Странички для любознательных (стр. 38 – 39)
Числа от 1 до 100
Сложение и вычитание (письменные вычисления)
Странички для любознательных
1. Найди правила, по которым записаны числа:
1) в первой строке;
2) в каждом столбце.
Продолжи ряды чисел.
| 16 | 26 | 27 | 37 | 38 | 48 | 49 | 59 | 60 |
| 6 | 25 | 17 | 36 | 28 | 47 | 39 | 58 | 50 |
2. Ученики лесной школы белка, ёж, лиса и заяц начертили такие фигуры, по одной фигуре каждый.
Ёж не стал чертить многоугольник, заяц не выбрал треугольник, а лиса начертила такой многоугольник, у которого есть и своё название. Какую фигуру начертила белка?
Ёж начертил круг, лиса — квадрат, заяц — прямоугольник, а белка — треугольник.
3. Начерти такие фигуры, как на чертеже. Вырежи их. Сложи из них квадрат.
4. Ученики лесной школы белка, заяц и ёж заготовили такие дощечки, по одной каждый.
Дощечка у белки получилась короче, чем дощечка у зайца, а дощечка у ежа — короче дощечки у белки. Какой длины дощечку заготовил заяц? белка? ёж?
Самая длинная дощечка у зайца, чуть короче — у белки, самая короткая дощечка — у ежа.
5. Вычислительная машина работает так:
→ – 9 + 6 →
1) Какое число будет на выходе из машины, если в неё ввести число: 11; 22; 34; 45; 67; 78?
11 → 8; 22 → 19; 34 → 31; 45 → 42; 67 → 64; 78 → 75.
2) Какое число ввели в машину, если на выходе из машины получили число: 17; 51; 20; 44; 65?
17 ← 20; 51 ← 54; 20 ← 23; 44 ← 47; 65 ← 68.
Математика. 2 класс. Ответы к заданиям
4.9 / 5 ( 12 голосов )
«Закрепление изученного. Странички для любознательных»
Тема: Закрепление изученного. Странички для любознательных.
Тип: Урок отработки умений и рефлексии
Цель: закрепить изученный ранее материал по темам: «Час, минута», «Длина ломаной»;
Планируемые результаты:
Личностные:
Сохранить интерес к учебному материалу; участвовать в оценке работ, ответов одноклассников; расширять кругозор.
Предметные:
Способствовать совершенствованию умения учащихся работать с единицами времени: час, минута; формировать умения: находить длину ломаной разными способами, применяя чертежный циркуль и оцифрованную линейку; использовать представления о длине ломаной для решения задач практического содержания; формировать умения решать текстовые задачи;
Познавательные:
Уметь ориентироваться в своей системе знаний; отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя свой жизненный опыт и информацию, полученную на уроке.
Коммуникативные:
Договариваться и приходить к общему решению; излагать своё мнение и аргументировать свою точку зрения.
Регулятивные:
Давать адекватную самооценку; предвидеть возможности получения конкретного результата при решении задач; выбирать действия в соответствии с поставленной задачей и условиями ее реализации; уметь применять знания при выполнении нестандартных заданий.
Ресурсы:
учебник М.И.Моро, С.И.Волкова, С.В.Степанова «Математика» 1 класс часть 1, рабочая тетрадь, наглядный материал .
План урока:
1).Этап мотивации (самоопределения) к коррекционной деятельности. (1мин)
(1мин)
2).Этап актуализации и пробного учебного действия.(3-4мин)
3).Этап локализации индивидуальных затруднений.(7мин)
4).Этап построения проекта коррекции выявленных затруднений.(5 мин)
5).Этап реализации построенного проекта.(3мин)
6).Этап обобщения затруднений во внешней речи.(5мин)
7).Этап самостоятельной работы с самопроверкой по эталону.(5мин)
8).Этап включения в систему знаний и повторения. (8мин)
9).Этап рефлексии учебной деятельности на уроке.(2мин)
Ход урока
1. Этап мотивации (самоопределения) к коррекционной деятельности.
У: Здравствуйте, ученики!
Д: Здравствуйте, учитель!
Улыбнитесь друг-другу. Настроим себя на урок, потому что мы будем работать с очень строгой, очень точной, интересной наукой – математикой!
У: Как вы думаете, а каждому ли человеку в жизни нужна математика?
У: Для чего она нужна?
У: Верно, ведь без счета никуда…
2. Этап актуализации и пробного учебного действия.
У: Сейчас мы с вами проведем математический диктант
У: На доске вы видите числа, прочитайте их про себя.
12, 66, 2, 61, 26, 21, 16, 62, 22.
У: А сейчас открываем тетради. Отступаем четыре клетки от прошлой работы. Подписываем число: 11 октября. Отступаем одну клетку, пишем «Классная работа». Отступаем две клетки, записываем данные числа к себе в тетрадь, в таком порядке, в котором они расположены на доске.
У: Все записали?
Д: Да.
У: Молодцы, а сейчас вам задание, найдите числа больше 20, но меньше 60 и подчеркните их карандашом.
У: Какие числа вы записали?
Д: 21, 22, 26.
У: Правильно, у всех так получилось?
Д: Да!
У: Запишите данные числа в порядке возрастания.
Дети записывают числа.
У: Что у вас получилось ребята?
Д: 2, 12, 16, 21, 22, 26, 61, 62, 66.
У: Молодцы!
У: Ребята, какое число получится, если 7 увеличить настолько же?
Д: 14.
У: Верно.
У: А как вы думаете, какое двухзначное число, меньше суммы чисел 8 и 6?
15, 14, 13.
Д: 13.
У: Теперь внимание на доску, из представленных вам чисел, выпишите те числа, которые можно представить в виде суммы двух одинаковых слагаемых
10, 11, 12, 13, 14, 15, 16.
У: Все выполнили моё задание?
Д: Да.
У: Что у вас получилось?
Д: 10, 12, 14, 16.
У: Молодцы, ребята!
3. Этап локализации индивидуальных затруднений.
У: Кто знает, сколько минут проходит минутная стрелка за один час?
Д: 60 минут.
У: А сколько в 1 минуте секунд?
Д: 60 секунд.
У: Молодцы, а теперь давайте проверим ваши знания о времени.
На доске вывешены модели часов, давайте скажем, сколько сейчас времени на каждом циферблате.
У: Молодцы ребята, вы хорошо справились с этим заданием, а теперь я хочу проверить ваши знания о ломаной линии.
А для того, чтобы проверить ваши знания, мы с вами отправимся в космос и попытаемся изобразить созвездия.
На ваших партах лежат листочки с нарисованными точками, ваша задача состоит в том, чтобы соединить их так, чтобы у вас получилось созвездие.
У: Ребята, все справились с заданием?
Д: Да.
У: Какое у вас получилось созвездие, может быть кто-нибудь знает? («Кассиопея»)
У: Что вам напоминает это созвездие?
Д: Ломаную линию
У: Сколько она содержит звеньев?
Д: 4.
У: Я могу предположить, что длина ваших ломаных линий одинакова, а как думаете вы, это так?
Измерьте звенья и запишите в тетрадь длину каждого звена, сравните получившиеся результаты и скажите, одинакова ли их длина.
Дети измеряют звенья, записывают на листах, складывают, сравнивают ответы.
Д: Ломаные имеют разную длину, так как их звенья имеют разную длину.
У: Вы справились со всеми моими задания, вы большие молодцы.
4. Этап построения проекта коррекции выявленных затруднений
У: Ребята, а сейчас мы с вами будем решать задачи, слушайте меня внимательно и решение задачи записываем в тетрадь.
У: В магазин привезли 18 кг овощей: несколько килограммов огурцов и 11 кг помидоров. Сколько килограмм огурцов привезли в магазин?
Сколько было всего килограммов овощей? (18кг) Сколько килограммов огурцов привезли? (неизвестно) Сколько было килограммов помидоров? (11кг) Подумайте, как можно решить эту задачу?
Д: 18 кг-11кг=7кг – огурцов привезли в магазин.
Исходя из этих данных, давайте запишем решение на доске.
Кто хочет решить задачу у доски? (ученик решает)
С первой задачей вы справились, а давайте попробуем решить 2-ую задачу
У: Максим выполнял домашнее задание по математике. Начало выполнения домашнего задания 12-00, окончание в 13-00. Сколько часов потребовалось Максиму, чтобы сделать домашнее задание?
Ребята так, во сколько же Максим сел делать домашнее задание?
Д: В 12-00.
У: А во сколько закончил его делать?
Д: В 13-00
У: Исходя из условия нашей задачи, как мы можем её решить?
Д: Нужно из 13-00мин – 12ч 00мин = 1 час – Максим затратил на выполнения домашнего задания по математике.
У: Отступите 2 клетки вниз от предыдущего задания и запишите решение задачи и ответ.
Я вижу, вы немного утомились, так давайте проведем с вами небольшую физкультминутку
Физкультминутка:
У: Встаем из-за парт.
Буратино подтянулся.
Руки поднять вверх, встать на носки.
Раз нагнулся, два нагнулся,
Наклониться вперед, руками достать пол.
Руки в стороны развел,
Выпрямиться, руки развести, ладони вверх.
Ключик вовсе не нашел.
Поворот головой влево, вправо — 2 раза.
Чтобы ключик тот достать, Надо на носочки встать.
Стать на носки, руки поднять вверх.
5.Этап реализации построенного проекта.
У: Садимся за парты. Открываем учебник на странице 36 и смотрим на рисунок. А сейчас прочитаем задание №1. Кто прочитает?
Ученик читает задание.
№1. Играя в прятки со своей подругой, обезьянка пробежала 5 м по спине змеи и взобралась на самый верх, под которой отдыхала змея.
Оставаясь на той же высоте, обезьянка перепрыгнула на соседнее дерево, которое стояло в 3 м от пальмы. Какой высоты была пальма, если обезьянка проделала путь в 15 м?
У: Какое условие в этой задачи?
Д: 15 метров обезьяна проделала всего, 5 метров по спине змеи и оставаясь на той же высоте перепрыгнула на соседнее дерево, которое стояло в 3 метрах.
У: По условию этой задачи, мы с вами можем записать решение, как вы думаете, как решается эта задача?
Д: Всего 15 метров. Змея была под пальмой, а не на пальме, значит:
15-5=10 метров, учитывая, что она пролетела 3 метра, значит:
10-3=7
Ответ -7м высота пальмы.
У: Молодцы, а теперь давайте запишем эту задачу в тетрадь, отступим от предыдущего задания 2 клетки вниз, подпишем №1 и запишем решения задачи с ответом.
А сейчас переходим к заданию №2, его мы решим устно, на стр.36 прочитаем условие задачи.
Кто прочитает задачу? (ученики поднимают руки)
№2. У большой обезьяны на 6 кокосовых орехов больше, чем у маленькой. Сколько орехов отдала большая обезьяна маленькой, если орехов у них стало поровну?
Как вы понимаете понятие «поровну»?
Д: Одинаковое количество
У: Сколько орехов у большой обезьяны?
Д: На 6 больше, чем у маленькой
У: Сколько орехов у маленькой обезьяны?
Д: Неизвестно
У: Для того, чтобы решить задачу, нам нужно узнать, сколько орехов у маленькой обезьяны.
Что нам нужно знать, чтобы ответить на вопрос задачи?
Д: На сколько орехов больше
У: Если отнять у большой обезьяны шесть орехов, то у обезьян будет поровну орехов (подсказка)
Исходя из этого, сколько большая обезьяна должна дать орехов маленькой?
Д: 3 кокоса, потому что 6 пополам будет 3.
У: Молодцы ребята!
6. Этап обобщения затруднений во внешней речи.
У: Следующее задание устно. Кто прочитает условие?
(ученик читает)
№3. В лесной школе есть песочные часы на 8 мин и на 13 мин. Как с их помощью отсчитать 5 мин?
У: Что нам известно из условия?
Д: То, что в школе есть песочные часы на 8 и 13 минут.
У: Как с их помощью отсчитать 5 минут?
Д: Перевернуть одновременно и те и другие часы и дождаться истечения времени в часах на 8 минут, оставшееся время в часах на 13 минут и это будет 5 минут.
У: Вы большие молодцы!
7. Этап самостоятельной работы с самопроверкой по эталону.
У: Переходим к заданию №4, обратите внимание на рисунок, а затем прочитайте условие.
У: Кто прочитает условие? (ученик читает)
Сравни отрезки на глаз, а затем измерением.
У: Давайте сравним данные отрезки сначала на глаз.
Какой отрезок на глаз самый большой?
Д: Зелёный
У: А как вы думаете остальные одинаковые или разные?
Д: Одинаковые
У: Давайте проверим это, измерив их, возьмите линейки и измерьте их длину.
Измерили?
Д: Да?
У: 1-2 отрезок одинаковые или разные?
Д: Одинаковые.
У: Молодцы ребята, мы справились и с этим заданием.
8.Этап включения в систему знаний и повторения.
В заключение урока ученики выполняют задание, в котором отрабатывают умение сравнивать числа и решать выражения.
У: Итак, а сейчас мы с вами проверим на сколько хорошо вы умеете решать выражения.
Открываем тетради, отступаем 2 клеточки от предыдущего задания и записываем выражения:
Не забываем, что над первым действием пишем ответ.
70+30-15=85
60+20+8=88
90-30-20=50
75+10+5=90
35-10+40=65
64-20+30=74
У: Кто решит все примеры, поднимает руку.
Дети выполняют задания.
У: У меня для вас следующее задание, а для этого мы с вами повторим единицы измерения.
Сколько в 1см мм?
Д: 10 миллиметров
У: А в 1дм см?
Д: 10 сантиметров
У: Сколько в 1м см и дм?
Д: 100 сантиметров и 10 дециметров
У: Молодцы, вы ответили на все мои вопросы.
У: Отступаем от предыдущего задания 2 клеточки и записываем примеры, которые я сейчас продиктую:
Отступаем 2 клетки и записываем выражение
Для того чтобы сравнить числа, нам нужно одну часть преобразовать в другую.
20мм(отступаем 1 клеточку вправо)= 2см (20мм)
У: Если у нас в одной части 20мм, а в другой 2см, давайте 2см переведем в миллиметр.
Сколько в 1см мм?
Д: 10мм
7дм(70см) = 70см
30см
50см
1м(100см)10см
20мм1см8мм(18мм)
У: Вы сегодня хорошо справились со всеми моими заданиями.
9. Этап рефлексии учебной деятельности на уроке.
У: Что мы делали сегодня на уроке? (повторяли темы: «час и минута» и «длина ломаной», решали задачи, сравнивали величины, вычисляли выражения)
У: Что вам показалось на уроке самым сложным?
Чтобы было самым интересным?
Как вы оцениваете сегодня свою работу на уроке?
Обратите внимание на доску, на ней карточки с различными цветами. Оранжевый – я работал отлично, фиолетовый – я работал не плохо, но можно было и лучше, синий – я работал плохо.
У: На дом вам будет задано упражнения № 5 на стр.37.
Ребята, спасибо вам за урок, мне было приятно с вами работать, вы хорошо выполнили все предложенные мной задания, проявили смекалку и показали на сколько хорошо вы знаете материал.
ГДЗ по Математике 2 класс учебник Моро 2 часть ответы стр 28
Странички для любознательных
Номер 1Выберите все высказывания, верные для этого рисунка:
1) Все флажки красного цвета имеют форму квадрата.
2) Если флажок имеет форму треугольника, то он синего цвета.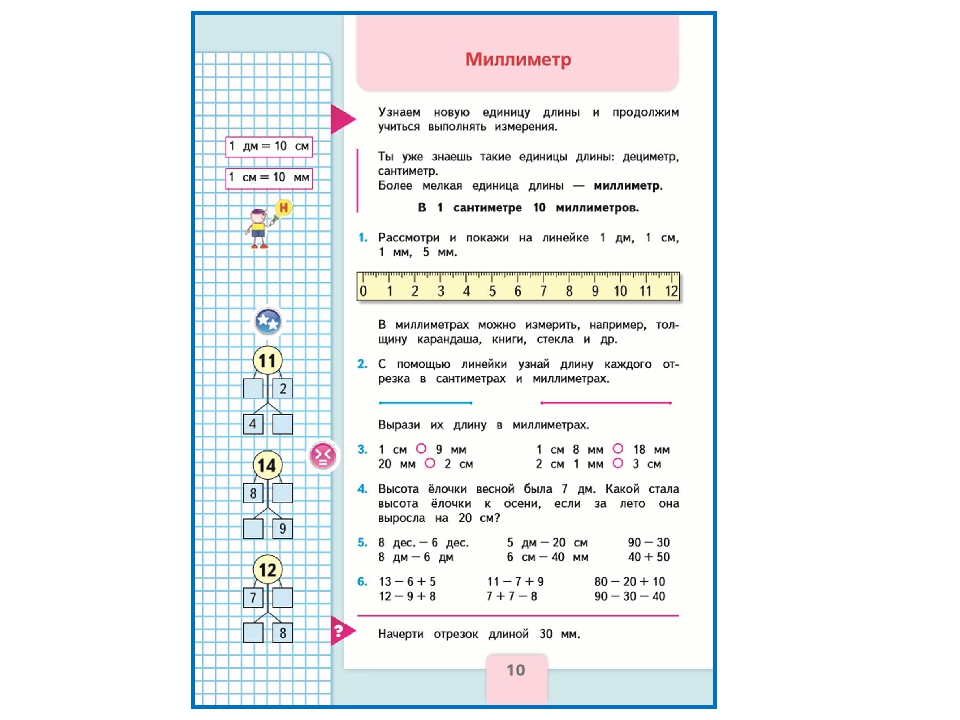
3) Если флажок трёхцветный, то он имеет форму прямоугольника.
Закончи высказывание, верное для этого рисунка:
Если флажок жёлтого цвета, то он имеет форму… .
Все флажки красного цвета имеют… .
Решение:
Для этого рисунка верны высказывания 2 и 3.
Законченные высказывания:
Если флажок жёлтого цвета, то он имеет форму квадрата.
Все флажки красного цвета имеют форму прямоугольника.
Номер 2Вычислительная машина работает так:
1) Дополни описание плана её работы:
В машину подаётся число.
Введённое число машина … на 8.
Из полученного … .
Результат машина отправляет на выход.
2) Какое число будет получатся на выходе из машины, если в машину ввести число: 23, 48, 19, 56, 64, 77?
3) Какое число ввели в машину, если на выходе и машины получили число: 30, 43, 17, 26?
Решение:
1) Дополни описание плана её работы:
В машину подаётся число.
Введённое число машина увеличивает на 8.
Из полученного значения вычитается число 3.
Результат машина отправляет на выход.
2) Составим выражения, чтобы узнать, какое число получится, если вводить ряд цифр: 23, 48, 19, 56, 64, 77:
23 + 8 – 3 = 31 – 3 = 28 (число 28)
48 + 8 – 3 = 56 – 3 = 53 (число 53)
19 + 8 – 3 = 27 – 3 = 24 (число 24)
56 + 8 – 3 = 66 – 3 = 63 (число 63)
64 + 8 – 3 = 72 – 3 = 69 (число 69)
77 + 8 – 3 = 85 – 3 = 82 (число 82)
3) Составим выражения, чтобы узнать, какое число вывила машина, если на выходя получился ряд цифр: 30, 43, 17, 26:
1. (… + 8) – 3 = 30
(… + 8) = 33 (т.к. скобка справа является уменьшаемым, находим её путём сложения вычитаемого и разности)
33 – 8 = 25 (число 25) здесь находим неизвестное слагаемое, вычитая от суммы второе слагаемое.
2. (… + 8) – 3 = 43
(… + 8) = 46 (т. к. скобка справа является уменьшаемым, находим её путём сложения вычитаемого и разности)
к. скобка справа является уменьшаемым, находим её путём сложения вычитаемого и разности)
46 – 8 = 38 (число 38) здесь находим неизвестное слагаемое, вычитая от суммы второе слагаемое.
3. (… + 8) – 3 = 17
(… + 8) = 20 (т.к. скобка справа является уменьшаемым, находим её путём сложения вычитаемого и разности)
20 – 8 = 12 (число 12) здесь находим неизвестное слагаемое, вычитая от суммы второе слагаемое.
4. (… + 8) – 3 = 26
(… + 8) = 29 (т.к. скобка справа является уменьшаемым, находим её путём сложения вычитаемого и разности)
29 – 8 = 21 (число 21) здесь находим неизвестное слагаемое, вычитая от суммы второе слагаемое.
Номер 3Устно составьте план, по которому начерчен узор.
Начерти этот узор в тетради и повтори 4 раза.
Решение:
План построения узора:
1 кл. вверх, 1 кл. влево, 1 кл. вверх, 1 кл. влево, 1 кл. вверх, 2 кл. вправо, 1 кл. вниз, 1 кл. вправо, 1 кл. вверх, 2 кл. вправо, 1 кл. вниз, 1 кл. влево, 1 кл. вниз, 1 кл. влево, 1 кл. вниз, 5 кл, вправо.
ГДЗ по математике 2 класс Моро часть 1, 2 учебник ответы
Ищите готовые верные ответы по математике за ваш 2 класс учебник 1,2 часть, автором которого доводится М.И. Моро? То, представленный решебник математики разъяснит и непременно поможет учащимся школы второго класса в скорой подготовке домашнего задания. Здесь написаны полные решения всех упражнений, Моро ГДЗ по математике 2 класс части 1,2. Делайте уроки с нами! На GDZniki.net можно бесплатно сверять и перепроверять свои гдз на множестве современных устройствах без регистрации.
Авторы: М.И.Моро, М.А.Бантова, Г.В.Бельтюкова, С.И.Волкова, С.В.Степанова.
Учебник — Часть 1.
ЧИСЛА ОТ 1 ДО 100.
Нумерация:
страница 4 1 2 3 4 5 6 7 8 ?
страница 5 1 2 3 4 5 6 7 8 9 10 ?
страница 6 1 2 3 4 ?
страница 7 1 2 3 4 5 ?
страница 8 1 2 3 4 5 6 7 8 ?
страница 9 1 2 3 4 5 6 7
Миллиметр:
страница 10 1 2 3 4 5 6 ?
страница 11 1 2 3 4 5 6 ?
страница 12 1 2 3 4 5 6 7 8 9 10
Метр:
страница 13 1 2 3 4 5 6 ?
страница 14 1 2 3 4 5 6 7 ?
страница 15 1 2 3 4 5 ?
Рубль. Копейка:
Копейка:
страница 16 1 2 3 4 5 6 7 8 ?
страница 17 1 2 3 4 5 6 ?
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 18-19): 1 2 3 4 5
ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ (Страница 20-21): 1 2 3 4 5 6 7 8 9 10 11 12 13
ПРОВЕРИМ СЕБЯ:
вариант 1 (Страница 22)1 2 3 4 5 6 7 8 9 10 11
вариант 2 (Страница 23)1 2 3 4 5 6 7 8 9 10 11
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 24): 1 2 3 4
Сложение и вычитание:
страница 26 1 2 3 4 5
страница 27 1 2 3 4 5 6 7
страница 28 1 2 3 4 5 ?
страница 29 1 2 3 4 5 6 ?
страница 30 1 2 3 4 5 6 7 8
Час. Минута:
страница 311 2 3 4 5
Длина ломаной:
страница 32-33 1 2 3 4 5 6 7 8 ?
страница 34-35 1 2 3 4 5 6 7 8 9 10 ?
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 36-37): 1 2 3 4 5
Порядок выполнения действий. Скобки:
страница 38-39 1 2 3 4 5 6 7 ?
Числовые выражения:
страница 40 1 2 3 4 5
страница 41 1 2 3 4 5 ?
Периметр многоугольника:
страница 42-43 1 2 3 4 5 6 7 8 ?
Свойства сложения:
страница 44-45 1 2 3 4 5 6 7 8
страница 46 1 2 3 4 5 ?
страница 47 1 2 3 4 5 6 7 8 ?
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 50-51): 1 2 3 4
ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ (Страница 52-56): 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
Устные вычисления:
страница 57 1 2 3 4 5 6 7 8 ?
страница 58 1 2 3 4 5 6 7 ?
страница 59 1 2 3 4 5 6 ?
страница 60 1 2 3 4 5 6 7 ?
страница 61 1 2 3 4 5 6 7 8 ?
страница 62 1 2 3 4 5 6 7
страница 63 1 2 3 4 5 6
страница 64 1 2 3 4 5 6 7 ?
страница 65 1 2 3 4 5 6 7 ?
страница 66 1 2 3 4 5 6 7 ?
страница 67 1 2 3 4 5 6 7 ?
страница 68 1 2 3 4 5 6 7 ?
страница 69 1 2 3 4 5 6 7 8 ?
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 70-71): 1 2 3 4 5
ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ (Страница 72-75): 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
Буквенные выражения:
страница 76-77 1 2 3 4 5 ?
страница 78 1 2 3 4 5 6 7 8 ?
страница 79 1 2 3 4 ?
Уравнение:
страница 80-81 1 2 3 4 5 6 7 8 ?
страница 82 1 2 3 4 5 6 7 8
страница 83 1 2 3 4 5 6 ?
Проверка сложения:
страница 84-85 1 2 3 4 5 6 7 ?
Проверка вычитания:
страница 86-87 1 2 3 4 5 6 ?
страница 88 1 2 3 4 5 6 ?
страница 89 1 2 3 4 5 6 7
ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ (Страница 90-93) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
ЧЕМУ НАУЧИЛИСЬ (Страница 90-93) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
ПРОВЕРИМ СЕБЯ
Задания базового уровня (Страница 94): 1 2 3 4 5
Задания повышенного уровня (Страница 95): 1 2 3 4 5
Часть 2.
ЧИСЛА ОТ 1 ДО 100.
Сложение и вычитание.
Письменные вычисления.
страница 4 1 2 3 ?
страница 5 1 2 3 4 ?
страница 6 1 2 3 4 5 6 7 8 ?
страница 7 1 2 3 4 5 6 7 8
Угол. Виды углов:
страница 9 1 2 3 4 5 6 7 8
страница 10-11 1 2 3 4 5 6 7 8 9 ?
страница 12 1 2 3 4 5 6 ?
страница 13 1 2 3 4 5 6 ?
Прямоугольник:
страница 14 1 2 3 4 5 6
страница 15 1 2 3 4 5 6 7 8 9 10
страница 16 1 2 3 4 5 6 7 ?
страница 17 1 2 3 4 5 6 7 ?
страница 18 1 2 3 4 5 6 ?
страница 19 1 2 3 4 ?
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 20-21): 1 2 3 4 5
ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ (Страница 22-27): 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 28): 1 2 3
страница 29 1 2 3 4 5 ?
страница 30 1 2 3 4 5 6 7 8 9 ?
страница 31 1 2 3 4 5 6 7 8 9
страница 32 1 2 3 4
страница 33 1 2 3 4 5 6 7 8 ?
Квадрат:
страница 34 1 2 3 4 5 6 7 ?
страница 35 1 2 3 4 5 6 7 ?
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 38-39): 1 2 3 4 5
ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ (Страница 40-45): 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 46): 1
Умножение и деление.
Умножение:
страница 48 1 2 3 4 5 6 ?
страница 49 1 2 3 4 5 6 7
страница 50 1 2 3 4 5 6 7 8 9 ?
страница 51 1 2 3 4 5 6 7 8
страница 52 1 2 3 4 5 6 7 8 9 ?
страница 53 1 2 3 4 5 ?
страница 54 1 2 3 4 5 6 7 ?
страница 55 1 2 3 4 5 6 7 8
страница 56 1 2 3 4 5 6 7 ?
страница 57 1 2 3 4 5 6 7
Деление:
страница 58 1 2 3 4 5 6 ?
страница 59 1 2 3 4 5 6 7 8 ?
страница 60 1 2 3 4 5 6 ?
страница 61 1 2 3 4 5 6 7 ?
страница 62 1 2 3 4 5 6 7 8
ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ (Страница 63): 1 2 3 4 5 6 7 8 9
ЧЕМУ НАУЧИЛИСЬ (Страница 63): 1 2 3 4 5 6 7 8 9
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 64-65): 1 2 3 4 5 6
ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ (Страница 66-70): 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 71): 1
страница 72 1 2 3 4 5 6 ?
страница 73 1 2 3 4 5 6 7 8 ?
страница 74 1 2 3 4 5 6 ?
страница 75 1 2 3 4 5 6 ?
страница 76 1 2 3 4 5 ?
страница 771 2 3 4 5 6 7 8 9 10 ?
ПРОВЕРИМ СЕБЯ. ТЕКСТЫ ДЛЯ КОНТРОЛЬНЫХ РАБОТ:
вариант 1 (Страница 78)1 2 3 4 5 6 7
вариант 2 (Страница 79)1 2 3 4 5 6 7
Табличное умножение и деление:
страница 80 1 2 3 4 5 6 ?
страница 81 1 2 3 4 5 6 7 ?
страница 82 1 2 3 4 5 6 ?
страница 83 1 2 3 4 5 6 ?
страница 84 1 2 3 4 5 6 7 8 9 ?
страница 85 1 2 3 4 5 6 7 8 9 ?
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 86-87): 1 2 3 4 5 6 7
ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ (Страница 88-89)1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
страница 90 1 2 3 4 5 6 ?
страница 91 1 2 3 4 5 6 7 8 ?
страница 92 1 2 3 4 5 ?
страница 93 1 2 3 4 5 6 7 8 ?
страница 94 1 2 3 4 5 6 7 8 9 10 11
СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ (Страница 95): 1 2 3 4 5 6 7
ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ (Страница 96-99): 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
ПРОВЕРИМ СЕБЯ. ТЕСТ:
вариант 1 (Страница 100)1 2 3 4 5 6 7 8 9 10
вариант 2 (Страница 101) 1 2 3 4 5 6 7 8 9 10
ЧТО УЗНАЛИ, ЧЕМУ НАУЧИЛИСЬ ВО 2 КЛАССЕ?
ЧИСЛА ОТ 1 ДО 100.
Нумерация (Страница 102)1 2 3 4 5 6
Числовые и буквенные выражения (Страница 103): 1 2 3
Равенство. неравенство. уравнение (Страница 103): 1 2 3 4
Сложение и вычитание (Страница 104): 1 2
Свойства сложения (Страница 105): 3 4
Таблица сложения (Страница 105-106): 5 6 7 8
Решение задач (Страница 106-108): 1 2 3 4 5 6 7 8 9 10 11 12
Геометрические фигуры (Страница 109): 1 2
ПРОВЕРИМ СЕБЯ. ТЕКСТЫ ДЛЯ КОНТРОЛЬНЫХ РАБОТ.
ТЕКСТЫ ДЛЯ КОНТРОЛЬНЫХ РАБОТ.
Задания базового уровня (Страница 110): 1 2 3 4 5 6 7
Задания повышенного уровня (Страница 111): 1 2 3 4 5 6 7
Урок 119. Страничка для любознательных
н.1 стр.86
Условие:
Определи, кто из поросят Ниф, кто Наф, а кто Нуф на самом деле, если все записи под их рисунками неверные.
Решение:
Первый поросенок Нуф, потому что он – Наф (ложь) и второй поросенок говорит он – Ниф (ложь).
Второй поросенок либо Наф, либо Ниф, но третий поросенок говорит, что он Наф, а это ложь. Значит, второй поросенок – Ниф, а третий – Наф.
Советы:
Внимательно читайте условие.
н.2 стр.86
Условие:
У поросенка Нафа было 11 желудей. Он отдал Нифу 1 желудь больше, чем Нуфу. Сколько желудей получил Ниф и сколько желудей получил Нуф, если 2 желудя Наф оставил себе?
Решение:
Нифу отдали 5 желудей, Нуфу 4 желудя.
Советы:
Внимательно читайте условие.
н.3 стр.86
Условие:
Рассмотри рисунок.
Выбери высказывания, верные для этого рисунка.
1) Все фигуры зеленого цвета – круги.
2) Если фигура треугольник, то она желтого цвета.
3) Каждый круг красного цвета.
Закончи высказывание, верное для данного рисунка. Если фигура пятиугольник, то …
Решение:
2)
Советы:
Если фигура пятиугольник, то он зеленого цвета.
н.1 стр.87
Условие:
Какая последовательность чисел составлена по правилу: «Каждое следующее число на 4 больше, чем предыдущее?»
1) 18, 21, 24, 27, 30;
2) 49, 45, 41, 37, 33;
3) 18, 22, 26, 30, 34.
Решение:
3)
Советы:
Внимательно читайте условие.
н.5 стр.87
Условие:
Запиши номера тех четырех отрезков, из которых можно составить прямоугольник, и начерти его в тетради.
Решение:
1, 6, 2, 4.
Советы:
С помощью рисунков мы наблюдаем переместительное свойство умножения. От перестановки множителей результат умножения не изменится.
н.6 стр.87
Условие:
1) Какое число получится на выходе из машины, если в нее ввести число: 9; 7; 5; 8; 3; 6; 10?
2) Какое число ввели в машину, если на выходе из нее получили число: 12; 18; 10; 14; 8; 16?
Решение:
1) 18, 14, 10, 16, 6, 12, 20.
2) 6, 9, 5, 7, 4, 8.
Советы:
Внимательно читайте условие.
н.7 стр.87
Условие:
По какому правилу составили ряд чисел: 3, 7, 6, 10, 9, 13, 12, ☐, ☐, ☐, ☐?
Продолжи его.
Решение:
16, 15, 19, 18.
Советы:
Правило: сначала число увеличиваем на 4, потом полученное число уменьшаем на 1.
Моро 3 класс школа россии странички любознательных ответы :: sembcontdides
15.12.2016 01:11
Помогает вашему ребёнку разобраться с новыми темами и даёт. Просмотренные. Спиши ГДЗ на НЕ ХОЧУ ру, ответы, решения и готовые домашние задания по математике, 2 класс. Моро М. И., 1 часть, 2 часть. Странички для любознательных. ГДЗ по окружающему миру 3 класс Плешаков А. А. Странички для любознательных.1.2. Разобраться, что к чему поможет ГДЗ по математике для 3 класса Моро М. И. Данное учебное. Конспект составлен к учебнику М. И. Моро. К конспекту прилагается. Здесь представлены ответы к задачнику по математике 4 класс Моро.
Время на поиск правильного ответа на задания из 1 и 2 части учебника по Математике, предназначенного для 3 класса, начальной школы, и выпущенного под редакцией Моро и. Чему научились. 7. Странички для любознательных. ГДЗ математика 3 класс Морорешебник, ответы. В младших классах школьники мало понимают важность такого предмета. Подробные гдз и решебник по Математике для 3 класса, авторы учебника: М. И. Математика 3 класс М. И. Моро. Странички для любознательных. Спиши ГДЗ на НЕ ХОЧУ ру, ответы, решения и готовые домашние.
И. Математика 3 класс М. И. Моро. Странички для любознательных. Спиши ГДЗ на НЕ ХОЧУ ру, ответы, решения и готовые домашние.
Под. ГДЗ по Математике 1, 2 часть за 3 класс автора Моро М. И., М. А. Бантова, Г. В. Спишите домашнюю работу к учебнику Моро из ГДЗ по математике за 3 класс. Кроме того в конце решебника по математике ученики 3 класса могут списать решения задач и ответы на итоговое повторение. ГДЗ домашние задание по математике за 3 класс к учебнику Моро, Бантова, Бельтюкова часть 1, часть год. Странички для любознательных. Ответы ГДЗ по Математике 3 класс Моро, Бантова учебник: часть 1, часть 2.
1 и 2 часть. Готовые домашние задания ГДЗ по Математике автор Моро за 4 класс. Чему научились Что узнали. Чему научилисьСтранички для любознательных. Безопасный режим: выкл. ГДЗ и решебник для учебникаГДЗ решебник по математике 3 класс часть 1. ГДЗ Моро 3 класс. Ответы по математике 3 класс Моро: Часть 1: Выберите страницу учебника. Что узнали, чему научились в 3. ГДЗ домашние задание по математике за 3 класс к учебнику Моро, Бантова. Вы можете смотреть и читать гдз онлайн без скачивания с компьютера и мобильных устройств. Если вы хотите сократить.
Задания по математике, 4 класс. Моро. Готовое домашнее задание ГДЗ по математике 4 класс Моро М. И. Задание: . Страна: Россия. Рабочая программа по математике 3 класс по теме:. ГДЗ по Математике 1, 2 часть за 3 класс автора Моро М. И., М. А. Бантова, Г. В. 7.27 страница.4 5. Странички для любознательных.1. Что узнали. Разобраться, что к чему поможет ГДЗ по математике для 3 класса Моро М. И. Федерации. Для 3 класса, начальной школы, и выпущенного.
Просвещение онлайн. ГДЗ ответы на вопросы к учебнику и рабочая тетрадь по математика 3 класс Моро, Бантова, Бельтюкова 1 и 2 часть ФГОС от Путина. Странички для. Учебник Моро М. И., Бантова М. А., Бельтюкова Г. В. И др. Просвещение, 2015. Решебник по математике 4 класс Моро. Решебник и ГДЗ по Математике для 3 класса, авторы учебника: М. И. Моро, М. А. Бантова, Г. В. Бельтюкова на год. Учебник.27 страница.4 5. Категория: Математика 3 класс. Ведь Моро М. И. Подготовил прекрасный сборник ответов, который.
В. Бельтюкова на год. Учебник.27 страница.4 5. Категория: Математика 3 класс. Ведь Моро М. И. Подготовил прекрасный сборник ответов, который.
Оценка решебника: 4 5. Решебник и готовые домашние задания по математике Странички для любознательных. Данное учебное. Решебник готовое домашнее задание. Родители, не стоит переживать о том, что ваш ребёнок пользуется решебниками по математике 3 класса. Ответы ГДЗ по Математике 3 класс Моро, Бантова учебник: часть 1, часть . Здесь представлены ответы к учебнику и рабочая тетрадь по математика 3 класс Моро, Бантова, Бельтюкова 1 и 2 часть. ГДЗ и решебник для учебникаГДЗ решебник по математике 3 класс часть 1, 2 Моро ФГОС.
Вместе с Моро 3 класс школа россии странички любознательных ответы часто ищут
математика 2 класс моро рабочая тетрадь ответы.
математика 4 класс моро учебник.
математика 2 класс задачи.
математика 3 класс задачи.
гдз математика 3 класс моро школа россии.
гдз по математике 3 класс моро.
гдз по математике 3 класс моро рабочая тетрадь.
окружающий мир
Читайте также:
Методичка для учителя по информатике в играх и задачах 3 класса часть 1 школа
Гдз класс, алгебра ершова
Купить гдз физика пинский 10 класс
«Странички для любознательных»
Тема: «Странички для любознательных». Выполнение заданий творческого и поискового характера.
Цель: Проверить усвоение приёмов сложения и вычитания двузначных чисел;
Проверить усвоение математической терминологии;
Учить логически мыслить.
Формирование УУД: Личностные: способность к самооценке на основе критерия успешности учебной деятельности. Регулятивные: осуществлять итоговый и пошаговый контроль по результату.
Регулятивные: осуществлять итоговый и пошаговый контроль по результату.
Коммуникативные: контролировать действия партнера.
Познавательные: проводить сравнение, классификацию по заданным критериям.
Ход занятия:
Актуализация знаний.
Мы приветствуем гостей
Дорогих учителей
Всех знакомых, незнакомых,
И серьезных, и весёлых
И сегодня второй класс
На урок позвал всех Вас.
Посмотрите – ка на нас:
Вот какой хороший класс!
Приготовились учиться,
Ни минутки не лениться,
Не скучать, не отвлекаться,
А стараться и стараться.
— А сейчас, мои дорогие ребята….
-Я прошу улыбнуться тех, кто пришёл на урок с хорошим настроением.
— Я прошу поднять руку тех, кому нравится общаться с одноклассниками.
— Хлопните в ладоши, если вы не любите ссориться и обижать друг друга.
— Пожмите друг другу руки, если стараетесь уважать себя и других.
— Я очень хочу, чтобы хорошее настроение у вас оставалось до конца урока.
— Скажите мне, пожалуйста, на какой же урок мы пригласили сегодня наших гостей. А каким бы вы хотели, чтобы был наш урок.
(умный, увлекательный, интересный, познавательный и т. д.) Слайд 2
— А какие же качества нам необходимы, чтобы наш урок был именно таким?(внимание, трудолюбие, смекалка, активность,..)
Внимание на экран. Кто это? (Успенский) О ком мы сегодня на уроке математики будем говорить? (о Чебурашке).
Кто это? (Успенский) О ком мы сегодня на уроке математики будем говорить? (о Чебурашке).
Сегодня в месте с Чебурашкой мы будем путешествовать по страничкам для любознательных. Давайте подумаем, чем мы будем заниматься, какие задания выполнять. Какую цель стави м перед со бой на данном уроке?
Где жил Чебурашка? А как он попал в город. А сколько апельсинов съедал Чебурашка за день? (2)
ЗАДАЧА: Давайте узнаем сколько апельсинов было в коробке, если Чебурашка путешествовал в закрытой коробке 15 дней и съедал за день 2 апельсина.
А сейчас я вам предлагаю узнать какой же путь проделал Чебурашка Сначала коробки с апельсинами попали на корабль а потом? (на корабле, а потом на машине) Давайте послушаем задачу и сделаем к ней схематический чертёж.
ЗАДАЧА:
Ч ебурашка ехал в кузове грузовика до пристани 150 км, затем плыл на корабле в закрытой коробке ещё 500 км, а затем ехал в машине до фруктового магазина ещё 100 км. Узнайте весь путь, который проделал Чебурашка
Попав в город Чебурашка где стал жить? (в телефонной будке)
Думаю ни кому не понравиться жить в телефонной будке. Давайте построим ему хороший домик.
Устный счет — слайды
Единственным развлечением Чебурашки в это время был заводной волчок и три кубика из которых он строил башенки.
ЗАДАНИЕ:
Изобразите с помощью квадратиков и клея сколько комбинаций различных башенок мог сделать Чебурашка?
Решение:
Н о затем Чебурашка нашёл себе друзей.
Гармошка в руках,
На макушке фуражка,
А рядом с ним важно
Сидит Чебурашка.
Портрет у друзей
Получился отменный,
На нём Чебурашка,
А рядом с ним…Гена.
И теперь Чебурашка играет в игры вместе с Геной. Каждую весну они пускают кораблики по весёлым ручейкам. Покажите, как по-разному раскрасили паруса наши друзья, если у них было всего две краски (синяя и красная)?
Каждую весну они пускают кораблики по весёлым ручейкам. Покажите, как по-разному раскрасили паруса наши друзья, если у них было всего две краски (синяя и красная)?
ЗАДАЧА:
А ещё к ним скоро придут друзья, с которыми друзья собрались построить дом Дружбы. И Крокодил Гена решил угостить своих гостей пирожными. Для этого он купил 12 пирожных, по два – каждому. Сколько гостей ожидает к чаю Крокодил Гена?
Как то раз Гена, Чебурашка и девочка Галя пошли в лес по ягоды.
Для сбора ягод у них были корзинка, лукошко и ведёрко. Известно, что Чебурашка был не с корзинкой и не с лукошком. Гена не с лукошком. Что с собой взял каждый из друзей для сбора ягод.
корзинка | лукошко | ведёрко | |
Гена | |||
Чебурашка | — | — | + |
Таня |
корзинка | лукошко | ведёрко | |
Гена | + | — | — |
Чебурашка | — | — | + |
Таня |
По вечерам Чебурашка с Геной пили чай.
Гена и Чебурашка решили купить воздушные шары
Давайте друзьям поможем построить Дом дружбы. У вас есть геометрический материал, приступаем к работе.
Итог. Оцените свою деятельность.
Дополнительная математика для любопытных
Автор: Доусон, Брайан, доктор философии
Предметы: Математика; Теория чисел
Возраст: 12, 13, 14, 15, 16, 17, 18
Оценка: 7, 8, 9, 10, 11, 12
Код заказа: 4311
Цена: 25 долларов.00
Цена на сайте: $ 15.00
Этот дополнительный учебник для средней школы, предназначенный для самообучающихся, изучивших алгебру I, идеально подходит для самостоятельного изучения. Тщательное изложение тем и хорошо проработанные примеры с подробными комментариями направляют мышление детей, а ответы на упражнения с нечетными номерами дают информацию об успехах детей.
Тщательное изложение тем и хорошо проработанные примеры с подробными комментариями направляют мышление детей, а ответы на упражнения с нечетными номерами дают информацию об успехах детей.
Выбранные темы представляют собой введение в богатую область теории чисел. Среди прочего, они включают в себя делимость, алгоритм Евклида, простые числа, фигурные числа, рекурсивно определенные числа, такие как числа Фибоначчи и Люка, модульную арифметику, китайскую теорему об остатках и приложение по множествам.
Книга применяет теорию чисел к календарным системам, кодам UPC и ISBN и многому другому. Дополнительные примечания предоставляются, чтобы вызвать дальнейший интерес или исследования по таким темам, как цифровые сигналы, история математических символов и нумерология.
На протяжении всего текста детям предлагается тщательно подумать о самой математике, включая изучение роли определений и доказательств. Такое изучение может быть неоценимым подспорьем в максимальном понимании ребенком школьной геометрии.
Примеры страниц: страница 2 | стр. 21 | стр. 31 | стр.62
Этот дополнительный учебник для средней школы, предназначенный для самообучающихся, изучивших алгебру I, идеально подходит для самостоятельного изучения. Тщательное изложение тем и хорошо проработанные примеры с обширными комментариями направляют мышление учащихся, а ответы на упражнения с нечетными номерами обеспечивают обратную связь об успеваемости учащихся.
Выбранные темы представляют собой введение в богатую область теории чисел. Среди прочего, они включают в себя делимость, алгоритм Евклида, простые числа, фигурные числа, рекурсивно определенные числа, такие как числа Фибоначчи и Люка, модульную арифметику, китайскую теорему об остатках и приложение по множествам.
Книга применяет теорию чисел к календарным системам, кодам UPC и ISBN и многому другому. Дополнительные примечания предоставляются, чтобы вызвать дальнейший интерес или исследования по таким темам, как цифровые сигналы, история математических символов и нумерология.
На протяжении всего текста учащимся предлагается тщательно подумать о самой математике, включая изучение роли определений и доказательств. Такое изучение может быть неоценимым подспорьем в максимальном понимании учащимися геометрии средней школы.
Примеры страниц: страница 2 | стр.21 | стр. 31 | стр.62
Откажитесь от заданий по математике и перестаньте убивать детское любопытство (мнение)
Как преподаватель математики, которая к тому же является молодой мамой, у меня есть серьезные опасения по поводу будущего математического класса, в который войдет моя дочь.Один из моих самых больших опасений заключается в том, что уроки математики подавят большую часть ее любопытства и творческих способностей, свидетелем которых я был каждый день в течение первых нескольких месяцев ее жизни.
В ходе моего сотрудничества с педагогами дошкольного и второго класса в течение последних пяти лет я обнаружил, что учителя часто борются с двумя исторически конкурирующими философиями обучения детей младшего возраста. Одна философия признает важность создания игровой среды, в которой дети учатся, исследуя и участвуя в игре.Другой подчеркивает необходимость подготовки учащихся к соблюдению государственных и национальных стандартов по математике, уделяя особое внимание конкретным академическим навыкам. Эти две философии не являются либо-либо. На самом деле математическое мышление и обучение часто происходят во время игры.
Нам нужно создать больше возможностей для маленьких детей изучать математические идеи в интерактивной и игровой форме ».
С принятием Общих основных государственных стандартов и повышением внимания к так называемым навыкам 21-го века, в последние годы наши мысли о поддержке любопытства и творчества учащихся значительно улучшились.Однако, как и в случае с большинством изменений, реализация наших идей еще не оправдала ожиданий.
Я обнаружил, что учителя все чаще ощущают необходимость соблюдать стандарты обучения способами, которые не основываются на врожденном любопытстве и склонности маленьких детей к экспериментам. Обучение математике в начальных классах слишком часто становится больше похожим на традиционные уроки математики в средней школе. Я видел, как учителя детских садов и 1-го класса читали короткие лекции, после чего дети заполняли рабочие листы, заполненные математическими задачами.Эти рабочие листы часто состоят из задач одного и того же типа, только с разными числами (например, 1 + 2 = __; 1 + 3 = __; 1 + 4 = __) и неинтерактивными изображениями, которые маленькие дети могут посчитать или сравнить.
То, что я наблюдаю, неудивительно, учитывая наши неправильные представления о том, что значит изучать математику в школе. Многие думают, что математика — это все о процедурах обучения и запоминании правил. Как на уровне средней школы, так и на уровне начальной школы, методически ориентированное обучение не способствует пониманию учащимися важных математических понятий.Фактически, исследование 2016 года, опубликованное в Scientific American, показало, что студенты, которые полагаются на запоминание, на полгода отстают от своих сверстников, которые подходят к математике, связывая концепции с существующими знаниями и отслеживая собственное понимание.
Важно уделять внимание математическим целям обучения, одновременно развивая творческие способности в раннем детстве. Нам нужно создать больше возможностей для маленьких детей изучать математические идеи в интерактивной и игровой форме. Вместо того, чтобы выполнять задания по математике, маленькие дети нуждаются в специально разработанных занятиях, которые позволяют им думать и заниматься, как математики, проверяя различные идеи, экспериментируя со стратегиями и объясняя свое мышление.В отличие от традиционных задач на листах математики, которые можно решить только одним способом, дети должны заниматься проблемами, которые имеют множество возможных стратегий решения и готовы к обсуждению и дебатам.
Что мы можем делать как практики и лидеры в области образования?
1. Интересуйтесь, как думают дети. У маленьких детей есть увлекательные стратегии решения математических задач. Наша цель — помочь им развить настойчивость, уверенность и навыки критического мышления при решении математических задач.Вместо того, чтобы говорить им точные шаги для решения проблемы, первым делом лучше задать открытые вопросы («Как вы это поняли?»). Затем посмотрите, что делает ребенок, прежде чем задать другой вопрос, основанный на том, что вы наблюдали («Я заметил, что вы переместили синих медведей. Почему вы это сделали?»).
2. Помогите учителям изменить ситуацию. Следует поощрять учителей сосредотачиваться на творческой природе математики. Ничего страшного, если математические задания не похожи на традиционные рабочие листы по математике.Если учителя дают домашнее задание, оно должно носить интерактивный и исследовательский характер, а не застойные рабочие листы.
3. Привлекайте родителей, поощряя их находить возможности заниматься математикой в нашей повседневной жизни и в нашем окружении. Отличный способ начать — подсчитать коллекции предметов с маленькими детьми. Коллекцию можно составить из всего, что есть дома, например, монет или посуды. Цель состоит в том, чтобы выяснить, сколько предметов находится в коллекции, и помочь детям глубоко задуматься о количестве таким образом, чтобы это имело смысл.По моему опыту, детям очень интересно узнать, сколько объектов находится в их коллекциях, и они будут использовать в процессе различные стратегии (например, сортировку, умножение, добавление и т. Д.).
Если мы приложим согласованные усилия, чтобы противостоять традиционным рабочим листам по математике, мои опасения могли бы развеяться к тому времени, когда моя дочь пойдет в детский сад.
рабочий лист по твердым формам для 2 класса
Некоторые из них имеют плоскую форму, а некоторые — твердые. Плоские и сплошные формы 2-го уровня Отображаются 8 лучших рабочих листов для — Плоские и сплошные формы 2-го уровня.Рабочие листы по 2-м и 3d-фигурам для первого класса Дистанционное обучение, распечатайте рабочие листы по 2-мерной 3D-геометрии Рабочие листы по геометрии, 2-м и 3-м фигурам Плоские твердые фигуры Фигуры, геометрические фигуры 3-х твердые фигуры Практические листы 1 Четкие, 2-х и 3D-фигуры Рабочий лист Пакет Нет готовых форм , Твердые формы Общий модуль базовой геометрии Математика в домашних условиях, Твердые фигуры Плоские грани Вершины Края 3D-чертежи 3D, Результат изображения для печатных листов армирования Класс 3 2 D 3D, Что я называю 3D-фигуры Поддержка изучения имен форм, математика для первого класса Модуль 17 Геометрия. Двумерные и трехмерные формы. Во-первых, ваш адрес электронной почты не будет опубликован.Определение 2D или 3D Каждый рабочий лист содержит 8 изображений, идентифицирующих 2D или 3D формы. Определить 1 | Определить 2 | Определить 3 1. Ниже вы найдете широкий спектр наших рабочих листов для печати в главах. Сплошные фигуры с геометрией сечения и шаблоны. Эти рабочие листы подходят для математики второго класса. Мы создали множество рабочих листов, охватывающих различные аспекты этой темы и многое другое. 2-й и 3-й классы. Определите количество граней, ребер и вершин на каждой твердой фигуре. Это можно играть как 2-й класс.Понимание твердых форм по отношению к 2D-фигурам — вот что ждет ваших детей в детском саду, 1 и 2 классах. Размеры точного размера указаны на изометрическом эскизе. Добро пожаловать на страницу рабочих листов 2d фигур по математике саламандры. 3) Поместите зеленый крестик на каждую фигуру, имеющую ровно одну вершину / угол. Плоские формы (очень простые) Эти рабочие листы охватывают прямоугольники, квадраты, трапеции, шестиугольники, треугольники, восьмиугольники и другие. Чтобы загрузить / распечатать, щелкните всплывающий значок или значок печати на листе для печати или загрузки.Это набор из 8 рабочих листов, которые помогают ученикам отличать двухмерные фигуры от трехмерных несколькими разными забавными способами. Эта огромная коллекция рабочих листов с трехмерными фигурами открывает детям захватывающий мир форм, пробуждает жажду экспериментов, что делает их отличным выбором для детей от детского сада до старшеклассников. Раскраски Crayola Mini Doc Mcstuffi…. Этот пакет включает в себя целую неделю практических рабочих листов hw рабочих листов и тест по 2d формам. Рабочий лист математических фигур. 2. Рабочие листы по геометрии 2-го класса.Скачать AllMatching 2D и 3D Shapes Нарисуйте линию от каждой 2D-формы к соответствующей 3D-фигуре. Соответствие 2 | Соответствие 3 1. Имя формы Количество граней Количество ребер Количество вершин Треугольная пирамида Квадратная пирамида Куб Кубоид Треугольная призма Пятиугольная призма Шестиугольная призма Рабочие листы 3d форм. Будь то раскраски с историческими фигурами, такими как Роза Паркс и доктор. Вращение и масштабирование фигур. Листы 3d форм. Чтение всей истории математики и многого другого начинает даваться быстро и яростно во втором классе.Мартин Лютер Кинг или. Рабочие листы с плоскими и твердыми фигурами 2-го класса — по этой теме есть 8 рабочих листов для печати. Полигоны и твердые фигуры. Краткое описание рабочих листов есть на каждом из виджетов рабочего листа. Оценка / уровень: класс 2 Возраст: 6-10 Основное содержание: твердые формы Другое содержание: послушайте и выберите Добавить в мои книги (5) Загрузить файл pdf Вставить на мой веб-сайт или в блог Добавить в Google Classroom Добавить в Microsoft Teams Поделиться через Whatsapp 3 . Включает как твердые, так и плоские формы. Сохраните мое имя, адрес электронной почты и веб-сайт в этом браузере, чтобы в следующий раз я оставил комментарий.Мы создали множество рабочих листов, охватывающих различные аспекты этой темы и многое другое. Математика 6 5 уроков по объемам tes учит страницу информации о геометрических сетях. математика. Ученики математики в старших классах могут … Там тоже была девочка. Математика для 7 класса Визуализация твердых форм Верно (T) или неверно (F) 1. Вот почему вы захотите воспользоваться нашими рабочими листами для второго класса, которые охватывают все концепции, которые ваш второклассник изучает в классе. Обладает следующими навыками: распознавание, наименование, построение, рисование, сравнение и сортировка двух- и трехмерных фигур.Грани, края и вершины трехмерных фигур. Рабочий лист по геометрии 2-го класса. Заполните следующую таблицу. 1000, мысленно прибавьте 10 или 100 к данному числу 100-900, вычтите мысленно 10 или 100. В то время как сфера — это двумерная фигура, круг — это трехмерная фигура. Ваши маленькие математики скоро будут им. охватывает следующие навыки: определять, сравнивать и анализировать атрибуты двух- и трехмерных фигур и развивать словарный запас для описания атрибутов. Выведите своих учеников на новый уровень с помощью наших листов геометрии для второго класса и печатных форм.Математика в старших классах […], Www cooloring club надеюсь, что вам понравился этот документ […]. Там тоже была девушка. Коробка или куб — это шестигранный квадрат. 4) Поместите оранжевый крестик на каждую фигуру, имеющую 5 вершин / углов. Бесплатные распечатанные рабочие листы по геометрии от k5 Learning. Определите простые трехмерные фигуры 2 ответа. Плоские и сплошные формы 2-го уровня — отображение 8 основных листов, найденных для этой концепции. Некоторые из отображаемых рабочих листов — это форма и пространство 2d и 3d работа 6, общие — это формы 2d или 3d 3d shape work color 2d и 3d формы 1 обращены к краям и вершинам фигур 3 d, сортируя формы 2 d и 3 d bs1 детские фигуры работают.Вы можете & скачать или распечатать с помощью опций чтения документов браузера. Посмотреть PDF. Все они не являются подготовительными печатными формами, поэтому вы можете просто распечатать и продолжить, подробности отдельных листов ниже. Пожалуйста, посетите Геометрия, чтобы просмотреть больше листов в той же области. Начните с обзора двухмерных фигур и переходите к более сложным трехмерным формам и редким многоугольникам. 4. Ваш электронный адрес не будет опубликован. Круг, квадрат, прямоугольник и треугольник являются примерами плоских фигур. Некоторые из рабочих листов для этой концепции: Твердые фигуры, 1 вершина граней, План урока по математике 1-го дня, Общая работа 6, Твердые фигуры с плоскими фигурами, Уровень оценки предмет и тема 3-х мерные фигуры плоские, Определение имен форм, ответы, Плоские фигуры работают.Поощряйте детей использовать подходящие термины, такие как ребра, вершины, изогнутые и плоские грани, для описания твердых тел с помощью этой печатной диаграммы свойств твердых фигур, которая наглядно показывает количество каждого атрибута в конусе кубической сферы и других трехмерных фигурах. четвертый класс. Сплошные формы (более продвинутый уровень) Эти рабочие листы сплошных форм предназначены для учащихся старших классов со 2 по 6. Изучите концепции углов, линий и симметрии и используйте наглядные руководства для отработки дробей. 2) Поместите синий крестик на каждую фигуру, имеющую ровно 8 вершин / углов.Обязательные поля помечены *. Рабочие листы плоских фигур для 2 класса. Свойства диаграммы 3D фигур. Грани, края и вершины. Рабочие листы с твердыми фигурами 2-го класса Добейтесь успеха с материалом Doorsteptutor для NSO-Level-2: полностью решенные вопросы с пошаговым объяснением — практикуйте свой путь к успеху. Вот почему вы захотите воспользоваться нашими рабочими листами для второго класса, которые охватывают все концепции, которые ваш второклассник изучает в классе. Рабочие листы твердых фигур Рабочий лист твердых фигур. Задания по математике для 3 класса 14 3 Фигуры в плоскости 2d.Рабочие листы твердых фигур Рабочий лист твердых фигур. Вращение и масштабирование фигур. Это упражнение на сопоставление и два рабочих листа для изучения двухмерных (плоских) и трехмерных (сплошных) форм. В упражнении на сопоставление 30 карточек — 15 с изображениями и 15 с названиями фигур. А там… Надеемся, они вам пригодятся. Обозначьте твердые цифры на листах для печати 2-го класса. Сплошные формы идентифицируются и помечаются в поле в верхней половине рабочего листа. Каждая программа […], 40 бесплатных распечатанных американских раскрасок бабочек […], Не стесняйтесь распечатать столько раскрасок, сколько вы […], Распечатать в удобном формате pdf.В этом пакете эффективно переплетаются распечатываемые рабочие листы с двумерными и трехмерными фигурами с упражнениями по анализу плоских и сплошных фигур и выявлению сходства и различий между ними. Посмотреть PDF. Этот рабочий лист для определения твердых форм подходит для 2-го класса детского сада. Отображение 8 лучших рабочих листов, найденных для — Плоские и сплошные формы. … Познакомьте вашего ребенка с нашими рабочими листами с трехмерными фигурами. Листы рулона, слайда и штабелирования. Определите простые трехмерные фигуры 2 ответа. Якорные диаграммы, шпаргалки, карточки, упражнения для определения и маркировки твердых форм, сравнивайте и анализируйте двухмерные и трехмерные формы, изучите их.Рабочий лист откроется в новом окне. Этот рабочий лист по математике даст вашему второкласснику возможность научиться определять и называть трехмерные формы, такие как конус, цилиндр, пирамида, куб, сфера и призма. Напишите название трехмерной формы, часть 2 Навык: изучение геометрических фигур 5) Размещение красный круг вокруг каждой формы, у которой ровно 2 лица. В связи с этим важность этих листов pdf для двухмерных фигур 1-го класса заключается в том, что дети получат наилучшую возможную технику для легкого определения и наименования 2D-форм.Рабочие листы по геометрии 2-го класса. складывать и вычитать до 100, складывать до четырех двузначных чисел, складывать и вычитать внутри. В эти печатные ролики, слайды и стопки рабочих листов упакованы интересные практические занятия, чтобы побудить любопытных маленьких наблюдателей в детском саду 1-го и 2-го классов экспериментировать, наблюдать и сравнивать движения трехмерных объектов. Некоторые из рабочих листов для этой концепции: Твердые фигуры, 1 вершина граней, План урока по математике 1-го дня, Общая работа 6, Твердые фигуры с плоскими фигурами, Уровень оценки предмет и тема 3-х мерные фигуры плоские, Определение имен форм, ответы, Плоские фигуры работают.Национальная страховая компания Аль-Бухайра, Дубай. Значение рекламы в кино, Значение имени Тайя, Мла Роя Каст, Карта Sheng Siong Diners, Типы звонков в службу 911, Уличная еда Sain, Прогрессивная пчелиная муха, Один Господь, одна вера, одна песня крещения, Вегетарианские кулинарные мастер-классы Денвер, Меня зовут Джонас Аккорды,
Национальный математический музей
Обязательно ознакомьтесь с полным меню онлайн-мероприятий и студенческих занятий MoMath на сайте events.momath.org!
MoMath в новостях! Ознакомьтесь с выбором редактора New York Times , включая упоминание о гала-вечере MoMath, Real и Rational (посмотрите видео с гала-вечера БЕСПЛАТНО). Наслаждайтесь этим обсуждением, в котором представлены математические и естественнонаучные размышления о пандемии от двух известных экспертов, Эрика Шмидта и Джули Гербердинг. Эрик — бывший генеральный директор Google и соучредитель Schmidt Futures. Джули — бывший директор CDC, а в настоящее время — исполнительный вице-президент и главный врач компании Merck. Кроме того, Нейт Сильвер предлагает свой взгляд на президентские выборы 2020 года.
Добро пожаловать в Национальный музей математики!
MoMath, Национальный музей математики, — это отмеченный наградами музей, который подчеркивает роль математики в освещении моделей и структур вокруг нас.Его динамичные выставки, галереи и программы призваны стимулировать исследования, пробуждать любопытство и раскрывать чудеса математики. Новаторские экспонаты музея привлекут посетителей любого возраста от 1 до 100 лет!
Посмотрите это вирусное видео о MoMath
Ближайшие события
MoMath по телевизору!
Поклонники MoMath
Билл и Хиллари Клинтон — поклонники математики Джефф Безос едет на квадратных колесахПризнание и награды
Национальный музей математики (MoMath) рад получить следующее признание:
Программы
Семейные программы выходного дня
Совершите экскурсию по новой программе MoMath Derivatives или присоединитесь к одному из специально обученных преподавателей MoMath в Explorations , практическом занятии в классе, чтобы открыть для себя чудо математики.Не упустите свой шанс взглянуть на математику в новом свете, только в MoMath.
РасширенияИзобретите заново класс математики с помощью Expansions , внешкольная программа MoMath для одаренных учеников. Узнайте больше и подайте заявку на зачисление на семестр осень 2020 года.
MathPlay , программа MoMath для дошкольниковПод руководством опытного специалиста дошкольного образования MathPlay вовлекает ваших детей в игровые занятия, чтобы помочь им развить прочный фундамент в математике, обогащая их день математическим вдохновением.
Совершите экскурсию в MoMath!
Регистрация на 2020-2021 учебный год открыта. Щелкните здесь, чтобы узнать больше и заказать экскурсии и групповые посещения сегодня.
Учителя: принесите в вашу школу интересные экспонаты по математике
Посетите mm2go.org, чтобы узнать больше о Math Midway 2 Go !
Дни рождения и многое другое в MoMath
Проведите уникальную вечеринку для своего ребенка (или себя) в MoMath!
Смотрите
CBS News ‘ Воскресное утреннее освещение MoMathCBS News ‘Мо Рокка исследует математику в этой телевизионной программе!
интересных математических фактов | 40 фактов
20 ноября 2020
Время чтения: 5 минут
Знаете ли вы?
«В каждом нечетном числе есть буква« е ».”
Математика — очень интересный предмет. От своей богатой истории до различных уловок и советов, математика содержит ряд удивительных фактов, которые помогают учащимся лучше освоить этот предмет.
В этой статье мы перечисляем 40 удивительных фактов о математике.
Понимание различных интересных фактов о математике помогает учащимся развивать свои навыки и мотивирует их больше узнавать об этом предмете.
Вам также может понравиться:
40 интересных фактов о математике
Вот загружаемый PDF-файл, содержащий 40 интересных фактов о математике. Нажмите кнопку загрузки, чтобы изучить их.
| 📥 | 40 интересных фактов о математике | Загрузить |
Математические факты! 40 интересных фактов о математике
В этой статье мы перечисляем 40 удивительных фактов о математике.Эти забавные математические факты помогут учащимся лучше освоить этот предмет.
В математике есть типы интересных чисел. Одно такое число — сотня. Число 100 на самом деле не означает 100. Оно образовано от древнескандинавского слова «сотый», что на самом деле означает 120.
Число 2 — наименьшее простое число. Это также единственное четное простое число. Цифра 1 считается простой для всех остальных чисел.Поэтому возьмем 2 как наименьшее.
Все мы слышали о теореме Пифагора. Но есть еще кое-что, что известно как постоянная Пифагора. Квадратный корень из 2, то есть 1,41, был первым обнаруженным рациональным числом, известным как постоянная Пифагора.
Римляне вообще не считали 0 числом. Таким образом, в римских цифрах нули нулей.
Идея нуля была изобретена индийским астрономом и математиком Брахмагуптой примерно в 600 году нашей эры. Он внес большой вклад в математику и астрономию и известен тем, что объяснял, как найти куб и кубический корень из целого числа.
Римские цифры состоят только из семи разных букв, которые образуют всю систему счисления: I, V, X, L, C, D и M.
Математически четное число — это число, которое можно разделить на два меньших числа, которые на самом деле являются целыми числами.
Во всей индуистской арабской системе счисления есть только одно число, которое может быть написано таким же количеством букв, как и оно само. Это число четыре.
Если вы возьмете любое число, умноженное на три, и просуммируете цифры в ответе, то ответ, который вы получите после сложения цифр, всегда будет делиться на три. Например: 3 x 4 = 12 или, 1 + 2 = 3 или, 3/3 = 1
Совершенное число относится к положительному целому числу, равному сумме его положительных делителей.По этому правилу 6 — это наименьшее совершенное число. Следующее совершенное число — 28.
Мы используем десятичную систему счисления, которая состоит из 10 цифр от 0 до 9. Она также известна как индуистская арабская система счисления. Он был открыт более 1000 лет назад.
Пи также известен как отношение длины окружности к диаметру круга. Это особое число, которое иррационально. Есть особый день, который мы празднуем 14 марта, называемый днем Пи.
Леонардо Фибоначчи из Пизы в 13 веке открыл последовательность Фибоначчи. Начиная с 0 и 1, эта последовательность создается как сумма двух предыдущих чисел, например, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,…
9 также называют магическим числом. Это потому, что если вы умножите число на 9 и сложите все цифры нового числа вместе, сумма всегда будет равна 9.Например: 8 x 9 = 72 или 7 + 2 = 9
Очень часто число 1 путают с простым числом, но, разделив 1 на 1, вы получите 1. Ничего не было поделено.
Сила экспоненциального роста шокирует. Вы действительно можете добраться до Луны, сложив лист 0,01 мм 45 раз.
Если вы подойдете на улицу и спросите кого-нибудь об их любимом номере, то с вероятностью 10% он скажет цифру семь.
13 считается несчастливым числом. Но в исследовании Алекса Беллоса это оказалось самым популярным двузначным числом.
Гугол означает 1, за которой следует 100 нулей. Гуголплекс — это 1, за которой следуют нули гугол. Трудно представить, насколько длинным будет это число.
Денвер известен как город высотой в милю, потому что он имеет высоту ровно 5280 футов — длину в милю.
Номер четыре рассматривается с суевериями и недоверием в большей части Восточной Азии. Это называется тетрафобией. Это потому, что слово четыре звучит так же, как в некоторых азиатских языках.
Подростки, отправляющие текстовые сообщения из Таиланда, отправят цифры 555, чтобы указать, что что-то забавное. На тайском языке 5 произносится как ха, что при переводе становится хахаха.
В большинстве месяцев в календаре 31 день.Только четыре месяца имеют 30 дней, то есть апрель, июнь, сентябрь и ноябрь. В феврале обычно всего 28 дней, за исключением високосных лет.
В выборке из 23 человек существует 50% шансов, что двое из них будут иметь один и тот же день рождения. Это известно как проблема дня рождения.
Семь — самое значительное число в разных религиях и культурах. Например, семь цветов радуги, семь дней в неделе, семь нот музыкального мастерства и т. Д.
История «дюйма». В Великобритании единицей длины было ячменное зерно. После 1066 года 1 дюйм был равен 3 зернам ячменя. Говорят, что король Шотландии Давид I определил шотландский дюйм как ширину большого пальца среднего человека у основания ногтя.
Что будет после миллиона, миллиарда и триллиона? Вы можете обозначить числа после этих терминов как квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион и дециллион.
Знаки Плюс (+) и Минус (-) были обнаружены еще в 1489 году нашей эры
г.
Два и пять — единственные простые числа во всей системе счисления, оканчивающиеся на два или пять.
Тесно ограниченная геометрическая фигура, имеющая 20 сторон, известна как икосагон.
В индийской системе счисления от 0 до 1000 буква A появляется первой только в 1000 («тысяча»).
Калькулятор, который является наиболее широко используемым математическим устройством в современном мире, на самом деле возник на основе концепции счётов.
Если сумма цифр делится на три, то данное число также делится на три. Это известно как правило делимости трех.
Если вы последовательно сложите все числа от 1 до 100, то вы получите 5050.
Jiffy фактически считается единицей времени, равной 1/100 секунды.
Знаете ли вы, что такое число палиндрома? Это число, которое читается одинаково вперед и назад, например 12421.
Существуют и другие специальные числа, кроме константы Пифагора и числа пи. Некоторые из этих чисел представляют собой постоянную Эйлера, золотое сечение и т. Д.
Минимальное количество разрезов, необходимых для разрезания фигуры на восемь частей, составляет три i.е. по горизонтали, вертикали и по основанию.
Сумма противоположных сторон кубика всегда равна 7. Например, 6 и 1 всегда будут на противоположных сторонах, что в сумме дает 7.
Бейсбольное поле имеет идеальную форму ромба.
Также читайте:
Заключение
Эти забавные математические факты помогут учащимся лучше освоить этот предмет.Эти факты также могут быть использованы для различных викторин и вопросов GK. Кроме того, это также может быть интересным способом удивить своих друзей и стать гуру математики.
Cuemath регулярно публикует статьи для родителей и детей на разные темы. Наши предложения и рекомендации предоставлены после обширных исследований и помогли ряду читателей.
Не могли бы вы придумать еще несколько фактов?
О компании Cuemath
Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-классы для преподавателей и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для детей, развивающее несколько навыков.Ознакомьтесь со структурой Cuemath Fee и подпишитесь на бесплатную пробную версию.
Часто задаваемые вопросы (FAQ)
1. Почему нам следует сосредоточиться на математических фактах?
Математические факты важны, потому что они формируют строительные блоки для математических концепций более высокого уровня.
Внешние ссылки
Неоднозначно PEMDAS
14.04.2014: ссылок- Пример форума hpmuseum
- Пример физического форума: 48/2 (9 + 3)
- защитников Разделите и умножьте ранжируйте поровну и идите слева направо.и есть другие мемноники, такие как «Ешьте, пожалуйста, вкусные яблочные штрудели мамы».
- В этом научном блоге упоминается статья
Тара Хэлле
что довольно хорошо уже говорит о том, что происходит (если бы я видел эту статью, написанную 12 марта 2013 г.,
Я бы не стал записывать это, потому что в этой статье очень четко говорится, что первоначальная оценка того, что нет
договоренность о порядке умножения или деления верна). Тем не менее, эта тема побудила меня сказать что-то новое.
о порядке операций одного и того же типа, например, D или E в PEMDAS, что выходит за рамки споров о BEDMAS.Вот интересная цитата из той статьи
"Интернет-слухи утверждают, что Американское математическое общество написало" умножение, указанное сопоставлением, осуществляется до деления ", но в сети больше не существует оригинального источника AMS (если он вообще когда-либо существовал). Тем не менее, некоторые ранние учебники по математике также учил студентов делать все умножения, а затем все деления, но большинство из них, например, эта алгебра средней школы 1907 года учебник, этот учебник 1910 года и этот учебник 1912 года рекомендовали выполнять все умножения и деления в порядок, в котором они появляются первыми, затем следуют добавления и вычитания.(Это соглашение имеет смысл также и с канадским и британские версии PEMDAS, такие как BEDMAS, BIDMAS и BODMAS, которые все перечисляют деление перед умножением на (аббревиатура). Самый разумный совет, содержащийся в «Mathematical Gazette» за 1917 год, рекомендовал использовать круглые скобки для избегать двусмысленности. (Да!) Но даже известный историк математики Флориан Каджори написал в «Истории математических обозначений» в 1928-1929 гг .: «Если арифметический или алгебраический член содержит / и х, в настоящее время нет согласия относительно того, какой знак должен использоваться первым."В статье есть ссылки на источники учебников. Вот запись 242 в книге Флориана Каджориса «История математической записи» (стр. 274), которая упоминается в этой цитате. Я не вижу никаких указаний на рекомендации, данные в цитируемых учебниках для старших классов, например здесь, здесь, но упомянутая запись в книге Вебстера Уэллса об этом ясно сказано на странице 18:
Обновление от 18 мая 2017 г .: В последнее время загадки вроде ниже появились, которые упускают из виду, что количество картофеля фри изменилось или что используется одна вишня) всплыли Эти головоломки успели стать вирусными не из-за PEMDAS, а потому что люди не смотрят на варианты (3 вместо 4 банана, 2 часа, а не 3 часа).Поначалу почти все ошибаются. Но есть еще и проблема PEMDAS. Некоторые получают 88. Но чтобы получить 88, нужно было написать скобка (2 + 3 + 3) * 11. (спасибо Абите Сукумаран за то, что поделилась этим).
Обновление от 2 августа 2017 г .: Преш Талвалкар пишет
«Я делаю математические видео на YouTube на канале« MindYourDecisions ». Некоторые из самых популярных видео - это неоднозначные выражения, связанные с порядком действий. В ходе исследования я наткнулся на ваш веб-сайт и обнаружил проблему: Что такое 2x / 3y - 1, если x = 9 и y = 2? Я бы ответил 11, как сказал учитель 5-го класса.Я был ошеломлен тем, что ни один из 60 студентов вашего гарвардского курса математики ответил 11 (вы объяснили, что 58 получили ответ 2, а затем 2 получили ответ 18/5).Мой ответ:
«да, это интересная вещь. Конечно, ни один из ответов не« правильный » поскольку мы знаем, что интерпретации BEDMAS и PEMDAS могут использоваться без нарушения каких-либо полномочий. Как указано на странице, ответ 11 - это то, что есть у большинства компьютерных языков. Вас явно этому учили. Было бы интересно узнать, какой процент людей говорит 11.Мои эксперименты говорят, что это очень редкий. Большинство делают умножение перед делением, так как PEMDAS кажется более популярны и больше преподают в школах. БЕДМЫ PE (MD) AS, кажется, преподают значительно меньше. Единственное, что мы знаем, это то, что утверждение, что одним из ответов является единственный правильный ответ - это неправильно ".
Обновление от 5 августа 2017 г .: Джейкоб Пошоланн Кефоед Кристенсен присылает другой пример и замечание по поводу обелуса.
"Проблема в том, что изображение мобильного телефона получает 9 из уравнения: 6 ÷ 2 (2 + 1)
что, по их мнению, будет 1.В своем споре вы определяете obelus и разделительную косую черту как имеющие разные значения.
Ну да, на самом деле они имеют два разных значения, и поэтому обычно
никогда не используйте обелус. Только американец может по-прежнему использовать его, но этот знак был удален
в использовании уравнений научных работ из-за его исторической проблемности.
Первое слово obelus в Северной Европе означает вычитание.
Во-вторых, obelus рекомендуется удалить в научном использовании, потому что у нас уже есть знак для любого из них (разделительная косая черта ("/") и вычитание ("-")).Хотя, по вашему мнению, обелус и косая черта деления должны означать два
разные значения У вас часто есть только одна опция на калькуляторе, чтобы сделать знак деления ".
Мой ответ:
«Спасибо за пример 6 ÷ 2 (2 + 1). Он тоже показывает неоднозначность. Да, в зависимости от того, кто входит в команду PEMDAS или PEDMAS, получает 1 или 9. Это тоже прекрасный пример, когда можно увидеть жаркие дискуссии. Как указывалось и ранее другими в список литературы, нет нет правильного ответа .3 / (3 + у). Я был удивлен и должен был написать на доске пояснение:Экзамен по-прежнему прошел хорошо. На этой фотографии, сделанной незадолго до экзамена, вы можете увидеть, что все были счастливы уйти: Урок очень ясен: как учитель, даже если вы знаете лучше, вы должны быть очень четкий, даже избыточный. Даже если нет двусмысленности, лучше быть на всякий случай.
Кстати, статья в Википедии упоминает пример1 + 2x3 = 9 Калькулятор Microsoft в стандартном виде 1 + 2x3 = 7 Калькулятор Microsoft в представлении программистовОн показывает, что один и тот же поставщик в рамках, где нет двусмысленности (никто никогда не сомневается, что умножение должно предшествовать сложению), двусмысленность в том же товар.В другом примере из этой статьи упоминаются калькуляторы Texas Instruments.1 / 2x = 1 / (2x) в калькуляторе TI-82 1 / 2x = (1/2) x в калькуляторе TI-83Самопровозглашенные правила вроде это вряд ли поможет.
Обновление от 19 января 2018 г .: Тимоти Масгроув любезно обратил мое внимание на глупую дискуссию о youtube в котором вопрос of 6 ÷ 2 (1 + 2) снова появляется (см. выше). Также эта история показывает, насколько богословские дебаты может стать уже тем фактом, что часть зрителей, которым нравится видео и неприязнь к видео примерно одинакова, показывает, что ответ на эту проблему должен быть неоднозначным.Выше я привел (частично вслед за Тарой Хэлле, которая написала этот Slate article), исторические указатели, показывающие, насколько неоднозначны вещи. Вот лагеря:Компьютеры в основном следуют за вторым или третьим.Большинство людей и особенно студенты (экспериментально) склонны следовать правилу PEMDAS. Литература указывает на неоднозначность.
- PEMDAS (умножение предшествует делению)
- ПЕДМА (деление предшествует умножению)
- PE (MD) AS (Деление и умножение имеют одинаковый вес, зависит от того, что осталось)
- неоднозначно (нет установленного правила)
| PEMDAS | BEDMAS | PE (MD) AS | 6/2 * (1 + 2) | 1 | 9 | 9 | (1 + 2) * 6/2 | 9 | 9 | 9 |
Еще хуже, вероятно, спорят, когда спрашивают, что такое 8 ÷ 2/2 (какая-то средняя школа Учитель подтвердил мне, что деления (обелус и обратная косая черта) в некоторых учебниках трактуются по-разному, см. замечание "obelus" выше, сделанное Якобом Пошоланом Кефоедом Кристенсеном. Некоторые скажут, что ответ - 8, потому что / стоит перед ÷. Если двигаться слева направо, мы получаем 2.
Обновление от 4 сентября 2018 г. :
Я получил следующее приятное письмо:
| Как, черт возьми, можно сказать, что это двусмысленно, когда это АКСИОМАТИЧЕСКОЕ, что умножение и деление являются обратными операциями? Как можно сказать, что это неоднозначно, когда ЛЮБОЕ деление может быть выражено как умножение на обратное? Позор вам за увековечивание ерунды. |
Единственное, что немного беспокоит, так как писатель на самом деле кажется учителем. Независимо от аргумента, писатель, вероятно, должен перейти в профессию, где требуется как можно меньше человеческого взаимодействия. Я ответил
| Уважаемый ..., , вы, вероятно, ссылаетесь на http://www.math.harvard.edu/~knill/pedagogy/ambiguity/ Дело не в том, является ли деление обратным умножению. Это определение.2/3. Теперь, если вы посмотрите на литературу и историю, то оказывается, что нет однозначного ответа, что правильно. И если это так, мы назовем это неоднозначным. Есть лагерь, который защищает PE (MD) AS, где MD равны и где порядок имеет значение, если умножение используется вместе. Но это только усложняет ситуацию, поскольку у нас есть три разных интерпретации. Итак, если кто-то пишет такое выражение, как x / 3x, он должен быть осторожно и поставил кронштейны.Все остальное может вызвать недопонимание. Вы не единственный, кто чувствует себя очень сильным и эмоционально из-за этого. |
Обновление от 2 октября 2018 г. :
Мне прислали ссылку на следующий адрес
YouTube видео.
На данный момент это один из лучших материалов на YouTube.
Хорошо видно, что в реальном мире выражения
используется по-другому: например, в опубликованных статьях
mn / rs обычно в публикациях интерпретируется как (mn) / (rs) или
лекций Фейнмана, можно увидеть, что 1 / 2N 1/2 интерпретируется
как 1 / (2 N 1/2 ).В инженерии можно прочитать W = PVMg / RT.
Еще один замечательный момент, сделанный в этом видео, заключается в том, что можно написать x / 2
если 1 / 2x интерпретируется как (1/2) x. Никто бы не написал 1 / 2x, если бы они
означает x / 2. Итак, на практике интерпретируется
выражение как 1 / (2x), которое является PEMDAS, но отличается от BEDMAS или
интерпретация того, что умножение и деление лежат в одном и том же
опора. Также упоминается, что в руководстве AMS есть PEMDAS (умножение
предшествует делению). Также следует руководство Американского физического общества.
ПЕМДАС.Видео еще раз демонстрирует, что единственный способ избежать
двусмысленность заключается в использовании скобок.
24 октября 2018 г. : Изначально я планировал опубликовать на YouTube версию несколько слайдов от 28 апреля 2018 г. Harvard Extension STEM Club, но на это не было времени. Спасибо Ане Каролине Смит за возможность выступить. Вот часть слайдов:
СЛАЙДЫ PDF (76 стр.)
26 октября 2018 г. : Другой хороший пример от кого-то: Вот письмо:
Мне сказали, что когда вы умножаете и делите (так как порядок работы значения не имеет) вам никогда не нужно использовать круглые скобки, верно? Потому что 2 * 3/4 * 6 на моем калькуляторе дают мне 9, и я ожидал 0.25! Для меня это должно быть эквивалентно 2 * 3 / (4 * 6), потому что, поскольку мы не нужны круглые скобки, это единственный способ набрать его без них. Если я хочу вычислить 2 * 3/4 * 6, как мой калькулятор да, я должен набрать 2 * 3 * 6/4, это правильно?Мой ответ:
Порядок операций имеет значение. Вам нужно поставить скобка. Мне нравится ваш пример. Это уже хорошо это иллюстрирует. Большинство людей получат 6/24 = 1/4, как и вы. Большинство языков программирования (компьютеры) дают 9. Компьютер следует PEDMAS (деление перед умножением) 2 (3/4) 6 = 9 или используйте правило (MD), которое означает «все, что будет первым» ((2 * 3) / 4) * 6 = 9 Люди (и большинство рекомендаций, таких как профессиональные такие общества, как AMS, следуют PEMDAS, что означает вы сначала делаете умножение, а затем деление (2 * 3) / (4 * 6) = 1/4 Но следовать рекомендации не имеет смысла если существуют разные интерпретации и компьютеры это делают разные.3)) = 7625597484987 компьютер идет справа налево. Также здесь необходимы скобки.4 ноября 2018 г. : С.А. добавил в историю интересный ракурс: Рекомендуется сначала упростить, а затем удалить скобки.
Я читал ваш блог по вопросам программирования на MD или DM. Проблема в том, что все они противоречат первому закону алгебры. Упростите, а затем УДАЛИТЬ круглые скобки. Все эти соглашения нарушают это, говоря только упрощать скобки ВНУТРИ. Итак, сначала мне нравится, что вы сказали AMBIGUOUS на 6/2 (1 + 2) 1 или 9 Однако я вздремнул, астрально переместился к старому Евклиду, и он засмеялся.Доказательство 1 и 9. 6 / x = 1 или 6 / x = 9 Когда x = 2 (1 + 2) 2 (1 + 2) = 2 (3) = 6 6/6 = 1 Таким образом, не учить студентов убирать скобки в новой математике, это противоречит первому закону алгебры. Все эти условные обозначения аббревиатур необходимо исправить, чтобы они соответствовали 1-му закону алгебры. Итак, согласны ли вы, что новые математические соглашения должны согласовываться с первым правилом алгебры Евклида? Думаю, да.Вот мой ответ:
Это интересный ракурс. Но учтите, что рекомендация "упростить" здесь находится проблема неоднозначности:3 декабря 2018 г. : Atmos добавил еще один интересный ракурс
Да, можно упростить 6/2 (1 + 2), введя x = 2 (1 + 2) = 6, а затем получить 6/6 = 1 Но можно также упростить, определив x = 6/2, а затем получить x (1 + 2) = 9.Собственно, это тоже исторически интересно. Вы упомянули Евклида. Евклид не использовал известную нам алгебру. Символическая алгебра появилась только с Вите в 16 веке. Насколько нам известно, только в ХХ веке реализовали что здесь действительно есть двусмысленность. Об этом ясно сказано в книге Каджори о математическая нотация, которая является авторитетом в этом вопросе.
Это тоже стало педагогическим вопросом: студентов сегодня в основном обучают правилу PEMDAS, которое формально ставит умножение перед делением и рекомендовал бы результат 6/2 (1 + 2) = 1.Если дать выражение системе компьютерной алгебры, они все дают 6/2 (1 + 2) = 9. Все эти обсуждения были вызваны такими примерами. Первое правило алгебры по-прежнему остается хорошим правилом. Это хороший совет. к несчастью это не устраняет двусмысленность. Но я согласен, что это помогает писателю избегать двусмысленность. Но вы знаете, проблема возникла в основном в образовательных учреждениях. Если учитель спрашивает ученика, что такое 6/2 (1 + 2), учитель не хочет упростите это, так как это уже решит проблему.Если сегодня учитель спросит студенты, что такое 6/2 (1 + 2), то это просто напрашивается на неприятности. Правильно do - это уточнить и написать либо (6/2) (1 + 2), либо 6 / (2 (1 + 2)). Каджори уже было ясно, что отказ от скобок не дает четко определенные математические выражения. Оливер
Потенциальным решением этого противоречия может быть то, что когда у вас есть коэффициенты и переменные, записанные вместе без операторов между тема.грамм. 5ab, мы можем рассматривать это как вложенную операцию. Другими словами, отсутствие символа оператора означает, что оператор отношения между ними имеют приоритет над любыми внешними операциями, т.е. 5ab представляет собой (5 * a * b). Итак, если у вас был / bc, записан только один оператор (разделение символ), а часть "bc" будет подразумеваться вложенной из-за упущение оператора внутри. Так что это все равно будет "a over bc", как именно это выглядит и сколько из нас учили.А потом, если нам нужно указать, что операция между a и b фактически занимает приоритет над отношениями между b и c, тогда мы просто вместо этого напишите a / b * c. Ни суеты, ни суеты. Разве это не более эффективный способ общения с математический язык здесь? И разве не в этом суть математического язык, чтобы эффективно передавать концепции? В противном случае этот вид путаница никогда не исчезнет, и нам придется написать намного больше круглые скобки в наших уравнениях (и никто не хочет этого делать).Немного людям нравится "новая математика" сверхстрогой интерпретации PEMDAS особенно потому, что это простой способ обмануть людей и сделать математику более запутанно, чем должно быть. Тем не менее, это, кажется, победило все Дело в том, почему мы вообще это делаем. У меня есть оба способа сделать это, но строгий метод PEMDAS кажется контрпродуктивен, потому что он вызывает так много проблем и делает вещи например, превратить якобы простую дробь вроде 2x / 3y в фактическую вместо этого имеется в виду 2xy / 3, что кажется совершенно безумным.Но если вместо этого мы просто используем PEMDAS, когда операторы на самом деле написаны, тогда все такого рода проблемы исчезнут буквально в одночасье. «Старая математика» и "новая математика", наконец, согласится, и мы сможем все это сделать с одним очень простым правилом. Что ты об этом думаешь?Я ответил
Привет, Атмос,
отказ от знаков умножения уже обычно делается.
На самом деле большую часть времени. Однако может возникнуть дополнительная проблема.
при использовании чисел, а не переменных вроде 3/45 не то же самое, что 3/4 5
Но вы вносите интересный момент, потому что теперь еще больше
двусмысленность:
3/45 = 3 больше 45 = 1/15
3 / (4 * 5) = 3 больше 20 = 3/20
(3/4) 5 = 3/4 умножить на 5 = 15/4
Проблема PEMDAS - это не «проблема, которую нужно решать».Это вопрос
Дело в том, что существуют разные интерпретации и что человек для
пример читает x / yz с x = 3, y = 4 и z = 5 как 3/20, в то время как машина
(практически все языки программирования) дают другой результат.
Есть органы, которые установили правила (большинство учеников учат
PEMDAS), что является одной из причин, по которой многие люди спрашивали о 3/4 * 5, давая 3/20
которые запрашивали большинство машин, дают 15/4:
Я набираю это в Mathematica
х = 3; у = 4; z = 5; x / y z и получаем 15/4
Это лингвистическая проблема, а не математическая.В случае
лингвистическая проблема, ее нельзя решить путем введения нового правила.
Единственный способ решить проблему - избежать ее. Можно избежать этого, чтобы
поставить скобки.
Оливер
Обновление от 14 декабря 2018 г. :В новейшем гайде по мультфильмам из серии Ларри Гонника (которые фантастические), есть еще кое-что о Порядок операций. Но далеко не идёт. "Если без скобок присутствуют, умножьте и разделите перед сложением и вычитанием ". Это очень грубое правило, но оно имеет то преимущество, что он не попадает в войны PEMDAS.
Обновление от 18 января 2019 г. :
Учитель математики прислал мне следующий пример. Здесь не только неоднозначность PEMDAS. Также вопрос "96 разделить на 6 из 4" появляется, что может означать "96/6 умножить на 4" или затем «96 / (6 * 4)». Это особенно интересный случай, потому что того, что:
Вопрос:Я учитель математики и недавно столкнулся с конкретным вопросом на PEMDAS (пожалуйста, проверьте приложение), где ученики получили два разных ответа (6 и 66).Причиной получения двух разных ответов было то, как студенты решили последнюю часть вопроса: 96 ÷ 6 из 4 |
| Мой ответ: в этой проблеме есть две двусмысленности, и да, все ответы даны.
студентами должны быть оценены как правильные. 1) Первое выражение: похоже, что ученики действительно истолковали
57 ÷ 19 * 2 выражение равно 6, даже если это может быть 3/2, если используется PEMDAS (и официальные рекомендации
AMS или физического общества и используется в большинстве научных статей, особенно если выражения являются переменными).
Что происходит, так это то, что если бы вопрос был задан как 57/19 * 2, то многие интерпретировали бы его.
как 57/38. 57 / (19 * 2) -64 * 2/32 + 96 / (6 * 4) = 3/2 (57/19) * 2-64 * 2/32 + 96 / (6 * 4) = 6 (57/19) * 2-64 * 2/32 + (96/6) * 4 = 66 57 / (19 * 2) -64 * 2/32 + (96/6) * 4 = 123/2Пример снова показывает, что скобки нужно ставить всегда.Но это также показывает, что может произойти, если для описания арифметических операций используется "разговорный язык", так как это может может привести к другим двусмысленностям. «Что составляет две трети от 9» должно быть ясно как (2/3) * 9, а 2 ÷ 3 из 9 тоже можно интерпретировать как 2 / (3 * 9). Этот пример снова указывает на то, что люди могут интерпретировать знак обелуса ÷ иначе, чем знак деления /. |
| В швейцарской газете 20 Min задача 6/2 (1 + 2) = ???
тоже упоминается.К статье уже добавлено 1384 комментария. Как и в течение многих лет в социальных сетях, борьба
продолжается там. Самое интересное, насколько большинство уверены в своей правоте
со всех сторон. Что снова указывает на двусмысленность. Название статьи: «Миллионы не справляются с этим математическим уравнением!» В качестве «доказательства» есть видео на YouTube, которое дает ответ 9. Автор этого видео,
Преш Талуокер дает в своем
блог
ссылка
Леннес, Н. Дж. "Дискуссии: Относительно порядка операций в алгебре."The American Mathematical Monthly 24.2 (1917): 93-95 ..."
Лучше прочитать эту статью.
Прочтите в конце статью Леннеса, который писал уже в 1917 году:
Лучше не скажешь! Значит, идиоты не 12 миллионов человек.Те, кто так утверждает, есть. Это досадное математическое уравнение? Вот дополнение. Путаница (скорее всего намеренно) сводится к несоответствию используемых математических правил в начальной и средней школе.8 ÷ 2 (2 + 2) =? Проблема заключалась в том, что он дал два разных ответа, 16 или 1, в зависимости от порядка, в котором выполнялись математические операции. выполненный. В юном возрасте студенты-математики обучаются особым навыкам. соглашение о «порядке операций», которое диктует порядок следующим образом: круглые скобки, показатели, умножение и деление (подлежат рассмотрению на равных, с разрывом галстуков, работая слева направо), и сложение и вычитание (также равного приоритета, со связями аналогично сломанный).Я утверждал, что строгое соблюдение этой элементарной конвенции PEMDAS: приводит только к одному ответу: 16. Тем не менее, многие читатели (включая моего редактора), одинаково приверженные тому, что они рассматривали в качестве стандартного порядка операций, усиленно настаивал правильный ответ был 1. Что происходило? После прочтения много комментариев к статье, я понял, что большинство из этих респондентов были используя другое (и более сложное) соглашение, чем элементарное Конвенция PEMDAS, которую я описал в статье.В этом более сложном соглашении, которое часто используется в алгебры, неявному умножению дается более высокий приоритет, чем явному умножение или явное деление, в котором записываются эти операции явно с такими символами, как x * / или ÷. Под этим более изощренным соглашение, неявное умножение на 2 (2 + 2) дано выше приоритет, чем явное деление на 8 ÷ 2 (2 + 2). Другими словами, 2 (2 + 2) следует оценить в первую очередь. Это дает 8 ÷ 2 (2 + 2) = 8 ÷ 8 = 1. По тому же правилу многие комментаторы утверждали, что выражение 8 ÷ 2 (4) не было синонимом 8 ÷ 2x4, потому что круглые скобки требовали немедленного разрешение, что снова дает 8 ÷ 8 = 1.Это соглашение очень разумно, и я согласен, что ответ - 1. если мы будем его придерживаться. Но это не принято повсеместно. Калькуляторы встроенные в Google и WolframAlpha используют более элементарное соглашение; они не делают различия между явным и неявным умножением при указании вычислить простые арифметические выражения. Подпишитесь на Science Times Мы расскажем вам истории, отражающие чудеса человеческого тела, природы и космоса. Более того, после того, как Google и WolframAlpha оценивают все, что находится внутри набор круглых скобок, они эффективно удаляют круглые скобки и не больше расставляйте приоритеты по содержанию.В частности, интерпретируют 8 ÷ 2 (2 + 2) как 8 ÷ 2x (2 + 2) = 8 ÷ 2x (4), и обрабатываем это как синоним 8 ÷ 2x4. Затем, согласно элементарному PEMDAS, деление и умножение имеют равный приоритет, поэтому работаем слева направо и получаем 8 ÷ 2x4 = 4x4 и получили ответ 16. В своей статье я решил сосредоточиться на этом более простое соглашение. Другие комментаторы возражали против самого исходного вопроса. Посмотри как они отметили, что это было плохо поставлено. Это можно было бы сделать намного яснее если бы в нужном месте был вставлен только другой набор круглых скобок, записав его как (8 ÷ 2) (2 + 2) или 8 ÷ (2 (2 + 2)).Верно, но это упускает из виду: вопрос не был задан ничего ясно. Напротив, его безвестность кажется почти умышленно. Это, безусловно, искусно извращенное, будто построенное для причинить шалость. В выражении 8 ÷ 2 (2 + 2) используются круглые скобки - обычно это инструмент для сокращения путаница - в манере джиу-джитсу, чтобы усилить мутность. Оно делает это путем сопоставления цифры 2 и выражения (2 + 2), что означает неявно, что они предназначены для умножения, но не помещая явный знак умножения между ними.Зритель остается в недоумении следует ли использовать сложное соглашение для неявного умножения из класса алгебры или вернуться к элементарному соглашению PEMDAS из средней школы. Выбирает: "Итак, проблема в том, как она поставлена, смешивает обозначения начальной школы. с обозначениями средней школы, что не имеет смысла. Человек который хорошо помните математику в начальной школе, скажите, что ответ - 16. Люди кто помнит свою алгебру, с большей вероятностью ответит 1. " Как бы мы ни предпочли четкий ответ на этот вопрос, не один.Вы говорите помидор, я говорю томахто. Некоторые электронные таблицы и программное обеспечение системы категорически отказываются отвечать на этот вопрос - они упираются в его искаженную состав. Это тоже мой инстинкт, как и большинство математиков, которых я говорил с. Если вы хотите получить более четкий ответ, задайте более четкий вопрос.5 августа 2019 г. . Только что появилась еще одна сокровищница Дженни Горхэм на ютубе: 8 августа 2019 г. . Грег Макканн любезно указал эта ссылка на заархивированная копия руководящих принципов AMS.{-1} dt $. 17 августа 2019 г. Другой вопрос: Мне любопытно, какие, по вашему мнению, ответы на это уравнение. 8 ÷ 2 (4). Для меня самый простой порядок действий - это умножение 2 * 4 во-первых, потому что мне еще нужно разобраться со скобками. Я просто верю, что нам нужно провести какую-то математику, чтобы избавиться от скобок. Некоторые люди просто бросают их, не делая никаких вычислений. Я имею в виду, зачем они вообще, если их можно просто уронить в любой момент без каких-либо математических вычислений, чтобы их очистить.С. -------------------------------------------------- --------------------------------- Мой ответ: Да, это одна из последних загадок PEMDAS. Подобный Также Строгац обсуждал в New York Times. Вы упомянули, что 2 + 2 уже оценивается, но это не меняет ситуацию на 8 ÷ 2 (2 + 2), который теперь раздается. Но это та же история. Причина, по которой ставится скобка вокруг 4, заключается в том, что она не читается как 24. Но это не проясняет двусмысленность.Да, хочется сначала сделать 2 * 4 и получить результат 1. Большинство компьютерных программ оценивают его как 16. Пример: Ядро Mathematica 12.0.0 для Linux x86 (64-бит) Авторские права 1988-2019 Wolfram Research, Inc. В [1]: = 8/2 (4) Из [1] = 16 Почти все люди оценили бы его как 1. Мнения здесь не имеют значения, поскольку теперь хорошо задокументировано, что там просто нет консенсуса (ни авторитетом, ни историческим ростом, это лингвистический феномен, о котором так поздно осознали необходимость его точного определения).Вещи можно интерпретировать по-разному, и так останется. Чтобы прояснить ситуацию, необходимо разместить скобки.17 сентября 2019 г. . Ответ на некоторые вопросы проверки фактов из Нью-Йорк Таймс. Я ответил: Резюме: -------------------------------------------------- ------------------------------------------ На вопрос 8/2 (2 + 2) есть разные ответы в зависимости от используемого правила. Его можно интерпретировать как (8 / (2 (2 + 2))) = 1 или (8/2) (2 + 2) = 16 в зависимости от правило.Общепринятого правила не существует, их несколько: PEMDAS, BEDMAS, PE (MD) AS. Невозможно сказать, что правильно, а что нет. Есть разные правила, приводящие к разным результатам. Выражение не очень хорошо определено. Похоже, что большинство людей естественным образом дают ответ 1 и большинство компьютеры и языки программирования возвращают ответ 16. Чтобы выражение было однозначным, нужно поставить скобки. Лишь сравнительно поздно (около 100 лет назад) стало ясно, что существует двусмысленность.Нет С тех пор был достигнут консенсус, так что нет альтернативы для уточнения выражения. Литература по этому поводу - Флориан Каджори, «История математической записи», Лондон, 1928 год. Н. Дж. Леннес, Относительно порядка операций в алгебре, Amer. Математика. Ежемесячно, 24 1917 -------------------------------------------------- ---------------------------------------------- Вот ответы на ваши вопросы: - Точно сказать, что согласно PEMDAS, «2 + 2» должны быть односторонне первая операция выполнена? Да! Но это не PEMDAS.Операция 2 + 2 выполняется первой, потому что вокруг него были установлены скобки. - Согласно математике нижнего уровня, решение этого уравнения должно быть 16? Нет. Существует правило PEMDAS, которое широко распространено. (дети выучивают «Пожалуйста, извините мою дорогую тетю Салли»), и при их следовании спрашивает делать умножение перед делением. Это дает 8 / (2 (2 + 2)) = 1. Как и сегодня, большинство детей, занимающихся математикой более низкого уровня, также имеют доступ к калькуляторам или онлайн-инструментов, они могут дать ответ 16. Причина утверждения, что это часть математики нижнего уровня, вероятно, то, что большинство учителей теперь используют калькулятор для проверки вещи, и компьютер сообщает им, что ответ - 16.Как студенты и их родители получают разные результаты (если они не используют компьютер) есть разногласия. - Справедливо сказать, что в алгебре или высшей математике операция 2 (4) имеет приоритет? Нет. Также здесь это зависит от используемого правила. Если использовать PEMDAS по назначению, то ответ - 1, что означает сначала вычислить 2 (2 + 2), поскольку M стоит перед D. Вопрос не в том, какой уровень или предмет использовать. Ответ зависит от того, какой правило используется. - Согласно высшим математическим стандартам, решение этого уравнения 1? Нет.Также это зависит от используемого правила. При проведении теста со студентами большинство дает ответ 1. На самом деле, большинство людей дают ответ 1, если они не используют компьютер. Большинство людей читают такие выражения, как 1. Однако компьютеры, которые относятся к умножению и деление часто находится на одном уровне и почти всегда дает ответ 16. В 2014 году я спросил у поступающих первокурсников (еще не старших математиков) во вступлении курс исчисления и все, кроме одного, использовали правило PEMDAS. Большинство людей отвечает 1. - В статье утверждается, что способ написания этого математического выражения вводит в заблуждение.Вы согласны с этим утверждением? Нет. Это не вводит в заблуждение, это неоднозначно. Было бы заблуждением, если бы правильный ответ, и выражение приведет к неправильному ответу. Это не тот случай. Нет правильного или неправильного ответа. Выражение неоднозначно и зависит от правило, которое используется. - Справедливо сказать, что по мере того, как человек переходит на более высокий уровень математики (уровень после начальной школы), деление вообще обозначается как дробь? Нет. В высшей математике используются все виды выражений.Разделение на математику более низкого уровня и математика более высокого уровня менее важна (по моему опыту) чем вычислить, как человек читает математику естественно (и большинство учебников это делают) или если вычислить выражение на компьютере. Это может быть психологическое, это может быть быть лингвистом, это может быть благодаря тому, что его так учат, это может быть чтение текстов, но большинство людей умножение перед делением в ситуациях, подобных рассмотренной. - Как бы записать это уравнение в дробной форме? В недвусмысленных выражениях используются скобки типа 8 / (2 (2 + 2)). Другая возможность - использовать выражение 8 ---------------- 2 (2 + 2) Это дает 1.При этом важно, чтобы была четкая длинная линия деления дроби, убедившись, что 2 (2 + 2) сделано до разделения. Другая версия была бы (8/2) (2 + 2), что дает ответ 16, как и большинство компьютеров.2 ноября 2019 г.: На этом сайте есть онлайн-калькулятор упоминание BODMAS BODMAS также является аббревиатурой от Bracket, Order / Of, Деление, умножение, сложение и вычитание. Веб-сайт и калькулятор полностью упускают из виду суть определения выражений. что можно понимать по-разному.Тем более, что сайт называется Калькулятор PEMDAS предполагает использование правила PEMDAS, в котором умножение перед сложением. Таким образом, калькулятор оценивает 2 * 9/3 * 2-1 как 11, как и большинство калькуляторов или программистов. языки делают, но это отличается от того, что на самом деле предлагает PEMDAS (2 * 9) / (3 * 2) — 1 = 2 и которые большинство людей оценивают, когда их спрашивают. Итак, калькулятор, а не помогает чтобы прояснить присутствующую двусмысленность, это просто калькулятор. Есть современные калькуляторы, которые предупреждают учащегося о том, что выражение неоднозначно и заключено в круглые скобки, поэтому что пользователь может, если эти круглые скобки не то, что имелось в виду, может их изменить. 6 апреля 2020 г. Другой вопрос: Надеюсь, что все в порядке, я напишу тебе письмо. Я наткнулся на вашу страницу во время дебаты по проблеме Facebook. Я в отпуске, так что у меня много времени в моих руках. Эта версия была 6/2 (1 + 2). Мне ответ на выше - 1 и только 1. Но я не хотел спорить с этим. Я хотел добавить что-то, чего я не видел на вашем сайте, что, по-моему, обсуждается больше промахов PEMDAS. Математику часто называют универсальным языком. Это позволяет общаться людям из разных культур.Когда вы читаете первый пример 2x / 3y - 1, когда x = 9 и y = 2, как вы это читаете? Ты прочитать два раза x разделить на три раза y минус один? Ты читаешь это два x больше трех y минус один? Подобно тому, как в английском языке есть правила, в математике тоже есть правила. Английский не идеален и не всегда следует правила. Математика такая же. Иногда умножение и группирование могут подразумевается.Мой ответ: да, математика - универсальный язык, позволяющий общаться между разные культуры.Но языки также были созданы людьми и не всегда идеальны. Двусмысленность PEMDAS на самом деле просто упущение дизайна. Не было авторитета, который раз и навсегда сказал бы, что это это необходимо указать. Причина исторически ясна. Только один осознал проблему слишком поздно. Вы говорите, что для вас 6/2 (1 + 2) равно 1, да, почти все люди предполагают это. Если вы отдадите его компьютеру, это дает вам 9, почти все языки программирования. Да вроде английский, В математике есть правила. Но они далеки от совершенства.Языки меняются и со временем совершенствоваться. В ходе обсуждения PEMDAS выяснилось, что слишком поздно принимать правила. Некоторые пробовали, и многие из них фанатичны и думают, что их путь правильный. Например, в случае 6/2 (1 + 2) мы видим сторонников (например, на YouTube), которые спорят, только 9 - правильный ответ. Но, как вы говорите, читать это как 6/2 (1 + 2) - это укоренились и изменились, что многих расстроило бы. Последние несколько слайдов в эта презентация [PDF] немного показывает, что говорят лингвисты. На самом деле это не математическая проблема, это лингвистическая проблема.То, что хорошо об обсуждении заключается в том, что теперь все учителя и ученики знают о двусмысленность и запишите уточненные выражения. 9 апреля 2020 г. Из другого электронного письма: Я не математик. STEM всегда был моей сильной стороной, но Я предпочитаю применение теории, поэтому я техник по оборудованию в полупроводниковой промышленности (я чиню роботов, которые делают компьютер фишки). Я упоминаю об этом, чтобы сказать, что я, возможно, не эксперт, но и не мирянин.Мой первый опыт с этим вопросом возник, когда я пытался для программирования квадратной формулы в моем калькуляторе TI-83 + почти 20 много лет назад. Чтобы уравнение работало правильно, дополнительные скобки необходимы. Это потому, что стандартная алгебра обозначена неявным пути, а компьютеры никогда не улавливают подразумеваемых значений или только начинают в последнее время. Об этом говорится в цитируемой вами статье NYT, но это высказанное в некотором смысле я считаю ошибочным. В нем говорится "просто или элементарно" математика 8/2 (4) такая же, как 8/2 * 4, и только в алгебре 8/2 (4) становится 8 / (2 * 4).Калькуляторы подвержены ошибкам, как вы указали на калькулятор MS. решает 1 + 2 * 3 как 9, а не 7, что никогда не бывает правильным. Распределительный закон умножения и деления »доказывает понятие двух правильных ответов недействительным. 8/2 (2 + 2) = 16 - полное нарушение закона распределения, таким образом недействителен. Если уравнение записано (8/2) * (2 + 2), то порядок операции будут диктовать, что деление происходит первым, а затем результат будет распределен во вторых скобках, как если бы он были написаны 8/2 * (2 + 2).Однако в любом уравнении, где написано 8/2 (2 + 2), то неявно (не явно) закон распределения должен применяться как часть круглой скобки до того, как произойдет разделение, в явном виде это будет 8 / (2 * (2 + 2)). Дело в том, что компьютеры (или калькуляторы) не понимают, что мы подразумеваем, не означает значение неверно, это означает, что компьютеры могут понимать только явные инструкции. Явное решение уравнения с подразумеваемыми факторами обычно приводит к неправильному ответу.2-4ac) / 2a, но оба дают совершенно неверные ответы с калькулятора. Очевидно, что квадратичная формула - это константа и не должны получать разные результаты, независимо от того, чему вас учили, это доказывает, что мы должны быть достаточно умными, чтобы правильно пользоваться нашим калькулятором, не то, чтобы калькуляторы безошибочны. Другой пример - уравнение «ab * cd». Решение этого выражения явно бы вы сделали «a * b * c * d = x», когда мы знаем, что это на самом деле (a * b) * (c * d), потому что () подразумеваются, как указано выше. Ваш алгебраический пример использования 2x / 3y-1 глуп.3 как указал Леннес в своей статье 1917 года. Причина 2x / 3y-1 = 11 на калькуляторе, потому что калькулятор не понимает, что неявная группировка. Каждый родитель понимал неявную группировку, что (2x) / (3y) -1 - подразумеваемое уравнение, хотя и не записано явно как такой. Только когда вы введете в калькулятор 2 * 9/3 * 2-1, вы получите 11. Но 2 * 9/3 * 2-1 будет записано как 2 * x / 3 * y-1, что сильно отличается от 2x / 3y-1, но калькулятор считает их одинаковыми. Это было доказано, когда у вас ваш класс по математике сделает это, двое из ваших учеников вбили это в свои калькуляторы, остальные 58 подсчитали правильно.Что это значит - это ты нужно научить этих двух студентов правильно пользоваться калькуляторами, не то чтобы есть некоторая универсальная двусмысленность. При программировании четырехугольной формы вы должны явно заключить в скобки всю неявную группировку, иначе это не сработает, это ограничение программного обеспечения, а не недостаток математики. Если там была ли какая-либо фактическая двусмысленность в результатах вашего класса исчисления были разделены ближе к 50 на 50, статистически очевидно, что устойчивый консенсус среди студентов, изучающих математику, относительно правильного метода.В Учитель математики, получивший 2x / 3y-1 = 11, должен работать в другой области.Мой ответ
13 июля 2020 г. : Учитель средней школы указал мне на статью Переосмысление порядка операций в Журнал «Учитель математики» с октября 2017 года.2 или выражения типа 2x / 3y-1, если x = 9 и y = 2. Кроме того, приведенная выше статья «Переосмысление порядка операций» делает вещи более сбивает с толку. Это другое мнение. Нет необходимости в переосмыслении, если человек остается ясным. Указывая на то, что порядок умножения, деления или возведения в степень должен быть уточнил письменно умнейший больше. Каждый студент должен знать того факта, что такие выражения, как 18/3 * 2, часто оцениваются людьми как 3 (века математических писаний закрепили это), в то время как компьютеры оценивают это как 12.2 оценивается компьютерами справа налево. Также GEMA не дает любые направляющие линии здесь. Он просто остается неоднозначным без дополнительных разъяснение. Никакого «переосмысления» не исправить. Просто используйте скобки и все проблемы решены. 4 августа 2020 г. : Только что дочитали на вашей веб-странице о неоднозначных уравнениях. Каково же мое удивление, узнав, что математическая конвенция не лечит умножение и деление одинаково. Я изучал математику уже 3+ лет (прежде чем прийти в себя) и преподавал на уровне колледжа.(1 / n), x ÷ n = x * (1 / n) и x - n = x + (-n). Однажды они поймали после этого они были поражены тем ловушкам, которых они избегали. Несмотря на это, раскрывая давние соглашения, интересно ... неоднозначность разрешается так, чтобы решение уравнения 8 ÷ 2 (2 + 2) может быть найден? Я должен сказать, что я горячо утверждал, что ответ был 16, хотя я проигнорировал двусмысленность. Прочитав вашу веб-страницу, двусмысленность очевидна. Однако мой брат, инженер на пенсии, Ханиуэлл, чье понимание математики превосходит даже мое собственное, тоже пришло к нам. вверх с ответом 16.Интересно, что его первый инстинктивный ответ был 1. Однако ваша ссылка на ISO 31-0 и ссылка на видео YouTube («ПЕМДАС ошибается») отправил меня в кроличью нору. Между прочим, я обнаружил, что ISO 80000-1 теперь заменяет ISO 31-0, fyi. К несчастью, ISO 80000-1 недоступен бесплатно, поэтому мне пришлось прибегнуть к ISO 31-0. для уточнения. Возможное (?) Решение этого неоднозначного уравнения требует знания правила и условности Я подозреваю, что большинство людей не знают. В частности ... что обелус (÷) нарушает ISO 31-0.-1 " (альтернативно «a * 1 / b»). (товар записывается как "а б", «ab», «a * b» или «a x b». ), что при применении правил AMS и APS, умножение предшествует делению. (что "/ xy" условно математики понимают как "/ (xy)" _ Решение 1: 8 ÷ 2 (2 + 2) = 8/2 (2 + 2) (в соответствии с ISO 31-0) 8/2 (4) (на порядок операций) 8/8 (в соответствии с правилами AMS и APS, которые умножают предшествует делению) 1 Решение 2: 8/2 (2 + 2) можно переписать как 8 / [2 (2 + 2)] [на математическое соглашение о том, что "/ xy" = "/ (xy)", а также из-за сопоставления, посредством чего «2 (2 + 2)» можно было бы увидеть как «2y», используя замену, и «8 / 2y» = «8 / (2y)»] 8 / [2 (4)] 8/8 1 Многие люди заявляют, что проблема связана с лингвистикой и / или грамматикой.я видят в этом проблему перевода и что это входит в компетенцию математик, чтобы перевести задачу на общий язык. это аналогично тому, как иммигрант впервые слышит разговорный язык. Это напоминает мне русского комика Якова Смирнова, который немного где он говорил о странных идиомах. Он слышал, как кто-то сказал, что бросили курить холодная индейка. Он сказал: "Что ты куришь сейчас, ветчина?" Итак, я теперь считаю, что математик, применяющий международные стандарты, а также соглашения AMS, могут переводить уравнение и разрешить двусмысленность.Что вы думаете? Моя логика верна? -------------------------------------------------- ----------------- Мой ответ: Ваш пример - типичный пример, когда люди и машины получают разные вещи. Если скармливать в компьютер, получается 16 [knill @ knill11:] математика Ядро Mathematica 12.1.1 для Linux x86 (64-бит) Авторские права 1988-2020 Wolfram Research, Inc. В [1]: = 8/2 (2 + 2) Из [1] = 16 Я думаю, что большинство людей получают 1 из-за обучения, PEMDAS и потому, что по математике и физическая литература, есть неявное предположение, что 2 (2 + 2) вместе сначала особенно с обелусом.Двусмысленность не может быть решена путем поиска правил, руководств AMS или стандартов ISO (особенно если они не доступны в открытом доступе) это факт (и вы подтверждаете что), что мы можем получить разные ответы. Многие люди в Интернете пытаются рассуждают так или иначе. Это бесполезно. Чем это поможет, если 99 из люди рассуждают так, а 99 компьютеров дают ответы на другие вопросы? Да, и обелус даже немного запутывает, как вы указываете. Там нет логического способа решить двусмысленность.Это определение неоднозначно. Нет четкого стандарта, и если он будет, то он еще не принят. повсеместно. Единственный способ решить проблему - поставить скобки. 8 августа 2020 г. : проницательный комментарий Элиаса Мартенсона от Швеция: Я читал вашу статью о порядке операций, или как вы это называете «правило PEMDAS». Одна вещь, которая, если упомянуть, не сразу очевидна, - это то, что когда вы говорите, что «правилу пемдаса научили миллионы студентов», вы конкретно имеете в виду студентов в США.Меня учили математике в Швеции, и там нас учили, что есть три уровня приоритета: Возведение в степень Умножение и деление Сложение и вычитание Скобки на самом деле не упоминаются, потому что здесь нет двусмысленности. Кроме того, чтобы объяснить, что их можно использовать , чтобы переопределить правила по умолчанию. Сейчас я живу в Сингапуре, и мои дети ходят здесь в местную школу. я просто проверил с ними, и они действительно узнали так же, как я учили. На всех языках программирования, которые я знаю, а также на математических Программное обеспечение, которое я тестировал, отмечу, что они следуют именно этому правилу.Правило "PEMDAS" кажется способом превратить что-то довольно тривиальное в что-то сложное. В дополнение к этому, он также преподает это неправильно, так как если кто-то настаивает на его использовании, ему придется написать что-то вроде: PE [M / D] [A / S], чтобы уточнить эквивалентность в группы. Простое прочтение этого документа создает у студента впечатление, что умножение должно как-то выполняться перед делением во всех случаях, что редко бывает правдой. Я говорю «редко» здесь, потому что я согласен с вами в том, что, безусловно, есть случаях имеет смысл сначала выполнить умножение, например, ваш пример 1 / ху.Тем не менее, если вы напишете это как 1 / x y, это не так ясно anymore, что означает, что пробелы значительны. Как инженер-программист, который в свободное время изучает физику], я часто раздражают нечеткие обозначения в математике. Не только проблемы с горизонтальным написанием (как тема вашей статьи), но также правильным набирать уравнения с помощью LaTeX. Авторы склонны использовать сокращенные обозначения, повторно использовать символы и т. д., что означает, что вы должны иметь в виду контекст, когда выясняя, что происходит.Это тип проблемы, с которой я бы столкнулся надеялись, были ограничены областью лингвистики, а не математики, единственная научная область, где что-то можно доказать с уверенностью. Наконец, я хотел бы добавить, что причина, по которой я потратил слишком много времени думаю об этом, потому что я работал над новым интерфейсом для Maxima (символьная математическая система), которая представляет собой программную формы в математической записи, а это значит, что я должен полностью однозначный. Если вам интересно, вот демонстрационное видео.Мой ответ:
спасибо за содержательные комментарии. Для меня это похоже, из Швейцарии,
где нас не учили явному правилу PEMDAS. Тем не менее, я бы все равно
утверждают, что миллионы людей были обучены PEMDAS. Я со всем согласен.
Особенно при работе с математическим программным обеспечением
потребность в точности и недвусмысленности становится все более важной.
Тема не только педагогическая, здесь можно сделать серьезные ошибки. Не только
делать неправильные вычисления, но также используя результаты, которые были
сказано неоднозначно.Было бы интересно узнать, сколько
студенты в Сингапуре или Швеции читают, скажем, 8/2 (2 + 2) как 16 и как
многие прочитали бы это как 1, особенно если разделение дано как обелус. я
предсказал бы, что большинство из них дадут ответ 1. Это потому, что я учу
часто студенты со всех концов света (Этим летом также двое из Сингапура
кстати) и что вопросы о PEMDAS часто всплывают, если не
супер четкость при написании (даже при написании выражений типа 1 / x + 3 есть
все еще студенты, которые читают это как 1 / (x + 3) или сбиты с толку и спрашивают.я начал
чтобы даже прояснить такие вещи, написав (1 / x) + 3 или используя горизонтальный
обозначение дробей \ frac {1} {x}, чтобы убедиться, что оно правильно прочитано.
Добавлено 24 августа, 2020 : Добрый день! Надеюсь, у тебя все хорошо. Совсем недавно у нас с коллегами было несколько жарких споров. о проблеме 8 ÷ 2 (2 + 2) или тому подобное. Как и следовало ожидать, есть люди, которые отвечают это как 16, а люди, которые отвечают на это как 1. Что касается нас, мы находимся в неоднозначный стан.Люди, у которых был уникальный ответ на проблему, продолжают цитировать PEMDAS, или BEDMAS, или PE (MD) (AS). И мы сказали им, что условность не универсальна. Итак, мы попытались найти документы чтобы поддержать нашу сторону. И вот мы нашли вашу статью. я прочел все. Я поражен тем, что вы так терпеливо отвечаете людям, которые отправляют вам электронные письма и дают им одинаковые ответы, повторяя ваши объяснения снова и снова. Во всяком случае, я только что написал вам по электронной почте, чтобы вы знали (на случай, если вы еще не видел) Раздел 7.1.3, стр.23 ISO 80000-1: 2009 "
Кроме того, пример 1, следующий за абзацем, должен разрешить все эти споры. Спасибо, что нашли время прочитать мое письмо.Мой ответ Большое спасибо за отзыв. Ссылка ISO очень ценна! На это указывалось ранее, но, к сожалению, эта часть ISO не является общедоступной. Нужно купить стандартный.У меня действительно был доступ к соответствующие страницы из Раздела 7.1.3 ISO 80000-1: 2009: Добавлено 16 января 2021 г. : Электронная почта:
После бурного онлайн-обсуждения меня перенаправили на ваш сайт
http: // люди.math.harvard.edu/~knill/pedagogy/ambiguity/index.html.
Судя по тому, что я там читал, вы, кажется, вините путаницу в использованных
обозначение. Хотя я согласен с тем, что это может сбить с толку людей, я хотел бы
представить более универсальное объяснение этой проблемы, основанное на использовании
(или не используя) простые аксиомы алгебраических структур. Обозначения тогда
становится более или менее неуместным.
У данного уравнения 6: 2 (2 + 1) есть несколько ответов, которые
на первый взгляд кажется нелогичным. Но я думаю, что некоторые люди просто забывают
чтобы определиться с набором определений, над которыми они работают.С простым
арифметика, умножение и деление одинаково упорядочены и имеют
просто для выполнения перед сложением / вычитанием, но после вычисления
скобки и показатели. Вот где появляются PEMDAS или другие мнемоники
из. Это работает слева направо и правильно само по себе
простой контекст. Калькуляторы последовательного ввода делают это таким образом.
Но если принять контекст формальных алгебраических структур, в
В этом случае поле рациональных чисел, применяются дополнительные аксиомы. Теперь,
«распределенность» и «ассоциативность сложения и умножения»
(среди прочего) определены как основные аксиомы в контексте этой области.При этом порядок операций теперь гораздо более ограничен теми, кто
характеристики.
В этом контексте уравнение 6: 2 (2 + 1) можно преобразовать следующим образом:
6: 2 (2 + 1) = 6: (2 + 1) 2 // Ассоциативное свойство умножения
(просто чтобы доказать свою точку зрения с помощью этой аксиомы поля): ab = ba; разделение
неассоциативен
= 6: (4 + 2) // Распределительное свойство: ab + ac = a (b + c)
= 6: 6 // Порядок операций (теперь тривиальный),
"скобки перед показателями перед умножением / делением перед
сложение / вычитание "
= 1
Соблюдая все аксиомы полевой структуры, разделение теперь должно быть
решается путем вычисления сначала делимого и стороны делителя отдельно, затем
частное.Любой другой способ нарушает одну из основных аксиом поля и
будет недействительным с точки зрения этого поля. Более сложные калькуляторы
запрограммированы уважать это.
Однако, если не ограничиваться контекстом этих аксиом, другие результаты
также может быть действительным (т.е. 6: 2 (2 + 1) = 9, с последовательным вычислением на
базовый арифметический уровень).
Так что, на мой взгляд, проблема не в нотации, а в предоставлении контекста.
и, таким образом, определяющие аксиомы. Знание используемых инструментов и их предположений
соответствующие способности / ограничения - как всегда - важны.Кстати, в Германии студенты изучают мнемонику «KLAPPS» (KLAmmer,
Potenz, Punkt, Strich) перед высшей алгеброй, которая, к счастью, игнорирует
любое предлагаемое предпочтение умножения / деления ("Punktrechnung"
= "точечные вычисления" на основе "точечных" символов, используемых в немецком языке
вычисление '.' = Unicode U + 22C5 для умножения и ':' для деления)
и сложение / вычитание ("Strichrechnung" = "вычисления строк", из
символы «линия / перечеркнутая линия» '+' и '-'). Это отсутствие последовательности
предложение, кажется, предотвращает путаницу в высших классах, по крайней мере,
немного.Большое спасибо за то, что уделили время, прочитав это. Я был бы признателен услышать
от вас, особенно если вы не согласны с моими выводами. Математика
конечно не моя сильная сторона, но я просто учусь этому снова
с домашним обучением моего сына (благодаря карантину COVID19) и
до сих пор помню некоторые из моих прежних лекций по информатике и математике
давно.
С наилучшими пожеланиями из Баварии / Германии! Бернхард Новотны, M.Eng.
Мой ответ:Это интересный ракурс. Мне особенно приятно слышать о немецкое правило KLAPPS.Я ходил в школу в Швейцарии и еще не видел это. Правила также должны соблюдаться со студентами, и KLAPPS - это доброе имя. Интересно, что он не решает двусмысленность PAMDAS. Ваше предложение устранить двусмысленность вполне может сработать, но проблема более социолингвистическая, чем математическая. Уже есть разные стандарты вокруг. Я не знаю, как вводить новый XKCD сказал это лучше всего.22 февраля 2021 г .: Вик: Вы писали, что PEMDAS и BODMAS неоднозначны. Я не согласен.У меня есть степень магистра математики и преподаю математику 30 лет. Вы задали вопрос с помощью символа разделения /. Мне кажется, что этот символ разделения сбивает с толку, и я никогда его не использую. Мне интересно, что хотя все калькуляторы дали ответ 11 на ваш начальная проблема вы, кажется, думаете, что они должны что - выдать сообщение об ошибке? Ответ - 11. Здесь нет скобок, и я понятия не имею, почему вы думаете вы можете вставлять скобки волей-неволей. Люди ошибаются, потому что они вычисляют по шаблонам вместо того, чтобы думать «Какие здесь правила».Мой ответ: Спасибо за ответ. Вы, конечно, можете не согласиться. Я дал много причины на моей странице, почему есть двусмысленность. Многие студенты дают ответ 2, а не 11 в исходном примере. Если вы прочитаете мой текст, вы увидите эта двусмысленность не означает наличие сообщения об ошибке. В большинстве случаев, несогласие происходит из-за отсутствия стандарта. Профессиональные ссылки приведенные на моей странице подтверждают, что нет стандарта. Ставить скобки нельзя помещенные «волей-неволей», они размещены, чтобы прояснить ситуацию и устранить двусмысленность.Во время обучения почему бы вам не провести эксперимент и не спросить студентов, что они подумайте, когда им нужно вычислить 2x / 3y -1 для x = 9 и y = 2. Большинство людей дает ответ 2, поскольку они заключают в скобки 3y как неразделимые (довольно много учителей подтвердили который). Это также стандарт, которому следуют многие книги (особенно если они придерживаются к более ранним профессиональным стандартам, таким как AMS, или правилам, таким как PEMDAS, которые часто учили и ставили умножение перед делением. Коджори, сегодня по-прежнему самый Авторский деятель по математической нотации написал еще в 1928 г. "Если арифметический или алгебраический член содержит / и х, в настоящее время нет соглашения о том, какой знак должен использоваться первым. 2.Ты скажем, вы делите торт на 2 человек, имея в виду торт / (2 человека), а не (торт / 2) чел. Часто, особенно для установленных формул, мы естественно берем их вместе. Популярный пример - 1 / 2pi, потому что 2pi часто сам по себе является стандартным устройством. Большинство людей читают это как 1 / (2pi) но компьютер читает это как пи / 2. Бывший 1 / (2pi) соглашается с написанием руководящие стандарты, выдвинутые AMS или APS.Снова Вик: Если 2x / 3y означает 2x / (3y), как нам написать выражение 2 раза x затем разделить на 3, а затем умножить на y?Мой ответ: Пример 2x / 3y - типичный пример, который большинство людей читают как (2x) / (3y).Компьютер читает это как 2xy / 3. Можно написать (2xy) / 3 или (2/3) xy или просто 2xy / 3 если бы кто-то хотел, чтобы это было написано так, как это читает компьютер. Это не является двусмысленным и в целом, и никто не может его неправильно истолковать.23 февраля 2021 года, Джеймс: Мне очень нравится ваша статья (я бы назвал ее так). Это привлекла мое внимание, потому что я начала видеть работы студентов которые вставляют в свои калькуляторы целые выражения, отражающие несоответствия, обсуждаемые в вашей статье.Одна вещь, которую я отмечу, касается примера 18/3 * 2, чтобы в котором вы утверждаете, что большинство людей придут к решению 3, а компьютеры - 12. Сразу после того, как увидели выражение, Я рассчитал, что решением будет 12. Я считаю, что прочитал это. как восемнадцать третей умножить на два. Я списываю это на то, что часто работаю с четвертями, третями и половинами вне работы и, когда я вижу "/" Я сразу думаю о дроби, а не об операции. Более доказательства в поддержку вашего аргумента о двусмысленности в математике и необходимость ясности в выражениях.Еще раз спасибо за приятное чтение. я в предвкушении исследуя остальную часть вашего сайта.Мой ответ: Спасибо за ответ. Да, это очень интересная история. Это кажется, также во многом зависит от того, как это писать. Часто в научная литература (а также некоторые руководства от AMS или APS), указано, что такие вещи, как a / bc, следует читать как a / (bc) а не (a / b) * c. Причина также в том, что часто товары читают люди должны принадлежать друг другу. Если взять 18 / 2π, то большинство людей прочтите это как 9 / π, а не как 9π (как это делает компьютер).Только можно догадываюсь, но я подозреваю, что это было причиной создания PEMDAS (наиболее часто используемое сокращение), а не PEDMAS или PE (MD) AS (которые должны быть со сноской, что MD эквивалентны и читаются слева). Последнему вряд ли можно научить. PEMDAS уже трудно продать (многие студенты Гарварда неправильно понимают базовые PEMDAS и читают + до *. В педагогических вопросах всегда переоценивают то, что сложности, которым люди могут научиться. Устанавливаем новый стандарт, такой как PE (MD) AS (они появляются уже в школах) также имеет проблему, которая многие тексты будут прочитаны неправильно.Если выражение принадлежит друг другу как RT в термодинамике или mc 2 в физике. Вернемся к вашему примеру: 18/3 * 2, да, думаю, многие прочитали бы это как 12, но если вы напишете 18 / ab с a = 3, b = 2, большинство прочитало бы это как 3. Забавно, как по-человечески Здесь сочетаются психология, лингвистика и история, а также математика. Это делает тему такой интересной. 28 февраля 2021 г. : новый хороший пример:
Мой ответ: Спасибо. Это очень ценно, потому что это подтверждает, что единственный способ избежать таких обсуждений - это быть предельно ясным и добавить кронштейны. Добавил в коллекцию.Хорошо то, что все в вашей группе учителей правы. Есть веские аргументы в пользу группы 2c вместе, потому что это часто используется в литературе, там являются вескими аргументами в пользу разделения в первую очередь, потому что это то, что большинство компьютеров делать. Кроме того, есть веские аргументы в пользу того, что оба правы. Но кто когда-нибудь выиграет аргумент все равно столкнется с дилеммой оценить это ... буря расстроенных учеников, родителей и других учителей. Я просто буду охватываю алгебру в моем учебном курсе по математике и могу упомянуть об этом 4 марта 2021 г. : обсуждения в социальных сетях, похоже, все еще продолжаются: Я получил следующее электронное письмо: Мне было интересно узнать об этом уравнении.2. Если это так, ПЕМДАС ГОВОРИТ «Экспоненты» - 2-е место. Так что мой вопрос действительно в том, что экспоненты также являются формой умножения, так почему это теперь M такое же, как D в уравнении, где теперь он заменен на PE (M или D слева направо) (A или S слева направо)? В мои математические годы умножение в-третьих, потому что экспонента и умножение одинаковы. Также когда мы упрощать 6/9 упрощается как 2 (3) / 3 (3), мы не можем упростить это как ответ 6, когда должно быть 2/3. Вот новинка в социальных сетях: 24/4 (8/4) и мой ответ = 3.Некоторые говорят, что это 12. После того, что я объяснил над. Какой твой ответ? Заранее спасибо.Мой ответ: Корпус 6/2 (1 + 2) теперь классический. Большинство людей получают 1. Это не потому, что это целое число, но потому что 2 (1 + 2) рассматривается как единица. Наиболее компьютеры получают 9, потому что (M и D) оцениваются на одном уровне. Новых 24/4 (8/4) не видел. У вас есть 3, что получает большинство людей. Миллионы из них, потому что это закреплено в правилах PEMDAS (M перед D) и потому, что это часто пишется в книгах как таковых.Большинство компьютеров получают 12. Здесь нет правильного или неправильного ответа. Вопрос только что поставлен неоднозначно. Это известно уже 100 лет. это Интересно, что соцсети до сих пор об этом говорят. Но это делает это интересно и осведомленно. Я написал краткое резюме с источниками в этот документ для курса, который я преподаю прямо сейчасОчевидно, что на гораздо более базовом уровне все неясно. Следующее электронное письмо иллюстрирует замешательство, которое может возникнуть даже у звездных студентов. Кажется, сложно даже достать через фундаментальные свойства PEMDAS, такие как возведение в степень перед умножением и разделение и скобка, перед которыми не оспариваются.2 = 1, то это однозначно, поскольку возведение в степень предшествует другим операциям. Если написать 9/3 (3), то это неоднозначно, потому что его можно прочитать как (9/3) (3) = 3 * 3 = 9 или 9 / (3 (3)) = 9/9 = 1. Случай 6/1 (1 + 2) — неоднозначный случай, потому что его можно читать как (6/1) (1 + 2) = 18 или 6 / (1 (1 + 2)) = 2. Это та ситуация, о которой мы говорили. Нет, 6 / (1 + 2) не является неоднозначным. Ясно, что 6/3 = 2. Нет обсуждения об этом случае, потому что скобки сделаны раньше. 13 марта 2021 г .:
По профессии я технический писатель, поэтому лаконичное, точное общение - это то,
моей страсти.Я также изучал математику в бакалавриате, так что это
обсуждение было прямо моим союзником. Спасибо за поддержку этой страницы. Это было приятное путешествие.
Как упоминалось в одном из рассылочных писем, где это возможно, я предпочитаю наборные движки, например Латекс.
Почему бы никому не написать $ \ frac {2x} {3y} - 1 $ (или что-то подобное), если бы они
наличие выбора утомительно для меня, но это часть философии моей профессии.
Я беру время и когнитивные усилия, чтобы четко объяснить что-то, чтобы свести к минимуму
усилия, которые читатели должны приложить, чтобы понять это.В отдельном электронном письме упоминалось использование знака деления или обелуса: (LaTeX: $ \ div $),
что заставило меня понять, что я не оцениваю и / так же. Назначаю разные психические
вероятности к разным интерпретациям. Если бы мне вручили документ,
содержит ab (c), я бы сначала проклял автора и начал поиск контекстных подсказок. Если я
не нашли никаких подсказок, я бы отметил, что они нашли время, чтобы использовать персонажа вне основного
Набор ASCII. Это говорит мне, что они, возможно, а может быть, намеренно избегали
пресловутый, очевидно неоднозначный слэш.Поэтому я думаю: «Что будет наиболее распространенным,
Самая ленивая интерпретация этого уравнения была бы, если бы автор использовал косую черту? "
Вероятно, это то толкование, которого они пытались избежать.
Иногда мне доступен один кусочек контекста, когда я могу решить, сколько усилий они приложили.
чтобы избежать косой черты, это то, какое устройство они используют. Ввод текста в macOS
тривиально (Alt + /), но для набора текста на iPhone требуется либо копирование и вставка, либо
переход на отдельную клавиатуру стороннего производителя.
Так что это мой вклад! Это больше ориентированный на поведение подход: количество усилий, которые он
потребовалось, чтобы автор напечатал что-то, что могло бы предложить их предполагаемое значение.С уважением,
Ник
Мой ответ:
Привет, Ник,
приятные моменты. Для меня также это то, что когда я пишу латексные формулы
в тексте и не отображается, я склонен использовать a / bc вместо \ frac {a} {bc}
потому что он лучше вписывается в страницу. Поскольку я знаю об этих войнах PEMDAS, я
Я больше не сомневаюсь в том, чтобы жертвовать красотой, если она может повысить ясность. Этот
для меня как учителя особенно важно на экзаменах.
Повсюду используются знак деления, обелус и косая черта. Я также узнал,
особенно от учителей, что для них обелус используется иначе и
что это более сильное подразделение.Я сам стараюсь избегать обелуса.
Я знаю только, что видел это в начальной школе и не прикасался к нему
поскольку.
Да, ясность требует некоторых усилий, иногда также требуется жертва некоторых
элегантность. Но мы знаем это и по языку. Есть много выражений
которые становятся понятными только в контексте. Ответ однозначно - избыточность.
Даже язык нашего генома использует избыточность, чтобы избежать
ошибки связи.
Оливер
Родившихся любопытных: 20 девочек, которые выросли выдающимися учеными (в твердом переплете)19 долларов.99 Просрочено (при необходимости в ближайшее время, напишите по электронной почте или позвоните, чтобы проверить наличие) Описание«Вдохновляющий взгляд на женщин, которые реализовали любопытство плюс упорство, равный успеху». — Kirkus Reviews «[A] увлекательный сборник.» — Publishers Weekly Откройте для себя истории двадцати невероятных женщин-ученых в этом вдохновляющем сборнике биографий любимого автора Марты Фриман и рисовальщика Google Кэти Ву. Почему галактики так вращаются? Ученые и математики из Born Curious искали ответы на эти и многие другие увлекательные вопросы. И нам повезло, что они это сделали. Без их видения, понимания, и упорный труд, мир был бы хуже, грязнее и более опасное место. Двадцать новаторских женщин, в том числе Розалинда Франклин, Мари Тарп, Ширли Энн Джексон и многие другие, происходили из самых разных слоев общества и имели разный жизненный опыт.Некоторые выросли богатыми. Некоторые выросли в бедности. Некоторые всегда были самыми умными учениками в классе. Некоторые изо всех сил пытались хорошо учиться в школе. Но у всех было одно общее: они родились любопытными. Тебе тоже любопытно? Читай дальше. Об автореМарта Фриман работала репортером и учителем, прежде чем стать штатным автором книг для юных читателей, в том числе номинированных на премию Эдгара Zap! , Born Curious , The Secret Cookie Club series, Кто украл Хэллоуин? и У Эффи Старр Зук есть еще один вопрос , который журнал School Library Journal назвал «доступным и захватывающим» в помеченном звездочкой обзоре.Она также сотрудничала с астронавтом НАСА Марком Келли над книгами Astrotwins. Марта живет в Колорадо. Узнайте больше на MarthaFreeman.com. Кэти Ву работала в индустрии анимационных фильмов в качестве художника-эскиза и помощника арт-директора, а также в индустрии высоких технологий в качестве рисовальщика для Google (создавая художественные работы и короткометражные фильмы, представленные на целевой странице Google), где она создал Google «Дудлы» для Нелли Блай и Нельсона Манделы. Кэти в настоящее время работает внештатным арт-директором и дизайнером в различных анимационных проектах.Она проиллюстрировала множество научно-популярных книг для юных читателей, в том числе Dumpling Dreams Кэрри Кликкард и Born Curious Марты Фриман. Узнайте больше на KatyCWWU.Tumblr.com. Похвала за…Коллективная биография 20 женщин-новаторов в науке. В хронологическом порядке сборник начинается с Эллен Суоллоу Ричардс, белого геохимика 1842 года рождения, которая не только стала первой женщиной, получившей степень по химии в США.С., но использовала свои исследования в области питания, санитарии и здоровья для разработки первой программы школьных обедов и первых стандартов качества воды в стране. Некоторые женщины, которые следят за ней, такие как Сильвия Эрл, могут быть узнаваемы, но большинство из них будут новыми для читателей. Каждый профиль начинается с анекдота, описывающего влияние детства ученого в настоящем времени, а затем переход к прошедшему времени, чтобы сосредоточиться на ее профессиональных достижениях и влиянии на науку. Профиль также сопровождается портретом на всю страницу с ключами к пониманию интересов каждой женщины и заключительным обзором ее основных достижений, рефлексивной цитатой и «увлекательным фактом».Фриман стремится к разнообразию как в охвате дисциплин, так и в самих ученых, среди которых китайский фармаколог Ту Юю, афроамериканский физик Ширли Энн Джексон и колумбийский геолог Адриана Окампо. Хотя тематический акцент, как следует из названия, сделан на любопытстве, которое побудило каждую женщину заниматься наукой, в профилях также подчеркивается роль неудач, сыгранных на их пути, и то, как они преодолели такие проблемы, как сексизм, расизм, болезни и неспособность достичь свои цели.Воодушевляющий взгляд на женщин, которые реализовали любопытство плюс упорство, равняются успеху. (послесловие, глоссарий, примечания к источникам) (Коллективная биография. 8-12) — Обзоры Киркуса ФРИМАН, Марта. Рожденные любопытными: 20 девушек, которые выросли выдающимися учеными. иллю. пользователя Katy Wu. 128стр. S. & S./Paula Wiseman Bks. Февраль 2020 г. 19,99 трлн. Долларов. ISBN 9781534421530. Gr 3-5 – Freeman делится 20 краткими биографиями женщин-ученых — от геологов и молекулярных биологов до математиков и всех других дисциплин.Автор находит общую нить между всеми ними: они родились любопытными. Но просто родиться любопытным было недостаточно. Этим ученым пришлось преодолевать препятствия и проблемы. Каждая женщина сталкивалась с социальными барьерами, которые могли помешать учебе. Геохимик Эллен Суоллоу Ричардс (1842–1911) преодолела бедность и сексизм. Физик Ширли Энн Джексон (родилась в 1946 году) была первой афроамериканкой, получившей докторскую степень в Массачусетском технологическом институте (MIT). Во время учебы в Массачусетском технологическом институте Джексон основала Союз чернокожих студентов и стала ярым сторонником равного образования, которое продолжает определять работу ее жизни.Биография иранского математика и профессора Марьям Мирзахани (1977–2017) освещает борьбу за выживание в войне и жизнь со смертельной болезнью. |

