Самостоятельные работы по геометрии. 10 класс | Материал по геометрии (10 класс):
Урок № 3 Геом. 10кл.
На дом:
1. Прямые a и b пересекаются в точке О, , , . Докажите, что прямые а и b и точка Р лежат в одной плоскости.
2. Плоскость содержит точки А, В, С, D, но не содержит точку М. Постройте точку К – точку пересечения прямой АВ и плоскости МСD. Лежит ли точка К в плоскости ?
Урок № 3 Геом. 10кл.
На дом:
1. Прямые a и b пересекаются в точке О, , , . Докажите, что прямые а и b и точка Р лежат в одной плоскости.
2. Плоскость содержит точки А, В, С, D, но не содержит точку М. Постройте точку К – точку пересечения прямой АВ и плоскости МСD. Лежит ли точка К в плоскости ?
Урок № 3 Геом. 10кл.
На дом:
1. Прямые a и b пересекаются в точке О, , , . Докажите, что прямые а и b и точка Р лежат в одной плоскости.
2. Плоскость содержит точки А, В, С, D, но не содержит точку М. Постройте точку К – точку пересечения прямой АВ и плоскости МСD. Лежит ли точка К в плоскости ?
Постройте точку К – точку пересечения прямой АВ и плоскости МСD. Лежит ли точка К в плоскости ?
Урок № 3 Геом. 10кл.
На дом:
1. Прямые a и b пересекаются в точке О, , , . Докажите, что прямые а и b и точка Р лежат в одной плоскости.
2. Плоскость содержит точки А, В, С, D, но не содержит точку М. Постройте точку К – точку пересечения прямой АВ и плоскости МСD. Лежит ли точка К в плоскости ?
Урок № 3 Геом. 10кл.
На дом:
1. Прямые a и b пересекаются в точке О, , , . Докажите, что прямые а и b и точка Р лежат в одной плоскости.
2. Плоскость содержит точки А, В, С, D, но не содержит точку М. Постройте точку К – точку пересечения прямой АВ и плоскости МСD. Лежит ли точка К в плоскости ?
Урок № 3 Геом. 10кл.
На дом:
1. Прямые a и b пересекаются в точке О, , , . Докажите, что прямые а и b и точка Р лежат в одной плоскости.
2. Плоскость содержит точки А, В, С, D, но не содержит точку М. Постройте точку К – точку пересечения прямой АВ и плоскости МСD. Лежит ли точка К в плоскости ?
Постройте точку К – точку пересечения прямой АВ и плоскости МСD. Лежит ли точка К в плоскости ?
Урок № 3 Геом. 10кл.
Математический диктант
Вариант I
1. Как называется раздел геометрии, изучающий фигуры в пространстве?
2. Назовите основные фигуры в пространстве.
3. Как называется раздел геометрии, изучающий фигуры в плоскости?
4. Сформулируйте аксиому А1.
5. Сформулируйте аксиому А3.
6. Сколько плоскостей можно провести через две точки?
7. Могут ли прямая и плоскость иметь лишь две общие точки?
Урок № 3 Геом. 10кл.
Математический диктант
Вариант II
1. Как называется раздел геометрии, изучающий фигуры на плоскости?
2. Как называется раздел геометрии, изучающий фигуры в пространстве?
3. Назовите основные фигуры в пространстве.
4. Сформулируйте аксиому А2.
5. Сколько плоскостей можно провести через прямую и не лежащую на ней точку?
6. Сколько плоскостей проходит через одну прямую?
7. Сколько может быть общих точек у прямой и плоскости?
Сколько может быть общих точек у прямой и плоскости?
Урок № 3 Геом. 10кл.
Математический диктант
Вариант I
1. Как называется раздел геометрии, изучающий фигуры в пространстве?
2. Назовите основные фигуры в пространстве.
3. Как называется раздел геометрии, изучающий фигуры в плоскости?
4. Сформулируйте аксиому А1.
5. Сформулируйте аксиому А3.
6. Сколько плоскостей можно провести через две точки?
7. Могут ли прямая и плоскость иметь лишь две общие точки?
Урок № 3 Геом. 10кл.
Математический диктант
Вариант II
1. Как называется раздел геометрии, изучающий фигуры на плоскости?
2. Как называется раздел геометрии, изучающий фигуры в пространстве?
3. Назовите основные фигуры в пространстве.
4. Сформулируйте аксиому А2.
5. Сколько плоскостей можно провести через прямую и не лежащую на ней точку?
6. Сколько плоскостей проходит через одну прямую?
7. Сколько может быть общих точек у прямой и плоскости?
Сколько может быть общих точек у прямой и плоскости?
Урок № 5 Геом. 10кл.
Самостоятельная работа
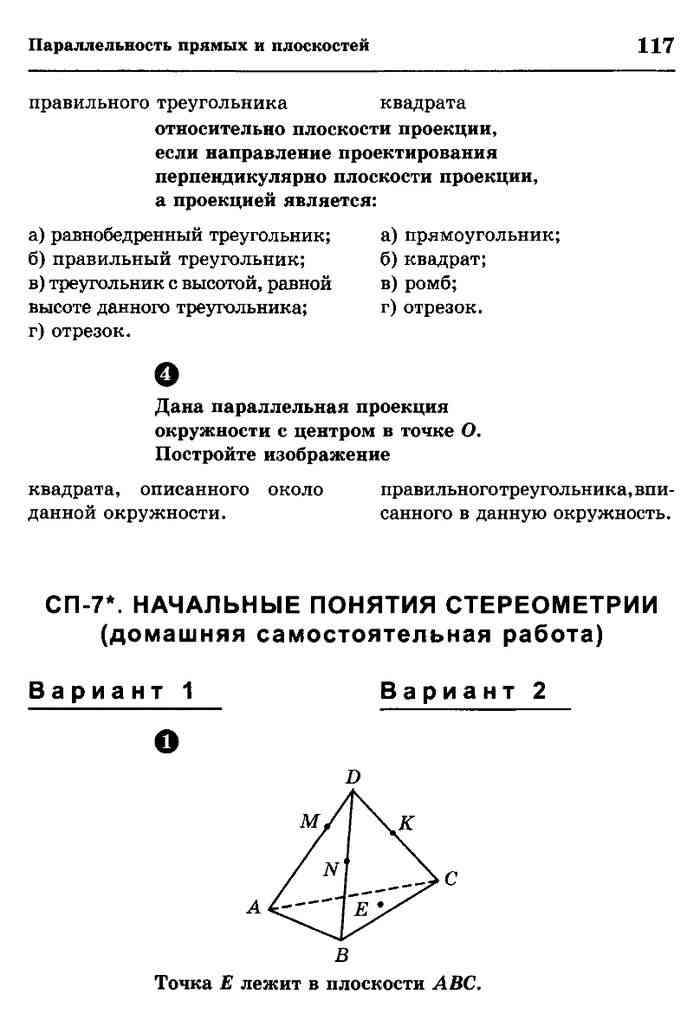
S 1. Пользуясь данным рисунком, назовите:
а) четыре точки, лежащие в плоскости SAB;
б) плоскость, в которой лежит прямая MN;
K C в) прямую, по которой пересекаются плос-
кости SAC и SBC;
A г) четыре точки, лежащие в плоскости АВС
N д) плоскость, в которой лежит прямая KN;
M е) прямую, по которой пересекаются плос-
B кости SAC и CAB.
2. Точка С – общая точка плоскости и . Прямая проходит через точку С. Верно ли, что плоскости и пересекаются по прямой с? Ответ объясните.
3. Плоскости и имеют три общие точки. Верно ли, что эти плоскости совпадают? Ответ обоснуйте.
4. Через прямую а и точку А можно провести две различные плоскости. Каково взаимное расположение прямой а и точки А? Ответ объясните.
5. Через А, В и С можно провести две различные плоскости. Каково взаимное расположение точек А, В и С? Ответ обоснуйте.
Урок № 5 Геом. 10кл.
Самостоятельная работа
S 1. Пользуясь данным рисунком, назовите:
а) четыре точки, лежащие в плоскости SAB;
б) плоскость, в которой лежит прямая MN;
K C в) прямую, по которой пересекаются плос-
кости SAC и SBC;
A г) четыре точки, лежащие в плоскости АВС
N д) плоскость, в которой лежит прямая KN;
M е) прямую, по которой пересекаются плос-
B кости SAC и CAB.
2. Точка С – общая точка плоскости и . Прямая проходит через точку С. Верно ли, что плоскости и пересекаются по прямой с? Ответ объясните.
3. Плоскости и имеют три общие точки. Верно ли, что эти плоскости совпадают? Ответ обоснуйте.
4. Через прямую а и точку А можно провести две различные плоскости. Каково взаимное расположение прямой а и точки А? Ответ объясните.
5. Через А, В и С можно провести две различные плоскости. Каково взаимное расположение точек А, В и С? Ответ обоснуйте.
Урок № 7 Геом. 10кл.
Самостоятельная работа
В
С
А А 1. Отрезок АВ не пересекает плоскость α.
Через середину отрезка С и концы отрезка
А и В проведены прямые, параллельные
α между собой и пересекающие плоскость α
в точках А1, В1, С1.
А1 С1 В1 Вычислить длину отрезка СС1, если
АА1 = 5, ВВ1 = 7.
А А 2. Точка М лежит на отрезке АВ. Отрезок
М АВ пересекается с плоскостью α в точке В.
Через А и М проведены параллельные
Прямые, пересекающие α в точках А1 и М1
А1 а) Докажите, что А1, М1 и В лежат на одной
В М1 прямой.
α б) Найдите длину отрезка АВ, если
АА1 : ММ1 = 3 : 2, АМ = 6.
Урок № 7 Геом. 10кл.
Самостоятельная работа
В
С
А А 1. Отрезок АВ не пересекает плоскость α.
Через середину отрезка С и концы отрезка
А и В проведены прямые, параллельные
α между собой и пересекающие плоскость α
в точках А1, В1, С1.
А1 С1 В1 Вычислить длину отрезка СС1, если
АА1 = 5, ВВ1 = 7.
А А 2. Точка М лежит на отрезке АВ. Отрезок
М АВ пересекается с плоскостью α в точке В.
Через А и М проведены параллельные
Прямые, пересекающие α в точках А1 и М1
А1 а) Докажите, что А1, М1 и В лежат на одной
В М1 прямой.
α б) Найдите длину отрезка АВ, если
АА1 : ММ1 = 3 : 2, АМ = 6.
Урок № 7 Геом. 10кл.
Работа в классе
1. Через основание АD трапеции АВСD проведена плоскость .
. Докажите, что прямая, проходящая через середины сторон АВ и СD, параллельна плоскости .
2. Дан ΔВСЕ. Плоскость, параллельная прямой СЕ, пересекает ВЕ
в точке Е1, а ВС – в точке С1.
Найдите ВС1, если С1Е1:СЕ = 3:8., ВС = 28см.
Урок № 7 Геом. 10кл.
Работа в классе
1. Через основание АD трапеции АВСD проведена плоскость .
Через основание АD трапеции АВСD проведена плоскость .
. Докажите, что прямая, проходящая через середины сторон АВ и СD, параллельна плоскости .
2. Дан ΔВСЕ. Плоскость, параллельная прямой СЕ, пересекает ВЕ
в точке Е1, а ВС – в точке С1.
Найдите ВС1, если С1Е1:СЕ = 3:8., ВС = 28см.
Урок № 7 Геом. 10кл.
Работа в классе
1. Через основание АD трапеции АВСD проведена плоскость .
. Докажите, что прямая, проходящая через середины сторон АВ и СD, параллельна плоскости .
2. Дан ΔВСЕ. Плоскость, параллельная прямой СЕ, пересекает ВЕ
в точке Е1, а ВС – в точке С1.
Найдите ВС1, если С1Е1:СЕ = 3:8., ВС = 28см.
Урок № 7 Геом. 10кл.
Работа в классе
1. Через основание АD трапеции АВСD проведена плоскость .
. Докажите, что прямая, проходящая через середины сторон АВ и СD, параллельна плоскости .
2. Дан ΔВСЕ. Плоскость, параллельная прямой СЕ, пересекает ВЕ
в точке Е1, а ВС – в точке С1.
Найдите ВС1, если С1Е1:СЕ = 3:8., ВС = 28см.
Урок № 7 Геом. 10кл.
Работа в классе
1. Через основание АD трапеции АВСD проведена плоскость .
. Докажите, что прямая, проходящая через середины сторон АВ и СD, параллельна плоскости .
2. Дан ΔВСЕ. Плоскость, параллельная прямой СЕ, пересекает ВЕ
в точке Е1, а ВС – в точке С1.
Найдите ВС1, если С1Е1:СЕ = 3:8., ВС = 28см.
Урок № 7 Геом. 10кл.
Работа в классе
1. Через основание АD трапеции АВСD проведена плоскость .
. Докажите, что прямая, проходящая через середины сторон АВ и СD, параллельна плоскости .
2. Дан ΔВСЕ. Плоскость, параллельная прямой СЕ, пересекает ВЕ
в точке Е1, а ВС – в точке С1.
Найдите ВС1, если С1Е1:СЕ = 3:8., ВС = 28см.
Урок № 7 Геом. 10кл.
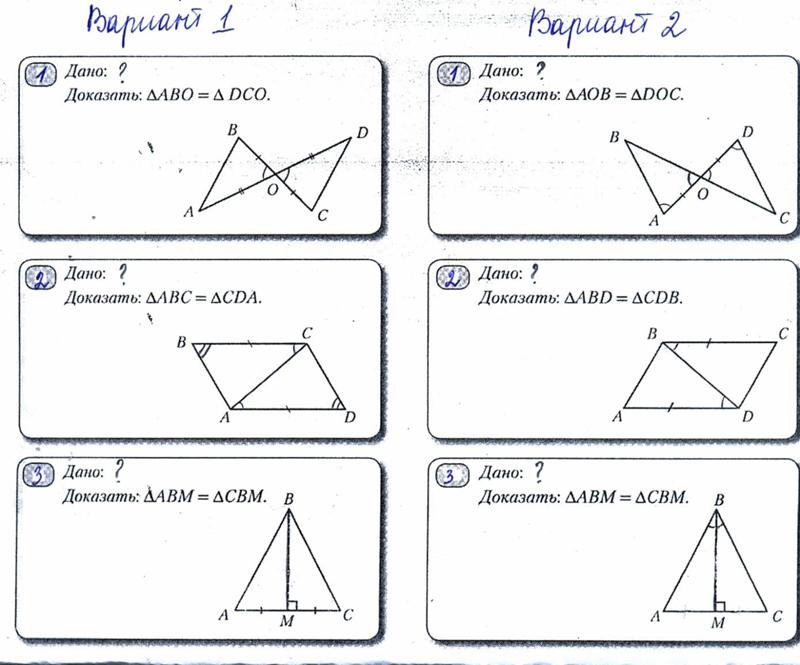
Самостоятельная работа.
Вариант I
В
1. Треугольник АВС и квадрат AEFC не
Треугольник АВС и квадрат AEFC не
К М лежат в одной плоскости. Точки К и М –
середины отрезков АВ и ВС соответственно.
А С а) Докажите, что КМ||EF.
б) Найдите КМ, если АЕ = 8см.
Е F
2. Плоскость проходит через основание АD трапеции АВСD.
Точки Е и F – середины отрезков АВ и СD соответственно.
Докажите, что ЕF||.
Урок № 7 Геом. 10кл.
Самостоятельная работа.
Вариант II
М N 1. Квадрат АВСD и трапеция KMNL не лежат
в одной плоскости. Точки А и D – середины
A D отрезков КМ и NL соответственно.
а) Докажите, что КL||ВС.
К L б) Найдите ВС, если KL = 10см, MN = 6см.
В С
2. Плоскость проходит через основание АС треугольника АВС.
Точки D и E – середины отрезков АВ и ВС соответственно.
Докажите, что DE||.
Урок № 7 Геом. 10кл.
Самостоятельная работа.
Вариант I
В
1. Треугольник АВС и квадрат AEFC не
К М лежат в одной плоскости. Точки К и М –
середины отрезков АВ и ВС соответственно.
А С а) Докажите, что КМ||EF.
б) Найдите КМ, если АЕ = 8см.
Е F
2. Плоскость проходит через основание АD трапеции АВСD.
Точки Е и F – середины отрезков АВ и СD соответственно.
Докажите, что ЕF||.
Урок № 7 Геом. 10кл.
Самостоятельная работа.
Вариант II
М N 1. Квадрат АВСD и трапеция KMNL не лежат
Квадрат АВСD и трапеция KMNL не лежат
в одной плоскости. Точки А и D – середины
A D отрезков КМ и NL соответственно.
а) Докажите, что КL||ВС.
К L б) Найдите ВС, если KL = 10см, MN = 6см.
В С
2. Плоскость проходит через основание АС треугольника АВС.
Точки D и E – середины отрезков АВ и ВС соответственно.
Докажите, что DE||.
Урок № 17 Геом. 10кл.
Задачи на построение сечений.
1. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его ребер (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
2. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся вершинами куба (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
3. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся либо вершинами куба, либо серединами его ребер (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
Урок № 17 Геом. 10кл.
Задачи на построение сечений.
1. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его ребер (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
2. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся вершинами куба (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
3. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся либо вершинами куба, либо серединами его ребер (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
Урок № 17 Геом. 10кл.
Задачи на построение сечений.
1. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его ребер (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
2. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся вершинами куба (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
3. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся либо вершинами куба, либо серединами его ребер (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
Урок № 17 Геом. 10кл.
Задачи на построение сечений.
1. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его ребер (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
2. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся вершинами куба (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
Найти периметр сечения, если ребро куба равно а.
3. Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся либо вершинами куба, либо серединами его ребер (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а.
Урок № 28 Геом. 10кл.
Решение задач
Задача 1.
Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед,
АD = 9 см, DC = 8 дм, DВ1 = 17 дм.
Найти: SBB1D1D.
Задача 2.
В треугольнике АВС: АВ = ВС = 10 см, АС = 12 см.
Через точку В к плоскости треугольника проведен перпендикуляр BD длиной 15 см.
а) Укажите проекцию треугольника DBC на плоскость АВС.
б) Найдите расстояние от точки D до плоскости АС.
Урок № 28 Геом. 10кл.
Решение задач
Задача 1.
Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед,
АD = 9 см, DC = 8 дм, DВ1 = 17 дм.
Найти: SBB1D1D.
Задача 2.
В треугольнике АВС: АВ = ВС = 10 см, АС = 12 см.
Через точку В к плоскости треугольника проведен перпендикуляр BD длиной 15 см.
а) Укажите проекцию треугольника DBC на плоскость АВС.
б) Найдите расстояние от точки D до плоскости АС.
Урок № 28 Геом. 10кл.
Решение задач
Задача 1.
Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед,
АD = 9 см, DC = 8 дм, DВ1 = 17 дм.
Найти: SBB1D1D.
Задача 2.
В треугольнике АВС: АВ = ВС = 10 см, АС = 12 см.
Через точку В к плоскости треугольника проведен перпендикуляр BD длиной 15 см.
а) Укажите проекцию треугольника DBC на плоскость АВС.
б) Найдите расстояние от точки D до плоскости АС.
Урок № 28 Геом. 10кл.
Решение задач
Задача 1.
Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед,
АD = 9 см, DC = 8 дм, DВ1 = 17 дм.
Найти: SBB1D1D.
Задача 2.
В треугольнике АВС: АВ = ВС = 10 см, АС = 12 см.
Через точку В к плоскости треугольника проведен перпендикуляр BD длиной 15 см.
а) Укажите проекцию треугольника DBC на плоскость АВС.
б) Найдите расстояние от точки D до плоскости АС.
Урок № 29 Геом. 10кл.
Решение задач
Задача 1.
Диагонали квадрата АВСD пересекается в точке О. SO – перпендикуляр к плоскости квадрата, SO = см.
а) Докажите равенство углов, образуемых прямыми SA, SC и SD с плоскостью квадрата.
б) Найдите эти углы, если периметр АВСD равен 32 см.
Задача 2.
В тетраэдре АВСD: . Докажите, что если перпен-дикуляры, проведенные из точки D к сторонам треугольника АВС, образуют равные углы с (АВС), то точка О – центр окружности, вписанной в треугольник АВС,
Урок № 29 Геом. 10кл.
Решение задач
Задача 1.
Диагонали квадрата АВСD пересекается в точке О. SO – перпендикуляр к плоскости квадрата, SO = см.
а) Докажите равенство углов, образуемых прямыми SA, SC и SD с плоскостью квадрата.
б) Найдите эти углы, если периметр АВСD равен 32 см.
Задача 2.
В тетраэдре АВСD: . Докажите, что если перпен-дикуляры, проведенные из точки D к сторонам треугольника АВС, образуют равные углы с (АВС), то точка О – центр окружности, вписанной в треугольник АВС,
Урок № 29 Геом. 10кл.
Решение задач
Задача 1.
Диагонали квадрата АВСD пересекается в точке О. SO – перпендикуляр к плоскости квадрата, SO = см.
а) Докажите равенство углов, образуемых прямыми SA, SC и SD с плоскостью квадрата.
б) Найдите эти углы, если периметр АВСD равен 32 см.
Задача 2.
В тетраэдре АВСD: . Докажите, что если перпен-дикуляры, проведенные из точки D к сторонам треугольника АВС, образуют равные углы с (АВС), то точка О – центр окружности, вписанной в треугольник АВС,
Урок № 29 Геом. 10кл.
Решение задач
Задача 1.
Диагонали квадрата АВСD пересекается в точке О. SO – перпендикуляр к плоскости квадрата, SO = см.
а) Докажите равенство углов, образуемых прямыми SA, SC и SD с плоскостью квадрата.
б) Найдите эти углы, если периметр АВСD равен 32 см.
Задача 2.
В тетраэдре АВСD: . Докажите, что если перпен-дикуляры, проведенные из точки D к сторонам треугольника АВС, образуют равные углы с (АВС), то точка О – центр окружности, вписанной в треугольник АВС,
Урок № 35 Геом. 10кл.
Самостоятельная работа.
1. Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед, АВ = 6см, АD=4см, АА1 =12см. Найдите АС1.
2. Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед, АВ = 4м, АD=3м, . Найдите Sбок.
3. Дан прямоугольный параллелепипед. Угол между диагональю основания и одной из его сторон равен β. Найдите площадь боковой поверхности параллелепипеда, если диагональ основания равна k.
Урок № 35 Геом. 10кл.
Самостоятельная работа.
1. Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед, АВ = 6см, АD=4см, АА1 =12см. Найдите АС1.
2. Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед, АВ = 4м, АD=3м, . Найдите Sбок.
Найдите Sбок.
3. Дан прямоугольный параллелепипед. Угол между диагональю основания и одной из его сторон равен β. Найдите площадь боковой поверхности параллелепипеда, если диагональ основания равна k.
Урок № 35 Геом. 10кл.
Самостоятельная работа.
1. Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед, АВ = 6см, АD=4см, АА1 =12см. Найдите АС1.
2. Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед, АВ = 4м, АD=3м, . Найдите Sбок.
3. Дан прямоугольный параллелепипед. Угол между диагональю основания и одной из его сторон равен β. Найдите площадь боковой поверхности параллелепипеда, если диагональ основания равна k.
Урок № 35 Геом. 10кл.
Самостоятельная работа.
1. Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед, АВ = 6см, АD=4см, АА1 =12см. Найдите АС1.
2. Дано: АВСDA1B1C1D1 – прямоугольный параллелепипед, АВ = 4м, АD=3м, . Найдите Sбок.
3. Дан прямоугольный параллелепипед. Угол между диагональю основания и одной из его сторон равен β. Найдите площадь боковой поверхности параллелепипеда, если диагональ основания равна k.
Найдите площадь боковой поверхности параллелепипеда, если диагональ основания равна k.
Урок № 35 Геом. 10кл.
Классная работа.
1. Диагональ куба равна 12см. Найдите: а) ребро куба; б) синус угла между диагональю куба и плоскостью одной из его граней.
2. Основанием прямоугольного параллелепипеда является квадрат, диагональ параллелепипеда равна см, а его измерения относятся как 2:2:1. Найдите: а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью основания.
3. В прямоугольном параллелепипеде измерения равны 6, 8, 10. Найти диагональ параллелепипеда и угол между диагональю параллелепипеда и плоскостью его основания.
4. В прямоугольном параллелепипеде измерения равны 5, 7, . Найти диагональ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью его основания.
5. Из вершины А прямоугольного ∆АВС () восстановлен перпендикуляр к плоскости АВС и на нем взят отрезок АМ=h. Точка М соединена с В и С. Найдите S∆VDC, если двугранный .
Найдите S∆VDC, если двугранный .
6. Точка М находится на расстоянии h от плоскости α. Проведены 2 наклонные МР и МQ (где Р и Q – основания наклонных), соответственно под углами 450 и 600. Найдите РQ, если , где О – основание перпендикуляра МО, МОα.
Урок № 35 Геом. 10кл.
Классная работа.
1. Диагональ куба равна 12см. Найдите: а) ребро куба; б) синус угла между диагональю куба и плоскостью одной из его граней.
2. Основанием прямоугольного параллелепипеда является квадрат, диагональ параллелепипеда равна см, а его измерения относятся как 2:2:1. Найдите: а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью основания.
3. В прямоугольном параллелепипеде измерения равны 6, 8, 10. Найти диагональ параллелепипеда и угол между диагональю параллелепипеда и плоскостью его основания.
4. В прямоугольном параллелепипеде измерения равны 5, 7, . Найти диагональ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью его основания.
5. Из вершины А прямоугольного ∆АВС () восстановлен перпендикуляр к плоскости АВС и на нем взят отрезок АМ=h. Точка М соединена с В и С. Найдите S∆VDC, если двугранный .
6. Точка М находится на расстоянии h от плоскости α. Проведены 2 наклонные МР и МQ (где Р и Q – основания наклонных), соответственно под углами 450 и 600. Найдите РQ, если , где О – основание перпендикуляра МО, МОα.
Урок № 38 Геом. 10кл.
Решите задачи
1. Дан прямоугольный параллелепипед АВСDA1B1C1D1, АВ = 4, АА1 =6,
А1С=. Найдите АD.
2. Дана прямая треугольная призма АВСА1В1С1, АС = ВС = 5, АВ =6 ,
ВDАС, . Найдите cosC1BC.
Урок № 38 Геом. 10кл.
Решите задачи
1. Дан прямоугольный параллелепипед АВСDA1B1C1D1, АВ = 4, АА1 =6,
А1С=. Найдите АD.
2. Дана прямая треугольная призма АВСА1В1С1, АС = ВС = 5, АВ =6 ,
ВDАС, . Найдите cosC1BC.
Урок № 38 Геом. 10кл.
Решите задачи
1. Дан прямоугольный параллелепипед АВСDA1B1C1D1, АВ = 4, АА1 =6,
А1С=. Найдите АD.
2. Дана прямая треугольная призма АВСА1В1С1, АС = ВС = 5, АВ =6 ,
ВDАС, . Найдите cosC1BC.
Урок № 38 Геом. 10кл.
Решите задачи
1. Дан прямоугольный параллелепипед АВСDA1B1C1D1, АВ = 4, АА1 =6,
А1С=. Найдите АD.
2. Дана прямая треугольная призма АВСА1В1С1, АС = ВС = 5, АВ =6 ,
ВDАС, . Найдите cosC1BC.
Урок № 38 Геом. 10кл.
Решите задачи
1. Дан прямоугольный параллелепипед АВСDA1B1C1D1, АВ = 4, АА1 =6,
А1С=. Найдите АD.
2. Дана прямая треугольная призма АВСА1В1С1, АС = ВС = 5, АВ =6 ,
ВDАС, . Найдите cosC1BC.
Урок № 38 Геом. 10кл.
Решите задачи
1. Дан прямоугольный параллелепипед АВСDA1B1C1D1, АВ = 4, АА1 =6,
А1С=. Найдите АD.
2. Дана прямая треугольная призма АВСА1В1С1, АС = ВС = 5, АВ =6 ,
ВDАС, . Найдите cosC1BC.
Найдите cosC1BC.
Урок № 41 Геом. 10кл.
Самостоятельная работа
Вариант I
1. Сторона основания правильной треугольной призмы равна 6 см, а диагональ боковой грани 10 см. Найдите площадь боковой и полной поверхности призмы.
2. Основание прямой призмы – ромб со стороной 5 см и тупым углом 1200. Боковая поверхность призмы имеет площадь 240 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
3. Основание прямой призмы – прямоугольный треугольник с катетами 15 и 20см. Большая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.
Урок № 41 Геом. 10кл.
Самостоятельная работа
Вариант II
1. Боковое ребро правильной треугольной призмы равно 9 см, а диагональ боковой грани равна 15 см. Найдите площадь боковой и полной поверхности призмы.
2. Основание прямой призмы – ромб с острым углом 600. Боковое ребро призмы равно 10 см, а площадь боковой поверхности – 240 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
3. Основание прямой призмы – прямоугольный треугольник с гипотенузой 25см и катетом 20см. Меньшая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.
Урок № 41 Геом. 10кл.
Самостоятельная работа
Вариант I
1. Сторона основания правильной треугольной призмы равна 6 см, а диагональ боковой грани 10 см. Найдите площадь боковой и полной поверхности призмы.
2. Основание прямой призмы – ромб со стороной 5 см и тупым углом 1200. Боковая поверхность призмы имеет площадь 240 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
3. Основание прямой призмы – прямоугольный треугольник с катетами 15 и 20см. Большая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.
Урок № 41 Геом. 10кл.
Самостоятельная работа
Вариант II
1. Боковое ребро правильной треугольной призмы равно 9 см, а диагональ боковой грани равна 15 см. Найдите площадь боковой и полной поверхности призмы.
2. Основание прямой призмы – ромб с острым углом 600. Боковое ребро призмы равно 10 см, а площадь боковой поверхности – 240 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
3. Основание прямой призмы – прямоугольный треугольник с гипотенузой 25см и катетом 20см. Меньшая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.
Урок № 44 Геом. 10кл.
Самостоятельная работа. Вариант I
1. Высота правильной треугольной пирамиды равна , радиус окружности, описанной около ее основания, 2а. Найдите : а) апофему пирамиды; б) угол между боковой гранью и основанием; в) площадь боковой поверхности; г) плоский угол при вершине пирамиды.
2. Основание пирамиды – прямоугольник со сторонами 6см и 8см. Высота пирамиды равна 12см и проходит через точку пересечения диагоналей основания. Найдите боковые ребра пирамиды.
Основание пирамиды – прямоугольник со сторонами 6см и 8см. Высота пирамиды равна 12см и проходит через точку пересечения диагоналей основания. Найдите боковые ребра пирамиды.
3. В правильной четырехугольной пирамиде сторона основания равна 6см, а угол наклона боковой грани к плоскости основания равен 600. найдите боковое ребро пирамиды.
4. Основанием пирамиды является треугольник со сторонами 12см, 10см, 10см. Каждая боковая грань наклонена к основанию под углом 450. Найдите площадь полной поверхности пирамиды.
Урок № 44 Геом. 10кл.
Самостоятельная работа. Вариант II
1. Апофема правильной четырехугольной пирамиды равна 2а. Высота пирамиды равна . Найдите: а) сторону основания пирамиды; б) угол между боковой гранью и основанием; в) площадь поверхности пирамиды; г) расстояние от центра основания пирамиды до плоскости боковой грани..
2. Основание пирамиды – ромб с диагоналями 10см и 18см. Высота пирамиды проходит через точку пересечения диагоналей ромба. Меньшее боковое ребро пирамиды равно 13см. Найдите большее боковые ребро пирамиды.
Меньшее боковое ребро пирамиды равно 13см. Найдите большее боковые ребро пирамиды.
3. Основанием пирамиды DABC является прямоугольный треугольник АВС, у которого гипотенуза АВ равна 29см, катет АС равен 21см. Ребро DA перпендикулярно к плоскости основания и равно 20см. Найдите площадь боковой поверхности пирамиды..
4. Основанием пирамиды является треугольник со сторонами 10см, 8см, 6см. Каждая боковая грань наклонена к основанию под углом 450. Найдите площадь полной поверхности пирамиды.
Урок № 44 Геом. 10кл.
Самостоятельная работа. Вариант I
1. Высота правильной треугольной пирамиды равна , радиус окружности, описанной около ее основания, 2а. Найдите : а) апофему пирамиды; б) угол между боковой гранью и основанием; в) площадь боковой поверхности; г) плоский угол при вершине пирамиды.
2. Основание пирамиды – прямоугольник со сторонами 6см и 8см. Высота пирамиды равна 12см и проходит через точку пересечения диагоналей основания. Найдите боковые ребра пирамиды.
Найдите боковые ребра пирамиды.
3. В правильной четырехугольной пирамиде сторона основания равна 6см, а угол наклона боковой грани к плоскости основания равен 600. найдите боковое ребро пирамиды.
4. Основанием пирамиды является треугольник со сторонами 12см, 10см, 10см. Каждая боковая грань наклонена к основанию под углом 450. Найдите площадь полной поверхности пирамиды.
Урок № 44 Геом. 10кл.
Самостоятельная работа. Вариант II
1. Апофема правильной четырехугольной пирамиды равна 2а. Высота пирамиды равна . Найдите: а) сторону основания пирамиды; б) угол между боковой гранью и основанием; в) площадь поверхности пирамиды; г) расстояние от центра основания пирамиды до плоскости боковой грани..
2. Основание пирамиды – ромб с диагоналями 10см и 18см. Высота пирамиды проходит через точку пересечения диагоналей ромба. Меньшее боковое ребро пирамиды равно 13см. Найдите большее боковые ребро пирамиды.
3. Основанием пирамиды DABC является прямоугольный треугольник АВС, у которого гипотенуза АВ равна 29см, катет АС равен 21см. Ребро DA перпендикулярно к плоскости основания и равно 20см. Найдите площадь боковой поверхности пирамиды..
Ребро DA перпендикулярно к плоскости основания и равно 20см. Найдите площадь боковой поверхности пирамиды..
4. Основанием пирамиды является треугольник со сторонами 10см, 8см, 6см. Каждая боковая грань наклонена к основанию под углом 450. Найдите площадь полной поверхности пирамиды.
Урок № 52 Геом. 10кл.
Решение задач
1. Высота правильной треугольной пирамиды равна , радиус окружности, описанной около ее основания, 2а. Найдите : а) апофему пирамиды; б) угол между боковой гранью и основанием; в) площадь боковой поверхности; г) плоский угол при вершине пирамиды.
2. Основание пирамиды – прямоугольник со сторонами 6см и 8см. Высота пирамиды равна 12см и проходит через точку пересечения диагоналей основания. Найдите боковые ребра пирамиды.
3. В правильной четырехугольной пирамиде сторона основания равна 6см, а угол наклона боковой грани к плоскости основания равен 600. найдите боковое ребро пирамиды.
4. Апофема правильной четырехугольной пирамиды равна 2а. Высота пирамиды равна . Найдите: а) сторону основания пирамиды; б) угол между боковой гранью и основанием; в) площадь поверхности пирамиды; г) расстояние от центра основания пирамиды до плоскости боковой грани..
Высота пирамиды равна . Найдите: а) сторону основания пирамиды; б) угол между боковой гранью и основанием; в) площадь поверхности пирамиды; г) расстояние от центра основания пирамиды до плоскости боковой грани..
2. Основание пирамиды – ромб с диагоналями 10см и 18см. Высота пирамиды проходит через точку пересечения диагоналей ромба. Меньшее боковое ребро пирамиды равно 13см. Найдите большее боковые ребро пирамиды.
Урок № 52 Геом. 10кл.
Решение задач
1. Высота правильной треугольной пирамиды равна , радиус окружности, описанной около ее основания, 2а. Найдите : а) апофему пирамиды; б) угол между боковой гранью и основанием; в) площадь боковой поверхности; г) плоский угол при вершине пирамиды.
2. Основание пирамиды – прямоугольник со сторонами 6см и 8см. Высота пирамиды равна 12см и проходит через точку пересечения диагоналей основания. Найдите боковые ребра пирамиды.
3. В правильной четырехугольной пирамиде сторона основания равна 6см, а угол наклона боковой грани к плоскости основания равен 600. найдите боковое ребро пирамиды.
найдите боковое ребро пирамиды.
4. Апофема правильной четырехугольной пирамиды равна 2а. Высота пирамиды равна . Найдите: а) сторону основания пирамиды; б) угол между боковой гранью и основанием; в) площадь поверхности пирамиды; г) расстояние от центра основания пирамиды до плоскости боковой грани..
2. Основание пирамиды – ромб с диагоналями 10см и 18см. Высота пирамиды проходит через точку пересечения диагоналей ромба. Меньшее боковое ребро пирамиды равно 13см. Найдите большее боковые ребро пирамиды.
Урок № 52 Геом. 10кл.
Домашнее задание
Тест
1. Из данных утверждений выберите верное:
а) все ребра правильной пирамиды равны;
б) площадь поверхности пирамиды равна половине произведения периметра основания на апофему;
в) боковые грани усеченной пирамиды – трапеции;
г) утверждения а – в не верны.
2. Найдите площадь боковой поверхности пирамиды, все грани которой наклонены к основанию под углом 600, а в основании лежит прямоугольный треугольник с катетами 3см и 6см.
а) 9см2; б) 10см2; в) 12см2; г) другой ответ.
3. В правильной четырехугольной пирамиде сторона основания равна 5см, а плоский угол при вершине пирамиды 600. Найдите боковое ребро пирамиды.
а) 6см; б) см; в) 5см; г) другой ответ.
4. В основанием пирамиды SABC лежит равнобедренный треугольник АВС, в котором ВС = 12см, а АВ = АС = 10см. Найдите площадь сечения ASM, если оно перпендикулярно плоскости основания, а все боковые ребра пирамиды равны 10см.
а) см2; б) см2; в) 31см2; г) другой ответ.
5. Боковые ребра пирамиды SABC равны между собой. SD – высота пирамиды. Точка D лежит внутри треугольника АВС. Треугольник АВС:
а) прямоугольный; б) остроугольный;
в) тупоугольный; г) недостаточно данных.
6. Найдите площадь диагоналей сечения правильной усеченной четырехугольной пирамиды, если ее высота равна см, а стороны основания 1см и 4см.
а) 10см2; б) 2,5см2; в) 5см2; г) другой ответ.
Урок № 52 Геом. 10кл.
Домашнее задание
Тест
1. Из данных утверждений выберите верное:
а) все ребра правильной пирамиды равны;
б) площадь поверхности пирамиды равна половине произведения периметра основания на апофему;
в) боковые грани усеченной пирамиды – трапеции;
г) утверждения а – в не верны.
2. Найдите площадь боковой поверхности пирамиды, все грани которой наклонены к основанию под углом 600, а в основании лежит прямоугольный треугольник с катетами 3см и 6см.
а) 9см2; б) 10см2; в) 12см2; г) другой ответ.
3. В правильной четырехугольной пирамиде сторона основания равна 5см, а плоский угол при вершине пирамиды 600. Найдите боковое ребро пирамиды.
а) 6см; б) см; в) 5см; г) другой ответ.
4. В основанием пирамиды SABC лежит равнобедренный треугольник АВС, в котором ВС = 12см, а АВ = АС = 10см. Найдите площадь сечения ASM, если оно перпендикулярно плоскости основания, а все боковые ребра пирамиды равны 10см.
Найдите площадь сечения ASM, если оно перпендикулярно плоскости основания, а все боковые ребра пирамиды равны 10см.
а) см2; б) см2; в) 31см2; г) другой ответ.
5. Боковые ребра пирамиды SABC равны между собой. SD – высота пирамиды. Точка D лежит внутри треугольника АВС. Треугольник АВС:
а) прямоугольный; б) остроугольный;
в) тупоугольный; г) недостаточно данных.
6. Найдите площадь диагоналей сечения правильной усеченной четырехугольной пирамиды, если ее высота равна см, а стороны основания 1см и 4см.
а) 10см2; б) 2,5см2; в) 5см2; г) другой ответ.
10 класс | ||||||||
Подготовила учитель математики МОУ Дугдинская СОШ Зейский район, Амурская область, Артющенко И. | ||||||||
да | нет | АМ | три | одну или бесконечно много | нет | да | три или не одной | |
да | нет | пересекаются | а | да | параллельны | нет | да | |
нет | нет | скрещивающиеся | АС | на плоскости | да | да | параллельность | |
да | нет | параллельны | параллелограмм | плоскости – параллельно – α | нет | нет | параллельны | плоскость параллельна данным прямым |
да | нет | 90° | ОВ | нет | а | α – a — b | ||
да | нет | прямоуг. | SD | угол АСО | да | нет | АВ | |
нет | нет | а ||α | ВМD | нет | нет | DСА | ||
да | нет | 5 | трапеция | нет | да | нет | ||
нет | нет | 0,5 | параллельны | -0,5 | пересекаются |
Навигация по странице:  |
|
Преподавание трехмерных фигур
Преподавание трехмерных фигур очень важно во 2-м классе. В мире так много реальных примеров трехмерных форм. Эти основы также помогут учащимся в их будущем обучении и занятиях по математике более высокого уровня в увлекательной игровой форме. Если вы ищете способ сделать уроки математики по геометрии практическими для своих учеников, ознакомьтесь с этими заданиями по геометрии трехмерных фигур для 2-го класса, чтобы добавить их в свои планы уроков.
Что такое трехмерные фигуры?
Трехмерные фигуры — это объемные фигуры, состоящие из трех измерений: длины, ширины и высоты. Они имеют толщину (глубину), что отличает их от 2D-форм.
Трехмерные фигуры — это объемные фигуры, состоящие из ребер, вершин и граней. Ребра составляют стороны формы. Вершины — это точки. Наконец, грани — это плоская поверхность, которая позволяет фигуре стоять.
Наконец, грани — это плоская поверхность, которая позволяет фигуре стоять.
Несколько примеров трехмерных фигур: кубы, прямоугольные призмы, сферы, конусы и цилиндры.
3D Shapes Geometry Anchor Charts
Одна из моих любимых стратегий для введения новых математических понятий — использование якорной диаграммы. Мне нравится создавать целую групповую якорную диаграмму со своими учениками, чтобы они могли вместе со мной пройтись по основам концепции.
Это вызывает интересную беседу, позволяет учащимся познакомиться с математическим словарем и дает им наглядное представление о концепции. Это очень важно при обучении трехмерным формам.
Хотя мне нравится создавать классную якорную диаграмму, которая будет отображаться в обстановке всей группы, учащимся также важно применять то, что они узнали об этой концепции.
После создания якорной диаграммы я предлагаю учащимся создать ее мини-версию в своих математических журналах. Это отличный справочник для студентов, к которому они могут вернуться в любое время во время математического блока. Это также отлично подходит для спирального обзора в течение года.
Это также отлично подходит для спирального обзора в течение года.
Теперь, когда вы знаете больше о том, что такое 3D-фигуры, и у вас есть надежная стратегия для ознакомления с ними ваших учеников, читайте дальше о различных способах преподавания 3D-фигур, которые являются практическими и очень увлекательными.
1. Сетки 3D Shape
При обучении трехмерным фигурам на уроке геометрии учащимся важно понимать взаимосвязь между двухмерными и трехмерными формами. Сети 3D-форм идеально подходят для того, чтобы разрушить эту связь.
Сеть трехмерной формы можно развернуть. Используя сети 3D-форм, учащиеся смогут увидеть, как будет выглядеть 3D-форма, если ее открыть и разложить плоско.
Таким образом, они могут точно видеть, какие 2D-формы использовались для построения фигуры, а также количество ребер, вершин и граней.
2. Построение 3D-фигур
Чем больше практических занятий получат учащиеся, когда вы преподаете им 3D-фигуры, тем лучше они поймут концепцию трех измерений и то, как они работают вместе для создания объемной формы.
Все, что вам нужно для создания трехмерных фигур, — это основные школьные принадлежности, такие как зубочистки и пластилин. Зубочистки представляют собой края строящихся фигур, а пластилин представляет собой вершины.
Этот фаворит в классе, потому что вы можете использовать зефир вместо пластилина, но я обнаружил, что пластилин создает более прочную форму и лучше держит все вместе.
Учащиеся могут использовать зубочистки и пластилин для создания различных трехмерных фигур на уроке геометрии.
Если вы ищете другие манипуляции и инструменты для использования в своем модуле геометрии, ознакомьтесь с этой записью в блоге.
3. Примеры фотографий с трехмерными фигурами из реальной жизни
Как я упоминал в начале этого поста, трехмерные фигуры повсюду в реальном мире. Учащиеся должны понимать, что формы можно найти в окружающем их мире, и уметь определять, когда реальный объект представляет собой трехмерную форму.
Вы можете обучать трехмерным формам в реальном мире, беря их на прогулку по школе или за ее пределами. Пока вы ходите, попросите учеников определить различные формы, которые они видят. Они даже могут записывать их в свой математический журнал.
Пока вы ходите, попросите учеников определить различные формы, которые они видят. Они даже могут записывать их в свой математический журнал.
Еще один способ укрепить практику работы с реальными трехмерными формами — включить использование реальных объектов и изображений. Вы можете делать это во время занятий по математике или самостоятельной практики.
4. Определите фигуры, которые не принадлежат
Когда ваши ученики будут работать с реальными фотографиями трехмерных фигур в геометрии, они начнут распознавать, когда формы похожи, а когда различаются.
Чтобы помочь им лучше понять трехмерные объекты реального мира, попросите их определить формы, которые не принадлежат к определенной категории. Это поощряет критическое мышление, поскольку они смотрят на атрибуты формы и выясняют, какая форма не соответствует остальным.
Эта карточка с заданием Нечетная фигура – интересный способ для учащихся идентифицировать фигуры и определить, какая из них не принадлежит. Они будут записывать свои ответы с карточек с заданиями в свои математические журналы, используя этот замечательный ресурс — задание «Нечетная фигура».
Они будут записывать свои ответы с карточек с заданиями в свои математические журналы, используя этот замечательный ресурс — задание «Нечетная фигура».
5. Повязки на голову по геометрии
При обучении геометрии вы хотите, чтобы занятия были как можно более увлекательными для максимального вовлечения учащихся. Это занятие с повязками на голову из моего раздела «Математика с подсказками по геометрии» — мой любимый способ заинтересовать детей при обучении трехмерным фигурам!
Учащиеся объединяются для игры в эту игру. Один учащийся надевает повязку на голову и прикрепляет карточку с фигурой спереди, не глядя. Они будут использовать анкету с вопросами о форме, чтобы задать своим товарищам по команде вопросы о форме, которую они носят.
Ответив на вопросы и услышав ответы, они будут обращаться к таблице форм, пока не поймут, какая у них форма.
Это занятие не только развлекает учащихся, но и требует, чтобы и ученик, носящий повязку, и другие товарищи по команде критически обдумывали форму и ее атрибуты.
6. Внедрение технологий
Включение технологий в преподавание уроков геометрии 3D-фигур — еще один способ вовлечь учащихся в процесс обучения. Это также позволяет учащимся работать с трехмерными фигурами по-другому.
Учащиеся могут практиковаться в определении фигур и их атрибутов с помощью этих карточек Geometry Boom. Эти интерактивные цифровые карточки с заданиями не являются подготовкой и представляют собой идеальный способ для учащихся практиковать самопроверку. Вы можете добавить этот замечательный ресурс в свои математические центры, использовать их для самостоятельной работы или поручить их своим первоклассникам.
Я надеюсь, что эти практические советы по обучению трехмерным фигурам с заданиями для 2-го класса дали вам больше идей для практических занятий в классе! Чтобы узнать больше о том, как преподавать геометрию, ознакомьтесь с этими сообщениями в блоге, чтобы заложить прочную основу для математических навыков:
- Упражнения по геометрии двумерных фигур
- 10 книг для обучения фигурам
- Математические манипуляции и инструменты для обучения геометрии
Прикрепите изображение ниже, чтобы сохранить этот пост на потом!
Math Fact Fluency Races: веселая и увлекательная игра для детей с математическими фактами
Свободное владение математическими фактами является ключевым фактором в начальных классах. К концу 2-го класса дети должны знать математические факты до
К концу 2-го класса дети должны знать математические факты до
. Подробнее »
Эффективные стратегии введения свойств сложения в 3-м классе
Вы учитель 3-го класса и ищете веселые и эффективные способы познакомить своих учеников со свойствами сложения? Если вы новичок в
Подробнее »
Обучение чувству чисел с помощью 10 простых упражнений с десятью рамками
Когда дело доходит до обучения чтению чисел, десять рамок являются важным инструментом, который студенты должны научиться использовать и применять. Включая десять кадров
Подробнее »
Геометрия и фигуры для детей: увлекательные занятия —
Изучайте и стройте с помощью геометрии и фигур для детей. Включено множество веселых математических заданий и БЕСПЛАТНОЕ задание по симметрии блоков узоров!
Вы искали Pinterest или гуглили, чтобы найти интересную, практическую геометрию и формы для детей? Вы ищете уроки и идеи для занятий, которые помогут вам лучше понять формы и геометрию? Тогда вы попали по адресу!
Геометрия и фигуры для детей
Математические советы и стратегии, необходимые для преподавания геометрии в начальных классах, находятся прямо здесь. У вас будет все необходимое, чтобы быстро внедрить множество геометрических заданий, игр и центров в свой класс или домой.
У вас будет все необходимое, чтобы быстро внедрить множество геометрических заданий, игр и центров в свой класс или домой.
Упражнения, книги, уроки по математике и другие ресурсы ( , включая БЕСПЛАТНЫЙ ) охватывают массу понятий геометрии и идеально подходят для детского сада, первого и второго класса. Кроме того, вы найдете ценные материалы по геометрии и советы по манипулированию, а также бесплатные подарки, которые вы можете получить уже сегодня! Этот пост наполнен огромным количеством полезной информации для вас во время вашего обучения.
Почему важно обучать детей геометрии и фигурам?
Детям нужно много возможностей, чтобы узнать о формах. Научиться определять и понимать, что представляют собой различные формы, а также их части, являются важными понятиями. Каждый день дети сталкиваются с формами в окружающей их среде. Они видят и взаимодействуют с ними повсюду ежедневно. Они должны уметь распознавать формы, озвучивать то, что видят, и понимать, почему они здесь.
Мы хотим, чтобы дети увидели форму и установили связь. Когда они смотрят на колесо автомобиля, мы хотим, чтобы они восприняли это изображение как круг, форму, которую они научились обозначать. В конце концов, мы хотим, чтобы дети научились различать формы и понимать формальные определения форм. Когда они смотрят на хлопушку, мы хотим, чтобы они восприняли это изображение как квадрат, поскольку у него четыре равные стороны.
По мере изучения каждой геометрической концепции дети переходят к следующему этапу понимания. Хорошее знание форм жизненно важно для дальнейшего изучения более сложных геометрических концепций.
Приведенные ниже упражнения помогут развить понимание форм. Используйте их так, как они описаны, или адаптируйте их к своим потребностям. Обсуждайте формы и поощряйте вопросы. Когда ребенок замечает фигуры в своем окружении, пусть они поделятся этим с классом! Находите время для веселых и увлекательных занятий по геометрии ежедневно в своем математическом центре и на бесплатных игровых площадках.
Геометрия и формы для занятий с детьми
Двухмерные фигуры
Первый этап в изучении геометрии – это умение идентифицировать, называть и описывать двухмерные фигуры. Говорите о формах всякий раз, когда вы их видите, и развешивайте плакаты с фигурами на стене, это полезно для детей! Имейте множество манипулятивных форм, доступных для изучения и «игры».
Упражнения
- Создайте подробную якорную диаграмму для каждой 2D-формы, которую вы обучаете. Нарисуйте фигуру, обозначьте ее и опишите, сколько сторон и углов у каждой из них.
- Научите фигуру с помощью запоминающейся песни или стихотворения, чтобы помочь им запомнить, как она называется и ее части.
- Используйте цветные палочки для эскимо, чтобы сформировать двухмерные фигуры с прямыми сторонами. Оставьте их в центре, чтобы дети могли собрать их самостоятельно.
- Играйте и творите с танграмами. Посмотрите, какие рисунки могут сделать дети.

- Выкройки блоков также являются забавными, практическими манипуляторами, которые побуждают детей к творчеству. Они являются идеальным дополнением к любой математической ванне!
- Достаньте геоборды и потренируйтесь формировать фигуры с помощью эластичных лент.
- Позвольте детям самостоятельно формировать фигуры с помощью Playdough.
- Закрепите знания о формах с помощью увлекательных распечатываемых заданий, идеально подходящих для начальной школы!
- Потренируйтесь формировать фигуры с помощью различных инструментов, таких как маркеры или наклейки.
- Делайте простые поделки, используя фигуры, вырезанные из плотной бумаги. Пусть они изобретают форму, комбинируя части формы, чтобы сделать новые.
- Проверьте понимание с помощью небольших целенаправленных задач. Быстро проверьте распознавание фигур с помощью карточек.

- Рисуйте фигуры для практики, используя Boogie Board или другой инструмент для рисования и стирания. Умение рисовать базовые формы необходимо для того, чтобы позже приступить к более сложным вещам.
Трехмерные фигуры
Как и в случае с двумерными фигурами, важно уметь идентифицировать, называть и описывать трехмерные фигуры! Наш мир состоит из трехмерных форм, и нам нужно распознавать их, чтобы понимать вещи. Удостоверьтесь, что у вас есть геометрические тела, которые можно держать и с которыми можно взаимодействовать, а также плакаты, на которые можно ссылаться.
Упражнения
- Создайте подробную якорную диаграмму для каждой трехмерной формы, которую вы обучаете. Нарисуйте фигуру, обозначьте ее и опишите, сколько ребер, вершин и граней у каждой из них.
- Научите трехмерную форму с помощью запоминающейся песни или стихотворения, чтобы помочь им запомнить, как она называется и ее части.

- Создавайте 3D-фигуры с помощью маленьких шариков скрученной глины и зубочисток, чтобы скрепить все вместе.
- Позвольте детям слепить геометрические фигуры из пластилина.
- Играйте в игры, чтобы улучшить понимание и распознавание геометрических тел: формы Bump и Scoot — два интересных варианта.
- Проявите творческий подход к пеноблокам и постройте башню или другое сооружение.
- Детям нравятся магнитные детали, которые можно соединять в трехмерные объекты. Имейте их в наличии во время бесплатной игры или во время STEM.
- Научите детей поэтапно рисовать твердую геометрическую фигуру. Они будут удивлены тем, насколько это просто!
- Просмотрите старые журналы, чтобы найти изображения различных трехмерных фигур. Добавьте изображения в якорную диаграмму класса.
- Головоломки, карточки с картинками и упражнения на сопоставление отлично подходят для запоминания форм и развития беглости речи.

Формы в окружающей среде
Основная цель обучения детей формам состоит в том, чтобы они могли видеть формы в окружающей среде и взаимодействовать с окружающей средой благодаря этому пониманию. Заставьте детей постоянно говорить о том, что они видят, и поощряйте их делиться.
Действия
- Создайте якорную диаграмму с примерами каждой формы в их мире. Пусть дети дают и рисуют предположения о том, как каждая фигура «выглядит…».
- Осмотрите класс и укажите на разные фигуры.
- Играйте в игры, в которых дети должны распознавать, какой объект имеет форму. Попробуйте эту игру в бинго!
- Отправляйтесь на поиски мусора снаружи и обратите внимание на увиденное.
- Сфотографируйте реальные примеры форм. Добавьте фотографии в карманную таблицу класса.
- Читайте книги о формах в реальном мире. «Форма вещей» — хорошая книга с множеством иллюстрированных примеров.

Сравнение и сортировка фигур
Предоставьте детям возможность сравнивать разные фигуры друг с другом. После того, как будет достигнуто понимание частей фигур, научите детей сортировать фигуры по одному или двум признакам.
Упражнения
- Раздайте небольшие группы двухмерных или трехмерных фигур на пару учащихся. Попросите их по очереди сортировать фигуры и пусть другой человек попытается угадать их правило сортировки.
- Разложите фигуры стопкой перед классом. Попросите их отсортировать фигуры по типу или по определенному правилу.
- Сортировка карточек с 2D- или 3D-изображениями по заданному атрибуту по классу или по центру
Симметрия
Расскажите детям младшего возраста об отражательной симметрии, которая является зеркальным отражением. Покажите детям, что если провести линию по центру изображения, обе стороны совпадут. Это называется линией симметрии. У одних фигур одна линия симметрии, у других больше. Познакомьте их также с симметрией, встречающейся в природе и окружающей их среде.
Познакомьте их также с симметрией, встречающейся в природе и окружающей их среде.
Деятельность
- Попросите детей найти симметричные предметы в классе и поделиться ими с классом.
- Выйдите на прогулку на природу и поищите симметричные вещи.
- Используйте блоки шаблонов для создания симметричных изображений. Получив половину изображения блока шаблона, создайте зеркальное отражение. Возьмите эти БЕСПЛАТНЫЕ карты симметрии блоков узоров ниже!
- Вместе с другом соберите конструкцию Lego, собрав одинаковые детали с обеих сторон.
- Постройте что-нибудь симметричное из небольших предметов, например из кубиков.
- Создайте произведение искусства, используя концепцию симметрии. Сложите лист бумаги и раскрасьте только с одной стороны. Сложите бумагу так, чтобы получились симметричные пятна краски.
Ресурсы по геометрии и фигурам для K-2
Действия, представленные в этом посте, можно найти в следующих ресурсах.
Группа геометрии и форм для детского сада
Геометрия для первого класса, группа
Блок геометрии и дробей для второго класса
Бесплатные изображения симметрии блоков шаблонов
Распечатайте набор этих блоков, чтобы использовать их вместе с блоками шаблонов, чтобы создать простой математический центр. Детям понравится создавать симметричные узоры!
Получите БЕСПЛАТНЫЕ изображения симметрии блоков шаблонов для вашего математического центра, нажав на изображение ниже .
Книги по геометрии и фигурам
Вверх, вниз и вокруг Кэтрин Айес
Вперед, формы, вперед, Дениз Флеминг
Когда линия изгибается… форма начинается, Ронда Грин
Формы, формы, формы, Тана Хобан
Форма вещей, Дэйл Энн Доддс Прыжок Стюарт Дж. Мерфи
Если бы вы были многоугольником Марси Абофф
Если бы вы были четырехугольником Марси Абофф
Жадный треугольник Мэрилин Бернс
Приготовьтесь! Дэвид Адлер
Три поросенка, один волк, семь волшебных форм Грейс Маккароне
Форма Генри Плакроуза
Формы мыши Эллен Уолш
Форма за формой Сьюз Макдональд
Формы! от National Geographic Kids
Капитан-невидимка и космические формы Стюарт Дж. Мерфи
Мерфи
Материалы по геометрии
Попробуйте комплексную программу Mindful Math
Узнайте о программе Mindful Math и о том, как она может изменить ваш математический блок в лучшую сторону! Эта всеобъемлющая учебная программа по математике доступна для детского сада, первого и второго класса.
Больше математических мероприятий для детей
Номер дневной деятельности
Добавление и вычитание до 20 действий для классной комнаты
Число. БЕСПЛАТНАЯ серия электронных писем Number Sense
Подпишитесь на серию электронных писем Building Number Sense, наполненных эффективными стратегиями, обязательными заданиями и БЕСПЛАТНЫМИ ресурсами для создания распорядка в вашем классе. Все, что вам нужно, чтобы помочь детям развить их чувство числа и в то же время весело провести время!
Имя
Личный адрес электронной почты
Мы используем это поле для обнаружения спам-ботов.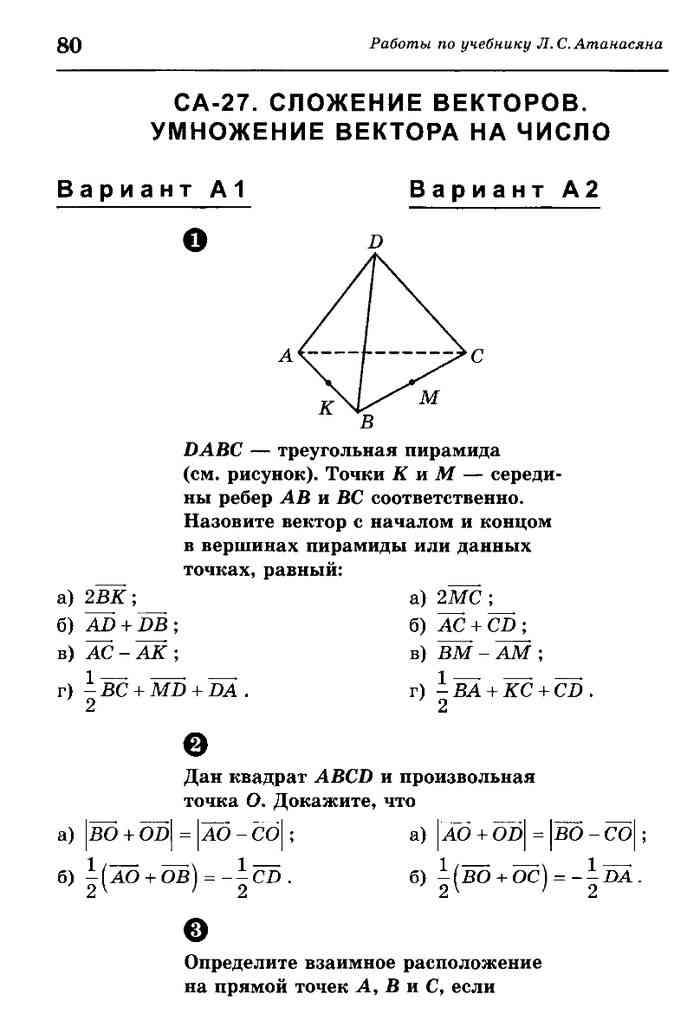 Если вы заполните это, вы будете отмечены как спамер.
Если вы заполните это, вы будете отмечены как спамер.
Я хочу получить бесплатный курс по электронной почте.
Эта форма собирает информацию, которую я буду использовать для отправки еженедельных электронных писем со стратегиями, рекламными акциями и ресурсами. Отписаться в любое время. Работает на ConvertKitРабота учителя геометрии
Перейти к результатам работы
Перейти к уточнению результатов
- Обзор
- Поиск
- Уточнить результаты
- Электронная почта
Ключевые слова
Расширьте область поиска
Уточните область поиска
Подпишитесь на уведомления о вакансиях Получайте новые вакансии для этого поиска по электронной почтеСоздать оповещение
- Хардвик, Массачусетс
- Школа Игл Хилл
Школа Игл Хилл объявляет набор на вакансию учителя математики на 2022-2023 учебный год.
 Первичное преподавание преподавателя…
Первичное преподавание преподавателя…Высшая работа
- Манассас, Вирджиния, США
- Конкурентный
- Государственные школы округа Принс-Уильям
СТАТУС РАБОТЫ: ОТКРЫТА В СИЛУ: 2022-23 ДАТА СООБЩЕНИЯ: 12.08.2022 ДАТА ЗАКРЫТИЯ: 01.06.2023 16:30 НОМЕР СООБЩЕНИЯ: 00043200 ШКОЛА/ОТДЕЛЕНИЕ: Hylton
- Такома Парк, Мэриленд, США
- Конкурентный
- Дон Боско Кристо Рей
Учитель геометрии Don Bosco Cristo Rey High School and Corporate Work Study Program ищет учителя геометрии на полный рабочий день для школы 2022-2023 y
- Вашингтон, округ Колумбия, США
- Конкурентный
- Э.Л. Государственная чартерная школа Хейнса
Учитель геометрии средней школы Хотите помочь создать более справедливый и добрый мир? Верите ли вы, что разнообразие — это мощная сила для школы
?- Нью-Йорк, NY
- Зависит от опыта, местоположения и т.
 д.
д. - Услуги по размещению ATOMS
Служба трудоустройства ATOMS поможет вам найти следующую работу преподавателя математики. ATOMS — это специализированная образовательная рекрутинговая фирма, специализирующаяся на подборе персонала.
- Нью-Йорк, Нью-Йорк
- От 61 000 долларов в год + льготы
- Чартерная школа New Heights Academy
УЧИТЕЛЬ МАТЕМАТИКИ В СТАРШИХ ШКОЛАХ ОСНОВНЫЕ ФУНКЦИИ Учителя будут планировать и проводить значимые учебные мероприятия, создавать возможности для максимального образования…
- Южная Америка, Северная Америка и Карибские острова
- Контракт обычно включает конкурентоспособную заработную плату и социальный пакет.
- Американские международные школы в Америке
Заинтересованы в преподавании на международном уровне? Наши американские международные школы расположены в Южной Америке, Северной Америке и на Карибских островах!
- Южная Америка, Северная Америка и Карибские острова
- Контракт обычно включает конкурентоспособную заработную плату и социальный пакет.



 В.
В. Через данную точку необходимо провести плоскость, содержащую ровно две из трех данных прямых.
Через данную точку необходимо провести плоскость, содержащую ровно две из трех данных прямых.


 Определите взаимное расположение прямых a и b .
Определите взаимное расположение прямых a и b . Как расположена эта фигура по отношению к данным прямым?
Как расположена эта фигура по отношению к данным прямым? Определите угол между данными прямыми, если a α, b || α.
Определите угол между данными прямыми, если a α, b || α.
 Назовите наибольшую сторону треугольника, если SС ВС.
Назовите наибольшую сторону треугольника, если SС ВС. Прямая а не лежит в плоскости α. Определите взаимное расположение прямой а и плоскости α, если а β.
Прямая а не лежит в плоскости α. Определите взаимное расположение прямой а и плоскости α, если а β.

 docx, Математика 1 курс индивидуальная работа КОМПЛЕКСНЫЕ ЧИСЛА.pdf, Практическая работа № 5.docx, контрольная работа 10 класс.docx, 1.2Практическая работа №2Чернышева С.А..docx, 1.1Практическая работа №1 Чернышева С.А..docx, Практическая работа №4 ФГОС 2021.docx, Практическая работа 4 Воронкина О.В. МАОУ СОШ с. Грузино Чудовск, контрольная работа 1 дошкольная педагогика 1.docx, +Самостоятельная работа №2.doc
docx, Математика 1 курс индивидуальная работа КОМПЛЕКСНЫЕ ЧИСЛА.pdf, Практическая работа № 5.docx, контрольная работа 10 класс.docx, 1.2Практическая работа №2Чернышева С.А..docx, 1.1Практическая работа №1 Чернышева С.А..docx, Практическая работа №4 ФГОС 2021.docx, Практическая работа 4 Воронкина О.В. МАОУ СОШ с. Грузино Чудовск, контрольная работа 1 дошкольная педагогика 1.docx, +Самостоятельная работа №2.doc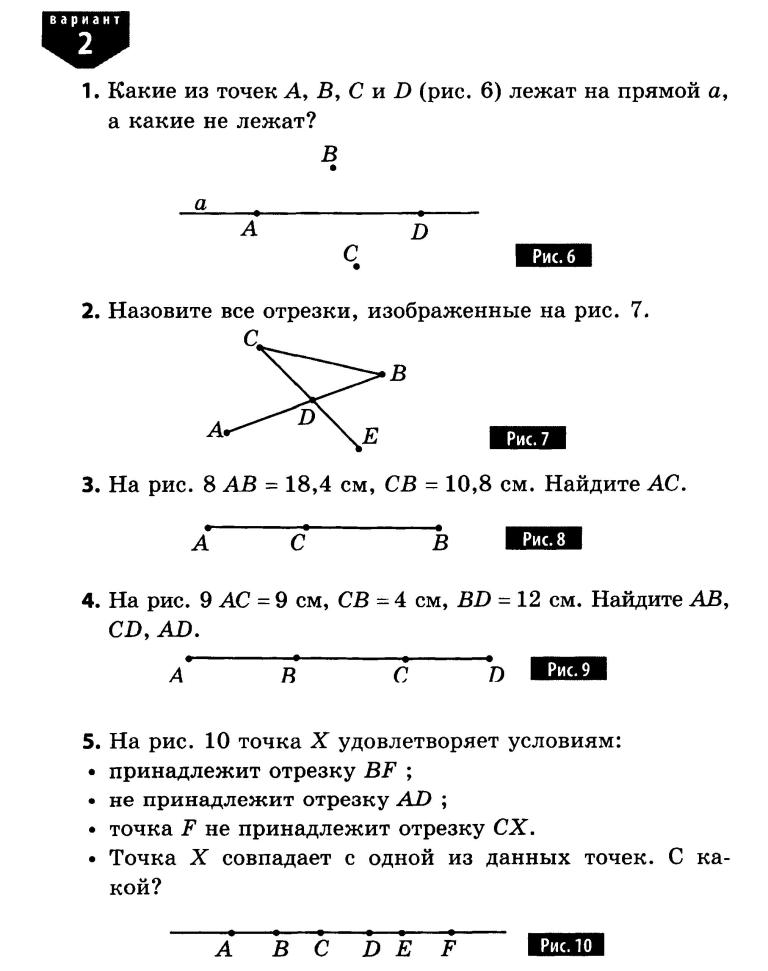 Найдите длины отрезков FS и DS
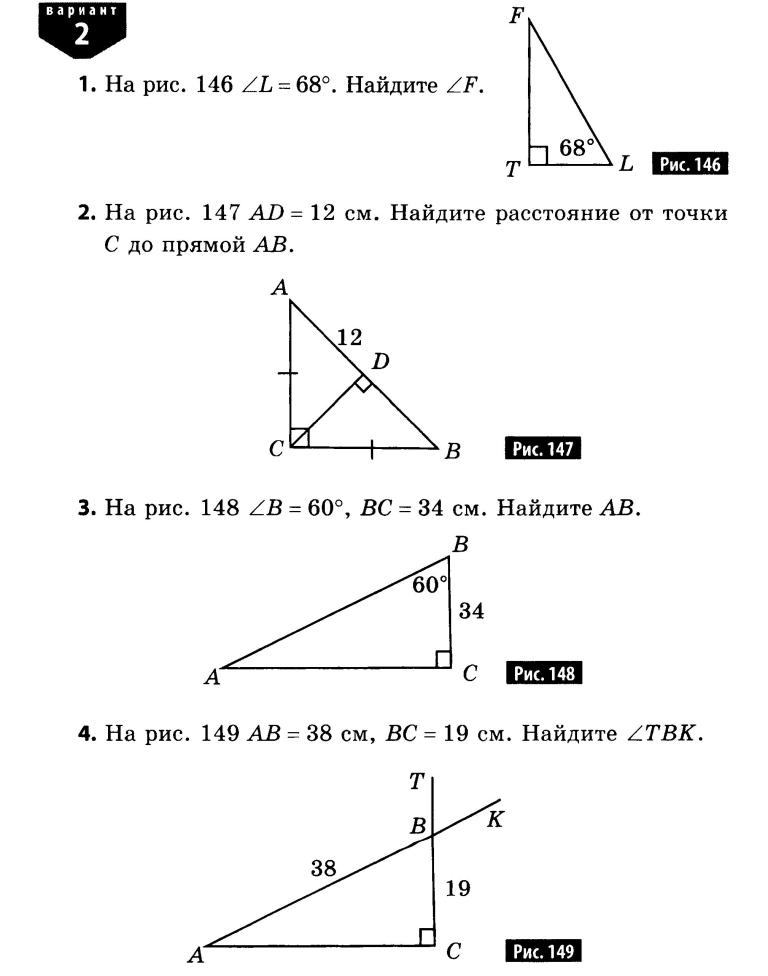
Найдите длины отрезков FS и DS На прямой m лежат точки M, N и К, причем MN = 85мм, NK = 12см. Какой может быть длина отрезка MK в сантиметрах? (1 способ)
На прямой m лежат точки M, N и К, причем MN = 85мм, NK = 12см. Какой может быть длина отрезка MK в сантиметрах? (1 способ) На отрезка АВ лежат точки С и D. Найдите длину отрезка СD, если АВ = 12 см, АС = 3 см, ВD = 4 см.
На отрезка АВ лежат точки С и D. Найдите длину отрезка СD, если АВ = 12 см, АС = 3 см, ВD = 4 см. На луче ОА отмечена точка S так, что ОS =5 см. Найдите отрезков ВS и АS
На луче ОА отмечена точка S так, что ОS =5 см. Найдите отрезков ВS и АS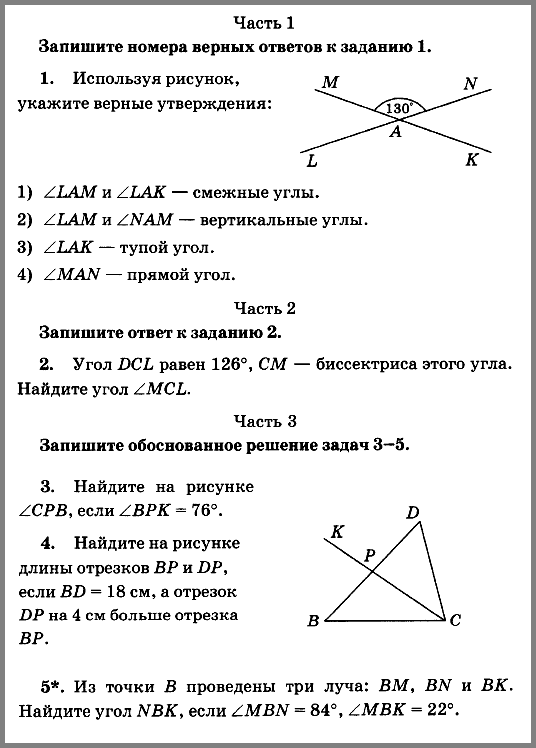


 Первичное преподавание преподавателя…
Первичное преподавание преподавателя… д.
д.