Решебник по математике питерсона 1 класс 3 часть: ГДЗ решебник по математике 1 класс Петерсон

Содержание

ГДЗ часть 1 Урок 9 математика 1 класс Петерсон

ГДЗ часть 1 Урок 9 математика 1 класс Петерсон Автор: Л.Г. Петерсон

Издательство: Ювента 2016

Серия: Учусь учиться

Тип книги: Учебник

Часть: 1, 2, 3

ГДЗ часть 1 Урок 13 математика 1 класс Петерсон

ГДЗ часть 1 Урок 13 математика 1 класс Петерсон
Автор: Л.

Г. Петерсон

Издательство: Ювента 2016

Серия: Учусь учиться

Тип книги: Учебник

Часть: 1, 2, 3

ГДЗ часть 1 Урок 14 математика 1 класс Петерсон

ГДЗ часть 1 Урок 14 математика 1 класс Петерсон
Автор: Л.

Г. Петерсон

Издательство: Ювента 2016

Серия: Учусь учиться

Тип книги: Учебник

Часть: 1, 2, 3

ГДЗ по Математике 3 класс рабочая тетрадь Петерсон часть 1, 2, 3

Математика – это очень сложная наука о свойствах и структуре объектов, которые положены в основание различных теорий. В нее входят следующие дисциплины: арифметика, геометрия, алгебра, тригонометрия, мат. анализ; все они применяют свои особые методы для достижения той ил иной цели. Конечно, у каждого вида разная степень сложности, однако ни один из них нельзя назвать простым или элементарным. Поэтому важно, чтобы школьники с самых первый дней обучения понимали материал. Ведь в таком возрасте ум очень гибкий и усваивать информацию проще. К тому же, с даже самыми базовыми навыками, потом легче постигать достаточно сложные темы.

К сожалению, ученики редко всерьез занимаются этим предметом. Когда формул для заучивания становится много больше, чем раньше, или когда задачи усложняются, ребята не хотят вникать и начинают списывать у кого-то или просто ничего не делают. Это ведет к ухудшению успеваемости, а в дальнейшем, к плохому результату на экзаменах. Конечно, все это ждет ребенка только в старшей школе, однако напрасно полагать, что пока необязательно задумываться об этом. Зачем создавать себе проблемы в будущем, если все можно решить, в настоящем! Нужно просто уделять немного времени индивидуальным занятиям с ребенком, приучать его к этому, что в будущем, он занимался самостоятельно. А отличным помощником в этом будет решебник. Вашему вниманию предлагается сборник, выпущенный издательством «Ювента» в 2016 году.

Какую пользу принесет учащимся учебно-методический комплекс по математике за 3 класс для рабочей тетради (автор: Л.Г. Петерсон)

Предложенный справочник очень удобен в использовании. Придя с работы, вам не придется по несколько часов искать нужную тему в интернете. Ведь онлайн-решебник имеет линейку для быстрой навигации по сайту. Достаточно будет просто включить интернет (на компьютере, телефоне, ноутбуке или планшете). Там вы сможете найти любую интересующую вас информацию, объясненную максимально простым и доступным языком. Задачник поможет не только мамам, папам и их детям, но и педагогам. Они с его помощью смогут составлять классные, самостоятельные и контрольные упражнения. Прочие преимущества:

круглосуточную доступность обеспечивает онлайн-режим;
исключительно верные ответы ко всем задачам;
издания регулярно обновляются;
понятный поиск по таблице;
положительные отзывы пользователей.

Содержание пособия по математике для 3 класса, рабочая тетрадь от Петерсон

Представленная книга включает в себя все разделы, необходимые для изучения на данном этапе обучения:

множество и его элементы;
формула объёма прямоугольного параллелепипеда;
диаграмма Венна. Знаки G и £;
деление с остатком;
умножение на двузначное и трехзначное число.

ГДЗ решебник по математике 1 класс Петерсон

Ответы на задания по математике за первый класс к учебнику Петерсон Л.Г.

Часть 1

Математическая игра:
1
Урок 1. Свойства предметов:
12
Урок 2. Свойства предметов:
12345
Урок 3. Свойства предметов:
1234567
Урок 4. Большие и маленькие:
12345
Урок 5. Группы предметов:
12
Урок 6. Группы предметов:
12345
Урок 7. Сравнение групп предметов:
12345678
Урок 8. Сравнение групп предметов:
123456789
Урок 9.

Сложение:
123456
Урок 10. Сложение:
123456
Урок 11. Вычитание:
1234567
Урок 12. Вычитание:
123456789
Урок 13. Выше, ниже:
1234567
Урок 14. Порядок:
1234567
Урок 15. Раньше, позже:
1234567
Урок 16. Один — много:
1234567
Урок 17. Один:
12345
Урок 18. Два:
1234
Урок 19. Три:
12345
Урок 22. Четыре:
123
Урок 24. Числовой отрезок:
12345678
Урок 25. Числовой отрезок:
1234567
Урок 26. Пять:
1234567
Урок 27. Пять:
12345678
Урок 28. Столько же:
1234567
Урок 29. Столько же:
1234567
Урок 31. Больше, меньше:
1234
Урок 32. Больше, меньше:
1234
Урок 33. Шесть:
12345
Урок 35. Точки и линии:
123456789
Урок 36. Компоненты сложения:
1234567
Урок 37. Области и границы:
123456789
Урок 38. Компоненты вычитания:
1234567
Урок 20. Числа 1 – 3:
1234
Урок 21.

Числа 1 – 3:
1234567
Урок 23. Числа 1 – 4:
1234567
Урок 30. Числа 1 – 5:
1234567
Урок 34. Числа 1 – 6:
123456

Часть 2

Математические игры:
123
Урок 1. Отрезок и его части:
1234567
Урок 2. Семь:
1234567
Урок 3. Ломаная линия. Многоугольник:
1234567
Урок 4. Выражения:
1234567
Урок 5. Выражения:
1234567
Урок 6. Выражения:
1234567
Урок 7. Восемь:
12345
Урок 10. Девять:
1234
Урок 11. Таблица сложения:
123456
Урок 12. Компоненты сложения:
123456
Урок 13. Компоненты вычитания:
1234567
Урок 14. Части фигур:
13456789
Урок 15. Части фигур:
1234567
Урок 16. Нуль:
123456789
Урок 17. Нуль:
12345678
Урок 18. Кубик Рубика:
1234567
Урок 19. Равные фигуры:
1234567
Урок 20. Равные фигуры:
1234567
Урок 21. Волшебные цифры:
12345678
Урок 22. Алфавитная нумерация:
1234567
Урок 23.

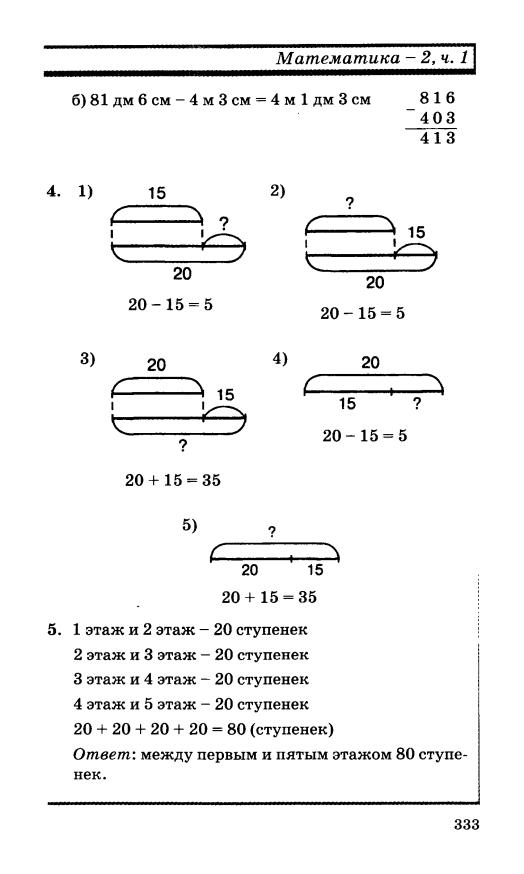Задача:
1234567
Урок 24. Задача:
1234567
Урок 25. Задача:
1234567
Урок 26. Задача:
1234567
Урок 27. Сравнение чисел:
123456
Урок 28. Задачи на сравнение:
1234567
Урок 29. Задачи на сравнение:
1234567
Урок 30. Задачи на сравнение:
123 4567
Урок 31. Задачи на сравнение:
12345678
Урок 32. Повторение:
12345678
Урок 8. Числа 1 – 8:
1234567
Урок 9. Числа 1 – 8:
123456

Часть 3

Повторение:
123456789101112131415161718192021222325262728293031323334353637383940414243444546
Урок 1. Величины. Длина:
1234
Урок 2. Величины. Длина:
123456789
Урок 3. Длина:
123456789
Урок 4. Масса:
123456789
Урок 5. Масса:
123456789
Урок 7. Свойства величин:
123456789
Урок 8. Свойства величин:
1234567
Урок 9. Свойства величин:
123456789
Урок 10. Решение задач:
123456789
Урок 11. Уравнения:
123456789
Урок 12.

Уравнения:
12345678
Урок 13. Уравнения:
12345678
Урок 14. Уравнения:
12345678910
Урок 15. Уравнения:
123456789
Урок 16. Уравнения:
1234567
Урок 17. Уравнения:
12345678
Урок 18. Единицы счета:
123456789
Урок 19. Единицы счета:
1234567
Урок 20. Десять:
123456789
Урок 21. Десять:
123456789
Урок 22. Десять:
12345678
Урок 23. Решение задач:
123456789
Урок 24. Счет десятками:
1234567
Урок 25. Круглые числа:
123456
Урок 26. Круглые числа:
123456789
Урок 27. Дециметр:
12345678910
Урок 28. Счет десятками и единицами:
12345678
Урок 29. Названия чисел до двадцати:
123456789
Урок 30. Названия чисел до двадцати:
12345678910
Урок 31. Названия чисел до двадцати:
123456789
Урок 32. Нумерация двузначных чисел:
12345678
Урок 33. Натуральный ряд:
12345678
Урок 34. Сравнение чисел:
123456789
Урок 35.

Сложение и вычитание двузначных чисел:
12345
Урок 36. Сложение и вычитание двузначных чисел:
12345678
Урок 37. Сложение и вычитание двузначных чисел:
123456789
Урок 38. Таблица сложения:
12345678
Урок 39. Таблица сложения:
12345678910
Урок 40. Таблица сложения:
12345678
Урок 41. Таблица сложения:
1234567
Урок 42. Таблица сложения:
12345678910
Урок 43. Таблица сложения:
123456789
Урок 44. Таблица сложения:
12345678
Урок 45. Таблица сложения:
12345678

Поделись ответами с друзьями в социальных сетях:

ГДЗ по математике 4 класс Петерсон 1, 2, 3 часть учебник

ГДЗ готовые домашние задания учебника по математике 4 класс Петерсон 1,2 и 3 часть ФГОС от Путина. Решебник (ответы на вопросы и задания) учебников и рабочих тетрадей необходим для проверки правильности домашних заданий без скачивания онлайн

Часть 1

1 урок.

Решение неравенства

1 2 3 4 5 6 7 8 9 10 11 12 13

2 урок. Множество решений

1 2 3 4 5 6 7 8 9 10 11 12 13 14

3 урок. Знаки больше или равно и меньше или равно

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

4 урок. Двойное неравенство

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

5 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

6 урок. Оценка суммы

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

7 урок. Оценка разности

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

8 урок. Оценка произведения

1 2 3 4 5 6 7 8 9 10 11 12

9 урок. Оценка частного

1 2 3 4 5 6 7 8 9 10 11 12 13 14

10 урок. Прикидка результатов арифметических действий

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

11 урок. Деление с однозначным частным

1 2 3 4 5 6 7 8 9 10 11 12

12 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

13 урок. Деление на двузначное и трехзначное число

1 2 3 4 5 6 7 8 9 10

14 урок

1 2 3 4 5 6 7 8 9

15 урок

1 2 3 4 5 6 7 8 9

16 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14

17 урок.

Оценка площади

1 2 3 4 5 6 7 8 9 10 11 12 13 14

18 урок. Приближенное вычисление площадей

1 2 3 4 5 6 7 8 9 10 11

19 урок. Измерения и дроби

1 2 3 4 5 6 7 8 9 10 11 12

20 урок. Из истории дробей

1 2 3 4 5

21 урок. Доли

1 2 3 4 5 6 7 8 9 10 11 12 13

22 урок. Сравнение долей

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

23 урок. Нахождение доли числа

1 2 3 4 5 6 7 8 9

24 урок. Проценты

1 2 3 4 5 6 7 8 9 10 11

25 урок. Нахождение числа по доле

1 2 3 4 5 6 7 8 9 10

26 урок

1 2 3 4 5 6 7 8 9 10 11 12

27 урок. Дроби

1 2 3 4 5 6 7 8 9 10 11 12

28 урок. Сравнение дробей

1 2 3 4 5 6 7 8 9 10 11 12 13

29 урок. Нахождение части числа

1 2 3 4 5 6 7 8 9 10 11 12 13 14

30 урок. Нахождение числа по его части

1 2 3 4 5 6 7 8 9 10 11 12 13 14

31 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

32 урок. Площадь прямоугольного треугольника

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Часть 2

1 урок. Деление и дроби

1 2 3 4 5 6 7 8 9 10 11 12 13 14

2 урок. Нахождение части, которую одно число составляет от другого

1 2 3 4 5 6 7 8 9 10 11 12

3 урок. Сложение дробей

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

4 урок. Вычитание дробей

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

5 урок. Правильные и неправильные дроби

1 2 3 4 5 6 7 8 9 10 11 12 13 14

6 урок. Правильные и неправильные части величин

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

7 урок. Задачи на части

1 2 3 4 5 6 7 8 9 10 11 12

8 урок. Смешанные числа

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

9 урок. Выделение целой части из неправильной дроби

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

10 урок. Запись смешанного числа в виде неправильной дроби

1 2 3 4 5 6 7 8 9 10 11 12 13 14

11 урок. Сложение и вычитание смешанных чисел

1 2 3 4 5 6 7 8 9 10 11 12

12 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

13 урок

1 2 3 4 5 6 7 8 9 10 11 12 13

14 урок

1 2 3 4 5 6 7 8 9 10 11 12

15 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

16 урок

1 2 3 4 5 6 7 8 9 10 11 12

17 урок. Шкалы

1 2 3 4 5 6 7 8 9 10 11 12 13 14

18 урок. Числовой луч

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

19 урок. Координаты на луче

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

20 урок. Расстояние между точками координатного луча

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

21 урок. Движение по координатному лучу

1 2 3 4 5 6 7 8 9 10 11 12

22 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14

23 урок. Одновременное движение по координатному лучу

1 2 3 4 5 6 7 8 9 10 11 12 13 14

24 урок. Скорость сближения и скорость удаления

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

25 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

26 урок. Встречное движение

1 2 3 4 5 6 7 8 9 10 11 12 13 14

27 урок. Движение в противоположных направлениях

1 2 3 4 5 6 7 8 9 10 11 12 13 14

28 урок. Движение вдогонку

1 2 3 4 5 6 7 8 9 10 11 12 13

29 урок. Движение с отставанием

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

30 урок. Формула одновременного движения

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

31 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

32 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14

33 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14

34 урок

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

35 урок. Действия над составными именованными числами

1 2 3 4 5 6 7 8 9 10 11 12

36 урок. Новые единицы площади

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Часть 3

Урок 1. Сравнение углов

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Урок 2. Развернутый угол. Смежные углы

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Урок 3. Решение задач

1 2 3 4 5 6 7 8 9 10 11 12

Урок 4. Измерение углов

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Урок 5. Угловой градус

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Урок 6. Транспортир

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Урок 7. Решение задач

1 2 3 4 5 6 7 8 9 10 12 13 14

Урок 8. Построение углов с помощью транспортира

1 2 3 4 5 6 7 8 9 10 11 12

Урок 9. Решение задач

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Урок 10. Центральный угол

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

Урок 11. Круговые диаграммы

1 2 3 5 6 7 8 9 10 11 12

Урок 12. Решение задач

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Урок 13. Столбчатые диаграммы

1 2 3 4 5 6 7 8

Урок 14. Решение задач

1 2 3 4 5 6 7 8 9 10

Урок 15. Пара элементов

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Урок 16. Передача изображений

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Урок 17. Решение задач

1 2 3 4 5 6 7 8 9 10

Урок 18. Координаты на плоскости

1 2 3 4 5 6 7 8 9 10

Урок 19. Построение точек по их координатам

1 2 3 4 5 6 7 8 9 10 11 12 13

Урок 20. Решение задач

1 2 3 4 5 6 7 8

Урок 21. Точки на осях координат

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Урок 22. Решение задач

1 2 3 4 5 6 7 8 9 10 11 12

Урок 23. График движения

1 2 3 4 5 6 7 8 9 10

Урок 24. Чтение и построение графиков движения

1 2 3 4 5 6 7 8 9

Урок 25. Графики одновременного движения

1 2 3 4 5 6 7 8 9

Урок 26. Составление рассказов по графикам движения

1 2 3 4 5 6 7 8 9 10 11

Урок 27. Решение задач

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Повторение

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 84 85 86 87

Приложение

1 Контрольные задания
2 Повторение

Гдз 1 класс петерсон перспектива :: thrivimvelec

Программам 1 3 и 1 4, а также для индивидуальной работы родителей с детьми. ГДЗ домашние задание по математике за 2 класс к учебнику петесона 2013 год часть 1, часть 2, часть 3. Введите в строку поиска только фамилию автора и класс. ГДЗ, Петерсон Л. Г. Страницы ответов. Спишите домашнюю работу по математике из ГДЗ 2 класса к трём частям учебника Петерсона. Подробный решебник гдз по Математике для 1 класса часть,.

Часть 1Выберите нужный номер урока. Следующая статьяГДЗ решебник Информатика 1 класс Горячев. ГДЗ. Петерсон Л. Г. Выберите издание решебника: Математика.1 класс. Петерсон Л. Г. Математика.1 класс. Петерсон Л. Г.2012г. Математика.1 класс. Читать онлайн: ГДЗ ответы, решебник Математика 1 класс Петерсон. Решебник ГДЗДомашние работы Математика Петерсон 1 класс Экзамен Дидактика Петерсон Математика 1 класс Методика Петерсон Построй свою математику. ПОИСК УЧЕБНИКА или ГДЗ. Вы здесь: Главная 1.

Класс Математика Математика 1 класс Петерсон. Загрузка. Математика 1 класс. ГДЗ по математике 1 класс Петерсон. Скачать ГДЗ Математика 1 класс Л. Г. Петерсон вы можете на Самые правильные ответы вы найдете здесь. Предыдущая статьяГДЗ Окружающий мир 1 класс Плешаков. Выберите интересующее вас упражнение из списка. Спиши сейчас онлайн. Порекомендовать ГДЗ в сообществах: Выберите следующее решение: Задание 1. Математика 1 класс Моро. Математика петерсон 1 класс перспектива. ГДЗ: Спиши готовые домашние задания часть.

Класс, решебник Л. Г. Петерсон, онлайн ответы на Учебник по математике для первого класса под авторством Л. Г. Петерсон не самый легкий для понимания. Задачи на повторение. Часть 1, Часть 2, Часть 3. Группа ВК Решебники Переводчик Калькулятор. Класс.1.2. Урок 16. Один — много. Номера заданий из ГДЗ удобно читать и смотреть онлайн с телефонов скачать нельзя. Математика 1 класс. Автор: М. И. Моро. Математика 1 класс Петерсон.

По математике за 1 класс, решебник Л. Г. Петерсон, онлайн ответы на Петерсон 2 кл 2012г таблица. Удобный решебник по математике за 1 класс в трёх частях 1, 2, 3 части поможет ученикам быстро списать решения нужных задачк учебнику Петерсона. Решебник по математике 3 класс, автор Петерсон. Решебник по математике 2 класс. Петерсон Л. Г. Математика 2 класс. ГДЗ и решебник для учебникаГДЗ решебник по математике 1 класс Петерсон Л. Г.

Авторы учебника: Л. Г. Петерсон 2016 год. Ответы ГДЗ по Математике 1 класс Л. Г. Петерсон Рабочая тетрадь. Часть год Ювента Скачать Онлайн и Бесплатно. Прямая ссылка на данную страницу: Код ссылки для вставки в блоги и веб страницы. Введите в строку поиска только фамилию автора и класс. Петерсон Л. Г. Ваши друзья не знают про этот решебник. ГДЗ: Спиши готовые домашние задания часть по математике за 1.

Онлайн. Здесь представлены ответы к учебнику по математике 3 класс Петерсон 1,2 и 3 часть. Математика 1 класс часть. Автор: Л. Г. Петерсон. ГДЗ ответы на вопросы учебника по математике 3 класс Петерсон 1, 2 и 3 часть ФГОС решебник от Путина. Подробный решебник гдз по Математике для 2 класса часть, авторы учебника: Петерсон Л. Г.2016 год. Он может быть использован для обучения математике младших школьников по.

Вместе с Гдз 1 класс петерсон перспектива часто ищут

петерсон 1 класс ответы 2015

петерсон 1 класс ответы 2016

гдз 1 класс математика рабочая тетрадь

петерсон математика 1 класс рабочая тетрадь скачать

петерсон 1 класс скачать бесплатно

петерсон 1 класс самостоятельные и контрольные работы

решебник по математике 1 класс дорофеев

решебник по математике 1 класс моро

Читайте также:

План конспект по аппликации для подготовительной группы осень

Гдз по математики класса автора виленкин

По географии решебник 7 класса обобщение атмосфера и биосфера з.андриевская и.п.галай 42 школы

Набор «Изучение арифметики» для 3 классов

В этом учебнике в твердом переплете 170 уроков. В нем рассматриваются навыки сложения и вычитания в 1 и 2 классах и преподаются факты умножения и деления с помощью таблицы 9 и простого двух- и трехэтапного умножения и деления. Другие рассматриваемые концепции — это значение дроби, эквиваленты меры, денежная стоимость и время. Введены смешанные вычисления и римские цифры.

Небольшая табличка с упражнениями на скорость дает возможность попрактиковаться в основных фактах.Дополнительная практика в математических фактах и задачах чтения предоставляется набором дополнительных мастеров черной линии, которые учителя могут копировать по мере необходимости.

Пособие для учителя содержит подробные инструкции для класса и показывает страницу ученика с заполненными ответами.

Брошюра с рабочими листами имеет отрывные листы, на которых представлены дополнительные концепции, помимо тех, которые изложены в учебнике, а также продвинутые практические занятия, которые помогут лучше подготовить учеников третьего класса к четвертому классу.

Рабочие листы для учителя — это ключ для ответов на рабочие листы буклета.

Дополнительные предметы (не включены):

Содержание руководства для учителя

Материалы для этого курса

Обзор этого курса

Учебные пособия

новых навыков, перечисленных по урокам
Уроки 1 — 170

1. Сложение — суммы 1-10

2. Вычитание — вычитание 1-10

3. Сложение / вычитание 1-10

4. Добавление столбца — суммы 10 и меньше

5. Сложение / вычитание — трижды 11, 12

6.Сложение / вычитание — триплет 13

7. Сложение / вычитание — триплет 14

8. Сложение / вычитание — триплет 15

9. Сложение / вычитание — триплет 16

10. Сложение / вычитание — Тройняшки 17, 18

15. Сложение / вычитание — 2 цифры плюс / минус 1 цифра

16. Дополнение — 2 цифры плюс 2 цифры

17. Вычитание — 2 цифры минус 2 цифры.
Смешанное вычисление — сложите, затем вычтите

19. Вычитание — 3 цифры минус 2 цифры

20.Сложение столбца — суммы 11-18

21. Дополнение — отнесите к десяткам
Смешанное вычисление — вычесть, затем прибавить

24. Дополнение — 3 цифры плюс 2 цифры

25. Дополнение — 3 цифры плюс 3 цифры.
Относить к сотням

27. Вычитание — заимствование из числа 10

32. Вычитание — брать / не брать

35. Вычитание — 3 цифры минус 3 цифры

36. Вычитание — заимствование от 100

38. Вычитание — заимствование из 0

41. Умножить на 1

43.Умножить на 2

47. Умножить на 3
Добавление столбца — 2 цифры

52. Смешанное вычисление — умножьте, затем сложите

53. Умножение — двузначное умножаемое

55. Умножить на 4

56. Сложение / вычитание — перенос / заимствование

57. Сложение / вычитание — перенос / заимствование / ничего

63. Разделить на 1

64. Разделить на 2

66. Разделить на 3

69. Разделить на 4

73. Умножить на 5

76. Умножение — трехзначное умножаемое

77.Разделите, чтобы найти ½

81. Разделить на 5

86. Разделите, чтобы найти ¼

89. Умножить на 6

96. Сложение — относить к числам 10 и 100

97. Разделить на 6

98. Divide — двузначный дивиденд с двузначным частным
Разделите, чтобы найти ⅓

105. Умножить на 7

106. Сложение / вычитание — десятичные знаки и символы доллара

113. Разделить на 7

121. Умножить на 8

124. Умножить — перенести на десятки

126.Разделите, чтобы найти ½, ¼, ⅓

129. Разделить на 8

133. Разделение — горизонтальное (÷)

137. Умножить на 9

138. Вычитание — заимствовать дважды

140. Деление — трехзначный дивиденд с двузначным частным

145. Разделить на 9

146. Умножение — переход к сотням

149. Divide — трехзначный дивиденд с трехзначным частным

153. Деление — просто длинное деление: трехзначное частное с остатком

Узоры

Индекс

Прочтите Интернет-руководство Egghead по геометрии от Peterson’s

, часть 1

49987.png

Глава 1

43581.png

Линии и точки

50773.png

Привет! Я умник. В этой главе я расскажу о следующих понятиях:

49995.png

Что такое линия? 1tip.jpg

Многие геометрические фигуры состоят из линий.

В геометрии слово линия всегда относится к прямой линии.

С технической точки зрения линии продолжаются бесконечно. Они распространяются в космос в обе стороны.

В геометрии это символ линии:

LineArrows.jpg

Стрелки означают, что линия продолжается бесконечно.

Именование строк

Чтобы назвать строку, поставьте рядом с ней букву. Линия на этом рисунке — это линия — .

LineSmallLabel-2.jpg

Что такое точка?

Точка — это определенное место на линии.

Мы почти никогда не видим точки сами по себе в геометрии плоскости. Обычно мы видим их на линиях.

PointonLineArrows.jpg

Примеры

Вот точка на линии p .

PointonLineArrowsSmallLabel-1.jpg

Вот точка на линии z .

PointonLineArrowsSmallLabel-2.jpg

Именование точек

В геометрии, когда мы видим точки на линии, они обычно имеют имена.

Примеры

Эта линия имеет точки B и C .

TwoPointsonLineArrows-1.jpg50866.png

Эта линия имеет точки D, E, и F .

ThreePointsonLineArrows-1.jpg

Точки используются для отображения местоположений на линии.

Практические вопросы

1. Назовите строки, показанные ниже. Назовите первую строку x , вторую строку y и третью строку z .

ThreeLineswithArrows.jpg

2. Назовите строки, показанные ниже. Назовите первую строку q , вторую строку r, и третью строку s .

ThreeLineswithArrows.jpg

3. Нарисуйте точки P и Q на строке ниже.

52240.png

4. Нарисуйте точки R и S на линии ниже. Назовите линию м .

52261.png

1tip_fmt1 Solutions

ThreeLineswithArrowsSmallLabels-1.jpg

ThreeLineswithArrowsSmallLabels-2.jpg 9019 9019 9019 может лежать на точках 9019 Q2009 и 9019 Q4 линия.В этом случае точка P находится слева.

TwoPointsonLineArrows-2.jpg

4. Точки R и S могут лежать в любом месте на линии. На этот раз справа находится точка S .

TwoPointsonLineArrowsSmallLabel-2.jpg

Другие геометрические термины: размеры, плоскости, постулаты и теоремы

Линии и точки — это два основных строительных блока в геометрии. Мы поговорим о них намного больше в оставшейся части этой главы.Прежде чем мы это сделаем, вам следует знать еще несколько концепций.

Размеры

Для измерения геометрических элементов мы обращаемся к различным размерам, таким как длина, высота и ширина. Точки — это единицы, не имеющие размеров. У них нет ни размера, ни длины; они просто указывают местоположения на линии.

Геометрические линии имеют одно измерение. Многие распространенные формы, такие как квадраты и другие плоские фигуры, имеют два измерения. Есть также сплошные фигуры, имеющие три измерения.Мы обсудим их в Части 2.

Плоскости

Плоскость — это особый геометрический компонент, образующий плоскую поверхность. Плоскость — это набор из трех или более точек, которые не находятся на одной прямой. Подобно тому, как линии бесконечно простираются в обе стороны, плоскости простираются бесконечно во всех направлениях. Вот изображение того, как обычно рисуются самолеты:

PlaneZ.jpg

Обратите внимание на заглавную букву Z в правом верхнем углу. Это этикетка самолета Z .

Постулаты 50039.png

Геометрия состоит не только из форм и фигур. Также он действует по определенным правилам. Эти правила определяют, что мы знаем о геометрии и как мы рассчитываем определенные измерения. Постулаты геометрии — это утверждения, которые принимаются как истинные. Они не требуют доказательств, и они не могут быть доказаны. Их принимают как данность.

Теоремы

Теорема похожа на геометрический постулат, за исключением того, что ее можно доказать.В то время как постулаты не могут быть доказаны и считаются истинными, истинность теорем можно показать с помощью ряда логических шагов.

Одна общая теорема, которую мы обсудим в следующей главе, — это теорема Пифагора. Он объясняет отношения между тремя сторонами прямоугольного треугольника. Используя теорему, вы можете найти длину недостающей стороны треугольника.

Линейные сегменты

Части линий иногда называют линейными сегментами .Отрезок линии означает часть линии.

На этом рисунке отрезок линии начинается в точке B и заканчивается в точке C .

TwoPointsonLineArrows-1.jpg

На этом рисунке отрезок линии начинается в точке D и заканчивается в точке E .

TwoPointsonLineArrows-3.jpg

На рисунке ниже представлены три отрезка линии.

ThreePointsonLineArrows-1.jpg

Один отрезок линии начинается в точке D и заканчивается в точке E .

Другой отрезок линии начинается в точке E и заканчивается в точке F .

Третий отрезок линии начинается в точке D и заканчивается в точке F .

Символы

В геометрии есть специальный символ, обозначающий отрезок линии.

50972.png

Линейный сегмент BC записывается как 44276.png

Практические вопросы

1. Как называется линейный сегмент ниже? Используйте символ для отрезка линии.

TwoPointsonLineArrows-4.jpg

2. Как называется сегмент линии ниже? Используйте символ для отрезка линии.

TwoPointsonLineArrows-5.jpg

3. Назовите отрезки линии, показанные на рисунке ниже.

ThreePointsonLineArrows-2.jpg

1tip_fmt1 Solutions

LineSegmentName-1.jpg

LineSegmentName-2.jpg

3. Все сегменты линии 90.ng о длине

Чтобы показать длину отрезка линии, пишем в измерении.

Примеры

Длина 44470.png — 4.

TwoPointsonLineLength-1.jpg

Длина 44521.png — 10.

TwoPointsonLineLength-2.jpg Иногда

Длина поиска 181s не отмечены. Мы можем использовать то, что знаем, чтобы найти недостающие длины.

Примеры

На рисунке ниже мы знаем, что длина 44568.png равна 5, а длина 44597.png равна 5.

ThreePointsonLineLength-1.jpg

Мы можем использовать то, что мы знаем, чтобы найти длину 44650.png. Если 44670.png равно 5, а 44695.png — 5, то 44717.png

ThreePointsonLineLength-2.jpg

Мы добавляем 44778.png плюс 44797.png, чтобы найти длину 44818.png.

Мы также можем использовать вычитание, чтобы найти недостающие длины.

На рисунке показано, что длина 44839.png равна 13, а длина 44875.png — 9.

FindingLengths-Subtraction1.jpg

Чтобы найти длину 44933.png вычтите длину 44957.png из длины 44981.png 13 — 9 = 4.

FindingLengths-Subtraction2.jpg

Длина 45035.png равна 4. Краткий способ записать измерения — использовать букву m.

В данном случае 45107.png

Практические вопросы

1. Какова длина линейного сегмента CD ниже?

TwoPointsonLineLength-3.jpg

2. Длина 45158.png равна 6. Длина 45185.png тоже равна 6.Запишите длину, указанную на рисунке ниже.

ThreePointsonLineArrows-3.jpg

3. Напишите длину отрезка QS на рисунке ниже.

ThreePointsonLineLength-3.jpg

4. Укажите длину отрезка BD на рисунке ниже.

ThreePointsonLineLength-5.jpg

5. Укажите длину отрезка YZ на рисунке ниже.

ThreePointsonLineLength-7.jpg

1tip_fmt1 Решения

1. Длина 45317.png составляет 20.

FigCh2-Page12.jpg

3. Мы добавляем 51321.png плюс 51316.png, чтобы найти длину 51311.png

ThreePointsonLineLength-4.jpg

4. Складываем 51341.png плюс 51334.png, чтобы найти длину 51328.png

ThreePointsonLineLength-6.jpg

5. Правильный ответ показан ниже.

ThreePointsonLineLength-8.jpg

Мы вычитаем 45637.png из 45663.png, чтобы найти длину 45685.png

51027.png

Отличная работа!

А как насчет единиц?

Обычно, когда мы измеряем длину, мы используем какую-то единицу. Например, длина может быть в футах или дюймах. Когда мы используем единицы измерения длины, мы просто записываем данную единицу. Например, размер 45741.png — 6 футов.

Units-1.jpg

Иногда приходится перемножать длины сторон фигуры. В этом случае, когда мы умножаем футы на футы, ответ должен быть выражен в квадратных футах: 6 футов × 4 фута = 24 квадратных фута.Если коротко, то это 24 фута².

Units-2.jpg

Сплошными цифрами можно умножить три измерения. В этом случае единицы выражаются в кубических единицах. Если бы мы умножили 6 футов на 4 фута на 2 фута, получилось бы 48 кубических футов. Мы могли бы записать это сокращенно как 48 футов³.

Units-3.jpg

В следующих главах мы будем больше работать с двухмерными и трехмерными формами.

Средние точки и лучи

Прежде чем мы закончим обсуждение точек и длины, вам нужно знать еще один тип точек.Это называется средней точкой .

Примеры

Средние точки — это точки, которые находятся на полпути между двумя точками на линии. Точка Y является средней точкой 45903.png

ThreePointsonLineLength-9.jpg

Длина 45955.png составляет 8. Точка Y попадает в середину 45977.png.

Точка C является средней точкой 45996.png.

ThreePointsonLineLength-1.jpg

Длина 46037.png составляет 10. Точка C находится на полпути между A и B .

Лучи

Луч — это участок линии, который начинается в одной точке, но продолжается бесконечно. Вот пример:

46064.png

Это луч ST . Это также можно было бы записать так:

FigCh2-Page14.jpg

Практические вопросы

1. Обведите среднюю точку линии ниже.

ThreePointsonLineLength-10.jpg

2. Обведите середину линии ниже.

ThreePointsonLineLength-12.jpg

3. Какой рисунок ниже?

FigCh2-Page15.jpg

A. Ray

B. Линия

C. Отрезок линии

4. Какой рисунок ниже?

51357.png

A. Ray

B. Линия

C. Отрезок линии

5. Какой рисунок ниже?

51364.png

A. Ray

B. Line

C. Линейный сегмент

1tip_fmt1 Solutions

ThreePointsonLineLength-11.jpg

Длина 46205.png — 14. Точка T находится на полпути между S и U .

ThreePointsonLineLength-13.jpg

Длина 46259.png составляет 4. Точка E находится на полпути между точкой D и точкой F .

3. Правильный ответ — B. Цифра представляет собой линию.

4. Правильный ответ — C. Фигура представляет собой отрезок линии.

5. Правильный ответ — A. Фигура — луч.

Параллельные линии

В геометрии есть некоторые особые типы линий. Первый тип называется параллельный.

Параллельные линии — это линии, которые не пересекаются. Они никогда не встречаются.

Примеры

Некоторые параллельные линии выглядят так:

ParallelLines.jpg51398.png

Если на обоих концах есть стрелки, они могут выглядеть так:

ParallelLinesArrows.jpg

Некоторые параллельные линии могут иметь метки. Параллельные линии ниже обозначены m и n :

ParallelLinesArrowsSmallLabels-1.jpg

Symbols

В геометрии почти каждый элемент имеет символ. Символ для параллельных линий: ||

Параллельные линии m и n в предыдущем примере показаны следующим символом:

m || n

Это означает, что линия m параллельна прямой n .

Иногда символ параллельной линии имеет наклон, например: //

Можно использовать любой тип символа. Вы, вероятно, увидите || символ чаще всего.

Пересекающиеся линии

Наряду с параллельными прямыми в геометрии существует еще пересекающихся прямых. Пересекающиеся линии — это линии, пересекающие друг друга.

Примеры

Вот несколько примеров того, как выглядят пересекающиеся линии:

IntersectingLines-1.jpgIntersectingLines-2.jpgIntersectingLines-3.jpg50321.png

Дополнительные примеры

Вот несколько пересекающихся линий со стрелками и метками:

IntersectingLinesArrowsSmallLabels-1.jpg

Нет каких-либо определенных символов для отображения пересекающихся линий. В геометрии пересекающиеся линии относятся к очень немногим элементам, у которых нет символа .

Практические вопросы

1. Нарисуйте символ «линия a параллельна линии b .»

blackboardonly.jpg

2. Нарисуйте линию a и линию b так, чтобы они были параллельны.

blackboardonly.jpg

3. Нарисуйте две линии, j и k , показывая, что j || k . Также покажите, что обе линии продолжаются вечно.

blackboardonly.jpg

4. Нарисуйте пересекающиеся линии x и y .

blackboardonly.jpg

5. Нарисуйте две линии показывает, что линия p пересекает линию q .

blackboardonly.jpg

1tip_fmt1 Solutions

1. Обозначение: a || b

ParallelLinesSmallLabels-2.jpgParallelLinesArrowSmallLabels-2.jpg

Оба верны!

ParallelLinesArrowSmallLabels-3.jpg

IntersectingLinesArrowsSmallLabels-2.jpg

IntersectingLinesArrowsSmallLabels 9163 9017 special type 9017 биссектриса. Биссектрисы или биссектрисы — это линии, пересекающие сегмент прямой в его средней точке. Помните средние точки? Средние точки — это точки, которые находятся на полпути между двумя точками на линии. Биссектрисы делят отрезок прямой на две равные части.

Примеры

На показанном рисунке линия м является биссектрисой. Он делит отрезок XZ на две равные части.

Bisectors-1.jpg

На этом рисунке 46818.png bisects 46847.png Как показано на рисунке, 46874.png

Bisectors-2.jpg

Практические вопросы

1. Отрезок линии VW делит пополам 46923.png в точке S . Если размер 46947.png равен 8, каков размер сегмента RS ?

Bisectors-3.jpg

2. Если 47002.png делит пополам 47027.png, какова мера 47051.png

Bisectors-5.jpg

3. Если сегмент CD делит сегмент пополам AB в точке E , какова мера отрезка EB ?

50728.png

4. Используя тот же рисунок, что и выше, определите размер AB .

5. На показанном рисунке отрезки линии HI и JK имеют одинаковую длину. Отрезок линии HI делит пополам 51661.png в точке L . Какова длина 51652.png

50738.png

1tip_fmt1 Solutions

1. Линейный сегмент VW делит пополам 47106.png в точке S . Следовательно, 47130.png и 47153.png равны. Нам говорят, что размер 47176.png равен 8. Разделите 47197.png на две равные части: 8 ÷ 2 = 4.

Bisectors-4.jpg

2. Нам говорят, что 47221.png bisects 47249.png . На рисунке показано, что 47273.png Следовательно, размер 47298.png также должен быть равен 7. Сложите 47322.png, чтобы определить длину 47353.png

Bisectors-6.jpg

3. Отрезок линии CD пополам отрезок AB на E . Это означает, что E является средней точкой линейного сегмента AB, , что означает, что линейные сегменты AE и EB равны.Нам говорят, что размер отрезка AE равен 7. Таким образом, размер отрезка EB также равен 7.

4. Мы знаем, что оба отрезка AE и EB измеряют 7. Сложив их вместе, мы получим 7 + 7 = 14. Размер отрезка AB равен 14.

5. Нам говорят, что 51679.png делит пополам 51693.png . На рисунке показано, что отрезок JL равен 8, что означает 51689 м.png = 16 (8 + 8). Нам говорят, что оба отрезка линии HI и JK равны, поэтому m 51675.png также равно 16.

Transversals

Прежде чем мы закончим тему строк, вам следует знать еще один тип строк. Это называется поперечным сечением .

Трансверсаль — это линия, пересекающая две другие прямые.

TwoLinesTransversalSmallLabels-1.jpg

Технически трансверсаль — это линия, которая пересекает две или более других прямых в той же плоскости в разных точках.

Важно то, что вы распознаете трансверсаль, когда видите ее.

TwoLinesTransversalSmallLabels-1 (REDARROW) .jpg

В данном случае линия c является поперечной. Он пересекает параллельные линии a и b .

1tip_fmt1

В геометрии мы обычно видим трансверсали, пересекающие две параллельные линии.

Практические вопросы

1. Нарисуйте трансверсаль x , пересекающую линии y и z .Показать прямые y и z как параллельные.

blackboardonly.jpg

2. Нарисуйте две параллельные линии, m и n , пересекаемые поперечной, t .

blackboardonly.jpg

3. Еще раз. Нарисуйте две линии, p || q , пересеченное поперечным, s .

blackboardonly.jpg

4. Нарисуйте три параллельные линии, t , u и v, пересекаются поперечной, w .

blackboardonly.jpg

5. Если линия пересекает три непараллельных линии, считается ли это поперечным?

1tip_fmt1 Solutions

TwoLinesTransversalSmallLabels-2.jpg

Line x может также наклоняться в другую сторону:

TwoLinesTransversalSmallLabels- .jpg

us

ФИЗ 240
УНИВЕРСИТЕТСКОЙ ФИЗИКИ I
ОСЕНЬ 2006

ИНСТРУКТОР: Др.Дорн Петерсон, Phys / Chem Bldg 1162, 568-6487, электронная почта: [email protected]

ВРЕМЯ ОФИСА: МВт 11-12, Вт, Чт 2-330, Проблемные сессии начиная с 2 ^-го неделя П, Чт 4-5. Я доступен и в другое время. Быстрый звонок, чтобы узнать, нахожусь ли я в офисе, наверное самый простой. Запланированный встречу можно назначить в классе или по электронной почте, если вы хотите быть уверены Я буду там, или ты хочешь провести подольше. Часто быстрое электронное письмо даст вам ответ быстрее, чем пытаться увидеть меня в моем офисе (а он часто работает по вечерам и выходные.)

ВЕБ-САЙТ КУРСА: http://csm.jmu.edu/physics/peterson/ph340/

ТЕКСТЫ: Требуется: Университет Physics by Ronald Lane Reese

КАЛЬКУЛЯТОР: Вам необходимо приобрести «синий» Sharp. Калькулятор EL-531WB-BL. Цена на Книжный магазин JMU стоит около 14 долларов. Он понадобится вам для викторин, лаборатории и тесты, поэтому обязательно приносите его на занятия каждый день. Это единственный калькулятор, который вам разрешено использовать. во время тестов, поэтому вам следует приобрести его заранее и привыкнуть к его использовать.

КАТАЛОГ ОПИСАНИЕ: PHYS 240. Университетская физика I. 3 кредита. Кинематика, динамика, сохранение энергии и импульса, колебательное движение, механика жидкости и волны. Дополнительный реквизит: MATH 232 или MATH 235

ОБЩЕЕ ОБРАЗОВАНИЕ: Этот курс удовлетворяет часть требований к кластеру 3 общеобразовательной программы. В частности, я считаю, что 240 и 140 л. вместе дают обширный охват целей обучения 1, 2, 5, 6 и 7 как указан в нижней части кластера 3 веб-страница.

ЭКЗАМЕН : Будет три экзамены в течение семестра и комплексный выпускной. Три «часовых» экзамена запланированы на воскресные вечера, так что у вас будет два часа на то, чтобы завершить тест, чтобы я мог сдать одинаковый экзамен по всем разделам. Планируются следующие испытания:

Дата	Разделы	Комната
Воскресенье, Октябрь1, , 19:00, ,	1-4	HHS 1301
Воскресенье, 29 октября, , 19:00	5-7	HHS 1301
Воскресенье, 19 ноября, , 19:00	8-10	HHS 1209 и 1210
Финал экзамен MW 9:05 разд., Ср, 13 декабря, 8:00 МВт 10:10 секта, Пн, 11 декабря, , 10:30	все	Phys / Chem 2212

Бывает, что по причинам, не зависящим от вас, вам может потребоваться изменить время для теста. Такие запросы будут рассматриваться гораздо более благосклонно, если они сделано хорошо перед тестом. Время от времени катастрофы забастовки в последнюю минуту, и предварительная договоренность не предусмотрена. В таком если вы обязаны связаться со мной по телефону, электронной почте или в записке в мой почтовый ящик физического факультета в течение следующих 24 часов.

ПРИМЕЧАНИЕ: Экзамен 3-го часа проводится в воскресенье перед каникулами в День Благодарения. Обвиняя вас мать за то, что купила вам невозвратный билет на самолет, который требует от вас уйти до этого времени (или другое не менее «хорошее» оправдание) не является поводом для того, чтобы я сдавал вам тест заранее или поздно.

ДОМАШНИЕ РАБОТЫ : Ваше понимание физика должна позволить вам применять принципы, которые вы изучаете, в новых ситуации и комбинации. Один из лучших способов изучить физику — это решение самых разных задач. Домашнее задание будет назначаться еженедельно и сдавать в понедельник. Вы можете обсудить домашнее задание с другими учениками в классе, и вы можете давать и получать подсказки и / или прямую помощь. Просто убедитесь, что кто-то другой не делает домашнее задание и «Показать» вам решение.Этого будет недостаточно, чтобы вы хорошо подготовились к тесты. Это твоя работа понять каждая домашняя задача достаточно хорошо, чтобы вы могли решить ее или подобное один. (Одно из самых больших разногласий между студентами и профессорами закончилось определение «похожий». Если ты понимаешь материал много чего похож. Если вы этого не сделаете, то ваше определение подобия тоже будет узкий. Утверждая, что вопросы теста «Совсем не похожи на домашнее задание» — еще один признак что вы не понимаете материала.)

Ваше выступление на домашнее задание будет оцениваться двумя способами. Каждый понедельник я выбираю одну из домашних задач, изменяю ее немного и дайте его вам как викторину в классе. Помимо возможности получить правильный ответ образованный человек способен четко объяснить, как они пришли к этот ответ. Так что я чувствую, что тебе нужно продемонстрируйте мне, что вы можете написать четкое и тщательное решение проблема физики. Каждое задание задачи будет 3 задачи, отмеченные звездочкой, и я ожидаю, что вы напишете четкую раствор, 1 на страницу.В классе я буду выберите один из них и соберите его. я будет оценивать эти проблемы на основе 50% ясности и 50% правильности.

ЧТЕНИЕ ВОПРОСЫ: Чтение для каждой недели будет назначена среда. Я хочу, чтобы ты проводил время за чтением критически. Вы должны спросить себя, если вы понимаете, о чем говорится. Ты должны взять на себя ответственность за ваш текст, записывая вопросы на полях как ты читаешь. По средам я ожидаю, что ты иметь напечатанный вопрос с вами в классе.Я соберу эти вопросы из 5 разные люди, проецируйте их на класс. Они будут оцениваться по шкале 0, 1 или 3 (в лучшем случае). Если я получу два практически эквивалентных вопросы от разных людей (возможно, они учатся вместе), они будут быть оцененным на основе или 0, 1. Итак, если вы работаете вместе в учебной группе (разрешено и поощряется) и генерирует вопросы в группе, было бы неплохо у вас есть 2 вопроса на случай, если 2 разных человека из вашей группы выбрал.

ДОПОЛНИТЕЛЬНЫЙ КРЕДИТ : Замены для изучение основного материала этого курса. Как следствие, будет не иметь дополнительного кредита для всего класса задания.

КОД ЧЕСТИ : Все работают в викторинах и экзамены должны быть вашей собственной работой, проводиться без сотрудничества или без разрешения помощь. Вы можете вместе работать над домашние задания.

Если вы не делал этого в последнее время, рекомендую вам прочитать хотя бы параграф B Кодекса чести.

СИСТЕМА ОЦЕНКИ:

Товар	Масса
Домашнее задание	25%
Экзамены	50%
Финал Экзамен	25%

МИССИЯ ЗАЯВЛЕНИЕ (требуется для счетчиков bean) : Этот курс соответствует физике Миссия кафедры состоит в том, чтобы служить частью ядра для основных физиков и как родственное требование для специальностей одного или нескольких других факультетов.

ПРОГРАММА КУРСА: Мы рассмотрим главы 1 через 12 Риз. Следующий список могут быть изменены в течение семестра.

гл. 1: все; Гл. 2: все; Гл. 3: все; Гл. 4: все; Гл. 5: все; Гл. 6: 1-2,6,9-11,13; Гл. 7: 1-6,8-9;

гл. 8: 1-10,12-20; Гл. 9: все; Гл. 10: 1-9,15-19; Гл. 11: все; Гл. 12: 1-20

Уровень 1 Раздел 1 Примеры вопросов

Уровень 1, Раздел 1

Ниже приведен пример того, что вы услышите во время раздела теста «Прослушивание».Контент на экране соответствует аудиоплеерам на всей странице. Вы также можете просмотреть стенограмму для каждого элемента, щелкнув ссылку под проигрывателем.

Просматривая вопросы, выберите подходящий ответ для каждого, щелкнув по нему. Когда вы ответили на все вопросы, нажмите «Показать все ответы» в конце страницы, чтобы выделить правильный ответ на каждый вопрос.

Эти типовые вопросы позволяют участникам теста выполнять типы заданий, представленные в тестах TOEFL ITP ^®.Они не предназначены для отображения того, как вопросы теста представлены в буклетах для тестов TOEFL ITP, или для имитации опыта тестирования.

Введение

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

В разделе теста на понимание речи на слух у вас будет возможность продемонстрировать свою способность понимать разговорный английский. Этот раздел состоит из трех частей со специальными указаниями для каждой части. Ответьте на все вопросы, исходя из того, что говорят или подразумевают выступающие в этом тесте.

Направления: В Части A вы услышите короткие разговоры между 2 людьми. После каждого разговора вы услышите вопрос о разговоре. Беседы и вопросы не будут повторяться.

Услышав вопрос, прочтите 4 возможных ответа на экране и выберите лучший ответ, щелкнув по нему.

Вот пример.

На записи вы услышите:

(Женщина) Мне не очень нравится эта картина.

(Мужчина) Я тоже.

(Рассказчик) Что означает этот человек?

На экране вы читаете:

Картина ему тоже не нравится.
Он не умеет красить.
Картины отсутствуют.
Он не знает, что делать.

Из разговора вы узнаете, что картина не нравится ни мужчине, ни женщине. Лучший ответ на вопрос «Что значит мужчина?» А: «Ему тоже не нравится картина». Следовательно, правильный выбор — А.

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

В разделе теста на понимание речи на слух у вас будет возможность продемонстрировать свою способность понимать разговорный английский. В этом разделе есть 3 части со специальными указаниями для каждой части. Ответьте на все вопросы, исходя из того, что говорят или подразумевают выступающие в этом тесте.

Часть A

Проезд

В Части A вы услышите короткие разговоры между 2 людьми.После каждого разговора вы услышите вопрос о разговоре. Беседы и вопросы не будут повторяться.

Услышав вопрос, прочтите 4 возможных ответа на экране и выберите лучший ответ, щелкнув по нему.

Вот пример.

На записи вы услышите:

На экране вы читаете:

Картина ему тоже не нравится.
Он не умеет красить.
Картины отсутствуют.
Он не знает, что делать.

Примеры вопросов для короткой беседы 1–3

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

(Рассказчик) Вопрос 1.

(Мужчина) Может, я сейчас запру компьютерную лабораторию, прежде чем идти домой?

(Женщина) Не беспокойтесь.Я пока не уйду — могу проверить по дороге.

(Рассказчик) Что, вероятно, сделает женщина?

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Ответ на вопрос 1:
1. Заблокируйте компьютерную лабораторию позже
2. Уйти с мужчиной
3. Купить новый замок для компьютерного класса
4. Покажите мужчине, где находится лаборатория

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

(Рассказчик) Вопрос 2.

(Мужчина) Вы не возражаете, если я выключу телевизор?

(Женщина) Я смотрю передачу.

(Рассказчик) Что имеет в виду женщина?

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Ответ на вопрос 2:
1. Мужчина тоже должен смотреть программу.
2. Мужчина должен оставить телевизор включенным.
3. Программа скоро закончится.
4. Она будет смотреть телевизор позже.

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

(Рассказчик) Вопрос 3.

(Женщина) Я слышала, что за выпускной экзамен по математике взимается плата.

(Мужчина) Да. И я могу быть коротким на один курс.

(Рассказчик) Что означает этот человек?

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Ответ на вопрос 3:
1. Он не уверен, какой курс выбрать.
2. Он может не соответствовать требованиям окончания.
3. Курс математики слишком короткий.
4. Дата выпуска изменена.

Часть B

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

Направления: В Части B вы услышите более продолжительные разговоры. После каждого разговора вы услышите несколько вопросов. Беседы и вопросы не будут повторяться.

Услышав вопрос, прочтите 4 возможных ответа на экране и выберите лучший ответ, щелкнув по нему.

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Проезд

В Части B вы услышите более длинные разговоры. После каждого разговора вы услышите несколько вопросов. Беседы и вопросы не будут повторяться.

Услышав вопрос, прочтите 4 возможных ответа на экране и выберите лучший ответ, щелкнув по нему.

Примеры вопросов для продолжительной беседы 4–7

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

(Рассказчик) Вопросы 4–7.Послушайте часть разговора между студентом и профессором.

(Мужчина) Привет, профессор Адамс. Меня зовут Ларри.

(Женщина) Привет, Ларри. Чем я могу помочь вам?

(Мужчина) Мне сказали, что вы размещаете студентов на стажировку по различным университетским программам.

(женщина) Да.

(Мужчина) Ну, меня интересует стажировка в университетском художественном музее … какие обязанности у стажеров, какая квалификация им нужна …

(Женщина) Извините, все вакансии на этот год заполнены…

(Мужчина) Ой! Но я только что увидел объявление на сайте музея сегодня утром.

(Женщина) К сожалению, веб-сайт устарел.

(Мужчина) Я хочу работать в музее после окончания учебы, и мой опыт работы отлично впишется в мое резюме. К тому же это единственная оплачиваемая стажировка в кампусе.

(Женщина) Я понимаю. Однако есть и другие способы получить опыт работы, даже если это не совсем то, что вам нужно. Например, библиотека ищет студентов-волонтеров.

(Мужчина) Библиотека? Но …

(Женщина) Ну, они планируют выставку фотографий, документирующих историю университета. И они ищут студентов-добровольцев, которые помогут просмотреть архивы и выбрать изображения, которые покажут, как университет изменился за последние сто лет.

(Человек) Хм …

(Женщина) Думаю, это всего лишь четырехнедельный проект. И, конечно же, это бесплатно.

(Мужчина) Но это было бы для моего резюме…

(Женщина) Именно так. Почему бы вам не прочитать описание должности — оно размещено на веб-сайте библиотеки. Если вам интересно, дайте мне знать, и я замолвлю за вас словечко перед Эмили Петерсон. Она директор выставок библиотеки и будет проводить собеседования с претендентами.

(Мужчина) Хорошо, я сделаю это прямо сейчас.

(Рассказчик) Вопрос 4. Что в основном обсуждают выступающие?

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Ответ на вопрос 4:
1. Возможности работы для студентов
2. Работа профессора в музее
3. Квалификация мужчины для работы
4. Возможная карьера мужчины после выпуска

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

(Рассказчик) Вопрос 5.Почему студент разочарован?

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Ответ на вопрос 5:
1. Он должен бросить работу в библиотеке.
2. Профессор не разрешает ему посещать ее занятия.
3. Университет недавно закрыл свой музей.
4. Стажировка, которую он хочет, недоступна.

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

(Рассказчик) Вопрос 6.Что будет представлено на выставке в университетской библиотеке?

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Ответ на вопрос 6:
1. Редкие книги
2. Картины
3. Фотографии
4. Исторические сводки

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

(Рассказчик) Вопрос 7. Что можно сделать о директоре выставок библиотеки Эмили Петерсон?

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Ответ на вопрос 7:
1. Она отберет волонтеров библиотеки.
2. Она изучала искусство у студента профессора.
3. Работала в художественном музее.
4. Недавно она присоединилась к библиотеке.

Часть C

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

Указания: В Части C теста вы услышите несколько выступлений. После каждого выступления вы услышите несколько вопросов. Переговоры и вопросы повторяться не будут.

Услышав вопрос, прочтите 4 возможных ответа на экране и выберите лучший ответ, щелкнув по нему.

Вот пример.

На записи вы услышите:

(Рассказчик) Послушайте, как инструктор рассказывает своему классу о телевизионной программе.

(Мужчина) Я хотел бы рассказать вам об интересной телепрограмме, которая будет показана в ближайший четверг. Он будет идти с 9 до 22 часов на 4 канале. Это часть сериала «Тайны биологии человека». Предметом программы является человеческий мозг — как он функционирует и как может работать со сбоями. Темы, которые будут затронуты, — это сны, память и депрессия.Эти темы иллюстрированы великолепной компьютерной анимацией, что облегчает понимание объяснений. Постарайтесь увидеть это шоу. Поскольку мы изучали нервную систему в классе, я знаю, что вы найдете это очень полезным.

Теперь послушайте образец вопроса.

(Рассказчик) Какова основная цель программы?

На экране вы читаете:

Для демонстрации новейшего использования компьютерной графики
Обсудить возможность экономической депрессии
Объяснить работу мозга
Чтобы инсценировать знаменитую детективную историю

Лучший ответ на вопрос «Какова основная цель программы?» это C «, чтобы объяснить работу мозга.»Следовательно, правильный выбор — это ответ C.

«.

А теперь послушайте еще один примерный вопрос.

(Рассказчик) Почему профессор рекомендует посмотреть программу?

На экране вы читаете:

Требуется для всех специальностей науки.
На нем будут представлены исследования профессора.
Может помочь зрителям улучшить свои навыки памяти.
Поможет с курсовой работой.

Лучший ответ на вопрос «Почему спикер рекомендует смотреть программу?» есть D, «Поможет с курсовой работой.»Поэтому правильный выбор — это ответ D.

«.

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Проезд

В Части C теста вы услышите несколько выступлений. После каждого выступления вы услышите несколько вопросов. Переговоры и вопросы повторяться не будут.

Услышав вопрос, прочтите 4 возможных ответа на экране и выберите лучший ответ, щелкнув по нему.

Вот пример.

На записи вы услышите:

Теперь послушайте образец вопроса.

На экране вы читаете:

Для демонстрации новейшего использования компьютерной графики
Обсудить возможность экономической депрессии
Объяснить работу мозга
Чтобы инсценировать знаменитую детективную историю

Лучший ответ на вопрос «Какова основная цель программы?» C, «Объяснять работу мозга». Следовательно, правильный выбор — это ответ C.

А теперь послушайте еще один примерный вопрос.

На экране вы читаете:

Требуется для всех специальностей науки.
На нем будут представлены исследования профессора.
Может помочь зрителям улучшить свои навыки памяти.
Поможет с курсовой работой.

Лучший ответ на вопрос «Почему спикер рекомендует смотреть программу?» стоит D, «Поможет с курсовой работой». Следовательно, правильный ответ — D.

Примеры вопросов для беседы 8–10

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

(Рассказчик) Вопросы 8–10.Послушайте выступление на уроке поведения животных.

(Мужчина) Сегодняшняя дискуссия посвящена обычной реакции животных — зевоту. Словарь определяет зевок как «непроизвольную реакцию на усталость или скуку». Это, безусловно, верно для зевки человека, но не обязательно для зевоты животного. У разных видов действие может иметь совершенно разное значение.

Например, некоторые животные зевают, чтобы запугать злоумышленников на своей территории. Примеры тому — рыбы и ящерицы. Бегемоты зевают, когда хотят уладить ссору.Наблюдателям кажется, что два бегемота зевают друг на друга целых два часа, прежде чем перестают ссориться.

Что касается социальных животных, таких как павианы или львы, они зевают, чтобы установить иерархию в социальных группах, а львы часто зевают, чтобы уменьшить социальную напряженность. Иногда животные зевают по строго физиологическим причинам, то есть для повышения уровня кислорода. И, как ни странно, когда они зевают по такой физической причине, они делают то же, что и люди — они пытаются подавить зевок, отводя взгляд или прикрывая рот.

(Рассказчик) Вопрос 8. В чем суть говорящего?

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Ответ на вопрос 8:
1. Животные зевают по ряду причин.
2. Зевота возникает только от усталости или скуки.
3. Человек зевает так же, как и другие животные.
4. Зевают только социальные животные.

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

(Рассказчик) Вопрос 9.По словам спикера, когда бегемоты могут зевать?

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Ответ на вопрос 9:
1. Когда плавают
2. Когда они ссорятся
3. Когда они общаются
4. Когда едят

=================== НАЧАТЬ РАСШИФРОВКУ СОДЕРЖАНИЯ ===================

(Рассказчик) Вопрос 10. Какая физиологическая причина зевоты упоминается?

=================== КОНЕЦ СОДЕРЖАНИЯ РАСШИФРОВКИ ===================

Ответ на вопрос 10:
1. Для тренировки мышц челюсти
2. Для устранения усталости
3. Чтобы получить больше силы для атаки
4. Чтобы получить больше кислорода

ответов

См. Также:

Новые тенденции в гендерной и математической успеваемости: метаанализ

Abstract

В этой статье мы используем метаанализ для анализа гендерных различий в недавних исследованиях успеваемости по математике.Во-первых, мы провели мета-анализ данных 242 исследований, опубликованных в период с 1990 по 2007 год, в которых участвовали 1 286 350 человек. В целом, d = 0,05, что указывает на отсутствие гендерных различий, и VR = 1,08, что указывает на почти равные мужские и женские различия. Во-вторых, мы проанализировали данные из больших наборов данных на основе вероятностной выборки подростков США за последние 20 лет: NLSY, NELS88, LSAY и NAEP. Величина эффекта для гендерного различия варьировала от -0,15 до +0,22. Коэффициенты дисперсии варьировались от 0.88 до 1,34. Взятые вместе, эти результаты подтверждают мнение о том, что мужчины и женщины одинаково успевают по математике.

Ключевые слова: успеваемость по математике, пол, метаанализ

Политические решения, такие как финансирование однополого образования, а также сохраняющийся стереотип о том, что девочки и женщины не обладают математическими способностями, требуют актуальной информации о гендерные различия в математической успеваемости. Такие стереотипы могут мешать женщинам поступать или продолжать карьеру в области науки, технологий, инженерии и математики (STEM).Сегодня женщины получают 45% дипломов бакалавриата по математике (NSF, 2008a), но женщины составляют лишь 17% преподавателей математики университетов (NSF, 2008b). Мы сообщаем о метаанализе последних исследований гендера и математики. Мы оцениваем величину гендерного различия и проверяем, изменяется ли оно в зависимости от таких факторов, как возраст и уровень сложности теста.

Стереотипы о гендере и математике

Математика и естественные науки стереотипны как мужские области (Fennema & Sherman, 1977; Hyde, Fennema, Ryan, Frost, & Hopp, 1990b, Nosek, et al, 2009).Стереотипы о неполноценности женщин по математике широко распространены среди детей и подростков, родителей и учителей. Хотя дети могут рассматривать мальчиков и девочек как равных по математическим способностям, они, тем не менее, считают, что взрослые мужчины лучше разбираются в математике, чем взрослые женщины (Steele, 2003). Неявные отношения, связывающие мужчин и математику, неоднократно демонстрировались в исследованиях студентов колледжей (например, Kiefer & Sekaquaptewa, 2007; Nosek, Banaji, & Greenwald, 2002).

Родители считают, что математические способности их сыновей выше, чем у их дочерей.В одном исследовании отцы оценили математический «IQ» своих сыновей в среднем в 110 баллов, а у дочерей — в 98 баллов; матери оценили 110 для сыновей и 104 для дочерей (Furnham et al., 2002; см. также Frome & Eccles, 1998). Учителя тоже склонны рассматривать математику как мужскую область. В частности, они переоценивают способности мальчиков по сравнению с девочками »(Li, 1999; но см. Helwig, Anderson, & Tindal, 2001).

Эти стереотипы вызывают беспокойство по нескольким причинам. Во-первых, говоря языком теории когнитивного социального обучения, стереотипы могут влиять на убеждения в компетентности или самоэффективность; корреляционное исследование действительно показывает, что стереотипы родителей и учителей в отношении пола и математики предсказывают восприятие детьми их собственных способностей, даже если фактическая успеваемость по математике контролируется (Bouchey & Harter, 2005; Frome & Eccles, 1998; Keller, 2001; Tiedemann, 2000). ).Убеждения в компетентности важны из-за их глубокого влияния на выбор человеком занятий и окружающей среды (Bandura, 1997; Bussey & Bandura, 1999). Согласно более раннему метаанализу, девочки сообщают о более низкой математической компетентности, чем мальчики, хотя разница невелика ( d = +16, Hyde et al., 1990b). В недавних исследованиях мальчики начальной школы по-прежнему сообщают о значительно более высоких убеждениях в математической компетентности, чем девочки (Else-Quest, Hyde, & Linn, 2010; Fredrick & Eccles, 2002; Lindberg, Hyde, & Hirsch, 2008; Watt, 2004).

Вторая проблема заключается в том, что стереотипы могут пагубно влиять на реальную производительность. Эффекты угрозы стереотипа (Steele, 1997; Steele & Aronson, 1995) были обнаружены для женщин, занимающихся математикой. В стандартной парадигме половине участников (талантливым студентам колледжа) говорят, что тест по математике, который они собираются сдавать, обычно показывает гендерные различия (состояние угрозы), а другой половине говорят, что тест по математике является гендерно справедливым и не показывает. гендерные различия (контроль).Исследования показывают, что студентки колледжа уступают по успеваемости по сравнению с мужчинами в условиях угрозы, но работают наравне с мужчинами в условиях контроля, что указывает на то, что подготовка к гендерным различиям в математике действительно ухудшает успеваемость девочек по математике (например, Ben-Zeev, Fein, & Inzlicht, 2005 ; Cadinu, Maass, Rosabianca, & Kiesner, 2005; Johns, Schmader, & Martens, 2005; Quinn & Spencer, 2001; Spencer, Steele, & Quinn, 1999). Эффекты угрозы стереотипа были обнаружены у детей еще в детском саду (Ambady, Shih, Kim, & Pittinsky, 2001).Другое исследование, измеряющее неявные стереотипы в отношении пола и математики, показало, что эти неявные стереотипы предсказывают успеваемость на курсе математического анализа (Kiefer & Sekaquaptewa, 2007).

Стереотипы играют роль в принятии политических решений, а также в принятии личных решений. Например, школы и штаты могут основывать решения о проведении однополых уроков математики на убеждении, что эти гендерные различия существуют (Arms, 2007).

Пол и успеваемость по математике

Стереотипы о неполноценности женщин по математике резко контрастируют с научными данными о реальной успеваемости.Метаанализ 1990 года обнаружил, что величина эффекта d = 0,15, у мужчин более высокие оценки, для гендерных различий в успеваемости по математике, усредненной по всем выборкам; однако в выборках из общей популяции (т. е. в национальных выборках, классах — в отличие от выборок с исключительно ранним развитием или низкими способностями) женщины набрали больше, но незначительно ( d = -0,05; Hyde, Fennema, & Lamon, 1990a ). Hedges и Nowell (1995), используя наборы данных, представляющие большие вероятностные выборки американских подростков, нашли d = 0.От 03 до 0,26 в разных наборах данных. Более того, до окончания средней школы девочки получают более высокие оценки на курсах математики, чем мальчики (Dwyer & Johnson, 1997; Kenney-Benson et al., 2006; Kimball, 1989). Короче говоря, предыдущее исследование показало, что гендерные различия в успеваемости по математике были очень небольшими и, в зависимости от выборки и критерия результатов, иногда в пользу мальчиков, а иногда в пользу девочек.

Некоторые особенности метаанализа 1990 г. (Hyde et al., 1990a) требуют более подробного описания.Используя компьютеризированный поиск литературы, исследователи определили 100 пригодных для использования исследований, которые дали 254 независимых размера эффекта, представляющих тестирование более 3 миллионов человек. Один из ключевых модераторов анализа изучал величину гендерных различий как функцию возраста и когнитивного уровня теста (вычисление считалось самым низким уровнем, понимание концепций считалось промежуточным, а решение сложных задач считалось самым высоким уровнем). В начальной и средней школе девочки лучше, чем мальчики, справлялись с вычислениями, но разница была небольшой ( d = −0.20 и -0,22 соответственно), а в старшей школе не было гендерных различий. Не было гендерной разницы в понимании математических понятий в любом возрасте. Что касается комплексного решения проблем, не было гендерных различий в начальной или средней школе, но гендерное различие в пользу мужчин проявилось в старшей школе ( d = 0,29). Это последнее гендерное различие, хотя и небольшое, вызывает беспокойство, потому что решение сложных проблем имеет решающее значение для карьеры в STEM.

Второй модераторский анализ изучал величину гендерных различий в успеваемости по математике в зависимости от этнической принадлежности выборки (Hyde et al., 1990а). Поразительным открытием было то, что небольшая гендерная разница в пользу мужчин была обнаружена для белых ( d = 0,13), но не для черных (-0,02) или латиноамериканцев (0,00).

Глубина знаний

Традиционно исследователи утверждали, что девочки могут справляться не хуже или даже лучше, чем мальчики, в тестах на вычисления, которые требуют относительно простых когнитивных процессов (например, Anastasi, 1958). Эти же исследователи пришли к выводу, что мужское превосходство проявляется в тестах, требующих более продвинутой когнитивной обработки, таких как решение сложных задач.Метаанализ 1990 года, проведенный Хайдом и его коллегами, предоставил некоторую поддержку этим идеям, хотя гендерные различия в решении сложных проблем не проявлялись до школьных лет и даже тогда не были значительными.

Современные исследователи математического образования концептуализируют эту проблему сложности когнитивных процессов как вопрос спроса на предметы и глубины знаний, необходимых для решения конкретной задачи. Уэбб (1999) разработал четырехуровневую структуру глубины знаний для определения когнитивной сложности заданий по математике при стандартизированных оценках.В этой структуре Уровень 1 (Отзыв) включает в себя отзыв информации, такой как факты или определения, а также выполнение простых алгоритмов. Уровень 2 (Навык / Концепция) включает элементы, которые требуют от учащихся принятия решений о том, как подойти к проблеме. Эти элементы обычно просят учащихся классифицировать, систематизировать, оценивать или сравнивать информацию. Уровень 3 (стратегическое мышление) включает сложные и абстрактные когнитивные требования, которые требуют от учащихся рассуждать, планировать и использовать доказательства. Уровень 4 (расширенное мышление) требует сложных рассуждений, планирования, развития и обдумывания в течение длительного периода времени.Задания на уровне 4 требуют, чтобы учащиеся соединяли идеи в области содержания или между областями содержания, поскольку они разрабатывают один подход к решению проблем из множества альтернатив. Эта структура глубины знаний использовалась для оценки когнитивных требований тестов, оценивающих успеваемость по математике в исследованиях, рассмотренных здесь.

Новые тенденции

С 1980-х годов произошли культурные сдвиги, которые требуют пересмотра гендерных различий в математике. В 80-е годы очевидным объяснением превосходства мужчин в решении сложных проблем, начиная с учебы в средней школе, были гендерные различия в выборе курса (Мис, Экклс-Парсонс и др., 1982).Девочки реже, чем мальчики, посещали углубленные курсы математики и углубленные научные курсы. Поскольку решение математических задач является важным компонентом курсов химии и физики, студенты могут изучать эти навыки на курсах естествознания так же, как и на курсах математики. Однако сегодня гендерный разрыв в изучении курсов исчез во всех областях, кроме физики. В выпускном классе средней школы 2005 г. 7,7% юношей и 7,8% девушек изучали математический анализ; 57,8% девочек и 50,6% мальчиков изучали химию; и 32.Физику изучали 8% девочек и 36,8% мальчиков (NSF, 2008c). Поскольку курсы, взятые учащимися, влияют на их успеваемость по математике, мы ожидаем, что гендерные различия в решении сложных задач в старшей школе уменьшились.

Кроме того, межнациональные данные показывают, что гендерный разрыв в успеваемости по математике сужается или даже обращается вспять в обществах с большим гендерным равенством (например, Швеция и Исландия), по сравнению с теми, кто имеет большее гендерное неравенство (например, Турция) (Else- Quest, Hyde, & Linn, 2010; Guiso, Monte, Sapienza, & Zingales, 2008).Поскольку за последние 30-40 лет Соединенные Штаты продвинулись к гендерному равенству, гендерный разрыв в успеваемости по математике должен был сократиться.

Результаты недавнего анализа данных государственных оценок успеваемости по математике свидетельствуют о том, что гендерный разрыв в успеваемости по математике в США действительно уменьшился или даже исчез (Hyde, Lindberg, Linn, Ellis, & Williams, 2008). Эти данные имели ряд ограничений и поднимали некоторые вопросы, которые заслуживают анализа в рамках более крупного исследования.Во-первых, они были основаны только на тестах, проведенных штатами для удовлетворения требований законодательства «Ни одного ребенка, оставленного без внимания». Предметы, затрагивающие уровни 3 или 4 глубины знания, заметно отсутствовали. Во-вторых, данные были получены только от учащихся 2–11 классов; Таким образом, тенденции в гендерных различиях после 11 класса (17 лет) не могли быть оценены. В-третьих, распределение показателей мужчин и женщин было доступно только для части выборки. Доступные результаты подняли интригующие вопросы о гендерных различиях в решении сложных проблем, поскольку в некоторых подгруппах женщины превосходили мужчин в верхней части распределения.

Гендер и изменчивость

Большая часть исследований была сосредоточена на гендерных различиях среднего уровня, но изменчивость (дисперсия) остается проблемой, даже когда средние значения схожи. Гипотеза большей мужской изменчивости была первоначально предложена в 1800-х годах и защищена такими учеными, как Чарльз Дарвин и Хэвлок Эллис, чтобы объяснить, почему существует избыток мужчин как в домах для умственно отсталых, так и среди гениев (Shields, 1982). С точки зрения современной статистики, гипотеза состоит в том, что, независимо от различий среднего уровня, мужчины имеют большую дисперсию, чем женщины, по интересующим интеллектуальным характеристикам.Таким образом, гипотеза утверждает, что мужчины с большей вероятностью, чем женщины, занимают как верхнюю, так и нижнюю часть статистического распределения успеваемости по математике. Обычно вычисляемая статистика представляет собой коэффициент дисперсии (VR), отношение мужской дисперсии к женской дисперсии. Таким образом, значения> 1,0 указывают на большую изменчивость самцов. Основываясь на данных нормирования тестов, Фейнголд (1992a) нашел VR 1,11 для числовых способностей DAT, 1,20 для SAT-Math и 1,02 для подтеста WAIS Arithmetic.Хеджес и Ноуэлл (1995) обнаружили, что показатель VR составляет от 1,05 до 1,25 для тестов по математике, проводимых среди национальных выборок подростков, таких как NLSY и NELS: 88. Анализ недавних данных оценки состояния, описанный ранее, показал, что VR находится в диапазоне от 1,11 до 1,21 (Hyde et al., 2008). Таким образом, есть некоторые свидетельства большей вариабельности успеваемости по математике среди мужчин, хотя коэффициенты дисперсии не очень однобокие. Гипотеза большей мужской изменчивости, конечно, является описанием данных, а не их объяснением, но, если она верна, она может частично объяснять обнаружение избытка самцов на очень высоких уровнях математических способностей (Hedges & Friedman, 1993). ).Одна из целей этого метаанализа состояла в том, чтобы повторно оценить гипотезу о большей мужской вариабельности для успеваемости по математике с использованием современных данных.

Текущее исследование

Несколько факторов требуют проведения нового метаанализа исследований гендерных и математических способностей. Во-первых, с момента проведения метаанализа 1990 г. было накоплено около 18 лет новых данных (Hyde et al., 1990a). Во-вторых, за последние два десятилетия произошли культурные сдвиги. В частности, девочки сейчас посещают углубленные курсы математики и некоторые курсы естествознания в старших классах школы с той же скоростью, что и мальчики, что сокращает разрыв в выборе курсов.Ожидается, что масштабы гендерных различий в успеваемости по математике будут даже меньше, чем это было в метаанализе 1990 года; Особый интерес представляет гендерное различие, благоприятствующее мальчикам в решении сложных проблем в старшей школе, и уменьшилось ли это различие в последние годы. В-третьих, продвинулись статистические методы метаанализа. Во время метаанализа 1990 г. были доступны только модели с фиксированными эффектами. С тех пор модели с фиксированными эффектами подверглись критике, и были разработаны модели со случайными эффектами и смешанные (Hedges & Vevea, 1998; Lipsey & Wilson, 2001).В текущем метаанализе используется модель смешанных эффектов, преимущества которой подробно описаны ниже.

Нашей целью в этом метаанализе было дать ответы на следующие вопросы:

Какова величина гендерных различий в успеваемости по математике с использованием метрики d ?
Меняется ли направление или величина гендерных различий в зависимости от глубины знаний, полученных в ходе теста?
С точки зрения развития, в каком возрасте появляются или исчезают гендерные различия?
Есть ли различия по U.S. этнических групп или народов, в направлении или величине гендерных различий?
Снизились ли масштабы гендерных различий в успеваемости по математике с 1990 по 2007 год?
Отличаются ли мужчины большей разницей в оценках, и если да, то насколько?

В исследовании 1 эти вопросы были рассмотрены с использованием традиционных методов метаанализа, которые включают выявление всех возможных исследований с использованием баз данных статей. В исследовании 2 вопросы рассматривались с использованием альтернативного метода, предложенного Hedges and Nowell (1995), который включает анализ недавних крупных национальных университетов.S. наборы данных, основанные на вероятностной выборке. Межнациональные наборы данных с вероятностной выборкой были проанализированы другими исследователями (Else-Quest, Hyde, & Linn, 2010; Guiso et al., 2008; Penner, 2008).

Исследование 2

Метод

Большие наборы данных в США

Из исследования 1 были исключены статьи, в которых сообщалось об анализе вторичных данных из крупных национальных наборов данных, поскольку исходные данные из этих исследований были получены непосредственно для отдельного анализа, который составляет Исследование 2. Наборы данных были включены в Исследование 2, если (а) они включали релевантную информацию об успеваемости по математике, (б) представляли данные, собранные после 1990 г., (в) были национально репрезентативными с большой выборкой и (г) предоставляли статистические данные как для мужчин, так и для женщин.Международные наборы данных были исключены из исследования 2, поскольку они были тщательно проанализированы в других источниках литературы (см. Else-Quest, Hyde, & Linn, 2010). Следующие большие наборы данных США были проанализированы в исследовании 2: Национальное лонгитюдное исследование молодежи — 1997 (NLSY97, Бюро статистики труда США, nd), Национальное лонгитюдное исследование в области образования (NELS88, Национальный центр исследований в области образования nda), Продольное исследование американской молодежи (LSAY, nd), и Национальная оценка образовательного прогресса (NAEP, Национальный центр исследований в области образования, n.d.b).

NLSY — 97 начал сбор данных в 1997 году и отслеживал студентов каждый год до 2002 года. При первой оценке 58,3% участников были белыми, 27,0% — черными, 1,7% — азиатскими американцами, 0,8% — американскими индейцами и 12,4% не сообщили об этнической принадлежности. Успеваемость по математике измерялась с помощью PIAT-R (Markwardt, 1998). Во время первого раунда сбора данных тест проводился для всех участников девятого класса или ниже. Во время второго раунда сбора данных тест проводился для всех участников, которые проходили тест во время первого раунда, а также тех, кому на 31 декабря 1996 года было не менее 12 лет.PIAT-R состоит из элементов с несколькими вариантами выбора в трех областях математического содержания: 1) основы (т.е. количество, размер и выбор формы), 2) основные факты (например, сложение, вычитание, умножение, деление) и 3) приложения ( т.е. алгебра, геометрия, дроби, задачи со словами и числовые отношения). Математическая оценка PIAT-R начинается с вопроса, соответствующего возрасту, и возрастает или уменьшается сложность до тех пор, пока юноша не установит «базовый», то есть когда юноша правильно ответит на пять последовательных вопросов.После достижения базального уровня сложность вопросов возрастает до тех пор, пока не будет достигнут «потолок», когда юноша неправильно ответит на пять из семи последовательных вопросов. Затем потолок корректируется с учетом неправильных ответов, полученных между базовым и потолочным значениями, и стандартизируется со средним значением 100 и стандартным отклонением 15. В текущем исследовании достижения по математике определяются с использованием стандартизированной оценки по математике PIAT-R для каждой оценки.

NELS88 — это лонгитюдное исследование, начавшееся с обследования 8-х классов в 1988 г. и отслеживавшее их в 10-м и 12-м классах в 1990 и 1992 гг.При первой оценке 67,0% участников были белыми, 12,2% — черными, 12,7% — латиноамериканскими, 6,3% — американскими азиатами и 1,6% не сообщили об этнической принадлежности. Математический тест NELS был разработан Службой образовательного тестирования и состоял из вопросов с несколькими вариантами ответов. Содержание задания включало арифметику, алгебру, геометрию, данные и вероятность, а также расширенные темы. Одна версия теста проводилась в базовом году, а три версии теста проводились во время первого и второго последующих наблюдений.В зависимости от результатов теста по математике в базовом году учащиеся были разделены на три группы (с низким, средним и высоким уровнем способностей), и им были назначены варианты теста по математике на первом и втором последующих занятиях в соответствии с их способностями. Каждый тест, независимо от способностей, оценивал навыки / знания, понимание и решение проблем во всех пяти областях содержания, описанных выше. В дополнение к тесту с множественным выбором, на экзамене 1992 года ученикам 12-х классов был предложен построенный ответный тест; этот тест включал элементы, исследующие измерения, геометрию и анализ данных.

Модель LSAY наблюдала за молодежью с 1987 по 1992 год с оценками каждый год с 7 по 12 классы. При первой оценке 70% участников были белыми, 11% — черными, 9,2% — латиноамериканцами, 3,5% — американцами азиатского происхождения, 1,5% были американскими индейцами, а 4,8% не сообщили об этнической принадлежности. На каждой оценке учащиеся проходили тест по математике с несколькими вариантами ответов, в ходе которого оценивались навыки геометрии, измерения, анализа данных, алгебры и простых операций (полный список задач см. На сайте http: // lsay.msu.edu/instruments_006.html).

Математическая оценка NAEP была единственной крупной базой данных США в текущем исследовании, которое не было продольным. Он состоял из двух разных исследований: оценки долгосрочных тенденций и основной оценки.

Оценка долгосрочных тенденций NAEP проводилась каждые четыре года с 1992 по 2004 год учащимся в возрасте 9, 13 и 17 лет. Этническое разнообразие было разным для каждой оценки и возрастной группы, но состояло из белых ( M = 74.07%, SD = 4,87), чернокожие ( M = 14,78%, SD = 1,31), латиноамериканцы ( M = 7,82%, SD = 3,31) и те, кто не указал этническую принадлежность ( M = 3,29%, SD = 1,38). Математическое оценивание в этом исследовании практически не изменилось с момента его начала в 1978 году. Оно включало как вопросы с множественным выбором, так и короткие построенные ответы, которые сосредоточены на математических навыках, включая числовые операции, измерения, алгебру и геометрию.

В отличие от данных о долгосрочных тенденциях, основная оценка NAEP отбирала учащихся по классам, а не по возрасту.Основная оценка давалась учащимся 4-х и 8-х классов каждые два года с 1990 по 2007 гг. В период с 1990 по 2000 гг. Были включены двенадцатиклассники. Этническое разнообразие было разным для каждой оценки и возрастной группы, но состояло из белых ( M = 67,07%, SD = 6,43), чернокожие, ( M = 15,94%, SD = 0,99), латиноамериканцы ( M = 11,89%, SD = 4,89), американцы азиатского происхождения ( M = 3,17%, SD = 1,66), американские индейцы ( M = 0.94%, SD = 0,42) и тех, кто не указал этническую принадлежность ( M = 3,29%, SD = 1,38). В математической части основной оценки NAEP использовались вопросы с множественным выбором, короткие построенные ответы и длинные построенные ответы. В дополнение к математическим навыкам, оцениваемым в ходе анализа долгосрочных тенденций, основной анализ также включал навыки анализа данных и вероятности.

Уникальным аспектом оценок NAEP является то, что оценки эффективности строятся с помощью IRT (теории ответов на вопросы).Таким образом, они не являются прямым отражением числа задач, которые любой учащийся понял правильно или неправильно. Скорее, образец правильных ответов используется для построения оценки «вероятного значения», которая отражает общее понимание учащимся математики. См. Мислеви, Джонсон и Мураки (1992) для дальнейшего обсуждения этого подхода и его преимуществ при оценке численности населения. Наш анализ основан на этих вероятных оценках шкалы значений, а также на соответствующих весах и стандартных ошибках, о которых сообщает NAEP.

Анализ данных

Анализ данных для исследования 2 был аналогичен исследованию 1. Были рассчитаны все величины эффекта, и была использована модель смешанных эффектов, чтобы определить, были ли размеры эффекта в каждом наборе данных неоднородными. Если величина эффекта была неоднородной, для прогнозирования гендерных различий в успеваемости по математике применялась взвешенная обычная регрессия наименьших квадратов.

Модерирующими переменными, использованными в исследовании 2, были возраст, год публикации, процентное соотношение каждого типа задач (числовое значение, алгебра, геометрия, измерение), процент проблем в каждом типе формата (множественный выбор, короткий ответ, открытый), и процент белых, черных и латиноамериканцев в каждой выборке.Как и в исследовании 1, также были рассчитаны коэффициенты дисперсии. Для больших наборов данных было доступно больше информации о характеристиках выборки и теста, чем было доступно для исследований, раскрытых в обзорах литературы в Исследовании 1. Таким образом, за исключением глубины знаний, мы смогли закодировать переменные-модераторы более подробно и с большим количеством деталей. модераторы, которые были закодированы как категориальные переменные в Исследовании 1, считались непрерывными переменными в Исследовании 2. Например, Исследование 1 закодировало, использовали ли тесты множественный выбор, короткий ответ или открытые вопросы, тогда как Исследование 2 закодировало процент вопросов в каждом формате. .

Результаты

Для всех наборов данных в исследовании 2 средневзвешенная величина эффекта составила d = +0,07. Средневзвешенный коэффициент дисперсии по всем наборам данных составил 1,09. Величина эффекта была неоднородной: Q _t (55) = 393,04, p <0,001, с компонентом дисперсии случайных эффектов 0,001. Различия между национальными наборами данных были значительным источником неоднородности Q _b (4, 55) = 43,12, p <.001; поэтому мы описываем результаты по каждому набору данных по очереди.

Величина эффекта для каждой оценки NLSY представлена в таблице 4. Средневзвешенная величина эффекта для всех шести оценок NLSY составила d = +0,08. Средневзвешенный коэффициент дисперсии составил 1,05. Размеры эффектов для NLSY-97 были однородными, Q _w (5) = 5,72, p = 0,33.

Величина эффекта для каждой оценки NELS: 88 представлена в таблице 5. Средневзвешенная величина эффекта по всем восьми оценкам составила d = +0.10. Средневзвешенный коэффициент дисперсии для NELS: 88 составил 0,94. Размеры эффекта в рамках NELS: 88 были неоднородными, Q _w (7) = 18,66, p <0,01.

Величина эффекта для каждой оценки LSAY представлена в таблице 6. Результаты LSAY указывают на небольшие или незначительные гендерные различия для каждой оценки. Средневзвешенная величина эффекта для всех шести оценок составила d = -0,07. Средневзвешенный коэффициент дисперсии составил 1,26. Размеры эффекта были однородными, Q _w (5) = 2.50, p = 0,78.

Величина эффекта для каждой оценки NAEP представлена в таблице 7. Результаты NAEP указали на небольшие или незначительные гендерные различия во всех классах. Средневзвешенная величина эффекта по всем 18 оценкам данных долгосрочного тренда составила d = +0,09. Средневзвешенная величина эффекта по всем 18 основным оценкам составила d = +0,06. Средневзвешенный коэффициент дисперсии для данных долгосрочного тренда составил 1,13, а для основной оценки — 1.04. Величина эффекта как для данных долгосрочного тренда, так и для основной оценки была однородной, Q _w (17) = 16,05, p = 0,52 и Q _w (17) = 12,88, p = 0,74 соответственно.

Неоднородность размеров эффекта в наборах данных указывает на то, что эти исследования не являются копиями друг друга, а скорее различаются по некоторым параметрам. Поэтому мы провели дополнительный анализ модерации, чтобы выяснить, могут ли характеристики выборки или тестовые характеристики объяснить неоднородность размеров эффекта в наборах данных.Эти анализы проводились с использованием аналога множественной регрессии, в которой каждый уровень каждого модератора вводился в качестве отдельного предиктора величины эффекта исследований. Результирующие бета-версии могут быть интерпретированы во многом как коэффициенты корреляции, с положительными значениями, указывающими на увеличение размера эффекта при увеличении значения модератора (относительное преимущество для мужчин), и отрицательными значениями, указывающими на уменьшение размера эффекта при увеличении значения модератора ( относительное преимущество для самок).

Как видно из таблицы 8, неоднородность исследований объясняется двумя аспектами тестов: тип задачи и математическое содержание. Что касается типа проблемы, тесты с более высокой долей множественного выбора и открытых заданий дали меньшую величину гендерного эффекта, тогда как тесты с более высокой долей коротких ответов дали большую величину гендерного эффекта. Это открытие удивило нас, учитывая, что три больших набора данных (LSAY, NLSY, NELS) имели 100% множественный выбор, и только один из них имел отрицательный общий размер эффекта; Если пункты с множественным выбором дают значительное преимущество для женщин, мы могли бы ожидать отрицательных эффектов во всех трех исследованиях.Поэтому мы провели дополнительный анализ, рассматривая только 36 размеров эффекта NAEP, у которых есть вариации в пропорции множественного выбора, коротких ответов и открытых вопросов. При рассмотрении только размеров эффекта NAEP мы обнаружили другую картину результатов, так что мужчины лучше справлялись с тестами с большей долей вопросов с множественным выбором (β = +.29), а женщины лучше справлялись с тестами с большей долей. коротких ответов и открытых заданий (βs = −32 и −19 соответственно).Таким образом, тип задачи оказал такое же влияние на гендерные различия в NAEP, что и в исследовании 1.

Что касается математического содержания, тесты с более высокой долей элементов алгебры дали меньшую величину эффекта (женщины справились относительно лучше), а тесты с более высокой долей элементов измерения давал больший эффект (мужчины выступали относительно лучше). Три других типа математического содержания не были значимыми предикторами величины эффекта в этом анализе.

Что касается глубины знаний, тесты, содержащие задания на уровне 3 или 4, дали больший эффект (мужчины лучше или женщины хуже).Все тесты содержали предметы на уровнях 1 и 2, и поэтому мы не могли исследовать конкретные эффекты предметов на этих уровнях.

Этнический состав выборки не повлиял на величину гендерных различий в успеваемости по математике. Однако возраст был незначительным предиктором величины эффекта ( p = 0,0516), при этом более старые выборки давали относительно большие гендерные различия в пользу мужчин.

Обсуждение

Мы предложили ответить на шесть вопросов с помощью этого метаанализа.Мы рассмотрим каждый вопрос по очереди.

Во-первых, каковы масштабы гендерных различий в успеваемости по математике, согласно современным исследованиям? Если взять исследование 1 и исследование 2 вместе, ответ, похоже, таков, что больше нет гендерных различий в успеваемости по математике. Для исследования 1 d значений составили в среднем +0,05 на основе данных от 1 286 350 человек. Для исследования 2, d значений в среднем составили +0,07 на основе данных от 1 309 587 человек. Эти результаты согласуются с недавним анализом U.S. данные о государственных оценках молодежи со 2 по 11 классы, которые показали, что девочки достигли паритета с мальчиками в успеваемости по математике (Hyde, Lindberg, Linn, Ellis, & Williams, 2008).

Во-вторых, меняется ли направление или величина гендерных различий в зависимости от глубины знаний, полученных в ходе теста? Сама по себе глубина знаний не была значимым предиктором различий в величине эффекта в исследовании 1. Однако исследование 2 показало, что может быть умеренное влияние глубины знаний на гендерные различия в успеваемости по математике, причем те, которые содержат большую долю предметы на уровне 3 или 4 в пользу мужчин.Эти результаты несовместимы с недавним анализом данных NAEP, в котором изучались гендерные различия по вопросам, отнесенным NAEP к категории трудных и к уровням 3 или 4 глубины знаний; в 12 ^{-м классе} среднее значение d = +0,07 или незначительная разница (Hyde et al., 2008). Однако одновременное изучение глубины знаний и возраста в исследовании 1 (таблица 3) указывает на преимущество мужчин (d = 0,16) в задачах уровня 3 или 4 в старшей школе, что согласуется с более ранним метаанализом Хайда. и коллеги (1990).Этот вывод, однако, основан только на 3 исследованиях, поэтому его следует интерпретировать с осторожностью. В очень немногих исследованиях использовались предметы, требующие такой большей глубины знаний, но это именно тот навык, который требуется для высокоуровневой карьеры в STEM.

В-третьих, с точки зрения развития, в каком возрасте появляются или исчезают гендерные различия? В соответствии с предыдущими метаанализами, являются ли гендерные различия более значительными в старшей школе, чем в начальной или средней школе? Наборы данных, рассмотренные в исследовании 2, показали незначительное увеличение величины эффекта с увеличением возраста (β = +.24). Это согласуется с результатами исследования 1, в котором были обнаружены гендерные различия, близкие к 0 для учащихся начальной и средней школы, и небольшие эффекты в пользу мужчин для учащихся старших классов и колледжей ( d s = +0,23 и +0,18, соответственно) . Эти результаты также не согласуются с данными Hyde et al. (2008) анализ данных государственных аттестаций, который показал отсутствие гендерных различий в успеваемости на любом уровне до 11 класса. Однако, опять же, важно одновременно учитывать возраст и глубину знаний, требуемых тестом.

В целом, мы пришли к выводу, что небольшая гендерная разница в пользу мужчин в решении сложных проблем все еще присутствует в старшей школе. Этот гендерный разрыв может объясняться множеством факторов. Как отмечалось ранее, девочки реже изучают физику, чем мальчики, и на уроках физики учат решать сложные задачи, возможно, даже больше, чем на уроках математики. Гендерные различия в моделях интереса могут играть роль (Su, Rounds, & Armstrong, 2009), хотя и эти модели формируются культурой.Более того, даже в самых недавних исследованиях родители и учителя дают более высокие оценки способностей мальчиков, чем девочек (Lindberg, Hyde, & Hirsch, 2008), а также влияние ожиданий родителей и учителей на оценки детьми их собственных способностей и их способностей. выбор курса хорошо задокументирован (Eccles, 1994; Jacobs, Davis-Kean, Bleeker, Eccles, & Malanchuk, 2005).

В-четвертых, существуют ли различия между этническими группами США или странами в направлении или величине гендерных различий? Что касается этнической принадлежности, таблица 2 показывает, что для исследования 1 была обнаружена небольшая гендерная разница в пользу мужчин среди белых, d = +0.13, но для всех этнических меньшинств вместе взятых, d = −.05. Этот результат аналогичен результату, полученному в метаанализе 1990 года (Hyde et al., 1990a), который обнаружил небольшое гендерное различие в пользу мужчин среди белых, но не различие для групп этнических меньшинств. В таблице 2 также показаны различия в величине эффекта в зависимости от национальности или региона мира. Наибольшая гендерная разница в пользу мужчин была обнаружена в исследованиях из Африки: d = +0,21, но даже это различие невелико.Наибольшая разница в пользу женщин была обнаружена в Центральной / Южной Америке и Мексике: d = -0,06. Эти различия в величине и направлении гендерных различий в успеваемости по математике согласуются с теми, которые были обнаружены при анализе международных наборов данных, таких как PISA и TIMSS. Эти другие исследования, кроме того, показали, что значения d для стран значительно коррелируют с показателями гендерного неравенства для этих стран (например, Else-Quest et al., 2010; Guiso et al., 2008; Пеннер, 2008).

В-пятых, уменьшились ли масштабы гендерных различий в успеваемости по математике с 1990 по 2007 год? Исследование 1 не обнаружило связи между годом публикации и величиной эффекта, что указывает на отсутствие заметной тенденции с течением времени к меньшим гендерным различиям. Это может быть связано с тем, что даже в 1990 году гендерные различия были уже небольшими (Hyde et al., 1990a), не оставляя места для дальнейшего сокращения.

В-шестых, демонстрируют ли мужчины большую разницу в оценках, и если да, то насколько? Общий коэффициент дисперсии в исследовании 1 был равен 1.07. То есть мужчины показали несколько большую дисперсию, но VR был недалеко от 1,0 или равных дисперсий. В исследовании 2 средний коэффициент дисперсии составлял 1,09, что опять же недалеко от 1,0. Кроме того, данные NELS: 88 (таблица 3) показывают, что несколько значений VR <1,0, что указывает на то, что большая изменчивость самцов не является повсеместной. Коэффициенты дисперсии менее 1,0 также были обнаружены в некоторых национальных и международных наборах данных (Hyde et al, 2008; Hyde & Mertz, 2009).

В целом, если рассматривать эти результаты в более широком контексте, гендер можно концептуализировать как один из многих предикторов успеваемости по математике.Другие факторы включают социально-экономический статус (SES), образование родителей и качество обучения. Мелхуиш и его коллеги (2008) сравнили величину эффекта 9 предикторов успеваемости детей по математике в возрасте 10 лет: вес при рождении, пол, SES, образование матери, образование отца, доход семьи, качество домашней учебной среды, эффективность дошкольного образования и начальная школа. эффективность. Поразительным открытием было то, что пол был самым слабым из этих 9 предикторов, то есть имел наименьший размер эффекта.Уровень образования матери, качество домашней учебной среды и эффективность начальной школы были гораздо более сильными предикторами. Наши выводы согласуются с выводами Мелхуиша и его коллег; пол не является сильным предиктором успеваемости по математике.

Значение

В целом результаты этих двух исследований убедительно свидетельствуют о гендерном сходстве в успеваемости по математике. Неоднородность результатов позволяет предположить, что существуют переменные-модераторы, которые могут прояснить структуру размеров эффекта.Выявление последовательных модераторов гендерных различий может быть усилено мерами, которые задействуют весь спектр математических рассуждений, включая вопросы, требующие последовательного рассуждения о сложных проблемах. Существование и величина гендерных различий в успеваемости по математике зависит от многих факторов, включая нацию, этническую принадлежность и возраст.

Эти выводы имеют несколько последствий для политики. Во-первых, эти результаты ставят под сомнение текущие тенденции развития однополых классов по математике.Сторонники однополого образования основывают свои аргументы отчасти на предположении, что девочки отстают от мальчиков в успеваемости по математике и должны находиться в защищенной среде, где только девочки, чтобы иметь возможность изучать математику (например, Streitmatter, 1999). Однако данные показывают, что девочки успевают по математике не хуже мальчиков, на основе 242 отдельных исследований (Исследование 1) и 4 крупных, тщательно отобранных национальных наборов данных по США (Исследование 2). Подавляющее большинство этих девочек и мальчиков учились в классах совместного обучения.Таким образом, аргумент о том, что успеваемость девочек по математике в гендерно интегрированных классах ухудшается, просто не подтверждается данными. Если мы хотим улучшить успеваемость учащихся по математике, нам лучше сосредоточиться не на поле, а на факторах, которые имеют большее влияние, таких как качество и выполнение учебной программы (Tarr et al., 2008), а также качество начальной школы и качества домашней учебной среды (Melhuish et al., 2008).

Во-вторых, нехватка заданий уровня 3 или 4 в оценках имеет серьезные последствия.Учитывая важность тестов по математике для школьной оценки в соответствии с законодательством «Ни один ребенок не отстает», учителя обычно преподают этот тест (Au, 2007). Если в тесте не будут выявлены навыки, необходимые гражданам, американские студенты окажутся в невыгодном положении. Кроме того, без доказательств, касающихся успеваемости учащихся по этим важным формам математического мышления, учителя, администраторы и политики не могут определить, какие учебные материалы или стратегии обучения способствуют повышению математических навыков.Наконец, тесты, которые не акцентируют внимание на решении сложных проблем или устойчивом рассуждении, сообщают учащимся неточную картину математики.

Эти результаты также имеют значение для развенчания стереотипов. В целом очевидно, что в США и некоторых других странах девочки достигли паритета с мальчиками в успеваемости по математике. Крайне важно, чтобы эта информация была широко известна, чтобы противодействовать стереотипам о неполноценности женщин в математике, которых придерживаются привратники, такие как родители и учителя, а также сами учащиеся.

Письмо и решение математических задач в 3 классе | Петерсен

Абстрактные

В этой статье рассматриваются письменные задания как методика поддержки математических стратегий решения учащихся в контексте Южноафриканской фазы Foundation. Это качественное тематическое исследование, в котором исследуется связь между использованием письма в математике и развитием у учащихся стратегий решения проблем и концептуального понимания. Исследование проводилось в пригородной школе Foundation Phase в Кейптауне, где учащиеся 3-го класса занимались письмом и математикой.Письменные задания были смоделированы для учащихся и реализованы ими, пока они занимались решением математических задач. Данные были собраны у выборки из восьми учащихся с разными способностями и включали письменные работы, интервью, полевые заметки и аудиозаписи обсуждений в группах способностей. Результаты показали улучшение в стратегиях и объяснениях, которые учащиеся использовали при решении математических задач, по сравнению с тем, как это было до того, как были реализованы письменные задания. Учащиеся смогли критически осмыслить свое мышление с помощью письменных стратегий и объяснений.Письменные задания были призваны помочь учащимся создавать и применять математические знания и навыки при разработке стратегий решения проблем.

Введение

Значение исследования

Учебная программа по математике, используемая в настоящее время в южноафриканских классах, делает упор на решение задач для развития критического мышления (Департамент базового образования Южной Африки [DBE] 2011a: 5).Однако, судя по результатам исследований южноафриканских учащихся в сравнительных международных исследованиях математики, таких как Тенденции в международных исследованиях математики и естествознания и Южноафриканский консорциум по мониторингу качества образования, есть опасения относительно их компетентности при решении математических задач и использования ими осмысленных стратегии (Ndlovu & Mji 2012). Несмотря на использование стандартизированных тестов, таких как Ежегодная национальная оценка (ANA) и провинциальные системные тесты, проводимые в Западной Капской провинции, результаты отражают разницу между способностью использовать процедурные и концептуальные знания.Учащиеся часто не достигают минимальных требований своего класса, особенно в области решения проблем. Отсутствие у учащихся базовых навыков счета в ANA, особенно в 3 и 4 классах, подчеркивается Graven et al. (2015: 69).

Как преподаватель на этапе Foundation, исследователь в течение многих лет наблюдал за учащимися при решении математических задач. Во время этих наблюдений учащиеся отразили свою некомпетентность в написании последовательных решений и объяснении своих решений учителю и / или сверстникам.Некоторые учащиеся, казалось, ждали инструкций от учителя, в которых описываются конкретные методы и процедуры для решения проблемы. Казалось, что учащимся обычно трудно применять математические концепции, которые они ранее усвоили, в своих стратегиях решения проблем.

Обзор литературы

Письмо необходимо для поддержки развития математических знаний и их применения в стратегиях решения проблем. Это помогает учащимся прояснить, определить и выразить свое мышление, а также изучить свои идеи и поразмышлять над тем, что они узнали, чтобы углубить и расширить свое понимание математических идей (Burns 1995: 13, 2007: 38; Jacobs & Ambrose 2009: 265 ).Письмо помогает учащимся разобраться в математических задачах: учащиеся учатся представлять и передавать свои мысли с помощью чисел, слов и изображений. В исследовании, проведенном Амаралом (2010), было обнаружено, что письмо по математике поддерживает процесс мышления. Использование разных стратегий и представлений при письме может быть связано с различными математическими способностями учащихся, которые понимают математические концепции на разных уровнях. Некоторые учащиеся могут писать и решать задачи на более сложных уровнях, чем другие, основываясь на своих предыдущих знаниях и уровнях концептуального понимания (Orton 2004: 25).Это выражается в использовании математических символов, как было обнаружено в исследовании, проведенном Мутоди и Мосимеге (2016: 203). Участники проявили трудности с пониманием сложности и абстрактной природы символов до того, как было освоено их концептуальное понимание математической идеи. По сравнению с этим исследованием, учащиеся участвовали в написании текстов других, чтобы сравнивать и извлекать уроки из стратегий своих сверстников, тем самым разрабатывая более продвинутые или изобретенные стратегии решения проблем, как предлагает Аскью (2013).

В предварительном и последующем тестировании исследования, основанного на вмешательстве 2-го уровня, проведенного Такане (в процессе) (Venkat & Askew 2016: 264), как и в этом исследовании, было очевидно, что стратегии учащихся становятся все более изощренными. Однако в центре внимания исследования Такане, по-видимому, был сделан больший упор на формирование смысла, чем на изощренность стратегий учащихся. Результаты исследования Tshesane и Venkat (2014) показывают, что использование конкретных моделей в качестве инструментов может привести к усложнению стратегий.Этот вывод, в котором использовалась модель числовой линии, коррелирует с этим исследованием в том, что письменные задания использовались в качестве модели или инструмента.

Бернс (1995) описывает различные типы письменных заданий и их цель в развитии концептуального понимания. Письменные задания, представленные в ее работе, были выполнены с учащимися из разных классов на протяжении от начальной школы до начальной школы. Поскольку это исследование было сосредоточено на подготовительном этапе, письменные задания Бернс были подходящими, поскольку в ее исследование входили учащиеся этих классов.Учебный план и заявление о политике оценивания «Математика для базового этапа» предусматривает, что учащиеся передают свои мысли устно и письменно с помощью рисунков и символов (South Africa DBE 2011a: 9). Выполнение письменных заданий позволило бы этому происходить в классе математики. Совместное письмо (Wilcox & Monroe 2011) было добавлено в это исследование, хотя и не напрямую из работы Бернса, поскольку оно связано с текущими руководящими принципами учебной программы, используемыми в Южной Африке. Совместное письмо — это элемент сбалансированного языкового подхода, при котором учащиеся и учитель пишут вместе (South Africa DBE 2011b: 12).

Выполнено пять письменных заданий. В «письме для решения математических задач» Бернс (1995: 69) предлагает учащимся решать, объяснять и обосновывать свое мышление, используя различные стратегии для проверки и интерпретации результатов. Учащиеся используют числа, изображения и слова, чтобы объяснить свои мысли, лежащие в основе своих стратегий решения. В «письме для записи (ведение журнала или журнала)» учащиеся постоянно ведут записи о том, что они делают и изучают на уроке математики, что может использоваться для записи своего мышления, когда они что-то замечают, делают наблюдение или сообщают об открытии. (Бернс 1995: 51).Они предоставляют учащимся возможность регулярно размышлять над уроками или концепциями математики, анализировать собственное обучение и налаживать письменный диалог между учителем и учеником. «Написание для объяснения» считается формой ведения заметок, когда учащиеся определяют математическое понятие или термин своими словами или резюмируют то, что они узнали (Freed 1994: 23). В этом письменном задании основное внимание уделяется способностям учащихся разъяснять и объяснять определенные математические концепции. «Написание статей о процессах мышления и обучения» позволяет учащимся мыслить не только на уроке математики.Учащиеся пишут о своих любимых или наименее любимых занятиях, качествах хорошего партнера по решению проблем, направлениях занятия или игры или письмах посетителям с описанием занятий по математике в классе (Burns 2007: 40). В «совместном письме» учитель и учащиеся формулируют математический рассказ или стихотворение, отражающее их понимание конкретной концепции. Учителя используют этот письменный опыт в классе математики для анализа и усвоения математических концепций и идей, а также для развития математической коммуникации (Wilcox & Monroe 2011: 526).Это письменное задание побуждает учащихся творчески и совместно использовать свои знания и понимание математики.

учащихся познакомили с использованием письменных заданий по математике, особенно в области решения проблем. Математические задачи и, в частности, текстовые задачи должны быть частью решения проблем. Хедденс и Спир (2006: 82) определяют решение проблемы как «(междисциплинарный) процесс, который человек использует для реагирования и преодоления препятствий или барьеров, когда решение или метод решения проблемы не сразу очевидны».Он включает в себя процесс мышления и рассуждений, который помогает концептуальному развитию, а не процессуальному развитию (O’Donnell 2006: 351). Хедденс и Спир (2006: 84) утверждают, что возможность применять концептуальные знания через решение проблем так же важна, как и понимание самих концепций, потому что это придает больше смысла и цели знаниям и навыкам, приобретенным учащимся. Этот процесс позволяет учащимся углубить свое концептуальное понимание и участвовать в процессе осмысления: они применяют и развивают свои математические знания (Schoenfeld 2013).По мере того, как учащиеся делают это, они, скорее всего, будут совершенствоваться в использовании стратегий решения проблем.

Теории Выготского о зоне ближайшего развития и присвоения легли в основу этого исследования. Эта теоретическая основа подходит для использования письменных заданий в классе математики, когда учащиеся решают математические задачи. Зона ближайшего развития (Выготский, 1978) определяется как:

Расстояние между фактическим уровнем развития, определяемым путем независимого решения проблем, и уровнем потенциального развития, определяемым путем решения проблем под руководством взрослых или в сотрудничестве с более способными сверстниками.(стр.86)

В этом исследовании писательская деятельность создала возможность для создания ZPD. Первоначально учащиеся занимались решением проблем, когда их использование стратегий и письменных объяснений было ограничено. Различные типы письменных заданий использовались для руководства и поддержки стратегий решения математических задач и объяснений в рамках ZPD, чтобы учащиеся могли сократить расстояние между их потенциальным развитием и фактическим развитием их независимых стратегий.Более знающий другой (MKO), будь то сверстник, родитель или учитель, формирует понимание посредством индивидуально подобранного темпа процесса решения проблемы (Bruner & Haste 1987: 8). В исследовании, проведенном Sonne и Graven (2014), было обнаружено, что математическая коммуникация и роль MKO могут играть решающую роль в разработке учащимися стратегий решения проблем. Учащиеся вместе участвуют в решении проблем в ZPD с возможностью объяснять и обсуждать математические концепции, встречающиеся в задачах.В таких ситуациях возникают строительные леса, которые, в свою очередь, приводят к формированию учащимся независимых знаний и способностей решать проблемы. В ZPD этого исследования методология письма в математике Бернса (1995) была представлена и реализована как инструмент, помогающий учащимся использовать стратегии решения проблем и поддерживать их при решении математических задач.

Теория присвоения Выготского, как объяснил Дуарте (2011), применима в этом исследовании, где есть размышления об объективной реальности в мыслях.Когда учащиеся занимались решением проблем и личным письмом, им была предоставлена возможность подобрать конкретную проблему, размышляя над концепциями в своем мышлении. Эта точка зрения подтверждается объяснением Аскью (2013), согласно которому через опыт учащиеся могут взаимодействовать с абстрактными концепциями независимо от того, достигли ли они определенной стадии развития.

Цели и задачи исследования

Это исследование было основано на следующем исследовательском вопросе:

Как различные типы письменных заданий помогают учащимся 3-го класса решать математические задачи?

Эта статья будет посвящена тому, насколько учащиеся 3-х классов способны выполнять письменные задания при решении математических задач.В нем сообщается о поддержке, которую письменные задания оказывают развитию стратегий решения проблем, фокусируясь на природе их представлений.

Методы исследования и разработки

Дизайн исследования

Это качественное тематическое исследование было систематическим, глубоким исследованием конкретного случая в его контексте с целью генерирования знаний (Rule & John 2011: 4). Предварительное и последующее тестирование проводилось в начале и в конце периода сбора данных, в ходе которого учащиеся 3-х классов решали пять математических задач, чтобы определить, улучшилось ли концептуальное понимание учащимися и стратегии решения проблем.Выборка из восьми учащихся была проинтервьюирована после предварительного и последующего тестирования, чтобы оценить степень вовлеченности учащихся в письменные задания, а также поддержку письменных заданий при разработке стратегий решения проблем. Письменные задания вводились систематически в качестве вмешательства для всех учащихся в классе в период сбора данных. Были проведены углубленные наблюдения за образцом письма учащихся, стратегиями решения проблем и концептуальным развитием.

Общие задачи по математике были даны всем участвующим учащимся во время предварительного тестирования, вмешательства и пост-теста.Задачи, связанные с основными операциями (сложение, вычитание, умножение и деление) с использованием целых чисел с различными диапазонами чисел, чтобы учесть различные группы математических способностей в классе. Хотя количество тестовых заданий было ограничено, учащиеся имели возможность решить 13 задач во время вмешательства. Эти проблемы были включены в данные, собранные для этого исследования. Обсуждения в группах способностей со всеми учащимися проводились после того, как учащиеся решили проблемы во время вмешательства.Учащиеся поделились своими стратегиями со своими сверстниками и их побудили критически осмыслить свои собственные стратегии, а также стратегии других.

Исследование проводилось в школе Foundation Phase с английским языком обучения в пригороде Кейптауна. Эта школа была выбрана для удобства, потому что исследователь был учителем в 3-м классе. Учащиеся преимущественно говорили и понимали английский язык. Один из пяти классов 3-го класса был выбран для удобного управления сбором данных для исследователя как учителя выбранного класса.Популяция состояла из всех учащихся участвующего класса, где письменные задания (Burns 1995; Wilcox & Monroe 2011) были смоделированы исследователем и реализованы учащимися в течение восьминедельного периода вмешательства. Данные были собраны из специально отобранной выборки из восьми учащихся. Они проявляли различные способности при решении и объяснении математических задач и представляли три группы математических способностей, представленные в классе 3 класса.

Сбор и анализ данных

Данные были собраны с помощью аудиозаписей интервью и обсуждений в группах способностей, письменных работ учащихся во время предварительного тестирования, вмешательства и пост-тестирования, а также полевых заметок.После предварительного и последующего тестирования образец был проинтервьюирован, чтобы изучить, как письмо использовалось при решении математических задач. Интервью были частично структурированы с гибким списком вопросов и ключевых тем, что позволяло проводить зондирование, уточняющие вопросы и углубленное исследование. После того, как учащиеся решили математические задачи во время вмешательства, различные группы математических способностей в классе обсудили свои решения и стратегии. Полевые заметки использовались для записи того, что учащиеся делали при решении математических задач.Диалог и беседа были написаны во время групповых обсуждений способностей и совместного письма между парами учащихся. Для целей этой статьи данные, собранные в ходе письменной работы учащихся, были проанализированы, чтобы изучить поддержку письменных заданий, оказываемых при разработке стратегий решения проблем через характер репрезентаций учащихся.

Процесс анализа включал в себя разработку первоначального понимания, кодирования, интерпретации и рисования последствий (Dana & Yendel-Hoppey 2009: 120).После того, как данные были расшифрованы и подготовлены, данные были прочитаны и перечитаны для извлечения и описания первоначальных выводов и отражения их общего значения. Следующим шагом было кодирование с использованием ATLAS.ti, компьютерной программы качественного анализа данных, где метки использовались для назначения различных тем или фокусов в данных (Rule & John 2011: 77). После изучения возможных рамок для анализа данных в этом исследовании, выборочные стратегии решения проблем учащихся были проанализированы и сопоставлены с использованием Системы обучения в цифрах (LFIN) Райта, Мартленда и Стаффорда (2006).LFIN инкапсулирует вероятные этапы и уровни изучения чисел, которые учащиеся проходят по мере развития своих математических знаний. LFIN включает в себя следующие области обучения числам: этапы раннего арифметического обучения (SEAL), числовые слова и числа, цепочку структурирования чисел, концептуальные знания разрядов, а также раннее умножение и деление. Хотя LFIN часто используется для анализа раннего обучения числам, он был надлежащим образом использован в этом исследовании, чтобы сосредоточить внимание и проанализировать уровень стратегий учащихся при решении математических задач со словами.В некотором смысле слова проблем были распакованы, чтобы проанализировать стратегии, связанные с числами в задачах. Венкат (2012) использовал этапы и уровни LFIN в аналогичном стиле в исследовательском проекте, который анализировал развитие и вмешательства в преподавание и изучение математики. Во вставках 1 и 2 показаны стадии ПЕЧАТИ и уровни раннего умножения и деления.

ВСТАВКА 1: Модель для этапов раннего обучения арифметике.

ВСТАВКА 2: Модель для ранних уровней умножения и деления.

Закодированные данные были интерпретированы, чтобы сообщить результаты, и выводы были сделаны для изучения степени, в которой учащиеся участвуют в письменных задачах, и поддержки письменных заданий, которые оказывают учащимся стратегии решения проблем.

Этические соображения

Для целей настоящего исследования разрешение было запрошено и предоставлено Департаментом образования Западного Кейптауна Технологического университета Кейп-Пенинсула, директором школы и родителями всех учащихся 3-го класса.Форма информированного согласия была прочитана и подписана родителями учащегося, предоставившими право участвовать в исследовании. Псевдонимы использовались для школы и всех участников, чтобы сохранить конфиденциальность.

Результаты и обсуждение

Во время выступления учащиеся выполняли пять письменных заданий. Следующие ниже примеры показывают, как учащиеся использовали задания и развивали математические знания посредством письма. Когда учащиеся познакомились с «записью для записи (ведение дневника или журнала)» (Burns 1995: 51), учащимся были представлены примеры того, как начинать предложения, которые помогут направить их мышление.На рисунке 1 показано, как Кайла использовала письменные подсказки для описания того, что произошло во время дневного урока математики. Во время вмешательства учащимся было дано несколько возможностей использовать «письмо для объяснения» (Freed 1994: 23). Письмо Бевана (рис. 2) проясняет его понимание пустой числовой строки после урока математики. На рисунках 3 и 4 показаны два разных примера того, как учащиеся писали, когда они «писали о процессах мышления и обучения» (Burns 2007: 40). Джемма описывает свое любимое занятие по математике на рисунке 3, а Беван определяет качества решателя задач на рисунке 4.

РИСУНОК 3: Джемма (процессы мышления и обучения).

РИСУНОК 4: Беван (Процессы мышления и обучения).

Предварительное и последующее тестирование, использованные в этом исследовании, помогли оценить уровни стратегий решения проблем, которые учащиеся использовали до и после выполнения различных типов письменных заданий.Этапы и уровни различных аспектов LFIN (Райт и др., 2006) обеспечили ясность и дифференциацию между стратегиями, которые учащиеся использовали при решении задач. Результаты предварительного тестирования показали, что большинству учащихся было трудно решать математические задачи со словами и передавать свои мысли посредством письма. Учащиеся иногда использовали стратегии, не соответствующие типу проблемы. Многие учащиеся в выбранном классе 3-го класса были ограничены в использовании методов решения математических задач на предварительном тесте.Их стратегии часто отражали более низкие этапы и уровни различных аспектов LFIN. Подсказки часто использовались в качестве стратегии в предварительном тесте (рис. 5) и в более ранней части письменного вмешательства. На этом этапе письменные объяснения учащихся были довольно ограниченными. Учащиеся, которые написали подробные объяснения при решении задач пост-теста, смогли предоставить подробные устные объяснения своих стратегий и процессов решения во время послетестовых интервью. Оказалось, что их использование письма помогло им понять свои стратегии и оправдать свое мышление при решении проблем (Burns 1995: 13).

Результаты показали улучшение уровня используемых стратегий решения проблем, поскольку учащиеся, например, меньше использовали подсчеты. Это улучшение было особенно очевидно среди учащихся ниже среднего, как показано на рисунках 6 и 7. Первоначально Джарред использовал перцепционный счет как стратегию для решения этой проблемы:

Завод по производству трициклов имеет в наличии 65 колес. Сколько трехколесных мотоциклов можно собрать с колесами?

Обсуждая письменный отзыв на следующий день, учащегося попросили объяснить, что, по его мнению, это означает, в то время как исследователь кружил свои подсчеты колес, чтобы образовать группу из трех колес.Эта техника была на уровне 1 (начальная группировка) раннего умножения и деления. Учащийся дал соответствующее словесное объяснение, что каждая группа представляет собой один трехколесный велосипед с тремя колесами. Он продолжал решать проблему самостоятельно. Позже, когда исследователь проанализировал то, что он сделал, стало ясно, что он все еще неверно истолковал проблему. Он продолжал кружить все свои подсчеты на группы по три, не считая своих подсчетов. Это заставило его выйти за рамки 65 колес, упомянутых в проблеме.Учитель написал объяснение, чтобы побудить к дальнейшим размышлениям о количестве подсчетов, необходимых для представления колес в задаче. Эта сложность понимания сложности символов до овладения концептуальным пониманием была выражена в исследовании Мутоди и Мосимеге (2016).

Проблема в заключительном тесте (рис. 7) была второй частью задачи, когда 39 родителей присутствовали на родительском собрании. Оно гласило:

После родительского собрания будет подан кофе.Из одного кофейника получается 5 чашек. Сколько чашек кофе нужно приготовить, если у каждого человека есть по одной чашке?

Джарред представил свою стратегию, используя рисунок, числа и слова, которые имели смысл. Его стратегия отражала образное составное группирование, третий уровень раннего умножения и деления. Он использовал повторное сложение таким образом, чтобы каждая группа была представлена как абстрактная составная единица (Райт и др., 2006). Он написал объяснение, в котором подробно описано, как он решил проблему (Jacobs & Ambrose 2009: 265).Он понимал математическую концепцию, необходимую в задаче — счет по пятеркам. Он не полагался на счет по одному и использовал стратегию, требующую мышления более высокого порядка. Однако он не стал предлагать раствор, который представлял собой восемь горшков кофе. На этом этапе учащиеся уже знакомы с концепцией счета по тройкам и пятеркам на предыдущих уроках математики. Стратегии, используемые в этих двух задачах одним и тем же учеником, показывают, как он продвинулся от первоначального использования счетчиков, когда он считал по одному, к счету в составных группах по пять человек без счетчиков позже, во время послетеста.Использование объяснений в письменных заданиях могло способствовать этому улучшению в использовании им стратегий решения проблем.

На рисунках 8 и 9 сравниваются стратегии и объяснения, используемые учеником выше среднего. Задача перед тестированием гласила:

В коробке 17 контактов. Сколько булавок будет в 6 коробках?

В этой предварительной задаче Джемма использовала деление вместо умножения. В пост-тесте она была единственным учеником, который использовал концептуальное значение места в своей стратегии решения проблем для решения следующей задачи:

Марк и Марта упаковали 81 стул.Марк собрал 48 стульев. Сколько упаковала Марта?

В своей стратегии она увеличила число на несколько десятков, чтобы вычислить разницу между 48 и 81. Она предоставила подробное объяснение своей стратегии в своих письмах, что подтвердило ее мышление, продемонстрировав более глубокое концептуальное понимание. Это улучшение в использовании ею более продвинутой стратегии, отражающей более высокий уровень LFIN, возможно, могло быть связано с письменным вмешательством, которое она получила.

На протяжении всего периода сбора данных учащимся предлагалось связать проблему, которую они решали, с математической концепцией или идеей.Первоначально некоторые учащиеся, особенно из групп со средним и ниже среднего уровня способностей, испытывали трудности с поиском математической концепции или идеи в рамках задачи. По мере развития письменного вмешательства учащиеся все больше вовлекались в письменные задания, поощряя их продумывать свои стратегии и решения, чтобы написать объяснение своего мышления (Burns 1995: 69). На рисунке 10 Джемма написала объяснение, которое помогло исследователю понять, как она решила проблему.Написав ответ, Джемме было предложено пересмотреть свою стратегию, найти свою ошибку и написать дальнейшее объяснение. Развитие их концептуального понимания было особенно очевидно во время заключительного теста, когда учащиеся индивидуально писали более подробные объяснения, включающие математические идеи.

Рисунок 11 представляет собой пример разработки стратегий решения проблем учащимися и их письменной речи во время вмешательства. Первоначальная стратегия Джеммы показывает, что она использовала подсчеты для решения следующей задачи:

32 птицы приземляются на птичий стол.Сейчас там 91 птица. Сколько птиц уже было на столе?

Учащимся была предоставлена возможность поделиться своими стратегиями решения проблем и объяснениями в ходе обсуждения в группе способностей. После изучения стратегий других учащихся Джемма смогла решить проблему, объединив свои концептуальные знания о числовой стоимости и вычитании, чтобы найти решение. После обсуждения она пришла к такому же решению, используя более изощренную стратегию. На этом этапе периода вмешательства ее письменные объяснения ее стратегий все еще были ограничены.

Большинство стратегий решения проблем, используемых учащимися в послетестировании, отражали более высокие стадии и уровни LFIN, предполагая, что они смогли связать математическое содержание и контекст проблемы со своими существующими знаниями (Orton 2004: 25). В некоторых случаях учащиеся комбинируют математические концепции в своих стратегиях, отображая более глубокое концептуальное понимание (рис. 12). По этой проблеме на собрание пришли 57 родителей. Было написано:

После родительского собрания будет подан кофе.Из одного кофейника получается 7 чашек. Сколько чашек кофе нужно приготовить, если у каждого человека есть по одной чашке?

Изначально этот ученик со средними способностями использовал стратегию удвоения до определенной степени и включил ее в повторяющуюся сумму сложения. Беван успешно объединил две стратегии из своих предшествующих знаний, что демонстрирует более глубокое концептуальное понимание. На этом этапе учащиеся не сталкивались с концепцией счета по семеркам. Он смог использовать свое знание удвоения чисел и добавления семи каждый раз вместо того, чтобы возвращаться к счетам и счету по единицам.

Эти результаты отражают, что мышление учащихся было конкретно присвоено через их стратегии и объяснения, когда они решали проблемы и участвовали в написании заданий. Учащиеся использовали пять письменных заданий, чтобы понять математические идеи и выразить свое мышление: их использование письма показало их индивидуальное развитие мышления.

Заключение Методика письма

Бернса (1995) использовалась в качестве средства поддержки математических стратегий решения учащихся в контексте Южноафриканской фазы Foundation.Письменные задания использовались в качестве вмешательства с классом учащихся 3-го класса в период сбора данных. Данные были собраны у выборки из восьми учащихся. Вмешательство продемонстрировало развитие их стратегий решения проблем по мере того, как они применяли свои концептуальные знания. К концу периода сбора данных учащиеся использовали более продвинутые стратегии. Приведенные примеры показывают, что существовала явная разница в характере представлений учащихся при сравнении результатов предварительного и последующего тестирования.

Пять письменных заданий были смоделированы для учащихся и реализованы во время вмешательства. Одна из письменных задач, «письмо для решения математических задач», использовалась во время предварительного и последующего тестирования. Использование учащимися этого письменного задания выявило степень, в которой учащиеся были способны выполнить хотя бы одно из письменных заданий. Это независимое использование письма предполагает, что использование письменных заданий может повысить способность учащихся описывать мышление, лежащее в основе их процессов решения, когда они участвуют в решении математических задач.Отобранные учащиеся смогли предоставить письменные объяснения своих решений, чтобы обосновать свои стратегии.

Цель этой статьи — вспомогательные письменные задания, которые даются учащимся 3-х классов при решении математических задач. Он исследовал степень, в которой учащиеся были в состоянии участвовать в письменных заданиях, и поддержку письменных заданий, которые оказывают на развитие стратегий решения проблем и характер репрезентаций учащихся. Хотя объем этой статьи ограничен, использование письменных методологий, таких как Бернс (1995), может быть полезно в контексте Южной Африки.Венкат и Аскью (2016) предлагают адаптировать материалы и педагогические подходы, такие как эта методология, для решения проблем и нужд южноафриканского класса математики.

Результаты этого исследования показывают, что письмо полезно в классе математики. Может потребоваться более всестороннее исследование использования каждого письменного задания для поддержки разработки стратегий решения проблем. Выступление учащихся может быть изучено во время групповых обсуждений способностей и совместной работы в связи с разработкой ими стратегий решения проблем.Дальнейшее углубленное исследование может быть проведено на начальном этапе, а также на старших классах, чтобы определить полезность письма по математике на всех этапах и этапах учебной программы по математике.

Благодарности

Это исследование частично стало возможным благодаря гранту Университетского исследовательского фонда Технологического университета полуострова Кейп

Конкурирующие интересы

Авторы заявляют, что у них нет финансовых или личных отношений, которые могли бы ненадлежащим образом повлиять на них при написании этой статьи.

Авторские работы

C.V. и С. были кураторами проекта. B.P., C.V. и С. соавтор проекта. Б.П. реализовали проект, собрали данные и проанализировали данные. B.P., C.V. и С. совместно сформулировал результаты, обсуждение и заключение.

Список литературы

Амарал, С.С., 2010, «Дискурсивные представления детей о своем математическом мышлении: исследование в области действия», магистерская диссертация, Университет Манитобы, Виннипег, МБ.

Аскью, М., 2013, «Посредничество в связи с числовыми связями обучения через призму научных концепций Выготского», Южноафриканский журнал детского образования 3 (2), 1–20. https://doi.org/10.4102/sajce.v3i2.37

Bruner, J. & Haste, H. (eds.), 1987, Осмысление смысла: конструирование мира ребенком , Рутледж, Лондон.

Burns, M., 1995, Письмо в классе математики: ресурс для 2–8 классов , Math Solutions, Саусалито, Калифорния.

Бернс, М., 2007, Об обучении математике: ресурс для K-8, Math Solutions, Саусалито, Калифорния.

Дана, Н.Ф. & Yendel-Hoppey, D., 2009, Руководство по рефлексивному педагогу по исследованиям в классе: обучение преподаванию и обучение обучению посредством опроса практикующего , Corwin Press, Thousand Oaks, CA.

Дуарте, Н., 2011, «Выготский и диалектическое присвоение реальности научным знанием», доклад, представленный в Международном обществе культурных и деятельностных исследований, Рим, 8 сентября.

Фрид, С., 1994, «Написание на уроках математики», Журнал адвентистского образования 56 (3), 22–26.

Грейвен, М., Стотт, Д., Мофу, З. и Ндонгени, С., 2015, «Определение этапов владения счетом для исправления базовых знаний с использованием числовой структуры обучения», в материалах 23-й ежегодной конференции. Южноафриканской ассоциации исследований в области математики, естествознания и технологического образования, Мапуту, Мозамбик, 13–16 января, стр.69–83.

Heddens, J.W. & Speer, W.R., 2006, Современная математика: концепции, методы обучения и учебные мероприятия , 11-е изд., Wiley, Hoboken, NJ.

Джейкобс, В. И Амброуз Р.К., 2009, «Максимальное использование сюжетных задач», Teaching Children Mathematics 15 (5), 260–266.

Мутоди, П. и Мосимеге, М., 2016, «Проблемы конструирования математического значения посредством символизации на уровне средней школы: некоторые учебные стратегии», в материалах 24-й ежегодной конференции Южноафриканской ассоциации исследований в области математики, естествознания. и технологическое образование, Претория, Южная Африка, 12–15 января, стр.196–207.

Ндлову, М. и Мджи, А., 2012, «Согласование между южноафриканскими стандартами оценки математики и системами оценки TIMSS», Pythagoras 33 (3), 182–190. https://doi.org/10.4102/pythagoras.v33i3.182

О’Доннелл, Б., 2006, «О том, как научиться лучше решать задачи», Обучение детей математике 12 (7), 346–351.

Ортон, А., 2004, Изучение математики: проблемы, теория и практика в классе , 3-е изд., Континуум, Лондон.

Рул, П. и Джон, В., 2011, Ваш путеводитель по тематическому исследованию , Ван Шайк, Претория.

Schoenfeld, A.H., 2013, «Размышления о теории и практике решения задач», The Mathematics Enthusiast 10 (1), 9–34.

Сонне, А. и Грейвен, М., 2014, «Исследование того, как навыки решения проблем могут быть развиты с использованием среды совместного обучения», презентация на 22-й ежегодной конференции Южноафриканской ассоциации исследований в области математики, естествознания и технологического образования. , Мапуту, Мозамбик, 13–16 января.

Южная Африка. Департамент базового образования (DBE), 2011a, Заявление об учебной программе и политике оценивания: английская математика , Департамент базового образования, Претория.

Южная Африка. Департамент базового образования (DBE), 2011b, Заявление об учебной программе и политике оценивания: английский домашний язык , Департамент базового образования, Претория.

Чесане Х. и Венкат Х., 2014, «Модели и стратегии для аддитивных отношений в первичной математике: результаты тематического исследования», доклад, представленный на материалах 22-й ежегодной конференции Южноафриканской ассоциации исследований в области математики. , Образование в области науки и технологий, Мапуту, Мозамбик, 13–16 января.

Венкат, Х., 2012, «Сообразительность и математика соединяются — начальная школа», презентация на Форуме практического сообщества, Йоханнесбург, 20–21 августа.

Венкат, Х. и Аскью, М., 2016, «Материалы,« заимствующие »и адаптируемые: обзор мероприятий« Большой книги »в классах начальной математики», доклад, представленный на материалах 24-й ежегодной конференции Южноафриканской ассоциации исследований. Магистр математики, естествознания и технологий, Претория, Южная Африка, 12–15 января.

Выготский Л.С., 1978, Разум в обществе: развитие высших психологических процессов , Издательство Гарвардского университета, Лондон.

ГДЗ часть 1 Урок 9 математика 1 класс Петерсон

Рекомендуем посмотреть

ГДЗ часть 1 Урок 13 математика 1 класс Петерсон

(adsbygoogle = window.adsbygoogle || []).push({}); Рекомендуем посмотреть

ГДЗ часть 1 Урок 14 математика 1 класс Петерсон

(adsbygoogle = window.adsbygoogle || []).push({}); Рекомендуем посмотреть

ГДЗ по Математике 3 класс рабочая тетрадь Петерсон часть 1, 2, 3

Какую пользу принесет учащимся учебно-методический комплекс по математике за 3 класс для рабочей тетради (автор: Л.Г. Петерсон)

Содержание пособия по математике для 3 класса, рабочая тетрадь от Петерсон

ГДЗ решебник по математике 1 класс Петерсон

Ответы на задания по математике за первый класс к учебнику Петерсон Л.Г.

Часть 1

Часть 2

Часть 3

ГДЗ по математике 4 класс Петерсон 1, 2, 3 часть учебник

Часть 1

1 урок.

2 урок. Множество решений

3 урок. Знаки больше или равно и меньше или равно

4 урок. Двойное неравенство

5 урок

6 урок. Оценка суммы

7 урок. Оценка разности

8 урок. Оценка произведения

9 урок. Оценка частного

10 урок. Прикидка результатов арифметических действий

11 урок. Деление с однозначным частным

12 урок

13 урок. Деление на двузначное и трехзначное число

14 урок

15 урок

16 урок

17 урок.

18 урок. Приближенное вычисление площадей

19 урок. Измерения и дроби

20 урок. Из истории дробей

21 урок. Доли

22 урок. Сравнение долей

23 урок. Нахождение доли числа

24 урок. Проценты

25 урок. Нахождение числа по доле

26 урок

27 урок. Дроби

28 урок. Сравнение дробей

29 урок. Нахождение части числа

30 урок. Нахождение числа по его части

31 урок

32 урок. Площадь прямоугольного треугольника

Часть 2

1 урок. Деление и дроби

2 урок. Нахождение части, которую одно число составляет от другого

3 урок. Сложение дробей

4 урок. Вычитание дробей

5 урок. Правильные и неправильные дроби

6 урок. Правильные и неправильные части величин

7 урок. Задачи на части

8 урок. Смешанные числа

9 урок. Выделение целой части из неправильной дроби

10 урок. Запись смешанного числа в виде неправильной дроби

11 урок. Сложение и вычитание смешанных чисел

12 урок

13 урок

14 урок

15 урок

16 урок

17 урок. Шкалы

18 урок. Числовой луч

19 урок. Координаты на луче

20 урок. Расстояние между точками координатного луча

21 урок. Движение по координатному лучу

22 урок

23 урок. Одновременное движение по координатному лучу

24 урок. Скорость сближения и скорость удаления

25 урок

26 урок. Встречное движение

27 урок. Движение в противоположных направлениях

28 урок. Движение вдогонку

29 урок. Движение с отставанием

30 урок. Формула одновременного движения

31 урок

Рекомендуем посмотреть

Рекомендуем посмотреть