ГДЗ по Математике 2 класс
ГДЗ по математике для 2 класса Моро – это сборник готовых домашних заданий по задачам и примерам из учебника по арифметике, составленного известными российскими авторами – М.И. Моро, М.А. Бантовой, Г.В. Бельтюковой и др. Он используется в большинстве общеобразовательных школ России.
Структура ГДЗ по учебнику математики второго класса от Моро
Во втором классе школьники знакомятся с базовыми понятиями арифметики, которые помогут им постигнуть алгебру и геометрию в старших классах, сформировать общее представление о предмете и науке. Они изучают числовой ряд от 1 до 100, порядок действий в сложных примерах, уравнения первого порядка с одной переменной. Они учатся рассчитывать периметр прямоугольника и проводить устные вычисления.
ГДЗ по математике 2 класса Моро, составленные на основе учебника 2015 года в его 6-м издании, включают в себя примеры и задачи на такие темы:
- числа от 1 до 100;
- проведение измерений, миллиметры и метры;
- денежная система исчислений: рубли и копейки;
- сложение и вычитание, скобки и порядок действий;
- измерение времени: часы и минуты;
- периметр многоугольника и длина ломаной линии;
- решение уравнений с одной переменной;
- угол и виды углов;
- прямоугольник и квадрат, их площадь и периметр;
- умножение, деление и их свойства.

Глубокое понимание представленных выше тем – гарантия успешного изучения алгебры и геометрии в старших классах. Ученики должны не просто списать примеры и задачки из решебника, но вникнуть в алгоритм решения.
Готовое домашнее задание для 2 класса на сайте ГДЗ Путина – замена репетиторов, помощь родителям, основа высокой успеваемости младших школьников.
Правильные решения от ГДЗ Путина по математике 2 класса к Моро
В интернете немало сайтов с готовыми домашними заданиями. В чем же преимущества портала ГДЗ от Путина для учеников младших классов и их родителей?
- наличие нескольких вариантов решения одной и той же задачи;
- ответы по самым свежим изданиям учебников российских школ;
- оформление готовых домашних заданий в соответствии с требованиями Министерства образования РФ;
- бесплатный доступ с любого устройства – смартфона, планшета, компьютера.
Эти критерии делают ГДЗ по математике 2 класса к учебнику Моро незаменимым помощником родителей. Теперь им не придется вникать в решения своего чада – подробные алгоритмы представлены на сайте, а также пользоваться дорогостоящими услугами репетиторов.
Теперь им не придется вникать в решения своего чада – подробные алгоритмы представлены на сайте, а также пользоваться дорогостоящими услугами репетиторов.
Ответы на задачки, примеры и уравнения в нескольких вариантах упростят постижение арифметики второклассниками – откроют им путь к постижению новых горизонтов в математике.
ГДЗ по Математике 2 класс Муравьева часть 1, 2
Авторы: Муравьева Г.Л., Урбан М.А..
Издательство: Национальный институт образования 2020
Математика – это такая дисциплина, с которой у младшеклассников чаще всего возникают сложности. Это связано с тем, что вчерашним первоклашкам приходится впервые погружаться в таинственный мир цифр и вычислительных действий. Времени на уроке учителю не всегда хватает, чтобы объяснить важную тему, а домашнее задание уже начинают задавать серьезное. Родители же не всегда успевают проверить тетради и проконтролировать своего ребенка. В результате – первые двойки, слезы, стресс у детей и недовольство у мам и пап. Чтобы избежать этого, стоит обратиться к ГДЗ по математике за 2 класс Муравьева
Родители же не всегда успевают проверить тетради и проконтролировать своего ребенка. В результате – первые двойки, слезы, стресс у детей и недовольство у мам и пап. Чтобы избежать этого, стоит обратиться к ГДЗ по математике за 2 класс Муравьева
Как устроен онлайн-решебник по математике за 2 класс Муравьева
Профессиональные и опытные методисты долго трудились над пособием, чтобы оно получилось удобным и понятным. В нем отражены такие основные темы, как:
- счет предметов;
- десятичные единицы;
- упорядочение и сравнение чисел;
- образование и запись числе от 1 до 1000000.
Среди родителей и педагогов бытует расхожее мнение о бесполезности и даже вреде сборников с готовыми зданиями. Эта точка зрения является ошибочной. Не нужно воспринимать такие справочники исключительно как шпаргалку для бездумного списывания. Для получения высоких результатов необходимо первоначально самостоятельно сделать все заданное на дом, только после этого разрешается сверить свои ответы с верными. В конце остаётся исправить выявленные ошибки. Регулярные занятия с ГДЗ по математике за 2 класс Г.Л.Муравьева, М.А.Урбан уже очень скоро повысят успеваемость, активность ученика на опросах, а хорошие оценки будут приносить ему радость.
В конце остаётся исправить выявленные ошибки. Регулярные занятия с ГДЗ по математике за 2 класс Г.Л.Муравьева, М.А.Урбан уже очень скоро повысят успеваемость, активность ученика на опросах, а хорошие оценки будут приносить ему радость.
Не стоит думать, что учебно-методический комплекс пригодится лишь учащимся с проблемами в учебе. Он будет полезным и другим пользователям. Отличники смогут легко и без чьей-то помощи подготовиться к любой самой сложной проверочной работе. Второклассникам, пропустившим урок по причине болезни, книга позволит самостоятельно усвоить новые параграфы. А преподаватели почерпнут из решебника множество увлекательных упражнений, разнообразив тем самым свой учебный план.
ГДЗ решебник по математике за 2 класс Моро с ответами
Авторы: М.И. Моро, М.А. Бантова, Г.В. Бельтюкова
Издательство: Просвещение 2015-2019
Серия: Школа России
Тип книги: Учебник
Часть:
Сборники с готовыми домашними заданиями, тестовыми заданиями появились уже довольно давно. Изначально собрания готовых пошаговых решений задач и примеров предназначались для повышения качества выполнения проверки домашнего задания родителями, учителями.
Изначально собрания готовых пошаговых решений задач и примеров предназначались для повышения качества выполнения проверки домашнего задания родителями, учителями.
Естественно, учеников такие сборники тоже заинтересовали, они стали использовать их в своих целях. К тому же, готовые решения служат отличным справочником по предмету, для которого они созданы. Так как в нем детально объясняется откуда берется какое-либо значение, а решение расписано поэтапно, это позволяет быстро освежить в памяти давно забытую школьную программу. Эта помощь особенно актуальна для родителей, и учителей. Так же из сборника можно использовать похожие примеры, как в домашнем задании у ребенка, это окажет ему небольшую помощь в выполнении.
Больше не обязательно что-то понимать в математике, для того чтобы помочь своему ребенку в решении домашнего задания, проверки оного. Стоит отметить, что ГДЗ существуют для всех точных наук для каждого класса обучения. К примеру есть решебник по математике 2 класс от автора Моро.
Часть 1. Страница учебника
4567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495Часть 2. Страница учебника
456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111Ученик больше не сможет обманывать родителей, выставляя некачественное, неверное решение задания за правильное, в целях экономия времени для своих целей. В то время, пособие с ответами существенно экономит свободное время родителей, позволяя за минуту узнать, правильно ли их ребенок выполнил задания. Гдз по математике 2 класс Моро поможет родителям детально объяснить в чем причина возможных ошибок своему ребенку.
Гдз по математике 2 класс Моро поможет родителям детально объяснить в чем причина возможных ошибок своему ребенку.
Ученик же, используя ответы к учебнику по математике 2 класс Моро так же сможет существенно сократить время, затрачиваемое на выполнение домашнего задания. Конечно, при бездумном списывании существенно снизится качество знаний по данному предмету. Поэтому не рекомендуется использованием учениками. Разве что допускается использовать отдельные страницы, где приведены похожие примеры, для демонстрации ответов к задачам или примеров какого-либо типа.
К тому же, авторы сборника решили расположить в конце раздел с заданиями, на которые не дается решения. Он предназначен для проверки собственных знаний, повышения их уровня.
Похожие решебники
ГДЗ, Ответы по Математике 2 класс Петерсон. Все решебники тут GDZ-na5.info
Готовые Домашние Задания, Решебник по Математике 2 класс Петерсон
ГДЗ: 2 класс. Математика. Математика.Петерсон Л.Г. |
Математика — это своенравная и сложная наука, которая требует от ученика значительных усилий и знаний. Задания по данной дисциплине имеют различные уровни сложности, поэтому школьнику требуется тратить множество времени на тщательную подготовку задания. Решение задач и уравнений может быть весьма сложным для ученика, особенно если он пропустил урок и не освоил новую тему.
Чтобы быть всегда подготовленным к урокам, можно обзавестись ГДЗ по Математике для 2 класса Петерсон
Ответы к домашним заданиям по Математике 2 класс. Петерсон
Часть-1.
Урок-01.
Урок-02.
Урок-03.
Урок-04.
Урок-05.
Урок-06.
Урок-07.
Урок-08.
Урок-09.
Урок-10.
Урок-11.
Урок-12.
Урок-13.
Урок-14.
Урок-15.
Урок-16.
Урок-17.
Урок-18.
Урок-19.
Урок-20.
Урок-21.
Урок-22.
Урок-23.
Урок-24.
Урок-25.
Урок-26.
Урок-27.
Урок-28.
Урок-29.
Урок-30.
Урок-31.
Урок-32.
Урок-33.
Урок-34.
Урок-35.
Урок-36.
Урок-37.
Урок-38.
Урок-39.
Урок-40.>
Часть-2.
Урок-01.
Урок-02.
Урок-03.
Урок-04.
Урок-05.
Урок-06.
Урок-07.
Урок-08.
Урок-09.
Урок-10.
Урок-11.
Урок-12.
Урок-13.
Урок-14.
Урок-15.
Урок-16.
Урок-17.
Урок-18.
Урок-19.
Урок-20.
Урок-21.
Урок-22.
Урок-23.
Урок-24.
Урок-25.
Урок-26.
Урок-27.
Урок-28.
Урок-29.
Урок-30.
Урок-31.

Урок-32.
Урок-33.
Урок-34.
Урок-35.
Урок-36.
Урок-37.
Урок-38.
Урок-39.
Часть-3.
Урок-01.
Урок-02.
Урок-03.
Урок-04.
Урок-05.
Урок-06.
Урок-07.
Урок-08.
Урок-09.
Урок-10.
Урок-11.
Урок-12.
Урок-13.
Урок-14.
Урок-15.
Урок-16.
Урок-17.
Урок-18.
Урок-19.
Урок-20.
Урок-21.
Урок-22.
Урок-23.
Урок-24.
Урок-25.
Урок-26.
Урок-27.
Урок-28.
Урок-30.
Урок-31.
Урок-32.
Урок-33.
Урок-34.
Урок-35.
Урок-36.
Урок-37.
Урок-38.
Урок-39.
Урок-40.
домашнее задание по математике второй класс
Gdz Po Matematike 2 Klass Moro Chast 1 2
Gdz Po Matematike 2 Klass Dorofeev Chast 1 2
Kniga Matematika 2 Klass Uchebnik V 2 H Chastyah Fgos Moro
Gdz Po Matematike 2 Klass Chebotarevskaya Chast 1 2
Gdz Matematika 2 Klass Moro Bantova Beltyukova Uchebnik
Gdz Po Matematike 2 Klass Dorofeev Chast 1 2
Gdz Po Matematike 2 Klass Moro Bantova Uchebnik Reshebnik
Domashnie Zadaniya Po Matematike 2 2 Klass Matematika 3 Klass
Gdz K Rabochej Tetradi Po Matematike 2 Klass Moro Volkova 1 2
Matematika 2 Klass Chast 2 Stranica 78 Moro Bantova Gdz
Matematika 2 Klass Chast 1 Stranica 60 Moro Bantova Gdz
Gotovye Domashnie Zadaniya Gdz Po Matematike Za 2 Klass
Gotovye Domashnie Zadaniya 1 11 Klass Onlajn
Gdz Po Matematike 2 Klass Rudnickaya Chast 1 2
Domashnee Zadanie Po Matematike Na Zimnie Kanikuly Dlya 2 Klassa
Gdz Po Matematike 2 Klass Stranica 7 Rabochaya Tetrad Chast 2 Moro
Gdz Po Matematike 2 Klass Rabochaya Tetrad Rudnickaya Yudacheva Chast
Gdz Po Matematike 2 Klass Proverochnye Raboty Volkova Moro Reshebnik
Matematika 2 Klass Chast 2 Stranica 95 Moro Bantova Gdz
Gdz Po Matematike 2 Klass Stranica 22 Rabochaya Tetrad Chast 1 Moro
Stranica 5 Zadanie 10 Matematika 2 Klass Moro Chast 1 Youtube
Gdz Po Matematike 2 Klass Chekinl Chast 1
Gdz Po Matematike 2 Klass Moro Rabochaya Tetrad Onlinegdz Net
Gdz Matematika 9 Klass Variant Book Activities Activities
Otvety Po Matematike Za 2 Klass 2 Chast Rabochaya Tetrad Dorofeev
Stranica 93 Reshenie Matematika 2 Klass 2 Chast Moro Onlinegdz
Gdz Po Matematike Istomina 2 Klass 2 Chast
Gdz Po Matematike 2 Klass Peterson Chast 1 2 3 Uchebnik
Agejchik N N Matematika Domashnie Zadaniya 2 Klass Chast 1 Pdf
Matematika 2 Klass Opiq
Gotovye Domashnie Zadaniya 2 Klass Programma Matematika 5 Klass
Gdz 2 Chasti Moro M I 2 Klass Matematika Chast 2 Stranicy
Stranica 89 Reshenie Matematika 2 Klass 1 Chast Moro Onlinegdz
Gdz Po Matematike Peterson 2 Klass 2 Chast
Matematika 2 Klass Chast 2 Stranica 51 Moro Bantova Gdz
Gdz Po Matematike 2 Klass Uchebnik Moro Volkova 2 Chast Str 54
Gdz Reshebnik Matematika 2 Klass Istomina N B
Stranica 85 Zadanie 6 Matematika 2 Klass Moro Chast 1 Youtube
Gdz Po Matematike 2 Klass Uchebnik Moro Volkova 1 Chast Str 58
Gdz 2 Klass Matematika Moro Volkova Stepanova Bantova
Gotovye Domashnie Zadaniya Matematika 2 Klass Rudnickaya Yudacheva
Gdz Po Matematike 1 Klass Uchebnik Moro Volkova 2 Chast Str 69
Stranica 26 Reshenie Matematika 2 Klass 1 Chast Moro Onlinegdz
Matematika 2 Klass Chast 2 Stranica 43 Moro Bantova Gdz
Gdz Po Matematike 3 Klass Rabochaya Tetrad 2 Chast Moro M I
Gdz Tetrad Po Matematike 2 Klass Zaharova 2
Gdz Reshebnik Po Matematike 2 Klass Moro
Domashnee Zadanie 2 Klass Matematika Math Words Math Equations
Stranica 88 Reshenie Matematika 2 Klass 1 Chast Moro Onlinegdz
Gdz Po Matematike 3 Klass Uchebnik 2 Chast Moro M I Bantova M
Gdz Po Matematike 2 Klass Stranica 53 Rabochaya Tetrad Chast 2 Moro
Matematika 2 Klass Chast 2 Stranica 42 Moro Bantova Gdz
Gotovye Domashnie Zadaniya Po Matematike 2 Klass Rudnickaya Zadacha
Gdz Po Matematike 2 Klass Uchebnik Moro Volkova 1 Chast Str 89
Gdz Po Matematike 2 Klass Moro
Gdz Matematika Moro 2 Klass Uchebnik 2 Chast Otvety Na Zadaniya
Gdz Po Matematike 2 Klass Proverochnye Raboty Mirakova
Stranica 64 Reshenie Matematika 2 Klass 1 Chast Moro Onlinegdz
Matematika 2 Klass Chast 1 Stranica 34 Moro Bantova Gdz
Stranica 63 Gdz Po Matematike 2 Klass Moro Chast 2
Gdz Po Matematike 4 Klass Moro Chast 1 2
Gdz Po Matematike 2 Klass Uchebnik Moro Volkova 1 Chast Str 33
Domashnie Zadanie Po Matematike 2 Klass
Kniga Matematika 2 Klass Uchebnik V 2 H Chastyah Fgos Moro
Gdz Po Matematike 2 Klass Bulycheva Gotovye Domashnie Zadaniya
Gotovye Domashnee Zadanie Po Matematike 1 Klass Moro Aldeting
Gdz Po Matematike 2 Klass Dorofeev Mirakova Buka S Podrobnymi
Gdz Po Matematike 2 Klass Moro Rabochaya Tetrad
Gdz Matematika 2 Klass G V Dorofeev T N Mirakova T B Buka
Gdz Reshebnik Po Matematike 3 Klass Moro Bantova Chast 1 2
Gdz Po Matematike 2 Klass Uchebnik Moro Volkova 2 Chast Str 68
Gotovoe Domashnee Zadanie Po Matematiki 2 Klass M I Moro Journal
Gdz Po Matematike 1 Klass Uchebnik Moro Volkova 2 Chast Str 73
Gdz Reshebnik Po Matematika 2 Klass Moro 1 I 2 Chast
Matematika 2 Klass Kartochki Zadanij 3 E Izd German O I
Gdz Reshebnik Po Matematike 3 Klass Moro Bantova Chast 1 2
Gdz Proverochnye Raboty Po Matematike 2 Klass Volkova
Gdz Po Matematike 2 Klass Uchebnik Moro Volkova 2 Chast Str 56
Kniga Matematika 2 Klass Proverochnye Raboty Svetlana
Matematika 2 Klass Chast 2 Stranica 79 Moro Bantova Gdz
Gdz Po Matematike 2 Klass Aleksandrova Chast 1 2
Otvety Na Domashnee Zadanie Po Matematike 2 Klass T M Chebotarevskaya
Gdz Dlya Teh Kto Lyubit Matematiku 2 Klass Moro Volkova Otvety Prakard
Gdz Matematika 2 Klass Kuznecova Trenirovochnye Primery Po
Tematicheskie Domashnie Zadaniya Po Matematike 2 Klass 92 Raboty
Gdz Po Matematike 2 Klass Moro M I Opredeli Na Skolko
Gdz Po Matematike 2 Klass Rabochaya Tetrad Zaharova Yudina Chast 1 2
Matematika 2 Klass Chast 1 Stranica 81 Moro Bantova Gdz
Matematika 2 Klass Chast 2 Stranica 15 Uprazhnenie 1 3 5 6
Gdz Po Matematike 2 Klass Uchebnik Moro Volkova 2 Chast Str 76
Reshebnik Gdz Kontrolnye Raboty Po Matematike 2 Klass Rudnickaya
Reshebnik Gdz Po Matematike Za 2 Klass
Chast 1 Str 88 6 Gdz Matematika 2 Klass Moro Skolkimi
Stranica 72 Gdz Po Matematike 2 Klass Moro Chast 2
Kniga Matematika 2 Klass Uchebnik Dlya Obsheobrazovatelnyh
Reshebnik Po Belorusskomu Yazyku Za 2 Klass Sviridenko
Gdz Po Matematike 2 Klass Stranica 52 Rabochaya Tetrad Chast 1 Moro
Matematika Domashnee Zadanie Dlya 12 Klassa Na 30 09
Gdz Po Matematike 2 Klass Zaharova Tetrad Dlya Samostoyatelnyh
Matematika 2 Klass Chast 2 Stranica 64 Moro Bantova Gdz
Решебник Математика 2 1 – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
Решебник Математика 2 1
Готовое Домашнее Задание По Алгебре
Ладыженский 5 Класс Учебник Гдз
Готовые Домашние Задания 10 Класс Алгебра
Гдз По Русскому Языку Класс Учебник
Гдз Биболетова
Гдз Развивайка По Математике 3 Класса
Решебник По Литературной Тетради 3 Класс
Гдз 10 Класс Сивоглазова
Немецкий Горизонты 11 Класс Гдз
Гдз Афанасьева Михеева Activity Book 8кл
Решебник По Математике 2 Виноградова
Гдз По Английскому 8 Рабочая Тетрадь
Гдз Дидактические Материалы 11 Класс Никольский
Гдз По Алгебре 14
Гдз Математика 2 Класс Стр 110
Перышкин 9 Гдз Учебник
Гдз Биология Лабораторная Работа
Гдз По Английскому 8 Афанасьева Михеева
Дорофеев 2 Класс Рабочая Тетрадь Гдз
Алгебра 8 Класс Дорофеев Суворова Гдз Учебник
Гдз Математика 4 Класс Решебник Задач
Решебник По Английскому 8 С Переводом
Решебник По Русскому Языку 8 Рабочая Тетрадь
Book 5 Класс Решебник
Гдз По Русскому 2 Класс Упр 19
Гдз По Физике 8 9 Класс
Гдз По Rainbow 11 Класс Афанасьева
Гдз По Русскому Языку Александрова Загоровская
Гдз По Английскому 6 Класс Афанасьева Верещагина
Литература 8 Класс Меркин Гдз Ответы
Гдз По Алгебре 9 Класс Фиолетовый Учебник
Гдз По Английскому 6 Класс Трубанева
Гдз Плешакова Новицкая 2 Часть
Гдз По Белорусскому Шестой Класс
Гитем Комарова Готовое Домашнее Задание 2 Класс
Гдз По Математике 5 Класс 1117
Гдз Математика 3 Класс Стр 4 Номер6
Гдз По Математике 1 Часть Кузнецова
Гдз По Русскому Языку Рыбченкова Александрова Загоровская
Гдз По Немецкому 7 Класс Вундеркинды
Учебник Решебник Немецкий 6 Класс
Гдз По Химии 8 Габриелян Остроумов
Гдз По Англ Языку 11 Класс Ваулина
Гдз По Англ Ваулина 8 Класс Учебник
Приложение К Учебнику 6 Класс Гдз
Гдз По Алгебре Восьмого Класса Мерзляк
Гдз Ваулина Рабочая Тетрадь
Впр Окружающий Мир Волкова Данилова Гдз
Гдз По Английскому Языку 22 Класс Spotlight
География 7 Класс Полярная Звезда Гдз
Голицынский 7 Ответы Гдз
Русский Язык 9 Класс Быстрова Гдз
Решебник По Математике 3 Часть Рудницкая
Гдз По Русскому Языку Рабочая Канакин
Гдз По Русскому 1 Класс Желтовская
Белорусские ГДЗ и Решебник за 2 класс по Математике часть 1 , часть 2 поможет Вам найти верный ответ на самый сложный номер задания Тип: Учебник . Издатель: Национальный институт образования 2019 год . Белорусские ГДЗ и Решебник за 2 класс по Математике часть . .
Издатель: Национальный институт образования 2019 год . Белорусские ГДЗ и Решебник за 2 класс по Математике часть . .
Онлайн решебник по Математике для 2 класса Чеботаревская Т .М ., Николаева В .В ., гдз и ответы к домашнему заданию . Решебник по Математике для 2 класса Чеботаревская Т .М .
Убедись в правильности решения задачи вместе с ГДЗ по Математике за 2 класс Муравьева Г .Л ., Урбан М .А . часть 1 , 2 . Ответы сделаны к книге 2019 года от Национальный институт образования .
ГДЗ (решебники ) по математике . Математика 5 класс . Герасимов В . Д ., Пирютко О . Н ., Лобанов А . П . 2019 Математика 6 класс . Л .Б . Шнеперман, Е .П . Кузнецов, Г .Л . Муравьёв и др .
ГДЗ решебник и ответы 2 класс, Математика , Моро М .И ., Волкова С .И ., Степанова С .В ., Бантова М .А ., Бельтюкова Г .В ., Учебник, 1 часть, год, 2019 год, 2019 год, 2019 год, 2020 год, 2020 год . Готовые домашние задания с подробными ответами .
Решебники, ГДЗ . 11 Класс . ГДЗ — поможет Вам сверить ответы к домашнему заданию по Математике Муравьева Г . Л ., Урбан М .А . 2 класс .
Л ., Урбан М .А . 2 класс .
Смотрите любимые видео, слушайте любимые песни, загружайте собственные ролики и делитесь ими с друзьями, близкими и целым миром .
Решебник по математике 2 класс — Моро, Волкова, Степанова 1 -2 часть (Учебник) . Правильные ответы онлайн! Бесплатно! Заходи! Первая содержит 95, вторая – 111 страниц . Для удобства к каждому развороту учебника приложен заполненный лист решебника .
Рабочая тетрадь является частью учебно-методического комплекса по математике для 2 класса авторов Г . Л . Муравьёвой, М . А . Урбан . Пособие может быть использовано на уроках как дополнительный материал для закрепления знаний, совершенствования умений и навыков . .
Математика и физика это вообще не для вас . Но теперь ваш ребёнок пошёл в школу, уже перешёл во второй класс, и вы, поэтому обязаны ему ГДЗ к учебнику по математике за 2 класс Моро Часть 1 , Часть 2 состоит из двух частей, что также и распространяется на решебник .
Решебник . X . Показать больше . По зосу «» не найдено ни одного решебника . Введите в строку поиска только фамилию автора и класс . Добавить книги в список » По зосу «» не найдено ни одной книги . Математика 2 класс .
По зосу «» не найдено ни одного решебника . Введите в строку поиска только фамилию автора и класс . Добавить книги в список » По зосу «» не найдено ни одной книги . Математика 2 класс .
Решебник по математике , 2 класс, Зак С . М ., К учебнику математики за 2 класс, Петерсон Л .Г ., .
Выполняй домашние задания по математике 2 класс с решебниками . Во втором классе программа по математике является гораздо более сложной, чем в первом . Во-первых, оценки будут уже настоящими и в журнале, а во-вторых, существенным образом увеличится уровень . .
ГДЗ и ответы к учебнику математики за 2 класс (Часть 1 – 2 ) Моро, Бантова, Волкова . Посмотрите также решебник к Раб .тетради Моро 2 класс .
Решебник по математике за 2 класс составлен с учетом рекомендаций опытных методистов . Здесь удобно смотреть способы решения В ГДЗ по математике 2 класс есть рисунки, наглядные таблички, понятные схемы, с помощью которых вы легко объясните полученный . .
Подробный решебник по математике для 5 класса, авторов Герасимов, Пирютко, 2019-2020 . Решебник – друг и наставник школьника . Пригодится подспорье и родителям . С ним припомнится школьная программа, а значит последует помощь ребенку .
Решебник – друг и наставник школьника . Пригодится подспорье и родителям . С ним припомнится школьная программа, а значит последует помощь ребенку .
Готовые Домашние Задания (ГДЗ) или решебники — это са необходи книга, которая должна лежать на полке у каждого современного Именно с ними вы и сможет свериться и выполнить домашку на отлично! Ответы по страницам для учебника ГДЗ Математика, Моро . .
Решебник — надежный консультант . Родители не всегда могут стать надежными помощниками — ведь без Квалифицированно справиться с математической наукой поможет «Математика 2 класс Учебник Моро, Бантова, Бельтюкова Школа России Просвещение» .
Ответы и решебник к учебнику часть 1 , 2 . Часть 2 . Страница 4 . Письменные вычисления: 1 ; 2; 3; Вопросы на полях
Именно поэтому решебники по математике за 2 класс лучше всего подходят для школьников, которые хотят учиться на «отлично» и блистать знаниями . Ученику достаточно сверить полученный ответ с тем, который приведен в сборнике, и дело сделано .
Белорусские ГДЗ и Решебник за 2 класс по Математике часть 1 , часть 2 поможет Вам найти верный ответ на самый сложный номер задания Тип: Учебник . Издатель: Национальный институт образования 2019 год . Белорусские ГДЗ и Решебник за 2 класс по Математике часть . .
Онлайн решебник по Математике для 2 класса Чеботаревская Т .М ., Николаева В .В ., гдз и ответы к домашнему заданию . Решебник по Математике для 2 класса Чеботаревская Т .М .
Убедись в правильности решения задачи вместе с ГДЗ по Математике за 2 класс Муравьева Г .Л ., Урбан М .А . часть 1 , 2 . Ответы сделаны к книге 2019 года от Национальный институт образования .
ГДЗ (решебники ) по математике . Математика 5 класс . Герасимов В . Д ., Пирютко О . Н ., Лобанов А . П . 2019 Математика 6 класс . Л .Б . Шнеперман, Е .П . Кузнецов, Г .Л . Муравьёв и др .
ГДЗ решебник и ответы 2 класс, Математика , Моро М .И ., Волкова С .И ., Степанова С .В ., Бантова М .А ., Бельтюкова Г .В ., Учебник, 1 часть, год, 2019 год, 2019 год, 2019 год, 2020 год, 2020 год . Готовые домашние задания с подробными ответами .
Готовые домашние задания с подробными ответами .
Решебники, ГДЗ . 11 Класс . ГДЗ — поможет Вам сверить ответы к домашнему заданию по Математике Муравьева Г .Л ., Урбан М .А . 2 класс .
Смотрите любимые видео, слушайте любимые песни, загружайте собственные ролики и делитесь ими с друзьями, близкими и целым миром .
Решебник по математике 2 класс — Моро, Волкова, Степанова 1 -2 часть (Учебник) . Правильные ответы онлайн! Бесплатно! Заходи! Первая содержит 95, вторая – 111 страниц . Для удобства к каждому развороту учебника приложен заполненный лист решебника .
Рабочая тетрадь является частью учебно-методического комплекса по математике для 2 класса авторов Г . Л . Муравьёвой, М . А . Урбан . Пособие может быть использовано на уроках как дополнительный материал для закрепления знаний, совершенствования умений и навыков . .
Математика и физика это вообще не для вас . Но теперь ваш ребёнок пошёл в школу, уже перешёл во второй класс, и вы, поэтому обязаны ему ГДЗ к учебнику по математике за 2 класс Моро Часть 1 , Часть 2 состоит из двух частей, что также и распространяется на решебник .
Решебник . X . Показать больше . По зосу «» не найдено ни одного решебника . Введите в строку поиска только фамилию автора и класс . Добавить книги в список » По зосу «» не найдено ни одной книги . Математика 2 класс .
Решебник по математике , 2 класс, Зак С . М ., К учебнику математики за 2 класс, Петерсон Л .Г ., .
Выполняй домашние задания по математике 2 класс с решебниками . Во втором классе программа по математике является гораздо более сложной, чем в первом . Во-первых, оценки будут уже настоящими и в журнале, а во-вторых, существенным образом увеличится уровень . .
ГДЗ и ответы к учебнику математики за 2 класс (Часть 1 – 2 ) Моро, Бантова, Волкова . Посмотрите также решебник к Раб .тетради Моро 2 класс .
Решебник по математике за 2 класс составлен с учетом рекомендаций опытных методистов . Здесь удобно смотреть способы решения В ГДЗ по математике 2 класс есть рисунки, наглядные таблички, понятные схемы, с помощью которых вы легко объясните полученный . .
.
Подробный решебник по математике для 5 класса, авторов Герасимов, Пирютко, 2019-2020 . Решебник – друг и наставник школьника . Пригодится подспорье и родителям . С ним припомнится школьная программа, а значит последует помощь ребенку .
Готовые Домашние Задания (ГДЗ) или решебники — это са необходи книга, которая должна лежать на полке у каждого современного Именно с ними вы и сможет свериться и выполнить домашку на отлично! Ответы по страницам для учебника ГДЗ Математика, Моро . .
Решебник — надежный консультант . Родители не всегда могут стать надежными помощниками — ведь без Квалифицированно справиться с математической наукой поможет «Математика 2 класс Учебник Моро, Бантова, Бельтюкова Школа России Просвещение» .
Ответы и решебник к учебнику часть 1 , 2 . Часть 2 . Страница 4 . Письменные вычисления: 1 ; 2; 3; Вопросы на полях
Именно поэтому решебники по математике за 2 класс лучше всего подходят для школьников, которые хотят учиться на «отлично» и блистать знаниями . Ученику достаточно сверить полученный ответ с тем, который приведен в сборнике, и дело сделано .
Ученику достаточно сверить полученный ответ с тем, который приведен в сборнике, и дело сделано .
ГДЗ по математике 2 класс Моро Бантова Бельтюкова учебник
Математика – предмет, в котором движение вперед невозможно без крепких базовых знаний. Это как лестница, где важна каждая ступенька. Многие математические законы используются и в других науках. В начальных классах малышу необходимо приобрести и закрепить основные понятия, научиться самостоятельно мыслить и организовывать себя. В этом поможет ГДЗ по математике для 2 класса, разработанный коллективом автором под руководством Марии Игнатьевны Моро.
Особенности пособия ГДЗ к учебнику Моро за 2 класс
Решебник по математике для 2-го класса М.И. Моро и других авторов соответствует требованиям Федерального государственного образовательного стандарта и входит в УМК «Школа России» для 1-4 класса М. Моро. Учебник выпущен компанией «Просвещение» и выдержал уже 12-е издание.
Моро. Учебник выпущен компанией «Просвещение» и выдержал уже 12-е издание.
Прекрасный педагог и учёный, М. Моро, посвятила 40 лет жизни созданию разнообразных учебных пособий. Своей целью она считала научить детей думать, мыслить логически, уметь применять научные принципы и знания в реальной жизни, а не механически считать по формулам и выполнять задания по шаблонам. Сборник прекрасно оформлен, каждый раздел снабжен цветными иллюстрациями. Чтобы избежать монотонности и сделать объяснения более наглядными, используются цветные заголовки, таблицы и графики. Для пометок и комментариев предусмотрены широкие поля.
Ребёнку будет интересно заниматься и приятно разглядывать картинки с весёлыми зверюшками. Ему несомненно понравятся разделы «Математика вокруг нас» и «Страничка для любознательных». Материал изложен доступным языком, в понятной лёгкой для восприятия малышом форме. Такое обучение напоминает увлекательную игру по разгадыванию загадок.
Пособие содержит задания разного уровня по принципу «от простого к сложному» и включает задания с решениями и ответами по всей программе 2-го класса по математике. Есть дополнительные задания для проверки усвоения пройденного материала.
Есть дополнительные задания для проверки усвоения пройденного материала.
Кому пригодится решебник Моро по математике для 2-го класса
Ребёнок в самом начале своего пути должен научиться организованности и ответственности, настойчивости в стремлении к цели. Это залог его успехов в дальнейшем. Самостоятельное решение задач по яркому сборнику поможет развить эти навыки. Подробные объяснения помогут ученику успешно справиться с примерами. Каждая маленькая победа над собой придаст ему уверенности в себе, своих силах. Он не будет бояться вызова к доске и не утратит интереса к учёбе.
Возможно, маленькому непоседе понадобится поддержка родителей, которым часто сложно разобраться, как доходчиво подать материал малышу. Пособие поможет научить малыша решать задачи и правильно оформлять для сдачи преподавателю. Преподаватели найдут в сборнике задачи для контрольных работ и проверки знаний учащихся по определённым темам.
Сборник ответов будет полезен учащимся:
- для самостоятельного выполнения домашних заданий;
- повторения пройденного материала;
- проработки сложных тем и углублённого изучения предмета;
- подготовки к контрольным и тестам;
- самостоятельной проверки знаний, выявления слабых мест и ошибок;
- восполнения пробелов из-за пропуска занятий или непонимания объяснений на уроке.

Преимущества использования пособия онлайн
Дети настолько привыкли пользоваться гаджетами, что и учебник в электронном виде воспринимается ими с большим энтузиазмом, выглядит современнее и приобретает в их глазах игровой формат. Использование сборника по математике онлайн имеет несомненные плюсы для учёбы:
- круглосуточная доступность;
- удобный поиск по номеру, теме;
- быстрое нахождение нужного ответа на задание;
- регулярное обновление;
- выбор вариантов решения;
- возможность использования на компьютере, смартфоне, планшете при наличии интернета.
Разумеется, в этой доступности кроется и опасность. Необходимо, чтобы ребенок не использовал пособие для списывания правильного решения задач на контрольных с помощью гаджета, а научился думать самостоятельно.
Какие темы рассмотрены в сборнике ответов
В пособие М. Моро включены полностью все темы, входящие в утвержденную учебную программу. Здесь вы найдёте подробные объяснения, задания и ответы для закрепления знаний по следующим темам:
- устный и письменный счёт от 1 до 100;
- сложение и вычитание, свойства и проверка;
- умножение и деление;
- таблица умножения;
- использование скобок и порядок вычислений;
- числовые и буквенные выражения;
- что такое «уравнение»;
- основные понятия о фигурах: угол, треугольник, прямоугольник, квадрат, многоугольник;
- проекции предметов на плоскости;
- единицы длины и времени;
- денежные единицы.

Красота и интуиция в преподавании математики
Аннотация
i Интуиция была определена как случайное возникновение и развитие событий в счастливой и полезной
путь. Beauty описывается в одном словаре как «сочетание качеств, таких как форма, цвет или форма,
доставляет удовольствие чувствам или приятно возвышает разум или дух.В этой статье приводятся примеры того, как эти
два аспекта опыта повлияли на то, что я хотел бы видеть в классах математики и в моей учебной программе
работа по развитию, чтобы породить их, до и через работу математики школы Чикагского университета
Проект.
Введение
iiВозможность написать эту статью возникла из-за того, что я получил одну из двух премий ISDDE 2017 года за пожизненные достижения в разработка и разработка учебной программы, другая — Кей Стейси.Этот документ основан на представленном пленарном докладе. на конференции ISDDE 2018 года в Голуэе, Ирландия.
Я бы не получил эту награду без работы многих других людей. Принято говорить, что мы работаем над плечи гигантов, но на самом деле мы работаем у ног таких людей, как Поля, Фрейденталь или Кляйн, а многочисленные великие математики и преподаватели на протяжении веков и со всего мира, которые создали область, которая является нашей игровая площадка.Но мы работаем плечом к плечу с нашими коллегами, коллегами и студентами, от которых мы многому учимся, и их труды нам помогают.
Получение этой награды особенное, потому что она исходит от моих коллег. Я хочу поблагодарить членов
наградный комитет, и особенно благодарю Боба и Барбару Рейс за их работу по составлению документов для моего
номинации и тем, кто написал письма поддержки. Эти люди внесли непосредственный вклад в мое получение этой награды.Но есть десятки других людей — нет, сотни других людей — без которых я бы не стоял раньше
ты. Некоторые из них будут указаны здесь, но я не могу назвать их всех.
Я хочу поблагодарить членов
наградный комитет, и особенно благодарю Боба и Барбару Рейс за их работу по составлению документов для моего
номинации и тем, кто написал письма поддержки. Эти люди внесли непосредственный вклад в мое получение этой награды.Но есть десятки других людей — нет, сотни других людей — без которых я бы не стоял раньше
ты. Некоторые из них будут указаны здесь, но я не могу назвать их всех.
Меня бы здесь не было, если бы не интуитивная интуиция, многие удачные обстоятельства, которые пришли ко мне без всякой работы. в моей части. Поэтому я решил сделать интуитивную интуицию одной из тем своих замечаний.
Удачная география
iiiЯ родился в Чикаго и, окончив среднюю школу, поступил в ведущий университет моего штата, Университет Иллинойса, потому что туда учился мой брат.За много лет до этого я решил, что хочу преподавать математику.
Мой первый образовательный курс назывался «Введение в образование», и я был в секции для будущих учителей математики. Учителем в этом классе был Кеннет Хендерсон, профессор математического образования и одаренный учитель. Несколько лет спустя среди его докторантов были Джон Досси и Том Куни. Предмет этого класса включал подробное изучение материалов средней школы, разработанных Комитетом по школьной математике Университета Иллинойса (UICSM).UICSM, начатый в 1951 году Максом Беберманом (Beberman, 1958), был первым из проектов «новой математики» в Соединенных Штатах (Kinsella, 1965).
Учителем в этом классе был Кеннет Хендерсон, профессор математического образования и одаренный учитель. Несколько лет спустя среди его докторантов были Джон Досси и Том Куни. Предмет этого класса включал подробное изучение материалов средней школы, разработанных Комитетом по школьной математике Университета Иллинойса (UICSM).UICSM, начатый в 1951 году Максом Беберманом (Beberman, 1958), был первым из проектов «новой математики» в Соединенных Штатах (Kinsella, 1965).
Материалы UICSM (UICSM, 1959; Beberman and Vaughan, 1964) начинались с урока, который в свое время был известен, переписки рукописным письмом между студентом из Соединенных Штатов и студентом на Аляске, в котором первый студент хочет чтобы помочь студенту с Аляски и, чтобы определить потребности студента с Аляски, задает студенту с Аляски несколько вопросов.
Среди них: «Убери 2 из 21.» Студент с Аляски пишет «1». «Сколько раз 3 переходит в 8?» Аляска
студент отвечает «дважды». «Напишите число больше 4. » Студент с Аляски пишет 4 .
» Студент с Аляски пишет 4 .
Целью урока было показать, что то, что вы пишете, является представлением концепции числа, а не самого числа. И то, что вы пишете, является числом, и этот урок научил различать число и число. Никто из нас, студентов университета, никогда не задумывался об этом различии.
UICSM очень осторожно использовал язык, но переборщил с этой конкретной идеей. Письмо, такое как x , используемое в уравнении, называлось не переменной, а местоимением , потому что оно означало
числительное так же, как местоимение заменяет существительное. Описание алгебраических свойств, таких как
распределительному свойству умножения над сложением предшествовали кванторы: ∀ a , ∀ b , ∀ c , a ( b + c ) = ab + ac.Существование личности было
описывается: ∃ b ∋∀ a , a + b = a . Тщательно основывая решение уравнений и манипуляции с алгебраическими выражениями на этих
свойств, UICSM принес математические системы и доказательства в изучение алгебры, идеи, которые ранее не
был частью исследования этого предмета.
Тщательно основывая решение уравнений и манипуляции с алгебраическими выражениями на этих
свойств, UICSM принес математические системы и доказательства в изучение алгебры, идеи, которые ранее не
был частью исследования этого предмета.
Мне понравился подход. Но более того, мне нравился тот факт, что к математике, которой меня учили одним способом, можно было подойти совершенно иначе.UICSM научил нас, что это не только нормально, но и более того, что это было ценно, — внимательно смотреть на то, чему учат, потому что тщательное изучение математики может привести к лучшему лечению.
В стране есть всего несколько других университетов, в которых я мог бы получить аналогичный урок. И почему я получил это образование? Потому что Иллинойс был моим государственным университетом, и мой брат учился там. Это случайность, случайное возникновение и развитие событий счастливым или благоприятным образом .
UICSM организовал алгебру последовательным образом. Это было красиво. Больше не нужно изучать изолированные правила. Все можно проследить до свойств поля действительных чисел.
Это было красиво. Больше не нужно изучать изолированные правила. Все можно проследить до свойств поля действительных чисел.
Пять лет спустя, когда я стал штатным учителем, я преподавал, используя материалы, на которые сильно повлиял SMSG, крупнейший из новых математических проектов в США. Как и в материалах штата Иллинойс, SMSG проследила свойства, используемые в алгебре, до свойства поля действительных чисел. Не такой серьезный подход, как UICSM, но опять же проявление возможности подойти к стандартному курсу математики существенно иным способом, чем существовавший ранее, способом, который был математически более последовательным, чем я когда-либо видел.Он отвечал критерию красоты, так как радовал мои чувства и возвысил мой разум и дух. Красота математики дает возможность иметь красивые уроки, разделы и курсы по математике.
Использование интуиции
iv Несколько лет назад я наблюдал, как одна из моих магистрантов преподавала в классе 12 -го класса вместе со своей ученицей. опыт преподавания.Темой дня было построение графиков в полярных координатах, и одним из примеров было построение графиков в полярных координатах.
кардиоидный (см. рисунок 1).
опыт преподавания.Темой дня было построение графиков в полярных координатах, и одним из примеров было построение графиков в полярных координатах.
кардиоидный (см. рисунок 1).
Кардиоида получила свое название, потому что она имеет форму сердца. Сидя в глубине комнаты, я понял, что свидание этот день как раз случилось 14 февраля года года, День святого Валентина в США (и во многих других странах по всему миру). мир). И поэтому я ждал, что этот студент-учитель укажет, что эта кривая примерно напоминает сердце на Валентинка.
О связи никогда не упоминалось. Это был традиционный класс предварительных вычислений, в котором связи между математикой и реальным миром почти полностью отсутствовали, и здесь был шанс показать хотя бы небольшую связь, но возможность была упущена. Это совпадение, что эта тема пришлась на День святого Валентина. Это была возможность для интуитивной прозорливости, случайной встречи, которая, я думаю, обрадовала бы студентов.
Это была возможность для интуитивной прозорливости, случайной встречи, которая, я думаю, обрадовала бы студентов.
Конечно, сердце Валентина не совсем похоже на кардиоиду, поэтому люди экспериментировали с различными
математические выражения для отображения графиков, которые больше похожи на валентинки или сердечки на игральных картах.На рисунке 2 показаны некоторые из разнообразных выражений, образующих кривые, похожие на кривые Валентина.
сердце. Мне особенно нравится средняя кривая в верхнем ряду, график уравнения 6 и градусов в x и и с довольно коротким алгебраическим описанием. При соответствующем масштабировании он почти соответствует валентинке.
сердце. Это прекрасный с эстетической точки зрения пример того, как алгебра может математически моделировать реальные объекты.Хорошо составленная учебная программа даст учащимся понять, что математика может моделировать даже сложные
геометрические фигуры. И он покажет или приведет ученика к другим красивым кривым с красивыми математическими
описания.
И он покажет или приведет ученика к другим красивым кривым с красивыми математическими
описания.
Источник: Вайсштейн, Эрик В. «Кривая сердца». Из MathWorld — Интернет-ресурс по Вольфрам. http://mathworld.wolfram.com/HeartCurve.html
Как этот студент-учитель мог пропустить связь между кардиоидой и Днем святого Валентина? Одна из причин в том, что наиболее распространенное размещение кардиоиды — горизонтальная линия симметрии.Другая причина в том, что кардиоида в учебной программе, потому что она дает хороший пример кривой, описанной в полярных координатах r и θ , а не x и y , а не из-за его связи с сердечками или валентинками. Рутина традиции часто мешают интуиции и часто приучают нас к красоте того, чему мы учим.
Элегантность преобразований
v Красота в математике принимает разные формы. Одна из форм — elegance . Будучи докторантом
В Мичиганском университете я искал темы, по которым я мог бы написать диссертацию, и Джозеф (Джо) Пейн, мой
советник, посоветовал мне изучить использование таких преобразований, как отражения, вращения, переводы и
так далее, в геометрии. Я изучил идею, и она мне понравилась. Я был очарован элегантностью определения
совпадающие цифры в этом подходе. В традиционном подходе требуется другое определение конгруэнтности для
каждый разный тип фигуры.Используя преобразования, нужно только одно определение. Таблица 1 показывает это.
Одна из форм — elegance . Будучи докторантом
В Мичиганском университете я искал темы, по которым я мог бы написать диссертацию, и Джозеф (Джо) Пейн, мой
советник, посоветовал мне изучить использование таких преобразований, как отражения, вращения, переводы и
так далее, в геометрии. Я изучил идею, и она мне понравилась. Я был очарован элегантностью определения
совпадающие цифры в этом подходе. В традиционном подходе требуется другое определение конгруэнтности для
каждый разный тип фигуры.Используя преобразования, нужно только одно определение. Таблица 1 показывает это.
Джо сказал, что эта идея заинтересовала не его, а Арт Коксфорд, более молодого профессора университета. Арт подумал, что это может быть обычная диссертация по учебной программе — напишите 3-недельный или 6-недельный блок, попробуйте его и сравните с традиционными классами, чтобы увидеть, есть ли какие-либо различия, но к этому времени мы с Кеном Хендерсоном уже уже написал рукопись для годичного предварительного расчета (Henderson, Usiskin & Zaring, 1971). Я утверждал, что трехнедельные и шестинедельные блоки никогда не влияют на то, что изучается в целом, поэтому мы должны написать годичный курс с использованием преобразований. И поэтому мы решили, что в течение следующего учебного года мы будем писать вместе, и каждый из нас будет пилотировать полный год 10 -го класса геометрии , используя то, что мы написали.
Я утверждал, что трехнедельные и шестинедельные блоки никогда не влияют на то, что изучается в целом, поэтому мы должны написать годичный курс с использованием преобразований. И поэтому мы решили, что в течение следующего учебного года мы будем писать вместе, и каждый из нас будет пилотировать полный год 10 -го класса геометрии , используя то, что мы написали.
Летом снова вспыхнула интуиция. Я работал помощником директора в летнем институте учителей Национального научного фонда США (NSF).В служебной библиотеке режиссера Фила Джонса я нашел книгу с использованием преобразований Transformatiemeetkunde , написанную голландской командой под руководством Рудольфа Трельстра (Troelstra, Haberman, deGroot & Bulens, 1965). В этой книге первое, что делается с фигурой, — это доказательство ее симметрии, из которой можно автоматически вывести многие другие свойства.
Например, одна из первых теорем, изученных в геометрии средней школы, заключается в том, что базовые углы равнобедренного
треугольник конгруэнтны, т. е.е., у них такая же мера. При традиционном подходе разделяем равнобедренные
треугольник на два треугольника, проведя отрезок от угла при вершине до середины основания
(Рисунок 3а).
Два образованных таким образом треугольника совпадают по SSS (сторона-сторона-сторона) и углам основания, что соответствует
углы этих треугольников, таким образом, должны совпадать. В подходе преобразования мы заключаем, что треугольник
собственное изображение под отражением над этой биссектрисой, и поскольку один базовый угол является изображением другого, они должны
быть конгруэнтным (рис. 3b).
е.е., у них такая же мера. При традиционном подходе разделяем равнобедренные
треугольник на два треугольника, проведя отрезок от угла при вершине до середины основания
(Рисунок 3а).
Два образованных таким образом треугольника совпадают по SSS (сторона-сторона-сторона) и углам основания, что соответствует
углы этих треугольников, таким образом, должны совпадать. В подходе преобразования мы заключаем, что треугольник
собственное изображение под отражением над этой биссектрисой, и поскольку один базовый угол является изображением другого, они должны
быть конгруэнтным (рис. 3b).
Подход с преобразованием основан на нашей интуиции относительно симметричных фигур и может быть применен к
получить некоторые основные свойства параллелограммов, прямоугольников, квадратов, правильных многоугольников, конических сечений и многих других
другие цифры (Coxford & Usiskin, 1971, 1972). В этом случае,
преобразования представляют собой элегантный и интуитивно понятный способ приближения к евклидовой геометрии, подходящий не только для
студенты, которые будут больше изучать математику, но также для студентов, которым трудно визуализировать и организовывать
свойства фигур.В моей докторской диссертации, предпринятой на основе пересмотра пилотных материалов, сравнивались
успеваемость и отношение 425 студентов, использующих эти материалы, 475 студентов, использующих традиционную геометрию
материалы (Усискин, 1972). Коммерческое издание включает в себя
доработка по результатам диссертационного исследования.
В этом случае,
преобразования представляют собой элегантный и интуитивно понятный способ приближения к евклидовой геометрии, подходящий не только для
студенты, которые будут больше изучать математику, но также для студентов, которым трудно визуализировать и организовывать
свойства фигур.В моей докторской диссертации, предпринятой на основе пересмотра пилотных материалов, сравнивались
успеваемость и отношение 425 студентов, использующих эти материалы, 475 студентов, использующих традиционную геометрию
материалы (Усискин, 1972). Коммерческое издание включает в себя
доработка по результатам диссертационного исследования.
Разработка курса Геометрия — подход к трансформации произошла в конце 1960-х годов, незадолго до того, как рисунки Эшера стали известны в США.S.A. Когда в 1971 году появилось коммерческое издание, Гарольд Джейкобс поместил рисунок Эшера на обложку своей знаменитой книги Mathematics — A Human Endeavor (1971). Вскоре работы Эшера стали заметны повсюду, слово мозаика вошло в наш словарный запас, и мы увидели совпадающих лошадей, птиц, рыб и всевозможные другие фигуры. Красивое искусство и красивая математика.
Вскоре работы Эшера стали заметны повсюду, слово мозаика вошло в наш словарный запас, и мы увидели совпадающих лошадей, птиц, рыб и всевозможные другие фигуры. Красивое искусство и красивая математика.
Исследование паттернов
viРяд людей описали математику как изучение закономерностей , то есть изучение сходства. в структуре.Пожалуй, самые известные работы по математике и шаблонам принадлежат Г. Харди (1940).
«Математик, как художник или поэт, создает узоры … Математические узоры, как и узор художника или поэта, должны быть красивыми, идеи, такие как цвета или слова, должны гармонично сочетаться друг с другом. . Красота — это первое испытание; в мире нет постоянного места для уродливой математики ».
Особенно приятно осознавать, что некоторые математические свойства, которые выглядят по-разному, являются экземплярами одного и того же паттерна.Но в этом плане математика вовсе не уникальна. Исследователи во всех областях ищут общие черты. Что делает математика, так это описывает модели алгебраически или геометрически, а затем изучает сами закономерности, часто без учета их происхождения.
Исследователи во всех областях ищут общие черты. Что делает математика, так это описывает модели алгебраически или геометрически, а затем изучает сами закономерности, часто без учета их происхождения.
Описание узоров настолько запечатлелось в нашем сознании, что буквы, которые мы используем, — это все, что нужно для обозначения настройка. В качестве примера в таблице 2 показаны шесть математически идентичных уравнений.В каждом произведении два числа — это третье число. Они различаются только буквами, используемыми для обозначения цифр, но этого достаточно, чтобы дайте нам знать, какую ситуацию они описывают. Читатель может захотеть рассмотреть правый столбец этой таблицы. и угадайте, что представляет собой каждое уравнение в левом столбце.
Другой пример значения букв связан с построением парабол, что является темой во всех США.
тексты по алгебре, обычно на втором году изучения алгебры. Студенты узнают, что вершина параболы с
уравнение y = ( x + 3) 2 + 5 можно увидеть в его уравнении. Сегодня они могут даже связать алгебру с геометрией, а именно с тем, что граф
of y = ( x + 3) 2 + 5 — это преобразованное изображение параболы с уравнением y = x 2 . Чего они не узнают из большинства американских учебников, так это
общая теорема, применимая ко всем переводным изображениям (Usiskin, 1975).В отношении, описанном предложением в x и y , следующие два процесса дают один и тот же график: (1) замена x на x — h и y x y — k ; (2) применяя перевод T ( x , y ) = ( x + h , y + k ) к графику исходного отношения. Немного
Следствия этой теоремы о переносе графов показаны в таблице 3.
Студенты узнают, что вершина параболы с
уравнение y = ( x + 3) 2 + 5 можно увидеть в его уравнении. Сегодня они могут даже связать алгебру с геометрией, а именно с тем, что граф
of y = ( x + 3) 2 + 5 — это преобразованное изображение параболы с уравнением y = x 2 . Чего они не узнают из большинства американских учебников, так это
общая теорема, применимая ко всем переводным изображениям (Usiskin, 1975).В отношении, описанном предложением в x и y , следующие два процесса дают один и тот же график: (1) замена x на x — h и y x y — k ; (2) применяя перевод T ( x , y ) = ( x + h , y + k ) к графику исходного отношения. Немного
Следствия этой теоремы о переносе графов показаны в таблице 3.
Непосредственные следствия теоремы о переводе графов пронизывают многие темы математики в старших классах. Однако,
они замаскированы, потому что конкретные буквы h и k , которые сигнализируют о величине
перевод обычно появляется только с кругом и параболой. Такие символы, как x 0 , y 0 , м ,
и b , и большинство студентов не понимают, что все следствия являются частными случаями одного и того же
теорема.Им не говорят, что графики функций синуса и косинуса конгруэнтны, и что графики всех
экспоненциальная и логарифмическая функции с одинаковым основанием конгруэнтны. В США на протяжении многих десятилетий
спор о том, что лучше иметь трехлетнюю последовательность алгебра-геометрия-алгебра или то, что называется
интегрированная последовательность. Вот замечательный пример интеграции алгебры и геометрии, которая должна быть в обоих
последовательности, но, насколько мне известно, можно найти только в материалах UCSMP. Но основа была сделана задолго до UCSMP.
существовал.
Но основа была сделана задолго до UCSMP.
существовал.
Переводы координатных графов, которые являются предметом теоремы о переносе графов, выполняются добавление фиксированных значений к координатам прообраза. Красивая соответствующая мультипликативная структура дает растягивает и сжимает графики. Мы называем эту теорему теоремой об изменении масштаба графа (Usiskin, 1975; Рубинштейн, Шульц, Сенк, Хакворт, МакКоннелл и Виктора, 1992).В отношении, описанном предложением в x и y , следующие два процесса дают один и тот же график (1) с заменой x на x / на и y by y / b ; (2) применение изменения масштаба T ( x , y ) = ( ax , на ) к графику исходного отношения.
Там, где мы складывали раньше, мы умножаем здесь. То, что мы вычитали раньше, мы делим.Опять же, есть множество полезных
следствия, наиболее частые из которых приведены в таблице 4. Среди следствий можно отметить, что все параболы
похоже, что все прямоугольные гиперболы похожи, и что графики всех экспоненциальных и логарифмических функций
похожи вне зависимости от базы. При создании учебной программы для студентов я счел важным включить эти
чудесные объединяющие теоремы — красивая элегантная математика.
Среди следствий можно отметить, что все параболы
похоже, что все прямоугольные гиперболы похожи, и что графики всех экспоненциальных и логарифмических функций
похожи вне зависимости от базы. При создании учебной программы для студентов я счел важным включить эти
чудесные объединяющие теоремы — красивая элегантная математика.
Приближение к алгебре через приложения
vii Пока я разыгрывал учебные проявления прекрасной математики матриц и связанных групп
с преобразованиями мой коллега из Чикагского университета Макс Белл писал о фундаментальных
важность приложений в изучении математики (Bell, 1972).Максимум
был мощным поборником включения реального мира в класс математики. Он утверждал (как
Торндайк,
Cobb, Orleans, Symonds, Wald & Woodyard. (1923)
десятилетия назад утверждал), что традиционные «проблемы со словами»
(или «сюжетные задачи»), встречающиеся в текстах по алгебре — касающихся монет, возраста или целых чисел — не были
актуальные приложения. Я убедился, что он прав.
Я убедился, что он прав.
В то время около трех четвертей выпускников средних школ в США.S.A. закончили один год алгебры, и только половина из них закончила второй год, однако книги для двух курсов были написаны в том же стиле, как если бы они были для одного и того же населения. Я чувствовал, что им нужны разные стили; первый курс должен был понравиться всем. Итак, в 1973 году я подал заявку и получил грант NSF на разработку начального курса алгебры, в котором алгебра будет разрабатываться из приложений, а также будут учиться вероятности и статистика. Я нашел типичную школу и наладил отношения, как и в других местах, а именно: вести уроки алгебры каждый день в течение всего года, а кто-то другой преподает тот же урок позже в тот же день классу таких же учеников.
Как начать такой курс? Макс писал об использовании чисел и четырех основных арифметических операциях, поэтому я начал с этого и расширил обсуждение до использования переменных. Это, естественно, привело бы к реальным ситуациям, приводящим к выражениям и линейным уравнениям типа a + x = b , ax = b , ax + b = c x + d , а также в различных проявлениях свойства распределения, построении графиков линий и, расширяя умножение до целых степеней, обсуждение может привести к сложному проценту и экспоненциальным функциям. Квадратичные выражения и уравнения могут быть обработаны стандартными приложениями для подсчета, площади и ускорения.
Квадратичные выражения и уравнения могут быть обработаны стандартными приложениями для подсчета, площади и ускорения.
Но я понятия не имел, как использовать приложения, чтобы получить полиномиальные выражения. А потом, в этом классе 9 -го класса , когда мы обсуждали сложные проценты, студент поднял руку с вопросом. Он сказал: «Я перебирал домашнее задание с моим отцом, и он спросил меня, имеет ли эта математика какое-либо отношение к сумме, которую мы платим за ипотека.Я подумал: «Его отец решил мою проблему». Отсюда урок по введению многочленов, которые я никогда не видел никого копировать. Урок начинается со следующей задачи (Usiskin, 1979), показанной здесь в Рисунок 4.
После того, как решение дается на уроке, ответ анализируется (как показано на рисунке 4), и различные компоненты полиномиального выражения изменяются, чтобы показать вклад коэффициентов и показателей. На этом этапе обучения общая формула для расчета стоимости ипотеки не является разумной, поскольку для этого требуется некоторое знание суммы конечного геометрического ряда. Но зародыш идеи здесь.
На этом этапе обучения общая формула для расчета стоимости ипотеки не является разумной, поскольку для этого требуется некоторое знание суммы конечного геометрического ряда. Но зародыш идеи здесь.
Я не знаю, как бы я подошел к полиномам в этом курсе, если бы этот студент не передал мне вопрос своего отца. Я знаю, что это был один из многих случаев, когда на содержание моих писем значительно повлияло то, что происходило в классе, когда я преподавал.Обучение повышает вероятность того, что произойдет что-то непредвиденное.
Интуиция и статистика
viiiСорок лет назад статистика в школьных учебниках по математике в США относилась только к вычислению среднего, медианы и модуляции, обычно выполнявшемуся в 7 и 8 классах перед старшей школой. Но в поисках реальных приложений математики с использованием алгебры я все время натыкался на статистику.
Serendipity поместила Билла Крускала в мой факультетский квартал. Билл был профессором статистики в Чикаго, в прошлом возглавлял этот факультет и был одним из первых членов объединенного комитета NCTM и Американской статистической ассоциации по статистике в школах. Я спросил Билла, будет ли он смотреть статистику в материалах по алгебре, которые я создавал, и он согласился.
Билл был профессором статистики в Чикаго, в прошлом возглавлял этот факультет и был одним из первых членов объединенного комитета NCTM и Американской статистической ассоциации по статистике в школах. Я спросил Билла, будет ли он смотреть статистику в материалах по алгебре, которые я создавал, и он согласился.
Билл был крутым читателем. Он нацарапал всю мою рукопись. Он утверждал, что статистика не является подмножеством математики. Это прикладная математика, такая как исследование операций или физика, потому что проблемы в статистике возникают не в математике, а для того, чтобы проводить статистику, человеку нужно знать не только математические, но и соответствующие математические знания.
Билл гордился тем, что работал статистиком в Чикаго. В Чикаго отдел статистики отделился от факультета математики вскоре после Второй мировой войны, и факультет статистики твердо верил, что статистика — это самостоятельная дисциплина. Первые строки книги The Nature of Statistics (Wallis & Roberts, 1954) подтверждают эту точку зрения.
«Статистика — это совокупность методов для принятия мудрых решений в условиях неопределенности… Эта современная концепция тема далека от той, которой обычно придерживаются обыватели.Действительно, даже пионеры статистических исследований принял его только в течение последнего десятилетия или около того ». (Уоллис и Робертс, 1954)
Для разработчиков учебных программ это различие заслуживает внимания. В математических текстах часто используются термины теоретическая вероятность и экспериментальная вероятность, чтобы различать, например, (теоретическую) вероятность подбрасывания честной монеты (½) и то, что вы получаете, когда подбрасываете монету (что-то около ½).Билл Крускал утверждал, что все вероятности являются теоретическими и что то, что математики называют экспериментальной вероятностью , более точно описывается как относительной частоты .
В книгах часто возникают проблемы со следующей формулировкой: Если вы подбросите честный кубик, какова вероятность выпадения 3 орлов подряд? Статистики сказали бы, что нельзя бросить честный кубик. Абсолютно невозможно определить, является ли кубик честным или нет. Вы можете только представить, что бросает честный кубик.Вы можете предположить, что игральная кость справедлива , а затем рассуждать на основании этого. Больше чем семантика. С этой точки зрения вероятностные проблемы представляют собой прекрасные примеры вывода из предполагаемых утверждений.
Статистика эволюционировала за последние четыре десятилетия. Более актуальное определение звучит так: «Статистика — это наука о данных». (Йейтс, Мур и Старнс, 2003 г.).
Применение арифметики
ix Десятилетие 1970-х было временем спада в математическом образовании в Соединенных Штатах, что очень похоже на наше нынешнее десятилетие.За исключением моего проекта по алгебре, NSF больше не финансировал разработку учебных программ по математике. Реакция на «новую математику» шестидесятых годов во многом была вызвана бихевиоризмом, в результате чего многие школы сосредоточились на поведенческих или производственных задачах, которые в основном были манипулятивными навыками в арифметике и алгебре, не слишком отличающимися от сегодняшнего Common Core (Центр ассоциации национальных губернаторов). for Best Practices, Совет директоров государственных школ, 2010 г.). Запрограммированные учебные материалы разбивали учебный план на небольшие этапы, не слишком отличавшиеся от сегодняшнего адаптивного формирующего и суммативного тестирования.И все это в одно десятилетие с появлением портативных калькуляторов. Чему можно было научить, если калькуляторы могли делать все арифметические операции?
Реакция на «новую математику» шестидесятых годов во многом была вызвана бихевиоризмом, в результате чего многие школы сосредоточились на поведенческих или производственных задачах, которые в основном были манипулятивными навыками в арифметике и алгебре, не слишком отличающимися от сегодняшнего Common Core (Центр ассоциации национальных губернаторов). for Best Practices, Совет директоров государственных школ, 2010 г.). Запрограммированные учебные материалы разбивали учебный план на небольшие этапы, не слишком отличавшиеся от сегодняшнего адаптивного формирующего и суммативного тестирования.И все это в одно десятилетие с появлением портативных калькуляторов. Чему можно было научить, если калькуляторы могли делать все арифметические операции?
В 1976 году нас с Максом Беллом попросила написать эссе по этому вопросу Мэрилин Сэйдам, которая вместе с Диком Шамуэем из Университета штата Огайо писала для NSF отчет об электронных калькуляторах (Suydam, 1976). Наше эссе объемом 75 страниц было приложением к этому отчету. И мы только поцарапали поверхность. Итак, мы обратились в NSF за грантом для написания материалов о применении арифметики, поскольку мы чувствовали, что с калькуляторами основное внимание в учебной программе должно уделяться использованию арифметики, а не арифметическим алгоритмам.В результате появилась рукопись объемом более 500 страниц (Usiskin & Bell, 1983), которую мы разбили на три части: числа, операции и маневры (переписывание, оценка, преобразование, отображение).
И мы только поцарапали поверхность. Итак, мы обратились в NSF за грантом для написания материалов о применении арифметики, поскольку мы чувствовали, что с калькуляторами основное внимание в учебной программе должно уделяться использованию арифметики, а не арифметическим алгоритмам.В результате появилась рукопись объемом более 500 страниц (Usiskin & Bell, 1983), которую мы разбили на три части: числа, операции и маневры (переписывание, оценка, преобразование, отображение).
Когда мы писали эту рукопись, стало очевидно, что назвал свойств операций арифметика в книгах — это чистая математика: умножение ассоциативно и коммутативно, имеет тождество 1, является распределительный над сложением и т. д.Но фундаментальный использует операций, которым не дается такой вид статус. Мы назвали эти значениями использования , и основные из них показаны в таблице 5. (Из Usiskin & Bell, 1983)
Наше мнение заключалось в том, что, поскольку именно эти значения использования сделали операции важными за пределами математики, они явились истоком абстракций, которые создали математику, и что значения использования должны быть свойствами, которым учат студентов с такой же важностью, как и чисто математические свойства. которые есть в учебной программе.
которые есть в учебной программе.
Другие (например, см. Карпентер, Мозер и Ромберг, 1982; или Стиглер, Фусон, Хэм и Ким, 1986) детализировали больше видов словесных задач, связанных с арифметическими операциями, чем мы, но наша точка зрения была с точки зрения основных значений из которого могут быть получены другие значения. В результате получается очень хорошее сочетание чистой и прикладной математики. Например, очевидно, что объединение и вынос отменяют друг друга, но также изменяются размер и соотношение. То есть, если две одинаковые фигурки имеют высоту 15 и 25 см, то деление на пропорции говорит нам, что большая фигурка составляет 5/3 высоты меньшей.Число 5/3 — коэффициент изменения размера; если мы умножим 15 на 5/3, получим 25. Точно так же и коэффициент ставки, и действие при умножении возникают из деления ставки. Если мы не раскрываем эти способы использования, мы обучаем точно так же, как этот ученик-учитель с кардиоидой; пользователи смотрят нам в глаза, но мы их игнорируем.
Теория Ван Хиле
xПримерно в это время Исаак Виршуп, профессор математики в университете, рекламировал теорию сцены, разработанную Пьером ван Хиле и Диной ван Хиле-Гельдоф, учениками Ганса Фройденталя в Нидерландах.Виршуп сообщил, что эту теорию использовал советский математик Пышкало при построении учебной программы для молодых студентов. Исследователи в США были увлечены теорией, которая предполагала, что ученик должен пройти следующие этапы в понимании геометрии и в таком порядке: распознавание, анализ, порядок, дедукция и строгость.
Теория изящная. Студент не может быть на уровне n по ван Хиле, не пройдя уровень n -1.То, что является внутренним на уровне n -1, становится внешним на уровне n . У каждого уровня есть свои языковые символы и своя сеть отношений. Два человека, рассуждающие на разных уровнях, не могут понять друг друга. Эта теория была использована для объяснения некоторых трудностей, с которыми учащиеся сталкивались на обычном в то время курсе геометрии в средней школе США
.
Я скептически относился к этой теории, особенно к первому свойству. Я чувствовал, что не прошел через эти стадии, как и многие другие представители моего поколения.В те дни студенты углублялись в изучение геометрии на уровне 3 или уровне 4. Мы с Шэрон Сенк, в то время докторантом, решили подать заявку на финансирование от Национального института образования на тест теории. Мы разработали грубый тест вопросов для каждого уровня, основанный на трудах Пьера и Дины ван Хиле, и провели его лично, когда он посетил Чикагский университет. Мы провели тест около 2400 студентов-геометров в 5 штатах США и обнаружили, как и предсказывал Виршуп, большинство студентов находятся на уровнях 1 и 2, и от них нельзя ожидать успеха в ориентированном на доказательства курсе геометрии.Мы также обнаружили, что есть студенты, которым нельзя присвоить уровень. Уровни разумно предсказывали успеваемость по курсу геометрии, как и простой тест содержания, проведенный в начале года.
Разработанный нами тест (Usiskin, 1982) был переведен как минимум на 10 языков и использован в десятках магистерских и докторских диссертаций. Диссертации. Практически каждый, кто использует тест, считает, что теория верна, и не считает, что наш тест был разработан для проверки теории.
Диссертации. Практически каждый, кто использует тест, считает, что теория верна, и не считает, что наш тест был разработан для проверки теории.
UCSMP и Serendipity
xiМоя связь с UCSMP возникла в результате того, что я снова оказался в нужном месте в нужное время. Осенью 1982 года, когда мы завершали исследование van Hiele и рукопись Applying Arithmetic , Изаак Виршуп работал над возможностью получения университетом 6-летнего гранта в размере 6 миллионов долларов от фонда Amoco Foundation. благотворительное подразделение Amoco Corporation (ныне BP), если бы мы были заинтересованы, и университет разрешил бы проект с такой беспрецедентной продолжительностью и финансированием.Не было очевидным, согласится ли университет на такой проект, потому что для чего-то такого масштаба требуется много офисных и рабочих помещений, а пространство является очень ценным товаром в университете.
Изаак и Пол Салли из Департамента математики, я, Ларри Хеджес и Сьюзан Стодольски из Департамента образования встречались еженедельно до весны 1983 года. Мы предложили проект K-12 по математике, который будет основываться на проделанной работе. мир, чтобы создать и протестировать полную учебную программу по математике для подавляющего большинства U.С. студенты. Нас поддержали руководители наших отделов Феликс Браудер и Чарльз Бидвелл. Два заведующих кафедрой, Изаак, Пол и я — пять профессоров — принесли наше дело ректору университета. Проректор сказал, что университет может предоставить место для проекта стоимостью 5 миллионов долларов. Мы знали, что нам нужно около 12 миллионов долларов, чтобы сделать то, что мы задумали (что эквивалентно примерно 30 миллионам долларов сегодня), но мы не сказали об этом ректору. Проректор одобрил проект при условии, что фонд Amoco не сократит другие выплаты университету.Фонд сдержал слово.
Мы предложили проект K-12 по математике, который будет основываться на проделанной работе. мир, чтобы создать и протестировать полную учебную программу по математике для подавляющего большинства U.С. студенты. Нас поддержали руководители наших отделов Феликс Браудер и Чарльз Бидвелл. Два заведующих кафедрой, Изаак, Пол и я — пять профессоров — принесли наше дело ректору университета. Проректор сказал, что университет может предоставить место для проекта стоимостью 5 миллионов долларов. Мы знали, что нам нужно около 12 миллионов долларов, чтобы сделать то, что мы задумали (что эквивалентно примерно 30 миллионам долларов сегодня), но мы не сказали об этом ректору. Проректор одобрил проект при условии, что фонд Amoco не сократит другие выплаты университету.Фонд сдержал слово.
С самого начала мы разделили проект на четыре компонента: компонент ресурсов, возглавляемый Изааком, который будет переводить материалы из других стран для поддержки работы элементарного компонента в классах K-6 и второстепенного компонента в классах 7-12, и компонент оценки, возглавляемый Ларри и Сьюзен, для количественного и качественного исследования работы, проделанной на уровне классов.
Было сочтено, что для изменений первая работа в K-6 должна быть связана с образованием учителей.Этим компонентом руководили Пол Салли и местный учитель Шейла Сконьер. Было понятно, что я буду направлять компонент 7-12. В отличие от тех, кто занимается с классами K-6, я чувствовал, что учителям 7-12 классов необходимо просмотреть материалы, прежде чем они будут заменены. Существование UCSMP предоставило уникальную возможность объединить различные работы, которые занимали мое время в течение предыдущих 16 лет. Это означало, что основные темы и многие подробные разработки более ранней работы — приложения, преобразования, использование калькуляционной технологии — могут быть перенесены.
В начале UCSMP Макс Белл был в отпуске из университета. Пройдет два года, прежде чем он вернется, а затем он приступит к проектированию и разработке учебной программы UCSMP для классов preK-6, учебной программы, все еще весьма успешной с коммерческой точки зрения под названием Everyday Mathematics (UCSMP, 2016). Сегодня эти усилия возглавляет Энди Айзекс. В Приложении A приводится полная информация об опубликованных, предпубликационных и тестовых версиях вторичных материалов UCSMP. При этом в приложении также указывается объем работы над коммерческими выпусками.
Сегодня эти усилия возглавляет Энди Айзекс. В Приложении A приводится полная информация об опубликованных, предпубликационных и тестовых версиях вторичных материалов UCSMP. При этом в приложении также указывается объем работы над коммерческими выпусками.
Два конкурирующих прекрасных аспекта математики
xiiВ европейской традиции мы склонны считать книгу Евклида Elements (Heath, 1956) первым учебником математики. Это определенно оказало наибольшее влияние на установление доказательства как определяющего фактора истинности математического утверждения. В этом отношении развитие всей геометрии и теории чисел в Elements является прекрасным. На протяжении двух тысячелетий он оказал большое влияние на преподавание геометрии в Европе, а затем и в Америке.
Алгебра развивается отдельно от геометрии. Хотя Декарт и Ферма разработали аналитическую геометрию в 1600-х годах, менее чем через полвека после новаторской работы Вите с переменными, Эйлера 1770 Vollständige Anleitung zur Algebra ( Полное руководство по алгебре) , прототипа текстов по алгебре, которые последовали, не содержит геометрии (Эйлер, 1972).
В конце 19 -го -го века, более 100 лет назад, два U.В национальных отчетах (Национальная ассоциация образования, 1894; Янг, 1899) установлен годичный курс алгебры, за которым следует годовой курс демонстративной геометрии, как 9 и 10 курсов для учащихся начального уровня по математике. «Демонстрационный» означал, что курс геометрии был очень ориентирован на доказательство, а теоремы демонстрировались доказательствами. Напротив, хотя правила или свойства будут приводиться в качестве обоснования шагов в решении уравнений или упрощении выражений, в курсе алгебры не упоминается доказательство.Постепенно за курсом геометрии последовал второй годичный курс алгебры, возможно, с некоторой тригонометрией, опять же с небольшими доказательствами или без них. Таким образом, последовательность алгебра-геометрия-алгебра закрепилась в большинстве школьных округов; более того, курсы алгебры содержали мало, если вообще не содержали геометрии, а курс геометрии содержал мало, если вообще вообще содержал алгебру. Сегодня эта последовательность начинается в 8 -м классе примерно для одной трети учащихся в США
Сегодня эта последовательность начинается в 8 -м классе примерно для одной трети учащихся в США
Работа с приложениями алгебры показала, что одна из причин, по которой студенты не могли применять алгебру, заключалась в том, что они не могли применять арифметику за пределами малых целых чисел.Работа ван Хиле показала, что большинство учеников поступили на курс геометрии в старшей школе со слишком слабыми знаниями геометрии, чтобы хорошо успеть на курсе. Итак, еще до начала UCSMP, я решил пойти в школу осенью 1983 года, чтобы написать и преподавать книгу, которая объединит приложения арифметики с подготовкой студентов к алгебре и геометрии. Эта книга стала Математика переходов .
В то время как Переходная математика писалась, мы пригласили шесть лучших специалистов по разработке учебных программ в стране в качестве консультативной группы, чтобы помочь определить, какими будут следующие пять курсов.Основная проблема касалась последовательности алгебра-геометрия-алгебра. С начала 20 — годов были сторонники интеграции алгебры и геометрии, то есть преподавания некоторой геометрии и некоторой алгебры каждый год, и книги, реализующие интегрированный учебный план, были нам известны, хотя их редко можно было найти в школах. Итак, один из первых вопросов, стоящих перед нами в UCSMP, заключался в том, должны ли мы интегрировать алгебру и геометрию в годы после Transition Mathematics .
С начала 20 — годов были сторонники интеграции алгебры и геометрии, то есть преподавания некоторой геометрии и некоторой алгебры каждый год, и книги, реализующие интегрированный учебный план, были нам известны, хотя их редко можно было найти в школах. Итак, один из первых вопросов, стоящих перед нами в UCSMP, заключался в том, должны ли мы интегрировать алгебру и геометрию в годы после Transition Mathematics .
Многие из консультативных групп, как известно, предпочитали трехлетнюю последовательность, которая охватывала бы традиционную алгебру и геометрическое содержание, не имея всей геометрии за один год. Результатом группового мышления стал первый год, который был почти полностью посвящен алгебре с небольшой геометрией, второй год, который начался с большого количества алгебры и закончился большим количеством геометрии, и третий год, который продолжил изучение геометрии и закончился много алгебры.
В конечном итоге это было мое решение сохранить последовательность алгебра-геометрия-алгебра, потому что альтернатива, созданная этой группой, была близка к этой последовательности, и я не хотел бороться с требованиями штата, округа и школы, которые обычно требовали двух курсов алгебры и одного. курс геометрии.Я чувствовал, что мы могли бы включать приложения геометрии в наши курсы алгебры и включать алгебру в наши курсы геометрии. Результатом стал первый курс, который можно было бы описать как «поезд алгебры», на котором пассажиры изучают арифметику, геометрию и статистику; второй курс, который можно было бы описать как «поезд геометрии», на котором пассажиры-алгебры; и второй курс «поезда алгебры», в котором участвуют геометрия и тригонометрия. Все это использует прекрасный аспект математики; что математика едина в том смысле, что результаты одного раздела математики могут быть использованы в другом.
курс геометрии.Я чувствовал, что мы могли бы включать приложения геометрии в наши курсы алгебры и включать алгебру в наши курсы геометрии. Результатом стал первый курс, который можно было бы описать как «поезд алгебры», на котором пассажиры изучают арифметику, геометрию и статистику; второй курс, который можно было бы описать как «поезд геометрии», на котором пассажиры-алгебры; и второй курс «поезда алгебры», в котором участвуют геометрия и тригонометрия. Все это использует прекрасный аспект математики; что математика едина в том смысле, что результаты одного раздела математики могут быть использованы в другом.
Традиционные ориентированные на доказательство курсы геометрии в США начали с того, что отметили, что точка, линия и плоскость — это три неопределенных термина, потому что мы не можем определить все термины, не имея круговых определений. Вместо определений утверждаются определенные постулаты, что неявно определяет, какой точкой, линией и плоскостью может быть; такие постулаты, как «есть ровно одна линия, проходящая через две точки» и «для данной точки и прямой есть ровно одна линия, содержащая эту точку и параллельная данной линии. «Большинству учителей и учеников наличие неопределенных терминов кажется слабостью. Но когда вы интегрируете алгебру в курс геометрии, она становится сильной стороной.
«Большинству учителей и учеников наличие неопределенных терминов кажется слабостью. Но когда вы интегрируете алгебру в курс геометрии, она становится сильной стороной.
UCSMP Геометрия (Coxford, Hirschhorn & Usiskin, 1991; Usiskin et al., 1997; Benson et al., 2009) начинается с геометрического представления точек и линий, в котором из постулатов типа «Через два в разных точках ровно одна линия ». учащихся заставляют думать, что точка обозначает место на плоской поверхности, а линии — это продолжение того, что мы рисуем с помощью линейок.Но затем, в следующем уроке, мы отметим, что те же постулаты охватывают геометрию, в которой точка — это упорядоченная пара действительных чисел, а линия — это набор упорядоченных пар, которые удовлетворяют уравнению формы. Таким образом, с самого начала курса геометрии мы оправдываем использование синтетических нечисловых методов, а также аналитической или координатной геометрии. Этот подход использует красоту дедукции, а также красоту единства математики, и он позволяет одновременно использовать алгебру и геометрию во всех последующих курсах.
Красота связей
xiiiОсновываясь на обсуждениях консультативной группы, мы решили, что последние два курса должны иметь по две темы: функции и статистика для курса 11 th и предварительные вычисления и дискретная математика для курса 12 th . Тригонометрия была добавлена к названию первого из этих курсов, чтобы сделать текст пригодным для использования в районах, где требовался курс тригонометрии.
Со статистикой в качестве «пассажира» в курсе алгебры и функциями и статистикой в качестве основных тем в курсе
11 -й класс , мы нашли много способов, которыми идеи одной из этих тем были связаны с идеями в
другой.Например, сигма-нотация, используемая в сериях, была введена необходимостью суммирования данных для вычисления
простая статистика уже на первом курсе алгебры. На курсе UCSMP 11 th мы смогли:
обсудить переводы изображений графиков функций и отношений вместе с добавлением или вычитанием константы из
все элементы в наборе данных, чтобы установить среднее значение 0. Мы могли бы обсудить масштабные преобразования графиков вместе с
масштабирование данных, когда мы хотели нормализовать эти данные до стандартного отклонения, равного 1.В таблице 6 показаны эти и другие
способы, которыми мы используем темы из статистики для мотивации или применения традиционных математических тем.
Мы могли бы обсудить масштабные преобразования графиков вместе с
масштабирование данных, когда мы хотели нормализовать эти данные до стандартного отклонения, равного 1.В таблице 6 показаны эти и другие
способы, которыми мы используем темы из статистики для мотивации или применения традиционных математических тем.
Последний курс UCSMP должен был объединить темы предварительного вычисления, необходимые для успеха в исчислении, с дискретной математикой, которая будет полезна в информатике. Таким образом, мы добавили год к стандартной академической школьной программе, но начали концентрированное изучение алгебры на год раньше, чем обычно. Имея предварительное вычисление и дискретную математику в качестве двух основных тем нашего курса 12 –, мы смогли объединить идеи, которые обычно разделяются.Например, мы смогли применить идеи формальной логики, чтобы объяснить, почему решение некоторых уравнений приводит к так называемым посторонним решениям. Мы могли бы обсудить факторизацию целых чисел вместе с факторизацией многочленов, простые целые числа вместе с простыми многочленами, наименьшее общее кратное целых чисел вместе с наименьшим общим кратным многочленов и так далее. И мы могли бы объединить идеи из этого курса с идеями из всех наших предыдущих курсов.
Мы могли бы обсудить факторизацию целых чисел вместе с факторизацией многочленов, простые целые числа вместе с простыми многочленами, наименьшее общее кратное целых чисел вместе с наименьшим общим кратным многочленов и так далее. И мы могли бы объединить идеи из этого курса с идеями из всех наших предыдущих курсов.
В 1623 году, когда Галилей написал в своей книге Il Saggiatore («Пробирный»), что Вселенная написана на языке математики, он был частью новаторского движения, принявшего то, что мы сегодня называем научным методом.Одна из целей школьной математики — познакомить учащихся с этим языком, но недостаточно ценится то, что язык математики может принимать разные формы, и необходимо научить учащихся, как переходить из одной формы в другую. Возможность разрабатывать многолетние учебные планы дала возможность обсуждать одну и ту же идею совершенно разными способами, обеспечивая прекрасные математические связи.
Рассмотрим понятие последовательных поворотов вокруг точки. Эволюция начинается в младших классах с физического
поворачивая, что мы можем измерять в градусах или оборотах, и мы добавляем эти меры, чтобы получить результат. Вращения
Около точки на плоскости находятся математическая модель физического действия. В геометрии, когда мы обсуждаем, что
иногда это называется «сложение углов» или «свойство смежного угла», мы обычно проводим руками, чтобы соединиться с
физическое действие, хотя евклидова геометрия статична — фигуры не двигаются.В координатной плоскости мы можем
представляют поворот относительно начала координат матрицей 2 x 2, а последовательные вращения — умножением матриц. Когда мы
запишите вращения величин x и y в матричной форме, как на рисунке 5, и умножьте
матрицы, получаем формулы для cos (x + y) и sin (x + y) в одну строку. Фактически, мы получаем каждый
формула дважды. Прекрасная математика.
Эволюция начинается в младших классах с физического
поворачивая, что мы можем измерять в градусах или оборотах, и мы добавляем эти меры, чтобы получить результат. Вращения
Около точки на плоскости находятся математическая модель физического действия. В геометрии, когда мы обсуждаем, что
иногда это называется «сложение углов» или «свойство смежного угла», мы обычно проводим руками, чтобы соединиться с
физическое действие, хотя евклидова геометрия статична — фигуры не двигаются.В координатной плоскости мы можем
представляют поворот относительно начала координат матрицей 2 x 2, а последовательные вращения — умножением матриц. Когда мы
запишите вращения величин x и y в матричной форме, как на рисунке 5, и умножьте
матрицы, получаем формулы для cos (x + y) и sin (x + y) в одну строку. Фактически, мы получаем каждый
формула дважды. Прекрасная математика.
Потому что хорошей и доступной математики для учащихся гораздо больше, чем мы можем уместить в школьной математике. учебной программы, если бы мы использовали только матрицы в этой настройке, было бы неэкономично тратить время на разработку
механизмы, необходимые для демонстрации элегантного вывода формулы для R x , которая используется на рисунке 5.Однако у матриц гораздо больше приложений, чем у этого — для понимания других преобразований, для решения
системы уравнений, к сетям и цепям Маркова.
учебной программы, если бы мы использовали только матрицы в этой настройке, было бы неэкономично тратить время на разработку
механизмы, необходимые для демонстрации элегантного вывода формулы для R x , которая используется на рисунке 5.Однако у матриц гораздо больше приложений, чем у этого — для понимания других преобразований, для решения
системы уравнений, к сетям и цепям Маркова.
Элегантная теория математического понимания
xivВ ходе пленарного выступления ICME в 2008 году Джереми Килпатрик отметил, что «математическое образование не похоже на другие области науки» (Artigue & Kilpatrick, 2008). Он процитировал заявление в Эрлангенском обращении Феликса Кляйна в 1872 году о том, что
«Каждое математическое поколение опирается на достижения своих предшественников, тогда как в других областях [включая математическое образование] часто бывает, что старые здания сносят раньше, чем можно будет построить новое.продолжить.”
Джереми отметил, что «мы не всегда начинаем полностью с нуля, но мы много сносим, а также строим».
Однако я считаю, что между математикой и математическим образованием есть промежуток, в котором есть вечные истины. В этом пространстве мы стремимся к тому, чтобы учащиеся «понимали» математику, которую они изучают. Для материалов UCSMP это понимание рассматривается открыто и включает четыре аспекта (Usiskin, 2015):
- измерение навыков-алгоритмов, которое варьируется от механического применения алгоритма до изучения алгоритмов и изобретения новых алгоритмов;
- измерение доказательства собственности, которое варьируется от механического обоснования свойств до написания доказательств и открытия новых свойств;
- измерение использования-приложения, которое варьируется от простейших применений, известных каждому, до использования известных математических моделей, а затем и изобретения новых; и
- измерение представления-метафоры, которое варьируется от повторения известных изображений математических идей до изобретения новых представлений.

Такой многогранный взгляд на понимание необходим, потому что для разных людей каждое из этих измерений преобладает над другими тремя по важности. Пресловутый «средний человек с улицы» склонен думать, что вы разбираетесь в математике, если знаете, как получить ответы на математические вопросы. Математики склонны рассматривать человека как понимающего математику, если он может ссылаться на свойства, объясняющие рассматриваемую математику. Инженеры склонны полагать, что вы не поймете математику по-настоящему, пока не сможете применить ее в реальных ситуациях.И многие психологи думают, что реального понимания означает способность каким-то образом представить математику, возможно, с помощью метафоры. Все эти четыре измерения присутствуют в преподавании и изучении математики и удивительно независимы друг от друга. Вот почему я называю их размерами. Практически для каждой концепции учебного плана UCSMP, на наших уроках и в наших тестах мы стремимся познакомить учащихся со всеми четырьмя измерениями. Кроме того, есть по крайней мере еще одно измерение в понимании математики — историко-социальное измерение — как математика развивалась и находилась под влиянием социальных сил; этот способ обычно игнорируется в классах.
Кроме того, есть по крайней мере еще одно измерение в понимании математики — историко-социальное измерение — как математика развивалась и находилась под влиянием социальных сил; этот способ обычно игнорируется в классах.
Одним из следствий многомерного взгляда на понимание является то, что мы постоянно вовлекались в геометрические представления числовых и алгебраических идей и в алгебраические представления геометрических идей. Таким образом, такой подход к пониманию помог нам воспользоваться преимуществом общего единства математики. И хотя это кажется сложным взглядом на понимание, в некотором смысле это элегантная структура для очень неизящной реальности.
Через некоторое время мы начали понимать, что наши авторы, как правило, предпочитали одно или два измерения понимания математики другим.При написании прозы и задач некоторые, как правило, фокусировались на навыках, некоторые — на математических свойствах, некоторые — на приложениях, некоторые — на представлениях, а некоторые — на историко-социальном измерении. Мы учли эти сильные стороны при формировании наших писательских команд, и я думаю, что это обогатило наши материалы.
Мы учли эти сильные стороны при формировании наших писательских команд, и я думаю, что это обогатило наши материалы.
Команды писателей и процесс письма
xv Составление хорошей учебной программы требует не только знания математики, но и умения писать понятный и интересный материал.С самого начала талантливые люди участвовали в написании текстов UCSMP (см. Ссылки на UCSMP в конце этого документа). После того, как я написал первый вариант Переходной математики , четыре очень умных и опытных местных учителя отредактировали материалы. Для каждого из других курсов мы выбрали опытных авторов в качестве руководителей групп. Джон МакКоннелл был главой отдела математики в местной средней школе и получил докторскую степень по математическому образованию в Северо-Западном университете, изучая отношения между учителями и студентами по алгебре 9 -го класса (МакКоннелл, 1978).Он стал руководителем нашей группы алгебры. Шэрон Сенк, учительница средней школы в Ньютоне, штат Массачусетс, преподавала ученикам геометрию и продвинутую алгебру. Кроме того, в исследовании ван Хиле она изучала успеваемость студентов по доказательству (Senk, 1985). Она согласилась возглавить группу продвинутой алгебры. Чтобы заполнить группы по алгебре, мы разместили рекламу на национальном уровне, попросили кандидатов прислать образцы письменных работ, а затем пригласили финалистов, чтобы оценить их способность работать с командой, чтобы планировать и писать на месте.Таким образом мы получили некоторых талантливых авторов. Что касается геометрии, мне удалось убедить Арта Коксфорда снова заняться этим.
Кроме того, в исследовании ван Хиле она изучала успеваемость студентов по доказательству (Senk, 1985). Она согласилась возглавить группу продвинутой алгебры. Чтобы заполнить группы по алгебре, мы разместили рекламу на национальном уровне, попросили кандидатов прислать образцы письменных работ, а затем пригласили финалистов, чтобы оценить их способность работать с командой, чтобы планировать и писать на месте.Таким образом мы получили некоторых талантливых авторов. Что касается геометрии, мне удалось убедить Арта Коксфорда снова заняться этим.
На последних двух курсах два человека разделили лидерство. Для курса мы первоначально называли функций и статистики , а теперь — FST , у нас были Рета Рубенштейн, тогда учитель в государственных школах Детройта, которая была замечательным автором в нашей группе продвинутой алгебры, и Джим Шульц, профессор из Университета штата Огайо (позже переехавшего в Университет Огайо), который уже написал замечательный учебник по математике для учителей начальной школы (Schultz, 1977). Для Precalculus and Discrete Mathematics мы убедили двух математиков, Тони Перессини и Сюзанну Эпп, стать соруководителями. Тони взял на себя инициативу в части предварительного вычисления, в то время как Сюзанна, написав учебник по дискретной математике для колледжа (Epp, 1990), взяла на себя инициативу по урокам дискретной математики.
Для Precalculus and Discrete Mathematics мы убедили двух математиков, Тони Перессини и Сюзанну Эпп, стать соруководителями. Тони взял на себя инициативу в части предварительного вычисления, в то время как Сюзанна, написав учебник по дискретной математике для колледжа (Epp, 1990), взяла на себя инициативу по урокам дискретной математики.
За исключением FST, который в основном писался вне университета, команды писателей работали летом от 6 до 8 недель, 5 дней в неделю в одной комнате, достаточно большой, чтобы разместить их с одним или двумя студентами-редакторами и справочными материалами.Встречи по планированию были постоянными. Я старался присутствовать на каждом собрании по планированию и был последним редактором на каждом уроке. Видимо, я был крутым редактором. Несколько лет назад на «жарке» после ужина в мою честь некоторые авторы подготовили скетч о моем редактировании. В скетче один из авторов прыгает от радости, когда видит, что написанное ею слово пережило мое редактирование — слово «the».
После того, как тексты по алгебре были написаны, мы поняли, что редакторы наших докторантов (Дэн Хиршхорн, Дора Аксой, Джим Фландерс, Барри Киссейн, Джефф Бирки и Грег Макрилл) делали много авторской работы, и мы сочли целесообразным идентифицировать их как авторов.Им помогали другие студенты университета, которые вычитывали текст и давали ответы и решения проблем. Студенты в университете также были нашими производителями, которые брали рукописный текст и переводили его в книжную форму, чтобы материалы могли быть протестированы на все большем количестве студентов. За эти годы мы наняли более 200 студентов Чикагского университета в качестве редакторов или помощников по производству.
Нашими полевыми тестовыми версиями были черно-белые издания в мягкой обложке или в спиральном переплете.В первых двух выпусках этой работой руководила Сьюзан Чанг. Режиссером третьего выпуска был Бен Бальскус. Когда наши книги стали коммерчески издаваться, наши издатели сделали полноцветное издание в твердом переплете и прилагаемое к нему издание для учителей. Но было исключение — под руководством Бена мы сами выполнили коммерческое производство двух последних книг третьего издания. Наличие редакторов в комнатах, прилегающих к окончательной постановке, было чрезвычайно эффективным и, на наш взгляд, беспрецедентным.
Но было исключение — под руководством Бена мы сами выполнили коммерческое производство двух последних книг третьего издания. Наличие редакторов в комнатах, прилегающих к окончательной постановке, было чрезвычайно эффективным и, на наш взгляд, беспрецедентным.
Также потребовалось провести большие исследования наших материалов. Сначала Ларри Хеджес и Сьюзан Стодольски руководили нашими итоговыми исследованиями. Через несколько лет нам стало ясно, что наше желание иметь независимых оценщиков в UCSMP оставило нас без некоторых видов данных, которые мы очень хотели. Например, нас очень интересовало влияние калькуляторов на обучение студентов, но оценщики думали, что это второстепенная проблема. В результате мы с Шэрон Сенк поделились большей частью работы над более поздними оценками первого издания.Затем Денисс Томпсон, которая начала с нами, будучи отобранной в конкурсе авторов, а затем стала докторантом, решила использовать тестирование Precalculus и Discrete Mathematics для своей докторской диссертации, а затем стала директором нашего исследования (Thompson , Senk, et al. , Несколько лет).
, Несколько лет).
Первое издание было закончено в 1991 году, и в результате продаж наш издатель попросил нас немедленно начать работу над вторым изданием. Для второго издания мы пригласили многих из авторов первого издания и повторили конкурс, чтобы заполнить авторские команды.Два новых имени появляются в трех книгах каждая: Дэвид Витонски, редактор, и Нильс Абель, учитель средней школы, который с тех пор много лет был главой отдела в Deerfield Academy, частной школе в Массачусетсе. Нильс воплощает принцип, который неоднократно подтверждался на протяжении многих лет, а именно, что в наших школах есть учителя математики, чьи знания и способности в области школьной математики не уступают любым университетским профессорам в нашей области. Второе издание было сделано к 1997 году.
Для третьего издания мы поменяли издателей и работали с 2005 по 2010. Мы также добавили курс, предшествующий Transition Mathematics, чтобы отразить изменения в США в концепции средней школы для 6-8 классов. Это чрезвычайно важно для многих. Автором этого издания была Натали Якуцин, которая пришла к нам в качестве опытного учителя, помогавшего редактировать первое издание Advanced Algebra . Для второго издания она отвечала за редактирование рукописей каждой книги.Затем она вернулась к преподаванию на полную ставку, но вернулась к написанию третьего издания, а совсем недавно она возглавила работу по созданию цифровой платформы для семи книг третьего издания.
Это чрезвычайно важно для многих. Автором этого издания была Натали Якуцин, которая пришла к нам в качестве опытного учителя, помогавшего редактировать первое издание Advanced Algebra . Для второго издания она отвечала за редактирование рукописей каждой книги.Затем она вернулась к преподаванию на полную ставку, но вернулась к написанию третьего издания, а совсем недавно она возглавила работу по созданию цифровой платформы для семи книг третьего издания.
Наконец, важно признать, что проект такого размера требует административной группы. Кэрол Сигел, наш офис-менеджер в течение трех десятилетий, руководила пятью из семи международных конференций, которые UCSMP проводил в Чикагском университете с 1985 года, включая две самые последние под эгидой Центра изучения математики, поддерживаемого NSF.Она также помогла отобрать всех кандидатов на редакционные и производственные должности в UCSMP, и благодаря ей и другому административному персоналу мы постоянно собирали необычайно хорошую команду поддержки для наших усилий по написанию, редактированию и производству.
Более подробную информацию о дизайне и разработке учебных материалов до и в рамках проекта математики школы Чикагского университета можно найти в бюллетенях UCSMP 1-40 на сайте http://ucsmp.uchicago.edu/newsletters, а также в Usiskin ( 2003); Usiskin (2007) и Reys & Reys (2014).
Резюме и благодарность
xvi В этой статье я попытался описать некоторые подробные размышления и работу, которые потребовались для разработки учебной программы UCSMP. Практически во всех случаях мы не были первопроходцами. Люди до нас разрабатывали учебную программу, включающую приложения и моделирование, включая преобразования, включая статистику и дискретную математику, используя новейшие технологии и работая над пониманием в математике. В Чикаго у меня была необычная возможность, предоставленная немногим людям — организовать и возглавить команду по разработке и написанию полной учебной программы по математике для средних школ.Эта работа не была бы известна сегодня, если бы не тот факт, что многие другие люди во всем мире работали над достижением тех же целей — над созданием актуальной, доступной для обучения и обучаемой программы математики для подавляющего большинства студентов.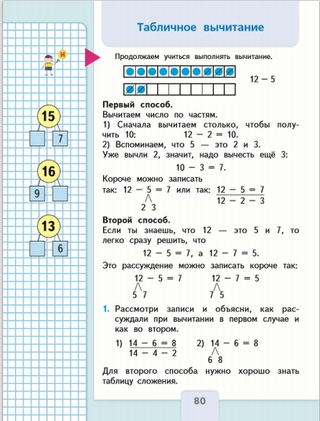
На нашу работу в начальной школе повлияли наши переводы советских учебников (Моро, Бантова, 1992; Моро, Бантова, Бельтюкова, 1992; Пчолько, Бантова, Моро и Пышкало, 1992; Усискин, 1997). На то, что у нас могут возникнуть ожидания в средних школах, повлияли наши переводы японских учебников (Kodaira, 1992), материалы Брайана Туэйтса и Джеффри Хаусона из SMP в США.К., работой Ганса Фройденталя, а затем и Института Фройденталя, Сола Гарфанкеля из COMAP, Могенса Нисса и Вернера Блюма и сотрудников ICTMA, занимающихся математическим моделированием и приложениями, новаторскими работами Джима Фея и Кэти Хайд в компьютерной алгебре. систем, работ Жана-Мари Лаборда и Ника Джекива в области динамической геометрии, а также работ Texas Instruments и Casio по созданию удобных и недорогих технологий для школ.
Даже со всем этим руководством мы не смогли бы выполнить эту работу без поддержки сотен школьных администраторов и учителей в наших формальных исследованиях и тысяч учителей, желающих преподавать материалы, значительно отличающиеся от тех, которые они видели или преподавали ранее.
Это замечательно, что у нас есть всемирное сообщество, посвященное улучшению учебных программ, которые мы даем студентам. Но мы не должны расслабляться. После периода замечательной разработки учебных программ по математике в США в 1990-х годах, который растянулся до 2000-х годов, в настоящее время в США практически нет разработки учебных программ. Общее ядро уничтожило разработку учебных программ по математике здесь. не только с его регрессивным контентом, возвращающим к основам, но и с созданием мегалитической структуры тестирования, которая затруднит реализацию будущих изменений.Нам нужно праздновать наши успехи, но мы должны остерегаться тех, кто хочет диктовать свое мнение об образовании, как будто это единственный путь.
Ссылки
xvii Джейкобс, Х. (1971). Математика — человеческие усилия . Бостон: W.H. Фримен.
Бостон: W.H. Фримен.
Моро, М.И. и Бантова М.А. (1992). Русский язык 2 класс Математика . Перевод Р. Х. Сильвермана. Чикаго: UCSMP.
Усискин, З. (1997). Изучение алгебры в классах K-4. Обучение детей математике 3 (6), стр. 346-356.
Приложение А.Тексты UCSMP для средних школ (6–12 классы)
xviiiПервое издание (коммерческое издание Glenview, IL: Scott Foresman)
Математика переходов . Залман Усискин, Джеймс Фландерс, Кэти Хайнс, Лидия Полонски, Сьюзен Портер и Стивен Виктора. Полевые испытания версий 1983-85 гг .; Полевые испытания в твердом переплете 1986 г . ; Скотт, Foresman изданий 1990, 1992
; Скотт, Foresman изданий 1990, 1992
Алгебра . Джон У. Макконнелл, Сьюзан Браун, Сьюзен Эддинс, Маргарет Хакворт, Лерой Сакс, Эрнест Вудворд, Джеймс Фландерс, Дэниел Хиршхорн, Кэти Хайнс, Лидия Полонски и Залман Усискин.Полевые испытания версий 1985-88 гг .; Скотт, Foresman изданий 1990, 1993
Геометрия . Артур Ф. Коксфорд младший, Дэниел Хиршхорн и Залман Усискин. Полевые испытания версий 1986-89 гг .; Скотт Форесман редакции 1991, 1993
Продвинутая алгебра . Шэрон Л. Сенк, Денисс Р. Томпсон, Стивен С. Виктора, Рета Рубенштейн, Джуди Халворсон, Джеймс Фландерс, Кэти Хайнс, Натали Джакусин, Джеральд Пиллсбери и Залман Усискин. Полевые испытания версий 1985-88 гг .; Скотт, Foresman изданий 1990, 1993
Функции, статистика и тригонометрия .Рета Н. Рубенштейн, Джеймс Э. Шульц, Шэрон Л. Сенк, Маргарет Хакворт, Джон У. МакКоннелл, Стивен С. Виктора, Дора Аксой, Джеймс Фландерс, Барри Киссан и Залман Усискин. Полевые испытания версий 1986-89 гг .; Скотт, Foresman edition 1992
Полевые испытания версий 1986-89 гг .; Скотт, Foresman edition 1992
Предварительные вычисления и дискретная математика . Энтони Л. Перессини, Сюзанна С. Эпп, Кэтлин А. Холлоуэлл, Сьюзан Браун, Уэйд Эллис младший, Джон У. Макконнелл, Джек Сортеберг, Денисс Р. Томпсон, Дора Аксой, Джеффри Д. Бирки, Грег Макрилл и Залман Усискин.Полевые испытания версий 1987-90 гг .; Скотт Форесман издание 1992 г.
Второе издание (коммерческое издание Glenview, IL: Scott Foresman and Scott Foresman — Addison Wesley, and Upper Saddle River, NJ: Prentice-Hall)
2Математика переходов . Залман Усискин, Кэти Хайнс Фельдман, Сюзанна Дэвис, Шэрон Малло, Глэдис Сандерс и Дэвид Витонски. Тестовая версия 1992-93; Скотт Форесман, издание 1995 г .; Скотт Форесман — Эддисон Уэсли издание 1998 г .; Издание Prentice Hall 2002
Алгебра. Джон В. МакКоннелл, Сьюзан Браун, Шэрон Л. Сенк, Тед Видерски, Скотт Андерсон и Залман Усискин. Тестовая версия 1992-93; Скотт Форесман издание 1996 г., Скотт Форесман — издание Эддисон Уэсли 1998 г .; Калифорнийское издание, 2000 г .; Издание Prentice Hall 2002
Тестовая версия 1992-93; Скотт Форесман издание 1996 г., Скотт Форесман — издание Эддисон Уэсли 1998 г .; Калифорнийское издание, 2000 г .; Издание Prentice Hall 2002
Геометрия . Залман Усискин, Дэниел Б. Хиршхорн, Вирджиния Хайстоун, Хестер Льюеллен, Николас Оппонг, Ричард ДиБьянка и Мерили Мэйр. Тестовая версия 1993-94; Скотт Форесман издание 1997 г .; Издание Prentice Hall 2002
Продвинутая алгебра .Шэрон Л. Сенк, Денисс Томпсон, Стивен С. Виктора, Залман Усискин, Нильс П. Абель, Сюзанна Левин и Марсия Вайнхольд. Тестовая версия 1993-94; Скотт Форесман издание 1996 г .; Издание Prentice Hall 2002
Функции, статистика и тригонометрия . Шэрон Л. Сенк, Джон В. МакКоннелл, Стивен С. Виктора, Залман Усискин, Нильс П. Абель, Вирджиния Хайстоун и Дэвид Витонски. Скотт Форесман — Эддисон Уэсли 1997
Предварительные вычисления и дискретная математика .Энтони Л. Перессини, Джон В. МакКоннелл, Залман Усискин, Нильс П. Абель и Дэвид Витонски. Скотт Форесман — Эддисон Уэсли 1998
Абель и Дэвид Витонски. Скотт Форесман — Эддисон Уэсли 1998
Третье издание (коммерческое издание Чикаго: Wright Group / McGraw-Hill; Чикаго: UChicagoSolutions)
3Математика перед переходом . Джон В. Макконнелл, Кэти Хайнс Фельдман, Дебора Хирес, Эмили Каллемейн, Энрике Ортис, Норин Виннингем, Карен Хант, Трой П. Регис, Михаэла Флоренс Сингер, Джон Вулф, Натали Джакусин и Залман Усискин.Полевые испытания версии 2006-07; Wright Group / McGraw-Hill издание 2009 г.
Математика переходов . Стивен С. Виктора, Эрика Чунг, Вирджиния Хайстоун, Кэтрин Капуцци, Дебора Хирес, Нева Меткалф, Сьюзен Сабрио, Натали Якуцин и Залман Усискин. Полевые испытания версии 2005-06; Wright Group / McGraw-Hill издание 2008 г .; UChicagoSolutions, выпуск 2016
Алгебра . Сьюзан Браун, Р. Джеймс Бренлин, Мэри Х. Уилтьер, Кэтрин М. Дегнер, Сьюзен К.Эддинс, Майкл Тодд Эдвардс, Нева Меткалф, Натали Якуцин и Залман Усискин. Полевые испытания версии 2005-06; Wright Group / McGraw-Hill издание 2008 г.
Полевые испытания версии 2005-06; Wright Group / McGraw-Hill издание 2008 г.
Геометрия . Джон Бенсон, Рэй Кляйн, Мэтью Дж. Миллер, Кэтрин Капуцци-Фейерштейн, Майкл Флетчер, Джордж Марино, Нэнси Пауэлл, Натали Якуцин и Залман Усискин. Полевые испытания версии 2006-07; Wright Group / McGraw-Hill издание 2009 г .; UChicagoSolutions, выпуск 2016
Продвинутая алгебра .Джеймс Фландерс, Маршал Лассак, Жан Сеч, Мишель Эггердинг, Пол Дж. Карафиол, Лин Макмаллин, Нил Вейсман и Залман Усискин. Полевые испытания версии 2006-07; Wright Group / McGraw-Hill издание 2009 г .; UChicagoSolutions, выпуск 2016
Функции, статистика и тригонометрия . Джон В. МакКоннелл, Сьюзен А. Браун, Пол Дж. Карафиол, Сара Брауэр, Мэри Айвз, Роза МакКаллаг, Натали Якукин и Залман Усискин. Полевые испытания версии 2007-08; Wright Group / McGraw-Hill издание 2010 г .; UChicagoSolutions, выпуск 2016
Предварительные вычисления и дискретная математика . Энтони Л. Перессини, Питер Д. ДеКрейн, Молли А. Рокстро, Стивен С. Виктора, Уорд Э. Кэнфилд, Мэри Хелен Уилтьер и Залман Усискин. Полевые испытания версии 2007-08; Wright Group / McGraw-Hill издание 2010 г .; UChicagoSolutions, выпуск 2016
Энтони Л. Перессини, Питер Д. ДеКрейн, Молли А. Рокстро, Стивен С. Виктора, Уорд Э. Кэнфилд, Мэри Хелен Уилтьер и Залман Усискин. Полевые испытания версии 2007-08; Wright Group / McGraw-Hill издание 2010 г .; UChicagoSolutions, выпуск 2016
Педагогические знания учителей в обучении стратегиям решения словесных задач
Подходы к определению словесных задач
В самом начале интервью мы хотели уточнить определение словесной проблемы и сузить круг словесных задач до рутинные проблемы со словами.Поэтому сначала мы попросили респондентов дать определение понятию «словесная проблема».
Респонденты подошли к вопросу двумя совершенно разными способами. С одной стороны, они могли подумать, что каждая задача, которую мы даем ученикам, выраженная словами, считается проблемой слов.
Бори, учитель начальных классов: Все, что также содержит буквы, а не только цифры. Когда есть несколько инструкций и восклицательный знак.
Другой подход также содержал ожидания относительно алгоритма решения текстовых задач.
Редактировать, учитель начальных классов: вычислительная задача, в которой задаче предшествует текстовая информация. Задачи и текст необходимо понять и записать знаками математического языка. В конце процесса решения дайте ответ на проблему.
Эти два типа подходов присутствуют во всех группах, как представлено в таблице 2.
Таблица 2 Количество участников в каждой подгруппе, принадлежащей к парадигмальным подходам, описанным Chapman (2006) Помимо общих категорий по Чепмену дальнейшие дихотомические переменные были получены из интервью.Одна из таких дихотомических переменных относится к тому, считали ли участники математические словесные задачи и математические задачи, заданные словами, одинаковыми. Тринадцать респондентов почувствовали резкое различие между словесной проблемой и проблемой, выраженной словами. Другой аспект, среди которого участников можно разделить на две группы, — это то, появился ли в их определении термин «операция» или нет. В 13 случаях (43,3%) слово «операция» появилось в определении, что может указывать на то, что эти респонденты рассматривали только словесные проблемы, которые можно решить с помощью операции.
В 13 случаях (43,3%) слово «операция» появилось в определении, что может указывать на то, что эти респонденты рассматривали только словесные проблемы, которые можно решить с помощью операции.
Мы дали понять, что в дальнейшем мы сосредоточимся на решении рутинных задач со словами.
Отношение и оценка трудности обучения словесным задачам
Семь вопросов интервью касались этой темы. Обычно участники считали преподавание словесных задач сложным. 23 респондента заявили, что преподавать по этой теме будет или будет очень сложно. Сложность объяснялась двумя факторами. С одной стороны, они думали, что повседневное концептуальное понимание учащимися проблематично, а с другой стороны, они не считали эту проблему математической или подлежащей развитию в математике.
Эржи, учитель начальных классов: Проблема в том, что у них нет повседневного опыта, а также у них есть концептуальные недостатки.
Детти, учитель начальных классов: Проблема заключается скорее в понимании, ученики замирают, когда слышат, что им нужно решить словесную задачу.
Девочки больше пугаются… Дети не знают сказок, поэтому тексты из сказок для них ничего не значат. Кроме того, в текстах много неизвестных слов.
Учителя видят несколько трудностей в том, как закодировать словесную задачу на языке математики.
Габи, учитель начальных классов: Мне кажется, дети это понимают с большим трудом, для них это абстрактное дело, чтобы подготовить план решения, записать расчет и проверить ответ. Это ограничивает детей, они запутываются, пугаются и паникуют, они что-то портят или что-то упускают.
Габи, учитель младших классов средней школы: Мой класс только что написал тест по задачам со словами, и я считаю, что мы были хорошо подготовлены, поскольку выполняли типовые задания.Однако когда ученикам приходилось сталкиваться с одной и той же проблемой с разными числами, они совершали ошибки и не могли применить изученные методы.
Андраш, учитель начальных классов: Есть проблема, на которую мы не можем повлиять: текстовые задачи часто являются инструментом тестирования на конкурсах и вступительных экзаменах.
В обучении существует огромное давление, что ученики должны уметь это делать. Очень сложно предоставить универсальные модели, которые работают во всех типах текстовых сред.
Юдит, учитель начальных классов: Когда алгоритм ясен и хорошо подготовлен, проблем нет.
Стоит отметить, что, по мнению семи участников, решение текстовых задач несложно. Шесть из них — учителя начальных классов, а один — учитель математики младших классов средней школы. Шесть из них дали определение в ответ на вопрос «Как вы определяете понятие словесной проблемы?» — ответ, который ограничивал значение словесной проблемы арифметическими операциями, оформленными в тексте. Они, вероятно, ограничивают свои преподавательские обязанности текстовыми задачами с прямой формулировкой, которые можно решить, выполнив одну арифметическую операцию.
Первые шаги обучения решению словесных задач
Третья часть интервью была посвящена анализу словесной задачи. Задача, проиллюстрированная на рис. 3, является самой первой проблемой со словами в учебнике нового поколения для первоклассников в Венгрии, который намеревается представить алгоритм решения задач со словами.
Задача, проиллюстрированная на рис. 3, является самой первой проблемой со словами в учебнике нового поколения для первоклассников в Венгрии, который намеревается представить алгоритм решения задач со словами.
Самая первая задача со словом в учебнике венгерских первоклассников (OFI 2016, стр. 102). Перевод текста задачи: Синица нашла 4 зерна пшеницы в одной кормушке для птиц и 6 семян подсолнечника в другой.Сколько всего семян нашла синичка? ». Перевод инструкций, выделенных жирным шрифтом сверху вниз, выглядит следующим образом: сделайте рисунок, запишите цифрами, запишите операцию и ответьте на вопрос
Мы считаем формулировку задачи сложной, поскольку она делает невозможно определить, могут ли быть другие семена, кроме пшеницы или подсолнечника, в одном или обоих кормушках, или же синицы нашли семена в другом месте, а не только в кормушках. Такой вид «разрушения» слова «проблема» аналогичен идее Фрейденталя, цитируемой Гриром (1997). Феномен «дидактического контракта», созданный Бруссо (см. Verschaffel et al. 2010), постоянно формируется и усиливается такими задачами в мире социальной среды класса.
Феномен «дидактического контракта», созданный Бруссо (см. Verschaffel et al. 2010), постоянно формируется и усиливается такими задачами в мире социальной среды класса.
Инструкции слева от рисунка (подготовить рисунок, записать числами, описать с помощью операции, ответить на вопрос) можно выполнить с трудом, создавая новые задачи помимо словесной задачи, которые дети, вероятно, решили с помощью сердце.
Агнес, учитель начальных классов: Мне это не нравится.В 1-м классе сбивает с толку, что два текста рядом друг с другом. Я думаю, что такие инструкции, как рисовать, записывать с операцией, ответ, не стоит там писать, потому что это моя (учительская) просьба. Я бы не стал учить алгоритм. Ученик все еще не может различить задачу и инструкции, принадлежащие алгоритму.
Рисование семян в кормушке кажется ненужным, так как в задании ученики должны отображать данные, а затем «считывать» числа с рисунка.
Андраш, учитель начальных классов: Я думаю, что эта задача не требует рисования, тем более что там стоит число, плюс, результат 10 и все.
Я считаю, что рисовать здесь излишне, это не вызов для школьников.
Еще одно возражение против задачи состоит в том, что ее реальность сомнительна.
Андраш, учитель начальной школы: Я думаю, что большинство словесных задач бесполезны. Вот почему я использую словесные задачи, созданные мной, но при этом важно, чтобы ученикам это нравилось.Какая разница, сколько всего того и этого, и что синица сначала съедает то, а потом то? Ребенок не мотивирован. У детей достаточно проблем, которые они должны решить в своей жизни.
Согласно одной интерпретации реалистичных задач, помимо того, что вещи в задачах должны быть обычными и реалистичными, они также должны быть значимыми и основанными на опыте по сравнению с задачами, которые являются лишь «прикрытием» для нерелевантных упражнений (English 2003 ). Однако мнения участников несколько разошлись.20 человек (66,7%) сочли задание полностью подходящим для обучения алгоритму словесных задач. Однако восемь из них отметили, что, возможно, необходимо заранее уточнить значение пшеницы, подсолнечника и семян.
Однако восемь из них отметили, что, возможно, необходимо заранее уточнить значение пшеницы, подсолнечника и семян.
Треть опрошенных сочла задание непригодным. Четверо из них заявили, что в нем содержится слишком много информации. Пятеро из них считали, что слова «пшеница-подсолнечник» могут быть незнакомы детям. Тем не менее, причины их взглядов не всегда совпадают с теми, с которыми согласны исследователи.
Габи, учитель математики младших классов: Как мне добавить пшеницу и подсолнечник? Мы всегда говорим, что не добавляем яблоко в грушу. В 5–8 классах мы можем добавлять только одинаковые выражения. Мы не можем добавлять подсолнечник к пшенице, потому что они не идентичны.
Только один учитель сказал, что формулировка задания неточная.
Юдит, учитель начальных классов: Не написано, что кормушек всего две. Вопрос не точный.
Две трети респондентов не сомневаются в правдивости текста.Среди сельских респондентов это соотношение составляет 76%.
Анна, учитель начальных классов: Когда класс любит природу и кормит птиц, это реально. Думаю, это реально, потому что здесь видели все виды семян в кормушке. Им это не странно.
16 респондентов (53%) считают, что рисунок помог в решении данной задачи. При этом 73% респондентов заявили, что рисунок всегда необходим при решении словесной задачи. В свете различий между 53% и 73% можно сделать вывод, что должен был быть лучший рисунок, связанный с самой первой проблемой, с которой дети сталкиваются в первом классе.
83% респондентов считают, что ответ полным предложением всегда необходим, и только 68% считают, что это необходимо и для этой задачи.
Агнес, учитель начальных классов: В общем, это необходимо, потому что усиливается ощущение, что это настоящая проблема. Затем я абстрагирую его и помещаю обратно в реальную среду. Потом проверяю, реально ли это. Я не думаю, что это хорошо, что ученики должны вставлять только числа.
Анна, учитель начальных классов: Вначале я не жду ответа с полным текстом.
В Венгрии и, судя по сравнению с учебниками, в Восточной Европе тоже важной традицией является ответ полными предложениями. Только пять респондентов сказали, что не ожидали бы текстового ответа от детей, и четверо из этих пяти респондентов были учителями до начала работы. Кажется, эта традиция тесно связана с оценочными тестами с высокими ставками, введенными в Венгрии, где многие баллы теряются, если не предоставляется текстовый ответ. Похоже, что действующие учителя считают подготовку к оцениванию важной, а предпрофессиональные учителя — нет (пока).
Методы и приемы, используемые при обучении решению словесных задач
Следующая группа вопросов касалась опыта преподавания. Эти вопросы не задавались учителям до начала работы. Важно, когда и как мы начнем обучать любому алгоритму, имеющему отношение к текстовым задачам. На наш взгляд, явное обучение стратегиям решения сомнительно, поскольку маленькие дети могут смешивать две вещи: решение проблемы и знание наизусть этапов процесса решения. Как правило, словесные задачи в первом классе можно решить за один этап, выполнив одну арифметическую операцию.Сложно объяснить, зачем нужен пошаговый алгоритм, когда ребенок уже знает ответ практически сразу после прочтения текста.
Как правило, словесные задачи в первом классе можно решить за один этап, выполнив одну арифметическую операцию.Сложно объяснить, зачем нужен пошаговый алгоритм, когда ребенок уже знает ответ практически сразу после прочтения текста.
79% респондентов сообщили, что начинают обучать явному алгоритму уже в первом классе, и для этого 91% из них выбирают простую словесную задачу с понятной формулировкой, которую можно решить с помощью одной операции, рассчитанной в уме.
Ильдико, учитель начальных классов: Хотя я преподаю это уже во втором семестре первого класса, мы обычно играем и не считаем.Например, они встают, когда им нужно добавить.
Только двое учителей высказали принципиально разное мнение.
Агнес, учитель начальных классов: Я начинаю с более сложной задачи в старших классах. Это имеет смысл только тогда, потому что до этого они не понимали, зачем им это делать.
Андраш, учитель начальных классов: Когда я начал преподавать, я думал, что мне придется начать с простых, но я понял, что проблема со словами действительно должна быть проблемой.
Когда ученик смотрит на него и сразу может решить, он не чувствует, что какой-либо алгоритм имеет смысл. Когда они смотрят на это и говорят 10, но ради учителя я напишу открытое предложение, все это становится самоцелью.
Мы спросили, с помощью каких методик обучения они помогают своим ученикам решать словесные задачи. Четко можно выделить две вещи: выделение текста (указали 48%) и поддержку понимания прочитанного.
Ильдико, учитель начальных классов: Они подчеркивают важные данные карандашом.
Мы попросили респондентов составить карту своих оценочных привычек, оценив решение следующей задачи, как если бы это было в тесте: «Бетти и Дори приглашают своих друзей на вечеринку. На каждом подносе 3 сыра, 5 салями и 3 бутерброда с ветчиной. Сколько всего бутербродов на 5 противнях? » Участники могли использовать любую систему подсчета баллов от дихотомической 0–1 до более совершенной системы подсчета баллов.
За правильное решение респонденты в среднем дали 5,2 балла. Минимум 3 (два для расчета, один для текстового ответа), максимум 10.Две трети респондентов выставили баллы в соответствии с этапами ожидаемого алгоритма. Из шагов алгоритма особенно важным они посчитали следующее: запись данных, написание открытого предложения, вычисление, текстовый ответ. Открытое предложение как образец было выделено в половине ответов.
Минимум 3 (два для расчета, один для текстового ответа), максимум 10.Две трети респондентов выставили баллы в соответствии с этапами ожидаемого алгоритма. Из шагов алгоритма особенно важным они посчитали следующее: запись данных, написание открытого предложения, вычисление, текстовый ответ. Открытое предложение как образец было выделено в половине ответов.
Боги, учитель начальных классов: В плане решения мы всегда пишем открытое предложение, и может быть несколько решений. Мы записываем это в манере, допускающей несколько решений.
Особенно важным оказался вопрос текстового ответа. Мы также спросили, ставили ли они балл за текстовый ответ, даже если расчет и решение задачи были неправильными. 19 респондентов заявили, что дали бы балл. Причины были следующие. Они либо не хотят дважды наказывать ученицу за ошибку, либо, как один учитель начальных классов осмелился признаться в своем замешательстве: «Это дилемма, потому что в принципе было бы справедливо поставить точку.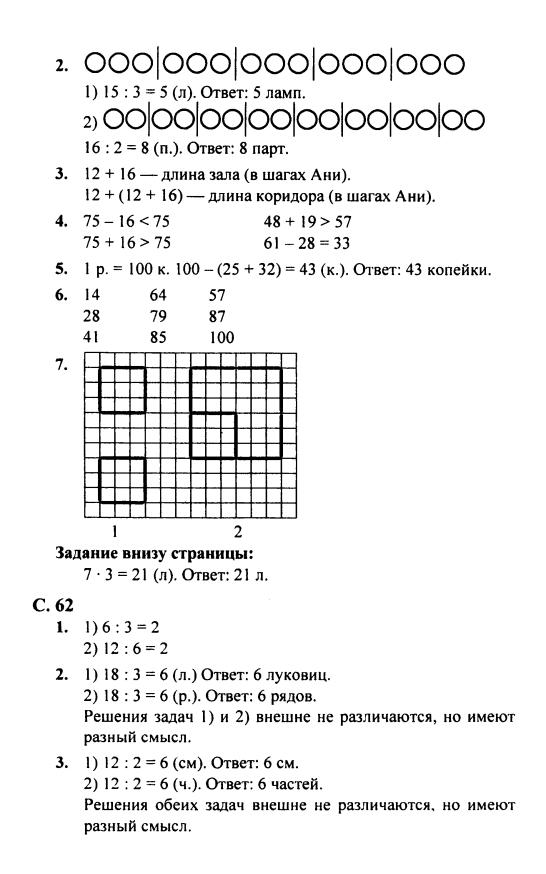 Поэтому я не знаю.”
Поэтому я не знаю.”
Мы спросили, какие еще модели они показали детям для решения словесных задач. Наш вопрос вызвал небольшую путаницу, и идей возникло не так много. Разделы рисования были упомянуты тремя учителями начальных классов, методом проб и ошибок два учителя математики младших классов средней школы, а таблицы одним учителем начальных классов были упомянуты в качестве возможных моделей решения словесных задач.
Собственные решения участников проблемы со словами
Интервью закончилось решением проблемы со словами от Verschaffel et al.(1994). «Карчи и Гюри вместе устраивают свой день рождения. Карчи пригласил 5 детей, Гюри пригласил 6 детей. Сколько детей было на вечеринке? »
Это типичная бессрочная задача, поскольку решение — это не одно определенное число. Есть несколько факторов, которые вы можете принять во внимание во время решения, которое показывает, что стратегия «искать числовые данные, а затем связывать их с соответствующей операцией» неэффективна. Были ли дети, которых пригласили оба организатора? Карчи и Гюри участвовали в вечеринке? Все ли приглашенные дети действительно пошли на праздник?
Были ли дети, которых пригласили оба организатора? Карчи и Гюри участвовали в вечеринке? Все ли приглашенные дети действительно пошли на праздник?
Мы попросили респондентов решить проблему со словом так, как они ожидали бы от своих второклассников.Нам было интересно, как участники интерпретируют это задание. Если они не распознали ловушку в задаче, мы спросили, будут ли они изменять решение в старших классах школы. Этой инструкцией мы мягко посоветовали им пересмотреть проблему. В Таблице 3 представлены решения в зависимости от оценок и опыта преподавания. Были определены четыре категории, и все ответы респондентов попали в одну из них. Самый сложный и реалистичный ответ пошел дальше простого выполнения арифметических операций с числами текста и открыл возможность различных возможных решений.Таким образом, «полное решение» содержало один или несколько числовых ответов (как и в трех других категориях ответов), а также замечание или сомнения относительно существования однозначного числового ответа.
Согласно Таблице 3, все подгруппы участников дали разные варианты ответов на этот вопрос. Обратите внимание, что эти шаблоны решений не являются их собственностью, но это те ответы, которые они ожидают от учеников 2-го класса.К сожалению, из этих ответов можно предположить, как их ученики будут вести себя, когда сталкиваются с реалистичными текстовыми проблемами в школе.
Школа Сен-Рафаэля: знакомьтесь с нашими учителями
Бакалавр, Раннее детство и вмешательство, Университет Маунт-Юнион Преподает с 2013 г., СГД с 2013 г. |
Мисс Лайонс любит быть частью Girls on the Run в St.Школа Рафаэля. Ей нравится делиться со студентами своей любовью к бегу и учить их быть сильными и позитивными молодыми женщинами.
MA, Учебный план и инструкции, Государственный университет Кливленда Бакалавр, образование, Янгстаунский государственный университет Преподает с 1995 г. |
ГоспожаРитцлер считает, что классы детского сада — самое счастливое место во всей школе! Ей нравится видеть улыбающиеся лица своих учеников и любовь к учебе! Помимо преподавания, г-жа Ритцлер является активным членом школьного консультативного совета и является представителем LPDC для нашего преподавательского состава.
Степень бакалавра, дошкольное образование и вмешательство, Дейтонский университет Мисс ДиПронио имеет B.S. в дошкольном образовании и вмешательстве от Дейтонского университета. Она преподает с 2017 года. Мисс ДиПронио рада присоединиться к общине Святого Рафаэля. Ей нравится, когда ее ученики заняты своей работой и хотят учиться. Мисс ДиПронио любит наблюдать за духовным и академическим ростом своих учеников. |
Магистр, Учебная программа, Государственный университет Боулинг-Грин Б. Преподает с 1999 г., СГД с 2014 г. |
Г-жа Сак говорит: «Это захватывающее время, чтобы стать частью школы Сен-Рафаэль!» Она рада видеть, как наши первоклассники растут в учебе, дружбе и отношениях с Иисусом.
B.A. Дошкольное образование, Университет Ксавьера |
г-жаДусек недавно окончил Университет Ксавьера со степенью бакалавра в области дошкольного образования. Она также имеет одобрение 4-го и 5-го классов. Она преподавала в классе для первого класса в общественных школах Сикамор в Цинциннати. Г-жа Дусек любит работать со своими учениками и наблюдать, как они растут в учебе, и она рада быть частью общины Святого Рафаэля!
M.Ed., Университет Олд Доминион бакалавр, дошкольное образование |
Г-жа Бруски говорит: «Я так рада, что преподаю в первом классе в Сен-Рафаэле! Я выросла в Эйвон-Лейк и посещала начальную школу Святого Иосифа, прежде чем поступить в среднюю школу Магнификат.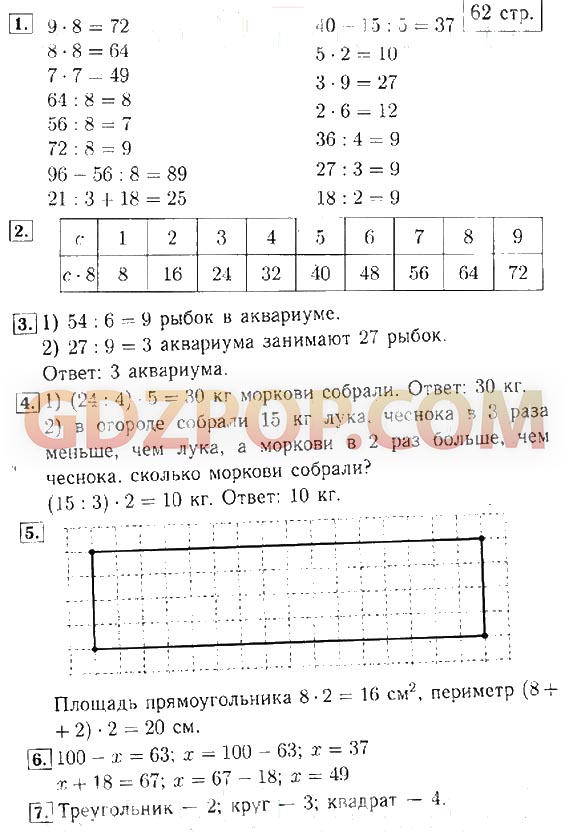 После окончания Магнификата я поступила в Университет Майами. где я получила степень бакалавра в области дошкольного образования. После окончания Университета Майами я вышла замуж за своего мужа Гранта, который в то время служил в армии.Я начал свою педагогическую карьеру в Миссисипи, Техасе и Вирджинии. После переезда в Вирджинию я смог начать свою карьеру в сфере образования. Я преподавал в государственных школах Норфолка (третий класс), государственных школах Вирджиния-Бич (первый класс) и католической школе Святого Иоанна Апостола (первый класс). Я провел несколько лет в школе Святого Иоанна Апостола, прежде чем вернуться в школу, чтобы получить степень магистра образования с упором на чтение в Университете Олд Доминион.Во время моего пребывания в Сент-Джонсе я был учителем-наставником, руководителем основной группы от дошкольного до второго класса, а также членом Совета по магистерской программе Ричмондской епархии. Я люблю образование и делюсь своей верой со своими учениками! Моя цель в классе — сделать так, чтобы они чувствовали себя уверенными, любимыми и рады приходить в школу каждый день! »
После окончания Магнификата я поступила в Университет Майами. где я получила степень бакалавра в области дошкольного образования. После окончания Университета Майами я вышла замуж за своего мужа Гранта, который в то время служил в армии.Я начал свою педагогическую карьеру в Миссисипи, Техасе и Вирджинии. После переезда в Вирджинию я смог начать свою карьеру в сфере образования. Я преподавал в государственных школах Норфолка (третий класс), государственных школах Вирджиния-Бич (первый класс) и католической школе Святого Иоанна Апостола (первый класс). Я провел несколько лет в школе Святого Иоанна Апостола, прежде чем вернуться в школу, чтобы получить степень магистра образования с упором на чтение в Университете Олд Доминион.Во время моего пребывания в Сент-Джонсе я был учителем-наставником, руководителем основной группы от дошкольного до второго класса, а также членом Совета по магистерской программе Ричмондской епархии. Я люблю образование и делюсь своей верой со своими учениками! Моя цель в классе — сделать так, чтобы они чувствовали себя уверенными, любимыми и рады приходить в школу каждый день! »
Бакалавр раннего детства и элементарного образования, Фронтсбургский государственный университет Преподает с 2000 г. МиссисМанфред начала свою педагогическую карьеру в округе Ховард, штат Мэриленд, в 2000 году. Переехав в Огайо, чтобы продолжить карьеру мужа, она быстро погрузилась в школу Святого Рафаэля. Г-жа Манфред начала волонтерство, в течение 2 лет была президентом школы и дома, заместителем учителя, помощником в 1-м классе, а затем в течение длительного периода времени в качестве помощника во 2-м классе. Приступить к команде 2-го класса в качестве штатного учителя просто как дома. Ей нравится смотреть, как ее второклассники растут в вере! |
Б.S. Дошкольное образование, Университет Джона Кэрролла, Преподает с 2019 г., СГД с 2019 г. |
Мисс О’Мэлли очень рада начать свою педагогическую карьеру в Saint Raphael в качестве учителя второго класса и наблюдать, как ее ученики растут как в классе, так и за его пределами. Она надеется на установление эффективных отношений со своими учениками в течение учебного года, поскольку она работает с ними для достижения их целей.
Она надеется на установление эффективных отношений со своими учениками в течение учебного года, поскольку она работает с ними для достижения их целей.
M.Ed. Начальное образование, Университет Джона Кэрролла B.B.A. Финансы и маркетинг, Университет Огайо, Преподает с 2003 г., СГД с 2017 г. |
После получения степени магистра начального образования г-жа Стенгер три года преподавала в муниципальном школьном округе Кливленда в качестве учителя первого и второго классов, а также тренера по грамотности.Г-жа Стенгертен провела следующие 10 лет в индустрии детских книг, редактируя и писая книги, а также разрабатывая руководства для учителей, которые будут использоваться в классах. Миссис
Стенгер был рад вернуться к преподаванию в 2017 году в качестве учителя второго класса в 2B! Ее любимые предметы — естественные науки и математика. Ей нравится читать, путешествовать, выгуливать собак и проводить время с мужем и тремя детьми.
Б.S. Начальное образование, Государственный университет Кливленда Преподает с 1993 г., СГД с 2001 г. |
Миссис Барретт гордится тем, как каждый класс становится семьей Комнаты 3, где мы проявляем уважение, сострадание и помогаем друг другу расти в нашей вере.
M.Ed., Reading Endorsement, Baldwin Walace College Б.S., Начальное образование, Специальное образование, Дейтонский университет Преподает с 2001 г., СГД с 2006 г. |
Г-жа Карнац очень рада вернуться в SRS в качестве учительницы 3-го класса. Свой педагогический стаж она начала здесь в 5-м классе. Г-жа Карнац была активным членом школы как родитель-волонтер и помогала составлять школьный ежегодник в течение последних 10 лет.
Б.А., начальное образование, Колледж Нотр-Дам штата Огайо Преподает с 1996 г. |
Г-жа Барко — увлеченный педагог, которому нравится проповедовать католическую веру и приносить любовь Иисуса в сердца своих учеников.
M.Ed., Ciriculum and Instruction with Reading Endorsement, Ashland University Б.С., Образование, Кливлендский государственный университет Преподает с 1990 г., СГД с 1990 г. |
Как учитель обществознания 4-го класса, г-жа Камола любит рассказывать ученикам факты о великом штате Огайо.
M.Ed., Учебная программа и инструкции с одобрением чтения, Кливлендский государственный университет Б.С., Образование, Университет Ашленда Преподает с 2000 г., СГД с 2005 г. |
Помимо преподавания, г-жа Сауто является активным тренером программы «Девушки в бегах». Ей также нравится работать с Raiders Club в течение недели. Будучи выпускницей SRS, а теперь и преподавателем, г-жа Сауто любит, что SRS — это место, где чувствуешь себя как дома и прививает сильный христианский характер каждому, кто проходит через него.
Будучи выпускницей SRS, а теперь и преподавателем, г-жа Сауто любит, что SRS — это место, где чувствуешь себя как дома и прививает сильный христианский характер каждому, кто проходит через него.
Б.S. Дошкольное образование и начальное образование; Я преподаю с 2015 года. Мне нравится преподавать математику и естественные науки. Дроби — моя любимая единица обучения в 4-м классе! Мне нравится позитивная атмосфера в классе и создание сильного сообщества. Мы так много узнаем вместе! Помимо преподавания, я люблю путешествовать, проводить время на улице и играть со своей собакой Мэй. |
М.Изд., Университет Джона Кэрролла BA, Университет Джона Кэрролла Преподает с 1996 г., СГД с 2006 г. |
Миссис Барри участвует в конкурсе пчел National Geography. Миссис Барри ценит нашу строгую религиозную программу в классе и за его пределами. Она ценит доктора Кереки, обитель Святого Игнатиана и Легион Марии. Миссис Барри любит поддерживать наших сотрудников через комитет Sunshine.Она заявляет: «SRS была благословением для моих детей и будет для вас тоже!»
Миссис Барри ценит нашу строгую религиозную программу в классе и за его пределами. Она ценит доктора Кереки, обитель Святого Игнатиана и Легион Марии. Миссис Барри любит поддерживать наших сотрудников через комитет Sunshine.Она заявляет: «SRS была благословением для моих детей и будет для вас тоже!»
M.Ed., обучение грамоте, Кливлендский государственный университет (текущий студент) Бакалавр, среднее образование, Государственный университет Боулинг Грин Преподает с 2008 г., СГД с 2009 г. |
Помимо преподавания, мисс Уэлш работает тренером программы «Девушки в бегах», которая способствует повышению самооценки и общего состояния здоровья молодых девушек.Ей нравится делиться своей любовью к чтению и письму со своими учениками, но больше всего ей нравится знакомиться с замечательными людьми, которые ее ученики.
Профессиональная лицензия, Государственный университет Боулинг-Грин Преподает с 1996 г. |
Миссис Уайз очень любит преподавать и изменять жизнь детей к лучшему.Помимо обучения математике, она является одним из тренеров команды соревнований по математике 5-6 классов. Миссис Уайз также является одним из тренеров научной олимпиады.
M.Ed., Curricullum and Development, Ashland University бакалавр, образование, Кливлендский государственный университет Преподает с 1998 г., СГД с 1998 г. |
На протяжении многих лет поощрение студентов к наблюдению и исследованию мира вокруг них было чрезвычайно полезным для миссис А.Руда. Ей выпала честь сопровождать многих наших студентов на региональных и государственных научных ярмарках, где они отлично проявили себя!
M. Ed., Университет Ашленда BS Ed., Государственный университет Огайо Преподает с 1984 г. |
Г-жа Сконсе модерирует «Класс чемпионов» и «Brain Brawl», которые представляют собой академические соревнования, в которых участвуют наши ученики 7 и 8 классов.Она чувствует себя счастливой, будучи частью семьи Святого Рафаэля, и любит поддерживать связь с бывшими учениками и слышать об их успехах в средней школе, колледже и за ее пределами. Она уже начала преподавать следующее поколение, или того, кого она называет «внучатыми учениками».
M.Ed., среднее образование, Государственный университет Огайо Бакалавр гуманитарных наук и семейные науки, Государственный университет Огайо Преподает с 2013 г., СГД с 2014 г. |
Мисс Хоффмайстер чувствует себя счастливой быть частью церкви Св.Сообщество школы Рафаэля и благодарит сообщество за теплый прием. Наряду с преподаванием, она с нетерпением ожидает участия в олимпиаде по науке и работе комитета по студенческой литургии.
Магистр наук, Молекулярная и целлюлозная биология, Кливлендский государственный университет B.D.S., наука, Университет Джона Кэрролла |
ГоспожаНоттингем — молекулярный и клеточный биолог по образованию.
У миссис Ноттингем есть B.D.S. наук от Университета Джона Кэрролла и магистра наук. в области молекулярной и клеточной биологии из CSU. Она проработала 10 лет в клинике Кливленда Клиник и Университетской клиники в области сердечно-сосудистой медицины и 5 лет в качестве консультанта по биомедицине для начинающих медицинских компаний.
Она любит готовить, играет на пианино и наслаждается прогулками по Бэй-Виллидж с мужем и 4 собаками.Элисон — жительница Бэй-Виллидж, живет со своим мужем Биллом и двумя детьми, которые учатся в школе Сен-Рафаэль.
|
ГоспожаЗейтц рада присоединиться к команде младших классов в качестве учителя религии в 7/8 классе и с нетерпением ждет встречи со всеми своими новыми учениками! Она родом из Ист-Сайда и живет в Уиллоуби-Хиллз со своим мужем Дэном и нашей дочерью Женевьев. Она любит Иисуса, кофе и все хитрости!
Б.С., Математика, Государственный университет Огайо Сертификат преподавателя, Университет Ашленда Преподает с 2007 г .; СГД с 2013 г. |
Г-н Вулфорд любит видеть, как ученики помогают друг другу в классе. Он гордится их сильным чувством общности.
Г-жа Тайберт говорит: «Я очень рада присоединиться к команде преподавателей Saint Raphael в этом году.Я преподаю испанский язык 18 лет и искренне верю, что меня призвали поделиться своей любовью и энергией к испанскому языку со своими учениками. Я выучил испанскую волю, живя в Хунине, Аргентина, когда был подростком. У меня также была возможность учиться за границей в Сеговии, Испания, во время учебы в Университете Огайо и в Куэрнаваке, Мексика, во время моей магистерской программы в Университете Ксавьера. У нас с мужем Майком двое детей: Эвелин (13 лет) и Джуд (9 лет). Оба моих ребенка заядлые футболисты, поэтому мы много времени проводим на полях.Я люблю читать, ходить в походы и путешествовать ».
M.Ed., Учебная программа и инструкции, Государственный университет Кливленда бакалавр, образование, Университет Маунт-Юнион Преподает с 2002 г., СГД с 2006 г. |
Г-жа Хирш любит наблюдать, как ее ученики становятся читателями и писателями. Она участвует в клубе «Сила пера и строителей».
M.Ed., Кливлендский государственный университет B.A., Болдуин Уоллес 2004 |
Г-жа Фиттс работает в школах с тех пор, как получила степень бакалавра музыкальной терапии в Музыкальной консерватории Болдуина-Уоллеса в 2004 году. Проработав полный рабочий день учителем музыки с особыми потребностями и преподавателем вокала по совместительству, почти десять. лет, она училась в Кливлендском государственном университете, чтобы получить степень магистра в области патологии речи в 2015 году.Мередит любит работать с детьми и включать игры и развлечения в терапию.
Уровень знаний в детском саду и более поздние результаты по математике
Кларк Б., Шинн М.Р. Предварительное расследование по выявлению и разработке первых
математических программ измерения на основе учебной программы. Обзор школьной психологии 2004; 33 (22): 234–248.
Клементс Д.Х., Сарама Дж. Экспериментальная оценка эффектов основанной на исследованиях дошкольной программы
по математике.Американский журнал исследований в области образования, 2008 г .; 45 (2): 443–494.
Копли, Дж. Маленький ребенок и математика. Вашингтон, округ Колумбия: Национальная ассоциация образования
детей младшего возраста; 2000.
Dehaene, S. Чувство числа: как разум создает математику. Нью-Йорк: издательство Оксфордского университета;
1997.
Департамент образования штата Делавэр. Он-лайн отчеты по программе тестирования студентов штата Делавэр: Statewide
summary — Math. 2007. Получено 12 сентября 2007 г. с http: // dstp.doe.k12.de.us/DSTPmart9
Даукер А. Индивидуальные различия в арифметике: значение для психологии, нейробиологии и образования
. Нью-Йорк: Психология Пресс; 2005.
Duncan GJ, Dowsett CJ, Classens A, Magnuson K, Huston AC, Klebanov P, et al. Готовность к школе и последующее достижение
. Психология развития 2008; 43 (6): 1428–1446. [PubMed: 18020822]
Фейгенсон Л., Дехаен С., Спелке Э. Основные системы чисел. Тенденции в когнитивных науках 2004; 8 (7):
307–314.[PubMed: 15242690]
Fuchs LS. Профилактические исследования в математике: улучшение результатов, построение идентификационных моделей и
понимание инвалидности. Журнал нарушений обучаемости, 2005 г .; 38 (4): 350–352. [PubMed: 16122068]
Фуллер Б., Райт Дж., Гесицки К., Канг Э. Измерение роста: как определить, что ни один ребенок не останется позади? Образовательный
Исследователь 2007; 36 (5): 268–278.
Geary DC. Отражения эволюции и культуры в детском познании: значение для математического
развития и обучения.Американский психолог 1995; 50 (1): 24–37. [PubMed: 7872578]
Гири, округ Колумбия, Хэмсон, Колорадо, Клад МК. Числовое и арифметическое познание: продольное исследование
процессов и концептуальных дефицитов у детей с нарушением обучаемости. Журнал экспериментального ребенка
Психология 2000; 77: 236–263. [PubMed: 11023658]
Гири, округ Колумбия, Клад МК, Берд-Крейвен Дж, ДеСото МС. Выбор стратегии в простом и сложном дополнении:
Вклады рабочей памяти и подсчета знаний для детей с математическими нарушениями.
Журнал экспериментальной детской психологии 2004; 88: 121–151. [PubMed: 15157755]
Geary DC, Hoard MK, Hamson CO. Численное и арифметическое познание: модели функций и дефицит
у детей с риском математической инвалидности. Журнал экспериментальной детской психологии
1999; 74: 213–239. [PubMed: 10527555]
Gersten R, Jordan NC, Flojo JR. Раннее выявление и вмешательство для учащихся с математическими трудностями
.Журнал нарушений обучаемости 2005; 38 (4): 293–304. [PubMed: 16122059]
Ginsburg, HP .; Lee, JS .; Бойд, JS. Математическое образование для детей младшего возраста: что это такое и как
продвигать его (Отчет о социальной политике, том 22, № 1). Анн-Арбор, Мичиган: Общество исследований детей
Развитие; 2008.
Гордон П. Численное познание без слов: данные из Амазонии. Наука 2004 Октябрь
15; 306: 496–499. [PubMed: 15319490]
Гриффин С. Развитие математической компетентности в дошкольном и раннем школьном возрасте: когнитивные основы
и стратегии обучения.В: Roher, JM., Редактор. Математическое познание. Гринвич,
Коннектикут: информационный век; 2002. с. 1-32.
Griffin, S .; Case, R .; Зиглер, RS. Классные уроки: объединение когнитивной теории и аудиторной практики.
В: МакГилли К., редактор. Rightstart: Обеспечение основных концептуальных предпосылок для первого формального обучения арифметике
учащимся из группы риска школьной неуспеваемости. Кембридж, Массачусетс: MIT Press; 1994. стр.
25-50.
Jordan, NC; Глаттинг, Дж.; Ramineni, C. Инструмент для проверки распознавания чисел для детей раннего возраста из группы риска на
математических трудностях. В: Даукер А., редактор. Математические трудности: Психология,
неврология и вмешательство. Нью-Йорк: Эльзевир; 2008. с. 45-58.
Jordan NC, Hanich LB, Kaplan D. Освоение арифметических фактов у маленьких детей: продольное исследование
. Журнал экспериментальной детской психологии 2003a; 85: 103–119. [PubMed: 12799164]
Jordan NC, Hanich LB, Kaplan D.Лонгитюдное исследование математических способностей у детей с
специфическими математическими трудностями в сравнении с детьми с коморбидной математикой и трудностями чтения.
Развитие ребенка 2003b; 74 (3): 834–850. [PubMed: 12795393]
Jordan et al. Page 14
Dev Psychol. Авторская рукопись; доступно в PMC 2009 25 ноября 2009 г.
NIH-PA Рукопись автора NIH-PA Рукопись автора NIH-PA Рукопись автора
Будущие развивающиеся технологии в секторе ветроэнергетики: европейская перспектива
Основные моменты
- •
Набор новых технологий в ветроэнергетическом секторе.
- •
Для каждой технологии был проведен анализ основных преимуществ и проблем.
- •
Определен потенциал для масштабирования каждой технологии.
- •
Оценены уровни технологической готовности и тенденции их развития.
Реферат
В этом документе представлен экспертный взгляд из Европы на будущие развивающиеся технологии в секторе ветроэнергетики с учетом их потенциала, проблем, приложений и готовности технологий, а также того, как они могут развиваться в ближайшие годы.Было установлено, что эти технологии исходят в основном из академического сектора, некоторых начинающих компаний и нескольких крупных промышленных предприятий. Были рассмотрены следующие области: воздушная ветроэнергетика, морские плавучие концепции, интеллектуальные роторы, устройства для сбора энергии ветра, роторы с лопастями, нетрадиционные системы передачи энергии, многороторные турбины, альтернативные опорные конструкции, модульные генераторы постоянного тока высокого напряжения , инновационные технологии изготовления лопастей, турбины с диффузорами и малые турбины.Также рассматривается будущая роль расширенного многомасштабного моделирования и доступности данных. Этот экспертный обзор показал, что для реализации многих из этих новых технологий потребуются дополнительные исследования. Тем не менее, необходимо определить синергию между фундаментальными и промышленными исследованиями, правильно направив государственное и частное финансирование в этих новых технологических областях, поскольку промышленное развитие может опережать более фундаментальные исследования быстрее, чем ожидалось.
Ключевые слова
Энергия ветра
Энергия ветра
Новые технологии
Уровень технологической готовности
Возобновляемые источники энергии
Рекомендуемые статьиЦитирующие статьи (0)
Просмотреть аннотацию© 2019 Авторы.Опубликовано Elsevier Ltd.
Рекомендуемые статьи
Цитирующие статьи
Детские игры, фильмы и книги K-3
Starfall не имеет рекламы, не собирает личную информацию от детей, не продает никакой информации и использует файлы cookie только для внутреннего управления сайтом. Используя этот сайт, вы соглашаетесь на использование файлов cookie и обновленную Политику конфиденциальности OK
Starfall.com® открылся в сентябре 2002 года как бесплатная общественная служба для обучения детей чтению.С тех пор он расширился, включив в него языковые искусства и математику для дошкольных учреждений, детских садов, первого, второго и третьего классов. Акцент Starfall на фонематической осведомленности, систематической последовательной фонетике и обычных словах в сочетании с аудиовизуальной интерактивностью оказался эффективным в обучении начинающих читателей. Мероприятия «Звездопад» основаны на исследованиях и соответствуют индивидуальным и общепринятым государственным стандартам по английскому языку и математике.
Программа делает упор на исследование, игру и позитивное подкрепление — побуждает детей становиться уверенными и внутренне мотивированными.Starfall — образовательная альтернатива другим развлечениям для детей и особенно эффективна для специального образования, домашнего обучения и развития английского языка (ELD, ELL, ESL). Он широко используется в школах, которые обслуживают детей с особыми потребностями и трудностями в обучении.
Наша недорогая программа членства расширяет бесплатный контент, включая анимированные песни, математику и упражнения по чтению для K-3. Членство также поддерживает производство новых книг, песен, образовательных игр и фильмов.
Программа, предоставленная некоммерческой организацией Starfall Education Foundation, была разработана доктором Стивеном Шутцем. В детстве Стивен с трудом учился читать из-за дислексии. Он хотел создать веб-сайт с бессистемными мультисенсорными интерактивными играми, которые позволят детям видеть, слышать и касаться во время обучения.
Принесено вам Крысой Заком. ™ Веб-сайт Starfall — это программная служба Starfall Education Foundation, общественной некоммерческой организации, 501 (c) (3).Starfall® и Starfall.com® являются зарегистрированными товарными знаками в США, Европейском Союзе и других странах. Авторские права © 2002–2021, компания Starfall Education. Все права защищены.
Еженедельная сводка суперинтенданта | Департамент образования Вайоминга
Уважаемые суперинтенданты,
Ноябрь — Месяц национального индейского наследия . Коренные американцы обогащают историю, разнообразие, культуру и будущее нашей страны и Вайоминга.
В 2017 году законопроект 76, Индийское образование для всех, был принят Законодательным собранием штата Вайоминг и был подписан.Вскоре после этого началась работа по разработке образовательных стандартов, чтобы каждый ученик в Вайоминге имел возможность узнать о племенах восточных шошонов и северных арапахо, которые имеют глубокие и постоянные корни в Вайоминге. Стандарты уже завершены и будут полностью внедрены в Вайоминге в следующем учебном году. В дополнение к стандартам «Индийское образование для всех» позволяет Министерству образования штата Вайоминг (WDE) напрямую сотрудничать со старейшинами племен, лидерами, преподавателями и другими людьми для создания хранилища учебных материалов и ресурсов.Стандарты образования и репозиторий ресурсов можно найти здесь.
Еще до того, как был принят закон, многие преподаватели Вайоминга рассказывали своим ученикам об истории, культуре, политике и многом другом коренных американцев. Есть много способов преподавать и учиться во время Национального месяца наследия коренных американцев (или в любой другой месяц. Вот несколько:
Баскетбол или ничего (Netflix)
Что было у нас (Amazon Prime)
Мисс Навахо (документальный фильм PBS)
Месяц наследия коренных американцев — ресурсы для учителей
Прямая ссылка на репозиторий WDE
В марте 2017 года тогдашний губернатор Мэтт Мид подписал закон № 76 «Индийское образование для всех».
В День ветеранов, 11 ноября, мы почтили память мужчин и женщин, служивших в вооруженных силах США. Рекомендую прочитать вдохновляющий рассказ о Кендрике Ласке. Он ушел из армии США и начал преподавать в средней школе. Если вы знаете ветерана или действующего военнослужащего мужчину или женщину, которые хотели бы стать учителем, в Вайоминге есть ресурсы:
Войска учителям — бывший преподаватель Вайоминга Билл Хардести работает напрямую со школами, высшими учебными заведениями и ветеранами, которые хотят стать учителями.
Центр обслуживания ветеранов Университета Вайоминга — ветеран армии Марти Мартинес тесно сотрудничает с ветеранами, когда они переходят в университетский городок и учатся в колледже.
Директор начальной школы Slade Хизер Моро возглавляет ассамблею награды Blue Ribbon в пятницу днем.
Slade Elementary и PODER Academy получили награды как Национальные школы с голубой лентой. У меня была возможность отпраздновать это событие виртуально со студентами и сотрудниками Slade.
«[Национальные] школы с голубой лентой показывают, что возможно, если сосредоточить внимание на учениках и их достижениях.


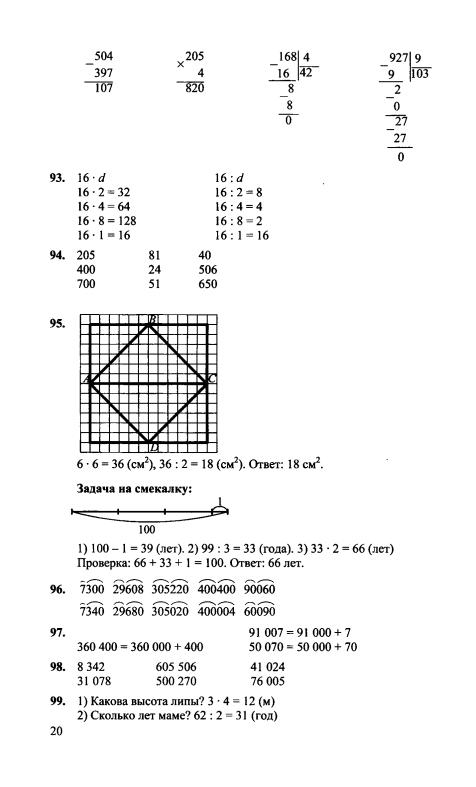


 продолжить.”
продолжить.” 
 Девочки больше пугаются… Дети не знают сказок, поэтому тексты из сказок для них ничего не значат. Кроме того, в текстах много неизвестных слов.
Девочки больше пугаются… Дети не знают сказок, поэтому тексты из сказок для них ничего не значат. Кроме того, в текстах много неизвестных слов. В обучении существует огромное давление, что ученики должны уметь это делать. Очень сложно предоставить универсальные модели, которые работают во всех типах текстовых сред.
В обучении существует огромное давление, что ученики должны уметь это делать. Очень сложно предоставить универсальные модели, которые работают во всех типах текстовых сред. Я считаю, что рисовать здесь излишне, это не вызов для школьников.
Я считаю, что рисовать здесь излишне, это не вызов для школьников.
 Когда ученик смотрит на него и сразу может решить, он не чувствует, что какой-либо алгоритм имеет смысл. Когда они смотрят на это и говорят 10, но ради учителя я напишу открытое предложение, все это становится самоцелью.
Когда ученик смотрит на него и сразу может решить, он не чувствует, что какой-либо алгоритм имеет смысл. Когда они смотрят на это и говорят 10, но ради учителя я напишу открытое предложение, все это становится самоцелью. , СГД с 2000 г.
, СГД с 2000 г. А., Элементарный (K-8) и Специальное изд. (K-12), Университет Мерсихерст
А., Элементарный (K-8) и Специальное изд. (K-12), Университет Мерсихерст , СГД с 2016 г.
, СГД с 2016 г. , СГД с 2003 г.
, СГД с 2003 г. , СГД с 2004 г.
, СГД с 2004 г. , SRS 1988-1990, 1998-настоящее время
, SRS 1988-1990, 1998-настоящее время A. Психология, Францисканский университет Стьюбенвилля, 2005 г.
A. Психология, Францисканский университет Стьюбенвилля, 2005 г.