ГДЗ решебник по алгебре 8 класс Макарычев, Миндюк, Нешков Учебник Просвещение
Алгебра 8 класс
Тип пособия: Учебник
Авторы: Макарычев, Миндюк, Нешков
Издательство: «Просвещение»
Науку, которая изучает величины и действия над ними называют алгеброй. Это один из древнейших разделов математики. Она очень важна как для развития общества, так и для отдельно взятого индивидуума. Её знания необходимы практически во всех сферах деятельности. Экономика, строительство, наука и многое другое, где алгебраические знания являются основой. В рамках школьной программы математику начинают изучать с первого класса и на протяжении всего процесса обучения совершенствуют свои навыки и умения вплоть до выпуска.
Чему научат уроки алгебры
Учебный курс восьмого класса направлен на изучение рациональных дробей, числовых неравенств, а также ребята познакомятся со свойствами квадратного корня и действиями над ним. Осваивая предмет они научатся:
- Правильно использовать алгебраические термины и понятия.

- При помощи уравнений решать задачи.
- Пользоваться изученными формулами.
- Строить графики квадратичной функции.
- Применять на практике изученный материал.
Основная цель дисциплины научить школьника логически мыслить, рассуждать, делать выводы, анализировать и находить закономерности.
Неоценимая помощь решебника
Алгебра – это один из сложных предметов. Многие ученики не совсем успешно усваивают учебный материал. Допускаемые ошибки, непонимание, пробелы в знаниях, все это негативно отражается на оценках и успеваемости. Хорошим помощником в такой ситуации станет «ГДЗ по Алгебре 8 класс Учебник Макарычев, Миндюк, Нешков (Просвещение)». Сборник содержит правильные и подробно расписанные онлайн-ответы. Они представлены абсолютно ко всем номерам упражнений учебника. С их помощью ученик сможет не только проверить правильное выполнение домашней работы, но и:
- понять ход решения задач и уравнений;
- разобраться со сложной темой и понять суть вопроса;
- сэкономить своё время и силы на поиск необходимой информации;
- заранее подготовиться к предстоящему уроку.

Решебник даст возможность подтянуть знания и оценки в самые кратчайшие сроки. Регулярное использование ГДЗ только положительным образом отразится на успеваемости, к тому же школьник всегда будет подготовлен к любой самостоятельной работе.
Краткая характеристика ученика
Хорошим пособием для получения качественных знаний по предмету является учебник по алгебре за 8 класс авторы Макарычев, Миндюк. Материал пособия расписан понятным и доступным языком, даны подробные инструкции с примерами к особо сложным заданиям. Определения и формулы выделены отдельным шрифтом, а наличие дополнительной информации способствует лучшему усвоению дисциплины.
Задания из учебника
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897898899900901902903904905906907908909910911912913914915916917918919920921922923924925926927928929930931932933934935936937938939940941942943944945946947948949950951952953954955956957958959960961962963964965966967968969970971972973974975976977978979980981982983984985986987988989990991992993994995996997998999100010011002100310041005100610071008100910101011101210131014101510161017101810191020102110221023102410251026102710281029103010311032103310341035103610371038103910401041104210431044104510461047104810491050105110521053105410551056105710581059106010611062106310641065106610671068106910701071107210731074107510761077107810791080108110821083108410851086108710881089109010911092109310941095109610971098109911001101110211031104110511061107110811091110111111121113111411151116111711181119112011211122112311241125112611271128112911301131113211331134113511361137113811391140114111421143114411451146114711481149115011511152Контрольные вопросы и задания
§1§2§3§4§5§6§7§8§9§10§11§12§13Похожие ГДЗ Алгебра 8 класс
Алгебра 8 класс
Дидактические материалы
Жохов, Макарычев, Миндюк
«Просвещение»
Алгебра 8 класс
УМК
Самостоятельные и контрольные работы
Глазков, Гаиашвили
«Экзамен»
Алгебра 8 класс
УМК
Рабочая тетрадь
Ерина
«Экзамен»
Алгебра 8 класс
Учебник (углубленный уровень)
Макарычев, Миндюк, Нешков
«Просвещение»
Задания из учебника: 1
Видеорешение
youtube.com/embed/FsYcPHFEEoQ» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>ГДЗ решебник Алгебра за 8 класс Арефьева, Пирютко (Учебник) «Народная асвета»
Алгебра 8 классУчебникАрефьева, Пирютко«Народная асвета»
Что изучает предмет
Осваивая алгебраическую науку ученик научиться:
- Точно и грамотно излагать свои мысли.
- Обосновывать свои суждения и доказывать утверждения.
- Пользоваться формулами и уметь их применять при решении задач.
- Решать неравенства и уравнения.
Учебник по алгебре за 8 класс авторы Арефьева, Пирютко станет прекрасным пособием для получения этих знаний и умений по предмету. Здесь ученик познакомится с квадратными корнями, уравнениями, неравенствами, а также с квадратичными функциями. Огромное количество заданий, которые представлены в пособии, станут отличной тренировочной базой для закрепления пройдённого материала. Издание полностью соответствует ФГОС и рекомендовано для общеобразовательных школ.
Издание полностью соответствует ФГОС и рекомендовано для общеобразовательных школ.
Чем полезен решебник
Очень часто восьмиклассник из-за сложности современной учебной программы испытывает настоящие трудности в понимании материала. Поможет с этим справиться ГДЗ «Алгебра 8 класс Учебник Арефьева, Пирютко Народная Асвета». Правильные и подробно расписанные онлайн-ответы имеются к каждому номеру упражнений учебного пособия. С их помощью ученик сможет проверить правильное выполнение домашней работы, качественно подготовиться к проверке знаний на уроке, при этом экономя своё время и силы. Систематическое применение решебника положительным образом скажется на знаниях, оценках и успеваемости.
Глава1. Задания
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402Глава1.
 Я проверяю свои знания12345678910
Я проверяю свои знания12345678910Глава1. Практическая математика
123Глава1. Исследовательское заданиеГлава1. Готовимся к олимпиаде
12Глава 2. Задания
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244Глава 2. Я проверяю свои знания
12345678910Глава 2. Практическая математика
12345Глава 2. Исследовательское заданиеГлава 2. Готовимся к олимпиаде
123Глава 3. Задания
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237Глава 3.
 Я проверяю свои знания12345678910
Я проверяю свои знания12345678910Глава 3. Практическая математика
1234Глава 3. Исследовательское задание
12Глава 3. Готовимся к олимпиаде
12Глава 4. Задания
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116Глава 4. Я проверяю свои знания
12345678910Глава 4. Практическая математика
12Глава 4. Исследовательское заданиеГлава 4. Готовимся к олимпиаде
12Повторение
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112Вопросы к параграфу
1234567891011121314151617181920Глава1. Задания: 1
◄ Предыдущий
Следующий ►
Условие
Решение
◄ Предыдущий
Следующий ►
ГДЗ по алгебре для 8 класса от Спиши фан
- org/Book»>
Рабочая Тетрадь по алгебре 8 класс Муравин Г.К.
Авторы: Муравин Г.К., Муравина О.В.
Решебник по алгебре 8 класс Г.К. Муравин
Авторы: Г.К. Муравин, К.С. Муравин, О.В. Муравина
Рабочая Тетрадь по алгебре 8 класс Минаева С.С.
Авторы: Минаева С.С., Рослова Л.О.
Решебник по алгебре 8 класс Ш.А. Алимов
Авторы: Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров
- org/Book»>
Решебник по алгебре 8 класс Ю.Н. Макарычев, Углубленный уровень
Авторы: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов
Контрольные Работы по алгебре 8 класс Мерзляк А.Г.
Авторы: Мерзляк А.Г., Полонский В.Б, Прокопенко Н.С., Якир М.С.
Рабочая Тетрадь по алгебре 8 класс Колягин Ю. М.
Авторы: Колягин Ю. М., Ткачева М.
 В., Федорова Н.Е.
В., Федорова Н.Е.
Сборник Задач по алгебре 8 класс Кузнецова Е.П.
Авторы: Кузнецова Е.П., Муравьева Г.Л., Шнеперман Л.Б.
Решебник по алгебре 8 класс Г.В. Дорофеев
Авторы: Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова
Решебник по алгебре 8 класс Мерзляк А.Г.
Авторы: Мерзляк А.Г., Полонский В.Б., Якир М.С.
Задачник по алгебре 8 класс Мордкович А.Г., Базовый уровень
Авторы: Мордкович А.Г., Александрова Л.А., Тульчинская Е.Е., Мишустина Т.Н.
org/Book»>
Решебник по алгебре 8 класс А.Г. Мерзляк
Авторы: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир
Решебник по алгебре 8 класс Біляніна О.Я.
Авторы: Біляніна О.Я., Кінащук Н.Л., Черевко І.М.
-
Решебник по алгебре 8 класс Истер О.С.
Автор: Истер О.С.
Решебник по алгебре 8 класс Е.П. Кузнецова
Авторы: Е.П. Кузнецова, Г.Л. Муравьева, Л.Б. Шнеперман, Б.Ю. Ящин
org/Book»>
Решебник по алгебре 8 класс С.М. Никольский
Авторы: С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин
Решебник по алгебре 8 класс Бевз Г.П.
Авторы: Бевз Г.П., Бевз В.Г.
Сборник Задач по алгебре 8 класс А.Г. Мерзляк
Авторы: А.Г. Мерзляк, В.Б. Полонський, Ю.М. Рабінович, М.С. Якір
Решебник по алгебре 8 класс Ю.Н. Макарычев
Авторы: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова
org/Book»>
Дидактические Материалы по алгебре 8 класс Жохов В.И.
Авторы: Жохов В.И., Макарычев Ю.Н., Миндюк Н.Г.
Самостоятельные И Контрольные Работы по алгебре 8 класс А.П. Ершова
Авторы: А.П. Ершова, В.В. Голобородько, А.С. Ершова
Сборник Задач по алгебре 8 класс Галицкий М.Л.
Авторы: Галицкий М.Л., Гольдман А.М., Звавич Л.И.
Дидактические Материалы по алгебре 8 класс Мерзляк А.Г.
Авторы: Мерзляк А.Г., Полонский В.Б., Рабинович М.

Задачник по алгебре 8 класс А.Г. Мордкович, Углубленный уровень
Авторы: А.Г. Мордкович, Л.И. Звавич, А.Р. Рязановский, Л.А. Александрова
Решебник по алгебре 8 класс Мерзляк А.Г., Углубленный уровень
Авторы: Мерзляк А.Г., Поляков В.М.
Решебник по алгебре 8 класс Петерсон Л.Г.
Авторы: Петерсон Л.Г., Агаханов Н.Х., Петрович А.Ю.
org/Book»>Дидактические Материалы по алгебре 8 класс Попов М.А.
Автор: Попов М.А.
Контрольные Работы по алгебре 8 класс Мордкович А.Г., Углубленный уровень
Автор: Мордкович А.Г.
Дидактические Материалы по алгебре 8 класс Звавич Л.И.
Авторы: Звавич Л.И., Дьяконова Н.В.
Дидактические Материалы по алгебре 8 класс Ткачева М.В.
Авторы: Ткачева М.В., Федорова Н.Е., Шабунин М.И.
org/Book»>Контрольно-Измерительные Материалы (Ким) по алгебре 8 класс Черноруцкий В.В.
Автор: Черноруцкий В.В.
Решебник по алгебре 8 класс Колягин Ю.М.
Авторы: Колягин Ю.М., Ткачева М.В., Федорова Н.Е.
Контрольные Работы по алгебре 8 класс Кузнецова Л.В.
Авторы: Кузнецова Л.В., Минаева С.С., Рослова Л.О.
Контрольные Работы по алгебре 8 класс Александрова Л.А., Базовый уровень
Автор: Александрова Л.А.
org/Book»>Самостоятельные Работы по алгебре 8 класс Александрова Л.А., Углубленный уровень
Автор: Александрова Л.А.
Самостоятельные Работы по алгебре 8 класс Александрова Л.А., Базовый уровень
Автор: Александрова Л.А.
Решебник по алгебре 8 класс Арефьева И.Г.
Авторы: Арефьева И.Г., Пирютко О.Н.
Тематические Тесты по алгебре 8 класс Чулков П.В.
Авторы: Чулков П.В., Струков Т.С.
org/Book»>Самостоятельные И Контрольные Работы по алгебре 8 класс Мерзляк А.Г., Углубленный уровень
Авторы: Мерзляк А.Г., Полонский В.В., Рабинович Е.М.
Дидактические Материалы по алгебре 8 класс Потапов М.К.
Автор: Потапов М.К.
Тематические Тесты по алгебре 8 класс Дудницын Ю.П.
Авторы: Дудницын Ю.П., Кронгауз В.Л.
Дидактические Материалы по алгебре 8 класс Евстафьева Л.П.
Авторы: Евстафьева Л.П., Карп А.П.
org/Book»>Тесты по алгебре 8 класс Мордкович А.Г., Базовый уровень
Авторы: Мордкович А.Г., Тульчинская Е.Е.
Тематические Тесты по алгебре 8 класс Кузнецова Л.В.
Авторы: Кузнецова Л.В., Минаева С.С., Рослова Л.О.
Тематические Тесты по алгебре 8 класс Ткачева М.В.
Автор: Ткачева М.В.
Рабочая Тетрадь по алгебре 8 класс Миндюк Н.Г.
Авторы: Миндюк Н.Г., Шлыкова И.С.
org/Book»>Рабочая Тетрадь по алгебре 8 класс Зубарева И.И.
Авторы: Зубарева И.И., Мильштейн М.С.
Рабочая Тетрадь по алгебре 8 класс Мерзляк А.Г.
Авторы: Мерзляк А.Г., Полонский В.Б., Якир М.С.
Решебник по алгебре 8 класс Тарасенкова Н.А.
Авторы: Тарасенкова Н.А., Богатырева И.М., Коломиец О.М., Сердюк З.О.
Решебник по алгебре 8 класс Кравчук В.Р.
Авторы: Кравчук В.Р., Пидручна М.В., Янченко Г. М.
org/Book»>Дидактические Материалы по алгебре 8 класс Феоктистов И.Е., Углубленный уровень
Автор: Феоктистов И.Е.
Тестовый Контроль Знаний по алгебре 8 класс Гальперина А.Р.
Автор: Гальперина А.Р.
Решебник по алгебре 8 класс Бунимович Е.А.
Авторы: Бунимович Е.А., Кузнецова Л.В., Минаева С.С., Рослова Л.О.
Решебник по алгебре 8 класс Абылкасымова А.Е.
Авторы: Абылкасымова А.Е., Кучер Т.П., Корчевский В.Е. ., Жумагулова З.А.
org/Book»>Решебник по алгебре 8 класс Мордкович А.Г.
Авторы: Мордкович А.Г., Семенов П.В., Александрова Л.А., Мардахаева Е.Л.
Решебник по алгебре 8 класс Шыныбеков А.Н.
Авторы: Шыныбеков А.Н., Шыныбеков Д.А., Жумабаев Р.Н.
Рабочая Тетрадь по алгебре 8 класс М.К. Потапов
Авторы: М.К. Потапов, А.В. Шевкин
Контрольные Работы по алгебре 8 класс Шуркова М.В.
Автор: Шуркова М.В.
org/Book»>Рабочая Тетрадь по алгебре 8 класс Шуркова М.В.
Автор: Шуркова М.В.
Задачник-Тренажёр по алгебре 8 класс Е.А. Бунимович
Авторы: Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова
Тетрадь Контрольных Тестовых Работ по алгебре 8 класс В.И. Стокоз
Автор: В.И. Стокоз
Тесты по алгебре 8 класс С.Г. Журавлев
Авторы: С.Г. Журавлев, В.В. Ермаков, Ю.В. Перепелкина, В.А. Свентковский
org/Book»>Тесты по алгебре 8 класс Ю.А. Глазков
Авторы: Ю.А. Глазков, М.Я. Гаиашвили
Тесты по алгебре 8 класс Е.М. Ключникова
Авторы: Е.М. Ключникова, И.В. Комиссарова
Контрольные Работы по алгебре 8 класс Ю.П. Дудницын
Авторы: Ю.П. Дудницын, B.Л. Кронгауз
Рабочая Тетрадь по алгебре 8 класс Т.М. Ерина
Автор: Т.М. Ерина
org/Book»>Решебник по алгебре 8 класс Солтан Г.Н.
Авторы: Солтан Г.Н., Солтан А.Е., Жумадилова А.Ж.
Практикум по алгебре 8 класс Левитас Г.Г., Базовый уровень
Автор: Левитас Г.Г.
Рабочая Тетрадь по алгебре 8 класс Журавлев С.Г.
Авторы: Журавлев С.Г., Перепелкина Ю.В.
Контрольные И Самостоятельные Работы по алгебре 8 класс Попов М.А.
Автор: Попов М.А.
org/Book»>Рабочая Тетрадь по алгебре 8 класс Ключникова Е.М.
Авторы: Ключникова Е.М., Комиссарова И.В.
Дидактические Материалы по алгебре 8 класс Зив Б.Г.
Авторы: Зив Б.Г., Гольдич В.А.
Контрольно-Измерительные Материалы (Ким) по алгебре 8 класс Ю. А. Глазков
Авторы: Ю. А. Глазков, М. Я. Гаиашвили, В. И. Ахременкова
Самостоятельные И Контрольные Работы по алгебре 8 класс Глазков Ю.А.
Авторы: Глазков Ю.А., Гаиашвили М.Я.
org/Book»>Математические Диктанты, Контрольные Работы (Методическое Пособие) по алгебре 8 класс Буцко Е.В.
Авторы: Буцко Е.В., Мерзляк А.Г., Полонский В.Б., Якир М.С.
Контрольные Работы (Методическое Пособие) по алгебре 8 класс Буцко Е.В., Углубленный уровень
Авторы: Буцко Е.В., Мерзляк А.Г., Полонский В.Б., Якир М.С.
Поурочные Разработки по алгебре 8 класс Рурукин А.Н.
Автор: Рурукин А.Н.
Тематические Проверочные Работы по алгебре 8 класс Александрова Л.
 А.
А.Автор: Александрова Л.А.
Самостоятельные И Контрольные Работы по алгебре 8 класс Петерсон Л.Г.
Авторы: Петерсон Л.Г., Баханова О.В.
Если $\operatorname{dim} G(0, T) = n$, то 8.26 показывает, что $0$ является единственным собственным значением $T$. Если $\operatorname{dim} G(0, T) = n – 1$, остается место только для еще одного собственного значения с кратностью $1$.
5. Решение. Каждый собственный вектор также является обобщенным собственным вектором, так что в прямом направлении мы можем привести рассуждения, подобные аргументам в упражнении 3, где размерности подходят только в том случае, если каждое собственное пространство равно соответствующему ему обобщенному (поскольку первое подмножество последнего). Другое направление очевидно с 8.23. 9{n-2} = \operatorname{диапазон} T$. Теперь 8.5 завершает доказательство.
Другое направление очевидно с 8.23. 9{n-2} = \operatorname{диапазон} T$. Теперь 8.5 завершает доказательство.
9. Решение: Имейте в виду, что когда мы упоминаем здесь размер матрицы размером $n$ на $n$, мы имеем в виду $n$, а не $n$, умноженное на $n$.
Пусть $V$ — векторное пространство, размерность которого равна размеру $A$ (или $B$, поскольку они одинаковы). Выбрать базис $V$ и определить $S, T \in \mathcal{L}(V)$ так, что $\mathcal{M}(S) = A$ и $\mathcal{M}(T) = B $. Тогда $\mathcal{M}(ST) = AB$.
Пусть $d_j$ равно размеру $A_j$ (или $B_j$, потому что они одинаковые). Рассмотрим список, состоящий из первых $d_1$ векторов в выбранном базисе. $A$ и $B$ показывают, что оболочки этих векторов инвариантны относительно $S$ и $T$.
Аналогично, длина следующих $d_2$ векторов после этого списка также инвариантна относительно $T$. Продолжая в том же духе, мы видим, что существует $m$ различных списков последовательных векторов без пересечений в выбранном базисе, промежутки которых инвариантны относительно $S$ и $T$.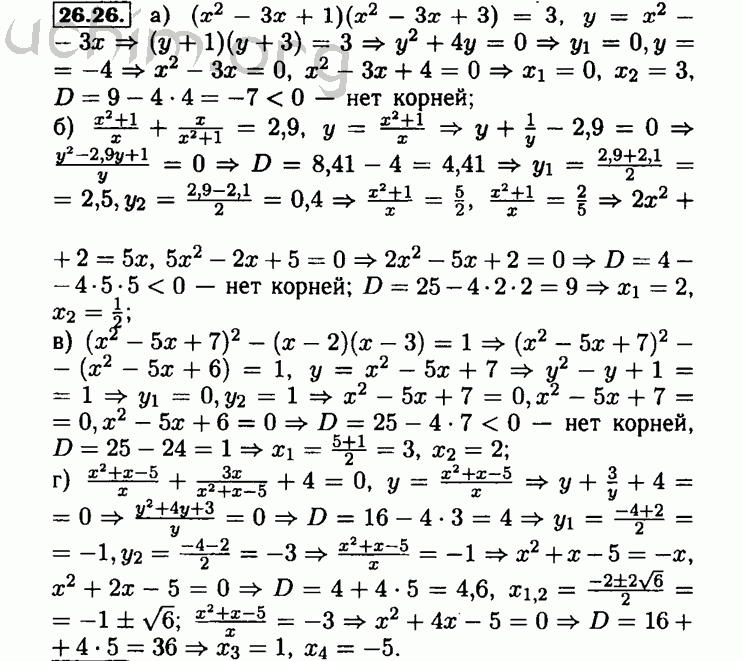
Пусть $U_1, \dots, U_m$ обозначают такие промежутки. Ясно, что $\mathcal{M}(S|_{U_j}) = A_j$ и $\mathcal{M}(T|_{U_j}) = B_j$ для каждого $j$. Следовательно, $\mathcal{M}(S|_{U_j}T|_{U_j}) = A_jB_j$, поэтому легко видеть, что $\mathcal{M}(ST)$ (равное $AB$) имеет желаемая форма.
10. Решение: Пусть $v_1, \dots, v_n$ обозначают базис $V$, состоящий из обобщенных собственных векторов $T$ (существующий по 8.23). Определите $\langle \cdot, \cdot \rangle: V \times V \to \mathbb{C}$ по
$$ \langle a_1 v_1 + \dots + a_n v_n, b_1 v_1 + \dots + b_n v_n \rangle = a_1\overline{b_1} + \dots + a_n\overline{b_n}, $$, где $a$ и $b$ — комплексные числа. Вы можете проверить, что $\langle \cdot, \cdot \rangle$ — правильно определенный скалярный продукт на $V$. Таким образом, $v_1, \dots, v_n$ — ортонормированный базис в $V$. Более того, обобщенные собственные пространства $T$ ортогональны друг другу. Отсюда следует, что если $v \in G(\beta, T)$, то
$$ P_{G(\alpha, T)} v = \begin{cases} v, \text{ if } \alpha = \beta\\ 0, \text{ if } \alpha \neq \beta \end{ case} \tag{$*$} $$, где $P_{G(\alpha, T)}$ — ортогональная проекция $V$ на $G(\alpha, T)$.
Пусть $\lambda_1, \dots, \lambda_m$ обозначают различные собственные значения $T$. Имеем
$$ T = T|_{G(\lambda_1, T)}P_{G(\lambda_1, T)} + \dots + T|_{G(\lambda_m, T)}P_{G(\ лямбда_м, Т)}. $$ Для каждого $j = 1, \dots, m$ можно написать $T|_{G(\lambda_j, T)} = \lambda_j I + N_j$, где $N_j$ — нильпотентный оператор, при котором $G (\lambda_j, T)$ инвариантно (см. 8.21 (c)). Поэтому
$$ \begin{align} T &= (\lambda_1 I + N_1)P_{G(\lambda_1, T)} + \dots + (\lambda_m I + N_m)P_{G(\lambda_m, T)}\ \ &= \underbrace{\lambda_1 P_{G(\lambda_1, T)} + \dots + \lambda_m P_{G(\lambda_m, T)}}_\text{(4)} + \underbrace{N_1P_{G (\lambda_1, T)} + \dots + N_mP_{G(\lambda_m, T)}}_\text{(5)}. \end{aligned} $$ Исправьте $k \in \{1, \dots, n\}$. Тогда $v_k \in G(\lambda_j, T)$ для некоторого $j \in \{1, \dots m\}$. $(*)$ показывает, что $(4)$ отображает $v_k$ в $\lambda_j v_k$. Следовательно, $v_1, \dots, v_n$ — базис собственных векторов $(4)$, а значит, $(4)$ диагонализируем. $(*)$ также показывает, что $(5)$ отображает $v_k$ в $N_j v_k$. 2(v_j – u)$ в промежутке первых $j – 3$ векторов базиса, затем в диапазоне первых $n – 4$, и так до тех пор, пока он не окажется в диапазоне пустого списка, то есть $\{0\}$. Это означает, что $v_j – u \in G(\lambda, T)$ для некоторого $u \in \operatorname{span}(v_1, \dots, v_{j-1})$.
2(v_j – u)$ в промежутке первых $j – 3$ векторов базиса, затем в диапазоне первых $n – 4$, и так до тех пор, пока он не окажется в диапазоне пустого списка, то есть $\{0\}$. Это означает, что $v_j – u \in G(\lambda, T)$ для некоторого $u \in \operatorname{span}(v_1, \dots, v_{j-1})$.
Пусть $\nu_1, \dots, \nu_d$ обозначают векторы выбранного базиса $V$, соответствующие столбцам $\mathcal{M}(T)$, в которых фигурирует $\lambda$, и в порядок их появления на базе. Мы можем повторить предыдущий процесс и найти $u_1, \dots, u_d$ таких
$$ \nu_1 – u_1, \dots, \nu_d – u_d \in G(\lambda, T), \tag{6} $$, где каждый $u_k$ находится в промежутке базисных векторов, предшествующих $\nu_k$. Мы утверждаем, что этот список линейно независим. Чтобы увидеть это, зафиксируйте $k \in \{1, \dots, d\}$. Предположим, что $\nu_k$ — это $j$-й базисный вектор, т. е. $\nu_k = v_j$. Это означает, что
$$ \operatorname{span}(\nu_1 – u_1, \dots, \nu_{k-1} – u_{k-1}) \subset \operatorname{span}(v_1, \dots, v_{j-1 }). 4)$ на 92(z-3)$.
4)$ на 92(z-3)$.
7. Решение: Согласно упражнению 4 в разделе 5B мы имеем
$$ V = \operatorname{null} P \oplus \operatorname{range} P. \tag{1} $$ Легко проверить, что если $v \in \operatorname{range} P$, тогда $Pv = v$. Таким образом,
$$ \operatorname{null} P \subset G(0, T) \text{ и } \operatorname{range} P \subset G(1, T). Тогда из $$ $(1)$ и 8.26 следует, что эти включения на самом деле являются равенствами, что и дает желаемый результат.
8. Решение: Пусть $p$ обозначает минимальный многочлен от $T$. У нас есть 9{-1}$ дает желаемый результат (обратите внимание, что $a_0$ отличен от нуля в упражнении 8).
12. Решение: Предположим, что $V$ имеет базис, состоящий из собственных векторов $T$. Пусть $\lambda_1, \dots, \lambda_m$ обозначают различные собственные значения $T$. Тогда легко увидеть, что
$$ (T – \lambda_1 I) \cdots (T – \lambda_m I) = 0 $$, применяя левую часть уравнения к каждому из базисных векторов, поскольку скобки коммутируют . По 8.46 $(z – \lambda_1) \cdots (z – \lambda_m)$ является полиномом, кратным минимальному многочлену от $T$. Этот многочлен не имеет повторяющихся нулей. Следовательно, минимальный многочлен не имеет повторяющихся нулей.
По 8.46 $(z – \lambda_1) \cdots (z – \lambda_m)$ является полиномом, кратным минимальному многочлену от $T$. Этот многочлен не имеет повторяющихся нулей. Следовательно, минимальный многочлен не имеет повторяющихся нулей.
Обратно, предположим, что минимальный многочлен от $T$, назовем его $p$, не имеет повторяющихся нулей. По 8.23 $T$ имеет базис обобщенных собственных векторов. Пусть $v$ — один вектор в этом базисе. Тогда $v \in G(\lambda, T)$ для некоторого собственного значения $\lambda$ оператора $T$. По 8.49 $\lambda$ равно нулю $p$. Таким образом, мы можем написать $p(z) = (z – \lambda)q(z)$ для некоторого многочлена $q$ с $q(\lambda) \neq 0$. Имеем
$$ 0 = p(T)v = q(T)(T – \lambda)v. $$ Обратите внимание, что $(T – \alpha)\hat{v} \neq 0$ для всех ненулевых $\hat{v} \in G(\lambda, T)$ и всех $\alpha \in \mathbb{F }$ с $\alpha \neq \lambda$. Отсюда следует, что $(T – \lambda)v = 0$, так как $G(\lambda, T)$ инвариантен относительно любого многочлена от $T$ и, значит, из $(T-\lambda I)v \neq 0$ следует $q(T)(T-\lambda I) \neq 0$ (поскольку мы можем факторизовать $q(T)$ и $\lambda$ не является нулем $q$). Следовательно, $v$ является собственным вектором $T$, а базис $V$, состоящий из обобщенных собственных векторов $T$, на самом деле состоит из собственных векторов $T$.
Следовательно, $v$ является собственным вектором $T$, а базис $V$, состоящий из обобщенных собственных векторов $T$, на самом деле состоит из собственных векторов $T$.
13. Решение: Если $\mathbb{F} = \mathbb{C}$, это непосредственно следует из предыдущего упражнения из комплексной спектральной теоремы (7.24).
14. Решение. Как видно из решения упражнения 10, постоянный член характеристического полинома, равный $p(0)$, равен $1$ или $-1$, умноженному на произведение собственных значений из $S$ возведены в их соответствующие кратности. Все собственные значения $S$ имеют абсолютное значение $1$ (см. 7.43 (b)), следовательно, $|p(0)| = 1$. 92$ с $n$.
(b) По существу то же самое, что и доказательство 8.46.
Пусть $q$ обозначает минимальный многочлен от $T$. Тогда также имеем $q(T)v = 0$. Кроме того, $\deg p \ge \deg q$. По алгоритму деления для полиномов (4.8) существуют $s, r \in \mathbb{P}(\mathbb{F})$ такие, что $$ p = sq + r $$ и $\deg r < \deg д$. Отсюда следует, что
Отсюда следует, что
$$ 0 = p(T)v = s(T)q(T)v + r(T)v = r(T)v. $$ По тем же рассуждениям, что и при доказательстве, следует, что $r = 0$.
16. Решение: у нас есть 9*) = 0$, присоединение каждой стороны, как мы сделали выше, показывает, что $\overline{p}(T) = 0$, где $\overline{p}$ равно $p$ с сопряженными коэффициентами. Но $\deg \overline{p} < m$, что является противоречием, поскольку минимальный многочлен от $T$ имеет степень $m$.
17. Решение: Характеристический многочлен $T$, назовем его $q$, имеет степень $\dim V$ (см. 8.36) и является полиномиальным кратным минимального многочлена $T$ (см. 8.48), назовите это $p$. Так как $q$ кратно $q$, то $q = ps$ для некоторого многочлена $s$, а так как $\deg q = \deg p$, то $\deg s = 0$. Следовательно, $s$ — константа. Поскольку они оба моничны, $s = 1$, и они должны быть равны.
19. Решение: Это следует непосредственно из упражнения 11 в разделе 8B.
20. Решение: Это немного очевидно, если вы понимаете, что
$$ \dim G(\lambda, T) = \dim G(\lambda, T|_{V_1}) + \dots + G(\ lambda, T|_{V_m}) \tag{2} $$ для каждого $\lambda \in \mathbb{F}$. Это верно, потому что подпространства в правой части уравнения содержатся в $G(\lambda, T)$ и потому, что когда мы записываем каждое $V_j$ как прямую сумму обобщенных собственных пространств $T|_{V_j}$ в уравнении
Это верно, потому что подпространства в правой части уравнения содержатся в $G(\lambda, T)$ и потому, что когда мы записываем каждое $V_j$ как прямую сумму обобщенных собственных пространств $T|_{V_j}$ в уравнении
$$ V = V_1 \oplus \dots \oplus V_m $$ размеры подходят только при условии, что $(2)$ истинно.
Как определить, что уравнение не имеет решения
Все ресурсы по алгебре 1
10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept
Алгебра 1 Помощь » Уравнения / Неравенства » Системы уравнений » Линейные/рациональные/переменные уравнения » Как узнать, когда уравнение не имеет решения
Решить рациональное уравнение:
Возможные ответы:
или
Нет решения
Правильный ответ:
Правильный ответ:
. Правильный ответ:
Правильный ответ:
. Объяснение:
При работе с рациональными уравнениями мы должны сначала отметить домен, который состоит из всех действительных чисел, кроме и . То есть это значения , которые сделают уравнение неопределенным. Поскольку наименьший общий знаменатель , и равен , мы можем умножить каждый член на LCD, чтобы исключить знаменатели и сократить уравнение до . Комбинируя подобные термины, мы получаем . Разделив обе части уравнения на константу, получим ответ . Однако это решение НЕ находится в домене. Таким образом, НЕТ РЕШЕНИЯ, потому что это посторонний ответ.
Сообщить об ошибке
Найдите набор решений:
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Ни один из других ответов.
Объяснение:
Используйте метод подстановки, чтобы найти набор решений.
1)
2)
Решите уравнение 2 для y:
Подставить в уравнение 1:
Если уравнение 1 решить для переменной, а затем подставить во второе уравнение, будет получен аналогичный результат. Это потому, что эти два уравнения имеют Нет решения . Измените оба уравнения в форму пересечения наклона и нарисуйте график для визуализации. Эти линии параллельны; они не могут пересекаться.
*Любой метод поиска решения этой системы уравнений приведет к отрицательному ответу.
Сообщить об ошибке
Сколько решений имеет приведенное ниже уравнение?
Возможные ответы:
Infinite
One
Три
No Solutions
Два
Правильный ответ:
No Solutions
8. Объяснение:
Объяснение:
Чтобы узнать, сколько решений имеет уравнение, вам нужно посмотреть на константы и коэффициенты.
Коэффициенты — это числа рядом с переменными.
Константы — это числа без переменных.
Если коэффициенты одинаковы с обеих сторон, то стороны не будут равны, поэтому решений не будет.
Сначала используйте свойство распределения с правой стороны.
Нет решения
Отчет о ошибке
Решение:
Возможные ответы:
Правильный ответ:
.0005 Объяснение: Сначала разложите числитель на множители. Перепишите уравнение. Термины могут быть удалены. Вычесть единицу с обеих сторон. Однако давайте подставим этот ответ обратно в исходное уравнение, чтобы проверить, получим ли мы в качестве ответа. Упростите левую сторону. Левая часть не удовлетворяет уравнению, потому что дробь не делится на ноль. Следовательно, недопустимо. Ответ: Отчет о ошибке Решение для: Возможные ответы: Нет решения
. Правильный ответ:
888
888
888
88
8
Объяснение:Объедините одинаковые члены в каждой части уравнения:
Затем вычтите из обеих частей.
Затем вычтите с обеих сторон.
Это бессмысленно; поэтому решения уравнения нет.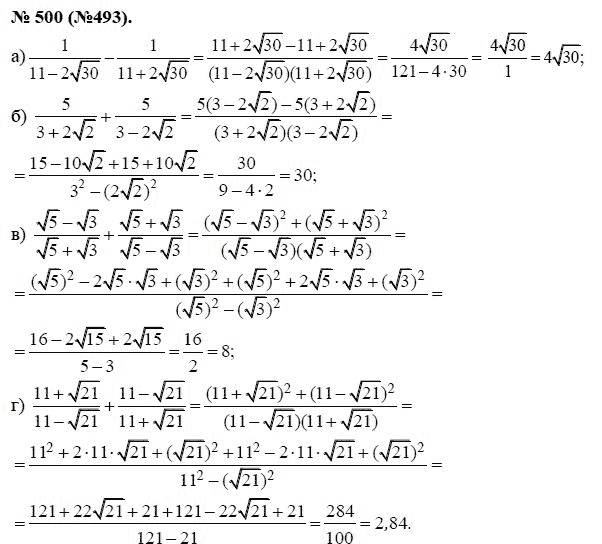
Отчет о ошибке
Решение уравнения:
Возможные ответы:
Нет решения
Правильный ответ:
Правильный ответ:
. Правильный ответ:
. Правильный ответ:
. Объяснение:
Обратите внимание, что конечное значение отрицательное. Любое отрицательное или положительное значение, находящееся внутри знака абсолютного значения, должно привести к положительному значению.
Если мы разделим уравнение на положительное и отрицательное решения, мы получим:
Решите первое уравнение.
Ответ на вопрос:
Решите второе уравнение.




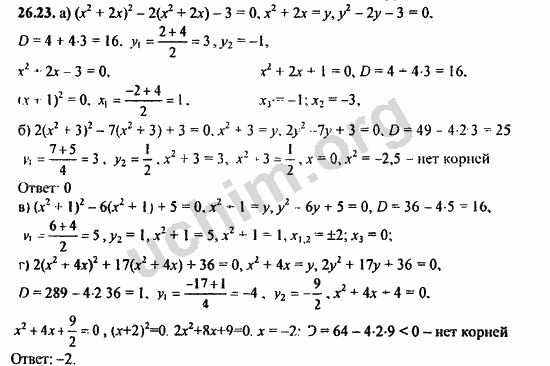 В., Федорова Н.Е.
В., Федорова Н.Е.
 А.
А.