Тесты по Математике для 5 класса
Реши задачу, запиши ответ без единиц измерения.
Математика 5 класс | Автор: Беспаалова Марина Владимировна | ID: 13645 | Дата: 10.8.2021
С помощью теста можно проверить умение суммировать смешанные дроби.
Математика 5 класс | Автор: Набатова Мирослава Дмитриевна | ID: 13644 | Дата: 10.8.2021
Отработка навыков вычислительной деятельности, закрепление знаний по теме «Понятие смешанного числа»
Математика 5 класс | Автор: Набатова Мирослава Дмитриевна | ID: 13643 | Дата: 10.8.2021
Небольшой тест для проверки знаний учеников пятых классов по пройденному материалу
Математика 5 класс | Автор: Илона | ID: 13642 | Дата: 9.8.2021
Тест предназначен для отработки умения округлять десятичные дроби.
Математика 5 класс | Автор: Высокова Нина Фадеевна | ID: 13641 | Дата: 9.
Умножение десятичных дробей
Математика 5 класс | Автор: Мусина Вероника Алексеевна | ID: 13366 | Дата: 27.7.2021
Проверяет вычислительные навыки.
Математика 5 класс | Автор: Набатова Мирослава Дмитриевна | ID: 13363 | Дата: 27.7.2021
Задание на деление десятичных дробей
Математика 5 класс | Автор: Телегина Елена Яковлевна | ID: 13361 | Дата: 27.7.2021
Тест состоит из 20 вопросов. Предназначен для проверки знаний учащихся по теме » Задачи на проценты».
Математика 5 класс | Автор: Таркина Кристина Эдуардовна | ID: 13341 | Дата: 25.7.2021
Проверить навыки сокращения обыкновенных дробей, нахождения НОД двух чисел.
Математика 5 класс | Автор: Набатова Мирослава Дмитриевна | ID: 13364 | Дата: 13.7.2021
Страница 1 из 23
Математика 5 класс темы уроков
По математике в 5 классе темы уроков будут посвящены сложению и вычитанию, умножению, делению натуральных чисел. Далее переходят к изучению дробных чисел с акцентом на десятичных дробях. Рассматривают сложение, умножение, округление, сопоставление, деление, вычитание десятичных дробей.
Далее переходят к изучению дробных чисел с акцентом на десятичных дробях. Рассматривают сложение, умножение, округление, сопоставление, деление, вычитание десятичных дробей.
Кроме того, выделяют время на основы площадей и объёмов, использование инструментов и шкал для измерений веса, расстояний, объёмов. Данный этап имеет огромную ценность для использования математики в повседневной жизни, поэтому подойти к нему надо особенно внимательно.
Натуральные числа
Начнём программу с изучения натуральных чисел. Так будет проще для усвоения последующего материала:
- Позиционная и непозиционная система счисления. Десятеричная, шестнадцатеричная, восьмеричная система счисления.
- Понятие числа и цифры. Происхождение цифр. Узнаем о том, как их записывали разные народы мира.
- Точка, прямая, луч и линия. Этот этап является фундаментом для всей геометрии.
- Отрезок, его сравнение и выяснение длины.
- Различные единицы измерения массы, расстояний, объёмов.

- Плоскость, бесконечность, фигуры, угол, треугольник, ломаная линия.
- Измерительные приборы и шкалы. Часовые, минутные и секундные стрелки.
- Сопоставление натуральных чисел, различные знаки равенства.
Вычитание и сложение натуральных чисел
На последующих двух этапах изучаются основные методы и законы математики, так что к ним следует отнестись внимательно. Важной темой уроков по математике за 5 класс является то, что можно делать с натуральными числами. Берутся за изучение со сложений и вычислений:
Деление и умножение натуральных чисел
Заканчивают изучение умножением и делением:
- Умножение и его характеристики
- Деление, особенности и характеристики
- Деление с остатком и без него
- Математическая запись. Языковая архитектура и математическая лингвистика
- Упрощение выражений – поиск его значения по одной или нескольким переменным
- Последовательность действий при решении уравнений.
 Зачем нужны скобки. Равноправность сложения и вычитания, а также деления и умножения. Прерогатива деления и умножения над такими действиями, как сложение и вычитание
Зачем нужны скобки. Равноправность сложения и вычитания, а также деления и умножения. Прерогатива деления и умножения над такими действиями, как сложение и вычитание - Степень числа. Последовательность математических действий с нею. Квадрат и куб
- Решение уравнений на движение
Объёмы и площади
Эти знания являются фундаментом для моделирования техники, а также других вещей и явлений. Изучают на примере прямоугольников и параллелепипедов:
- Формулы. Определение, теорема, тождество, экспериментальная формула
- Площадь. Единицы измерения. Соотношение квадратных миллиметров, сантиметров, метров
- Нахождение площади прямоугольника
- Квадрат
- Старинные способы измерения площадей
- Грани, углы, плоскости прямоугольного параллелепипеда
- Поиск площади поверхности
- Понятие и нахождение объёма
- Системы измерения объёмов
- Объём куба и прямоугольного параллелепипеда
- Окружность и круг.
 Дуга, радиус, диаметр
Дуга, радиус, диаметр
Дробные числа
Дроби – самая сложная тема в этом году, так что надо её разбирать, не торопясь, и внимательно. В математике за 5 класс в темы уроков входит исследование различных видов дробей:
- Простые дроби и их построение, характеристики
- Зачем требуется дробное обозначение
- Правильные и неправильные дроби
- Сопоставление и определение обыкновенных дробей
- Вычитание и сложение дробей с идентичными и разными знаменателями
- Поиск части и целого
- Неправильные дроби и их классификация
- Смешанные числа
- Арифметические операции со смешанными числами
Десятичные дроби, их вычитание и сложение
Далее надо научиться использовать дроби в математических вычислениях. А сначала – вычитание и сложение:
- Десятичные дроби, определение и характеристики
- Их изображение и прочтение
- Правила сравнения
- Сопоставление на системе координат
- Вычитание и сложение в столбик
- Округление с недостатком и избытком
Десятичные дроби, деление и умножение
Заканчивают исследование десятичных дробей разбором их деления и умножения:
- Деление и умножение на 10, 100, 0,1, 0,01.
 Сдвигание запятой при отсутствии цифр
Сдвигание запятой при отсутствии цифр - Деление и умножение десятичных дробей
- Среднее арифметическое
Инструменты для вычислений и измерений
Эта группа уроков откроет для вас математику как мировую культуру, а также её важность для научно-технического прогресса. Далее проходят различные математические инструменты:
- Полный, развернутый, прямой, острый, тупой угол
- Градусы. Транспортир и его применение. Установление углов
- Биссектриса и медиана
- Проценты. Поиск процента от числа. Умножение и деление на проценты
- Круговые диаграммы
Основы комбинаторики
Последняя тема уроков по математике за 5 класс – комбинаторика. Теоремы сложения и умножения. Применение теорем в реальной жизни. Логика перебора. Парадокс Монти Холла. На этом заканчивается программа.
Заключение
Цель на этом этапе – получить знания для практического применения их в жизни. Данный раздел поможет построить логическое критическое мышление, разовьёт способность мыслить абстрактно.
Основные правила математики с примерами. 5 класс — Сайт учителя математики Косыхиной Н.В.
Основные правила математики с примерами. 5 класс
Содержание
- Натуральные числа
- Сравнение натуральных чисел
- Свойства сложения
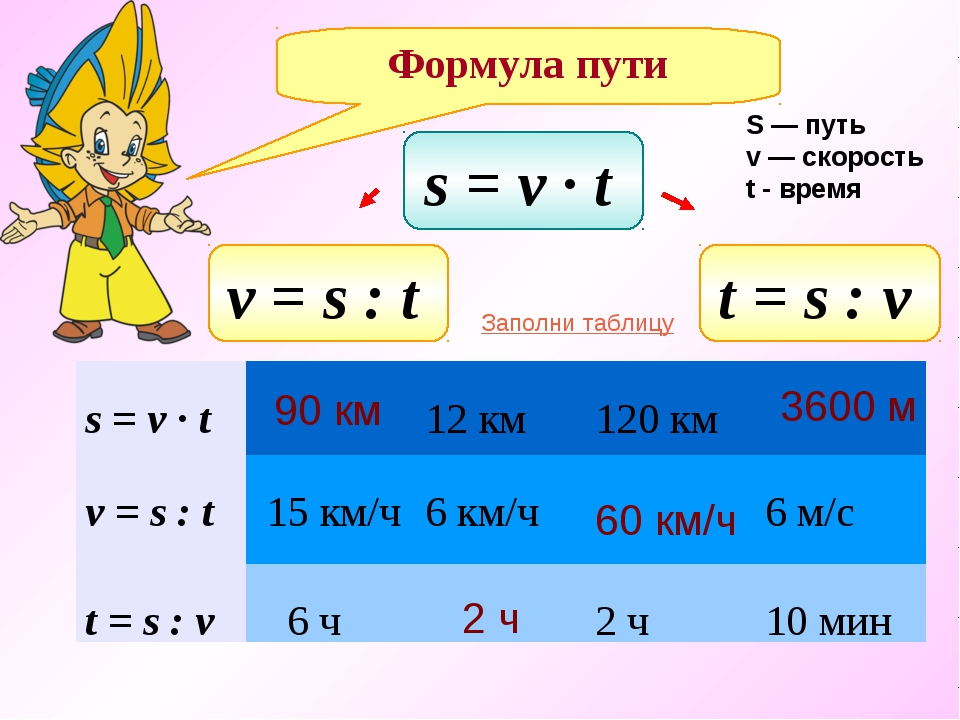
- Формула пути
- Корень уравнения
- Правила решения уравнений
- Отрезок, прямая, луч
- Угол, биссектриса угла
- Углы: развернутый, прямой, острый, тупой
- Многоугольники. Равные фигуры
- Треугольники: остроугольный, прямоугольный, тупоугольный
- Треугольники: равнобедренный, равносторонний, разносторонний
Натуральные числа
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т.
Сравнение натуральных чисел
Число меньше любого натурального числа.
0<1, 0<100
Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.
4352⏟4>999⏟3
Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр
3561>3559
Свойства сложения
Переместительный закон:
15+10=10+15
Сочетательный закон:
(23+15)+25=23+(15+25)
Формула пути
S=V·t,где S — пройденный путь, V — скорость движения, t — время, за которое пройден путь S
Корень уравнения
Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.
2·x+10=16
x = 3 — корень, так как 2·3+10=16
Что значит «Решить уравнение»
Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.
Правила решения уравнений
- Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
20слагаемое+xслагаемое=100суммаx = 100 — 20x = 80
- Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
xуменьшаемое—10вычитаемое=40разностьx = 40 + 10x = 50
- Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
50уменьшаемое—xвычитаемое=40разностьx = 50 — 40x = 10
- Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
xмножитель·7множитель=56произведениеx = 56 : 7x = 8
- Чтобы найти неизвестное делимое, надо делитель умножить на частное.
xделимое:8делитель=9частноеx = 9 · 8x = 72
- Чтобы найти неизвестный делитель, надо делимое разделить на частное.
42делимое:xделитель=7частноеx = 42 : 7x = 6
Отрезок, прямая, луч
Отрезок
Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)
Свойство длины отрезка
Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .
Равные отрезки
Два отрезка называют равными, если они совмещаются при наложении.
Свойство прямой
Через две точки проходит только одна прямая.
Измерить отрезок
Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
Ломаная
Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом
Луч
Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
Угол, биссектриса угла
Угол
Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.
Равные углы
Два угла называют равными, если они совмещаются при наложении.
Свойство величины угла
Если между сторонами угла ∠ провести луч , то градусная мера ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.
Биссектриса угла
Луч, который делит угол на два равных угла, называется биссектрисой угла.
Углы: развернутый, прямой, острый, тупой
Развернутый угол
Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.
Прямой угол
Угол, градусная мера которого равна 90°, называют прямым.
Острый угол
Угол, градусная мера которого меньше 90°, называют острым.
Тупой угол
Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
Многоугольники. Равные фигуры
Равные многоугольники
Два многоугольники называют равными, если они совмещаются при наложении.
Равные фигуры
Две фигуры называют равными, если они совмещаются при наложении.
Треугольники: остроугольный, прямоугольный, тупоугольный
Остроугольный треугольник
Если все углы треугольника острые, то его называют остроугольным треугольником.
Прямоугольный треугольник
Если один из углов треугольника прямой, то его называют прямоугольным треугольником.
Тупоугольный треугольник
Если один из углов треугольника тупой, то его называют тупоугольным треугольником.
Треугольники: равнобедренный, равносторонний, разносторонний
Равнобедренный треугольник
Если две стороны треугольника равны, то его называют равнобедренным треугольником.
Равносторонний треугольник
Если три стороны треугольника равны, то его называют равносторонним треугольником.
Периметр равностороннего треугольника
Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле
Разносторонний треугольник
Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.
Прямоугольник. Квадрат. Периметр
Прямоугольник
Если в четырехугольнике все углы прямые, то его называют прямоугольником.
Свойство прямоугольника
Противоположные стороны прямоугольника равны.
Периметр прямоугольника
Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле
Квадрат
Прямоугольник, у которого все стороны равны, называют квадратом.
Периметр квадрата
Если сторона квадрата равна , то его периметр вычисляют по формуле .
Умножение. Свойства умножения
Умножение
- Если один из двух множителей равен 1, то произведение равно второму множителю.
- Если один из множителей равен нулю, то произведение равно нулю.
- Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Свойства умножения
- Переместительный закон умножения:
- Сочетательный закон умножения:
- Распределительное свойство умножения относительно сложения:
2·(3+10) = 2·3 + 2·103·11 + 3·4 = 3·(11 + 4)
- Распределительное свойство умножения относительно вычитания:
2·(15—7) = 2·15 — 2·73·10 — 3·4 = 3·(10 — 4)
Деление.
 Деление с остатком
Деление с остаткомДеление
Для натуральных чисел равенство является правильным, если является правильным равенство
15 : 5 = 3 -правильное равенство, так как равенство 5 · 3 = 15 верное
В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.
На ноль делить нельзя.
Для любого натурального числа правильными являются равенства:
,
Деление с остатком
, где — делимое, — делитель, — неполное частное, — остаток, .
154делимое=50делитель · 3неполное частное + 4остаток, 4<50
Если остаток равен нулю, то говорят, что число делится нацело на число .
Площадь. Площадь квадрата, прямоугольника
Свойства площади фигуры
Равные фигуры имеют равные площади;
Площадь фигуры равна сумме площадей фигур, из которых она состоит.
Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.
Площадь квадрата
,
где — площадь квадрата, — длина его стороны.
Объем. Объем прямоугольного параллелепипеда, куба
Свойства объема фигуры
Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.
Объем прямоугольного параллелепипеда
- ,
где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;
, где — площадь поверхности прямоугольного параллелепипеда.
- ,
где — площадь основания параллелепипеда, — его высота.
Объем куба
,
где — объем куба, — длина его ребра.
Дроби: правильная, неправильная, сравнение дробей
Правильная дробь
Дробь, числитель которой меньше знаменателя, называют правильной
Неправильная дробь
Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.
Сравнение дробей
- Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.

- Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.
- Все правильные дроби меньше единицы, а неправильные — больше или равны единице.
- Любая неправильная дробь больше любой правильной дроби.
Сложение и вычитание дробей с одинаковыми знаменателями
- Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
- Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Сложение и вычитание смешанных чисел
- Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
- Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

Преобразование неправильной дроби в смешанное число
Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно
- числитель разделить на знаменатель;
- полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.
227= смешанное число? 7322—211 227=317
Преобразование смешанного числа в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь нужно
- целую часть числа умножить на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- эту сумму записать как числитель неправильной дроби;
- в его знаменателе записать знаменатель дробной части смешанного числа.
523= неправильная дробь?523=5*3+23=15+23=173
Десятичные дроби: свойства, сравнение, округление
Свойства десятичной дроби
Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.
Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.
2,23 = 2,230 = 2,230000005,50000=5,50000=5,5
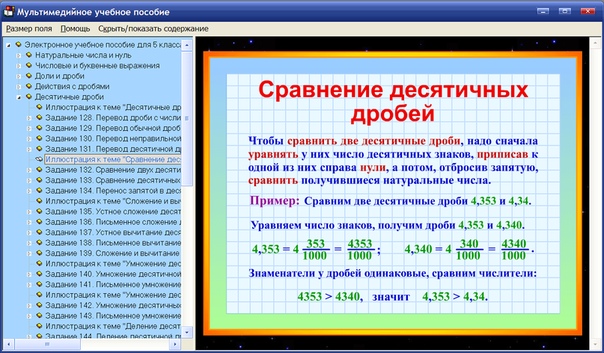
Сравнение десятичных дробей
Из двух десятичных дробей больше та, у которой целая часть больше.
Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо
- с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
- после чего сравнить полученные дроби поразрядно.
Сравнить 5,03 и 5,0375.5,03⏟2=5,0300⏟4 и 5,0375⏟4 ; 5,0300 < 5,0375.
Округление десятичных дробей
Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо
- все следующие за этим разрядом цифры отбросить.
- если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4, то последнюю из цифр, которые оставляют, не меняют;
- если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.

Округлить 5,248 и 3,952:а) до десятых:5,248≈5,2; 3,952≈4,0;б) до сотых:5,248≈5,25;3,952≈3,95.
Десятичные дроби: сложение, вычитание
Сложение десятичных дробей
Чтобы найти сумму двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
- сложить полученные числа так, как складывают натуральные числа;
- поставить в полученной сумме запятую под запятыми.
Сложить 2,5 и 3,623.2,500⏟3 и 3,263⏟3;2,500+3,2635,763
Вычитание десятичных дробей
Чтобы найти разность двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
- выполнить вычитание так, как вычитают натуральные числа;
- поставить в полученной разности запятую под запятыми.
Вычесть 3,27 и 3,009.3,270⏟3 и 3,009⏟3;3,270—3,0090,261
Десятичные дроби: умножение, деление
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
- перемножить их как натуральные числа, не обращая внимания на запятые;
- в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Умножить 1,5 и 2,25.2×2,2511,5+1125225·33,375 —количество цифр после запятой
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.
Умножить 1,235 на 10, 100, 1000.а) на 10:1,235 ×10⏟1=12,35б) на 100:1,235 ×100⏟2 = 123,5в) на 1000:1,235 ×1000⏟3=1235,0 = 1235
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.
Умножить 512,3 на 0,1, 0,01 и 0,001.а) на 0,1:512,3 ×0,1⏟1=51,23б) на 0,01:512,3 ×0,01⏟2=5,123в) на 0,001:512,3 ×0,001⏟3=0,5123
Деление десятичных дробей
Чтобы разделить десятичную дробь на десятичную, надо:
- перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
- выполнить деление на натуральное число.
Разделить 24,2 на 0,02.24,2 : 0,02⏟ 2= 2420,0 : 2 = 2420 : 2 = 1210.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.
Разделить 25,5 на 10, 100, 1000.а) на 10:25,5 : 10⏟1=2,55;б) на 100:25,5 : 100⏟2=0,255;в) на 1000:25,5 : 1000⏟3=0,0255;
Среднее арифметическое
Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.
Найти среднее арифметическое чисел 15, 25 и 20.
15+25+20⏞сумма чисел3⏟количество чисел = 603= 20Примечание:
Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.
Здесь
Vсредняя =Sобщtобщ .1) 200 + 120 = 320(км) -весь путь;
2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;
3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;
4) 4 + 4 = 8(ч) — все время;
5) 320 : 8 = 40(км/ч) — средняя скорость.
Ответ: 40 км/ч.
Процент
Процентом называют сотую часть величины или числа 1%=
Найти 4% от числа 20.20 : 100 = 0,2 (0,2 —это 1% от числа 20);0,2 × 4 =0,8( 0,8—искомое число).Или 4% = 4100 = 0,04;0,04 ×20 = 0,8.
Математика 5 класс Основной блок
Математика 5 класс Основной блок создатель Светлана Урусова1. Натуральные числа
1.1. Натуральные числа и шкалы
1.1.1. Обозначение натуральных чисел
1.1.2. Отрезок. Длина отрезка. Треугольник.
1.1.3. Плоскость. Прямая. Луч.
1.1.4. Шкалы и координаты
1.1.5. Сравнение натуральных чисел
1.1.6. Отрезок. Длина отрезка. Треугольник.
1.2. Сложение и вычитание натуральных чисел
1.2.1. Сложение натуральных чисел и его свойства
1.2.2. Вычитание натуральных чисел и его свойства
1.2.3. Числовые и буквенные выражения
1.2.4. Буквенная запись свойств сложения и вычитания
1.2.5. Уравнение
1.3. Умножение и деление натуральных чисел
1.3.1. Умножение натуральных чисел и его свойства
1.3.2. Деление натуральных чисел и его свойства
1.3.3. Деление с остатком
1.3.4. Упрощение математических выражений с использование правил сложения, вычитания, умножения и деления натуральных чисел
1.3.5. Порядок выполнения действий
1.3.6. Степень числа. Квадрат и куб числа.
1.4. Площади и объемы
1.4.1. Понятие формулы
1.4.2. Отрезок. Длина отрезка. Треугольник.
1.4.3. Площадь. Формула площади прямоугольника.
1.4.4. Единицы измерения площадей.
1.4.5. Прямоугольный параллелипипед
1.4.6. Объемы. Объем прямоугольного параллелепипеда.
2. Дробные числа
2.1. Обыкновенные дроби
2.1.1. Доли. Обыкновенные дроби
2.1.2. Окружность и круг
2.1.3. Сравнение дробей
2.1.4. Правильные и неправильные дроби
2.1.5. Сложение и вычитание дробей с одинаковым знаменателем
2.1.6. Деление и дроби
2.1.7. Смешанные числа
2.1.8. Сложение и вычитание смешанных чисел
2.2. Десятичные дроби
2.2.1. Десятичная запись дробных чисел
2.2.2. Сравнение десятичных дробей
2.2.3. Сложение и вычитание десятичных дробей
2.2.4. Приближенные значения чисел. Округление чисел.
2.2.5. Окружность и круг
2.3. Умножение и деление десятичных дробей
2.3.1. Умножение десятичных дробей на натуральные числа
2.3.2. Деление десятичных дробей на натуральные числа
2.3.3. Умножение десятичных дробей
2.3.4. Деление на десятичную дробь
2.3.5. Среднее арифметическое
2.4. Инструменты для вычислений и измерений
2.4.1. Микрокалькулятор
2.4.2. Проценты
2.4.3. Угол. Прямой и развернутый угол. Чертёжный треугольник.
Как решить проблемы с математикой
«Нужно преподавать математику как особую теорию красоты»
Psychologies: Почему у многих детей математика вызывает скуку, страх, отвращение?
Александр Лобок, психолог: Это означает только одно: она принципиально неправильно для этого ребенка преподается в школе. Множество детей переживают унижение математикой. Долгие школьные годы они испытывают чувство своей непроходимой математической тупости, а учитель поддерживает это чувство либо в щадящей форме («Что поделаешь, у него гуманитарные мозги!»), либо в циничной и злобной («Ну ты тупой!»).
Многие учителя убеждены, что математические способности — «от бога» и что причина «невменяемости» миллионов детей, не понимающих математику, в их природной ограниченности. Тогда как задача школы — помочь каждому ребенку почувствовать математический азарт и желание заниматься. Если этот интерес и любовь возникнут, ребенок будет гораздо более успешен — в том числе и в традиционном математическом обучении.
Чаще всего проблемы возникают у детей гуманитарного склада. Как в них пробудить этот азарт?
Для детей-гуманитариев важно почувствовать смысл. А традиционная школьная программа довольно часто предлагает математику как набор абстрактной «цифири», даже не пытаясь объяснить ученикам, что математика — это прежде всего философия, позволяющая совершенно по-новому взглянуть на окружающий мир. Если же детям открыть дверцу в смыслы того, чем занимается математика, — у них появляется азарт и интерес.
Например, когда объясняешь и показываешь, что математика — это такое особое волшебство, которое позволяет обсчитать весь мир. И значит, найти что-то фундаментально общее во всем мире. Например, все можно взвесить, измерить — на этом основании сравнить мальчика Петю, его любимую кошку и папин автомобиль. И вообще, оказывается, сравнить можно все во Вселенной!
А еще дети не подозревают, что математика наполнена внутренней красотой, — им тоже об этом никто не рассказывает. А ведь любая последовательность орнаментов или игра архитектурных форм — это математика. И если детям преподавать математику как особую теорию красоты, это очень может их зацепить.
Значит ли это, что освоить школьный курс математики по силам каждому ребенку?
В том виде, в каком он сегодня существует, — разумеется, нет. Да это и не нужно. А вот постигнуть эстетические и философские основания математики — это по силам и нужно всем. Благодаря этому интерес к математике — причем к самой традиционной — возникает у каждого ребенка. В том числе у тех, кто всю жизнь этот предмет ненавидел и считал себя неспособным.
Но что же делать родителям, чьи дети учатся в традиционной школе и не справляются с математикой?
Это всегда глубоко индивидуальная проблема. Но общая рекомендация может быть такой: надо найти такого педагога, который по-настоящему увлечен и математикой, и детьми.
Стало известно, когда начнутся ВПР в 2022 году
https://sn.ria.ru/20210817/rosobrnadzor-1746108056.html
Стало известно, когда начнутся ВПР в 2022 году
Стало известно, когда начнутся ВПР в 2022 году — РИА Новости, 17.08.2021
Стало известно, когда начнутся ВПР в 2022 году
Всероссийские проверочные работы в 2022 году начнутся 1 марта с контрольных у старших классов, сообщает пресс-служба Рособрнадзора. РИА Новости, 17.08.2021
2021-08-17T16:37
2021-08-17T16:37
2021-08-17T16:37
общество
сн_образование
социальный навигатор
россия
всероссийские проверочные работы (впр)
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdn25.img.ria.ru/images/07e4/0b/09/1583783688_0:170:3038:1879_1920x0_80_0_0_49dcdbb5ce617ef338353f2e106a8490.jpg
МОСКВА, 17 авг — РИА Новости. Всероссийские проверочные работы в 2022 году начнутся 1 марта с контрольных у старших классов, сообщает пресс-служба Рособрнадзора.Отмечается, что впервые в 2022 году учащиеся 7 классов будут сдавать ВПР по двум обязательным предметам и двум, выбранным случайно. Решение о том, сдавать ли ВПР оканчивающим 10 и 11 классы, как и в предыдущие годы, будут принимать сами школы. Проверочные работы у одиннадцатиклассников должны проходить по тем предметам, которые они не выбрали для сдачи на ЕГЭ.Конкретные даты проведения ВПР для каждого класса и предмета школы определят самостоятельно в рамках установленного расписанием периода.»Начнется проведение ВПР в 2022 году с проверочных работ для 10 и 11 классов. С 1 марта по 25 марта десятиклассники будут сдавать географию. Одиннадцатиклассники – историю, биологию, географию, физику, химию и иностранные языки (английский, немецкий или французский)», – добавили в ведомстве.В соответствии с утвержденным расписанием, с 15 марта по 20 мая 2022 года ученики 4-8 классов напишут проверочные работы по русскому языку и математике. В этот же период четвероклассники, помимо русского языка и математики, сдадут ВПР по предмету «Окружающий мир», а ученики 5 классов – по биологии и истории.С 1 апреля по 20 мая учащихся 7 классов ждет мониторинг качества подготовки по английскому, немецкому и французскому языкам.Также с 15 марта по 20 мая для параллелей 6-8 классов пройдут ВПР по истории, биологии, географии, обществознанию, 7 и 8 классов – по истории, биологии, географии, обществознанию и физике, 8 классов – по истории, биологии, географии, обществознанию, физике и химии. Проверочные работы в 6-8 классах будут проводиться для каждого класса по двум обязательным предметам (русский язык и математика) и двум предметам на основе случайного выбора.Информация о распределении предметов по классам в параллели будет предоставлена в образовательную организацию через личный кабинет в Федеральной информационной системе оценки качества образования.Результаты ВПР могут быть использованы образовательными организациями для совершенствования образовательного процесса, а органами управления образованием – для анализа текущего состояния системы образования и формирования программ ее развития. Не предусмотрено использование результатов ВПР для оценки деятельности образовательных организаций, преподавателей, региональных и муниципальных органов управления образованием.
https://sn.ria.ru/20210408/rosobrnadzor-1727354446.html
https://sn.ria.ru/20210316/rosobrnadzor-1601433716.html
россия
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2021
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
Новости
ru-RU
https://sn.ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
https://cdn25.img.ria.ru/images/07e4/0b/09/1583783688_154:0:2885:2048_1920x0_80_0_0_0347fd78250da7ec8c9b5b23d0ea26c5.jpgРИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
общество, сн_образование, социальный навигатор, россия, всероссийские проверочные работы (впр)
МОСКВА, 17 авг — РИА Новости. Всероссийские проверочные работы в 2022 году начнутся 1 марта с контрольных у старших классов, сообщает пресс-служба Рособрнадзора.
«Приказом Федеральной службы по надзору в сфере образования и науки утверждено расписание проведения всероссийских проверочных работ (ВПР) в 2022 году для обучающихся в общеобразовательных организациях», – говорится в сообщении.
Отмечается, что впервые в 2022 году учащиеся 7 классов будут сдавать ВПР по двум обязательным предметам и двум, выбранным случайно. Решение о том, сдавать ли ВПР оканчивающим 10 и 11 классы, как и в предыдущие годы, будут принимать сами школы. Проверочные работы у одиннадцатиклассников должны проходить по тем предметам, которые они не выбрали для сдачи на ЕГЭ.
Конкретные даты проведения ВПР для каждого класса и предмета школы определят самостоятельно в рамках установленного расписанием периода.
«Начнется проведение ВПР в 2022 году с проверочных работ для 10 и 11 классов. С 1 марта по 25 марта десятиклассники будут сдавать географию. Одиннадцатиклассники – историю, биологию, географию, физику, химию и иностранные языки (английский, немецкий или французский)», – добавили в ведомстве.
8 апреля, 12:53
Перехода только на ВПР в школах не будет, заявили в РособрнадзореВ соответствии с утвержденным расписанием, с 15 марта по 20 мая 2022 года ученики 4-8 классов напишут проверочные работы по русскому языку и математике. В этот же период четвероклассники, помимо русского языка и математики, сдадут ВПР по предмету «Окружающий мир», а ученики 5 классов – по биологии и истории.
С 1 апреля по 20 мая учащихся 7 классов ждет мониторинг качества подготовки по английскому, немецкому и французскому языкам.
Также с 15 марта по 20 мая для параллелей 6-8 классов пройдут ВПР по истории, биологии, географии, обществознанию, 7 и 8 классов – по истории, биологии, географии, обществознанию и физике, 8 классов – по истории, биологии, географии, обществознанию, физике и химии. Проверочные работы в 6-8 классах будут проводиться для каждого класса по двум обязательным предметам (русский язык и математика) и двум предметам на основе случайного выбора.
Информация о распределении предметов по классам в параллели будет предоставлена в образовательную организацию через личный кабинет в Федеральной информационной системе оценки качества образования.
Результаты ВПР могут быть использованы образовательными организациями для совершенствования образовательного процесса, а органами управления образованием – для анализа текущего состояния системы образования и формирования программ ее развития. Не предусмотрено использование результатов ВПР для оценки деятельности образовательных организаций, преподавателей, региональных и муниципальных органов управления образованием.
16 марта, 11:03
Музаев рассказал, как планируется сократить время проведения ВПРОтец 9-летней Алисы Тепляковой промедлил с платным поступлением в МГУ
В пресс-службе факультета психологии МГУ «МК» сообщили: «Мы зачислили абитуриентов, которые по баллам прошли на бюджет. Алисы Тепляковой среди них нет.
Говорить о том, что Алиса прошла, можно будет после того, как родители придут заключать договор об оказании платных образовательных услуг».
Сам же Евгений нам ответил так: «С психфаком все хорошо, договоры еще неделю точно можно подписывать. Алиса в любом случае поступила». Ранее в интервью «МК» Евгений говорил: «Учеба для нее – по возрасту. Она играет со сверстниками, и, естественно, с 20-летними дядями и тетями в университете ей говорить не о чем. Она там будет учиться, а не контакты налаживать».
Семья Тепляковых – это мама, папа и семеро детей, разница между которыми составляет примерно полтора года. Алиса – старшая, и у нее единственной имя, привычное нашему слуху. Остальных зовут необычно и очень красиво. Хеймдалль, Лейя, Терра, Айлунг, Фейлунг и Тесей. Самому маленькому, Тесею, всего 2 месяца. Как известно, так звали героя греческой мифологии, который убил Минотавра. И это имя брату выбрала Алиса.
Младшим братьям Фейлунгу и Айлунгу – соответственно, годик и два. Айлунг и Фейлунг – китайские имена, «дракон любви» и «летящий дракон». Далее следуют девочки: Терре – четыре, а Лейе – пять. Терра означает Земля. Лейя – цветок. Хеймдаллем звали скандинавского бога, сына Одина. Хеймдаллю Теплякову семь лет.
У Евгения Теплякова несколько высших образований, он психолог, преподаватель психологии, математик, программист. Окончил на «отлично» психфак МГУ. Позже получил еще один красный диплом МГУ по специальностям математика и кибернетика.
Папа Евгений Тепляков с детьми. Фото: Из личного архиваСейчас, по словам Евгения, он работает как раз по специальности (имеется в виду «психолог-преподаватель») – воспитателем семейного детского сада, состоящего из собственных детей, и получает за это зарплату от государства.
Его жена Наталья тоже имеет два высших образования – математическое и финансовое. Несколько лет супруги жили в Китае, Евгений учился там в докторантуре, тогда у них было еще только двое детей, Алиса и Хеймдалль. Видимо, два китайских имени у детей – дань тем годам и этой стране. На своей странице в ЖЖ родители описывают себя так: «Математики, биологи, психологи, философы, экономисты, программисты. Порой социологи, если сильно захотеть – то и политологи. Немного автомеханики, чуть-чуть филологи. Местами спортсмены. Педагоги еще».
Самое удивительное, что не только Алиса, но и вообще все дети Тепляковых в своем развитии намного опережают сверстников. Поэтому отец категорически возражает, когда Алису называют вундеркиндом. Все дети в одной семье вундеркинды? Так не бывает. Семья Тепляковых на своем примере доказывает, что любой ребенок, если только с ним правильно заниматься с самого детства, может добиться таких же успехов и освоить школьную программу гораздо раньше, чем это запрограммировано нашей системой образования.
При этом отец уверяет, что его дети вовсе не лишены детства и учеба их не напрягает.
«Садиков и школ у нас нет, поэтому очень тяжело»
– Вы с Натальей всегда хотели большую семью? – спрашиваю Евгения.
– Нет, мы никогда этого не хотели, я вообще единственный ребенок в семье. Но потом оказалось, что большая семья – это здорово, – отвечает глава семейства.
Все дети на домашнем обучении, учат их сами родители.
Четырехлетняя Терра в этом году идет в первый класс. Лейя в пять лет заканчивает программу четвертого класса.
Пока что больше других детей прославилась Алиса, хотя ее семилетний брат Хеймдалль (по-домашнему «Хемик») от нее ничуть не отстает. В пять лет он уже был призером по множеству предметов школьного этапа олимпиад – по биологии 6-го класса, биологии 7-го класса, математики 5-го и 6-го класса, обществознание 6-го класса и экологии 6-го класса. По словам отца, Хемику чуть-чуть не хватило баллов, чтобы попасть в число призеров муниципального этапа по биологии 7-го класса.
Его сестра Алиса в 7 лет была в призерах олимпиад по математике 8-го класса, математике 9-го класса, экономике 8-9-х классов, экологии и обществознанию.
В этом году семилетний Хемик сдал ОГЭ и получил аттестат за 9-й класс. Так же, как и Алиса в прошлом году. Напомним, что в этом году, в свои восемь, девочка сдала ЕГЭ, получила аттестат за полную одиннадцатилетку и сдала дополнительные вступительные испытания на факультет психологии МГУ.
– У них объективно высокий интеллект, очень высокие результаты для их возраста, – говорит о детях Евгений. – Мы, кстати, уже устали бороться, опровергать миф о «феноменальной памяти» Алисы, который запустили некоторые эксперты по психологии, при том что они ее даже не видели, не общались с ней…
Ректор МГУ Виктор Садовничий и сотрудники психфака сразу же, как только Алиса подала документы, подтвердили, что готовы оказать ей любую поддержку в случае зачисления.
Алиса Теплякова. Фото: Из личного архиваНа вопросы, как Тепляковым удается организовать обучение детей на дому при таком количестве братьев и сестер, среди которых есть и совсем малыши, как они организуют домашнее хозяйство в таких стесненных условиях (Тепляковы вдевятером живут в однокомнатной квартире 30 кв. м в столице) и кто им помогает, Евгений отвечает: «Да никак у нас ничего не организовано. Бабушки и дедушки не помогают, сказали, что «это ваши проблемы». Садиков и школ у нас нет, поэтому приходится тяжело. Мы бы с удовольствием обратились к кому-то за помощью, но не к кому. Какой смысл писать про наш быт? Это не имеет отношения к образованию».
При этом Евгений замечает, что, «если бы они могли заниматься с детьми в нормальных условиях, результаты были бы еще выше».
– Как у вас распределены обязанности с супругой? Кто учит детей, а кто занимается хозяйством?
– Мы оба занимаемся всем.
– Получается, вы должны помнить всю школьную программу, чтобы учить детей всем предметам?
– Зачем ее помнить, она же есть! Мы всем предметам учим. Математике учу и я, и Наталья, жена даже больше меня. Хотя она больше специализируется на «началке» – учит детей читать, писать, у меня бы терпения не хватило.
Маркс плюс советская методика
Евгений Тепляков рассказывает, что в среднем его дети тратят на учебу в день по три-четыре часа, и «четверть этого времени, а может быть, треть, а если скоро экзамен, отданы чтению учебной и научно-популярной литературы. А там уже начинается наша работа – понять, что ребенок не понял, почему не понял и как ему это объяснить».
Отец уникально «продвинутых» детей раскрыл секреты их методики.
– Если говорить о методике, то это серьезная научная работа, огромная методология. Я ее не изобретал, я взял то, что есть. Я стою на базе деятельностного подхода. Деятельностный подход стоит на базе марксистской общенаучной методологии. («Деятельностный метод обучения – это организация учебного процесса, в котором главное место отводится активной и разносторонней, в максимальной степени самостоятельной познавательной деятельности школьника» – Авт.) А Маркс, в свою очередь, стоит на Гегеле. Это советская школа, советские методики, советская психология и педагогика… Например, были такие экспериментальные классы по методике Эльконина-Давыдова в 70-80-е годы. Есть очень много обучающих фильмов в Интернете на эту тему, в которых показывают, как дети в первом и во втором классе разбирают чуть ли не на вузовской уровне русский язык, математику. Эти фильмы смотришь на одном дыхании, потому что то, что в них показывают, это невероятно. Были работы Виктора Шаталова, когда он выступал и показывал, что, например, многое из программы пятого класса можно пройти за полчаса.
– А как вы пришли к тому, чтобы обучать ваших детей по ускоренной программе, не как всех учат?
– Почему «не как всех»? Ваш ребенок наверняка тоже пошел в первый класс, уже умея читать и считать? По статистике, 70% детей приходят читающими-пишущими в школу, при этом школьная программа предполагает, что они начинают с нуля. А дальше мы сталкиваемся с парадоксом: вы приводите в школу ребенка, который уже знает, по сути, программу первого, а кто-то и второго класса, а кто-то, может, и четвертого. То, что мы смогли пройти за пять лет 11-летку, это не к нам вопрос, а к 11-летке. Когда в России школьная программа 4-го класса заканчивается темой чисел больше тысячи, а ребенку в это время уже почти 12 лет, то это очень странно.
– Своего ребенка я планировала отдать в первый класс в 6 лет и 1 месяц (столько ей было на 1 сентября). Однако нам отсоветовали это делать: «Зачем вам лишать ее детства? Пусть в школу пойдет через год, ей будет легче». Следуя вашей логике, мы зря их послушали?
– В России же была сначала десятилетка. Потом сказали, что первый класс – это бывшая «подготовишка», и лучше, чтобы дети учились в школе, а не в садике (потому что в школе педагоги лучше). И начали брать с 6 лет. И одновременно существовали две системы: в одной брали с 6 лет, в другой брали с семи, но «прыгали» через класс. Потом, в 2001 году, это все отменили, сказали, что «все идут с семи», и никто через класс не прыгает. И получилась в итоге странная вещь: в Советском Союзе была десятилетка, шли с семи и оканчивали в 17 лет. А сейчас 11-летка, и тоже идут с семи. И оканчивают в 18 лет.
Я учился в белорусской школе, и там в первый класс поступают в шесть лет. Даже если тебе в сентябре шесть, то ты идешь. В Белоруссии нельзя пойти с семи, надо писать объяснительную, почему твой ребенок занимает место в детском садике. А ведь это соседняя с нами республика, и там живут абсолютно такие же дети. И в Украине то же самое, и в Казахстане.
Поэтому у нас получается, что дети сидят в своих классах по возрасту, а чем они там занимаются – никого не волнует. Попробуйте скажите в классе, что «я не понял», вам ответят – ваши проблемы, нанимайте репетитора. А попробуйте сказать наоборот – «эта тема легкая, я ее уже прошел». Вам ответят – это ваши проблемы, мы ее еще проходим. В лучшем случае, разрешат почитать книгу на задней парте. В этом вся проблема. Не в нас и не в Алисе. Ну в 10 лет бы окончил другой ребенок 11-летку, ну в 12. Дело не в возрасте. А в том, что ему некуда идти вперед.
Очень многие дети сталкиваются с таким. Их ведут к психологам, которые объясняют им, что «надо остановиться, что сейчас не надо еще учиться, идите развивайтесь, в Монтессори играйте…». Это я, как психолог, могу им сказать, что они говорят ерунду, но я представляю и знаю, скольких родителей они остановили. Даже вы на своем примере в этим столкнулись, когда в 6 лет вам сказали — да лучше отдохните годик!
Фото: Из личного архива– Есть же специализированные школы, школы с углубленным изучением того или иного предмета.
– Нам все школы отказали. Мы хотели Алису отдать в пять лет сразу во второй класс. Если бы ее взяли, мы были бы довольны. Нам школа «Интеллектуал» прямым текстом ответила, что изучение программы по школе России не является показателем одаренности, и, несмотря на то, что ваш ребенок в четыре года сдал программу пятого класса, она может поступить в пятый класс не раньше 11 лет.
Сотни тысяч детей в таких случаях останавливаются. Наша история в том, что мы не остановились.
О «лишении детства»
– Многие считают, что «всему свое время», школьная программа как раз и рассчитана на то, чтобы на загружать сильно мозги детей, чтобы они постепенно осваивали все предметы. Наверняка главная причина нападок на вас – что вы «лишаете своих детей детства».
– Те же самые люди, которые нас спрашивают, зачем лишать детей детства, сами «выпихивают» своих детей в 16 лет работать со словами «А что это ты сидишь на моей шее?», а он, несчастный, еще и 9-й класс не успел окончить, потому что с 8 лет пошел в школу.
Мы лишаем детства детей? Я вам приведу один комментарий. Человек пишет нам: «Я работаю 8-10 часов в сутки, у меня ипотека, мне нужно спортом заниматься, я хочу еще своей личной жизнью заняться, поэтому – где я возьму еще 3-4 часа на ребенка? Это все ерунда, чем вы занимаетесь, все должно быть по возрасту, ребенок должен быть социализирован». То есть это не мы лишаем ребенка детства, а скорее такие родители, как этот. А мы лишаем родителей возможности откупиться и сказать, что «все нормально». Система же выполняет функцию передержки.
Всем плевать, какое детство у ребенка – в садике, в школе. Нравится ему в лагере, не нравится – часто ли ребенка забирают из лагеря, если ему там не нравится? Нет. А в садик отдают в 8 утра, забирают в 7 вечера. И считают, что у них детство хорошее. То есть на самом деле ребенок многим мешает.
А про своих детей скажу, что им нравится то, чем они занимаются.
– На чем вы делаете акцент в их обучении?
– Главное – чтение. Это очень важно. Об этом говорил Сухомлинский, и многие другие педагоги и ученые. Алиса, например, любит читать много разных книг. Она читает все. Но, конечно, больше всего она любит сказки, волшебные истории. Гоголя прочла очень много. Она не читала произведения, которые меня раздражают, – «Войну и мир», к примеру. Она читала и Достоевского, и Грибоедова, и Тургенева, и Толстого. Другое дело, что она из этого понимала. Но она читала.
– Что же она вынесла из того же Толстого, ведь у нее нет достаточного жизненного опыта, чтобы понимать те или иные вещи из взрослых произведений?
– Вопрос, что она вынесла из классики, вообще не имеет смысла. Давайте поговорим про теорию коммуникации: я вам говорю слова, которые уже искажаются на выходе, вы слышите и интерпретируете их по-своему, и получается, вы считываете вообще другое сообщение, а не то, которое я хочу до вас донести? Ну, это нормально. Можно поговорить о концепции значения личностного смысла, который у каждого свой… Я не спрашиваю у детей, что они вынесли из прочитанного, это ситуация экзамена, а мы все время говорим о безоценочности.
– Алиса играет со сверстниками, есть у нее друзья?
– У наших детей много друзей для игр. Если у вас дети-погодки, они, конечно, будут ругаться, ссориться, драться, но они реально очень близкие люди. Простой пример – это близнецы. Им, кроме друг друга, больше никто особо и не нужен. Они самые близкие люди на всю жизнь. Что касается Алисы, то она и вне дома общается, на детских площадках у нее есть друзья – и ровесники, и более старшие. Проблема в том, что Алиса – старший ребенок в многодетной семье, она лидер, хочет всеми управлять. Соответственно, старшие дети ей это не особо-то дадут. А она хочет, чтобы все было, как она скажет, чтобы все играли, как она скажет.
«Вундеркинда» можно сделать из любого
Главный вопрос, волнующий родителей, которые мечтают вырастить ребенка, опережающего сверстников в развитии, – влияют ли гены, должен ли быть какой-то особенный, врожденный склад ума?
Евгений Тепляков убежден, что – нет, не влияют. Нет от природы одаренных детей. Их можно сделать такими только с помощью силы образования, которое вы им даете. Или не даете.
– Как только вы говорите о таланте, вы снимаете с себя ответственность. Например, у учителя есть класс, 30 человек. Он должен их научить. Удобнее всего сказать: вот этим дано, а этим – нет. Потому что тогда вы ни в чем не виноваты. Что с ними мучиться, если им «не дано»?
В большинстве случаев талантом называется результат, который получен не при вас, и вы не знаете, откуда он взялся. Я не слышал, чтобы в Кении рождались ученые высокого уровня в 50-е годы ХХ века. Потому что в Кении не было банально школ.
С другой стороны, возьмите такой замечательный пример – евреи-ашкеназы (субэтническая группа евреев – Авт.). У них был ценз оседлости, им не разрешали выезжать с территории Белоруссии и Польши, и для того чтобы выехать, в конце 19 века, у них должна была быть либо ученая степень, либо медицинская степень. Поэтому у них была очень высокая ценность образования. Для них это был единственный способ вырваться из нищеты. Они очень сильно вкладывались в образование. И, как итог, мы видим множество выдающихся личностей, которые эмигрировали в Америку. И еще огромное количество еврейских детей с высоченными результатами, которых учили дома.
И в советской России тоже было очень много еврейских детей, которые занимались математикой, музыкой, физикой и достигали высоких результатов. Потому что у них была очень высокая ценность образования. Это же прекрасно. Они реально очень сильно вкладывались в своих детей. И добивались прекраснейших результатов.
Алиса и ее брат Хеймдалль. Фото: Из личного архиваА сейчас, если мы посмотрим на уровень образования в Израиле, то увидим по рейтингу международных образований 2018 года, что в Израиле оно посредственное. Это не имеет никакого отношения к генетике, к тому, что генетически интеллект как-то по-особенному распределен. У китайцев, например, в садике ребенка с трех лет начинают учить иероглифам. Они их пишут, прописывают. И в младших группах у них уже есть учебники. Мы ходили в китайский садик, когда там жили, и мы это знаем. И известно, что по рейтингу международных сопоставлений у китайцев самый высокий в мире уровень образования.
– Иными словами, любой ребенок, если с ним заниматься с самого детства, может добиться таких же успехов к своим юным годам, как и ваши дети?
– Возьмем хорошего тренера в спорте. Спросите его, может ли он вывести на уровень кандидата ребенка, если у него есть только мотивация, но ребенок пока особо ничего не умеет? С большой вероятностью (если только он подходит по необходимым в данном виде спорта физическим параметрам), он сдаст на КМС, если только будет серьезно «впахивать».
– Точно так же и с детским умом?
– Да. Если с ребенком НЕ заниматься, то он и НЕ разовьется. Это очевидно. Несомненно, это сложно, нужно искать мотивацию, нужно простраивать подход, в каждом конкретном предмете есть своя образовательная траектория. Это отдельная методологическая задача – как правильно, как лучше преподавать физику и так далее. Поскольку я преподаватель психологии по первому диплому, я могу преподавать любой предмет.
– Как вы занимаетесь со своими самыми маленькими детьми, которым год и два?
– Когда у вас маленький ребенок, как вы с ним занимаетесь? Разговариваете, показываете предметы, стараетесь, чтобы он новые слова учил.
Существует тест развития ребенка от рождения до 42 месяцев. Три шкалы – шкала моторного, психического и социального развития. Эти три шкалы измеряют, насколько ваш ребенок соответствует возрастным нормам. Вы можете опираться на тест, чтобы узнать, где у ребенка зона ближайшего развития, то есть какие навыки должны у него возникать в ближайшее время при нормальном развитии. Естественно, оно может несколько отличаться от этого.
До раннего возраста, до 3-3,5 лет вы можете примерно смотреть на возрастные нормы. Например, во сколько ребенок должен начать ползать, сидеть, в каком возрасте он должен ставить кубики один на другой, в каком возрасте он должен различать цвета и так далее, по разным навыкам. Понятно, что человек, который не является психологом и педагогом, скорее всего, не сможет на это опираться…
Если говорить об Алисе, то складывать буквы и читать слова она начала с трех лет. До этого учили ее буквам, она их знала в полтора годика. Но до трех лет у нее не получалось читать.
Фейлунг. Фото: Из личного архива«Не учить – преступление»
– Тот факт, что вы проживаете с семерыми детьми в однокомнатной квартире, не может не шокировать. Многодетным семьям разве не положена помощь от государства в получении жилья?
– Мы прекрасно знаем, что никто нам квартиру не даст. Сейчас получают квартиры те, кто встал в очередь до 2005 года. Мы не встали в очередь, нас не ставят. Сейчас до сих пор получают те, кто встал в 1999, 2000 годах.
Сейчас квартиры дают только семьям с приемными детьми, если вы заберете у города, например, семь детей. Сначала такую квартиру дают в аренду, а когда дети вырастают, и у государства нет к вам претензий, ее позволяют приватизировать.
Удивительно, но детей Тепляковых наша система образования будто бы не замечает.
– Реакция на Алису, на нашу семью абсолютно неадекватная, – продолжает Евгений. – Есть реестр одаренных детей, и, насколько мы можем судить, кого попало туда не берут. Но нас туда не включают, там четкие критерии, мы по ним не проходим.
Единственное, за что мы бьемся — чтобы многочисленные логопеды и психологи перестали пропагандировать бред, что детям нельзя идти вперед. У нас есть знакомая, ребенок которой тоже шел с опережением программы. Поступил в лицей. И там у него возникла проблема с «составом числа 16». Состав, который требовалось указать, был для тех детей, кто еще через десяток переходить не умеет. А тот ребенок давно умел.
Вызывают маму в школу и говорят: «Ваш ребенок тупой, не хотите забрать документы из лицея?». Она говорит, как же тупой, если он и складывает, и делит, и умножает числа, все умеет! А ей говорят, а нам это вообще не интересно. Он мешает нам вести уроки. Мама забрала документы, они перешли в обычную школу. Ребенок шел вперед, а ему говорят – не положено! У нас таких не любят. Любят, чтобы было, как положено.
– Если ваши все дети, как и Алиса, рано поступят в вузы, им и работать придется раньше начать?
– Если захотят. «Выпихивать» их мы не планируем. Вы поймите, у нас нет бизнес-плана, мы просто учим детей. Не учить – преступление.
Онлайн-программа по математике для 5-х классов
Посмотреть демо наших уроков!Математика — очень важный компонент пятого класса образования. Учитесь вы на дому или нет, помощь вашему ребенку в достижении необходимых математических целей в 5-м классе позволяет ему быть подготовленным, уверенным и знающим при поступлении в среднюю школу и за ее пределами. Без твердого понимания основ изучать более сложную математику в будущем будет все труднее.
На этой странице представлена информация о том, на что следует обращать внимание в учебной программе пятого класса по математике, о том, что должен знать пятиклассник, о задачах по математике и многом другом.
Какую математику должен знать 5-классник?
В пятом классе ученики математики предсказывают относительный размер решений сложения, вычитания, умножения и деления целых чисел, сложения, вычитания и умножения дробей, десятичных и смешанных чисел. Кроме того, они должны были достичь мастерства в исчислении, округлении, деньгах, а также в обычной и метрической системе, и это лишь некоторые из них.
Ниже приведены некоторые понятия, которые должен знать пятиклассник.
- Округление чисел до ближайших десяти, сотен, тысяч, десяти тысяч и сотен тысяч
- Использование частичных произведений и умножение в уме
- Деление с двузначными делителями
- Порядок и сравнение дробей
- Сравнение периметра и площади
Посетите страницу программы Time4Learning по математике и последовательности действий для 5-го класса, чтобы узнать обо всех концепциях, которые ваш ребенок усвоит при использовании нашей учебной программы.
Задачи по математике для 5 класса
Ниже приведены лишь некоторые из математических целей 5-го класса, которые должен достичь ваш ребенок. Подбирая комплексную и эффективную учебную программу по математике для пятого класса, ваш ребенок будет изучать все важные концепции и темы, необходимые для перехода в шестой класс.
- Использование разряда для сложения, вычитания, умножения и деления десятичных знаков
- Применяйте формулы для решения различных стандартных задач длины / веса / вместимости / температуры
- Рассчитать вероятность события
Кроме того, Time4MathFacts помогает свободно владеть математическими фактами с помощью интерактивных и игровых видеоуроков, которые помогают студентам практиковать и усваивать важные математические факты, а также сложение, вычитание, умножение и деление.
Почему стоит выбрать программу Time4Learning для 5-го класса по математике
Учебная программа пятого класса по математике Time4Learning — это комплексная онлайн-программа, в которой преподаются важные математические концепции с использованием интерактивного мультимедийного подхода. Студентам преподается материал, и у них есть много возможностей попрактиковаться. Задания с выставлением оценок, а также викторины помогают оценить понимание, в то время как автоматическое выставление оценок и ведение записей позволяют родителям отслеживать, как развиваются их дети.
Учебную программу по математике для 5-го класса Time4Learning можно использовать в качестве основной учебной программы в вашем домашнем обучении или в качестве дополнения к практике по математике в пятом классе. Многие родители также используют Time4Learning как инструмент летнего обучения, чтобы предотвратить ужасную летнюю утечку мозгов.
Ниже приведены некоторые особенности и преимущества, которые вы можете ожидать при использовании учебной программы по математике Time4Learning для пятого класса.
Как полный учебный план
| В качестве дополнения
|
Дополнительные ресурсы для домашнего обучения 5-го класса
Четыре основных математических понятия, которые ваши дети изучают в 5–6 классах | Scholastic
С пятого класса на шестой может произойти значительный скачок в знаниях математики, и мне нравится думать об этом как о переходе через мост. Чем больше мы соединим мост, тем лучше наши дети будут чувствовать себя в средней школе.Пятый класс — это кульминация всего, что ученики узнали на начальном уровне, а шестой класс можно рассматривать как отправную точку для средней школы. И независимо от того, как устроена средняя школа вашего ребенка, между этими оценками существует четкая связь. Чем более комфортно дети усваивают эти концепции к концу шестого класса, тем лучше они будут подготовлены к средней школе.
Вот четыре основных математических понятия, которые ваш ребенок усвоит в пятом и шестом классе:
1.Система счисления. В пятом классе ученики сосредотачиваются на сложении, вычитании, умножении и делении целых чисел, дробей и десятичных знаков. Ваш ребенок научится свободно вычислять эти типы чисел и понимать взаимосвязь между ними. Студенты также должны уметь использовать эти числа в реальных сценариях. В шестом классе дети продолжают понимать эти числа, а также знакомятся с отрицательными числами. Они начнут определять рациональные числа и целые числа в числовой строке, а также сравнивать их.Использование моделей значительно улучшит понимание ребенком этих концепций.
Поощряйте своего ребенка:
- Распознавайте и вычисляйте, используя дроби и десятичные дроби в реальном мире. Например, попросите ребенка вычислить скидку на распродаже; сумма налога при совершении покупок; найдите кончик счета или объясните спортивную статистику.
- Используйте дробные линейки для вычислений (сложение, вычитание, умножение или деление).
Изображение предоставлено: LearnZillion
- Найдите примеры положительных и отрицательных чисел в реальном мире (температура, расстояние, уровень моря и т. Д.)) и используйте модели, чтобы понять взаимосвязь между ними.
Изображение любезно предоставлено: положительное влияние Math
2. Коэффициенты. Ученики будут использовать свои знания о дробях и десятичных дробях в пятом классе для соотношения разума и оценки задач в шестом классе. Детям нужно будет связать свое понимание умножения и деления с реальными задачами с использованием соотношений. Они будут использовать модели (диаграммы, таблицы, двойные числовые линии и т. Д.), Чтобы помочь им установить эти связи и решить проблемы с удельной стоимостью.Студенты также узнают о процентах и о том, как они соотносятся с дробями и десятичными знаками.
Поощряйте своего ребенка:
- Найдите примеры соотношений в реальном мире. Например, « Соотношение крыльев и клювов в скворечнике зоопарка было 2: 1, потому что на каждые 2 крыла приходился 1 клюв».
- Используйте модели, чтобы понять проблемы соотношения и скорости:
Изображение предоставлено: 6-й класс мистера Пратта
Изображение предоставлено: nzmaths.
- Создавайте реальные проблемы, используя понимание соотношений. Например, « В этом рецепте соотношение 3 стакана муки к 4 стаканам сахара, поэтому на каждый стакан сахара приходится 3/4 стакана муки».
3. Выражения и уравнения. Учащиеся начинают понимать разницу между выражением и уравнением. Они используют переменные для представления неизвестного числа как в выражениях, так и в уравнениях. Ученики пятого и шестого классов следуют соответствующему порядку действий для решения задач, включая скобки и показатели.Ваши дети начинают читать, интерпретировать и писать выражения и уравнения, а также решать уравнения с одной переменной.
Поощряйте своего ребенка:
- Различайте выражение и уравнение и поймите значение знака равенства:
Выражение: 4y + 2
Уравнение: 4y + 2 = 14
- Решайте проблемы, используя аббревиатуру PEMDAS:
Изображение предоставлено coolmath.com
- Легко читать и писать выражения: Вычтите n из 8 дюймов как 8 — n.
- Создавайте и решайте реальные проблемы с помощью переменных. Например: « Аренда катка стоит 100 долларов плюс 5 долларов на человека. Напишите выражение, чтобы найти стоимость для любого количества (n) человек. Сколько стоит 25 человек? Ответ: 100 + 5n; так что для 25 человек = 100 + 5 (25) = 225 ».
4. Геометрия: Учащиеся продолжают классифицировать фигуры по категориям в зависимости от их свойств.Ваш ребенок научится находить площадь треугольников и некоторых четырехугольников. Они научатся вычислять объем трехмерных фигур, используя целые числа и дробные части. Учащиеся начинают использовать представление реальных проблем путем нанесения точек на координатную плоскость.
Поощряйте своего ребенка:
- Поймите разницу между поиском площади двухмерной фигуры и поиском объема трехмерной фигуры. Укажите на разные предметы и спросите, найдет ли ваш ребенок площадь или объем этой фигуры.Например, «Вы можете найти площадь или объем этого заднего двора?» Или: «Вы бы нашли объем этого бассейна?»
- Используйте соответствующий словарь при описании различных многоугольников и геометрических свойств. Например, «Что такое параллельные прямые?» Ответ: «Две линии на плоскости, которые никогда не пересекаются. Они всегда находятся на одинаковом расстоянии друг от друга».
- Используйте их обучение в третьем классе, чтобы понять, как найти площадь прямоугольника или найти значение треугольника:
Изображение предоставлено: Департамент математического образования Университета Джорджии
- Развивайте понимание координатной плоскости и начинайте наносить точки, используя реальные сценарии (используя миллиметровую бумагу).Например, «На карте библиотека расположена в (-2, 2), здание мэрии — в (0,2), а средняя школа — в (0,0). Представьте местоположения в виде точек на координатной сетке с единицей измерения 1 миля ».
Не волнуйтесь, если эти концепции сначала покажутся немного пугающими. Помните, что вы не посещали ежегодные уроки математики, которые опираются друг на друга, как ваши дети. (Сначала может показаться, что ваши дети понимают это лучше, чем вы!)
Но в этом суть нашей серии блогов «Основные математические концепции».Мы хотим, чтобы и вы, , также были наделены пониманием этих математических концепций. Вы можете быстро начать обучение своих детей, вы можете идти в ногу с ними, но это поможет вам больше общаться со своим ребенком по тому, что часто является сложным предметом.
У вас есть вопросы об этих концепциях или другие вопросы по математике вашего ребенка? Отправьте их Дженнифер здесь, чтобы она могла ответить в следующем блоге. Или поделитесь ими с нами на странице Scholastic Parents в Facebook.
Изображение предоставлено: © Oktay Ortakcioglu / iStockphoto
Пятиклассный курс математики
В следующем списке представлены основные математические концепции, которые необходимо освоить к концу 5-го класса учебного года.Предполагается, что они овладеют концепциями в предыдущем классе, кроме того, учащиеся изучают основы алгебры, геометрии и теории вероятностей, на которые будут опираться в последующие годы.
Номера
- Считайте печатные числа до 100 000 и найдите, сравните, упорядочивайте, представляйте, оценивайте и идентифицируйте числа до 100 000, используя обычные и развернутые формы
- Полное понимание разряда справа и слева от 0-4 разряда
- Сосчитайте по комбинациям 3, 4, 6, 7, 8, 9 и 10, 11 и 12 до 144
- Факты умножения сохраняются в памяти до 12 таблиц X (также необходимо понимать факты деления)
- Разбирать десятичные дроби с точностью до тысячных 0.013 и уметь складывать и вычитать десятичные дроби.
- Продемонстрировать твердое понимание дробей и связанных с ними десятичных знаков с точностью до сотых долей.
- Умножение и деление десятичных знаков
- Рассказывать о математическом мышлении при решении задач — выбор подходящей стратегии
- Выберите подходящие методы решения проблем в текстовых задачах для вышеуказанных операций
Измерения
- Полное понимание дюймов, футов, ярдов, миль, миллиметров, сантиметров, метров, километров и применение этих терминов к действиям по решению проблем
- Точно измерьте и сделайте соответствующие оценки того, какие единицы измерения применимы.
- Создавать или иллюстрировать предметы, используя различные единицы измерения
- Оценить и точно округлить
- Считывание и запись дат с использованием различных методов (10 января 2002 г., 10 февраля 2002 г. и т. Д.)
- Деньги составляют 1000,00 долларов на внесение сдачи и решение проблем
- Изучите и решите проблемы измерения окружности, периметра, объема, вместимости и площади, объясните правила и примените формулы
Геометрия
- Определение, сортировка, классификация, построение, измерение и применение различных геометрических форм и фигур и задач
- Полное понимание геометрических свойств и соотношений
- Классифицировать треугольники по свойствам и типам сторон (тупые, равнобедренные) и т. Д.
- Определите двумерные сети, которыми представлены твердые тела, и постройте сети
- Измерение и построение различных треугольников и углов с помощью транспортира
- Исследуйте и обнаруживайте мозаичные узоры, покрывающие плоскость и мозаику
- Понимать систему координат как на картах, так и на сетках
Алгебра / Паттерн
- Идентифицировать, создавать, анализировать и расширять шаблоны и описывать правила с помощью более чем одной переменной
- Определите значения в уравнениях, когда в четырех операциях отсутствуют пропущенные члены, и предоставьте правила
- Определить количество пропущенных значений, если задано уравнение, включающее более 1 операции
- Продемонстрируйте эквивалентность в уравнениях с помощью 4 операций
Вероятность
- Спроектировать обследования, собрать данные и записать их надлежащим образом, уметь обсуждать результаты
- Построить множество графиков и соответствующим образом пометить их, а также указать разницу между выбором одного графа над другим
- Обсудить реальную потребность в данных и сборе данных
- Чтение, анализ и интерпретация данных в виде различных графиков и т. Д.
- Us древовидные диаграммы для организации данных, принятия решения о собранных и отсортированных данных и записи результатов
- Проведите вероятностные эксперименты и примените логические рассуждения к результатам
- Прогнозировать вероятность на основе исходной информации
Все классы
математических навыков, которые ваш ребенок усвоит в пятом классе
Изучая математику в пятом классе, ваш ребенок расширит понимание десятичных и дробных чисел, а также изучит числовые выражения, объем и графики.Об этом много! Помогите своему ребенку преуспеть в математике в пятом классе, узнав больше о том, чем он будет заниматься.
В течение года ваш ребенок будет:
1. Решать числовые выражения
У вашего ребенка был большой опыт решения задач с помощью четырех операций. Теперь ваш ребенок еще больше разовьет это понимание, научившись использовать круглые скобки в числовых выражениях и оценивать выражения с их помощью. Ваш ребенок узнает о порядке операций и сначала решит части выражений в скобках.
Помогите своему ребенку попрактиковаться в понимании порядка операций, давая ему более длинные выражения для оценки, как со скобками, так и без них. Дайте ребенку такое же выражение, но с другим расположением скобок. Поговорите с ребенком о том, как круглые скобки повлияли на выражение.
2. Работа с десятичными дробями
В пятом классе ученики учатся читать, писать и сравнивать десятичные дроби с тысячными. Они также практикуют сложение, вычитание, умножение и деление десятичных дробей до сотых, что может быть непросто!
Поддержите своего ребенка, рассказав о различных стратегиях.Попросите ребенка использовать рисунки или модели, чтобы попытаться визуализировать решаемые им десятичные задачи. Например, нарисуйте сетку 10х10 и попросите ребенка увидеть каждый квадрат как сотую. Используйте сетку, чтобы визуализировать десятичные дроби при решении задач.
3. Сложение и вычитание дробей с разными знаменателями
В четвертом классе ученики научились сравнивать дроби с разными числителями или знаменателями. Теперь они расширят это понимание, научившись складывать и вычитать дроби с разными знаменателями, находя общие знаменатели.
Предложите вашему ребенку выполнить реальные задания на сложение и вычитание. Например, при приготовлении пищи вы можете попросить ребенка рассчитать стакана муки + ½ стакана муки. Помогите своему ребенку связать общие знаменатели с их знаниями об умножении, подумав об общих кратных. ( Посетите нашу страницу о дробях, чтобы освежить свои знания о дробях!)4. Умножение и деление дробей
Работа с дробями не заканчивается сложением и вычитанием! Пятиклассники готовы умножать дроби на целые числа или дроби.Они также будут делить единичные дроби (дроби, где числитель 1) на целые числа и целые числа на единичные дроби.
Эти понятия могут быть непростыми, поэтому вместо того, чтобы объяснять их вашему ребенку, попросите его объяснить их вам. Возможность быть учителем может помочь вашему ребенку развить более глубокое понимание и даст вам возможность увидеть, насколько хорошо все это усваивается.
5. Измерьте объем
Четвероклассники имеют опыт измерения длины и веса.Но в этом году они познакомятся с новым типом измерения: объемом. Студенты научатся измерять объемы, считая единичные кубы, используя кубические сантиметры, кубические дюймы и кубические футы. Они узнают формулу для вычисления объема кубов и прямоугольных призм (объем = длина x ширина x высота)
У вас есть ребенок замечает количество напитков, которые потребляет ваша семья. Поговорите о том, как емкости разного размера, например, 2-литровые и 1-литровые бутылки, вмещают разное количество жидкости.
6. Точки графика на координатной плоскости
В пятом классе ученики узнают, как в системе координат есть ось x и ось y, и как точки могут быть заданы по их координатам (x, y).
Попросите вашего ребенка нарисовать координатную плоскость с помощью графической бумаги и потренируйтесь, когда ребенок находит определенные точки. Такие игры, как «Морской бой», также могут быть отличным способом попрактиковаться в представлении о координатах. Если у вас нет настольной игры, вот как вы можете играть в Морской бой, используя ручку и бумагу!
На протяжении всего пятого класса обучения вашего ребенка находите возможности проверить и услышать, что он изучает.Математика в пятом классе может быть сложной, так что воспользуйтесь этой возможностью, чтобы улучшить свои навыки!
Нашли это полезным? Ознакомьтесь с нашими руководствами по математике от детского сада до 5 класса
Написано Лили Джонс, Лили любит учиться всему. Она была воспитателем детского сада и первого класса, инструктором по обучению, разработчиком учебной программы и наставником учителей. Она любит смотреть на мир с любопытством и вдохновлять людей всех возрастов любить учиться. Она живет в Калифорнии с мужем, двумя детьми и маленькой собачкой.
О Komodo — Komodo — это увлекательный и эффективный способ улучшить математические навыки K-5. Komodo, разработанный для детей от 5 до 11 лет для использования в домашних условиях, использует небольшой и частый подход к изучению математики (15 минут, три-пять раз в неделю), который вписывается в напряженный семейный распорядок. Komodo помогает пользователям развить беглость и уверенность в математике — , не задерживая их надолго .
Узнайте больше о Komodo и о том, как он помогает тысячам детей каждый год лучше учиться математике — вы даже можете попробовать Komodo бесплатно.
Математика / Цели обучения математике в пятом классе
Цели обучения математике в пятом классе
Числа и операции Подсчет, наборы чисел, представления чисел, сравнение и порядковые номера, значение места
- отрицательные числа в контексте.
- Поймите концепции ценности через миллионы.
- Считать по сотням тысяч и миллионам.
- Сравните и закажите целые числа до 10 000 000.
- Экспресс-номера до 10 000 000 в различных формах.
- Умножение многозначных чисел.
- Найдите частные, относящиеся к многозначным дивидендам.
- Решать задачи умножения и деления.
- Выберите наиболее полезную форму частного и интерпретируйте остаток.
- Используйте оценку и мысленную математику для оценки сумм, разностей, произведений и частных.
- Модель десятичных дробей с использованием тысячных долей.
- Разберитесь в концепции разряда тысячных долей.
- Перевести десятичные дроби в дроби.
- Сложить и вычесть десятичные знаки.
- Умножайте и делите десятичные дроби на целые числа.
- Решите задачи с умножением и делением десятичных знаков.
- Преобразование дробей в десятичные.
- Связать дроби и выражения деления.
- Сложить и вычесть разные дроби и смешанные числа.
- Умножайте правильные дроби, неправильные дроби, смешанные числа и целые числа.
- Разделите дроби на целые числа.
- Решайте задачи со словами сложения, вычитания, умножения и деления дробей.
- Используйте передаточные числа для решения проблем.
- Найдите эквивалентные соотношения.
- Решите проблемы с процом.
- Перевести дроби в проценты.
- Найдите процент числа.
Алгебраическое мышление
Шаблоны и свойства
- Выявление, описание и расширение числовых шаблонов, включающих все операции.
- Найдите правила для завершения числовых шаблонов.
- Поймите взаимосвязь между числами и символами в формулах для площади поверхности и объема.
- Опишите числовые отношения в контексте.
- Используйте буквы как переменные.
- Напишите и решите числовые предложения для одно-, двух- и трехэтапных реальных задач.
- Напишите и решите уравнения.
- Граф линейных уравнений.
- Упростите алгебраические выражения.
- Понять равенство и неравенство.
- Используйте порядок операций в числовых выражениях с двумя или более операциями.
Геометрия и измерения
Линии и углы
- Нанесите сумму углов на прямую линию.
- Накладываем сумму углов в точке.
- Применить свойство вертикальных углов пересекающихся линий.
- Примените свойства правого, равнобедренного и равностороннего треугольников.
- Примените сумму углов треугольника.
- Примените свойства параллелограмма, ромба и трапеции.
- Продемонстрируйте, что сумма длин любых двух сторон треугольника больше, чем длина третьей стороны.
- Определите и классифицируйте призмы и пирамиды.
- Укажите твердое тело, которое можно сделать из сети.
- Обозначьте цилиндры, сферы и конусы.
- Опишите цилиндры, сферы и конусы по количеству и типу граней, а также количеству ребер и вершин.
- Построить твердые тела с помощью единичных кубов.
- Найдите площадь треугольника как продолжение площади прямоугольника.
- Оценить и измерить объем в кубических единицах.
- Используйте сетку прямоугольной призмы, чтобы найти ее площадь.
- Нанесите точки на координатную сетку.
Анализ данных
Сбор, классификация, организация, представление, интерпретация и анализ данных
- Представьте данные в виде двойной столбчатой диаграммы.
- Анализируйте данные на двойной гистограмме.
Вероятность
Исследование результатов и экспресс-вероятность
- Определите экспериментальную вероятность результата.
- Сравните результаты эксперимента с теоретической вероятностью.
- Найдите все возможные комбинации, перечислив, составив древовидную диаграмму и умножив.
Пятый класс | Инструменты 4 Учителя NC
Учебная база ВведениеЦель этого документа — связать и упорядочить математические идеи, чтобы позволить учителям планировать возможности обучения для учащихся, чтобы развить последовательное понимание математики.Кластеры и последовательность предназначены для того, чтобы помочь учащимся осмыслить связи между математическими идеями и процедурами. Это осмысление происходит сверхурочно. Следовательно, концепции включаются в несколько кластеров с возрастающей глубиной. Они строятся в течение года, начиная с концептуального понимания и постепенно приближаясь к процессуальной беглости.
Каждый кластер включает список связанных стандартов контента и диапазон предлагаемой продолжительности. Стандарты указывают на математические ожидания учащихся к концу учебного года.Стандарты вводятся и разрабатываются в течение года, поэтому тот факт, что стандарт контента указан в конкретном кластере, не означает, что он должен быть освоен в кластере. В некоторых кластерах зачеркивание в стандартах контента обозначает часть стандарта этому мы научимся позже. В других кластерах появляется полный стандарт, но предложения о предполагаемом фокусе указываются в описании кластера. Поскольку стандарты могут быть включены в кластеры задолго до ожидаемого успеваемости, формирующая оценка является важным инструментом для планирования обучения и отчетности об успеваемости учащихся.Эта оценка естественным образом происходит, когда учителя развивают математическое мышление и рассуждения учащихся во время выполнения математических задач.
Особые стандарты математической практики указаны для каждого кластера. Перечисленные предложения являются руководством для учителей. Хотя перечисленные практики могут особенно хорошо подходить для содержания кластера, это не означает, что они будут единственными практиками, которые будут использовать студенты. Студенты, выполняющие сложные математические задачи, естественно, будут заниматься многими математическими практиками, как и математикой.Во время обучения учителя могут наблюдать и решать другие практики, которые учащиеся используют, помимо тех, которые перечислены в кластере.
Каждый кластер включает раздел под названием «Что такое математика?» который описывает важные концепции и связи в рамках стандартов, необходимых учащимся для понимания и использования математики. Второй раздел под названием «Важные соображения» содержит рекомендации, основанные на прогрессе учащихся, а также идеи и модели для обучения в ситуациях, связанных с решением проблем.Решение проблем и математические рассуждения определяют, что значит заниматься математикой. Богатые задания (включая задачи со словами) предоставляют учащимся конкретный контекст для использования при знакомстве с новой математикой. Позже работа с такими задачами позволяет учащимся развить понимание и в конечном итоге продемонстрировать мастерство. Богатые задачи с несколькими точками входа и выхода позволяют естественным образом дифференцировать обучение и доступны для всех студентов.
Первоначальный кластер в каждом классе включает в себя построение математического сообщества.Изучение математики предполагает продуктивную борьбу во время решения проблем и содержательную беседу, когда учащиеся делятся стратегиями и объясняют свое мышление. Для этого требуется, чтобы отдельные ученики обладали математическим складом ума, верой в то, что они могут учиться и заниматься математикой, поэтому они будут рисковать при решении нестандартных задач. Вместе учащиеся должны публично делиться идеями, критикуя математические идеи со сверстниками и учителем. Безопасное сообщество, в котором ошибки и борьба ценятся как возможности для обучения, очень важны.Математические нормы о том, как учащиеся делают и говорят о математике, должны быть четко установлены таким же образом, как и другие распорядки и ожидания, вводимые в начале учебного года.
Учебная программа 5-го класса
Ниже приведены необходимые навыки со ссылками на ресурсы, которые помогут в освоении этого навыка. Мы также поощряем множество упражнений и работу с книгами. Curriculum Home
Важно: это только руководство.
Обратитесь в местный орган управления образованием, чтобы узнать их требования.
Класс 5 | Умножение
☐ Используйте различные стратегии для умножения трехзначного числа на трехзначное. Примечание. Умножение на что-либо большее, чем трехзначный множитель / множимое, должно выполняться с использованием технологий.
☐ Уметь умножать на отрицательные числа
☐ Развивайте свободное владение языком с помощью умножения до 12x
5 класс | Деление
☐ Используйте различные стратегии для деления трех- или четырехзначных чисел на одно- или двузначные числа. Примечание. Деление на что-либо большее, чем двузначный делитель, должно выполняться с использованием технологий.
☐ Легко проверить, может ли одно число быть равномерно разделено на другое, используя правила делимости.
5 класс | Числа
☐ Чтение и запись целых чисел в миллионы
☐ Помните, что некоторые числа делятся только на одно и сами по себе (простое число), а другие имеют несколько делителей (составные)
☐ Вычислить кратное целого числа и наименьшее общее кратное двух чисел
☐ Определите факторы данного числа
☐ Найдите общие делители и наибольший общий делитель двух чисел
☐ Вычислить арифметическое выражение, используя порядок операций, включая умножение, деление, сложение, вычитание и скобки
☐ Сравните и закажите номера в миллионы
☐ Округление чисел до сотых и до ближайших 10 000
☐ Поймите структуру разрядных значений десятичной системы счисления: * 10 единиц = 1 десятка * 10 десятков = 1 сотня * 10 сот = 1 тысяча * 10 тысяч = 1 десять тысяч * 10 десятков тысяч = 1 сотня тысяч * 10 сотен тысяч = 1 миллион
☐ Поймите разницу между множителем и кратным целому числу,
5 класс | Десятичные знаки
☐ Сравните десятичные дроби, используя, или =
☐ Используйте различные стратегии для сложения, вычитания, умножения и деления десятичных знаков до тысячных
☐ Чтение, запись и порядок десятичных дробей с точностью до тысячных
☐ Конвертировать проценты в десятичные числа
5 класс | Дроби
☐ Упростите дроби до наименьших значений
☐ Преобразование неправильных дробей в смешанные числа и смешанных чисел в неправильные дроби
☐ Используйте различные стратегии для сложения и вычитания дробей с одинаковыми знаменателями
☐ Сложить и вычесть смешанные числа с одинаковыми знаменателями
☐ Оценивайте суммы и разности дробей с одинаковыми знаменателями.
☐ Создайте эквивалентные дроби, учитывая дробь
☐ Сравните и упорядочьте дроби, включая отличные от знаменателей (с использованием числовой линии и без нее). Примечание: часто используемые дроби, такие как те, которые могут быть указаны на линейке, мерной чашке и т. Д.
☐ Сравните дроби, используя, или =
☐ Сложение, вычитание, умножение и деление дробей (включая смешанные дроби), знаменателями которых являются степени десятичных дробей.
☐ Разделите дробь на целое число
☐ Умножить дробь на целое число
☐ Выражайте десятичные дроби как эквивалент дробей со знаменателями, которые являются степенями 10
☐ Перевести проценты в дроби
5 класс | Проценты
☐ Поймите, что процент означает часть 100
☐ Преобразование дробей или десятичных знаков в проценты
5 класс | Передаточные числа
☐ Понять концепцию передаточного числа
☐ Экспресс-коэффициенты в разных формах
5 класс | Измерение
☐ Используйте линейку для измерения с точностью до сантиметра или миллиметра
☐ Определите личные рекомендации для метрических единиц длины
☐ Определите общепринятые эквивалентные единицы длины (метрические)
☐ Преобразование длины в метрическую систему
☐ Определите инструменты и методы, необходимые для измерения с надлежащим уровнем точности: длины и углы
☐ Измерьте и начертите углы с помощью транспортира
☐ Понять температуру
☐ Понимание температурных шкал Цельсия и Фаренгейта, включая точки замерзания и кипения воды по двум шкалам
☐ Используйте линейку для измерения с точностью до дюйма, 1/2, 1/4 или 1/8 дюйма
☐ Определите личные рекомендации для стандартных единиц длины США
☐ Определите общепринятые эквивалентные единицы длины (США)
☐ Преобразование длины в системе США
5 класс | Время
☐ Вычислить прошедшее время в часах и минутах
☐ Преобразование времени из минут и секунд в секунды или часов и минут в минуты
5 класс | Геометрия (плоскость)
☐ Вычислить формулу периметра для заданных входных значений
☐ Рассчитать периметр правильных и неправильных многоугольников
☐ Определить соответствующие части равных треугольников
☐ Определить и провести линии симметрии основных геометрических фигур
☐ Постройте точки для образования основных геометрических фигур (определите и классифицируйте)
☐ Расчет периметра основных геометрических фигур, нарисованных на координатной плоскости (прямоугольники и фигуры, состоящие из прямоугольников, имеющих стороны с целой длиной и параллельных осям)
☐ Обозначить пары одинаковых треугольников или других геометрических фигур
☐ Определить соотношение сторон одинаковых треугольников
☐ Классифицируйте четырехугольники по свойствам их углов и сторон
☐ Знайте, что сумма внутренних углов четырехугольника составляет 360 градусов
☐ Классифицируйте треугольники по свойствам их углов и сторон
☐ Знайте, что сумма внутренних углов треугольника составляет 180 градусов
☐ Найдите недостающий угол, если даны два угла треугольника
☐ Определить пары совпадающих треугольников или других геометрических фигур
☐ Знайте, что прямой угол равен 90 градусам, прямой угол — 180 градусов, а полный круг — 360 градусов.
☐ Поймите, что подразумевается под порядком симметрии вращения плоской формы, и узнайте, как найти его значение.
☐ Разберитесь, что подразумевается под правильными и неправильными многоугольниками; выпуклые и вогнутые многоугольники; и сложные многоугольники.
☐ Понять, что подразумевается под точечной симметрией
☐ Понять, что подразумевается под вершиной угла и прилегающими углами
5 класс | Геометрия (твердое тело)
☐ Понять платоновы тела
☐ Постройте модели Платоновых тел из их сетей.
☐ Понимать многогранники и классифицировать их как Платоновы тела, призмы, пирамиды и т. Д.
5 класс | Алгебра
☐ Определите и используйте соответствующую терминологию при обращении к константам, переменным и алгебраическим выражениям
☐ Перевести простые словесные выражения в алгебраические
☐ Подставить присвоенные значения в выражения переменных и оценить, используя порядок операций
☐ Решите простые одношаговые уравнения, используя основные целочисленные факты
☐ Решите и объясните простые одношаговые уравнения, используя обратные операции с целыми числами
☐ Создавайте и объясняйте закономерности и алгебраические отношения (пример: 2,4,6,8… алгебраически 2n (удвоение))
☐ Создавайте алгебраические или геометрические узоры, используя конкретные объекты или визуальные рисунки (например, вращайте и закрашивайте геометрические фигуры)
☐ Знайте разницу между закрытым и открытым предложением.
5 класс | Координаты
☐ Определите и нанесите точки в первом квадранте
5 класс | Логика
☐ Используйте логические рассуждения для решения задач, требующих различных навыков
5 класс | Данные
☐ Собирать и записывать данные из различных источников (например,г., газеты, журналы, опросы, диаграммы и обзоры)
☐ Отображение данных в виде линейного графика, чтобы показать увеличение или уменьшение с течением времени
☐ Вычислить среднее значение для данного набора данных и использовать для описания набора данных
☐ Формулируйте выводы и делайте прогнозы по графикам
5 класс | Оценка
☐ Обосновать обоснованность оценки
☐ Оценка сумм, разностей, произведений и частных десятичных знаков
☐ Обоснуйте обоснованность ответов с помощью оценки
5 класс | Вероятность
☐ Перечислите возможные результаты для эксперимента с одним событием
☐ Запишите результаты эксперимента с использованием дробей / соотношений
☐ Создайте образец пространства и определите вероятность одного события, учитывая простой эксперимент (например,г.



 Зачем нужны скобки. Равноправность сложения и вычитания, а также деления и умножения. Прерогатива деления и умножения над такими действиями, как сложение и вычитание
Зачем нужны скобки. Равноправность сложения и вычитания, а также деления и умножения. Прерогатива деления и умножения над такими действиями, как сложение и вычитание Дуга, радиус, диаметр
Дуга, радиус, диаметр Сдвигание запятой при отсутствии цифр
Сдвигание запятой при отсутствии цифр