Решаем задачу по математике 3 класс (Петерсон, чтоб ее!): bloha_v_svitere — LiveJournal
?- Образование
- Cancel
Дублирую: заполни проспуски.
17 часов 5 минут — 9 часов 30 минут = 16 часов ? минут Вообще-то тут уже далеко не 16 часов ? минут, а вполне определенные 7 часов 35 минут
А от полученного времени (7 часов 35 минут) невозможно вычесть 9 часов 30 минут.
Или если предлагается из 16 часов ? минут вычесть 9 часрв 30 минут, то минуты к 16 часам мне ставить произвольные?
«Кому бы еще спокойной ночи пожелать?» (с)*
*если не знаете этого анекдота, пишите, расскажу.
Tags: 3 класс, Петерсон, школа
Subscribe
Помогите решить задачу по математике (3 класс)
Я очень скромно оцениваю свои математические способности. Но мне кажется, что в условии задачи чего-то не хватает: В одном куске 12 м ткани, а во…
Очередная петерсонная задача по математике (1 класс)
Ох уж эта Петерсон и ее учебник по математике для начальной школы! У меня такое ощущение, что она росла на загадках: «Плывут два крокодила. Один…
Помогите решить задачу по математике (1 класс)
У меня с логикой плохо. Номер 4 — найти закономерность и вставить пропущенные цифры. Намекните на закономерность, а цифры, может, уже сообразим…
Помогите решить задачу по математике (3 класс)
Надо мне взять тэг у antep_fistik «Бурасы Туркие». Что такое — не знаю, но это очень точно характеризует мое понимание…
Задача по математике 2-й класс
Я что-то опять туплю и прошу помощи зала.
 Задача такая: Андрей забил в три раза больше голов, чем Толя. А Толя на шесть голов больше, чем Андрей.…
Задача такая: Андрей забил в три раза больше голов, чем Толя. А Толя на шесть голов больше, чем Андрей.…Помогите решить задачу по математике (2 класс)
С аэродрома поднялось в воздух d пар самолетов, а b самолетов осталось. На сколько больше самолетов осталось, чем улетело? Вариант: b — d*2…
Photo
Hint http://pics.livejournal.com/igrick/pic/000r1edq
Помогите решить задачу по математике (3 класс)
Я очень скромно оцениваю свои математические способности. Но мне кажется, что в условии задачи чего-то не хватает: В одном куске 12 м ткани, а во…
Очередная петерсонная задача по математике (1 класс)
Ох уж эта Петерсон и ее учебник по математике для начальной школы! У меня такое ощущение, что она росла на загадках: «Плывут два крокодила. Один…
Помогите решить задачу по математике (1 класс)
У меня с логикой плохо. Номер 4 — найти закономерность и вставить пропущенные цифры.
 Намекните на закономерность, а цифры, может, уже сообразим…
Намекните на закономерность, а цифры, может, уже сообразим…Помогите решить задачу по математике (3 класс)
Надо мне взять тэг у antep_fistik «Бурасы Туркие». Что такое — не знаю, но это очень точно характеризует мое понимание…
Задача по математике 2-й класс
Я что-то опять туплю и прошу помощи зала. Задача такая: Андрей забил в три раза больше голов, чем Толя. А Толя на шесть голов больше, чем Андрей.…
Помогите решить задачу по математике (2 класс)
С аэродрома поднялось в воздух d пар самолетов, а b самолетов осталось. На сколько больше самолетов осталось, чем улетело? Вариант: b — d*2…
Урок математики 3 класс. Л.Г.Петерсон. Тема «Формула работы»
I. Организационный момент.
— Сейчас урок математики.
II. Мотивация к учебной деятельности.
— Давайте прочитаем хором высказывание
Человек лишь тогда чего-то добивается, когда он верит в свои силы. (немецкий философ Андреас Фейербах)
(немецкий философ Андреас Фейербах)
— О каких качествах идет речь?
— Как эти качества могут нам пригодиться?
III. Актуализация знаний.
— В математике часто используются формулы.
— Какие формулы вы знаете?
— А зачем они нужны? (Чтобы решать похожие и обратные задачи)
– Рассмотрите таблицу. О каких величинах можно составить задачи.
— Составьте задачи по данным таблицы.
s | v | t |
? | 60 км/ч | 4ч |
540 км | ? | 6ч |
57км | 19км/ч | ? |
S=v•t t=s:v v=a•b•c s= a•b v=s:t
— Какие формулы вы будете использовать для решения этих задач? Подчеркнем их и прочитаем.
— Запишите в тетради только ответы этих задач.
— Давайте проверим с помощью сигнальных кругов.
-Те, кто не ошибся в решении задач, поставьте на полях +.
IV. Пробное действие.
— Запишите формулу, для решения следующей задачи.
«Одна швея за 5ч сшила 20 фартуков, другая за 4ч сшила 16 таких же фартуков. Какая швея работает быстрее?»
— Какие формулы записали? А кто не записал никакой формулы?
— В чем трудность? (Не могу записать формулу для такой задачи)
— Почему возникло затруднение? (Не знаем такой формулы)
— О чем эта задача? (о работе)
— Какие величины есть в задаче? (время работы, скорость работы)
— Какая новая величина? (работа)
— Как же можно назвать эту формулу? (формула работы)
V. Сообщение темы урока и постановка целей.
Сообщение темы урока и постановка целей.
— Итак тема урока «Формула работы»
— Какие же цели мы поставим на сегодняшний урок?
Цели урока:
1. Узнать формулу работы.
2. Научиться решать задачи по формуле работы.
VI. Решение учебной задачи. Открытие нового знания.
— Заполним таблицу к задаче.
— О каких величинах идет речь в этой задаче?
(о времени, количестве выполненной работы)
— Если сказано «быстрей», то о какой величине идет речь?
— Какие задачи напоминает? (задачи на движение)
— Как же найти скорость работы? (всю работу разделить на время)
— В математике скорость работы принято обозначать v, так же, как и в задачах на движение.
Вся выполненная работа – А,
Время, затраченное на работу – t, так же, как и в задачах на движение.
— Попробуйте сами записать формулу, по которой можно найти скорость работы. v=A: t
— А теперь выведем формулу работы.
— Чем является А? (А – делимое, чтобы найти делимое, нужно частное умножить на делитель)
— Прочитайте получившуюся формулу. A=v•t
— Какую еще формулу можно вывести? t= A: v
— А теперь сверим с текстом на доске.
— Что нового узнали, почитав текст?
(Скорость еще называют производительностью)
— Что же мы подразумеваем под словом работа?
VII. Физминутка.
Физминутка.
— Объясните, как вы понимаете смысл следующих высказываний? (с. 44 № 1)
— Давайте еще раз озвучим цели урока.
— Узнали формулу работы? Прочитайте ее.
— Какие формулы вывели? Прочитайте их.
VIII. Первичное закрепление.
— Какой была вторая цель?
(Научиться решать задачи по формуле работы.)
— Предлагаю выполнить следующие задания:
1. Составить и решить задачи по таблице.
A | v | t |
? | 4 детали/мин | 5 мин |
160 скворечников | ? | 8 дней |
120 шт. | 60 шт/ч | ? |
A=v•t v=A: t t= A: v
— Запишите решение этих задач.
-Проверим решение задач через документ-камеру.
— Какую формулы выбрали для решения задач?
— Покажите, какую формулу использовали для нахождения неизвестной величины.
— Те, кто не ошибся в решении задач, поставьте на полях +.
2. Практическая работа (индивидуальные карточки с примерами)
— А сейчас вы попробуете вычислить производительность своего умственного труда.
— Будем решать на время примеры, а данные заносить в таблицу.
Вся работа A | Производительность V | Время работы t |
… | ? | 2мин |
3. Взаимопроверка
— Давайте проверим правильность решения.
— Запишите количество правильных ответов в таблицу.
— Если количество правильных ответов не меньше 10 – поставьте себе +
— Как узнать производительность? Какой формулой воспользуемся? (v=A: t)
— Вычислите свою производительность.
(количество правильных примеров разделить на 2 мин)
-Где в жизни может пригодиться умение находить производительность, объем работы, время работы?
IX. Контроль достижения целей.
Контроль достижения целей.
— А теперь вернемся к задаче, которая вызвала затруднение.
— Какую же формулу выберем?
— Запишите самостоятельно решение этой задачи в тетрадь.
— Проверим решение.
— Те, кто правильно решил задачу, поставьте на полях +.
X. Рефлексия.
— Итак, какой была тема урока?
— Какие цели мы поставили на урок? Прочитайте формулу работы.
— Достигли этих целей?
— Помогли ли нам в достижении поставленных целей те качества, о которых мы говорили в начале урока.?
XI. Д/з с. 44 № 4, № 5.
Матология по классам | Pearson в Канаде
Mathology Grade Three включает следующие компоненты, которые можно приобрести вместе или по отдельности:
Mathology Grade 3 Activity Kit: 32 увлекательных игры и задания, разработанные для поддержки понимания учащимися математики.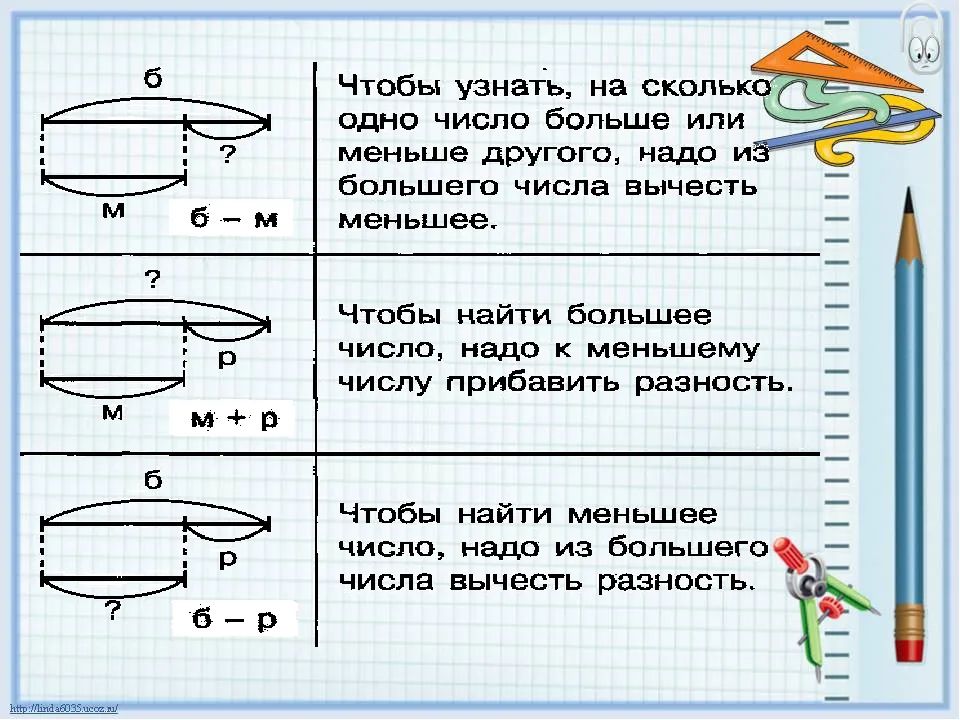
18 художественная и научно-популярная литература Маленькие книжки по математике и пособия для учителей, предназначенные для того, чтобы вовлечь учащихся в развитие математических навыков и словарного запаса на раннем этапе.
Mathology Математические коврики 3–4 классы: 44 ламинированных математических коврика, которые можно списывать при стирании, чтобы помочь учащимся представлять, демонстрировать и иллюстрировать свое понимание математических концепций.
Mathology.ca: Наш онлайн-центр для учителей, предназначенный для улучшения:
- Поиск
- Планирование
- Обучение
- Оценка и отслеживание
- Профессиональное обучение
Все в одном удобном он-лайн месте.
Благодарности Авторы
Предварительно просмотрите компоненты ниже.
Благодарности
Reviewers
Adams, Tina
School District #22, Vernon, BC
Auger, Marianne
Trillium Lakelands District School Board, ON
Ball, Sandra
Консультант (на пенсии), Британская Колумбия
Битти, Рут
Факультет образования, Университет Лейкхед,
Белески, Джейн
Школьный округ № 44, Северный Ванкувер, Британская Колумбия
БУРДА, LOIS
Программа STECOIST), STED), STED), STINGENTINT), STED), STED), STED), STED), STED), STED), STED), STED), STED), STED), STED), STED), STED), STED), STED), STED), STED), STED), STED), LOIS

Кейв, Филлис
Консультант по раннему развитию (на пенсии), ON
Chamberland, Jennifer
Школьный совет округа Halton 90, ON0003
Collison, Lisa
Kawartha Pine Ridge District School Board, ON
Cooper, Kate
Faculty of Education, Lakehead University, ON
Cunningham, Sheila
Saskatchewan Rivers Отдел государственных школ, SK
ДиЛиберо, Энн Мари
Районный школьный совет Ниагары, Онтарио
Фризен, Ким
School District #22, Vernon, BC
Gauthier, Liliane
Educational Consultant, SK
Goulden, Wendy
Coordinator of Elementar Programs (Retired), ON
Hartmann , Дебора
Тренер по учебной программе (на пенсии), ON
Highet, Maxine
Школьный совет католического округа Йорк, ON
Johns0006
Тренер по математике, PEI
Lajambe, Heather
Math Lead, Kakisiwew School, Ochapowace Nation, SK
Lawrence, Patricia
9003 9003
Horte School, LAIRIE School,
9003 9003
. Ли, Меган
Ли, Меган Школьный округ № 22, Вернон, Британская Колумбия
Мало, Сильвия
Консультант по математике, AB
9, Мишель Маккей0006
Школьный совет округа Пил,
McTavish, Claire
Greater Saskatoon Catholic School , Heather
Школьный совет округа Блууотер, ON
Morgan, Nancy
Католические школы Элк-Айленда, AB
Niebergall, Miranda
Parkland School Division, AB
O’Leary, Andrea
Trillium Lakelands District School Board, ON
Pemberton, Kerry
Annapolis Valley Regional Centre for Education , NS
Simmons, Wilma
Консультант (на пенсии), ON
Солецкий, Улана
Математика, AB Edmontons, консультант0054
Steiner, Lana
Good Spirit School Division, SK
Strangway, Lynn
Toronto District School Board, ON
Taylor, Sarah
Peterborough Victoria Northumberland and Clarington Школьный совет католического округа, ON
Трейнор, Патрис
Консультант по вопросам образования, Британская Колумбия
Аппер, Крейг
Отдел государственной школы Форт МакМюррей, AB
Vandesande, Debbie
Школьный округ #22, Вернон, BC
, Varty, Gerry
, Mathemattan Lyn
Консультант (на пенсии), ON
Vianzon, Monaliza
Pembina Trails School Division, MB
Webb,06 Kyle 9 Webb,060003
Regina Catholic Schools, SK
Wiebe, Jerrold
Pembina Trails School Division, MB
Wines, Deborah
Trillium Lakelands District School Board, ON
Witz, Leah
Независимая школа, ON
Пирсон выражает благодарность следующим источникам за иллюстрации, фотографии и другие материалы, использованные в Матологии для 3 класса.
Illustrations and Photos
Classroom Activity Kit
OVERVIEW
Sam Edwards/Caia Image/Age fotostock
MLB Calla’s Jingle Dress: Cindy Revell
MLB Planting Seeds: Joanna Czernichowska
STUDENT CARDS
Номер
Состав: студенческие билеты 1A, 1B, 4A, 4B, 8A, 8B, 9A, 9B, 12A, 12B, 18A, 18B
Вивиана Гарофоли: студенческие билеты 2A, 2B
Student Cardes 3A , 3Б
Холли Купер: студенческие билеты 5A, 5B
Диего Вайсберг: студенческие билеты 6A, 6B
Энни Беттс: студенческие билеты 7A, 7B
Энтони Льюис: студенческие билеты 10
Синди Ревелл:
9002 901 02 901 02 11 11 студенческие билеты Сачико Йошикава: студенческие билеты 11C, 11DКоллин Мэдден: студенческие билеты 13A, 13B
Джо Тейлор: студенческие билеты 14A
Трейси Сабин: студенческие билеты 14B
Хавьер Хоакин: студенческие билеты 15A, 020 Cтудент 90:003B 90:003B 90:003B 90:00002 Карточки 16А, 16В
Джон Стюарт: Студенческие билеты 17A, 17B
Марк Раффл: Студенческие билеты 19A, 19B
Студенческий билет 1A (фон, знак скорости, торт, подарочный пакет, майка, дом, общественный автобус): Ilina93/Shutterstock; Лестер Балахадиа/Shutterstock; Алессандро Гарофало/Newscom; рабочий/Шаттерсток; Роман Гориелов/Алами; джазмхх/Shutterstock; Джефф Уайт/Shutterstock
Студенческий билет 1B (фон, дверь, Си-Эн Тауэр, экскаватор, знак назначения, дом, книга): Ilina93/Shutterstock; К. Деча/Shutterstock; Сунцюань Дэн/Shutterstock; cbphoto/Алами; АрлифтАтоз2205/Шаттерсток; джазмхх/Shutterstock; М-Рэкхэм/Шаттерсток
Деча/Shutterstock; Сунцюань Дэн/Shutterstock; cbphoto/Алами; АрлифтАтоз2205/Шаттерсток; джазмхх/Shutterstock; М-Рэкхэм/Шаттерсток
Студенческие билеты 4A, 4B (фон): S-F/Shutterstock
Студенческие билеты 9A, 9B (плитка шоколада, деревянная линейка, значок батареи, счетчик красного медведя, счетчик синего медведя, счетчик зеленого медведя): PandaStudio/Shutterstock; Электронный вектор/Shutterstock; Колонко/Шаттерсток; Мама Фила/Shutterstock; Мама Фила/Shutterstock; Phil’s Mommy/Shutterstock
Студенческий билет 12A (фон, желтые стикеры, булавки): Texturis/Shutterstock; Владимир Саныч/Shutterstock; Людмила Харламова/Shutterstock и Зурбанов Алексей/Shutterstock
Студенческий билет 12B (фон, синие стикеры, булавки): Texturis/Shutterstock; В. Фокин/Шаттерсток; Людмила Харламова/Shutterstock и Зурбанов Алексей/Shutterstock
Студенческие билеты 13А, 13Б (шаги): Виктория Матыня/Shutterstock
Студенческий билет 14А (наушники, звуковая система, ноутбук, КЛЛ): dantess/Shutterstock; CapturePB/Shutterstock; ittoilmatar/Shutterstock; Wuttichok Panichiwarapun/Shutterstock
Студенческие билеты 15A, 15B (пластиковая бутылка с водой, бинт): DenisMArt/Shutterstock; Коптер Пиксель/Shutterstock
Студенческие карты 18A, 18B (арахисовое масло, тунец, ломтики сыра, хлеб, малина, банка фасоли, поднос с йогуртом, макароны, коробка с хлопьями, апельсиновый сок, мороженое, бананы, морковь, молоко): Africa Studio/Shutterstock; Китч Бейн / Shutterstock; The_Pixel/Shutterstock; Ратикова/Shutterstock; ДжениФото/Шаттерсток; Арвинд Балараман/Shutterstock; Фотофермер/Шаттерсток; Гуляш/Шаттерсток;
Гтс/Шаттерсток; с-тс/Шаттерсток; Вита Пахай/Shutterstock; Макс Народенко/Shutterstock; Лоренцо Аркобассо/Shutterstock; s-ts / Shutterstock
Студенческие карты 19A, 19b (фоновая): Arigato/Shutterstock
Паттерны и алгебра
Джон Курц: Студенческие карты 20A, 20B
Соединение: студенческие карты 21a, 21b, 22a, 22B
Студент. 22A (фиолетовая кнопка в форме звезды, синяя кнопка в форме треугольника, темно-фиолетовая кнопка в форме звезды, заглавные буквы X и заглавные буквы Y, строчная буква y): monemi/Shutterstock; Ричард Петерсон/Шаттерсток; монэми/Shutterstock; Бриллиантовая студия/Shutterstock; БелаяБарби/Shutterstock
22A (фиолетовая кнопка в форме звезды, синяя кнопка в форме треугольника, темно-фиолетовая кнопка в форме звезды, заглавные буквы X и заглавные буквы Y, строчная буква y): monemi/Shutterstock; Ричард Петерсон/Шаттерсток; монэми/Shutterstock; Бриллиантовая студия/Shutterstock; БелаяБарби/Shutterstock
Студенческий билет 22B (красная квадратная табличка, пуговицы): маленькая птичка/Shutterstock; Picsfive/Shutterstock
Measurement
Steve Bjorkman: Student Cards 23A, 23B
Fabiana Faiallo: Student Cards 24A, 24B
Composure: Student Cards 25A, 25B, 25C, 25D
Geometry
Самообладание: студенческие билеты 26A, 26B, 27A, 27B
Christos Skaltsas: студенческие билеты 28A, 28B, 28C, 28D
Valentina Belloni: студенческие билеты 29A, 29B
студенческие билеты 27A, 27B (деревянная фоторамка): TR STOK/Shutterstock 31A, 31B, 32A, 32B
Студенческие билеты 31A, 31B (фон): stockcreations/Shutterstock
Маты по математике
Иллюстрации Джованни Джорджи Пьерфранчески . Изображения счетов воспроизведены с разрешения Банка Канады.
Изображения счетов воспроизведены с разрешения Банка Канады.
Mathology.ca
УРОКИ
Иллюстрации Джованни Джорджи Пьерфранчески, Джона Курца Изображения монет © Королевский монетный двор Канады, 2021. Все права защищены. Изображения счетов воспроизведены с разрешения Банка Канады.
Номер
Урок 1 (фото в разделе «До»): Adam Borg/Shutterstock; RuskaPixs/Shutterstock; DSO Media/Shutterstock
Урок 4 (фото в разделе «До»): JayTee88/Shutterstock; Фотография Имрана Хана / Shutterstock; эрмесс/Shutterstock
Урок 5 (фото в разделах «До» и «Работа над этим»): Лаура Уотсон; Gucio_55/Shutterstock
Урок 9 (фото в разделе «До»): Tom Barrett
Урок 11 (фото в разделе «Дополнительный мини-урок»): Dave Whamond
Урок 25 (фото в разделе «До»): 32 пикселя/Shutterstock
Урок 27 (фото в разделе «До»): Mark Sykes/Alamy Stock Photo
Урок 37 (фото в разделе «До»): Юлиан Велчев/Shutterstock; Робертиндиана/Шаттерсток; пануват фимфа/Shutterstock
Паттерны и алгебра
Урок 1 (фото в ‘до’): Leanne Franson
Урок 3 (фото в ‘до’): PD Studio/Shutterstock
Измерение
Урок . 1 (фото в «Word Wall»): Nertuz/Shutterstock; vvoe/Shutterstock
1 (фото в «Word Wall»): Nertuz/Shutterstock; vvoe/Shutterstock
Урок 6 (фото в разделе «Работа над этим»): Мария Тревино
Геометрия
Урок 4 (фото в разделе «До»): VanoVasaio/Shutterstock; Мария Драйфхаут/Shutterstock; Ташатуванго/Шаттерсток; анмбф/Шаттерсток; EHStockphoto/Shutterstock
Урок 5 (фото в разделе «Консолидация»): Wangkun Jia/Shutterstock
Урок 7 (фото в разделе «До»): Shutterstock
Урок 8 (фото в разделе «До»): Потапов Александр/Shutterstock; Данита Делимонт/Алами Фото со стока; studiovin/Shutterstock
Урок 11 (фото в разделе «До»): Chris Hil/Shutterstock; Elly Godfroy/Shutterstock
Урок 12 (фотографии в «Консолидации» и «Дополнительном мини-уроке»): Slanapotam/Shutterstock; катастрофа_OL/Shutterstock; дизайн/Shutterstock; © Anders Hingel/Saatchi Gallery
Урок 20 (фото в разделе «До»): pavels/Shutterstock; донатас1205/Shutterstock; Erhan Inga/Shutterstock
Урок 21 (Фото в «До»): Art By Isla Townsend-Rahman
Reproducibles
Иллюстрации от Giovanni Giorgi Pierfranceschi
Номер
Номер
9/Номер
9003 Толстяк Джеки/Шаттерсток; Стив Уайт; Толстяк Джеки/Шаттерсток; Ричард Браун/Алами Фото со стока; Толстый Джеки / ShutterstockГеометрия
Мастер 52: Чернецкая Наталья/Shutterstock
Мастер 57: MK studio/Shutterstock; Сипарис/Шаттерсток; mayakova/Shutterstock
Мастер 69: Ольга Мильцова/Shutterstock
Мастер 72: Искусство Ислы Таунсенд-Рахман
ПРАКТИКА, ВЫХОДНОЙ БИЛЕТ И ПОКАЖИТЕ ЧТО ВЫ ЗНАЕТЕ
Иллюстрации John PieresnchiCo Королевский монетный двор Канады 2021 г. — Все права
— Все права
защищены.
Number
Lesson 1 (photo in ‘Practice’): pockygallery/Shutterstock
Technical Art
Math Mats
Giovanni Giorgi Pierfranceschi
Mathology.ca
LESSONS
Giovanni Giorgi Pierfranceschi , John Kurtz
ВОСПРОИЗВОДИМЫЕ РЕПРОДУКТЫ
Giovanni Giorgi Pierfranceschi
ПРАКТИКА, ВЫХОДНОЙ БИЛЕТ И ПОКАЖИТЕ, ЧТО ВЫ ЗНАЕТЕ
Giovanni Giorgi Pierfranceschi, John Kurtz
Авторы
Тара Флинн — педагог, исследователь, автор и редактор. В качестве научного директора исследовательской программы доктора Кэти Брюс (Trent Math Education Research Collective) Тара была удостоена чести работать с сотнями преданных своему делу педагогов-новаторов, исследующих преподавание и изучение математики, особенно в области пространственного мышления и дробей. Этот совместный подход к исследованиям привел к таким вкладам, как документ Министерства образования Онтарио Обращая внимание на пространственное мышление (соавтор), ресурс Pearson Принимая форму: занятия по развитию геометрического и пространственного мышления, классы K–2 (соавтор и руководитель редакционного проекта) и ресурс ETFO Learning Through Исследования учителей: руководство для вашего исследовательского путешествия (основной автор). Педагог в третьем поколении, Тара твердо верит в государственное образование и значимое участие педагогов в исследованиях, чтобы результаты этой работы отражали и поддерживали бесконечно сложный мир в классе.
Педагог в третьем поколении, Тара твердо верит в государственное образование и значимое участие педагогов в исследованиях, чтобы результаты этой работы отражали и поддерживали бесконечно сложный мир в классе.
Дженнифер Картер — окружной координатор школьного округа Вернон в Британской Колумбии. У нее есть опыт преподавания в начальных классах, в том числе 15 лет в 1–3 классах. Дженнифер является исполнительным членом Ассоциации учителей математики Британской Колумбии (BCAMT), членом сети BC Numeracy Network, председателем внутренней сети математики и адъюнкт-профессором Университета Британской Колумбии (UBCO).
Лариса Люцив последние 15 лет работала учителем в Совете католической школы Эдмонтона. Она преподавала в 1-м, 2-м и 3-м классах и сейчас работает воспитателем детского сада в 9-м классе. Она провела 10 лет в школе Св. Франциска Ассизского, школе языка и культуры кри Нехия Пиматисивин. Лариса считает, что каждый ребенок может добиться успеха, если завязываются отношения, которые помогают раскрыть таланты и интересы учеников.
Кили Мартин проработал в Окружном школьном совете Ниагары 12 лет учителем начальных классов, инструктором, а в последнее время — учителем учебных ресурсов. Она увлечена своей ролью учебного лидера, поддерживая учителей в разработке увлекательных уроков, которые используют обучение, основанное на исследованиях, и удовлетворяют потребности разных учащихся. Как творческий и заботливый педагог, она любит учиться вместе со своими коллегами и учениками, используя их уникальные математические способности, чтобы глубже понять, как математика связана с окружающим миром.
Энн Пиджен работает педагогом 27 лет. Она имела честь работать в различных ролях, в том числе: Координатор обучения по математике, что дало ей возможность посещать бесчисленные классы математики, работая с преданными учителями посредством совместных исследований; Сотрудник по успеваемости учащихся Министерства образования Онтарио, содействующий профессиональному обучению математике на уровне провинций, регионов и школ; и классный руководитель, где она делится своей любовью к преподаванию математики со студентами и коллегами.
В 2016 году Энн была удостоена награды Ассоциации координаторов математики Онтарио (OMCA) за выдающиеся достижения и инновации в области математического образования. Она получила степень магистра в области образования в Университете Западного Онтарио, где заинтересовалась отношениями части и целого и развитием понимания студентами операций. Недавно она участвовала в исследовании преподавания и изучения дробей посредством честного обмена. Энн — гордая мать двух замечательных мальчиков.
Джонатан Со () — гордый учитель школьного совета округа Пил в Онтарио. Он преподавал во 2–8 классах и в настоящее время является учителем 4 класса. Джонатан всегда стремится поощрять творчество и исследования в своей семье, учениках и коллегах. Он получил степень магистра в области образования, сосредоточившись на том, как его вопросы повлияли на изучение учащимися взаимосвязей части и целого в дробях. Джонатан интересуется математикой, оцениванием и технологиями, и он увлечен исследованиями и бесконечными возможностями, которые они открывают для учащихся. Джонатан — спикер TEDx, выступавший на различных семинарах по всей Канаде. Он гордый родитель 3 замечательных маленьких детей, заядлый бегун и любитель галстуков-бабочек.
Джонатан — спикер TEDx, выступавший на различных семинарах по всей Канаде. Он гордый родитель 3 замечательных маленьких детей, заядлый бегун и любитель галстуков-бабочек.
Эрик Тизер имела возможность работать в системе начального математического образования Онтарио почти 20 лет. Его различные роли включали классного руководителя, тренера по математике и консультанта. Эрик также был президентом Ассоциации координаторов математики Онтарио (OMCA) и недавно преподавал дополнительные курсы повышения квалификации в Педагогическом колледже Онтарио. Он по-прежнему в восторге от работы со студентами и преподавателями, поскольку они ищут математику в своем мире способами, которые помогают им рассуждать и понимать математику, которую они изучают.
Венди Вес более 40 лет работала в сфере образования в Манитобе классным руководителем, учителем вспомогательных служб и консультантом отдела дошкольного образования, занимаясь улучшением навыков грамотности и счета в классах K–4. Она провела множество семинаров по математике для детей младшего возраста, включая «Первые шаги в профессиональном развитии математики». Венди твердо убеждена, что когда учителя понимают концептуальные идеи, лежащие в основе математики, могут наблюдать и исследовать то, что знают учащиеся, и иметь репертуар надежных учебных действий, обучение учащихся математике значительно улучшится.
Она провела множество семинаров по математике для детей младшего возраста, включая «Первые шаги в профессиональном развитии математики». Венди твердо убеждена, что когда учителя понимают концептуальные идеи, лежащие в основе математики, могут наблюдать и исследовать то, что знают учащиеся, и иметь репертуар надежных учебных действий, обучение учащихся математике значительно улучшится.
Хизер Джелли проработала в школьном совете округа Йорк 31 год, прежде чем недавно вышла на пенсию. Как ранний учитель начальных классов, Хизер использовала множество возможностей для лидерства, чтобы сотрудничать с педагогами, в том числе была преподавателем в школьном классе, тренером по грамотности и тренером по математике. Последние 4 года она провела в совете директоров, работая консультантом по математике и раннему обучению. На протяжении своей карьеры Хизер посчастливилось участвовать в невероятном профессиональном обучении с известными исследователями/авторами в области грамотности, устной речи и математики. Она твердо убеждена, что все учащиеся способны и компетентны, если у них есть время и возможность показать, что они знают. Она верит в способность преподавателей развивать понимание устной речи и ее связи с изучением математики, в частности, в обучении тому, как поощрять голос учащихся.
Она твердо убеждена, что все учащиеся способны и компетентны, если у них есть время и возможность показать, что они знают. Она верит в способность преподавателей развивать понимание устной речи и ее связи с изучением математики, в частности, в обучении тому, как поощрять голос учащихся.
Шелли Йерли
После 8 лет работы руководителем отдела математики в провинции по заданию Совета директоров по вопросам образования Онтарио (CODE), Шелли вернулась к преподаванию математики в классе Trillium Lakelands DSB. Во время выполнения задания ключевым проектом в ее портфолио было исследование действий под руководством доктора Кэти Брюс из Трентского университета, которое было сосредоточено на преподавании и изучении дробей. В этой работе, являющейся партнерством между CODE, Трентским университетом и Министерством образования Онтарио, участвовали учащиеся и преподаватели классов K–12 нескольких школьных советов округа Онтарио. Шелли также сыграла роль в разработке многочисленных ресурсов и профессиональной поддержки обучения для педагогов K-12, включая серию «Внимание к…» и провинциальные программы GAINS Math CAMPPP. Шелли работала в ряде комитетов, в том числе в Комитете по образовательным материалам NCTM (2014–2017 гг.), Сети практических исследований Исполнительного комитета Америки (2009 г.–2014 г.), Министерство образования Онтарио, объединяющее практику и исследования — Консультативная группа по математике (2007–2010 гг.), а также в качестве исполнительного члена Ассоциации координаторов математики Онтарио (2002–2006 гг.). Страсть педагогов к обучению и стремление к качественным образовательным задачам, основанным на исследованиях, вдохновляет Шелли продолжать поддерживать более тесное соответствие между исследованиями и практикой в классе.
Шелли работала в ряде комитетов, в том числе в Комитете по образовательным материалам NCTM (2014–2017 гг.), Сети практических исследований Исполнительного комитета Америки (2009 г.–2014 г.), Министерство образования Онтарио, объединяющее практику и исследования — Консультативная группа по математике (2007–2010 гг.), а также в качестве исполнительного члена Ассоциации координаторов математики Онтарио (2002–2006 гг.). Страсть педагогов к обучению и стремление к качественным образовательным задачам, основанным на исследованиях, вдохновляет Шелли продолжать поддерживать более тесное соответствие между исследованиями и практикой в классе.
Морин Постникофф более 25 лет работает педагогом в школьном округе Кутеней-Колумбия в Британской Колумбии. За это время она взяла на себя множество ролей и обязанностей на всех уровнях своего округа. Карьера Морин началась с работы учителем по вызову, репетитором по математике и тренером, а затем в течение 12 лет переросла в преподавание математики в средней школе. В 2007 году она получила степень магистра в области лидерства и учебной программы. Желание изменить ситуацию с учениками в более раннем возрасте (особенно в арифметике) привело к смене должностей и изменению педагогики. Проработав 5 лет в начальной школе, Морин взяла на себя роль районного координатора по обучению. В течение 3 лет она помогала учителям и учащимся внедрять новую учебную программу Британской Колумбии и работала в различных провинциальных командах по планированию и консультированию. В настоящее время Морин снова можно найти в начальной школе Фрутвейл, где она преподает все предметы увлеченным ученикам 6 и 7 классов. Будучи учителем на протяжении всей жизни, она любит путешествовать по всему миру, подтверждая свою веру в то, что лучшее обучение происходит путем изучения и получения опыта для себя.
В 2007 году она получила степень магистра в области лидерства и учебной программы. Желание изменить ситуацию с учениками в более раннем возрасте (особенно в арифметике) привело к смене должностей и изменению педагогики. Проработав 5 лет в начальной школе, Морин взяла на себя роль районного координатора по обучению. В течение 3 лет она помогала учителям и учащимся внедрять новую учебную программу Британской Колумбии и работала в различных провинциальных командах по планированию и консультированию. В настоящее время Морин снова можно найти в начальной школе Фрутвейл, где она преподает все предметы увлеченным ученикам 6 и 7 классов. Будучи учителем на протяжении всей жизни, она любит путешествовать по всему миру, подтверждая свою веру в то, что лучшее обучение происходит путем изучения и получения опыта для себя.
Новые компоненты для 3 класса
Буклет с математическими ковриками для 3–4 классов
44 ламинированных коврика по математике с надписями и стиранием, предназначенные для помощи учащимся:
- Представлять, демонстрировать и иллюстрировать свое понимание математических понятий.

- Будьте критичны и изобретательны, делая математические выборы, предположения и решения.
- Сохраняйте позитивную мотивацию и настойчивость, решая сложные математические задачи.
- Поделитесь своим мнением.
Посмотреть математические коврики в действии
Что внутри?
Виртуальный образец Купить
Комплект заданий для 3 класса
- Помогите учителям уверенно проводить насыщенные уроки математики
- Поддержка различных настроек класса (весь класс, небольшая группа, учебные центры и онлайн-обучение)
- Вовлекайте учащихся всех уровней, повышая уверенность в своих математических навыках
- Помогите учителям быстро распознать стратегии учащихся и определить следующие шаги с помощью практических формирующих оценок.
 Поддержка
Поддержка - Продвижение учащихся по ступеням изучения математики
- Приобретайте прочные базовые знания об основных навыках в течение года
**Все материалы для учителей можно найти на сайте Mathology.ca
Что внутри комплекта для занятий для 3 класса Купить
Маленькие книги для 3 класса
В 3 классе есть 18 маленьких книжек по математике. Они отлично подходят для занятий дома и поддерживают как математику, так и грамотность.
Фантастические путешествия
Большая идея: Числа связаны во многих отношениях.
- оценка количества до 1000
- сравнить/заказать количество до 1000
Хоккей Домашнее задание
Большая идея: количества и числа могут быть сгруппированы по единицам или разделены на единицы.
- разделить целое на равные части (доли)
- сравнить дроби
В поисках Бастера
Большая идея: количества и числа могут быть сгруппированы по единицам или разделены на единицы.
- составить до 1000 на основе позиционного значения
- сравнить/заказать номера с 1000
Как работают числа
Большая идея: количества и числа могут быть сгруппированы по единицам или разделены на единицы.
- составление/разложение трехзначных чисел
- поиск и использование шаблонов чисел
Математика заставляет меня смеяться
Большая идея: количества и числа можно складывать и вычитать, чтобы определить, сколько или сколько.
- добавить/вычесть до 1000
- оценивайте, сравнивайте и заказывайте номера по номеру 1000
Уличная вечеринка
Большая идея: количества и числа можно складывать и вычитать, чтобы определить, сколько или сколько.
- добавить/вычесть до 1000
- сравнить/заказать номера до 1000 (доработка)
Посадка семян
Большая идея: количества и числа можно складывать и вычитать, чтобы определить, сколько или сколько.
- добавить/вычесть до 1000
- разработка концепции умножения
Спортивный лагерь
Большая идея: количества и числа можно умножать (путем группировки единиц) и делить (путем разделения на единицы), чтобы определить, сколько или сколько.
- моделировать и решать проблемы равного группирования/совместного использования
- относятся сложение к умножению, вычитание к делению
Джингл-платье Каллы
Большая идея: количества и числа можно умножать (путем группировки единиц) и делить (путем разделения на единицы), чтобы определить, сколько или сколько.
- умножить и разделить на 50
- прибавить и вычесть до 100
Чудесные шедевры Намира
Большая идея: закономерности можно описать математически.
- исследование моделей роста и сокращения (доработка)
- использовать уравнения для представления простых моделей увеличения и уменьшения
Неделя испытаний
Большая идея: закономерности можно описать математически.
- использовать свойства равенства для решения задач
- использовать язык алгебры
Козий остров
Большая идея: единицы измерения можно использовать для измерения и сравнения атрибутов.
- измерение времени, температуры и длины
- изучить единицы измерения и их отношения
Измерения О ВАС!
Большая идея: единицы измерения можно использовать для измерения и сравнения атрибутов.
- оценка, измерение и сравнение атрибутов
- определить и связать меры
Вызов Кролика
Большая идея: единицы измерения можно использовать для измерения и сравнения атрибутов.
- оценка, измерение и сравнение площади
- оценка, измерение и сравнение периметра
ЗАМЕЧАТЕЛЬНЫЕ Здания
Большая идея: Формы и тела можно исследовать и сравнивать на основе атрибутов.
- идентифицировать, описывать и сравнивать двухмерные формы и трехмерные тела
- составление и разложение двухмерных фигур и трехмерных тел
Экскурсия по галерее
Большая идея: Формы и твердые тела можно преобразовывать разными способами.
- описание и сравнение трансформаций
- идентифицировать, описывать и сравнивать двухмерные формы
Добро пожаловать в природный парк
Большая идея: сбор и отображение данных может помочь нам прогнозировать и интерпретировать ситуации.
- интерпретировать диаграммы, таблицы, пиктограммы и гистограммы
- делать выводы из отображения данных
Шанс
Большая идея: сбор и отображение данных может помочь нам прогнозировать и интерпретировать ситуации.
- изучить вероятность различных исходов
- исследовать честность игр
Виртуальный образец Купить
Представляем Mathology.ca
Простой, экономящий время онлайн-инструмент планирования для учителей, содержащий разнообразные математические задания и педагогическую поддержку.
Mathology.ca помогает учителям:
- Искать высококачественные уроки по математике и/или добавлять свои любимые уроки
- Создавайте собственные планы уроков или используйте наши еженедельные и годовые планы
- Преподавание с использованием карточек с заданиями по математике и/или книжек по математике, а также включенных цифровых ресурсов и инструментов
- Оценивайте и отслеживайте учащихся с помощью простого в использовании, практичного и мощного инструмента оценки
- Доступ к коротким актуальным профессиональным обучающим видео в любое время и в любом месте
30-дневная бесплатная пробная подписка на веб-семинары
Значение в цифрах
Чтобы узнать больше о тестировании в классе по математике для третьего класса и о том, как оно разрабатывается для поддержки учащихся третьего класса и их учителей, прочитайте рассказ Дафферин-Пила, учителя третьего класса, Норали Ярра, здесь.
«Когда прибыли ресурсы, это было как Рождество в коробке. Столько ресурсов было. И все они разработаны с расчетом на семи-восьмилетнего ребенка; есть всплески цвета, много животных и игровое обучение»
Норали Ярра
Заинтересованы в математике?
Запрос дополнительной информации
Свяжитесь для получения дополнительной информации
Для получения дополнительной информации о математике 3 класса, пожалуйста, свяжитесь с вашим местным менеджером по работе с клиентами Pearson Canada здесь.
facebook.com/pearsonk12
@PearsonMathology
Обратитесь к торговому представителю
Расстройство исполнительного функционирования и математика
Эван — симпатичный ученик четвертого класса, у которого много друзей, но у него проблемы в школе, особенно с математикой. В прошлом году ему поставили диагноз СДВГ из-за его поведения, связанного с концентрацией внимания. Эван думает, что понимает материал, но дома с трудом выполняет домашнюю работу. Больше всего он чувствует себя побежденным, когда проходит тесты по главам и модульные тесты, где ему трудно понять, с чего начать различные многошаговые задачи. Во многих задачах ответы Эвана выглядят как догадки, а не как результат систематического подхода к решению проблем. Эван разочарован работой и потерял мотивацию. Учитель говорит ему, что он мог бы выполнить работу, если бы просто приложил больше усилий.
Эван думает, что понимает материал, но дома с трудом выполняет домашнюю работу. Больше всего он чувствует себя побежденным, когда проходит тесты по главам и модульные тесты, где ему трудно понять, с чего начать различные многошаговые задачи. Во многих задачах ответы Эвана выглядят как догадки, а не как результат систематического подхода к решению проблем. Эван разочарован работой и потерял мотивацию. Учитель говорит ему, что он мог бы выполнить работу, если бы просто приложил больше усилий.
То, что происходит с Эваном, мало чем отличается от того, что происходит со многими учениками с СДВГ. Эван хочет хорошо успевать по математике, но испытывает трудности с многоэтапным решением задач и переходом от одного типа задач к другому. Хотя он хочет добиться успеха, его более низкая успеваемость заставила его устать от попыток улучшить, что привело к отсутствию усилий в математике. Эти характеристики указывают на проблемы с исполнительным функционированием (EF).
Исследователи Рассел Баркли, Кевин Мерфи и Мариеллен Фишер обнаружили, что у учащихся с СДВГ часто возникают проблемы с исполнительными функциями. EF ученика проявляется в том, как он регулирует свое собственное учебное поведение, что имеет решающее значение для успеха в нескольких аспектах жизни, включая изучение математики (Clements et al., 2016). Как правило, УФ включает три компонента: саморегуляцию, рабочую память и восстановление. Каждая из этих областей влияет друг на друга.
СаморегуляцияСаморегуляция проявляется как импульсивность в подходе к решению проблем. Это может проявиться, когда математика показана как серия быстрых трюков, содержание которых не понимается до того, как будет вычислен ответ. Для Эвана это особенно хлопотно. В четвертом классе математика становится все более сложной, особенно с текстовыми задачами. В этой задаче (EngageNY, 2019, стр. 10) Эван должен проанализировать текстовую задачу, разработать точный подход и вычислить ответ:
Мистер Фуллер хочет поставить забор вокруг своего прямоугольного двора. Ширина двора 55 футов, а длина 75 футов. Сколько футов ограждения нужно мистеру Фуллеру?
Ширина двора 55 футов, а длина 75 футов. Сколько футов ограждения нужно мистеру Фуллеру?
- 130
- 260
- 3 905
- 4 125
Если Эвану не хватает саморегуляции, чтобы прочитать и проанализировать задачу, он может увидеть компоненты словесной задачи 55 футов и 75 футов, а также увидеть, что ответом является вопрос о футах. Итак, используя свою относительную вычислительную мощь, он просто прибавляет 55 + 75, чтобы получить 130. Рассматривая 130 как первый вариант ответа, A , он уверен, что прав. В конце концов, то, что он вычислил, сначала проявляется в вариантах ответов. В этой задаче Эвану не удается интерпретировать проблему как решение для периметра из-за его импульсивности в процессе решения проблемы.
Чтобы помочь таким учащимся, как Эван, рассмотрите возможность предоставления шагов по решению проблем. Хотя было показано, что многие подходы помогают, даже трехступенчатая когнитивная стратегия (Скажи, Спроси, Проверь) улучшит решение задач учащимися и поможет развить саморегуляцию (Монтегю, 2008).
| Скажи | Эван читает задачу, спрашивая себя, понимает ли он представленную информацию. |
| Спросите | Эван строит внутренний диалог, задавая себе вопросы об информации, например: «Что задает вопрос?» и «Как мне использовать информацию в задаче, чтобы ответить на вопрос?» Эван может даже перефразировать слово «проблема», чтобы увидеть, представлена ли информация в понятной ему манере. |
| Чек | Эван сравнивает свой ответ с заданным вопросом. |
Эта когнитивная стратегия поможет Эвану научиться саморегуляции при решении проблемы, чтобы он отвечал на нее обдуманно, а не импульсивно.
Рабочая память Рабочая память демонстрируется путем хранения информации при обработке события, так что информация сохраняется и может быть эффективно обработана и вызвана для использования в подходящее время (Witzel, 2016). Различные компоненты рабочей памяти служат предикторами математических рассуждений учащегося (Meyer, 2010). В частности, зрительно-пространственная рабочая память (VSWM) влияет на подходы учащихся к решению арифметических задач (Ashkenazi, 2013) и общую успеваемость по математике (Allen, 2019).). VSWM похож на блокнот, где учащиеся могут мысленно представлять числа и арифметику, например, на числовой прямой или с помощью модели области. Слишком часто учащиеся с трудностями в математике не используют ВСМ при решении арифметических задач (Ашкенази, 2013). Таким образом, важно помочь учащимся построить ментальные образы математики, чтобы помочь учащимся развить VSWM.
Различные компоненты рабочей памяти служат предикторами математических рассуждений учащегося (Meyer, 2010). В частности, зрительно-пространственная рабочая память (VSWM) влияет на подходы учащихся к решению арифметических задач (Ashkenazi, 2013) и общую успеваемость по математике (Allen, 2019).). VSWM похож на блокнот, где учащиеся могут мысленно представлять числа и арифметику, например, на числовой прямой или с помощью модели области. Слишком часто учащиеся с трудностями в математике не используют ВСМ при решении арифметических задач (Ашкенази, 2013). Таким образом, важно помочь учащимся построить ментальные образы математики, чтобы помочь учащимся развить VSWM.
Хотя использование когнитивных стратегий помогает учащимся решать математические задачи, включение визуальных представлений улучшает успеваемость учащихся (Swanson, 2015). В том же примере с периметром, показанном ранее, Эвану нужно предложить нарисовать визуальное представление, которое будет отображать событие решения проблемы, чтобы помочь его VSWM.
На этапе Спросить Эван должен нарисовать визуальное представление, чтобы помочь построить внутренний диалог.
| 75 футов | |
| 55 футов |
Это визуальное представление поможет ему изучить различные параметры, с которыми он, возможно, уже знаком (например, периметр и площадь). Задавая себе вопрос о том, что задает проблема, он настраивает свое визуальное представление, чтобы легче представить периметр забора.
| 75 футов | ||
| 55 футов | 55 футов | |
| 75 футов |
Во время проверки в рамках когнитивной стратегии он сравнивает свой рисунок со своим ответом в 260 футов, помогая ему увидеть связь между проблемой и его подходом.
Восстановление Восстановление — это способность переключать внимание с одной конструкции на другую и приспосабливаться к новым требованиям. Джосвик и коллеги (2019 г.) подчеркнул важность помощи учащимся научиться переключаться с одной задачи на другую и найти подходящую и эффективную стратегию для решения новой задачи.
Джосвик и коллеги (2019 г.) подчеркнул важность помощи учащимся научиться переключаться с одной задачи на другую и найти подходящую и эффективную стратегию для решения новой задачи.
Эван только что решил задачу, требующую понимания и вычисления периметра. Поэтому он будет склонен решать за периметром подобные задачи. Возьмем, к примеру, эту словесную проблему (EngageNY, 2019, стр. 11):
Мисс Петерсон хочет заменить всю напольную плитку на своей кухне. Пол кухни 12 футов в длину и 7 футов в ширину. Если у г-жи Петерсон уже есть 45 квадратных плиток в один фут, сколько еще плиток в один фут ей нужно, чтобы полностью покрыть кухонный пол?
Вместо этого Эвану нужно перезапустить свою когнитивную стратегию. Это может быть сложно для ученика, который борется с EF. Чтобы помочь учащемуся переключаться с задачи на задачу, рассмотрите возможность предоставления органайзера подсказок для запуска задач. В этом примере учитель дает Эвану органайзер с подсказками, которые соответствуют его когнитивной стратегии решения проблем, и Эван заполняет пробелы, чтобы начать. В этом примере учитель также выделяет жирным шрифтом подсказку, чтобы указать Эвану, что делать.
В этом примере учитель также выделяет жирным шрифтом подсказку, чтобы указать Эвану, что делать.
| В чем проблема? | Сколько квадратных плиток размером в один фут еще необходимо? | ||||||||||
| Что уже дано? | Длина | 12 футов | |||||||||
| Ширина | 7 футов | ||||||||||
| Квадратные плитки, которые у нее уже есть | 45 | ||||||||||
| Нарисуйте изображение, соответствующее задаче |
| ||||||||||
| Нам нужно найти площадь. Почему? | Мне нужно знать размер всего этажа | ||||||||||
| Тогда что нам делать? Почему? | Я вычитаю количество плиток, которые у нее уже есть. Это позволяет мне узнать, сколько еще плиток ей нужно. Это позволяет мне узнать, сколько еще плиток ей нужно. | ||||||||||
| Область расчета 12 футов x 7ft = 84ft 2 84FT 2 — 45FT 2 = 39FT 2 еще необходимо. Мисс Петерсон все еще нужно 39 плиток. | |||||||||||
Предоставляя органайзер подсказок, Эван может видеть, что ему нужно для решения проблемы. Он завершает каждый шаг в органайзере, прежде чем начнет свой расчет. Это не только помогает ему более эффективно переключаться с задачи на задачу, но также дает ему сигналы для саморегуляции и визуальной рабочей памяти. По мере того как Эван привыкает к переключению задач, учитель будет сокращать количество подсказок, чтобы со временем и успехом Эван стал более независимым.
Эффективные стратегии помогают в изучении математики Для решения исполнительных функций в математике требуется тщательное планирование и реализация стратегии, чтобы не только удовлетворить потребности учащегося, но и использовать сильные стороны учащегося. В примере с Эваном учитель включил когнитивную стратегию, визуальное представление и организатор подсказок.
В примере с Эваном учитель включил когнитивную стратегию, визуальное представление и организатор подсказок.
Существует много других способов помочь учащимся с дефицитом УФ, например, сосредоточить внимание на автоматизме операционных фактов, чтобы уменьшить будущую когнитивную нагрузку, и использовать подход позитивного поведения для поощрения усилий. Борьба с исполнительными функциями не обязательно должна останавливать процесс обучения математике. Скорее, это призыв к более эффективным стратегиям.
Брэдли Витцель, доктор философии , отмеченный наградами преподаватель и почетный профессор педагогики Аделаиды Уорт Дэниэлс в Университете Западной Каролины. В качестве школьного учителя, а до этого в качестве младшего педагога, он работал в разных условиях, обучая в основном математике и естественным наукам хорошо успевающих учащихся с ограниченными возможностями. Доктор Витцель написал множество книг, глав в книгах и учебных пособий, а также несколько десятков научных и практических статей.
 Он разработал и представил шесть образовательных видеороликов и провел более 500 семинаров и презентаций на конференциях. Самое главное, он отец двоих детей, муж педагога и сын двух педагогов.
Он разработал и представил шесть образовательных видеороликов и провел более 500 семинаров и презентаций на конференциях. Самое главное, он отец двоих детей, муж педагога и сын двух педагогов. ССЫЛКИ И ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Аллен, К., Хиггинс, С. и Адамс, Дж. (2013). Связь между зрительно-пространственной рабочей памятью и математическими способностями у детей школьного возраста: систематический обзор.
Educational Psychology Review, 31, 509–531. https://doi.org/10.1007/s10648-019-09470-8Ашкенази С., Розенберг-Ли М., Меткалф А.В.С., Свигарт А.Г. и Менон В. (2013). Зрительно-пространственная рабочая память является важным источником общей уязвимости домена в развитии арифметического познания.
Нейропсихология, 51 (11), 2305-2317.Баркли, Р.А., Мерфи, К.Р., и Фишер, М. (2008).
СДВГ у взрослых: что говорит наука. Нью-Йорк: Guilford Press. Клементс, Д.Х., Сарама, Дж. , и Гермерот, К. (2016). Обучение исполнительной функции и ранняя математика: Направления причинно-следственных связей. Early Childhood Research Quarterly, 36(3), 79–90. заниматьсяNY. (2019, июнь). Программа тестирования штата Нью-Йорк. 4 класс. Тест по математике. Выпущенные вопросы. Доступно по адресу https://www.engageny.org/resource/released-2019.-3-8-ela-and-mathematics-state-test-questions
, и Гермерот, К. (2016). Обучение исполнительной функции и ранняя математика: Направления причинно-следственных связей. Early Childhood Research Quarterly, 36(3), 79–90. заниматьсяNY. (2019, июнь). Программа тестирования штата Нью-Йорк. 4 класс. Тест по математике. Выпущенные вопросы. Доступно по адресу https://www.engageny.org/resource/released-2019.-3-8-ela-and-mathematics-state-test-questionsДжосвик, К., Клементс, Д.Х., Сарама, Дж., Банс, Х.В., и Дэй-Хесс, К.А. (2019). Двойное воздействие: математика и исполнительная функция.
Обучение детей математике, 25 (7), 416-426.Монтегю, М. (2008). Стратегии саморегуляции для улучшения решения математических задач для учащихся с ограниченными возможностями обучения.
Ежеквартальный выпуск по нарушению обучаемости, 31 , 37–44.Swanson, HL, Lussier, CM, & Orosco, MJ (2015). Когнитивные стратегии, рабочая память и рост в решении словесных задач у детей с математическими трудностями.



 Задача такая: Андрей забил в три раза больше голов, чем Толя. А Толя на шесть голов больше, чем Андрей.…
Задача такая: Андрей забил в три раза больше голов, чем Толя. А Толя на шесть голов больше, чем Андрей.… Намекните на закономерность, а цифры, может, уже сообразим…
Намекните на закономерность, а цифры, может, уже сообразим…

 Поддержка
Поддержка