Ответы математика зубарева 5: ГДЗ по математике 5 класс рабочая тетрадь Зубарева ответы

Определение 1. Расстояние от точки на координатной прямой до нуля называется модулем числа , являющегося координатой данной точки (рис. 1).

Пример 1 . Заметим, что модули противоположных чисел равны и неотрицательны, так как это расстояние, и оно не может быть отрицательным, а расстояния от чисел, симметричных относительно нуля, до начала координат равны.

Определение 2. .

Пример 2. Рассмотрим одну из задач, поставленных в предыдущем примере, для демонстрации эквивалентности введенных определений. , как видим, при отрицательном числе под знаком модуля добавление перед ним еще одного минуса дает неотрицательный результат, как следует из определения модуля.

Последствия. Расстояние между двумя точками с координатами на координатной прямой можно найти следующим образом независимо от взаимного расположения точек (рис. 2).

1. Модуль любого числа неотрицательный

2. Модуль произведения есть произведение модулей

3. Модуль частный — это частные модули

Пример 3. Решить уравнение.

Решение. Воспользуемся вторым определением модуля: и запишем наше уравнение в виде системы уравнений для различных вариантов расширения модуля.

Пример 4. Решить уравнение.

Решение. Аналогично решению предыдущего примера получаем, что .

Пример 5. Решить уравнение.

Решение. Решим через следствие из первого определения модуля: . Изобразим это на числовой оси с учетом того, что искомый корень будет находиться на расстоянии 2 от точки 3 (рис. 3).

На основании рисунка получаем корни уравнения: , так как точки с этими координатами находятся на расстоянии 2 от точки 3, как и требуется в уравнении.

Ответ. .

Пример 6. Решить уравнение.

Решение. По сравнению с предыдущей задачей есть только одно осложнение — это отсутствие полного сходства с формулировкой следствия о расстоянии между числами на оси координат, так как под знаком модуля стоит знак плюс, а не знак минус . Но привести его к нужному виду несложно, что мы и сделаем:

Изобразим это на числовой оси аналогично предыдущему решению (рис. 4).

Корни уравнения .

Ответ. .

Пример 7. Решить уравнение.

Решение. Это уравнение немного сложнее предыдущего, так как неизвестное стоит на втором месте и со знаком минус, кроме того, оно еще и с числовым множителем. Для решения первой задачи воспользуемся одним из свойств модуля и получим:

Для решения второй задачи произведем замену переменных: , что приведет нас к простейшему уравнению . Согласно второму определению модуля . Подставляем эти корни в уравнение замены и получаем два линейных уравнения:

Ответ. .

Достаточно часто в ходе решения задач с корнями возникают модули, и следует обращать внимание на ситуации, в которых они возникают.

При первом взгляде на это тождество могут возникнуть вопросы: «а зачем там модуль?» и «почему тождество ложное?». Оказывается, на второй вопрос можно привести простой контрпример: если то должно быть истинным, что равносильно, а это не тождество.

После этого может возникнуть вопрос: «Решает ли такое тождество проблему», но на это предложение есть и контрпример. Если тогда должно быть истинным, то что эквивалентно, и это неверное тождество.

Соответственно, если вспомнить, что квадратный корень из неотрицательного числа является неотрицательным числом, а значение модуля неотрицательно, становится понятно, почему приведенное выше утверждение верно:

.

Пример 8. Вычислить значение выражения .

Решение. В таких задачах важно не сразу бездумно избавляться от рута, а использовать вышеуказанное тождество, т.к.

Состоит из положительных (натуральных) чисел, отрицательных чисел и нуля.

Все отрицательные числа и только они меньше нуля. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.

Для каждого натурального числа n существует одно и только одно отрицательное число, обозначаемое -n , которое дополняет n до нуля: n + (− n ) = 0 . Оба номера называются напротив друг друга . Вычитание целого числа из эквивалентно прибавлению к его противоположности: -a .

Свойства отрицательных чисел

Отрицательные числа подчиняются почти тем же правилам, что и натуральные числа, но имеют некоторые особенности.

Исторический очерк

Литература

• Выгодский М.Я. Справочник по элементарной математике. — М.: АСТ, 2003. — ISBN 5-17-009554-6
• Глейзер Г.И. История математики в школе. — М.: Просвещение, 1964. — 376 с.

Ссылки

Фонд Викимедиа. 2010 .

• Причинение вреда по неосторожности
• Неотропикс

Смотреть что такое «Неотрицательное число» в других словарях:

действительное число — Вещественное или действительное число — это математическая абстракция, возникшая из-за необходимости измерения геометрических и физических величин окружающего нас мира, а также выполнения таких операций, как извлечение корня, вычисление логарифмов , решение… … Википедия

обычно небольшое неотрицательное целое число — Часть кодирования, которая представляет неограниченные неотрицательные целые значения, но где малые значения чаще встречаются (ITU T X.691). Темы… … Справочник технического переводчика

РЕАЛЬНОЕ ЧИСЛО — действительное число, положительное число, отрицательное число или нуль. Понятие числа чисел возникло путем расширения понятия рационального числа. Необходимость этого расширения обусловлена ​​как практическим использованием математики в выражении… … Математическая энциклопедия

Простое число — Простое число — это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя. Все остальные натуральные числа, кроме одного, называются составными. Таким образом, все натуральные числа больше единицы… … Википедия

натуральное число — ▲ целочисленное выражение, действительное, число натуральное число неотрицательное целое; выражает количество отдельных целочисленных объектов, в которых l. агрегаты; обозначают количество действительных целых объектов; числовое выражение. четыре… Идеографический словарь русского языка

Десятичная — Десятичная дробь — это разновидность дроби, представляющая собой способ представления действительных чисел в виде, где знак дроби: либо, либо, десятичная точка, служащая разделителем между целой и дробной частями числа. число… … Википедия Википедия 9(2))) символы плюс и минус задают не знак выражения, которому они предшествуют, а знак арифметической операции, поэтому знак результата может быть любым, он определяется только после того, как выражение было вычислено.

Помимо арифметики понятие знака используется и в других разделах математики, в том числе для нечисловых математических объектов (см. ниже). Понятие знака важно и в тех разделах физики, где физические величины делятся на два класса, условно называемые положительными и отрицательными, — например, электрические заряды, положительная и отрицательная обратная связь, различные силы притяжения и отталкивания.

Знак числа

Положительные и отрицательные числа

Нулю не присваивается никакого знака, т. е. + 0 (\displaystyle +0) и − 0 (\displaystyle -0) — одно и то же число в арифметике. В математическом анализе значение символов + 0 (\displaystyle +0) и − 0 (\displaystyle -0) может различаться, см. об этом Отрицательный и положительный нуль; в информатике компьютерное кодирование двух нулей (целочисленный тип) может отличаться, см. прямой код.

В связи с вышеизложенным вводятся еще несколько полезных терминов:

• Число неотрицательное , если оно больше или равно нулю.
• Число неположительное , если оно меньше или равно нулю.
• Положительные ненулевые числа и отрицательные ненулевые числа иногда (чтобы подчеркнуть, что они ненулевые) называются «строго положительными» и «строго отрицательными» соответственно.

Та же самая терминология иногда используется для реальных функций. Например, функция называется положительной 9029.5 если все ее значения положительные, неотрицательные , если все ее значения неотрицательные и т.д. Еще говорят, что функция положительна/отрицательна на данном интервале ее определения..

Пример использования функции см. в статье Квадратный корень#Комплексные числа.

Модуль (абсолютное значение) числа

Если число x (\displaystyle x) опустить знак, то полученное значение называется модуль или абсолютное значение числа x (\displaystyle x), оно обозначается | х | . (\displaystyle |x|.) Примеры: | 3 | = 3; | − 3 | = 3. (\displaystyle |3|=3;\ |(-3)|=3.)

Для любых действительных чисел a , b (\displaystyle a,b) выполняются следующие свойства.

Знак нечисловых объектов

Знак угла

Значение угла на плоскости считается положительным, если он измерен против часовой стрелки, в противном случае — отрицательным. Аналогично классифицируются два случая вращения:

• вращение на плоскости — например, вращение на (–90°) происходит по часовой стрелке;
• вращение в пространстве вокруг ориентированной оси обычно считается положительным, если выполняется «правило буравчика», в противном случае оно считается отрицательным.

Знак направления

В аналитической геометрии и физике продвижения по заданной прямой или кривой часто условно делят на положительные и отрицательные. Такое деление может зависеть от постановки задачи или от выбранной системы координат. Например, при вычислении длины дуги кривой часто удобно приписывать этой длине знак минус в одном из двух возможных направлений.

Вход в компьютер

старший бит
0	1	1	1	1	1	1	1	=	127
0	1	1	1	1	1	1	0	=	126
0	0	0	0	0	0	1	0	=	2
0	0	0	0	0	0	0	1	=	1
0	0	0	0	0	0	0	0	=	0
1	1	1	1	1	1	1	1	=	−1
1	1	1	1	1	1	1	0	=	−2
1	0	0	0	0	0	0	1	=	−127
1	0	0	0	0	0	0	0	=	−128
Для представления знака целого числа большинство компьютеров используют

по модулю числа само это число называется, если оно неотрицательно, или тем же числом с обратным знаком, если оно отрицательно.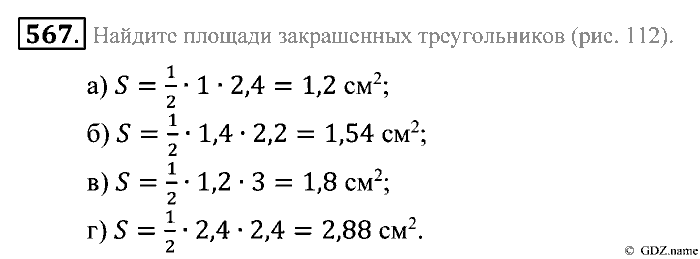

Например, модуль 5 равен 5, а модуль -5 тоже 5.

То есть под модулем числа понимается абсолютная величина, абсолютная величина этого числа без учета его знак.

Обозначается следующим образом: |5|, | Х |, | и | и т.д.

правило :

Объяснение :

|5| = 5
Это читается так: модуль числа 5 равен 5.

|–5| = –(–5) = 5
Это читается так: модуль числа -5 равен 5.

|0| = 0
Это читается так: модуль нуля равен нулю.

Свойства модуля:

1) Модуль числа является неотрицательным числом: | и | ≥ 0 2) Модули противоположных чисел равны: | и | = |– a | 3) Квадрат модуля числа равен квадрату этого числа: | и | 2 = a2 4) Модуль произведения чисел равен произведению модулей этих чисел: | а · б | = | и | · | б | 6) Модуль частных номеров равен отношению модулей этих номеров: | и : б | = | и | : | б | 7) Модуль суммы чисел меньше или равен сумме их модулей: | а + б | ≤ | и | + | б | 8) Модуль разности чисел меньше или равен сумме их модулей: | а – б | ≤ | и | + | б | 9) Модуль суммы/разности чисел больше или равен модулю разности их модулей: | а ± б | ≥ || и | – | б || 10) Из знака модуля можно вынести постоянный положительный коэффициент: | м · и | = м · | a |, m >0 11) Степень числа можно вынести из знака модуля: | и к | = | и | k, если k существует 12) Если | и | = | б |, тогда а = ± б

Геометрический смысл модуля.

Модуль числа — это расстояние от нуля до этого числа.

Например, снова возьмем число 5. Расстояние от 0 до 5 такое же, как и от 0 до -5 (рис. 1). А когда нам важно знать только длину отрезка, то знак не имеет не только значения, но и смысла. Однако это не совсем так: мы измеряем расстояние только положительными числами — или неотрицательными числами. Пусть значение деления нашей шкалы равно 1 см. Тогда длина отрезка от нуля до 5 равна 5 см, от нуля до -5 тоже 5 см.

На практике расстояние часто измеряют не только от нуля — точкой отсчета может быть любое число (рис. 2). Но суть от этого не меняется. Запись вида |a – b| выражает расстояние между точками a и b на числовой прямой.

Пример 1 . Решить уравнение | Х – 1| = 3.

Решение .

Смысл уравнения в том, что расстояние между точками X и 1 равно 3 (рис. 2). Следовательно, от точки 1 отсчитываем три деления влево и три деления вправо — и ясно видим оба значения X :
X 1 = –2, X 2 = 4.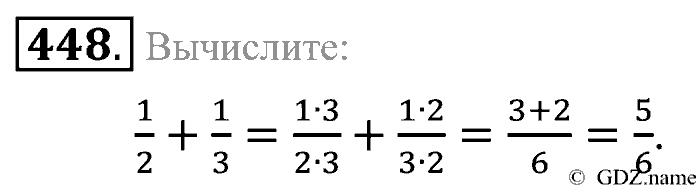

Мы можем вычислить.

│ X – 1 = 3
│ X – 1 = –3

│ X = 3 + 1
│ X = –3 + 1

│ X = 4
│ х = –2.

Ответ: X 1 = –2; X 2 = 4.

Пример 2 . Найдите модуль выражения:

Решение .

Давайте сначала выясним, является ли выражение положительным или отрицательным. Для этого преобразуем выражение так, чтобы оно состояло из однородных чисел. Не будем искать корень из 5 — это довольно сложно. Поступим проще: возведем 3 и 10 в корень. Затем мы сравниваем величину чисел, составляющих разницу:

3 = √9. Следовательно, 3√5 = √9 √5 = √45

10 = √100.

Мы видим, что первое число меньше второго. Это означает, что выражение отрицательное, то есть его ответ меньше нуля:

3√5 – 10

Но по правилу модуль отрицательного числа равен тому же числу с обратным знаком. У нас есть отрицательное выражение. Поэтому необходимо изменить его знак на противоположный. Противоположностью 3√5 — 10 является -(3√5 — 10). Раскроем в нем скобки — и получим ответ:

–(3√5 – 10) = –3√5 + 10 = 10 – 3√5.

Ответить .

Как считывать данные в Simulink через внешний порт PCIe? — MATLAB Answers

17 просмотров (последние 30 дней)

Отредактировано: Илья Зубарев 15 июня 2016 г.

Получение радиочастотных данных через USRP x300 с использованием блока SDRu Receiver в Simulink. У меня уже есть это, работающее с 1Gb Ethernet на ноутбуке. Я пытаюсь получать данные быстрее и определил соединение Ethernet как мое узкое место в данных.

Я приобрел карту PCIe для ноутбука NI-8360B (как указано в руководстве USRP), получил драйверы и могу зарегистрировать ее существование в Matlab с помощью функций findsdru и probesdru. На данный момент я должен иметь возможность принимать данные через него. Однако я не знаю, как адресовать блок приемника SDRu для работы через порт PCIe.

Проблема в том, что при проверке устройства не возвращается IP-адрес, а блок приемника запрашивает его. Раньше я сопоставлял свое Ethernet-соединение с IP-адресом 1-гигабитного порта USRP (который я получаю из функций findsdru и probesdru). Затем введите их в настройки приемника SDRu, и вперед.

Я просмотрела всю документацию, которую смогла найти. Драйверы устройств работают, устройство включено, и я могу обнаружить его в диспетчере устройств, командной строке и даже в Matlab. Я полагаю, что он работает правильно. Я просто не могу получить данные через него. Что мне не хватает?

Есть ли способ установить IP-адрес для слота PCIe?

Или, может быть, мне нужно установить адрес этого порта в USRP?

Есть ли способ запустить блок приема SDRu без IP-адреса?

Может быть, мне следует использовать другой блок Simulink?

Может быть что-то в настройках Simulink, чего я еще не нашел?

Ответы (0)

Произошла ошибка

Не удалось выполнить действие из-за изменений, внесенных на страницу. Перезагрузите страницу, чтобы увидеть ее обновленное состояние.