ГДЗ по Математике для 2 класса Александрова Э.И. часть 1, 2 на 5
Автор: Александрова Э.И..
Издательство: Вита-Пресс 2016
«ГДЗ по математике 2 класс Александрова (Вита-Пресс)» – помощь для школьника на втором году учебы. Конечно, каждый родитель пытается подсказать ребенку решение, ведь в начальной школе нет сложных тем и загруженности информацией, но часто не так просто вспомнить правильные алгоритмы действий. Для того чтобы донести ученику материал, требуется педагогический опыт и умение преподнести.
В течение урока преподаватель объясняет максимально понятно, но то, что в классе кажется легким, дома ребенок уже может и забыть. Именно для того, чтобы легко воспроизвести и все вспомнить и были разработаны готовые домашние задания.
Что дает решебник по математике для 2 класса от Александровой
Чтобы получить весь спектр знаний, необходимо регулярно заниматься учебой, и зачастую нужны несколько источников, которые будут дополнять друг друга. Использование онлайн-ответов при освоении предмета имеет очевидные плюсы. И это не только списывание. Преимуществами пособия являются:
- – круглосуточная возможность доступа из любого места и устройства;
- – удобный способ поиска по номеру задания;
- – подробное объяснение каждого решения;
- – выводы к упражнениям, которые помогают научиться правильно формулировать ответ;
- – верные ответы на каждую задачу.
Даже если второклассник находится вне дома, или у него каникулы, он без труда сможет воспользоваться решебником и восстановить в памяти пройденный материал.
Структура ГДЗ
Учебник поможет лучше понять практические задания, потренироваться и таким образом повысить свои оценки. Пособие разработано в соответствии с программой и включает такие темы:
- Неравенства и уравнения.
- Арифметические действия столбиком.
- Работа со скобками.
- Задачи.
- Умножение и деление.
- Основы геометрии, работа с отрезками и ломанными.
Решения вмещаются в двух частях, по несколько глав каждая, где помимо ответов ученик получает вопросы для самоконтроля и дополнительные задания, направленные на тренировку практических навыков и лучшего понимания темы. «ГДЗ по математике за 2 класс Александрова Э. И. (Вита-Пресс)»
ГДЗ Математика 2 класс Моро, Бантова, Бельтюкова Учебник 1, 2 часть
Авторы: Моро М.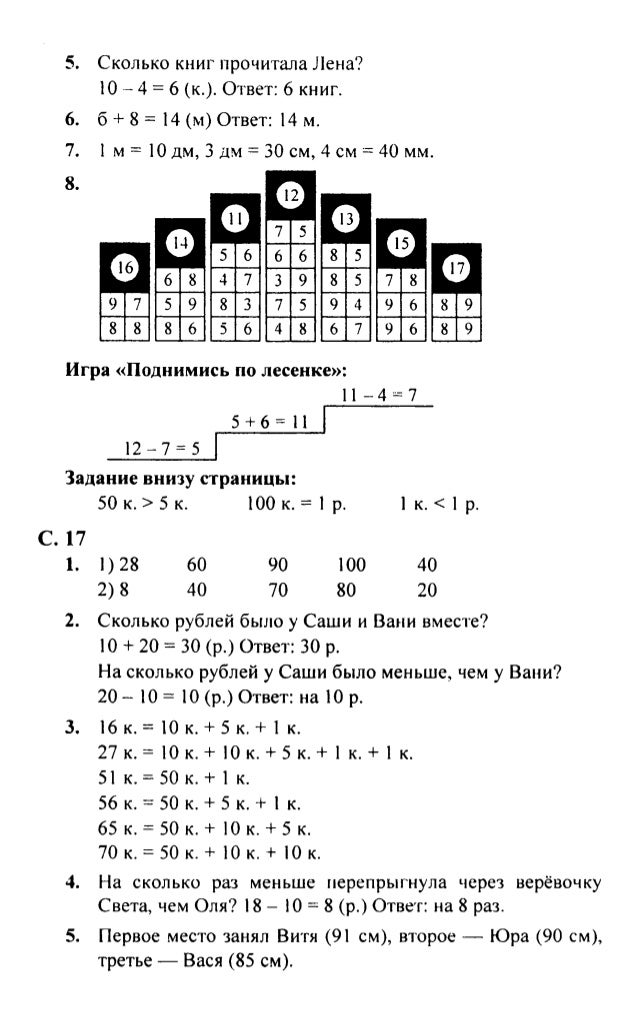 И., Бантова М. А., Бельтюкова Г. В. и др.
И., Бантова М. А., Бельтюкова Г. В. и др.
Издательство: Просвещение
Тип: Учебник
Во втором классе ребята продолжат изучать математику. Только теперь она будет немного труднее чем раньше. Разумеется, все понимают, что малышам очень трудно вычислять или решать какой-нибудь пример. Тогда они могут заглянуть в ГДЗ по математике для 2 класса Моро и разобрать то, что не понятно.
В начальном классе очень важно отработать умения вычислять простые выражения. Школьникам это пригодится для дальнейшего обучения, ведь в следующем классе у них уже встретятся сложные примеры или даже уравнения.
Часть 1
Выберите страницу
Часть 1
Выберите страницу
Авторы постарались создать такой учебник, в котором дети будут изучать простую математику без лени или незаинтересованности. Не стоит забывать о том, что в процессе создания этого пособия присутствовал еще один автор. Это – Бельтюкова Галина Викторовна. Она создала более двадцати книг, посвященным математике для начального класса.
Учебник разделен на 2 части. В 1 и 2 части 2 класса Моро ребята будут изучать такие темы, как: простые единицы измерения, числа до 100, периметры фигур, примеры со скобкой, выражения в которых есть буквы и другие.
Сейчас вы нигде не встретите ребенка, который ни разу не заглядывал в решебник. Это потому, что на дворе век технологий, у всех есть доступ к интернету, а значит и к готовым домашним заданиям.
Бывает такое, что во втором классе классный руководитель не силен в математике, но по правилам должен преподавать его. Можно догадаться, что он не даст все необходимые знания по этому предмету. Детям останется только полагаться на свой ум, на помощь от родителей или списать все с гдз.
Если ребенок является самым старшим, то конечно с ним будут заниматься родители, они будут подсказывать как решить то или иное упражнение. А вот если он, к примеру младший, то родители положат ответственность на старшего. А как мы знаем, старшим нет дела до младших. В итоге ребенок остается без помощи.
В таком случае многие семьи нанимают платных репетиторов. Но они могут дать не те знания. Например, ребенок проходит по программе математики 2 класса Моро, Бантовой вычитание столбиком, а репетитор может обучить ребенка вычитанию 5 класса.
Из этого следует сделать вывод о том, что наилучшей помощью будет заглянуть в наш решебник. У нас вы найдете абсолютно все ответы к каждому заданию. К тому же у нас будет и подробное решение, поэтому школьник обязательно все поймет. Ответы предоставлены без каких-либо ошибок, поэтому сверяться с другими сайтами необязательно.
ГДЗ 4 Страница учебника Моро 2 класс 1 часть по Математике
Ответы к странице 41.
1)1,3,6,8,12,15,17,19,20.
2)17,18,19
15,16,17
8,9,10,11,12,13,14,15.
2.
| Увеличь на 3: | Уменьши на 2: | ||||||||
| 4 | 7 | 6 | 5 | 10 | 12 | 8 | 9 | 7 | 10 |
| 7 | 10 | 9 | 8 | 13 | 10 | 6 | 7 | 5 | 8 |
3.
1) С ответом 10:
7+3=10
8+2=10
4+6=10
9+1=10
2)С ответом 6:
10-4=6
8-2=6
9-3=6
7-1=6
4.
Задача 1
10+6=16(к)
Ответ: всего 16 карандашей.
Задача 2
Меняю вопрос: На сколько меньше карандашей во второй коробке, чем в первой?
10-6=4(к)
Ответ: на 4 карандаша меньше.
5.
1) 5+5=10(т.)
2)10-2=8(т.)
Ответ: было 10 тетрадей, осталось 8 тетрадей.
6.
Красный отрезок длиннее синего на 1 см.
7.
| 2+6=8 | 8-4=4 | 7-6+8=9 | 10-0=10 |
| 2+7=9 | 9-5=4 | 9-7+5=7 | 18+0=18 |
8.
1)Как можно назвать эти фигуры одним словом?
Многоугольники.
2) Почему каждую фигуру можно назвать лишней?
Фигура 1 треугольник, остальные четырёхугольники.
Фигура 2 розового цвета, остальные синего.
Фигура 3 самая большая, и у неё все стороны разной длины, а у квадрата и треугольника стороны равны между собой.
9.
10.
1 способ
| 1 группа — сложение | 2 группа — вычитание |
| 6+3=9 2+8=10 3+6=9 8+2=10 | 9-6=3 10-2=8 9-3=6 10-8=2 |
2 способ
| 1 группа — числа 3, 6 и 9 | 1 группа — число 2, 8 и 10 |
| 6+3=9 9-6=3 3+6=9 9-3=6 | 2+8=10 10-2=8 8+2=10 10-8=2 |
ГДЗ по географии 7 класс Домогацких ответы на вопросы в учебнике
ГДЗ готовые домашние задания учебника по географии 7 класс Домогацких Алексеевский часть 1, 2 ФГОС от Путина.
Часть 1
§1. Суша в океане
§2. Геологическое время
§3. Строение земной коры
§4. Литосферные плиты и современный рельеф
§5. Платформы и равнины
§6. Складчатые пояса и горы
Итоговые задания по теме раздела
§7. Пояса планеты
§8. Воздушные массы и климатические пояса
§9. Климатообразующие факторы
Итоговые задания по теме раздела
§10. Мировой океан и его части
§11. Движение вод Мирового океана
§12. Жизнь в океане
§13. Особенности отдельных океанов
Итоговые задания по теме раздела
§14. Географическая оболочка
§15. Зональность географической оболочки
Итоговые задания по теме раздела
§16. Освоение Земли человеком
§18. Население Земли
§19. Страны мира
Итоговые задания по теме раздела
§20. Географическое положение и история исследования Африки
§21.
 Геологическое строение и рельеф Африки
Геологическое строение и рельеф Африки§22. Климат Африки
§23. Гидрография Африки
§24. Разнообразие природы Африки
§25. Население Африки
§26. Регионы Африки — Северная и Западная Африка
§27. Регионы Африки — Центральная, Восточная и Южная Африка
Итоговые задания по теме раздела
Часть 2
§28. Географическое положение и история исследования Австралии
§29. Компоненты природы Австралии
§30. Особенности природы Австралии
§31. Австралийский Союз
§32. Океания
Итоговые задания по теме раздела
§33. Географическое положение и история исследования Антарктиды
§34. Особенности природы Антарктиды
Итоговые задания по теме раздела
§36. Геологическое строение и рельеф Южной Америки
§37. Климат Южной Америки
§38. Гидрография Южной Америки
§39. Разнообразие природы Южной Америки
§40. Население Южной Америки
§41.
 Регионы Южной Америки
Регионы Южной АмерикиИтоговые задания по теме раздела
§42. Географическое положение Северной Америки. История открытий и исследований
§43. Геологическое строение и рельеф Северной Америки
§44. Климат Северной Америки
§45. Гидрография Северной Америки
§46. Разнообразие природы Северной Америки
§47. Население Северной Америки
§48. Регионы Северной Америки
Итоговые задания по теме раздела
§49. Географическое положение и история исследования Евразии
§50. Геологическое строение и рельеф Евразии
§51. Климат Евразии
§52. Гидрография Евразии
§54. Население Евразии
§55. Регионы Европы
§56. Регионы Азии — Юго-Западная, Восточная и Центральная Азия
§57. Регионы Азии — Южная и Юго-Восточная Азия
Итоговые задания по теме раздела
§58. Природа и человек
Варианты адаптированной образовательной программы для детей с ограниченными возможностями здоровья
Инклюзивное образование в школах можно встретить все чаще и чаще. С каждым годом совершенствуется нормативная база, которая определяет особенности обучения детей с ОВЗ. Указанные нормативные акты являются основополагающими при разработке АООП для детей с ОВЗ. В зависимости от проблем, которые испытывает ребенок ПМПК определяет для каждого ребенка индивидуальный вариант обучения. Чем отличаются варианты обучения друг от друга? Что означает кодировка в рекомендациях ПМПК для обучающегося с ОВЗ? С такими вопросами нередко сталкиваются родители детей с ОВЗ и педагоги, которые обучают особенных детей.
С каждым годом совершенствуется нормативная база, которая определяет особенности обучения детей с ОВЗ. Указанные нормативные акты являются основополагающими при разработке АООП для детей с ОВЗ. В зависимости от проблем, которые испытывает ребенок ПМПК определяет для каждого ребенка индивидуальный вариант обучения. Чем отличаются варианты обучения друг от друга? Что означает кодировка в рекомендациях ПМПК для обучающегося с ОВЗ? С такими вопросами нередко сталкиваются родители детей с ОВЗ и педагоги, которые обучают особенных детей.
- Письмо Минобрнауки России от 23.05.2016 N ВК-1074/07 «О совершенствовании деятельности психолого-медико-педагогических комиссий».
- Письмо Министерства образования и науки РФ от 11 марта 2016 г. № ВК-452/07 «О введении ФГОС ОВЗ»
- Постановление главного государственного санитарного врача Российской Федерации от 10.07.2015 года № 26 «Об утверждении СанПиН 2.4.2.3286–15 «Санитарно-эпидемиологические требования к условиям и организации обучения и воспитания в организациях, осуществляющих образовательную деятельность по адаптированным основным общеобразовательным программам для обучающихся с ограниченными возможностями здоровья».

- Федеральный закон № 273-ФЗ от 29.12.2012 «Об Образовании в Российской Федерации» (далее — Закон).
При отсутствии клинически значимых особенностей в физическом и (или) психическом развитии ребенку рекомендуется основная образовательная программа дошкольного (ДОО), начального (НОО), основного общего (ООО) или среднего общего образования.
Если у ребенка выявлены особенности развития, подтвержденные ПМПК, квалифицируемые как ОВЗ, то такому ребенку рекомендуется обучение по образовательной программе, учитывающей его трудности, «приспособленной» к наличию особых образовательных потребностей. Такая адаптированная основная общеобразовательная программа далее будет обозначаться как АООП определенного вида, основой определения которой является клиническая сущность имеющихся у ребенка нарушений.
Отличительные особенности вариантов обучения по адаптированной программе лиц с ограниченными возможностями здоровья
Варианты АООП конкретизируют условия получения образования для всех категорий обучающихся с ОВЗ: ряд АООП НОО ОВЗ «2» предполагает четыре варианта получения образования, АООП НОО для слабослышащих и слабовидящих обучающихся — три варианта, АООП НОО для обучающихся с тяжелыми нарушениями речи (ТНР) и задержкой психического развития (ЗПР) — два варианта и, наконец, АООП О УО (ИН) — два варианта. По вариантам 3 и 4 АООП НОО ОВЗ обучаются дети, имеющие сочетание сенсорных, других нарушений и умственную отсталость (интеллектуальные нарушения).
По вариантам 3 и 4 АООП НОО ОВЗ обучаются дети, имеющие сочетание сенсорных, других нарушений и умственную отсталость (интеллектуальные нарушения).
1-й вариант предполагает, что обучающийся получает образование, полностью соответствующее по итоговым достижениям к моменту завершения обучения, образованию сверстников, находясь в их среде и в те же сроки обучения.
Обучение по первому варианту свидетельствует о том, что ребенок обучается по общему с детьми без ОВЗ учебному плану. Его особые образовательные потребности удовлетворяются в ходе внеурочной работы. Суть потребностей и, соответственно, необходимого сопровождения, обозначена в соответствующем приложении ФГОС НОО ОВЗ и ПрАООП. Конкретное содержание сопровождения устанавливается консилиумом образовательной организации (ПМПк ОО), ПМПК обозначает лишь основные его направления. Обучение по варианту 1 ФГОС НОО ОВЗ может быть организовано по основной образовательной программе, при необходимости — в соответствии с индивидуальным учебным планом. Обучение по индивидуальному учебному плану в пределах осваиваемых общеобразовательных программ осуществляется в порядке, установленном локальными нормативными актами образовательной организации. При прохождении обучения в соответствии с индивидуальным учебным планом его продолжительность может быть изменена образовательной организацией с учетом особенностей и образовательных потребностей конкретного обучающегося. АООП для таких обучающихся разрабатывается в части программы коррекционной работы, которая реализуется во внеурочной деятельности.
Обучение по индивидуальному учебному плану в пределах осваиваемых общеобразовательных программ осуществляется в порядке, установленном локальными нормативными актами образовательной организации. При прохождении обучения в соответствии с индивидуальным учебным планом его продолжительность может быть изменена образовательной организацией с учетом особенностей и образовательных потребностей конкретного обучающегося. АООП для таких обучающихся разрабатывается в части программы коррекционной работы, которая реализуется во внеурочной деятельности.
2-й вариант предполагает, что обучающийся получает образование в пролонгированные сроки обучения. Обучение по второму варианту свидетельствует о том, что уровень сложности образовательной программы ниже, в учебный план включены курсы коррекционно-развивающей области, обозначенные во ФГОС и АООП. Наряду с академическими достижениями внимание обращено и к формированию сферы жизненной компетенции. Рабочая группа образовательной организации, созданная локальным актом, вносит необходимые дополнения в ПрАООП, касающиеся оценки достижений в области жизненной компетенции и содержания программы коррекционной работы. Вариант 2 предусматривает обучение по АООП с изменениями в содержательном и организационном разделах (программы отдельных учебных предметов, курсов коррекционно-развивающей области и курсов внеурочной деятельности, реализующиеся на основе УП), что предполагает дополнительные условия в общеобразовательном классе.
Вариант 2 предусматривает обучение по АООП с изменениями в содержательном и организационном разделах (программы отдельных учебных предметов, курсов коррекционно-развивающей области и курсов внеурочной деятельности, реализующиеся на основе УП), что предполагает дополнительные условия в общеобразовательном классе.
3-й вариант предполагает, что обучающийся получает образование, которое по содержанию и итоговым достижениям не соотносится к моменту завершения школьного обучения с содержанием и итоговыми достижениями сверстников, не имеющих дополнительные ограничения по возможностям здоровья, в пролонгированные сроки (для обучающихся с нарушением слуха, зрения, опорно-двигательного аппарата, расстройством аутистического спектра и умственной отсталостью). Обучение по третьему варианту ФГОС НОО ОВЗ означает, что у ребенка при ведущем нарушении, обозначенном в стандарте (глухие, слабослышащие, позднооглохшие, слепые, слабовидящие, с нарушениями опорно-двигательного аппарата, с расстройствами аутистического спектра), имеется умственная отсталость (интеллектуальные нарушения) в легкой степени выраженности (F 70 в соответствии с МКБ-10). Академический компонент образовательной программы в этом случае не имеет первоочередного значения, особое внимание уделяется развитию сферы жизненной компетенции. Вариант 3 ФГОС НОО ОВЗ (вариант 1 ФГОС О УО (ИН) предполагает выдачу свидетельства об обучении. ПрАООП имеют еще более существенные отличия в содержательном и организационном разделах.
Академический компонент образовательной программы в этом случае не имеет первоочередного значения, особое внимание уделяется развитию сферы жизненной компетенции. Вариант 3 ФГОС НОО ОВЗ (вариант 1 ФГОС О УО (ИН) предполагает выдачу свидетельства об обучении. ПрАООП имеют еще более существенные отличия в содержательном и организационном разделах.
4-й вариант предполагает, что обучающийся получает образование, которое по содержанию и итоговым достижениям не соотносится к моменту завершения школьного обучения с содержанием и итоговыми достижениями сверстников, не имеющих дополнительные ограничения по возможностям здоровья, в пролонгированные сроки (для обучающихся с умственной отсталостью (умеренной, тяжелой, глубокой степени, тяжелыми и множественными нарушениями развития). На основе данного варианта программы образовательная организация разрабатывает специальную индивидуальную программу развития (СИПР).
Обучение по четвертому варианту ФГОС НОО ОВЗ означает, что основному нарушению (из перечисленных выше) сопутствует умственная отсталость в умеренной или более тяжелой степени (F71, F72 в соответствии с МКБ-10). Ребенок обучается по специальной индивидуальной программе развития (СИПР), содержание которой устанавливается исходя из его актуальных возможностей. Вариант 4 ФГОС НОО ОВЗ (вариант 2 ФГОС О УО (ИН) означает необходимость получения образования по специальной индивидуальной программе развития (далее — СИПР). Подобные программы принципиально отличаются по содержанию и формам организации образовательного процесса; специальные условия, позволяющие работать с ребенком, в каждом случае конкретизируются ПМПК. В большинстве случаев условия, соответствующие особым образовательным потребностям таких обучающихся, могут быть созданы, в том числе на базе различных центров, реализующих комплексную помощь детям с ОВЗ.
Ребенок обучается по специальной индивидуальной программе развития (СИПР), содержание которой устанавливается исходя из его актуальных возможностей. Вариант 4 ФГОС НОО ОВЗ (вариант 2 ФГОС О УО (ИН) означает необходимость получения образования по специальной индивидуальной программе развития (далее — СИПР). Подобные программы принципиально отличаются по содержанию и формам организации образовательного процесса; специальные условия, позволяющие работать с ребенком, в каждом случае конкретизируются ПМПК. В большинстве случаев условия, соответствующие особым образовательным потребностям таких обучающихся, могут быть созданы, в том числе на базе различных центров, реализующих комплексную помощь детям с ОВЗ.
Также стоит отметить, что в соответствии с Законом лицам с ограниченными возможностями здоровья (с различными формами умственной отсталости), не имеющим основного общего и среднего общего образования и обучавшимся по адаптированным основным общеобразовательным программам, выдается свидетельство об обучении по образцу и в порядке, которые устанавливаются федеральным органом исполнительной власти, осуществляющим функции по выработке государственной политики и нормативно-правовому регулированию в сфере образования.
Рекомендованная ПМПК образовательная программа шифруется обозначенным для нарушения кодом и указанием после точки варианта АООП. Вариант АООП рекомендуется коллегиально на основании всех диагностических материалов, представленных специалистами, анализа анамнестичесикх сведений, психолого-педагогической характеристики, общей оценки социальной ситуации развития. Коды для заключений ПМПК выглядят следующим образом:
| Категория детей с ОВЗ | Варианты программ ФГОС НОО обучающихся с ОВЗ и ФГОС О УО |
| глухие | 1.1, 1.2, 1.3, 1.4 |
| слабослышащие | 2.1, 2.2, 2.3 |
| слепые | 3.1, 3.2, 3.3, 3.4 |
| слабовидящие | 4.1, 4.2, 4.3 |
| с тяжелыми нарушениями речи | 5.1, 5.2 |
| с нарушениями ОДА | 6.1, 6.2, 6.3, 6.4 |
| с задержкой психического развития | 7.1, 7.2 |
| с расстройствами аутистического спектра | 8. 1, 8.2, 8.3, 8.4 1, 8.2, 8.3, 8.4 |
| с умственной отсталостью (интеллектуальными нарушениями) | Пр. N 1599, вар. 1 Пр. N 1599, вар. 2 |
Ч. 3 ст. 55 ФЗ-273 Закона определяет особый порядок приема детей на обучение по АООП — только с согласия родителей (законных представителей) и на основании рекомендаций ПМПК.
В отдельных статьях Закона говорится об организации образования лиц с ОВЗ, инвалидностью. К категории детей-инвалидов относятся дети до 18 лет, имеющие значительные ограничения жизнедеятельности, приводящие к социальной дезадаптации, вследствие нарушений развития и роста ребенка, способностей к самообслуживанию, передвижению, ориентации, контролю за своим поведением, обучению, общению, трудовой деятельности в будущем. Инвалидность устанавливается учреждениями медико-социальной экспертизы. Обучающийся с ОВЗ может не иметь инвалидность.
Подробное описание вариантов АООП для различных категорий обучающихся с ОВЗ.
АООП НОО для глухих обучающихся
Вариант 1.1. предназначен для образования глухих детей (со слуховыми аппаратами и/или имплантами), которые достигают к моменту поступления в школу уровня развития (в том числе и речевого), близкого возрастной норме, имеют положительный опыт общения со слышащими сверстниками.
Вариант 1.2. предназначен для глухих детей, не имеющих дополнительных ограничений здоровья, препятствующих получению НОО в условиях, учитывающих их общие и особые образовательные потребности, связанные, в том числе, с овладением словесной речью (в устной и письменной формах), жизненными компетенциями, способствующими наиболее полноценному личностному развитию, планомерному введению в более сложную социальную среду, поэтапному расширение социальных контактов, в том числе со слышащими сверстниками и взрослыми.
В спорных случаях (вариант 1.2 или 1.3) на момент поступления ребенка в школу следует рекомендовать более сложную образовательную среду (вариант 1. 2), а в случае, если обучающийся не достигает минимального уровня овладения предметными результатами по всем или большинству учебных предметов в течение года, то по рекомендации ПМПК и с согласия родителей (законных представителей) образовательная организация может перевести обучающегося на обучение по варианту 1.3.
2), а в случае, если обучающийся не достигает минимального уровня овладения предметными результатами по всем или большинству учебных предметов в течение года, то по рекомендации ПМПК и с согласия родителей (законных представителей) образовательная организация может перевести обучающегося на обучение по варианту 1.3.
Вариант 1.3. предназначен для образования глухих обучающихся с легкой умственной отсталостью (интеллектуальными нарушениями), а также глухих детей с задержкой психического развития церебрально-органического происхождения, в результате которой длительное время отмечается функциональная незрелость центральной нервной системы.
Вариант 1.4. предназначен для образования детей, имеющих, помимо глухоты, другие тяжелые множественные нарушения развития (ТМНР): умственную отсталость в умеренной, тяжелой или глубокой степени, которая может сочетаться с нарушениями зрения, опорно-двигательного аппарата, расстройствами аутистического спектра,
эмоционально-волевой сферы и быть выражена в различной степени тяжести, быть осложнена текущими соматическими заболеваниями и психическими расстройствами.
АООП НОО для слабослышащих и позднооглохших обучающихся
Вариант 2.1. предназначен для слабослышащих и позднооглохших обучающихся, которые достигли к моменту поступления в школу уровня развития, близкого возрастной норме, и имеют положительный опыт общения со слышащими сверстниками; понимают обращенную к ним устную речь; их собственная речь должна быть внятной, т. е. понятной для окружающих.
Вариант 2.2. рекомендуется обучающимся, уровень психического развития которых отстает от возрастной нормы (но не достигает степени умственной отсталости), а также в случаях, если они плохо понимают обращенную к ним речь, говорят малопонятно для окружающих, опыт общения со слышащими сверстниками отсутствует (достаточно одного из этих условий).
Вариант 2.3. предназначен слабослышащих и позднооглохших обучающимися с легкой умственной отсталостью (интеллектуальными нарушениями).
АООП НОО для слепых обучающихся
Вариант 3. 1. предназначен для слепых, которые достигли уровня общего развития, полностью соответствующего требованиям, предъявляемым к уровню развития обучающихся, поступающих в школу, и у которых развиты компенсаторные способы деятельности, необходимые для систематического обучения.
1. предназначен для слепых, которые достигли уровня общего развития, полностью соответствующего требованиям, предъявляемым к уровню развития обучающихся, поступающих в школу, и у которых развиты компенсаторные способы деятельности, необходимые для систематического обучения.
Вариант 3.2. предназначен для слепых, которые не смогли достичь уровня общего развития, полностью соответствующего требованиям, предъявляемым к уровню развития обучающихся, поступающих в школу; не достигли на момент поступления в образовательную организацию достаточного уровня развития компенсаторных способов деятельности, необходимых для систематического обучения, но при этом имеют достаточно большие потенциальные возможности.
Вариант 3.3. предназначен для обучающихся, имеющих сочетание слепоты и легкой умственной отсталости, что значительно осложняет развитие и использование компенсаторных способов деятельности, необходимых для систематического обучения.
Вариант 3. 4. предназначен для обучающихся, имеющих сочетание слепоты с умеренной и тяжелой умственной отсталостью, что затрудняет формирование элементарных способов деятельности, овладение учебными знаниями, умениями и навыками.
4. предназначен для обучающихся, имеющих сочетание слепоты с умеренной и тяжелой умственной отсталостью, что затрудняет формирование элементарных способов деятельности, овладение учебными знаниями, умениями и навыками.
АООП НОО для слабовидящих обучающихся
Вариант 4.1. предназначен для слабовидящих, которые достигли уровня общего развития, полностью соответствующего требованиям, предъявляемым к уровню развития обучающихся, поступающих в школу, и у которых развиты компенсаторные способы деятельности.
Вариант 4.2. предназначен для слабовидящих, которые не смогли достичь уровня общего развития, полностью соответствующего требованиям, предъявляемым к уровню развития обучающихся, поступающих в школу; не достигли на момент поступления в образовательную организацию достаточного уровня развития компенсаторных способов деятельности, необходимых для систематического обучения, но при этом имеют достаточно большие потенциальные возможности.
Вариант 4.3. предназначен для обучающихся, имеющих сочетание слабовидения с легкой умственной отсталостью (с интеллектуальной недостаточностью), что значительно осложняет развитие и использование компенсаторных способов деятельности, необходимых для систематического обучения.
АООП НОО для обучающихся с тяжелыми нарушениями речи (ТНР)
Вариант 5.1. предполагает обучение в общеобразовательном классе по общей программе при обязательном наличии логопедического сопровождения, осуществляемого в совместной работе учителя-логопеда с учителем. Предназначен для обучающихся с фонетико-фонематическим или фонетическим недоразвитием речи (сложная дислалия; легкая степень выраженности дизартрии, заикания; ринолалия), дети с общим недоразвитием речи III — IV уровней речевого развития (выделенных Р. Е. Левиной и Т. Б. Филичевой), у которых, как правило, оказываются нарушенными все компоненты языка, дети с нарушениями чтения и письма. Дети не должны иметь очевидной задержки психического развития.
Дети не должны иметь очевидной задержки психического развития.
Вариант 5.2. предназначен для обучающихся, находящихся на II и III уровнях речевого развития (по Р. Е. Левиной), являющихся следствием алалии, афазии, дизартрии, ринолалии, заикания. Показанием для выбора этого варианта являются также тяжелые нарушения чтения и письма. Этот же вариант рекомендуется обучающимся, не имеющим общего недоразвития речи при тяжелой степени выраженности заикания, однако для них дополнительный год обучения в первом классе не предусматривается.
АООП НОО для обучающихся с нарушениями опорно-двигательного аппарата (НОДА)
Вариант 6.1. адресован обучающимся с НОДА, достигшим к моменту поступления в школу уровня развития, близкого к возрастной норме, и имеющим положительный опыт общения со здоровыми сверстниками. Образовательная организация должна иметь условия, позволяющие организовать среду и рабочее место обучающегося в соответствии с ограничениями его здоровья и обеспечить реализацию программы коррекционной работы, соответствующей его особым образовательным потребностям.
Вариант 6.2. рекомендуется обучающимся, обнаруживающим помимо двигательных нарушений, негрубую задержку психического развития.
Вариант 6.3. предназначен для образования детей, имеющих помимо двигательных нарушений легкую умственную отсталость.
Вариант 6.4. предназначен для образования детей, имеющих тяжелые множественные нарушения развития (ТМНР). В структуре ТМНР — умственная отсталость в умеренной, тяжелой или глубокой степени, сочетающаяся с двигательными нарушениями, а в ряде случаев еще и с другими расстройствами (сенсорной, эмоционально-волевой патологией), а также соматическими расстройствами.
АООП НОО для обучающихся с ЗПР
Вариант 7.1. рекомендуется обучающимся, у которых отмечаются трудности произвольной саморегуляции, проявляющейся в условиях деятельности и организованного поведения, а также устойчивые признаки общей социально-эмоциональной незрелости. Кроме того, у данной категории обучающихся могут быть признаки легкой органической недостаточности центральной нервной системы (ЦНС), выражающиеся в повышенной психической истощаемости с сопутствующим снижением умственной работоспособности и устойчивости к интеллектуальным и эмоциональным нагрузкам, а также типичные, в разной степени выраженные, дисфункции в сферах пространственных представлений, зрительно-моторной координации, фонетико-фонематического развития, нейродинамики и др. Одним из важнейших условий включения обучающегося с ЗПР в среду сверстников без ограничений здоровья является устойчивость форм адаптивного поведения. Обязательным условием является психолого-педагогическое сопровождение обучающегося, согласованная работа учителя начальных классов с педагогами, реализующими программу коррекционной работы, содержание которой для каждого обучающегося определяется с учетом его особых образовательных потребностей на основе рекомендаций ПМПК.
Одним из важнейших условий включения обучающегося с ЗПР в среду сверстников без ограничений здоровья является устойчивость форм адаптивного поведения. Обязательным условием является психолого-педагогическое сопровождение обучающегося, согласованная работа учителя начальных классов с педагогами, реализующими программу коррекционной работы, содержание которой для каждого обучающегося определяется с учетом его особых образовательных потребностей на основе рекомендаций ПМПК.
Вариант 7.2. адресован обучающимся с ЗПР, которые характеризуются уровнем развития ниже возрастной нормы, отставание может проявляться в целом или локально в отдельных функциях (замедленный темп или неравномерное становление познавательной деятельности). Отмечаются нарушения внимания, памяти, восприятия и других познавательных процессов, умственной работоспособности и целенаправленности деятельности, в той или иной степени затрудняющие усвоение школьных норм и школьную адаптацию в целом. Произвольность, самоконтроль, саморегуляция в поведении и деятельности, как правило, сформированы недостаточно. Обучаемость удовлетворительная, но часто избирательная и неустойчивая, зависящая от уровня сложности и субъективной привлекательности вида деятельности, а также от актуального эмоционального состояния. Возможна неадаптивность поведения, связанная как с недостаточным пониманием социальных норм, так и с нарушением эмоциональной регуляции, гиперактивностью. В этом случае предполагается, что они получают образование, сопоставимое с таковым для детей, не имеющих ограничений здоровья, в специальном классе или соответствующей образовательной организации.
Обучаемость удовлетворительная, но часто избирательная и неустойчивая, зависящая от уровня сложности и субъективной привлекательности вида деятельности, а также от актуального эмоционального состояния. Возможна неадаптивность поведения, связанная как с недостаточным пониманием социальных норм, так и с нарушением эмоциональной регуляции, гиперактивностью. В этом случае предполагается, что они получают образование, сопоставимое с таковым для детей, не имеющих ограничений здоровья, в специальном классе или соответствующей образовательной организации.
АООП НОО для обучающихся с расстройствами аутентического спектра (РАС)
Одним из специальных условий является организация диагностического и пропедевтического периодов, продолжительность которых регулируется рекомендациями ПМПК и может составлять от одного месяца до года. Эти подготовительные периоды обучения реализуются в организациях, осуществляющих образовательную деятельность в рамках одного или нескольких вариантов АООП НОО обучающихся с РАС, и предполагают уточнение и конкретизацию особенностей аффективных, коммуникативных, интеллектуальных, речевых и поведенческих расстройств обучающихся с целью уточнения или определения варианта АООП для дальнейшего их обучения. В процессе школьного обучения сохраняется возможность перехода ребенка с одного варианта стандарта на другой (основанием для этого является заключение ПМПК).
В процессе школьного обучения сохраняется возможность перехода ребенка с одного варианта стандарта на другой (основанием для этого является заключение ПМПК).
Вариант 8.1. рекомендуется обучающимся, имеющим формально сопоставимый с нормой уровень психоречевого развития, когда до поступления в школу ребенок имел опыт подготовки к ней в группе детей. Вместе с тем, даже имея высокие интеллектуальные способности, эти дети для успешного освоения начального образования в условиях полной инклюзии нуждаются в систематической психолого-педагогической и организационной поддержке, обеспечивающей удовлетворение их особых образовательных потребностей, реализуемой на основе сугубо индивидуальной программы коррекционной работы, касающейся в первую очередь развития различных аспектов сферы жизненной компетенции.
Вариант 8.2. предполагает менее высокие интеллектуальные способности обучающегося или отсутствие опыта подготовки к школьному обучению в группе сверстников, поэтому длительность получения начального образования пролонгируется на один год. Ребенок может находиться в среде сверстников с ОВЗ, имеющих нарушения, не противоречащие удовлетворению его особых образовательных потребностей (например, в специальном коррекционном классе вместе с обучающимися по вариантам 5.2 или 6.2 или 7.2). Предполагается, что при выборе этого варианта АООП академический компонент будет освоен обучающимися с РАС в объеме, сопоставимом с таковым во ФГОС НОО. Неуспеваемость по отдельному предмету не является основанием изменения на другие варианты АООП.
Вариант 8.3. рекомендуется при сочетании РАС с легкой умственной отсталостью. Отличие от варианта 8.2 в том, что не требуется, чтобы академический компонент был освоен в объеме, сопоставимом с таковым во ФГОС НОО, поэтому может находиться в специальном коррекционном классе с обучающимися, имеющими умственную отсталость (интеллектуальные нарушения), другие ОВЗ либо в среде сверстников без ОВЗ. Особые образовательные потребности, касающиеся развития различных аспектов сферы жизненной компетенции, должны реализовываться в соответствии с таковыми для обучающихся с РАС. В сфере академической компетентности при обучении по этому варианту выделяется два уровня достижений: минимальный и достаточный.
Вариант 8.4. рекомендуется обучающимся с РАС, осложненными умственной отсталостью (умеренной, тяжелой, глубокой, тяжелыми и множественными нарушениями развития). На основе данного варианта организация разрабатывает специальную индивидуальную программу развития (СИПР), учитывающую индивидуальные образовательные потребности обучающегося, включение в образовательную среду осуществляется постепенно и дозированно.
Во ФГОС НОО ОВЗ и ФГОС О УО предполагается изменение образовательного маршрута, программ и условий получения образования обучающимися с ОВЗ на основе комплексной оценки личностных, метапредметных и предметных результатов освоения АООП НОО, заключения ПМПК и мнения родителей (законных представителей).
В соответствии с Законом реализация АООП НОО может быть организована как совместно с другими обучающимися, так и в отдельных классах, группах или в отдельных организациях. Основным механизмом реализации АООП является учебный план (УП), в том числе индивидуальный учебный план.
Пифагорка — Ментальная арифметика Мытищи, счеты Соробан, Абакус. Центр развития интеллекта в Мытищах (Московская область) — отзывы, курсы, занятия
Счеты Соробан
Любой родитель хочет видеть своего ребенка счастливым, успешным и самостоятельным
Как это сделать? Где этому учат? Может ли обычный детский сад, школа обеспечить все это?
Мы предлагаем дать шанс самому ребенку!
В основе занятий по ментальной арифметике в г. Мытищи — японская система развития интеллектуальных способностей при помощи счет соробан (абакус).
15 минут ежедневных занятий ментальной арифметикой на счетах соробан помогают заложить новые нейронные связи, развить самостоятельность, способность к принятию решений, внимательность, фотографическую память, а отсюда и дальнейшие успехи в учебе, спорте, работе и жизни.
Вам, наверное, встречалась такая статистика — только 5% людей достигают значительных успехов в жизни. Остальные 95% лишь мечтают об этом, но их мечты почему-то не сбываются.
Всего один навык, полученный до 12 лет, способен изменить будущее вашего ребенка
Почему так происходит, и можем ли мы изменить эту статистику для наших детей?
Наукой доказано: способность к успеху зависит от гармоничного развития правого и левого полушарий мозга. К сожалению, у большей части населения земного шара развитие левого полушария значительно преобладает над правым. Иными словами, логическое мышление развито хорошо. Зато творческое мышление — интуиция, выбор правильных путей и поступков — работает из рук вон плохо.
Получается, что если нам с вами развить правое полушарие до уровня левого, то мы обретем способность к успеху?
В какой-то степени — да. Но гораздо более серьезных результатов достигнет здесь не взрослый, а ребенок 5-12 лет. Именно в этом возрасте мозг наиболее пластичен. Поэтому наша методика разработана специально для детей.
Что такое Ментальная арифметика?
Ментальная арифметика высокоэффективная программа развития умственных способностей при помощи арифметических вычислений на счетах (абакус, соробан), так называемый быстрый счет:
подходит для детей от 4 до 16 лет;
развивает самостоятельность, инициативность, умение критически оценивать себя;
работает уже в 52 странах мира (США, Канада, Великобритания, Австрия, Испания, Австралия, Япония, Малайзия, Таиланд, Китай и др.).
Счеты называют «древним калькулятором» — их придумали наши предки еще 2500 лет назад. Почему же сегодня эта система вычислений вновь стала популярной?
В отличие от обычной арифметики упражнения на счетах задействуют оба полушария головного мозга. Причем, их развитие происходит согласованно и гармонично.
Как это происходит?
Развитие левого полушария:
- стимуляция мелкой моторики;
- наглядное представление результата арифметических действий.
Развитие правого полушария:
- использование в равной степени правой и левой руки;
- работа в уме с воображаемыми счетами.
«Побочный эффект» методики — быстрый счет в уме
Приведем такой пример: в Японии дети в обязательном порядке изучают соробан (японские счеты) в младших классах. Такой подход к образованию уже дал результаты. Японские школьники из года в год побеждают на международных математических олимпиадах, что стало даже традицией.
В Китае решать задачи с трехзначными числами дети умеют уже в детском саду. Взгляните сами — кажется невероятным, но это факт:
Однако смысл Ментальной арифметики вовсе не в навыке считать в уме. Это всего лишь полезный побочный эффект. А сами счеты абакус — не «калькулятор» и даже не математический тренажер.
Ментальная арифметика развивает способность к успеху в любом деле
Занятия Ментальной арифметикой помогают натренировать нейронные связи головного мозга вашего ребенка, развивают скорость и качество его мышления. Это можно сравнить со спортивными тренировками.
Представьте, что вдруг…
Вы оказались среди участников Чемпионата мира по велоспорту. Вот-вот раздастся сигнал старта, а вы в последний раз гоняли на велике в 5-м классе. Есть ли у вас шансы среди спортсменов, тренировавших этот навык несколько лет?
Так же и с интеллектом. Проверено: с любыми задачами в учебе, карьере, увлечениях и т.п. тренированный мозг справляется легче и быстрее, чем нетренированный.
Продолжим спортивную аналогию. Чтобы стать олимпийским чемпионом, спортом нужно заниматься с детства. Точно так же и с Ментальной арифметикой и счетами соробан. По заявлению китайских и японских педагогов, если упражняться на счетах одновременно начнут взрослый и ребенок — взрослый не достигнет тех же результатов, что и ребенок. Именно потому важно начать тренировать мозг вовремя.
Что дает вашему ребенку освоение Ментальной арифметики (по отзывам наших родителей)
Программа рассчитана на 2 года, но первые результаты родители обычно замечают уже через 3-4 месяца.
Рост успеваемости в школе (даже в музыкальной)
Математика
Уже после 2-х месяцев обучения оценки по математике у сына заметно улучшились. Однажды мы с мужем на кухне считали вслух какие-то трёхзначные числа, а Кирилл вдруг моментально дал ответ без калькулятора!
Волкова Екатерина Владимировна
Математика и чтение
Никита стал намного лучше считать и читать. Мы видим, что этот уровень выше, чем у сверстников-первоклассников
Лаушкин Олег Александрович
Все предметы
К сожалению, мы занимались только 1 раз в неделю. Но успеваемость уже улучшилась по всем предметам. Этот учебный год мы закончили без троек!
Маринина Елена Анатольевна
Музыка
Мы ещё занимаемся по классу фортепиано (а это мелкая моторика), и Артём стал одинаково успешно играть как левой, так и правой рукой!
Лячина Ирина
Самостоятельность и уверенность в себе
Катя стала собранной и уверенной в себе, говорит: «Я всё равно это сделаю!». Стала такой самостоятельной, что я могу спокойно доверить ей выполнение сложного школьного задания без моего участия.
Маринина Елена Анатольевна
Ребёнка хвалят, плечи расправились, самооценка поднялась.
Борисова Ольга
Мой сын посещает занятия 3 месяца, поэтому о каких-то глобальных изменениях говорить пока рано. Но то, что он теперь самостоятельно выполняет домашнее задание, это точно.
Лячина Ирина
Победы в конкурсах и олимпиадах (не только математических)
А ещё Макар выиграл Олимпиаду по математике в школе…
Костина Дина Борисовна
Учебный год с Ментальной арифметикой стал для нас особенно успешным. Мой сын Сергей занял призовые места в городском конкурсе научных проектов и конкурсе «Ученик Года»
Пронина Мария Сергеевна
Как проходят занятия по ментальной арифметике в городе Мытищи?
Ваш ребенок тренирует навыки работы со счетами постепенно, с переходом от простого к сложному. Занятия проходят 2 раза в неделю по 1 часу плюс домашние занятия по 15 минут в день. В итоге к концу программы ваш ребенок уже свободно складывает, вычитает, умножает и делит в уме двух-,и даже трехзначные числа.
Но вот вопрос: может ли нормальный ребенок прилежно заниматься одним и тем же целый час? Конечно, нет! И поэтому мы придумали вот что…
Особая программа Ментальной арифметики от «Пифагорки»
Традиция упражнений со счетами пришла к нам из Азии, где дети гораздо послушнее, а авторитет старших непререкаем. Там нет понятия «скучно на уроке», зато есть строгая дисциплина. Иное дело — наши дети. Практика показывает, что длительные тренировки на счетах даются им с трудом, возникает утомление и потеря интереса.
Поэтому мы чередуем занятия на счетах играми, заданиями на развитие памяти и внимания, упражнениями для глаз и осанки. Получается двойная польза!
Но и это еще не все.
Обучение Ментальной арифметике часто предлагают по аналогии со школьными уроками — в группах, по общему плану. При этом совершенно не учитываются индивидуальные (генетические) особенности ребенка. Например, один успеет за занятие прорешать 3 страницы учебника, а другой всего 1 или даже половину. Все дети разные, у каждого своя скорость.
У нас дети тоже занимаются в группах. Но при этом задания даются каждому ребенку индивидуально, с учетом его возможностей. Поэтому у нас весело, интересно и результативно!
В отличие от курсов английского, сын ни разу не сказал про ментальную арифметику: «Мама, а может, не пойдём?». Нас впечатлили результаты, поэтому мы планируем шестилетнюю дочку также записать на этот курс. (Пронина Мария Сергеевна).
Почему ментальную арифметику лучше всего изучать именно в «Пифагорке»?
Вот какие результаты показывают ученики ЦРИ «Пифагорка» в городе Мытищи:
С вашим ребенком занимаются:
педагоги и психологи с опытом работы с детьми в детском саду и школе;
преподаватели высшей категории;
победители областных и всероссийских конкурсов педагогического мастерства.
Все наши педагоги прошли обучение технологии «Ментальная арифметика» в Центрах повышения квалификации.
Приглашаем на обучение успеху!
Не упустите время. Помните — для достижения максимального результата начинать занятия Ментальной арифметикой нужно уже сегодня!
Уникальные результаты по ментальной арифметике в «Пифагорке»
Воспитанница ЦРИ «Пифагорка» (Санкт-Петербург) Виктория Алиева показала удивительные математические способности на ТВ шоу «Удивительные люди».
Остались еще вопросы? Добро пожаловать в раздел Вопросы и ответы по ментальной арифметике.
Также вы можете ознакомиться со статьями по ментальной арифметике.
Урок 35. понятие скорости. единицы скорости — Математика — 4 класс
Математика, 4 класс
Урок № 35. Понятие скорости. Единицы скорости
Перечень вопросов, рассматриваемых в теме:
— что такое «скорость»?
— какими единицами измеряется скорость?
— как вычислить скорость?
Глоссарий по теме:
Скорость – это расстояние, пройденное объектом за единицу времени.
Скорость – это величина, её можно измерять и сравнивать.
Чтобы узнать скорость движения, нужно расстояние разделить на время.
Основная и дополнительная литература по теме урока:
1. Моро М.И., Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 — М.; Просвещение, 2017. – с.5-7
2. Моро М.И., Волкова С.И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.3
3. Волкова С.И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.54
Теоретический материал для самостоятельного изучения
Наверняка вы замечали, что в окружающем нас мире постоянно что-то движется. Что-то движется быстрее, а что-то медленнее. Например, по дороге идёт человек, едет автомобиль, в воздухе летит самолёт. Все они движутся, но автомобиль движется быстрее человека, а самолёт быстрее автомобиля. В математике величиной характеризующей быстроту движения объектов, является скорость.
Кто бежит быстрее, зебра или страус, если зебра бежит со скоростью 60 км/ч, а страус за минуту пробегает 500м?
Легковая машина прошла 160 км за 2 часа. В течение каждого часа она проходила одинаковое расстояние. Сколько километров проходила эта машина за один час?
Чтобы найти, какое расстояние машина проехала за один час, нужно все пройденное расстояние, 160 км, разделить на время, 2 часа. Таким образом, скорость движения машины – 80 километров в час. Иначе можно сказать, что за один час машина проходила 80 километров.
Сокращенно записывается так: 80 км/ч.
160 : 2 = 80 км/ч
Космический корабль пролетает 8 тысяч метров в секунду. Его скорость можно записать так: 8000 м/с.
Вы знаете, что 1000 м = 1 км. Значит, скорость космического корабля можно записать иначе: 8000 м/с = 8 км/с.
Например, черепаха за минуту проползает пять метров, это значит, что скорость движения черепахи – пять метров в минуту. Улитка за одну секунду может проползти один сантиметр, то есть скорость улитки – один сантиметр в секунду.
Скорость движения – это расстояние, пройденное за единицу времени.
Единицей времени может быть одна секунда, одна минута или один час.
Чтобы узнать скорость движения, нужно расстояние разделить на время.
Скорость = Расстояние : Время
Задания тренировочного модуля:
1. Соотнесите значение скорости с объектом.
Объект | Значение скорости |
черепаха | 90 км/ч |
человек | 700 км/ч |
автомобиль | 5 м/мин |
самолёт | 8 км/с |
ракета | 5 км/ч |
Правильный вариант:
Объект | Значение скорости |
черепаха | 5 м/мин |
человек | 5 км/ч |
автомобиль | 90 км/ч |
самолёт | 700 км/ч |
ракета | 8 км/с |
2. Дед Мороз послал погоню за злым Волшебником, похитившим Снегурочку. Подчеркните имена посланников Деда Мороза, которые смогут догнать похитителя.
Правильный вариант: волк, медведь, олень
3. Выберите один правильный вариант ответа.
Скорость – это величина, которая показывает:
1. пройденный объектом путь;
2. как быстро движется объект;
3. какой путь проходит объект за единицу времени.
Правильный вариант: какой путь проходит объект за единицу времени.
Математика стержней и посохов
Математика для христианской жизни Серии«Математическая программа Rod and Staff — это черно-белая, прямолинейная, серьезная, традиционная математика с упором на тренировку и запоминание, а также практическое применение с помощью текстовых задач. Ранее изученные концепции постоянно пересматриваются». —Кэти Даффи
Эта серия статей разработана с учетом следующих целей: (1) подчеркнуть правильные библейские ценности; (2) научить полезным фактам и навыкам с числами; (3) уделять сбалансированное внимание концепциям, вычислениям и приложениям; (4) дать ученику возможность проводить уроки с минимальной помощью учителя; и (5) включать в себя задачи чтения или рассуждения, которые включают духовный урок, библейский принцип, вызов или некоторую полезность в повседневной жизни.
Числовые факты и навыки преподаются традиционным методом. Цель состоит в том, чтобы подготовить студента к труду в Царстве Божьем и во славу Божью. Используются реалистичные задачи из повседневной жизни. Многие задачи расположены по горизонтали, что поможет ученику развить умственные арифметические навыки. Эта серия была написана с убеждением, что эффективно обучать одной математической операции непрерывно в течение нескольких недель (подход с углубленным изучением), а не изучать одну концепцию сегодня, другую завтра и так далее, а затем повторять цикл (спиральный подход).
Сильный акцент делается на овладении навыками и старается обеспечить достаточное количество упражнений, чтобы средний ученик мог это сделать. Включены дополнительные листы практики, обычно в форме мастеров черной линии, которые могут быть скопированы учителями по мере необходимости для проведения дополнительных упражнений. Также предусмотрены скоростные упражнения, в которых упор делается сначала на точность, а затем на скорость.
Уроки для первых двух классов имеют форму рабочей тетради. Классы 3 и выше представлены в форме многоразовой книги в твердом переплете.Текст ученика включен как часть пособия для учителя.
Примечание по алгебре:
Поскольку алгебра не вводится до 7 класса, в младших классах предусмотрены упражнения, включающие смешанные операции, для практики со смешанными вычислениями, и их следует выполнять в последовательном порядке. Стандартный алгебраический порядок операций вводится вместе с алгебраическими выражениями в 7 классе.
Кроме того, хотя в 7-м и 8-м классах вводятся некоторые алгебраические понятия, и некоторые пользователи считают, что для достаточной подготовки к изучению алгебры I этот курс не задуман как тщательный курс предварительной алгебры.Rod and Staff разрабатывает курс алгебры, но на его подготовку уйдет несколько лет.
Просмотр области действия и диаграммы последовательности. Чтобы увидеть оглавление и образцы уроков, нажмите на наборы учебных программ ниже.
Загрузите тест на размещение (напишите нам, чтобы получить ответ)
% PDF-1.4 % 562 0 объект > эндобдж xref 562 153 0000000016 00000 н. 0000003430 00000 н. 0000003568 00000 н. 0000003719 00000 н. 0000007749 00000 н. 0000008248 00000 н. 0000008315 00000 н. 0000008462 00000 п. 0000008574 00000 н. 0000008735 00000 н. 0000008918 00000 н. 0000009029 00000 н. 0000009141 00000 п. 0000009265 00000 н. 0000009474 00000 н. 0000009575 00000 н. 0000009690 00000 н. 0000009819 00000 п. 0000009940 00000 н. 0000010066 00000 п. 0000010186 00000 п. 0000010307 00000 п. 0000010425 00000 п. 0000010598 00000 п. 0000010717 00000 п. 0000010821 00000 п. 0000010939 00000 п. 0000011056 00000 п. 0000011173 00000 п. 0000011293 00000 п. 0000011468 00000 п. 0000011576 00000 п. 0000011680 00000 п. 0000011811 00000 п. 0000011934 00000 п. 0000012060 00000 п. 0000012178 00000 п. 0000012348 00000 п. 0000012453 00000 п. 0000012563 00000 п. 0000012693 00000 п. 0000012815 00000 п. 0000012941 00000 п. 0000013067 00000 п. 0000013190 00000 п. 0000013374 00000 п. 0000013482 00000 п. 0000013603 00000 п. 0000013726 00000 п. 0000013847 00000 п. 0000013964 00000 п. 0000014088 00000 п. 0000014225 00000 п. 0000014332 00000 п. 0000014432 00000 п. 0000014560 00000 п. 0000014688 00000 п. 0000014815 00000 п. 0000014937 00000 п. 0000015085 00000 п. 0000015233 00000 п. 0000015381 00000 п. 0000015529 00000 п. 0000015677 00000 п. 0000015825 00000 п. 0000015973 00000 п. 0000016121 00000 п. 0000016269 00000 п. 0000016417 00000 п. 0000016565 00000 п. 0000016713 00000 п. 0000016861 00000 п. 0000017010 00000 п. 0000017159 00000 п. 0000017308 00000 п. 0000017457 00000 п. 0000017606 00000 п. 0000017755 00000 п. 0000017904 00000 п. 0000018053 00000 п. 0000018202 00000 п. 0000018351 00000 п. 0000018500 00000 п. 0000018649 00000 п. 0000018798 00000 п. 0000018947 00000 п. 0000019096 00000 п. 0000019245 00000 п. 0000019394 00000 п. 0000019543 00000 п. 0000019787 00000 п. 0000020050 00000 н. 0000020352 00000 п. 0000020641 00000 п. 0000020662 00000 п. 0000021132 00000 п. 0000021154 00000 п. 0000021981 00000 п. 0000022003 00000 п. 0000022352 00000 п. 0000022774 00000 п. 0000023203 00000 п. 0000023225 00000 п. 0000023529 00000 п. 0000023550 00000 п. 0000023591 00000 п. 0000026250 00000 п. 0000026273 00000 п. 0000028016 00000 п. 0000028039 00000 п. 0000028153 00000 п. 0000029503 00000 п. 0000029731 00000 п. 0000030356 00000 п. 0000030414 00000 п. 0000030635 00000 п. 0000030676 00000 п. 0000031207 00000 п. 0000031771 00000 п. 0000031978 00000 п. 0000032185 00000 п. 0000032207 00000 п. 0000032761 00000 п. 0000032962 00000 п. 0000033628 00000 п. 0000033650 00000 п. 0000034087 00000 п. 0000034109 00000 п. 0000034513 00000 п. 0000034535 00000 п. 0000034921 00000 п. 0000034943 00000 п. 0000035355 00000 п. 0000035377 00000 п. pu € I7i_8,8PPp) / П-4 / V 1 / Длина 40 >> эндобдж 565 0 объект > / Кодировка> >> / DA (ɔg \ nKMU) >> эндобдж 713 0 объект > ручей qjG: 4REIX / & FI; 8} kʉ + n; oDxp? _suÚ # P} 3ܜ #} wy8lx (+ SvDT> Z «.Ȅ 縺 d
Пойди по математике, 1 класс Ответы на вопросы PDF
Вы ищете мгновенную помощь в выполнении домашних заданий для решения концептуальных математических задач для 1-го класса? Тогда это направление станет вашим идеальным выбором. Здесь наши предметные эксперты приложили совместные усилия для предоставления HMH Go Math Grade 1 Answer Krey , согласованной в соответствии с Учебниками по математике для 1 класса. Go Math Grade 1 Primary School Solution Key учит всем простым и сложным базовым математическим навыкам и помогает вашим детям учиться глубокому мышлению и проявлять некоторое влияние на обычный образ мышления.Следовательно, загрузите по главам HMG Go Math Answer Key для учеников 1-го класса из следующих модулей и начните обучение эффективным образом.
Бесплатная загрузка PDF-файла главы Wise HMH Go Math Grade 1 Ключ решения
Доступ по предоставленным ссылкам поможет вам больше в расширении ваших знаний по предмету и получить прочную основу для математических концепций. Здесь мы перечислили по главам Go Math Grade 1 Answer Key PDF Online для бесплатной загрузки. Нажмите на быструю ссылку на соответствующую главу и получите ключ от HMH Go Math First Grade Solution Key в автономном режиме для лучшей подготовки.
Начальная школа Перейти по математике 1 класс Ответы Ключевые PDF-файлы всех глав охватывают вопросы из 1–12 уроков, обзоры глав, тесты по главам, дополнительные практики, контрольные точки в середине главы и т. Д. Итак, соберите файл в формате pdf для первого класса. ключ решения математики и начать подготовку к различным предстоящим экзаменам.
Преимущества обращения в начальную школу по математике. Ответы для первого класса PDF
Учащиеся, которые рады узнать о преимуществах ключа ответов для первого класса Go Math , могут внимательно изучить этот раздел и подготовиться к получению высоких оценок на экзаменах.
- Прежде всего, предоставленный ключ решения 1-го класса по математике HMH Go поможет улучшить ваши знания по предмету и повысить вашу уверенность при сдаче экзаменов.
- Он наполнен вопросами и ответами по каждой главе и уроку. Таким образом, студенты могут полностью усвоить концепцию и легко практиковаться в ситуациях в реальном времени.
- Все основные понятия математики 1 класса помогут вашим детям понять сложные математические концепции в предстоящих классах.
- Последовательная практика с использованием ответов 1 класса по учебнику HMH Go по математике поможет вам добиться успеха на экзаменах.
- Начальная школа Go Math Grade First Solutions сгруппированы по главам в соответствии с последним учебным планом общих основных государственных стандартов.
Часто задаваемые вопросы по HMH Go Math Grade 1. Ключ к ответу Скачать бесплатно PDF
1. Помогает ли учащимся достичь высоких результатов при решении всех вопросов из «Перейти к математике» для 1-го класса?
Да, учащиеся 1-го класса могут легко получить высокие оценки на экзаменах, решая и упражняясь с помощью ключа ответов по математике го.Он включает в себя решенные и нерешенные вопросы из всех глав, обзоры глав, тесты глав и т. Д. Итак, хорошо подготовьтесь, используя ключ ответа HMH Go Math для первого класса.
2. Где я могу получить ключ к решению по математике для 1 степени по главам?
Вы можете получить ключ решения Chapter Wise Grade 1 HMH Go Math Solution на нашем надежном и надежном веб-сайте, например, Gomathanswerkey.com
3. Как бесплатно скачать ключ с ответами для первого класса по математике в формате pdf?
Просто нажав на доступные ссылки в формате pdf, вы можете бесплатно получить доступ к отформатированному ключу с ответом для первого класса по математике Go Math и загрузить его.Итак, загрузите офлайн и больше практикуйтесь, чтобы получать хорошие оценки на различных экзаменах.
Помогите вашему ребенку развить ранние математические навыки • НОЛЬ ДО ТРЕХ
Дети используют первые математические навыки в повседневных делах и занятиях. Это хорошая новость, поскольку эти навыки важны для подготовки к школе. Но ранняя математика не означает вынимать калькулятор во время игры. Еще до того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания посредством повседневного взаимодействия.Например, у Томаса две машины; Джозеф хочет один. После того, как Томас поделился одной, он видит, что у него осталась одна машина (Bowman, Donovan, & Burns, 2001, стр. 201). Другие математические навыки приобретаются в ходе повседневных занятий, которыми вы делитесь с ребенком — например, подсчета шагов по мере того, как вы поднимаетесь или опускаетесь. Неформальные занятия, подобные этой, дают детям толчок к формальному обучению математике, которое начинается в школе.
Какие математические знания понадобятся вашему ребенку в начальной школе? Ранние математические концепции и навыки, на которых строится учебная программа по математике в первом классе, включают: (Bowman et al., 2001, с. 76).
Размер, форма и узоры
Умение считать вербально (сначала вперед, потом назад)
Распознавающие цифры
Определение большего и меньшего количества
Понимание однозначного соответствия (т. Е. Сопоставление наборов или знание, в какой группе их четыре, а в какой пять)
Ключевые математические навыки для школы
Более продвинутые математические навыки основаны на начальном математическом «фундаменте» — точно так же, как дом построен на прочном фундаменте.В первые годы жизни вы можете помочь своему ребенку начать развивать математические навыки в раннем возрасте, представив такие идеи, как: (Из Diezmann & Yelland, 2000 и Fromboluti & Rinck, 1999.)
Number Sense
Это умение точно считать — первый нападающий. Затем, позже в школе, дети научатся считать в обратном порядке. Более сложный навык, связанный с чувством чисел, — это способность видеть отношения между числами, например, сложение и вычитание. Бен (2 года) увидел кексы на тарелке.Он сосчитал со своим отцом: «Один, два, три, четыре, пять, шесть… »
Представительство
Оформление математических идей «реальными» с помощью слов, картинок, символов и предметов (например, блоков). Кейси (3 года) собирался на пикник. Он аккуратно разложил четыре пластмассовые тарелки и четыре пластмассовых стакана: «Так что всей семьей приехать на пикник!» В его семье было четыре члена; он смог применить эту информацию к выбранному количеству тарелок и чашек.
Пространственное чувство
Позже в школе дети будут называть это «геометрией».«Но для малышей он знакомит с идеями формы, размера, пространства, положения, направления и движения. Азиз (28 месяцев) хихикал внизу слайда. «Что тут смешного?» — недоумевала его тетя. «Я поднялся, — сказал Азиз, — а потом спустился!»
Измерение
Технически это определение длины, высоты и веса объекта в таких единицах, как дюймы, футы или фунты. Измерение времени (например, в минутах) также относится к этой области навыков. Габриэлла (36 месяцев) снова и снова спрашивала свою Абуэлу: «Сделать печенье? Я сделаю это! » Ее Абуэла показала ей, как наполнить мерный стакан сахаром.«Нам нужны две чашки, Габи. Наполните его один раз и положите в миску, а затем снова наполните ».
Оценка
Это способность сделать хорошее предположение о количестве или размере чего-либо. Маленьким детям это сделать очень сложно. Вы можете помочь им, показав им значение таких слов, как больше, меньше, больше, меньше, больше, меньше чем. Нолан (30 месяцев) посмотрел на два рогалика: один был обычным, другой — мини-бубликом. Его отец спросил: «Какой из них ты предпочитаешь?» Нолан указал на обычный рогалик.Его отец сказал: «Ты, должно быть, голоден! Этот рогалик больше. Этот бублик меньше. Хорошо, я дам тебе большую. Скоро завтрак! »
Паттерны
Узоры — это вещи, числа, формы, изображения, которые логически повторяются. Шаблоны помогают детям научиться делать прогнозы, понимать, что будет дальше, устанавливать логические связи и использовать навыки рассуждения. Ава (27 месяцев) указала на Луну: «Луна. Солнце переходит ночь-ночь. Дедушка подобрал ее: «Да, маленькая Ава.Утром выходит солнце, а луна уходит. Ночью солнце засыпает, а луна выходит играть. Но пора Аве спать, прямо как солнце.
Решение проблем
Способность продумать проблему, признать, что к ответу существует более одного пути. Это означает использование прошлых знаний и навыков логического мышления для поиска ответа. Карл (15 месяцев) посмотрел на сортировщик формы — пластиковый барабан с тремя отверстиями в верхней части.Отверстия имели форму треугольника, круга и квадрата. Карл посмотрел на массивные фигуры на полу. Он поднял треугольник. Он положил его в свой месяц, а затем ударил им об пол. Он коснулся краев пальцами. Затем он попытался засунуть его в каждую дырочку новой игрушки. Сюрприз! Он упал в отверстие треугольника! Карл потянулся к другому блоку, на этот раз круглому…
Математика: одна часть целого
Математические навыки — это лишь часть более широкой сети навыков, которые дети развивают в раннем возрасте, включая языковые, физические и социальные навыки.Каждая из этих областей навыков зависит от других и влияет на них.
Трина (18 месяцев) укладывала блоки. Она положила два квадратных блока один на другой, а затем треугольный. Она обнаружила, что никакие блоки больше не будут балансировать на вершине блока треугольной формы. Она взглянула на своего отца и показала ему блок, который ей не удалось достичь, чтобы оставаться на вершине, по сути говоря ему своим жестом: «Папа, мне нужна помощь, чтобы разобраться в этом». Ее отец показал ей, что, если она снимет треугольный блок и вместо него воспользуется квадратным, она сможет сложить еще больше.Затем она добавила еще два блока к своей башне, прежде чем с гордостью показать свое творение отцу: «Дада, Оок! Оу! »
В этом обычном взаимодействии вы можете увидеть, как все области разработки Trina работают вместе. Ее физические способности позволяют ей манипулировать блоками и использовать свои мыслительные способности для выполнения своего плана по постройке башни. Она использует свой язык и социальные навыки, когда просит помощи у отца. Ее эффективное общение позволяет папе реагировать и оказывать необходимую помощь (дальнейшее развитие ее социальных навыков, поскольку она считает себя важным и хорошим коммуникатором).Это еще больше укрепляет ее мыслительные способности, поскольку она узнает, как решить проблему увеличения высоты башни.
Что вы можете сделать
Приведенные ниже советы показывают, как вы можете помочь своему ребенку освоить математические навыки в раннем возрасте, опираясь на его природное любопытство и весело проводя время вместе. (Примечание: большинство этих советов предназначены для детей старшего возраста — в возрасте от 2 до 3 лет. Дети младшего возраста могут быть представлены рассказам и песням, используя повторение, рифмы и числа.)
Прибавьте форму.
Играть с сортировщиками формы. Поговорите с ребенком о каждой форме — посчитайте стороны, опишите цвета. Создавайте свои собственные фигуры, вырезая большие фигуры из цветной плотной бумаги. Попросите ребенка «прыгнуть по кругу» или «запрыгнуть на красную фигуру».
Подсчитайте и отсортируйте.
Соберите корзину с маленькими игрушками, ракушками, камешками или пуговицами. Считайте их вместе с ребенком. Отсортируйте их по размеру, цвету или предназначению (то есть все машины в одной стопке, все животные в другой).
Сделайте звонок.
Вместе со своей 3-летней дочкой начните учить ее адрес и номер телефона своего дома. Поговорите с ребенком о том, что у каждого дома есть номер, и как его дом или квартира входят в серию, каждая со своим номером.
Какой это размер?
Обратите внимание на размеры объектов в мире вокруг вас: этот розовый бумажник самый большой. Синий кошелек самый маленький. Попросите ребенка подумать о своем размере по сравнению с другими предметами («Вы помещаетесь под столом? Под стулом?»).
Теперь ты готовишь!
Наполнять, перемешивать и наливать могут даже маленькие дети. Благодаря этим упражнениям дети естественным образом учатся считать, измерять, складывать и оценивать.
Уходи прочь.
Прогулка дает детям множество возможностей сравнить (какой камень больше?), Оценить (сколько желудей мы нашли?), Отметить сходства и различия (есть ли у утки мех, как у кролика?) И классифицировать (посмотреть, есть ли можно найти красные листья). Вы также можете поговорить о размере (делая большие и маленькие шаги), оценить расстояние (находится ли парк рядом с нашим домом или далеко?) И потренироваться в счете (давайте посчитаем, сколько шагов мы дойдем до угла).
Время картинки.
Используйте песочные часы, секундомер или таймер для коротких (1–3 минут) занятий. Это помогает детям развить чувство времени и понять, что на одни дела уходит больше времени, чем на другие.
Прибавьте форму.
Укажите на разные формы и цвета, которые вы видите в течение дня. Во время прогулки вы можете увидеть знак в форме треугольника желтого цвета. Внутри магазина вы можете увидеть красный прямоугольник.
Прочтите и пой свои числа.
Пойте песни, которые рифмуются, повторяются или содержат числа.Песни закрепляют закономерности (что тоже является математическим навыком). Они также являются интересным способом попрактиковаться в языке и развить социальные навыки, такие как сотрудничество.
Начни сегодня.
Используйте календарь, чтобы говорить о дате, дне недели и погоде. Календари усиливают подсчет, последовательности и закономерности. Развивайте навыки логического мышления, говоря о холодной погоде и спрашивая ребенка: что мы надеваем, когда холодно? Это побуждает вашего ребенка находить связь между холодной погодой и теплой одеждой.
Раздать.
Попросите ребенка помочь в распределении таких предметов, как закуски, или в разложении салфеток на обеденном столе. Помогите ему дать каждому ребенку по крекеру. Это помогает детям понимать индивидуальную переписку. Когда вы раздаете предметы, подчеркните концепцию числа: «Один для вас, один для меня, один для папы». Или: «Мы надеваем обувь: раз, два».
Большой на блоках.
Дайте вашему ребенку возможность поиграть с деревянными кубиками, пластиковыми блокировками, пустыми коробками, пакетами для молока и т. Д.Сложение этих игрушек в стопку и манипулирование ими помогает детям узнать о формах и отношениях между формами (например, два треугольника образуют квадрат). Скворечники и чашки для детей младшего возраста помогают им понять взаимосвязь между объектами разного размера.
Туннельное время.
Откройте большие картонные коробки с каждого конца, чтобы превратить их в туннель. Это помогает детям понять, где находится их тело в пространстве и по отношению к другим объектам.
Длинное и короткое.
Отрежьте несколько (3-5) кусочков ленты, пряжи или бумаги разной длины. Поговорите о таких идеях, как длинные и короткие. Расположите ребенка в порядке от самого длинного к самому короткому.
Учитесь на ощупь.
Вырежьте фигуры — круг, квадрат, треугольник — из прочного картона. Пусть ваш ребенок коснется фигуры открытыми, а затем закрытыми глазами.
Образец воспроизведения.
Развлекайтесь с выкройками, позволяя детям раскладывать сухие макароны, крупные бусины, различные виды сухих хлопьев или кусочки бумаги разными узорами или рисунками.Во время этого занятия внимательно наблюдайте за ребенком, чтобы не подавиться, и уберите все предметы, когда закончите.
Обучение стирке.
Сделайте работу по дому интересной. Сортируя белье, попросите ребенка сделать стопку рубашек и стопку носков. Спросите его, какая стопка больше (оценка). Вместе посчитайте, сколько рубашек. Посмотрите, сможет ли он сделать пары носков: вы можете вынуть два носка и сложить их в стопку? (Не беспокойтесь, если они не совпадают! Это упражнение больше связано с подсчетом, чем с сопоставлением.)
Детская площадка по математике.
Пока ваш ребенок играет, сравнивайте его по росту (высокий / низкий), положению (больше / меньше) или размеру (большой / маленький).
Платье для успеха в математике.
Попросите ребенка выбрать рубашку на день. Спросите: Какого цвета ваша рубашка? Да, желтый. Можете ли вы найти в своей комнате что-нибудь желтое? Когда вашему ребенку приблизится три года и старше, обратите внимание на узоры на его одежде — например, полосы, цвета, формы или изображения: я вижу узор на вашей рубашке.Есть полосы, которые идут красным, синим, красным, синим. Или ваша рубашка покрыта пони — большой пони рядом с маленьким пони, по всей вашей рубашке!
Графические игры.
Когда вашему ребенку исполнится три года и больше, составьте таблицу, на которой ребенок сможет наклеивать стикер каждый раз, когда идет дождь или каждый раз в солнечную погоду. В конце недели вы можете вместе прикинуть, в каком столбце больше или меньше наклеек, и подсчитать, сколько, чтобы быть уверенным.
Список литературы
Боуман, Б.Т., Донован М.С. и Бернс М.С. (ред.). (2001). Стремятся учиться: обучение наших дошкольников. Вашингтон, округ Колумбия: Национальная академия наук.
Diezmann, C., & Yelland, N.J. (2000). Развитие математической грамотности в раннем детстве. В Йелланде, штат Нью-Джерси (ред.), Содействие осмысленному обучению: инновации в обучении профессионалов дошкольного образования. (стр. 47–58). Вашингтон, округ Колумбия: Национальная ассоциация образования детей младшего возраста.
Фромболути, К.С. и Ринк Н. (1999 июнь). Раннее детство: где начинается обучение. Министерство образования США, Управление исследований и совершенствования образования, Национальный институт развития и образования детей младшего возраста. Получено 11 мая 2018 г. по адресу https://www2.ed.gov/pubs/EarlyMath/title.html
.Многопредметные: Учителя детства (1–6 классы) Часть вторая: Практический опрос по математике
Многопредметный опрос: Учителя детства (1–6 классы) Часть вторая: Опросник для практических занятий по математикеНазвание вопроса
Ландшафтный дизайнер оформляет внутренний дворик из серого и белого камня.Схема конструкции представлена ниже.
Название вопроса
* 1. Какое уравнение можно использовать для определения общей площади патио в квадратных футах?
Название вопроса
* 2.Ученик использует растворимую смесь лимонада, чтобы приготовить 7 кувшинов лимонада для школьных мероприятий. Учащийся использует 2/8 стакана смеси для каждого кувшина. Какое общее количество смеси использует ученик?
Название вопроса
* 3.Какое выражение эквивалентно 32?
Название вопроса
График системы линейных уравнений показан ниже.
Название вопроса
* 4.Какая упорядоченная пара является наилучшей оценкой для решения этой системы линейных уравнений?
Название вопроса
* 5.Какое выражение представляет собой факторизацию 32m + 56mp?
Название вопроса
* 6.Средний радиус Земли составляет 6 371,0 км, а средний радиус Луны — 1 737,5 км. Какова приблизительная разница между средней длиной окружности Земли и Земли Луны в километрах?
Название вопроса
* 7.Сотрудник по продажам в магазине электроники может выбрать один из двух вариантов заработной платы, показанных ниже.
- 115 долларов в неделю плюс 9,5% комиссионных от общих продаж торгового партнера
- 450 $ в неделю без комиссии
Средний общий объем продаж торгового партнера в прошлом году составил 125 000 долларов. В чем разница между двумя вариантами заработной платы, исходя из средней продолжительности последних лет?
Название вопроса
Выражение и четыре возможных значения этого выражения показаны ниже.
Название вопроса
* 8. Какое лучшее значение для выражения?
Название вопроса
* 9.Тренировка спортсмена состоит из 10 минут разминки, 25 минут подъема тяжестей и 15 минут бега на беговой дорожке. Каково отношение количества минут, в течение которых спортсмен поднимает тяжести, к общему количеству минут тренировки?
Название вопроса
На графике ниже показана взаимосвязь между количеством человек в группе и общей стоимостью билетов для входа на спортивное мероприятие.
Название вопроса
* 10. Какая точка на графике представляет собой единицу стоимости?
Название вопроса
Компания по производству хлопьев случайным образом кладет одно цветное призовое кольцо в каждую коробку с хлопьями.Есть 6 колец разного цвета. Цвета колец в каждой из 50 коробок с хлопьями показаны в таблице ниже.
Название вопроса
* 11. Исходя из данных, какова вероятность того, что в следующей коробке с хлопьями будет синее или желтое кольцо?
Название вопроса
* 12.В партии новых книг для библиотеки 5/12 книг были стихами, а 2/5 — биографиями. Остальные книги в партии были загадками. Какая доля книг в партии была загадкой?
Название вопроса
Ниже показаны параллелограмм и четыре выражения.
Название вопроса
* 13. Какое выражение можно использовать для определения площади параллелограмма?
Название вопроса
Ученик использует блоки размером 1 кубический дюйм, чтобы сделать правую прямоугольную призму, показанную ниже.
Название вопроса
* 14. Затем ученик делает меньшую правую прямоугольную призму, используя 1/4 кубиков.Каков объем в кубических дюймах меньшей правой прямоугольной призмы?
Название вопроса
Ниже показаны четыре экспоненциальных выражения.
Название вопроса
* 15.Какое экспоненциальное выражение равно 2
-5 X 2 8 ?Название вопроса
Скорость света в вакууме составляет 299 792 458 метров в секунду. В вопросе викторины учащимся предлагается записать в научных обозначениях наилучшее приближение скорости света.Ниже показаны ответы четырех студентов.
Название вопроса
* 16. Какой ответ является наилучшим приближением скорости света, записанной в научных обозначениях?
Название вопроса
Высота ракеты в выбранные моменты времени указана в таблице ниже.
Название вопроса
* 17. Основываясь на этих данных, какое утверждение
, а не является действительным заключением?Название вопроса
Ниже показаны четыре возможные функции.
Название вопроса
* 18. Какая функция является вершиной формы
f ( x ) = 3 x 2 + 12 x + 11?Название вопроса
Ниже показаны четыре функции.
Название вопроса
* 19. Какая функция будет иметь наибольшее значение при увеличении x выше 25?
Название вопроса
Учащийся проверяет значения, которые сделают KLM прямоугольным треугольником, когда отрезок линии LN соответствует высоте, а KM = 16, как показано ниже.
Название вопроса
* 20. При какой длине треугольник KLM будет прямоугольным?
СЧЕТ
т
Для работы этого сайта требуется Javascript, пожалуйста, включите.
Математика 1 класса — Кембриджские государственные школы
В 1 классе учебное время должно быть сосредоточено на четырех критических областях: (1) развитие понимания сложения, вычитания и стратегий сложения и вычитания в пределах 20; (2) развитие понимания отношений целых чисел и значений разряда, в том числе группировки десятков и единиц; (3) развитие понимания линейного измерения и измерения длины как повторяющихся единиц длины; и (4) рассуждения об атрибутах, а также составление и разложение геометрических фигур.
Читать письмо семьям | Загрузить объем и последовательность (pdf)
Поддержка вашего ребенка в 1-м классе по математике
Совет школ большого города создал «дорожные карты» для родителей, чтобы дать родителям рекомендации относительно того, что их ребенок будет изучать по математике и как они могут поддержать это обучение. Эти родительские дорожные карты также предоставляют трехлетние снимки, показывающие, как отобранные стандарты прогрессируют из года в год:
Дорожная карта для родителей: поддержка вашего ребенка в математике
Guía Para Los Padres: Apoyando A Su Hijo En Matemáticas
Стандарты математической практики
В рамках 2011 года вводится
Стандарты математической практики
Эти стандарты дополняют стандарты содержания, так что учащиеся все активнее взаимодействуют с предметом по мере того, как они растут в математической зрелости и опыте на протяжении младших, средних и старших классов школы.Эти стандарты одинаковы для всех классов от дошкольного до 12 класса.
Объяснение того, как стандарты могут быть выделены в Уровне 1, можно найти здесь
Эти восемь практик можно сгруппировать в следующие категории, как показано в таблице ниже:
Образцы мышления продуктивного математического мыслителя: | Рассуждение и объяснение |
Моделирование и использование инструментов | |
Видеть структуру и обобщать |
Стандарты содержания, которые должны быть охвачены в 1-м классе
Направленность обучения в 1-м классе определяется Структурой учебной программы по математике штата Массачусетс 2011, которую можно найти на
Сайт Департамента начального и среднего образования
Чтобы узнать об основных стандартах Common Core в математике, щелкните здесь
Math
Студенты лучше всего изучают математику, когда у них есть возможность «заниматься математикой».Студенты должны работать над сложными проблемами, делиться своими мыслями с другими и использовать свое мышление для построения и углубления понимания. Этот процесс предоставит нашим студентам навыки, необходимые для поступления в колледж или более подготовленной работы.
Стандарты обучения
Стандарты обучения математике нового поколения штата Нью-Йорк представляют собой установленные руководящие принципы того, что каждый ученик должен знать и уметь делать по математике с классов K-12. Узнайте больше о стандартах математики.Чтобы узнать больше об основной учебной программе г. Нью-Йорка, см. Оценки ниже:
Ресурсы для семьи
Вот несколько занятий, которые можно попробовать дома:
Готовка
Следующие шаги, использование дробей и соотношений и измерение количеств — это всего лишь некоторые навыки, которые мы используем, чтобы приготовить даже базовые рецепты. А когда вы готовите вместе, вы вместе с ребенком можете приготовить вкусные блюда!
Покупки
При совершении покупок поощряйте детей обращать внимание на размеры, вес, вместимость и измерения жидкости.Попросите ребенка:
- найти самый большой контейнер с молоком и объяснить, почему он вмещает больше, чем другие контейнеры
- сравните размер и стоимость двух или более предметов, чтобы определить наилучшее значение
- подсчитайте количество предметов в вашем cart
- оцените стоимость предметов.
- определите, сколько денег можно ожидать в обмен на сдачу.
Повседневная жизнь
. Проведите беседы, относящиеся к повседневной жизни, и включите математические вопросы.Во время путешествия используйте вопрос «Когда мы туда доберемся?» Как возможность подвести некоторые подсчеты:
- посчитайте количество съездов и / или остановок, прежде чем вы доберетесь до пункта назначения
- поговорите о милях до пункта назначения
- спросите, как быстро вы едете, чтобы ваш ребенок мог ответить
В повседневной жизни вы всегда можете задавать «удивительные» вопросы, например:
- Какого роста это дерево?
- Сколько мест в этой комнате?
- Сколько людей стоят перед нами на этой линии?
Обдумайте эти вопросы вместе и попросите ребенка рассказать вам, о чем они думали, чтобы получить свои ответы.
Цифры и фигуры
Цифры и фигуры нас окружают! Найдите числа и формы в окружающей среде (адреса, спортивная статистика, прогноз погоды, номерные знаки, цены, знаки) и обсудите, что они означают и как используются.
Сколько времени это займет?
Изучите время, попросив ребенка оценить, а затем измерить, сколько времени требуется для выполнения различных действий. Какие из оценок вашего ребенка были близки к реальному времени? Какие были дальше всего? Попросите их назвать занятие, которое, по их мнению, займет менее пяти минут, затем попробуйте его и посмотрите, насколько точным было их предположение.Не забывайте отмечать время начала и окончания каждого действия, чтобы увидеть, как долго оно длилось; это поможет детям понять течение времени.
Пазлы и оригами
Пазлы помогают развивать пространственные навыки. Умение замечать формы и узоры в пазлах позволит вашему ребенку легко усвоить концепции геометрии, которым его обучают в школе.
Оригами (японское искусство складывания бумаги) укрепляет понимание формы и симметрии, а также требует от детей следовать указаниям в последовательном порядке.
Сыграть в игры
Настольные игры, такие как «Монополия», «Улики», «Желоба и лестницы» и многие другие, дают возможность попрактиковаться в математических навыках, вычислениях и логических рассуждениях. Карточные игры, такие как Twenty-One и Hearts, дадут вашему ребенку возможность попрактиковаться в базовых вычислениях.
Ресурсы для преподавателей
Учителя и другие преподаватели могут найти учебную программу и учебные материалы на сайте We Teach NYC.
.

