Ответ по геометрии: Ответы по геометрии на вопросы и задачи с подробным решением

Билеты и ответы по геометрии

Билеты и вопросы

• формат doc
• размер 13.98 КБ
• добавлен 04 октября 2011 г.

2011, 12 стр.

Аксиомы стереометрии.
Теорема о существовании и единственности плоскости, проходящей через данную прямую и точку вне ее.
Параллелепипед, его элементы.
Теорема о точке пересечения диагоналей параллелепипеда.
Параллельные прямые (определение).
Теорема о существовании и единственности прямой, параллельной данной и проходящей через точку, не лежащую на этой прямой.
Вывод формулы площади сферы.
Прямая, параллельная плоскости (определение).

Признак параллельности прамой и плоскости.
Конус.
Вывод формулы объема конуса.
Параллельные плоскости (определение).
Признак параллельности двух плоскостей.
Вывод формулы объема пирамиды.
Теорема об отрезках параллельных прямых, заключенных между двумя параллельными плоскостями.
Касательная плоскость (определение).
Теорема о касательной плоскости шара (сферы).
Прямая, перпендикулярная плоскости (определение).
Признак перпендикулярности прямой и плоскости.
Площадь боковой поверхности пирамиды.
Теорема о боковой поверхности правильной пирамиды.
Теорема о трех перпендикулярах.
Вывод формулы объема шара.
Перпендикулярные плоскости (определение).
Признак перпендикулярности двух плоскостей.
Прямая призма (определение).
Теорема о боковой поверхности прямой призмы.
Задача о боковой поверхности наклонной призмы.
Теорема о двух прямых, перпендикулярных плоскости.
Прямоугольный параллелепипед (определение).
Теорема о квадрате диагоналей прямоугольного параллелепипеда.
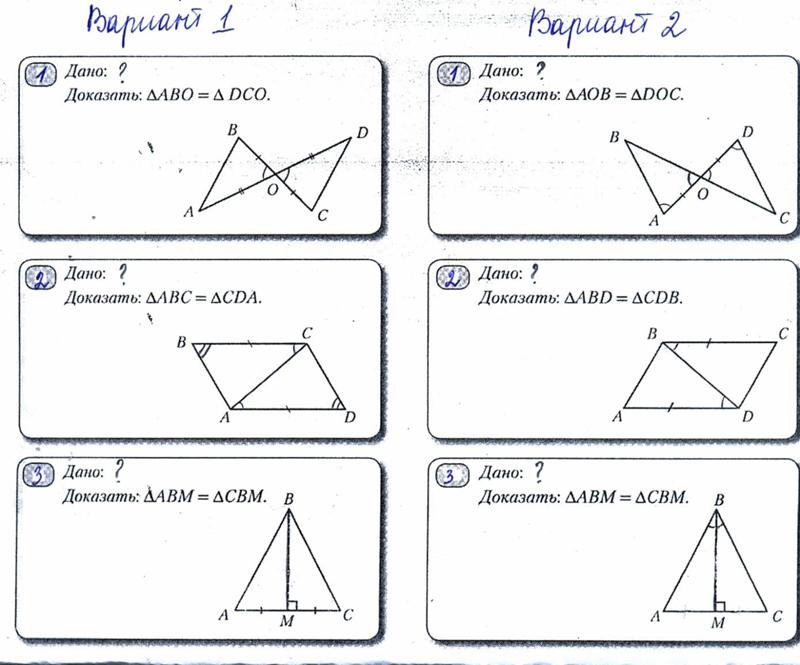
Теорема о плоскости, перпендикулярной одной из двух параллельных прямых (или обратная ей теорема).
Теорема о противолежащих гранях параллелепипеда.

Смотрите также

• формат djvu
• размер 6.32 МБ
• добавлен 05 апреля 2011 г.

Предлагаемый «Курс Опытной Геометрии» ставит себе целью изложить в популярной форме элементарный курс геометрии в объеме, необходимом для применения геометрических знаний в практической жизни. В основу этого курса положен индуктивно-лабораторный метод.

• формат djvu
• размер 7.91 МБ
• добавлен 12 января 2011 г.

20-е изд. — М.: Просвещение, 2010. — 384 с. В этом учебнике геометрии много задач: есть задачи и практические задания к каждому параграфу, дополнительные задачи к каждой главе и, наконец, задачи повышенной трудности.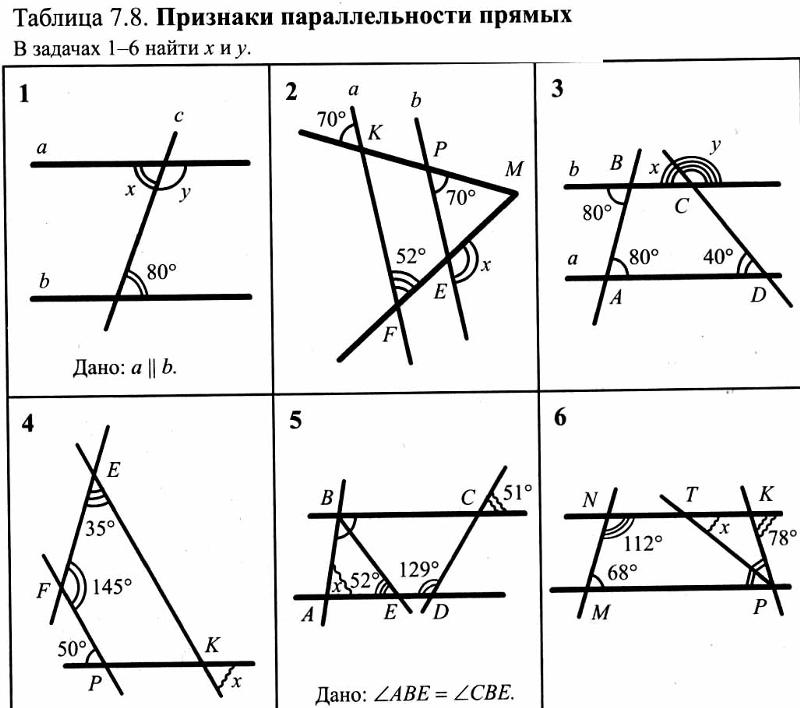 Основными являются задачи к параграфу. Более трудные задачи отмечены звездочкой. В конце книги к задачам даны ответы и указания. Учебник для 7 — 9 классов общеобразовательных учреждений.

Билеты и вопросы

• формат doc
• размер 41.77 КБ
• добавлен 11 января 2011 г.

Стр. 10. Экзаменационные билеты по геометрии. 10 билетов. Аксиомы стереометрии. Параллелепипед, его элементы. Параллельные прямые (определение). Вывод формулы площади сферы. Прямая, параллельная плоскости (определение). Вывод формулы объема конуса. Параллельные плоскости (определение). Вывод формулы объема пирамиды. Касательная плоскость (определение). Прямая, перпендикулярная плоскости (определение). Площадь боковой поверхности пирамиды. Т…

• формат djvu
• размер 9. 87 МБ
• добавлен 07 сентября 2011 г.

Новое изд., испр. и доп. — М.: МЦНМО, 2011. — 640 с. В учебнике изложен курс геометрии для 10–11 классов средней школы (профильный уровень). Подробно разобран теоретический материал и многочисленные задачи. В каждой главе приводятся задачи для самостоятельного решения, к которым даны ответы и указания. Наряду со «стандартными» широко представлены «нестандартные» задачи, в том числе задачи математических олимпиад разного уровня и вступительных э…

• формат djvu
• размер 3.53 МБ
• добавлен 18 марта 2011 г.

— М.; «Обериг», 1994. – 209с. Пособие, написанное известным педагогом, специалистом школьной геометрии, включает как векторные задачи, так и смешанные задачи классической геометрии, решаемые с помощью векторов. В книге решены векторные задачи из сборников задач по математике под редакцией М. И. Сканави разных изданий. Для учащихся школ и техникумов, лицеев и гимназий, классов с углубленным изучением математики, абитуриентов, студентов, учителей и…

• формат pdf
• размер 1.43 МБ
• добавлен 12 июня 2011 г.

Уфа, 1998 Книга представляет собой учебное пособие по курсу оснований геометрии. Она адресована студентам-математикам, а также школьникам 7-11 классов для самостоятельного углубленного изучения геометрии и для использования в кружках и факультативных занятиях.

• формат djvu
• размер 2.34 МБ
• добавлен 25 декабря 2009 г.

Библиотечка Квант, выпуск 31 — М.: Наука, 1984. — 160 с. Сборник содержит 340 задач по стереометрии и состоит из двух разделов. В первом разделе помещены в основном задачи вычислительного характера. Сюда же включены в виде задач некоторые теоремы и факты стереометрии, непосредственно примыкающие школьному курсу. Во втором разделе собраны различные геометрические факты, неравенства, задачи на геoмeтpические места точек, элементы геометрии тетраэд…

• формат djvu
• размер 2.79 МБ
• добавлен 07 апреля 2011 г.

Библиотечка Квант, выпуск 31. — М.: Наука, 1984. — 160 с. Полностью распознано. Сборник содержит 340 задач по стереометрии и состоит из двух разделов. В первом разделе помещены в основном задачи вычислительного характера. Сюда же включены в виде задач некоторые теоремы и факты стереометрии, непосредственно примыкающие школьному курсу. Во втором разделе собраны различные геометрические факты, неравенства, задачи на геoмeтpические места точек, эле.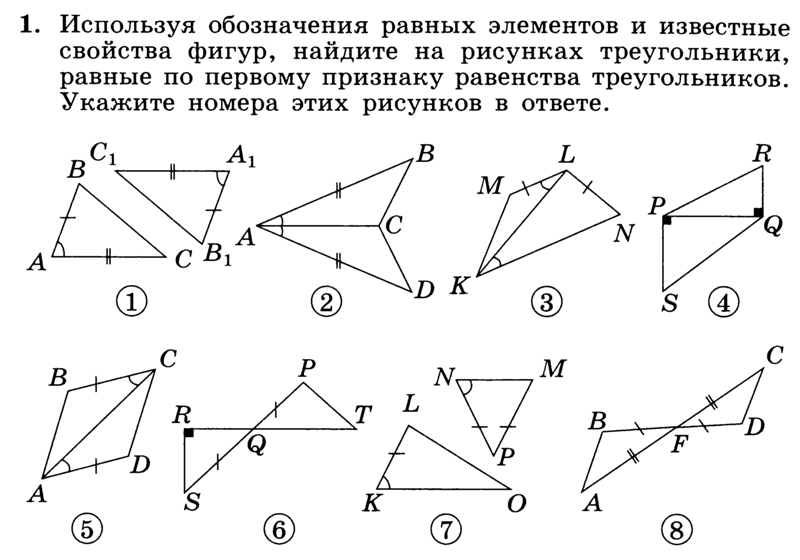

..

• формат djvu
• размер 4.05 МБ
• добавлен 27 января 2011 г.

М.: Государственное издательство технико-теоретической литературы, 1955. — 280 с. Эта книга, состоящая из двух томов, посвящена элементарной геометрии. В течение главным образом XIX века в элементарной геометрии был накоплен весьма обширный материал. Было доказано много красивых и неожиданных теорем о кругах, треугольниках, многоугольниках и т. д.; из элементарной геометрии выделились даже целые «науки», как геометрия треугольника или геометрия…

• формат djvu
• размер 8.64 МБ
• добавлен 27 января 2011 г.

М.: Государственное издательство технико-теоретической литературы, 1956. — 611 с. Эта книга, состоящая из двух томов, посвящена элементарной геометрии. В течение главным образом XIX века в элементарной геометрии был накоплен весьма обширный материал. Было доказано много красивых и неожиданных теорем о кругах, треугольниках, многоугольниках и т. д.; из элементарной геометрии выделились даже целые «науки», как геометрия треугольника или геометрия…

В чем важность планиметрии и пространственной геометрии?

содержание

Каково значение плоской и пространственной геометрии?

Аннотация: Изучение плоскостной и пространственной геометрии имеет большое значение для школьника, помогает в развитии навыков абстрагирования, решении бытовых задач для вычисления и сравнения результатов, а также в распознавании свойств геометрических фигур.

Какое значение имеет плоскостная геометрия?

Изучение геометрии необходимо для полного развития человека, поскольку оно помогает понять мир, развивает логическое мышление и обеспечивает лучшее понимание других областей знаний из-за большого значения, которое геометрия приобретает в повседневной жизни человека. .

В чем разница и важность планиметрии и пространственной геометрии?

Планиметрия — это изучение фигур в двух измерениях, таких как квадраты, круги, прямоугольники и треугольники. В то время как пространственная геометрия изучает фигуры в трех измерениях, то есть кубы, сферы, параллелепипеды и пирамиды.

Каково значение пространственной геометрии в повседневной жизни?

С помощью Пространственной геометрии можно обнаружить характеристики и свойства геометрических тел, а также разработать формулы для расчета объема и площади этих тел.

В чем основное отличие пространственных геометрических фигур от плоских?

Наиболее важное различие между плоскими и пространственными фигурами заключается в количестве измерений, необходимых для определения этих фигур. Фигура называется плоской, если для ее определения необходимы только два измерения.

Где применять пространственную геометрию?

Наиболее распространенные расчеты в пространственной геометрии заключаются в определении длин кривых, площадей поверхностей и объемов твердотельных областей. Другие пространственные геометрические фигуры: цилиндр, конус, сфера. «Платоновы тела» — это выпуклые многогранники, известные с античных времен.

Что такое пространственная геометрия?

Пространственная геометрия — это анализ тел в пространстве, то есть геометрия для трехмерных объектов, в отличие от плоской геометрии, изучающей двумерные фигуры. Как и последний, первый возникает на основе примитивных понятий, а именно: точка, линия, плоскость и пространство.

Что такое пространственные геометрические фигуры?

Примеры пространственных фигур: пирамида, призма, куб, сфера, цилиндр и др.

Каково применение планиметрии в нашей повседневной жизни?

Дорожные знаки, дома и строения — вот некоторые из примеров, где присутствует геометрия.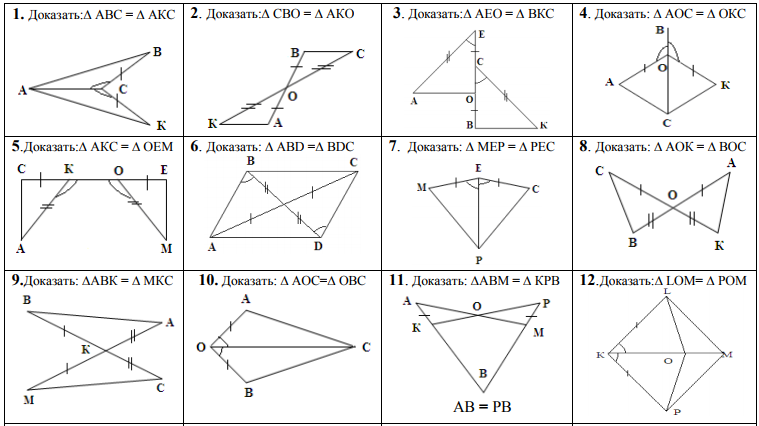 Другой известный пример – наш национальный флаг. В нем можно распознать различные фигуры, такие как прямоугольник, ромб и круг — все это фигуры, являющиеся частью геометрии.

Как пространственная геометрия присутствует в зданиях и каково ее значение?

В настоящее время геометрия считается одним из основных предметов с математическим приложением, связанным с отраслью гражданского строительства, а также с архитектурой. Именно с помощью форм и геометрических расчетов специалисты, связанные с этими областями, зарисовывают планы домов, зданий, улиц, площадей.

Правильно ли говорить, что геометрию можно разделить на планиметрию, пространственную геометрию и аналитическую геометрию?

Геометрия — раздел математики, изучающий измерения и свойства фигур, подразделяющийся, помимо пространственной геометрии, на две подобласти: плоскостную геометрию (отвечающую за изучение плоскости и пространства) и аналитическую геометрию (которая связана с алгеброй и математический анализ).

Что такое плоские геометрические фигуры?

Основными плоскими фигурами являются треугольник, круг, квадрат, прямоугольник, ромб и трапеция, и каждая из них имеет формулу вычисления площади. Стоит отметить, что область изучается в планиметрии, геометрии для двухмерных объектов.

Какое значение имеет преподавание геометрии в начальной школе?

Геометрия важна в глобальном становлении школьника и для его интеллектуального развития. Геометрическое знание развивает идеи, позволяющие понять мир, в котором оно действует, пространство, которое его окружает, исследуя и открывая действия, дающие ему ощущение этого пространства.

Какова основная цель обучения геометрии или пространственному знанию?

Правильный ответ: сравнивать величины одного вида, различать предметы и величины и измерять величины.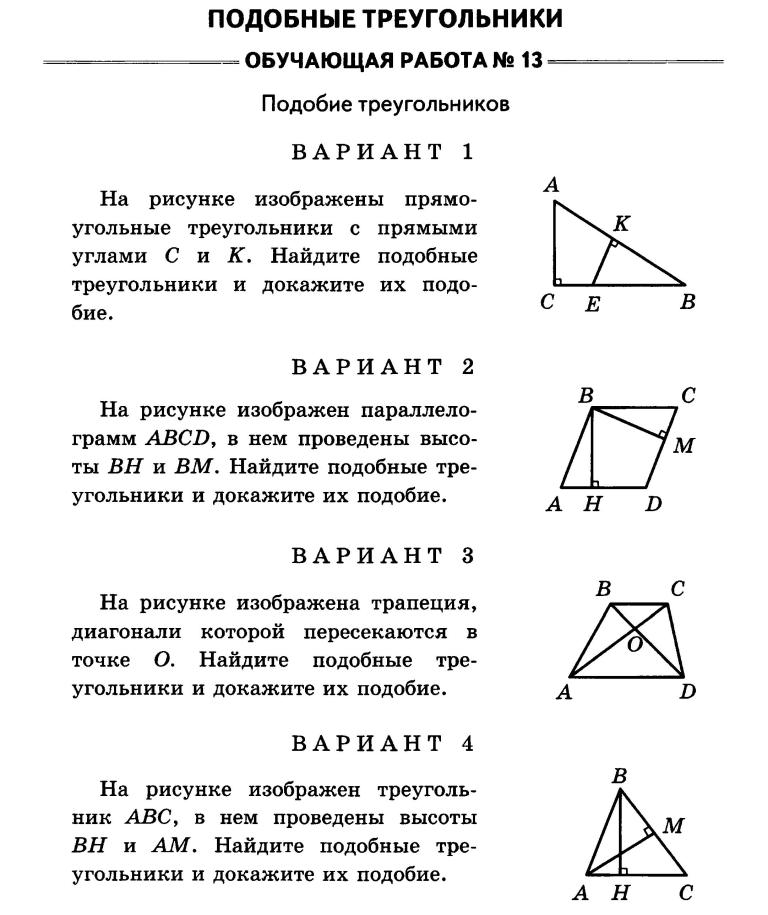

Что нужно знать для изучения пространственной геометрии?

Если это все еще не хорошо, вы можете узнать, что изучать по базовой математике для плоской и пространственной геометрии.

Основные предметы базовой геометрии

• Счет;
• Прямой;
• Плоский;
• углы;
• декартова плоскость;
• Геометрические тела;
• Подобие треугольников;
• Теорема Пифагора;

Какая пространственная геометрическая фигура имеет только неплоские поверхности?

Неплоские или пространственные геометрические фигуры#

• Конус.
• Мяч.
• Пирамида.
• Цилиндр.

Сколько фигурок самолетов?

Что такое плоские фигуры

В геометрии наиболее известны формы плоских фигур: круг, квадрат, треугольник, прямоугольник, трапеция, шестиугольник, пятиугольник, параллелограмм и ромб.

Почему куб не плоская фигура?

Строить геометрические фигуры в пространстве можно только в том случае, если число измерений фигуры равно или меньше числа измерений пространства. Таким образом, невозможно построить круг в одномерном пространстве, ни куб на плоскости, ни квадрат внутри прямой, ни конус в одномерном пространстве.

Что изучает планиметрия?

Планиметрия посвящена объектам, принадлежащим плоскости, то есть имеющим только ширину и длину. Она также известна как евклидова геометрия.

Как возникла планиметрия?

Первые занятия по плоской геометрии относятся к Древней Греции, ее также можно назвать евклидовой геометрией в честь Евклида Александрийского (360 г. на принципах Платона.

Что такое плоские фигуры?

Мы называем плоской фигурой любую фигуру, имеющую два измерения. Нас окружают плоские фигуры, такие как квадраты, круги, треугольники и другие формы. Плоские фигуры имеют два измерения. Плоские фигуры присутствуют во все времена в быту.

Как работать с пространственной геометрией?

Начните занятие с представления некоторых объектов в виде многогранников, чтобы можно было изучить некоторые элементы, принадлежащие к твердым телам. каждая грань также является вершиной многогранника. Пример куба: куб имеет длину, ширину и высоту (3 измерения) и состоит из 6 квадратов (плоских фигур).

Сколько в нем пространственных геометрических фигур?

Пространственные геометрические фигуры# Пространственная геометрия изучает различные геометрические тела, среди основных у нас есть: цилиндр, куб, конус, сфера, параллелепипед и пирамида.

Кто создал геометрию?

Евклид, великий математик и писатель, жил, вероятно, в XNUMX веке до нашей эры и считается отцом геометрии. Он первым собрал всю геометрию в единое произведение под названием «Элементы». Этот математик основывал планиметрию на пяти постулатах.

Где сегодня можно использовать геометрию?

Обычно геометрия рассматривается как незначительная для студента. Овладение этим содержанием следует поощрять путем исследования исторических фактов о геометрии и ее применениях в строительстве, сельском хозяйстве, животноводстве и решении задач, связанных с расчетами и измерениями.

Что еще относится к планиметрии?

Площади плоских фигур, которые падают больше всего, это: Площадь параллелограмма (с помощью которой можно также вычислить площадь прямоугольника и площадь квадрата, поскольку они являются параллелограммами). Статью на эту тему можно найти здесь; Площадь круга.

Как работать с плоской геометрией в дошкольном образовании?

Ниже приведены некоторые интересные упражнения, которые помогут в изучении геометрических фигур.

1. Пазлы из геометрических фигур.
2. Детали для контурной геометрической фигуры.
3. Маски животных с носами геометрических фигур.

Как рассчитать плоскую и пространственную геометрию?

Формулы геометрии пространства

1. Когда мы собираемся изучать пространство, плоскостная геометрия приобретает другое измерение.
2. Чтобы рассчитать объем призмы, просто умножьте площадь основания на высоту.
3. Куб — это правильный многогранник, у которого все стороны равны.

Образована ли геометрическая фигура всеми точками плоскости, находящимися на одинаковом расстоянии от фиксированной точки этой плоскости?

Окружность – это плоская геометрическая фигура, образованная объединением точек, находящихся на одинаковом расстоянии от фиксированной точки.

Как работать с плоскими фигурами?

Рекомендации: Начните урок, спросив учащихся, могут ли они сказать, что такое плоские фигуры, и привести несколько примеров. Проверьте, какие фигуры они смогли изобразить как плоские фигуры. Запишите их ответы на доске и попросите их назвать каждый из них. Позже исследуйте некоторые из них.

Что такое неплоская фигура?

Неплоские формы

Это фигуры с тремя измерениями: длина, высота и ширина. Неплоские формы также называют геометрическими телами. Они подразделяются на многогранники и не многогранники. Чтобы узнать больше о геометрических телах, прочтите также пространственную геометрию.

Что такое плоские области?

Некоторые плоские области напоминают хорошо известные многоугольники, такие как треугольник, квадрат, прямоугольник, ромб, параллелограмм, трапеция, пятиугольник, шестиугольник и другие, где каждый из них имеет определенную формулу для определения площади его поверхности.

Каковы преимущества геометрии?

Ниже приведены некоторые из основных преимуществ использования технологий.

• Более быстрое выравнивание.
• Более точное выравнивание.
• Больше экономии топлива.
• Больше устойчивости при движении.
• Меньший износ подвески.

Какое значение имеет геометрия в математике?

Геометрия чрезвычайно важна в повседневной жизни людей, так как развивает наглядное мышление, и без этой способности они вряд ли смогут решать различные геометризированные жизненные ситуации; Они также не смогут использовать геометрию как фактор для понимания и решения вопросов…

Каков вклад геометрии в человечество?

Создание неевклидовой геометрии стало важной вехой в истории математики. С эволюцией евклидовой геометрии в неевклидову геометрию были открыты и представлены обществу новые понятия, новые теории, в качестве примера можно привести теорию относительности Альберта Эйнштейна.

Как пространственная геометрия присутствует в зданиях и каково ее значение?

В настоящее время геометрия считается одним из основных предметов с математическим приложением, связанным с отраслью гражданского строительства, а также с архитектурой. Именно с помощью форм и геометрических расчетов специалисты, связанные с этими областями, зарисовывают планы домов, зданий, улиц, площадей.

Какова основная цель обучения геометрии или пространственному знанию?

Правильный ответ: сравнивать величины одного вида, различать предметы и величины и измерять величины.

Что такое плоскость пространственной геометрии?

Плоскость представляет собой набор выровненных линий и, следовательно, это также набор точек. Объект, образованный таким выравниванием линий, представляет собой плоскую поверхность, которая не искривляется и бесконечна во всех направлениях. На плоскости можно рисовать фигуры, которые кроме длины имеют ширину.

Какое значение имеет геометрия в топографии?

В области топографии часто используется часть математики, связанная с планиметрией, аналитикой и тригонометрией, для преобразования показаний углов и расстояний, выполненных в поле, в плоские координаты и вычисления площадей.

Справка по геометрии — Бесплатная справка по математике

Нужна помощь по геометрии? У нас есть более тридцати отличных уроков геометрии, разбитых на общие темы. Обязательно просмотрите все темы, чтобы найти то, что вам нужно, или выполните поиск по ключевому слову.

Линии графика

• Асимптоты
• Домен и диапазон
• Нахождение асимптот
• Нахождение горизонтальных асимптот
• Форма уклона точки
• Форма пересечения склонов
• Наклон линии
• Ось X-Y
• Построение параболы

Формы

• Треугольники
• 30-60-90 Прямоугольный треугольник
• Параллелограммы
• Трапеции
• Специальные параллелограммы
• Конгруэнтные треугольники
• Равнобедренные треугольники
• полигонов

Углы, линии и точки

• Формула расстояний
• Мир углов
• Специальные уголки
• Параллельные линии
• Длина сегмента линии
• Сумма углов треугольника
• Внешние углы треугольника
• Внутренние углы многоугольника
• Неравенства треугольников
• Формула средней точки

Другие уроки

• Заполнение уравнений квадрата в круге
• Среднее геометрическое
• Геометрические термины
• Словарь по геометрии

Формулы

• Формулы площади
• Формулы периметра
• Площадь поверхности
• Объемные формулы

Другое

• Важный словарь по геометрии
• Вертикальные углы

Уроки с других сайтов:

• Площади, объемы, площади поверхности
• Длина окружности
• Классификация углов
• Конические сечения/круги
• Внутренние углы правильных многоугольников
• Основы многоугольника
• Теорема Пифагора
• Трехмерные фигуры

Последние вопросы по геометрии

Почему мы не можем определить последовательные числа на прямой с действительными числами? Воскресенье, 12 февраля 2023 г.

Подобие треугольников Воскресенье, 12 февраля 2023 г.0125 Воскресенье, 12 февраля 2023 г.

Интегральный вопрос Лебега Воскресенье, 12 февраля 2023 г.

Статистика: как найти среднее+медиану этого вопроса? Воскресенье, 12 февраля 2023 г.

Избранный урок

Прочтите о свойствах прямоугольных треугольников 30-60-90.

Ресурсы для репетиторов

Онлайн-уроки по математике и ссылки могут быть действительно полезными, если у вас есть конкретный вопрос или вы ищете освежение знаний по определенной теме. Но если вам нужна дополнительная помощь, вам может понадобиться репетитор по геометрии. Будь то друг или учитель в школе, местный репетитор или онлайн-репетитор, реальный человек может быстрее ответить на вопросы и объяснить вещи, которые вы не понимаете, лучше, чем любой урок или доска объявлений.

Геометрия: ключ ответа

Здесь представлены ответы и решения для задания «Вставь меня, тренер!» ящики для упражнений, организованные по секциям.

Снятие бремени с доказательств

1. Да
2. Теорема 8.3: Если два угла дополняют один и тот же угол, то эти два угла равны.

A и B дополняют друг друга, а C и B дополняют друг друга.

Дано: А и В комплементарны, а С и В комплементарны.

Докажите: A ~= C.

	Заявления	Причины
1.	А и В комплементарны, а С и В комплементарны.	Дано
2.	мА + мВ = 90°, мКл + мБ = 90°	Определение дополнительного
3.	мА = 90° — мБ, мКл = 90° — мБ	Свойство вычитания равенства
4.	мА = мКл	Замена (этап 3)
5.	А ~= С	Определение ~=

Доказательство связи между сегментами и углами

1. Если E находится между D и F, то DE = DF EF.

E находится между D и F.

Дано: E находится между D и F

Докажите: DE = DF EF.

	Заявления	Причины
1.	E находится между D и F	Дано
2.	D, E и F являются коллинеарными точками, а E находится на ¯DF	Определение между
3.	DE + EF = DF	Постулат сложения сегментов
4.	DE = DF EF	Свойство вычитания равенства

2. Если BD делит ABC на два угла, ABD и DBC, то mABC = mABC — mDBC.

BD делит ABC на два угла, ABD и DBC.

Дано: BD делит ABC на два угла, ABD и DBC

Докажите: mABD = mABC — mDBC.

	Заявления	Причины
1.	BD делит ABC на два угла, ABD и DBC	Дано
2.	мАБД + мДБК = мАВС	Постулат сложения углов
3.	мАБД = мАВС — мДБК	Свойство вычитания равенства

3. Биссектриса угла единственна.

ABC с двумя биссектрисами угла: BD и BE.

Дано: ABC с двумя биссектрисами угла: BD и BE.

Докажите: mDBC = 0.

	Заявления	Причины
1.	BD и BE делят пополам ABC	Дано
2.	ABC ~= DBC и ABE ~= EBC	Определение биссектрисы ангела
3.	mABD = mDBC и mABE ~= mEBC	Определение ~=
4.	mABD + mDBE + mEBC = mABC	Постулат сложения углов
5.	mABD + mDBC = mABC и mABE + mEBC = mABC	Постулат сложения углов
6.	2mABD = mABC и 2mEBC = mABC	Замена (этапы 3 и 5)
7.	mABD = mABC / 2 и mEBC = mABC / 2	Алгебра
8.	mABC / 2 + mDBE + mABC / 2 = mABC	Замена (этапы 4 и 7)
9.	мАВС + мДБЭ = мАВС	Алгебра
10.	мДБЭ = 0	Свойство вычитания равенства

4. Дополнение к прямому углу есть прямой угол.

A и B — смежные углы, а A — прямой угол.

Дано: А и В — смежные углы, А — прямой угол.

Докажите: угол B прямой.

	Заявления	Причины
1.	A и B — смежные углы, а A — прямой угол	Дано
2.	мА + мБ = 180º	Определение дополнительных углов
3.	мА = 90°	Определение прямого угла
4.	90° + mB = 180°	Замена (шаги 2 и 3)
5.	мБ = 90º	Алгебра
6.	B — прямой угол	Определение прямого угла

Доказательство связи между строками

1. m6 = 105°, m8 = 75°
2. Теорема 10.3: Если две параллельные прямые пересечены секущей, то противоположные внешние углы равны.

м.п. разрез поперечным t.

Дано: l m, разрезанный секущей t.

Докажите: 1 ~= 3.

	Заявления	Причины
1.	л м разрез поперечной т	Дано
2.	1 и 2 — вертикальные углы	Определение вертикальных углов
3.	2 и 3 соответствующие углы	Определение соответствующих углов
4.	2 ~= 3	Постулат 10.1
5.	1 ~= 2	Теорема 8.1
6.	1 ~= 3	Переходное свойство 3.

3. Теорема 10.5. Если две параллельные прямые пересечены секущей, то внешние углы по одну сторону от секущей являются дополнительными углами.

м.п. срезанный поперечным t.

Дано: l m, разрезанный секущей t.

Докажите: 1 и 3 являются дополнительными.

Заявление

		Причины
1.	л м разрез поперечной т	Дано
2.	1 и 2 — дополнительные углы, а m1 + m2 = 180º	Определение дополнительных углов
3.	2 и 3 соответствующие углы	Определение соответствующих углов
4.	2 ~= 3	Постулат 10.1
5.	м2 ~= м3	Определение ~=
6.	м1 + м3 = 180º	Замена (этапы 2 и 5)
7.	1 и 3 являются дополнительными	Определение дополнительного

 

Лучшие 3D-принтеры

Заинтересованы в 3D-печати?

Мы изучили основные моменты, которые следует учитывать при покупке 3D-принтера, и выбрали лучшие принтеры 2020 года в зависимости от ваших потребностей.

ПОЛУЧИТЬ ПЕЧАТЬ

 

4. Теорема 10.9. Если две прямые пересечены секущей так, что внешние углы равны, то эти прямые параллельны.

Прямые l и m пересекаются секущей t.

Дано: Прямые l и m пересекаются секущей t, где 1 ~= 3.

Докажите: l m.

Заявление

		Причины
1.	Прямые l и m пересекаются секущей t с 1 ~= 3	Дано
2.	1 и 2 — вертикальные углы	Определение вертикальных углов
3.	1 ~= 2	Теорема 8.1
4.	2 ~= 3	Транзитивное свойство ~=.
5.	2 и 3 соответствующие углы	Определение соответствующих углов
6.	л м	Теорема 10.7

5. Теорема 10.11. Если две прямые пересечены секущей так, что внешние углы по одну сторону от этой секущей смежны, то эти прямые параллельны.

Линии l и m пересекаются t секущей t.

Дано: Прямые l и m пересекаются секущей t, углы 1 и 3 — смежные.

Докажите: l m.

Заявление

		Причины
1.	Прямые l и m пересекаются секущей t, а 1 представляет собой 3 дополнительных угла	Дано
2.	2 и 1 дополнительные уголки	Определение дополнительных углов
3.	3 ~= 2	Пример 2
4.	3 и 2 соответствующие углы	Определение соответствующих углов
5.	л м	Теорема 10.7

Компания двоих. Три треугольника

1. Тупоугольный равнобедренный треугольник
2. Острые углы прямоугольного треугольника дополняют друг друга.

ABC — прямоугольный треугольник.

Дано: треугольник ABC прямоугольный, угол B прямой.

Докажите: A и C — дополнительные углы.

Заявление

		Причины
1.	ABC — прямоугольный треугольник, а B — прямой угол	Дано
2.	мБ = 90º	Определение прямого угла
3.	мА + мВ + мКл = 180º	Теорема 11.1
4.	мА + 90° + мКл = 180°	Замена (шаги 2 и 3)
5.	мА + мКл = 90º	Алгебра
6.	A и C являются дополнительными углами	Определение дополнительных углов

3. Теорема 11.3: Мера внешнего угла треугольника равна сумме мер двух несмежных внутренних углов.

ABC с внешним углом BCD.

Заявление 7.

		Причины
1.	ABC с наружным уголком BCD	Дано
2.	DCA — прямой угол, mDCA = 180º	Определение прямого угла
3.	мБЦА + мБЦД = мДКА	Постулат сложения углов
4.	мБЦА + мБЦД = 180º	Замена (шаги 2 и 3)
5.	mBAC + mABC + mBCA = 180º	Теорема 11.1
6.	мБАК + мАБК + мБЦА = мБЦА + мБЦД	Замена (этапы 4 и 5)
мБАЦ + мАБК = мБЦД	Свойство вычитания равенства

4. 12 единиц ²

5. 30 единиц ²

6. Нет, треугольник с такими длинами сторон нарушил бы неравенство треугольника.

Конгруэнтные треугольники

1. Рефлексивное свойство: ABC ~= ABC.

Свойство симметрии: если ABC ~= DEF, то DEF ~= ABC.

Переходное свойство: если ABC ~= DEF и DEF ~= RST, то ABC ~= RST.

2. Доказательство: если ¯AC ~= ¯CD и ACB ~= DCB, как показано на рис.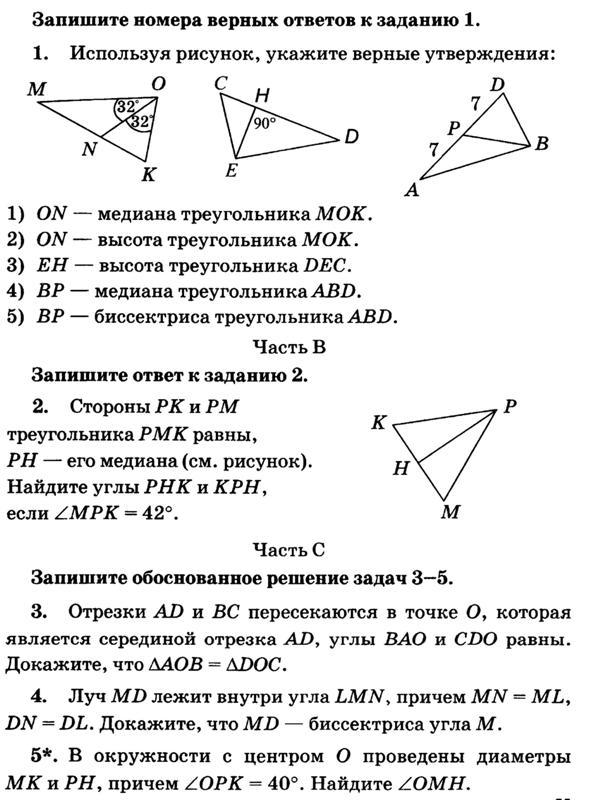 12.5, то ACB ~= DCB.

Заявление

		Причины
1.	¯AC ~= ¯CD и ACB ~= DCB	Дано
2.	¯БК ~= ¯БК	Рефлексивное свойство ~=
3.	ACB ~= DCB	Постулат SAS

3. Если ¯CB ¯AD и ACB ~= DCB, как показано на рис. 12.8, то ACB ~= DCB.

Заявление

		Причины
1.	¯CB ¯AD и ACB ~= DCB	Дано
2.	углы ABC и DBC прямые	Определение
3.	mABC = 90° и mDBC = 90°	Определение прямых углов
4.	мАВС = мДВС	Замена (этап 3)
5.	АВС ~= ДБК	Определение ~=
6.	¯БК ~= ¯БК	Рефлексивное свойство ~=
7.	ACB ~= DCB	Постулат АСА

4. Если ¯CB ¯AD и CAB ~= CDB, как показано на рис. 12.10, то ACB~= DCB.

Заявление

		Причины
1.	¯CB ¯AD и CAB ~= CDB	Дано
2.	углы ABC и DBC прямые	Определение
3.	mABC = 90° и mDBC = 90°	Определение прямых углов
4.	мАВС = мДВС	Замена (этап 3)
5.	АВС ~= ДБК	Определение ~=
6.	¯БК ~= ¯БК	Рефлексивное свойство ~=
7.	ACB ~= DCB	ААС Теорема

5. Если ¯CB ¯AD и ¯AC ~= ¯CD, как показано на рис. 12.12, то ACB ~= DCB.

Заявление

		Причины
1.	¯CB ¯AD и ¯AC ~= ¯CD	Дано
2.	ABC и DBC — прямоугольные треугольники	Определение прямоугольного треугольника
3.	¯БК ~= ¯БК	Рефлексивное свойство ~=
4.	ACB ~= DCB	HL Теорема для прямоугольных треугольников

6. Если P ~= R и M — середина ¯PR, как показано на рис. 12.17, то N ~= Q.

Заявление

		Причины
1.	P ~= R и M — середина ¯PR	Дано
2.	¯PM ~= ¯MR	Определение средней точки
3.	NMP и RMQ — вертикальные углы	Определение вертикальных углов
4.	NMP ~= RMQ	Теорема 8.1
5.	PMN ~= RMQ	Постулат АСА
6.	Н ~= Q	КПОКТАК

Похожие треугольники

1. х = 11
2. х = 12
3. 40° и 140°
4. Если A ~= D, как показано на рис. 13.6, то ^BC / _AB = ^CE / _DE .

Заявление

		Причины
1.	А ~= Д	Дано
2.	BCA и DCE — вертикальные углы	Определение вертикальных углов
3.	БКА ~= ДКЭ	Теорема 8.1
4.	ACB ~ DCE	AA Теорема подобия
5.	BC / AB = CE / DE	КССТАП

5. 150 футов.

Открытие дверей с помощью подобных треугольников

1. Если прямая параллельна одной стороне треугольника и проходит через середину второй стороны, то она проходит через середину третьей стороны.

¯DE ¯AC, а D — середина ¯AB.

Дано: ¯DE ¯AC и D – середина ¯AB.

Докажите: E — середина ¯BC.

Заявление до н.э. БЭ г. до н.э.

		Причины
1.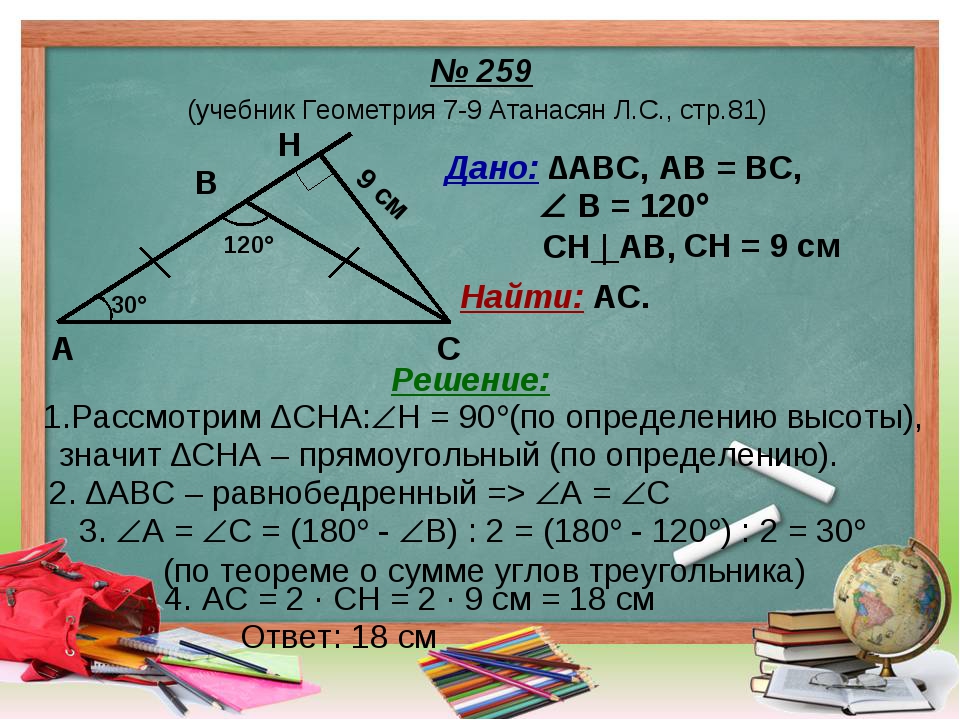	¯DE ¯AC, а D — середина ¯AB.	Дано
2.	¯DE ¯AC и пересекается поперечной AB	Определение поперечной
3.	BDE и BAC соответствующие углы	Определение соответствующих углов
4.	БДЭ ~= БАК	Постулат 10.1
5.	Б ~= Б	Рефлексивное свойство ~=
6.	ABC ~ DBE	AA Теорема подобия
7.	ДБ / АБ = БЭ / БЭ	КССТАП
8.	ДБ = АВ / 2	Теорема 9.1
9.	ДБ / АВ = 1 / 2	Алгебра
10.	1 / 2 = БЭ / БЭ	Замена (этапы 7 и 9)
11.	г. до н.э. = 2BE	Алгебра
12.	БЭ + ЕС =	Постулат сложения сегментов
13.	БЭ + ЕС = 2БЭ	Замена (этапы 11 и 12)
14.	ЕС =	Алгебра
15.	E — середина ¯	Определение средней точки

2. AC = 43, AB = 8, RS = 16, RT = 83

3. AC = 42, BC = 42

Четырехугольники на первый план

1. АД = 63, ВС = 27, РС = 45
2. ¯AX, ¯CZ и ¯DY

Трапеция ABCD с показанными четырьмя высотами XB CY.

3. Теорема 15.5. В воздушном змее одна пара противоположных углов конгруэнтна.

Воздушный змей ABCD.

Дано: Воздушный змей ABCD.

Докажите: B ~= D.

Заявление

		Причины
1.	ABCD — воздушный змей	Дано
2.	¯AB ~= ¯AD и ¯BC ~= ¯DC	Определение воздушного змея
3.	¯AC ~= ¯AC	Рефлексивное свойство ~=
4.	АВС ~= АЦП	Постулат ССС
5.	Б ~= Д	КПОКТАК

4. Теорема 15.6. Диагонали воздушного змея перпендикулярны, а диагональ, противоположная конгруэнтным углам, делит другую диагональ пополам.

Воздушный змей ABCD.

Дано: Воздушный змей ABCD.

Докажите: ¯BD ¯AC и ¯BM ~= ¯MD.

Заявление

		Причины
1.	ABCD — воздушный змей	Дано
2.	¯AB ~= ¯AD и ¯BC ~= ¯DC	Определение воздушного змея
3.	¯AC ~= ¯AC	Рефлексивное свойство ~=
4.	АВС ~= АЦП	Постулат ССС
5.	БАК ~= ЦАП	КПОКТАК
6.	¯AM ~= ¯AM	Рефлексивное свойство ~=
7.	ПРО ~= АДМ	Постулат SAS
8.	¯BM ~= ¯MD	КПОКТАК
9.	БМА ~= прямой доступ к памяти	КПОКТАК
10.	мБМА = мДМА	Определение ~=
11.	MBD — прямой угол, а mBMD = 180º	Определение прямого угла
12.	мБМА + мДМА = мБМД	Постулат сложения углов
13.	мБМА + мДМА = 180º	Замена (шаги 9 и 10)
14.	2mBMA = 180º	Замена (шаги 9 и 12)
15.	мБМА = 90º	Алгебра
16.	BMA прямоугольный	Определение прямого угла
17.	¯BD ¯AC	Определение

5. Теорема 15.9: Противоположные углы параллелограмма равны.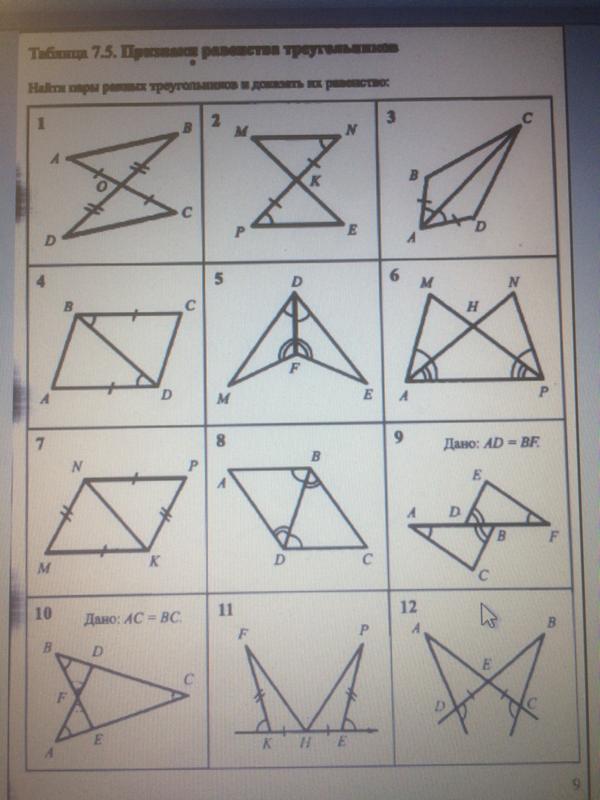

Параллелограмм ABCD.

Дано: Параллелограмм ABCD.

Докажите: ABC ~= ADC.

Заявление

		Причины
1.	Параллелограмм ABCD имеет диагональ ¯AC.	Дано
2.	ABC ~= CDA	Теорема 15.7
3.	АВС ~= АЦП	КПОКТАК

6. 144 шт. ²

7. 180 шт. ²

8. Воздушный змей ABCD имеет площадь 48 шт.

Параллелограмм ABCD имеет площадь 150 единиц ² .

Прямоугольник ABCD имеет площадь 104 единицы ² .

Ромб ABCD имеет площадь ³⁵ / ₂ шт. ² .

Анатомия круга

1. Окружность: 20 футов, длина ˆRST = ¹⁵⁵ / ₁₈ футов
2. 9 футов ²
3. 15 футов ²
4. 28º

Единичный круг и тригонометрия

1. ³ / ₃₄ = ³³⁴ / ₃₄
2. ¹ / ₃ = ³ / ₃
3. Коэффициент тангенса = ⁴⁰ / ₃ , коэффициент синуса = ⁴⁰ / ₇
4. отношение тангенса = ⁵ / ₅₆ = ⁵⁵⁶ / ₅₆ , отношение косинуса = ⁵⁶ / ₉

Выдержки из Полное руководство идиота по геометрии © 2004 Дениз Сечеи, доктор философии.