Гдз и решебник Математика 1 класс Захарова, Юдина — Тетрадь для самостоятельной работы
Математика 1 классТетрадь для самостоятельной работыПерспективная начальная школаЗахарова, Юдина«Академкнига»
Первый класс — всегда ответственный период для ребенка, который ассоциируется со сменой обстановки, уровня и степени ответственности перехода в целом. Это сложно морально и физически изменить привычную обстановку детского сада на школу, и приспособиться к ней.
Сложность предмета для первоклассников
Первым, что бросается в глаза родителю — более сложная школьная программа. Уже с первого класса, к детям можно относиться как к студентам, которые приходят в школу за знаниями, и, в зависимости от серьезности хорошо или плохо обучаются.
Большое количество предметов и домашнего задания может вызвать определенные трудности у родителей во время проверки. Ведь помимо большого количества дисциплин, детей интересуют прогулки, игры, друзья, и другое.
С целью облегчения процесса проверки домашнего задания, были разработаны специальные учебные пособия, именуемые ГДЗ — готовое домашнее задание.
Рабочая тетрадь по математике Захаровой для 1-ого класса
Готовое домашнее задание по «Математике рабочая тетрадь для 1 класса», авторами которой являются Захарова и Юдина включает в себя ответы и решения на все задания, представленные в тетради: а их более 120 страниц.
Польза ГДЗ
Использование готового домашнего задания приносит пользу как родителям, так и детям:
- В первую очередь, ГДЗ помогает родителям при проверке его у ребенка. Иногда бывает совсем мало времени на то, чтобы вспоминать школьные годы и следить за этапностью решения в тетради ребенка. В таким ситуациях, можно просто сверить решение пособия и ребенка, и если что-то будет неправильно, помочь ему или направить его на правильное решение.
- Ребенок, в свою очередь, может также воспользоваться сервисом ГДЗ.
Однако, вам лучше сразу приучить его сверять ответы, а не списывать. Только так он сможет научиться не только самостоятельно искать решения, но и исправлять допущенные ошибки, в случае несоответствия с ГДЗ.
Однако, вам лучше сразу приучить его сверять ответы, а не списывать. Только так он сможет научиться не только самостоятельно искать решения, но и исправлять допущенные ошибки, в случае несоответствия с ГДЗ.ГДЗ по математике 2 класс рабочая тетрадь Захарова Юдина
Авторы: О. А. Захарова, Е. П. Юдина
Издательство: Академкнига
Тип книги: Тетрадь для самостоятельной работы
ГДЗ рабочая тетрадь Математика в вопросах и заданиях. 2 класс. Тетрадь для самостоятельной работы. О. А. Захаровой, Е. П. Юдиной. Издательство Академкнига/Учебник. Серия Математика. Состоит из двух частей (1 часть – 64 страницы, 2 часть – 80 страниц).
Математическое развитие второклассников, формирование системы необходимых знаний по предмету, развитие познавательного интереса к математике, а также к умственной деятельности являются первостепенными задачами, стоящими перед заданиями рабочей тетради. Юные школьники освоят разрядность сотен, смогут провести сравнение трехзначных чисел, сложить числа столбиком.
На ЯГДЗ Вы сможете найти решебник ГДЗ, в котором собраны решения всех упражнений, входщих в состав рабочей тетради. Успешное интеллектуальное развитие, самостоятельный поиск и обработка информации станут итогом работы с нашим изданием. Привычка проверять выполненное решение позволит предотвратить получение нежелательных оценок.
Часть 1
1 Математика и летние каникулы
1 2 3 4 5
2 Счёт десятками и круглые десятки
1 2 3
3 Числовые равенства и числовые неравенства
1 2 3 4 5
4 Числовые выражения и их значения
1 2 3
5 Сложение круглых десятков
1 2 3 4
6 Вычитание круглых десятков
1 2 3
7 Десятки и единицы
1 2 3 4
8 Краткая запись задачи
1 2 3
9 Килограмм.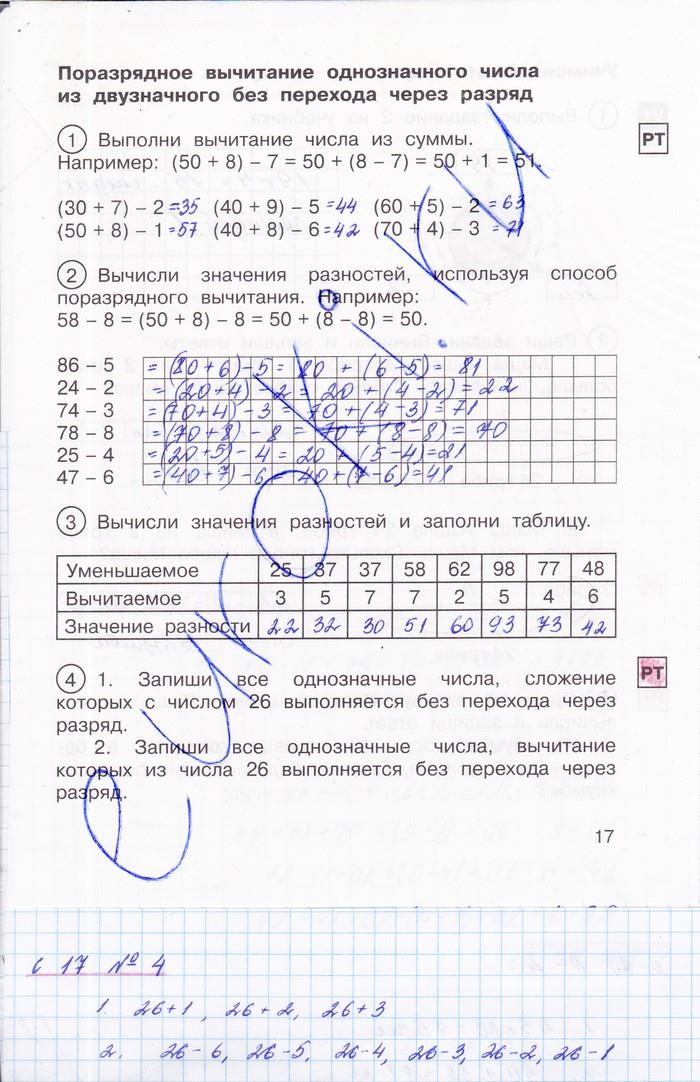
Сколько килограммов
1 2 3
10 Учимся решать задачи
1 2 3 4
11 Прямая бесконечна
1 2
12 Сложение круглых десятков с однозначными числами
1 2 3
13 Поразрядное сложение двузначного числа и однозначного без перехода через разряд
1 2 3 4
14 Поразрядное вычитание однозначного числа из двузначного без перехода через разряд
1 2 3 4
15 Учимся решать задачи
1 2 3
16 Прямая и луч
1 2 3
17 Сложение круглого десятка и двузначного числа
1 2 3 4
18 Вычитание круглого десятка из двузначного числа
1 2 3 4
19 Дополнение до круглого десятка
1 2 3
20 Сложение двузначного числа и однозначного с переходом через разряд
1 2 3 4 5
21 Вычитание однозначного числа из круглого десятка
1 2 3 4
22 Поразрядное вычитание однозначного числа из двузначного с переходом через разряд
1 2 3 4
23 Угол
1 2 3
24 Прямой, острый и тупой углы
1 2
25 Последовательность чисел
1 2 3
26 Углы многоугольника
1 2 3
27 Разностное сравнение чисел
1 2 3
28 Задачи на разностное сравнение чисел
1 2 3
29 Двузначное число больше однозначного
1 2 3 4 5
30 Сравнение двузначных чисел
1 2 3 4
31 Прямоугольник и квадрат
1 2 3 4
32 Поразрядное сложение двузначных чисел без перехода через разряд
1 2 3 4
33 Поразрядное сложение двузначных чисел с переходом через разряд
1 2 3 4 5
34 Десять десятков, или сотня
1 2 3 4 5
35 Дециметр и метр
1 2 3 4
36 Килограмм и центнер
1 2 3
37 Сантиметр и метр
1 2 3 4
38 Сумма и произведение.
Знак умножения
1 2 3
39 Произведение и множители
1 2
40 Значение произведения и умножение
1 2 3 4 5
41 Перестановка множителей
1 2
42 Умножение числа 0 и на число 0
1 2 3 4
43 Умножение числа 1 и на число 1
1 2 3 4 5 6
44 Длина ломаной линии
1 2 3 4 5
45 Умножение числа 1 на однозначные числа
1 2 3 4
46 Умножение числа 2 на однозначные числа
1 2 3
47 Периметр многоугольника
1 2 3 4 5
48 Периметр прямоугольника
1 2 3 4
49 Умножение числа 3 на однозначные числа
1 2 3 4
50 Умножение числа 4 на однозначные числа
1 2 3 4 5
51 Умножение и сложение — порядок выполнения действий
1 2 3 4
52 Периметр квадрата
1 2 3 4 5
53 Умножение числа 5 на однозначные числа
1 2 3 4
54 Умножение числа 6 на однозначные числа
1 2 3 4
55 Умножение числа 7 на однозначные числа
1 2 3 4
56 Умножение числа 8 на однозначные числа
1 2 3 4
57 Умножение числа 9 на однозначные числа
1 2 3 4
58 Увеличение в несколько раз
1 2 3
59 Работа с данными
1 2
60 Геометрические фигуры и геометрические величины
1
61 Таблица умножения
Таблица умножения
Часть 2
1 Счет десятками и круглое число десятков
1 2 3
2 Разряд сотен и названия круглых сотен
1 2 3 4
3 Сложение круглых сотен
1 2 3 4
4 Вычитание круглых сотен
1 2 3 4
5 Трехзначное число как сумма разрядных слагаемых
1 2 3 4
6 Трехзначное число – сума круглых сотен и двузначного или однозначного числа
1 2 3
7 Трехзначное число больше двузначного
1 2 3 4
8 Сравнение трехзначных чисел
1 2 3 4 5
9 Одно условие и несколько требований
1 2 3 4 5
10 Введение дополнительных требований
1 2 3 4
11 Запись решения задачи по действиям
1 2 3
12 Запись решения задачи в виде одного выражения
1 2 3 4 5
13 Запись сложения в строчку и столбиком
1 2 3 4
14 Способ сложения столбиком
1 2 3 4 5 6 7 8
15 Окружность и круг
1 2 3
16 Центр и радиус
1 2 3 4 5
17 Радиус и диаметр
1 2 3 4 5
18 Равные фигуры
1 2 3
19 Вычитание суммы из суммы
1 2 3 4
20 Поразрядное вычитание чисел без перехода через разряд
1 2 3 4
21 Поразрядное вычитание чисел с переходом через разряд
1 2 3
22 Запись вычитания в строчку и столбиком
1 2 3 4
23 Способ вычитания столбиком
1 2 3 4 5 6 7 8 9
24 Умножение и вычитание — порядок выполнения действий
1 2 3 4
25 Вычисления с помощью калькулятора
1 2 3 4
26 Известное и неизвестное
1 2 3
27 Числовое равенство и уравнение
1 2 3 4 5
28 Как найти неизвестное слагаемое
1 2 3
29 Как найти неизвестное вычитаемое
1 2 3
30 Как найти неизвестное уменьшаемое
1 2 3
31 Учимся решать уравнения
1 2 3
32 Распредели предметы поровну
1 2 3 4
33 Деление.
Знак деление
1 2 3 4
34 Частное и его значение
1 2
35 Делимое и делитель
1 2 3 4
36 Деление и вычитание
1 2 3 4 5 6
37 Деление и измерение
1 2
38 Деление пополам и половина
1 2 3 4
39 Деление на несколько равных частей и доля
1 2 3 4 5
40 Уменьшение в несколько раз
1 2 3
41 Действия первой и второй ступеней
1 2
42 Сколько прошло времени — Солнечные и песочные часы
1 2 3 4 5
43 Который час — Полдень и полночь
1 2 3
44 Циферблат и римские цифры
1 2 3 4 5
45 Час и минута
1 2 3 4 5 6 7
46 Откладываем равные отрезки
1 2 3 4
47 Числа на числовом луче
1 2 3
48 Натуральный ряд чисел
1 2 3 4 5 6
49 Час и сутки
1 2 3 4
50 Сутки и неделя
1 2 3 4
51 Сутки и месяц
1 2 3 4
52 Месяц и год
1 2 3 4
53 Календарь
1 2 3 4
54 Год и век
1 2 3
55 Данные и искомое
1 2
56 Обратная задача
1 2 3 4
57 Обратная задача и проверка решения данной задачи
1 2 3 4 5
58 Запись решения задачи в виде уравнения
1 2
59 Учимся решать задачи с помощью уравнений
1 2
60 Геометрические построения с помощью циркуля и линейки
1 2 3 4
61 Вычисляем значения выражений
1 2 3 4 5 6 7 8 9
62 Решаем задачи и делаем проверку
1 2 3
63 Время-дата и время-продолжительность
1 2
64 Геометрические фигуры и геометрические величины
1
65 Учимся составлять последовательности чисел
1 2 3 4
НУШ Математика.
1 класс. Рабочая тетрадь к учебнику С. А. Скворцовой, О. В. Оноприенко. В 2 частях. ЧАСТЬ 2Называем компоненты и результат действия вычитания
Складываем и вычитаем числа
Измеряем длины отрезков
Строим отрезки заданной длины
Изучаем выражения на два действия
Прибавляем и вычитаем число 3
Исследуем таблицы сложения и вычитания числа 3
Прибавляем и вычитаем числа 0, 1, 2, 3
Прибавляем и вычитаем числа 0, 1, 2, 3
Готовимся к изучению задач
Прибавляем и вычитаем число 4
Прибавляем и вычитаем число 4
Знакомимся с задачей
Узнаём о составляющих задачи
Исследуем задачи
Исследуем таблицы сложения и вычитания числа 4
Прибавляем и вычитаем числа 0, 1, 2, 3, 4
Открываем способ сложения и вычитания числа 5
Прибавляем и вычитаем число 5
Исследуем таблицы сложения и вычитания числа 5
Учимся выполнять арифметические действия с величинами
Складываем и вычитаем числа по частям Сравниваем величины
Исследуем таблицы сложения чисел второй пятёрки
Готовимся к изучению вычитания чисел 6, 7, 8, 9
Готовимся к изучению вычитания чисел 6, 7, 8, 9
Составляем краткую запись задачи
Вычитаем числа 6, 7, 8, 9
Вычитаем числа 6, 7, 8, 9
Составляем краткую запись задач
Находим неизвестное уменьшаемое или вычитаемое
Вычитаем числа второй пятёрки
Сравниваем число и математическое выражение
Исследуем таблицы вычитания чисел второй пятёрки
Сравниваем число и математическое выражение
Сравниваем математические выражения
Измеряем массы предметов
Измеряем ёмкости сосудов
Записываем задачу кратко
Исследуем свойства величин
Исследуем счётную единицу «десяток»
Сравниваем, складываем и вычитаем десятки
Получаем круглые числа
Складываем и вычитаем круглые числа
Исследуем единицу измерения длины «дециметр»
Образуем числа второго десятка
Записываем числа второго десятка
Записываем числа второго десятка
Записываем числа первой сотни
Сравниваем числа в пределах 100
Складываем и вычитаем на основе десятичного состава чисел второго десятка
Складываем и вычитаем на основе десятичного состава чисел первой сотни
Складываем и вычитаем на основе десятичного состава чисел первой сотни
Прибавляем и вычитаем число 1
Складываем и вычитаем числа на основе нумерации
Обобщаем знания о нумерации чисел первой сотни
Прибавляем и вычитаем однозначное число
Складываем и вычитаем числа
Складываем и вычитаем числа
Складываем и вычитаем числа
Исследуем задачи
Находим неизвестное вычитаемое или уменьшаемое
Знакомимся с задачами на нахождение неизвестного уменьшаемого или вычитаемого
Решаем задачи
Исследуем составляющие задач
Знакомимся со сложением и вычитанием двузначных чисел
Знакомимся с единицей измерения времени «сутки»
Определяем время по часам
Узнаём о продолжительности суток
Складываем и вычитаем числа
Определяем стоимость товара
Знакомимся с единицей измерения длины «метр»
Складываем и вычитаем числа Повторяем изученное
Складываем и вычитаем числа Повторяем изученное
Захарова 1 клас — snt63.
ruСкачать захарова 1 клас doc
Книга учебник СССР «Математика» 1 класс для учителей Моро Бантова Бельтюкова. р. Таганрог р. Подписаться на новые лоты по запросу «Книга учебник Захарова Фещенко \»Математика\» для 1 класса 3ч, г». Регистрация не требуется. В случае появления на продаже новых лотов удовлетворяющих вашим условиям, вы получите письмо на указанный адрес со списком наименований.
Вы сможете отписаться от получения этих уведомлений в любой момент. Гдз и решебник Математика 1 класс Захарова, Юдина — Рабочая тетрадь. Математика 1 класс. Серия: Перспективная начальная школа. Тип пособия: Рабочая тетрадь. Авторы: Захарова, Юдина. Издательство: «Академкнига». Для чего нужна математика. Математику изучают с первого класса. Но это – не только цифры и элементарные действия. Ученики узнают о способах решения каких-то задач, уравнений и примеров.
ГДЗ — поможет Вам сверить ответы к домашнему заданию по Математике Захарова О.А., Юдина Е.П. тетрадь для самостоятельной работы 1 класс.
Решения выполнены к издательству Академкнига Авторы: Захарова О.А., Юдина Е.П.. Тип: тетрадь для самостоятельной работы. Издательство: Академкнига Перспективная начальная школа Чтобы читать и смотреть Математика в вопросах и заданиях 1 класс Тетрадь самостоятельной работы Захарова Юдина часть 2, нажмите на нужные страницы.
Появятся изображения с бесплатными учебными материалами. Онлайн Математика в вопросах и заданиях 1 класс Тетрадь самостоятельной работы Захарова Юдина часть 2 бесплатно читать. Смотри школьные учебники (не гдз) на образовательном ресурсе — Рабочая-тетрадь-и-учебник.ком.
ГДЗ по Математике 1 класс Захарова О.А., Юдина Е.П. тетрадь для самостоятельной работы. Показать решебники. В закладки. Приветствуем на образовательном портале Еуроки. Здесь вы найдете ГДЗ с подробным и полным решением упражнений (номеров) по Математике тетрадь для самостоятельной работы за 1 класс, автор: Захарова О.А., Юдина Е.П.
Издательство: Академкнига. тетрадь №1. страница.
Здесь вы найдете тетрадь для самостоятельной работы по Математике 1 класса Часть 1, 2, авторы: Захарова О.А., Юдина Е.П., от издательства: Академкнига ГДЗ содержит все ответы на вопросы и поможет Вам правильно выполнить домашнее задание.
Ответы к учебнику по математике 1 класс Чекин Часть 1, 2 можно скачать здесь. Введите номер задания. Тетрадь №1. Страницы.
ГДЗ к тетради для самостоятельной работы часть 1, 2 по математике за 1 класс авторов Захарова, Юдина года издания. На этой странице вы можете посмотреть решения заданий с любой страницы рабочей тетради. Выберите страницу и вы перейдете в раздел с готовыми ответами к конкретной странице рабочей тетради. 1 класс» Захарова, Серова. Захарова, Серова: Поурочные разработки по математике. 1 класс. Пособие содержит подробные поурочные разработки по математике для 1 класса и ориентировано на учителей, работающих по развивающей системе Л.В.
Занкова. Сценарии уроков написаны в занимательной форме, включают различные виды игр, задания на развитие смекалки и логики, веселые задачи, загадки, конкурсы, интересный дополнительный материал.
Похожее:
(PDF) Построение диаграмм бегущих волн (1 + n) -мерного модифицированного уравнения Захарова-Кузнецова в физике плазмы
[70] Дж. Л. Г. Гирао, Х. М. Басконус, А. Кумар, О моделях новой волны недавно расширенного
Нелинейное (2 + 1) -мерное уравнение Буссинеска четвертого порядка, Математика, 8 (3), 341, (2020).
[71] В. Гао, М. Сенель, Г. Йель, Х. М. Басконус, Б. Сенель, Новые сложные волновые структуры для электрической модели линии передачи
, возникающие в сетевой системе, Aims Mathematics, 5 (3), 1881 −1892, (2020).
[72] К. Ван, З.
Ни, В. Се, Дж. Гао, К. Чжоу, В. Лю, Управление темным солитоном на основе дисперсии и нелинейности
для нелинейного уравнения Шрёдингера третьего порядка, Optik 184 , (2019), 370–376.
[73] YY Wang, CQ Dai, YQ Xu, J. Zheng, Y. Fan, Динамика нелокальных и локализованных пространственно-временных солитонов
для частично нелокального нелинейного уравнения Шрёдингера, Nonlinear Dyn, 92,1261-1269, (2018).
[74] J. t. Ли, Ю. Чжу, Дж. З. Хан, В. Цинь, К.q. Дай, С. з. Ван, Скалярные и векторные мультипольные и вихревые солитоны
в пространственно-модулированных кубико-квинтических нелинейных средах, Нелинейная динамика, 91,757–765, (2018).
[75] Х. Лю, В. Лю, Х. Трики, К. Чжоу, А. Бисвас, Периодические затухающие колебания между солитонными взаимодействиями для нелинейного уравнения Шрёдингера с переменным коэффициентом высокого порядка, Нелинейная динамика,
96 801 −809, (2019).
[76] Г. З. Ву, К. К. Дай, Неавтономные солитонные решения дробно-нелинейного дробного нелинейного уравнения с переменным коэффициентом
Уравнение Шрёдингера, Appl Math Lett 106, (2020), 106365.
[77] X. Ян, Д. Хо, X. Хун, Периодическая передача и управление оптическими солитонами в оптических волокнах, Optik
216, 164752, (2020).
[78] X. Fan, T. Qu, S. Huang, X. Chen, M. Cao, Q. Zhou, W. Liu, Аналитическое исследование влияния
эффектов высшего порядка на оптические солитоны в волокне. лазер, Optik 186, (2019), 326–331.
[79] CQ Dai, YY Wang, Y. Fan, DG Yu, Реконструкция устойчивости гауссовских пространственных солитонов
в пяти-семеричных нелинейных материалах при PT -симметричных потенциалах, Nonlinear Dyn, 92,1351 —
1358, (2018).
[80] SJ Chen, JN Lin, YY Wang, Солитонные решения и их устойчивость трех (2 + 1) -мерных
PT -симметричных нелинейных уравнений Шредингера с дифракцией и нелинейностями высшего порядка, Optik
194 , (2019), 162753.
[81] X. Дж. Янг, Д. Балеану, М. П. Лазаревич, М. С. Кайич, Дробные краевые задачи для интегральных
и дифференциальных уравнений с локальными дробными операторами, Тепловая наука, 19 (3), 959–966, (2015).
[82] X. Guan, W. Liu, Q. Zhou, A. Biswas, Преобразование Дарбу и аналитические решения для обобщенного уравнения
super-NLS-mKdV, Нелинейная динамика, 98,1491 −1500, (2019) .
24
Оптимальные решения дробного порядка Уравнения Захарова – Кузнецова
В этой статье асимптотический метод оптимальных гомотопий расширен для получения приближенных решений двумерных дифференциальных уравнений в частных производных дробного порядка. Уравнение Захарова – Кузнецова дробного порядка решается в качестве тестового примера, а дробные производные по времени описываются в смысле Капуто.Решения задачи вычисляются в виде быстро сходящихся рядов с легко вычисляемыми компонентами с помощью Mathematica. Достоверность предложенного метода дана при сравнении с другими методами в литературе. Полученные результаты показали, что метод является мощным и эффективным для нахождения решения многомерных уравнений с частными производными дробного порядка.
1. Введение
Дробное исчисление — это просто расширение исчисления целочисленного порядка.
В течение многих лет предполагалось, что дробное исчисление является чистым предметом математики и не имеет таких приложений в реальных явлениях, но сейчас эта концепция неверна из-за недавнего применения дробного исчисления при моделировании распространения звуковых волн в жестких условиях. пористые материалы [1], распространение ультразвуковых волн в губчатой кости человека [2], вязкоупругие свойства мягких биологических тканей [3], проблема отслеживания пути в автономных электромобилях [4] и т. д. В центре внимания находятся дифференциальные уравнения дробного порядка. внимание многих исследований в связи с их частым применением в областях электромагнитной, электрохимии, акустики, материаловедения, физики, вязкоупругости и техники [5–9].Подобные задачи более сложны по сравнению с дифференциальными уравнениями целого порядка. Из-за сложности дробного исчисления большинство дифференциальных уравнений дробного порядка не имеют точных решений, и в качестве альтернативы для решения этих типов уравнений широко используются приближенные методы [10–14].
Некоторые из недавних методов для приближенных решений дифференциальных уравнений дробного порядка — это метод разложения Адомиана (ADM), метод гомотопических возмущений (HPM), вариационный итерационный метод (VIM), метод гомотопического анализа (HAM) и т. Д.[15–26].
Маринка и Херисану ввели асимптотический метод оптимальных гомотопий (OHAM) для решения нелинейных дифференциальных уравнений, который сделал методы возмущений независимыми от предположения о малых параметрах и огромной вычислительной работе [27–31]. Метод был недавно расширен Sarwar et al. для решения дифференциальных уравнений дробного порядка [32–35].
В этой статье формулировка OHAM расширена до двумерных дифференциальных уравнений в частных производных дробного порядка.В частности, расширенная формулировка демонстрируется на иллюстративных примерах следующей дробной версии уравнений Захарова – Кузнецова, кратко называемой FZK ():
В приведенном выше уравнении — параметр, описывающий теорию дробной производной, — произвольные константы и целые числа.
которые определяют поведение слабонелинейных ионно-звуковых волн в плазме, содержащей холодные ионы и горячие изотермические электроны, в присутствии однородного магнитного поля. Уравнение FZK решалось многими исследователями с использованием различных методов.Некоторые из недавних хорошо известных методик: [36–40].
Настоящая статья состоит из шести разделов. В разделе 2 приведены некоторые основные определения и свойства дробного исчисления. Раздел 3 посвящен анализу OHAM для двумерных дифференциальных уравнений в частных производных дробного порядка. В разделе 4 приведены приближенные решения 1 -го порядка уравнений FZK (2, 2, 2) и FZK (3, 3, 3), в которых дробные производные по времени описаны в смысле Капуто.В разделе 5 сравниваются результаты приближенного решения 1 -го порядка с помощью предложенного метода с использованием вариационного итерационного метода (VIM) 3 -го порядка , алгоритма возмущений-итераций (PIA) и метода ряда остаточных степеней (RPS).
) решения [36, 37]. Во всех случаях предлагаемый метод дает лучшие результаты.
2. Основные определения
В этом разделе приводятся некоторые определения и результаты из литературы, которые имеют отношение к текущей работе.Риман – Лиувилль, Велиль, Рейзе, Компос и Капуто предложили множество определений.
Определение 1. Говорят, что действительная функция, находится в пространстве, если существует действительное число, такое, что =, где, и говорят, что она находится в пространстве, если только если.
Определение 2. Оператор дробного интеграла Римана – Лиувилля порядка функции определяется следующим образом: Когда мы формулируем модель реальных задач с дробным исчислением, оператор Римана – Лиувилля имеет определенные недостатки.Капуто предложил модифицированный дробно-дифференциальный оператор в своей работе по теории вязкоупругости.
Определение 3. Дробная производная от в смысле Капуто определяется как
Определение 4.
Если и, то свойства оператора можно найти в литературе. Отметим следующее:
For. существует почти для каждого. . . .
3. Анализ OHAM для PDE дробного порядка
В этом разделе вводится OHAM для уравнения в частных производных дробного порядка.Предлагаемый метод представлен в следующих этапах. Шаг 1: запишите общее уравнение с частными производными дробного порядка как С учетом начальных условий. В приведенных выше уравнениях — это оператор дробной производной Капуто или Римана – Лиувилля, является дифференциальным оператором, является неизвестной функцией и является известной аналитической функцией, является n-кортеж, который обозначает пространственные независимые переменные и представляет временную независимую переменную, соответственно. Шаг 2: построить оптимальную гомотопию для дифференциального уравнения с частными производными дробного порядка, которое в уравнении (7) является параметром вложения и вспомогательной функцией, которая удовлетворяет следующему соотношению: для и.
Решение быстро сходится к точному решению по мере увеличения значения в интервале. Эффективность OHAM зависит от построения и определения вспомогательной функции, которая контролирует сходимость решения. Вспомогательная функция может быть записана в виде В приведенном выше уравнении, являются параметрами управления сходимостью и являются функцией от. Шаг 3: расширяя ряд Тейлора примерно, у нас есть Замечания: из уравнения (9) ясно, что сходимость ряда зависит от вспомогательного параметра управления сходимостью. степени после подстановки уравнения (10) в уравнение (7), мы получаем нулевой порядок, 1 -й порядок , 2 -й порядок и задачи высокого порядка: Шаг 5: эти задачи содержат дробные производные по времени.Поэтому мы применяем оператор к вышеуказанным задачам и получаем серию решений следующим образом: Помещая вышеуказанные решения в уравнение (12), можно получить приближенное решение. Остаток получается путем подстановки приближенного решения в уравнение (5). Шаг 6: параметры контроля сходимости могут быть найдены либо методом Ритца, либо методом коллокации, либо методом Галеркина, либо методом наименьших квадратов.
В этой презентации для расчета параметров управления сходимостью используется метод наименьших квадратов, в котором мы сначала строим функционал: Затем параметры управления сходимостью вычисляются путем решения следующей системы: Приближенное решение получается путем подстановки оптимальных значений параметры управления сходимостью в уравнении (10).Метод наименьших квадратов является мощным методом и использовался во многих других методах, таких как метод оптимальных гомотопических возмущений (OHPM) и метод оптимальных вспомогательных функций (OAFM) для вычисления оптимальных значений произвольных констант [41, 42].
4. Сходимость OHAM
Если ряд (10) сходится к, где получается из задачи нулевого порядка и деформации K-порядка, то является точным решением (5).
Доказательство. , так как ряд сходится, его можно записать так, и оно верно, что на самом деле выполняется следующее уравнение: Теперь мы имеем то, что удовлетворяет. Теперь, если выбрано правильно, то уравнение приводит к тому, что является точным решением.
5. Применение OHAM
5.1. Дробное время FZK (2, 2, 2)
Рассмотрим следующее уравнение дробного времени FZK (2, 2, 2) с начальным условием
Точное решение уравнения (22) для, где — произвольная константа.
Используя формулировку OHAM, описанную в разделе 3, мы имеем задачу нулевого порядка: проблема первого порядка:
Решения вышеуказанных проблем следующие:
Приближенное решение 1 st порядка OHAM дается формулой следующее выражение:
5.2. Дробное время FZK (3, 3, 3)
Рассмотрим следующее уравнение дробного времени FZK (2, 2, 2) с начальным условием
Точное решение уравнения (22) для, где — произвольная константа.
Используя формулировку OHAM, описанную в разделе 3, мы имеем задачу нулевого порядка: проблема первого порядка:
Решения вышеуказанных проблем следующие:
Приближенное решение 1 st порядка OHAM дается формулой следующее выражение:
6.Результаты и обсуждение
Состав ОНАМ испытан по формуле FZK.
Mathematica 7 используется для большинства вычислительных работ.
В таблице 1 показаны оптимальные значения параметров управления сходимостью для уравнений FZK (2, 2, 2) и FZK (3, 3, 3) при различных значениях В таблицах 2 и 3 результаты, полученные по 1 st аппроксимация предлагаемого метода для уравнения FZK (2, 2, 2) сравнивается с аппроксимацией 3 rd порядка итерационного алгоритма возмущений (PIA) и метода ряда остаточных мощностей (RPS) при различных значениях.В таблицах 4 и 5 результаты, полученные с помощью аппроксимации 1 -го порядка предложенного метода, сравниваются с аппроксимацией 3 -го порядка VIM для уравнения FZK (3, 3, 3). На рисунках 1–4 представлены трехмерные графики зависимости точного и приближенного решения предложенным методом для уравнения ФЗК (2, 2, 2). На рисунках 1 и 2 представлены трехмерные графики зависимости точного и приближенного решения предложенным методом для уравнения ФЗК (3, 3, 3). На рис. 5 представлены двухмерные графики приближенного решения предложенным методом для уравнения ФЗК (2, 2, 2) при различных значениях.
На рис. 6 представлены двухмерные графики приближенного решения предложенным методом для уравнения ФЗК (3, 3, 3) при различных значениях.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4
4
. к точным решениям. 7. ЗаключениеРешение OHAM 1 -го порядка дает более обнадеживающие результаты по сравнению с 3-мя приближениями порядка -го порядка для PIA, RPS и VIM. Из полученных результатов сделан вывод, что предложенный метод очень эффективен и удобен для решения многомерных уравнений в частных производных дробного порядка. Точность метода можно еще больше повысить за счет приближения более высокого порядка. Доступность данныхВ ходе исследования данные не генерировались и не анализировались. Конфликт интересовАвторы заявляют об отсутствии конфликта интересов в отношении публикации этой статьи. Вклад авторовВсе авторы внесли равный и значительный вклад в написание этой статьи. Все авторы прочитали и одобрили окончательную рукопись. БлагодарностиАвторы выражают благодарность отделу математики AWKUM за помощь и поддержку в завершении этой работы. % PDF-1.4 % 1 0 объект > эндобдж 7 0 объект /Заголовок /Тема / Автор /Режиссер / Ключевые слова / CreationDate (D: 20211103215611-00’00 ‘) / ModDate (D: 20200816215650 + 02’00 ‘) / В ловушке / Ложь /PTEX.Fullbanner (Это pdfTeX, версия 3.14159265-2.6-1.40.20 \ (TeX Live 2019 / Debian \) kpathsea версия 6.3.1) >> эндобдж 2 0 obj > эндобдж 3 0 obj > эндобдж 4 0 obj > эндобдж 5 0 obj > эндобдж 6 0 obj > эндобдж 8 0 объект > эндобдж 9 0 объект > эндобдж 10 0 obj > эндобдж 11 0 объект > эндобдж 12 0 объект > эндобдж 13 0 объект > эндобдж 14 0 объект > эндобдж 15 0 объект > эндобдж 16 0 объект > эндобдж 17 0 объект > эндобдж 18 0 объект > эндобдж 19 0 объект > эндобдж 20 0 объект > эндобдж 21 0 объект > эндобдж 22 0 объект > эндобдж 23 0 объект > эндобдж 24 0 объект > эндобдж 25 0 объект > эндобдж 26 0 объект > эндобдж 27 0 объект > эндобдж 28 0 объект > эндобдж 29 0 объект > эндобдж 30 0 объект > эндобдж 31 0 объект > эндобдж 32 0 объект > эндобдж 33 0 объект > эндобдж 34 0 объект > эндобдж 35 0 объект > эндобдж 36 0 объект > эндобдж 37 0 объект > эндобдж 38 0 объект > эндобдж 39 0 объект > эндобдж 40 0 объект > эндобдж 41 0 объект > эндобдж 42 0 объект > эндобдж 43 0 объект > эндобдж 44 0 объект > эндобдж 45 0 объект > эндобдж 46 0 объект > эндобдж 47 0 объект > эндобдж 48 0 объект > эндобдж 49 0 объект > эндобдж 50 0 объект > эндобдж 51 0 объект > эндобдж 52 0 объект > эндобдж 53 0 объект > эндобдж 54 0 объект > эндобдж 55 0 объект > эндобдж 56 0 объект > эндобдж 57 0 объект > эндобдж 58 0 объект > эндобдж 59 0 объект > эндобдж 60 0 объект > эндобдж 61 0 объект > эндобдж 62 0 объект > эндобдж 63 0 объект > эндобдж 64 0 объект > эндобдж 65 0 объект > эндобдж 66 0 объект > эндобдж 67 0 объект > эндобдж 68 0 объект > эндобдж 69 0 объект > эндобдж 70 0 объект > эндобдж 71 0 объект > эндобдж 72 0 объект > эндобдж 73 0 объект > эндобдж 74 0 объект > эндобдж 75 0 объект > эндобдж 76 0 объект > эндобдж 77 0 объект > эндобдж 78 0 объект > эндобдж 79 0 объект > эндобдж 80 0 объект > эндобдж 81 0 объект > эндобдж 82 0 объект > эндобдж 83 0 объект > эндобдж 84 0 объект > эндобдж 85 0 объект > эндобдж 86 0 объект > эндобдж 87 0 объект > эндобдж 88 0 объект > эндобдж 89 0 объект > эндобдж 90 0 объект > эндобдж 91 0 объект > эндобдж 92 0 объект > эндобдж 93 0 объект > эндобдж 94 0 объект > эндобдж 95 0 объект > эндобдж 96 0 объект > эндобдж 97 0 объект > эндобдж 98 0 объект > эндобдж 99 0 объект > эндобдж 100 0 объект > эндобдж 101 0 объект > эндобдж 102 0 объект > эндобдж 103 0 объект > эндобдж 104 0 объект > эндобдж 105 0 объект > эндобдж 106 0 объект > эндобдж 107 0 объект > эндобдж 108 0 объект > эндобдж 109 0 объект > эндобдж 110 0 объект > эндобдж 111 0 объект > эндобдж 112 0 объект > эндобдж 113 0 объект > эндобдж 114 0 объект > эндобдж 115 0 объект > эндобдж 116 0 объект > эндобдж 117 0 объект > эндобдж 118 0 объект > эндобдж 119 0 объект > эндобдж 120 0 объект > эндобдж 121 0 объект > эндобдж 122 0 объект > эндобдж 123 0 объект > эндобдж 124 0 объект > эндобдж 125 0 объект > эндобдж 126 0 объект > эндобдж 127 0 объект > эндобдж 128 0 объект > эндобдж 129 0 объект > эндобдж 130 0 объект > эндобдж 131 0 объект > эндобдж 132 0 объект > эндобдж 133 0 объект > эндобдж 134 0 объект > эндобдж 135 0 объект > эндобдж 136 0 объект > эндобдж 137 0 объект > эндобдж 138 0 объект > эндобдж 139 0 объект > эндобдж 140 0 объект > эндобдж 141 0 объект > эндобдж 142 0 объект > эндобдж 143 0 объект > эндобдж 144 0 объект > эндобдж 145 0 объект > эндобдж 146 0 объект > эндобдж 147 0 объект > эндобдж 148 0 объект > эндобдж 149 0 объект > эндобдж 150 0 объект > / ProcSet [/ PDF / Text / ImageC / ImageB / ImageI] >> эндобдж 151 0 объект > транслировать x ڝ XɎ6 + (! H & Hn-ȡ5% `Np% K0 $ SH> R ^ / nKN Ք | É_i-. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
29675 × 10 −5