Контрольные работы по геометрии 7 класс | Методическая разработка по геометрии (7 класс) по теме:
Контрольные работы
по геометрии
7 класс
Контрольная работа №1
по теме «Основные свойства простейших геометрических фигур.
Смежные и вертикальные углы.»
Вариант 1.
1. На луче с началом в точке А отмечены точки В и С.
Найдите отрезок ВС, если АВ=9,2 см, АС=2,4 см. Какая из точек лежит между двумя другими?
2.Один из углов ,образовавшихся при пересечении двух прямых, в четыре раза меньше другого. Найдите эти углы.
3. Луч с – биссектриса угла (ab). Луч d — биссектриса
угла (ac).
Найдите
4.*Дано:
Найти:
Вариант 2.
1. На луче с началом в точке А отмечены точки В и С.
Найдите отрезок ВС, если АВ=3,8 см,АС=5,6 см.Какая из точек лежит между двумя другими?
2. Один из углов, образовавшихся при пересечении двух прямых, на 70° больше другого.
Найдите эти углы
3. Луч с – биссектриса
Луч с – биссектриса
Найдите
4.*Дано:
Найти:
Контрольная работа №2
по теме «Треугольники»
Вариант 1
1. Отрезки АВ и СD имеют общую середину О. Докажите, что
2. Луч АD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что
3. Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану BB1 к боковой стороне АС.
Контрольная работа №2
Вариант 2.
1. Отрезки МЕ и РК точкой D делятся пополам. Докажите, что
2.На сторонах угла D отмечены точки М и К так, что DМ=DК. Точка Р лежит внутри угла D и РК=РМ. Докажите, что луч DР – биссектриса угла МDК.
3. Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А.
Контрольная работа №3
Вариант 1.
1. Отрезки ЕF и РQ пересекаются в их середине М. Докажите ,что РЕ||QF .
2. Отрезок DМ- биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если
Контрольная работа №3
Вариант 2.
1. Отрезки MN и EF пересекаются в их середине P. Докажите ,что EN||MF .
2. Отрезок AD- биссектриса треугольника ABC. Через точку D проведена прямая, параллельная стороне AB и пересекающая сторону AC в точке F. Найдите углы треугольника ADF, если
Контрольная работа №4.
Вариант 1.
1.
Найдите сторону АВ треугольника АВС.
2. В треугольнике CDE точка М лежит
на стороне СЕ, причём DM.
3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
Контрольная работа №4.
Вариант 2.
1.
Найдите сторону АС треугольника АВС.
2. В треугольнике MNP точка K лежит
на стороне MN, причём
3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
Контрольная работа №5
Вариант 1
1. В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причём ОК=9 см. Найдите расстояние от точки О до прямой МN .
2. Постройте прямоугольный треугольник по гипотенузе и острому углу.
Дополнительное задание.
С помощью циркуля и линейки постройте угол 150˚.
Контрольная работа №5
Вариант 2.
1. В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса ЕF , причём FC=13 см. Найдите расстояние от точки F до прямой DE .
2. Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.
Дополнительное задание.
С помощью циркуля и линейки постройте угол 105˚.
Контрольная работа № 1 Тема: Параллельность прямых и плоскостей | |
1 вариант 1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно. а) Каково взаимное положение прямых ЕF и АВ? б) Чему равен угол между прямыми ЕF и АВ, если АВС = 150°? Поясните. 2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками. а) Выполните рисунок к задаче. б) Докажите, что полученный четырехугольник есть ромб. | 2 вариант 1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC. а) Каково взаимное положение прямых РK и АВ? б) Чему равен угол между прямыми РK и АВ, если АВС = 40° и ВСА = 80°? Поясните. 2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2. а) Выполните рисунок к задаче. б) Докажите, что четырехугольник MNEK есть трапеция. |
Контрольная работа № 2 Тема: Параллельность плоскостей. | |
1 вариант 1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4. 3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1. | 2 вариант 1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5. 3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3. |
Контрольная работа № 3 Тема: Перпендикулярность прямых и плоскостей | |
1 вариант 1. а) ребро куба; б) косинус угла между диагональю куба и плоскостью одной из его граней. 2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла DABM, в) найдите синус угла между плоскостью ромба и плоскостью α | 2 вариант 1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите: а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью его основания. 2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла BADM, в) Найдите синус угла между плоскостью квадрата и плоскостью α. |
Контрольная работа № 4 Тема: Многогранники | |
1 вариант 1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. а) высоту ромба; б) высоту параллелепипеда; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда | 2 вариант 1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны a и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите: а) меньшую высоту параллелограмма; б) угол между плоскостью АВС1 и плоскостью основания; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда. |
ECE598MAB: Геометрическая теория управления | М.-А. Белаббас
Преподавательский состав
- М.-А. Белаббас, офис: CSL 166, электронная почта:
[email protected]
Ассистент: Линда Стимсон, CSL 153. - Часы работы по предварительной записи.
Время собраний
Класс собирается во вторник и четверг с 14:00 до 15:20 в ECEB 3017.
Домашние задания
На протяжении всего курса будет задано примерно 4-5 домашних заданий. Домашнее задание предназначено для того, чтобы помочь вам проверить и углубить свое понимание материала, пройденного в классе, или материала, который не пройден.
HW1
HW2
HW3
HW4
Код для HW2
Экзамены
- Нет финального экзамена, но финальный проект с письменным отчетом (4-8 Pages) и или Prentation Prentation 30 Mins Prentation и или Mins Prentation). Или или или Prentation Prentath )
Учебник
Обязательных учебников нет. Конспекты лекций будут выкладываться по мере прохождения.
Конспекты лекций будут выкладываться по мере прохождения.
Предварительные условия
Официальными предварительными условиями для этого курса являются ECE 515 (Теория и проектирование систем управления) и ECE 528 (Нелинейные системы). На практике должно быть достаточно хорошего понимания линейной алгебры, многомерного исчисления и готовности проделать дополнительную работу, чтобы заполнить возможные пробелы в вашем опыте. Если вы попадаете в эту последнюю категорию, пожалуйста, сначала обсудите со мной.
Заметки
Здесь будут размещены записи лекций. Они находятся в стадии разработки, поэтому, пожалуйста, проверяйте наличие обновленных версий.
Главы 0–2 (18 января 2018 г.)
Главы 0–4 (5 февраля 2018 г.)
Ch 5 Observability
Ссылка для стабилизации обратной связи [Ссылка исправлена — напишите мне, если она не работает]
Линеаризация обратной связи и градиент потоки на многообразиях ссылка
Введение в дифференциальную геометрию для управления pdf
Ссылки
Статья Брокетта «Ранние дни геометрического управления» хорошо читает об историческом развитии области. (для опубликованной версии перейдите по этой ссылке; вы можете получить к ней доступ, если находитесь в кампусе или используете кампусную VPN)
(для опубликованной версии перейдите по этой ссылке; вы можете получить к ней доступ, если находитесь в кампусе или используете кампусную VPN)
Следующие книги полезны для понимания отдельных частей пройденного материала.
- W. Boothby, Введение в дифференциальную геометрию и группы Ли , Academic Press, NY, 1976.
- Фрэнк Уорнер,
- Альберто Исидори Нелинейные системы управления: введение , второе изд. Спрингер, Нью-Йорк, 1989. .
- Р. Абрахам и Дж. Марсден, Основы механики (второе изд.) Addison-Wesley, Reading, Mass., 1979.
- В.И. Арнольд, Математические методы в классической механике , Springer-Verlag New York, 1989.
- Велимир Юрджевич, Геометрическая теория управления , издательство Кембриджского университета, Кембридж, Англия, 1997.
- Энтони Блох, Неголономная механика и управление , Springer-Verlag NY, 2003
- RW Brockett, Конечномерные линейные системы , J.
 Wiley, NY, 1970.
Wiley, NY, 1970. Франческо Булло и Эндрю Д. Льюис, Геометрический контроль механических систем , Springer-Verlag, 2004
запрос ссылки — Дифференциальная геометрия для нелинейной теории управления
спросилИзменено 4 года, 5 месяцев назад
Просмотрено 2к раз
$\begingroup$
Я студент инженерного факультета, и мне нужно получить хорошее представление о некоторых понятиях дифференциальной геометрии, таких как многообразия, диффеоморфизмы, распределения и т. д. Я не могу найти правильный начальный путь. Как начать изучение предмета с азов?
Мне нужен материал для изучения геометрической нелинейной теории управления. Любые дальнейшие предложения приветствуются.
Любые дальнейшие предложения приветствуются.
- дифференциальная геометрия
- запрос-справка
- теория управления
$\endgroup$
6
$\begingroup$
На случай, если кому-то еще в поиске попадется этот вопрос. Если вы хотите изучить его для целей нелинейного управления, Нелинейная динамическая система управления s Неймейера и ван дер Шафта дает хорошее введение, плюс вы ясно видите, где что используется, например, теорема Фробениуса. Теперь, если вы хотите узнать больше о дифференциальной геометрии, я бы посоветовал прочитать любую книгу Джона М. Ли, особенно 9.0071 Введение в гладкие коллекторы . Тогда, если вы хотите продолжить, у таких людей, как Джеррольд Марсден, Гектор Суссманн и Эндрю Льюис, есть фантастический материал, связанный с геометрическим контролем. Особенно книга «Многообразия, тензорный анализ и приложения » содержит, как мне кажется, всю математику, связанную с управлением и динамическими системами, с геометрической точки зрения.



 Тетраэдр и параллелепипед.
Тетраэдр и параллелепипед.
 Диагональ куба равна 6 см. Найдите:
Диагональ куба равна 6 см. Найдите:
 Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:
Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите: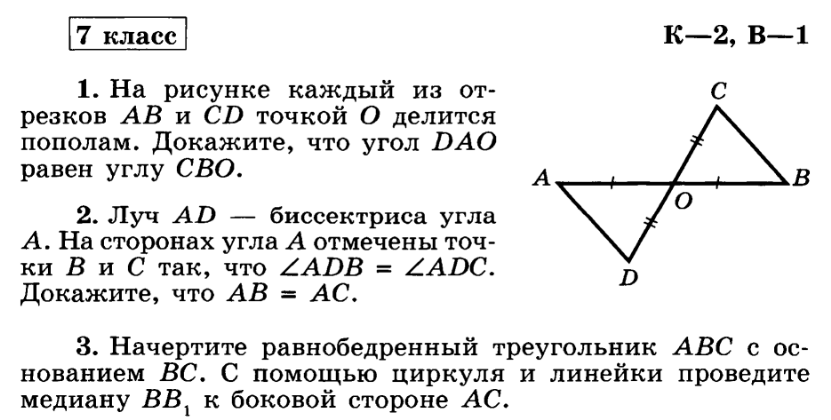
 Wiley, NY, 1970.
Wiley, NY, 1970.