Контрольная работа вариант 1 по алгебре: Алгебра 8 Макарычев КР-1 Вариант 1

Содержание

Контрольные работы по алгебре в двух вариантах в виде тестов (7 класс)

Автор: Майорова Евгения Ивановна

учитель математики

МБОУ г.Астрахани «СОШ №36»

Контрольные работы по алгебре 7 класс

по учебнику Ю.Н. Макарычев, Н. Г. Миндюк.

За основу взяты контрольные работы под редакцией

В.И. Жохова.

Контрольные работы в двух вариантах, содержат 5 заданий, выделены задания на выполнение обязательного стандарта математического образования, одно из заданий контрольных работ представлено в виде теста.

КОНТРОЛЬНАЯ РАБОТА №1

ВАРИАНТ 1

1. Найдите значение числового выражения:

(2/7 + 3/14)(7,5 – 13,5)

1) -4 2) -3 3) 4 4) 3

2. Упростите выражение:

а) 5а – 3b – 8а + 12 b

б) 16с + (3с – 2) – (5с + 7)

в) 7 – 3(6y – 4)

3. Сравните значения выражений 0,5х – 4 и 0,6х – 3 при х = 5

4. Упростите выражение 6,3х – 4 – 3(7,2х + 0,3) и найдите его значение при х = ⅔

5. В прямоугольном листе жести со сторонами х см и y см вырезали квадратное отверстие со стороной 5 см. Найдите площадь оставшейся части. Решите задачу при х = 13, y = 22.

КОНТРОЛЬНАЯ РАБОТА №1

ВАРИАНТ 2

2. Найдите значение числового выражения:

(2/7 + 3/14)( — 7,5 + 13,5)

1) -4 2) -3 3) 4 4) 3

2. Упростите выражение:

а) 3а + 7b – 6а — 4 b

б) 8с + (5 – с) – (7 + 11с)

в) 4 – 5(3y + 8)

3. Сравните значения выражений 3 – 0,2а и 5 – 0,3а при а = 16

4. Упростите выражение 3,2 а – 7 – 7(2,1а — 0,3) и найдите его значение при а = 3/5

5. В кинотеатре n рядов по m мест в каждом. На дневной сеанс были проданы билеты на первые 7 рядов. Сколько незаполненных мест было во время сеанса? Решите задачу при n = 21, m = 35.

КОНТРОЛЬНАЯ РАБОТА №2

ВАРИАНТ 1

1. Решите уравнение:

2х + 1 = 3х — 4

1) -5 2) 1 3) 5 4) свой ответ

2. Решите уравнение:

а) ⅔ х = -6 б) 1,6(5х – 1) = 1,8х – 4,7

3. Турист проехал в 7 раз большее расстояние, чем прошел пешком. Весь путь туриста составил 24 км. Какое расстояние турист проехал?

4. При каком значении переменной значение выражения 3 – 2с на 4 меньше значения выражения 5с + 1 ?

5. Длина прямоугольника на 6 см больше ширины. Найдите площадь прямоугольника, если его периметр равен 48 см.

КОНТРОЛЬНАЯ РАБОТА №2

ВАРИАНТ 2

1. Решите уравнение:

— 2х + 1 = — х — 6

1) — 7 2) 5 3) 7 4) свой ответ

2. Решите уравнение:

а) — ⅜ х = 24 б) 2(0,6х + 1,85) = 1,3х + 0,7

3. На одной полке на 15 книг большее, чем другой. Всего на двух полках 53 книги. Сколько книг на каждой полке?

4. При каком значении переменной значение выражения 4а + 8 на 3 больше значения выражения 3 – 2а ?

5. Ширина прямоугольника в 2 раза меньше длины. Найдите площадь прямоугольника, если его периметр равен 120 см.

КОНТРОЛЬНАЯ РАБОТА №3

ВАРИАНТ 1

1. Функция задана формулой у = ½х – 7. Найдите:

а) значение функции, соответствующее значению аргумента, равному 4;

б) значение аргумента, при котором значение функции равно -8.

2. а) Постройте график функции у= 3х – 4.

б) С помощью графика функции найдите значение функции, соответствующее значению аргумента 2,5.

3. В одной системе координат постройте графики функций у = — 0,5х и у = 2.

4. Проходит ли график функции у = — 5х + 11 через точку М(6; -41)?

5. Каково взаимное расположение графиков функции у = 15х — 51 и у = — 15х + 39 ?

1) параллельные 2) пересекаются 3) перпендикулярные

КОНТРОЛЬНАЯ РАБОТА №3

ВАРИАНТ 2

1. Функция задана формулой у = 5 — ⅓х. Найдите:

а) значение функции, соответствующее значению аргумента, равному -6;

б) значение аргумента, при котором значение функции равно -1.

2. а) Постройте график функции у= -2х + 5.

б) С помощью графика функции найдите значение функции, соответствующее значению аргумента -0,5.

3. В одной системе координат постройте графики функций у = 0,5х и у = -5.

4. Проходит ли график функции у = — 7х — 3 через точку М(4; -25)?

5. Каково взаимное расположение графиков функции у = -21х — 15 и у = 21х + 69 ?

1) пересекаются 2) параллельные 3) перпендикулярные

КОНТРОЛЬНАЯ РАБОТА №4

ВАРИАНТ 1

1. Выполните действия:

а) х⁵ х¹¹б) х¹⁵: х³

1) х^-6 2) х¹⁶ 3) х⁵⁵ 1) х¹⁸ 2) х⁵ 3) х¹²

2. Выполните действия:

а) (х⁴)⁷ б) (3х⁶)³

3. Упростите выражение:

а) 4а²с (- 2,5ас⁴) б) ( -2 х¹⁰ у⁶)⁴

4. Постройте график функции у = х²

С помощью графика определите:

а) значение функции при х = -1,5;

б) значение переменной х при у(х) = 3.

5. Найдите значение выражения:

а) 3¹¹ 9³ б) 3х³ – 1 при х = -⅓

27⁵

6. Упростите выражение (- 1 ½ х⁵у¹³)³ 0,08 х⁷у

КОНТРОЛЬНАЯ РАБОТА №4

ВАРИАНТ 2

1. Выполните действия:

а) х⁹ х¹³б) х¹⁸: х⁶

1) х^-4 2) х¹¹⁷ 3) х²² 1) х³ 2) х¹² 3) х²⁴

2. Выполните действия:

а) (х⁷)⁴ б) (2х³)⁵

3. Упростите выражение:

а) -7а⁵с³ 1,5ас б) ( -3 х⁴ у¹³)³

4. Постройте график функции у = х²

С помощью графика определите:

а) значение функции при х = 2,5;

б) значение переменной х при у(х) = 5.

5. Найдите значение выражения:

а) 8³ 2⁴ б) 2 — 7х² при х = -½

4⁵

6. Упростите выражение (- 2½ х¹⁵у⁴)² 0,04 ху⁷

КОНТРОЛЬНАЯ РАБОТА №5

ВАРИАНТ 1

1. Упростите выражение -12х + 3ху – 2( х +3ху)

а) 10х – 3ху б) -14х + 9ху в) -10х + 9ху г) -14х – 3ху

2. Решите уравнение:

30 + 5(3х – 1) = 35х – 25

3. Вынесите общий множитель за скобки:

а) 7ха – 7хb б) 16ху² + 12х²у

4. По плану тракторная бригада должна была вспахать поле за 14 дней. Бригада вспахивала ежедневно на 5 га больше, чем намечалось по плану. И потому закончила пахоту за 12 дней. Сколько гектаров было вспахано?

5. Решите уравнение:

а) 4х + 5 3х – 2 2х – 5

6 4 3

б) х

2 + ⅛ х = 0

КОНТРОЛЬНАЯ РАБОТА №5

ВАРИАНТ 2

1. Упростите выражение -12х + 3ху – 2( х +3ху)

а) 10х – 3ху б) -14х + 9ху в) -10х + 9ху г) -14х – 3ху

2. Решите уравнение:

10х — 5 = 6(8х + 3) – 5х

3. Вынесите общий множитель за скобки:

а) 8ха + 4хb б) 18ху³ + 12х²у

4. Заказ по выпуску машин должен быть выполнен по плану за 20 дней. Но завод выпускал ежедневно по 2 машины сверх плана и поэтому выполнил заказ за 18 дней. Сколько машин должен был выпускать завод ежедневно по плану ?

5. Решите уравнение:

а) 7х — 4 8 – 2х 3х + 3

9 6 4

б) 2х² — х = 0

КОНТРОЛЬНАЯ РАБОТА №6

ВАРИАНТ 1

1. Представьте в виде многочлена:

а) ( у – 4)(у – 5) б) (х – 3)(х² + 2х – 6)

в) (3а + 2b)(5а – b)

2. Разложите на множители:

а) b(b + 1) – 3(b + 1) б) са – сb + 2а — 2b

3. Упростите выражение:

(а²– b²)(2а + b) — аb( а + b)

а ) 2а³ +в³ – 3ав² б) 2а³ — в³ – 3ав²в)^{2а³ — в³ + 3ав²}

4. Докажите тождество: ( х — 3)( х + 4) = х( х + 1) – 12.

5. Ширина прямоугольника вдвое меньше его длины. Если ширину увеличить на 3 см, а длину – на 2 см, то площадь прямоугольника увеличится на 78 см². Найдите длину и ширину прямоугольника.

КОНТРОЛЬНАЯ РАБОТА №6

ВАРИАНТ 2

1. Представьте в виде многочлена:

а) ( у + 7)(у – 2) б) (х + 5)(х² — 3х + 8)

в) (4а — b)(6а + 3b)

2. Разложите на множители:

а) у(а — b) – 2(b + а) б) 3х – 3у + ах — ау

3. Упростите выражение:

(а²– b²)(2а + b) — аb( а + b)

а ) 2а³ +в³ – 3ав² б) 2а³ — в³ – 3ав²в)^{2а³ — в³ + 3ав²}

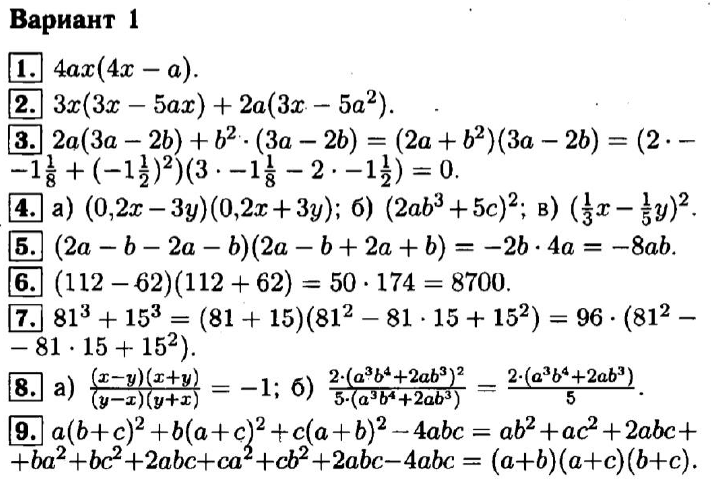4. Докажите тождество: а( а – 2) – 8 = ( а + 2)(а – 4).

5. Длина прямоугольника на 12 см больше его ширины. Если длину увеличить на 3 см, а ширину – на 2 см, то площадь прямоугольника увеличится на 80 см². Найдите длину и ширину прямоугольника.

КОНТРОЛЬНАЯ РАБОТА №7

ВАРИАНТ 1

1. Преобразуйте в многочлен:

1) (а – 3)² 2) (2у + 5)²

3) (4а – b)( 4а + b) 4) (х² + 1)( х² – 1)

2. Разложите на множители:

1) с² – 0,25 2) х² – 8х + 16

3. Найдите значение выражения: (х + 4)² – (х — 2)(х + 2) при х = 0,125

а) — 21 б) 12 с) 21 д) — 12

4. Выполните действия:

а) 2(3х – 2у)(3х + 2у) б) (а – 5)² – (а + 5)²

в) ( а³ + b²)²

5. Решите уравнение:

9у² – 25 = 0

КОНТРОЛЬНАЯ РАБОТА №7

ВАРИАНТ 2

1. Преобразуйте в многочлен:

1) (а + 4)² 2) (3у — с)²

3) (2а – 5)( 2а + 5) 4) (х² + у)( х² – у)

2. Разложите на множители:

1) 0,36 — с² 2) а² + 10а + 25

3. Найдите значение выражения: (а — 2 b)² + 4 b( а – b) при х = 0,12

а) 144 б) – 0,144 с) 0,0144 д) 0,24

4. Выполните действия:

а) 3(1 + 2ху)( 1 — 2ху) б) (а + b)² – (а — b)²

в) ( х² — у³)²

5. Решите уравнение:

16у² – 49 = 0

КОНТРОЛЬНАЯ РАБОТА №8

ВАРИАНТ 1

1. Преобразуйте в многочлен:

а) (а – 2)( а + 2) – 2а(5 – а)

б) (у – 9)² – 3у(у + 1)

в) 3(х – 4) ² – 3х²

2. Разложите на множители:

а) 25х – х³ б) 2х² – 20х + 50

3. Найдите значение выражения а² – 4bс, если а = 6, b = -11, с = -10

а) 452 б) -202 в) -404 г) 476

4. Упростите выражение:

(с² – b)² – (с² — 1)(с² + 1) + 2bс²

5. Докажите тождество:

(а + b)² – (а – b)² = 4аb

КОНТРОЛЬНАЯ РАБОТА №8

ВАРИАНТ 2

1. Преобразуйте в многочлен:

а) 4х(2х – 1) – (х – 3)(х + 3)

б) (х + 3)(х – 11) + (х + 6)²

в) 7(а + b) ² – 14аb

2. Разложите на множители:

а) у³ — 49у б) -3а² – 6аb — 3b²

3. Найдите значение выражения а² – 4bс, если а = 6, b = -11, с = -10

а) 452 б) -202 в) -404 г) 476

4. Упростите выражение:

(а — 1)²(а + 1) + (а + 1)( а — 1)

5. Докажите тождество:

(х — у)² + (х + у)² = 2(х² + у²)

КОНТРОЛЬНАЯ РАБОТА ЗА КУРС 7 КЛАССА

ВАРИАНТ 1

1. Найдите значение выражения:

¼ х³ + 3у² при х = -2 и у = -1

1) 5 2) -1 3) 1 4) -5

2. Решите систему уравнений:

х + 2у = 11,

5х – 3у = 3

1) (4 ; 3) 2) (3 ; 4) 3) (- 4 ; 3) 4) (-4 ; -3)

3. Решите уравнение:

-0,4(1,5х – 2) = 1 – 0,5(2х + 1)

1) — ¾ 2) ¾ 3) 1⅓ 4) — 1⅓

4. Пешеход рассчитал, что, двигаясь с определенной скоростью, намеченный путь он пройдет за 2,5 часа. Но он шел со скоростью, превышающей намеченную на 1 км/ч, поэтому прошел путь за 2 часа. Найдите длину пути.

5. а) Постройте график функции у = 3 – 2х

б) Принадлежит ли графику функции точка М (8; -19)?

КОНТРОЛЬНАЯ РАБОТА ЗА КУРС 7 КЛАССА

ВАРИАНТ 2

1. Найдите значение выражения:

¼ х³ + 3у² при х = -2 и у = -1

1) 5 2) -1 3) 1 4) -5

2. Решите систему уравнений:

х + 2у = 11,

5х – 3у = 3

1) (4 ; 3) 2) (3 ; 4) 3) (- 4 ; 3) 4) (-4 ; -3)

3. Решите уравнение:

-0,4(1,5х – 2) = 1 – 0,5(2х + 1)

1) — ¾ 2) ¾ 3) 1⅓ 4) — 1⅓

4. Велосипедист должен был проехать весь путь с определенной скоростью за 2 часа. Но он ехал со скоростью, превышающей намеченную на 3 км/ч, поэтому на весь путь затратил 1⅔ часа. Найдите длину пути.

5. а) Постройте график функции у = 2 – 3х

б) Принадлежит ли графику функции точка М (9; -25)?

Итоговая контрольная работа по алгебре за курс 7 класса

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Итоговая контрольная работа по алгебре за курс 7 класса (учебник А. Г. Мордковича) составлена в 2- вариантах + подготовительный вариант. Первая часть содержит 12 заданий базового уровня сложности, вторая часть состоит из 4-х заданий повышенного уровня сложности.

Вариант 1

Часть 1

А1

Найдите значение выражения: .

1) ; 2) ; 3) ; 4)

А2

Найдите число, 20% которого равны 100.

1) 500; 2) 800; 3) 20; 4) 80.

Представьте выражение в виде многочлена.

А3

1) ; 2) ;

3); 4).

А4

Из формулы силы выразите массу .

1) ; 2) ; 3) ; 4) .

А5

Упростите выражение .

1) ; 2) ; 3) ; 4) .

А6

Раскройте скобки и приведите подобные слагаемые в выражении:

1) ; 2) ; 3) ; 4) .

А7

Выполните действия: .

1) ; 2) ; 3) ; 4) .

А8

Упростите выражение и найдите его значение при , .

1) ; 2) ; 3) ; 4) .

А9

Вычислите: .

1) 3, 2) 40,5; 3) 27; 4) 9.

А10

Какая из точек принадлежит графику линейного уравнения ?

1) A; 2) D; 3)B; 4)C.

А11

Решите уравнение: .

Ответ _________

А12

Соотнесите функции, заданные формулами, с их графиками (см. рис.1).

1) 2) 3)

А	Б	В

Часть 2

Задания с развернутым ответом.

(решения запишите на специальном бланке)

В1

Реши систему уравнений:

В2

Выполните разложение на множители: .

В3

Решите уравнение: .

В4

Решите задачу с помощью системы уравнений:

В 15 одинаковых пакетов и 5 одинаковых коробок расфасовали 2400 г конфет. В каждую коробку уместилось на 20г конфет больше, чем в каждый пакет. Сколько граммов конфет было в каждом пакете и каждой коробке?

Вариант 2

Часть 1

А1

Найдите значение выражения: .

1) ; 2) ; 3) ; 4) .

А2

Найдите 25% от числа 120.

1) 480; 2) 30 ; 3) 90; 4) 160.

А3

Представьте выражение в виде многочлена

1) ; 2) ;

3); 4).

А4

Из формулы потенциальной энергии выразите .

1) ; 2) ; 3) ; 4) .

А5

Упростите выражение .

1) ; 2); 3); 4).

А6

Раскройте скобки и приведите подобные слагаемые в выражении:

1) ; 2) ; 3) ; 4) .

А7

Выполните действия: .

1) ; 2) ; 3) ; 4) .

А8

Упростите выражение и найдите его значение при .

1) ; 2) ; 3) 24; 4) .

А9

Вычислите: .

1) 5; 2) 3; 3) 25; 4) 2,5.

А10

Какая из точек принадлежит графику линейного уравнения ?

1) A; 2) С; 3)B; 4)D.

А11

Решите уравнение: .

Ответ ____________________________

А12

Соотнесите функции, заданные формулами, с их графиками (см. рис.1).

1) ; 2) ; 3) .

А	Б	В

Часть 2

Задания с развернутым ответом.

(решения запишите на специальном бланке)

В1

Реши систему уравнений :

В2

Выполните разложение на множители: .

В3

Решите уравнение: .

В4

Решите задачу с помощью системы уравнений.

Двое рабочих изготовили по одинаковому количеству деталей. Первый выполнил свою работу за 5ч, а второй за 4ч, так как изготовлял на 12 деталей в час больше второго. Сколько деталей изготовил каждый рабочий?

Подготовительный вариант

итоговой контрольной работы по алгебре

Часть 1

А1

Найдите значение выражения:

1) 14; 2) -2; 3) -3; 4) 3.

А2

Найдите 75% от числа 120.

1) 180; 2) 30; 3) 90; 4) 80.

А3

Представьте выражение в виде многочлена

А4

Выразите переменную у из уравнения 2x – y = 5.

1) y = –2x – 5;

2) y = 2x – 5;

3) y = 5 – 2x;

4) y = 2x + 5.

А5

Упростите выражение

А6

Раскройте скобки (2а – 7в)(7в + 2а).

А7

Выполните действия:

А8

Упростите выражение и найдите его значение при .

1) ; 2) ; 3) 24; 4) .

А9

Вычислите: .

1) 9; 2) 27; 3) 81; 4) 3.

А10

Какая из точек принадлежит графику линейной функции у = 1.5х – 2:

А(- 10; 2), В(0; -2), С(3; 4), Е(5; — 2).

1) A; 2) С; 3)B; 4)Е.

А11

Решите уравнение: 2,1 (2х -3) + 8,9х = — 9,4.

Ответ ________________________________

А12

Укажите рисунок, на котором изображен график линейного уравнения x + 4 = 0

Часть 2

Задания с развернутым ответом.

(решение запишите на специальном бланке)

В1

Реши систему уравнений :

В2

Выполните разложение на множители:

В3

Решите уравнение: .

В4

Решите задачу с помощью системы уравнений:

Дано два числа. Если первое число удвоить и к нему прибавить второе число, то получим 21. Если же к первому числу добавить удвоенное второе число, то получим 27. Найдите эти числа.

итоговая контрольная работа по алгебре, 7 класс
PDF / 410.67 Кб

F Математические фразы, символы и формулы. Вводная статистика

Математически написанные фразы на английском языке

Когда английский говорит:	Интерпретируйте это как:
X не меньше 4.	Х ≥ 4
Минимум X равен 4.	Х ≥ 4
X не менее 4.	Х ≥ 4
X больше или равно 4.	Х ≥ 4
X не больше 4.	Х ≤ 4
Максимальное число X равно 4.	Х ≤ 4
X не более 4.	Х ≤ 4
X меньше или равно 4,	Х ≤ 4
X не превышает 4.	Х ≤ 4
X больше 4.	Х > 4
X больше 4.	Х > 4
X превышает 4.	Х > 4
X меньше 4.	Х < 4
X меньше, чем 4.	Х < 4
Х равно 4.	Х = 4
Х равно 4.	Х = 4
X равно 4.	Х = 4
X не равно 4.	Х ≠ 4
X не равно 4.	Х ≠ 4
X не то же самое, что 4.	Х ≠ 4
X отличается от 4.	Х ≠ 4

Стол F1

Формулы

Формула 1: факториал

n!=n(n−1)(n−2)…(1)n!=n(n−1)(n−2)…(1)

0!=10!=1

Формула 2: Комбинации

(nr)=n!(n−r)!r!(nr)=n!(n−r)!r!

Формула 3: Биномиальное распределение

X~B(n,p)X~B(n,p)

P(X=x)=(nx)pxqn−xP(X=x)=(nx)pxqn −x, для x=0,1,2,…,nx=0,1,2,…,n

Формула 4: геометрическое распределение

X~G(p)X~G(p)

P(X=x)=qx−1pP(X=x)=qx−1p, для x=1,2,3,. ..x=1,2,3,…

Формула 5: Гипергеометрическое распределение

X~H(r,b,n)X~H(r,b,n)

P(X=x)=((rx)(bn−x)(r+bn))P( X=x)=((rx)(bn−x)(r+bn))

Формула 6: Распределение Пуассона

X~P(μ)X~P(μ)

P(X=x)=μxe−μx!P(X=x)=μxe−μx!

Формула 7: Равномерное распределение

X~U(a,b)X~U(a,b)

f(X)=1b−af(X)=1b−a, a

Формула 8: Экспоненциальное распределение

X~Exp(m)X~Exp(m)

f(x)=me−mxm>0,x≥0f(x)=me−mxm>0,x ≥0

Формула 9: Нормальное распределение X~N(μ,σ2)X~N(μ,σ2)

f(x)=1σ2πe−(x−μ)22σ2f(x)=1σ2πe−(x−μ) 22σ2 , –∞

Формула 10: Гамма-функция

Γ(z)=∫∞0xz-1e-xdxΓ(z)=∫∞0xz-1e-xdxz>0z>0

Г(12)=πГ(12)=π

Γ(m+1)=m! Γ(m+1)=m! для мм, неотрицательное целое число

иначе: Γ(a+1)=aΓ(a)Γ(a+1)=aΓ(a)

Формула 11:

t -распределение Стьюдента

X~tdfX~tdf

f(x)= (1+x2n)−(n+1)2Γ(n+12)nπΓ(n2)f(x)=(1+x2n)−(n+1)2Γ(n+12)nπΓ(n2)

Х=ZYnX=ZYn

Z~N(0,1),Y~Xdf2Z~N(0,1),Y~Xdf2, nn = степени свободы

Формула 12: распределение хи-квадрат

X~Χdf2X~Χdf2

f(x)=xn−22e−x22n2Γ(n2)f(x)=xn−22e−x22n2Γ(n2), x>0x>0 , nn = положительное целое число и степени свободы

Формула 13: распределение F

X~Fdf(n),df(d)X~Fdf(n),df(d)

df(n)=df(n)=степени свободы для числителя

df(d)=df(d)=степени свободы для знаменателя

f(x)=Γ(u+v2)Γ(u2)Γ(v2)(uv)u2x(u2−1)[1+(uv)x−0,5(u+v)]f(x)= Γ(u+v2)Γ(u2)Γ(v2)(uv)u2x(u2−1)[1+(uv)x−0,5(u+v)]

X=YuWvX=YuWv, YY, WW хи-квадрат

Символы и их значения

Ошибка

Глава (1-я использованная)	Символ	Разговорный	Значение
Выборка и данные		Квадратный корень из	то же
Выборка и данные	ππ	Пи	3. 14159… (конкретный номер)
Описательная статистика	Q ₁	Первый квартиль	первый квартиль
Описательная статистика	Q ₂	Вторая четверть	второй квартиль
Описательная статистика	Q ₃	Третий квартиль	третий квартиль
Описательная статистика	ИКР	межквартильный диапазон	Q ₃ – Q ₁ = IQR
Описательная статистика	х¯х¯	х-бар	выборочное среднее
Описательная статистика	мкм	мю	населения означает
Описательная статистика	s s _x sx	с	стандартное отклонение выборки
Описательная статистика	s2s2sx2sx2	с в квадрате	выборочная дисперсия
Описательная статистика	σσσxσx σx	сигма	стандартное отклонение населения
Описательная статистика	σ2σ2σx2σx2	сигма в квадрате	дисперсия населения
Описательная статистика	ΣΣ	заглавная сигма	сумма
Вероятностные темы	{}{}	кронштейны	установить обозначение
Вероятностные темы	нержавеющая сталь	С	место для образца
Вероятностные темы	АА	Событие А	событие А
Вероятностные темы	П(А)П(А)	вероятность А	вероятность появления А
Вероятностные темы	П(А\|Б)П(А\|Б)	вероятность А при заданном В	проб. A произошло при условии, что B произошло
Вероятностные темы	П(А ИЛИ В)П(А ИЛИ В)	проб. А или В	проб. из A или B или обоих встречающихся
Вероятностные темы	Р(А И Б)Р(А И Б)	проб. А и В	проб. событий А и В (одновременно)
Вероятностные темы	А ′	A-prime, дополнение к A	дополнение к A, а не к A
Вероятностные темы	П ( А ‘)	проб. комплекта A	то же
Вероятностные темы	Г ₁	зеленый при первом выборе	то же
Вероятностные темы	П ( Г ₁)	проб. зеленого на первом выборе	то же
Дискретные случайные величины	ПДФ	проб. функция распределения	то же
Дискретные случайные величины	Х	х	случайная величина X
Дискретные случайные величины	Х ~	дистрибутив X	то же
Дискретные случайные величины	Б	биномиальное распределение	то же
Дискретные случайные величины	Г	геометрическое распределение	то же
Дискретные случайные величины	Н	гипергеометрический р-н.	то же
Дискретные случайные величины	П	Пуассон р-н.	то же
Дискретные случайные величины	λλ	Лямбда	среднее значение распределения Пуассона
Дискретные случайные величины	≥≥	больше или равно	то же
Дискретные случайные величины	≤≤	меньше или равно	то же
Дискретные случайные величины	=	равно	то же
Дискретные случайные величины	≠	не равно	то же
Непрерывные случайные величины	ф ( х )	ф из х	функция x
Непрерывные случайные величины	пдф	проб. функция плотности	то же
Непрерывные случайные величины	У	равномерное распределение	то же
Непрерывные случайные величины	Опыт	экспоненциальное распределение	то же
Непрерывные случайные величины	к	к	критическое значение
Непрерывные случайные величины	f ( х ) =	f из x равно	то же
Непрерывные случайные величины	м	м	скорость затухания (для exp. dist.)
Нормальное распределение	Н	нормальное распределение	то же
Нормальное распределение	я	z — счет	то же
Нормальное распределение	З	стандартное нормальное расстояние.	то же
Центральная предельная теорема	ЦЛТ	Центральная предельная теорема	то же
Центральная предельная теорема	Х¯Х¯	X -бар	случайная величина X -бар
Центральная предельная теорема	мксмкс	среднее X	среднее X
Центральная предельная теорема	мкс¯мкс¯	среднее значение X -бар	среднее X — бар
Центральная предельная теорема	σxσx	стандартное отклонение X	то же
Центральная предельная теорема	σx¯σx¯	стандартное отклонение X -бар	то же
Центральная предельная теорема	ΣXΣX	сумма X	то же
Центральная предельная теорема	ΣxΣx	сумма х	то же
Доверительные интервалы	Класс	уровень достоверности	то же
Доверительные интервалы	КИ	доверительный интервал	тот же
Доверительные интервалы	ЭБМ	, связанная со средним значением	то же
Доверительные интервалы	ЕБП	ошибка связана с пропорцией	то же
Доверительные интервалы	т	Студенческая т -распределение	то же
Доверительные интервалы	дф	степеней свободы	то же
Доверительные интервалы	тα2тα2	студент t с a /2 области в правом хвосте	то же
Доверительные интервалы 9	q — первичный; q — шляпа	образец доля отказа
Проверка гипотез	H0H0	H — нет, H — sub 0	нулевая гипотеза
Проверка гипотез	Ха-Ха	H-, H -sub	альтернативная гипотеза
Проверка гипотез	х2х2	H -1, H -sub 1	альтернативная гипотеза
Проверка гипотез	αα	альфа	вероятность ошибки первого рода
Проверка гипотез	ββ	бета	вероятность ошибки второго рода
Проверка гипотез	Х1¯-Х2¯Х1¯-Х2¯	X 1 бар минус X 2 бара	разница в выборке означает
Проверка гипотез	мк1-мк2мк1-мк2	мю -1 минус мю -2	разница в населении означает
Проверка гипотез	П’1-П’2П’1-П’2	P 1-значный минус P 2-простой	разница в пропорциях образца
Проверка гипотез	р1-р2р1-р2	р 1 минус р 2	разница в пропорциях населения
Распределение хи-квадрат	Х2Х2	Кю -квадрат	Хи-квадрат
Распределение хи-квадрат	ОО	Наблюдается	Наблюдаемая частота
Распределение хи-квадрат	ЕЕ	Ожидается	Ожидаемая частота
Линейная регрессия и корреляция 9	у — шляпа	оценочное значение y
Линейная регрессия и корреляция	рр	коэффициент корреляции	то же
Линейная регрессия и корреляция	εε	ошибка	то же
Линейная регрессия и корреляция	СШЭ	Сумма квадратов ошибок	то же
Линейная регрессия и корреляция	1,9 с	1,9 раза с	пороговое значение для выбросов
F – Распределение и дисперсионный анализ	Ф	F -отношение	F -соотношение

Стол F2 Символы и их значения

Алгебраические рассуждения и варианты задач с битой и мячом: Решение изоморфной алгебры сначала облегчает решение задач позже

. 2017 дек; 24(6):1922-1928.

doi: 10.3758/s13423-017-1241-8.

Джером Д Гувер ¹ , Элис Ф. Хили ²

Принадлежности

¹ Факультет психологии и неврологии, Университет Колорадо в Боулдере, Боулдер, Колорадо, 80309-0345, США.
² Факультет психологии и неврологии, Университет Колорадо в Боулдере, Боулдер, Колорадо, 80309-0345, США. Элис.Хили@Colorado.EDU.

PMID: 28197896
DOI: 10.3758/с13423-017-1241-8

Джером Д. Гувер и др. Психон Бык Преподобный. 2017 дек.

. 2017 дек; 24(6):1922-1928.

doi: 10.3758/s13423-017-1241-8.

Авторы

Джером Д Гувер ¹ , Элис Ф. Хили ²

Принадлежности

¹ Факультет психологии и неврологии, Университет Колорадо в Боулдере, Боулдер, Колорадо, 80309-0345, США.
² Факультет психологии и неврологии, Колорадский университет в Боулдере, Боулдер, Колорадо, 80309-0345, США. Элис.Хили@Colorado.EDU.

PMID: 28197896
DOI: 10. 3758/с13423-017-1241-8

Абстрактный

Классическая задача о бите и мяче широко используется для измерения предвзятости и правильности рассуждений при принятии решений. Студенты вузов в подавляющем большинстве склонны давать предвзятый ответ на этот вопрос. В какой степени рассуждающие могут изменить свои суждения и, в частности, возможно ли облегчить решение проблемы, побуждая участников рассматривать проблему с алгебраической точки зрения? Сто девяносто семь участников были набраны для изучения влияния алгебраических подсказок как стратегии устранения предвзятости на варианты задачи о бите и мяче. Участники, которым было предложено рассмотреть проблему алгебраически, значительно чаще давали правильные ответы по сравнению с контрольными участниками. Большая часть этого подсказочного эффекта была ограничена условием, которое требовало от участников решения изоморфных алгебраических уравнений, соответствующих структуре типов вопросов с битой и мячом. На последующий критический вопрос с разными предметами и суммами в долларах, представленными без подсказки, участники смогли обобщить полученную информацию, чтобы значительно уменьшить общую предвзятость. Было также обнаружено, что математическая тревожность в значительной степени связана с точностью решения задач с битой и мячом. Эти результаты показывают, что при определенных условиях алгебраическое рассуждение является эффективной стратегией устранения предубеждений в вариантах задач с битой и мячом, и предоставляют первое документальное свидетельство влияния математической тревожности на результаты теста на когнитивное отражение.

Ключевые слова: Алгебраическое рассуждение; Когнитивный рефлексивный тест; Устранение предвзятости; Принятие решения; Суждение; математическая тревожность; Рассуждение.

Цитируется

Метаанализ связи между математической тревогой и математическими достижениями.
Баррозу С., Гэнли К.М., Макгроу А.Л., Гир Э.А., Харт С.А., Докур М.С. Баррозу С. и др. Психологический бык. 2021 фев; 147(2):134-168. дои: 10.1037/bul0000307. Epub 2020 29 октября. Психологический бык. 2021. PMID: 33119346 Бесплатная статья ЧВК.
Проблема с битой и мячом: более веские доказательства в поддержку процесса сознательной ошибки.
Гувер Д.Д., Хили А.Ф. Гувер Дж. Д. и др. Решение (Wash DC). 2019 окт;6(4):369-380. дои: 10.1037/dec0000107. Epub 2019 14 марта. Решение (Wash DC). 2019. PMID: 31632998 Бесплатная статья ЧВК.

использованная литература

1. Анну Рев Психол. 2008;59:255-78 — пабмед
1. Перспектива Psychol Sci.

Контрольные работы по алгебре в двух вариантах в виде тестов (7 класс)

Итоговая контрольная работа по алгебре за курс 7 класса

F Математические фразы, символы и формулы. Вводная статистика

Математически написанные фразы на английском языке

Формулы

Формула 1: факториал

Формула 2: Комбинации

Формула 3: Биномиальное распределение

Формула 4: геометрическое распределение

Формула 5: Гипергеометрическое распределение

Формула 6: Распределение Пуассона

Формула 7: Равномерное распределение

Формула 8: Экспоненциальное распределение

Формула 10: Гамма-функция

Формула 11:

Формула 12: распределение хи-квадрат

Формула 13: распределение F

Символы и их значения

Алгебраические рассуждения и варианты задач с битой и мячом: Решение изоморфной алгебры сначала облегчает решение задач позже

Принадлежности

Авторы

Принадлежности

Абстрактный

Похожие статьи

Цитируется

использованная литература

Добавить комментарий Отменить ответ