Урок 34. решение задач. часть 1 — Математика — 2 класс
Математика, 2 класс
Урок № 34. Решение задач.
Перечень вопросов, рассматриваемых в теме:
— Как составить план решения задачи?
Глоссарий по теме:
Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.
Выражение – формула, выражающая какие–либо математические отношения.
Схема — своеобразный чертёж, в котором составные части — его элементы и связи между ними изображены условно, без соблюдения масштаба.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –5-е изд. – М.: Просвещение, 2014. – с.10, 11.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций.
- Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.18.
Математика. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. С. И. Волкова – М.: Просвещение, 2017. – с.41.
Теоретический материал для самостоятельного изучения
Посмотрите на эти изображения. Знакомы ли нам они? Да, это схемы задач.
Мы умеем составлять схемы к задачам и по схемам находить задачу.
Определим, какая схема подходит к задаче.
В этой задаче мы находим целое.
Подходит такая схема.
Выберем схему ко второй задаче.
В этой задаче мы находим часть
от целого. Подходит данная схема.
И к последней схеме мы составим такую задачу:
Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?
Папа поймал на рыбалке 6 окуней и 8 лещей.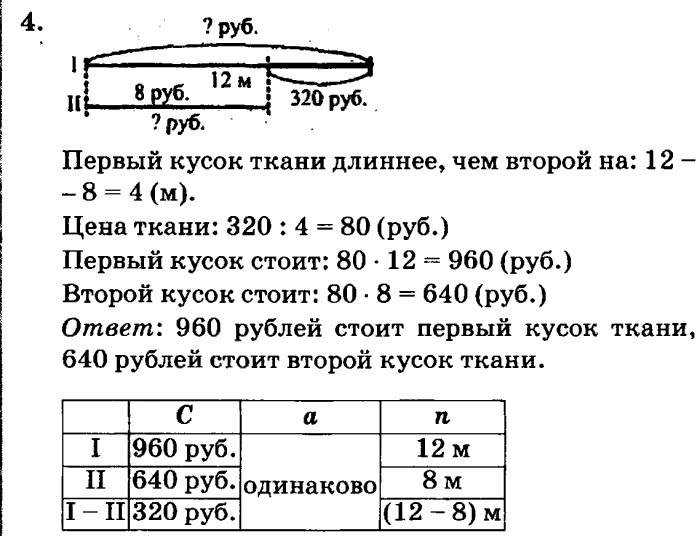
Сколько всего рыб поймал папа?
Рассмотрите такую схему.
Знакома ли она вам? С такими схемами мы ещё не встречались. Это схемы рассуждения при поиске решения задачи. Составим схему рассуждения при решении уже известной нам задачи. «Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?». Для решения задачи начнём рассуждать от вопроса, составляя при этом схему. Что нужно найти в задаче? «Сколько всего рыб поймал папа?»
Ставим в схеме знак вопроса.
Что для этого достаточно знать?
Верно, нужно знать, сколько и каких рыб поймал папа.
Это окуни и лещи. Ставим числа 8 и 6,
рисуем стрелки к вопросу.
Можем ли мы ответить на вопрос задачи?
Да.
8 + 6 = 14 (р.) поймал папа
Попробуем составить схему рассуждения к более сложной задаче.
«Папа поймал на рыбалке 8 окуней, а сын на 2 рыбы меньше. Сколько всего рыб поймали папа и сын?».
Что нужно узнать в задаче? «Сколько всего рыб поймали папа и сын?»
Ставим в схеме знак вопроса.
Что для этого достаточно знать?
Верно, нужно знать сколько рыб поймал папа
и сколько рыб поймал сын. Рисуем два круга и стрелки к вопросу.
Что из этого мы знаем, а что нужно найти?Правильно, мы знаем сколько рыб поймал папа. Ставим число восемь в схему.
Но мы не знаем, сколько рыб поймал сын.
Ставим знак вопроса.
Что нужно знать, чтобы сосчитать рыб, которых поймал сын?
Нужно знать количество рыб у папы и
на сколько меньше поймал рыб сын.
Рисуем два круга и стрелки к вопросу.Ставим в схему числа восемь и два.
Каким будет первое действие? Узнаем, сколько рыб поймал сын.
1) 8 – 2 = 6 (р.) поймал сын.
Ответили мы на вопрос задачи? Нет. Каким будет второе действие?
Узнаем, сколько всего рыб поймали папа и сын.
2) 8 + 6 = 14 (р.) поймали всего.
Вывод: Для выбора способа решения задачи, мы выстраиваем цепочку рассуждения. Её можно представить в виде схемы. Составляя схему рассуждения «от вопроса к данным», мы отвечаем на такие вопросы: «Что достаточно знать, чтобы ответить на вопрос задачи? Что мы знаем уже? Как найти то, что ещё неизвестно?».
Текст задачи можно моделировать разными способами: в виде схематического чертежа, таблицы, диаграммы.
Тренировочные задания.
1.Выберите схему рассуждения, подходящую к задаче «Юра съел 9 конфет, а Коля на 4 конфеты меньше. Сколько конфет съели мальчики?»
Правильные ответы:
2. Дополните диаграмму данными из текста.
Сел Миша на пенёк, съел пирожок… А ещё две баранки, пять пончиков и девять яблок.
Правильные ответы:
Страница 93 — ГДЗ Математика 2 класс. Моро, Бантова, Бельтюкова, Волкова, Степанова. Учебник часть 1
Вернуться к содержанию учебника
Что узнали. Чему научились
Вопрос
24. Выполни действия и проверь вычитание сложением, а сложение вычитанием.
| 80 — 7 | 63 + 30 | 78 — 40 | 26 + 4 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Как изменялось уменьшаемое? вычитаемое? разность?
Подсказка
Повтори действия с двузначными числами.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
26. У фермера было 3 лошади, коров на 8 больше, а овец столько, сколько лошадей и коров вместе. Сколько было овец?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
27.
В автобусе ехали 10 мужчин и 6 женщин. На остановке сели ещё 2 человека и никто не вышел. Сколько стало …?
Подсказка
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
28. На строительстве дома работали 20 каменщиков и 16 маляров. На другую работу перевели 8 человек. Сколько человек осталось на строительстве?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
29.
В пруду зоопарка плавали 6 лебедей, 12 гусей, а уток на 3 меньше, чем лебедей и гусей вместе. Сколько уток плавало в пруду?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
30. Дима нёс сумку с фруктами. Масса сумки 1 кг, а масса фруктов на 7 кг больше. На какой вопрос ответишь, выполнив действия:
1) 1 + 7; 2) 1 + (1 + 7)?
Подсказка
Повтори, что такое масса и в чём она измеряется.
От перемены мест слагаемых сумма не изменится.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
31. Составь по схематическому чертежу задачу и реши её.
Подсказка
Повтори, из каких частей состоит задача?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Найди периметр каждой фигуры:
Подсказка
Повтори, как найти периметр многоугольника.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
© budu5.com, 2021
Пользовательское соглашение
Copyright
Тесты онлайн по математике для 2 класса
Здесь выложены онлайн тесты по математике за 2 класс на тему «Математические задачи, Сложение и вычитание до 100, и Умножение и деление» и другие. Тесты составлены с учетом школьной программы по математике для 2 класса на основе того, что должен знать и уметь ребенок в этом возрасте. А именно:
Математические задачи для 2 класса.
Задачи на нахождение неизвестного слагаемого, неизвестного уменьшаемого и неизвестного вычитаемого. Решение задач в 2 действия на сложение и вычитание. Решение задач в одно действие на умножение и деление (с числами 2 и 3 из таблицы умножения). Порядок выполнения действий в выражениях, содержащих 2-3 действия (со скобками и без них). При этом, кроме простых выражений из программы 1 класса, в этих задачах используются новые (более сложные) выражения: прибавление одноцифрового числа к двухцифровому (45+7), отнимание одноцифрового числа от двухцифрового (45-7), прибавление и отнимание двухцифровых чисел (45+27, 45-27). Также в этих задачах используются меры длины (миллиметры, сантиметры, дециметры, метры), разменная монета (рубли, копейки), единицы измерения веса (киллограмм, центнер), единицы измерения ёмкости (литр).
Сложение и вычитание до 100 для 2 класса. Новая счетная единица – десяток.. Счет десятками. Образование и названия чисел, их десятичный состав.
Запись и чтение чисел. Числа однозначные и двузначные. Порядок следования чисел при счете. Сравнение чисел. Единицы длины: сантиметр, дециметр, миллиметр, метр. Соотношения между ними. Единицы времени: час, минута. Соотношение между ними. Определение времени по часам с точностью до минуты. Монеты (набор и размен). Задачи на нахождение неизвестного слагаемого, неизвестного уменьшаемого и неизвестного вычитаемого. Решение задач в 2 действия на сложение и вычитание. Устные и письменные приемы сложения и вычитания чисел в пределах 100. Числовое выражение и его значение. Порядок действий в выражениях, содержащих 2 действия (со скобками и без них). Сочетательное свойство сложения. Использование переместительного и сочетательного свойств сложения для рационализации вычислений.
Умножение и деление для 2 класса. Конкретный смысл и названия действий умножения и деления. Знаки умножения • (точка) и деления : (две точки). (В тестах знак умножения заменяется на «х»).
Названия компонентов и результата умножения (деления), их использование при чтении и записи выражений. Переместительное свойство умножения. Взаимосвязи между компонентами и результатом действия умножения; их использование при рассмотрении деления с числом 10 и при составлении таблиц умножения и деления с числами 2, 3. Порядок выполнения действий в выражениях, содержащих 2-3 действия (со скобками и без них). Периметр прямоугольника (квадрата). Решение задач в одно действие на умножение и деление.
Дальше вы можете пройти по порядку (или вразброс) тесты по математике за 2 класс. Желаем успехов!
Тесты
В этом тесте тебе нужно решить 10 математических задач на нахождение суммы для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на нахождение суммы для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на нахождение суммы для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на нахождение остатка для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на нахождение остатка для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на нахождение остатка для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на тему «Больше, меньше» для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на тему «Больше, меньше» для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного третьего слагаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного третьего слагаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного уменьшаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного уменьшаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на разностное сравнение для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на разностное сравнение для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на разностное сравнение для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с косвенными вопросами для 2 класса.
В этом тесте тебе нужно решить все примеры на сложение в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на сложение в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на сложение в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на сложение с переходом через десяток в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на вычитание в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на вычитание в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на вычитание в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на вычитание с переходом через десяток для 2 класса.
В этом тесте тебе нужно решить все примеры на вычитание с переходом через десяток для 2 класса.
В этом тесте тебе нужно проверить свои знания таблицы умножения с числами «2» и «3» для 2 класса.
В этом тесте тебе нужно увеличивать или уменьшать число «2» в заданное количество раз, а также увеличивать и уменьшать другие числа в 3 раза
В этом тесте тебе нужно увеличивать или уменьшать число «3» в заданное количество раз, а также увеличивать и уменьшать другие числа в 3 раза
В этом тесте тебе нужно пройти математический диктант, в котором нужно решать выражения с числом «2».
В этом тесте тебе нужно пройти математический диктант, в котором нужно решать выражения с числом «3».
В этом тесте тебе нужно решить примеры, состоящие из нескольких действий, руководствуясь при этом правилом порядка математических действий.
В этом тесте тебе нужно решить 10 математических заданий, в которых ты сможешь проверить не только математические способности, но и логическое мышление.
ГДЗ, Ответы по Математике 2 класс Рудницкая. Все решебники тут GDZ-na5.info
Готовые Домашние Задания, Решебник по Математике 2 класс Рудницкая
ГДЗ: 2 класс. Математика.Рудницкая В.Н. 2014 г. |
Ты ученик второго класса и не успел вовремя подготовить домашнее задание или ты колеблешься в правильности его решений. Тогда воспользуйся специальным решебником с ГДЗ по Математике 2- ых классов, но в применении его нет ничего необычного, не списывай, попробуй решить сам, и если не получиться, то подгляди. Может быть, уже довольно позднее время, за окном ночь, и ты задержался, не успел по некоторым обстоятельствам подготовиться, а ранним утром подниматься на первый урок? Побереги своё здоровье и продли себе сон. Ведь в будущей жизни будут такие задачи, на которые решебника и не найти.
Ответы к домашним заданиям по Математике 2 класс.
РудницкаяЧасть-1
Числа 10,20,30…,100
Двузначные числа и их запись
Луч и его обозначение
Числовой луч
Соотношения между единицами длины
Многоугольники и его элементы
Сложение и вычитание вида 26+2
Запись сложения столбиком
Запись вычитания столбиком
Сложение двузначных чисел
Вычитание двузначных чисел
Периметр многоугольника
Окружность, её центр и радиус
Взаимное расположение фигур на плоскости
Умножение и деление на 2. Половина числа
Умножение и деление на 3. Треть числа
Умножение и деление на 4.
Четверть числа
Доп. задачи
Числа и вычисления
Величины
Геометрические фигуры
Часть-2
Умножение и деление на 5. Пятая часть числа
Умножение и деление на 6. Шестая часть числа
Площадь фигуры. Единицы площади
Умножение и деление на 7. Седьмая часть числа
Умножение и деление на 8. Восьмая часть числа
Умножение и деление на 9. Девятая часть числа
Во сколько раз больше или меньше
Решение задач на увеличение и уменьшение в раз
Нахождение нескольких долей числа
Названия чисел в записях действий
Числовые выражения
Составление числовых выражений
Прямой угол
Прямоугольник.
Квадрат
Свойства прямоугольника
Площадь прямоугольника
Доп. задачи
Слож.вычит.умнож.делен. в пределах 100
Арифметич. задачи
|
|
..» учителям
..» родителямЗадачи для 1 — 2 класса
Примеры решения задач по математике
Задача №1
В шкафу стояло 39 книг.
Сколько книг переставили на полку?Решение:
39 — 25 = 14 (кн.)Ответ: на полку переставили 14 книг.
Когда на полку переставили несколько книжек, их там осталось 25.
Задача №2
Когда со стоянки уехало 4 машины, там осталось ещё 26.
Сколько машин было на стоянке?Решение:
26 + 4 = 30 (маш.)Ответ: на стоянке было 30 машин.
Задача №3
У Олега было 15 почтовых марок. 5 марок он использовал.
Сколько марок осталось у Олега?Решение:
15 — 5 = 10 (мар.)Ответ: у Олега осталось 10 марок.
Задача №4
На элеватор привезли 45 т ржи, а пшеницы 15 т.
Сколько всего зерна привезли на элеватор?Решение:
45 + 15 = 60 (т)Ответ: на элеватор привезли 60 тонн зерна.
Задача №5
Петя собрал по теме «Космос» 25 марок, а по теме «Флот» только 9.
Сколько всего марок в Петиной коллекции?Решение:
25 + 9 = 31 (мар.)Ответ: в Петиной коллекции 31 марка.
Задача №6
В ларёк привезли 15 ящиков яблок и 8 ящиков слив.
Сколько всего привезли ящиков с фруктами?Решение:
15 + 8 = 23 (ящ.)Ответ: в ларёк привезли 23 ящика с фруктами.
Задача №7
Бабушка посадила 16 кустиков клубники, а внучка 5.
Сколько всего кустиков клубники они посадили?Решение:
16 + 5 = 21 (кус.)Ответ: они посадили 21 куст клубники.
Задача №8
В школьную столовую привезли 15 кг картофеля, через 2 дня ещё 10 кг.
Сколько всего килограммов картофеля привезли?Решение:
15 + 10 = 25 (кг)Ответ: всего привезли 25 кг картофеля.
Задача №9
На стройку привезли 5 ящиков больших гвоздей и 8 ящиков маленьких.
Сколько всего привезли ящиков с гвоздями?Решение:
5 + 8 = 13 (ящ.)Ответ: на стройку привезли 13 ящиков с гвоздями.
Задача №10
Дедушка налил в бочку 18 вёдер воды и привёз в сад. Из бочки, под кусты, вылили 7 вёдер воды.
Сколько вёдер воды осталось бочке?Решение:
18 — 7 = 11 (вёд.)Ответ: в бочке осталось 11 вёдер воды.
Домашнее задание
Чтобы легко и быстро решать аналогичные задачи нужно закрепить знания выполнив несколько заданий самостоятельно.
Пример 1
На праздник 9 Мая дети читали стихи. Девочки прочитали 7 стихов, а мальчики 9. Сколько всего прочитали стихотворений?
Пример 2
Оля помогала маме мыть посуду. Мама помыла 6 тарелок, а Оля помыла 3 чашки. Сколько всего вымыто посуды?
Пример 3
К новогоднему празднику ученики украсили школьный класс. Девочки вырезали из бумаги 15 снежинок, а мальчики 20 хлопушек. Сколько всего украшений сделали ученики?
Пример 4
В классе на подоконниках окнон стоят 36 горшков с цветками. На первом подоконнике стоят 12 горшков, на втором 14. Сколько горшков на третьем подоконнике?
Пример 5
У Коли в аквариуме 18 рыбок – 9 скалярий и 11 барбусов. Коля подарил Ване 4 скалярия, а Пете 4 барбуса.
Реши задачу и дай ответ.
Сколько рыбок каждой породы осталось у Коли?Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter
задач Word: частично | Математика для 2-го класса
Как решать задачи с частичным словом
Фермер Джо посадил 6 помидоров. Фермер Бен посадил 13 помидоров. Сколько помидоров посадили фермер Джо и фермер Бен всего ?
Это называется Задача целого слова .
Когда вам дают двух частей, вам нужно найти целое.
Для этого вы сложите детали вместе.
Когда вам дают одну часть и все , вам нужно найти недостающую часть .
Для этого нужно вычесть заданную часть из целого.
😀 Совет: решить подобные проблемы может быть непросто.
Итак, вам действительно нужно хорошо читать подсказки. 😌
Давай попробуем.
Шаг 1. Соберите улики.
У нас есть две части, но не целое.
Нам нужно найти целое.
Шаг 2. Нарисуйте рисунок или диаграмму целиком.
Как нам разобраться в целом?
Верно!
👉 Нам нужно сложить две части вместе.
Шаг 3. Напишите уравнение.
6 + 13 = 19
Шаг 4.
Запишите ответ словесным предложением.
Фермер Джо и фермер Бен посадили 19 помидоров.
Другой пример
Как насчет решения другой проблемы?
Сара испекла 18 кексов. 10 были шоколадными. Остальное было ванилью. Сколько ванильных кексов испекла Сара?
Шаг 1. Соберите улики.
Мы видим, что у нас есть целое.
У нас тоже есть одна часть.
Шаг 2. Нарисуйте рисунок или диаграмму целиком.
Исходя из нашего рисунка, что нам делать?
Верно! Нам нужно найти недостающую часть.
👉 вычитаем заданную часть из целого.
Шаг 3. Напишите уравнение.
18–10 = 8
Шаг 4. Напишите словесное предложение.
Сара испекла 8 ванильных кексов.
Отличная работа! 👏
Смотри и учисьТеперь можно переходить к практике! 💪
задач Word для K-2 — Где происходит волшебство
Всем привет!
Обычно я получаю около 4 или 5 писем в неделю от учителей, которые купили мои ресурсы по текстовым задачам для детского сада, 1-го и 2-го классов.Большинство вопросов, которые я получаю, связаны с учащимися, которым трудно понять, что им делать, когда они сталкиваются с ситуациями сложения и вычитания.
Как я уже много раз говорил ранее, я не занимаюсь математикой. Собственно говоря, я был одним из тех студентов, которые ненавидели это из-за беспокойства по поводу математики. Я, однако, выполнил свою «домашнюю работу», не позволяя своим ученикам (и моим собственным мальчикам) доходить до этой точки, и сегодня я хочу предложить вам некоторое понимание.
Существует три основных уровня развития, когда дело доходит до решения проблем:
- Моделирование–> Прямое моделирование должно быть вашим шагом №1 в том, чтобы помочь вашим ученикам понять и развить чувство контекста и отношений при изучении того, как решать текстовые задачи.Я написал ЗДЕСЬ о том, как помочь студентам обнаружить взаимосвязи в задачах рассказа. Вы не можете ожидать, что ваши ученики будут использовать и применять какую-либо стратегию без предварительного моделирования. Позвольте детям использовать свои пальцы, если они находятся в K или 1st, или даже если они недостаточно знакомы с ситуациями сложения и вычитания. Им понадобится МНОГО возможностей, чтобы взаимодействовать, слушать, терпеть неудачу и добиваться успеха. Некоторые стратегии моделирования: использование пальцев, рисунков или использование реальных объектов.
Им понадобится МНОГО возможностей, чтобы взаимодействовать, слушать, терпеть неудачу и добиваться успеха. Некоторые стратегии моделирования: использование пальцев, рисунков или использование реальных объектов.- Счетные стратегии -> Учащимся, которые используют счетные стратегии для решения сюжетных задач, вероятно, не нужно моделировать каждое число.Когда вы видите, что ваши ученики используют стратегии подсчета, они, вероятно, больше осведомлены об отношениях в задаче рассказа. Некоторые из их стратегий подсчета можно придумать, а другие вам придется смоделировать в рамках своего руководства по стимуляции. Это несколько якорных диаграмм со стратегиями подсчета (сложения и вычитания), которые я составлял в прошлом со своими учениками.
- Полученные факты -> Хорошо, это этап, на котором ваши ученики действительно демонстрируют свои знания и беглость числовых фактов.Обычно я могу сказать, когда мои ученики составляют и раскладывают числа, компенсируют их, ищут способы использовать контрольные числа. и т.д. Я написал ЗДЕСЬ о контрольных цифрах. С другой стороны, на этом этапе студенты уже занимаются вычислениями. И с вычислениями приходит потребность решить. Иногда это стремление решать и вычислять может отвлекать наших студентов от осмысления и анализа проблемы рассказа. Когда вы начнете наблюдать это, вы можете попробовать убрать цифры из слов «проблемы». Таким образом, у них нет другого выбора, кроме как разобраться в контексте и отношениях.
и т.д. Я написал ЗДЕСЬ о контрольных цифрах. С другой стороны, на этом этапе студенты уже занимаются вычислениями. И с вычислениями приходит потребность решить. Иногда это стремление решать и вычислять может отвлекать наших студентов от осмысления и анализа проблемы рассказа. Когда вы начнете наблюдать это, вы можете попробовать убрать цифры из слов «проблемы». Таким образом, у них нет другого выбора, кроме как разобраться в контексте и отношениях.
Существует около 14-15 типов задач со словами. Некоторые из них сложнее других, но к концу 2-го класса, когда дети познакомятся со всеми типами, они должны свободно владеть этими ситуациями сложения и вычитания.
На мой взгляд, сначала следует ввести словесные задачи «соединить» и «разделить». Их легче решить, потому что они включают в себя реальные действия, которые дети могут смоделировать или разыграть.
Эти два типа задач со словами идеально подходят для введения и закрепления концепции «часть-часть-целое» с использованием числовых связей.
По опыту я говорю вам: проблемы с неизвестным запуском и неизвестными изменениями всегда будут немного сложнее, чем другие. Это потому, что когда мои ученики готовятся к моделированию проблемы, они не знают, с чего начать… потому что начало неизвестно!
Задачи со словом «часть-часть-целое» — это очень весело. Я учил их, когда преподавал в первом классе пару лет назад, и мы обычно использовали их как возможность развить концептуальное понимание и составить комбинации.Также они идеально подходят для использования с Рекенрексом!
Самым сложным типом задач со словами для понимания для моих студентов было сравнение. Есть кое-что в формулировке и используемом языке:
- меньше
- менее
- подробнее
- больше
- больше
Привет, словарь второго уровня!
Это особенно верно для изучающих английский язык и для студентов с плохим восприятием чисел и / или очень слабым языковым опытом.
Типовые задачи сравнения слов обеспечивают идеальный контекст для вас, чтобы представить и обучить стратегиям с использованием гистограмм.
Я буду писать об этом позже.
Вы можете скачать шпаргалки по этим типам задач ЗДЕСЬ!
Пожалуйста, сделайте мне одолжение и не учите своих учеников решать задачи со словами, используя ключевые слова. Будь вы младший учитель или опытный, не говорите своим ученикам, что «всего» означает прибавление, а «левый» означает вычитание. Я понимаю, что когда мы приближаемся к сезону тестирования, мы можем прибегнуть к этому, особенно если у нас есть ученики, которые все еще борются.Но ради всего святого, это уводит от настоящего концептуального понимания, и мы лишь паршиво исправляем вещи.
Что он сказал.
Ключевые слова вводят в заблуждение … правда в том, что не во многих задачах рассказа есть ключевые слова, и ваши ученики также не смогут решать многоступенчатые задачи со словами.
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ УЗНАТЬ О НАШИХ РЕСУРСАХ ПРОБЛЕМЫ WORD ДЛЯ ДЕТСКОГО САДА, ПЕРВЫЙ И ВТОРОЙ КЛАСС.
Вы можете получить БЕСПЛАТНЫЙ образец моих задач со словом для первого и второго класса ЗДЕСЬ!
Вы также можете получить ПОЛНУЮ продукцию в моем магазине TPT.
Надеюсь, вам понравился этот пост, спасибо, что прочитали!
ТОРГОВЫЙ СПИСОК
Как обучать задачам на сложение и вычитание слов
Мои ученики пытались решить , как решать задачи на сложение и вычитание слов , и казалось, что это длилось вечно. Они могли подчеркнуть вопрос и найти числа. В большинстве случаев мои ученики просто складывали два числа, не понимая сути проблемы.
Уф.
Можете рассказать?
Я большой сторонник того, чтобы НЕ учить спискам ключевых слов. Просто он не работает одинаково для всех задач. Это ярлык, ведущий к сбоям в математическом мышлении. Я подробно расскажу о том, почему это не работает, в книге «Проблема с использованием ключевых слов для решения проблем со словами».
Вы можете узнать больше о ресурсе «Проблемы со сложением и вычитанием слов», который я использую в своем классе, в этом сообщении в блоге.
Ниже приведены пять стратегий решения математических задач, которые можно использовать при обучении текстовым задачам с использованием любых ресурсов.
Итак, как мне учить словесные задачи? Это довольно сложно, но очень весело, когда вы в нее входите.
Основные компоненты обучения задачам на сложение и вычитание слов включают:
- Обучение соотношению чисел s — Как учитель, знайте тип задачи и помогайте ученикам решать действия в задаче
- Различайте Числа — дайте учащимся только правильные числа, чтобы они могли прочитать задачу, не увязнув в вычислениях.
- Используйте академический словарь — и будьте последовательны в том, что вы используете.
- Прекратить поиск «ответа» — дело не в ответе; речь идет о процессе
- Различия между моделями и стратегиями — одна связана с соотношением чисел, а другая — с тем, как учащиеся «решают» или вычисляют задачу.
Учите соотношению чисел в задачах со словами
Я учу задачи со словами, удаляя числа. Звучит странно, правда? Устранение отвлекающих факторов на числа помогает учащимся сосредоточиться на ситуации, в которой возникла проблема, и понять действие или взаимосвязь чисел.
Это также мешает студентам решить задачу до того, как мы поговорим о соотношении чисел.
Когда я преподаю задачи со словами, я даю студентам задачи с пробелами и без чисел. Сначала поговорим о действии в проблеме. Мы определяем, добавляется ли что-то к чему-то или берется из чего-то еще. Это становится нашим уравнением. Мы определяем, что нам нужно решить, и составляем уравнение с пробелами и квадратом для неизвестного числа.
___ + ___ = unknown
Вы хотите получить бесплатный образец словесных задач, которые я использую в своем классе? Щелкните ссылку или изображение ниже.БЕСПЛАТНЫЙ образец задач Word по типу задачи
Различайте числа в словах Задачи
Только после того, как мы обсудим задачу, я даю учащимся числа. Я разделяю числа в зависимости от потребностей студентов. В начале года мы все делаем одни и те же числа, чтобы я мог убедиться, что студенты понимают процесс.
После того, как ученики ознакомятся с процессом, я начинаю давать разным ученикам разные числа в зависимости от их уровня математического мышления.
Я также меняю числа в течение года, с однозначных на двузначные числа. Прелесть пустых мест в том, что я могу поставить в задачу любые числа, какие захочу, чтобы практиковать стратегии, над которыми мы работали в классе.
В какой-то момент мы действительно создаем список слов, но не список ключевых слов. Мы создаем список действий или глаголов и определяем, объединяют ли эти действия что-то или разделяют. Сколько вы можете придумать? Вот несколько идей:
Присоединиться: положил, получил, взял, купил, сделал
Отдельно: съел, потерял, отложил, уронил, использовал
Не бойтесь использовать академический словарный запас
Я учу своих учеников определять начало проблемы, заменяет в проблеме, а приводит к проблеме.Я учу их искать неизвестное . Это все слова, которые мы используем при решении задач, и мы узнаем структуру проблемы со словом через словарь и соотношение чисел.
Фактически, использование одного и того же словаря для разных типов задач помогает учащимся увидеть взаимосвязь чисел на более глубоком уровне.
Возьмите эти примеры, можете ли вы определить начало , изменить и результат в каждой задаче?
Подсказка: посмотрите на код, используемый для типа проблемы, в правом нижнем углу.
Для задач сравнения мы используем следующие термины: больше , меньше , больше и меньше . Попробуйте эти задачи и посмотрите, сможете ли вы определить компоненты словесных проблем.
Прекратите искать «ответ»
Это самое сложное заблуждение, чтобы разрушить его. Студенты не решают словесную задачу, чтобы найти «ответ». Хотя ответ помогает мне, учителю, понять, понял ли ученик взаимосвязь чисел, я хочу, чтобы ученики могли объяснить свой процесс и понять глубину словесных задач.
Ладно, они первоклассники и второклассники. Я знаю.
Мои ученики после инструктажа все еще могут объяснить, что они начинают ed с одного числа. Проблема , результат ред в другом другом номере.
Затем учащиеся знают, что они ищут изменение между этими двумя числами.
Все дело в отношениях.
Различия между моделями и стратегиями
Пару лет назад я наткнулся на эту статью о необходимости помочь студентам разработать адекватные модели для понимания взаимосвязи чисел в задаче.
В голове перегорела лампочка. Мне нужно было провести различие между моделями студентов, которые используют для понимания взаимосвязи чисел в задаче, и стратегиями для решения вычислений в задаче. Эти две вещи работают в тандеме, но очень разные.
Модели — это визуальные способы представления проблем. Стратегии — это способы, которыми ученик решает проблему, складывая и разбирая числа.
Самое главное в моделях — отойти от них.Я знаю, это звучит странно.
Вы так долго учите студентов пользоваться моделями, а потом уже не хотите, чтобы они использовали модели. На самом деле, вы хотите, чтобы студенты двигались к повышению эффективности.
Младшие ученики будут разыгрывать задачи, рисовать задачи с помощью репрезентаций и рисовать задачи с помощью кругов или линий. Двигайте учащихся к эффективности. По мере того, как числа становятся больше, модель должна представлять взаимосвязь чисел
Это яркий пример перехода от модели с перевернутой v к модели стержней.
Вот ученик, переходящий от рисования кругов к использованию перевернутой буквы v.
Учащиеся должны твердо использовать одну модель, прежде чем переходить на другую. Они могут даже использовать два одновременно, пока они выясняют сходство между моделями.
Учащиеся также должны уметь создавать свои собственные модели. Вы увидите, как я иногда давал студентам копии модели, которые они могли наклеить в свои тетради, а иногда студенты рисовали свои собственные модели. Они должны нести ответственность за выбор того, что им лучше всего подходит.Начните обучение с конкретных моделей, а затем позвольте учащимся выбрать одну из них.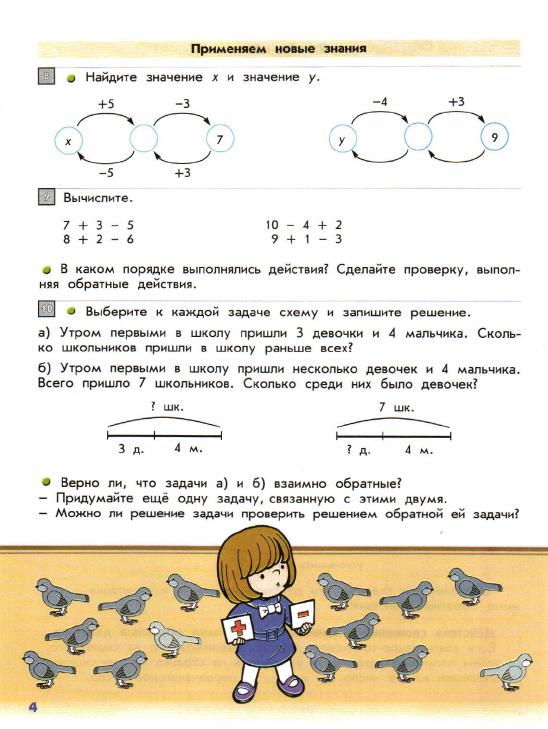
Всегда подталкивайте студентов к более эффективным моделям.
То же самое и со стратегиями вычислений. Изучите стратегии сначала на практике математических фактов, прежде чем применять их к задачам со словами, чтобы учащиеся поняли стратегии и могли быстро выбрать одну из них. При обучении сосредоточьтесь на одной или двух стратегиях. Когда учащиеся овладеют некоторыми стратегиями, предложите им выбрать стратегии, которые подходят для решения различных задач.
Будьте целеустремленными в числах, которые вы выбираете для своих задач со словами. Различные наборы чисел поддаются разным стратегиям и разным моделям. Используйте числовые наборы, которые студенты уже отработали на вычислительной технике. Если вы научили делать 10, используйте числа, которые дают 10. Если вы работаете над сложением без перегруппировки, используйте эти наборы чисел. Чем больше связей вы сможете установить между вычислением и решением проблемы, тем лучше.
Приведенные выше примеры в основном предназначены для задач объединения и разделения.
Неудивительно, что нашим ученикам так сложно сравнивать задачи, поскольку мы не учим их в той же степени, что и объединять и разделять задачи. Нашим ученикам нужно еще больше практики с такими типами задач, потому что соотношение чисел более абстрактное. Но я оставлю это для другого сообщения в блоге.
Вам нужен БЕСПЛАТНЫЙ образец ресурса, который я использую для обучения задачам сложения и вычитания слов по типу задачи ? Щелкните эту ссылку или изображение ниже.
Полный ресурс также доступен в моем магазине для покупки и на сайте Teachers Pay Teachers .
Возможно, вас заинтересует. . .
Задания для печати 1 класса по математике
Наши рабочие листы по математике для 1-го класса выровнены непосредственно с Core
Стандарты учебной программы для 1-го класса. Каждый стандарт полностью охвачен. Эти области в домашних листах, рабочих листах и викторинах.
Мы также добавляем дополнительные материалы, которые выходят за рамки стандартов.
которые мы находим во всех остальных тестах для этого уровня.Некоторые дополнения включают наши плакаты по математике для 1 класса. Эти рабочие листы по математике предназначены для учащихся 1-го класса как с математическим уровнем, так и с уровнем чтения. Также не забудьте посетить наши тесты по математике для 1 класса, чтобы оценить свой уровень достижений в этом классе.
Операции и подсказки на листах по алгебре
- Словесные задачи на сложение и вычитание (OA.1) — эти рабочие листы сосредоточены на задачах, которые выражаются в словесной форме и требуют вычисления единственной суммы или разницы для решения ситуационного упражнения.
- Одноместный Вычитание цифр (1.OA.A.1) — мы знакомим студентов с основной концепцией математической разницы.
- Простой Задачи на вычитание слов (1.OA.A.1) — мы берем различия в концепциях и применяем их к задачам со словами.
- Фиксированный
Целочисленное вычитание до 12 (относится к 1.OA.A.1) — учащиеся работают над удалением только одного определенного числа для различных целых чисел от 12 и ниже. Отличный раздел для работы над математическими фактами для первого класса.
- Проблемы со сложением слов (до 20) — (OA.2) — Эти рабочие листы представляют проблемы, которые можно найти в форме предложений и включают суммы, которые в сумме не превышают двадцати.
- Простой Задача со словом сложения (1.OA.A.2) — здесь вы должны начать со всего набора задач со словом.
- Свойства операций как стратегии (OA.3) — эти рабочие листы рассматривают общие математические свойства учащихся на этом уровне. Основа здесь — ассоциативные и коммутативные свойства.
- Вычитание и неизвестные слагаемые (до 20) ( OA.4) — это действительно учебник для подготовки студентов к пошаговой алгебре.
- Отсутствует Операции (сложение и вычитание) (1.OA.B.4) — Сообщите нам, чего не хватает в этих задачах. Подсказка: это оператор.
- Вычитание Числа с цифрами (относится к 1.OA.4) — мы начинаем переход от целых чисел к картинкам.
- Связать счет с сложением
и вычитание (1. OA.B.5). Если подумать, обе эти операции в точности похожи на счет. Двигаясь в ту или иную сторону. Мы делаем это очевидным для студентов.
- Сложение и вычитание в пределах 20 (1.OA.C.6) — Мы сохраняем суммы и различие чуть меньше двадцати.
- Семейства математических фактов (1.OA.C.6, 1.OA.B, 3.OA.4) — Семейства фактов — это группы чисел, которые почти систематичны в том смысле, что их можно переставлять для сложения и вычитания. Это действительно поможет вам быстро освоить основные операции.
- Rapid Fire Horizontal Addition Math Facts (1.OA.C.6) — это задачи с суммированием слева направо.
- Rapid Fire Horizontal Subtraction Math Facts (1.OA.C.6) — То же, что и выше, но мы вычитаем.
- Rapid Fire Vertical Addition Math Facts (1.OA.C.6) — Это здорово, чтобы поддерживать ваш уровень практики.
- Скорострельное вертикальное вычитание
Математические факты (1.OA.C.6) — это формат, к которому привыкло большинство студентов, но в реальном мире все немного более плавно.
- Number Bonds (1.OA.C.6) — интересный способ закрепить этот навык как для учеников, так и для учителей.
- Работа со знаками равенства ( OA.7) — это основа работы с уравнениями.
- Неизвестные номера в «Суммы и различия» (OA.8) — это помогает учащимся правильно переходить к задачам со словами.
- Подсчет (до 120) ( 1.NBT.1) — Это действительно помогает перейти к обучению формированию сумм и разностей.
- Одно и десятки знаков — 1.NBT.2) — Учащиеся начинают понимать значение заполнителя и разрядного значения.
- Сравните двузначные числа (1.NBT.3) — здесь появляются значения больше, меньше и равные.
- Одноместный Сложение цифр (1.NBT.C.4) — Учащиеся начинают складывать два однозначных числа вместе.
- Сложение чисел (Менее 100) (1.NBT.4) — В этом разделе начинаются соединения двух и трех пар чисел.
- На десять больше или на десять меньше
— 1. NBT.5) — Это отлично подходит для изучения силы десяти и, в конечном итоге, перехода к показателям.
- Визуальная сумма и разница Проблемы со словами (1.NBT.6) — здесь вам нужно сбалансировать несколько частей: предложения, целые числа и визуальные эффекты, которые представляют собой целые числа.
- Непрямая длина Word Problems (1.MD.1) — вы будете использовать другие доступные ссылки, чтобы найти установленные меры.
- Проблемы с длиной слова В единицах измерения (1.MD.2) — мы используем отдельные значения для работы с метрическими и стандартными американскими единицами длины.
- часов с половиной часов Время (1.MD.3) — В данном случае минутная стрелка всегда находится на уровне двенадцати или шести.
- Организация и понимание Данные (1.MD.4) — учащиеся узнают, как сделать данные более понятными для себя и своей аудитории.
- Атрибуты форм (G.1) — Каждая форма имеет что-то уникальное.
- Создание двумерных фигур (G.2) — Это стандартные формы, и мы просим вас нарисовать их с нуля.
- Разбиение кругов и прямоугольники (G.3) — вы разделите эти геометрические фигуры на части, руководствуясь записанными указаниями.
Отличный раздел для работы над математическими фактами для первого класса.
OA.B.5). Если подумать, обе эти операции в точности похожи на счет. Двигаясь в ту или иную сторону. Мы делаем это очевидным для студентов.
Рабочие листы с числами и основанием десяти
NBT.5) — Это отлично подходит для изучения силы десяти и, в конечном итоге, перехода к показателям.Таблицы измерений и данных
Рабочие листы по геометрии
Что изучают в классе ученики математики 1-го класса?
Учащиеся 1-х классов стремятся расширить свои навыки, которым они научились в детском саду и дошкольном учреждении.В учебной программе первого класса основной упор делается на построение основ математики. Вот некоторые вещи, которые они изучают на уроках математики в первом классе:
— Подсчет до 100 в небольшие группы, такие как 2, 5 и 10. Это помогает им научиться распознавать и записывать числа до 100.
— Они изучают понятие «больше чем» или «равно», а также основные математические операции, такие как сложение, вычитание, деление и умножение.
— Они изучают использование символов при использовании основных математических операций, таких как «+», «-», «« =, ».
»
— Сложение чисел до 100 в их голове.
— Учимся делать простое вычитание.
— Рабочее сложение и вычитание с помощью монет.
— Учимся определять простые закономерности.
— Изучение основных единиц измерения, таких как длина, вес, рост.
— Понимание и выполнение простых дробей (1/2, 1/3, 1/4).
— Научиться определять время по аналоговым часам и выучить разные термины для определения времени.
При изучении концепций математической учебной программы следует иметь в виду, что она следует спиральной учебной программе.Это означает, что год за годом мы вращаемся по спирали и опираемся на старые знания. Итак, в 1 классе вы развиваете навыки, которым изначально научились в детском саду. Когда вы дойдете до 2-го класса, вы будете развивать навыки, полученные в 1-м классе. Это означает, что если мы что-то не освоим, мы увидим это снова. Это дает нам шанс на этот раз сделать все правильно. Но это также указывает на то, что если у вас есть вредные привычки и вы их не исправляете, они станут для вас проблемой в будущем.
Задачи по математике для KidZone
[1 класс] [Оценка 2] [3-й степени] [Оценка 4] [5 класс]
Введение:
Задачи Word отсортированы по классам, а внутри каждой оценки — по тема.Я всегда нахожу, что предоставление сезонного рабочего листа помогает сохранить мои дочь взволнована своей работой.
Уровни обучения являются ориентировочными — пожалуйста, используйте свой суждение, основанное на способностях и рвении вашего ребенка (моя старшая дочь всегда использовала оценку ниже, тогда как моя младшая дочь кажется оценкой или два выше — иди прикинь). Имейте в виду, что задачи по математике со словами требуются навыки чтения, понимания и математики, чтобы ребенок, хорошо разбирающийся в основные математические уравнения могут оказаться труднее, чем вы ожидаете, столкнувшись с с математическими задачами со словом.
Все задачи со словами
динамические (другими словами, они регенерируют новую проблему каждый раз, когда вы их открываете
или нажмите «Обновить» в своем браузере).
Слова в частном
проблема не изменится, но цифры изменятся. Дети, которые борются
преобразование словесной задачи в математическое уравнение будет обнадеживающим
(создание уверенности), чтобы снова обратиться к одним и тем же словесным подсказкам с разными
числа, поэтому рассмотрите возможность печати пары повторений каждой проблемы.
В классе вы можете создать проблему для партнеров или группы
ученики решают вместе, а затем воссоздают то же
проблема для детей делать соло.
Со своей старшей дочерью однажды я понял, насколько она
боролся с математикой, когда ее нельзя было записать в красивом аккуратном уравнении, я
часто решали с ней математическую задачу (выполняя большую часть работы
я), а затем предоставил ей несколько повторений той же проблемы с
разные числа для нее, чтобы сделать соло. Через несколько недель она
смог сделать их без прохождения от мамы. Она одна из
те ребята, которые говорят: «Это слишком сложно!» довольно быстро так
укрепление доверия важно — если она думает, что не может что-то сделать
она не может — если она думает, что может сделать что-то, что может.
Теперь как сделать
Я убеждаю ее, что она МОЖЕТ содержать свою комнату в чистоте? * смеяться *
Общие задачи со словами для 1-го класса
— Мешки с фасолью
— Ведра
— Собачьи кости
— Время в школу (рисунок предложения)Тематические задачи со словами для 1 класса
Примечание: проблема генерируется с новыми числами каждый раз, когда вы нажимаете
Задачи со словами 2 степени
Тематические задачи со словами для 2 класса
Примечание: проблема возникает с новыми числами каждый раз, когда вы нажимаете
Задачи со словом 3 степени
Тематические задачи со словами для 3 класса
Примечание: проблема генерируется с новыми числами каждый раз, когда вы нажимаете
Задачи со словами для 4-го класса
Тематические задачи со словами для 4 класса
Примечание: проблема генерируется с новыми числами каждый раз, когда вы нажимаете
Задачи 5 класса
Тематические задачи со словами для 5 класса
Примечание: проблема генерируется с новыми числами каждый раз, когда вы нажимаете
Часть Часть Целая Деятельность | Фея Поппинс
Рози | Размещено |
ШтырьЭти упражнения помогают детям понять, что числа могут быть представлены по-разному.Дети также узнают о реальных семьях.
Учебная часть, часть целиком
Обучение детей принципам «часть-часть-целое» помогает им узнать, что числа могут быть представлены по-разному, например четыре как 1 и 3, 2 и 2 или 4 и 0. В принципе, каждое число можно разделить на две части. . Дети также учатся изображать отношения «часть-часть-целое» в диаграммах и числовых предложениях.
Полезные учебные пособия
Соединение кубов и звеньев отлично подходит для моделирования числа как двух частей целого.Вы также можете использовать дешевую альтернативу — цветные скрепки или бумажную цепочку. Лучше всего, если вы ограничите количество цветов только двумя, чтобы дети могли легко видеть две части числа.
Представляем часть-часть-целое
Составьте число из двух цветных соединительных кубиков (или чего-то подобного). Например, на фото ниже семерка состоит из двух частей.
Первая часть состоит из 4 синих кубиков , а вторая часть состоит из 3 розовых кубиков .Это говорит нам о том, что вместе числа 4 и 3 составляют семь. Изучите другие способы сделать семь, по-прежнему используя те же два цвета. Ниже приведены некоторые упражнения, предназначенные для дальнейшего обучения части-части-целому.
Штифт
Задание 1 — Рабочие коврики, состоящие из частей, целые
Для этого упражнения вам понадобятся соединительные кубики или звенья, ламинированный рабочий коврик и стираемый маркер. Есть несколько разных рабочих ковриков на выбор. Начните с простых циновок, на которых есть место, чтобы написать только одно числовое предложение, а затем используйте маты для семейной работы.
Как играть…
Детям нужно использовать соединительные кубики, чтобы моделировать целое число из двух частей. Затем они пишут числовое предложение на рабочем коврике. Есть карточки с заданиями, которые вы можете использовать, или дети могут просто научиться составлять разные числа самостоятельно.
Бросок кубика может быть интересным способом выбора числа для работы.
Задание 2 — Запись и протирание ковриков
Эти маты, заполняющие пустую часть, необходимо ламинировать или поместить в прозрачный рукав, чтобы их можно было использовать со стираемым маркером.Есть четыре уровня на выбор, я рекомендую начать с уровня 1, где дети в основном складывают две части вместе, чтобы вычислить недостающее целое число. Хорошо иметь соединительные кубики или ссылки для детей, которым сложно найти ответы в уме.
Как играть…
Напишите недостающий номер в пустом поле. Уровень 1 и уровень 2 сосредоточены на вычислении недостающих целых чисел. Уровни 3 и 4 сосредоточены на отработке недостающих частей целого числа.
Штифт
Задание 3 — Листы частично частично целиком
Они бывают разных уровней и начинаются с простых чисел. Детям нужно вычислить недостающее целое число или недостающий номер детали. Листы с ответами прилагаются.
Пример — Стиль 1
Штифт
Пример — Стиль 2
Штифт
Задание 4 — Факты Семейные рабочие коврики и карточки
Для этого упражнения вам понадобятся соединительные кубики или звенья, ламинированный рабочий коврик и стираемый маркер.Есть также карточки задач, которые вы можете использовать.
Дети начинают с решения задачи «часть-часть-целое». Далее им нужно смоделировать число с помощью соединительных кубиков. Наконец, им нужно написать числовые предложения на коврике для семейной работы.
Штифт
Задание 5 — Рабочие листы для семьи
Они бывают разных уровней и начинаются с простых семейств фактов. Детям нужно написать числовые предложения на сложение и вычитание для каждой семьи фактов.Листы с ответами прилагаются.
Штифт
Чтобы узнать больше об этих мероприятиях, щелкните здесь.
Штифт
Если вам нужны дополнительные практические ресурсы, часть часть часть целиком, не забудьте взять карты сложения ламы ниже.
Они лучше всего подходят для детей детского сада и первого класса.
Штифт
Штифт
9 советов и приемов для решения задач со словами
Привет! Меня зовут Джо-Эллен из Love Believe Teach с Джо-Эллен Фуди, и я рада быть приглашенным блогером для Рэйчел Линетт.
Давайте поговорим о… проблемах со словами. Я могу начать с того, что скажу вам, что люблю учить детей решать задачи со словами, но не буду. Проблемы со словом сложны. Двухэтапные задачи со словами еще сложнее, и научить их решать, возможно, будет самым сложным навыком, которому вы обучаете в течение всего года. Хуже всего то, что вы ничего не можете с этим поделать. Неа! Нада! Задачи со словами есть в каждой математической программе, в каждом классе, в каждом стандартизированном математическом тесте, и они являются важным навыком, которым ученики должны овладеть, чтобы выжить в нашем мире.И это наша главная цель, верно?
Итак, вот что я нашел наиболее полезным и наименее болезненным для учащихся способом научиться решать сложные словесные задачи.
Не ожидайте 100% мастерства после одного урока. Этого просто не произойдет. Я знаю, что это может быть трудно понять, но этот навык требует ВРЕМЕНИ и очень много. К сожалению, от этого никуда не деться.
Признайте, что задачи со словами сложны и вашим ученикам потребуется много практики с ними.Почему-то произнесение этого вслух делает весь процесс немного менее пугающим.
Используйте много, много, много форм практики. Я не могу этого достаточно подчеркнуть. Если у вас нет ученика, обладающего сверхспособностью решать задачи с чудодейственным словом, вашим ученикам понадобится ОЧЕНЬ много практики. Студентам нужны непосредственные инструкции всего класса, время с партнером, самостоятельные занятия для практики, веселые игры «вставай и двигайся», центры карточек с заданиями и домашние задания. Да, вам нужно привлечь родителей ваших учеников к тому, чтобы помочь их детям справиться с этими трудными проблемами.Разнообразие важно для того, чтобы ваши ученики продолжали практиковаться и улучшать свои навыки.
Обучайте, переучивайте, а затем, по прошествии некоторого времени, переучивайте снова. Иногда детям нужно время, чтобы усвоить все трюки, которым вы их научили. Поэтому после первого вводного урока подождите немного и повторите его с помощью короткого мини-урока, чтобы освежить их сознание. Повторяйте мини-уроки столько раз, сколько нужно.
Ох, ох! Я сказал это. И да, я имел это в виду.От этого никуда не деться. Судя по моему опыту, да, у меня его более 18 лет, студентам нужно много-много практики, чтобы справиться с задачами со словом. Иногда, просто иногда, может помочь решить проблему за проблемой. Вы можете мне не поверить, но для детей они действительно воспринимают это как вызов. Поверьте мне!
Вот как я это делаю: сначала я раздаю лист с упражнениями №1 с одной или двумя задачами. Я даю студентам время закончить, и как только они заканчивают, они проверяют его.Если они все поймут правильно, я немедленно даю им страницу №2. Затем я повторяю процесс снова и снова, пока не почувствую, что они устают.
Вы узнаете, когда ваш класс достигнет дневного максимума. Они начнут отказываться от задания, не будут работать так усердно, «веселье» больше не витает в воздухе, и вот тогда я понимаю, что пора переходить к следующему занятию.
Другой способ попрактиковаться — превратить его в игру, чтобы увидеть, сколько задач класс может правильно решить за x минут. Начните со слов: «Мы будем выполнять столько задач, сколько сможем за пять минут.На своей отметке, готовься! Ваш класс будет думать, что они играют в игру, а не решают сложные задачи со словами. Вы можете легко отслеживать, сколько задач класс решил правильно в установленные сроки. Если вы повторите эту игру несколько раз, вы увидите, что их общее количество становится все выше и выше по мере роста их навыков. Затем посмотрите, как ваш класс отмечает свои достижения. Они это заслужили!
БЕСПЛАТНАЯ ЗАДАЧА, состоящая из двух слов, которая поможет вашим ученикам начать практиковаться.Я считаю, что наиболее эффективно начинать с одной задачи на странице, а учащиеся работают над тремя задачами на странице.
Да, некоторым детям они нужны. Им нужна система, которой нужно следовать. Я обнаружил, что дать студентам одну простую и понятную стратегию — лучший способ помочь этим студентам. Для них это просто не так запутанно. Убедитесь, что вы выбрали удачную стратегию!
Вот слово «план атаки», которое я использую со своими второклассниками:
- Шаг 1. Прочтите проблему и подумайте: «В чем проблема?»
- Шаг 2. Перечитайте проблему и подумайте: «В чем проблема?»
- Шаг 3. Спланируйте «атаку» и подумайте: «Как лучше всего решить эту проблему?»
- Шаг 4. Решите проблему и подумайте: «Какую операцию мне следует использовать?»
- Шаг 5. Проверьте свой ответ и подумайте: «Имеет ли мой ответ смысл? Моя математика верна? »
Да, мы учителя и должны учить, но иногда дети просто не понимают, что мы говорим или как мы что-то объясняем.Это не делает нас плохими учителями; считайте это тайной юного ума. Все, что вам нужно сделать, это разделить студентов на пары, которые борются с кем-то, кто пытается справиться с проблемами.
Прежде чем вы это узнаете, каждый с легкостью справится с этими проблемами со словами!
Попросите учащихся написать свои собственные задачи со словами, а затем попросите друга решить их. Как только ваши ученики научатся решать задачи со словами, вы увидите, как их понимание этих задач будет расти.
Поговорите о том, что есть много разных способов решить словесную проблему, и что на 100% нормально решать проблему с помощью стратегии, отличной от чьей-либо другой.Примите эту идею и скажите своим ученикам, что все наши умы уникальны и решение этих проблем просто должно иметь смысл для вас.
Итак, вот и все. Я искренне надеюсь, что вы сможете найти несколько идей, которые сможете сразу же реализовать в своем собственном классе. Для большинства студентов проблемы со словами являются сложной задачей, но они никуда не денутся. Итак, давайте просто сделаем их чем-то, над чем мы будем работать вместе. Если у вас есть какие-либо советы и приемы, которые сработали для ваших учеников, я хотел бы услышать о них в комментариях ниже.