Геометрия вопросы для повторения к главе 1 ответы: ГДЗ (решебник) по геометрии 7-9 класс Атанасян, Бутузов, Кадомцев – РЕШАТОР!

Вопросы для повторения к главе 5 атанасян. Вопросы для повторения к главе V. Вопрос5. Каковы главные обязанности гражданина

На вопрос Вопросы для повторения к Главе 5 Геометрия 7-9 класс Атанасян заданный автором Егор Кротов лучший ответ это Вот:

Ответ от Двутавровый [новичек]
какая фигура называется ломаной

Ответ от росомаха [новичек]
Нужны ответы на вопросы для повторения к главе 5 к учебнику геометрии 7-9 класс атанасян (с 114-115 учебника)

Ответ от Никита Суворов [новичек]
Нужны ответы на вопросы (1-22) к гллаве 5

Ответ от старослужащий [новичек]
Нужны ответы на вопросы для повторения к главе 5 к учебнику геометрии 7-9 класс атанасян 113-114 стр

Ответ от Ўлия Хачирова [новичек]
ОТВЕТЫ НА ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ К ГЛАВЕ 5
1. Ломаная — это фигура, не лежащая на одной прямой.
Звенья — это отрезки, из которых составлена ломаная.
Концы отрезков — вершины ломаной
Длина ломаной — сумма длин всех звеньев.
2. . Многоугольник — это геометрическая фигура, состоящие из замкнутой ломаной.

Сторона — один отрезок многоугольника
Диагональ — отрезок соединяющий две любые не соседние вершины.
Вершина — место пересечений линий в многоугольнике
Периметр — длина ломаной.
3. Выпуклый многоугольник — это мнгоугольник, который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
4. (n -2) . 1800
n — кол- во углов
5. стр. 99 Так как сумма углов выпуклого n-угольника равна (n-2)*180?, то сумма углов четырёхугольника равна 360?
6. ——
7. Параллелограмм — это четырёхугольник, у которого противолежащие стороны попарно параллельны. Является выпуклым четырехугольником.
8-9
Для параллелограмма верно свойство: Противолежащие стороны попарно равны.
А еще есть признак параллелограма: если в четырехугольнике противолежащие стороны попарно равны, то он паралеллограмм.
10 — 101-102
11. Трапеция — четырёхугольник у которого две стороны параллельны а две другие не параллельны
Стороны — основания и боковые стороны.
12 Трапеция, у которой боковые стороны равны между собой, называется равнобедренной.
Трапеция, один из углов которой прямой, называется прямоугольной.
14 Прямоугольник — это паралелограмм, у которого все углы прямые
Док-во на стр. 108
14 стр. 108
15. Ромб — это паралелограмм, у которого все стороны равны. Док-во — стр. 109.
17.Квадрат — прямоугольник, у которого все стороны равны.
18 Две точки называются симметричными относительно прямой а, если это прямая проходит через середину отрезка и перпендикулярна к нему.
19. . Фигура называется симметричной относительно прямой а, если каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
20. Две точки называются симметричными относительно точки О, если О — середина отрезка.
21.Фигура называется симметричной относительной точки О, если каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

1. Объясните, какая фигура называется ломаной. Что такое звенья, вершины и длина ломаной?

2. Объясните, какая ломаная называется многоугольником. Что такое вершины, стороны, периметр и диагонали многоугольника?

3. Какой многоугольник называется выпуклым? Объясните, какие углы называются углами выпуклого многоугольника.

4. Выведите формулу для вычисления суммы углов выпуклого n-угольника.

5. Докажите, что сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360°.

6. Начертите четырёхугольник и покажите его диагонали, противоположные стороны и противоположные вершины.

7. Чему равна сумма углов выпуклого четырёхугольника?

8. Дайте определение параллелограмма. Является ли параллелограмм выпуклым четырёхугольником?

9. Докажите, что в параллелограмме противоположные стороны равны и противоположные углы равны.

10. Докажите, что диагонали параллелограмма точкой пересечения делятся пополам.

11. Сформулируйте и докажите утверждения о признаках параллелограмма.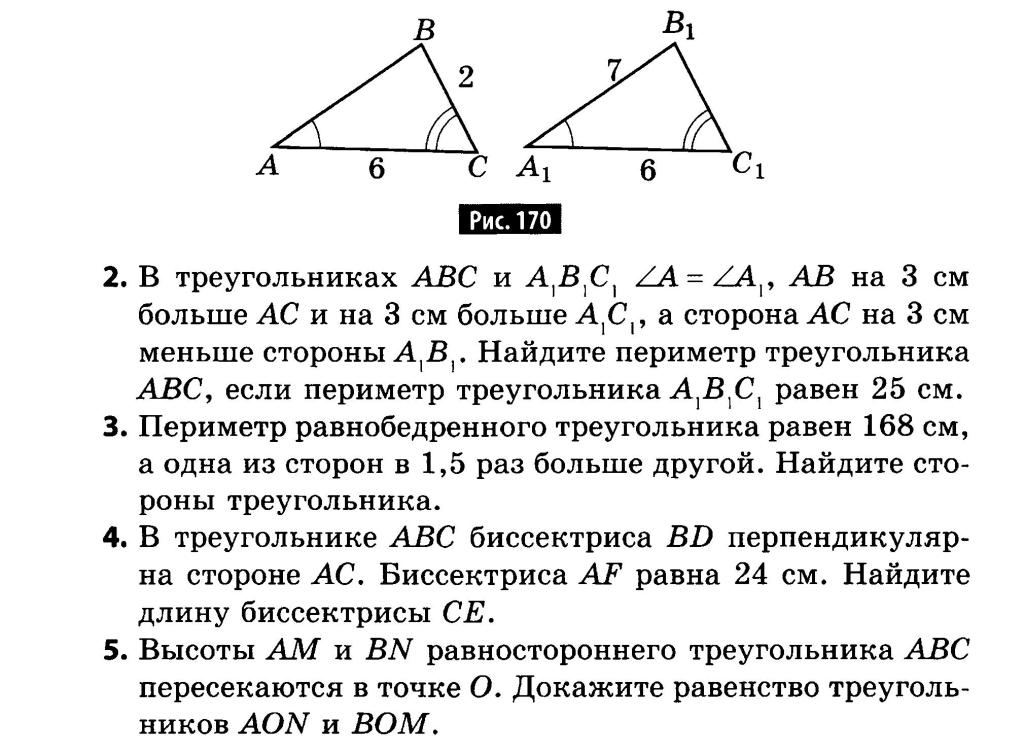

12. Какой четырёхугольник называется трапецией? Как называются стороны трапеции?

13. Какая трапеция называется равнобедренной? прямоугольной?

14. Какой четырёхугольник называется прямоугольником? Докажите, что диагонали прямоугольника равны.

15. Докажите, что если в параллелограмме диагонали равны, то параллелограмм является прямоугольником.

16. Какой четырёхугольник называется ромбом? Докажите, что диагонали ромба взаимно перпендикулярны и делят его углы пополам.

17. Какой четырёхугольник называется квадратом? Перечислите основные свойства квадрата.

18. Какие две точки называются симметричными относительно данной прямой?

19. Какая фигура называется симметричной относительно данной прямой?

20. Какие две точки называются симметричными относительно данной точки?

21. Какая фигура называется симметричной относительно данной точки?

22. Приведите примеры фигур, обладающих: а) осевой симметрией; б) центральной симметрией; в) и осевой, и центральной симметрией.

Дополнительные задачи

424. Докажите, что если не все углы выпуклого четырёхугольника равны друг другу, то хотя бы один из них тупой.

425. Периметр параллелограмма ABCD равен 46 см, АВ = 14 см. Какую сторону параллелограмма пересекает биссектриса угла А? Найдите отрезки, которые образуются при этом пересечении.

426. Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.

427. Через произвольную точку основания равнобедренного треугольника проведены прямые, параллельные боковым сторонам треугольника. Докажите, что периметр получившегося четырёхугольника равен сумме боковых сторон данного треугольника.

428. В параллелограмме, смежные стороны которого не равны, проведены биссектрисы углов. Докажите, что при их пересечении образуется прямоугольник.

429. Докажите, что выпуклый четырёхугольник является параллелограммом, если сумма углов, прилежащих к каждой из двух смежных сторон, равна 180°.

430. Докажите, что выпуклый четырёхугольник является параллелограммом, если его противоположные углы попарно равны.

431. Точка К — середина медианы AM треугольника АВС. Прямая ВК пересекает сторону АС в точке D. Докажите, что AD = 1/2 AC

432. Точки М и N — середины сторон AD и ВС параллелограмма ABCD. Докажите, что прямые AN и МС делят диагональ BD на три равные части.

433. Из вершины В ромба ABCD проведены перпендикуляры ВК и ВМ к прямым AD и DC. Докажите, что луч BD является биссектрисой угла КВМ.

434. Докажите, что точка пересечения диагоналей ромба равноудалена от его сторон.

435. Докажите, что середина отрезка, соединяющего вершину треугольника с любой точкой противоположной стороны, лежит на отрезке с концами в серединах двух других сторон.

436. Диагональ АС квадрата ABCD равна 18,4 см. Прямая, проходящая через точку А и перпендикулярная к прямой АС, пересекает прямые ВС и CD соответственно в точках М и N. Найдите MN.

437. На диагонали АС квадрата ABCD взята точка М так, что АМ = АВ. Через точку М проведена прямая, перпендикулярная к прямой АС и пересекающая ВС в точке Н. Докажите, что ВН = НМ = МС.

438. В трапеции ABCD с большим основанием AD диагональ АС перпендикулярна к боковой стороне CD, ∠B АС = ∠CAD. Найдите AD, если периметр трапеции равен 20 см, a ∠D = 60°.

439. Сумма углов при одном из оснований трапеции равна 90°. Докажите, что отрезок, соединяющий середины оснований трапеции, равен их полуразности.

440. На двух сторонах треугольника вне его построены квадраты. Докажите, что отрезок, соединяющий концы сторон квадратов, выходящих из одной вершины треугольника, в два раза больше медианы треугольника, выходящей из той же вершины.

441. Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии.

442. Докажите, что точка пересечения диагоналей параллелограмма является его центром симметрии.

443. Сколько центров симметрии имеет пара параллельных прямых?

444. Докажите, что если фигура имеет две взаимно перпендикулярные оси симметрии, то точка их пересечения является центром симметрии фигуры.

Ответы к задачам

425. Пересекает сторону CD; 9см и 5см.

426. 3см, 4см, 3см.

428. Указание. Воспользоваться задачей 400.

430. Указание. Воспользоваться теоремой о сумме углов выпуклого четырёхугольника и задачей 429.

431. Указание. Через точку М провести прямую, параллельную ВК, и воспользоваться задачей 385.

432. Указание. Воспользоваться задачей 385.

433. Указание. Сначала доказать, что Δ BKD = Δ BMD.

435. Указание. Воспользоваться задачей 384.

436. 36,8см. Указание. Использовать диагональ BD.

437. Указание. Сначала доказать, что Δ АВН = Δ АМН.

438. 8см. Указание. Воспользоваться задачей 389, а.

439. Указание. Через середину меньшего основания провести прямые, параллельные боковым сторонам, и воспользоваться задачей 404.

440. Указание. Пусть EF — отрезок, соединяющий концы сторон квадратов, выходящих из вершины А треугольника АВС. Рассмотреть точку D, симметричную точке А относительно середины стороны ВС, и доказать, что Δ ABD = Δ EAF.

441. Указание. Воспользоваться задачей 420.

443. Бесконечное множество.

444. Указание. Пусть а и b — взаимно перпендикулярные оси симметрии фигуры и О — точка их пересечения. Сначала доказать, что если точки М и М 1 симметричны относительно прямой а, а М 1 и М 2 симметричны относительно прямой b, то М и М 2 симметричны относительно точки О.

Готовые домашние задания к учебнику геометрии для учащихся 7-9 классов, авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина , издательство Просвещение на 2015 — 2016 учебный год.

Ребята, в 7-9 классе вы будете изучать такой интересный предмет как геометрия. Чтобы в дальнейшем не иметь проблем с пониманием этого урока, необходимо с самого начала усердно работать.

В предыдущих классах вы уже познакомились с некоторыми геометрическими фигурами. В этом гуду вы расширите этот минимум познания. Весь курс делится на два раздела: планиметрию и стереометрию. В 7 и 8 классе вы будете рассматривать фигуры на плоскости — это раздел планиметрия. В 9 классе свойства фигур в пространстве — стереометрия.

Часто возникает ситуация, когда не получается исходя из условия сделать правильный рисунок, нарисовать в пространстве все детали и тогда геометрия кажется неподъёмным для вас предметом. Если у вас начнутся такие трудности, тогда рекомендуем использовать наш гдз по геометрии за 7-9 класс Л.С. Атанасяна, который размещён ниже.

ГДЗ Геометрия 7 класс рабочая тетрадь Атанасян можно скачать .

ГДЗ Геометрия 8 класс рабочая тетрадь Атанасян можно скачать .

ГДЗ Геометрия 9 класс рабочая тетрадь Атанасян можно скачать .

ГДЗ к дидактическим материалам по геометрии за 7 класс Зив Б.Г. можно скачать .

ГДЗ к дидактическим материалам по геометрии за 8 класс Зив Б.Г. можно скачать .

ГДЗ к дидактическим материалам по геометрии за 9 класс Зив Б.Г. можно скачать .

ГДЗ к самостоятельным и контрольным работам по геометрии за 7-9 классы Иченская М.А. можно скачать .

ГДЗ к сборнику заданий по геометрии за 7 класс Ершова А. П. можно скачать .

ГДЗ к сборнику заданий по геометрии за 8 класс Ершова А.П. можно скачать .

ГДЗ к рабочей тетради по геометрии за 9 класс Мищенко Т.М. можно скачать .

ГДЗ к тематическим тестам по геометрии за 7 класс Мищенко Т.М. можно скачать .

ГДЗ к тематическим тестам по геометрии за 8 класс Мищенко Т.М. можно скачать

Вопрос1. Объясни, что означает слово «патриот».

Ответ. Патриот – это тот, кто любит свою Родину, желает ей успехов и не жалеет ради этих успехов сил и даже жизни, но он также видит недостатки Родины и старается их исправить, при этом он уважает другие народы.

Вопрос2. Что изображено на гербе Российской Федерации?

Ответ. На гербе Российской Федерации изображён красный щит. На фоне этого щита золотой двухглавый орёл, на каждой из голов по короне, а сверху – ещё одна большая корона (символы царской власти), в одной лапе орёл держит скипетр (царский жезл), а в другой – державу (символ земного шара с крестов – символом христианства). На груди орла всадник, который вонзает копьё в дракона.

Вопрос3. Что означают цвета российского Государственного флага?

Ответ. Цвета российского Государственного флага в начале были взяты Петром I с голландского, но они приобрели своё значение: внизу – красный – мир мифический, выше – небесный, голубой, ещё выше – белый – мир божественный.

Вопрос4. Каковы права гражданина, дающие ему возможность участвовать в управлении делами государства?

Ответ. Граждане имеют право участвовать в выборах и быть избранными на пост Президента Российской Федерации, в Государственную Думу Российской Федерации, в органы местного самоуправления. Они также имеют право голосовать на референдумах.

Вопрос5. Каковы главные обязанности гражданина?

Ответ. Обязанности:

1) соблюдать конституцию и другие законы;

2) защищать свою страну;

3) беречь памятники истории и культуры;

4) бережно относиться к природным богатствам;

5) платить законно установленные налоги и сборы.

Ответ. Достойный гражданин, конечно же, должен добросовестно исполнять все обязанности гражданина. Он радуется и огорчается когда видит успехи и неудачи своей страны. Именно поэтому он всеми силами стремиться сделать страну лучше, указывает на её недостатки, потому что уверен: тогда успехов будет больше, а неудач меньше.

Вопрос7. Почему мы говорим, что народ нашей страны многонациональный?

Ответ. Потому что в Российской Федерации проживает много разных национальностей (некоторые многочисленны, другие совсем небольшие, самые маленькие насчитывают всего несколько тысяч человек). Но при этом все национальности составляют один народ, люди из этого народа – россияне.

Вопрос8. Почему русский язык называют языком межнационального общения?

Ответ. У каждой национальности есть свой язык, который остальные национальности не знают. И только на русском языке говорят по всей стране, человека, который говорит на нём могут понять представители всех национальностей, потому русский язык и называется межнациональным.

Вопрос9. Почему культуру нашей страны называют многонациональной?

Ответ. Потому что у каждой из национальностей Российской Федерации есть своя культура (не на всех их языках писали великие поэты и писатели, но у всех есть хотя бы сказки, колыбельные и т. д.), но все культуры разных национальностей составляют одну общую культуру нашей страны.

Вопрос10. Как складывается многонациональная культура?

Ответ. Русский народ в своё время собрал вокруг Москвы земли, которые сегодня составляют Россию. В начале Московское княжество подчинило себе несколько окрестных, потом оно стало главой всей Северо-Западной Руси, а потом Российское государство стало включать в свой состав самые разные окрестные народы, особенно быстро оно расширялось на Восток.

Вопрос11. Что такое национальность?

Ответ. Принадлежность человека к определённой нации называется национальностью. Признаки такой принадлежности: язык, культура и, главное, понимание людьми того, что они едины и относятся к этой национальности.

Геометрия 7 Атанасян Задачи 156-185

Дополнительные задачи №№ 156-185 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями, а также вопросы для повторения к Главе II «ТРЕУГОЛЬНИКИ». Геометрия 7 Атанасян Задачи 156-185 + ответы.

◄ Задачи 143-155   ОГЛАВЛЕНИЕ учебника

Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях.

Дополнительные вопросы к главе 2 «Треугольники»

Вопросы для повторения к главе II.

Дополнительные задачи №№ 156-185

Геометрия 7 класс (УМК Атанасян)

  Вопросы для повторения к главе II.

• 1. Объясните, какая фигура называется треугольником. Начертите треугольник и покажите его стороны, вершины и углы. Что такое периметр треугольника?
• 2. Какие треугольники называются равными?
• 3. Что такое теорема и доказательство теоремы?
• 4. Сформулируйте и докажите теорему, выражающую первый признак равенства треугольников.
• 5. Объясните, какой отрезок называется перпендикуляром, проведённым из данной точки к данной прямой.
• 6. Сформулируйте и докажите теорему о перпендикуляре, проведённом из данной точки к данной прямой.
• 7. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?
• 8. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?
• 9. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
• 10. Какой треугольник называется равнобедренным? Как называются его стороны?
• 11. Какой треугольник называется равносторонним?
• 12. Докажите, что углы при основании равнобедренного треугольника равны.
• 13. Сформулируйте и докажите теорему о биссектрисе равнобедренного треугольника. ‘
• 14. Сформулируйте и докажите теорему, выражающую второй признак равенства треугольников.
• 15. Сформулируйте и докажите теорему, выражающую третий признак равенства треугольников.
• 16. Что такое определение? Дайте определение окружности. Что такое центр, радиус, хорда и диаметр окружности?
• 17. Объясните, как отложить на данном луче от его начала отрезок, равный данному.
• 18. Объясните, как отложить от данного луча угол, равный данному.
• 19. Объясните, как построить биссектрису данного угла.
• 20. Объясните, как построить прямую, проходящую через данную точку, лежащую на данной прямой, и перпендикулярную к этой прямой.
• 21. Объясните, как построить середину данного отрезка.

 

  Дополнительные задачи №№ 156-185

№ 156. □ Периметр треугольника АВС равен 15 см. Сторона ВС больше стороны АВ на 2 см, а сторона АВ меньше стороны АС на 1 см. Найдите стороны треугольника.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 157. □ В равнобедренном треугольнике основание больше боковой стороны на 2 см, но меньше суммы боковых сторон на 3 см. Найдите стороны треугольника.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 158. Основание равнобедренного треугольника равно 8 см. Медиана, проведённая к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2 см больше периметра другого. Найдите боковую сторону данного треугольника.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 159. Докажите, что два равнобедренных треугольника равны, если боковая сторона и угол, противолежащий основанию, одного треугольника соответственно равны боковой стороне и углу, противолежащему основанию, другого треугольника.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 160. Прямая а проходит через середину отрезка АВ и перпендикулярна к нему. Докажите, что: а) каждая точка прямой а равноудалена от точек А и В; б) каждая точка, равноудалённая от точек А и В, лежит на прямой а.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 161. В треугольниках АВС и А₁В₁С₁ медианы AM и А₁М₁ равны, ВС = В₁С₁ и ∠AMB = ∠A₁M₁B₁. Докажите, что ΔАВС = ΔА₁В₁С₁.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 162. На рисунке 92 треугольник ADE равнобедренный, DE — основание. Докажите, что:
а) если BD = СЕ, то ∠CAD = ∠BAE и АВ = АС; б) если ∠CAD = ∠BAE, то BD = CE и АВ = АС.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 163. Докажите, что середины сторон равнобедренного треугольника являются вершинами другого равнобедренного треугольника.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 164. На сторонах равностороннего треугольника АВС отложены равные отрезки AD, BE и CF, как показано на рисунке 93. Точки D, Е, F соединены отрезками. Докажите, что треугольник DEF — равносторонний.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 165. Отрезки АВ и CD пересекаются в их общей середине О. На отрезках АС и BD отмечены точки К и К₁ так, что АК = ВК₁. Докажите, что: а) ОК = ОК₁; б) точка О лежит на прямой КК₁.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 166. Отрезки АВ и CD пересекаются в их общей середине О. Точки М и N — середины отрезков АС и BD. Докажите, что точка О — середина отрезка MN.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 167. Стороны равностороннего треугольника АВС продолжены, как показано на рисунке 94, на равные отрезки AD, СЕ, BF. Докажите, что треугольник DEF — равносторонний.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 168. В треугольнике ABC ∠A = 38°, ∠B = 110°, ∠C = 32°. На стороне АС отмечены точки D и Е так, что точка D лежит на отрезке АЕ, BD = DA, ВЕ = ЕС. Найдите угол DBE.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 169. На рисунке 95 OC = OD, ОВ = ОЕ. Докажите, что AB = EF. Объясните способ измерения ширины озера (отрезка АВ на рисунке 95), основанный на этой задаче.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 170. Докажите, что треугольники АВС и АХВХСХ равны, если АВ = АХВХ, ∠A = ∠AX, AD = AXDX, где AD и AXDX — биссектрисы треугольников.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 171. В треугольниках АВС и ADC стороны ВС и AD равны и пересекаются в точке О, ∠OAC = ∠OCA.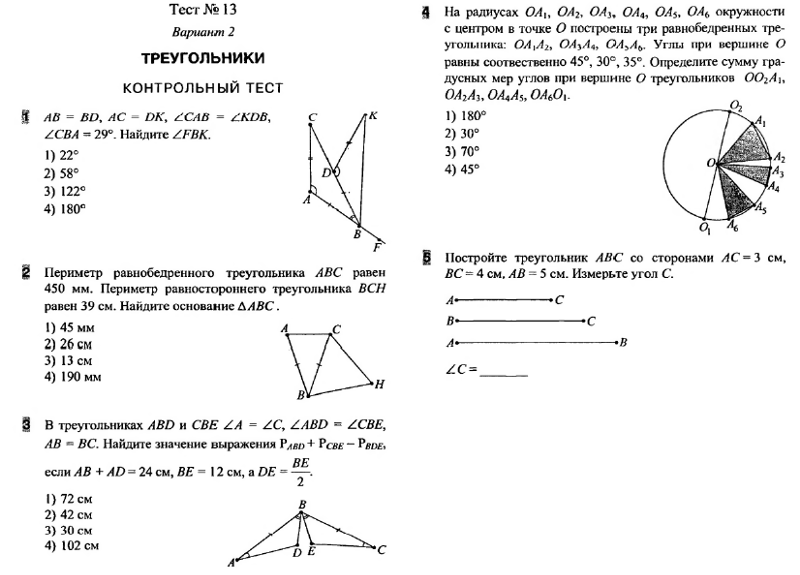 Докажите, что треугольники АВО и СDO равны.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 172. На рисунке 96 AC = AD, AB ⊥ CD. Докажите, что BC = BD и ∠ACB = ∠ADB.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 173. * Докажите, что угол, смежный с углом треугольника, больше каждого из двух других углов треугольника.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 174. * Докажите, что ΔАВС = ΔА₁В₁С₁, если ∠A = ∠A₁, ∠B = ∠B₁, ВС = В₁С₁.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 175. * На сторонах угла XOY отмечены точки А, В, С и D так, что ОА = ОВ, AC = BD (рис. 97). Прямые AD и ВС пересекаются в точке Е. Докажите, что луч ОЕ — биссектриса угла XOY. Опишите способ построения биссектрисы угла, основанный на этом факте.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 176. * Докажите, что треугольники АВС и А₁В₁С₁ равны, если АВ = А₁В₁, АС = А₁С₁, AM = А₁М₁, где AM и А₁М₁ — медианы треугольников.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 177. * Даны два треугольника: АВС и А₁В₁С₁. Известно, что АВ = А₁В₁, АС = А₁С₁, ∠A = ∠AX. На сторонах АС и ВС треугольника АВС взяты соответственно точки К и L, а на сторонах А₁С₁ и В₁С₁ треугольника А₁В₁С₁ — точки К₁ и L₁ так, что АК = А₁К₁, LC = L₁C₁. Докажите, что: a) KL = K₁L₁, б) AL = A₁L₁.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 178. * Даны три точки А, В, С, лежащие на одной прямой, и точка D, не лежащая на этой прямой. Докажите, что по крайней мере два из трёх отрезков AD, BD и CD не равны друг другу.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 179. * На боковых сторонах АВ и АС равнобедренного треугольника АВС отмечены точки Р и Q так, что ∠PXB = ∠QXC, где X — середина основания ВС. Докажите, что BQ = CP.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 180. Постройте окружность данного радиуса, проходящую через данную точку, с центром на данной прямой.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 181. Постройте окружность данного радиуса, проходящую через две данные точки.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 182. Даны прямая а, точки А, В и отрезок PQ. Постройте треугольник АВС так, чтобы вершина С лежала на прямой а и AC = PQ.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 183. Даны окружность, точки А, В и отрезок PQ. Постройте треугольник АВС так, чтобы вершина С лежала на данной окружности и AC = PQ.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 184. На стороне ВС треугольника АВС постройте точку, равноудалённую от вершин А и С.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

№ 185. С помощью циркуля и линейки разделите данный отрезок на четыре равные части.

Нажмите на спойлер, чтобы увидеть ОТВЕТ

 

---

 

◄ Задачи 143-155 ОГЛАВЛЕНИЕ учебника

Вы смотрели: Дополнительные задачи №№ 156-185 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями, а также вопросы для повторения к Главе II «ТРЕУГОЛЬНИКИ». Геометрия 7 Атанасян Задачи 156-185 + Ответы.

7 класс. Геометрия. Атанасян. Учебник. Ответы к стр. 66

Параллельные прямые

Аксиома параллельных прямых
Об аксиомах геометрии. Аксиома параллельных прямых. Теоремы об углах, образованных двумя параллельными прямыми и секущей. Углы с соответственно параллельными или перпендикулярным сторонами

Ответы к стр. 66

Задачи

208. Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50°. Найдите эти углы.

Д а н о
α||b
c — секущая
∠1 — ∠2 = 50°

Н а й т и
∠1 — ?
∠2 — ?

Р е ш е н и е
Так как ∠1 и ∠2 — односторонние при α||b и секущей с, то ∠1 + ∠2 = 180°. ∠1 — ∠2 = 50° ⇒ ∠1 = 50° + ∠2. Тогда ∠1 + ∠2 = 50° + ∠2 + ∠2 = 180° или 2∠2 = 130° или ∠2 = 65°, а ∠1 = 50° + ∠2 = 50° + 65° = 115°.

О т в е т: ∠1 = 115°, ∠2 = 65°.

209. На рисунке 120 α||b, c||d, ∠4 = 45°. Найдите углы 1, 2 и 3.

Д а н о
α||b
c||d
∠4 = 45°

Н а й т и
∠1 — ?
∠2 — ?
∠3 — ?

Р е ш е н и е
∠4 и ∠2 — соответственные углы при α||b и секущей d, значит ∠4 = ∠2 = 45°. ∠3 и ∠4 — смежные, значит ∠3 + ∠4 = 180° ⇒ ∠3 = 180° — ∠4 = 180° — 45° = 135°. ∠1 и ∠3 — внутренние накрест лежащие углы при c||d и секущей α, значит ∠1 = ∠3 = 135°.

О т в е т: ∠1 = 135°, ∠2 = 45°, ∠3 = 135°.

210. Два тела Р₁ и Р₂ подвешены на концах нити, перекинутой через блоки А и В (рис. 121). Третье тело Р₃ подвешено на той же нити в точке С и уравновешивает тела Р₁ и Р₂. (При этом АР₁||BР₂||СР₃.) Докажите, что ∠ACB = ∠CAP₁ + ∠CBP₂.

Д а н о
Рисунок
АР₁||BР₂||СР₃

Д о к а з а т ь
∠ACB = ∠CAP₁ + ∠CBP₂

Д о к а з а т е л ь с и в о
Дополнительное построение: луч СD.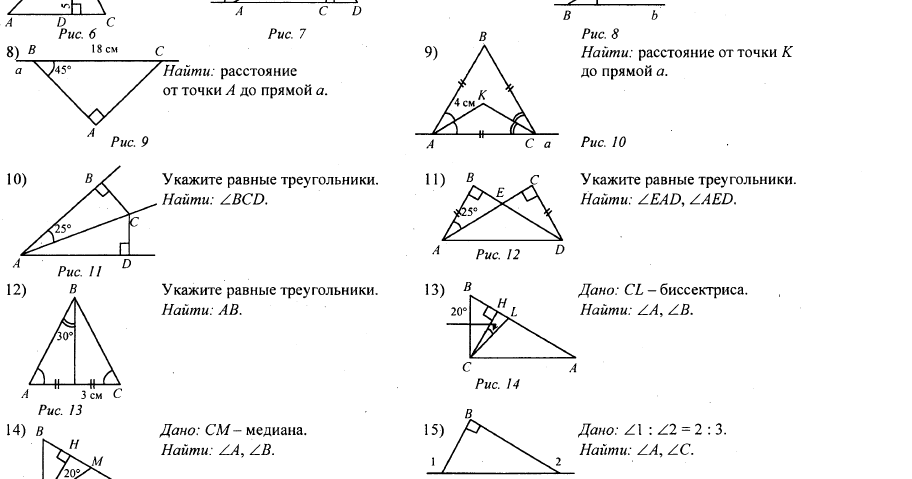 ∠ACB = ∠ACD + ∠DCB. ∠CAP₁ и ∠ACD — внутренние накрест лежащие углы при АР₁||СР₃ и секущей АС, значит ∠CAP₁ = ∠ACD. ∠CBP₂ и ∠DCB — внутренние накрест лежащие углы при СР3||ВР2 и секущей СВ, значит ∠CBP₂ = ∠DCB. Тогда ∠ACB = ∠ACD + ∠DCB = ∠CAP₁ + ∠CBP₂.

О т в е т: ∠ACB = ∠CAP₁ + ∠CBP₂.

211. Две параллельные прямые пересечены секущей. Докажите, что: а) биссектрисы накрест лежащих углов параллельны; б) биссектрисы односторонних углов перпендикулярны.

Д а н о
α||b
с — секущая

Д о к а з а т ь
а) KF||CL
б) KF⏊CK

Д о к а з а т е л ь с и в о
а) ∠ACF и ∠CFE — внутренние накрест лежащие углы при α||b и секущей c, значит ∠ACF = ∠CFE. ∠ACF = ∠1 + ∠2, ∠1 = ∠2, так как CL — биссектриса ∠ACF. ∠CFE = ∠3 + ∠4, ∠3 = ∠4, так как KF — биссектриса ∠CFE. Следовательно, ∠1 = ∠2 = ∠3 = ∠4. ∠3 и ∠1 — внутренние накрест лежащие углы при KF и CL и секущей CF, ∠3 = ∠1, значит KF||CL.

б) ∠ACF и ∠DFC — внутренние односторонние углы при α||b и секущей c, значит ∠ACF + ∠DFC = 180°. ∠ACF = ∠1 + ∠2, ∠1 = ∠2, так как CK — биссектриса ∠ACF. ∠DFC = ∠3 + ∠4, ∠3 = ∠4, так как KF — биссектриса ∠DFC. Рассмотрим ΔCFK: ∠KCF + ∠CFK + ∠FKC = ∠1 + ∠3 + ∠FKC = 180°. ∠1 + ∠3 = ¹/₂ ∠ACF + ¹/₂ ∠DFC = ¹/₂(∠ACF + ∠DFC) = ¹/₂•180° = 90°. Тогда ∠1 + ∠3 + ∠FKC = 90° + ∠FKC = 180° ⇒ ∠FKC = 180° — 90° = 90°. Так как ∠FKC = 90°, то KF⏊CK.

О т в е т: а) KF||CL, б) KF⏊CK

212. Прямые, содержащие высоты АА₁ и ВВ₁ треугольника АВС, пересекаются в точке Н, угол В — тупой, ∠С = 20°. Найдите угол АНВ.

Д а н о
ΔAВС
АА₁, ВВ₁ — высота
АА₁ ∩ ВВ₁ в т. Н
∠С = 20°
∠В — тупой

Н а й т и
∠АНВ

Р е ш е н и е
Рассмотри ΔВВ₁С: ∠ВВ₁С = 90°, так как ВВ₁ — высота к АС. Тогда ∠ВВ₁С + ∠В₁СВ + ∠СВВ₁ = 180° ⇒ ∠СВВ₁ = 180° — ∠ВВ₁С — ∠В₁СВ = 180° — 90° — 20° = 70°.
Рассмотрим ΔНВА₁: ∠НА₁В = 90°, так как АА₁ — высота к ВС. ∠НВА₁ = ∠СВВ₁ = 70° — так как вертикальные. ∠АНВ = А₁НВ. Тогда ∠НВА₁ + ∠ВА₁Н + ∠А₁НВ = 180° ⇒ ∠А₁НВ = 180° — ∠НВА₁ — ∠НА₁В = 180° — 70° — 90° = 20°.

О т в е т: ∠АНВ = 20°.

Вопросы для повторения к главе III

1. Дайте определение параллельных прямых. Какие два отрезка называются параллельными?

Две прямые на плоскости называются параллельными, если они не пересекаются. Два отрезка называются параллельными, если они лежат на параллельных прямых.

2. Что такое секущая по отношению к двум прямым? Назовите пары углов, которые образуются при пересечении двух прямых секущей.

Прямая с называется секущей по отношению к прямым α и b, если она пересекает их в двух точках.

Внутренние накрест лежащие углы: 3 и 6, 4 и 5 — попарно равны.
Внешние накрест лежащие углы: 1 и 8, 2 и 7 — попарно равны.
Внутренние односторонние углы: 4 и 6, 3 и 5 — их сумма 180°.
Внешние односторонние углы: 1 и 7, 2 и 8 — их сумма 180°.
Соответственные углы: 1 и 5, 2 и 6, 3 и 7, 4 и 8 — попарно равны.

3. Докажите, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Д а н о
с ∩ α, с ∩ b
∠1 = ∠2

Д о к а з а т ь
α||b

Д о к а з а т е л ь с и в о
Из середины О отрезка АВ проведём перпендикуляр ОН к прямой α. На прямой b от точки В отложим отрезок ВН₁, равный отрезку АН и проведём отрезок ОН₁. Треугольники ОНА и ОН₁В равны по двум сторонам и углу между ними (АО = ВО, АН = ВН₁, ∠1 = ∠2), поэтому ∠3 = ∠4 и ∠5 = ∠6. Из равенства ∠3 = ∠4 следует, что точка Н₁ лежит на продолжении луча ОН, то есть точки Н, О и Н₁ лежат на одной прямой, а из равенства ∠5 = ∠6 следует, что угол 6 — прямой (так как угол 5 — прямой). Итак, прямые α и b перпендикулярны к прямой НН₁, поэтому они параллельны.

О т в е т: α||b.

4. Докажите, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Д а н о
с ∩ α, с ∩ b
∠1 = ∠2

Д о к а з а т ь
α||b

Д о к а з а т е л ь с и в о
Так как углы 2 и 3 — вертикальные, то ∠2 = ∠3. Из этих двух равенств следует, что ∠1 = ∠3. Но углы 1 и 3 — накрест лежащие, поэтому прямые α и b параллельны.

О т в е т: α||b.

5. Докажите, что если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Д а н о
с ∩ α, с ∩ b
∠1 + ∠4 = 180°

Д о к а з а т ь
α||b

Д о к а з а т е л ь с и в о
Так как углы 3 и 4 — смежные, то ∠3 + ∠4 = 180°. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые α и b параллельны.

О т в е т: α||b.

6. Расскажите о практических способах проведения параллельных прямых.

На практике параллельные прямые проводят с помощью: чертёжного угольника и линейки, рейсшины (в чертёжной практике), малки (две деревянные планки, скреплённые шарниром) при столярных работах.

7. Объясните, какие утверждения называются аксиомами. Приведите примеры аксиом.

Аксиомы — утверждения о свойствах геометрических фигур, принимаемые в качестве исходных положений, на основе которых доказываются далее теоремы и вообще строится вся геометрия.
Через любые две точки проходит прямая, и притом только одна.
На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.

8. Докажите, что через данную точку, не лежащую на данной прямой, проходит прямая, параллельная данной.

Утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом и само является аксиомой.

9. Сформулируйте аксиому параллельных прямых.

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

10. Какое утверждение называется следствием? Докажите, что прямая, пересекающая одну из двух параллельных прямых, пересекает и другую.

Следствия — утверждения, которые выводятся непосредственно из аксиом или теорем.

Пусть прямые α и b параллельны и прямая с пересекает прямую α в точке М. Если бы прямая с не пересекала прямую b, то через точку М проходили бы две прямые (прямые α и с), параллельные прямой b. Но это противоречит аксиоме параллельных прямых, и, значит, прямая с пересекает прямую b.

ГДЗ. Ответы по геометрии. 7 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.

Геометрия. 7 класс

Ежедневные задания по геометрии — BMA Math with Viv

Ċ

Chapter 12 Assignments.pdf Просмотреть Скачать

409к

т. 2

7 мая 2015 г. , 5:19

[email protected]

Ċ

Геометрия Гл. 12 Review.pdf Посмотреть Скачать

989к

т. 2

345к

т. 2

360к

т. 2

org

Ċ

Геометрия Гл. 11 Review.pdf Посмотреть Скачать

1022к

т. 2

351к

т. 2

14 апр. 2015 г., 4:23

[email protected]

	Ċ	круговые отношения summary.pdf Посмотреть Скачать		345к	т. 2	26 марта 2015 г., 14:10	[email protected]
	Ċ	Geom Ch 10 Notes and Practice. pdf Посмотреть Скачать		369к	т. 2	16 февраля 2015 г., 16:42	[email protected]
	Ċ	Геометрия Гл. 10 практических тестов. Ответы.pdf Просмотреть Скачать		386к	т. 2	16 февраля 2015 г., 16:42	[email protected]
	Ċ	Геометрия Гл. 10 Обзор Ответы.pdf Посмотреть Скачать		т. 2	16 февраля 2015 г., 16:42	[email protected]

	Ċ	Geom Ch 8 Notes and Practice.pdf Посмотреть Скачать		т. 2	16 февраля 2015 г., 16:43	[email protected]
	Ċ	Геометрия Гл. 8 Практический тест Ответы.pdf Посмотреть Скачать		461к	т. 2	16 февраля 2015 г., 16:43	[email protected]
	Ċ	Геометрия Гл. 8 Обзор Ответы.pdf Посмотреть Скачать		934k	т. 2	16 февраля 2015 г., 16:43	[email protected]

	Ċ	Geom Ch 7 Notes and Practice.pdf Посмотреть Скачать		362к	т. 3	16 февраля 2015 г. , 16:37	[email protected]
	Ċ	Геометрия Гл. 7 Практический тест.pdf Посмотреть Скачать		403к	т. 3	16 февраля 2015 г., 16:37	[email protected]
	Ċ	Геометрия Гл. 7 Review.pdf Посмотреть Скачать		т. 3	16 февраля 2015 г., 16:37	[email protected]

	Ċ	Geom Ch 6 Notes and Practice.pdf Посмотреть Скачать		365к	т. 3	16 февраля 2015 г., 16:37	vbuckley@burkemtnacademy. org
	Ċ	Геометрия Глава 6 Обзор Ответы.pdf Посмотреть Скачать		948к	т. 3	16 февраля 2015 г., 16:37	[email protected]
	Ċ	Geometry Chapter 6 Test Answers.pdf Посмотреть Скачать		439к	т. 3	16 февраля 2015 г., 16:37	[email protected]

	Ċ	Geom Ch 5 Notes and Practice.pdf Посмотреть Скачать		367k	т. 3	16 февраля 2015 г., 16:36	[email protected]
	–	Геом Ч. 5 Ортоцентр треугольника Вид				16 февраля 2015 г., 16:36	[email protected]
	Ċ	Геом Ч. 5 Обзор ответов.pdf Посмотреть Скачать		831к	т. 3	16 февраля 2015 г., 16:36	[email protected]
	Ċ	Геом. Ч. 5 Test Answers.pdf Посмотреть Скачать		437к	т. 3	16 февраля 2015 г., 16:36	[email protected]

	Ċ	Геом Ч. 4 дополнительных практических ответа.pdf Посмотреть Скачать		349k	т. 3	16 февраля 2015 г., 16:36	[email protected]
	Ċ	Geom Ch 4 Notes and Practice.pdf Посмотреть Скачать		307к	т. 3	16 февраля 2015 г., 16:36	[email protected]

	Ċ	Геом Ч. 3 Book Test Answers.pdf Посмотреть Скачать		353k	т. 3	16 февраля 2015 г., 16:35	[email protected]
	Ċ	Геом Ч. 3 дополнительных практических ответа.pdf Просмотреть Скачать		200к	т. 3	16 февраля 2015 г. , 16:35	[email protected]
	Ċ	Geom Ch 3 Notes and Practice.pdf Посмотреть Скачать		275к	т. 3	16 февраля 2015 г., 16:35	[email protected]
	Ċ	Геом Ч. 3 Обзор Ответы.pdf Посмотреть Скачать		845к	т. 3	16 февраля 2015 г., 16:35	[email protected]

	Э	2.3_practice_on_lodetachment_and_losyllogism.doc Посмотреть Скачать		28к	т. 3	16 февраля 2015 г., 16:34	vbuckley@burkemtnacademy. org
	–	Построение биссектрисы угла на Geogebra Вид				16 февраля 2015 г., 16:34	[email protected]
	Ċ	Геом Ч. 2 Book Test Answers.pdf Посмотреть Скачать		397k	т. 4	16 февраля 2015 г., 16:34	[email protected]
	Ċ	Геом Ч. 2 дополнительных практических ответа.pdf Просмотреть Скачать		214k	т. 4	16 февраля 2015 г., 16:34	[email protected]
	Ċ	Geom Ch 2 Notes and Practice. pdf Посмотреть Скачать		274k	т. 3	16 февраля 2015 г., 16:34	[email protected]
	Ċ	Геом Ч. 2 Обзор Ответы.pdf Посмотреть Скачать		855к	т. 4	16 февраля 2015 г., 16:35	[email protected]
	Ċ	законы логики WS.pdf Посмотреть Скачать		«> 89k	т. 3	16 февраля 2015 г., 16:34	[email protected]

	Ċ	Геом Ч. 1 Book Test Answers.pdf Посмотреть Скачать		367k	т. 3	16 февраля 2015 г., 16:33	[email protected]
	Ċ	Геом Ч. 1 Extra Practice Answers.pdf Посмотреть Скачать		168к	т. 3	16 февраля 2015 г., 16:33	[email protected]
	Ċ	Геом Ч. 1 Обзор Answers.pdf Посмотреть Скачать		930k	т. 3	16 февраля 2015 г., 16:33	[email protected]

	Ċ	First Day Response.pdf Посмотреть Скачать		108к	т. 3	16 февраля 2015 г. , 16:33	[email protected]
	Ċ	Geometry First Week.pdf Посмотреть Скачать		296k	т. 3	16 февраля 2015 г., 16:33	[email protected]

Giaramita, Dorothy / Honors Geometry Calendar

7/23 Домашнее задание: обзор Syllabus Online и Sign и верните зеленую форму

Summer Packet 1-28

9

555.

Приведенные ниже заметки в PowerPoint полезны учащимся для повторения понятий по алгебре 1 при подготовке к Летнему тесту понятий на следующей неделе.

Добавление и вычитание радикалов, разделяющих радикалы, решающие системы с использованием элиминационных факторинг из GCF

Факторинг специальных случаев, факторинг, когда A = 1 факторинг, когда A не = 1 Умножающие экспоненты Умножающие полиномы

.

Решение систем с использованием исключения    Решение систем с использованием подстановки, часть 1    Решение систем с использованием подстановки, часть 2

  

            HW: Летний пакет 48-55 и стартовый рабочий лист 1.1 1,2, 5, 6a, 7, 8, 9ab

                  12,14)

7/25             HW: Summer packet 56-64 and finish 1.1 worksheet  

7/26             Quiz on 1.1   HW: Summer packet 29-47

                   

                                         

7/29             HW: Study

7 /30–7/31  Летний тест понятий   HW: 1,2 ws

8/1 HW: 1,3 WS

8/2 HW: 1,4 WS

8/5 HW: 1,5 WS

8/6-8/7

Quiz 1.1-1.5 90

5555555555555 года. /8 HW: 1,7 и 1,8

8/9 HW: 1,9

8/13

2,1 Примечания

8/14 2,2 Примечания

8/15-15.16666666666666666666666666666666666666666666666666666666666666666666666666666.

Пн.: 2,1 н.с. и 2,2 н.с.

8/19 HW: 2,3 и 2,4

8/20-8/21 HW: 2,5 WS и 2,6 WS

8/22 HW: 2,7 WS

5 8/23 Глава 2 Группа 2 Группа HW: 2,7 WS

55555555555. 2.8 WS

8/26 Обзор

8/27-8/28 Обзор CH 3 HW: Due On Fri. 3.1ws (или стр. 114 1,2,3,4abc,5ab на миллиметровой бумаге)

8/29              Глава 2 тест

8.

9/9 HW: 3,6 WS

9/10 HW: 3,7 WS

9/11 HW: 3,8 WS

9/12-9/13 CH 3 Quiz и CH 3 Обзор

55555559/13 CH 3 и CH 3 Обзор

9 0002

5555559/13 CH 3 и CH 3. 16                Обзор

9/17-9/18     Тест по главе 3  HW: срок выполнения в четверг. 4.1 WS

9/19 HW: 4,3 WS

9/20 HW: 4,4 WS

9/23 HW: 4,5 WS и 4,6 WS

9/24-9/25 4,2 В.

9/26 Обзор

9/27 CH 4 Тест

Печать: Глава 5 Домашнее задание 5.

1 5,2 5,3 5,4 5,5 5,6 5,7

10/15-10/16 HW: 5,1 Вт.0856

10/17                5.3

10/18                5.4

 

10/21                5.5

10/22-10/23    Chapter 5 Quiz    HW:5.6 ws 

10/24                5.7

10/25                Review

10/28          Review Ch 5 and start 6.1 notes

10/29-10/30  Chapter 5 Test    HW: 6.1 ws

10/31                HW: No homework

11/1         6.2 ws

 

 

11/ 4                6,3

11/5-11/6 Глава 6 Викторина 7.1

11/7 7.2

11/8 7.3

11/12-11/13 7.4 и начало обзора

11/14. /15            

Тест по главе 7

 

 

18/11 

 

18/11        Большие идеи (Clever.com) Глава 4 Преобразования

                    4.1 Translations   HW: 4.1 ws

11/19         4.

2 Reflections     HW: 4.2 ws

11/20         4.3 Rotations       HW: 4.3 ws

11/21-11/22  Review 4.1-4.3 and   Quiz 4.1-4.3 

11/25    4.4 Congruence and Transformations HW: 4.4 ws 

11/26  4.5 Dilations HW:4.5 ws

 

   

 

12/2   Review    

12/3-12/4    Transformations Test

12 /5           Уравнения параллельных и перпендикулярных прямых ws  

12/6 Pythagorean Theoorem WS

12/9 Flex Final Review WS

12/10-12/11 Quiz

12/12 О. О НАВОЧЕРЕНИЕ WS 1-21

12/13. 1

. 4,6

 

3-й квартал

1/7-1/8    HW: 8.1 Часть 1, статьи 1–8 и 8.1 Часть 2, статьи 1–8 

(или стр. 329 4bc, 7,8,9,11,12, 13,15 и стр. 330 14AB, 18,20,21,22ABC, 24,25,26)

1/9 HW: 8,2 WS

1/10 HW: 8,3 WS Skip 3

1/13 8,4 ws

14/1/15   Тест 8.

1–8.4 и  HW: 8.5

16 1         Обзор теста

17/1         Глава 8 Тест   

4 9 00064

           Print: Trig Homework (9.9,9.10, Law of Sines, Law of Cosines, Mixed Trig Applications)

 

 

1/21-1/22   9.1 and  9.2

1/23    9.3

1/24  9.4

1/27 9,5

1/28-1/29 9,6 и обзор викторины 9.1-9,5

1/30 9,7 HW: 9,7 Часть 1

1/31 QUIZ на 9.1-9,5 HW: 9,7 HW: 9.7. 2

 

2/3          9,8

2/4–2/5   Обзор 

2/6 9.7a WS

2/7 Тест на 9.1-9.8

2/10 9,9 и 9,10

2/11-12 9,9 и 9.10

2/13/11-19.9 и 9.10

2/1355 2/1355 2/1355 2/1355 2/1355 2/1355 2/13556 2/13/12/12 9,9 и 9.10

2/1355 2/13/11. 2/14 Закон косинусов

2/18-2/19 Смешанные приложения и обзор

2/20 Обзор

2/21 Тест тригея (9,9, 9.10, Закон о сини, Закон о косиенях.

и смешанные триггерные приложения)

 

24/2        10.1 и  10.9

              HW: 10.1 ws 1,2,4,5 (или стр. 443 5,8,14,17abc)

              и 10.9 ws 1-6 (или стр. 501 2abc, 3abc, 5ab, 6ab, 6bc, 6bc

2/25 10,2 и 10,3

HW: 10,2 WS 1,2,4-6 (или Page 448 6,7AB, 11,12,13) ​​

и 10,3 WS 4-8,11 (или страница 454 9ABCD , 10abc, 11,12,13ab, 19ab)

2/26         10,4 ws 1-5, 7-9 (или стр. 464 5,10-13, 16,17,19)

27-2/28 10.5 и 10.6 примечания HW: секущие углы ws 1-18 и Sec-Tan Tan-Tan ws 1-16

3/2 10,7 и 10,8 Примечания. 8-12,15-16

10,7 1-5,8,10 Стр. 489 3,5,7,9.10,15,17

10,8 1-9 Стр. 495 3-13

Домашнее задание: пересмотр 1-10

3/6 ГЛАВА 10 Тест

4-й квартал

3/24-3/25 11,1 и 11.2

3/2/24-3/25 11,1 и 11.2

3/266.198956 2

5918 9.198955918 9.

3/24-3/25 11,1 и 11.

2

3/266/2 24-3/25 11,1 и 11.2

9008 3/2669 298.

3/24-3/25 11,1 и 11.2

9008 3/2669 298.

. 3/30-3/31 11,5

4/1-4/2 11,6

4/3 11,7

4/6 11,8

4/7-4/8 Обзор

4/9 Глава 11 Тесто.

 

 

4/13        12.1

4/14     12.2 

4/15     12.3

4/16-4/17   12.4

 

4/20       12.5 and 12.6 

4/21-4/22  Review 

4/23 ГЛАВА 12 Тест

4/24 13.1

4/27 13,2

4/28-4/29 13,3

4/30 13.4

9

555556

4/30. 5/4    Обзор главы 13 

5/5–5/6   Глава 13 тест

5/7 Большие идеи (Clever.com) 12.1 и 12.2

5/8 BI 12.3

5/11 BI 12.4

5/12-5/13 BI 12.5 и обзор

55555/14/13 BI

.

21-5/22     Повторение итогового экзамена

5/26 Обзор для окончательного экзамена

.

Ключ к ответу Глава 1 — Предварительный расчет

1 Попытайся

1.1 Функции и обозначения функций

1.

1. ⓐ да
2. ⓑ да. (Примечание: если бы два игрока разделили, скажем, 4-е место, то имя не зависело бы от ранга.)

2.

w=f(d)w=f(d)

3.

да

4.

г(5)=1г(5)=1

5.

м=8м=8

6.

y=f(x)=x32y=f(x)=x32

7.

г(1)=8г(1)=8

8.

х=0х=0 или х=2х=2

9.

1. ⓐ да, поскольку на каждом банковском счете в любой момент времени имеется только один остаток
2. ⓑ нет, т. к. баланс на нескольких банковских счетах может быть одинаковым
3. ⓒ нет, так как одному и тому же выходу может соответствовать более одного входа.

10.

1. ⓐ Да, буквенная оценка зависит от процентной оценки;
2. ⓑ Нет, не один к одному. Мы можем получить 100 различных процентных чисел, но только около пяти возможных буквенных оценок, поэтому не может быть только одного процентного числа, соответствующего каждой буквенной оценке.

11.

да

12.

Нет, потому что он не проходит тест горизонтальной линии.

1,2 Домен и диапазон

1.

{−5,0,5,10,15}{−5,0,5,10,15}

2.

(−∞,∞)(−∞,∞)

3.

(-∞,12)∪(12,∞)(-∞,12)∪(12,∞)

4.

[−52,∞)[−52,∞)

5.

1. ⓐ значения меньше или равные –2, или значения больше или равные –1 и меньше 3;
2. ⓑ {x|x≤−2or−1≤x<3}{x|x≤−2or−1≤x<3} ;
3. ⓒ (−∞,−2]∪[−1,3)(−∞,−2]∪[−1,3)

6.

домен = [1950,2002] диапазон = [47,000,000,89,000,000]

7.

домен: (-∞,2];(-∞,2]; диапазон: (-∞,0](-∞,0]

8.

1,3 Скорость изменения и поведение графиков

1.

2,84 доллара – 2,315 доллара лет = 0,535 доллара года = 0,106 доллара 2,84 – 2,315 доллара года = 0,535 доллара года = 0,106 доллара США в год.

2.

1212

3.

а+7а+7

4.

Локальный максимум приходится на (−1,28),(−1,28), а локальный минимум приходится на (5,−80).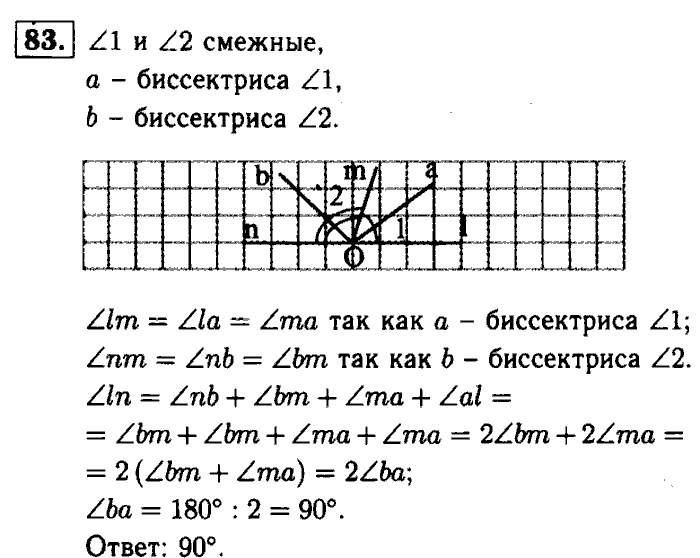 (5,−80). Функция возрастает на (−∞,−1)∪(5,∞)(−∞,−1)∪(5,∞) и убывает на (−1,5).(−1,5).

1,4 Состав функций

1.

(fg)(x)=f(x)g(x)=(x−1)(x2−1)=x3−x2−x+1(f−g)(x)=f(x)− g(x)=(x−1)−(x2−1)=x−x2(fg)(x)=f(x)g(x)=(x−1)(x2−1)=x3−x2 −x+1(f−g)(x)=f(x)−g(x)=(x−1)−(x2−1)=x−x2

Нет, функции разные.

2.

Гравитационная сила все еще является силой, поэтому a(G(r))a(G(r)) имеет смысл как ускорение планеты на расстоянии r от Солнца (из-за гравитации), но G (a(F))G(a(F)) не имеет смысла.

3.

f(g(1))=f(3)=3f(g(1))=f(3)=3 и g(f(4))=g(1)=3g(f(4)) =g(1)=3

4.

г(ж(2))=г(5)=3г(ж(2))=г(5)=3

5.

1. ⓐ 8
2. ⓑ 20

6.

[−4,0)∪(0,∞)[−4,0)∪(0,∞)

7.

Возможный ответ:

g(x)=4+x2g(x)=4+x2
h(x)=43−xh(x)=43−x
f=h∘gf=h∘g

1,5 Преобразование функций

1.

b(t)=h(t)+10=−4,9t2+30t+10b(t)=h(t)+10=−4,9t2+30t+10

2.

Графики f(x)f(x) и g(x)g(x) показаны ниже. Преобразование представляет собой горизонтальный сдвиг. Функция смещена влево на 2 единицы.

3.

4.

г(х)=1х-1+1г(х)=1х-1+1

5.

6.

1. ⓐ

   г(х)=-f(х)г(х)=-f(х)

   хх	-2	0	2	4
   г(х)г(х)	−5−5	−10−10	−15−15	−20−20

2. ⓑ

   ч(х)=f(-х)ч(х)=f(-х)

   хх	-2	0	2	4
   ч(х)ч(х)	15	10	5	неизвестно

7.

Примечание: g(x)=f(−x)g(x)=f(−x) выглядит так же, как f(x)f(x).

8.

даже

9.

хх	2	4	6	8
г(х)г(х)	9	12	15	0

10.

г(х)=3х-2г(х)=3х-2

11.

g(x)=f(13x)g(x)=f(13x) поэтому, используя функцию квадратного корня, мы получаем g(x)=13xg(x)=13x

1,6 Функции абсолютного значения

1.

|x−2|≤3|x−2|≤3

2.

с использованием переменной pp для прохождения, |p−80|≤20|p−80|≤20

3.

f(x)=−|x+2|+3f(x)=−|x+2|+3

4.

х=-1х=-1 или х=2х=2

5.

f(0)=1,f(0)=1, поэтому график пересекает вертикальную ось в точке (0,1).(0,1).f(x)=0f(x)=0, когда x= −5x=−5 и x=1x=1, поэтому график пересекает горизонтальную ось в точках (−5,0)(−5,0) и (1,0).(1,0).

6.

-8≤x≤4-8≤x≤4

7.

k≤1k≤1 или k≥7;k≥7; в интервальной записи это будет (−∞,1]∪[7,∞)(−∞,1]∪[7,∞)

1,7 Обратные функции

1.

ч(2)=6ч(2)=6

3.

Да

4.

Область определения функции f−1f−1 равна (−∞,−2)(−∞,−2), а область значений функции f−1f−1 равна (1,∞). (1,∞).

5.

1. f(60)=50.f(60)=50. За 60 минут пройдено 50 миль.
2. f−1(60)=70.f−1(60)=70. Чтобы проехать 60 миль, потребуется 70 минут.

6.

а. 3; б. 5.6

7.

х=3у+5х=3у+5

8.

f−1(x)=(2−x)2;без домена:[0,∞);без домена−1:(−∞,2]f−1(x)=(2−x)2;без домена: [0,∞);domainoff−1:(−∞,2]

9.

1.1 Секционные упражнения

1.

Отношение представляет собой набор упорядоченных пар. Функция — это особый вид отношения, в котором никакие две упорядоченные пары не имеют одинаковых первых координат.

3.

Когда вертикальная линия пересекает график отношения более одного раза, это означает, что для данного входа существует более одного выхода. При любом конкретном входном значении может быть только один выход, если отношение должно быть функцией.

5.

Когда горизонтальная линия пересекает график функции более одного раза, это означает, что для данного выхода имеется более одного входа. Функция является однозначной, если каждый выход соответствует только одному входу.

7.

функция

9.

функция

11.

функция

13.

функция

15.

функция

17.

функция

19.

функция

21.

функция

23.

функция

25.

не функция

27.

f(−3)=−11;f(−3)=−11;
f(2)=−1;f(2)=−1;
f(-a)=-2a-5;f(-a)=-2a-5;
-f(а)=-2а+5;-f(а)=-2а+5;
f(a+h)=2a+2h−5f(a+h)=2a+2h−5

29.

f(−3)=5+5;f(−3)=5+5;
f(2)=5;f(2)=5;
f(-a)=2+a+5;f(-a)=2+a+5;
-f(a)=-2-a-5;-f(a)=-2-a-5;
f(a+h)=2−a−h+5f(a+h)=2−a−h+5

31.

f(−3)=2;f(−3)=2;f(2)=1−3=−2;f(2)=1−3=−2;
f(−a)=|−a−1|−|−a+1|;f(−a)=|−a−1|−|−a+1|;
-f(a)=-|a-1|+|a+1|;-f(a)=-|a-1|+|a+1|;
f(a+h)=|a+h−1|−|a+h+1|f(a+h)=|a+h−1|−|a+h+1|

33.

g(x)−g(a)x−a=x+a+2,x≠ag(x)−g(a)x−a=x+a+2,x≠a

35.

1. ⓐ f(−2)=14;f(−2)=14;
2. ⓑ х=3х=3

37.

1. ⓐ f(5)=10;f(5)=10;
2. ⓑ х=-1х=-1 или х=4х=4

39.

1. ⓐ f(t)=6−23t;f(t)=6−23t;
2. ⓑ f(−3)=8;f(−3)=8;
3. ⓒ т=6т=6

41.

не функция

43.

функция

45.

функция

47.

функция

49.

функция

51.

функция

53.

1. ⓐ f(0)=1;f(0)=1;
2. ⓑ f(x)=−3,x=−2f(x)=−3,x=−2 или x=2x=2

55.

не является функцией, поэтому это также не функция «один к одному»

57.

Функция «один к одному»

59.

функция, но не один к одному

61.

функция

63.

функция

65.

не функция

67.

f(x)=1,x=2f(x)=1,x=2

69.

f(-2)=14;f(-1)=11;f(0)=8;f(1)=5;f(2)=2f(-2)=14;f(-1) =11;f(0)=8;f(1)=5;f(2)=2

71.

f(−2)=4; f(-1)=4,414;f(0)=4,732;f(1)=5;f(2)=5,236f(-2)=4; f(−1)=4,414;f(0)=4,732;f(1)=5;f(2)=5,236

73.

f(−2)=19;f(−1)=13;f(0)=1;f(1)=3;f(2)=9f(−2)=19;f(−1) =13;f(0)=1;f(1)=3;f(2)=9

75.

20

77.

[0, 100][0, 100]

79.

[−0,001, 0,001][−0,001, 0,001]

81.

[−1 000 000, 1 000 000][–1 000 000, 1 000 000]

83.

[0, 10][0, 10]

85.

[−0,1,0,1][−0,1,0,1]

87.

[−100, 100][−100, 100]

89.

1. ⓐ г(5000)=50;г(5000)=50;
2. ⓑ Количество кубических ярдов земли, необходимое для сада площадью 100 квадратных футов, равно 1.

91.

1. ⓐ Высота ракеты над землей через 1 секунду составляет 200 футов.
2. ⓑ высота ракеты над землей через 2 секунды составляет 350 футов.

1.2 Секционные упражнения

1.

Область определения функции зависит от того, какие значения независимой переменной делают функцию неопределенной или мнимой.

3.

Нет ограничений на xx для f(x)=x3f(x)=x3, потому что вы можете извлечь кубический корень из любого действительного числа. Таким образом, областью определения являются все действительные числа (−∞,∞).(−∞,∞). Имея дело с набором действительных чисел, вы не можете извлечь квадратный корень из отрицательных чисел. Таким образом, значения xx ограничены для f(x)=xf(x)=x неотрицательными числами, а домен равен [0,∞).[0,∞).

5.

Нарисуйте график каждой формулы кусочной функции в соответствующей области. Используйте один и тот же масштаб для осей xx и yy для каждого графика. Укажите инклюзивные конечные точки сплошным кружком, а исключительные конечные точки — незаштрихованным кружком. Используйте стрелку, чтобы указать −∞−∞ или ∞.∞. Объедините графики, чтобы найти график кусочной функции.

7.

(−∞,∞)(−∞,∞)

9.

(-∞,3](-∞,3]

11.

(-∞,∞)(-∞,∞)

13.

(-∞,∞)(-∞,∞)

15.

(-∞,-12)∪(-12,∞)(-∞,-12)∪(-12,∞)

17.

(-∞,-11)∪(-11,2)∪(2,∞)(-∞,-11)∪(-11,2)∪(2,∞)

19.

(-∞,-3)∪(-3,5)∪(5,∞)(-∞,-3)∪(-3,5)∪(5,∞)

21.

(-∞,5)(-∞,5)

23.

[6,∞)[6,∞)

25.

(-∞,-9)∪(-9,9)∪(9,∞)(-∞,-9)∪(-9,9)∪(9,∞)

27.

домен: (2,8],(2,8), диапазон [6,8)[6,8)

29.

домен: [−4, 4],[−4, 4], диапазон: [0, 2][0, 2]

31.

домен: [-5,3),[-5,3), диапазон: [0,2][0,2]

33.

домен: (−∞,1],(−∞,1], диапазон: [0,∞)[0,∞)

35.

домен: [−6,−16]∪[16,6];[−6,−16]∪[16,6]; диапазон: [−6,−16]∪[16,6][−6,−16]∪[16,6]

37.

домен: [−3,∞);[−3,∞); диапазон: [0,∞)[0,∞)

39.

домен: (−∞,∞)(−∞,∞)

41.

домен: (−∞,∞)(−∞,∞)

43.

домен: (−∞,∞)(−∞,∞)

45.

домен: (−∞,∞)(−∞,∞)

47.

f(−3)=1;f(−2)=0;f(−1)=0;f(0)=0f(−3)=1;f(−2)=0;f(− 1)=0;f(0)=0

49.

f(-1)=-4;f(0)=6;f(2)=20;f(4)=34f(-1)=-4;f(0)=6;f(2) =20;f(4)=34

51.

f(-1)=-5;f(0)=3;f(2)=3;f(4)=16f(-1)=-5;f(0)=3;f(2) =3;f(4)=16

53.

домен: (−∞,1)∪(1,∞)(−∞,1)∪(1,∞)

55.

окно: [-0,5,-0,1];[-0,5,-0,1]; диапазон: [4100][4100]

окно: [0.1,0.5];[0.1,0.5]; диапазон: [4100][4100]

57.

[0,8][0,8]

59.

Много ответов. Одна функция: f(x)=1x−2.f(x)=1x−2.

1.3 Секционные упражнения

1.

Да, средняя скорость изменения всех линейных функций постоянна.

3.

Абсолютный максимум и минимум относятся ко всему графику, тогда как локальные экстремумы относятся только к определенной области вокруг открытого интервала.

5.

4(б+1)4(б+1)

9.

4x+2h5x+2h

11.

−113(13+ч)−113(13+ч)

13.

3ч3+9ч+93ч3+9ч+9

15.

4х+2ч-34х+2ч-3

17.

4343

19.

возрастание на (−∞,−2,5)∪(1,∞),(−∞,−2,5)∪(1,∞), уменьшение на (−2,5,1)(−2,5,1)

21.

возрастает по (−∞,1)∪(3,4),(−∞,1)∪(3,4), убывает по (1,3)∪(4,∞)(1,3)∪( 4,∞)

23.

локальный максимум: (−3,50),(−3,50), локальный минимум: (3,−50)(3,−50)

25.

абсолютный максимум приблизительно на уровне (7,150),(7,150), абсолютный минимум приблизительно на уровне (-7,5,-220)(-7,5,-220)

27.

а. –3000; б. –1250

29.

-4

31.

27

33.

–0,167

35.

Локальный минимум на (3,−22),(3,−22), убывающий на (−∞,3),(−∞,3), возрастающий на (3,∞)(3,∞)

37.

Локальный минимум на (−2,−2),(−2,−2), убывающий на (−3,−2),(−3,−2), возрастающий на (−2,∞)(−2 ,∞)

39.

Локальный максимум в точках (−0,5,6),(−0,5,6), локальные минимумы в точках (−3,25,−47)(−3,25,−47) и (2,1,−32),(2,1,−32) , убывающая на (−∞,−3,25)(−∞,−3,25) и (−0,5,2,1),(−0,5,2,1), возрастающая на (−3,25,−0,5)(−3,25,−0,5) и ( 2.1,∞)(2.1,∞)

43.

б=5б=5

45.

2,7 галлона в минуту

47.

примерно –0,6 миллиграмма в день

1.

4 Секционные упражнения

1.

Найдите числа, при которых функция в знаменателе gg равна нулю, и проверьте любые другие ограничения домена для ff и g,g, такие как корень с четным индексом или нули в знаменателе.

3.

Да. Пример ответа: пусть f(x)=x+1 и g(x)=x-1.f(x)=x+1 и g(x)=x-1. Тогда f(g(x))=f(x−1)=(x−1)+1=xf(g(x))=f(x−1)=(x−1)+1=x и g (f(x))=g(x+1)=(x+1)−1=x.g(f(x))=g(x+1)=(x+1)−1=x. Итак, f∘g=g∘f.f∘g=g∘f.

5.

(f+g)(x)=2x+6,(f+g)(x)=2x+6, домен: (−∞,∞)(−∞,∞)

(f−g)( x)=2×2+2x−6,(f−g)(x)=2×2+2x−6, домен: (−∞,∞)(−∞,∞)

(fg)(x)=−x4− 2×3+6×2+12x,(fg)(x)=-x4-2×3+6×2+12x, домен: (-∞,∞)(-∞,∞)

(fg)(x)=x2+2×6-x2 ,(fg)(x)=x2+2×6−x2, область определения: (−∞,−6)∪(−6,6)∪(6,∞)(−∞,−6)∪(−6,6) ∪(6,∞)

7.

(f+g)(x)=4×3+8×2+12x,(f+g)(x)=4×3+8×2+12x, домен: (−∞,0)∪(0,∞)(−∞, 0)∪(0,∞)

(f−g)(x)=4×3+8×2−12x,(f−g)(x)=4×3+8×2−12x, область определения: (−∞,0)∪( 0,∞)(−∞,0)∪(0,∞)

(fg)(x)=x+2,(fg)(x)=x+2, домен: (−∞,0)∪(0,∞)(−∞,0)∪(0,∞)

(fg)(x)=4×3+8×2,(fg)(x)=4×3+8×2, домен: (−∞,0)∪(0,∞)(−∞,0)∪(0,∞)

9.

(f+g)(x)=3×2+x−5,(f+g)(x)=3×2+x−5, домен: [5,∞)[5,∞)

(f−g )(x)=3×2−x−5,(f−g)(x)=3×2−x−5, домен: [5,∞)[5,∞)

(fg)(x)=3x2x−5 ,(fg)(x)=3x2x−5, домен: [5,∞)[5,∞)

(fg)(x)=3x2x−5,(fg)(x)=3x2x−5, домен: (5,∞)(5,∞)

11.

1. ⓐ 3
2. ⓑ f(g(x))=2(3x−5)2+1;f(g(x))=2(3x−5)2+1;
3. ⓒ g(f)(x))=6×2−2;g(f)(x))=6×2−2;
4. ⓓ (g∘g)(x)=3(3x−5)−5=9x−20;(g∘g)(x)=3(3x−5)−5=9x−20;
5. ⓔ (f∘f)(−2)=163(f∘f)(−2)=163

13.

f(g(x))=x2+3+2,g(f(x))=x+4x+7f(g(x))=x2+3+2,g(f(x))= х+4х+7

15.

f(g(x))=x+1×33=x+13x,g(f(x))=x3+1xf(g(x))=x+1×33=x+13x,g(f(x) )=x3+1x

17.

(f∘g)(x)=12x+4−4=x2,(g∘f)(x)=2x−4(f∘g)(x)=12x+4−4=x2,(g ∘f)(x)=2x−4

19.

f(g(h(x)))=(1x+3)2+1f(g(h(x)))=(1x+3)2+1

21.

• ⓐ Текст (g∘f)(x)=−32−4x;(g∘f)(x)=−32−4x;
• ⓑ(−∞,12)(−∞,12)

23.

1. ⓐ (0,2)∪(2,∞);(0,2)∪(2,∞);
2. ⓑ (−∞,−2)∪(2,∞);(−∞,−2)∪(2,∞); в. (0,∞)(0,∞)

25.

(1,∞)(1,∞)

27.

образец: f(x)=x3g(x)=x−5f(x)=x3g(x)=x−5

29.

образец: f(x)=4xg(x)=(x+2)2f(x)=4xg(x)=(x+2)2

31.

образец: f(x)=x3g(x)=12x−3f(x)=x3g(x)=12x−3

33.

образец: f(x)=x4g(x)=3x−2x+5f(x)=x4g(x)=3x−2x+5

35.

образец: f(x)=xf(x)=x
g(x)=2x+6g(x)=2x+6

37.

образец: f(x)=x3f(x)=x3
g(x)=(x−1)g(x)=(x−1)

39.

образец: f(x)=x3f(x)=x3
g(x)=1x−2g(x)=1x−2

41.

образец: f(x)=xf(x)=x
g(x)=2x−13x+4g(x)=2x−13x+4

67.

11

73.

f(g(0))=27,g(f(0))=-94f(g(0))=27,g(f(0))=-94

75.

f(g(0))=15,g(f(0))=5f(g(0))=15,g(f(0))=5

77.

18×2+60x+5118×2+60x+51

79.

г∘g(x)=9x+20g∘g(x)=9x+20

83.

(−∞,∞)(−∞,∞)

85.

Ложь

87.

(f∘g)(6)=6(f∘g)(6)=6; (g∘f)(6)=6(g∘f)(6)=6

89.

(f∘g)(11)=11,(g∘f)(11)=11(f∘g)(11)=11,(g∘f)(11)=11

93.

A(t)=π(25t+2)2A(t)=π(25t+2)2 и A(2)=π(254)2=2500πA(2)=π(254)2=2500π квадрат дюймов

95.

A(5)=π(2(5)+1)2=121πA(5)=π(2(5)+1)2=121π квадратных единиц

97.

• ⓐ N(T(t))=23(5t+1,5)2−56(5t+1,5)+1;N(T(t))=23(5t+1,5)2−56(5t+1,5) )+1;
• ⓑ 3,38 часа

1.5 Секционные упражнения

1.

Горизонтальный сдвиг возникает, когда константа добавляется или вычитается из входных данных. Вертикальные сдвиги возникают, когда константа добавляется к выходным данным или вычитается из них.

3.

Горизонтальное сжатие получается, когда константа больше 1 умножается на вход. Вертикальное сжатие получается, когда константа от 0 до 1 умножается на выход.

5.

Для функции f,f замените (-x)(-x) на (x)(x) в f(x).f(x). Упрощать. Если результирующая функция совпадает с исходной функцией f(−x)=f(x),f(−x)=f(x), то функция четная. Если результирующая функция противоположна исходной функции, f(-x)=-f(x),f(-x)=-f(x), то исходная функция нечетна. Если функция не та же самая или противоположная, то функция не является ни нечетной, ни четной.

7.

г(х)=|х-1|-3г(х)=|х-1|-3

9.

г(х)=1(х+4)2+2г(х)=1(х+4)2+2

11.

График f(x+43)f(x+43) представляет собой горизонтальный сдвиг влево на 43 единицы графика f.f.

13.

График f(x-4)f(x-4) представляет собой горизонтальный сдвиг вправо на 4 единицы графика f.f.

15.

График f(x)+8f(x)+8 представляет собой вертикальный сдвиг вверх на 8 единиц графика f.f.

17.

График f(x)−7f(x)−7 представляет собой вертикальный сдвиг вниз на 7 единиц графика f.f.

19.

График f(x+4)−1f(x+4)−1 представляет собой горизонтальный сдвиг влево на 4 единицы и вертикальный сдвиг вниз на 1 единицу графика f. f.

21.

убывающая на (−∞,−3)(−∞,−3) и возрастающая на (−3,∞)(−3,∞)

23.

убывает на [0,∞)[0,∞)

25.

27.

29.

31.

g(x)=f(x-1),h(x)=f(x)+1g(x)=f(x-1),h(x)=f(x)+1

33.

f(x)=|x-3|−2f(x)=|x-3|−2

35.

f(x)=x+3−1f(x)=x+3−1

37.

f(x)=(x-2)2f(x)=(x-2)2

39.

f(x)=|x+3|−2f(x)=|x+3|−2

41.

f(x)=-xf(x)=-x

43.

f(x)=-(x+1)2+2f(x)=-(x+1)2+2

45.

f(x)=−x+1f(x)=−x+1

47.

даже

49.

нечетный

51.

четный

53.

График gg является вертикальным отражением (по оси xx) графика f.f.

55.

График gg представляет собой вертикальное растяжение в 4 раза графика f.f.

57.

График gg представляет собой горизонтальное сжатие в 1515 раз графика f.f.

59.

График gg представляет собой горизонтальное растяжение в 3 раза графика f.f.

61.

График gg представляет собой горизонтальное отражение по оси yy и вертикальное растяжение в 3 раза графика f.f.

63.

g(x)=|−4x|g(x)=|−4x|

65.

г(х)=13(х+2)2-3г(х)=13(х+2)2-3

67.

г(х)=12(х-5)2+1г(х)=12(х-5)2+1

69.

График функции f(x)=x2f(x)=x2 сдвинут влево на 1 единицу, вытянут по вертикали в 4 раза и сдвинут вниз на 5 единиц.

71.

График f(x)=|x|f(x)=|x| растягивается по вертикали в 2 раза, сдвигается по горизонтали на 4 единицы вправо, отражается поперек горизонтальной оси, а затем смещается по вертикали на 3 единицы вверх.

73.

График функции f(x)=x3f(x)=x3 сжат по вертикали в 12,12 раза.

75.

График функции растягивается по горизонтали в 3 раза, а затем смещается по вертикали вниз на 3 единицы.

77.

График f(x)=xf(x)=x сдвигается вправо на 4 единицы, а затем отражается по вертикальной линии x=4.x=4.

79.

81.

1.

6 Секционные упражнения

1.

Изолируйте член абсолютного значения так, чтобы уравнение имело вид |A|=B.|A|=B. Составьте одно уравнение, установив выражение внутри символа абсолютного значения, A,A, равным выражению на другой стороне уравнения, B.B. Составьте второе уравнение, установив AA равным противоположному выражению на другой стороне уравнения. уравнение, −B.−B. Решите каждое уравнение относительно переменной.

3.

График функции абсолютного значения не пересекает ось хх, поэтому график либо полностью выше, либо полностью ниже оси хх.

5.

Сначала определите граничные точки, найдя решение(я) уравнения. Используйте граничные точки, чтобы сформировать возможные интервалы решения. Выберите тестовое значение в каждом интервале, чтобы определить, какие значения удовлетворяют неравенству.

7.

|x+4|=12|x+4|=12

9.

|f(x)−8|<0,03|f(x)−8|<0,03

11.

{1,11}{1,11}

13.

{-94 134}{-94 134}

15.

{103 203}{103 203}

17.

{115 295}{115 295}

19.

{52,72}{52,72}

21.

Нет решения

23.

{−57,27}{−57,27}

25.

(0,−8);(−6,0),(4,0)(0,−8);(−6,0),(4,0)

27.

(0,−7);(0,−7); нет xx-перехватов

29.

(−∞,−8)∪(12,∞)(−∞,−8)∪(12,∞)

31.

−43≤x≤4−43≤x≤4

33.

(−∞,−83]∪[6,∞)(−∞,−83]∪[6,∞)

35.

(-∞,-83]∪[16,∞)(-∞,-83]∪[16,∞)

37.

39.

41.

43.

45.

47.

49.

51.

53.

диапазон: [0,20][0,20]

55.

х-х- пересечения:

57.

(-∞,∞)(-∞,∞)

59.

Не существует решения для aa, которое предохранило бы функцию от перехвата yy. Функция абсолютного значения всегда пересекает точку пересечения yy, когда x=0.x=0.

61.

|p−0,08|≤0,015|p−0,08|≤0,015

63.

|x−5,0|≤0,01|x−5,0|≤0,01

1.7 Секционные упражнения

1.

Каждый выход функции должен иметь ровно один выход, чтобы функция была однозначной. Если какая-либо горизонтальная линия пересекает график функции более одного раза, это означает, что значения yy повторяются и функция не является взаимно однозначной. Если ни одна горизонтальная линия не пересекает график функции более одного раза, то значения yy не повторяются, и функция является взаимно однозначной.

3.

Да. Например, f(x)=1xf(x)=1x является обратным самому себе.

5.

Для заданной функции y=f(x),y=f(x) найти xx через y.y. Поменяйте местами xx и y.y. Решите новое уравнение для y.y. Выражение для yy обратное: y=f−1(x).y=f−1(x).

7.

f−1(x)=x−3f−1(x)=x−3

9.

f−1(x)=2−xf−1(x)=2−x

11.

f-1(x)=-2xx-1f-1(x)=-2xx-1

13.

область f(x):[−7,∞);f−1(x)=x−7f(x):[−7,∞);f−1(x)=x−7

15.

область f(x):[0,∞);f−1(x)=x+5f(x):[0,∞);f−1(x)=x+5

16.

• ⓐ f(g(x))=xf(g(x))=x и g(f(x))=x.g(f(x))=x.
• ⓑ Это говорит нам о том, что ff и gg являются обратными функциями

17.

f(g(x))=x,g(f(x))=xf(g(x))=x,g(f(x))=x

19.

один к одному

21.

один к одному

23.

не один к одному

25.

33

27.

22

29.

31.

[2,10][2,10]

33.

66

35.

−4−4

37.

00

39.

11

41.

хх	1	4	7	12	16
f-1(x)f-1(x)	3	6	9	13	14

43.

f−1(x)=(1+x)1/3f−1(x)=(1+x)1/3

45.

f−1(x)=59(x−32).f−1(x)=59(x−32). Учитывая температуру по Фаренгейту, x,x, эта формула позволяет рассчитать температуру по Цельсию.

47.

t(d)=d50,t(d)=d50,t(180)=18050.t(180)=18050. Время прохождения автомобилем 180 миль составляет 3,6 часа.

Обзор упражнений

1.

функция

3.

не функция

5.

f(−3)=−27;f(−3)=−27;f(2)=−2;f(2)=−2;f(−a)=−2a2−3a;f(− а)=-2а2-3а;
-f(a)=2a2-3a;-f(a)=2a2-3a;f(a+h)=-2a2+3a-4ah+3h-2h3f(a+h)=-2a2+3a-4ah +3ч−2ч3

7.

один к одному

9.

функция

11.

функция

13.

15.

22

17.

x=-1,8x=-1,8 или  или x=1,8 или x=1,8

19.

−64+80a−16a2−1+a=−16a+64−64+80a−16a2−1+a=−16a+64

21.

(-∞,-2)∪(-2,6)∪(6,∞)(-∞,-2)∪(-2,6)∪(6,∞)

23.

25.

3131

27.

возрастание (2,∞);(2,∞); убывающая (−∞,2)(−∞,2)

29.

возрастание (−3,1);(−3,1); постоянная (−∞,−3)∪(1,∞)(−∞,−3)∪(1,∞)

31.

локальный минимум (−2,−3);(−2,−3); локальный максимум (1,3)(1,3)

33.

Абсолютный максимум: 10

35.

(f∘g)(x)=17−18x;(g∘f)(x)=−7−18x(f∘g)(x)=17−18x;(g∘f)(x)= −7−18x

37.

(f∘g)(x)=1x+2;(f∘g)(x)=1x+2;(g∘f)(x)=1x+2(g∘f)(x)=1x +2

39.

(f∘g)(x)=1+x1+4x,x≠0,x≠−14(f∘g)(x)=1+x1+4x,x≠0,x≠−14

41.

(f∘g)(x)=1x,x>0(f∘g)(x)=1x,x>0

43.

образец: g(x)=2x−13x+4;f(x)=xg(x)=2x−13x+4;f(x)=x

45.

47.

49.

51.

53.

55.

f(x)=|x−3|f(x)=|x−3|

57.

даже

59.

нечетный

61.

даже

63.

f(x)=12|x+2|+1f(x)=12|x+2|+1

65.

f(x)=−3|x−3|+3f(x)=−3|x−3|+3

67.

69.

х=-22,х=14х=-22,х=14

71.

(−53,3)(−53,3)

73.

f−1(x)=x-1f−1(x)=x-1

77.

Функция один к одному.

78.

Функция не является однозначной.

79.

55

Практический тест

1.

Отношение является функцией.

3.

−16

5.

График представляет собой параболу, и он не проходит тест горизонтальной линии.

7.

2a2-a2a2-a

9.

−2(а+б)+1−2(а+б)+1

11.

22

13.

15.

дажечетный

17.

нечетный

19.

х=-7х=-7 и х=10х=10

21.

f−1(x)=x+53f−1(x)=x+53

23.