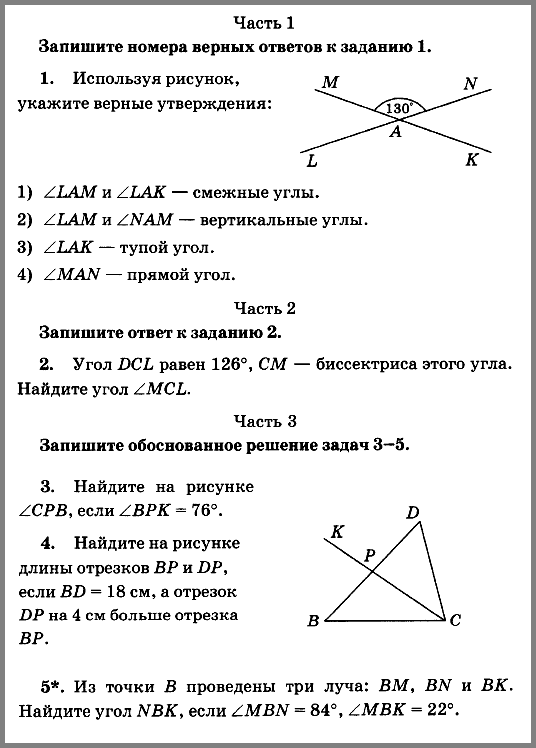
Контрольная работа № 1. Векторы | |
1 вариант. 1. Начертите два неколлинеарных вектора и . Постройте векторы, равные: а) ; б) 2. На стороне ВС ромба АВСD лежит точкаК такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы через векторы и . 3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции. 4.* В треугольнике АВС О – точка пересечения медиан. Выразите вектор через векторы и . | 2 вариант 1. Начертите два неколлинеарных вектора и . Постройте векторы, равные: а) ; б) 2. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы через векторы и 3. В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. 4. * В треугольнике МNK О – точка пересечения медиан, . Найдите число k. |
Контрольная работа № 2. Метод координат. | |
1 вариант. 1. Найдите координаты и длину вектора , если . 2. Напишите уравнение окружности с центром в точкеА (- 3;2), проходящей через точку В (0; — 2). 3. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N (2; 4), К (2; — 2). а) Докажите, что Δ- равнобедренный; б) Найдите высоту, проведённую из вершины М. 4. * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( — 1; 3 ) и К( 0; 2 ). | 2 вариант. 1). Найдите координаты и длину вектора , если . 2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ). 3). Треугольник СDЕ задан координатами своих вершин: С (2; 2), D (6; 5), Е (5; — 2). а) Докажите, что Δ- равнобедренный; б) Найдите биссектрису, проведённую из вершины С. 4. * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; — 3 ) и С( 2; 0 ). |
Контрольная работа № 3. Соотношения между сторонами и углами треугольника. | |
1 вариант
В = 600, ВС = Найдите АС.
7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
| 2 вариант
D = 450, СЕ =Найдите DE.
5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
|
Контрольная работа № 4. Длина окружности и площадь круга. | |
1 вариант 1. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 2. Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 1200. Чему равна площадь соответствующего данной дуге кругового сектора? 3. Периметр правильного треугольника, вписанного в окружность, равен Найдите периметр правильного шестиугольника, описанного около той же окружности. | 2 вариант 1. 2. Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора? 3. Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность. |
Контрольная работа № 5. Движения. | |
1 вариант 1. Начертите ромб АВСD. Постройте образ этого ромба: а) при симметрии относительно точки С; б) при симметрии относительно прямой АВ; в) при параллельном переносе на вектор ; г) при повороте вокруг точки D на 600 по часовой стрелке. 2. Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр. 3. * Начертите два параллельных отрезка, длины которых равны. | 2 вариант 1. Начертите параллелограмм АВСD. Постройте образ этого параллелограмма: а) при симметрии относительно точки D; б) при симметрии относительно прямой CD; в) при параллельном переносе на вектор ; г) при повороте вокруг точки А на 450 против часовой стрелки. 2. Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей. 3.* Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой. |
Найдите среднюю линию трапеции.
Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см.
начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой.Умк Атанасян Контрольная Работа – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
Умк Атанасян Контрольная Работа
Опубликовано 06.12.2013 — 16:14 — Наталья Сергееевна
Контрольные работы к учебнику геометрия Атанасян Л.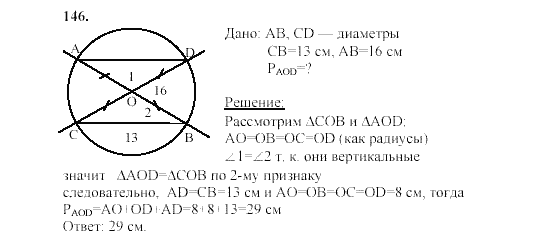
С. 7,8 классы
Контрольная работа № 1.
1 вариант.
1). Три точки В, С , и D лежат на одной прямой. Известно, что ВD = 17 см, DC = 25 см. Какой может быть длина отрезка ВС ?
2). Сумма вертикальных углов МОЕ и DOC, образованных при пересечении прямых МС и DE, равна 204 0 . Найдите угол МОD .
3). С помощью транспортира начертите угол, равный 78 0 , и проведите биссектрису смежного с ним угла.
2 вариант.
1). Три точки М, N и К лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МК ?
2). Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108 0 . Найдите угол ВОD .
3). С помощью транспортира начертите угол, равный 132 0 , и проведите биссектрису одного из смежных с ним углов.
Контрольная работа № 2.
1 вариант.
1). На рисунке 1 отрезки АВ и СD имеют общую середину О. Докажите, что .
С
А O
В
2). Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что АDВ = А DС . Докажите, что АВ = АС .
3). В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5 : 2 . Найдите стороны треугольника.
2 вариант.
1). На рисунке 1 отрезки МЕ и РК точкой D делятся пополам. Докажите, что КМD = РЕD.
М К
D
2). На сторонах угла D отмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла D и РК = РМ .
Докажите, что луч DР – биссектриса угла МDК .
3). В равнобедренном треугольнике с периметром 56 см основание относится к боковой стороне как 2 : 3 . Найдите стороны треугольника.
Контрольная работа № 3.
1 вариант .
1). Отрезки EF и PQ пересекаются в их середине М. Докажите, что РЕ // QF .
2). Отрезок DM – биссектриса треугольника CDE . Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N . Найдите углы треугольника DMN , если .
3). На рисунке АС // ВD , точка М – середина отрезка АВ . Докажите, что М – середина отрезка CD .
D
M
A B
2 вариант.
1). Отрезки МN и ЕF пересекаются в их середине Р.
Докажите, что ЕN // МF .
2). Отрезок AD – биссектриса треугольника АВС . Через точку D проведена прямая, параллельная стороне FD и пересекающая сторону АС в точке F . Найдите углы треугольника АDF , если .
3). На рисунке AB // DC, АВ = DC. Докажите, что точка О – середина отрезков АС и ВD .
В С
О
А D
Контрольная работа № 4.
1 вариант.
1). На рисунке: . Найдите сторону АВ треугольника АВС .
Е
B М
А
C D
F
2).
В треугольнике СDE точка М лежит на стороне СЕ , причём — острый. Докажите, что DE > DM .
3). Периметр равнобедренного тупоугольного треугольника равен 45 см , а одна из его сторон больше другой на 9 см . Найдите стороны треугольника.
2 вариант.
1). На рисунке: . Найдите сторону АС треугольника АВС.
Е М
A С
В
D F
2). В треугольнике MNP точка К лежит на стороне MN , причём — острый. Докажите , что КР < МР.
3). Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
Контрольная работа № 5.
1 вариант.
1). В остроугольном треугольнике МNP биссектриса угла М пересекает высоту NK в точке О , причём ОК = 9 см . Найдите расстояние от точки О до прямой МN .
2). Постройте прямоугольный треугольник по гипотенузе и острому углу.
3). Один из углов прямоугольного треугольника равен 60 0 , а сумма гипотенузы и меньшего катета равна 42 см . Найдите гипотенузу .
2 вариант.
1). В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF , причём FC = 13 см . Найдите расстояние от точки F до прямой DE .
2). Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.
3). В треугольнике АВС , биссектрисы углов А и С пересекаются в точке О . Найдите угол АОС.
Итоговая контрольная работа
1 вариант.
1). В равнобедренном треугольнике АВС с основанием АС угол В равен 42 0 .
Найдите два других угла треугольника АВС.
2). Величины смежных углов пропорциональны числам 5 и 7. Найдите разность между этими углами.
3). В прямоугольном треугольнике АВС , , АС = 10 см , СD АВ, DE АС. Найдите АЕ .
4). В треугольнике МРК угол Р составляет 60 0 угла К , а угол М на 4 0 больше угла Р . Найдите угол Р .
2 вариант.
1). В равнобедренном треугольнике АВС с основанием АС сумма углов А и С равна 156 0 . Найдите углы треугольника АВС .
2). Величины смежных углов пропорциональны числам 4 и 11. Найдите разность между этими углами.
3). В прямоугольном треугольнике АВС , , ВС = 18 см , СК АВ, КМ ВС. Найдите МВ.
4). В треугольнике BDE угол В составляет 30 0 угла D , а угол Е на 19 0 больше угла D . Найдите угол В .
Контрольная работа № 1.
1). Диагонали прямоугольника ABCD пересекается в точке О, ABO = 36°.
Найдите AOD.
2). Найдите углы прямоугольной трапеции, если один из ее углов равен 20°.
3). Стороны параллелограмма относятся как 1 : 2 , а его периметр равен 30 см . Найдите стороны параллелограмма.
4). В равнобокой трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции.
5).* Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 30°, АМ = 4 см . Найдите длину диагонали BD ромба, если точка М лежит на стороне AD.
1). Диагонали прямоугольника MNKP пересекаются в точке О, MON= 64°. Найдите ОМР. 2). Найдите углы равнобокой трапеции, если один из ее углов на 30° больше второго.
3). Стороны параллелограмма относятся как 3 : 1 , а его периметр равен 40 см . Найдите стороны параллелограмма.
4). В прямоугольной трапеции разность углов при одной из боковых сторон равна 48°. Найдите углы трапеции.
5).* Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 3 0°, длина диагонали АС равна 6 см .
Найдите AM, если точка М лежит на продолжении стороны AD.
Контрольная работа № 2.
1). Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
2). Катеты прямоугольного треугольника равны 6 и 8 см . Найдите гипотенузу и площадь треугольника.
3). Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см .
4).* В прямоугольной трапеции АВСК большая боковая сторона равна 3 см, угол К равен 45°, а высота СН делит основание АК пополам. Найдите площадь трапеции.
2 вариант.
1). Сторона треугольника равна 12 см , а высота, проведенная к ней, в три раза меньше высоты. Найдите площадь треугольника.
2). Один из катетов прямоугольного треугольника равен 12 см , а гипотенуза 13 см . Найдите второй катет и гипотенузу треугольника.
3). Диагонали ромба равны 10 и 12 см .
Найдите его площадь и периметр.
4).* В прямоугольной трапеции ABCD большая боковая сторона равна 8 см , угол А равен 60°, а высота ВН делит основание AD пополам. Найдите площадь трапеции.
Контрольная работа № 3.
1 вариант.
1). По рис. A = B, СО = 4, DO = 6, АО = 5 .
Найти : а). ОВ ; б). АС : BD; в). .
2). В треугольнике ABC сторона АВ = 4 см , ВС = 7 см , АС = 6 см , а в треугольнике MNK сторона МК = 8 см, MN =12 см, KN = 14 см . Найдите углы треугольника MNK, если A = 80°, B = 60°.
3). Прямая пересекает стороны треугольника ABC в точках М и К соответственно так, что МК || АС, ВМ : АМ = 1 : 4 . Найдите периметр треугольника ВМК , если периметр треугольника ABC равен 25 см .
4). В трапеции ABCD (AD и ВС основания) диагонали пересекаются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см 2.
2 вариант.
1). По рис. РЕ || NK, MP = 8, MN = 12, ME = 6. Найти : а) . МК ; б). РЕ : NК ; в). .
2). В ∆ АВС АВ = 12 см, ВС = 18 см, В = 70 0 , а в ∆ МNК МN = 6 см, NК = 9 см, N = 70 0 . Найдите сторону АС и угол С треугольника АВС , если МК = 7 см, К = 60 0 .
3). Отрезки АВ и CD пересекаются в точке О так, что ACO = BDO, АО : ОВ = 2:3. Найдите периметр треугольника АСО, если периметр треугольника BOD равен 21 см .
4). В трапеции ABCD ( AD и ВС основания) диагонали пересекаются в точке О, = 32 см 2 , = 8 см 2 . Найдите меньшее основание трапеции, если большее из них равно 10 см .
Контрольная работа № 4.
1 вариант.
1). Средние линии треугольника относятся как 2 : 2 : 4, а периметр треугольника равен 45 см . Найдите стороны треугольника.
2).
Медианы треугольника ABC пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС и пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите EF, если сторона АС равна 15 см.
3). В прямоугольном треугольнике ABC ( C = 90° ) АС = 5 см, ВС = 5 см . Найдите угол В и гипотенузу АВ.
4). В треугольнике ABC A = , C = , сторона ВС = 7 см, ВН – высота. Найдите АН.
5). В трапеции ABCD продолжения боковых сторон пересекаются в точке К, причем точка В — середина отрезка АК. Найдите сумму оснований трапеции, если AD = 12 см .
1). Стороны треугольника относятся как 4 : 5 : 6 , а периметр треугольника, образованного его средними линиями, равен 30 см . Найдите средние линии треугольника.
2). Медианы треугольника MNK пересекаются в точке О. Через точку О проведена прямая, параллельная стороне МК и пересекающая стороны MN и NK в точках А и В соответственно. Найдите МК, если длина отрезка АВ равна 12 см.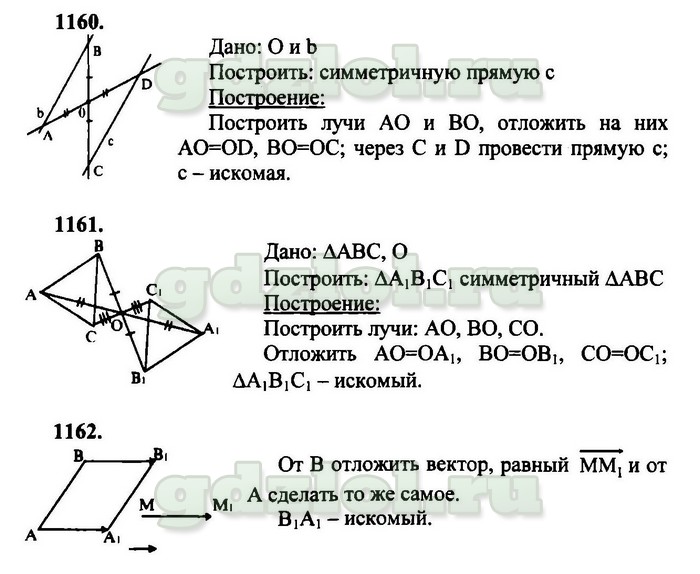
3). В прямоугольном треугольнике РКТ ( T = 90° ), РТ = 7 см , КТ = 1 см . Найдите угол К и гипотенузу КР.
4). В треугольнике ABC A = , C = , высота ВН равна 4 см . Найдите АС.
5). В трапеции MNKP продолжения боковых сторон пересекаются в точке Е, причем ЕК = КР. Найдите разность оснований трапеции, если NK = 7 см .
1 вариант.
1). АВ и АС — отрезки касательных, проведенных к окружности радиуса 9 см . Найдите длины отрезков АС и АО, если АВ = 12 см .
2). По рисунку АВ : BC = 11 : 12. Найти: BCA, BAC.
радиусом 16 см описана около треугольника ABC так, что угол OAB равен 30°, угол OCB равен 45°. Найдите стороны АВ и ВС треугольника.
2 вариант.
1). MN и МК — отрезки касательных, проведенных к окружности радиуса 5 см . Найдите MN и МК, если МО = 13 см .
2). По рисунку AB : АС=5 : 3. Найти: BOC, ABC.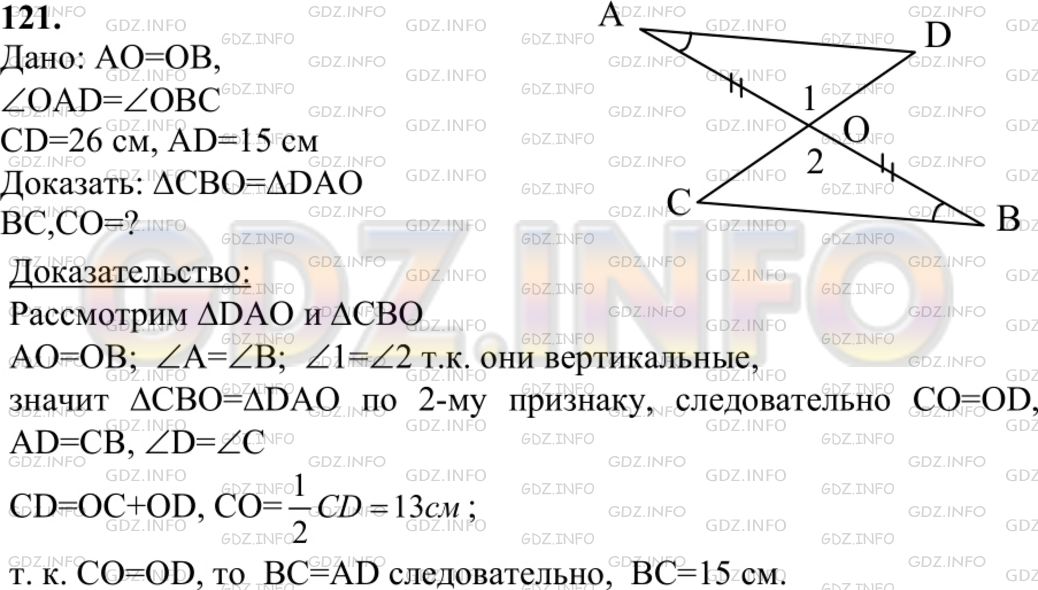
AF = 4 см , ВF = 16 см , CF = DF. Найдите CD .
Это первая контрольная работа по теме «Параллелограм и его виды»…
Первая контрольная работа по теме «Параллелограм и его виды»…
Контрольная работа содержит 4 задания части А1, А2, А3, А4 и 1 задание части В1…
Контрольная работа № 1 Простейшие задачи в координатах Вариант 11. Найдите координаты вектора , если А (5; –1; 3), В (2; –2; 4).2. Даны векторы (3; 1; –2) и (1; 4; –3). Найдите .3. Изобрази…
Работа состоит из 7 заданий: 4 задания базового уровня, 5,6,7 повышенного уровня. Работа рассчитана на 45 мин.Критерии оценивания: оценка «5» — за любые правильно выполненные 6 заданий…
Итоговая контрольная работа по геометрии 8 класс по учебнику Атанасян Л.С….
Контрольная работа по геометрии в 2-х вариантах….
Контрольная работа № 5.
Геометрия 7 Контрольные работы Атанасян — УчительPRO
Примерные контрольные работы по геометрии по УМК .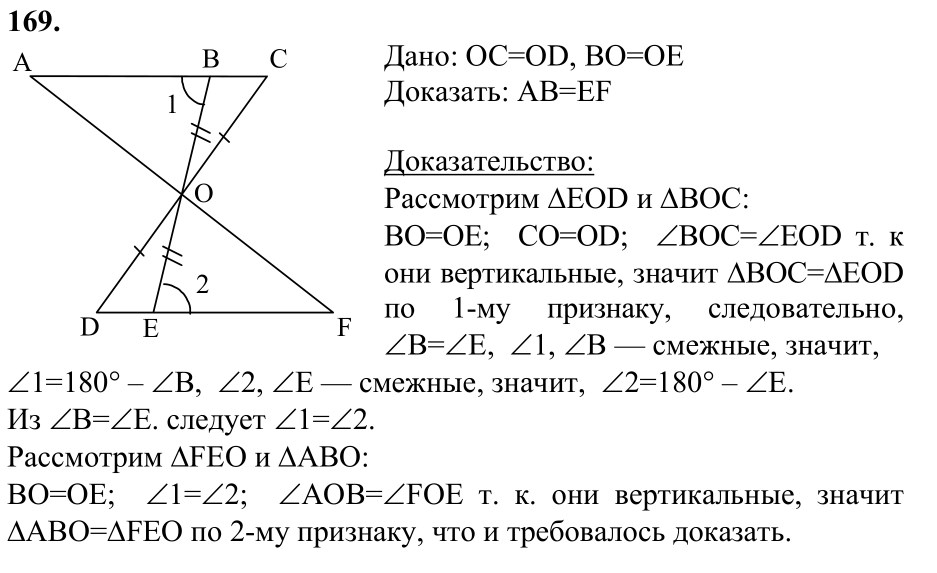
..
Контрольные работы по геометрии по учебнику Атанасян …
Геометрия 7 Атанасян (Мельникова) | КОНТРОЛЬНЫЕ РАБОТЫ
Геометрия 7 Атанасян (Мельникова) | КОНТРОЛЬНЫЕ РАБОТЫ
Контрольные работы по геометрии 8 класс ( Атанасян ) скачать
Геометрия в 7 классе, контрольные работы по Атанасяну за…
Примерные контрольные работы по геометрии по УМК …
ГДЗ Геометрия 7-9 класс Иченская, Атанасян — Тетрадь для…
контрольные работы по геометрии 7 класс атанасян — поиск…
Контрольные работы по геометрии 10 класс УМК Атанасян
ГДЗ: Геометрия 7-9 класс Иченская, Атанасян — Тетрадь для…
ГДЗ Геометрия 7, 8, 9 класс самостоятельные и контрольные …
Геометрия. 8 класс. Контрольные работы к учебнику… | Лабиринт
Отчет По Практике В Юридической Клинике Университета
Эссе На Тему Чорос Гуркин Патриот Родины
Эссе На Тему Путешествие Атома Азота
Готовые Эссе По Обществознанию Егэ
Контрольные Работы К Учебнику Верещагиной 5 Класс
Развитие исследований в области математического образования
%PDF-1.