ГДЗ к сборнику Ершовой, Голобородько Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса ОНЛАЙН
Избранное / Решебники (ГДЗ) для школьников
Решебник к сборнику задач «Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса.— М.: Илекса,— 2012,— 238 с.» Рукопись. — 2013
В решебнике представлены подробные решения задач из сборника «Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса.— М.: Илекса,— 2012,— 238 с.» Уровни сложности А и Б (в некоторых работах решены варианты В).
Решебник поможет Вам проверить правильность решения задач и упражнений.
Страницы решебника представлены в виде слайдов. Кликните на нужный слайд, чтобы прочитать содержание страницы.
Внимание! Рукопись не проверялась, возможны ошибки!
АЛГЕБРА
Рациональные дроби
С-1. Рациональные выражения. Сокращение дробей
Рациональные выражения. Сокращение дробей
С-2. Сложение и вычитание дробей
К-1. Рациональные дроби.
Сложение и вычитание дробей
С-3. Умножение и деление дробей. Возведение дроби в степень
С-4. Преобразование рациональных выражений
С-6. Обратная пропорциональность и ее график
К-2. Рациональные дроби
Квадратные корни
С-7. Арифметический квадратный корень
С-8. Уравнение х2 = а. Функция у = a/х
С-9. Квадратный корень из произведения, дроби, степени
К-3. Арифметический квадратный корень и его свойства
С-10. Внесение и вынесение множителя в квадратных корнях
С-11. Преобразование выражений, содержащих квадратные корни
К-4. Применение свойств арифметического квадратного корня
Квадратные уравнения
С-13. Неполные квадратные уравнения
Неполные квадратные уравнения
С-14. Формула корней квадратного уравнения
С-15. Решение задач с помощью квадратных уравнений. Теорема Виета
К-5. Квадратные уравнения
С-17. Дробные рациональные уравнения
С-18. Применение дробных рациональных уравнений. Решение задач
К-6. Дробные рациональные уравнения
Неравенства
С-19. Свойства числовых неравенств
К-7. Числовые неравенства и их свойства
С-20. Линейные неравенства с одной переменной
С-21. Системы линейных неравенств
К-8. Линейные неравенства и системы неравенств с одной переменной
Степень с рациональным показателем
С-23. Степень с отрицательным показателем
К-9. Степень с целым показателем
К-10. Годовая контрольная работа
ГЕОМЕТРИЯ (по Погорелову)
Четырехугольники
СП-1. Свойства и признаки параллелограмма
Свойства и признаки параллелограмма
СП-2. Прямоугольник. Ромб. Квадрат
КП-1. Параллелограмм
СП-3. Теорема Фалеса. Средняя линия треугольника
СП-4. Трапеция. Средняя линия трапеции
КП-2. Трапеция. Средние линии треугольника и трапеции
Теорема Пифагора
СП-6. Теорема Пифагора
СП-7. Теорема, обратная теореме Пифагора. Перпендикуляр и наклонная
СП-8. Неравенство треугольника
КП-3. Теорема Пифагора
СП-10. Решение прямоугольных треугольников
СП-11. Свойства тригонометрических функций
КП-4. Прямоугольный треугольник (итоговая контрольная работа)
Декартовы координаты на плоскости
СП-12. Координаты середины отрезка.
Расстояние между точками. Уравнение окружности
СП-13. Уравнение прямой
КП-5. Декартовы координаты
Движение
СП-15.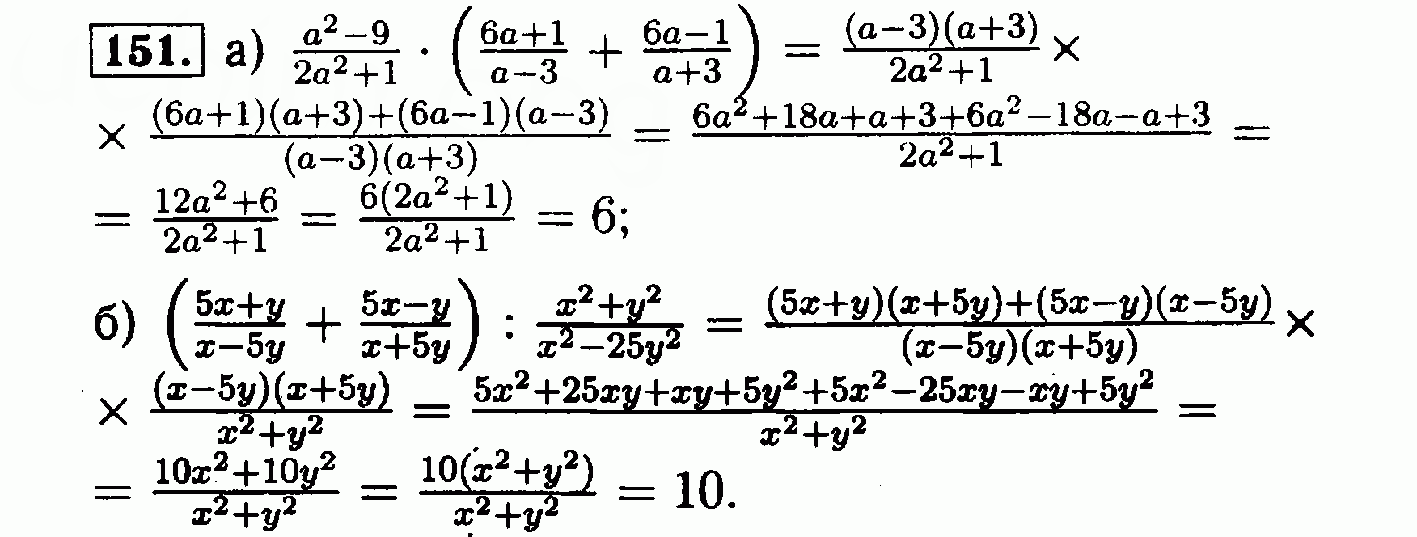 Движение и его свойства. Центральная
Движение и его свойства. Центральная
и осевая симметрии. Поворот
СП-16. Параллельный перенос
Векторы
СП-17. Понятие вектора. Равенство векторов
СП-18. Действия с векторами в координатной форме. Коллинеарные векторы
СП-19. Действия с векторами в геометрической форме
СП-20. Скалярное произведение
КП-6. Векторы
КП-7. Годовая контрольная работа
ГЕОМЕТРИЯ по учебнику Атанасяна
Четырехугольники
СА-1. Свойства и признаки параллелограмма
СА-2.Прямоугольник. Ромб. Квадрат
КА-1. Четырехугольники
Площадь
СА-4.Площадь прямоугольника, квадрата
СА-5.Площадь параллелограмма, ромба, треугольника
СА-6.Площадь трапеции
СА-7.Теорема Пифагора
КА-2. Площади. Теорема Пифагора
Подобные треугольники
СА-9. Определение подобных треугольников. Свойство биссектрисы угла треугольника
Свойство биссектрисы угла треугольника
СА-10. Признаки подобия треугольников
КА-3. Подобие треугольников
СА-11. Применение подобия к решению задач
СА-12. Соотношения между сторонами и углами прямоугольного треугольника
КА-4. Применение подобия к решению задач. Соотношения между сторонами и углами прямоугольного треугольника
Окружность
СА-14. Касательная к окружности
СА-15. Центральные и вписанные углы
СА-16. Теорема о произведении отрезков пересекающихся хорд. Замечательные точки треугольника
СА-17. Вписанная и описанная окружности
КА-5. Окружность
Векторы
СА-19. Сложение и вычитание векторов
СА-20. Умножение вектора на число
СА-21. Средняя линия трапеции
КА-6. Векторы. Применение векторов к решению задач
КА-7. Годовая контрольная работа
ВНИМАНИЕ! Все права на публикацию рукописей принадлежат сайту gdz.
 math-helper.ru. Копирование и распространение материалов запрещено! Тегиалгебра 8 класс ершова решебникгдз ершовагеометрия 8 класс ершова решебникершова алгебра ответыершова геометрия ответыЕршова решебник 8 классрешебник алгебра 8 ершоварешебник геометрия 8 ершоварешебник ершова голобородько 8 классрешения ершова 8 класс
math-helper.ru. Копирование и распространение материалов запрещено! Тегиалгебра 8 класс ершова решебникгдз ершовагеометрия 8 класс ершова решебникершова алгебра ответыершова геометрия ответыЕршова решебник 8 классрешебник алгебра 8 ершоварешебник геометрия 8 ершоварешебник ершова голобородько 8 классрешения ершова 8 классteifuddnighbatt1989
Моя страница
- Стартовая страница
- нижней страницы
- Контакт
- решебник по физике упражнение 19 номер 2 7 клаl
- гдз к сборнику контрольных работ
- ответы на 6 тест немецкий язык 6 класс зверло
- гдз по математике 4 класс м.
 и. моро в тетради
и. моро в тетради - гдз по русскому языку 6 класс 446 баранов
- гдз по дидактическим материалам 8 класс ал
- ответы на 3 раундап по английскому языку
- алгебра и начало математического анализа
- решебники высшей математики
- скачать бесплатно решебник для enjoy english
- бесплатный решебники гдз
- решебник по математике 5 класс зубарева мо
- верещагина и афанасьева англ.
 яз. 5 класс гдз
яз. 5 класс гдз - гдз.збирнык мерзляк
- решебник по математике 1 — 4класс
- ответы на кроссворд по биологии каменскоk
- гдз 8 класс ладыжская
- решебник для построения графика функции
- гдз по русскому языку а.и.власенков л.м.рыбч&
- гдз — алгебра, мордкович за 7 класс
- гдз по матиматике5класс вилинкин выпус2009 го
- ответы управление торговлей сертификаци
- гдз алгебра 7 дорофеев суворова
- гдз англ яз кузовлёв
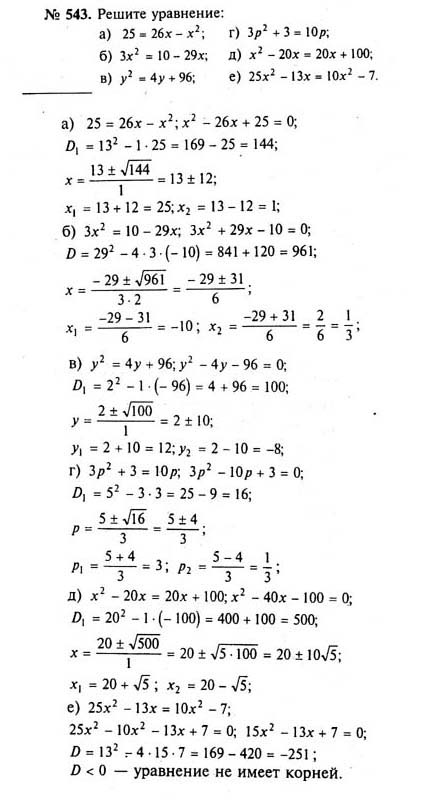 ru. Хотите тоже свой сайт?
ru. Хотите тоже свой сайт?Зарегистрироваться бесплатно
|
Эта статья цитируется в 21 научных статей (всего в 22 статей) Определенная иерархия множеств. Ю. Л. Ершов Полный текст PDF (858 кБ) Поступила: 11.01.1968 Библиографические базы данных: Тип документа: Артикул Язык: Русский Цитата: Ю. Л. Ершов, “Одна иерархия множеств. I», Алгебра и логика, 7:1 (1968), 47–74 Цитирование в формате AMSBIB Варианты соединения: Цикл статей
Эта публикация цитируется в следующих статьях:
Цитирование статей в Google Scholar: русские цитаты,
английские цитаты | QR-? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домашняя страница Николая Баженова
Опросы
- Основы теории онлайновых структур, Бюлл.
 Симб. Журнал., 2019, 25:2, 141-181. С Родом Дауни, Искандером Калимуллиным и Александром Мельниковым. Предварительная версия.
Симб. Журнал., 2019, 25:2, 141-181. С Родом Дауни, Искандером Калимуллиным и Александром Мельниковым. Предварительная версия. - Спектры категоричности вычислимых структур, Журнал математических наук, 2021, 256:1, 34-50. Полнотекстовый доступ. Это перевод статьи, опубликованной в 2018 году.
Автоматические и полиномиальные структуры, пунктуальная вычислимость
- Полурешетки Роджерса пунктуальных нумераций, Math. Структура вычисл. наук, 2022, 32:2, 164-188. С Манатом Мустафой и Сергеем Оспичевым. Это журнальная версия доклада конференции TAMC-2020 «Полурешётки точечных нумераций»
- Спектры точечной категоричности вычислимо категоричных структур, Алгебра и логика, 2021, 60:3, 223-228. С Искандером Калимуллиным. Полнотекстовый доступ.
- Онлайн-презентации конечно порожденных структур, Теор. вычисл. наук, 2020, 844, 195-216. С Искандером Калимуллиным, Александром Мельниковым и Кен Мэн Нг. [препринтная версия].
- Полурешетки точечных нумераций, в Proceedings of TAMC-2020 (Lect.
 Notes Comput. Sci., 12337), 1-12. С Манатом Мустафой и Сергеем Оспичевым. [скачать в формате pdf] Окончательная аутентифицированная версия доступна в Интернете по адресу https://doi.org/10.1007/9.78-3-030-59267-7_1
Notes Comput. Sci., 12337), 1-12. С Манатом Мустафой и Сергеем Оспичевым. [скачать в формате pdf] Окончательная аутентифицированная версия доступна в Интернете по адресу https://doi.org/10.1007/9.78-3-030-59267-7_1 - Определимые подмножества алгебраических структур с полиномиальным временем, в Proceedings of CSR-2020 (Lect. Notes Comput. Sci., 12159), 142–154. [скачать в формате pdf] Окончательная аутентифицированная версия доступна в Интернете по адресу https://doi.org/10.1007/978-3-030-50026-9_10 .
- Автоматические и полиномиальные алгебраические структуры, J. Symb. Журнал., 2019, 84:4, 16:30-1669. С Мэтью Харрисоном-Трейнором, Искандером Калимуллиным, Александром Мельниковым и Кен Мэн Нг.
Алгоритмическое обучение
- Вычисление сложности изменения сознания при изучении алгебраических структур, в Proceedings of CiE-2022 (Lect. Notes Comput. Sci., 13359), 1-12. С Витторио Чиприани и Лукой Сан Мауро.
- О тьюринговой сложности изучения конечных семейств алгебраических структур, J.
 Log. Вычисл., 2021, 31:7, 1891-1900. С Лукой Сан Мауро. [архив: 2106.14515]
Log. Вычисл., 2021, 31:7, 1891-1900. С Лукой Сан Мауро. [архив: 2106.14515] - Изучение семейств алгебраических структур по информатору, инф. Comput., 2020, 275, article id 104590. Совместно с Екатериной Фокиной и Лукой Сан Мауро. [arXiv:1905.01601]
Отношения эквивалентности, вычислимая сводимость и вычислимо перечислимые структуры
- Примитивно-рекурсивные отношения эквивалентности и их примитивно-рекурсивная сложность, Вычислимость, 2022, 11:3-4, 187-221. С Кен Мэн Нг, Лукой Сан Мауро и Андреа Сорби. [архив: 2109.04055]
- Хорошо-заказы, реализованные в.э. отношения эквивалентности, в Proceedings of CiE-2022 (Lect. Notes Comput. Sci., 13359), 13-23. С Максимом Зубковым.
- Вычислимость сводимости для вычислимых линейных порядков типа ω, Journal of Mathematical Sciences, 2022, 267:4, 429-443. С Акнуром Аскарбеккызы и Биржаном Калмурзаевым.
- Наборы индексов для классов положительных предпорядков, Алгебра и логика, 2022, 61:1, 30-53.
 С Биржаном Калмурзаевым и Марией Торебековой.
С Биржаном Калмурзаевым и Марией Торебековой. - Вычислимая вложимость для алгебраических структур, Asian-European J. Math., 2022, 15:7, идентификатор статьи 2250126. С Манатом Мустафой.
- О вычислительном содержании теории борелевских отношений эквивалентности, Препринт Обервольфаха OWP-2021-06. С Бенуа Монином, Лукой Сан Мауро и Рафаэлем Заморой.
- Структура вычислимо перечислимых отношений предпорядка, Алгебра и логика, 2020, 59:3, 201-215. С Серикжаном Бадаевым и Биржаном Калмурзаевым. Полнотекстовый доступ.
- Классификация отношений эквивалентности в иерархии Ершова, Арх. Мат. Логика, 2020, 59:7-8, 835-864. С Манатом Мустафой, Лукой Сан Мауро, Андреа Сорби и Марсом Ямалеевым.
- Минимальные отношения эквивалентности в гиперарифметических и аналитических иерархиях, Лобачевский Ю. Матем., 2020, 41:2, 145-150. С Манатом Мустафой, Лукой Сан Мауро и Марсом Ямалеевым. Полнотекстовый доступ.
- Слабо предполные отношения эквивалентности в иерархии Ершова, Алгебра и логика, 2019, 58:3, 199-213.
 С Биржаном Калмурзаевым. Полнотекстовый доступ.
С Биржаном Калмурзаевым. Полнотекстовый доступ. - Вычислимые изоморфизмы дистрибутивных решеток, в Proceedings TAMC-2019 (Lect. Notes Comput. Sci., 11436), 28-41. С Манатом Мустафой и Марсом Ямалеевым.
- О темных вычислимо перечислимых отношениях эквивалентности, Сиб. Мат. Ж., 2018, 59:1, 22-30. С Биржаном Калмурзаевым. Полнотекстовый доступ.
- Булевых алгебр, реализуемых в.п. отношения эквивалентности, Сибирские электронные математические известия, 2017, 14, 848-855. С Манатом Мустафой, Фрэнком Стефаном и Марсом Ямалеевым.
Теория нумерации и смежные темы
- Сложность Σ 0 n -классификации определяемых подмножеств, Arch. Мат. Логика, опубликованная в Интернете. Со Светланой Александровой и Максимом Зубковым. Полнотекстовый доступ.
- Минимальные обобщенные вычислимые нумерации и семейства положительных предпорядков, Алгебра и логика, 2022, 61:3, 188-206. С Асылбеком Исаховым, Биржаном Калмурзаевым и Фаризой Ракымжанкызы.

- О двух типах решеток понятий в теории нумерации, в Proceedings TAMC-2022 (Lect. Notes Comput. Sci., 13571), 79-92. С Манатом Мустафой и Анваром Нуракуновым.
- Полурешетки Роджерса предельно монотонных нумераций, Math. Журнал. Q., 2022, 68:2, 213-226. С Манатом Мустафой и Жансая Тлеулиевой.
- Теории полурешеток Роджерса аналитических нумераций, Лобачевский Ж. Матем., 2021, 42:4, 701-708. С Манатом Мустафой и Жансая Тлеулиевой. Полнотекстовый доступ.
- Об универсальных парах в иерархии Ершова, Сиб. Мат. Ж., 2021, 62:1, 23-31. С Манатом Мустафой и Сергеем Оспичевым. Полнотекстовый доступ.
- Нумерации в аналитической иерархии, Алгебра и логика, 2020, 59:5, 404-407. С Манатом Мустафой, Сергеем Оспичевым и Марсом Ямалеевым. Полнотекстовый доступ.
- Ограниченная сводимость для вычислимых нумераций, в Proceedings of CiE-2019 (Lect. Notes Comput. Sci., 11558), 96-107. С Манатом Мустафой и Сергеем Оспичевым.
- Элементарные теории и наследственная неразрешимость для полурешеток нумераций, Arch.
 Мат. Логика, 2019, 58:3-4, 485-500. С Манатом Мустафой и Марсом Ямалеевым. Полнотекстовый доступ.
Мат. Логика, 2019, 58:3-4, 485-500. С Манатом Мустафой и Марсом Ямалеевым. Полнотекстовый доступ. - Полурешетки Роджерса для семейств отношений эквивалентности в иерархии Ершова, Сиб. Мат. Ж., 2019, 60:2, 223-234. С Биржаном Калмурзаевым. Полнотекстовый доступ.
Вычислимые группы
- Разложения разрешимых абелевых групп, Int. Журнал алгебраических вычислений, 2020, 30:1, 49-90. С Сергеем Гончаровым и Александром Мельниковым.
- Набор индексов автоустойчивых относительно сильных конструктивизаций групп, Сиб. Мат. Ж., 2017, 58:1, 72-77. С Сергеем Гончаровым и Маргаритой Марчук. Полнотекстовый доступ.
Спектры степеней отношений
- Внутренняя сложность рекурсивных функций на натуральных числах со стандартным порядком, в Proceedings of STACS-2022 (LIPIcs – Leibniz Int. Proc. Inform., 219), 8:1-8:20. С Дариушем Калочинским и Михаем Вроцлавским.
HKSS-Универсальные классы структур
- Вычислимые алгебры Гейтинга с выделенными атомами и коатомами, J.
 Logic Lang. инф., опубликовано в сети. Это журнальная версия доклада конференции ICLA-2021 «О теоретико-вычислимых свойствах гейтинговых алгебр». Полнотекстовый доступ.
Logic Lang. инф., опубликовано в сети. Это журнальная версия доклада конференции ICLA-2021 «О теоретико-вычислимых свойствах гейтинговых алгебр». Полнотекстовый доступ. - Об эффективной универсальности мереологических теорий, Math. Журнал. Q., 2022, 68:1, 48-66. С Син-Чиен Цай.
- HKSS-полнота модальных алгебр, Сибирские электронные математические известия, 2021, 18:2, 923-930.
- О теоретико-вычислимых свойствах алгебр Гейтинга, в Proceedings of ICLA-2021, 25-29.
- Вычислимые контактные алгебры, Фундамент. Информ., 2019, 167:4, 257-269.
- Спектры категоричности полимодальных алгебр, Studia Logica, 2016, 104:6, 1083-1097. Полнотекстовый доступ.
Бивложимые структуры
- О бивложимой категоричности алгебраических структур, Ann. Чистое приложение Логика, 2022, 173:3, id статьи 103060. С Дино Россеггером и Максимом Зубковым. [arXiv:2005.07829]
- Степени бивложимой категоричности, Вычислимость, 2021, 10:1, 1-16.
 С Екатериной Фокиной, Дино Россеггером и Лукой Сан Мауро. [arXiv:1907.03553]
С Екатериной Фокиной, Дино Россеггером и Лукой Сан Мауро. [arXiv:1907.03553] - Степени бивложимой категоричности структур эквивалентности, Arch. Мат. Логика, 2019, 58:5-6, 543-563. С Екатериной Фокиной, Дино Россеггером и Лукой Сан Мауро. Полнотекстовый доступ.
- Вычислимая бивложимая категоричность, Алгебра и логика, 2018, 57:5, 392-396. С Екатериной Фокиной, Дино Россеггером и Лукой Сан Мауро. Полнотекстовый доступ.
- Вычислимая бивложимая категоричность структур эквивалентности, в материалах 11-го Всегреческого симпозиума по логике (Дельфы, Греция, 12–16 июля 2017 г.), 126–132. С Екатериной Фокиной, Дино Россеггером и Лукой Сан Мауро.
Вычислимые вложения для классов структур
- Вычислимые вложения для пар линейных порядков, Алгебра и логика, 2021, 60:3, 163-187. С Христо Ганчевым и Стефаном Ватевым. Полнотекстовый доступ. Это журнальная версия статьи конференции CiE-2019 «Эффективные вложения для пар структур»
- Примечание о вычислимых вложениях для ординалов и их обратных значений в Proceedings of CiE-2020 (Lect.
 Notes Comput. Sci., 12098), 1–13. Со Стефаном Ватевым.
Notes Comput. Sci., 12098), 1–13. Со Стефаном Ватевым. - Эффективные вложения для пар структур, в Proceedings of CiE-2019 (Lect. Notes Comput. Sci., 11558), 84–95. С Христо Ганчевым и Стефаном Ватевым.
- Вычислимые по Тьюрингу вложения, вычислимая бесконечная эквивалентность и линейные порядки [скачать в формате pdf], в Proceedings of CiE-2017 (Lect. Notes Comput. Sci., 10307), 141-151. Окончательная публикация доступна в Springer по адресу http://dx.doi.org/10.1007/978-3-319-58741-7_15 .
Эффективная категория
- О спектрах категоричности локально конечных графов, Сиб. Мат. Ж., 2021, 62:5, 796-804. С Маргаритой Марчук. Полнотекстовый доступ.
- Сильные степени категоричности и слабой плотности, Лобачевский Ж. Матем., 2020, 41:9, 1630-1639. С Искандером Калимуллиным и Марсом Ямалеевым. Полнотекстовый доступ.
- Линейные порядки и спектры категоричности, в материалах 14-й и 15-й азиатских логических конференций. Сингапур: World Scientific, 2019.
 С. 35-52.
С. 35-52. - Степени категоричности и спектральная размерность, J. Symb. Журнал., 2018, 83:1, 103-116. С Искандером Калимуллиным и Марсом Ямалеевым.
- Степени автоустойчивости первичных булевых алгебр, Алгебра и логика, 2018, 57:2, 98-114. С Маргаритой Марчук. Полнотекстовый доступ.
- Степени категоричности для простых и однородных моделей, в Proceedings of CiE-2018 (Lect. Notes Comput. Sci., 10936), 40-49. С Маргаритой Марчук.
- Вычислимость дистрибутивных решеток, Сиб. Мат. Ж., 2017, 58:6, 959-970. С Андреем Фроловым, Искандером Калимуллиным и Александром Мельниковым. Полнотекстовый доступ.
- Эффективная категоричность для дистрибутивных решеток и алгебр Гейтинга, Лобачевский Я. Матем., 2017, 38:4, 600-614. Полнотекстовый доступ.
- Степени категоричности жестких конструкций, в Proceedings of CiE-2017 (Lect. Notes Comput. Sci., 10307), 152-161. С Марсом Ямалеевым.
- Примечание об эффективной категоричности для линейных порядков, в Proceedings of TAMC-2017 (Lect.
 Notes Comput. Sci., 10185), 85-96.
Notes Comput. Sci., 10185), 85-96. - Степени автоустойчивости линейных порядков и линейно упорядоченных абелевых групп, Алгебра и логика, 2016, 55:4, 257-273. Полнотекстовый доступ.
- Степени категоричности против сильных степеней категоричности, Алгебра и логика, 2016, 55:2, 173-177. С Искандером Калимуллиным и Марсом Ямалеевым. Полнотекстовый доступ.
- Теорема ветвления и вычислимая категоричность в иерархии Ершова, Алгебра и логика, 2015, 54:2, 91-104. Полнотекстовый доступ
- Спектры автоустойчивости булевых алгебр, Алгебра и логика, 2014, 53:6, 502-505. Полнотекстовый доступ.
- Δ 0 2 -категоричность булевых алгебр, J. Math. наук, 2014, 203:4, 444-454. Полнотекстовый доступ.
- Гиперарифметическая категоричность булевых алгебр типа B(ω α ×η), J. Math. наук, 2014, 202:1, 40-49. Полнотекстовый доступ
- Степени категоричности для суператомных булевых алгебр, Алгебра и логика, 2013, 52:3, 179-187.
 Полнотекстовый доступ
Полнотекстовый доступ
Эффективная категоричность для разрешимых структур (автоустойчивость относительно сильных конструктивизаций)
- Замечание о разрешимой категоричности и множествах индексов, Сибирские электронные математические известия, 2020, 17, 1013-1026. С Маргаритой Марчук.
- Построение разрешимых графов из разрешимых структур, Алгебра и логика, 2019, 58:5, 369-382. С Мэтью Харрисон-Трейнор. Полнотекстовый доступ.
- Степени автоустойчивости относительно сильных конструктивизаций графов, Сиб. Мат. Ж., 2018, 59:4, 565-577. С Маргаритой Марчук. Полнотекстовый доступ
- Спектры автоустойчивости разрешимых структур, Матем. Структура вычисл. наук, 2018, 28:3, 392-411.
- Степени автоустойчивости относительно сильных конструктивизаций булевых алгебр, Алгебра и логика, 2016, 55:2, 87-102. Полнотекстовый доступ.
- Индексное множество линейных порядков, автоустойчивых относительно сильных конструктивизаций, Вестн.
 Новосибирск. Гос. ун-та, сер. Мат. мех. Поставить в известность. , 2015, 15:3, 51-60. С Сергеем Гончаровым и Маргаритой Марчук. Английский перевод: Набор индексов линейных порядков, автоустойчивых относительно сильных конструктивизаций, J. Math. наук, 2017, 221:6, 840-848. Полнотекстовый доступ.
Новосибирск. Гос. ун-та, сер. Мат. мех. Поставить в известность. , 2015, 15:3, 51-60. С Сергеем Гончаровым и Маргаритой Марчук. Английский перевод: Набор индексов линейных порядков, автоустойчивых относительно сильных конструктивизаций, J. Math. наук, 2017, 221:6, 840-848. Полнотекстовый доступ. - Индексные множества автоустойчивых относительно сильных конструктивизаций конструктивных моделей для знакомых классов, Докл. Матем., 2015, 92:2, 525-527. С Сергеем Гончаровым и Маргаритой Марчук. Полнотекстовый доступ.
- Простая модель без степени автоустойчивости по отношению к сильным конструктивизациям [скачать в формате pdf], в Proceedings of CiE-2015 (Lect. Notes Comput. Sci., 9136), 117-126.
Окончательная публикация доступна по адресу link.springer.com, DOI 10.1007/978-3-319-20028-6_12. - Множество индексов булевых алгебр, автоустойчивых относительно сильных конструктивизаций, Сиб. Мат. Ж., 2015, 56:3, 393-404. С Сергеем Гончаровым и Маргаритой Марчук.
 Полнотекстовый доступ.
Полнотекстовый доступ.
Другие работы по теории вычислимости
- Приближенные приближенные рассуждения: Нечеткие множества и иерархия Ершова, в Трудах ЛОРИ 2021 (Lect. Notes Comput. Sci., 13039), 1-13. С Манатом Мустафой, Сергеем Оспичевым и Лукой Сан Мауро. [arXiv: 2107.10033].
- Заметка о вычислимых различающих раскрасках, Лобачевский Ж. Матем., 2021, 42:4, 693-700. С Ноамом Гринбергом, Александром Мельниковым, Расселом Миллером и Кен Мэн Нг. Полнотекстовый доступ.
Теория списков
- О разрешимости списочных структур, Сиб. Мат. Ж., 2019, 60:3, 377-388. Со Светланой Александровой. Полнотекстовый доступ.
- Автоматические структуры и теория списков, Сибирские электронные математические известия, 2015, 12, 714-722.
Булевы алгебры с выделенными эндоморфизмами
- Булевы алгебры с выделенными эндоморфизмами и порождающими деревьями, Вестн. Новосибирск. Гос. ун-та, сер. Мат. мех.
 Поставить в известность. , 2015, 15:1, 29-44. Английский перевод: Булевы алгебры с выделенными эндоморфизмами и порождающими деревьями, J. Math. наук, 2016, 215:4, 460-474. Полнотекстовый доступ.
Поставить в известность. , 2015, 15:1, 29-44. Английский перевод: Булевы алгебры с выделенными эндоморфизмами и порождающими деревьями, J. Math. наук, 2016, 215:4, 460-474. Полнотекстовый доступ. - Д.к.э. степени категоричности булевых алгебр с выделенным автоморфизмом, Вестн. Новосибирск. Гос. ун-та, сер. Мат. мех. Поставить в известность. , 2014, 14:1, 19-27. Английский перевод: 2-вычислимо перечислимые степени категоричности булевых алгебр с выделенными автоморфизмами, J. Math. наук, 2015, 211:6, 738-746. Полнотекстовый доступ.
- Вычислимые нумерации класса булевых алгебр с выделенными эндоморфизмами, Алгебра и логика, 2013, 52:5, 355-366. Полнотекстовый доступ.
- Вычислимая категоричность булевой алгебры B(ω) с выделенным автоморфизмом, Алгебра и логика, 2013, 52:2, 89-97. С Региной Тухбатуллиной. Полнотекстовый доступ.
- Конструктивизируемость булевой алгебры B(ω) с выделенным автоморфизмом, Алгебра и логика, 2012, 51:5, 384-403.



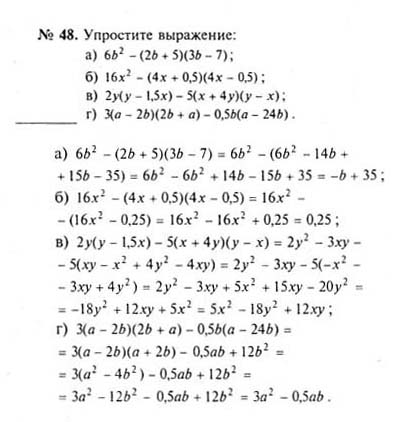 и. моро в тетради
и. моро в тетради яз. 5 класс гдз
яз. 5 класс гдз я
я Я
Я  Файзрахманов, “Разложимость низких 2-вычислимо перечислимых степеней и скачки Тьюринга в иерархии Ершова”, Изв. (Из. ВУЗ), 54:12 (2010), 51–58
Файзрахманов, “Разложимость низких 2-вычислимо перечислимых степеней и скачки Тьюринга в иерархии Ершова”, Изв. (Из. ВУЗ), 54:12 (2010), 51–58  е. степеней», Учен. зап. Казань. ун-та. сер. физ.-матем. науки, 154, вып. Казань, Изд-во Казанского ун-та, 2, 2012, 152–158
е. степеней», Учен. зап. Казань. ун-та. сер. физ.-матем. науки, 154, вып. Казань, Изд-во Казанского ун-та, 2, 2012, 152–158  А., Макниколл Т.Х., Мельников А.Г., “О сложности классификации пространств Лебега”, J. Symb. Log., 85:3 (2020), PII S0022481220000638, 1254–1288
А., Макниколл Т.Х., Мельников А.Г., “О сложности классификации пространств Лебега”, J. Symb. Log., 85:3 (2020), PII S0022481220000638, 1254–1288  Симб. Журнал., 2019, 25:2, 141-181. С Родом Дауни, Искандером Калимуллиным и Александром Мельниковым. Предварительная версия.
Симб. Журнал., 2019, 25:2, 141-181. С Родом Дауни, Искандером Калимуллиным и Александром Мельниковым. Предварительная версия. Notes Comput. Sci., 12337), 1-12. С Манатом Мустафой и Сергеем Оспичевым. [скачать в формате pdf] Окончательная аутентифицированная версия доступна в Интернете по адресу https://doi.org/10.1007/9.78-3-030-59267-7_1
Notes Comput. Sci., 12337), 1-12. С Манатом Мустафой и Сергеем Оспичевым. [скачать в формате pdf] Окончательная аутентифицированная версия доступна в Интернете по адресу https://doi.org/10.1007/9.78-3-030-59267-7_1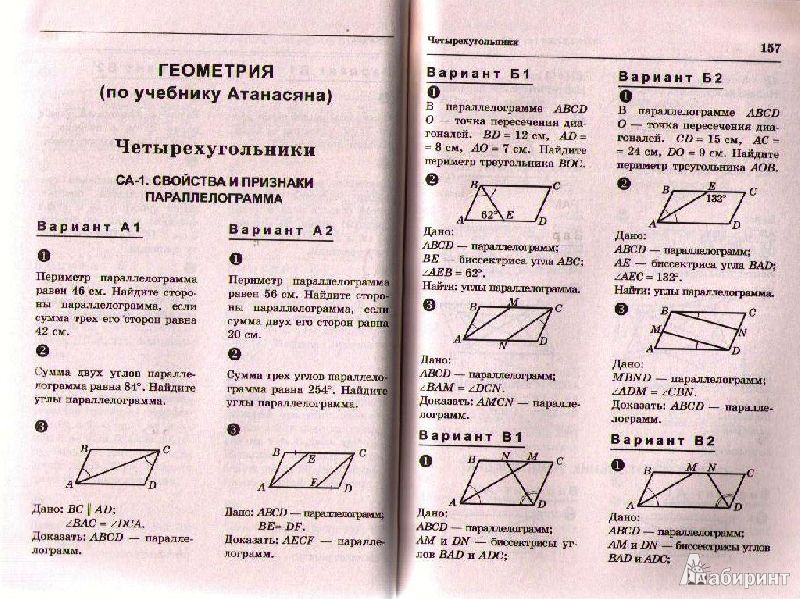 Log. Вычисл., 2021, 31:7, 1891-1900. С Лукой Сан Мауро. [архив: 2106.14515]
Log. Вычисл., 2021, 31:7, 1891-1900. С Лукой Сан Мауро. [архив: 2106.14515] С Биржаном Калмурзаевым и Марией Торебековой.
С Биржаном Калмурзаевым и Марией Торебековой. С Биржаном Калмурзаевым. Полнотекстовый доступ.
С Биржаном Калмурзаевым. Полнотекстовый доступ.
 Мат. Логика, 2019, 58:3-4, 485-500. С Манатом Мустафой и Марсом Ямалеевым. Полнотекстовый доступ.
Мат. Логика, 2019, 58:3-4, 485-500. С Манатом Мустафой и Марсом Ямалеевым. Полнотекстовый доступ. Logic Lang. инф., опубликовано в сети. Это журнальная версия доклада конференции ICLA-2021 «О теоретико-вычислимых свойствах гейтинговых алгебр». Полнотекстовый доступ.
Logic Lang. инф., опубликовано в сети. Это журнальная версия доклада конференции ICLA-2021 «О теоретико-вычислимых свойствах гейтинговых алгебр». Полнотекстовый доступ. С Екатериной Фокиной, Дино Россеггером и Лукой Сан Мауро. [arXiv:1907.03553]
С Екатериной Фокиной, Дино Россеггером и Лукой Сан Мауро. [arXiv:1907.03553] Notes Comput. Sci., 12098), 1–13. Со Стефаном Ватевым.
Notes Comput. Sci., 12098), 1–13. Со Стефаном Ватевым. С. 35-52.
С. 35-52.