Гдз геом 9 кл: Решебники по геометрии за 9 класс — Решеба

ГДЗ,Геометрия,9 класс,Атанасян Л.С. – Рамблер/класс

741 вопрос

749 ответов

Изобразите № 1240 ГДЗ Геометрия 9 класс Атанасян Л.С.

Изобразите тетраэдр DABC, отметьте точку К на ребре DC и точки М и N граней АВС и ACD. Постройте сечение тетраэдра плоскостью MNK. (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Выручайте № 1287 ГДЗ Геометрия 9 класс Атанасян Л.С.

Пусть ABCD — квадрат, а A1B1C1 — правильный треугольник, вписанные в окружность радиуса R. Докажите, что сумма
АВ + А1B1, равна (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Докажите № 1256 ГДЗ Геометрия 9 класс Атанасян Л.С.

Вершины четырёхугольника ABCD имеют координаты А(х1;у1), В (х2; у2), С(х3;у3) и D (х4; у4). Докажите, что этот четырёхугольник является (Подробнее…)

ГДЗГеометрия9 классАтанасян Л. С.

Постройте отрезок № 1166 ГДЗ Геометрия 9 класс Атанасян Л.С.

Постройте отрезок А1В1 который получается из данного отрезка АВ поворотом вокруг данного центра О: а) на 120° по часовой стрелке; б) на (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Докажите № 1279 ГДЗ Геометрия 9 класс Атанасян Л.С.

На рисунке 370 изображён правильный десятиугольник, вписанный в окружность радиуса R, АС — биссектриса угла ОАВ.
Докажите, что:  (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Найдите объём № 1221 ГДЗ Геометрия 9 класс Атанасян Л.С.

Найдите объём конуса, если площадь его основания равна Q, а площадь боковой поверхности равна Р

ГДЗГеометрия9 классАтанасян Л.С.

Найдите радиус № 1246 ГДЗ Геометрия 9 класс Атанасян Л.С.

Высота цилиндра на 12 см больше его радиуса, а площадь полной поверхности равна 288π см2. Найдите радиус основания и высоту цилиндра. (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Найдите № 1212 ГДЗ Геометрия 9 класс Атанасян Л.С.

Найдите объём правильной четырёхугольной пирамиды, если сторона её основания равна т, а плоский угол (т. е. угол грани) при вершине (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Надо найти № 1243 ГДЗ Геометрия 9 класс Атанасян Л.С.

В правильной n-угольной пирамиде плоский угол при вершине равен а, а сторона основания равна а. Найдите объём пирамиды.

ГДЗГеометрия9 классАтанасян Л.С.

Выручайте № 1293 ГДЗ Геометрия 9 класс Атанасян Л.С.

Докажите, что два параллелограмма равны, если диагонали и угол между ними одного параллелограмма соответственно равны диагоналям и углу (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Выручайте № 1175 ГДЗ Геометрия 9 класс Атанасян Л. С.

Даны прямая а и точки М и N, лежащие по одну сторону от неё. Докажите, что на прямой а существует единственная точка X, такая, что (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Докажите № 1148 ГДЗ Геометрия 9 класс Атанасян Л.С.

Докажите, что при осевой симметрии плоскости:
а) прямая, параллельная оси симметрии, отображается на прямую, параллельную оси (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Найдите отношение № 1215 ГДЗ Геометрия 9 класс Атанасян Л.С.

В цилиндр вписана правильная n призма (т. е. основания призмы вписаны в основания цилиндра). Найдите отношение объёмов призмы и (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Вычислите площади № 1223 ГДЗ Геометрия 9 класс Атанасян Л.С.

Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Вычислите площади боковой и полной поверхностей (Подробнее. ..)

ГДЗГеометрия9 классАтанасян Л.С.

Изобразите № 1235 ГДЗ Геометрия 9 класс Атанасян Л.С.

Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью BKL, где К — середина ребра АА1, a L — середина ребра СС1. (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Хелп № 1117 ГДЗ Геометрия 9 класс Атанасян Л.С.

Найдите площадь круга, вписанного: а) в равносторонний треугольник со стороной а; б) в прямоугольный треугольник с катетом а и (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Найдите № 1207 ГДЗ Геометрия 9 класс Атанасян Л.С.

Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей равна 8 см. Найдите боковые рёбра пирамиды, если (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Найдите площадь № 1241 ГДЗ Геометрия 9 класс Атанасян Л.С.

Основанием пирамиды является параллелограмм со сторонами 5 м и 4 м и меньшей диагональю 3 м. Высота пирамиды проходит через точку (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Найдите отношения № 1096 ГДЗ Геометрия 9 класс Атанасян Л.С.

Стороны правильного треугольника, квадрата и правильного шестиугольника равны друг другу. Найдите отношения площадей этих (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Докажите № 1177 ГДЗ Геометрия 9 класс Атанасян Л.С.

Медианы АА1, ВВ1 и СС1 треугольника АВС пересекаются в точке М. Точки А2, В2 и С2 являются соответственно серединами отрезков AM, ВМ и (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

ГДЗ по Геометрии 9 класс Мерзляк

С каждым годом программа по геометрии становиться все сложнее. В девятом класс она продолжает изучение векторов и координат на плоскости, рассматриваются представления о тригонометрических функциях угла. Каждый теоретический материал закрепляется решением задач на пройденную тему. Именно подобные решения и вызывают у учащегося массу сложностей. Закрепить свои знания и разобраться со всеми трудностями, встречающимися при выполнении домашнего задания, отлично поможет задачник к учебнику в виде ГДЗ по геометрии за 9 класс (авторы: Мерзляк, Полонский, Якир). Он намного облегчит учебу девятиклассника. Пособие соответствует всем требованиям, предъявляемым ФГОС и рабочей программой основного образования.

Учебник разбит на пять глав. В первой рассматриваются способы решения треугольников. Из второй ученик узнает, какими свойствами обладают правильные многоугольники. О расстоянии между точками и о методе координат описано в третьем разделе. В четвертом сосредоточены понятия о векторах, действия с ними и их применение. В последней главе речь пойдет уже о стереометрии. Начальные сведения, переход от плоских фигур к объемным. Школьник научится выполнять чертежи к задачам.

Учеба на отлично с онлайн-ГДЗ по геометрии за 9 класс Мерзляка

Изучить этот сложный материал поможет решебник, который является отличной шпаргалкой на протяжении всего учебного года. Он поможет каждому девятикласснику:

• пополнить и углубить свои знания по предмету;
• повысить успеваемость;
• быстро и безошибочно выполнить домашнее задание;
• наиболее эффективно подготовиться к предстоящей итоговой аттестации.

Онлайн-формат сократит время на поисках нужного материала, пособие можно использовать в любом месте, где имеется доступ к Интернету.

Педагог сможет использовать материал сборника для составления своей индивидуальной программы, которая поможет ему донести до каждого ученика все нюансы, имеющиеся в этой дисциплине.

Решебник по геометрии для 9 класса Мерзляка вполне сможет помочь родителям заменить репетитора. Тем самым они смогут помочь своему ребенку не только правильно выполнить то или иное упражнение, но и наиболее эффективно подготовиться к экзаменам.

Дополнительное ГДЗ

• Упражнения

• Вопросы к параграфам

  • § 1
  • § 2
  • § 3
  • § 4
  • § 5
  • § 6
  • § 7
  • § 8
  • § 9
  • § 10
  • § 11
  • § 12
  • § 13
  • § 14
  • § 15
  • § 16
  • § 17
  • § 18
  • § 19
  • § 20

• Когда сделаны уроки (1 глава)

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6

• Проверь себя

  • 1
  • 2
  • 3
  • 4
  • 5

Часть учеников относит геометрию к числу самых интересных предметов из всех, которые они проходят в девятом классе. С таким утверждением согласны далеко не все. Учащимся необходимо обладать большим багажом знаний, чтобы хорошо успевать по этому предмету и приносить домой положительные оценки. Но не стоит отчаиваться тем, кто пока не может похвастаться хорошей успеваемостью. Им стоит обратить внимание на «ГДЗ по геометрии 9 класс Мерзляк (Вентана-Граф)».

Пособие содержит в себе много полезной информации:

1. Верные ключи ко всем номерам из оригинального учебника.
2. Развернутые описания хода каждого решения.
3. Детальные разъяснения от составлявших его методистов.

Высока вероятность, что ребенок, разобравшись в геометрии, сможет найти себя. Быть может, это направление станет ему настолько интересно, что он решит развивать свои познания в дальнейшей жизни. К примеру хороший высокооплачиваемый инженер должен знать немало из курса геометрии.

Отличительные черты ГДЗ

Дополнительное онлайн-пособие облегчит учебную жизни девятиклассника. Все потому, что в нем собрано огромное количество нужных и, главное, достоверных сведений. Учебник разбит на несколько разделов, каждый из которых содержит в себе важную инф-цию. Среди тем, что предстоит освоить подросткам:

• свойства многоугольников;
• расстояние от точки А до В и методы вычисления координат;
• применение вектора;
• подробный разбор стереометрии.

Каждый школьник знает, что мало просто решить задачу – ее нужно верно оформить. Авторы книги позаботились об учениках и предоставили им несколько примеров оформления рабочей тетради. В справочнике также можно найти инструкцию по выполнению чертежей.

Что даст использование онлайн-решебника по геометрии для 9 класса от Мерзляка

Решебник сможет с легкостью заменить репетитора. Над его созданием около шести лет работали опытные теоретики, времени и сил ушло много. Это говорит о том, что «ГДЗ по геометрии за 9 класс Мерзляк, Полонский, Якир(Вентана-граф)» является консультантом, созданным не для простого списывания, а ради углубленного изучения предмета. С помощью задачника учащийся сможет развить в себе способность мыслить математически, что не может не пригодиться во взрослой жизни. В онлайн-сборнике есть информация касаемо теорем и способов их доказательства, так что онлайн-издание поможет школьнику еще и улучшить свою речь и научит грамотно и логически высказывать свои мысли.

С геометрией в 9 классе могут возникнуть трудности у многих детей. Ведь на носу переводной экзамен, а это значит что нужно срочно повторять пройденный материал и как-то выучить новый. Школьникам очень сложно бывает уместить всю поступающую и уже поступившую информацию в своей голове. Множество теорем, правил и формул, которые нужно знать, скорее всего, вызовут у детей отчаяние и могут даже оттолкнуть от качественного разбора всего материала. Конечно, школьная программа рассчитана повторение материала прошлых лет, но стандартных 45 минут в школе бывает недостаточно, чтобы ребенок получил все необходимые знания, тем более новых тем в этой дисциплине будет очень много.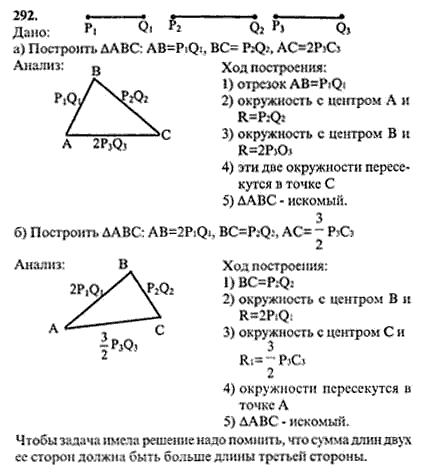 Конечно, учителя стараются снабдить ребят всей информацией, которая может понадобиться в ходе экзамена и в дальнейшей жизни. Но так как времени всегда не хватает, зачастую приходится нанимать репетиторов, чтобы школьник был подготовлен ко всем нюансам в самых сложных заданиях. Но и в школьном учебнике могут найтись задачи, которые создадут трудности для многих, а тратить с репетитором время на это не хочется.

В этой ситуации школьнику поможет онлайн-решебник по геометрии за 9 класс от автора А. Г. Мерзляк, Издательство: Вентана-граф, 2016 год.

Если ребенок прогуливал уроки или не может понять какую-либо тему, то еще рано отчаиваться, ведь можно быстро нагнать сверстников, проходя непонятные темы и прорешивая задачи. Благодаря представленному справочнику ребята получат возможность делать это самостоятельно. Также данный сборник будет полезен отличникам, которые захотят свериться с правильными ответами, не тратя время на проверку учителем или на поиски ответа в интернете.

Какую еще пользу может принести учебно-методический комплекс по геометрии за 9 класс (авторы: Мерзляк, Полонский, Якир)

Пользу этот сборник принесет не только учащимся, но и родителям, которым будет проще помогать ребенку с домашней работой и объяснять непонятные моменты, ведь в решениях написаны подробные комментарии. Прочие преимущества:

• четкое, ясное изложение материала, правильные ответы ко всем заданиям;
• открывается на любой удобной для вас платформе;
• верные и актуальные примеры оформления;
• возможность изучения разделов самостоятельно.

Содержание справочника по геометрии для 9 класса от Мерзляк

Это пособие включает в себя все главы, рекомендуемые к изучению на данный период обучения:

• формулы для нахождения площади треугольников;
• правильные многоугольники;
• расстояние между двумя точками;
• угловой коэффициент прямой.

Статистика ячеек S2 | S2Geometry

Это приблизительные диапазоны площадей ячейки S2 на каждом уровне. Средний размер возвращается функцией S2Cell.AverageArea() , гарантированно находится в пределах коэффициента 1,5 от верхнего и нижнего пределов диапазона. Кроме того, были выбраны два случайных местоположения для предоставления примера края ячейки. длины.

уровень	минимальная площадь	максимальная площадь	средняя площадь	шт.		Случайная ячейка 1 (Великобритания) мин. длина ребра	Случайная ячейка 1 (Великобритания) макс. длина ребра		Случайная ячейка 2 (США) мин. длина ребра	Случайная ячейка 2 (США) макс. длина ребра	Количество ячеек
00	85011012. 19	85011012.19	85011012.19	км 2		7842 км	7842 км		7842 км	7842 км	6
01	21252753.05	21252753.05	21252753.05	км 2		3921 км	5004 км		3921 км	5004 км	24
02	4919708.23	6026521.16	5313188.26	км 2		1825 км	2489 км		1825 км	2489 км	96
03	1055377.48	1646455,50	1328297. 07	км 2		840 км	1167 км		1130 км	1310 км	384
04	231564.06	413918.15	332074.27	км 2		432 км	609 км		579 км	636 км	1536
05	53798,67	104297.91	83018.57	км 2		210 км	298 км		287 км	315 ​​км	6К
06	12948,81	26113.30	20754,64	км 2		108 км	151 км		143 км	156 км	24К
07	3175,44	6529. 09	5188,66	км 2		54 км	76 км		72 км	78 км	98К
08	786,20	1632,45	1297.17	км 2		27 км	38 км		36 км	39 км	393К
09	195,59	408.12	324,29	км 2		14 км	19 км		18 км	20 км	1573К
10	48,78	102.03	81.07	км 2		7 км	9 км		9 км	10 км	6М
11	12. 18	25,51	20,27	км 2		3 км	5 км		4 км	5 км	25М
12	3,04	6,38	5,07	км 2		1699 м	2 км		2 км	2 км	100М
13	0,76	1,59	1,27	км 2		850 м	1185 м		1123 м	1225 м	402М
14	0,19	0,40	0,32	км 2		425 м	593 м		562 м	613 м	1610М
15	47520. 30	99638,93	79172,67	м 2		212 м	296 м		281 м	306 м	6Б
16	11880.08	24909,73	19793.17	м 2		106 м	148 м		140 м	153 м	25Б
17	2970.02	6227.43	4948,29	м 2		53 м	74 м		70 м	77 м	103Б
18	742,50	1556,86	1237.07	м 2		27 м	37 м		35 м	38 м	412Б
19	185,63	389,21	309,27	м 2		13 м	19 м		18 м	19 м	1649Б
20	46,41	97,30	77,32	м 2		7 м	9 м		9 м	10 м	7Т
21	11,60	24,33	19,33	м 2		3 м	5 м		4 м	5 м	26Т
22	2,90	6,08	4,83	м 2		166 см	2 м		2 м	2 м	105Т
23	0,73	1,52	1,21	м 2		83 см	116 см		110 см	120 см	422Т
24	0,18	0,38	0,30	м 2		41 см	58 см		55 см	60 см	1689Т
25	453,19	950. 23	755,05	см 2		21 см	29 см		27 см	30 см	7e15
26	113,30	237,56	188,76	см 2		10 см	14 см		14 см	15 см	27e15
27	28,32	59,39	47,19	см 2		5 см	7 см		7 см	7 см	108e15
28	7,08	14,85	11,80	см 2		2 см	4 см		3 см	4 см	432e15
29	1,77	3,71	2,95	см 2		12 мм	18 мм		17 мм	18 мм	1729e15
30	0,44	0,93	0,74	см 2		6 мм	9 мм		8 мм	9 мм	7e18

Эволюция: как геометрия формирует разделение труда

1. Мерлин Стапс,
2. Корина Тарнита,

1. Департамент экологии и эволюционной биологии, Принстонский университет, США;

Наше тело состоит из клеток, выполняющих определенные функции: эритроциты переносят кислород, клетки сетчатки обнаруживают свет, а иммунные клетки борются с патогенами. Однако самые ранние многоклеточные организмы не имели таких специализированных клеток, и то, как впервые возникло разделение труда между клетками, остается неизвестным (Bonner, 2000; Brunet and King, 2017; van Gestel, Tarnita, 2017).

Одним из наиболее хорошо изученных примеров разделения труда является разделение труда между зародышевыми клетками, которые размножаются, и соматическими клетками, единственной целью которых является обеспечение выживания зародышевых клеток. Дифференциация между зародышевыми и соматическими клетками неоднократно развивалась и происходит даже у простых многоклеточных организмов с гораздо меньшим количеством типов клеток, чем у животных, таких как зеленые водоросли или социальные амебы. Поскольку невозможно определить, какое давление отбора приводило к эволюции дифференцировки зародышевых и соматических клеток сотни миллионов лет назад, биологи обратились к математическим моделям, чтобы понять, как возникли зародышевые и соматические клетки (Гаврилец, 2010; Мишод, 2007).

Модели эволюции дифференцировки зародышевой сомы исходят из предположения, что клетки внутри многоклеточной группы могут инвестировать ресурсы в выживание группы, размножение или их комбинацию. Используя эти модели, исследователи могут задаться вопросом, какие условия позволяют развиваться специализированным клеткам, которые инвестируют только в размножение (зародыши) или выживание (сома). Предыдущая работа показала, что разделение труда может развиваться только в строгих условиях, когда специализированные клетки должны лучше (то есть более эффективно) выполнять свою работу, чем неспециализированные клетки (Michod, 2007). Но эти условия, возможно, не обязательно были соблюдены на раннем этапе эволюции разделения труда.

Теперь в eLife Питер Юнкер, Уильям Рэтклифф и их коллеги из Технологического института Джорджии, включая Дэвида Янни и Шейна Якобина в качестве первых авторов, Педро Маркеса-Закариаса и Джошуа Вайца, сообщают, что геометрия некоторых ранних многоклеточных организмов может облегчили развитие разделения труда (Yanni et al.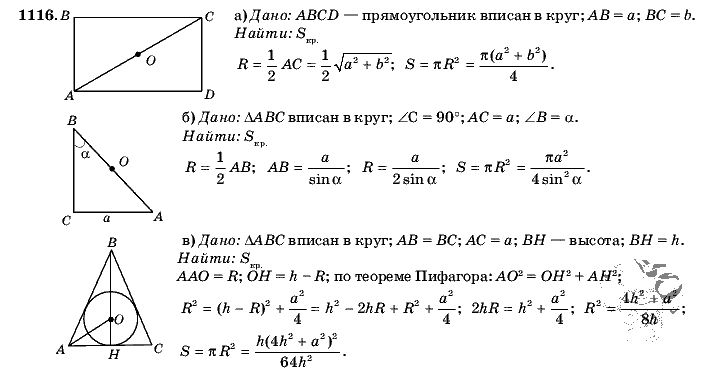 , 2020). Команда разработала модель дифференцировки зародыша и сомы, которая включает пространственную структуру. В то время как более ранние модели предполагают, что инвестиции в выживание объединяются и распределяются между всеми ячейками, модель, созданная Yanni et al. предполагает, что инвестиции клетки в выживание распределяются только с непосредственными соседями (рис. 1). В этой установке форма многоклеточной группы играет решающую роль, поскольку она определяет, какие клетки являются соседними.

Как геометрия влияет на дифференцировку клеток.

У многих многоклеточных организмов развилась дифференцировка зародыш-сома — разделение труда между зародышевыми клетками, специализирующимися на размножении, и соматическими клетками, которые помогают организму выживать. Янни и др. показывают, что многоклеточные организмы с разреженной клеточной геометрией, такой как структура, показанная здесь, с большей вероятностью будут развивать дифференцировку зародыш-сома. В таких организмах зародышевые клетки (фиолетовые) могут чередоваться с соматическими клетками (синие), поэтому инвестиции в выживание, сделанные соматическими клетками, приносят пользу исключительно зародышевым клеткам (серые стрелки).

Янни и др. обнаружили, что «разреженная» геометрия, в которой клетки имеют мало соседей, такие как нити и деревья, особенно способствует эволюции дифференцировки зародышевой сомы. В этих структурах регулярно расположенные клетки берут на себя роль зародыша, в то время как промежуточные клетки становятся соматическими, чтобы поддерживать репродуктивные клетки (рис. 1). Таким образом, инвестиции в выживание, сделанные соматическими клетками, теперь распределяются исключительно с зародышевыми клетками, а не со всеми клетками в группе, включая другие соматические клетки. Янни и др. показали, что такое эффективное разделение преимуществ выживания ослабляет условия, при которых может развиваться разделение труда: в разреженных многоклеточных геометриях разделение труда может быть благоприятным даже тогда, когда специализированные клетки немного менее эффективны, чем неспециализированные.

Интересно, что во многих существующих многоклеточных организмах пространственная организация зародышевых и соматических клеток повторяет модель, предсказанную моделью. Например, у цианобактерий роль соматических клеток берут на себя специализированные фиксаторы азота, регулярно расположенные вдоль филаментов для поддержки окружающих репродуктивных клеток (Flores and Herrero, 2010). И хотя сложные многоклеточные организмы, которые находятся за пределами досягаемости этой модели, обычно не имеют регулярно расположенных зародышевых клеток, проблески предсказанной организации все же можно увидеть. Например, яйцеклетки плодовой мушки развиваются из скопления взаимосвязанных клеток, из которых только одна становится яйцеклеткой, а окружающие клетки берут на себя вспомогательную роль (Bastock, St Johnston, 2008; Алсус и др., 2018).

В то время как модели, такие как Yanni et al. проливают свет на эволюционные силы, формирующие дифференцировку клеток, они мало говорят нам о лежащих в их основе механизмах (Márquez-Zacarías et al. , 2020). Эти находки, однако, дают многообещающее представление: если дифференцировка зародышевой сомы связана со специфической пространственной организацией, то ее эволюция требует механизмов развития, которые позволяют клеткам дифференцироваться в соответствии с их местоположением. Будущая цель состоит в том, чтобы понять, как такие механизмы развития возникли в ходе эволюции.

Каталожные номера

1. 1. Алсус JI
   2. Вильютрейкс P
   3. Ступ N
   4. Шварцман С.Ю.
   5. Дункель J

   (2018) Энтропийные эффекты в упаковках деревьев клеточных линий

   Nature Physics 14 :1016–1021.

   https://doi.org/10.1038/s41567-018-0202-0

   • пабмед
   • Google ученый
2. 1. Басток R
   2. Сент-Джонстон D

   (2008) Дрозофила оогенез

   Современная биология 18 :R1082–R1087.

   https://doi.org/10.1016/j.cub.2008.09.011

   • пабмед
   • Google ученый

3. Книга

   1. Боннер JT

   (2000) Первые сигналы: эволюция многоклеточного развития

   Princeton University Press.

   https://doi.org/10.1515/9781400830589

   • Google ученый
4. 1. Брюнет Т
   2. Король N

   (2017) Происхождение многоклеточности животных и дифференцировка клеток

   Клетка развития 43 :124–140.

   https://doi.org/10.1016/j.devcel.2017.09.016

   • пабмед
   • Google ученый
5. 1. Флорес E
   2. Эрреро А

   (2010) Компартментальная функция посредством дифференцировки клеток у нитчатых цианобактерий

   Nature Reviews Microbiology 8 :39–50.

   https://doi.org/10.1038/nrmicro2242

   • пабмед
   • Google ученый
6. 1. Гаврилец С

   (2010) Быстрый переход к разделению труда через эволюцию пластичности развития

   PLOS Вычислительная биология 6 :e1000805.

   https://doi.org/10.1371/journal.pcbi.1000805

   • пабмед
   • Google ученый
7. 1. Маркес-Закариас P
   2. Пино
   ринггитов
   3. Гомес М
   4. Велиз-Куба А
   5. Мурругарра Д
   6. Рэтклифф туалет
   7. Никлас KJ

   (2020) Эволюция клеточной дифференцировки: от гипотез к моделям

   Тенденции экологии и эволюции 13.

   https://doi.org/10.1016/j.tree.2020.07.013

   • Google ученый
8. 1. Мишо RE

   (2007) Эволюция индивидуальности при переходе от одноклеточной к многоклеточной жизни

   PNAS 104 :8613–8618.

   https://doi.org/10.1073/pnas.0701489104

   • пабмед 909:30
   • Google ученый
9. 1. ван Гестель J
   2. Тарнита CE

   (2017) О происхождении биологического строения с упором на многоклеточность

   PNAS 114 :11018–11026.

   https://doi.org/10.1073/pnas.1704631114

   • пабмед
   • Google ученый
10. 1. Янни Д
    2. Якобин S
    3. Маркес-Закариас P
    4. Вайц JS
    5. Рэтклифф туалет
    6. Юнкер ПИ 909:30

    (2020) Топологические ограничения ранней многоклеточности благоприятствуют репродуктивному разделению труда

    eLife 9 :e54348.

    https://doi.org/10.7554/eLife.54348

    • пабмед
    • Google ученый

Статья и информация об авторе

Сведения об авторе

1. Merlijn Staps

   Merlijn Staps находится на кафедре экологии и эволюционной биологии Принстонского университета, Принстон, США

   Конкурирующие интересы

   Конкурирующие интересы не заявлены «Этот ORCID iD идентифицирует автора этой статьи:» 0000-0003-4869-4817

2. Корина Тарнита

   Корина Тарнита работает на факультете экологии и эволюционной биологии Принстонского университета, Принстон, США

   Для корреспонденции

   [email protected]

   Конкурирующие интересы

   Конкурирующие интересы не заявлены «Этот ORCID iD идентифицирует автора этой статьи:» 0000-0003-4476-0012

История публикаций

1. Версия записи опубликована: 3 ноября 2020 г. (версия 1)

Авторское право

© Staps and Tarnita, 2020 г.

Эта статья распространяется в соответствии с условиями лицензии Creative Commons Attribution, которая разрешает неограниченное использование и распространение при условии указания оригинального автора и источника.

Показатели

Число цитирований статей, полученное путем опроса самых высоких значений из следующих источников: Crossref, PubMed Central, Scopus.

Ссылки для скачивания

Список ссылок, состоящий из двух частей, для загрузки статьи или частей статьи в различных форматах.

Загрузки (ссылка для скачивания статьи в формате PDF)

• Статья PDF

Открытые цитаты (ссылки для открытия цитат из этой статьи в различных онлайн-сервисах управления ссылками)

• Менделей
• ЧитатьКуб»>

Процитируйте эту статью (ссылки для загрузки цитат из этой статьи в форматах, совместимых с различными инструментами управления ссылками)

1. Мерлин Стапс
2. Корина Тарнита

(2020)

Эволюция: как геометрия формирует разделение труда

eLife 9 :e63328.