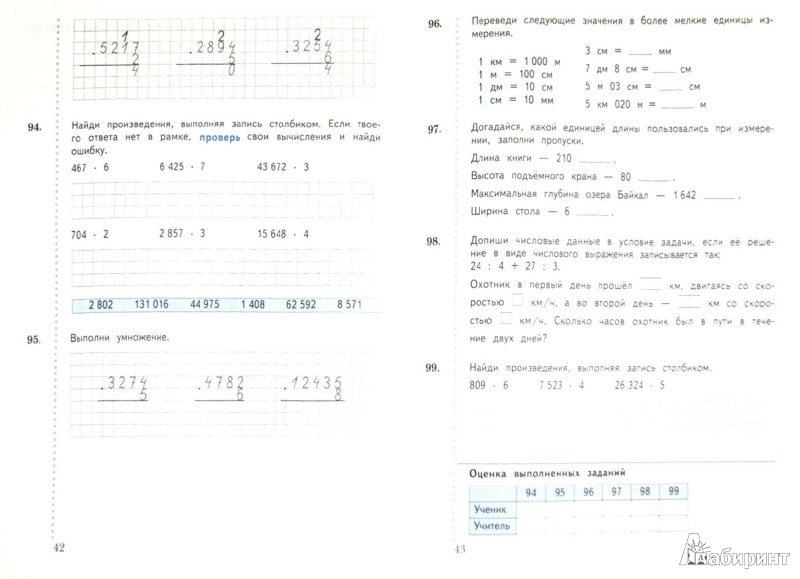
ГДЗ по математике для 3 класса рабочая тетрадь Дружим с математикой Кочурова Е.Э.
Авторы: Кочурова Е.Э.
Решебник по математике для 3 класса рабочая тетрадь Дружим с математикой, Кочурова Е.Э. . Подробные и качественные решения задач ФГОС онлайн от Спиши фан.
Задания
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179
gejocem гдз по математике 4 класс рабочая тетрадь кочурова дружим с математикой ответы
投稿日：2017年04月10日（月）
Ссылка:
http://onakygu.
sabemo.ru/5/64/gdz-po-matematike-4-klass-rabochaya-tetrad-kochurova-druzhim-s-matematikoy-otvety
гдз по математике 4 класс рабочая тетрадь кочурова дружим с математикой ответы
гдз по математике.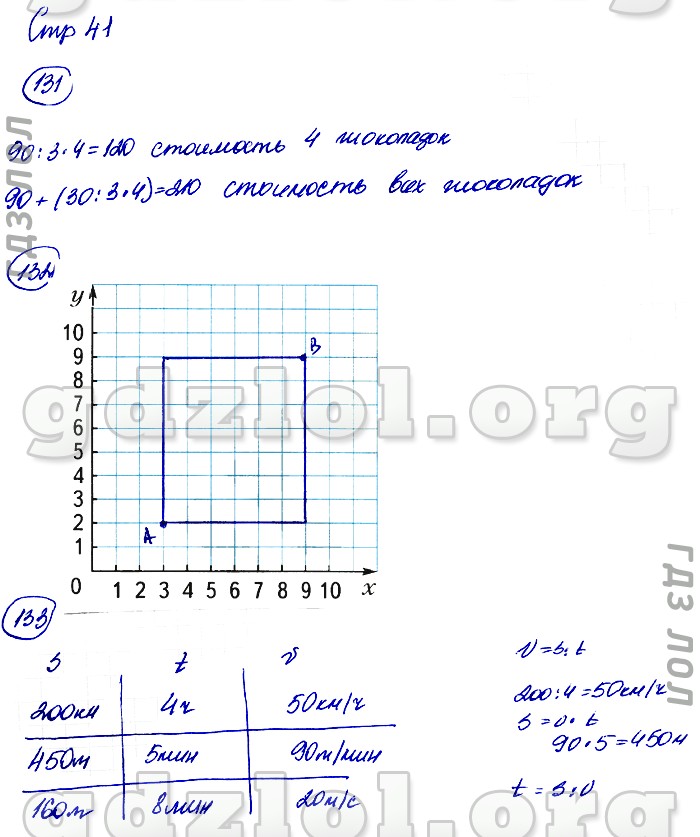
Talk Math With Your Friends
Talk Math With Your Friends (TMWYF) — это еженедельный виртуальный коллоквиум по математике. Спикер будет выступать в течение 45 минут, а затем 15 минут на вопросы и обсуждение. Выступления будут записываться и размещаться при условии согласия спикера.
Нажмите кнопку ниже, чтобы присоединиться к нам в прямом эфире через Zoom каждый четверг с 3:30 до 4:30 по восточному времени (с 12:30 до 1:30 по тихоокеанскому времени). Более подробная информация находится на нашей странице информации о Zoom.
Присоединяйтесь через Zoom по четвергам в 15:30 по восточному времени!
12 мая 2022 г. 15:30–16:30 по восточному времени (12:30–13:30 по тихоокеанскому времени). Боланле Салаам, Университет Джорджии
Студенты думают сквозь призму реального анализа: необходимые знания, необходимость времени и пути продвижения вперед «понимание» и «обучение» — непостижимые состояния по своей сути; не существует механизма, позволяющего исследователю или преподавателю заглянуть в мысли студентов. Это естественным образом приводит к опоре на письменные и устные высказывания учащихся, наблюдаемые действия и успеваемость как на ключевые источники понимания того, как учащиеся занимаются математикой.
В этом докладе обсуждаются теоретические последствия несоответствия между письменными, принятыми и достигнутыми целями учебной программы по математике в пространстве K-16 через призму первой недели студента курса реального анализа для выпускников. Я использую теорию коммуникации Сфарда, чтобы выявить нюансы рассогласования учебных целей, и представляю два новых инструмента, основанных на деревьях реализации Сфарда (я назвал эти дискурсивные карты и вызванные деревья), которые могут помочь в изучении продвинутого математического мышления учащихся. Я воспользуюсь первой страницей первой главы книги Рудина «Реальный и комплексный анализ» (3Е), чтобы мотивировать дискуссию.
Приглашаем всех на этот разговор; он будет доступен любому, кто знаком с основами исчисления одной переменной вплоть до интегрирования. Вся другая соответствующая справочная информация будет предоставлена. Зрителям будет предоставлена возможность создавать дискурсивные карты и / или вызванные деревья, поэтому, пожалуйста, присоединяйтесь к устройству, на котором вы можете рисовать на сенсорном экране или на котором вам удобно писать с помощью мыши.
Если вы решите внести свой рисунок в этот сеанс, ваше имя будет автоматически анонимизировано.
Для заинтересованных слушателей я предлагаю несколько вопросов для рассмотрения перед выступлением, которые подчеркивают потенциальную возможность различий в том, что ожидается от мышления студентов экспертами-математиками, и в том, как студенты описывают свое собственное мышление:
Прочитать первое страница абстрактной главы об интеграции Рудина, где делается краткое введение в теорию интеграции Лебега. Каков самый высокий уровень математического содержания, с которым, по вашему мнению, должен быть знаком студент, чтобы следовать этому введению?
На каких предыдущих курсах, по вашему мнению, учащийся должен был ознакомиться с содержанием, которое вы назвали в ответ на первый вопрос?
Какие связи, по вашему мнению, должен установить учащийся с содержанием K-16, чтобы понять смысл этого введения? Какие связи вы делаете с предыдущим контентом K-16, чтобы понять смысл этого вступления?
Пожалуйста, не стесняйтесь обсуждать свои мысли по электронной почте на bsalaam at uga dot edu или делиться ими во время дискуссионной части выступления.
Следите за обновлениями!
Четверг 3: 30-4: 30 вечера по восточному (12: 30-1: 30 Тихоокеанский регион)
2/10 — Майкл Барани
3/3 — Дэн МакКуллан
3 3/3 /17 — Adriana Salerno
3/31 — OURFA 2 M 2
4/14 — Mandy Jansen
5/5 — Nicole Joseph, Ashli-Ann Douglas, Mariah Harmon
5/12 — Bolanle Salaam
Переседование — Shraddha Shirude
- . Во время бурного изучения математики в колледже Ванесса Сан писала о своем положительном и отрицательном опыте в математике как об исцелении, как о выражении своей радости и боли от утраты любви к математике и как о призыве к действию для тех, кто в математическое сообщество, чтобы прислушиваться к потребностям своих студентов и коллег.
На этом сеансе Ванесса обнажит свою душу, прочитает некоторые стихи и мемуары, которые она написала, а также обсудит истории, лежащие в их основе.14 апреля 2022 г. 15:30–16:30 по восточному времени (12:30–13:30 по тихоокеанскому времени). Д-р Аманда Янсен, Университет Делавэра
Черновой набросок Математика: повторение для обучения
Целью этого занятия является обсуждение интеграции использования черновика и повторения в преподавание математики. Учителя K-12 сообщают, что наброски и исправления на уроках математики могут создать безопасное пространство для учеников, чтобы они могли поделиться своими мыслями, сосредоточиться на понимании, а не на получении ответов, и подчеркнуть, что обучение — это постоянный, непрерывный процесс развития мышления. Я поделюсь идеями учителей классов K-12 о том, как они интегрируют наброски и исправления в свои уроки математики, чтобы вызвать обсуждение.
5 мая 2022 г. 15:30–16:30 по восточному времени (12:30–13:30 по тихоокеанскому времени). Николь Джозеф, Эшли-Энн Дуглас, Мэрайя Хармон, Университет Вандербильта
«Мне нравится делать больше практических вещей, чем просто рабочие листы:» истории чернокожих школьниц об их опыте в городских классах математики
В этом исследовании использовалась математическая педагогика черных феминисток, чтобы понять опыт 48 чернокожих девочек 10 и 11 классов в средних классах математики. Повышение их голоса привело к знаниям, созданным чернокожими девочками, которые показали, что они часто сталкивались с равнодушными учителями, учебными программами и занятиями, которые не были интересными, и неблагоприятная учебная среда. Такой опыт ограничивал их восприятие полезности математики вне школы и их будущей карьеры. Результаты также показали, что их предыдущий и текущий опыт в математике не способствовал положительной математической идентичности.
Последствия для учителей, общих педагогов, чернокожих девочек, и их семьи обсуждаются, а затем Ap Приложение C, в котором перечислены действия, которые учителя математики могут предпринять сейчас, чтобы начать оказывать поддержку чернокожим девочкам в своих классах.31 марта 2022 г., 15:30–16:30 по восточному времени (12:30–13:30 по тихоокеанскому времени). Люк Ситон, Ванесса Сан и Ли Трент; the Online Undergraduate Resource Fair for the Advancement and Alliance of Marginalized Mathematicians (OURFA 2 M 2 ) [website, padlet1, padlet2]
Lessons from OURFA 2 M 2
Ярмарка онлайн-ресурсов для бакалавров, посвященная продвижению и альянсу маргинализированных математиков (OURFA 2 M 2 ) — это ежегодная онлайн-конференция, организованная нынешними и недавними студентами бакалавриата.
Мы разработали конференцию, чтобы соединить недопредставленных и маргинализированных студентов-математиков с ресурсами для построения карьеры, предоставить им пространство для студентов и самих студентов, а также укрепить их уверенность посредством представительства и поощрения. Наша конференция привлекает более 350 зарегистрировавшихся, включая студентов и профессиональных математиков, для общения и различных личных, профессиональных и технических переговоров.В этом выступлении мы опираемся как на наш личный опыт, так и на то, что мы узнали в ходе организации конференции. Мы выясним, в чем не хватает нынешнего наставничества студентов, и предложим способы, которыми преподаватели могут работать над поиском решений. Мы также поделимся тем, как преподаватели и другие специалисты могут улучшить свою защиту маргинализированных математиков и другие организационные усилия.
17 марта 2022 г. 15:30–16:30 по восточному времени (12:30–13:30 по тихоокеанскому времени).
Адриана Салерно, Колледж Бейтса и Национальный научный фондКонструкции оригами высших измерений
Оригами — древнее искусство, которое и по сей день продолжает приносить как художественные, так и научные открытия. В 2012 году Бюлер, Батлер, де Лони и Грэм еще больше расширили эти идеи, разработав математическую конструкцию, вдохновленную оригами, в которой мы итеративно строим точки на сложной плоскости («бумаге») из набора начальных точек ( или «исходные точки») и линии через эти точки с заданными углами (или допустимыми «сгибами» на нашей бумаге). Любые две линии с этими заданными углами через исходные точки, которые пересекаются, создают новую точку, и, повторяя этот процесс для каждой сформированной пары точек, мы создаем подмножество комплексной плоскости. Мы распространяем ранее известные результаты об алгебраической и геометрической структуре этих множеств на более высокие измерения.
В случае, когда полученное множество представляет собой решетку, мы исследуем связь между множеством углов и образующими решетки и определяем, как введение нового угла изменяет решетку. (Совместная работа с Девиной Банерджи и Сарой Чари).3 марта 2022 г. 15:30–16:30 по восточному времени (12:30–13:30 по тихоокеанскому времени). Dan McQuillan, Norwich University
Вершинно-магические полные маркировки графов [ слайды ]
Полная маркировка графа G есть присвоение целых чисел, v, 1,2,… +e, к v вершинам и e ребрам G. Вес вершины равен сумме ее «метки» с суммой меток инцидентных ей ребер. Полная маркировка является вершинной магией (или VMTL), если вес каждой вершины является константой, называемой магической константой для VMTL. Вопросы легко сформулировать и разумно решить.
Многие результаты и доказательства весьма элегантны. Остается много открытых проблем, доступных для студентов бакалавриата. В этом докладе будут обсуждаться несколько прошлых успехов в исследованиях бакалавриата и возможные будущие проекты.10 февраля 2022 г. 15:30–16:30 по восточному времени (12:30–13:30 по тихоокеанскому времени). Майкл Барани, Эдинбургский университет
Можно ли спасти глобальную математику? Должно ли это быть?
Сегодня для математиков обычно и во многих случаях ожидается взаимодействие с работой и людьми из других стран и часто с других континентов. Математики часто путешествуют на большие расстояния по своему призванию, и нередко карьера строится за счет международной миграции. Я определяю глобальную математику как отдельный исторический феномен в современной истории математики и утверждаю, что ее следует понимать как недавнее, временное, случайное и ненадежное развитие, объясняя в процессе, что делает этот аргумент важным для историков математики.
На этом сеансе Ванесса обнажит свою душу, прочитает некоторые стихи и мемуары, которые она написала, а также обсудит истории, лежащие в их основе.
Последствия для учителей, общих педагогов, чернокожих девочек, и их семьи обсуждаются, а затем Ap Приложение C, в котором перечислены действия, которые учителя математики могут предпринять сейчас, чтобы начать оказывать поддержку чернокожим девочкам в своих классах.
Мы разработали конференцию, чтобы соединить недопредставленных и маргинализированных студентов-математиков с ресурсами для построения карьеры, предоставить им пространство для студентов и самих студентов, а также укрепить их уверенность посредством представительства и поощрения. Наша конференция привлекает более 350 зарегистрировавшихся, включая студентов и профессиональных математиков, для общения и различных личных, профессиональных и технических переговоров.
Адриана Салерно, Колледж Бейтса и Национальный научный фонд
В случае, когда полученное множество представляет собой решетку, мы исследуем связь между множеством углов и образующими решетки и определяем, как введение нового угла изменяет решетку. (Совместная работа с Девиной Банерджи и Сарой Чари).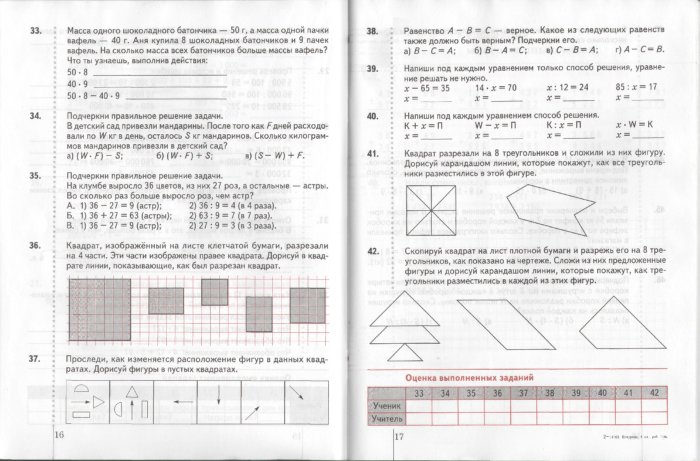
Многие результаты и доказательства весьма элегантны. Остается много открытых проблем, доступных для студентов бакалавриата. В этом докладе будут обсуждаться несколько прошлых успехов в исследованиях бакалавриата и возможные будущие проекты.