ГДЗ по геометрии 9 класс от Путина: решебники
ГДЗ по геометрии для 9 класса – это решебники по предмету, которые содержат готовые решения и ответы на упражнения базовых учебников, используемых в большинстве российских школ.
ГДЗ от Путина по геометрии для 9 класса – основа подготовки к экзаменам
По окончании 9 класса школьников ожидает цикл итоговых экзаменов, которые позволяют им получить свидетельство о неполном среднем образовании. Одним из самых сложных предметов школьной программы, который требует особого внимания в преддверии ГИА является геометрия.
Многие ребята испытывают затруднения в ходе выполнения домашней работы ввиду того, что задачки по предмету требуют не только идеального знания теории, но также абстрактного мышления и умения интерпретировать условия упражнения в зрительные образы.
В связи с этим серьезным подспорьем школьников становятся решебники по геометрии для 9 класса, которые содержат задачки по таким темам курса, как:
- метод координат и уравнения плоских фигур;
- соотношения между углами и сторонами треугольника – синус, косинус, тангенс, котангенс;
- скалярное произведение векторов;
- длина и площадь круга.
В учебниках рассматривается сложное и практически важное понятие движения, которое проявляется в феноменах центральной и осевой симметрии.
Онлайн-решебники от Путина по геометрии для 9 класса – удобный помощник девятиклассника
Широкий круг тем, углубленное изучение аксиом геометрии порой требует значительных временных затрат: школьники сидят над задачками по геометрии все оставшееся от учебы время. Для того чтобы существенно сократить временные затраты на подготовку домашней работы по геометрии стоит воспользоваться онлайн-решебниками.
На нашем сайте представлены практические пособия по всем основным учебникам по геометрии в самом актуальном варианте. Интерфейс ресурса максимально адаптирован под потребности пользователей:
- решение можно найти в один клик, выбрав нужный номер в приведенной выше таблице;
- использовать сайт можно с телефона, планшета, компьютера (ноутбука).
Всем школьникам, которые решат воспользоваться решебниками на нашем сайте предоставляется бесплатный доступ к онлайн сервисам.
При помощи одного из них можно моментально рассчитать площадь треугольника.
ГДЗ по Геометрии за 9 класс A.Г. Мерзляк, B.Б. Полонский
Геометрия 9 класс A.Г. Мерзляк
Авторы: A.Г. Мерзляк, B.Б. Полонский, М.С. Якир
Изучение фигур в пространстве необходимо в школьной программе для подготовки к поступлению в ВУЗы. Точные дисциплины считают самыми тяжёлыми для освоения и сдачи. Школьникам приходится заучивать много формул, шудировать материал и сдавать обязательный экзамен. Чтобы хорошо подготовиться к ОГЭ, следует много заниматься и тратить на это силы и внимание. Представленное «ГДЗ по Геометрии за 9 класс Мерзляк, Вентана-граф» откроет возможность отработки и проверки знаний по предмету.
ГДЗ по Геометрии за 9 класс Мерзляк выпускникам в помощь
В выпускном классе сдаётся ОГЭ по предметам, которые понадобятся для поступления в высшие учебные заведения.
Обычно, у ребят не остается свободного времени на решение домашних заданий, потому что все силы уходят на экзамены, репетиторов и дополнительные курсы. Поэтому на помощь приходят готовые материалы. Таким образом, школьники смогут без затруднений понять необходимую тему и выполнить по ней работу дома. Плюсы использования ГДЗ: быстрая и удобная проверка заданий, экономия времени для внешкольных занятий и доступное, полное и понятное разъяснение материала. Тем самым, девятиклассники смогут экономить время на домашние задания, при этом, успевая уделять внимание подготовке к экзаменам.
Структура учебника
На уроках геометрии в 9 классе ученики оттачивают знания по пройденному ранее материалу, учатся решать задачи, находить координаты и знакомятся с новыми геометрическими фигурами. Решение заданий в решебнике подробно расписано для более глубокого осмысления важности тем, понимания и применения алгоритмов к задачам. ГДЗ состоит из следующих разделов:
- 886 полностью решенных упражнений.
- Вопросы и ответы к параграфам учебника.
- Задания по типу «Проверь себя».
- Несколько примеров решения к работам.
- Подсказки и аннотации к усложненным упражнениям.
Таким образом, пособие поможет ученикам освоить школьный материал в сжатый срок. Родителям не придётся повторять весь учебник и нанимать репетитора. Учебник имеет две формы. Электронная версия находится на интернет – платформе. Чтобы найти нужное ГДЗ следует лишь иметь при себе мобильное устройство, ноутбук, планшет или компьютер, и доступ к сети. Это очень удобно, ведь теперь не нужно ходить по книжным магазинам в поисках решебника. Ответы есть всегда в интернете.
«ГДЗ по Геометрии за 9 класс А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Вентана-граф» поможет в решении сложных и непонятных домашних заданий. Полная версия есть в онлайн-варианте. Это лучший способ подготовиться к экзаменам и контрольным.Страница не найдена
Новости
Заведующая отделом по связям с общественностью Общероссийского профсоюза образования Елена Елшина рассказала о подарках ко Дню учителя.
1 окт
Минпросвещения и Рособрнадзор опубликовали проект расписания проведения Единого государственного экзамена (ЕГЭ) и Основного государственного экзамена (ОГЭ) в 2022 году.
1 октСледователи возбудили уголовное дело после сообщений о том, что более 20 учеников гимназии в Брянске обратились за медпомощью с признаками кишечной инфекции. Об этом сообщили в региональном главке СК России.
1 окт
Генеральный консул КНР в Санкт-Петербурге Ван Вэньли прокомментировала популярность ЕГЭ по китайскому языку.
Более 20 учеников гимназии № 3 в Брянске обратились в больницу с признаками кишечной инфекции, сообщила директор департамента образования и науки области Елена Егорова.
30 сен
Научный руководитель Института всеобщей истории РАН Александр Чубарьян рассказал о Всемирном конгрессе школьных учителей истории, который открывается в понедельник, 4 октября, в Москве.
30 сен
Мальчик пострадал при стрельбе в школе в американском городе Мемфис, штат Теннесси.
Геометрия шестерен и прикладная теория Эпизод 1, часть 10, стр.
Нгай Шан: 08.08.2014, 12:21
P1: GDZ / SPH P2: GDZ CB672-09 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля , 2004 0:16 9.4 Анализ контакта зубов 253 Рисунок 9.4.2: Применяемые системы координат. Численное решение системы нелинейных уравнений основано на применении соответствующей подпрограммы; см., например, More et al. [1980] и Visual Numerics, Inc. [1998]. Первое предположение о решении может быть получено из данных, полученных в результате локального синтеза.Мы проиллюстрируем обсуждаемый метод TCA следующей простой задачей плоской передачи. Задача 9.4.1. Рассмотрим три системы координат S 1, S 2 и S f, жестко связанные с ведущей шестерней 1, ведомой шестерней 2 и рамой f соответственно (рис. 9.4.2). Шестерня 1 снабжена эвольвентным профилем 1, который представлен в S 1 следующими уравнениями (рис.
9.4.3): x 1 = r b1 (sin θ 1 — θ 1 cos θ 1), y 1 = r b1 ( cos θ 1 + θ 1 sin θ 1), z 1 = 0. (9.4.23) Рисунок 9.4.3: Профиль 1 передачи 1.P1: GDZ / SPH P2: GDZ CB672-09 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0:16 254 Компьютерное моделирование зацепления и контакта Рисунок 9.4.4: Профиль 2 шестерни 2. Передача 2 — это снабженный эвольвентным профилем 2, который представлен в S 2 уравнениями (рис. 9.4.4) x 2 = r b2 (−sinθ 2 + θ 2 cos θ 2), y 2 = r b2 (−cosθ 2 — θ 2 sin θ 2), z 2 = 0. (9.4.24) Решение Применение основного принципа анализа контакта зубьев позволяет нам определить условия зацепления 1 и 2 в системе координат S f, используя следующую процедуру. : (1) Определим единичные нормали n 1 и n 2 к 1 и 2 в системах координат S 1 и S 2 соответственно.Единичные нормали к 1 и 2 должны иметь одинаковую ориентацию в точке касания профилей. (2) Затем представим профили 1 и 2 в системе координат S f и выведем уравнения их касания. (3) Используя уравнения касания, можно получить три уравнения следующей структуры: f 1 [(θ 1 — φ 1), (θ 2 + φ 2)] = 0 (9.
4.25) f 2 [(θ 1 — φ 1), r b1, r b2, E] = 0 (9.4.26) f 3 [θ 1, θ 2, r b1, r b2, E, (θ 1 — φ 1)] = 0. (9.4 .27) P1: GDZ / SPH P2: GDZ CB672-09 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0:16 9.4 Анализ контакта зубьев 255 (4) Анализ полученных уравнений показывает, что отношение dφ 1 / dφ 2 является постоянным и представлено как dφ 1 dφ 2 = — dθ 1 dθ 2 = r b2 г b1. (5) Мы можем определить линию действия по вектор-функции r (1) f (θ 1 — φ 1) и доказать, что линия действия является прямой линией. Ориентацию линии действия можно определить с помощью скалярного произведения af · (−if), где af = ∂r (1) f ∂θ 1 ∂r (1) f ∂θ 1 — единичный вектор линии действия.Процедура вывода следующая: Шаг 1: Уравнения (9.4.23) дают следующие выражения для единичной нормали к 1: n 1 = t 1 × k 1 = cos θ 1 i 1 — sin θ 1 j 1 ( при условии θ 1 = 0). (9.4.28) Здесь t 1 — единичная касательная к 1; k 1 — единичный вектор оси z 1. Шаг 2: Аналогичным образом, используя уравнения. (9.4.
24) получаем, что n 2 = k 2 × t 2 = cos θ 2 i 2 — sin θ 2 j 2. (9.4.29) Здесь t 2 — единичная касательная к 2; k 2 — единичный вектор оси z 2. Порядок кофакторов в уравнении.(9.4.29) обеспечивает ориентацию n 2, как показано на рис. 9.4.4. Шаг 3. Используя матричные уравнения r (i) f = M fi ri (θ i), n (i) f = L fi ni (θ i) (i = 1, 2), (9.4.30), получаем следующее уравнения касания: r (1) f (θ 1, φ 1) = r (2) f (θ 2, φ 2), n (1) f (θ 1, φ 1) = n (2) f (θ 2, φ 2). (9.4.31) Шаг 4. Векторные уравнения. (9.4.31) дает следующую систему скалярных уравнений: r b1 [sin (θ 1 — φ 1) — θ 1 cos (θ 1 — φ 1)] −r b2 [−sin (θ 2 + φ 2) + θ 2 cos (θ 2 + φ 2)] = 0 (9.4.32) r b1 [cos (θ 1 — φ 1) + θ 1 sin (θ 1 — φ 1)] −r b2 [−cos (θ 2 + φ 2) — θ 2 sin (θ 2 + φ 2)] — E = 0 (9.4.33) cos (θ 1 — φ 1) — cos (θ 2 + φ 2) = 0 (9.4.34) sin (θ 1 — φ 1) — sin (θ 2 + φ 2) = 0. (9.4.35 ) Шаг 5: Анализ уравнений. (9.4.34) и (9.4.35) получаем θ 1 — φ 1 = θ 2 + φ 2. (9.4.36) P1: GDZ / SPH P2: GDZ CB672-09 CB672 / Litvin CB672 / Litvin-v2.
cls 27 февраля 2004 г. 0:16 256 Компьютерное моделирование сеточных и контактных уравнений (9.4.32) и (9.4. 33), рассматриваемые одновременно, дают следующие соотношения: cos (θ 1 — φ 1) — r b1 + r b2 E = 0 (9.4.37) r b1 θ 1 + r b2 θ 2 — E sin (θ 1 — φ 1) = 0.(9.4.38) Система уравнений. (9.4.36) — (9.4.38) имеет структуру системы уравнений. (9.4.25) — (9.4.27) обсуждалось выше. Уравнения (9.4.36) — (9.4.38) дают θ 1 — φ 1 = θ 2 + φ 2 = const. (9.4.39) r b1 θ 1 + r b2 θ 2 = const. (9.4.40) Шаг 6: Дифференцирование уравнений. (9.4.39) и (9.4.40) получаем, что передаточное число постоянное и может быть представлено следующим образом: m 12 = dφ 1 dφ 2 = — dθ 1 dθ 2 = r b2 r b1. (9.4.41) Шаг 7: Линия действий представлена уравнением r (1) f = r b1 [sin (θ 1 — φ 1) — θ 1 cos (θ 1 — φ 1)] if + r b1 [cos (θ 1 — φ 1) + θ 1 sin (θ 1 — φ 1)] jf (9.4.42), где (θ 1 — φ 1) постоянная [см. (9.4.39)]. Векторная функция r (1) f (θ 1) является линейной, потому что (θ 1 — φ 1) = константа, а линия действия представляет собой прямую линию.
Единичный вектор линии действия представлен как af = ∂r (1) f ∂θ 1 ∂r (1) f ∂θ 1 = −cos (θ 1 — φ 1 ), если + sin (θ 1 — φ 1) jf. (9.4.43) Ориентация линии действия определяется скалярным произведением a f · (−i f) = cos (θ 1 — φ 1) = r b1 + r b2 E. (9.4.44) Линия действия проходит через точку I, лежащую на оси y f.Из (9.4.42) следует, что когда x (I) f = 0, имеем y (I) f = r b1 cos (θ 1 — φ 1). (9.4.45) Используя уравнения. (9.4.44) и (9.4.45) получаем y (I) f = r b1 r b1 + r b2 E = E 1 + m 12. (9.4.46) Схема действий показана на рис. 9.4.5. Легко проверить, что линия действия касается окружностей основания шестерни. Подчеркнем, что расположение и ориентация линии действия зависит от выбранного межцентрового расстояния E (учитывая заданные радиусы r b1 и r b2 базовых окружностей). P1: GDZ / SPH P2: GDZ CB672-09 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0:16 9.5 Применение анализа методом конечных элементов для проектирования зубчатых передач 257 Рисунок 9.
4.5: Расположение и ориентация линии действия. 9.5 ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО АНАЛИЗА ДЛЯ ПРОЕКТИРОВАНИЯ ЗУБЧАТЫХ ПРИВОДОВ Применение конечно-элементного анализа позволяет нам выполнять (i) анализ напряжений, (ii) исследование образования контакта подшипников и (iii) обнаружение сильных областей контактных напряжений. внутри цикла создания сетки. Такой подход требует (i) разработки зацепления конечных элементов зубчатой передачи, (ii) определения контактирующих поверхностей и (iii) установления граничных условий для нагружения зубчатой передачи.В этом разделе описывается подход авторов к конечно-элементному анализу при проектировании зубчатых колес. Подход основан на применении компьютерной программы общего назначения, представленной Hibbit, Karlsson & Sirensen, Inc. [1998]. Основные особенности разработанного подхода заключаются в следующем: (а) Конечно-элементная сетка создается автоматически с использованием уравнений поверхностей зубьев и обода. Узлы конечного зацепления получаются как точки поверхностей зубьев шестерни.
Таким образом, исключается потеря точности, связанная с разработкой твердотельных моделей с использованием компьютерных программ САПР (автоматизированного проектирования).Граничные условия для анализа напряжений шестерни и шестерни также устанавливаются автоматически. P1: GDZ / SPH P2: GDZ CB672-09 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0:16 258 Компьютерное моделирование зацепления и контакта (b) Модули для автоматического создания моделей конечных элементов интегрированы в систему. разработанные компьютерные программы. Следовательно, создание моделей конечных элементов может быть выполнено легко и быстро для любого положения контакта цикла зацепления. Кроме того, можно исследовать образование контакта подшипников и обнаруживать появление краевого контакта и области сильного контакта.Применение компьютерных программ САПР для разработки конечно-элементных моделей является промежуточным этапом существующего подхода к применению конечно-элементного анализа и имеет следующие недостатки: (1) Определение проволочных моделей, образованных шлицами, осуществляется численно.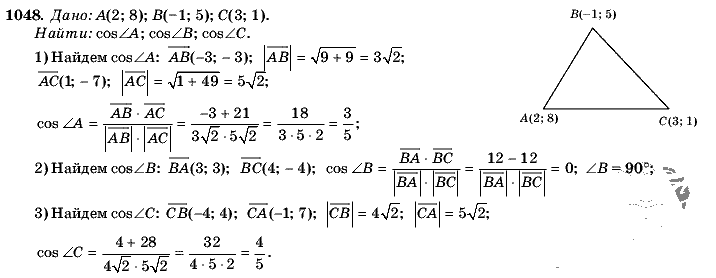
Проволочные модели состоят из плоских участков зубьев шестерен, которые используются для создания твердотельных моделей. (2) Конечно-элементные сетки твердотельных моделей требуют применения компьютерных программ для конечно-элементного анализа.(3) Необходимо определить граничные условия для конечноэлементных сеток. (4) Увеличение плоских участков зубьев шестерни улучшает точность проволочных и твердотельных моделей, но требует больших затрат времени. (5) Разработки, описанные выше, должны выполняться опытными пользователями компьютерных программ САПР, являются дорогостоящими с точки зрения времени и должны выполняться для каждого заданного случая проектирования зубчатых колес различной геометрии, для каждого положения зацепления и для различные расследования.Модифицированный подход, представленный в этом разделе, лишен упомянутых выше недостатков и может быть резюмирован следующим образом: Шаг 1: Используя уравнения обеих сторон поверхностей шестерни или зубьев шестерни и частей соответствующего обода, мы можем аналитически представить объем проектируемого корпуса.
На рис. 9.5.1 (а) показан спроектированный корпус для однозубой модели шестерни модифицированной эвольвентной косозубой зубчатой передачи. Шаг 2: Вспомогательные промежуточные поверхности с 1 по 6, показанные на рис. 9.5.1 (b), также определяются аналитически.Поверхности с 1 по 6 позволяют нам разделить зуб на шесть частей и контролировать дискретность этих подобъемов зуба на конечные элементы. Шаг 3: Аналитическое определение координат узлов выполняется с учетом количества искомых элементов в продольном и профильном направлениях [Рис. 9.5.1 (с)]. Подчеркнем, что все узлы конечноэлементной сетки определяются аналитически, и те, которые лежат на промежуточных поверхностях зуба, действительно являются точками, принадлежащими реальной поверхности.Шаг 4: Дискретизация модели конечными элементами с использованием узлов, определенных на предыдущем шаге, выполняется, как показано на рис. 9.5.1 (d). Шаг 5: Установка граничных условий для шестерни и шестерни выполняется автоматически следующим образом: (i) Узлы по бокам и в нижней части обода шестерни считаются фиксированными [Рис.
9.5.2 (а)]. P1: GDZ / SPH P2: GDZ CB672-09 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0:16 9.5 Применение конечноэлементного анализа для проектирования зубчатых передач 259 Рисунок 9.5.1: Иллюстрация (а) объема проектируемого тела, (б) вспомогательных промежуточных поверхностей, (в) определения узлов для всего объема и (г) дискретизации объема по конечным элементам. (ii) Узлы на двух сторонах и в нижней части обода шестерни образуют жесткую поверхность [Рис. 9.5.2 (b)]. Жесткие поверхности — это трехмерные геометрические структуры, которые не могут быть деформированы, но могут выполнять поступательное движение или вращение как твердые тела (Hibbit, Karlsson & Sirensen, Inc. [1998]).Они также очень рентабельны, потому что переменные, связанные с жесткой поверхностью, представляют собой перемещения и вращения одного узла, известного как опорный узел твердого тела [Рис. 9.5.2 (b)]. Базовый узел твердого тела расположен на оси вращения шестерни со всеми степенями свободы, за исключением вращения вокруг оси вращения шестерни, зафиксированной на нуле.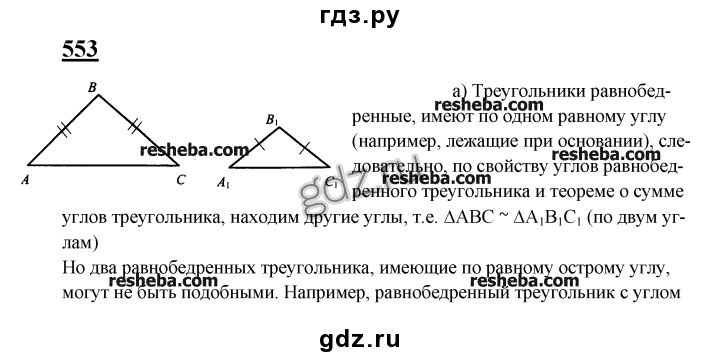
Крутящий момент прикладывается непосредственно к оставшейся степени свободы опорного узла твердого тела [Рис. 9.5.2 (b)]. Шаг 6: Определение контактных поверхностей для контактного алгоритма компьютерной программы с конечными элементами (Hibbit, Karlsson & Sirensen, Inc.[1998]) также выполняется автоматически и требует определения главной и подчиненной поверхностей. Обычно эталонная поверхность выбирается как поверхность более жесткого тела или как поверхность с более крупной сеткой, если две поверхности находятся на структурах с сопоставимой жесткостью. P1: GDZ / SPH P2: GDZ CB672-09 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0:16 260 Компьютерное моделирование зацепления и контакта Рис. 9.5.2: (a) Граничные условия для шестерни; (b) схематическое изображение граничных условий и приложения крутящего момента для шестерни.На рисунках с 9.5.3 по 9.5.5 показаны примеры конечно-элементных моделей конической зубчатой передачи со спиральной зубчатой передачей, косозубой зубчатой передачи и зубчатой передачи с торцевым червяком и коническим червяком, соответственно.
9.6 КРАЙНЫЙ КОНТАКТ Наиболее перспективная конструкция зубчатой передачи должна основываться на локализации контакта подшипника с поверхностями зубьев шестерни. Поверхности зубьев шестерни с локализованным контактом подшипников находятся в точке P1: GDZ / SPH P2: GDZ CB672-09 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0:16 9.6 Контакт кромок 261 Рисунок 9.5.3: Модель конечных элементов всей спиральной конической зубчатой передачи.контакт в любое мгновение, но не на линии. Однако в настоящее время существуют зубчатые передачи с поверхностями зубьев, которые все еще находятся в прямом контакте. Фактически, из-за ошибок совмещения теоретический мгновенный контакт на линии превращается в точечный, но он может сопровождаться краевым контактом (см. Ниже). Моделирование зацепления поверхностей зуба, находящихся в мгновенном точечном контакте, может выполняться компьютерными программами TCA (см. Раздел 9.4) на основе непрерывного касания поверхностей зуба, которые имеют общую нормаль в мгновенном точечном контакте.
Рисунок 9.5.4: Конечноэлементная модель всей винтовой зубчатой передачи. P1: GDZ / SPH P2: GDZ CB672-09 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0:16 262 Компьютерное моделирование зацепления и контакта Рис. 9.5.5: Модель конечных элементов червячной передачи. с коническим червяком. Контакт кромок означает, что вместо касания поверхностей кромка поверхности зуба одной шестерни находится в зацеплении с поверхностью зуба сопряженной шестерни. Контакт края может быть представлен следующими уравнениями: r (1) f (u 1 (θ 1), θ 1, φ 1) = r (2) f (u 2, θ 2, φ 2) (9.6.1) ∂r (1) f ∂θ 1 · N (2) f = 0. (9.6.2) Здесь r (1) f (u 1 (θ 1), θ 1, φ 1) представляет край поверхность зуба шестерни; ∂r (1) f / ∂θ 1 — касательная к ребру. Система уравнений (9.6.1) и (9.6.2) представляет собой систему четырех нелинейных уравнений с четырьмя неизвестными: θ 1, u 2, θ 2, φ 2; φ 1 — входной параметр. Аналогичные уравнения могут быть получены для случая касания кромки поверхности зуба шестерни с поверхностью зуба шестерни.
Контакт кромок может происходить в двух случаях: (i) когда поверхности зубьев шестерни изначально находятся в прямом контакте, и (ii) когда поверхности зубьев шестерни находятся в точечном контакте.Каждый случай обсуждается отдельно. Краевой контакт поверхностей зубьев шестерни, которые изначально находятся в прямом контакте. Мы начинаем обсуждение со случая прямозубых шестерен. На рисунке 9.6.1 (а) показано, что поверхности зубьев шестерни 1 и 2 идеальной зубчатой передачи касаются линии L 1 –L 2. Теперь учтите, что шестерни смещены, а оси шестерен пересекаются или пересекаются. Тогда кромка E 1 поверхности зуба шестерни будет касаться поверхности зуба 2 шестерни в точке M. Пути контакта на поверхностях зуба шестерни показаны на рис.9.6.2 (а). Преобразование движения сопровождается функцией ошибок передачи, показанной на рис. 9.6.2 (б). Перенос зацепления в конце цикла зацепления сопровождается скачком угловой скорости, при этом неизбежны вибрация и шум. Точно так же можно обсудить краевой контакт косозубых шестерен с параллельными осями, вызванный угловым смещением, таким как угол пересечения осей шестерен и разница углов винтовой линии шестерни.
Краевого контакта смещенных шестерен, поверхности зубьев которых изначально находятся в прямом контакте, можно избежать путем применения измененной топологии поверхностей зубьев.Такая топология […] … P1: FHA / JTH CB672 -10 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0: 19 10 .2 Геометрия эвольвентных кривых 2 71 Рисунок 10 .2.4: Расширенная эвольвентная кривая Используя подход, аналогичный рассмотренному выше, мы получаем следующие уравнения: x = (rb ∓ h) sin φ — rb φ cos φ y = (rb ∓ h) cos φ + rb φ sin φ (10 .2 .11) Верхний знак в уравнениях (10 .2 .11) соответствует вытянутой эвольвенте (рис. 10 .2.4), и. .. соответствующее смещение е реечного ножа (рис. 10.5 .1) можно определить из уравнения (10 .5 .1) с требованием, чтобы αG ≥ 0. Тогда получаем tg αc — 4P (a — e) ≥ 0 N sin 2αc (10 .5.5) Выражение (10 .5.5 ) с a = 1 / P дает N sin2 αc — 2 (1 — Pe) ≥ 0 N sin αc cos αc (10 .5.6) Учитывая (10 .5.6) и (10 .5.4) одновременно, получаем Pe ≥ Nmin — N Nmin (10 .5.7) Здесь Pe представляет собой алгебраическое безразмерное значение .
.. эвольвентная кривая P1: FHA / JTH CB672 -10 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0: 19 272 Прямозубые эвольвентные шестерни Рисунок 10.2.6: Спираль Архимеда Существует частный случай, когда h = rb и вытянутая эвольвентная кривая превращается в спираль Архимеда (рис. 10 .2.6), определяемую уравнением Mo M = r = rb φ (см. Также задачу 1. 6 .1 ) Другой частный случай — когда h = 0 и кривая (10 .2 .11) является условной … Две ветви эвольвентной кривой (10 .2 .1) P1: FHA / JTH CB672 -10 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0: 19 270 Эвольвентные прямозубые шестерни, где OP = rb [sin φ cos φ] T PM = PM [- cos φ (10.2.2) sin φ] T (10 .2.3) (ii) Из-за качения без скольжения имеем PM = MoP = rb φ (10 .2.4) Здесь φ — угол поворота при перекатывающем движении (iii) Уравнения (10 .2 .1) до (10 .2.4) дают x = rb (sin φ — φ cos … зацепление стойки и зубчатой передачи Вращение варочной панели имитирует перемещение воображаемой стойки P1: FHA / JTH CB672 -10 CB672 / Litvin CB672 / Litvin-v2.
cls 27 февраля 2004 г. (a) Подача варочной панели (b) Рисунок 10 .3.5: Генерация варочной панелью Рисунок 10 .3.6: Генерация формирователем 0:19 P1: FHA / JTH CB672 -10 CB672 / Литвин CB672 / Литвин-v2.cls 27 февраля 2004 г. 0: 19 Эвольвентные цилиндрические зубчатые колеса 278 Рис. 10 .3.7: Зацепление зубчатого колеса и формирователя … создание прямозубого эвольвентного зубчатого колеса с помощью реечного станка показано на рис. 10 .3 .1 Зубчатая передача, которую необходимо разрезать вращается с угловой скоростью ω вокруг O, а зуборез поступает со скоростью v. Скорость | v | и угловая скорость ω связаны уравнением N v = rp = ω 2P (10 .3 .1) P1: FHA / JTH CB672 -10 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0: 19 274 Spur Эвольвентные шестерни Рисунок 10.3 .1: Создание эвольвенты … (рис. 10 .3.4) — это отрезок прямой линии, равный pc (напомним, что делительная окружность — это центрод, входящий в зацепление с зуборезкой). Диаметр диаметра равен представлен как P = π N = d pc (10 .
4 .1) P1: FHA / JTH CB672 -10 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0: 19 10 .4 Пропорции зубчатых элементов 279 Рисунок 10 .4 .1: Параметры зубьев шестерни и определяются как количество зубьев шестерни. .. Numerics, Inc [19 98]) Приближенное представление, но с высокой точностью обратной функции α (θ) (θ = tan α — α) было предложено Ченгом [19 92]: α = (3θ) 1/3 — 9 2/3 5/3 2 2 1/3 7/3 θ + 3 θ — 3 θ + ··· 5 17 5 17 5 для θ и 10.2.5) … 2) рекомендуется 267 P1: FHA / JTH CB672 -10 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 268 0: 19 прямозубые эвольвентные шестерни Рис. 10 .2 .1: эвольвентные и эволюционные 10 .2 ГЕОМЕТРИЯ ИНВОЛЮТНЫХ КРИВЫХ В дальнейшем мы будем рассматривать обычные, расширенные и укороченные эвольвентные кривые (см. Раздел 1. 6) Мы начнем с общих определений эволюты и эвольвенты плоской кривой Эволюты и Эволюты Учтите, что … теперь, когда число зубьев шестерни N увеличено, но P и αc сохранены на тех же значениях. При N> N радиусы делительной окружности и основания.
Рис. 10.3.3: Стойка как частный случай зубчатого колеса P1: FHA / JTH CB672 -10 CB672 / Litvin CB672 / Litvin-v2.cls 27 февраля 2004 г. 0: 19 276 Прямозубые эвольвентные шестерни Рисунок 10 .3.4: Параметры окружности реечного резака rp и rb соответственно; центр . 1, который представлен в S 1 следующими уравнениями (рис. 9.4.3): x 1 = r b1 (sin θ 1 — θ 1 cos θ 1), y 1 = r b1 (cos θ 1 + θ 1 sin θ 1), z 1 = 0. (9.4.23) Рисунок 9.4.3: Профиль 1 шестерни. следует: m 12 = dφ 1 dφ 2 = — dθ 1 dθ 2 = r b2 r b1.(9.4. 41) Шаг 7: Линия действий представлена уравнением r (1) f = r b1 [sin (θ 1 — φ 1) — θ 1 cos (θ 1 — φ 1)] if + r b1 [cos (θ 1 — φ 1). уравнения: r (1) f (u 1 (θ 1), θ 1, φ 1) = r (2) f (u 2, θ 2, φ 2) (9.6.1) ∂r (1) f ∂θ 1 · N (2) f = 0. (9.6.2) Здесь r (1) f (u 1 (θ 1), θ 1, φ 1) представляет край поверхности зуба шестерни; ∂r (1) f / ∂θ 1 is
Xem thêm: Gear Geometry and Applied Theory Episode 1 Part 10 pps, Gear Geometry and Applied Theory Episode 1 Part 10 pps, Gear Geometry and Applied Theory Episode 1 Part 10 pps
Аналогии с поведением океана при разделении континентов западной впадины Вудларк
Taylor, B.
, Goodliffe, A. Martinez, F. & Hey, R. Nature 374 , 534–537 (1995).
ADS CAS Статья Google ученый
Дэвис, Х. Л., Саймондс, П. А. и Риппер, И. Д. Bur. Шахтер. Ресурс. J. Austr. Геол. Geophys. 9 , 49–68 (1984).
Google ученый
Дэвис, Х. Л. Am. J. Sci. 280-А 171–191 (1981).
Google ученый
Дэвис, Х. Л. и Уоррен Р. Г.
ADS Статья Google ученый
Хилл, Э. Дж., Болдуин, С. Л. и Листер, Г. С. Геология 20 , 907–910 (1992).
ADS Статья Google ученый
Хилл, Э.Дж. И Болдуин, С. Л. J. Метаморф. Геол. 11 , 261–277 (1993).
ADS CAS Статья Google ученый
Листер, Г. С. и Болдуин, С. Л. Геология 21 , 607–610 (1993).
ADS Статья Google ученый
Болдуин, С. Л., Листер, Г. С., Хилл, Э. Дж., Фостер, А. и Макдугалл, И. Тектоника 12 , 611–628 (1993).
ADS Статья Google ученый
Биннс, Р. А. и др. Proc. Pacific Rim Congr. 87 , 531–535 (1987).
Google ученый
Биннс, Р. А. и др. Пер. Являюсь. геофизики. ООН. 67 , 1231 (1986).
Google ученый
Куртильо, В., Gaedeano, A. & LeMouel, J. L. Планета Земля. Sci. Lett. 47 , 144–160 (1980).
ADS Статья Google ученый
Вик, Г.
Э. J. geophys. Res. 87 , 10677–10688 (1982).
ADS Статья Google ученый
Куртильо, В. Тектоника 1 , 239–250 (1982).
ADS Статья Google ученый
Стеклер, М.С. и тенБринк, У. Планета Земля. Sci. Lett. 79 , 120–132 (1986).
ADS Статья Google ученый
Актон Г. Д. и Стейн С. Тектоника 10 , 501–526 (1991).
ADS Статья Google ученый
Courtillot, V. et al. J. geophys. Res. 89 , 3315–3333 (1984).
ADS CAS Статья Google ученый
Вайссель, Дж. К., Тейлор, Б. и Карнер, Г. Д. Тектонофизика 87 , 253–277 (1982).
ADS Статья Google ученый
Тейлор, Б.
в Морская геология, геофизика и геохимия бассейна Вудларк — Соломоновы Острова (ред. Тейлор, Б. и Экзон, штат Нью-Йорк) 25–48 (Циркум-Тихоокеанский совет по энергетическим и минеральным ресурсам, Хьюстон, Техас, 1987 г.).
Google ученый
Бак, W. R. J. geophys. Res. 96 , 201610–20178 (1991).
Артикул Google ученый
Фридево, К. и Исакс, Б. Планета Земля. Sci. Lett. 71 , 305–314 (1984).
ADS Статья Google ученый
Муттер, Дж.C. et al. Trans Am. Geophys. ООН. 73 , 536 (1992).
ADS Google ученый
Гудлифф, А., Тейлор, Б., Мартинес, Ф. и Хей, Р. Пер. Являюсь. геофизики. ООН. 74 , 606 (1994).
Google ученый
Беннес В.
ADS Статья Google ученый
Mutter, J. C., Mutter, C. Z., Abers, G. A. & Fang, J. Trans. Являюсь. геофизики. ООН. 74 , 412 (1993).
Артикул Google ученый
Эй, Р. Н. Планета Земля. Sci. Lett. 37 , 321–325 (1977).
ADS Статья Google ученый
Эй, Р.N., Kleinrock, M.C., Miller, S.P., Atwater, T.M. & Searle, R.C. J. geophys. Res. 91 , 3369–3393 (1986).
ADS Статья Google ученый
Searle, R. & Francheteau, J. Mar. Geophys. Res. 8 , 95–129 (1986).
Google ученый
Аберс Г. А. Геология 19 , 1205–1208 (1991).
ADS Статья Google ученый
Листер Г. С., Этередж М. А. и Симондс П. А. Геология 12 , 246–250 (1986).
ADS Статья Google ученый
Англия, П. С. Geophys. J. R. Astr Soc. 70 , 295–321 (1982).
ADS Статья Google ученый
Муттер, Дж.С. Nature 374 , 499–500 (1995).
ADS CAS Статья Google ученый
Скачать Geometría Gdz 9 ° Grado Atanasiano для ПК бесплатно — максимальная версия
- Командная установка с BlueStacks
- Быстрая установка с Nox App Player
Установить для ПК с
Gracias и BlueStacks подбирают приложения для Android на ПК.BlueStacks работает с классическим интерфейсом Android. En lugar de utilizar gestos táctiles, este móvil virtual se controla con el ratón y el teclado.
- En primer lugar, debe instalar el software Bluestacks en su computadora or computadora portátil: descargar BlueStacks
- Después de Bluestacks, ahora debe descargar el archivo APK de Geometría Gdz 9 ° Grado — Atanasón la1910clic Aqurado 10 Bluestacks устанавливается на ПК / Ноутбук. En la barra de herramientas de la esquina izquierda, encontrará una opción de Agregar APK.Загрузите архивный APK, используя параметры в Bluestacks. Haga clic en eso.
- Te preguntará acerca de la ubicación donde guardaste el APK descargado. En mi caso, lo he guardado en el escritorio, así que estoy seleccionando eso.
- Ahora instalará automáticamente la aplicación en Bluestacks. Encontrará el Geometría Gdz 9 ° Grado — Atanasiano en la pestaña de aplicaciones en la pantalla main de la ventana Bluestacks.
- Ahora, я есть список для использования Geometría Gdz 9 ° Grado — Atanasiano en la PC.Aquí está el Geometría Gdz 9 ° Grado — Atanasiano que se ejecuta con éxito en mi PC después de la instalación y hace clic en la aplicación.
Cómo instalarlo Geometría Gdz 9 ° Grado — Atanasiano for PC con Nox App Player
Nox App Player — это программа, которая предназначена для использования в качестве эмулятора для Android, чтобы использовать его для использования в игре. Store sin necesidad de utilizar un dispositivo móvil. Результат очень полезен для обычных пользователей, которые используются для устройств Android.
- En primer lugar, debe descargar el воспроизводчик де ла aplicación Nox — https://es.bignox.com/, haga clic en el software for comenzar la instalación en su computadora / computadora portátil.
- Ahora, скачать из архива APK воды.
- Después de la instalación, abra el воспроизводитель NOX. En la esquina derecha de la caja de herramientas, encontrará una opción de ‘Agregar APK’.
