Сходинки 8 клас алгебра мерзляк гдз
Скачать сходинки 8 клас алгебра мерзляк гдз rtf
Подробное решение номер ГДЗ Алгебра 8 класс Мерзляк номер Решебник. Лучшие бесплатные решебники и готовое домашнее задание ко всем школьным учебникам УРОКУ.НЕТ. Предмет: Алгебра. Класс: 8 класс.
Автор: Мерзляк. Загрузи своё решение домашки и заработай на этом отметки! Добавить своё решение. Польза ГДЗ по алгебре за 8 класс Мерзляка. В сборнике содержатся девятьсот тридцать восемь упражнений, шесть заданий для самопроверки, ответы к вопросам по двадцати трем параграфам и дополнительные номера для решения задач. Благодаря обширным решениям, ученики могут: подтянуть свои познания; вникнуть в суть каждой темы; научиться выполнять даже самые заковыристые задания.
Проверка д/з с пособием занимает очень мало времени, не нужно будет по несколько раз пересчитывать ответы, чтобы удостовериться в отсутствии ошибок.
Готовые домашние задания с 1 по 11 класс. Главная»» ГДЗ Алгебра 8 класс»» ГДЗ решебник по Алгебре 8 класс Мерзляк А.
ГДЗ по Алгебре 8 класс Мерзляк А.Г., Полонский В.Б. ГДЗ. Алгебра 8 класс. Мерзляк А.Г., Полонский В.Б. 1. 2. Домашняя работа по алгебре за 8 класс к учебнику авторов А.Г. Мерзляк, В.Б. Полонский, М.С.
Якир. «Алгебра 7 класс: учебник для учащихся общеобразовательных организаций (углубленное изучение)». В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Мерзляк А.Г. Алгебра: 8 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.М.
Поляков. — 2-е изд., стереотип. — М., Алгебра 8 Контрольные Мерзляк. Цитаты контрольных работ и ответы на задачи контрольных работ из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ А.Г. Мерзляк, В.Б. Полонский, Е.М.Рабинович и др. — М.: Вентана-Граф, ». Представленные ниже контрольные работы в 2-х вариантах ориентированы на учебник «Алгебра 8» авторов А.Г. Мерзляк, В.Б.
Полонский, М. С. Якир системы УМК «Алгоритм успеха». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
С. Якир системы УМК «Алгоритм успеха». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
Нажмите на необходимую вам тему контрольной работы.
Решебник. Готовые Домашние Задания для 8 класса по Алгебре. Мерзляк, Полонский. г. Автор підручника: А.Г. Мерзляк, В.Б. Полонський, Ю.М. Рабінович, М.С. Якір. Видавництво: Харків, «Гімназія». Рік видання: Кількість сторінок: Формат підручника: PDF. Дивитись онлайн та читати відповіді до підручника Збірник задач і контрольних робіт Алгебра 8 клас А.Г. Мерзляк, В.Б. Полонський, Ю.М. Рабінович, М.С.
Якір (Варіант 1, 2, 3 онлайн) – Нова програма рік. Дивитись відповідь: ← Назад. Вперед →. Дивитись інші ГДЗ онлайн. ГДЗ (решебники) — подробные готовые домашние задания Алгебра за 8 класс Мерзляк, Полонский, Якир. Учебник по алгебре за 8 класс автор Мерзляк, Полонский поспособствует получению качественных навыков и умений по предмету. Пособие имеет тематическую структуру, материал изложен простым и доступным языком.
Определения, теоремы и термины выделены отдельным шрифтом, а для закрепления пройдённых тем в конце каждого параграфа имеются задания с подробными примерами решений.
doc, fb2, txt, PDFПохожее:
Гдз алгебра 8 клас мерзляк мегарешеба
Скачать гдз алгебра 8 клас мерзляк мегарешеба rtf
8 класс. Авторы: Мерзляк А.Г., Полонский В.Б., Якира М.С., Издательство: Серия: Страна: Перейти к решебнику по новой программе >. Алгебра. 8 клас. Мерзляк А. Г., Полонський В.
Алгебра. 8 клас. Мерзляк А. Г., Полонський В.
Б., Якір M. С. рік. Проверь себя. Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6. Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 Задание 22 Задание 23 Задание 24 Задание 25 Задание 26 Задание 27 Задание 28 Задание 29 Задание ГДЗ 8 класс» Алгебра.
Решебник «Алгебра 8 клас, А. Г. Мерзляк». Идет загрузка решебника Другие решебники: Алгебра. Почти у каждого ученика возникают трудности при выполнении домашнего задания. Наш сервис поможет Вам в решении или проверке упражнений по предмету Алгебра. Предлагаем вам Решебник «Алгебра 8 клас, А. Г. Мерзляк», с помощью которого вы повысите свои оценки за короткий срок.
Этот Решебник «Алгебра 8 клас, А. Г. Мерзляк» будет полезен не только учащимся но и их родителям, при помощи которого они освежат в памяти знания полученные много лет назад.
Готовые домашние задания по учебнику Алгебра уже просмотрело человек. Чтобы читать и смотреть Учебник Алгебра 8 класс Мерзляк Полонский Якир, нажмите на нужные страницы. Появятся изображения с бесплатными учебными материалами. В комментариях вы можете сверяться и делиться готовыми ответами на домашнее задание, создавая свой интерактивный решебник к сложным упражнениям.
В обновленном решебнике ГДЗ Мерзляк Полонский 8 класс ответы были перепроверены специалистами и выложены для работы в режиме онлайн, что позволит его использовать практически везде, где есть сеть интернет. А удобная мобильная версия станет приятным дополнением для тех, кто любит списывать даже во время занятия по алгебре.
Готовое домашние задание (гдз, решебник) по алгебре за 8 класс к учебнику для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С.
Якир. — М.: Вентана-Граф, ГДЗ по Алгебре 8 класс: Мерзляк А.Г. Издание: Алгебра. 8 класс. Учебник для учащихся общеобразовательных учреждений / А. Г. Мерзляк, В.Б. Полонский, М.С. Якир. Вентана-Граф. г.
Г. Мерзляк, В.Б. Полонский, М.С. Якир. Вентана-Граф. г.
ГДЗ по Алгебре за 8 класс А.Г. Мерзляк, В.Б. Полонский ФГОС. Авторы: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Издательство: Вентана-граф Выполнения заданий за 8 класс по Алгебре А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, от издательства: Вентана-граф ФГОС, не простое занятие, поэтому ГДЗ поможем Вам сверить ответы к заданиям. Рекомендуем посмотреть. title=»ГДЗ к рабочей тетради по алгебре за 8 класс Мерзляк А.Г.»> ГДЗ к рабочей тетради по алгебре за 8 класс Мерзляк А.Г.
Издательство: Вентана-граф. Серия: Алгоритм успеха. title=»ГДЗ к дидактическим материа. «Алгебра 8 класс» Авт. учебника А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Издательство М.: Вентана-Граф. 4 часов в неделю, часов в год. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА 8 класс Алгебра. Рабочая программа по алгебре разработана в соответствии с Примерной программой основного общего образования по математике, с учётом требований федерального компо Читать еще. ГДЗ. 8 клас. Алгебра.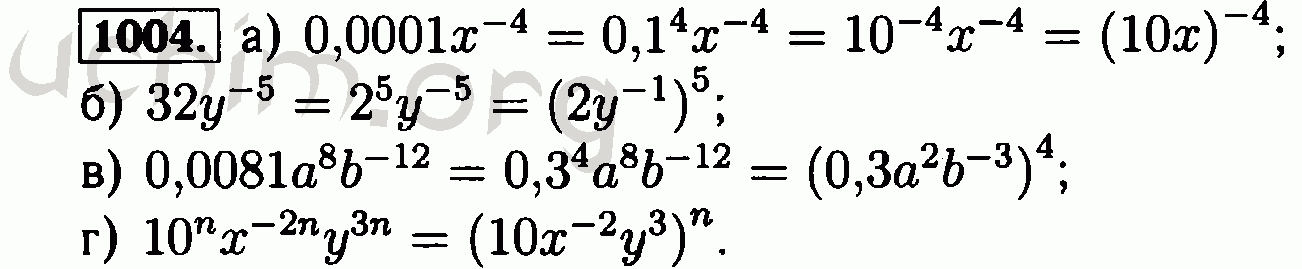 ГДЗ до підручника з алгебри 8 клас А.Г.
ГДЗ до підручника з алгебри 8 клас А.Г.
Мерзляк, В.Б. Полонський рік. ГДЗ до підручника з алгебри 8 клас А.Г. Мерзляк, В.Б. Полонський рік. 1 2 3 4 5. Рейтинг ГДЗ — на основі голосів (Ваша оцінка —). Обери відповідь до вправи. Готова домашня робота з алгебри для 8 класу. Рішення та відповіді до підручника з алгебри для 8 класу. Говорячи конкретно: якщо автори Вашого підручника – А.Г.
Мерзляк та В.Б. Полонський, то Ви на правильному сайті з правильними цілями, адже наші відповіді складені саме для цієї книжки. Сумніви і складнощі – не знайомі поняття для учнів, у яких є ГДЗ. Іноді навіть дорослі потребують поради фахівця або додаткового джерела інформації.
fb2, rtf, txt, fb2Похожее:
Гдз алгебра 8 клас алгебра мерзляк полонський якір
Скачать гдз алгебра 8 клас алгебра мерзляк полонський якір txt
Гдз и решебник Алгебра 8 класс Мерзляк, Полонский, Якир — Учебник.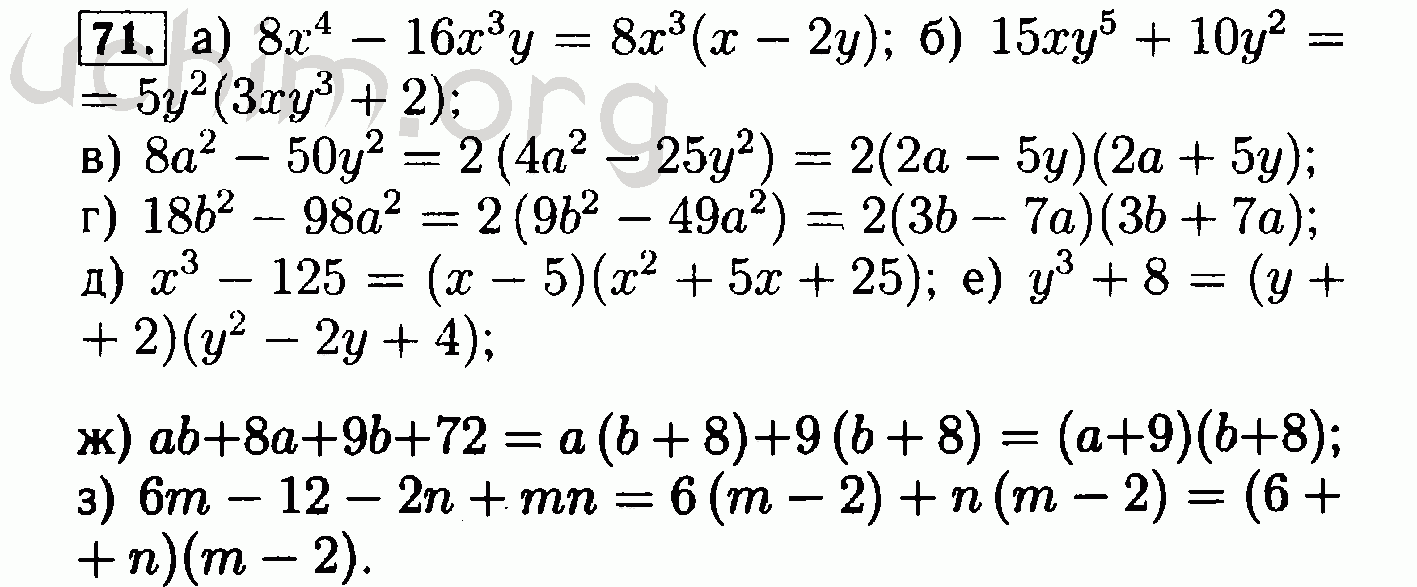 Алгебра 8 класс. Тип пособия: Учебник. Авторы: Мерзляк, Полонский, Якир. Издательство: «Вентана-Граф». Алгебра – это раздел математики изучающий свойства различных величин и действия над ними. Эта наука возникла ещё в древности под влиянием нужд общества в решении общих однотипных задач. В рамках школьной программы учебный курс за восьмой класс познакомит учеников с такими понятиями как квадратный корень и рациональные дроби, ребята подробно изучат их свойства и освоят действия над ними.
Алгебра 8 класс. Тип пособия: Учебник. Авторы: Мерзляк, Полонский, Якир. Издательство: «Вентана-Граф». Алгебра – это раздел математики изучающий свойства различных величин и действия над ними. Эта наука возникла ещё в древности под влиянием нужд общества в решении общих однотипных задач. В рамках школьной программы учебный курс за восьмой класс познакомит учеников с такими понятиями как квадратный корень и рациональные дроби, ребята подробно изучат их свойства и освоят действия над ними.
Помимо этого они получат знания о числовых неравенствах и степенях с целым показателем. Восьмиклассники научатся. «Алгебра 8 класс: учебник для учащихся общеобразовательных организаций». В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Мерзляк А.Г.
Алгебра: 8 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, — с.». Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по геометрии. , (х-р): (х + у), d Целые и дробные выражения называют рациональными выражениями.
, (х-р): (х + у), d Целые и дробные выражения называют рациональными выражениями.
В «ГДЗ по Алгебре 8 класс Учебник Мерзляк, Полонский, Якир Вентана-Граф» даны верные варианты ответов задач и подробно расписаны вопросы по темам учебника.
Пособие строго структурировано согласно книге, задания следуют строго по номерам и названиям параграфов. Польза Готового Домашнего Задания. Авторы издательств книг по учебным дисциплинам повышают строгость материала, не учитывая разные степени подготовки школьников и их усваиваемость. В результате у некоторых детей образуется каша в голове, с которой он сам редко способен справиться самостоятельно.
В таком случае онлайн-решебник станет отли. Выполнения заданий за 8 класс по Алгебре А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, от издательства: Вентана-граф ФГОС, не простое занятие, поэтому ГДЗ поможем Вам сверить ответы к заданиям. Рекомендуем посмотреть. title=»ГДЗ к рабочей тетради по алгебре за 8 класс Мерзляк А.Г.»> ГДЗ к рабочей тетради по алгебре за 8 класс Мерзляк А.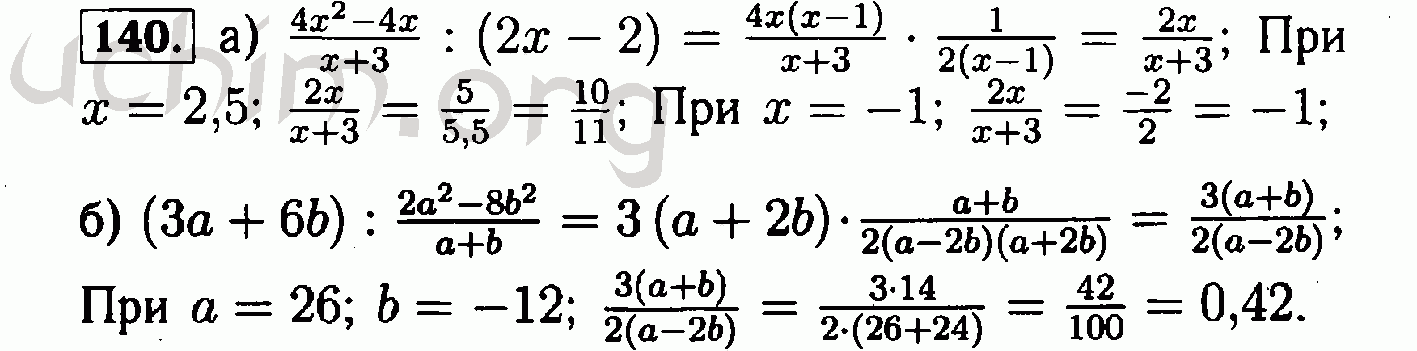 Г.
Г.
Издательство: Вентана-граф. Серия: Алгоритм успеха. title=»ГДЗ к дидактическим материалам по алгебре за 8 класс Мерзляк А.Г.»> ГДЗ к дидактическим материалам по алгебре за 8 класс Мерзляк А.Г.
Издательство: Вентана-граф. Серия: Алг.
Убедись в правильности решения задачи вместе с ГДЗ по Алгебре за 8 класс А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Ответы сделаны к книге года от Вентана-граф ФГОС. ГДЗ к рабочей тетради по алгебре за 8 класс Мерзляк А.Г. можно посмотреть тут. ГДЗ к дидактическим материалам по алгебре за 8 класс Мерзляк А.Г. можно посмотреть тут. ГДЗ по алгебре 8 класс углубленное изучение Мерзляк А.Г.
можно посмотреть тут. быстрый поиск. Номера. ГДЗ gj алгебре Мерзляка А.Г., Полонского В.Б., Якира М.С. за 8 класс, решебник включает ответы к основным заданиям учебника. Чтобы материал усваивался легче, Мерзляк и соавторы поделили упражнения на простые и сложные, а также добавили рубрику с нестандартными задачками для развития творческого потенциала учеников.
Но что если у школьника нет огромных способностей к математике? Предмет поддаётся изучению с трудом, а на носу контрольная? Решебник по алгебре для 8 класса поможет подготовиться эффективно и без стресса. Ответы даны с подробным алгоритмом решения, так что сможет разобраться даже школьник, пропустивший тему. Підручник «Алгебра» за авторства Мерзляка А.
Г. орієнтований на поглиблене вивчення математики учнями восьмих класів. Посібник схвалено Міністерством освіти і науки України. Надруковано видавництвом «Гімназія» у році у місті Харків. Алгебра 8 кл. г.Мерзляк А.Г., Полонський В.Б., Якіра М.С. Як знайти необхідне готове рішення д/з?
1 Зліва виберіть розділ або підрозділ: 2 Під кожним завданням є відкриті коментарі. Сайт ГДЗ пропонує тобі правильно вирішити домашнє завдання, звіривши його з нашими готовими домашніми завданнями. Увага Уточнюй, звіряй, перевіряй, але не списуй! Якщо тобі не вистачає інформації або ти чогось не зрозумів, звернися до адміністратора сайту!.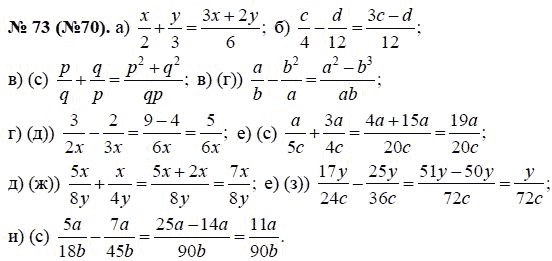
Похожее:
ГДЗ по алгебре 8 класс: решебники готовых домашних заданий
ГДЗ по алгебре для 8 класса – это решебники по предмету, которые содержат базу готовых ответов и решений на все примеры, уравнения, задачки школьного курса алгебры. Они формируются на основании учебников по алгебре, используемых в российских средних школах.
Стоит ли школьникам использовать решебники по алгебре в 8 классе?
Применение решебников в процессе выполнения домашней работы – вопрос спорный. Многие педагоги и родители выступают против такой практики, что совершенно необоснованно. Дело в том, что в курсе алгебры 8 класса представлены отнюдь не простые темы, постичь которые дано не каждому ребенку:
- способы преобразования рациональных выражений;
- график функций у=√х и у=К/х;
- свойства квадратного корня и квадратичная функция и функция;
- решение квадратных уравнений и теорема Виета;
- свойства иррациональных уравнений и неравенств.

Такой внушительный объем сведений требует от школьников максимальной концентрации памяти и внимания, ответственности и значительных временных затрат. при таком раскладе действенным помощником становится решебник по алгебре для 8 класса, который помогает в деле проверки выполненного домашнего задания, ликвидации пробелов в знаниях за 8 класс, разбора сложных задач и примеров, а также подготовки к контрольным и экзаменам.
Поиск ответа по условию – уникальная опция нашего сайта по гдз алгебре восьмого класса
Немало ресурсов Рунета предлагают пользователям базы готовых ответов и решений по алгебре. Среди многочисленных конкурентов наш ресурс выделяется спектром уникальных, значимых для школьников и их родителей свойств:
- Во-первых, на нем собраны самые свежие решебники по алгебре за 8 класс;
- Во-вторых, поиск готового ответа займет всего пару секунд – достаточно лишь указать в строке поиска номер задачки или часть ее условия;
- В-третьих, сайт адаптирован под ПК, нетбуки, ноутбуки, телефоны и планшеты.

Регулярное обновление сборников ГДЗ, возможность использования базы ответов в бесплатном режиме и без регистрации – дополнительные достоинства нашего сайта. Онлайн-решебники – важная составляющая блестящего выполнения домашних и классных работ по алгебре в 8 классе.
Гдз 8 клас алгебра мерзляк вшколе
Скачать гдз 8 клас алгебра мерзляк вшколе doc
Убедись в правильности решения задачи вместе с ГДЗ по Алгебре за 8 класс А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Ответы сделаны к книге года от Вентана-граф ФГОС. ГДЗ к дидактическим материалам по алгебре за 8 класс Мерзляк А.Г. можно посмотреть тут. ГДЗ по алгебре 8 класс углубленное изучение Мерзляк А.Г. можно посмотреть тут. быстрый поиск. Номера. Контрольные работы по алгебре 8 класс с ответами (УМК Мерзляк, Полонский, Рабинович). Дидактические материалы. Алгебра 8 Контрольные Мерзляк. Выберите необходимую вам тему контрольной работы.
В начале указана цитата (материал контрольной работы) из учебного пособия «Алгебра 8 класс. Дидактические материалы/ А.Г.
Дидактические материалы/ А.Г.
Мерзляк, В.Б. Полонский, Е.М.Рабинович и др. — М.: Вентана-Граф». Каждая цитата представлена в форме удобной для проверки знаний (на одной странице). Затем представлены решения и ответы (нет в пособии). При постоянном использовании данных контрольных работ (в 4-х вариантах) рекомендуем КУПИТЬ книгу: Мерзляк, Рабинович, Полонский: Алгебра. 8 класс. Готові домашні роботи з алгебри для учнів 8-х класів, автори: Мерзляк А.
Г., Полонський В. Б., Якір М. С. ГДЗ видані у році по новій програмі. ГДЗ по алгебре 8 класс Мерзляк содержит девятьсот тридцать восемь номеров, где даны примеры решения по всем имеющимся в школьной программе задачам. Исчерпывающие ответы помогут школьникам проверить себя и поработать над ошибками. Помимо этого, в сборнике представлены вопросы по параграфам и задания для самопроверки.
ГДЗ 8 класс» Алгебра. Решебник «Алгебра 8 клас, А. Г. Мерзляк». Идет загрузка решебника Другие решебники: Алгебра. Почти у каждого ученика возникают трудности при выполнении домашнего задания. Наш сервис поможет Вам в решении или проверке упражнений по предмету Алгебра. Предлагаем вам Решебник «Алгебра 8 клас, А. Г. Мерзляк», с помощью которого вы повысите свои оценки за короткий срок.
Наш сервис поможет Вам в решении или проверке упражнений по предмету Алгебра. Предлагаем вам Решебник «Алгебра 8 клас, А. Г. Мерзляк», с помощью которого вы повысите свои оценки за короткий срок.
Этот Решебник «Алгебра 8 клас, А. Г. Мерзляк» будет полезен не только учащимся но и их родителям, при помощи которого они освежат в памяти знания полученные много лет назад. Готовые домашние задания по учебнику Алгебра уже просмотрело человек.
ГДЗ Путина предоставляет Вам готовые решения по Алгебре за 8 класс. Решебник от А.Г. Мерзляк, В.Б. Полонский, М.С. Якир содержит верные ответы и подробное описание заданий по всему курсу обучения. ГДЗ: готовые ответы по алгебре за 8 класс, решебник Мерзляк, Алгоритм успеха ФГОС, онлайн решения на flowerdecor64.ru Алгебра в средней школе является одним из главных предметов, поэтому часов в программе ФГОС ей предоставлено предостаточно.
Ученик, который в будущем планирует получить профессию, связанную с математикой, должен уделять максимальное количество времени данному предмету. Отличным способом для устранения данной проблемы является ГДЗ по алгебре за 8 класс Мерзляк. Он рассматривается как дополнительный источник информации, содержит тематические тесты на разные задачи, а также верные ответы к ним. Готовые Домашние Задания. Решебник по Алгебре. 8 класс. Мерзляк, Полонский. г.
Отличным способом для устранения данной проблемы является ГДЗ по алгебре за 8 класс Мерзляк. Он рассматривается как дополнительный источник информации, содержит тематические тесты на разные задачи, а также верные ответы к ним. Готовые Домашние Задания. Решебник по Алгебре. 8 класс. Мерзляк, Полонский. г.
Похожее:
Гдз алгебра 8 клас якір мерзляк полонський
Скачать гдз алгебра 8 клас якір мерзляк полонський djvu
О решебнике А. Г. Мерзляк, В.Б. Полонский, М.С. Якир. Другие решебники по алгебре для 8 классa. А.Г. Мерзляк, В.Б. Полонський, М. Якiр А. Мерзляк, В. Полонський, М. Якiр. Ш.А. Алимов Алимов Ш. А. и др. В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк Жохов В. И., Макарычев Ю. Н., Миндюк Н. Г., Их нельзя скачать (в формате pdf), зато можно бесплатно смотреть задания (упражнения, задачи, тесты с вариантами, контрольные, лабораторные и проверочные работы) для подготовки к ВПР, КДР, экзаменам ГИА, ОГЭ, ЕГЭ — нажмите на № номер страницы.
Г. Мерзляк, В.Б. Полонский, М.С. Якир. Другие решебники по алгебре для 8 классa. А.Г. Мерзляк, В.Б. Полонський, М. Якiр А. Мерзляк, В. Полонський, М. Якiр. Ш.А. Алимов Алимов Ш. А. и др. В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк Жохов В. И., Макарычев Ю. Н., Миндюк Н. Г., Их нельзя скачать (в формате pdf), зато можно бесплатно смотреть задания (упражнения, задачи, тесты с вариантами, контрольные, лабораторные и проверочные работы) для подготовки к ВПР, КДР, экзаменам ГИА, ОГЭ, ЕГЭ — нажмите на № номер страницы.
; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 30; 31; 32; 33; 34; 35; 36; 37; 38; 39; 40; 41; 42; 43; 44; 45; 46; 47; 48; 49; 50; 51; 52; 53; 54; 55; 56; 57; 58; 59; 60; 61; 62; 63; 64; 65; 66; 67; 68; 69; 70; 71; 72; 73; 74; 75; 76; 77; 78; 79; 80; 81; 82; 83; 84; 85; 86; 87; Готовые домашние задания (ГДЗ) к учебнику по алгебре за 8 класс, авторы: А.Г.
Мерзляк, В.Б. Полонский, М.С. Якир. ГДЗ к дидактическим материалам по алгебре за 8 класс Мерзляк можно смотреть здесь. Номера задач. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 ГДЗ gj алгебре Мерзляка А.Г., Полонского В.Б., Якира М.С.
Номера задач. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 ГДЗ gj алгебре Мерзляка А.Г., Полонского В.Б., Якира М.С.
за 8 класс, решебник включает ответы к основным заданиям учебника. Чтобы материал усваивался легче, Мерзляк и соавторы поделили упражнения на простые и сложные, а также добавили рубрику с нестандартными задачками для развития творческого потенциала учеников. Но что если у школьника нет огромных способностей к математике? Предмет поддаётся изучению с трудом, а на носу контрольная? Решебник по алгебре для 8 класса поможет подготовиться эффективно и без стресса. Ответы даны с подробным алгоритмом решения, так что сможет разобраться даже школьник, пропустивший тему.
Новые и подробные решебники и гдз по алгебре за 8 класс. Авторы: Мерзляк А.Г., Полонский В.Б., Якир М.С.. Издательство: Гимназия. С удобным интерфейсом от Путина орг. С удобным интерфейсом от Путина орг. ГДЗ к учебнику по Алгебре за 8 класс Мерзляк, Полонский для Российских школ можно скачать здесь.
С удобным интерфейсом от Путина орг. ГДЗ к учебнику по Алгебре за 8 класс Мерзляк, Полонский для Российских школ можно скачать здесь.
Вправи. 1.
А.Г. Мерзляк, В.Б. Полонський, М.С. Якір. ГДЗ 8 класс» Алгебра. Решебник (ГДЗ) «Алгебра 8 клас, А.Г. Мерзляк, В.Б. Полонський, М.С.
Якір». Наш сервис поможет Вам в решении или проверке упражнений по предмету Алгебра. Предлагаем вам Решебник (ГДЗ) «Алгебра 8 клас, А.Г. Мерзляк, В.Б. Полонський, М.С. Якір», с помощью которого вы повысите свои оценки за короткий срок. Этот Решебник (ГДЗ) «Алгебра 8 клас, А.Г. Мерзляк, В.Б. Полонський, М.С.
Якір» будет полезен не только учащимся но и их родителям, при помощи которого они освежат в памяти знания полученные много лет назад. Готовые домашние задания по учебнику Алгебра уже просмотрело человек.
О решебнике А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Другие решебники по алгебре для 8 классa. А.Г. Мерзляк, В.Б. Полонський, М. Якiр А. Мерзляк, В. Полонський, М. Якiр. Ш. А. Алимов Алимов Ш. А. и др. В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк Жохов В. И., Макарычев Ю. Н., Миндюк Н. Г., Авторы: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Онлайн решебник по Алгебре для 8 класса А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, гдз и ответы к домашнему заданию. ГДЗ к рабочей тетради по алгебре за 8 класс Мерзляк А.Г.
А. Алимов Алимов Ш. А. и др. В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк Жохов В. И., Макарычев Ю. Н., Миндюк Н. Г., Авторы: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Онлайн решебник по Алгебре для 8 класса А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, гдз и ответы к домашнему заданию. ГДЗ к рабочей тетради по алгебре за 8 класс Мерзляк А.Г.
можно скачать здесь. ГДЗ к дидактическим материалам по алгебре за 8 класс Мерзляк А.Г. можно скачать здесь. Номера. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99
EPUB, rtf, doc, rtfПохожее:
 в відповіді 6 клас
в відповіді 6 клас
Алгебра 8 клас мерзляк для русских школ
Скачать алгебра 8 клас мерзляк для русских школ fb2
«Алгебра 7 класс: учебник для учащихся общеобразовательных организаций (углубленное изучение)». В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Мерзляк А.Г. Алгебра: 8 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.М. Поляков. — 2-е изд., стереотип. — М., — с.». Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по алгебре.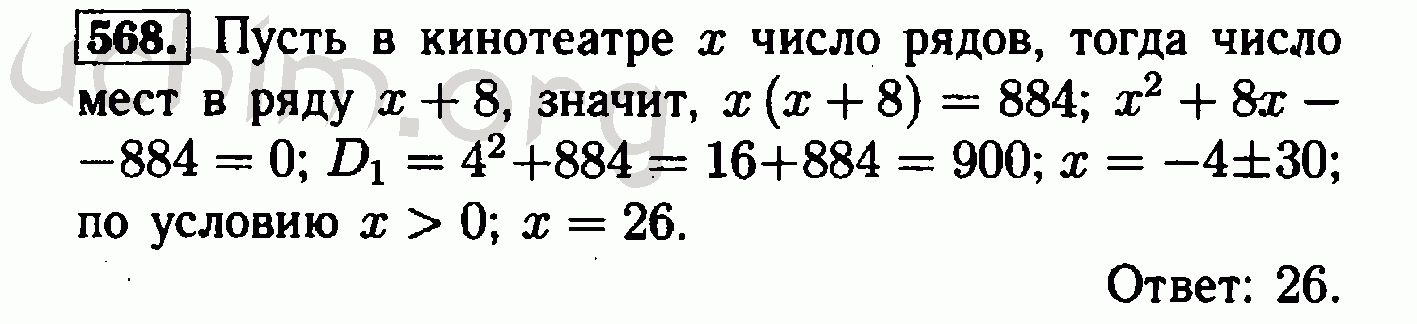
Учебник находится здесь: fabrika61.ru Авторы, издание: Мерзляк А. Г., Полонский В. Б., Якир М. С. Нравится. Твитнуть. Список заданий. 2. 5. 7. О решебнике А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Другие решебники по алгебре для 8 классa. Л.А. Александрова, А.Г. Мордкович Л. А. Александрова (при участии Мордкович А. Г.) Ю.Н. Макарычев Ю.Н. Макарычев; Под ред. С.А. Теляковского — е изд. —М.: Просвещение, г.
А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская А.Г. Мордкович, Т.Н. Мишустина, Е.Е.Тульчинская. — М.: Мнемозина, г. В.И. Жохов, Ю.Н. Макарычев, Н.Г.
Миндюк В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. Алгебра 8 класс — Мерзляк. видео просмотров Обновлен 24 апр. г. Ещё. Алгебра 8 класс Мерзляк Полонский Якир. GDZ Ru. GDZ Ru. • 2. Текущее видео. № 1 — Алгебра 8 класс Мерзляк. GDZ Ru. GDZ Ru. • 3. Текущее видео.
№ 2 — Алгебра 8 класс Мерзляк. GDZ Ru. GDZ Ru. • 4. Текущее видео. № 3 — Алгебра 8 класс Мерзляк. GDZ Ru. GDZ Ru. • 5. Текущее видео. № 4 — Алгебра 8 класс Мерзляк. GDZ Ru. GDZ Ru. • 6. Текущее видео. № 5 — Алгебра 8 класс Мерзляк. GDZ Ru. GDZ Ru. • 7. Текущее видео. № 6 — Алгебра 8 класс Мерзляк. GDZ Ru.
GDZ Ru. GDZ Ru. • 6. Текущее видео. № 5 — Алгебра 8 класс Мерзляк. GDZ Ru. GDZ Ru. • 7. Текущее видео. № 6 — Алгебра 8 класс Мерзляк. GDZ Ru.
GDZ Ru. • 8. Текущее видео. № 7 — Алгебра 8 класс Мерзляк. GDZ Ru. GDZ Ru. • 9. Текущее видео. № 8 — Алгебра 8. Алгебра 8 класс. Учебник. Мерзляк, Полонский, Якир. Вентана-Граф. Программа по алгебре. ГДЗ по алгебре 8 класс Мерзляк содержит девятьсот тридцать восемь номеров, где даны примеры решения по всем имеющимся в школьной программе задачам.
Исчерпывающие ответы помогут школьникам проверить себя и поработать над ошибками. Помимо этого, в сборнике представлены вопросы по параграфам и задания для самопроверки. Что дает ГДЗ. Это только в сказках все бывает легко и просто, а в школе приходится трудиться, причем очень усердно.
Многие подростки просто не выдерживают подобной нагрузки и начинают путаться в уроках, заданиях и т. д. В итоге это приводит к. ГДЗ Алгебра 8 класс Алгоритм успеха. авторы: А.Г. Мерзляк, В.Б. Полонский, М.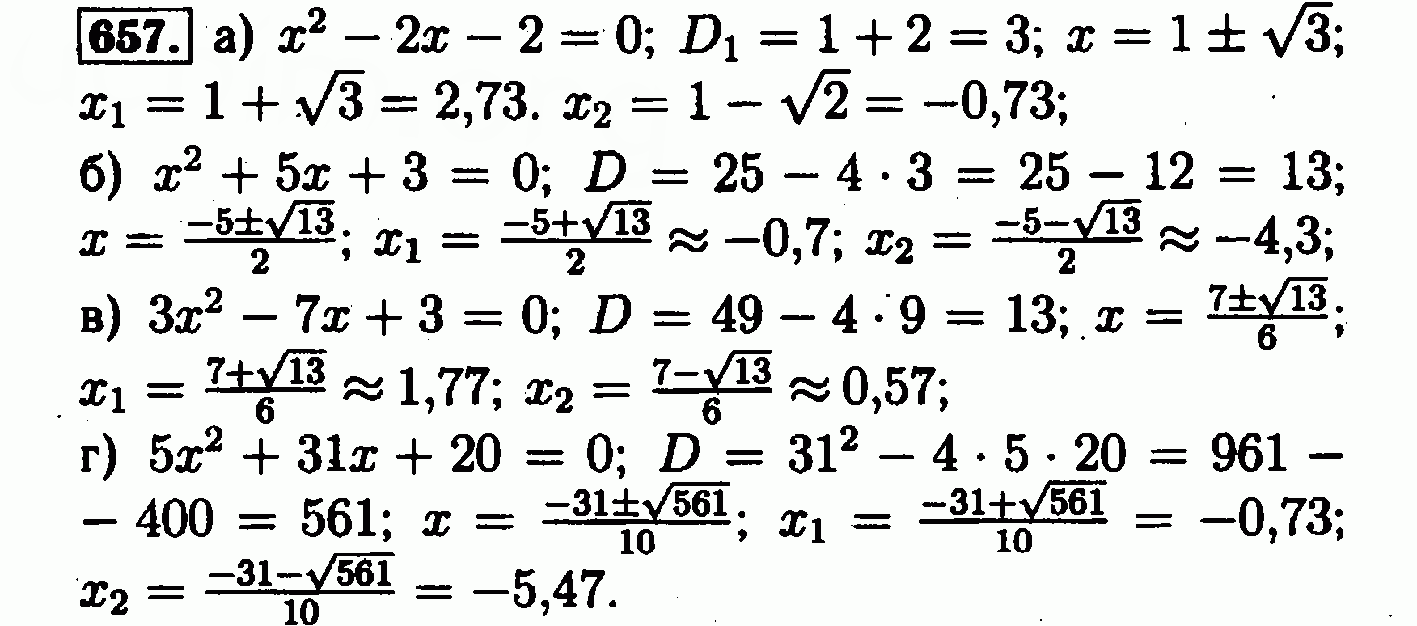 С. Якир. Наверное, для вас не будет являться секретом тот факт, что овладению хорошим уровнем знаний по математике способствует регулярное выполнение упражнения разного уровня сложности. Чтобы обеспечить надлежащую самостоятельную подготовку, настоятельно рекомендуем воспользоваться ГДЗ по учебнику Алгебра 8 класс, написанным коллективом авторов Мерзляк, Полонский и Якир. Решебник по учебнику Алгебра 8 класса под редакцией Мерзляка станет настоящим помощником при самостоятельной работе, которая обязательно повысит вашу успеваемость в школе.
С. Якир. Наверное, для вас не будет являться секретом тот факт, что овладению хорошим уровнем знаний по математике способствует регулярное выполнение упражнения разного уровня сложности. Чтобы обеспечить надлежащую самостоятельную подготовку, настоятельно рекомендуем воспользоваться ГДЗ по учебнику Алгебра 8 класс, написанным коллективом авторов Мерзляк, Полонский и Якир. Решебник по учебнику Алгебра 8 класса под редакцией Мерзляка станет настоящим помощником при самостоятельной работе, которая обязательно повысит вашу успеваемость в школе.
Номера.
Решебник (ГДЗ) Алгебра 8 клас А.Г. Мерзляк, В.Б. Полонський, M.С. Якір ( рік). Авторы: А.Г. Мерзляк, В.Б. Полонський, M.С. Якір. Год: |. Класс: 8 |. Предмет: Алгебра |. Для того, чтобы удостоверится в выполненной вами домашней работе по алгебре и получить высокий балл в школе, ребятам потребуется помощь цифрового пособия.
Смотри на нашем сайте решебник Алгебра 8 клас А.Г. Мерзляк, В.Б. Полонський, M.С. Якір года. Как быстро проверить знания? После того, как Вы выполнили уравнение или задачу на черновике — откройте интернет и зайдите к нам на сайт.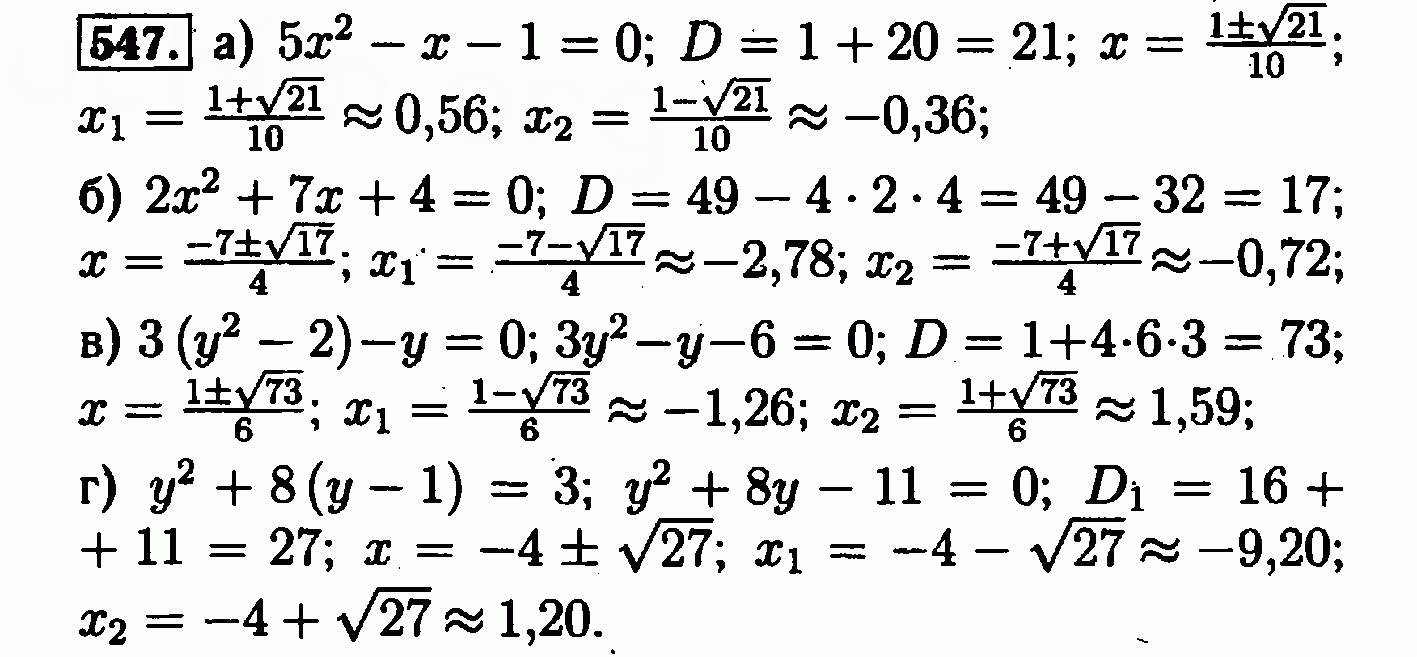 Там Вы найдете решебник и сможете сверить все примеры всего за несколько минут, а потом переписать все в чистовик. Как найти ответ и задание?. А.
Там Вы найдете решебник и сможете сверить все примеры всего за несколько минут, а потом переписать все в чистовик. Как найти ответ и задание?. А.
Г. Мерзляк, В. М. Поляков) системы «Алгоритм успеха». Содержание учебника соответствует федеральному государственному. Учебник предназначен для углублённого изучения алгебры в 8 классе и входит в комплект из трёх книг: «Алгебра. 7 класс», «Алгебра.
8 класс», «Алгебра. 9 класс» (авт. А. Г. Мерзляк, В. М. Поляков) системы «Алгоритм успеха». Содержание учебника соответствует федеральному государственному образовательному стандарту основного общего образования ( г.). Рубрика: Алгебра / 8 класс. Автор: Автор: А. Г. Мерзляк, В. М. Поляков. Год: Для учеников: 8 класс. Язык учебника: Русский. Формат: PDF. Страниц: Стара програма: Алгебра. 8 класс Мерзляк А. Г., Полонский В. Б., Якира М.
С. «Алгебра. 8 класс» ГДЗ. Мерзляк А. Г., Полонский В. Б., Якира М. С. Відповіді до підручника з алгебри для 8 класу Мерзляк. Ответы к учебнику по алгебре для 8 класса Мерзляк.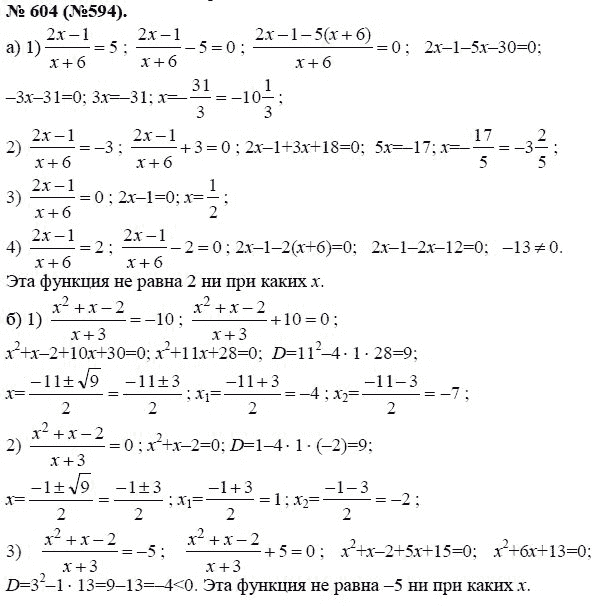 Проверь себя. Задания.
Проверь себя. Задания.
Похожее:
слабая идемпотентная 2-монада в nLab
СодержаниеКонтекст
2-х категорийная теория
Теория 2 категорий
Определения
Трансферы между двумя категориями
Морфизмы в 2-х категориях
Конструкции 2-х категорий
Ограничения в 2-х категориях
Конструкции по 2-м категориям
Идея
Слабая идемпотентная 2-монада , также называемая монадой Кока – Цоберляйна или KZ , кодирует определенный вид структуры, подобной свойствам, которую категория или, в более общем смысле, объект 2-категории, может нести.
Типичными примерами являются 2-монады TT на Cat, которые переводят категорию CC в свободное кополение TCT C группы CC при заданном классе копределов — тогда алгебре? TC → CT C \ to C — категория CC со всеми такими копределами, которые, конечно, по существу уникальны. Более того, для заданных таким образом совместных категорий CC и DD, функтора F: C → DF \ Colon C \ to D и диаграммы SS в CC существует единственная стрелка colimTFS → F (colimS) colim TFS \ to F (colim S), задаваемый универсальным свойством копредела.Именно это свойство обобщает слабая идемпотентность.
Определение
2-монада TT на 2-категории KK называется слабо-идемпотентной , если заданы любые две (строгие) TT-алгебры a: TA → Aa \ colt TA \ to A, b: TB → Bb \ двоеточие TB \ в B и морфизм f: A → Bf \ двоеточие A \ в B, существует единственная 2-клетка f¯: b∘Tf⇒f∘a \ bar f \ двоеточие b \ circ T f \ Rightarrow f \ circ a превращение (f, f¯) (f, \ bar f) в слабый морфизм TT-алгебр:
TA → TfTBa ↓ ⇙f¯ ↓ bA → fB \ array { T A & \ overset {T f} {\ to} & T B \\ a \ downarrow & \ swArrow \ bar f & \ downarrow b \\ A & \ underset {f} {\ to} & B }Двойная монада TT называется colax-идемпотентной , если f: A → Bf \ двоеточие A \ to B порождает TT-морфизм colax (f, f˜) (f, \ tilde f):
TA → TfTBa ↓ ⇗f˜ ↓ bA → fB \ array { T A & \ overset {T f} {\ to} & T B \\ a \ downarrow & \ neArrow \ тильда f & \ downarrow b \\ A & \ underset {f} {\ to} & B }Эквивалентные условия
Теорема
2-монада TT, как указано выше, с единицей η: 1 → T \ eta: 1 \ to T, слабо-идемпотентна тогда и только тогда, когда для любой TT-алгебры a: TA → Aa \ Colon TA \ to A существует 2-ячейка θa: 1⇒ηA∘a \ theta_a \ columns 1 \ Rightarrow \ eta_A \ circ a такая, что (θa, 11A) (\ theta_a, 1_ {1_A}) — единица и счетчик присоединения aηAa \ dashv \ eta_A. 2 A \ to T A — это TT-алгебра на TAT A, а ηA: A → TA \ eta_A \ двоеточие A \ to T A — это морфизм основного объекта aa на объект μA \ mu_A. Таким образом, существует единственный η¯A: μA∘TηA = 1TA⇒ηA∘a \ bar \ eta_A \ Colon \ mu_A \ circ T \ eta_A = 1_ {TA} \ Rightarrow \ eta_A \ circ, превращающий ηA \ eta_A в слабый ТТ-морфизм. Установите θa = η¯A \ theta_a = \ bar \ eta_A. Тогда равенства треугольников требуют, чтобы:
2 A \ to T A — это TT-алгебра на TAT A, а ηA: A → TA \ eta_A \ двоеточие A \ to T A — это морфизм основного объекта aa на объект μA \ mu_A. Таким образом, существует единственный η¯A: μA∘TηA = 1TA⇒ηA∘a \ bar \ eta_A \ Colon \ mu_A \ circ T \ eta_A = 1_ {TA} \ Rightarrow \ eta_A \ circ, превращающий ηA \ eta_A в слабый ТТ-морфизм. Установите θa = η¯A \ theta_a = \ bar \ eta_A. Тогда равенства треугольников требуют, чтобы:
aη¯A: a⇒a∘ηA∘a = aa \ bar \ eta_A \ двоеточие a \ Rightarrow a \ circ \ eta_A \ circ a = a равно 1a1_a. Составной a∘η¯Aa \ circ \ bar \ eta_A делает ηAa \ circ \ eta_A слабым TT-морфизмом от aa до aa (вставьте η¯A \ bar \ eta_A с тождественным квадратом a∘μA = a∘Taa \ circ \ mu_A = a \ circ T a).Но a∘ηA = 1Aa \ circ \ eta_A = 1_A, и 1a1_a также превращает это в слабый TT-морфизм, поэтому по уникальности aη¯A = 1aa \ bar \ eta_A = 1_a.
η¯AηA: ηA⇒ηA∘a∘ηA = ηA \ bar \ eta_A \ eta_A \ Colon \ eta_A \ Rightarrow \ eta_A \ circ a \ circ \ eta_A = \ eta_A равно 1ηA1 _ {\ eta_A}.
 Но это непосредственно следует из условия единичной когерентности для слабого TT-морфизма η¯A \ bar \ eta_A.
Но это непосредственно следует из условия единичной когерентности для слабого TT-морфизма η¯A \ bar \ eta_A.
Наоборот, предположим, что θa \ theta_a, алгебры a, ba, b на A, BA, B и f: A → Bf \ двоеточие A \ to B заданы.Возьмем f¯ \ bar f в качестве сопряжения с 1f: b∘Tf∘ηA = f⇒f1_f \ columns b \ circ T f \ circ \ eta A = f \ Rightarrow f относительно присоединений a⊣ηAa \ dashv \ eta_A и 1⊣11 \ dashv 1, который в данном случае задается путем вставки с помощью θa \ theta_a, поэтому мы имеем, что f¯ = b∘Tf∘θa \ bar f = b \ circ T f \ circ \ theta_a. Партнер f¯ \ bar f, в свою очередь, задается формулой f¯∘ηA \ bar f \ circ \ eta_A, что, поскольку маты соответствуют биективно, равно 1f1_f. Итак, f¯ \ bar f удовлетворяет условию единицы.
Рассмотрим диаграммы, выражающие условие умножения: поскольку a∘μA = a∘Taa \ circ \ mu_A = a \ circ T a (и то же самое для bb), их границы равны, поэтому у нас есть 2-клетки α, β: b∘Tb∘T2f⇒f∘a∘Ta \ alpha, \ beta \ двоеточие b \ circ T b \ circ T ^ 2 f \ Rightarrow f \ circ a \ circ T a.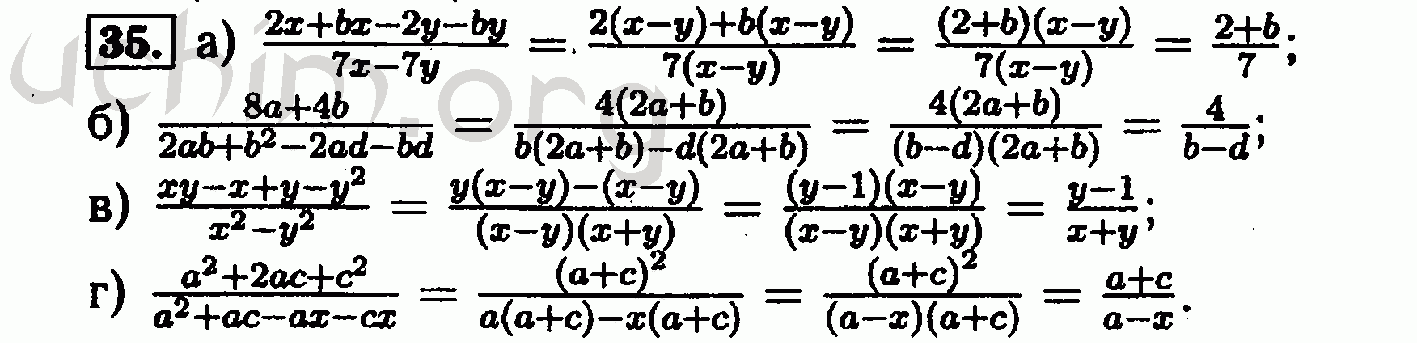 2} \ to \ eta T \ circ \ mu Making (ℓ, 1): μ⊣ηT (\ ell, 1) \ Colon \ mu \ dashv \ eta T. И наоборот, для алгебры a: TA → Aa \ Colon TA \ to A 2-ячейка θa \ theta_a задается формулой Ta∘ℓA∘TηAT a \ circ \ ell_A \ circ T \ eta_A.
2} \ to \ eta T \ circ \ mu Making (ℓ, 1): μ⊣ηT (\ ell, 1) \ Colon \ mu \ dashv \ eta T. И наоборот, для алгебры a: TA → Aa \ Colon TA \ to A 2-ячейка θa \ theta_a задается формулой Ta∘ℓA∘TηAT a \ circ \ ell_A \ circ T \ eta_A.
Другое, но эквивалентное условие состоит в том, что существует модификация d: Tη → ηTd \ двоеточие T \ eta \ в \ eta T такая, что dη = 1d \ eta = 1 и μd = 1 \ mu d = 1; и для данного ℓ \ ell, как указано выше, dd определяется как ℓ∘Tη \ ell \ circ T \ eta.
Эти различные условия можно также рассматривать как способ сказать, что присоединение Эйленберга-Мура для TT является слабым идемпотентным 2-присоединением.Таким образом, TT является слабой идемпотентной 2-монадой именно тогда, когда это 2-присоединение является слабым идемпотентным, и, следовательно, также, когда это 2-монада, индуцированная неким слабым идемпотентным 2-присоединением.
Двойным образом, чтобы TT был colax-идемпотентным, необходимо и достаточно, чтобы выполнялось любое из следующих условий.
Для любой TT-алгебры a: TA → Aa \ двоеточие TA \ to A существует 2-ячейка ζa: ηA∘a⇒1 \ zeta_a \ columns \ eta_A \ circ a \ Rightarrow 1 такая, что (1, ζa): ηA⊣a (1, \ zeta_a) \ двоеточие \ eta_A \ dashv a.
Имеется модификация m: μ∘ηT → 1m \ двоеточие \ mu \ circ \ eta T \ to 1, делающее (1, m): ηT⊣μ (1, m) \ двоеточие \ eta T \ dashv \ mu.
Существует модификация e: ηT → Tηe \ colon \ eta T \ к T \ eta такая, что eη = 1e \ eta = 1 и μe = 1 \ mu e = 1.
Алгебры
Теорема дает необходимое условие для того, чтобы объект AA допускал структуру TT-алгебры, а именно, что ηA: A → TA \ eta_A: A \ to T A допускает левый сопряженный элемент с единичной коэтилитой. В случае псевдоалгебр этого необходимого условия также достаточно.
Теорема
Задать структуру псевдо-TT-алгебры на объекте AA равносильно заданию левого сопряженного к ηA: A → TA \ eta_A: A \ к T A с обратимой счетной частью.
В частности, объект допускает не более одной структуры псевдо TT-алгебры с точностью до единственного изоморфизма. Таким образом, структура TT-алгебры — это структура, подобная свойствам.
Во многих случаях интересно рассмотреть псевдо TT-алгебры, для которых структура алгебры TA → AT A \ to A имеет дополнительный левый сопряженный элемент, образующий присоединенную тройку.Подобные алгебры иногда называют непрерывными алгебрами.
Примеры
Как упоминалось выше, стандартными примерами нестрогих идемпотентных 2-монад являются монады на CatCat, алгебры которых являются категориями со всеми копределами указанного класса. В этом случае 2-монада — это операция свободного копополнения. Соответственно, существуют колакс-идемпотентные 2-монады, которые примыкают к границам указанного класса. Обратное утверждение дано (PowerCattaniWinskel), который показал, что 2-монада является монадой для свободных совместных дополнений тогда и только тогда, когда она слабо идемпотентна и единица η \ eta плотна (плюс условие когерентности).
Другим важным примером colax-идемпотентной монады является монада на Cat / BCat / B, которая переводит p: E → Bp \ двоеточие E \ в B в проекцию B / p → pB / p \ в p из категории запятых. . Алгебры этой монады — расслоения Гротендика над BB; см. также расслоение в 2-категории. Монада p↦p / Bp \ mapsto p / B слабо-идемпотентна, а ее алгебры являются опфибрациями.
Последнее на самом деле является частным случаем общей ситуации. Если TT — (2-) монада, относительно которой можно определить обобщенные мультикатегории, то часто она индуцирует слабую идемпотентную 2-монаду T˜ \ tilde {T} на 2-категории таких обобщенных мультикатегорий (также известных как «виртуальные TT -алгебры »), такие что (псевдо) T˜ \ tilde {T} -алгебры эквивалентны (псевдо) TT-алгебрам.Когда TT — это 2-монада, алгебры которой являются строгими 2-функторами B → CatB \ to Cat и чьи псевдоалгебры являются псевдофункторами B → CatB \ to Cat, то виртуальная TT-алгебра является категорией над BB, и это псевдо T˜ \ tilde {T} -алгебра как раз тогда, когда это опфибрация. Аналогично, существует слабая идемпотентная 2-монада на 2-категории мультикатегорий, псевдоалгебры которых являются моноидальными категориями, и так далее.
Аналогично, существует слабая идемпотентная 2-монада на 2-категории мультикатегорий, псевдоалгебры которых являются моноидальными категориями, и так далее.
Недвижимость
псевдодистрибутивных законов, включающих слабые идемпотентные 2-монады, имеют особенно красивую форму; см. (Мармолехо) и (Уокер).
Для обычных 1-монад существует представление Манеса в виде «троек Клейсли» с первичными данными семейства единичных морфизмов и подъемов, избегая итерации эндофунктора. Подобное представление существует для слабых идемпотентных 2-монад, как показано в Marmolejo-Wood (2012). Затем в Walker (2017) показано, что при условии, что единицы этого представления полностью верны (отражение полной верности вложения Йонеды) (почти), все аксиомы структуры Йонеды выполняются.В случаях, когда размер не играет роли, например, В идеальном завершении позы эти два понятия совпадают. Для получения дополнительной информации см. Структуру Йонеды или Уокера (2017).

Список литературы
Классические ссылки:
Макс Келли, Стив Лэк, О структурах, подобных свойствам , TAC 3 (9), 1997. (аннотация)
Андерс Кок, Монады, конструкции которых примыкают к блокам , Орхусский препринт 1972/73 No.35. (pdf)
Андерс Кок, Монады, конструкции которых примыкают к единицам , JPAA 104: 41–59, 1995.
Ross Street, Волокна в двух категориях , Cah. Верхний. Геом. Diff. XXI № 2 (1980). (число)
Volker Zöberlein, Доктрины по двум категориям , Math. Zeitschrift 148 (1976) стр. 267-279. (гдз)
«Учебные» описания концепции можно найти в
Особые грани концепции изучены в
.Marta Bunge, Жестко ограниченное завершение , TAC 28 no.8 (2013) стр 213-240. (аннотация)
Марта Бунге, Джонатон Фанк, О состоянии объекта бикоммы для KZ-доктрин , JPAA 143 (1999) pp.
 69-105.
69-105.А. Дж. Пауэр, Г. Л. Каттани, Г. Винскель, Результат представления для свободных совместных завершений , JPAA 151: 273–286, 2000 doi
Их законы распределения попадают в центр внимания в
- Франсиско Мармолехо, Распределительные законы для псевдомонад , TAC
Франсиско Мармолехо, Ричард Дж.Wood, Расширения Кан и слабые идемпотентные псевдомонады , TAC 26 № 1 (2012) стр. 1-19. (аннотация)
Чарльз Уолкер, Распределительные законы через допустимость , arXiv
Отношение к структурам Йонеды связано с
- Чарльз Уокер, Yoneda Structures и KZ Doctrines , arxiv
Логико-синтаксическая сторона рассматривается в
Публикации: Лоуренс Р. Тейлор
Ссылки The Math Reviews (MR) будут работать, только если у вас есть подписка на MathSciNet.
После записи MR обычно есть еще одна ссылка в строке. Это либо ссылка на один из архивов,
arXiv (arXiv.org),
JSTOR (jstor.org),
GT (Геометрия и топология),
GDZ (Архив в Геттингене),
NUMDAM (проект NUMDAM)
или куда-нибудь еще. Репринт — это копия репринта, отправленная автору; препринт — это какая-то версия
статьи перед публикацией — опубликованная версия является окончательной.
Ссылка $$$ означает, что все, что я смог найти, это ссылка, по которой вы сможете купить статью.Некоторые статьи имеют более одной ссылки на источник.
Это либо ссылка на один из архивов,
arXiv (arXiv.org),
JSTOR (jstor.org),
GT (Геометрия и топология),
GDZ (Архив в Геттингене),
NUMDAM (проект NUMDAM)
или куда-нибудь еще. Репринт — это копия репринта, отправленная автору; препринт — это какая-то версия
статьи перед публикацией — опубликованная версия является окончательной.
Ссылка $$$ означает, что все, что я смог найти, это ссылка, по которой вы сможете купить статью.Некоторые статьи имеют более одной ссылки на источник.
Вот версия списка AmsRef. Порядок записей такой же, как ниже.
[62] Основная последовательность расслоения и второй набор когомотопий.Лоуренс Р. Тейлор. Труды Freedman Fest , Geom. Тополь. Моногр., 18 , Геом. Тополь. Publ., Coventry (2012) 235–251.
MR 3084240 журнал arXiv
[61] Контроль неопределенности в тройных произведениях Месси.
Лоуренс Р. Тейлор. Геом. Dedicata, 148 , 371-389, 2010.
MR 2721632 журнал
[60] Функторы Макки и бисет.
И. Хэмблтон, Л. Р. Тейлор и Э. Б. Уильямс. Геом. Dedicata, 148 , 157-174, 2010.
MR 2721623 журнал arXiv
[59] Платье индукции и фактор Бернсайда Зеленое кольцо.
Ян Хэмблтон, Лоуренс Р. Тейлор и Брюс Уильямс. Теория алгебр. Чисел, 3 , 511-541, 2009.
MR 2578887 (2011e: 20009) журнал arXiv
[58] Бирациональность эталонных карт с помощью хирургии.
Скотт Ноллет, Лоуренс Р. Тейлор и Фредерико Ксавье. J. Reine Angew. Math., 627 , 83-95, 2009.
MR 2494914 журнал arXiv
[57] Квадратичные улучшения поверхностей: два исчезающих результата.
Лоуренс Р. Тейлор.4 $.
Лоуренс Р. Тейлор. Asian J. Math., 12 , 285-287, 2008.
MR 2453556 журнал arXiv
[55] Неориентированные геометрические функторы.
Лоуренс Р. Тейлор. Forum Math., 20 , 457-467, 2008.
MR 2418201 журнал arXiv
[54] Примеры экзотических стратификаций.
Брюс Хьюз, Лоуренс Р. Тейлор, Шмуэль Вайнбергер и Брюс Уильямс. Геом.Topol., 11 , 1477-1505, 2007.
MR 2326949 GT
[53] Комплексные спиновые структуры на 3-многообразиях.
Лоуренс Р. Тейлор. Геометрия и топология многообразий , Fields Inst. Commun., 47 , амер. Математика. Soc. (2005) 313-317.
MR 2189941 (2006к: 57072) препринт
[52] Обзор 4-многообразий глазами хирургии.
Робион К. Кирби и Лоуренс Р. Тейлор. Обзоры по теории хирургии, Vol.2 , Ann. математики. Stud., 149 , Princeton Univ. Press (2001) 387-421.
MR 1818779 (2002a: 57028) arXiv
[51] Натянутые сферы коразмерности один нечетного порядка.
Лоуренс Р. Тейлор. Геометрия и топология: Орхус (1998) , Contemp. Матем., 258 , амер. Математика. Soc. (2000) 369-375.
Soc. (2000) 369-375.
MR 1778118 (2001к: 53124) arXiv
[50] Управляемые гомеоморфизмы над многообразиями неположительной кривизны.
Брюс Хьюз, Ларри Тейлор и Брюс Уильямс. Canad. Математика. Бык., 43 , 343-354, 2000.
MR 1776062 (2001г: 57041) перепечатка
[49] Окрестности в стратифицированных пространствах с двумя слоями.
Брюс Хьюз, Лоуренс Р. Тейлор, Шмуэль Вайнбергер и Брюс Уильямс.
Топология , 39 , 873-919, 2000.
MR 1763954 (2001e: 57026) перепечатать arXiv
[48] Руководство по вычислению групп препятствий к операциям для конечных групп.
Ян Хэмблтон и Лоуренс Р. Тейлор. Обзоры по теории хирургии, Vol. 1 , Ann. математики. Stud., 145 , Princeton Univ. Press (2000) 225-274.
MR 1747537 (2001e: 19007) перепечатка
[47] Гладкие евклидовы 4-пространства с небольшим количеством симметрий.
Лоуренс Р. Тейлор. Труды Kirbyfest , Geom. Тополь. Моногр., 2 , Геом. Тополь. Publ., Coventry (1999) 563-569 (электронная).
Тейлор. Труды Kirbyfest , Geom. Тополь. Моногр., 2 , Геом. Тополь. Publ., Coventry (1999) 563-569 (электронная).
MR 1734424 (2000j: 57063) GT arXiv
[46] Модули рациональных перестановок для конечных групп.
Ян Хэмблтон и Лоуренс Р. Тейлор. Math. Z., 231 , 707-726, 1999.
MR 1709492 (2000i: 20013) перепечатка
[45] Инвариант гладких $ 4 $ -многообразий.
Лоуренс Р. Тейлор. Геом. Topol., 1 , 71-89 (электронная), 1997.
MR 1483766 (98i: 57034) GT
[44] О размерности бесконечных покрытий.
W. G. Dwyer, S. Stolz и L.R. Taylor. Proc. Амер.Математика. Soc., 124 , 2235-2239, 1996.
MR 1307514 (96i: 57022) AMS
[43] Жесткость расслоений над многообразиями неположительной кривизны.
С. Б. Хьюз, Л. Р. Тейлор и Э. Б. Уильямс.
Топология , 34 , 565-574, 1995.
MR 1341809 (97a: 55019) перепечатка
[42] Ограниченные гомеоморфизмы над многообразиями Адамара.
С. Б. Хьюз, Л. Р. Тейлор и Э. Б. Уильямс. Math.Scand., 73 , 161-176, 1993.
MR 1269255 (95h: 57042) журнал
[41] К теории представлений, связанной с когомологиями конфигурационных пространств.
Ф. Р. Коэн и Л. Р. Тейлор. Алгебраическая топология , Contemp. Math., 146 , амер. Математика. Soc. (1993) 91-109.
MR 1224909 (94i: 57057) перепечатка
[40] Приблизительные расслоения многообразия — это приблизительно пучки.
С.Брюс Хьюз, Лоуренс Р. Тейлор и Э. Брюс Уильямс. Forum Math., 3 , 309-325, 1991.
MR 1115949 (92k: 57040) ГДЗ
[39] $ Pin $ -структуры на низкоразмерных многообразиях.
Р. К. Кирби и Л. Р. Тейлор. Геометрия низкоразмерных многообразий, 2 , London Math. Soc. Lecture Note Ser. + $.
+ $.
Р. К. Кирби и Л. Р. Тейлор. Комментарий. Математика. Helv., 65 , 434-447, 1990.
MR 1069818 (91h: 57025) ГДЗ
[37] Теоремы обнаружения для $ K $ -теории и $ L $ -теории.
И. Хэмблтон, Лоуренс Тейлор и Брюс Уильямс. J. Pure Appl. Алгебра, 63 , 247-299, 1990.
MR 1047584 (91b: 18015) PDF
[36] Теории расслоений для топологических многообразий.
К. Б. Хьюз, Л.Р. Тейлор и Э. Б. Уильямс. Пер. Амер. Математика. Soc., 319 , 1-65, 1990.
MR 1010410 (91e: 57035) AMS
[35] О гомологиях конфигурационных пространств.
C.-F. Бёдигхаймер, Ф. Коэн и Л. Тейлор.
Топология , 28 , 111-123, 1989.
MR 991102 (90h: 57031) перепечатка
[34] На $ G_n (RG) $ для $ G $ конечная нильпотентная группа.
И. Хэмблтон, Л. Р. Тейлор и Э. Б.Уильямс. J. Algebra, 116 , 466-470, 1988.
MR 953163 (89h: 20008) перепечатка
[33] Гомологии функциональных пространств.
Ф. Р. Коэн и Л. Р. Тейлор. Math. Z., 198 , 299-316, 1988.
MR 946606 (89d: 55017) ГДЗ
[32] Логарифмические описания групп Уайтхеда и групп классов для $ p $ -групп.
Роберт Оливер и Лоуренс Р. Тейлор. Mem. Амер. Математика.Soc., 76 , vi + 97, 1988.
MR 938472 (89k: 18024) $$$
[31] Операция с конечной фундаментальной группой.
И. Хэмблтон, Р. Дж. Милграм, Л. Тейлор и Б. Уильямс. Proc. Лондонская математика. Soc. (3), 56 , 349-379, 1988.
MR 922660 (89c: 57043) перепечатка
[30] Круглая $ L $ -теория.
I. Hambleton, A. Ranicki и L. Taylor. J. Pure Appl. Алгебра, 47 , 131-154, 1987.
MR 6 (88i: 18010) перепечатка
[29] Универсальное сглаживание четырехмерного пространства.
Майкл Х. Фридман и Лоуренс Р. Тейлор. J. Differential Geom., 24 , 69-78, 1986.
MR 857376 (88a: 57044) перепечатка
[28] Относительные инварианты Рохлина.
Лоуренс Р. Тейлор. Topology Appl., 18 , 259-280, 1984.
MR 769295 (86g: 57027) перепечатка
[27] Теория сглаживания и работа Фридмана о четырехмерных многообразиях.
Ричард Лашоф и Лоуренс Тейлор. Алгебраическая топология, Орхус, 1982, , Конспект лекций по математике, 1051 , Springer (1984) 271-292.
MR 764584 (86b: 57009) препринт
[26] Введение в карты между хирургическими группами обструкции.
Ян Хэмблтон, Лоуренс Тейлор и Брюс Уильямс. Алгебраическая топология, Орхус, 1982, , Конспект лекций по математике, 1051 , Springer (1984) 49-127.
MR 764576 (86b: 57017) перепечатка
[25] Отображения Джеймса и кольцевые пространства $ E_n $.-reshenie-25.16.jpg)
Ф. Р. Коэн, Дж. П. Мэй и Л. Р. Тейлор. Пер. Амер. Математика. Soc., 281 , 285-295, 1984.
MR 719670 (85 м: 55010) AMS
[24] Отображения Джеймса, отображения Сигала и теорема Кана-Придди.
Дж. Карузо, Ф. Р. Коэн, Дж. П. Мэй и Л. Р. Тейлор. Пер. Амер. Математика. Soc., 281 , 243-283, 1984.
MR 719669 (86 г: 55007) AMS
[23] Гомологии функциональных пространств.
Ф.Р. Коэн и Л. Р. Тейлор. Труды Северо-Западной конференции по теории гомотопий (Эванстон, Иллинойс, 1982) , Contemp. Матем., 19 , амер. Математика. Soc. (1983) 39-50.
MR 711041 (85d: 55016) перепечатка
[22] Обобщенные теоремы о расщеплении.
Дж. П. Мэй и Л. Р. Тейлор. Math. Proc. Cambridge Philos. Soc., 93 , 73-86, 1983.
MR 684277 (84b: 55014) перепечатка
[21] Теорема о топологической разрешающей способности.
Селман Акбулут и Лоуренс Тейлор. Inst. Hautes \ ‘Etudes Sci. Publ. Math., , 163-195, 1981.
MR 623537 (83e: 57015) NUMDAM
[20] $ K (Z, 0) $ и $ K (Z_2,0) $ как спектры Тома.
Ф. Р. Коэн, Дж. П. Мэй и Л. Р. Тейлор. Illinois J. Math., 25 , 99-106, 1981.
MR 602900 (82h: 55008) перепечатка
[19] Тангенциальные гомотопические эквивалентности.
Иб Мадсен, Лоуренс Р.Тейлор и Брюс Уильямс. Комментарий. Математика. Helv., 55 , 445-484, 1980.
MR 593058 (82f: 57015) ГДЗ
[18] Теорема о топологической разрешающей способности.
Селман Акбулут и Ларри Тейлор. Бык. Амер. Математика. Soc. (N.S.), 2 , 174-176, 1980.
MR 551757 (82a: 57018)
[17] О родах сучков.
Лоуренс Р. Тейлор. Топология многообразий малой размерности (Proc.Вторая конференция в Сассексе, Chelwood Gate, 1977) , Lecture Notes In Math.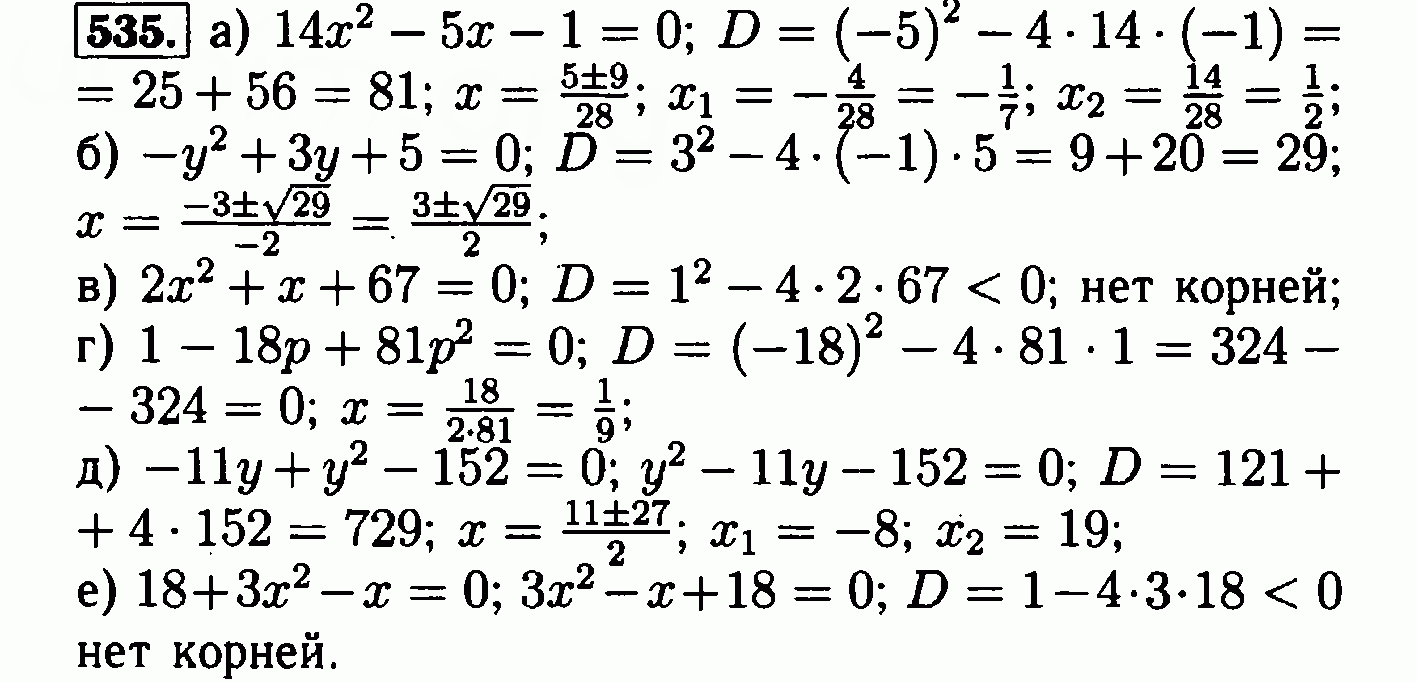 , 722 , Springer (1979) 144-154.
, 722 , Springer (1979) 144-154.
MR 547461 (82м: 57011) опубликованная версия
[16] Операционные пространства: формулы и структура.
Лоуренс Тейлор и Брюс Уильямс. Алгебраическая топология, Ватерлоо, 1978 (Proc. Conf., Univ. Waterloo, Waterloo, Ont., 1978) , Lecture Notes in Math., 741 , Springer (1979) 170-195.
MR 557167 (81к: 57034) препринт
[15] Местная хирургия: основы и применение.
Лоуренс Тейлор и Брюс Уильямс. Алгебраическая топология, Орхус 1978 (Proc. Sympos., Univ. Орхус, Орхус, 1978) , Lecture Notes In Math., 763 , Springer (1979) 673-695.
MR 561246 (81d: 57024) препринт
[14] Разделение еще нескольких пространств.
Ф. Р. Коэн, Дж. П. Мэй и Л. Р. Тейлор. Math. Proc. Cambridge Philos. Soc., 86 , 227-236, 1979.
MR 538744 (81b: 55016) перепечатка
[13] Препятствие конечности стенки для расслоения.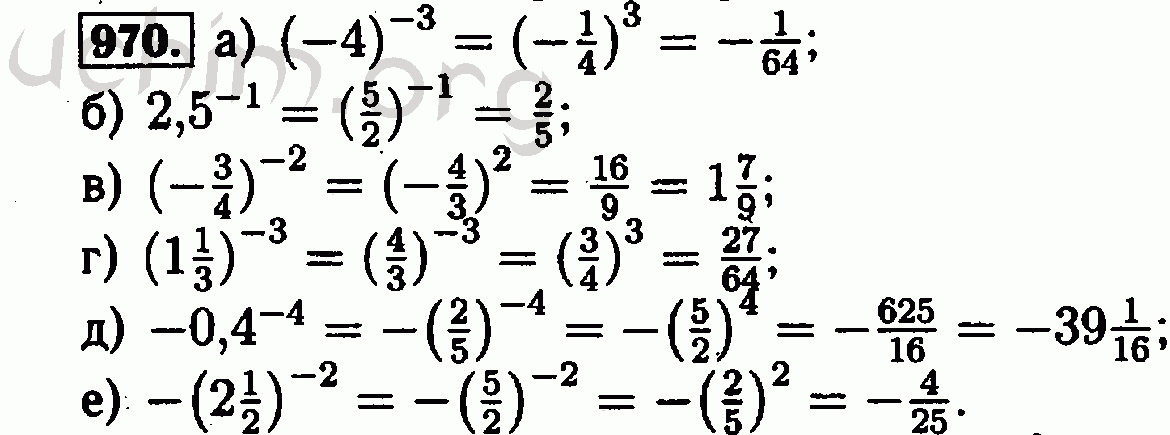
Эрик Кьяер Педерсен и Лоуренс Р. Тейлор. амер. J. Math., 100 , 887-896, 1978.
MR 509078 (80 г: 55030) JSTOR
[12] Вычисления когомологий Гельфанда-Фукса, когомологий функциональных пространств и когомологий конфигурационных пространств.
Ф. Р. Коэн и Л. Р. Тейлор. Геометрические приложения теории гомотопий (Proc. Conf., Evanston, Ill., 1977), I , Lecture Notes in Math., 657 , Springer (1978) 106-143.
MR 513543 (80f: 58050) перепечатка
[11] Гомотопическая теория Дольбо.
Джозеф Нейзендорфер и Лоуренс Тейлор. Пер. Амер. Математика. Soc., 245 , 183-210, 1978.
MR 511405 (80f: 32004) JSTOR
[10] Разбиение некоторых пространств $ CX $.
Ф. Р. Коэн, Дж. П. Мэй и Л. Р. Тейлор. Math. Proc. Cambridge Philos. Soc., 84 , 465-496, 1978.
MR 503007 (80a: 55010) перепечатка
[9] Конфигурационные пространства: приложения к когомологиям Гельфанда-Фукса. * $.
* $.
Найджел Рэй, Роберт Свитцер и Ларри Тейлор. Mem. Амер. Математика. Soc., 12 , ix + 66, 1977 г.
MR 0461520 (57 # 1505) $$$
[6] $ Λ $ -расщепляющих $ 4 $ -многообразий.
Майкл Х. Фридман и Лоуренс Тейлор.
Топология , 16 , 181-184, 1977 г.
MR 0442954 (56 # 1329) перепечатка
[5] Теории $ 2 $ -локальных кобордизмов.
Лоуренс Р. Тейлор. J. London Math. Soc. (2), 14 , 303-308, 1976.
MR 0431142 (55 # 4144) перепечатка
[4] Подпись ссылок.
Луи Х. Кауфман и Лоуренс Р. Тейлор. Пер. Амер. Математика. Soc., 216 , 351-365, 1976.
MR 0388373 (52 # 9210) JSTOR
[3] Хирургические группы и внутренние автоморфизмы.
Лоуренс Р. Тейлор. Алгебраическая $ K $ -теория. III: Эрмитова $ K $ -теория и геометрические приложения , Springer (1973) 471-477. Конспект лекций по математике. , Vol. 343.
, Vol. 343.
MR 0405460 (53 # 9253) PDF
[2] Теорема Уайтхеда в собственной категории.
Ф. Т. Фаррелл, Л. Р. Тейлор и Дж. Б. Вагонер. Compositio Math., 27 , 1-23, 1973.
MR 0334226 (48 # 12545) NUMDAM
[1] Остатки последовательностей, подобных Фибоначчи.
Лоуренс Тейлор. Кварт Фибоначчи, 5 , 298-304, 1967.
MR 0222022 (36 # 5074) PDF
ГДЗ Скачать приложение 2021 — Бесплатно
Описание ГДЗ
Миллионы бесплатных приложений для Android доступны в 9apps.30,000+ пользователи скачали последнюю версию ГДЗ 2017 в 9Apps бесплатно каждую неделю! Хотя поначалу вы, наверное, этого не заметите. Это горячее приложение было выпущено 23 мая 2017 г. Наслаждайтесь игрой с новыми потрясающими функциями!
Если вы не хотите самостоятельно писать домашнее задание, воспользуйтесь нашими готовыми ds!
Это приложение позволяет вам получить доступ к домашнему заданию
Дисциплина, предметы, которые мы рассматриваем в нашем приложении:
математика, алгебра, русский язык, английский язык, геометрия, физика, химия, биология, география, безопасность жизни, социальные науки, история , Немецкий, компьютерные науки, мир вокруг нас, литература.
Также есть примечания и комментарии по каждому классу.
Удобный формат, вы можете скачать GDZ на телефон.
Внимание!
Программа не хранит в себе никаких данных и не нарушает права составителей GDZ.
Ready-ds помогают студентам получить оценки 4 и 5!
Пока студент переписывает готовые документы, он вспоминает, как решить эту проблему и стать умнее.
В нашей коллекции есть такие разделы:
— ГДЗ по русскому языку 6 класс
— ГДЗ по алгебре 9 класс
— ГДЗ Путин
— ГДЗ по алгебре 7 класс
— ГДЗ по русскому языку 7 класс
— ГДЗ по математике 5 класс
— ГДЗ по алгебре 8
— ГДЗ Русский язык 8 класс
— ГДЗ Геометрия 8 класс
— ГДЗ от Путина
Например, в заданиях ГДЗ по алгебре 9 класс использовать свежие решения задач.Аспиранты «Наших» решают уравнения и записывают ответы на GDZ Algebra 7 класс.
Мы постарались сделать отличную программу, чтобы вам было удобно ею пользоваться.
Многие решенбники уже содержат старые затортые ответы и учителя их знают. Также в этом году мы предлагаем наш решебник с уникальными, свежими ответами.
Также в этом году мы предлагаем наш решебник с уникальными, свежими ответами.
Причем на каждое дополнение есть ответ, чтобы вы понимали, как была решена проблема.
Известный ГДЗ Путин тоже есть в нашем приложении, в нем очень удобно сортировать информацию.
Написано много ответов на ГДЗ по русскому языку 7 класс, сочиняет и составляет филологические задачи.
Наше приложение — это не только актуальные старшекласники, но и полезная информация GDZ по математике 5 класс, GDZ Algebra 8 класс, GDZ Русский язык 8 класс.
Наши специалисты разработали это приложение, чтобы вы лучше учились и запоминали больше информации.
GDZ Geometry Grade 8 очень полный и подробно описан в разделах приложения.
Мы используем такие форматы, как ответы Путина на ГДЗ.
Попробуйте наши ready-ds, и вы останетесь довольны !!!
Также предлагаем Вам расширенный ответ GDZ Algebra Grade 9 и GDZ Algebra Grade 7
Также есть видеоответы GDZ по русскому языку и GDZ Grade 7 по математике 5 класс.


 Но это непосредственно следует из условия единичной когерентности для слабого TT-морфизма η¯A \ bar \ eta_A.
Но это непосредственно следует из условия единичной когерентности для слабого TT-морфизма η¯A \ bar \ eta_A.
 69-105.
69-105.