гдз математика Мерзляк 6 клас
математика
українська мова
українська література
англійська мова
французька мова
німецька мова
біологія
географія
всесвітня історія
інформатика
Обери свій клас
- Вы здесь:
- Главная
- Математика 6 Мерзляк
- Вправа 1001 гдз математика 6 клас мерзляк
1
2
3
4
5
6
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
132
133
134
135
136
137
138
139
150 151 152 153 154 155 156 157 158 159
160 161 162 163 164 165 166 167 168 169
170 171 172 173 174 175 176 177 178 179
180 181 182 183 184 185 186 187 188 189
190 191 192 193 194 195 196 197 198 199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
280 281 282 283 284 285 286 287 288 289
290 291 292 293 294 295 296 297 298 299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
420 421 422 423 424 425 426 427 428 429
430 431 432 433 434 435 436 437 438 439
440 441 442 443 444 445 446 447 448 449
450 451 452 453 454 455 456 457 458 459
460 461 462 463 464 465 466 467 468 469
470 471 472 473 474 475 476 477 478 479
480 481 482 483 484 485 486 487 488 489
490 491 492 493 494 495 496 497 498 499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
550 551 552 553 554 555 556 557 558 559
560 561 562 563 564 565 566 567 568 569
570 571 572 573 574 575 576 577 578 579
580 581 582 583 584 585 586 587 588 589
590 591 592 593 594 595 596 597 598 599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
680 681 682 683 684 685 686 687 688 689
690 691 692 693 694 695 696 697 698 699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
776
777
778
779
780
781
782
783
784
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
801
802
803
804
805
806
807
808
809
810
811
812
813
814
815
816
817
818
819
820
821
822
823
824
825
826
827
828
829
830
831
832
833
834
835
836
837
838
839
840
841
842
843
844
845
846
847
848
849
850
851
852
853
854
855
856
857
858
859
860
861
862
863
864
865
866
867
868
869
870
871
872
873
874
875
876
877
878
879
880
881
882
883
884
885
886
887
888
889
890
891
892
893
894
895
896
897
898
899
900
901
902
903
904
905
906
907
908
909
910
911
912
913
914
915
916
917
918
919
920
921
922
923
924
925
926
927
928
929
930
931
932
933
934
935
936
937
938
939
940
941
942
943
944
945
946
947
948
949
950
951
952
953
954
955
956
957
958
959
960
961
962
963
964
965
966
967
968
969
970
971
972
973
974
975
976
977
978
979
980
981
982
983
984
985
986
987
988
989
990
991
992
993
994
995
996
997
998
999
1000
1001
1002
1003
1004
1005
1006
1007
1008
1009
1010
1011
1012
1013
1014
1015
1016
1017
1018
1019
1020
1021
1022
1023
1024
1025
1026
1027
1028
1029
1030
1031
1032
1033
1034
1035
1036
1037
1038
1039
1040
1041
1042
1043
1044
1045
1046
1047
1048
1049
1060 1061 1062 1063 1064 1065 1066 1067 1068 1069
1070 1071 1072 1073 1074 1075 1076 1077 1078 1079
1080 1081 1082 1083 1084 1085 1086 1087 1088 1089
1090 1091 1092 1093 1094 1095 1096 1097 1098 1099
1100
1101
1102
1103
1104
1105
1106
1107
1108
1109
1110
1111
1112
1113
1114
1115
1116
1117
1118
1119
1120
1121
1122
1123
1124
1125
1126
1127
1128
1129
1130
1131
1132
1133
1134
1135
1136
1137
1138
1139
1140
1141
1142
1143
1144
1145
1146
1147
1148
1149
1150
1151
1152
1153
1154
1155
1156
1157
1158
1159
1160
1161
1162
1163
1164
1165
1166
1167
1168
1169
1180 1181 1182 1183 1184 1185 1186 1187 1188 1189
1190 1191 1192 1193 1194 1195 1196 1197 1198 1199
1200
1201
1202
1203
1204
1205
1206
1207
1208
1209
1210
1211
1212
1213
1214
1215
1216
1217
1218
1219
1220
1221
1222
1223
1224
1225
1226
1227
1228
1229
1230
1231
1232
1233
1234
1235
1236
1237
1238
1239
1240
1241
1242
1243
1244
1245
1246
1247
1248
1249
1250
1251
1252
1253
1254
1255
1256
1257
1258
1259
1260
1261
1262
1263
1264
1265
1266
1267
1268
1269
1270
1271
1272
1273
1274
1275
1276
1277
1278
1279
1280
1281
1282
1283
1284
1285
1286
1287
1288
1289
1300
1301
1302
1303
1304
1305
1306
1307
1308
1309
1310
1311
1312
1313
1314
1315
1316
1317
1318
1319
1320
1321
1322
1323
1324
1325
1326
1327
1328
1329
1330
1331
1332
1333
1334
1335
1336
1337
1338
1339
1340
1341
1342
1343
1344
1345
1346
1347
1348
1349
1350
1351
1352
1353
1354
1355
1356
1357
1358
1359
1360
1361
1362
1363
1364
1365
1366
1367
1368
1369
1370
1371
1372
1373
1374
1375
1376
1377
1378
1379
1380
1381
1382
1383
1384
1385
1386
1387
1388
Любі друзі, будь-ласка, використовуйте ❤️гдз 6 клас математика Мерзляк❤️ Якір Полонський для отримання знань та їх корекції, не обманюйте себе в першу чергу і вчителів. Якщо ви просто переписали, не розуміючи як розв’язується цей приклад, ви зробили погано лише собі. Запам’ятайте це. Я і вся наша команда дуже надіємося на те, що в нашій країні з кожним роком збільшується кількість батьків, які допомогають своїх дітям розв’язувати математику, а наша праця у вигляді гдз 6 клас математика Мерзляк Якір Полонський буде допомогати вам в цьому.
Якщо ви просто переписали, не розуміючи як розв’язується цей приклад, ви зробили погано лише собі. Запам’ятайте це. Я і вся наша команда дуже надіємося на те, що в нашій країні з кожним роком збільшується кількість батьків, які допомогають своїх дітям розв’язувати математику, а наша праця у вигляді гдз 6 клас математика Мерзляк Якір Полонський буде допомогати вам в цьому.
ГДЗ (решебник) Математика 6 клас Мерзляк. Відповіді до підручника
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
Автори:А.Г. Мерзляк, В.Б. Полонський, М.С. Якір
Видавництво:Гімназія, Харьков
Рік видання:2014
Відповіді (ответы):пыдручник (учебник)
СХОЖІ ГДЗ І ПІДРУЧНИКИ
Математика Збірник задач 6 клас Мерзляк 2014 (Укр.)
ГДЗ (Ответы, решебник) Робочий Зошит Математика 6 клас Мерзляк
підручник
§ 1. ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ№ 1 — 186
1. Дільники і кратні№ 1 — 39
Дільники і кратні№ 1 — 39
2. Ознаки подільності на 10, на 5 і на 1№ 40-72
3. Ознаки подільності на 9 і на З№ 73-103
4. Прості й складені числа№ 104-137
5. Найбільший спільний дільник№ 138 — 162
6. Найменше спільне кратне№ 163-186
§ 2. ЗВИЧАЙНІ ДРОБИ№ 187 — 571
7. Основна властивість дробу№ 187 — 209
8. Скорочення дробів№ 210-235
9. Зведення дробів до спільного знаменника. Порівняння дробів№ 236-265
10. Додавання і віднімання дробів№ 266-327
11. Множення дробів№ 328-383
12. Знаходження дробу від числа№ 384-428
13. Взаємно обернені числа№ 429-441
14. Ділення дробів№ 442-492
15. Знаходження числа за заданим значенням його дробу№ 493-535
16. Перетворення звичайних дробів у десяткові№ 536-545
17. Нескінченні періодичні десяткові дроби№ 546-556
18. Десяткове наближення звичайного дробу№ 557 — 571
§ 3. ВІДНОШЕННЯ І ПРОПОРЦІЇ№ 572 — 827
19. Відношення№ 572-598
20. Пропорції№ 599 — 630
Пропорції№ 599 — 630
21. Відсоткове відношення двох чисел№ 631 — 659
22. Пряма і обернена пропорційна залежність№ 660-679
23. Поділ числа у заданому відношенні№ 680-698
24. Коло і круг№ 699-730
25. Довжина кола. Площа круга№ 731-766
26. Циліндр, конус, куля№ 767-782
27. Діаграми№ 783-801
28. Випадкові події. Ймовірність випадкової події№ 802-827
§ 4. РАЦІОНАЛЬНІ ЧИСЛА І ДІЇ З НИМИ№ 828 — 1295
29. Додатні і від’ємні числа№ 828-843
30. Координатна пряма№ 844-868
31. Цілі числа. Раціональні числа№ 869-890
32. Модуль числа№ 891-915
33. Порівняння чисел№ 916-949
34. Додавання раціональних чисел№ 950-973
35. Властивості додавання раціональних чисел№ 974-989
36. Віднімання раціональних чисел№ 990-1019
37. Множення раціональних чисел№ 1020-1050
38. Переставна і сполучна властивості множення раціональних чисел. Коефіцієнт№ 1051-1070
39. Розподільна властивість множення№ 1071-1109
40. Ділення раціональних чисел№ 1110-1137
Ділення раціональних чисел№ 1110-1137
41. Розв’язування рівнянь№ 1138-1167
42. Розв’язування задач за допомогою рівнянь№ 1168-1209
43. Перпендикулярні прямі№ 1210-1236
44. Паралельні прямі№ 1237-1252
45. Координатна площина№ 1253-1283
46. Графіки№ 1284-1295
Вправи для повторення за курс 6 класу№ 1296-1388
«ПЕРЕВІРТЕ СЕБЕ» в тестовій формі№ Задания № 1 — № 6
Поділитися:
Якщо є питання чи побажання пишіть у коментарі:
| Страна: | СССР СССР |
|---|---|
| Научная область: | |
| Место работы: | |
| Альма-матер: | |
| Награды и призы: |
Дополнительный множитель. Приведение дробей к новому знаменателю – правило и примеры. Правило приведения дробей к заданному знаменателю
Главная » Отчет по практике » Дополнительный множитель. Приведение дробей к новому знаменателю – правило и примеры. Правило приведения дробей к указанному знаменателю
Первоначально я хотел включить методы общего знаменателя в параграф «Сложение и вычитание дробей». Но информации было так много, и важность ее так велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Но информации было так много, и важность ее так велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, допустим, у нас есть две дроби с разными знаменателями. И мы хотим убедиться, что знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомним, звучит так:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же ненулевое число.
Таким образом, при правильном выборе множителей знаменатели дробей уравняются — этот процесс называется приведением к общему знаменателю. А искомые числа, «выравнивающие» знаменатели, называются дополнительными множителями.
Зачем вообще нужно приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. Другого способа выполнить эту операцию нет;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно облегчает эту задачу;
- Решение задач на доли и проценты.
 Проценты — это, по сути, обычные выражения, содержащие дроби.
Проценты — это, по сути, обычные выражения, содержащие дроби.
Есть много способов найти числа, которые при умножении делают знаменатели дробей равными. Мы рассмотрим только три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Перекрестное умножение
Самый простой и надежный способ, который гарантированно выровняет знаменатели. Идем дальше: умножаем первую дробь на знаменатель второй дроби, а вторую на знаменатель первой. В результате знаменатели обеих дробей станут равны произведению исходных знаменателей. Взгляните:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получаем:
Да все так просто. Если вы только начинаете учить дроби, лучше работать по этому методу – так вы застрахуете себя от многих ошибок и гарантированно получите результат.
Единственным недостатком этого метода является то, что вам придется много считать, потому что знаменатели перемножаются «навылет», и в результате могут получиться очень большие числа. Это плата за надежность.
Это плата за надежность.
Метод общих делителей
Этот прием позволяет существенно сократить расчеты, но, к сожалению, применяется редко. Метод выглядит следующим образом:
- Прежде чем продолжить (т. е. методом перекрестного анализа), взгляните на знаменатели. Возможно, один из них (тот, что больше) делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем дроби с меньшим знаменателем.
- В этом случае дробь с большим знаменателем вообще не нужно ни на что умножать — это экономия. При этом резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Обратите внимание, что 84:21=4; 72:12=6. Так как в обоих случаях один знаменатель делится на другой без остатка, применяем метод общих множителей. У нас есть:
Обратите внимание, что вторая дробь вообще ни на что не умножалась. Фактически, мы вдвое сократили объем вычислений!
Кстати, дроби в этом примере я взял не случайно. Если вам интересно, попробуйте посчитать их крест-накрест. После сокращения ответы будут такими же, но работы будет гораздо больше.
Если вам интересно, попробуйте посчитать их крест-накрест. После сокращения ответы будут такими же, но работы будет гораздо больше.
В этом сила метода общих делителей, но, повторяю, его можно применять только тогда, когда один из знаменателей делится на другой без остатка. Что достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы, по сути, пытаемся найти число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них не обязательно будет равно прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 подойдет число 24, так как 24: 8 = 3; 24 : 12 = 2. Это число много меньше произведения 8 12 = 96.
Наименьшее число, которое делится на каждый из знаменателей, называется их наименьшим общим кратным (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК (a; b).
Например, НОК (16; 24) = 48; НЦМ (8; 12) = 24.
Если вы сможете найти такое число, общий объем вычислений будет минимальным. Взгляните на примеры:
Задача. Найдите значения выражений:
Обратите внимание, что 234 = 117·2; 351 = 117 3. Множители 2 и 3 взаимно просты (у них нет общих делителей, кроме 1), а множитель 117 является общим. Следовательно, НОК (234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 4. Множители 3 и 4 взаимно просты, а множитель 5 — обычный. Следовательно, НОК (15; 20) = 5 3 4 = 60.
Теперь приведем дроби к общему знаменателю:
Обратите внимание, насколько полезным было разложение исходных знаменателей на множители:
- Найдя те же множители, мы сразу пришли к наименьшему общему кратному, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, какие факторы «недостают» для каждой из дробей. Например, 234 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.

Чтобы оценить, какой колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить те же примеры, используя метод крест-накрест. Без калькулятора, конечно. Думаю после этого комментарии будут лишними.
Не думайте, что в реальных примерах не будет таких сложных дробей. Они постоянно встречаются, и вышеперечисленные задания не предел!
Проблема только в том, как найти этот самый NOC. Иногда все находится за несколько секунд буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Мы не будем касаться этого здесь.
Схема приведения общего знаменателя
- Необходимо определить, какое будет наименьшее общее кратное для знаменателей дробей. Если вы имеете дело со смешанным или целым числом, то его необходимо сначала превратить в дробь, а уж потом определить наименьшее общее кратное. Чтобы преобразовать целое число в дробь, нужно в числителе написать само число, а в знаменателе единицу.
 Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратилось в дробь, нужно умножить целое число на знаменатель и прибавить к нему числитель. Пример: 8 целых чисел и 3/5 в виде дроби = 8х5 + 3/5 = 43/5.
Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратилось в дробь, нужно умножить целое число на знаменатель и прибавить к нему числитель. Пример: 8 целых чисел и 3/5 в виде дроби = 8х5 + 3/5 = 43/5. - После этого необходимо найти дополнительный множитель, который определяется путем деления НОЗ на знаменатель каждой дроби.
- Последним шагом является умножение дроби на дополнительный коэффициент.
Важно помнить, что приведение к общему знаменателю необходимо не только для сложения или вычитания. Чтобы сравнить несколько дробей с разными знаменателями, также нужно сначала каждую из них привести к общему знаменателю.
Общий знаменатель дробей
Для того чтобы понять, как привести дробь к общему знаменателю, нужно понимать некоторые свойства дробей. Итак, важным свойством, используемым для приведения к НКД, является равенство дробей. Другими словами, если числитель и знаменатель дроби умножить на число, то в результате получится дробь, равная предыдущей. В качестве примера возьмем следующий пример. Для того чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, нужно сделать следующее:
В качестве примера возьмем следующий пример. Для того чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, нужно сделать следующее:
- Сначала найдите наименьшее общее кратное знаменателей. В этом случае для чисел 9 и 6 НОК будет равен 18.
- Определите дополнительные коэффициенты для каждой из дробей. Это делается следующим образом. Делим НОК на знаменатель каждой из дробей, в результате получаем 18:9=2, а 18:6=3. Эти числа будут дополнительными множителями.
- Вносим две фракции в НОЗ. При умножении дроби на число необходимо умножить и числитель, и знаменатель. Дробь 5/9можно умножить на дополнительный коэффициент 2, в результате чего получится дробь, равная этой — 10/18. То же самое делаем со второй дробью: 5/6 умножаем на 3, получается 15/18.
Как видно из примера, представленного выше, обе дроби были приведены к наименьшему общему знаменателю. Чтобы окончательно разобраться, как найти общий знаменатель, нужно усвоить еще одно свойство дробей. Он заключается в том, что числитель и знаменатель дроби можно сократить на одно и то же число, которое называется общим делителем. Например, 12/30 можно уменьшить до 2/5, разделив его на общий множитель 6.
Он заключается в том, что числитель и знаменатель дроби можно сократить на одно и то же число, которое называется общим делителем. Например, 12/30 можно уменьшить до 2/5, разделив его на общий множитель 6.
Чтобы понять, как складывать дроби с разными знаменателями, давайте сначала изучим правило, а затем рассмотрим конкретные примеры.
Чтобы складывать или вычитать дроби с разными знаменателями, нужно:
1) Найти (НОЗ) заданные дроби.
2) Найдите дополнительный множитель для каждой дроби. Для этого новый знаменатель нужно разделить на старый.
3) Умножьте числитель и знаменатель каждой дроби на дополнительный коэффициент и сложите или вычтите дроби с одинаковыми знаменателями.
4) Проверить правильность и несократимость полученной дроби.
В следующих примерах нужно складывать или вычитать дроби с разными знаменателями:
1) Чтобы вычесть дроби с разными знаменателями, сначала ищем наименьший общий знаменатель этих дробей. Выберите большее из чисел и проверьте, делится ли оно на меньшее. 25 не делится на 20. Умножьте 25 на 2. 50 на 20 не делится. Умножьте 25 на 3. 75 на 20 не делится. Умножьте 25 на 4,100 и разделите на 20. Следовательно, наименьший общий знаменатель равен 100.
Выберите большее из чисел и проверьте, делится ли оно на меньшее. 25 не делится на 20. Умножьте 25 на 2. 50 на 20 не делится. Умножьте 25 на 3. 75 на 20 не делится. Умножьте 25 на 4,100 и разделите на 20. Следовательно, наименьший общий знаменатель равен 100.
2) Чтобы найти дополнительный множитель для каждой дроби, надо новый знаменатель разделить на старый. 100:25=4, 100:20=5. Соответственно к первой дроби дополнительный множитель 4, ко второй — 5.
3) Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычесть дроби по правилу вычитания дробей с одинаковыми знаменателями.
4) Полученная дробь правильная и неприводимая. Так что это ответ.
1) Чтобы сложить дроби с разными знаменателями, сначала ищем наименьший общий знаменатель. 16 не делится на 12. 16∙2=32 не делится на 12. 16∙3=48 делится на 12. Значит 48 это НОЗ.
2) 48:16=3, 48:12=4. Это дополнительные множители для каждой дроби.
3) умножить числитель и знаменатель каждой дроби на дополнительный множитель и сложить новые дроби.
4) Полученная дробь правильная и неприводимая.
1) 30 не делится на 20. 30∙2 = 60 разделить на 20. Значит 60 — наименьший общий знаменатель этих дробей.
2) чтобы найти дополнительный множитель для каждой дроби, новый знаменатель нужно разделить на старый: 60:20=3, 60:30=2.
3) умножить числитель и знаменатель каждой дроби на дополнительный множитель и вычесть новые дроби.
4) полученная дробь на 5.
1) 8 не делится на 6. 8 ∙ 2 = 16 не делится на 6. 8 ∙ 3 = 24 делится и на 4, и на 6. Итак, 24 является НОЗ.
2) чтобы найти дополнительный множитель для каждой дроби, нужно новый знаменатель разделить на старый. 24:8=3, 24:4=6, 24:6=4. Значит, 3, 6 и 4 являются дополнительными множителями к первой, второй и третьей дробям.
3) умножить числитель и знаменатель каждой долбы на дополнительный коэффициент. Добавить и вычесть. Полученная дробь неверна, поэтому необходимо выбрать целую часть.
В этом уроке мы рассмотрим приведение дробей к общему знаменателю и решим задачи на эту тему. Дадим определение понятиям общего знаменателя и дополнительного множителя, вспомним о взаимно простых числах. Определим понятие наименьшего общего знаменателя (НОД) и решим ряд задач на его нахождение.
Дадим определение понятиям общего знаменателя и дополнительного множителя, вспомним о взаимно простых числах. Определим понятие наименьшего общего знаменателя (НОД) и решим ряд задач на его нахождение.
Тема: Сложение и вычитание дробей с разными знаменателями
Урок: Приведение дробей к общему знаменателю
Повторение. Основное свойство дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная дробь.
Например, числитель и знаменатель дроби можно разделить на 2. Получаем дробь. Эта операция называется сокращением дроби. Также можно выполнить обратное преобразование, умножив числитель и знаменатель дроби на 2. В этом случае говорят, что мы привели дробь к новому знаменателю. Число 2 называется дополнительным фактором.
Выход. Дробь можно привести к любому знаменателю, кратному знаменателю данной дроби. Чтобы привести дробь к новому знаменателю, ее числитель и знаменатель умножают на дополнительный множитель.
1. Приведите дробь к знаменателю 35.
35 кратно 7, то есть 35 делится на 7 без остатка. Это означает, что такое преобразование возможно. Найдем дополнительный множитель. Для этого делим 35 на 7. Получаем 5. Умножаем числитель и знаменатель исходной дроби на 5.
2. Приведите дробь к знаменателю 18.
Найдем дополнительный множитель. Для этого разделите новый знаменатель на исходный. Получаем 3. Умножаем числитель и знаменатель этой дроби на 3.
3. Приводим дробь к знаменателю 60.
Деление 60 на 15 дает нам дополнительный множитель. Это 4. Умножить числитель и знаменатель на 4.
4. Привести дробь к знаменателю 24
В простых случаях приведение к новому знаменателю производится в уме. Дополнительный множитель принято указывать только вне скобок чуть правее и выше исходной дроби.
Дробь можно привести к знаменателю 15, а дробь можно привести к знаменателю 15. Дроби также имеют общий знаменатель 15.
Общий знаменатель дробей может быть любым общим кратным их знаменатели. Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей этих дробей.
Пример. Приведите дробь к наименьшему общему знаменателю.
Сначала найдите наименьшее общее кратное знаменателей этих дробей. Это число равно 12. Найдем дополнительный множитель для первой и для второй дроби. Для этого разделите 12 на 4 и 6. Три — это дополнительный множитель для первой дроби, а два — для второй. Приведем дроби к знаменателю 12.
Мы привели дроби к общему знаменателю, то есть нашли равные им дроби, у которых один и тот же знаменатель.
Правило. Чтобы привести дроби к наименьшему общему знаменателю, нужно
Сначала найдите наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
Во-вторых, разделить наименьший общий знаменатель на знаменатели этих дробей, то есть найти дополнительный множитель для каждой дроби.
В-третьих, умножьте числитель и знаменатель каждой дроби на дополнительный множитель.
а) Приведите дробь и к общему знаменателю.
Наименьший общий знаменатель равен 12. Дополнительный множитель для первой дроби равен 4, а для второй 3. Привести дроби к знаменателю 24.
б) Привести дробь и к общему знаменателю.
Наименьший общий знаменатель равен 45. Деление 45 на 9 на 15 дает 5 и 3 соответственно. Приведите дроби к знаменателю 45.
в) Приведите дробь и к общему знаменателю.
Общий знаменатель равен 24. Дополнительные делители равны 2 и 3 соответственно.
Иногда бывает трудно устно найти наименьшее общее кратное для знаменателей этих дробей. Затем с помощью простых множителей находятся общий знаменатель и дополнительные множители.
Привести дробь и к общему знаменателю.
Разобьем числа 60 и 168 на простые множители. Напишем разложение числа 60 и добавим недостающие множители 2 и 7 из второго разложения. Умножьте 60 на 14, чтобы получить общий знаменатель 840. Дополнительный множитель для первой дроби равен 14. Дополнительный множитель для второй дроби равен 5. Приведите дроби к общему знаменателю 840.
Умножьте 60 на 14, чтобы получить общий знаменатель 840. Дополнительный множитель для первой дроби равен 14. Дополнительный множитель для второй дроби равен 5. Приведите дроби к общему знаменателю 840.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемосина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математики 5-6 класс. — ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6 классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О. и другие. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.
Вы можете скачать книги, перечисленные в разделе 1.2. этого урока.


 Г. Мерзляк, В.Б. Полонский, М.С. Якира. Содержит правильные ответы на все упражнения из учебника для 5 класса издательства Вентана-Граф 2016 года. Информация в пособии актуальна и на 2019 год.. ГДЗ пользуется большим успехом у школьных учителей и частных преподавателей, которые на основе готового материала создают свои уникальные конспекты.
Г. Мерзляк, В.Б. Полонский, М.С. Якира. Содержит правильные ответы на все упражнения из учебника для 5 класса издательства Вентана-Граф 2016 года. Информация в пособии актуальна и на 2019 год.. ГДЗ пользуется большим успехом у школьных учителей и частных преподавателей, которые на основе готового материала создают свои уникальные конспекты.



 28 июля 1958 г.) — советский и украинский педагог, учитель математики, автор учебно-методической литературы, народный учитель Украины, полный кавалер ордена «За заслуги».
28 июля 1958 г.) — советский и украинский педагог, учитель математики, автор учебно-методической литературы, народный учитель Украины, полный кавалер ордена «За заслуги». — Харьков: Гимназия, 2008.
— Харьков: Гимназия, 2008. Г. Мерзляк, Д.А. Номировский, В.Б. Полонский, М.С. Якир. Алгебра и начало анализа. 10 класс (углубленное изучение). — Харьков: Гимназия, 2010.
Г. Мерзляк, Д.А. Номировский, В.Б. Полонский, М.С. Якир. Алгебра и начало анализа. 10 класс (углубленное изучение). — Харьков: Гимназия, 2010. Г. Мерзляк, В.Б. Полонский, М.С. Якир. Алгебра. 7 класс (углубленное изучение). — Москва: Вентана-Граф, 2013.
Г. Мерзляк, В.Б. Полонский, М.С. Якир. Алгебра. 7 класс (углубленное изучение). — Москва: Вентана-Граф, 2013.

 Глаза его смотрели на вошедших.
Глаза его смотрели на вошедших. 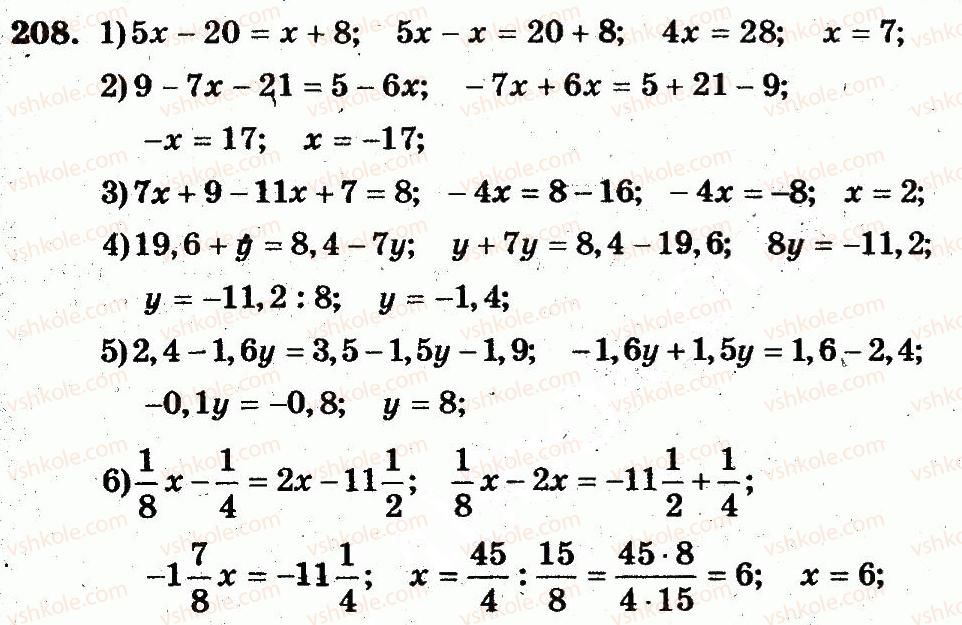
 Он, чуткий, нежный князь Андрей, как мог он сказать это с той, которую он любил и которая любила его! Если бы он думал жить, то сказал бы это менее холодно-оскорбительным тоном. Если бы он не знал, что умрет, то как бы ему не было жалко ее, как он мог сказать это при ней! Объяснение этому могло быть только одно, это то, что ему было все равно, и все-таки потому, что ему открылось что-то другое, самое важное.
Он, чуткий, нежный князь Андрей, как мог он сказать это с той, которую он любил и которая любила его! Если бы он думал жить, то сказал бы это менее холодно-оскорбительным тоном. Если бы он не знал, что умрет, то как бы ему не было жалко ее, как он мог сказать это при ней! Объяснение этому могло быть только одно, это то, что ему было все равно, и все-таки потому, что ему открылось что-то другое, самое важное. 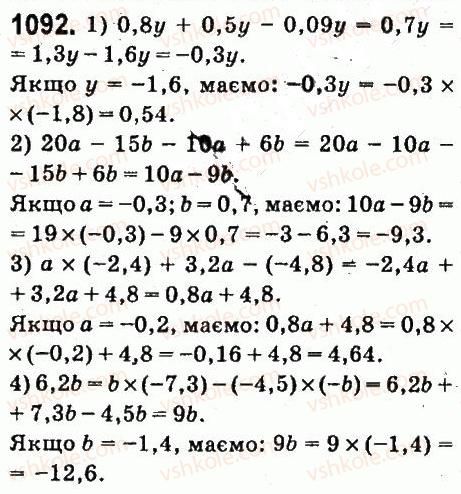 — Он писал здесь, что вы ему очень понравились, — продолжал он просто, спокойно, видимо, не в силах понять всего того сложного значения, какое имели его слова для живых людей. — Ежели бы и вы его полюбили, то очень хорошо… чтобы вы вышли замуж, — прибавил он несколько побыстрее, как бы обрадовавшись тем словам, которые давно искал и нашел наконец . Княжна Марья слышала его слова, но они не имели для нее другого значения, кроме того, что доказывали, как ужасно далеко он был теперь от всего живого.
— Он писал здесь, что вы ему очень понравились, — продолжал он просто, спокойно, видимо, не в силах понять всего того сложного значения, какое имели его слова для живых людей. — Ежели бы и вы его полюбили, то очень хорошо… чтобы вы вышли замуж, — прибавил он несколько побыстрее, как бы обрадовавшись тем словам, которые давно искал и нашел наконец . Княжна Марья слышала его слова, но они не имели для нее другого значения, кроме того, что доказывали, как ужасно далеко он был теперь от всего живого.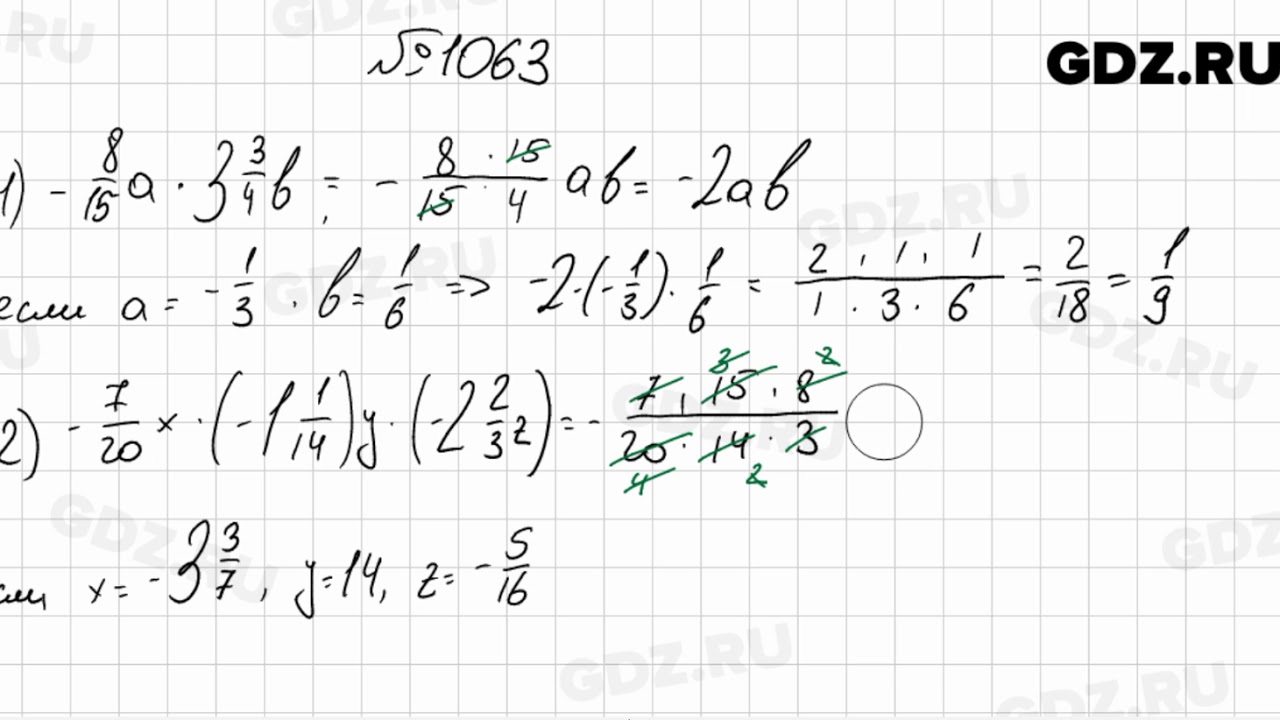
 С другой стороны, в сборник включены задачи, давно ставшие математическим фольклором, авторов которых мы просто не знаем. По этим причинам нам пришлось отказаться от наших первоначальных намерений.
С другой стороны, в сборник включены задачи, давно ставшие математическим фольклором, авторов которых мы просто не знаем. По этим причинам нам пришлось отказаться от наших первоначальных намерений.  Мерзляк А.Г., Полонский В.Б., Якир М.С. 1993 — fileskachat.com, скачать быстро и бесплатно.
Мерзляк А.Г., Полонский В.Б., Якир М.С. 1993 — fileskachat.com, скачать быстро и бесплатно. Проценты — это, по сути, обычные выражения, содержащие дроби.
Проценты — это, по сути, обычные выражения, содержащие дроби.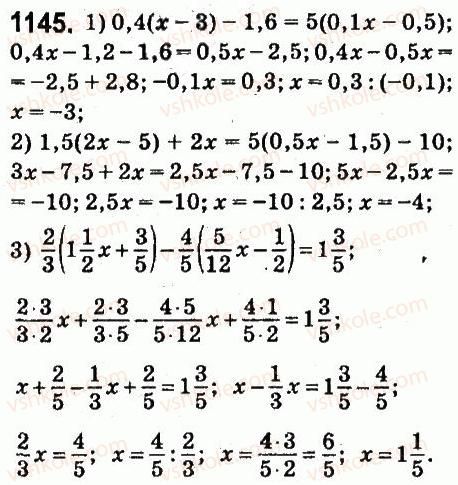 Например, НОК (16; 24) = 48; НЦМ (8; 12) = 24.
Например, НОК (16; 24) = 48; НЦМ (8; 12) = 24.
 Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратилось в дробь, нужно умножить целое число на знаменатель и прибавить к нему числитель. Пример: 8 целых чисел и 3/5 в виде дроби = 8х5 + 3/5 = 43/5.
Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратилось в дробь, нужно умножить целое число на знаменатель и прибавить к нему числитель. Пример: 8 целых чисел и 3/5 в виде дроби = 8х5 + 3/5 = 43/5.