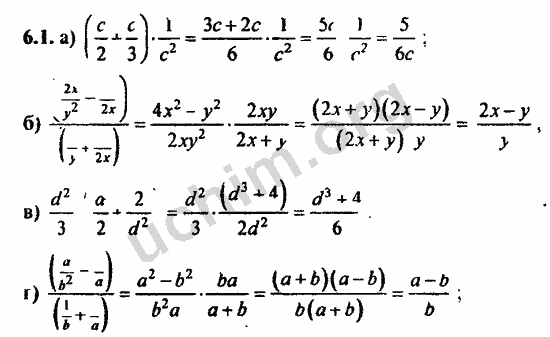1 гдз по алгебре: Номер №1 — ГДЗ по Алгебре 7 класс: Мерзляк А.Г.

ГДЗ Алгебра 7 класс Никольский, Потапов, Решетников

• Алгебра 7 класс
• Серия: МГУ — школе.
• Тип пособия: Учебник
• Авторы: Никольский, Потапов, Решетников
• Издательство: «Просвещение»

Задания для самоконтроля

123456789101112131415161718

Задания на исследование

123456789101112131415

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057067077087097107117127137147157167177187197207217227237247257267277287297307317327337347357367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797807817827837847857867877887897907917927937947957967977987998008018028038048058068078088098108118128138148158168178188198208218228238248258268278288298308318328338348358368378388398408418428438448458468478488498508518528538548558568578588598608618628638648658668678688698708718728738748758768778788798808818828838848858868878888898908918928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132

Задания для самоконтроля: 1

Условие

Решебник №1

Решебник №2

Учим алгебру правильно

Многие школьники после разделения привычной им математики на алгебру и геометрию начинают теряться. Более сложный материал и непонятные формулы нередко становятся причиной падения успеваемости. Если с самого начала не наладить учебный процесс, то в дальнейшем исправить ситуацию будет значительно труднее. Для полного понимания алгебры необходимо не только внимательно слушать учителя, штудировать учебник, но и пользоваться дополнительными методическими пособиями, такими как ГДЗ.

Седьмой класс готовит учеников к более углубленному изучению предмета. Так как данная дисциплина очень сложна, то и относиться к ней надо с повышенным вниманием. Программа в этом году предстоит тоже весьма непростая. Действительные числа, алгебраические и линейные уравнения — это одно из немногого с чем придется столкнуться школьникам на уроках.

Немаловажным является полное осознание материала, так как малейшее недопонимание или отсутствие в школе по болезни даже в течении пары дней, может привести к тому, что предмет перестанет нравиться и оценки по нему значительно снизятся. Чтобы этого не произошло, детям и их родителям предлагают воспользоваться решебником к учебнику «Алгебра 7 класс Учебник Никольский, Потапов, Решетников, Шевкин (Просвещение, 2015г.)». Это пособие поможет поддерживать свои знания на должном уровне.

Что включено в ГДЗ

В сборнике содержится 1132 основных задания, а так же задачи на исследование и для самоконтроля. Они полностью охватывают учебный курс этого года. Авторы предоставили ребятам:

• обширные ответы;
• подробные решения;
• дополнительные материалы.

Все это призвано помочь ученикам глубже вникнуть в тематику и избежать ошибок, которые повлияют на их успеваемость. ГДЗ по Алгебре 7 класс Никольский станет незаменимым помощником каждого школьника. Самостоятельные и контрольные работы уже не будут представлять какой-либо сложности, ведь к ним можно заранее подготовиться. Вся необходимая для этого информация представлена на страницах данного справочника, и доступна к просмотру онлайн круглосуточно, так что ученики могут работать в удобное для себя время.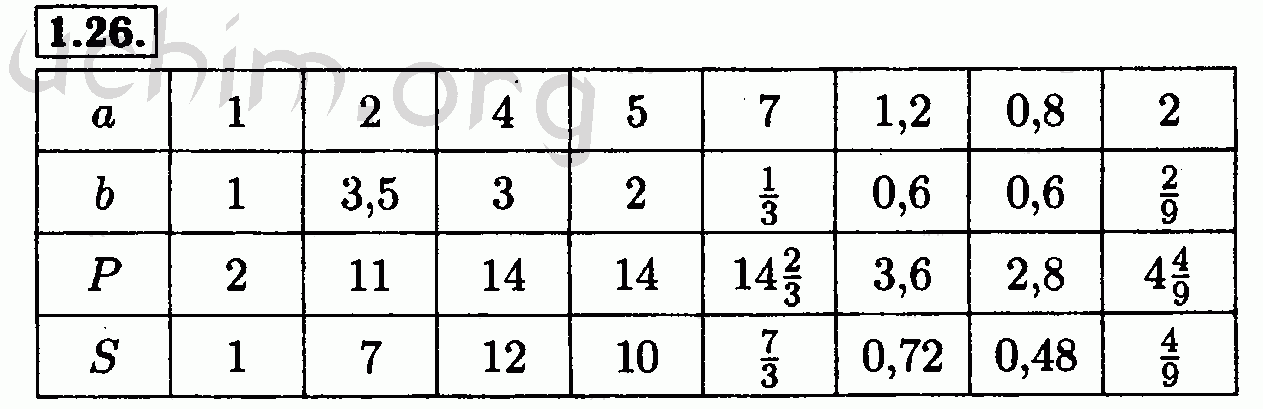

Чего ожидать от решебника

Изучение алгебры требует максимальной отдачи от учащихся. Это не тот предмет, который можно просто задвинуть на задний план, не вникая в его суть. Но именно так и стараются поступить многие дети, не отдавая себе отчета в том, что одна неправильно понятая тема негативно повлияет на понимание дисциплины в целом. Поэтому ребятам необходимо:

1. Внимательно разбирать параграфы.
2. Не стесняться задавать вопросы в случае недопонимания.
3. Выполнять все задания учителя.
4. Проводить в обязательном порядке работу над ошибками.
5. Пользоваться ГДЗ для самоконтроля.

Кроме того, это руководство будет полезно не только ученикам, но и их родителям. Его плюсы заключаются в полной доступности заданий даже для людей, которые мало что понимают в данном предмете или основательно его подзабыли. Решебник к учебнику «Алгебра 7 класс Никольский (Просвещение)» поможет любому школьнику подтянуть свои знания, а взрослым — в любой момент проконтролировать учебный процесс и проверить уровень подготовки своих отпрысков.

Решебником нередко пользуются и учителя. Данное пособие помогаем им сэкономить время на проверке тетрадей своих подопечных, составить план урока и нередко задания для контрольных они выбирают именно из ГДЗ по алгебре. Школьникам стоит иметь это ввиду, чтобы заблаговременно проштудировать материалы и не испытывать затруднений при очередной внеплановой проверочной работе.

Насколько продуктивно использование ГДЗ

Учитывая большие нагрузки, которые предстоит испытать школьникам в этом году, не приходится удивляться, что многие из них просто теряют интерес к учебе. Ребята просто не успевают заниматься внеурочной деятельностью, выполнять многочисленные задания и посещать дополнительные секции. Кроме того, им необходимо выделить еще достаточно времени на отдых, иначе на следующий день они просто не смогут сосредоточиться на уроках. Естественно при таком раскладе учащиеся начинают искать всевозможные способы облегчить себе жизнь. Чаще всего ребята прибегают к списыванию. Такой способ только на первых порах приносит положительный результат, а потом начинаются проблемы.

Намного эффективнее использовать в учебном процессе решебник, который позволит существенно сократить время на выполнение домашнего задания и усвоение текущего материала. С этим пособием под рукой ученики могут не переживать, что что-то не успеют или упустят. Авторы постарались максимально адаптировать представленные сведения для пользователей с любым уровнем знаний, так что даже двоечники смогут стать отличниками при должном усердии.

Как правильно пользоваться онлайн-решебником

Некоторые школьники считают, что не нужно прикладывать особых усилий, чтобы пользоваться ГДЗ по алгебре 7 класс Учебник Никольский (Просвещение). Но это не совсем так. Ведь если просто бездумно списывать информацию, то нужные знания просто не отложатся в памяти, что в дальнейшем негативно скажется при проведении проверочных мероприятий. Поэтому необходимо придерживаться нескольких элементарных правил:

• всегда изучать теорию;
• все задания выполнять самостоятельно;
• проверять себя при помощи ГДЗ;
• искать причины возникновения ошибок;
• закреплять изученное.

Если действовать по этому алгоритму, то можно с легкостью разобрать даже самые сложные алгебраические темы. При этом полученными познаниями школьники смогут воспользоваться и в дальнейшем, а не просто позабудут все через пару недель. Решебник находится в круглосуточном онлайн-доступе, поэтому открыть его можно с любого современного гаджета, подключенного к интернету. Это дает возможность воспользоваться подсказками непосредственно перед уроком, что гарантирует получение пятерки и за устный ответ и за письменную работу.

Гдз по Алгебре. 1-11 класс

Алгебра и начала анализа 11 класс

А.Н. Колмогоров и др.

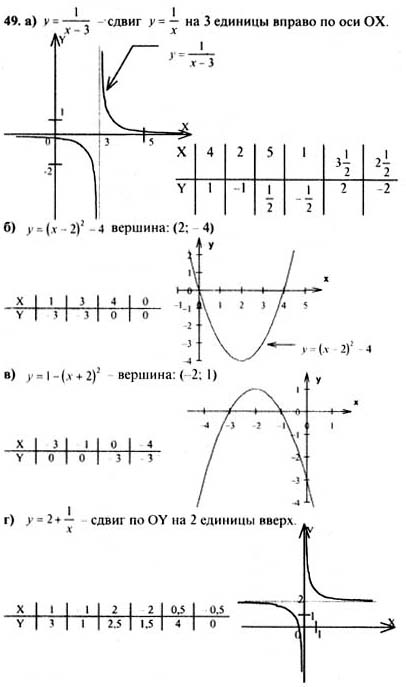
«М.: Просвещение»

Алгебра и начала анализа 11 класс

С.А. Шестаков

«М.: Внешсигма, 2004»

Алгебра и начала анализа 11 класс

Ш.А. Алимов и др.

«М.: Просвещение»

Алгебра и начала анализа 11 класс. Задачник

А.Г. Мордкович, Л.О. Денищева, Т.А. Корешкова,Т.Н. Мишустина, Е.Е. Тульчинская

«М.: Мнемозина, 2001»

Алгебра и начала анализа 11 класс. Задачник

А.Г. Мордкович

«М.: Мнемозина»

Алгебра и начала анализа 11 класс. Контрольные работы

А.Г. Мордкович, Е.Е. Тульчинская

«М.: Мнемозина»

Дидактические материалы по алгебре и началам анализа для 11 класса

Б.М. Ивлев, С.М. Саакян,С.И. Шварцбурд

«М.: Просвещение»

Сборник заданий для подготовки и проведения письменного экзамена 11 класс

Г.В. Дорофеев, Г.К. Муравин, Е.А. Седова

«М.: Дрофа»

Сборник задач по математике для поступающих в вузы.

М.И. Сканави

Алгебра и начала анализа 10 класс

А.Н. Колмогоров

«М.: Просвещение»

Алгебра и начала анализа 10 класс

Ш.А. Алимов и др.

«М.: Просвещение»

Алгебра и начала анализа 10 класс. Задачник

А.Г. Мордкович, Л.О. Денищева, Т.А. Корешкова,Т.Н. Мишустина, Е.Е. Тульчинская

«М.: «Мнемозина», 2001 »

Алгебра и начала анализа 10 класс. Задачник

А.Г. Мордкович и др.

«М.: Мнемозина»

Алгебра и начала анализа 10 класс. Контрольные работы

А.Г. Мордкович, Е.Е. Тульчинская

«М.: Мнемозина»

Дидактические материалы по алгебре и начала анализа для 10 класса

Б. М. Ивлев, С.М. Саакян, С.И. Шварцбург

«М.: Просвещение, 1999»

Сборник задач по математике для поступающих в вузы

М.И. Сканави

Алгебра, задачник часть 2

Мордкович, Мишустина, Тульчинская

«М.: Мнемозина. 2003, 2005 и 2007 год»

Алгебра. Сборник заданий для подготовки к ГИА в 9 классе

Л.В. Кузнецова, С.Б. Суворова

«М.: Просвещение, 2010 год»

Алгебра. Сборник заданий для подготовки к ГИА в 9 классе

Л.В. Кузнецова и др.

«6-е изд. — М.:Просвещение, 2011 год»

Алгебра. Учебник для 9 класса.

Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.

«М.: «Просвещение», 2001 — 2014»

Алгебра 9 класс

Ю.

Н. Макарычев

Алгебра 9 класс

Ю.Н. Макарычев

«М.: Просвещение, 2007»

Алгебра 9 класс

Ю.Н. Макарычев

«М.: Просвещение, 2012»

Алгебра 9 класс. Дидактические материалы

Ю.Н. Макарычев, Н.Г. Миндюк, Л.Б. Крайнева

Алгебра 9 класс. Дидактические материалы

Ю.Н. Макарычев, Н.Г. Миндюк, Л.Б. Крайнева

«М.: Просвещение, 2005-2010 »

Алгебра 9 класс. Дидактические материалы

Ю.Н. Макарычев, Н.Г. Миндюк

«М.: Просвещение, 2003»

Алгебра 9 класс. Контрольные работы

Ю.П. Дудницын, Е.Е. Тульчинская

«М.: Мнемозина»

Алгебра 9 класс задачник в двух частях, ч. 2

А.Г. Мордкович

«М.: Мнемозина, 2015»

Алгебра 9.

Макарычев

«1999-2000 год»

Алгебра и начала анализа. Сборник задач для подготовки и проведения итоговой аттестации за курс средней шк.

С. Шестаков

«М.: Астрель, 2003-2004»

Дидактические материалы по алгебре для 9 класса

Б.Г. Зив, В.А. Гольдич

«СПб: Петроглиф, 2004»

Рабочая тетрадь по алгебре 9 класс. К учебнику А.Г. Мордкович

Е.М. Ключникова И.В. Комиссарова

Рабочая тетрадь по алгебре 9 класс. К учебнику Ю.М. Колягин

М.В. Ткачёва Н.Е. Фёдорова М.И. Шабунин

Рабочая тетрадь по алгебре 9 класс. Часть 1

И. Г. Миндюк И.С. Шлыкова

Рабочая тетрадь по алгебре 9 класс. Часть 1

С.С. Минаева, Л.О. Рослова

Рабочая тетрадь по алгебре 9 класс. Часть 2

И.Г. Миндюк И.С. Шлыкова

Рабочая тетрадь по алгебре 9 класс. Часть 2

С.С. Минаева, Л.О. Рослова

Сборник заданий для проведения письм. экзамена по алгебре за курс осн. школы. 9 класс

Л.В. Кузнецова и др.

«7-е изд., стереотип. — М.: Дрофа, 2002 год»

Сборник задач. Алгебра 8 и 9 класс.

Галицкий, Гольдман, Звавич

«М.: Просвещение, от 2011 года»

Алгебра

Ю.Н. Макарычев, Волошина B.C.

«Просвещение, 2012 год»

Алгебра. Учебник для 8 класса

Ш.А. Алимов и др.

«М.: Просвещение, 2012, 2013, 2014, 2015»

Алгебра 8 класс

А.Г. Мордкович, Т.Н. Мишустина, Е.Е.Тульчинская

«4-е изд. — М.: Мнемозина, старый учебник 2002г»

Алгебра 8 класс

Никольский С.М., Шульцева О.В.

«М.: Просвещение, 2011-2015 гг»

Алгебра 8 класс. Старый учебник.

Ш.А. Алимов

«М.: Просвещение, 2001-2011 год»

Алгебра 8 класс задачник. 2 часть.

Мордкович А.Г., Мишустина Т.Н., Тульчинская Е.Е.

«М.: Мнемозина, 2003-2015 гг.»

Алгебре 8 класс. Учебник для общеобразовательных учреждений

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б

«М.: Просвещение, 2003-2015 гг»

Дидактические материалы Алгебра 8 класс.

Макарычев Ю.Н., Жохов В.И., Миндюк Н.Г.

«М.: Просвещение, Решения и ответы к контрольным работам 2011-2015 гг.»

Дидактические материалы по алгебре для 8 класса

Б.Г. Зив, В.А. Гольдич

«7-е изд. — СПб:Петроглиф, 2010»

Контрольно измерительные материалы по алгебре 8 класс

Черноруцкий В.В.

Рабочая тетрадь по алгебре 8 класс. К учебнику А.Г. Мордкович. Часть 1

Е.М. Ключникова, И.В. Комиссарова

Рабочая тетрадь по алгебре 8 класс. К учебнику А.Г. Мордкович. Часть 2

Е.М. Ключникова, И.В. Комиссарова

Рабочая тетрадь по алгебре 8 класс. К учебнику Ю.Н. Макарычев

Т.М. Ерина

Рабочая тетрадь по алгебре 8 класс. Часть 1

Г. К. Муравин, О. В. Муравина

Рабочая тетрадь по алгебре 8 класс. Часть 1

И.И. Зубарева, М.С. Мильштейн

Рабочая тетрадь по алгебре 8 класс. Часть 1

Н.Г. Миндюк И.С. Шлыкова

Рабочая тетрадь по алгебре 8 класс. Часть 1

С.С. Минаева Л.О. Рослова

Рабочая тетрадь по алгебре 8 класс. Часть 1

Юрий Колягин, Мария Ткачева, Надежда Федорова, Михаил Шабунин

Рабочая тетрадь по алгебре 8 класс. Часть 2

Г. К. Муравин, О. В. Муравина

Рабочая тетрадь по алгебре 8 класс. Часть 2

Н.Г. Миндюк И.С. Шлыкова

Рабочая тетрадь по алгебре 8 класс. Часть 2

С.С. Минаева Л.О. Рослова

Рабочая тетрадь по алгебре 8 класс. Часть 2

Юрий Колягин, Мария Ткачева, Надежда Федорова, Михаил Шабунин

Сборник задач по алгебре 8-9 класс

М.Л. Галицкий, А.М. Гольдман, Л.И.Звавич

«М.: Просвещение, 2011»

Алгебра. Контрольные работы 7 класс

Ю.П. Дудницин, Е.Е. Тульчинская

«М.: Мнемозина, 2006 год, 8-е издание»

Алгебра. Контрольные работы 7 класс

Ю.П. Дудницин

«М.: Мнемозина, 2000 год, 2-е изд.»

Алгебра 7 класс

Алимов Ш.А.

«М.: Просвещение, Год: с 2012 по 2014»

Алгебра 7 класс

Ю.Н. Макарычев, Н. Г. Миндюк, К.И. Нешков, С.Б. Суворова

«М.: Просвещение, 2013-2015 год»

Алгебра 7 класс. Дидактические материалы

Л.И. Звавич, Л.В. Кузнецова

«М.: Просвещение, 2011 год»

Алгебра 7 класс : в двух частях. задачник

А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская

«М.: «Мнемозина», 2003 »

Алгебра 7 класс задачник. Часть 2.

А.Г. Мордкович и др.

«М.: Мнемозина, 2010 год, 14-е изд. стер.»

Дидактические материалы по алгебре для 7 класса

Б.Г. Зив, В.А. Гольдич

«11 изд. — СПб:Петроглиф 2010 год»

Контрольные работы — Алгебра 7-9 классы.

А.Г. Мордкович

Рабочая тетрадь алгебра

Макарычев

Рабочая тетрадь по алгебре 7 класс

С. С. Минаева Л.О. Рослова

Рабочая тетрадь по алгебре 7 класс. К учебнику А.Г. Мордкович

Е.М. Ключникова И.В. Комиссарова

Рабочая тетрадь по алгебре 7 класс. Часть 1

Г. К. Муравин, О. В. Муравина

Рабочая тетрадь по алгебре 7 класс. Часть 1. К учебнику Ш.А. Алимов

Ю.М. Колягин М.В. Ткачева

Рабочая тетрадь по алгебре 7 класс. Часть 1. К учебнику Ю.Н. Макарычев

Т.М. Ерина

Рабочая тетрадь по алгебре 7 класс. Часть 2

Г. К. Муравин, О. В. Муравина

Рабочая тетрадь по алгебре 7 класс. Часть 2. К учебнику Ш.А. Алимов

Ю.М. Колягин М.В. Ткачева

Рабочая тетрадь по алгебре 7 класс Часть 2.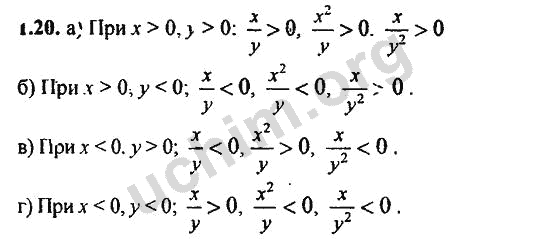 К учебнику Ю.Н. Макарычев

Т.М. Ерина

Рабочая тетрадь по алгебре 7 класс №1

И.И. Зубарева, М.С. Мильштейн

Рабочая тетрадь по алгебре 7 класс №2

И.И. Зубарева, М.С. Мильштейн

ГДЗ по математике 1 класс учебник Моро 1, 2 часть

Часть 1. Страницы

• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76
• 77
• 78
• 79
• 80
• 81
• 82
• 83
• 84
• 85
• 86
• 87
• 88
• 89
• 90
• 91
• 92
• 93
• 94
• 95
• 96
• 97
• 98
• 99
• 100
• 101
• 102
• 103
• 104
• 105
• 106
• 107
• 108
• 109
• 110
• 111
• 112
• 113
• 114
• 115
• 116
• 117
• 118
• 119
• 120
• 121
• 122
• 123
• 124
• 125
• 126
• 127

Часть 2.

Страницы

• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76
• 77
• 78
• 79
• 80
• 81
• 82
• 83
• 84
• 85
• 86
• 87
• 88
• 89
• 90
• 91
• 92
• 93
• 94
• 95
• 96
• 97
• 98
• 99
• 100
• 101
• 102
• 103
• 104
• 105
• 106
• 107
• 108
• 109
• 110
• 111

Дополнительное ГДЗ Моро

• Рабочая тетрадь по математике 1 класс Моро, Волкова
• Проверочные работы по математике 1 класс Волкова 

Рекомендуем посмотреть

• Рабочая тетрадь по окружающему миру 1 класс Плешаков
• Учебник по русскому языку 1 класс Канакина, Горецкий
• Рабочая тетрадь по русскому языку 1 класс Канакина, Горецкий

Описание

Сборник готовых домашних заданий по учебнику М. И. Моро, С.И. Волковой, С. В. Степановой «Математика 1 класс» демонстрирует принципы выполнения основных номеров.

Для удобства материал разбит на две части. Страницы ГДЗ строго соответствуют учебнику. Имеются необходимые пояснения к аналитическим заданиям, краткие записи задач на сложение, вычитание, чертежи, неравенства.

Преимущество пособия состоит в том, что оно представляет решения упражнений под чертой, что не всегда встречается у авторов других ГДЗ.

Высококачественные иллюстрации выглядят чётко, разборчиво. Наглядное объяснение алгоритмов помогает понять принципы решения, поэтапной записи, итогового оформления. Это позволяет оперативно передавать навыки работы детям.

Ваше сообщение отправлено!

+

GDZ In Algebra Class 7-11 APK Скачать для Android

Главная→ Приложения→ Образование

Загрузить APK →

ГДЗ по алгебре 7-11 класс приложение

В приложении вы найдете ГДЗ на учебники и задачники авторов Макарычева, Мордковича, Алимова, Мерзляка, Николая, Миндюка, Колягина, Суворова и других. Алгебра — очень важная школьная дисциплина, она фактически готовит вас к началу математического анализа. Основные возможности приложения: 1) Поиск по автору и теме. 2) Поиск класса (ГДЗ представлен для 7, 8, 9, 10 и 11 классы). Все представленные решения и ответы предоставлены исключительно в целях самопроверки и контроля домашних заданий. Не забудьте оценить ГДЗ по алгебре 7-11 класс.

Показать больше

Последняя версия

ГДЗ по алгебре 7-11 класс

Последняя версия   

Другие версии

Горячее приложение

Гугл ТВ

ООО «Гугл»

3,9 5Б+

Ютуб

ООО «Гугл»

4.2 10Б+

Карты Google

ООО «Гугл»

4.1 10Б+

Мессенджер

Meta Platforms, Inc.

4.1 5Б+

Google Дуэт

ООО «Гугл»

4,6 5Б+

Gmail

ООО «Гугл»

4.2 10Б+

Google Chrome: быстрый и безопасный

ООО «Гугл»

4.2 10Б+

MX-плеер

MX Media (ранее J2 Interactive)

4.4 1Б+

Google Просмотр улиц

ООО «Гугл»

4.2 1Б+

Dropbox: безопасное облачное хранилище

Dropbox, Inc.

4.3 1Б+

Google Презентации

ООО «Гугл»

4. 1 1Б+

Майкрософт OneDrive

Корпорация Майкрософт

4,6 1Б+

Лучшие загрузки

Кахут! Играйте и создавайте викторины

Кахут!

4.7 50 млн+

Напоминание: Школьное общение

Напомнить101

4.4 10 млн+

Розеттский камень: учись, практикуйся и говори на языках

Розетта Стоун Лтд

4.7 10 млн+

ABCmouse.com

Возраст обучения, Inc.

4 10 млн+

Класс Додзё

Класс Додзё

4.8 10 млн+

Lingokids: обучающие игры для детей

Lingokids — Изучение английского языка для детей

4. 3 10 млн+

Star Walk 2 Ads+ Просмотр карты звездного неба

Технология Вито

4,5 10 млн+

Баббель — Изучайте языки

Баббель

4.6 10 млн+

Детское видео PBS

PBS ДЛЯ ДЕТЕЙ

4.4 10 млн+

PictureThis — Идентификатор растений

ООО «Глорити»

4.7 10 млн+

SkyView® Lite

Одиннадцатый Терминал

4.4 10 млн+

Quizlet: языки и словарный запас

Quizlet Inc.

4,5 10 млн+

Домашняя страница Кай-Вен Лана — Математические ссылки

Домашняя страница Кай-Вен Лана — Математические ссылки Интернет-ресурсы Люди

---

Интернет-ресурсы

• Информация
  • Полный поиск MathSciNet
  • MR Поиск
  • Диссертации и тезисы ProQuest через Университет Миннесоты
  • Списки конференций/семинаров по: Сеть теории чисел Киран Кедлая Рави Вакил MathMeetings. net
• Журналы/серии онлайн (бесплатно или через Миннесотский университет)
  • Успехи в математике
  • Алгебра и теория чисел
  • Американский математический журнал Проект МУЗА JSTOR
  • Алгебраическая геометрия
  • Анналы Института Фурье
  • Annales Scientifiques de l’École Normale Supérieure
  • Анналы математики
  • Азиатский математический журнал
  • Бюллетень Математического общества Франции
  • Бюллетень математических наук
  • Бюллетень Американского математического общества
  • Математические комментарии Helvetici 1-71 72-
  • Коммуникации в алгебре
  • Математическая композиция 1–104 105–139 105-
  • Дискретная математика
  • Документа Математика
  • Математический журнал Герцога 1–100 все
  • Экспериментальная математика
  • Форум математики, Пи
  • Форум математики, Sigma
  • Функциональный анализ и его приложения
  • Математические изобретения Спрингер ГДЗ
  • Уведомления о международных математических исследованиях
  • Journal de Théorie des Nombres de Bordeaux
  • Journal für die reine und angewandte Mathematik (Журнал Крелла)
  • Журнал алгебры
  • Журнал алгебраической геометрии
  • Журнал дифференциальной геометрии
  • Журнал Американского математического общества АМС JSTOR
  • Журнал Института математики Жюссье
  • Журнал математического общества Японии Проект Евклид J-ЭТАП
  • Журнал теории чисел
  • Журнал символьных вычислений
  • Конспекты лекций по математике
  • Математическая рукопись
  • Скандинавская математика
  • Математика
  • Математический Аннален Спрингер ГДЗ
  • Письма о математических исследованиях
  • Mathematische Nachrichten
  • Математическая газета Спрингер ГДЗ
  • Мичиганский математический журнал
  • Уведомления Американского математического общества
  • Тихоокеанский математический журнал 1–176 официальный
  • Труды Американского математического общества АМС JSTOR
  • Труды Эдинбургского математического общества
  • Труды Лондонского математического общества
  • Публикации mathématiques de l’I. H.E.S.
  • Чистая и прикладная математика Ежеквартально
  • Rendiconti del Seminario Matematico della Università di Padova
  • Теория представлений
  • Исследования в области теории чисел
  • Исследования в области математических наук
  • Труды Американского математического общества АМС JSTOR
• Документы Архивы
  • Открытые математические заметки AMS
  • Архивы Гротендик
  • Архив электронной печати arXiv.org
  • Фронт математики ArXiv
  • Геометрический семинар Ленглендса Чикагского университета
  • Электронная библиотека по математике, математические журналы
  • Страница курса Гейтсгори
  • Göttinger Digitalisierungs-Zentrum
  • Труды ICM
  • ICTP 2003: Высшая школа основ алгебраической геометрии
  • JStor
  • NUMDAM — нумерация документов по древней математике
  • Проект МУЗА
  • НаукаПрямой
• Темы, представляющие общий интерес
  • Теория чисел
    • Сеть теории чисел
      • Домашние страницы/ведомственные списки специалистов по теории чисел
      • Вещи, представляющие интерес для теоретиков чисел
    • Список теории чисел
  • Список теоретиков представлений
  • Проект математической генеалогии
  • Ассоциация сотрудников Николя Бурбаки

---

человек

Ахмед Аббес; Нориюки Абэ (阿部紀行) ; Джеффри Адамс; Валерий Алексеев; Патрик Аллен; Екатерина Америкак; Джузеппе Анкона; Грег В. Андерсон; Фабрицио Андреатта; Том М. Апостол; Дону Арапура; Константин Ардаков; Сара Ариас-де-Рейна; Джеймс Артур; Авнер Эш; Джозеф Аюб.

Мэтью Бейкер; Бенджамин Баккер; Франческо Бальдассарри; Пол Франк Баум; Кай Беренд; Ребекка Белловин; Лоран Бергер; Тобиас Бергер; Владимир Беркович; Джозеф Бернштейн; Пьер Бертело; Александр Бертолони Мели; Бхаргав Бхатт; Кошер Биркар; Дон Блазиус; Спенсер Блох; Гебхард Бёкле; Ричард Э. Борчердс; Найджел Бостон; Жан Бурген; Джордж Боксер; Паскаль Бойер; Риккардо Браска; Александр Браверман; Кристоф Брей; Оливье Бринон; Мишель Брион; Патрик Броснан; Бен Брубейкер; Ян Хендрик Брюнье; Дэниел Бамп; Дэвид Бернс; Эшай А. Бурунгейл; Кевин Баззард.

Фрэнк Калегари; Ана Караиани; Хуай-Дун Цао (曹怀东) ; Дэниел Каро; Билл Кассельман; Франсеск Кастелла; Кястутис Чеснавичюс; Чинг-Ли Чай (翟敬立) ; Шарлотта Чан; Юнкай Чен (陳榮凱) ; Миаофэн Чен (陈苗芬) ; Цао-Сянь Чен (陳朝銑) ; Chuangxun Cheng (程创勋) ; Вэнь-Чен Чи (紀文鎮) ; Масатака Чида (千田雅隆) ; Гаэтан Шевенье; Бруно Чиареллотто; Тед Чинбург; Ионут Чокан-Фонтанине; Джеймс В. Когделл; Пьер Колмез; Ален Конн; Брайан Конрад; Кейт Конрад; Дэвид А. Кокс; Кристоф Корнут; Джон Кремона.

Анри Дармон; Жан-Франсуа Дат; Стивен ДеБакер; Марк Андреа де Катальдо; Айз Йохан де Йонг; Пьер Делинь; Лассина Дембеле; Кристофер Денинджер; Эхуд де Шалит; Фред Даймонд; Йивэнь Дин (丁一文) ; Луис Виктор Дьелефе; Младен Димитров; Габриэль Доспинеску.

Гарольд М. Эдвардс; Эллен Э. Эйшен; Джордан С. Элленберг; Ноам Д. Элкис; Мэтью Эмертон; Элен Эно; Рон Эванс.

Лоран Фарг; Тобиас Финис; Джессика Финцен; Маттиас Флах; Йенс Франке; Эберхард Фрайтаг; Хавьер Фресан; Эдвард Френкель; Йенс Функе.

Деннис Гейтсгори; Хуэй Гао (高辉) ; Цзыян Гао (高紫阳) Пол Гаррет; Тоби Джи; Стивен Гелбарт; Джейс Р. Гетц; Дориан Голдфельд; Роу Гудман; Эяль З. Горен; Марк Горески; Ульрих Герц; Дэвид Госс; Фернандо К. Гувеа; Ральф Гринберг; Майкл Грехениг; Бенедикт Х. Гросс; Самуил Грушевский.

Томас Дж. Хейнс; Пол Хамахер; Дэвид Хансен; Шуши Харашита (原下秀士) ; Гюнтер Хардер; Майкл Харрис; Урс Хартл; Шин Хаттори (服部新) Йохен Хайнлот; Деннис А. Хейхал; Сюйхуа Хэ (何旭華) ; Ойген Хеллманн; Дэвид Хелм; Флориан Херциг; Харузо Хида (肥田晴三) ; Марк Хиндри; Вэй Хо; Мел Хохстер; Фриц Хорманн; Бен Ховард; Мин-Лунь Се (謝銘倫) ; Юнцюань Ху (胡永泉) ; Цзин-Сун Хуан (黄劲松) ; Клаус Хулек; Джеймс Э. Хамфрис.

Ацуши Ичино (市野篤史) ; Люк Иллюзи; Тамоцу Икэда (池田保) ; Наоки Имаи (今井直毅) ; Тецуши Ито (伊藤哲史) .

Эрве Жаке; Йенс Карстен Янцен; Фрейзер Джарвис; Личжэнь Цзи (季理真) ; Дихуа Цзян (江迪华) ; Кристиан Йоханссон; Андрей Йорза.

Ташо Калета; Масаки Кашивара (柏原正樹) ; Джесси Касс; Пейман Кассаи; Фумихару Като (加藤文元) ; Николас М. Кац; Киран Шридхара Кедлая; Чандрашекхар Кхаре; Минхён Ким; Вансу Ким; Марк Кисин; Бруно Клинглер; Энтони В. Кнапп; Шиничи Кобаяши (小林真一) ; Тошиюки Кобаяши (小林俊行) ; Янош Коллар; Нил Коблиц; Арно Крет; Даниэль Криз; Стивен С. Кудла.

Жан-Пьер Лабес; Лоран Лафорг; Винсент Лафорг; Джеффри С. Лагариас; Роберт П. Ленглендс; Раду Лаза; Роберт Лазарсфельд; Мин Хо Ли; Антонио Лей; Хендрик В. Ленстра-младший; Брэндон В. Левин; Марк Левин; Чао Ли (李超) ; Цзянь-Шу Ли (勵建書) ; Цзюнь Ли (李骏) ; Шичжан Ли (李时璋) ; Вэнь-Цзин Винни Ли (李文卿) ; Вэнь-Вэй Ли (李文威) ; Цзе Линь (林洁) ; Байин Лю (刘柏英) ; Руочуань Лю (刘若川) ; Тонг Лю (刘通) ; Ифэн Лю (刘一峰) ; Элон Линденштраус; Алекс Любоцкий; Дэвид Леффлер; Эдуард Дж.Н. Лоойенга; Оттмар Лоос; Иван Лосев; Джонатан Любин; Джудит Людвиг; Джейкоб Лурье; Джордж Люстиг; Геннадий Любезник; Сергей Лысенко.

Роберт Д. Макферсон; Кирти Мадапуси Пера; Елена Мантован; Владимир Маркович; Саймон Маршалл; Филипп Мезонобе; Ахил Мэтью; Барри Мазур; Ёити Миэда (三枝洋一) ; Лука Мильорини; Джон Миллсон; Джеймс С. Милн; Шиничи Мотидзуки (望月新一) ; Колетт Мёглин; Фарид Мокране; Бен Мунен; Софи Морель; Лоран Море-Байи; Мэтью Морроу; Гэри Л. Маллен; Дэвид Мамфорд; Виджая Кумар Мурти; Рам Мурти.

Дэвид Надлер; Арвинд Н. Наир; Ику Накамура (中村郁) ; Джеймс Ньютон; Бо Чау Нго; Марк-Юбер Николь; Весава Низио; Рутгер Нут.

Тадаши Очиай (落合理) ; Андрей Одлызко; Артур Огус; Мартин Олссон; Кен Оно; Франс Оорт; Фабрис Оргогозо.

Lue Pan (潘略) ; Георгиос (Джордж) Паппас; Стефан Патрикис; Аннегрет Пол; Бернадетт Перрен-Риу; Джонатан Пила; Винсент Пиллони; Ричард Пинк; Аарон Пикстон; Аарон Поллак; Дэвид Поллак; Роберт Поллак; Патрик Поло; Бьорн Пунен; Флориан Поп; Михнеа Попа; ; Дипендра Прасад; Гопал Прасад; Картик Прасанна.

Джозеф Рабинофф; Ниранджан Рамачандран; Динакар Рамакришнан; Лоренцо Рамеро; Майкл Рапопорт; Кеннет А. Рибет; Тимо Ришарц; Джованни Россо: Сандра Розенштайн; Карл Рубин; Зеев Рудник.

Клод Саббах; Маса-Хико Сайто (齋藤政彦) ; Такеши Сайто (斎藤毅) ; Яннис Сакелларидис; Алиреза Салехи Голсефиди; Лесли Д. Сапер; Питер Сарнак; Шу Сасаки (佐々木秀) ; Фумихиро Сато (佐藤文広) ; Гордон Савин; Дэвид Сэвитт; Уилл Савин; Эйтан Саяг; Пьер Шапира; Майкл Шейн; Вильфрид Шмид; Ральф Шмидт; Питер Шнайдер; Питер Шольце; Рене Шуф; Бенджамин Шраен; Мехмет Халюк Şengün; Фрейдун Шахиди; Анант Шанкар; Арул Шанкар; Ромьяр Шарифи; Сюй Шэнь (申旭) ; Кодзи Симидзу (清水康司) ; Суг Ву Шин (申皙宇) ; Алиса Сильверберг; Джозеф Х. Сильверман; Эндрю Сноуден; Клаус М. Соренсен; Каннан Сундарараджан; Стивен Спербер; Флориан Спранг; Джейсон Старр; Уильям А.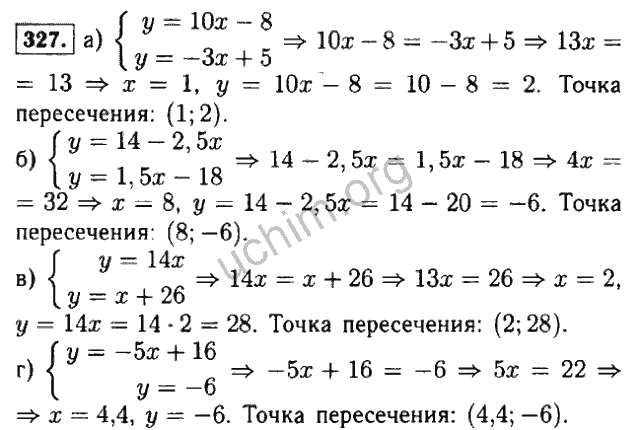 Штейн; Гленн Стивенс; Матиас Штраух; Бенуа Стро; Июнь Су (苏钧) ; Биньонг Сун (孙斌勇) .

Марко Тадич; Ленни Тельман; Оливье Тайби; Рамин Таклоо-Бигаш; Гарри Тамвакис; Юньцин Тан (唐云清) ; Такаси Танигучи (谷口隆) ; Ричард Тейлор; Салим Тайу; Джереми Тейтельбаум; Николай Темплиер; Джек Торн; Е Тянь (田野) ; Жак Тилуин; Питер Э. Трапа; Дэвид Треуманн; Джейкоб Цимерман.

Эммануэль Ульмо; Дуглас Алмер; Эрик Урбан.

Джерард ван дер Гир; Вееравалли С. Варадараджан; Энтони Варильи-Альварадо; Ила Варма Адриан Васиу; Акшай Венкатеш; Марина Вязовская; Эккарт Фивег; Ева Виманн; Мари-Франс Виньерас; Кари Вилонен; Бьянка Вирай; Анджело Вистоли; Владимир Воеводский; Клэр Вуазен; Пол Войта; Дэвид Воган; Фелипе Волох.

Мишель Вальдшмидт; Жан-Лу Вальдспургер; Чен Ван (万忱) ; Дацин Ван (万大庆) ; Синь Ван (万昕) ; Чин-Лунг Ван (王金龍) ; Лоуренс С. Вашингтон; Чарльз А. Вейбель; Джаред Вайнштейн; Райнер Вайсауэр; Кирстен Викельгрен; Габор Визе; Ченянь Ву (吴晨彦) ; Дмитрий Висс.

Лян Сяо (肖梁) ; Цзюньи Се (谢俊逸) ; Чэньян Сюй (许晨阳) ; Даксин Сюй (许大昕) ; Конг Сюэ (английский) ; Тин Сюэ (薛婷) .

Андрей Яфаев; Тунхай Ян (杨同海) ; Сай-Ки Юнг (楊世琪) ; Александр Юцис; Чиа-Фу Ю (余家富) ; Дженг-Доу Ю (余正道) ; Тони Юэ Ю (余越) . Синьи Юань (袁新意) ; Чживэй Юнь (恽之玮) .

Сара Зербес; Шоу-Ву Чжан (张寿武) ; Вэй Чжан (张伟) ; Вэйчжэ Чжэн (郑维喆) ; Ронг Чжоу; Чен-Бо Чжу (朱程波) ; Ихан Чжу (朱艺航) ; Пол Циглер; Майкл Зив; Томас Зинк; Дэвид Зюрик-Браун; Давид Зывина.

Алгебра 1 — Что такое Алгебра 1? Задачи, темы, формулы

Алгебра 1 или элементарная алгебра включает в себя традиционные темы, изучаемые в курсе современной элементарной алгебры.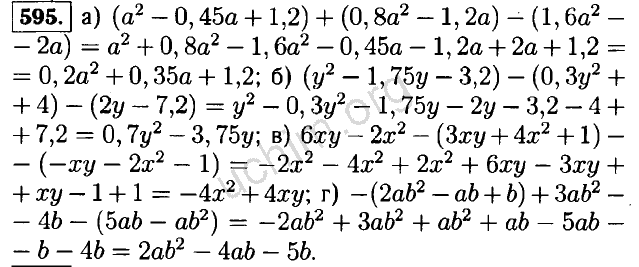 Основные арифметические операции включают числа наряду с математическими операциями, такими как +, -, x, ÷. В то время как алгебра включает такие переменные, как x, y, z, и математические операции, такие как сложение, вычитание, умножение и деление, для формирования осмысленного математического выражения.

Алгебра помогает представить различные ситуации или проблемы в виде математических выражений. Понятия, относящиеся к алгебре 1 или элементарной алгебре, включают в себя переменные, оценку выражений и уравнений, свойства равенств и неравенств, решение алгебраических уравнений и линейных уравнений с одной или двумя переменными и так далее.

1.	Что такое Алгебра 1?
2.	Алгебра 1 Темы
3.	Законы алгебры 1
4.	Алгебра 1 Формулы
5.	Разница между Алгеброй 1 и Алгеброй 2
6.	Алгебра 1: советы и рекомендации
7.	Часто задаваемые вопросы по алгебре 1

Что такое Алгебра 1?

Алгебра 1  состоит из общих/основных понятий алгебры. Он вводит оценочные уравнения и неравенства, действительные числа и их свойства, которые включают аддитивные и мультипликативные тождества, обратные операции, а также дистрибутивные и коммутативные свойства. В алгебре 1 мы также познакомимся с концепцией многочленов, а также включим немного геометрии для вычисления площади, объема и периметров фигур с использованием алгебраических выражений вместо чисел.

Алгебра 1 или элементарная алгебра связана с решением алгебраических выражений для правильного ответа. В алгебре 1 простые переменные, такие как x, y, представлены в виде уравнения. В зависимости от степени переменной уравнения можно разделить на различные типы, а именно линейные уравнения, квадратные уравнения, кубические уравнения и так далее. Линейные уравнения имеют вид ax + b = c, ax + by + c = 0, ax + by + cz + d = 0. Элементарная алгебра, основанная на степени переменных, разветвляется на квадратные уравнения и полиномы. Общая форма представления квадратного уравнения: ax ² + bx + c = 0, а для полиномиального уравнения это ax ⁿ + bx ^n-1 + cx ^n-2 + …..k = 0.

Правила для различных свойств в алгебре 1 можно лучше понять, как показано ниже,

Алгебра 1 Темы

Алгебра разделена на многочисленные темы, чтобы помочь в детальном изучении. Алгебра 1 разделена на 12 глав, и каждая глава разделена на несколько уроков. Эти 12 глав в Алгебре 1 даны как:

Глава 1. Вещественные числа и операции с ними

• Целые числа
• Дроби
• Экспоненты
• ПЕМДАС

Глава 2. Линейные уравнения и неравенства

• Переменные выражения
• Линейные уравнения
• Соотношение
• Доля

Глава 3.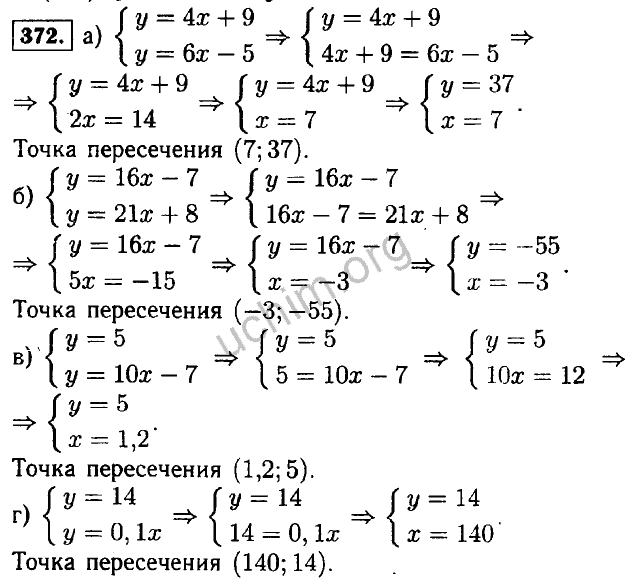 Введение в функции

• Что такое функции?
• Полиномиальные функции
• Визуализация функций с помощью графиков
• Арифметические и геометрические прогрессии

Глава 4: Линии графика

• Декартова система
• Графики линейных уравнений
• Перпендикулярная линия
• Параллельные линии

Глава 5. Решение линейных систем

• Решение линейных систем методом замены
• Решение линейных систем перекрестным умножением
• Решатель системы уравнений
• Решения линейного уравнения

Глава 6. Многочлены и их операции

• Многочлены
• Полиномиальные выражения
• Полином энной степени
• Умножение многочленов

Глава 7. Факторинг и решение методом факторизации

• Что такое фактор?
• Методы факторинга
• Факторизация алгебраических выражений
• Факторизация квадратных уравнений

Глава 8. Экспоненты и экспоненциальные функции

• Экспоненты
• Экспоненциальные функции
• Иррациональные Показатели
• Операции с экспоненциальными членами

Глава 9. Рациональные выражения и уравнения

• Рациональные числа
• Рациональная функция
• Нецелочисленные рациональные показатели
• Упрощение рациональных выражений

Глава 10. Подкоренные выражения и уравнения

• Surds
• Квадрат и квадратный корень
• Рационализация
• Рационализировать знаменатель

Глава 11. Решение квадратных уравнений и построение графиков парабол

• Квадратные и квадратные корни
• Квадратичная формула
• График квадратичной функции
• Комплексные числа и комплексные решения

Глава 12: Анализ данных и вероятность

• Обработка данных
• Вероятность и статистика
• Категориальные данные
• Перестановки и комбинации

Законы алгебры 1

Основными законами алгебры являются ассоциативные, коммутативные и дистрибутивные законы, представленные в таблице ниже:

Имя свойства	Определение	Пример
Коммутативное право на добавление	(а + б) = (б + а). Согласно свойству коммутативности, перестановка позиций операндов в операции не влияет на результат.	Если (4x + 3x) = 7x, то (3x + 4x) = 7x
Коммутативный закон для умножения	(а × б) = (б × а). Согласно свойству коммутативности, перестановка позиций операндов в операции не влияет на результат.	Если (2x × 4) = 8x, то (4 × 2x) = 8x
Ассоциативный закон Для дополнения	а + (б + в) = (а + б) + в. Эта группировка слагаемых не влияет на сумму.	Если 3у + (4у + 5у) = (3у + 9у) = 12у, тогда (3у + 4у) + 5у = ​​7у + 5у = ​​12у
Ассоциативный закон умножения	а × (б × с) = б × (а × с). Эта группа факторов не влияет на продукт.	Если 3a × (2b × 5c) = 3a × (10bc) = 30abc, то (3a × 2b) × 5c = 6ab × 5ac = 30abc ​​
Дистрибутивное право Дополнение	а × (б + с) = (а × б) + (а × с). Сложение двух чисел и последующее их умножение на третье дает тот же результат, что и умножение двух чисел по отдельности на третье с последующим сложением полученного результата.	Если 4x × (3y + 2y) = (4x × 5y) = 20xy, то (4x × 3y) + (4x × 2y) = 12xy + 8xy = 20xy
Распределительный закон для вычитания	а × (б — с) = (а × б) — (а × с). Вычитание двух чисел и последующее их умножение на третье дает тот же результат, что и умножение двух чисел по отдельности на третье с последующим вычитанием полученного результата.	Если 4x × (3y — 2y) = (4x × y) = 4xy, то (4x × 3y) — (4x × 2y) = 12xy — 8xy = 4xy

Алгебра 1 Формулы

Вот список формул, которые очень полезны при решении задач по алгебре 1.

• Алгебраические идентичности:
  (A + B) ² = A ² + 2AB + B ²
  (A — B) ² = A ² 6666666666666666666666666666666666666666666666666666666666 гг. a + b)(a — b) = a ²  — b ²
  (x + a)(x + b) = x ²  + x(a + b) + ab
  (a + b) ³  = а ³  + 3а ² б + 3аб ²  + б ³
  (A- B) ³ = A ³ — 3A ² B + 3AB ² — B ³
  A ^{3 9060 + B} 3 3 ³ 3 ^{3 3 3 3 3 3 3 3 3} 3 + B ^{3 (A 3 3 3 + B 3 . а 2  — ab + b 2 ) ​​
  а 3  — b 3  = (a — b)(a 2  + ab + b 2 ) 2  = а 2  + b 2  + c 2  + 2ab + 2bc + 2ca}
• Свойства показателей:
  a ^m . а ^н  = а ^{m + n}
  a ^m /a ⁿ  = a ^{m — n}
  (a ^m ) ​​ ⁿ  = an
  (ab) ^м  = a ^м . б ^м
  а ⁰  = 1
  а ^-м  = 1/а ^м
• Формулы линейных уравнений:
  Общая форма: ax + by = c
  Форма пересечения наклона: y = mx + b
  Двухточечная форма: y−y ₁ =m(x−x ₁ )
  Форма пересечения: x/a + y/ б = 1
  Вертикальная линия через (p, q): x = p
  Горизонтальная линия через (p, q): y = q
• Формулы квадратных уравнений:
  Стандартная форма квадратного уравнения: ax ² + bx + c = 0,
  Вершинная форма квадратного уравнения: a (x — h) ² + k = 0
  Квадратная формула: Корни квадратного уравнения ax ²  + bx + c = 0 определяются как x = [-b ± √(b² — 4ac)]/2a.
• Формулы арифметической последовательности:
  n ^-й  член, a _n =a ₁ +(n−1)d
  Сумма = n/2 [2a + (n — 1) d] (OR) n/2 [a ₁ + a _п ]
• Формулы геометрической последовательности:
  n ^th  член геометрической прогрессии равен a _n  = a · r ^{n — 1} .
  Сумма n слагаемых, S _n  = a (r ⁿ  – 1)/(r–1)
  Сумма бесконечных слагаемых, S = a/(1–r)
• Формула средней скорости изменения: [f(b) — f(a)] / (b — a)
• Формула сложных процентов: A = P (1 + r / n) ^{n t}  
• Статистические формулы:
  Среднее значение = (Сумма наблюдений) ÷ (Общее количество наблюдений)
  Среднее значение сгруппированных данных =  Σf _i /N
  Медиана, когда n нечетно:  [(n + 1)/2]  срок; Медиана, когда n четное: [(n/2) ^th  term + ((n/2) + 1) ^th  term]/2
  Диапазон = Максимум — Минимум
  Межквартильный диапазон = Верхний квартиль — Нижний квартиль

Разница между Алгеброй 1 и Алгеброй 2

Алгебру 1 и Алгебру 2 можно отличить по сложности и использованию алгебраических выражений. В следующей таблице поясняются важные различия между алгеброй 1 и алгеброй 2.

Алгебра 1	Алгебра 2
Алгебра 1 знакомит вас с общими понятиями алгебры. Вы узнаете о переменных, функциях и самых важных понятиях во всей алгебре.	Алгебра 2 гораздо более продвинутая. Это также гораздо более разнообразно: вы узнаете обо всем, от логарифмов и комплексных чисел до неявных функций и коник до фундаментальной теоремы алгебры.
Алгебра 1 помогает учащимся получить базовые знания по темам алгебры.	Алгебра 2 повышает сложность и понимание тем, изучаемых в алгебре 1.
На этом уроке учащиеся узнают, как манипулировать показателями степени или многочленами, записывать их в более простой форме и т. д.	В этом учащиеся учатся применять навыки, полученные таким образом в алгебре 1, а также изучают более сложные методы.
Алгебра 1 сосредоточена на решении уравнений и неравенств	Алгебра 2 концентрируется на дополнительных типах уравнений, таких как экспоненциальные и логарифмические уравнения.
Алгебра 1 необходима для понимания алгебры 2.	Алгебра 2 необходима для понимания концепций исчисления.

Советы и рекомендации по алгебре 1

• Чтобы понять Алгебру 1, нам нужно быть знакомым с темами доалгебры, такими как целые числа, одношаговые уравнения, многошаговые уравнения, неравенства и уравнения, графики и функции, проценты, вероятности, введение в геометрию и, правильно треугольники. Как только мы пройдем переподготовку, мы сможем перейти к алгебре 1.
• При умножении двух рациональных выражений в алгебре всегда есть риск получить ложные решения или посторонние решения, поэтому будьте осторожны с расчетной частью.
• Мы можем добавлять многочлены, просто добавляя одинаковые члены, чтобы объединить два многочлена в один.

Важные замечания по алгебре 1:

• Свойство неравенства сложения: прибавление одного и того же числа к каждой стороне неравенства дает эквивалентное неравенство.
• Отрицательные показатели: обратные величины положительных показателей в экспоненциальных функциях.
• Свойство отношения степеней: Оно говорит нам, что при делении степеней по одному и тому же основанию нам просто нужно вычесть степени.
• Константы имеют мономиальную степень 0.

☛ Похожие темы:

• Математический калькулятор
• Алгебра Калькулятор
• Калькулятор алгебраических формул

 

Алгебра 1 Задачи

1. Пример 1: Используя законы и свойства алгебры 1, оцените выражение (4 × (x + 2)), где x = 5. x в 4 × (x + 2), мы получаем, 4 × (5 + 2) = 4 × 7 = 28,

   Ответ: 28

2. Пример 2: Решите данное выражение для значения x, 4 + 3 = x.
   Решение:

   Дано, 4 + 3 = х. Мы просто сделаем сложение данного выражения и получим значение x. 4 + 3 равно 7 или x = 4 + 3 = 7.

   Ответ:  Следовательно, значение x равно 7.

3. Пример 3: Решите данное выражение, используя правила алгебры 1 для значения y, 2y + 16 = 32,

   Решение:

   Дано, 2y + 16 = 32. Решим уравнение относительно y.

   2y = 32 — 16 дает 2y = 16, y = 8.

   Ответ: Следовательно, значение y равно 8.

перейти к слайду перейти к слайду перейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по алгебре 1

 

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы по алгебре 1

Чему вы научитесь на уроке алгебры 1?

Алгебра 1 или Элементарная алгебра включает основные традиционные темы, изучаемые в курсе современной элементарной алгебры. Основные арифметические операции включают числа наряду с математическими операциями, такими как +, -, x, ÷. В то время как алгебра включает в себя переменные, такие как x, y, z, и математические операции, такие как сложение, вычитание, умножение и деление, для формирования осмысленного математического выражения.

Что считается алгеброй 1?

Алгебра 1 состоит из общих понятий алгебры. Он вводит оценочные уравнения и неравенства, действительные числа и их свойства, которые включают аддитивные и мультипликативные тождества, обратные операции, а также дистрибутивные и коммутативные свойства.

В чем разница между алгеброй 1 и алгеброй 2?

Разницу между Алгеброй 1 и Алгеброй 2 можно понять, используя следующие пункты:

• Алгебра 1 помогает учащимся получить базовые знания по темам алгебры, в то время как алгебра 2 повышает сложность и понимание тем, изучаемых в алгебре 1.
• На алгебре 1 учащиеся учатся работать с показателями степени или многочленами и записывать их в более простой форме и т. д., а на алгебре 2 учащиеся учатся применять навыки, полученные таким образом на алгебре 1, а также изучают более сложные приемы.
• Алгебра 1 сосредоточена на решении уравнений и неравенств. Но алгебра 2 концентрируется на дополнительных типах уравнений, таких как показательные и логарифмические уравнения.
• Алгебра 1 необходима для понимания алгебры 2, тогда как алгебра 2 необходима для понимания понятий, возникающих в исчислении.

Что такое стандартная форма в алгебре 1?

Стандартная форма в Алгебре 1 — это форма записи данного математического понятия, такого как уравнение, число или выражение, в форме, которая следует определенным правилам.

Как быстро выучить алгебру 1?

Понятия алгебры 1 можно освоить, следуя определенным инструкциям. Ключевые моменты, приведенные ниже, помогут вам обеспечить тщательное графическое изображение элементарной алгебры.

• Сосредоточьтесь на основных арифметических понятиях.
• Помните правило PEMDAS.
• Научитесь четко различать роли переменных, констант, показателей степени, отрицательных и положительных чисел.
• Проведите тщательную ревизию формул.
• Работа над практическими задачами.

Какой класс алгебры 1?

Алгебра 1 или элементарная алгебра — это первый математический предмет, который вы должны пройти в средней школе. В этой части алгебры мы изучаем действительные числа, изучаем решение, написание и графическое отображение линейных уравнений. Также в Алгебру 1.9 включены многочлены, а также квадратные уравнения и функции.0003

Какие темы рассматриваются в Алгебре 1?

Темы, затронутые в алгебре 1, разделены на разные главы. Эти главы можно разделить на следующие категории:

• Реальные числа и их операции
• Линейные уравнения и неравенства
• Введение в функции
• Графические линии
• Решение линейных систем
• Многочлены и их операции
• Факторинг и решение методом факторинга
• Экспоненты и экспоненциальные функции
• Рациональные выражения и уравнения
• Основные выражения и уравнения
• Решение квадратных уравнений и построение графиков парабол
• Анализ данных и вероятность

Алгебра 1 или 2 сложнее?

Алгебра 1 — это базовый блок алгебры 2. Алгебра 2 — более высокий и сложный курс, поэтому алгебра 2 намного сложнее, чем алгебра 1.