ГДЗ(дүж) решения для учебника Геометрия Солтан 9 класс 2020 KZGDZ.COM
Авторы: Солтан Г., Солтан А., Жумадилова А.
Издательство: Келешек-2030
Год: 2020
Электронный учебник
К 9 классу ученик должен знать и уметь разбираться в геометрических фигурах, их свойствах. В новом курсе предмета Геометрия девятиклассника ждут такие темы как: векторы, преобразование плоскости, решение треугольников, окружность и многоугольники. Чтобы не попасть впросак при разборе трудных упражнений, предлагаем воспользоваться решебником для учебника от автора Солтан Г., тут разобраны все задания дисциплины, приведены правильные ответы с пояснениями. Осваивать теоремы станет намного проще даже самым отстающим ребятам. С ГДЗ знания приобретают осмысленный характер, их можно применять для более сложных задач, интегрировать в смежные науки.
Повторение курса геометрии 8 класса.
Упражнение
6789101112131415171920212223242526272829
I.
Векторы1. Понятие вектора. Коллинеарные векторы
Упражнение
3334353637383941
2. Сложение и вычитание векторов
Упражнение
4345464950515253545556
3. Умножение вектора на число. Критерий коллинеарности двух векторов
Упражнение
6162636466676869707172
4. Разложение вектора по двум неколлинеарным векторам.
Упражнение
737475767778798081828384
5. Координаты вектора.
Упражнение
87889093949596979899100101
6. Угол между векторами. Скалярное произведение двух векторов.
Упражнение
103104105
106107108109110112113114115116117118119120
7. Применение векторов при решении задач
Упражнение
121122124126127128
8.
Упражнения на повторение раздела «Векторы»Упражнение
129131132133134135136138139140141142144145
Проверь себя!
Упражнение
148 3B148 4B148 5C
II. Преобразования плоскости.
9. Преобразование плоскости. Движение и его виды
Упражнение
149150151153154155157
10. Применение движений к решению задач
Упражнение
158159160161164165
11. Преобразования гомотетии и подобия, их свойства
Упражнение
166167168169170171172
12. Подобные треугольники
Упражнение
174175176177178179180181182183184185186187188189190
13. Подобные многоугольники
Упражнение
192193194195196197
198199200
14. Применение гомотетии и подобия при решении задач.
Упражнение
202203204205206207208
15. Упражнения на повторение раздела «Преобразования плоскости»
Упражнение
209210211212213214215216217218219220221222223224
Проверь себя!
Упражнение
225 4B225 5С
III. Решение треугольников.
16. Теорема синусов
Упражнение
226227228229230231232233234235
17. Теорема косинусов
Упражнение
236237238239240241242243244245246
18. Решение треугольников
Упражнение
247248249250251253254255256257258259
19. Углы, вписанные в окружность, и их свойства
Упражнение
260262263264265266267268269
20. Свойства касательной и секущей, пересекающихся хорд окружности
Упражнение
270271272273274275276277278279
21.
Применение тригонометрии к выводу формул площадей треугольника и решению задачУпражнение
280281282283284285286287288289290291292293294295296297298299300301302303
22. Упражнения на повторение раздела «Решение треугольников»
Упражнение
304305306307308309310311312313
Проверь себя!
Упражнение
314 4В
IV. Окружность. Многоугольники
23. Вписанные в окружность четырехугольники
Упражнение
316317318319320321
24. Описанные около окружности четырехугольники
Упражнение
322323324325326327328329330331332333334
25. Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него
Упражнение
336337338339340341342
26. Нахождение длин сторон и площадей правильных многоугольников.
Упражнение
343344345346347348349
27. Длина окружности и ее дуги
Упражнение
351352353354355356357358359360361362
363364365366367368
28. Площадь круга, его сектора и сегмента
Упражнение
370371372373374375376377378379380381382383384385
29. Упражнения на повторение раздела «Окружность. Многоугольники»
Упражнение
386387388389390391392393394395396397398399400401402403404405406407408409
Повторение курса геометрии 9 класса
Упражнение
411412413414415416417418419420421422423424425426427428430431433434435436437438439440441442443444445446
447448449450451452
К 9 классу ученик должен знать и уметь разбираться в геометрических фигурах, их свойствах. В новом курсе предмета Геометрия девятиклассника ждут такие темы как: векторы, преобразование плоскости, решение треугольников, окружность и многоугольники.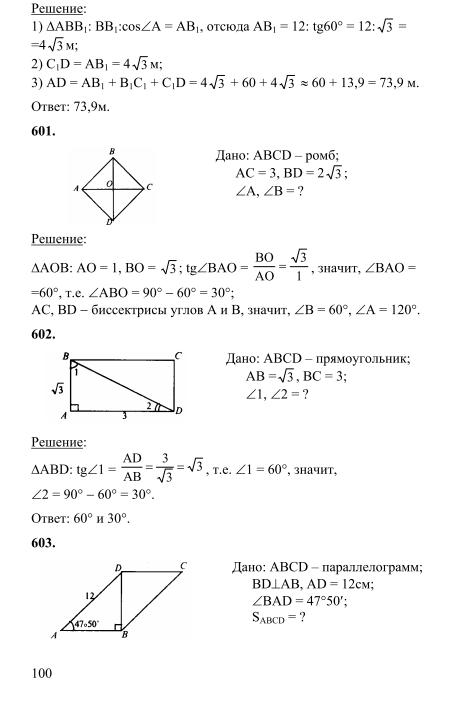
Чтобы не попасть впросак при разборе трудных упражнений, предлагаем воспользоваться решебником для учебника от автора Солтан Г., тут разобраны все задания дисциплины, приведены правильные ответы с пояснениями. Осваивать теоремы станет намного проще даже самым отстающим ребятам. С ГДЗ знания приобретают осмысленный характер, их можно применять для более сложных задач, интегрировать в смежные науки.
А.В. Погорелов. Геометрия. 9 класс. §11. Контрольные вопросы, ответы — Решебник
Страница 1 из 2
Вопрос 1. Что такое преобразование подобия?
Ответ. Преобразование фигуры \(F\) в фигуру \(F’\) называется преобразованием подобия, если при этом проеобразовании расстояния между точками изменяются в одно и то же число раз (рис. 233). Это значит, что если произвольные точки \(X\), \(Y\) фигуры \(F\) при преобразовании подобия переходят в точки \(X’\), \(Y’\) фигуры \(F’\), то \(X’Y’ = k\cdot XY\), причем число \(k\) — одно и то же для всех точек \(X\), \(Y\).
Число \(k\) называется коэффициентом подобия. При \(k = 1\) преобразование подобия, очевидно, является движением.
Вопрос 2. Что такое гомотетия (центр гомотетии, коэффициент гомотетии)?
Ответ. Пусть \(F\) — данная фигура и \(O\) — фиксированная точка (рис. 234). Проведем через произвольную точку \(X\) фигуры \(F\) луч \(OX\) и отложим на нем отрезок \(OX’\), равный \(k\cdot OX\), где \(k\) — положительное число. Преобразование фигуры \(F\), при котором каждая ее точка \(X\) переходит в точку \(X’\), построенную указанным способом, называется
Вопрос 3. Докажите, что гомотетия есть преобразование подобия.
Ответ. Теорема 11.1. Гомотетия есть преобразование подобия.
Доказательство. Пусть \(O\) — центр гомотетии, \(k\) — коэффициент гомотетии, \(X\) и \(Y\) — две произвольные точки фигуры (рис.
235).
При гомотетии точки \(X\) и \(Y\) переходят в точки \(X’\) и \(Y’\) на лучах \(OX\) и \(OY\) соответственно, причем \(OX’ = k\cdot OX\), \(OY’ = k\cdot OY\). Отсюда следуют векторные равенства
\(\overline{OX’} = k\overline{OX},\, \overline{OY’} = k\overline{OY}\).
Вычитая эти равенства почленно, получим:
\(\overline{OY’} — \overline{OX’} = k(\overline{OY} — \overline{OX})\).
Так как \(\overline{OY’} — \overline{OX’} = \overline{X’Y’}\), \(\overline{OY} — \overline{OX} = \overline{XY}\), то \(\overline{X’Y’} = k\overline{XY}\). Значит, \(|\overline{X’Y’}| = k|\overline{XY}|\), т.е. \(X’Y’ = kXY\). Следовательно, гомотетия есть преобразование подобия. Теорема доказана.
Вопрос 4. Какие свойства преобразования подобия вы знаете? Докажите, что преобразование подобия сохраняет углы между полупрямыми.
Ответ. Так же как и для движения, доказывается, что при преобразовании подобия три точки \(A, B, C\), лежащие на одной прямой, переходят в три точки \(A_1, B_1, C_1\), также лежащие на одной прямой.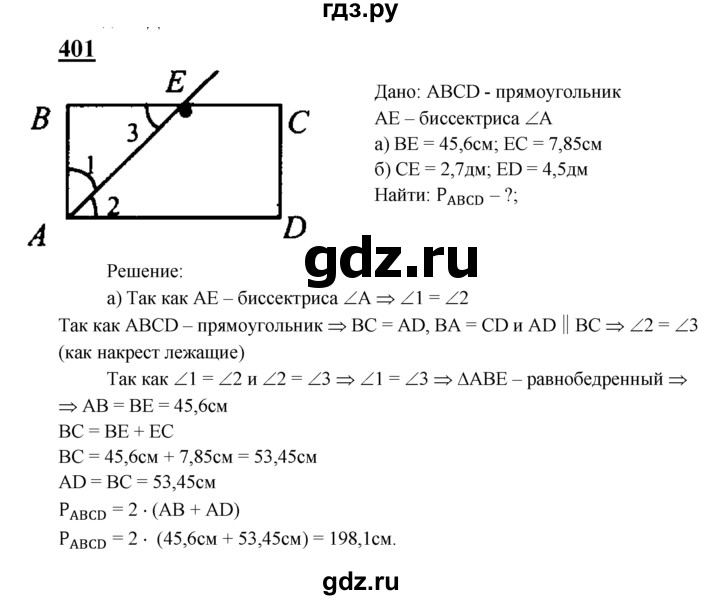
Причем если точка \(B\) лежит между точками \(A\) и \(C\), то точка \(B_1\) лежит между точками \(A_1\) и \(C_1\). Отсюда следует, что
Докажем, что преобразование подобия сохраняет углы между полупрямыми.
Действительно, пусть угол \(ABC\) преобразованием подобия с коэффициентом \(k\) переводится в угол \(A_1B_1C_1\) (рис. 237). Подвергнем угол \(ABC\) преобразованию гомотетии относительно его вершины \(B\) с коэффициентом гомотетии \(k\). При этом точки \(A\) и \(C\) перейдут в точки \(A_2\) и \(C_2\). Треугольники \(A_2BC_2\) и \(A_1B_1C_1\) равны по третьему признаку. Из равенства треугольников следует равенство углов \(A_2BC_2\) и \(A_1B_1C_1\). Значит, углы \(ABC\) и \(A_1B_1C_1\) равны, что и требовалось доказать.
Вопрос 5. Какие фигуры называются подобными?
Ответ. Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия.
Вопрос 6. Каким знаком обозначается подобие фигур? Как записывается подобие треугольников?
Ответ. Для обозначения подобия фигур используется специальный значок: \(\sim\).
Запись \(F\sim F’\) читается так: «Фигура \(F\) подобна фигуре \(F’\)».
Запись подобия треугольников \(ABC\) и \(A_1B_1C_1\): \(\triangle ABC \sim \triangle A_1B_1C_1\).
Вопрос 7. Сформулируйте и докажите признак подобия треугольников по двум углам.
Ответ. Теорема 11.2. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство. Пусть у треугольников \(ABC\) и \(A_1B_1C_1\) \(\angle A = \angle A_1\), \(\angle B = \angle B_1\). Докажем, что \(\triangle ABC \sim \triangle A_1B_1C_1\).
Пусть \(k = \frac{AB}{A_1B_1}\). Подвергнем треугольник \(A_1B_1C_1\) преобразованию подобия с коэффициентом подобия \(k\), например гомотетии (рис. 238).
Так как треугольники \(A_1B_1C_1\) и \(A_2B_2C_2\) гомотетичны и, значит, подобны, а треугольники \(A_2B_2C_2\) и \(ABC\) равны и поэтому тоже подобны, то треугольники \(A_1B_1C_1\) и \(ABC\) подобны.
Теорема доказана.
Вопрос 8. Сформулируйте и докажите признак подобия треугольников по двум сторонам и углу между ними.
Ответ. Теорема 11.3. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
Доказательство (аналогично доказательству теоремы 11.2). Пусть у треугольников \(ABC\) и \(A_1B_1C_1\) \(\angle C = \angle C_1\) и \(AC = kA_1C_1\), \(BC = kB_1C_1\). Докажем, что \(\triangle ABC \sim \triangle A_1B_1C_1\).
Подвергнем треугольник \(A_1B_1C_1\) преобразованию подобия с коэффициентом подобия \(k\), например гомотетии (рис. 240). При этом получим некоторый треугольник \(A_2B_2C_2\), равный треугольнику \(ABC\). Действительно, так как преобразование подобия сохраняет углы, то \(\angle C_2 = \angle C_1\). А значит, у треугольников \(ABC\) и \(A_2B_2C_2\) \(\angle C = \angle C_2\). Далее, \(A_2C_2 = kA_1C_1 = AC\), \(B_2C_2 = kB_1C_1 = BC\). Следовательно, треугольники \(ABC\) и \(A_2B_2C_2\) равны по первому признаку (по двум сторонам и углу между ними).
Так как треугольники \(A_1B_1C_1\) и \(A_2B_2C_2\) гомотетичны и, значит, подобны, а треугольники \(A_2B_2C_2\) и \(ABC\) равны и поэтому тоже подобны, то треугольники \(A_1B_1C_1\) и \(ABC\) подобны.
Теорема доказана.
Вопрос 9. Сформулируйте и докажите признак подобия треугольников по трем сторонам.
Ответ. Теорема 11.4. Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Доказательство (аналогично доказательству теоремы 11.2). Пусть у треугольников \(ABC\) и \(A_1B_1C_1\) \(AB = kA_1B_1\), \(AC = kA_1C_1\), \(BC = kB_1C_1\). Докажем, что \(\triangle ABC \sim \triangle A_1B_1C_1\).
Подвергнем треугольник \(A_1B_1C_1\) преобразованию подобия с коэффициентом подобия \(k\), например гомотетии (рис. 242). При этом получим некоторый треугольник \(A_2B_2C_2\), равный треугольнику \(ABC\). Действительно, у треугольников соответствующие стороны равны:
\(A_2B_2 = kA_1B_1 = AB\),
\(A_2C_2 = kA_1C_1 = AC\),
\(B_2C_2 = kB_1C_1 = BC\).
Следовательно, треугольники \(ABC\) и \(A_2B_2C_2\) равны по третьему признаку (по трем сторонам).
Так как треугольники \(A_1B_1C_1\) и \(A_2B_2C_2\) гомотетичны и, значит, подобны, а треугольники \(A_2B_2C_2\) и \(ABC\) равны и поэтому тоже подобны, то треугольники \(A_1B_1C_1\) и \(ABC\) подобны.