Привет. Решим уравнение? 74 Алгебра 9 класс Макарычев – Рамблер/класс
Привет. Решим уравнение? 74 Алгебра 9 класс Макарычев – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Решите уравнение:
а) 3(х + 4)2 = 10x 4- 32;
б) 31x + 77 = 15(x + 1)2.
ответы
Запросто!
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
10 класс
11 класс
Химия
похожие вопросы 5
150 Алгебра 9 класс Макарычев Помогите решить графически
Решите графически уравнение:
а) х3 = 2; б) х3 = 4; в) х3 = -5.
ЭкзаменыАлгебра9 классМакарычев Ю.Н.ГДЗ
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А.Н.Алгебра
Васильевых. 50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 13 ОГЭ Русский язык 9 класс Однородное подчинение придаточных
50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 13 ОГЭ Русский язык 9 класс Однородное подчинение придаточных
Среди предложений 21-29:
(21) И Митрофанов услышал в этом смехе и прощение себе, и даже какое-то (Подробнее…)
ГДЗРусский языкОГЭ9 классВасильевых И.П.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
ГДЗЕГЭРусский языкЦыбулько И.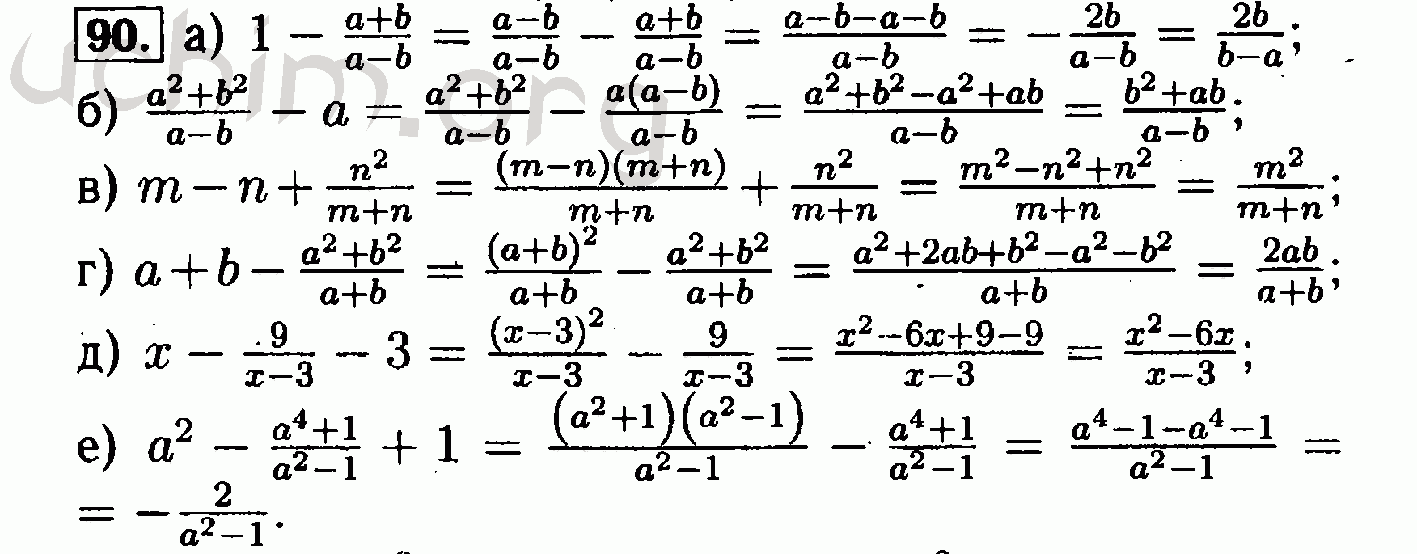 П.
П.
Алгебра. 9 класс. Учебник Макарычев Ю. Н.
- Главная /
- Каталог /
- Основное образование (5-9 классы) /
- Математика, Алгебра, Геометрия /
-
Алгебра.
 9 класс. Учебник
9 класс. Учебник
Линия УМК: Алгебра. Макарычев Ю.Н. (7-9)
Серия: Нет
Автор: Макарычев Ю. Н.
Номер ФПУ : 1.1.2.4.2.4.3
1 009,00 ₽
Нет в наличии
Аннотация
Учебник «Алгебра. 9 класс», является частью завершённой предметной линии учебников по алгебре для учащихся 7—9 классов общеобразовательных организаций.Наличие в каждом пункте учебника заданий разного уровня, помеченных специальными знаками, нацеливает учащихся на мобилизацию своих сил для перехода на более высокую ступень в усвоении материала. Учащимся, проявляющим интерес и склонности к математике, предлагаются усложнённые задания в дополнительных пунктах под рубрикой «Для тех, кто хочет знать больше». Тематика этих дополнительных пунктов определена так, что теоретический материал и система упражнений в них расширяют основной материал главы и выводят учащихся за пределы школьной программы по математике. Например, главу «Уравнения и неравенства с одной переменной» завершает пункт «Некоторые приёмы решения целых уравнений». Раздел «Задачи повышенной трудности предоставляет учащимся возможность испытать радость при решении задач олимпиадного уровня. Таким образом, учебник создаёт предпосылки для построения каждым учащимся индивидуальной образовательной траектории при изучении алгебры.
Учащимся, проявляющим интерес и склонности к математике, предлагаются усложнённые задания в дополнительных пунктах под рубрикой «Для тех, кто хочет знать больше». Тематика этих дополнительных пунктов определена так, что теоретический материал и система упражнений в них расширяют основной материал главы и выводят учащихся за пределы школьной программы по математике. Например, главу «Уравнения и неравенства с одной переменной» завершает пункт «Некоторые приёмы решения целых уравнений». Раздел «Задачи повышенной трудности предоставляет учащимся возможность испытать радость при решении задач олимпиадного уровня. Таким образом, учебник создаёт предпосылки для построения каждым учащимся индивидуальной образовательной траектории при изучении алгебры.
| Артикул | 13-0032-12 |
| ISBN | 978-5-09-101247-7 |
| Год титула | 2022 |
| Размеры, мм | 170x220x18 |
| Количество страниц | 288 |
| Красочность | черно-белая |
| Вес, кг | 0,4100 |
| Класс/Возраст |
9 кл. |
| Предмет | Алгебра |
| Издательство | Просвещение |
Учился по ней в 9 классе, книга хорошая.
6 учителей рассказывают свои секреты о том, как повысить успеваемость учащихся средних классов по математике – The 74
Получайте подобные истории прямо на почту. Подпишитесь на информационный бюллетень 74
Успеваемость по математике в средней школе резко упала во время пандемии, но коренные проблемы существуют гораздо дольше.
Вот типичный сценарий: ученик преуспевает в элементарной математике, ему нравятся манипуляции, игры и словесные задачи, удобные для детей. Затем приливы меняются. Когда в уравнение вступают более абстрактные мысли, некогда любимый предмет ученика становится источником беспокойства и поражения.
В средней школе учащиеся также могут столкнуться со стеной обучения из-за неустраненных пробелов в обучении. По словам Шелли Берр, которая поддерживает 42 школьных округа округа Аллегейни, штат Пенсильвания, школьные округа Allegheny Intermediate Unit и является сертифицированным тренером Data Wise в Гарварде, еще до пандемии учащиеся приходили в среднюю школу с пробелами в знаниях основных математических понятий. Те основы, которые не были закреплены в начальной школе, создают барьеры для изучения новых, более сложных навыков.
Заполнить эти пробелы в навыках при переходе к контенту уровня сложности непросто. «Учителям сложно преподавать контент на уровне класса», — говорит Берр, отмечая, что иногда им приходится заново обучать навыкам двух-трех предыдущих классов. По ее словам, расписание занятий по математике в средней школе обычно предполагает ежедневное изучение нового навыка, что не учитывает прогресс в приобретении навыков.
По ее словам, расписание занятий по математике в средней школе обычно предполагает ежедневное изучение нового навыка, что не учитывает прогресс в приобретении навыков.
Несмотря на то, что свежий подход к обучению учителей является частью решения, инновационные классные учителя уже делают успехи в правильном направлении. Их стратегии включают в себя использование конкретных инструментов, помогающих молодым умам понять абстрактные концепции, предоставление учащимся выбора и изменение мышления, чтобы они рассматривали ошибки как часть процесса.
Учителям нужно руководство, чтобы сосредоточиться на ключевых навыках
Бёрр отмечает, что учителя не обязательно обучены определять навыки, которые должны быть у каждого класса, чтобы в дальнейшем оставаться знатоками математики. Если учителя должны отдавать предпочтение овладению одними навыками, а не другими, ключевое значение имеет знание того, какие из них являются наиболее важными.
Исследование, проведенное в 2017 году Региональной образовательной лабораторной программой совместно с некоторыми лидерами образования штата Миссури, выявило пять широких категорий: соотношения и пропорциональные отношения, система счисления, выражения и уравнения, геометрия и статистика/вероятность. Мастерство в этих областях больше всего ассоциировалось с успехом в алгебре I.
Мастерство в этих областях больше всего ассоциировалось с успехом в алгебре I.
Бёрр говорит: «Самым большим предиктором успеха в алгебре является детсадовское чувство числа».
Бетонные инструменты формируют абстрактное понимание
Маловероятно, что учащиеся средней школы будут играть с плиткой, рисовать и работать руками, но учащиеся в этом возрасте все еще нуждаются в таких занятиях, чтобы преуспеть в математике. Берр призывает учителей использовать манипулятивные приемы даже в средней школе, чтобы помочь учащимся перейти от конкретного к абстрактному пониманию. Она указывает на такие инструменты, как блоки с основанием 10 до пятого класса, манипулятивные дроби, помогающие детям «видеть это по-разному», и плитки алгебры.
Если бы школа могла выбрать только один практический инструмент для средней школы, говорит она, алгебраические плитки были бы обязательными для всего, от помощи в визуализации целых чисел до решения многошаговых уравнений. Пандемия также показала педагогам, что виртуальные алгебраические плитки тоже могут работать.
Снимки класса Освещайте путь
Мы рассмотрели лучшие практики средних школ по всей стране, где учителя активно работают над тем, чтобы вовлечь учащихся в изучение математики и ликвидировать пробелы в обучении. Вот некоторые из их основных стратегий охвата учащихся средних классов:
Предоставьте поколению Z немедленную обратную связь, к которой они привыкли, — ошибки и все такое пункт назначения, шутит Эйб. Вместо этого преднамеренная и немедленная обратная связь с помощью таких инструментов, как NearPod и Socrative, повышает вовлеченность и своевременное улучшение в ее классе. С помощью этих инструментов она анонимно отображает работу нескольких учащихся одновременно, работая со студентами, чтобы определить, что пошло не так.
«Они привыкли к тому, что их стимулируют технологии, и хотят мгновенной обратной связи, того немедленного удовлетворения, которое приходит от некоторых технических инструментов, которые я использую», — говорит она. Для Nearpod она загружает все свои уроки, давая обратную связь в режиме реального времени. «Это сильно отличается от ручки и бумаги… когда я не могу охватить всех 30 учеников в классе». Она говорит, что обнаружение ошибок сразу же приводит к «преднамеренному обсуждению» их работы, а не к представлению своих собственных.
«Это сильно отличается от ручки и бумаги… когда я не могу охватить всех 30 учеников в классе». Она говорит, что обнаружение ошибок сразу же приводит к «преднамеренному обсуждению» их работы, а не к представлению своих собственных.
Формирование культуры, в которой «Ошибки очень популярны» — математическая аббревиатура, которую она использует, — норма, потому что каждый день учащиеся видят как ошибки, так и примеры. Технические инструменты, которые она использует, позволяют естественным образом обнаруживать ошибки по мере их возникновения, поэтому ученики привыкли совершать их и получать немедленную обратную связь. Она также не использует домашнее задание, так как ученики получают много практики и обратной связи во время занятий.
Использование нематематических предметов для превращения абстрактного в конкретное
Элиза Мерфи, директор по преподаванию и обучению Чартерной школы искусств Нью-Йорка
Отрицательные числа могут вызывать трудности у учащихся средних классов, говорит Мерфи. «Очень трудно понять, почему, когда вы вычитаете отрицательное число, оно становится положительным… это не имеет никакого смысла». Но легче, когда у детей есть конкретные аналогии, такие как подводные лодки, уходящие под воду, или приготовление супа горячее или холоднее с помощью кубиков льда.
«Очень трудно понять, почему, когда вы вычитаете отрицательное число, оно становится положительным… это не имеет никакого смысла». Но легче, когда у детей есть конкретные аналогии, такие как подводные лодки, уходящие под воду, или приготовление супа горячее или холоднее с помощью кубиков льда.
Детям также предлагается создать свои собственные реальные примеры математики в действии, часто связанные с музыкой или искусством. Например, учителя математики в седьмом классе хотели, чтобы ученики использовали пропорции в проекте. Некоторые использовали масштабные коэффициенты для увеличения собственных рисунков. Другие играли музыкальное произведение, чтобы продемонстрировать интервалы или соотношение частот в нотах, составляющих музыкальный аккорд. В третьем варианте учащиеся увеличили рецепт, чтобы накормить весь класс, а затем приготовили его для всех.
В восьмом классе учителя математики использовали художественный проект, чтобы закрепить понимание учащихся о пересечениях, линиях, пересекающих две параллельные линии, и углах, которые они образуют. Студенты должны были выглянуть за пределы классной комнаты, чтобы найти примеры пересечений в своем доме или районе. Сфотографировав свой пример, они использовали онлайн-транспортир для измерения образовавшихся углов, наблюдая, дополняют ли они друг друга.
Студенты должны были выглянуть за пределы классной комнаты, чтобы найти примеры пересечений в своем доме или районе. Сфотографировав свой пример, они использовали онлайн-транспортир для измерения образовавшихся углов, наблюдая, дополняют ли они друг друга.
Решение реальных проблем
Жанна Хайбрехтс, главный академический офис Stratford School , несколько филиалов в Калифорнии
школа.
«Когда ученики средней школы Стратфорда спрашивают своих учителей математики: «Зачем нам это учить?», мы думаем, что они заслуживают ответа, — говорит Хайбрехтс. «Учителя регулярно включают реальные задачи, которые иллюстрируют полезность принципов, благодаря чему курсы по математике кажутся гораздо более актуальными».
Например, одним из популярных упражнений является проектирование смартфона и расчет необходимого объема памяти. В другом разделе студенты проектируют крышу, покрытую солнечными панелями, рассчитывая шаг, необходимый для оптимизации захвата энергии. Она говорит, что это помогает смягчить абстрактность курсов алгебры и геометрии в средней школе.
Она говорит, что это помогает смягчить абстрактность курсов алгебры и геометрии в средней школе.
Постановка целей и отслеживание мастерства
Сара Бреслин, заместитель директора средней школы Brooklyn Lab, Нью-Йорк
Когда Бреслин увидела несоответствие между «выходными билетами» учащихся в классе и их промежуточной оценкой, она работала с учителями, чтобы построить план профессионального развития. Программа под названием Shift the Lift предполагает перенос умственной нагрузки по решению задач с учителя на ученика. Он разработан, чтобы помочь учителям определить конкретные стандарты, которые чаще всего ставят учеников в тупик, и помочь им принять мышление роста, когда они работают над их освоением.
Учителя ставят «сверхконкретные цели» для каждого ученика, продвигают независимую практику и используют выходные билеты два-три раза в неделю, чтобы измерить прогресс в достижении этих целей, — говорит она. Выходные билеты измеряют, насколько хорошо учащиеся овладевают данной темой, и оценивают свои рабочие привычки. Бреслин говорит, что когда студенты начинают Shift the Lift, в среднем только около 55% оправдывают ожидания. Всего пять недель спустя это число обычно вырастает до 89%.
Бреслин говорит, что когда студенты начинают Shift the Lift, в среднем только около 55% оправдывают ожидания. Всего пять недель спустя это число обычно вырастает до 89%.
Предоставление учащимся возможности самим решать, как продемонстрировать свое понимание
Эшли Бараттини и Эйприл Риган, со-учителя восьмого класса, The Urban Assembly School for Leadership & Empowerment, Бруклин
Не каждый день можно увидеть итоговую оценку в виде подкаста, брошюры, Tik Tok или швейный проект. Но это норма для учеников Бараттини и Риган, для которых выбор является фундаментальным аспектом повышения вовлеченности в математику в средней школе. Бараттини вспоминает прошлогоднюю студентку, которая рассмотрела варианты для тестирования и вместо этого предложила проект вышивки, демонстрирующий ее новые математические знания. Учителя были более чем счастливы повиноваться.
От охоты за мусором до станций, от мини-уроков со всей группой до небольших учебных групп, «предоставление им возможности продемонстрировать свои знания и показать, как они изучают математику и понимают ее», — говорит Риган. Уроки в их классе длятся максимум 10 минут, и они дают домашнее задание только раз в несколько недель, примерно пять-шесть вопросов, по одному из каждого недавно проведенного урока для дополнительной практики.
Уроки в их классе длятся максимум 10 минут, и они дают домашнее задание только раз в несколько недель, примерно пять-шесть вопросов, по одному из каждого недавно проведенного урока для дополнительной практики.
Рейган говорит: «Мне нравится слышать в конце занятия, когда ученик говорит: «На самом деле, сегодня было очень весело».
Первоначально эта статья появилась на Ed Post .
Получайте подобные истории прямо на свой почтовый ящик. Подпишитесь на информационный бюллетень 74
Как найти диапазон — Алгебра 1
Все ресурсы по Алгебре 1
10 Диагностических тестов 557 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущий 1 2 3 4 5 6 7 8 9… 12 13 Далее →
Алгебра 1 Помощь » Статистика и вероятность » Как найти диапазон
Мы хотим создать трехзначный код для кодового замка. Допускаются только цифры от 0 до 9, и цифры могут повторяться. Сколько таких кодов можно сгенерировать?
Допускаются только цифры от 0 до 9, и цифры могут повторяться. Сколько таких кодов можно сгенерировать?
Возможные ответы:
Правильный ответ:
Объяснение:
Первая позиция может быть заполнена 10 способами, и, поскольку разрешено повторение, 2-я позиция может быть заполнена 10 способами, и аналогично третья позиция может быть заполнена 10 способами, что дает нам правильный ответ
Сообщить об ошибке
Вам дан следующий набор чисел:
2, 8, 3, 6, 9, 10, 5
Найдите диапазон.
Возможные ответы:
Правильный ответ:
Объяснение:
Диапазон представляет собой разницу между самым низким и самым высоким числом в наборе чисел.
Наименьшее число в наборе чисел — 2, а наибольшее число — 10. Таким образом, диапазон рассчитывается как
Итак, 8 — это диапазон.
Сообщить об ошибке
Оценка:
Возможные ответы:
Правильный ответ:
Объяснение:
Это комбинированная проблема. Все, что нам нужно для решения этой задачи, — это формула комбинации:
Теперь
и
Вместо того, чтобы искать ответы для всех этих факториалов, обратите внимание, что они имеют много одинаковых членов и поэтому могут быть отменены.
Сообщить об ошибке
Учитель оценивает тесты и записывает результаты в свои записи. Очки записываются следующим образом: 81, 91, 83, 88, 74, 98, 81, 94, 68, 92, 77, 79, 83, 91, 81, 84, 85, 81, 85, 79, 83, 81. , 83.
Какой диапазон?
Возможные ответы:
Правильный ответ:
Объяснение:
Диапазон статистики — это просто разница между наибольшим и наименьшим значением.
Наибольшее число в наборе — 98, а наименьшее — 68.
Вычтите, чтобы найти диапазон:
Сообщить об ошибке
Учитывая набор тестов, каков диапазон?
Возможные ответы:
Правильный ответ:
Объяснение:
Диапазон — это разница между наименьшим и наибольшим числом. Наименьшее значение — 77, а наибольшее — 9.8.
98 – 77 = 21
Сообщить об ошибке
Диапазон следующего набора данных – 18. Какое возможное значение для ?
Возможные ответы:
Нельзя определить
Правильный ответ:
Объяснение:
Расположите известные значения в наборе в порядке номеров: {–5, –2, 1, 3, 5, 7, 7, 10}. Диапазон — это разница между наибольшим значением и наименьшим значением.
Диапазон — это разница между наибольшим значением и наименьшим значением.
x должно быть либо наибольшим, либо наименьшим значением в наборе.
диапазон = х – наименьшее значение
18 = х – (–5)
18 = х + 5
13 = х
ИЛИ
диапазон = наибольшее значение – х
–20 х 0 9002 18 = х18 = 8 = –x
–8 = x
Сообщить об ошибке
На приведенной выше диаграмме показана конкретная неделя работы в рекламной фирме. Каков диапазон почасовых ставок рабочих?
Возможные ответы:
Правильный ответ:
Объяснение:
Диапазон представляет собой разницу между наибольшим и наименьшим значением.
Сообщить об ошибке
Каков диапазон набора?
Возможные ответы:
Правильный ответ:
Объяснение:
Диапазон определяется как разница между наибольшим и наименьшим числом в наборе. Здесь наибольшее число – , а наименьшее – .
Здесь наибольшее число – , а наименьшее – .
Таким образом, диапазон равен
– мода, – среднее значение, а 6 – медиана.
Сообщить об ошибке
В наборе чисел какой диапазон?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы определить диапазон этого набора данных, возьмите наибольшее число и вычтите из него наименьшее число.
Самое большое число в наборе — десять.
Наименьшее число в наборе .
Вычесть оба числа.
Сообщить об ошибке
Найдите диапазон следующего набора чисел.
Возможные ответы:
Правильный ответ:
Объяснение:
Вычтите наименьшее число (4) из наибольшего (52), чтобы получить 48.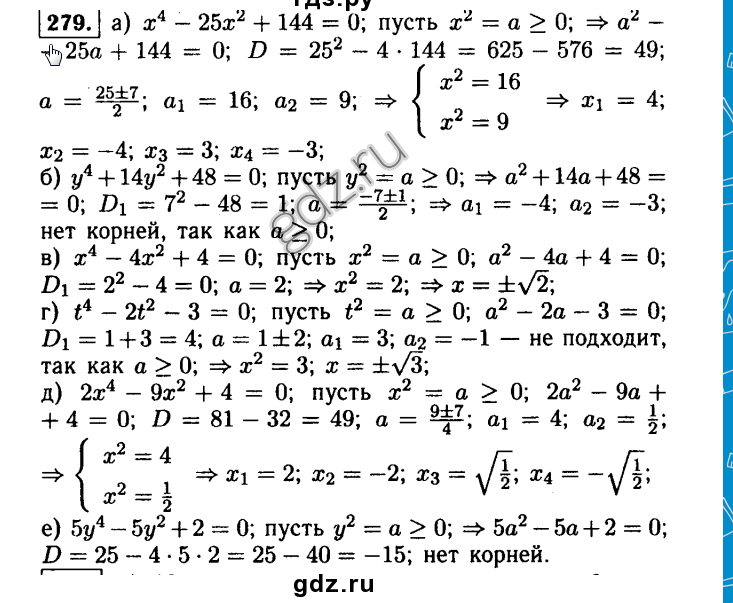


 9 класс. Учебник
9 класс. Учебник