ГДЗ по Геометрия 7-9 класс Атанасян
ГДЗ по Геометрия 7-9 класс Атанасян Л.С.
Подробный решебник (ГДЗ) по Геометрии за 7-9 класс
Автор: Атанасян Л.С.
Глава I. Начальные геометрические сведения
§ 1. Прямая и отрезок
1. Точки, прямые, отрезки
2. Провешивание прямой на местности
Практические задания
§ 2. Луч и угол
- 3. Луч
- 4. Угол
- Практические задания
§ 3. Сравнение отрезков и углов
5. Равенство геометрических фигур
6. Сравнение отрезков и углов
Задачи
§ 4. Измерение отрезков
7. Длина отрезка
8. Единицы измерения. Измерительные инструменты
Практические задания
Задачи
§ 5. Измерение углов
9. Градусная мера угла
10. Измерение углов на местности
Практические задания
Задачи
§ 6. Перпендикулярные прямые
Перпендикулярные прямые
11. Смежные и вертикальные углы
12. Перпендикулярные прямые
13. Построение прямых углов на местности
Практические задания
Задачи
Вопросы для повторения к главе I
Дополнительные задачи
Глава II. Треугольники
§ 1. Первый признак равенства треугольников
14. Треугольник
15. Первый признак равенства треугольников
Практические задания
Задачи
§ 2. Медианы, биссектрисы и высоты треугольника
16. Перпендикуляр к прямой
17. Медианы, биссектрисы и высоты треугольника
18. Свойства равнобедренного треугольника
Практические задания
Задачи
§ 3. Второй и третий признаки равенства треугольников
19. Второй признак равенства треугольников
20. Третий признак равенства треугольников
Задачи
§ 4. Задачи на построение
21. Окружность
22. Построения циркулем и линейкой
23. Примеры задач на построение
Примеры задач на построение
Задачи
Вопросы для повторения к главе II
Дополнительные задачи
Глава III. Параллельные прямые
§ 1. Признаки параллельности двух прямых
24. Определение параллельных прямых
25. Признаки параллельности двух прямых
26. Практические способы построения параллельных прямых
Задачи
§ 2. Аксиома параллельных прямых
27. Об аксиомах геометрии
28. Аксиома параллельных прямых
29. Теоремы об углах, образованных двумя параллельными прямыми и секущей
30. Углы с соответственно параллельными или перпендикулярными сторонами
Задачи
Вопросы для повторения к главе III
Дополнительные задачи
Глава IV. Соотношения между сторонами и углами треугольника
§ 1. Сумма углов треугольника
31. Теорема о сумме углов треугольника
32. Остроугольный, прямоугольный и тупоугольный треугольники
Задачи
§ 2. Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника
33. Теорема о соотношениях между сторонами и углами треугольника
34. Неравенство треугольника
Задачи
§ 3. Прямоугольные треугольники
35. Некоторые свойства прямоугольных треугольников
36. Признаки равенства прямоугольных треугольников
37*. Уголковый отражатель
Задачи
§ 4. Построение треугольника по трём элементам
38. Расстояние от точки до прямой. Расстояние между параллельными прямыми
39. Построение треугольника по трём элементам
Задачи
Вопросы для повторения к главе IV
Дополнительные задачи
Задачи повышенной трудности
Задачи к главе I
Задачи к главе II
Задачи к главам III и IV
Глава V. Четырёхугольники
§ 1. Многоугольники
40. Многоугольник
41. Выпуклый многоугольник
42. Четырёхугольник
Задачи
§ 2. Параллелограмм и трапеция
43. Параллелограмм
Параллелограмм
44. Признаки параллелограмма
45. Трапеция
Задачи
§ 3. Прямоугольник, ромб, квадрат
46. Прямоугольник
47. Ромб и квадрат
48. Осевая и центральная симметрии
Задачи
Вопросы для повторения к главе V
Дополнительные задачи
Глава VI. Площадь
§ 1. Площадь многоугольника
49. Понятие площади многоугольника
50*. Площадь квадрата
51. Площадь прямоугольника
Задачи
§ 2. Площади параллелограмма, треугольника и трапеции
52. Площадь параллелограмма
53. Площадь треугольника
54. Площадь трапеции
Задачи
§ 3. Теорема Пифагора
55. Теорема Пифагора
56. Теорема, обратная теореме Пифагора
57. Формула Герона
Задачи
Вопросы для повторения к главе VI
Дополнительные задачи
Глава VII. Подобные треугольники
§ 1. Определение подобных треугольников
58. Пропорциональные отрезки
Пропорциональные отрезки
59. Определение подобных треугольников
60. Отношение площадей подобных треугольников
Задачи
§ 2. Признаки подобия треугольников
61. Первый признак подобия треугольников
62. Второй признак подобия треугольников
63. Третий признак подобия треугольников
Задачи
§ 3. Применение подобия к доказательству теорем и решению задач
64. Средняя линия треугольника
65. Пропорциональные отрезки в прямоугольном треугольнике
66. Практические приложения подобия треугольников
67. О подобии произвольных фигур
Задачи
§ 4. Соотношения между сторонами и углами прямоугольного треугольника
68. Синус, косинус и тангенс острого угла прямоугольного треугольника
69. Значения синуса, косинуса и тангенса для углов 30°, 45° и 60°
Задачи
Вопросы для повторения к главе VI
Дополнительные задачи
Глава VIII. Окружность
§ 1. Касательная к окружности
Касательная к окружности
70. Взаимное расположение прямой и окружности
71. Касательная к окружности
Задачи
§ 2. Центральные и вписанные углы
72. Градусная мера дуги окружности
73. Теорема о вписанном угле
Задачи
§ 3. Четыре замечательные точки треугольника
74. Свойства биссектрисы угла
75. Свойства серединного перпендикуляра к отрезку
76. Теорема о пересечении высот треугольника
Задачи
§ 4. Вписанная и описанная окружности
77. Вписанная окружность
78. Описанная окружность
Задачи
Вопросы для повторения к главе VIII
Дополнительные задачи
Глава IX. Векторы
§ 1. Понятие вектора
79. Понятие вектора
80. Равенство векторов
81. Откладывание вектора от данной точки
Практические задания
Задачи
§ 2. Сложение и вычитание векторов
- 82.
 Сумма двух векторов
Сумма двух векторов - 83. Законы сложения векторов. Правило параллелограмма
- 84. Сумма нескольких векторов
- 85. Вычитание векторов
- Практические задания
- Задачи
§ 3. Умножение вектора на число. Применение векторов к решению задач
86. Произведение вектора на число
87. Применение векторов к решению задач
88. Средняя линия трапеции
Практические задания
Задачи
Вопросы для повторения к главе IX
Дополнительные задачи
Задачи повышенной трудности
Задачи к главе V
Задачи к главе VI
Задачи к главе VI
Задачи к главе VIII
Задачи к главе IX
Глава X. Метод координат
§ 1. Координаты вектора
89. Разложение вектора по двум неколлинеарным векторам
90. Координаты вектора
Задачи
§ 2. Простейшие задачи в координатах
91. Связь между координатами вектора и координатами его начала и конца
92. Простейшие задачи в координатах
Простейшие задачи в координатах
Задачи
§ 3. Уравнения окружности и прямой
93. Уравнение линии на плоскости
94. Уравнение окружности
95. Уравнение прямой
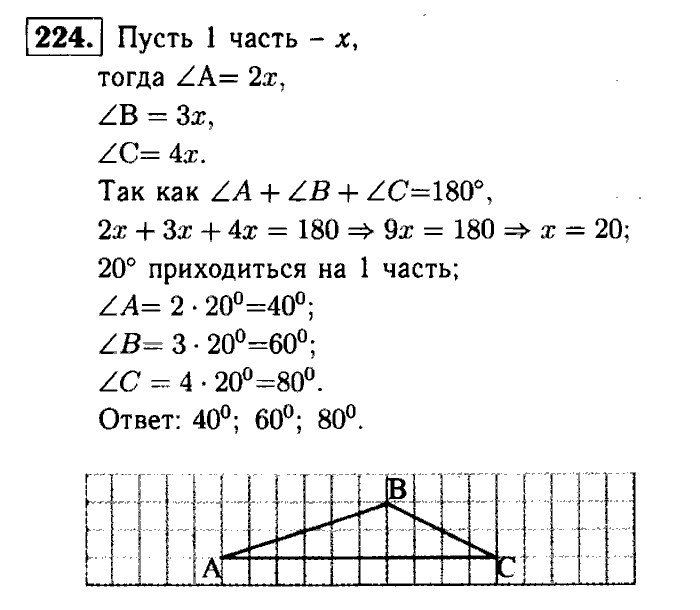
96. Взаимное расположение двух окружностей
Задачи
Вопросы для повторения к главе X
Дополнительные задачи
Глава XI. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
§ 1. Синус, косинус, тангенс, котангенс угла
97. Синус, косинус, тангенс, котангенс
98. Основное тригонометрическое тождество. Формулы приведения
99. Формулы для вычисления координат точки
Задачи
§ 2. Соотношения между сторонами и углами треугольника
100. Теорема о площади треугольника
101. Теорема синусов
102. Теорема косинусов
103. Решение треугольников
104. Измерительные работы
Задачи
§ 3. Скалярное произведение векторов
105. Угол между векторами
Угол между векторами
106. Скалярное произведение векторов
107. Скалярное произведение в координатах
108. Свойства скалярного произведения векторов
Задачи
Вопросы для повторения к главе XI
Дополнительные задачи
Глава XII. Длина окружности и площадь круга
§ 1. Правильные многоугольники
109. Правильный многоугольник
110. Окружность, описанная около правильного многоугольника
111. Окружность, вписанная в правильный многоугольник
112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
113. Построение правильных многоугольников
Задачи
§ 2. Длина окружности и площадь круга
114. Длина окружности
115. Площадь круга
116. Площадь кругового сектора
Задачи
Вопросы для повторения к главе XII
Дополнительные задачи
Глава XIII. Движения
§ 1. Понятие движения
117. Отображение плоскости на себя
Отображение плоскости на себя
118. Понятие движения
119*. Наложения и движения
Задачи
§ 2. Параллельный перенос и поворот
120. Параллельный перенос
121. Поворот
Задачи
Вопросы для повторения к главе XIII
Дополнительные задачи
Глава XIV. Начальные сведения из стереометрии
§ 1. Многогранники
122. Предмет стереометрии
123. Многогранник
124. Призма
125. Параллелепипед
126. Объём тела
127. Свойства прямоугольного параллелепипеда
128. Пирамида
Задачи
§ 2. Тела и поверхности вращения
129. Цилиндр
130. Конус
131. Сфера и шар
Задачи
Вопросы для повторения к главе XIV
Дополнительные задачи
Задачи повышенной трудности
Задачи к главе X
Задачи к главе XI
Задачи к главе XII
Задачи к главе XIII
Задачи к главе XIV
Исследовательские задачи
Темы рефератов
Приложения
1. Об аксиомах планиметрии
Об аксиомах планиметрии
2. Некоторые сведения о развитии геометрии
Геометрия 8 Атанасян Учебник | Частная школа. 8 класс
Ознакомительная версия с цитатами из учебника для принятия решения о покупке книги: Геометрия. 7-9 классы. Учебник для общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина — М.: Просвещение. Нажмите на изображение обложки книги, чтобы перейти в Интернет-магазин!
Содержание учебника «Геометрия 8 класс. Атанасян» позволяет достичь планируемых результатов обучения, предусмотренных ФГОС основного общего образования. Учебник включает трёхступенчатую систему задач, а также исследовательские задачи, темы рефератов, список рекомендуемой литературы, что позволит учащимся расширить и углубить свои знания по геометрии. Специально для родителей даны ОТВЕТЫ и РЕШЕНИЯ на задачи из учебника (ГДЗ).
Геометрия — одна из самых древних наук, она возникла очень давно, ещё до нашей эры. В переводе с греческого слово «геометрия» означает «землемерие» («гео» —по-гречески земля, а «метрео» — мерить). Такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, проведении дорог, строительстве зданий и других сооружений. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями и построениями. Таким образом, геометрия возникла на основе практической деятельности людей, а в дальнейшем сформировалась как самостоятельная наука, занимающаяся изучением геометрических фигур.
В переводе с греческого слово «геометрия» означает «землемерие» («гео» —по-гречески земля, а «метрео» — мерить). Такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, проведении дорог, строительстве зданий и других сооружений. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями и построениями. Таким образом, геометрия возникла на основе практической деятельности людей, а в дальнейшем сформировалась как самостоятельная наука, занимающаяся изучением геометрических фигур.
Глава V. Четырёхугольники
§ 1. Многоугольники (40. Многоугольник. 41. Выпуклый многоугольник. 42. Четырёхугольник).
Задачи №№ 363 — 370 с Решениями и Ответами
§ 2. Параллелограмм и трапеция (43. Параллелограмм. 44. Признаки параллелограмма. 45. Трапеция).
45. Трапеция).
Задачи №№ 371 — 398 с Ответами и решениями
§ 3. Прямоугольник, ромб, квадрат (46. Прямоугольник. 47. Ромб и квадрат. 48. Осевая и центральная симметрии).
Задачи №№ 399 — 423 с Ответами и решениями
Вопросы для повторения к главе 5. Дополнительные задачи.
Задачи №№ 424 — 444 с Ответами и решениями
Глава VI. Площадь
§ 1. Площадь многоугольника (49. Понятие площади многоугольника. 50*. Площадь квадрата. 51. Площадь прямоугольника).
Задачи №№ 445 — 458 с Ответами и решениями
§ 2. Площади параллелограмма, треугольника и трапеции (52. Площадь параллелограмма. 53. Площадь треугольника. 54. Площадь трапеции).
Задачи №№ 459 — 482 с Ответами и решениями
§ 3. Теорема Пифагора (55. Теорема Пифагора. 56. Теорема, обратная теореме Пифагора. 57. Формула Герона).
57. Формула Герона).
Задачи №№ 483 — 499 с Ответами и решениями
Вопросы для повторения к главе 6. Дополнительные задачи.
Глава VII Подобные треугольники
§ 1. Определение подобных треугольников (58. Пропорциональные отрезки. 59. Определение подобных треугольников. 60. Отношение площадей подобных треугольников).
§ 2. Признаки подобия треугольников (61. Первый признак подобия треугольников. 62. Второй признак подобия треугольников. 63. Третий признак подобия треугольников).
§ 3. Применение подобия к доказательству теорем и решению задач (64. Средняя линия треугольника. 65. Пропорциональные отрезки в прямоугольном треугольнике. 66. Практические приложения подобия треугольников. 67. О подобии произвольных фигур).
§ 4. Соотношения между сторонами и углами прямоугольного треугольника (68. Синус, косинус и тангенс острого угла прямоугольного треугольника. 69. Значения синуса, косинуса и тангенса для углов 30°, 45° и 60°).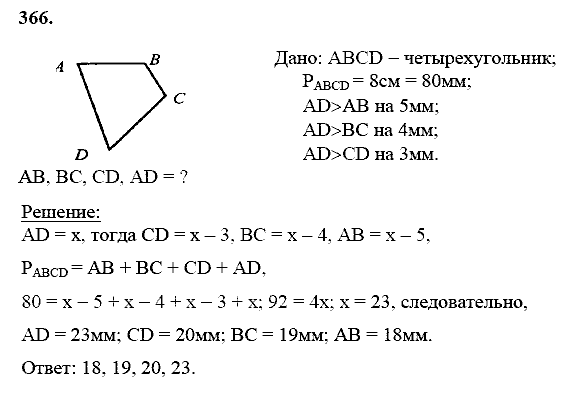
Вопросы для повторения к главе 7. Дополнительные задачи.
Глава VIII Окружность
§ 1. Касательная к окружности (70. Взаимное расположение прямой и окружности. 71. Касательная к окружности).
§ 2. Центральные и вписанные углы (72. Градусная мера дуги окружности. 73. Теорема о вписанном угле).
§ 3. Четыре замечательные точки треугольника (74. Свойства биссектрисы угла. 75. Свойства серединного перпендикуляра к отрезку. 76. Теорема о пересечении высот треугольника).
§ 4. Вписанная и описанная окружности (77. Вписанная окружность. 78. Описанная окружность).
Вопросы для повторения к главе 8. Дополнительные задачи.
Глава IX Векторы.
§ 1. Понятие вектора (79. Понятие вектора. 80. Равенство векторов. 81. Откладывание вектора от данной точки).
§ 2. Сложение и вычитание векторов (82. Сумма двух векторов. 83. Законы сложения векторов. Правило параллелограмма. 84. Сумма нескольких векторов.
§ 3. Умножение вектора на число. Применение векторов к решению задач (86. Произведение вектора на число. 87. Применение векторов к решению задач. 88. Средняя линия трапеции).
Вопросы для повторения к главе 9. Дополнительные задачи.
Вы смотрели: Ознакомительная версия с цитатами из учебника для принятия решения о покупке книги: Геометрия. 7-9 классы. Учебник для общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина — М.: Просвещение.
Геометрия 8 Атанасян Учебник ОГЛАВЛЕНИЕ:
Глава V. Четырёхугольники
Глава VI. Площадь
Глава VII Подобные треугольники
Глава VIII Окружность
Глава IX Векторы.
Скоро будут опубликованы остальные темы учебника. Если Вам необходим какой-то раздел или задачи, то напишите нам в поле для комментариев, мы не обещаем, но постараемся сделать быстрее.
Если Вы не согласны с решением заданий, то напишите в поле для комментариев на соответствующей странице № задачи, который по Вашему мнению решен неправильно, с указанием своего ответа.
Просмотров: 17 613
Вопросы для повторения к главе I. Вопросы для повторения к главе VI Вопросы для повторения к главе 8
1. Какова последовательность звеньев в цепочке формирования затрат на качество и стоимости фарфоровой посуды?
2. Какие подразделения предприятия обеспечивают качество изготовленной продукции?
3. Объяснить роль планового отдела, бухгалтерии, отдела подготовки производства в обеспечении качества продукции.
4. Сравните функции отдела снабжения и отдела сбыта в обеспечении качества продукции.
5. Какие затраты на качество формируются на «исполнительном» уровне отделов?
6. Перечислить состав управленческих затрат на качество. Чем они отличаются от производственных?
7. Какие затраты на качество относятся на базовым, а какие к дополнительным? Есть ли среди них повторяющиеся?
8. Объясните различия между внутренней
и внешней информацией о качестве
продукции.
Объясните различия между внутренней
и внешней информацией о качестве
продукции.
9. Как можно ускорить получение выводов о предмете исследования по первичным данным?
10. Назовите формы регистрации данных, позволяющие увидеть зависимость между затратами и влияющими на них факторами.
11. В чем преимущество сметы затрат перед другими носителями информации?
12. Перечислите этапы построения диаграммы рассеивания. Можно ли по ней определить наличие и направление связи между результативным и факторным показателями?
13. Какое расположение точек на диаграмме рассеивания свидетельствует о положительной, отрицательной корреляции, о ее отсутствии?
14. Каковы принципы применения ФСА?
15. Назовите основания классификации функций изделия. Какова взаимосвязь между ними?
16. Охарактеризуйте этапы ФСА?
17. В чем заключается принцип Эйзенхауэра в ФСА?
18. Можно ли с помощью табличной формы выявить функции изделия, подлежащие усовершенствованию или ликвидации?
19. Что такое матричная таблица выбора
изделий для производства? Назовите
показатели, позволяющие сделать этот
выбор.
Что такое матричная таблица выбора
изделий для производства? Назовите
показатели, позволяющие сделать этот
выбор.
20. Как рассчитывается коэффициент корреляции между параметрами качества и затратами на его создание?
21. Как с помощью индексного метода определить влияние качества на затраты на продукцию?
22. В чем недостатки методов балльной оценки и удельной цены? Какова область их применения?
23. Где и как применяется показатель «выход годного»?
24. Как рассчитывается обобщающий коэффициент качества?
25. Как определить объем продукции, потерянной предприятием вследствие возникновения брака и затрат на его исправление?
26. Каковы направления определения экономической эффективности от внедрения более качественной продукции? Чем они различаются и что общего в расчете показателя экономической эффективности во всех случаях?
27. В каких направлениях проектного анализа используют преимущественно формальные или неформальные методы? Почему?
28.
29. С помощью каких показателей можно оценить конкурентоспособность продукции?
30. Покажите важность проектного анализа и внедрения новой продукции для региона нахождения производителя.
31. Отражаются ли затраты, связанные с качеством продукции в балльной цене, в удельной цене изделия?
32. Находят ли отражение затраты на качество в показателе рентабельного продукции? Объясните ваше мнение.
ГДЗ Геометрия 7 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ Геометрия 8 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ Геометрия 9 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ к дидактическим материалам по геометрии за 7 класс Зив Б.Г. можно скачать .
ГДЗ к дидактическим материалам по геометрии за 8 класс Зив Б.Г. можно скачать .
ГДЗ к дидактическим материалам по геометрии за 9 класс Зив Б.Г. можно скачать .
ГДЗ к самостоятельным и контрольным работам по геометрии за 7-9 классы Иченская М.
ГДЗ к сборнику заданий по геометрии за 7 класс Ершова А.П. можно скачать .
ГДЗ к сборнику заданий по геометрии за 8 класс Ершова А.П. можно скачать .
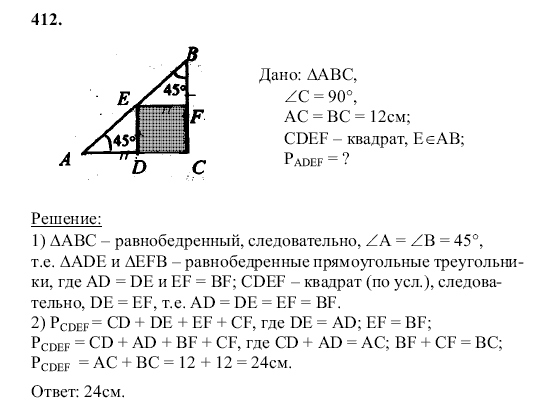
ГДЗ к рабочей тетради по геометрии за 9 класс Мищенко Т.М. можно скачать .
ГДЗ к тематическим тестам по геометрии за 7 класс Мищенко Т.М. можно скачать .
ГДЗ к тематическим тестам по геометрии за 8 класс Мищенко Т.М. можно скачать .
ГДЗ к тематическим тестам по геометрии за 9 класс Мищенко Т.М. можно скачать .
ГДЗ к контрольным работам по геометрии за 7 класс Мельникова Н.Б. можно скачать .
ГДЗ к контрольным работам по геометрии за 8 класс Мельникова Н.Б. можно скачать .
ГДЗ к контрольным работам по геометрии за 9 класс Мельникова Н.Б. можно скачать .
ГДЗ к рабочей тетради по геометрии за 9 класс Глазков Ю.А. Егупова М.В. можно скачать .
Родителям нередко приходится слышать жалобы ребёнка о том, что он не понимает тот или иной предмет. Чаще всего это точные науки: алгебра, геометрия, физика. Некоторые родители стараются нанять репетитора, а другие скачивают своим детям ГДЗ по геометрии к учебнику Атанасяна. Конечно, просто бездумное списывание с ответов не сможет привести к положительному результату. Но если школьник будет сверять свои задания, пользоваться изданием для повторения или изучения материала, чтобы на уроке быть уже подготовленным, вы увидите, что знания станут крепче, а предмет понятней.
Решебник по геометрии за 7 класс подойдёт также для углубленного изучения, выполнения заданий повышенной сложности. Так как пособие ежегодно подвергается изменениям и дополнениям, родители могут не беспокоиться в правильности всех ответов. Благодаря этой книге школьник может не бояться за получение неудовлетворительных оценок — они останутся в прошлом. А при регулярном изучении предмета и повышении своих знаний вы увидите, как с каждым разом всё легче и легче становится выполнить задание.
Чаще всего это точные науки: алгебра, геометрия, физика. Некоторые родители стараются нанять репетитора, а другие скачивают своим детям ГДЗ по геометрии к учебнику Атанасяна. Конечно, просто бездумное списывание с ответов не сможет привести к положительному результату. Но если школьник будет сверять свои задания, пользоваться изданием для повторения или изучения материала, чтобы на уроке быть уже подготовленным, вы увидите, что знания станут крепче, а предмет понятней.
Решебник по геометрии за 7 класс подойдёт также для углубленного изучения, выполнения заданий повышенной сложности. Так как пособие ежегодно подвергается изменениям и дополнениям, родители могут не беспокоиться в правильности всех ответов. Благодаря этой книге школьник может не бояться за получение неудовлетворительных оценок — они останутся в прошлом. А при регулярном изучении предмета и повышении своих знаний вы увидите, как с каждым разом всё легче и легче становится выполнить задание.
Готовые домашние задания к учебнику геометрии для учащихся 7-9 классов, авторы: Л. С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина
, издательство Просвещение на 2015 — 2016 учебный год.
С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина
, издательство Просвещение на 2015 — 2016 учебный год.
Ребята, в 7-9 классе вы будете изучать такой интересный предмет как геометрия. Чтобы в дальнейшем не иметь проблем с пониманием этого урока, необходимо с самого начала усердно работать.
В предыдущих классах вы уже познакомились с некоторыми геометрическими фигурами. В этом гуду вы расширите этот минимум познания. Весь курс делится на два раздела: планиметрию и стереометрию. В 7 и 8 классе вы будете рассматривать фигуры на плоскости — это раздел планиметрия. В 9 классе свойства фигур в пространстве — стереометрия.
Часто возникает ситуация, когда не получается исходя из условия сделать правильный рисунок, нарисовать в пространстве все детали и тогда геометрия кажется неподъёмным для вас предметом. Если у вас начнутся такие трудности, тогда рекомендуем использовать наш гдз по геометрии за 7-9 класс Л.С. Атанасяна, который размещён ниже.
ГДЗ Геометрия 7 класс рабочая тетрадь Атанасян можно скачать
.
ГДЗ Геометрия 8 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ Геометрия 9 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ к дидактическим материалам по геометрии за 7 класс Зив Б.Г. можно скачать .
ГДЗ к дидактическим материалам по геометрии за 8 класс Зив Б.Г. можно скачать .
ГДЗ к дидактическим материалам по геометрии за 9 класс Зив Б.Г. можно скачать .
ГДЗ к самостоятельным и контрольным работам по геометрии за 7-9 классы Иченская М.А. можно скачать .
ГДЗ к сборнику заданий по геометрии за 7 класс Ершова А.П. можно скачать .
ГДЗ к сборнику заданий по геометрии за 8 класс Ершова А.П. можно скачать .
ГДЗ к рабочей тетради по геометрии за 9 класс Мищенко Т.М. можно скачать .
ГДЗ к тематическим тестам по геометрии за 7 класс Мищенко Т.М. можно скачать .
ГДЗ к тематическим тестам по геометрии за 8 класс Мищенко Т.М. можно скачать
1 Приведите примеры векторных величин, известных вам из курса физики.
2 Дайте определение вектора. Объясните, какой вектор называется нулевым.
3 Что называется длиной ненулевого вектора? Чему равна длина нулевого вектора?
4 Какие векторы называются коллинеарными? Изобразите на рисунке сонаправленные векторы и и противоположно направленные векторы
5 Дайте определение равных векторов.
6 Объясните смысл выражения: «Вектор отложен от точки А». Докажите, что от любой точки можно отложить вектор, равный данному, и притом только один.
7 Объясните, какой вектор называется суммой двух векторов. В чём заключается правило треугольника сложения двух векторов?
8 Докажите, что для любого вектора справедливо равенство
9 Сформулируйте и докажите теорему о законах сложения векторов.
10 В чём заключается правило параллелограмма сложения двух неколлинеарных векторов?
11 В чём заключается правило многоугольника сложения нескольких векторов?
12 Какой вектор называется разностью двух векторов? Постройте разность двух данных векторов.
13 Какой вектор называется противоположным данному? Сформулируйте и докажите теорему о разности векторов.
14 Какой вектор называется произведением данного вектора на данное число?
15 Чему равно произведение
16 Могут ли векторы быть неколлинеарными?
17 Сформулируйте основные свойства умножения вектора на число.
18 Приведите пример применения векторов к решению геометрических задач.
19 Какой отрезок называется средней линией трапеции?
20 Сформулируйте и докажите теорему о средней линии трапеции.
Дополнительные задачи к главе IX
800. Докажите, что если векторы сонаправлены, то а если противоположно направлены, причём то
801. Докажите, что для любых векторов справедливы неравенства
802. На стороне ВС треугольника АВС отмечена точка N так, что BN = 2NC. Выразите вектор через векторы
803. На сторонах MN и NP треугольника MNP отмечены соответственно точки X и Y так, что
804. Основание AD трапеции ABCD в три раза больше основания ВС. На стороне AD отмечена такая точка К, что Выразите векторы через векторы
На стороне AD отмечена такая точка К, что Выразите векторы через векторы
805. Три точки А, В и С расположены так, что Докажите, что для любой точки О справедливо равенство
806. Точка С делит отрезок АВ в отношении m: n, считая от точки А. Докажите, что для любой точки О справедливо равенство
1. Расскажите, как измеряются площади многоугольников.
2. Сформулируйте основные свойства площадей многоугольников.
3. Какие многоугольники называются равновеликими и какие равносоставленными?
4. Сформулируйте и докажите теорему о вычислении площади прямоугольника.
5. Сформулируйте и докажите теорему о вычислении площади параллелограмма.
6. Сформулируйте и докажите теорему о вычислении площади треугольника. Как вычислить площадь прямоугольного треугольника по его катетам?
7. Сформулируйте и докажите теорему об отношении площадей двух треугольников, имеющих по равному углу.
8. Сформулируйте и докажите теорему о вычислении площади трапеции.
9. Сформулируйте и докажите теорему Пифагора.
10. Сформулируйте и докажите теорему, обратную теореме Пифагора.
11. Какие треугольники называются пифагоровыми? Приведите примеры пифагоровых треугольников.
12. Какая формула площади треугольника называется формулой Герона? Выведите эту формулу.
Дополнительные задачи
500. Докажите, что площадь квадрата, построенного на катете равнобедренного прямоугольного треугольника, вдвое больше площади квадрата, построенного на высоте, проведённой к гипотенузе.
501. Площадь земельного участка равна 27 га. Выразите площадь этого же участка: а) в квадратных метрах; б) в квадратных километрах.
502. Высоты параллелограмма равны 5 см и 4 см, а периметр равен 42 см. Найдите площадь параллелограмма.
503. Найдите периметр параллелограмма, если его площадь равна 24 см 2 , а точка пересечения диагоналей удалена от сторон на 2 см и 3 см.
504. Меньшая сторона параллелограмма равна 29 см. Перпендикуляр, проведённый из точки пересечения диагоналей к большей стороне, делит её на отрезки, равные 33 см и 12 см. Найдите площадь параллелограмма.
Найдите площадь параллелограмма.
505. Докажите, что из всех треугольников, у которых одна сторона равна а, а другая — b, наибольшую площадь имеет тот, у которого эти стороны перпендикулярны.
506. Как провести две прямые через вершину квадрата, чтобы разделить его на три фигуры, площади которых равны?
507.* Каждая сторона одного треугольника больше любой стороны другого треугольника. Следует ли из этого, что площадь первого треугольника больше площади второго треугольника?
508.* Докажите, что сумма расстояний от точки на основании равнобедренного треугольника до боковых сторон не зависит от положения этой точки.
509. Докажите, что сумма расстояний от точки, лежащей внутри равностороннего треугольника, до его сторон не зависит от положения этой точки.
510.* Через точку D, лежащую на стороне ВС треугольника АВС, проведены прямые, параллельные двум другим сторонам и пересекающие стороны АВ и АС соответственно в точках Е и F. Докажите, что треугольники CDE и BDF равновеликие.
511. В трапеции ABCD с боковыми сторонами АВ и CD диагонали пересекаются в точке О.
а) Сравните площади треугольников ABD и ACD.
б) Сравните площади треугольников АВО и СDO.
в) Докажите, что выполняется равенство ОА ОВ = ОС OD.
512.* Основания трапеции равны а и b. Отрезок с концами на боковых сторонах трапеции, параллельный основаниям, разделяет трапецию на две равновеликие трапеции. Найдите длину этого отрезка.
513. Диагонали ромба равны 18 м и 24 м. Найдите периметр ромба и расстояние между параллельными сторонами.
514. Площадь ромба равна 540 см 2 , а одна из его диагоналей равна 4,5 дм. Найдите расстояние от точки пересечения диагоналей до стороны ромба.
515. Найдите площадь равнобедренного треугольника, если: а) боковая сторона равна 20 см, а угол при основании равен 30°; б) высота, проведённая к боковой стороне, равна 6 см и образует с основанием угол в 45°.
516. В треугольнике АВС ВС = 34 см. Перпендикуляр MN, проведённый из середины ВС к прямой АС, делит сторону АС на отрезки AN = 25 см и NC= 15 см. Найдите площадь треугольника АВС.
Найдите площадь треугольника АВС.
517. Найдите площадь четырёхугольника ABCD, в котором АВ = 5 см, ВС = 13 см, CD = 9 см, DA = 15 см, АС = 12 см.
518. Найдите площадь равнобедренной трапеции, если: а) её меньшее основание равно 18 см, высота — 9 см и острый угол равен 45°; б) её основания равны 16 см и 30 см, а диагонали взаимно перпендикулярны.
519. Найдите площадь равнобедренной трапеции, у которой высота равна h, а диагонали взаимно перпендикулярны.
520. Диагонали равнобедренной трапеции взаимно перпендикулярны, а сумма оснований равна 2а. Найдите площадь трапеции.
521. Докажите, что если диагонали четырёхугольника ABCD взаимно перпендикулярны, то AD 2 + ВС 2 = АВ 2 + CD 2 .
522. В равнобедренной трапеции ABCD с основаниями AD = 17 см, ВС = 5 см и боковой стороной АВ = 10 см через вершину В проведена прямая, делящая диагональ АС пополам и пересекающая основание AD в точке М. Найдите площадь треугольника BDM.
523. Два квадрата со стороной а имеют одну общую вершину, причём сторона одного из них лежит на диагонали другого. Найдите площадь общей части этих квадратов.
Найдите площадь общей части этих квадратов.
524. Стороны треугольника равны 13 см, 5 см и 12 см. Найдите площадь этого треугольника.
525. Расстояние от точки М, лежащей внутри треугольника АВС, до прямой АВ равно 6 см, а до прямой АС равно 2 см. Найдите расстояние от точки М до прямой ВС, если АВ=13см, ВС = 14 см, АС = 15 см.
526. В ромбе высота, равная см, составляет 2/3 большей диагонали. Найдите площадь ромба.
527. В равнобедренной трапеции диагональ равна 10 см, а высота равна 6 см. Найдите площадь трапеции.
528. В трапеции ABCD диагонали пересекаются в точке О. Найдите площадь треугольника АОВ, если боковая сторона CD трапеции равна 12 см, а расстояние от точки О до прямой CD равно 5 см.
529. Диагонали четырёхугольника равны 16 см и 20 см и пересекаются под углом в 30°. Найдите площадь этого четырёхугольника.
530. В равнобедренном треугольнике АВС с основанием ВС высота AD равна 8 см. Найдите площадь треугольника АВС, если медиана DM треугольника ADC равна 8 см.
531. Стороны АВ и ВС прямоугольника ABCD равны соответственно 6 см и 8 см. Прямая, проходящая через вершину С и перпендикулярная к прямой BD, пересекает сторону AD в точке М, а диагональ BD — в точке К. Найдите площадь четырёхугольника АВКМ.
532. В треугольнике АВС проведена высота ВН. Докажите, что если:
а) угол А острый, то ВС 2 = АВ 2 + АС 2 — 2АС АН;
б) угол А тупой, то ВС 2 = АВ 2 + АС 2 + 2АС АН.
Ответы к задачам
Вопросы для повторения к главе 12. Вопросы для повторения к главе IX. Применение метода координат к решению задач
Готовые домашние задания к учебнику геометрии для учащихся 7-9 классов, авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина , издательство Просвещение на 2015 — 2016 учебный год.
Ребята, в 7-9 классе вы будете изучать такой интересный предмет как геометрия. Чтобы в дальнейшем не иметь проблем с пониманием этого урока, необходимо с самого начала усердно работать.
В предыдущих классах вы уже познакомились с некоторыми геометрическими фигурами. В этом гуду вы расширите этот минимум познания. Весь курс делится на два раздела: планиметрию и стереометрию. В 7 и 8 классе вы будете рассматривать фигуры на плоскости — это раздел планиметрия. В 9 классе свойства фигур в пространстве — стереометрия.
Часто возникает ситуация, когда не получается исходя из условия сделать правильный рисунок, нарисовать в пространстве все детали и тогда геометрия кажется неподъёмным для вас предметом. Если у вас начнутся такие трудности, тогда рекомендуем использовать наш гдз по геометрии за 7-9 класс Л.С. Атанасяна, который размещён ниже.
ГДЗ Геометрия 7 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ Геометрия 8 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ Геометрия 9 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ к дидактическим материалам по геометрии за 7 класс Зив Б.Г. можно скачать .
ГДЗ к дидактическим материалам по геометрии за 8 класс Зив Б. Г. можно скачать
.
Г. можно скачать
.
ГДЗ к дидактическим материалам по геометрии за 9 класс Зив Б.Г. можно скачать .
ГДЗ к самостоятельным и контрольным работам по геометрии за 7-9 классы Иченская М.А. можно скачать .
ГДЗ к сборнику заданий по геометрии за 7 класс Ершова А.П. можно скачать .
ГДЗ к сборнику заданий по геометрии за 8 класс Ершова А.П. можно скачать .
ГДЗ к рабочей тетради по геометрии за 9 класс Мищенко Т.М. можно скачать .
ГДЗ к тематическим тестам по геометрии за 7 класс Мищенко Т.М. можно скачать .
ГДЗ к тематическим тестам по геометрии за 8 класс Мищенко Т.М. можно скачать
ГДЗ Геометрия 7 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ Геометрия 8 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ Геометрия 9 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ к дидактическим материалам по геометрии за 7 класс Зив Б.Г. можно скачать .
ГДЗ к дидактическим материалам по геометрии за 8 класс Зив Б.Г. можно скачать
.
ГДЗ к дидактическим материалам по геометрии за 9 класс Зив Б.Г. можно скачать .
ГДЗ к самостоятельным и контрольным работам по геометрии за 7-9 классы Иченская М.А. можно скачать .
ГДЗ к сборнику заданий по геометрии за 7 класс Ершова А.П. можно скачать .
ГДЗ к сборнику заданий по геометрии за 8 класс Ершова А.П. можно скачать .
ГДЗ к рабочей тетради по геометрии за 9 класс Мищенко Т.М. можно скачать .
ГДЗ к тематическим тестам по геометрии за 7 класс Мищенко Т.М. можно скачать .
ГДЗ к тематическим тестам по геометрии за 8 класс Мищенко Т.М. можно скачать .
ГДЗ к тематическим тестам по геометрии за 9 класс Мищенко Т.М. можно скачать .
ГДЗ к контрольным работам по геометрии за 7 класс Мельникова Н.Б. можно скачать .
ГДЗ к контрольным работам по геометрии за 8 класс Мельникова Н.Б. можно скачать .
ГДЗ к контрольным работам по геометрии за 9 класс Мельникова Н.Б. можно скачать .
ГДЗ к рабочей тетради по геометрии за 9 класс Глазков Ю. А. Егупова М.В. можно скачать
.
А. Егупова М.В. можно скачать
.
Родителям нередко приходится слышать жалобы ребёнка о том, что он не понимает тот или иной предмет. Чаще всего это точные науки: алгебра, геометрия, физика. Некоторые родители стараются нанять репетитора, а другие скачивают своим детям ГДЗ по геометрии к учебнику Атанасяна. Конечно, просто бездумное списывание с ответов не сможет привести к положительному результату. Но если школьник будет сверять свои задания, пользоваться изданием для повторения или изучения материала, чтобы на уроке быть уже подготовленным, вы увидите, что знания станут крепче, а предмет понятней.
Решебник по геометрии за 7 класс подойдёт также для углубленного изучения, выполнения заданий повышенной сложности. Так как пособие ежегодно подвергается изменениям и дополнениям, родители могут не беспокоиться в правильности всех ответов. Благодаря этой книге школьник может не бояться за получение неудовлетворительных оценок — они останутся в прошлом. А при регулярном изучении предмета и повышении своих знаний вы увидите, как с каждым разом всё легче и легче становится выполнить задание.
1. Сколько прямых можно провести через две точки?
2. Сколько общих точек могут иметь две прямые?
3. Объясните, что такое отрезок.
4. Объясните, что такое луч. Как обозначаются лучи?
5. Какая фигура называется углом? Объясните, что такое вершина и стороны угла.
6. Какой угол называется развёрнутым?
7. Какие фигуры называются равными?
8. Объясните, как сравнить два отрезка.
9. Какая точка называется серединой отрезка?
10. Объясните, как сравнить два угла.
11. Какой луч называется биссектрисой угла?
12. Точка С делит отрезок АВ на два отрезка. Как найти длину отрезка АВ, если известны длины отрезков АС и СВ?
13. Какими инструментами пользуются для измерения расстояний?
14. Что такое градусная мера угла?
15. Луч ОС делит угол АОВ на два угла. Как найти градусную меру угла АОВ, если известны градусные меры углов АОС и СОВ?
16. Какой угол называется острым? прямым? тупым?
17. Какие углы называются смежными? Чему равна сумма смежных углов?
18. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы?
Какие углы называются вертикальными? Каким свойством обладают вертикальные углы?
19. Какие прямые называются перпендикулярными?
20. Объясните, почему две прямые, перпендикулярные к третьей, не пересекаются.
21. Какие приборы применяют для построения прямых углов на местности?
Дополнительные задачи к главе I
71. Отметьте четыре точки так, чтобы никакие три не лежали на одной прямой. Через каждую пару точек проведите прямую. Сколько получилось прямых?
72. Даны четыре прямые, каждые две из которых пересекаются. Сколько точек пересечения имеют эти прямые, если через каждую точку пересечения проходят только две прямые?
73. Сколько неразвёрнутых углов образуется при пересечении трёх прямых, проходящих через одну точку?
74. Точка N лежит на отрезке МР. Расстояние между точками М и Р равно 24 см, а расстояние между точками N и М в два раза больше расстояния между точками N и Р. Найдите расстояние:
75. Три точки К, L, М лежат на одной прямой, КL = 6 см, LM = 10 см. Каким может быть расстояние КМ? Для каждого из возможных случаев сделайте чертёж.
Каким может быть расстояние КМ? Для каждого из возможных случаев сделайте чертёж.
76. Отрезок АВ длины а разделён точками Р и Q на три отрезка АР, PQ и QB так, что АР — 2PQ = 2QB. Найдите расстояние между:
77. Отрезок длины m разделён:
Найдите расстояние между серединами крайних частей.
78. Отрезок в 36 см разделён на четыре не равные друг другу части. Расстояние между серединами крайних частей равно 30 см. Найдите расстояние между серединами средних частей.
79. Точки А, В и С лежат на одной прямой, точки М и N — середины отрезков АВ и АС. Докажите, что BC = 2MN.
80. Известно, что ZAOB = 35°, ZBOC = 50°. Найдите угол АОС. Для каждого из возможных случаев сделайте чертёж с помощью линейки и транспортира.
81. Угол hk равен 120°, а угол hm равен 150°. Найдите угол km. Для каждого из возможных случаев сделайте чертёж.
82. Найдите смежные углы, если:
83. Найдите угол, образованный биссектрисами двух смежных углов.
84. Докажите, что биссектрисы вертикальных углов лежат на одной прямой.
85. Докажите, что если биссектрисы углов АВС и CBD перпендикулярны, то точки А, В и D лежат на одной прямой.
86. Даны две пересекающиеся прямые а и b и точка А, не лежащая на этих прямых. Через точку А проведены прямые m и n так, что m⊥a, n⊥b. Докажите, что прямые m и n не совпадают.
1. Что называется отношением двух отрезков?
2. В каком случае говорят, что отрезки АВ и CD пропорциональны отрезкам А 1 В 1 и С 1 D 1 ?
3. Дайте определение подобных треугольников.
4. Сформулируйте и докажите теорему об отношении площадей подобных треугольников.
5. Сформулируйте и докажите теорему, выражающую первый признак подобия треугольников.
6. Сформулируйте и докажите теорему, выражающую второй признак подобия треугольников.
7. Сформулируйте и докажите теорему, выражающую третий признак подобия треугольников.
8. Какой отрезок называется средней линией треугольника? Сформулируйте и докажите теорему о средней линии треугольника.
9. Докажите, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2: 1, считая от вершины.
10. Сформулируйте и докажите утверждение о том, что высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на подобные треугольники.
11. Сформулируйте и докажите утверждения о пропорциональных отрезках в прямоугольном треугольнике.
12. Приведите пример решения задачи на построение методом подобия.
13. Расскажите, как определить на местности высоту предмета и расстояние до недоступной точки.
14. Объясните, какие две фигуры называются подобными. Что такое коэффициент подобия фигур?
15. Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника?
16. Докажите, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
17. Какое равенство называют основным тригонометрическим тождеством?
18. Чему равны значения синуса, косинуса и тангенса для углов 30°, 45°, 60°? Ответ обоснуйте.
Дополнительные задачи
604. Треугольники АВС и А 1 В 1 С 1 подобны, АВ = 6 см, ВС- 9 см, С А = 10 см. Наибольшая сторона треугольника А 1 В 1 С 1 равна 7,5 см. Найдите две другие стороны треугольника А 1 В 1 С 1 .
605. Диагональ АС трапеции ABCD делит её на два подобных треугольника. Докажите, что АС 2 = а b, где а и b — основания трапеции.
606. Биссектрисы MD и NK треугольника MNP пересекаются в точке О. Найдите отношение OK: ON, если MN = 5 см, NP = 3 см, МР = 7 см.
607. Основание равнобедренного треугольника относится к боковой стороне как 4: 3, а высота, проведённая к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
608. На продолжении боковой стороны ОВ равнобедренного треугольника АО В с основанием АВ взята точка С так, что точка В лежит между точками О и С. Отрезок АС пересекает биссектрису угла АОВ в точке М. Докажите, что AM
609. На стороне ВС треугольника АВС взята точка D так, что Докажите, что AD — биссектриса треугольника АВС.
610. Прямая, параллельная стороне АВ треугольника АВС, делит сторону АС в отношении 2: 7, считая от вершины А. Найдите стороны отсечённого треугольника, если АВ = 10см, ВС = 18 см, СА = 21,6 см.
611. Докажите, что медиана AM треугольника АВС делит пополам любой отрезок, параллельный стороне ВС, концы которого лежат на сторонах АВ и АС.
612. Два шеста АВ и CD разной длины а и b установлены вертикально на некотором расстоянии друг от друга так, как показано на рисунке 210. Концы А и D, В и С соединены верёвками, которые пересекаются в точке О. По данным рисунка докажите, что:
Найдите х и докажите, что х не зависит от расстояния d между шестами АВ и CD.
Рис. 210
613. Докажите, что треугольники АВС и А 1 В 1 С 1 подобны, если:
а) , где ВМ и В 1 М 1 — медианы треугольников;
б) ∠А = ∠A 1 , , где ВН и В 1 Н 1 — высоты треугольников АВС и A 1 B 1 C 1 .
614. Диагонали прямоугольной трапеции ABCD с прямым углом А взаимно перпендикулярны. Основание АВ равно 6 см, а боковая сторона AD равна 4 см. Найдите DC, DB и СВ.
Основание АВ равно 6 см, а боковая сторона AD равна 4 см. Найдите DC, DB и СВ.
615.* Отрезок с концами на боковых сторонах трапеции параллелен её основаниям и проходит через точку пересечения диагоналей. Найдите длину этого отрезка, если основания трапеции равны а и b.
616. Докажите, что вершины треугольника равноудалены от прямой, содержащей его среднюю линию.
617. Докажите, что середины сторон ромба являются вершинами прямоугольника.
618. Точки М и N являются соответственно серединами сторон CD и ВС параллелограмма ABCD. Докажите, что прямые AM и AN делят диагональ BD на три равные части.
619. Биссектриса внешнего угла при вершине А треугольника АВС пересекает прямую ВС в точке D. Докажите, что .
620. В треугольнике АВС (АВ≠ АС) через середину стороны ВС проведена прямая, параллельная биссектрисе угла А, которая пересекает прямые АВ и АС соответственно в точках D и Е. Докажите, что BD = CE.
621. В трапеции ABCD с основаниями AD и ВС сумма оснований равна b, диагональ АС равна a, ∠ACB = α. Найдите площадь трапеции.
Найдите площадь трапеции.
622. На стороне AD параллелограмма ABCD отмечена точка К так, что AK = 1/4 KD. Диагональ АС и отрезок В К пересекаются в точке Р. Найдите площадь параллелограмма ABCD, если площадь треугольника АРК равна 1 см 2 .
623. В прямоугольной трапеции ABCD с основаниями AD и ВС ∠A = ∠B = 90°, ∠ACD = 90°, ВС = 4 см, AD = 16 см. Найдите углы С и D трапеции.
624. Докажите, что медианы треугольника разбивают его на шесть треугольников, площади которых попарно равны.
625. Основание AD равнобедренной трапеции ABCD в 5 раз больше основания ВС. Высота ВН пересекает диагональ АС в точке М, площадь треугольника АМН равна 4 см 2 . Найдите площадь трапеции ABCD.
626. Докажите, что треугольники АВС и А 1 В 1 С 1 подобны, если где AD и A 1 D 1 — биссектрисы треугольников.
Задачи на построение
627. Дан треугольник АВС. Постройте треугольник А1В1С1, подобный треугольнику АВС, площадь которого в два раза больше площади треугольника АВС.
628. Даны три отрезка, длины которых соответственно равны а, b и с. Постройте отрезок, длина которого равна .
Даны три отрезка, длины которых соответственно равны а, b и с. Постройте отрезок, длина которого равна .
629. Постройте треугольник, если даны середины его сторон.
630. Постройте треугольник по стороне и медианам, проведённым к двум другим сторонам.
Ответы к задачам
Современные дети регулярно сталкиваются с ситуациями, когда возникают определенные проблемы с домашней работой. Причины таких обстоятельств могут быть довольно разными – лень, болезни, невнимательность. Особенно часто так бывает с Геометрией, которая имеет много непонятных упражнений. В случае если возникли проблемы, то старшеклассники – начинают лихорадочно искать варианты разрешения подобных сложностей. Действительно, кто-то обращается к родственникам, друзьям, репетиторам, а кто-то ищет ГДЗ , которые сделаны профессионалами, не допускающими ошибок.
Благодаря бурному развитию интернет технологий теперь есть великолепный шанс отыскать требуемые задачи при помощи специализированной площадки. Главное ответственно отнестись к вопросу, чтобы готовые Д/З имели высокое качество и были полностью понятны. Разумеется, надо доверять данным, размещенным на тех онлайн-ресурсах, которые сумели себя зарекомендовать с сильной стороны. Только на таких ресурсах содержится качественная информация по домашке, которой можно воспользоваться, когда возникнет в необходимость.
Главное ответственно отнестись к вопросу, чтобы готовые Д/З имели высокое качество и были полностью понятны. Разумеется, надо доверять данным, размещенным на тех онлайн-ресурсах, которые сумели себя зарекомендовать с сильной стороны. Только на таких ресурсах содержится качественная информация по домашке, которой можно воспользоваться, когда возникнет в необходимость.
Представленный решебник будет рациональным выбором для отдельных ситуаций. В нем есть максимально грамотные и развернутые ответы, по геометрии для учеников с 7 по 9 классов . Они подходят для учебников авторов — Атанасян и Бутузов . Вы сможете на данной интернет странице быстро сверить результаты, и поднимете реальный уровень познаний и эрудиции по такому сложному предмету. Поэтому ей нередко пользуются школьники и их родители.
Высококвалифицированная администрация портала серьезно позаботилась, чтобы материал был написан в доступной и понятной форме. В случае если, выходят в свет новые книги, тут сразу появляются ответы на новые номера. В этом смогли уже неоднократно удостовериться многочисленные посетители портала.
В этом смогли уже неоднократно удостовериться многочисленные посетители портала.
Важно понимать, если появляются сложности с учебой по базовым дисциплинам, то стоит позаботиться чтобы они разрешались. Не нужно затягивать, это приводит к крайне неприятным последствиям. Эта онлайн страница сможет служить отличным местом, где можно осуществлять сверку правильности исполнения номеров, которые задали преподаватели. Уже многие подростки ее используют, и оставили о ней множество хороших откликов. Это неудивительно, благодаря ей, есть прекрасная возможность получать высокие оценки и добиваться лучшей успеваемости в школе.
ГДЗ Геометрия 7 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ Геометрия 8 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ Геометрия 9 класс рабочая тетрадь Атанасян можно скачать .
ГДЗ к дидактическим материалам по геометрии за 7 класс Зив Б.Г. можно скачать .
ГДЗ к дидактическим материалам по геометрии за 8 класс Зив Б.Г. можно скачать
.
ГДЗ к дидактическим материалам по геометрии за 9 класс Зив Б.Г. можно скачать .
ГДЗ к самостоятельным и контрольным работам по геометрии за 7-9 классы Иченская М.А. можно скачать .
ГДЗ к сборнику заданий по геометрии за 7 класс Ершова А.П. можно скачать .
ГДЗ к сборнику заданий по геометрии за 8 класс Ершова А.П. можно скачать .
ГДЗ к рабочей тетради по геометрии за 9 класс Мищенко Т.М. можно скачать
ГДЗ упражнение 510 русский язык 10‐11 класс Гольцова, Шамшин – Telegraph
➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!
ГДЗ упражнение 510 русский язык 10‐11 класс Гольцова, Шамшин
Подробное решение упражнение № 510 по русскому языку для учащихся 10 ‐11 класса Инновационная школа Базовый уровень, авторов Гольцова , Шамшин, Мищерина 2020 . Авторы : Н .Г . Гольцова , И .В . Шамшин , М .А . Мищерина . Издательство: Русское слово 2020 .
Использование ГДЗ Гольцова 10 -11 позволяет экономить время, быстро находить допущенные обучающимися ошибки Учебник под авторством Гольцова (для учащихся 10 классов, а также выпускных 11 классов) предназначен как для обычных школ, так и для учебных заведений с . .
.
Онлайн решебник по Русскому языку для 10 ‐11 класса Н .Г . Гольцова , И .В . Шамшин , М .А . Мищерина, гдз и ответы к домашнему заданию . Авторы: Н .Г . Гольцова , И .В . Шамшин, М .А . Мищерина .
Гольцова , Шамшин . «Русское слово», . Обобщающие контрольно-тренировочные упражнения и диктанты . Упражнение №510 .
Подробный решебник (ГДЗ ) по Русскому языку за 10 ‐11 (десятый‐одиннадцатый ) класс — готовый ответ упражнение — 510 . Авторы: Н .Г . Гольцова , И .В . Шамшин , М .А . Мищерина . Издательство: Русское слово 2020 год . Тип: Учебник, Инновационная школа, Базовый уровень .
Польза ГДЗ по русскому языку за 10 -11 класс Гольцовой (Базовый уровень: часть 1, 2) . В последние два учебных года учащимся предстоит Онлайн-решебник по русскому для 10 -11 класса (авторы: Н . Г . Гольцова , И . В . Шамшин, М . А . Мищерина) не является источником для . .
На этой странице размещены все ГДЗ к учебнику по русскому языку за 10 -11 классы авторов Н .Г . Гольцова , И . В . Шамшин года издания . Все задания данного решебника подробно рассмотрены и решены авторами, ученикам остается только списывать и забыть о домашних . .
В . Шамшин года издания . Все задания данного решебника подробно рассмотрены и решены авторами, ученикам остается только списывать и забыть о домашних . .
Следует отметить, что ГДЗ по Гольцовой за 10 и 11 класс предусмотрено только для подсказки правильного решения, а не для бездумного Книга «Все домашние работы к учебнику: Русский язык 10 —11 классы Н . Г . Гольцова , И . В . Шамшин » содержит выполненные упражнения .
Онлайн ГДЗ по учебнику Русский язык 10 -11 класс : Гольцова Н .Г . ГДЗ к упр . № 510 , Русский язык , 10 -11 класс , Гольцова Н .Г ., Шамшин И .В ., Мищерина М .А .
Гольцова , Шамшин . Русское слово . год . ГДЗ (решебник) по русскому языку 10 -11 класс Гольцова , Шамшин . Базовый уровень . Старшеклассники два года испытывают постоянный стресс из-за чересчур больших нагрузок в школе и страха плохо сдать ЕГЭ .
Русский язык 10 -11 класс . Учебник . Гольцова , Шамшин . Поэтому так важно делать домашние упражнения на совесть, разбирая и запоминая новые правила и темы по русскому языку в В 10 -11 классе русский язык богат на новые правила и термины, а также дополнен . .
.
ГДЗ и решебник по русскому языку за 10 -11 класс Гольцова , Шамшин — ответы онлайн . Русский язык остается одним из наиболее используемых на пространстве СНГ Каких правил нужно придерживаться при использовании ГДЗ по русскому языку за10 -11 класс Гольцовой .
Ответы к упражнениям по русскому языку за 10 и 11 класс к учебнику Гольцовой , Шамшина часть 1, 2 . Проверка домашнего задания . Ответы к учебнику Гольцовой , Шамшина , русский 10 и 11 класс .
Разбор упражнений из школьного учебника по русскому языку за 10 -11 класс авторов: Гольцова Т .И . Шамшин Ф .Н . Дополнительное пояснение бесплатно в ответах из ГДЗ . Гольцова Н .Г ., Шамшин И .В ., Мищерина М .А . «Русское слово» Часть 1, 2 .
Решебник . Готовые Домашние Задания для 10 -11 классов по Русскому языку . Гольцова Н .Г . .
Подробное решение упражнение № 510 по русскому языку для учащихся 10 ‐11 класса Инновационная школа Базовый уровень, авторов Гольцова , Шамшин, Мищерина 2020 . Авторы : Н . Г . Гольцова , И .В . Шамшин , М .А . Мищерина . Издательство: Русское слово 2020 .
Г . Гольцова , И .В . Шамшин , М .А . Мищерина . Издательство: Русское слово 2020 .
Использование ГДЗ Гольцова 10 -11 позволяет экономить время, быстро находить допущенные обучающимися ошибки Учебник под авторством Гольцова (для учащихся 10 классов, а также выпускных 11 классов) предназначен как для обычных школ, так и для учебных заведений с . .
Онлайн решебник по Русскому языку для 10 ‐11 класса Н .Г . Гольцова , И .В . Шамшин , М .А . Мищерина, гдз и ответы к домашнему заданию . Авторы: Н .Г . Гольцова , И .В . Шамшин, М .А . Мищерина .
Гольцова , Шамшин . «Русское слово», . Обобщающие контрольно-тренировочные упражнения и диктанты . Упражнение №510 .
Подробный решебник (ГДЗ ) по Русскому языку за 10 ‐11 (десятый‐одиннадцатый ) класс — готовый ответ упражнение — 510 . Авторы: Н .Г . Гольцова , И .В . Шамшин , М .А . Мищерина . Издательство: Русское слово 2020 год . Тип: Учебник, Инновационная школа, Базовый уровень .
Польза ГДЗ по русскому языку за 10 -11 класс Гольцовой (Базовый уровень: часть 1, 2) . В последние два учебных года учащимся предстоит Онлайн-решебник по русскому для 10 -11 класса (авторы: Н . Г . Гольцова , И . В . Шамшин, М . А . Мищерина) не является источником для . .
В последние два учебных года учащимся предстоит Онлайн-решебник по русскому для 10 -11 класса (авторы: Н . Г . Гольцова , И . В . Шамшин, М . А . Мищерина) не является источником для . .
На этой странице размещены все ГДЗ к учебнику по русскому языку за 10 -11 классы авторов Н .Г . Гольцова , И .В . Шамшин года издания . Все задания данного решебника подробно рассмотрены и решены авторами, ученикам остается только списывать и забыть о домашних . .
Следует отметить, что ГДЗ по Гольцовой за 10 и 11 класс предусмотрено только для подсказки правильного решения, а не для бездумного Книга «Все домашние работы к учебнику: Русский язык 10 —11 классы Н . Г . Гольцова , И . В . Шамшин » содержит выполненные упражнения .
Онлайн ГДЗ по учебнику Русский язык 10 -11 класс : Гольцова Н .Г . ГДЗ к упр . № 510 , Русский язык , 10 -11 класс , Гольцова Н .Г ., Шамшин И .В ., Мищерина М .А .
Гольцова , Шамшин . Русское слово . год . ГДЗ (решебник) по русскому языку 10 -11 класс Гольцова , Шамшин . Базовый уровень . Старшеклассники два года испытывают постоянный стресс из-за чересчур больших нагрузок в школе и страха плохо сдать ЕГЭ .
Базовый уровень . Старшеклассники два года испытывают постоянный стресс из-за чересчур больших нагрузок в школе и страха плохо сдать ЕГЭ .
Русский язык 10 -11 класс . Учебник . Гольцова , Шамшин . Поэтому так важно делать домашние упражнения на совесть, разбирая и запоминая новые правила и темы по русскому языку в В 10 -11 классе русский язык богат на новые правила и термины, а также дополнен . .
ГДЗ и решебник по русскому языку за 10 -11 класс Гольцова , Шамшин — ответы онлайн . Русский язык остается одним из наиболее используемых на пространстве СНГ Каких правил нужно придерживаться при использовании ГДЗ по русскому языку за10 -11 класс Гольцовой .
Ответы к упражнениям по русскому языку за 10 и 11 класс к учебнику Гольцовой , Шамшина часть 1, 2 . Проверка домашнего задания . Ответы к учебнику Гольцовой , Шамшина , русский 10 и 11 класс .
Разбор упражнений из школьного учебника по русскому языку за 10 -11 класс авторов: Гольцова Т .И . Шамшин Ф .Н . Дополнительное пояснение бесплатно в ответах из ГДЗ . Гольцова Н .Г ., Шамшин И .В ., Мищерина М .А . «Русское слово» Часть 1, 2 .
Гольцова Н .Г ., Шамшин И .В ., Мищерина М .А . «Русское слово» Часть 1, 2 .
Решебник . Готовые Домашние Задания для 10 -11 классов по Русскому языку . Гольцова Н .Г . .
ГДЗ задание для повторения 259 алгебра 10 класс Никольский, Потапов
ГДЗ Вопросы и задания к главе IX 5 история 6 класс Агибалов, Донской
ГДЗ задача повышенной трудности 16 физика 9 класс Задачник Генденштейн, Кирик
ГДЗ упражнение 352 русский язык 3 класс Нечаева, Яковлева
ГДЗ задание 671 математика 5 класс Никольский, Потапов
ГДЗ контрольная работа / контрольная работа №2 / подготовительный вариант 4 алгебра 7 класс дидактические материалы Феоктистов
ГДЗ § / § 22 61 алгебра 10 класс задачник Мордкович, Денищева
ГДЗ упражнение 9 английский язык 7 класс сборник упражнений к учебнику Биболетовой Барашкова
ГДЗ страница 132 английский язык 9 класс spotlight Эванс, Дули
ГДЗ параграф 17 17.26 геометрия 7 класс Мерзляк, Поляков
ГДЗ промежуточное тестирование 50 английский язык 11 класс Контрольные (тестовые) задания Эванс, Дули
ГДЗ номер 380 математика 5 класс Дорофеев, Шарыгин
ГДЗ это ты знаешь и умеешь / часть 1. страница 69 русский язык 3 класс Бунеев, Бунеева
страница 69 русский язык 3 класс Бунеев, Бунеева
ГДЗ страница 181 английский язык 9 класс Афанасьева, Михеева
ГДЗ часть 1. страница 138 английский язык 2 класс Верещагина, Бондаренко
ГДЗ Математика 5 класс рабочая тетрадь Бунимович, Дорофеев
ГДЗ задание 1212 математика 5 класс Никольский, Потапов
ГДЗ упражнение 245 русский язык 5 класс Быстрова, Александрова
ГДЗ параграф 13 2 алгебра 9 класс рабочая тетрадь Миндюк, Шлыкова
ГДЗ проверь себя / страница 42 1 алгебра 7 класс Дорофеев, Суворова
ГДЗ часть №2 127 математика 6 класс Петерсон, Дорофеев
ГДЗ учебник 2019 / часть 2. упражнение 575 (1463) математика 6 класс Виленкин, Жохов
ГДЗ страница 69 биология 7 класс Сонин, Захаров
ГДЗ по русскому языку 3 класс проверочные и контрольные работы Бунеева Решебник
ГДЗ задание 64 русский язык 5 класс рабочая тетрадь Бабайцева, Беднарская
ГДЗ вопросы в конце параграфа / § 23 2 химия 11 класс Габриелян, Лысова
ГДЗ Учебник 2019 / часть 2 244 (1093) математика 5 класс Виленкин, Жохов
ГДЗ самостоятельная работа / вариант 3 300 математика 6 класс дидактические материалы Чесноков, Нешков
ГДЗ задания для самопроверки / завдання №4 18 алгебра 8 класс Кравчук, Пидручна
ГДЗ unit 1 73 английский язык 9 класс Enjoy English Биболетова, Бабушис
ГДЗ упражнение 453 русский язык 8 класс практика Пичугов, Еремеева
ГДЗ номер 1349 математика 6 класс Мерзляк, Полонский
ГДЗ §34 34. 20 алгебра 10‐11 класс Учебник, Задачник Мордкович, Семенов
20 алгебра 10‐11 класс Учебник, Задачник Мордкович, Семенов
ГДЗ часть 1 202 математика 3 класс Истомина
ГДЗ номер 83 алгебра 7 класс Мерзляк, Полонский
ГДЗ часть 2. упражнение 80 математика 4 класс рабочая тетрадь Рудницкая, Юдачева
ГДЗ § 9. формулы сложения. 9.31 алгебра 10 класс Никольский, Потапов
ГДЗ страница 38 английский язык 8 класс Любченко, Любченко
ГДЗ задание 283 математика 5 класс Рабочая тетрадь Муравин, Муравина
ГДЗ номер 813 математика 6 класс Мерзляк, Полонский
ГДЗ страница 44 английский язык 8 класс spotlight Ваулина, Дули
ГДЗ часть 3 38 русский язык 3 класс Каленчук, Чуракова
ГДЗ параграф 11 5 геометрия 7‐9 класс Погорелов
ГДЗ № 706 математика 5 класс Зубарева, Мордкович
ГДЗ урок Урок 74 математика 1 класс рабочая тетрадь Кочурова
ГДЗ по литературе 7 класс Меркин Решебник
ГДЗ вариант 2 195 математика 5 класс дидактические материалы Мерзляк, Полонский
ГДЗ самостоятельные работы / СР-20 / вариант 1 3 алгебра 9 класс дидактические материалы Потапов, ШевкинВ
ГДЗ номер / § 1 21 алгебра 11 класс Никольский, Потапов
ГДЗ часть 1 (страница) 309 литература 7 класс Меркин
Решебник ГДЗ 2 Класс Дорофеев
Скачать Решебник По Математике 5
ГДЗ По Химии 10 Габриелян Маскаев
ГДЗ По Английскому Четвертый Класс Биболетова
ГДЗ По Алгебре 8 Мордкович Задачник 2020
Большие идеи Ответы по математике и геометрии Глава 9 Прямоугольные треугольники и тригонометрия – Большие идеи по математике Ответы
Вы стремитесь сделать своего ребенка более умным и подкованным в математике? Не беспокойтесь, мы нашли лучшее решение, которое избавит вас от стресса. Вот лучшее руководство по подготовке, которое поможет вашим детям и заставит их сосредоточиться на концепциях соответствующего класса. Большие идеи Математическая геометрия Ответы Глава 9 Прямоугольные треугольники и тригонометрия — это то, что мы обсуждаем в приведенных выше строках. С помощью BIM Geometry Ch 9Ключ решения, вы можете быстро получить предметные навыки и получить самые высокие оценки на экзаменах. Обучение на основе веселья и активности — это простой и простой способ тщательно понять концепции и прояснить свои сомнения за минимальное время.
Вот лучшее руководство по подготовке, которое поможет вашим детям и заставит их сосредоточиться на концепциях соответствующего класса. Большие идеи Математическая геометрия Ответы Глава 9 Прямоугольные треугольники и тригонометрия — это то, что мы обсуждаем в приведенных выше строках. С помощью BIM Geometry Ch 9Ключ решения, вы можете быстро получить предметные навыки и получить самые высокие оценки на экзаменах. Обучение на основе веселья и активности — это простой и простой способ тщательно понять концепции и прояснить свои сомнения за минимальное время.
Хотите получить больше баллов по главе 9 «Прямоугольные треугольники и тригонометрия»? Загрузите BIM Geometry Chapter 9 Right Triangles and Trigonometry Answer key Pdf бесплатно по ссылкам ниже. После загрузки мудрых уроков больших идей по математике, ключ решения для геометрии, глава 9, учащихся должны эффективно начать подготовку и часто пересматривать ее. Ознакомьтесь со ссылками, доступными здесь, и коснитесь соответствующей ссылки на урок в старшей школе Big Ideas Math Geometry ch 9 Solution Book, чтобы узнать вопросы, затронутые в практических тестах, тестах по главам, оценках и т. д. по концепциям прямоугольных треугольников и тригонометрии.
д. по концепциям прямоугольных треугольников и тригонометрии.
Прямоугольные треугольники и тригонометрия Поддержание математических знаний
Упростите выражение.
Вопрос 1.
√75
Ответ:
квадратный корень из 75 = 5625.
Объяснение:
В приведенном выше вопросе,
при этом,
√75.
квадратный корень из 75 = 75 х 75.
75 х 75 = 5625.
√75 = 5625.
Вопрос 2.
√270
Ответ:
квадратный корень из 270 = 72 900.
Объяснение:
В приведенном выше вопросе,
при этом,
√270.
квадратный корень из 270 = 270 х 270.
270 х 270 = 72900,
√270 = 72900,
Вопрос 3.
√135
Ответ:
квадратный корень из 135 = 18225.
Объяснение:
В приведенном выше вопросе
при условии, что
√135.
квадратный корень из 135 = 135 х 135.
135 х 135 = 18225.
√135 = 18 225.
Вопрос 4.
\(\frac{2}{\sqrt{7}}\)
Ответ:
2/49 = 0,04.
Объяснение:
В приведенном выше вопросе
при условии, что
квадратный корень из 7 = 7 x 7.
7 x 7 = 49.
\(\frac{2}{\sqrt{7}}\) .
2/49 = 0,04.
Вопрос 5.
\(\frac{5}{\sqrt{2}}\)
Ответ:
5/4 = 1,25.
Объяснение:
В приведенном выше вопросе
учитывая, что
квадратный корень из 2 = 2 x 2.
2 x 2 = 4.
\(\frac{5}{\sqrt{2}}\) .
5/4 = 1,25.
Вопрос 6.
\(\frac{12}{\sqrt{6}}\)
Ответ:
12/36 = 0,33.
Объяснение:
В приведенном выше вопросе
при условии, что
квадратный корень из 6 = 6 х 6.
6 х 6 = 36,
\(\frac{12}{\sqrt{6}}\).
12/36 = 0,33.
Решите пропорцию.
Вопрос 7.
\(\frac{x}{12}=\frac{3}{4}\)
Ответ:
x = 9.
Объяснение:
В приведенном выше вопросе
дано что
\(\frac{x}{12}=\frac{3}{4}\)
x/12 = 3/4.
4 х = 12 х 3.
4 х = 36.
х = 36/4.
x = 9.
Вопрос 8.
\(\frac{x}{3}=\frac{5}{2}\)
Ответ:
x = 7,5.
Объяснение:
В приведенном выше вопросе
, учитывая, что
\(\frac{x}{3}=\frac{5}{2}\)
x/3 = 5/2.
2x = 5×3.
2x = 15.
x = 15/2.
х = 7,5.
Вопрос 9.
\(\frac{4}{x}=\frac{7}{56}\)
Ответ:
x = 32.
Объяснение:
В приведенном выше вопросе дано
что
\(\frac{4}{x}=\frac{7}{56}\)
4/x = 7/56.
7 х = 56 х 4.
7 х = 224.
х = 224/7.
x = 32.
Вопрос 10.
\(\frac{10}{23}=\frac{4}{x}\)
Ответ:
х = 9,2.
Объяснение:
В заданном выше вопросе
при условии, что
\(\frac{10}{23}=\frac{4}{x}\)
x/4 = 10/23.
10х = 23 х 4.
10х = 92.
х = 92/10.
х = 9,2.
Вопрос 11.
\(\frac{x+1}{2}=\frac{21}{14}\)
Ответ:
x = 135.
Объяснение:
В приведенном выше вопросе
, учитывая, что
\(\frac{x + 1}{2}=\frac{21}{14}\)
x + 12 x 2 = 21 × 14.
2x + 24= 294 .
2x = 294 – 24,
2х = 270.
х = 270/2.
x = 135.
Вопрос 12.
\(\frac{9}{3 x-15}=\frac{3}{12}\)
Ответ:
x = 6,33.
Объяснение:
В приведенном выше вопросе
при условии, что
\(\frac{9}{3 x-15}=\frac{3}{12}\)
27x – 135 = 3×12.
27х = 36 + 135.
27х = 171.
х = 171/27.
х = 6,33.
Вопрос 13.
РЕЗЮМЕ
Свойство произведения квадратных корней позволяет упростить извлечение квадратного корня из произведения. Вы можете упростить квадратный корень из суммы? разницы? Объяснять.
Ответ:
Да, я могу упростить квадратный корень из суммы.
Объяснение:
В приведенном выше вопросе
при условии, что
Свойство произведения квадратных корней позволяет упростить квадратный корень из произведения.
√3 + 1 = √4.
√4 = 4 х 4.
16.
√3 – 1 = √2.
√2 = 2 x 2.
4.
Прямоугольные треугольники и тригонометрия Математические упражнения
Мониторинг прогресса в стандартном положении. Каковы точные координаты его вершин?
Каковы точные координаты его вершин?
Ответ:
Сумма всех углов треугольника = 180°
Если один 30°, а другой равен 90°
180° – 120° = 60°
Вопрос 2.
Используйте программу динамической геометрии для построения прямоугольного треугольника с острый угол 20° и 70° в стандартном положении. Каковы приблизительные координаты его вершин?
Ответ:
Дано,
Используйте программу динамической геометрии для построения прямоугольного треугольника с остроугольными размерами 20° и 70° в стандартном положении.
Вершины A(0,0), B(0,9,0) и C(0.9, 0.3)
9.1 Теорема Пифагора
Исследование 1
Доказательство теоремы Пифагора без слов
Работа с партнером.
а. Начертите и вырежьте прямоугольный треугольник с катетами а и b и гипотенузой с.
Ответ:
В заданном выше вопросе,
при том, что
доказательство теоремы Пифагора без слов.
а 2 + б 2 = в 2.
б. Сделайте три копии вашего прямоугольного треугольника. Расположите все треугольники тура так, чтобы они образовали большой квадрат, как показано на рисунке.
Ответ:
a 2 + b 2 = c 2.
Объяснение:
В приведенном выше вопросе,
учитывая это,
сделайте три копии вашего прямоугольного треугольника.
а 2 + б 2 = в 2.
в. Найдите площадь большого квадрата через a, b и c, суммировав площади треугольников и маленького квадрата.
Ответ:
Площадь большого квадрата = a 2 x b 2.
Объяснение:
В приведенном выше вопросе
учитывая, что
площадь квадрата = l x b.
, где l = длина, а b = ширина.
площадь квадрата = a x b.
площадь = a 2 x b 2.
d. Скопируйте большой квадрат. Разделите его на два меньших квадрата и два прямоугольника одинакового размера, как показано на рисунке.
Ответ:
Разделите квадрат на два прямоугольника одинакового размера с размерами a и b, квадрат размера a и другой квадрат размера b следующим образом:
Искомый квадрат с двумя прямоугольниками одинакового размера размерами a и b, квадратом размера a и другим квадратом размера b.
эл. Найдите площадь большого квадрата через a и b, суммировав площади прямоугольников и меньших квадратов.
Ответ:
Площадь большого квадрата по размерам малых квадратов и прямоугольников равна a² + b² + 2ab
f. Сравните свои ответы к частям (c) и (e). Объясните, как это доказывает теорему Пифагора.
Ответ:
a 2 + b 2 = c 2.
Объяснение:
В приведенном выше вопросе
при условии, что
Длина а и b равна гипотенузе.
a 2 + b 2 = c 2.
где a = одна сторона и b = одна сторона.
Исследование 2
Доказательство теоремы Пифагора
Работа с партнером:
a. Нарисуйте прямоугольный треугольник с катетами а и b и гипотенузой с, как показано на рисунке. Нарисуйте высоту от C до \(\overline{A B}\) Обозначьте длины, как показано.
Нарисуйте прямоугольный треугольник с катетами а и b и гипотенузой с, как показано на рисунке. Нарисуйте высоту от C до \(\overline{A B}\) Обозначьте длины, как показано.
Ответ:
A 2 + B 2 = C 2.
Объяснение:
В вышеуказанном вопросе,
, данный,
A 2 + B
2 = = 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 . 2.
б. Объясните, почему ∆ABC, ∆ACD и ∆CBD похожи.
Ответ:
В прямоугольном треугольнике все углы равны.
Объяснение:
В приведенном выше вопросе
при условии, что
∆ABC, ∆ACD и ∆CBD аналогичны.
В прямоугольном треугольнике все углы равны.
РЕЗЮМЕ
Чтобы хорошо разбираться в математике, нужно знать и гибко использовать различные свойства операций и объектов.
Ответ:
c. Напишите доказательство в два столбца, используя подобные треугольники в части (b), чтобы доказать, что a 2 + b 2 = c 2
Объяснение:
В заданном выше вопросе
при том, что
В теореме Пифагора.
a 2 + b 2 = c 2
длина гипотенузы т.е. равна длинам двух сторон.
a 2 + b 2 = c 2
Сообщите свой ответ
Вопрос 3.
Как вы можете доказать теорему Пифагора?
Ответ:
a 2 + b 2 = c 2
Объяснение:
В приведенном выше вопросе
при этом,
В теореме Пифагора
длина гипотенузы равна длине двух других сторон.
гипотенуза = c.
длина = а.
ширина = b.
a 2 + b 2 = c 2
Вопрос 4.
Воспользуйтесь Интернетом или другим звуковым ресурсом, чтобы найти способ доказать теорему Пифагора, отличный от исследований 1 и 2.
Ответ:
Урок 9.1 Теорема Пифагора
Мониторинг прогресса
Найдите значение x. Затем скажите, образуют ли длины сторон пифагорову тройку.
Вопрос 1.
Ответ:
х = √52.
Объяснение:
В приведенном выше вопросе
при условии, что
длины сторон равны 6 и 4. 36 + 16 = с2
52 = с2.
с = √52.
Вопрос 2.
Ответ:
x = 4.
Объяснение:
В приведенном выше вопросе
при условии, что
длины сторон равны 3 и 5.
х2 + 3 х 3 = 5 х 5.
х2 + 9 = 25. 16.
х = 4.
Вопрос 3.
Анемометр – прибор для измерения скорости ветра. Показанный анемометр прикреплен к вершине столба. Опорные тросы прикреплены к столбу на высоте 5 футов над землей. Каждая опорная проволока имеет длину 6 футов. На каком расстоянии от основания столба каждый провод прикреплен к земле?
Ответ:
х = √11.
Объяснение:
В приведенном выше вопросе
при условии, что
Анемометр – это устройство, используемое для измерения скорости ветра.
опорных тросов прикреплены к столбу на высоте 5 футов над землей.
Каждый поддерживающий трос имеет длину 6 футов.
d2 + 6 x 6 = 5 x 5.
d2 + 36 = 25.
d2 = 25 – 36.
d2 = 11.
d = √11.
Определите, является ли треугольник прямоугольным.
Вопрос 4.
Ответ:
Да, треугольник прямоугольный.
Объяснение:
В приведенном выше вопросе
учитывая, что
гипотенуза = 3 √34.
одна сторона = 15.
другая сторона = 9.
значит треугольник прямоугольный.
Вопрос 5.
Ответ:
Да, треугольник является актуальным треугольником.
Объяснение:
В приведенном выше вопросе
учитывая, что
гипотенуза = 22,
одна сторона = 26,
другая сторона = 14,
, значит треугольник остроугольный.
Вопрос 6.
Убедитесь, что отрезки с длинами 3, 4 и 6 образуют треугольник. Треугольник остроугольный, прямоугольный или тупоугольный?
Ответ:
Да, длины треугольника образуют остроугольный треугольник.
Объяснение:
В приведенном выше вопросе
учитывая, что
длины сторон 3, 4 и 6 образуют треугольник.
6 х 6 = 3 х 3 + 4 х 4.
36 = 9 + 16.
36 = 25.
поэтому длина треугольника образует остроугольный треугольник.
Вопрос 7.
Убедитесь, что отрезки с длинами 2,1, 2,8 и 3,5 образуют треугольник. Треугольник остроугольный, прямоугольный или тупоугольный?
Ответ:
2,1 + 2,8 > 3,5
4,9 > 3,5 > 2,8
5,6 > 2,8 > 2,1
6,3 > 2,1
Поскольку все неравенства верны, отрезки с длинами 2,1, 2,8 и 3,5 образуют треугольник.
Упражнение 9.1 Теорема Пифагора
Словарь и проверка основных понятий
Вопрос 1.
СЛОВАРЬ
Что такое тройка Пифагора?
Ответ:
Вопрос 2.
РАЗНЫЕ СЛОВА, ОДИНАКОВЫЙ ВОПРОС
Что отличается? Найдите «оба» ответа.
Найдите длину большей стороны.
Ответ:
Длина наибольшей стороны = 5.
Объяснение:
В приведенном выше вопросе
учитывая, что
длины сторон равны 3 и 4. равны длинам сторон.
X = 4 x 4 + 3 x 3.
X x X = 16 + 9.
X x X = 25.
X = 5.
Найдите длину гипотенузы
Ответ:
Длина гипотенузы = 5.
Объяснение:
В приведенном выше вопросе
при условии, что
длины сторон равны 3 и 4.
по теореме Пифагора
самая длинная сторона равна длинам сторон.
X = 4 x 4 + 3 x 3.
X x X = 16 + 9.
X x X = 25.
X = 5.
Найдите длину самого длинного участка.
Ответ:
Длина самой длинной стороны = 5.
Объяснение:
В приведенном выше вопросе
учитывая, что
длины сторон равны 3 и 4. равны длинам сторон.
X = 4 x 4 + 3 x 3.
X x X = 16 + 9.
X x X = 25.
X = 5.
Найдите длину стороны, противоположной прямому углу.
Ответ:
Длина стороны, противоположной прямому углу = 5.
Объяснение:
В приведенном выше вопросе
учитывая, что
длины сторон равны 3 и 4.
в пифагорейской треоэме
самая длинная сторона равна длинам сторон.
X = 4 x 4 + 3 x 3.
X x X = 16 + 9.
X x X = 25.
X = 5.
Мониторинг прогресса и моделирование с помощью математики
В упражнениях 3-6 найдите значение х. Затем скажите, образуют ли длины сторон пифагорову тройку.
Вопрос 3.
Ответ:
Вопрос 4.
Ответ:
Длина x = 34.
Объяснение:
В приведенном выше вопросе
учитывая, что
длины сторон равны 30 и 16. равны длинам сторон.
X = 16 x 16 + 30 x 30.
X x X = 256 + 900.
X x X = 1156.
X = 34.
Вопрос 5.
Ответ:
Вопрос 15. 009002 Вопрос 6. 009002 Ответ:
Длина х = 7,2.
Объяснение:
В приведенном выше вопросе
при условии, что
длины сторон равны 6 и 4.
в пифагорейской треоэме
самая длинная сторона равна длинам сторон.
Х = 4 х 4 + 6 х 6.
Х х Х = 16 + 36.
Х х Х = 52.
Х = 7,2.
В упражнениях 7–10 найдите значение x. Затем скажите, образуют ли длины сторон пифагорову тройку.
Вопрос 7.
Ответ:
Вопрос 8.
Ответ:
Длина X = 25,6.
Объяснение:
В приведенном выше вопросе
учитывая, что
длины сторон равны 24 и 9.
в пифагорейской треоэме
самая длинная сторона равна длинам сторон.
Х = 24 х 24 + 9 х 9.
Х х Х = 576 + 81.
Х х Х = 657.
Х = 25,6.
Вопрос 9.
Ответ:
Вопрос 10.
Ответ:
Длина x = 11,4.
Объяснение:
В приведенном выше вопросе,
учитывая, что
длины сторон равны 7 и 9.
в треоэме Пифагора,
самая длинная сторона равна длинам сторон.
Х = 7 х 7 + 9 х 9.
Х х Х = 49 + 81.
Х х Х = 130.
Х = 11,4.
АНАЛИЗ ОШИБОК
В упражнениях 11 и 12 опишите и исправьте ошибку при использовании теоремы Пифагора (теорема 9. 1).
1).
Вопрос 11.
Ответ:
Вопрос 12.
Ответ:
x = 24.
Объяснение:
В приведенном выше вопросе
при условии, что
длины сторон равны 26 и 10.
26 х 26 = а х а + 10 х 10.
676 = а х а + 100.
676 – 100 = а х а.
576 = а х а.
a = 24.
x = 24.
Вопрос 13.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Пожарная лестница образует прямоугольный треугольник, как показано на рисунке. Используйте теорему Пифагора (теорема 9.1), чтобы приблизительно определить расстояние между двумя платформами. (См. пример 3.)
Ответ:
Вопрос 14.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Щит баскетбольного кольца образует с опорными стержнями прямоугольный треугольник, как показано на рисунке. Используйте теорему Пифагора (теорема 9.1), чтобы приблизительно определить расстояние между стержнями, где они соприкасаются со щитом.
Ответ:
х = 9,1.
Объяснение:
В приведенном выше вопросе,
учитывая, что
длины сторон равны 13,4 и 9,8.
13,4 х 13,4 = Х х Х + 9,8 х 9,8.
179,56 = Х х Х + 96,04.
1790,56 – 96,04 = Х х Х.
83,52 = Х х Х.
Х = 9,1.
В упражнениях 15–20 скажите, является ли треугольник прямоугольным.
Вопрос 15.
Ответ:
Вопрос 16.
Ответ:
Нет, треугольник не прямоугольный.
Объяснение:
В приведенном выше вопросе,
учитывая, что
длины сторон равны 23 и 11,4.
гипотенуза = 21,2.
21,2 х 21,2 = 23 х 23 + 11,4 х 11,4.
449,44 = 529 + 1290,96.
449,44 = 658,96.
449 не равно 658,96.
, значит треугольник не прямоугольный.
Вопрос 17.
Ответ:
Вопрос 18.
Ответ:
Нет, треугольник не прямоугольный.
Объяснение:
В заданном выше вопросе
учитывая, что
длины сторон равны 5 и 1.
гипотенуза = √26.
26 х 26 = 5 х 5 + 1 х 1.
676 = 25 + 1.
676 = 26.
676 не равно 26,
значит треугольник не прямоугольный.
Вопрос 19.
Ответ:
Вопрос 20.
Ответ:
Да, треугольник образует прямоугольный.
Объяснение:
В приведенном выше вопросе
учитывая, что
длины сторон равны 80 и 39.
гипотенуза = 89.
89 х 89 = 80 х 80 + 39 х 39.
7921 = 6400 + 1521
7921 = 7921
7921 равно 7921
, поэтому треугольник образует прямоугольный.
В упражнениях 21–28 убедитесь, что длины сегментов образуют треугольник. Треугольник остроугольный, прямоугольный или тупоугольный?
Вопрос 21.
10, 11 и 14
Ответ:
Вопрос 22.
6, 8 и 10
Ответ:
Да, треугольник образует прямоугольный.
Объяснение:
В приведенном выше вопросе
учитывая, что
длины сторон равны 8 и 6.
гипотенуза = 10.
10 х 10 = 8 х 8 + 6 х 6.
100 = 64 + 36
100 = 100.
100 равно 100.
, поэтому треугольник образует прямоугольный.
Вопрос 23.
12, 16 и 20
Ответ:
Вопрос 24.
15, 20 и 36
Ответ:
Да, треугольник тупоугольный.
Объяснение:
В приведенном выше вопросе
учитывая, что
длины сторон равны 15 и 20.
гипотенуза = 36.
36 х 36 = 20 х 20 + 15 х 15.
1296 = 400 + 225
1296 > 625
1296 больше 625,
, поэтому треугольник не является тупоугольным.
Вопрос 25.
5.3, 6.7 и 7.8
Ответ:
Вопрос 26.
4.1, 8.2 и 12.2
Ответ:
Нет, треугольник тупоугольный.
Объяснение:
В приведенном выше вопросе,
учитывая, что
длины сторон равны 4,1 и 8,2.
гипотенуза = 12,2.
12,2 х 12,2 = 4,1 х 4,1 + 8,2 х 8,2`.
148,84 = 16,81 + 67,24.
148,84 > 84,05.
148,84 больше 84,05.
, значит треугольник тупоугольный.
Вопрос 27.
24, 30 и 6√43
Ответ:
Вопрос 28.
10, 15 и 5√13
Ответ:
Да, треугольник остроугольный.
Объяснение:
В заданном выше вопросе
учитывая, что
длины сторон равны 10 и 5√13.
гипотенуза = 15.
15 х 15 = 10 х 10 + 5√13 х 5√13.
225 = 100 + 34,81.
225 < 134,81.
225 меньше 134,81.
, так что треугольник остроугольный.
Вопрос 29.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
В бейсболе длина путей между последовательными базами составляет 90 футов, и пути образуют прямые углы. Игрок на первой базе пытается украсть вторую базу. Какое расстояние должен пройти мяч от домашней площадки до второй базы, чтобы вывести игрока?
Ответ:
Вопрос 30.
ОБОСНОВАНИЕ
Вы делаете подрамник для картины из подрамников. Прямоугольная картина будет иметь длину 10 дюймов и ширину 8 дюймов. Как с помощью линейки убедиться, что углы кадра равны 9?0°
Ответ:
х = 12,8.
Объяснение:
В заданном выше вопросе
учитывая, что
длины сторон равны 10 и 8.
гипотенуза = x.
Х х Х = 10 х 10 + 8 х 8.
Х = 100 + 64.
Х = 12,8.
В упражнениях 31–34 найдите площадь равнобедренного треугольника.
Вопрос 31.
Ответ:
Вопрос 32.
Ответ:
Площадь равнобедренного треугольника = 12 футов.
Объяснение:
В приведенном выше вопросе
, учитывая, что
основание = 32 фута.
гипотенуза = 20 футов.
a 2 + b 2 = c 2
h x h + 16 x 16 = 20 x 20.
h x h + 256 = 400.
h x h = 400 – 5 h x h = 400 – 5 ч 152 152 x
h
значит площадь равнобедренного треугольника = 12 фт.
Объяснение:
В приведенном выше вопросе
при том, что
основание = 28 м.
гипотенуза = 50 м.
A 2 + B 2 = C 2
H x H + 14 x 14 = 50 x 50.
H x H + 196 = 2500.
H x H = 2500 — 196.
H x H = 2304.
H = 48 M. .
значит площадь равнобедренного треугольника = 48м.
Вопрос 35.
АНАЛИЗ ОТНОШЕНИЙ
Обоснуйте формулу расстояния, используя теорему Пифагора (Тон. 9. 1).
Ответ:
Вопрос 36.
КАК ВЫ ЭТО ВИДИТЕ?
Откуда вы знаете, что угол ∠C прямой, не используя теорему Пифагора (теорема 9.1)?
Ответ:
Да, треугольник образует прямоугольный.
Объяснение:
В приведенном выше вопросе
учитывая, что
длины сторон равны 8 и 6.
гипотенуза = 10.
10 х 10 = 8 х 8 + 6 х 6.
100 = 64 + 36 .
100 = 100.
100 равно 100.
, поэтому треугольник образует прямоугольный.
Вопрос 37.
РЕШЕНИЕ ПРОБЛЕМ
Вы делаете воздушного змея и вам нужно выяснить, сколько креплений купить. Вам понадобится крепление по периметру воздушного змея. Переплет поставляется в упаковках по два метра. Сколько пакетов нужно купить?
Сколько пакетов нужно купить?
Ответ:
Вопрос 38.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Используйте теорему Пифагора (теорема 9.1) для доказательства теоремы о сравнении катетов и гипотенуз (HL) (теорема 5.9).
Ответ:
Вопрос 39.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Докажите утверждение, обратное теореме Пифагора (теорема 9.2). (Подсказка: нарисуйте ∆ABC со сторонами a, b и c, где c — длина наибольшей стороны. Затем нарисуйте прямоугольный треугольник со сторонами a, b и x, где x — длина гипотенузы. Сравните длины c и x.)
Ответ:
Вопрос 40.
НАВОДИТ НА МЫСЛИ
Рассмотрим два целых числа m и n. где м > п. Порождают ли следующие выражения пифагорейскую тройку? Если да, то докажите свой ответ. Если нет, приведите контрпример.
2MN, M 2 — N 2 , M 2 + N 2
Ответ:
Вопрос 41.
. тройной, потому что 72 2 + 75 2 не равно квадрату положительного целого числа. Ваш друг прав? Объясните свои рассуждения.
Ваш друг прав? Объясните свои рассуждения.
Ответ:
Вопрос 42.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Скопируйте и завершите доказательство теоремы Пифагора о неравенствах (теорема 9.3) когда с 2 < а 2 + b 2 .
Дано В ∆ABC, c 2 < a 2 + b 2 , где c — длина
самой длинной стороны.
∆PQR имеет длины сторон a, b и x, где x — длина гипотенузы, а ∠R — прямой угол.
Докажите, что треугольник ∆ABC остроугольный.
| Выписки | Причины |
| 1. В ∆ABC C2 < (12 + h3, где c — длина наибольшей стороны. ∆PQR имеет длины сторон a, b и x, где x — длина гипотенузы, и ∠R угол прямой | 1. _____________________________ |
| 2. а 2 + б 2 = х 2 | 2. _____________________________ |
| 3. с 2 < г 2 | 3. _____________________________ _____________________________ |
| 4. с < х | 4. Извлеките положительный квадратный корень из каждой стороны. |
| 5. м ∠ R = 90° | 5. _____________________________ |
| 6. м ∠ С < м ∠ R | 6. Обращение к теореме о шарнирах (теорема 6.13) |
| 7. м ∠ С < 90° | 7. _____________________________ |
| 8. ∠C — острый угол. | 8. _____________________________ |
| 9. ∆ABC — остроугольный треугольник. | 9. _____________________________ |
Ответ:
Вопрос 43.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Докажите теорему Пифагора о неравенствах (теорема 9.3) когда с 2 > а 2 + b 2 . (Подсказка: вернитесь к упражнению 42.)
Ответ:
Поддержание математических навыков
Упростите выражение, рационализировав знаменатель.
Вопрос 44.
\(\frac{7}{\sqrt{2}}\)
Ответ:
7/√2 = 7√2/2.
Объяснение:
В заданном выше вопросе
при условии, что
\(\frac{7}{\sqrt{2}}\) = 7/√2.
7/√2 = 7/√2 x √2 /√2 .
7 √2 /√4.
7√2/2.
Вопрос 45.
\(\frac{14}{\sqrt{3}}\)
Ответ:
Вопрос 46.
\(\frac{8}{\sqrt{2}}\)
Ответ:
8/√2 = 8√2/2.
Объяснение:
В заданном выше вопросе
при условии, что
\(\frac{8}{\sqrt{2}}\) = 8/√2.
8/√2 = 8/√2 х √2 /√2 .
8 √2 /√4.
8√2/2.
Вопрос 47.
\(\frac{12}{\sqrt{3}}\)
Ответ:
9.2 Специальные прямоугольные треугольники
Исследование 1
Соотношения сторон равнобедренного прямоугольного треугольника
Работа с партнером:
а. Используйте программное обеспечение для динамической геометрии, чтобы построить равнобедренный прямоугольный треугольник с длиной катета 4 единицы.
Ответ:
б. Найдите меры острого угла. Объясните, почему этот треугольник называется треугольником 45° – 45° – 90°.
Ответ:
c. Найдите точные отношения длин сторон (используя квадратные корни).
\(\frac{A B}{A C}\) = ____________
\(\frac{A B}{B C}\) = ____________
\(\frac{A B}{B C}\) = ____________
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ
Чтобы хорошо разбираться в математике, вам необходимо выражать числовые ответы с точностью, соответствующей контексту задачи.
Ответ:
d. Повторите части (а) и (с) для нескольких других равнобедренных прямоугольных треугольников. Используйте полученные результаты, чтобы составить гипотезу об отношении длин сторон равнобедренного прямоугольного треугольника.
Ответ:
Разведка 2
Работа с партнером.
а. Используйте программное обеспечение для динамической геометрии, чтобы построить прямоугольный треугольник с острыми углами 30 ° и 60 ° (треугольник 30 ° — 60 ° — 90 °), где длина более короткого катета составляет 3 единицы.
б. Найдите точные отношения длин сторон (используя квадратные корни).
\(\frac{A B}{A C}\) = ____________
\(\frac{A B}{B C}\) = ____________
\(\frac{A B}{B C}\) = ____________
Ответ:
C. Повторите части (a) и (b) для нескольких других треугольников 30° – 60° – 90°. Используйте полученные результаты, чтобы написать гипотезу об отношении длин сторон 30° – 60° – 9треугольник 0°.
Ответ:
Сообщите свой ответ
Вопрос 3.
Как соотносятся длины сторон треугольников с углами 45°- 45° – 90°? Треугольники 30° – 60° – 90°?
Ответ:
Один из треугольников называется треугольниками 45, 45 и 90. Углы треугольника равны 45 градусов, 45 градусов и 90 градусов. Тогда это равнобедренный прямоугольный треугольник.
Другой треугольник — это треугольники 30, 60 и 90. Углы треугольника равны 30 градусов, 60 градусов и 90 градусов.
В обоих треугольниках длина гипотенузы равна квадратному корню из суммы квадратов катетов треугольника.
Урок 9.2 Особые прямоугольные треугольники
Мониторинг прогресса
Найдите значение переменной. Запишите ответ в простейшей форме.
Вопрос 1.
Ответ:
x = 4
Объяснение:
(2√2)² = x² + x²
8 = 2x²
x² = 4
x = 4 05 9 0 9 9 0 9 9 0 9 Вопрос0002 Ответ:
Y = 2
Объяснение:
Y² = 2 + 2
Y² = 4
Y = 2
Вопрос 3.
Ответ:
x = 3, y = 2чина
:
более длинный катет = более короткий катет • √3
x = √3 • √3
x = 3
гипотенуза = более короткий катет • 2
= √3 • 2 = 2√3
Вопрос 4
Ответ:
h = 2 √3
Объяснение:
более длинная сторона = более короткая сторона • √3
h = 2√3
Вопрос 5.
Логотип на мусорном ведре напоминает равносторонний треугольник со стороной 6 сантиметров. Приблизительно площадь логотипа.
Ответ:
Площадь равна \(\frac { 1 }{ 3√3 } \)
Объяснение:
Площадь = \(\frac { √3 }{ 4 } \) a²
= \(\frac { √ 3 }{ 4 } \)(6)²
= \(\frac { 1 }{ 3√3 } \)
Вопрос 6.
Кузов самосвала поднимают, чтобы высыпать песок. На какой высоте находится тело длиной 14 футов от рамы, когда оно наклонено вверх на угол 60°?
Ответ:
Высота 28/3 фута — это тело длиной 14 футов от рамы, когда оно наклонено вверх на угол 60°.
Объяснение:
Высота тела под углом 90 градусов = 14 футов
Высота тела под углом 1 градус = 14/90
Высота тела под углом 60 градусов = 14 x 60/90
= 14 x 2/3
= 28/3 фута
Упражнение 9.2 Особые прямоугольные треугольники
Словарь и проверка основных понятий
Вопрос 1.
СЛОВАРЬ
Назовите два особых прямоугольных треугольника по величине их углов.
Ответ:
Вопрос 2.
ПИСЬМО
Объясните, почему в равнобедренном прямоугольном треугольнике острые углы всегда равны 45°.
Ответ:
Поскольку острые углы прямоугольного равнобедренного треугольника должны быть конгруэнтны по теореме об углах при основании и дополнять друг друга, их меры должны быть равны 90°/2 = 45°.
Мониторинг прогресса и моделирование с помощью математики
В упражнениях 3–6 найдите значение x. Запишите ответ в простейшей форме.
Вопрос 3.
Ответ:
Вопрос 4.
Ответ:
x = 10
Объяснение:
гипотенуза = катет • √2
x = 5√2 • √2
x = 10
Вопрос 5.
Ответ:
Вопрос 6.
Ответ:
x = \(\frac) { 9 }{ √90 }
Объяснение:
гипотенуза = катет • √2
9 = x • √2
x = \(\frac { 9 }{ √2 } \)
В упражнениях 7–10 найдите значения x и y. Запишите ответы в простейшей форме.
Вопрос 7.
Ответ:
Вопрос 8.
Ответ:
x = 3, y = 6
Объяснение:
гипотенуза = 2 • более короткий катет
y = 2 • 3
y = 6
более длинный катет = √3 • более короткий катет
3√3 = √3x
x = 3
Вопрос 9.
Ответ:
Вопрос 10.
Ответ:
x = 18, y = 6√3
Объяснение:
гипотенуза = 2 • более короткое катет более короткая нога
х = √3 . 6√3
6√3
x = 18
АНАЛИЗ ОШИБОК
В упражнениях 11 и 12 опишите и исправьте ошибку при нахождении длины гипотенузы.
Вопрос 11.
Ответ:
Вопрос 12.
Ответ:
гипотенуза = катет • √2 = √5 . √2 = √10
В упражнениях 13 и 14 нарисуйте описанную фигуру. Найдите указанную длину. Округлите десятичные ответы до десятых.
Вопрос 13.
Длина стороны равностороннего треугольника равна 5 сантиметрам. Найдите длину высоты.
Ответ:
Вопрос 14.
Периметр квадрата равен 36 дюймов. Найдите длину диагонали.
Ответ:
Длина диагонали равна 9√2
Объяснение:
Сторона квадрата = 36/4 = 9
Диагональ квадрата = √2a = √2(9) = 9√2
В упражнении 15 и 16, найдите площадь фигуры. Округлите десятичные ответы до десятых.
Вопрос 15.
Ответ:
Вопрос 16.
Ответ:
Площадь 40√(1/3) кв.м. • более короткая ветвь
более короткая ветвь = 4/√3
h² = 16/3 + 16
h² = 16(4/3)
h = 8√(1/3)
Площадь параллелограмма = 5(8√(1/3)) = 40√(1/3) ) кв. м
м
Вопрос 17.
РЕШЕНИЕ ЗАДАЧ
Каждая половина разводного моста имеет длину около 284 футов. На какую высоту поднимется разводной мост, если x=30°? 45°? 60°?
Ответ:
Вопрос 18.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Гайка имеет форму правильного шестиугольника со стороной 1 сантиметр. Найдите значение х. (Подсказка: правильный шестиугольник можно разделить на шесть конгруэнтных треугольников.)
Ответ:
Длина стороны = 1 см
Правильный шестиугольник имеет шесть равных длин сторон. Линия, проведенная из центра в любую вершину, будет иметь ту же длину, что и любая сторона.
Это означает, что радиус равен длине стороны.
В результате, если провести линии от центра к каждой из вершин, говорят, что правильный шестиугольник
состоит из шести равносторонних треугольников.
Из диаграммы x = 2× апофема
Апофема — это расстояние от центра правильного многоугольника до середины стороны.
Используя теорему Пифагора, мы получили бы апофему
Гипотенуза² = противоположная² + соседняя²
1² = апофема² + (½)²
Апофема = √(1² -(½)²)
= √(1-¼) = √¾
Апофема = ½√3
x = 2× Apothem = 2 × ½√3
x = √3
Вопрос 19.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Напишите абзацное доказательство теоремы о треугольнике 45°-45°-90° ( Теорема 9.4).
Дан ∆DEF в виде треугольника с углами 45° – 45° – 90°.
Докажите, что гипотенуза в √2 раза длиннее каждого катета.
Ответ:
Вопрос 20.
КАК ВЫ ЭТО ВИДИТЕ?
На схеме показана часть колеса Феодора.
а. Какие треугольники, если они есть, являются треугольниками 45 ° — 45 ° — 90 °?
Ответ:
Требуется, какие треугольники являются треугольниками 45° – 45° – 90°.
Чтобы определить, какие треугольники являются треугольниками 45° – 45° – 90°.
Треугольник 45° – 45° – 90° является равнобедренным треугольником с двумя равными сторонами.
Выделенный треугольник – треугольник 45° – 45° – 90°.
б. Какие треугольники, если они есть, составляют 30° – 60° – 90° треугольники?
Ответ:
Требуется, какие треугольники являются треугольниками 30° – 60° – 90°.
Треугольник с углами 30° – 60° – 90° – это треугольник, у которого гипотенуза в два раза длиннее короткого катета, а более длинный катет в √3 раза длиннее короткого катета.
На данном рисунке видно, что у третьего треугольника гипотенуза в два раза длиннее короткого катета, а самый длинный катет в √3 раза длиннее самого короткого катета.
Выделенный треугольник – это треугольник 30° – 60° – 90°.
Вопрос 21.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Напишите абзацное доказательство теоремы о треугольнике 30° – 60° – 90° (теорема 9.5).
(Подсказка: постройте ∆JML, конгруэнтную ∆JKL.)
Дан треугольник ∆JKL с углами 30° 60° 9o°.
Докажите, что гипотенуза в два раза длиннее короткого катета, а более длинный катет в √3 раза длиннее короткого катета.
Ответ:
Вопрос 22.
НАВОДИТ НА МЫСЛЬ
Особый прямоугольный треугольник — это прямоугольный треугольник с рациональными размерами углов, длина каждой стороны которого содержит не более одного квадратного корня. Есть только три особых прямоугольных треугольника. Диаграмма ниже называется прямоугольником Эйля. Обозначьте стороны и углы на схеме. Опишите все три специальных прямоугольных треугольника.
Ответ:
Вопрос 23.
ПИСЬМО
Опишите два способа показать, что все равнобедренные прямоугольные треугольники подобны друг другу.
Ответ:
Вопрос 24.
СПОРЫ
Каждый треугольник на диаграмме представляет собой треугольник с углами 45° – 45° – 90°. На этапе 0 каждая сторона треугольника имеет длину 1 единица. Ваш брат утверждает, что длины катетов сложенных треугольников на каждом этапе уменьшаются вдвое. Таким образом, длина катета треугольника, добавленного на этапе 8, будет равна \(\frac{1}{256}\) единице. Ваш брат прав? Объясните свои рассуждения.
Ваш брат прав? Объясните свои рассуждения.
Ответ:
Дано,
Каждый треугольник на диаграмме представляет собой треугольник с углами 45° – 45° – 90°. На этапе 0 каждая сторона треугольника имеет длину 1 единица. Ваш брат утверждает, что длины катетов сложенных треугольников на каждом этапе уменьшаются вдвое. Таким образом, длина катета треугольника, добавленного на этапе 8, будет равна \(\frac{1}{256}\) единице.
На этапе 0: Длины сторон равнобедренного прямоугольного треугольника всегда являются отношением гипотенузы данного равнобедренного прямоугольного треугольника к константе √2.
Стадия 1: Это означает, что прямоугольный равнобедренный треугольник Стадии 0 будет иметь длину стороны, равную 1 единице. Это будут гипотенузы треугольников, образованных на этапе 1, поэтому длины сторон прямоугольных равнобедренных треугольников, образованных на этапе 1, будут равны
1/ √2 = √2/2 единиц.
Стадия 2: Это означает, что прямоугольный равнобедренный треугольник Стадии 1 будет иметь длины сторон, равные √2/2 единицы. Это будут гипотенузы треугольников, образованных на этапе 2, поэтому длины сторон прямоугольных равнобедренных треугольников, образованных на этапе 2, будут √2/2⋅√2 = 1/2 единицы. 98 = 1/16 единиц.
Это будут гипотенузы треугольников, образованных на этапе 2, поэтому длины сторон прямоугольных равнобедренных треугольников, образованных на этапе 2, будут √2/2⋅√2 = 1/2 единицы. 98 = 1/16 единиц.
Следовательно, утверждение брата неверно.
Вопрос 25.
ИСПОЛЬЗОВАНИЕ СТРУКТУРЫ
ΔTUV представляет собой треугольник 30° – 60° – 90°. где две вершины U (3, – 1) и V ( – 3, – 1), \(\overline{U V}\) является гипотенузой. и точка T находится в квадранте I. Найдите координаты точки T.
Ответ:
Поддержание математических знаний
Найдите значение x.
Вопрос 26.
ΔDEF ~ ΔLMN
Ответ:
х = 18
Объяснение:
\(\frac { DE }{LM } \) = \(\frac { DF }{ LN } \)
\(\frac { 12 }{ x } \) = \(\frac { 20 }{ 30 } \)
\ (\ frac { 12 }{ x } \) = \ (\ frac { 2 }{ 3 } \)
x = 12 (\ (\ frac { 3 }{ 2 } \)) = 18
Вопрос 27.
ΔABC ~ ΔQRS
Ответ:
Используйте программное обеспечение для динамической геометрии, чтобы построить правильный ∆ABC, как показано.
 Нарисуйте \(\overline{C D}\) так, чтобы это была высота от прямого угла до гипотенузы ∆ABC.
Нарисуйте \(\overline{C D}\) так, чтобы это была высота от прямого угла до гипотенузы ∆ABC. Ответ:
б. Среднее геометрическое двух положительных чисел a и b — это положительное число x, удовлетворяющее
\(\frac{a}{x}=\frac{x}{b}\)
x — среднее геометрическое a и b.
Напишите пропорцию длин сторон ∆CBD и ∆ACD так, чтобы CD было средним геометрическим двух других длин сторон. Используйте подобные треугольники, чтобы оправдать свои шаги.
Ответ:
c. Используйте пропорцию, которую вы написали в части (b), чтобы найти CD.
Ответ:
d. Обобщите пропорцию, которую вы написали в части (b). Затем напишите гипотезу о том, как среднее геометрическое связано с высотой от прямого угла до гипотенузы прямоугольного треугольника.
ПОСТРОЕНИЕ ЖЕСТКИХ АРГУМЕНТОВ
Чтобы хорошо разбираться в математике, вам необходимо понимать и использовать установленные предположения, определения и ранее установленные результаты при построении аргументов.
Ответ:
Исследование 2
Сравнение средних геометрических и арифметических
Работа с партнером:
Используйте электронную таблицу, чтобы найти среднее арифметическое и среднее геометрическое нескольких пар положительных чисел. Сравните два средства. Что ты заметил?
Ответ:
Формула среднего арифметического = сумма наблюдений/общее количество наблюдений.
Формула для среднего геометрического = квадратный корень из (ab)
Сообщите свой ответ
Вопрос 3.
Как связаны высоты и средние геометрические прямоугольных треугольников?
Ответ:
Теорема о высоте прямоугольного треугольника или теорема о среднем геометрическом является элементарной геометрией, которая связывает высоту на гипотенузе в прямоугольном треугольнике и отрезки из двух прямых. В нем говорится, что среднее геометрическое отрезков равно высоте.
Урок 9.3 Подобные прямоугольные треугольники
Мониторинг прогресса
Определите подобные треугольники.
Question 1.
Answer:
△QRS ~ △ QST
Question 2.
Answer:
△EFG ~ △ EHG
Question 3.
Answer:
△EGH ~ △EFG
\( \ frac { EF }{ EG } \) = \ (\ frac { GF }{ GH } \)
\ (\ frac { 5 }{ 3 } \) = \ (\ frac { 4 }{ x } \)
х = 2,4
Вопрос 4.
Ответ:
△JLM ~ △LMK
\(\frac { JL }{LM } \) = \(\frac { JM }{KM } \)
\(\frac { 13 }{ 5 } \) = \(\frac { 12 }{ x } \)
x = 4,615
Найдите среднее геометрическое двух чисел.
Вопрос 5.
12 и 27
Ответ:
x = √(12 x 27)
x = √324 = 18
Вопрос 6.
18 и 54
x = 31,17
Вопрос 7.
16 и 18
Ответ:
x = √(16 x 18) = √(288)
x = 16,970
Вопрос 8.
Найдите значение x в треугольнике слева.
Ответ:
x = √(9 x 4)
x = 6
Вопрос 9.
ЧТО ЕСЛИ?
В примере 5 расстояние по вертикали от земли до ваших глаз составляет 5,5 футов, а расстояние от вас до стены спортзала — 9 футов. Приблизительно высота стены тренажерного зала.
Приблизительно высота стены тренажерного зала.
Ответ:
9² = 5,5 x w
81 = 5,5 x w
w = 14,72
Высота стены = 14,72 + 5,5 = 20,22
Упражнение 9.3 Подобные прямоугольные треугольники
Проверка словарного запаса и основных понятий
Вопрос 1.
ЗАКОНЧИТЕ ПРЕДЛОЖЕНИЕ
Если высота проведена к гипотенузе прямоугольного треугольника, то два образовавшихся треугольника подобны исходному треугольнику а также ____________ .
Ответ:
Вопрос 2.
ПИСЬМО
Своими словами объясните среднее геометрическое.
Ответ:
Среднее геометрическое — это среднее значение или среднее, которое показывает центральную тенденцию набора чисел путем нахождения произведения их значений.
Мониторинг прогресса и моделирование с помощью математики
В упражнениях 3 и 4 найдите одинаковые треугольники.
Вопрос 3.
Ответ:
Вопрос 4.
Ответ:
△LKM ~ △LMN ~ △MKN
В упражнениях 5–10 найдите значение x.
Вопрос 5.
Ответ:
Вопрос 6.
Ответ:
x = 9,6
Объяснение:
ТС } \)
\(\frac { 20 }{ 16 } \) = \(\frac { 12 }{ x } \)
1,25 = \(\frac { 12 }{ x } \)
x = 9,6
Вопрос 7. Вопрос 8 \(\frac { 16 }{ 34 } \) = \(\frac { x }{ 30 } \)
x = 14,11
Вопрос 9.
Ответ:
Вопрос 10.
Ответ:
х = 2,77
Объяснение:
\(\frac { 5.8 }{ 3.5 } \) = \(\frac { 4.6 }{ x } \)
x = 2,77
В упражнениях 11–18 найдите среднее геометрическое двух чисел .
Вопрос 11.
8 и 32
Ответ:
Вопрос 12.
9 и 16
Ответ:
x = √ (9 x 16)
x = 12
Вопрос 13.
14 и 200015 Ответ. :
Вопрос 14.
25 и 35
Ответ:
х = √(25 х 35)
х = 29,5
Вопрос 15.
16 и 25
Ответ:
Вопрос 16.
8 и 28
Ответ:
x = √ (8 x 28)
x = 14,96
Вопрос 17.
17 и 36
Ответ: Ответ: Ответ: Ответ:.
Вопрос 18.
24 и 45
Ответ:
x = √(24 x 45)
x = 32,86
В упражнениях 19-26 найдите значение переменной.
Вопрос 19.
Ответ:
Вопрос 20.
Ответ:
y = √(5 x 8)
y = √40
y = 2√10
Вопрос 21.
Ответ:
Вопрос 22.
Ответ:
10 • 10 = 25 • x
100 = 25x
x = 4
Вопрос. 23.
Ответ:
Вопрос 24.
Ответ:
B² = 16 (16 + 6)
B² = 16 (22) = 352
B = 18,76
Вопрос 25.
Ответ:
Вопрос 26.
Ответ:
x² = 8(8 + 2)
x² = 8(10) = 80
x = 8,9
АНАЛИЗ ОШИБОК
В упражнениях 27 и 28 опишите и исправьте ошибку при написании уравнения для данной диаграммы.
Вопрос 27.
Ответ:
Вопрос 28.
Ответ:
d² = g • e
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В Упражнении 3s,
Вопрос 29.
Вы хотите определить высоту памятника в местном парке. Вы используете картонный квадрат, чтобы выровнять верх и низ памятника, как показано вверху слева. Ваш друг измеряет вертикальное расстояние от земли до вашего глаза и горизонтальное расстояние от вас до памятника. Примерная высота памятника.
Ответ:
Вопрос 30.
Ваш одноклассник стоит с другой стороны памятника. У нее есть кусок веревки, привязанный к основанию памятника. Она протягивает веревку к картонному квадрату, который она держит, выровненными вверху и внизу памятника. Используйте информацию на диаграмме выше, чтобы примерно определить высоту памятника. Получится ли у вас тот же ответ, что и в упражнении 29? Объясните свои рассуждения.
Ответ:
Высота равна стороне гипотенузы прямоугольного треугольника, образованного картоном и веревками, ведущими к вершине и низу памятника.
Приблизительная высота монумента 14,63 фута.
θ1 = арктан(5,5/7,2) = 37,37
90° = θ1 + θ2
θ2 = 90 – 37,37 = 52,62
тангенс(θ2) = d/7,2
d = 7,2 × тангенс(θ2) × d = 9007,2 d = 9007,2 (52,62)
tan(52,624) = 72/55
d = 7,2 × 72/55 = 9,43
высота памятника, h = d + 5,2
h = 9,43 + 5,2 = 14,63 фута Упражнения 31 – 34. Найдите значение(я) переменной(й).
Найдите значение(я) переменной(й).
Вопрос 31.
Ответ:
Вопрос 32.
Ответ:
\(\frac { 6 }{ b + 3 } \) = \(\frac { 8 }{ 6 } \)
36 = 8(b + 3)
36 = 8b + 24
8b = 12
b = \(\frac { 3 }{ 2 } \)
Вопрос 33.
Ответ:
Вопрос 34.
Ответ:
x = 6, 40, z = 53
Объяснение:
\(\frac { 24 }{ 32 } \) = \(\frac { 32 }{ x } \)
0,75 = \(\frac { 32 }{ x } \)
x = 42,66
y = √24² + 32²
y = √576 + 1024 = 40
z = √42,66² + 32² = √1819,87 + 1024 = 53
Вопрос 35.
ОБОСНОВАНИЕ
Используйте схему. Определите, какие пропорции верны. Выбрать все, что подходит.
(A) \(\frac{D B}{D C}=\frac{D A}{D B}\)
(B) \(\frac{B A}{C B}=\frac{C B}{B D}\ )
(C) \(\frac{C A}{B \Lambda}=\frac{BA}{C A}\)
(D) \(\frac{D B}{B C}=\frac{D A}{B A }\)
Ответ:
Вопрос 36.
АНАЛИЗ ОТНОШЕНИЙ
Вы конструируете воздушного змея в форме ромба. Вы знаете, что AD = 44,8 сантиметра, DC = 72 сантиметра и AC = 84,8 сантиметра. Вы хотите использовать прямую перекладину \(\overline{B D}\). Примерно, как долго это должно быть? Объясните свои рассуждения.
Вы знаете, что AD = 44,8 сантиметра, DC = 72 сантиметра и AC = 84,8 сантиметра. Вы хотите использовать прямую перекладину \(\overline{B D}\). Примерно, как долго это должно быть? Объясните свои рассуждения.
Ответ:
BD = 76,12
Объяснение:
AD = 44,8 см, DC = 72 см и AC = 84,8 см
Две непересекающиеся пары последовательных сторон конгруэнтны.
Итак, AD = AB = 44,8 см
DC = BC = 72 см
Диагонали перпендикулярны.
Итак, AC ⊥ BD
AC = AO + OC
AX = x + y = 84,8 — (i)
Перпендикуляр делит диагональ BD пополам на равные части, пусть это будет z.
BD = BO + OD
BD = z + z
Используя теорему Пифагора
44,8² = x² + z² —- (ii)
72² = y² + z² —– (iii)
Вычесть (ii) и (iii)
72² – 44,8² = y²+ z² – x² – z²
5184 – 2007,04 = (x + y) (x – y)
3176,96 = (84,8)(x – y)
37,464 = x – y — (iv)
Сложить (i) и (iv)
x + y + x – y = 84,8 + 37,464
2x = 122,264
x = 61,132
x + y = 84,8
61. 132 + y = 84,8
132 + y = 84,8
y = 23,668
44,8² = x² + z²
z = 38,06
BD = z + z
BD = 76,12
Вопрос 37.
Analyzing Returezing
Analyzing.
Вопрос 37.
. Теоремы о среднем (теоремы 9.7 и 9.8), чтобы найти AC и BD.
Ответ:
Вопрос 38.
КАК ВЫ ЭТО ВИДИТЕ?
В каком из следующих треугольников применима теорема о среднем геометрическом (высоте) (теорема 9.7)?
(A)
(B)
(C)
(D)
Ответ:
Длина каждого катета прямоугольного треугольника равна среднему геометрическому длин гипотенузы и отрезка гипотенузы которая прилегает к ноге.
CD² = AD × BD
CD/AD = BD/CD
Вариант B — правильный ответ.
Вопрос 39.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Используйте диаграмму ∆ABC. Перепишите и завершите доказательство теоремы Пифагора (теорема 9. 1).
1).
Дано В ∆ABC угол ∆BCA прямой.
Доказать c 2 = a 2 + b 2
| Заявления | Причины |
| 1. В ∆ABC угол ∠BCA прямой. | 1. ________________________________ |
| 2. Проведите перпендикуляр (высоту) от C до \(\overline{A B}\). | 2. Перпендикулярный постулат (постулат 3.2) |
| 3. в.э. = а 2 и ср = b 2 | 3. ________________________________ |
| 4. в.п. + б 2 = ___ + б 2 | 4. Аддитивное свойство равенства |
| 5. в.э + ср = а 2 + б 2 | 5. ________________________________ |
| 6. в(д + е) а 2 + б 2 | 6. ________________________________ |
| 7. е + е = ________ | 7. Постулат сложения сегментов (постулат 1. 2) 2) |
| 8. в • в = а 2 + б 2 | 8. ________________________________ |
| 9. в 2 = а 2 + б 2 | 9. Упрощение. |
Ответ:
Вопрос 40.
СПОРЫ
Ваш друг утверждает, что среднее геометрическое 4 и 9 равно 6, а затем маркирует треугольник, как показано на рисунке. Ваш друг прав? Объясните свои рассуждения.
Ответ:
G.M = √(4 x 9) = √36 = 6
Мой друг прав.
В упражнениях 41 и 42 используйте данные утверждения для доказательства теоремы.
Джин ∆ABC — прямоугольный треугольник.
Высота \(\overline{C D}\) приведена к гипотенузе \(\overline{A B}\).
Вопрос 41.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Докажите теорему о среднем геометрическом (высоте) (теорема 9.7) b, показывающую, что CD 2 = AD • BD.
Ответ:
Вопрос 42.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Докажите теорему о среднем геометрическом (поле) (теорема 9.8) b, показывающую, что CB 2 = DB • AB • AD 2 902 .
Ответ:
CB² = DB x AB
AC² = AD x AB
Доказательство:
Из данного треугольника
Мы знаем, что
CB/DB = AB/CD представляет собой уравнение 1
И
AC/AD = AB/AC представляет собой уравнение 2
Из уравнения 1
CB² = DB x AB
Из уравнения 2
AC² = AD x AB
Отсюда доказано.
Вопрос 43.
КРИТИЧЕСКОЕ МЫШЛЕНИЕ
Начертите прямоугольный равнобедренный треугольник и обозначьте длины двух катетов x. Затем проведите высоту к гипотенузе и обозначьте ее длину у. Теперь, используя теорему о подобия прямоугольных треугольников (теорема 9.6), нарисуйте три подобных треугольника с изображения и обозначьте длину стороны, равную либо x, либо y. Какой вывод вы можете сделать об отношениях между двумя меньшими треугольниками? Объясните свои рассуждения.
Ответ:
Вопрос 44.
НАВОДИТ НА МЫСЛЬ
Показаны среднее арифметическое и среднее геометрическое двух неотрицательных чисел x и y.
среднее арифметическое = \(\frac{x+y}{2}\)
среднее геометрическое = \(\sqrt{x y}\)
Напишите неравенство, связывающее эти два средних. Обосновать ответ.
Ответ:
Неравенство средних арифметических и геометрических. среднее арифметическое неотрицательных действительных чисел больше или равно среднему геометрическому тех же чисел.
Здесь x и y — два неотрицательных числа.
x + y/2 = квадратный корень из (xy) с равенством
Если x = y
Квадрат действительного числа всегда неотрицательный. По биномиальной формуле.
(a + или – b) ² = a² + или – 2ab + b
0 < или = (x – y) ²
= x² – 2xy + y²
= x² + 2xy + y² – 4xy
= (x + y) ² – 4xy
Отсюда (x + y) ² = 4xy с равенством
Когда (x – y) ² = 0, то x = y
Следовательно, AM и GM являются неравенством.
Вопрос 45.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Докажите теорему о подобии прямоугольного треугольника (теорему 9.6), доказав три утверждения о подобии.
Дан ∆ABC — прямоугольный треугольник.
Высота \(\overline{C D}\) обращается к hvpotenuse \(\overline{A B}\).
Докажите ∆CBD ~ ∆ABC, ∆ACD ~ ∆ABC,
∆CBD ~ ∆ACD
Ответ:
Поддержание математических способностей
Решите уравнение для x.
Вопрос 46.
13 = \(\frac{x}{5}\)
Ответ:
13 = \(\frac{x}{5}\)
x = 65
Вопрос 47.
29 = \(\frac{x}{4}\)
Ответ:
Вопрос 48.
9 = \(\frac{78}{x}\)
Ответ:
9 = \(\frac{78}{x}\)
9x = 78
x = 8,6
Вопрос 49.
30 = \( \frac{115}{x}\)
Ответ:
Тест с 9.1 по 9.3
Найдите значение x. Скажите, образуют ли длины сторон пифагорову тройку.
Вопрос 1.
Ответ:
х = 15
Объяснение:
x² = 9² + 12²
x² = 81 + 144
x² = 225
x = 15
Вопрос 2.
Ответ:
x = 10,63
Объяснение:
x² = 7b + 8m = 49 +
. 64
x = √113
x = 10,63
Вопрос 3.
Ответ:
x = 4√3
Объяснение:
8² = x² + 4²
64 = X² + 16
x = 48
x = 400. 3
Убедитесь, что длины сегментов образуют треугольник. Треугольник остроугольный, прямоугольный или тупоугольный?
(Раздел 9.1)
Вопрос 4.
24, 32 и 40
Ответ:
Треугольник – прямоугольный треугольник.
Объяснение:
40² = 1600
24² + 32² = 576 + 1024 = 1600
40² = 24² + 32²
Итак, треугольник является прямоугольным треугольником.
Вопрос 5.
7, 9 и 13
Ответ:
Треугольник тупоугольный.
Объяснение:
13² = 169
7² + 9² = 49 + 81 = 130
13² > 7² + 9²
Итак, треугольник является тупоугольным треугольником.
Вопрос 6.
12, 15 и 10√3
Ответ:
Треугольник остроугольный.
Объяснение:
15² = 225
12² + (10√3)² = 144 + 300 = 444
15² < 12² + (10√3)²
Итак, треугольник остроугольный.
Найдите значения x и y. Запишите свои ответы в простейшей форме. Вопрос 70002 Вопрос 8.
Ответ:
y = 8√3, x = 16
Объяснение:
более длинный участок = более короткий участок • √3
y = 8√3
x² = 8² + (8√3)² = 64 + 192
x = 16
Вопрос 9.
Ответ:
x = 5√2, y = 5√6
Объяснение:
более длинный участок = более короткий участок • √3
y = x015 9 = 5√6
гипотенуза = более короткий катет • 2
10√2 = 2x
x = 5√2
Найдите среднее геометрическое двух чисел.
Вопрос 10.
6 и 12 9Вопрос 11 и 26
Ответ:
G.M = √(18 • 26) = 6√13
Найдите подобные прямоугольные треугольники. Затем найдите значение переменной.
Вопрос 13.
Ответ:
x = √(8 • 4)
x = 4√2
Вопрос 14.
Ответ:
y = 005 √(9 √ 2006) Вопрос 15.
Ответ:
Учитывая, что
a = 12
b = 18
Формула для среднего геометрического: y = квадратный корень из (a x b)
y = квадратный корень из (12 x 18)
y = квадратный корень из (216)
y = 62,353
Вопрос 16.
Размеры телевизоров измеряются длиной их диагонали. Вы хотите купить телевизор диагональю не менее 40 дюймов. Стоит ли покупать показанный телевизор? Объясните свои рассуждения.
Ответ:
x² = 20,25² + 36²
x² = 410,0625 + 1296 = 1706,0625
x = 41,30
Да, я куплю телевизор.
Вопрос 17.
Каждый треугольник, показанный ниже, является прямоугольным.
а. Являются ли треугольники особыми прямоугольными? Объясните свои рассуждения.
Ответ:
A — подобный треугольник.
б. Перечислите все подобные треугольники. если есть.
Ответ:
B, C и D, E — подобные треугольники.
в. Найдите длины высот треугольников B и C.
Ответ:
Высота B = √(9 + 27) = 6
Высота C = √(36 + 72) = 6√3
9.4 Отношение касательной
Разведка 1
Расчет отношения касательной
2
а. Постройте ∆ABC, как показано на рисунке. Постройте сегменты, перпендикулярные \(\overline{A C}\), чтобы сформировать прямоугольные треугольники, которые имеют общую вершину A и дугу, подобную ∆ABC с вершинами, как показано.
Ответ:
б. Рассчитайте каждое заданное отношение, чтобы заполнить таблицу десятичных значений тангенса А для каждого прямоугольного треугольника. Что вы можете сделать вывод?
Ответ:
Разведка 2
Использование калькулятора
Работа с партнером: Используйте калькулятор с ключом тангенса для вычисления тангенса 36,87°. Вы получаете тот же результат, что и в Exploration 1? Объяснять.
ВНИМАНИЕ К ТОЧНОСТИ
Чтобы хорошо разбираться в математике, вам необходимо выражать числовые ответы с точностью, соответствующей контексту задачи.
Ответ:
Сообщите свой ответ
Вопрос 3.
Повторить исследование 1 для ∆ABC с вершинами A(0, 0), B(8, 5) и C(8, 0). Постройте семь перпендикулярных отрезков так, чтобы не все они пересекались \(\overline{A C}\) при целых значениях x. Обсудите свои результаты.
Ответ:
Вопрос 4.
Как с помощью прямоугольного треугольника найти тангенс острого угла? Существует ли единственный прямоугольный треугольник, который необходимо использовать?
Ответ:
По прямоугольному треугольнику можно определить тангенс любого острого угла, взяв отношение длины стороны, противолежащей углу, к длине стороны, прилегающей к острому углу.
Из любого прямоугольного треугольника можно определить тангенс острых углов на нем.
Урок 9.4 Отношение тангенса
Мониторинг прогресса
Найдите тангенс J и тангенс K. Запишите каждый ответ в виде дроби и десятичного числа, округленного до четырех знаков.
Вопрос 1.
Ответ:
tan K = \(\frac { противоположная сторона }{ смежная сторона } \) = \(\frac { JL }{ KL } \)
= \(\frac { 32 } { 24 } \) = \(\frac { 4 }{ 3 } \) = 1,33
tan J = \(\frac { KL }{ JL } \) = \(\ frac { 24 }{ 32 } \) = \ (\ гидроразрыва {3} {4} \) = 0,75
Вопрос 2.
Ответ:
tan K = \(\frac { LJ }{ LK } \) = \(\frac { 15 }{ 8 } \)
tan J = \(\frac { LK } { LJ } \) = \(\frac { 8 }{ 15 } \)
Найдите значение x. Округлите ответ до десятых.
Вопрос 3.
Ответ:
Tan 61 = \(\frac { 22 }{ x } \)
1,804 = \(\frac { 22 }{ x } \)
x = 12,1951
Вопрос 4.
Ответ:
tan 56 = \(\frac { x }{ 13 } \)
1,482 = \(\ frac { x }{ 13 } \)
x = 19,266
Вопрос 5.
ЧТО ЕСЛИ?
В примере 3 длина более короткого катета равна 5 вместо 1. Покажите, что тангенс угла 60° по-прежнему равен √3.
Ответ:
более длинный участок = более короткий участок • √3
= 5√3
tan 60 = \(\frac { 5√3 }{ 5 } \)
= √3
Вопрос 6.
Вы измеряете высота фонарного столба. Вы стоите в 40 дюймах от основания фонарного столба. Вы измеряете угол возвышения от земли до вершины фонарного столба и он равен 70°. Найдите высоту h фонарного столба с точностью до дюйма.
Ответ:
tan 70 = \(\frac { h }{ 40 } \)
2,7474 = \(\frac { h }{ 40 } \)
h = 109,896 в
Упражнение 9.4 Тангенсное отношение
Проверка словарного запаса и основных понятий
Вопрос 1.
ЗАВЕРШИТЕ ПРЕДЛОЖЕНИЕ
Отношение тангенсов сравнивает длину _________ с длиной ___________ .
Ответ:
Вопрос 2.
ПИСЬМО
Объясните, откуда вы знаете, что отношение тангенса является постоянным для данного измерения угла.
Ответ:
Когда два треугольника подобны, соответствующие стороны пропорциональны, что делает отношение постоянным для данного измерения острого угла.
Мониторинг прогресса и моделирование с помощью математики
В упражнениях 3–6 найдите тангенсы острых углов прямоугольного треугольника. Запишите каждый ответ в виде дроби и десятичной дроби, округленной до четырех знаков после запятой.
Вопрос 3.
Ответ:
Вопрос 4.
Ответ:
тангенс F = \(\frac { DE }{ EF } \) = \(\frac { 24 }{ 7 } \)
tan D = \(\frac { EF }{ DE } \) = \(\ frac { 7 }{ 24 } \)
Вопрос 5.
Ответ:
Вопрос 6.
Ответ:
tan K = \(\frac { JL }{ LK } \) = \(\frac { 3 }{ 5 } \)
tan J = \(\frac { LK }{ JL } \) = \(\frac { 5 }{ 3 } \)
В упражнениях 7–10 найдите значение x. Округлите ответ до десятых.
Вопрос 7.
Ответ:
Вопрос 8.
Ответ:
tan 27 = \(\frac { x }{ 15 } \)
0,509 = \(\frac { x }{ 15 } \)
x = 7,635
Вопрос 9.
Ответ:
Вопрос №10
АНАЛИЗ ОШИБОК
В упражнениях 11 и 12 опишите ошибку в выражении касательного отношения. Исправьте ошибку, если это возможно. В противном случае написать невозможно.
Вопрос 11.
ОТВЕТ:
Вопрос 12.
Ответ:
,
♂ = 30
♂ = 55
♂ + потряно 55 = 180
∠B = 180 – 85 = 95°
Подставляя значения в приведенное ниже уравнение
∠B ≠ 90°, треугольник не является прямоугольным.
tan55 = 18/11.0 невозможно.
Следовательно, треугольник ΔABC не является прямоугольным.
В упражнениях 13 и 14 используйте специальный прямоугольный треугольник, чтобы найти тангенс данной меры угла.
Вопрос 13.
45°
Ответ:
Вопрос 14.
30°
Ответ:
tan 30° = \(\frac { 1 }{ √3 } \)
5 105 90.090 Вопрос 1 С МАТЕМАТИКОЙ
Геодезист стоит в 118 футах от основания монумента Вашингтона. Геодезист измеряет угол возвышения от земли до вершины памятника и составляет 78°. Найдите высоту h монумента Вашингтона с точностью до фута.
Найдите высоту h монумента Вашингтона с точностью до фута.
Ответ:
Вопрос 16.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Ученые могут измерить глубину лунных кратеров h, глядя на фотографии теней. Длина тени, отбрасываемой краем кратера, составляет 500 метров. Угол подъема лучей Солнца 55°. Оцените глубину d кратера.
Ответ:
tan 55 = \(\frac { d }{ 500 } \)
1,428 = \(\frac { d }{ 500 } \)
d = 714 м
Глубина кратера 714 м
Вопрос 17.
ИСПОЛЬЗУЯ СТРУКТУРУ
Найдите тангенс меньшего острого угла в прямоугольном треугольнике со сторонами 5, 12 и 13.
Ответ:
Вопрос 18. угла в прямоугольном треугольнике с длинами сторон 3, 4 и 5.
Ответ:
tan x = \(\frac { 4 }{ 3 } \)
Вопрос 19.
ОБОСНОВАНИЕ
острый угол в прямоугольном треугольнике изменяется при увеличении меры угла? Обосновать ответ.
Ответ:
Вопрос 20.
КРИТИЧЕСКОЕ МЫШЛЕНИЕ
Для каких угловых мер тангенс острого угла в прямоугольном треугольнике равен 1? больше 1? меньше 1? Обосновать ответ.
Ответ:
Чтобы тангенс угла был равен 1, противоположная и прилежащая стороны прямоугольного треугольника должны быть одинаковыми. Это означает, что прямоугольный треугольник является равнобедренным прямоугольным треугольником, поэтому углы равны 45–45–90. Острый угол должен быть равен 1. Чтобы тангенс был больше 1, противоположная сторона должна быть больше, чем прилежащая сторона. Это означает, что угол должен быть между 45 и 90 градусов. Если тангенс меньше 1, это означает, что противоположная сторона должна быть меньше, чем прилежащая сторона. Острый угол должен быть между 0 и 45.
Вопрос 21.
СПОРЫ
В вашей гостиной есть раздвижная стеклянная дверь. Вы хотите купить навес для двери, длина которого будет достаточной, чтобы не пускать внутрь солнце, когда оно находится в самой высокой точке неба. Угол подъема лучей Солнца в этих точках равен 70°, а высота двери 8 футов. Ваша сестра утверждает, что вы можете определить, как далеко должен простираться выступ, умножив 8 на tan 70°. Ваша сестра права? Объяснять.
Угол подъема лучей Солнца в этих точках равен 70°, а высота двери 8 футов. Ваша сестра утверждает, что вы можете определить, как далеко должен простираться выступ, умножив 8 на tan 70°. Ваша сестра права? Объяснять.
Ответ:
Вопрос 22.
КАК ВЫ ЭТО ВИДИТЕ?
Напишите выражение для тангенса каждого острого угла прямоугольного треугольника. Объясните, как тангенс одного острого угла связан с тангенсом другого острого угла. Какой парой углов являются ∠A и ∠B?
Ответ:
tan A = \(\frac {BC }{AC} \) = \(\frac {a}{b} \)
tan B = \(\frac {AC}{BC} \) = \(\frac { b }{ a } \)
Вопрос 23.
ОБОСНОВАНИЕ
Объясните, почему невозможно найти тангенс прямого или тупого угла.
Ответ:
Вопрос 24.
НАВОДИТ НА МЫСЛИ
Чтобы создать диаграмму ниже. вы начинаете с равнобедренного прямоугольного треугольника с катетом длиной 1 единица. Тогда гипотенуза первого треугольника становится катетом второго треугольника, длина оставшегося катета которого равна 1 единице. Продолжайте диаграмму, пока не построите угол, тангенс которого равен \(\frac{1}{\sqrt{6}}\). Приблизительно оцените величину этого угла.
Продолжайте диаграмму, пока не построите угол, тангенс которого равен \(\frac{1}{\sqrt{6}}\). Приблизительно оцените величину этого угла.
Ответ:
Вопрос 25.
РЕШЕНИЕ ЗАДАЧ
Ваш класс фотографируется на лужайке. Фотограф находится в 14 футах от центра класса. Фотограф поворачивается на 50°, чтобы посмотреть в оба конца класса.
а. Какое расстояние между концами класса?
б. Фотограф поворачивается еще на 10° в любую сторону, чтобы увидеть конец диапазона камеры. Если каждому студенту нужно 2 фута пространства. сколько еще учеников может поместиться в конце каждого ряда? Объяснять.
Ответ:
Вопрос 26.
РЕШЕНИЕ ЗАДАЧИ
Найдите периметр фигуры. где AC = 26, AD = BF и D — середина \(\overline{A C}\).
Ответ:
AC = 26
AD = BF
D = середина AC
AD = CD = 26/2 = 13
AE = AD/sin(50) = 13/sin(50) = 17
ED = AD/tan50 = 13/tan50 = 10,9
AB = AC × tan35 = 26 × tan(35) = 18,2
18,2/26 = 13/GF. GF = 13 × 26/18,2 = 18,6
GF = 13 × 26/18,2 = 18,6
GF = HF = 18,6 подобными треугольниками
BG = BH = 22,7
BC = √(26² + 18,2²) = 31,7
GC = BC – BG
GC = 31,7 – 22,7 = 9
Периметр = AE + AB + BH + HF + GF + GC + CD
P = 17 + 18,2 + 22,7 + 18,6 + 18,6 + 9 + 13 = 117,1
Итак, периметр фигуры равен 117,1
Поддержание математических способностей
Найдите значение x.
Вопрос 27.
Ответ:
Вопрос 28.
Ответ:
длинная сторона = короткая сторона
x = 4,04
Вопрос 29.
Ответ:
9.5 Соотношения синусов и косинусов
Исследование 1
Работа с партнером: Используйте программу динамической геометрии.
а. Постройте ∆ABC, как показано на рисунке. Постройте сегменты, перпендикулярные \(\overline{A C}\), чтобы сформировать прямоугольные треугольники, которые имеют общую вершину A и подобны ∆ABC с вершинами, как показано.
Ответ:
б. Вычислите каждое заданное отношение, чтобы заполнить таблицу десятичных значений sin A и cos A для каждого прямоугольного треугольника. Какой вывод вы можете сделать?
Вычислите каждое заданное отношение, чтобы заполнить таблицу десятичных значений sin A и cos A для каждого прямоугольного треугольника. Какой вывод вы можете сделать?
Ответ:
Сообщите свой ответ
Вопрос 2.
Как с помощью прямоугольного треугольника найти синус и косинус острого угла? Существует ли единственный прямоугольный треугольник, который необходимо использовать?
Ответ:
Предположим, что острые углы прямоугольного треугольника прибавлены к 90 градусам.
Мы знаем, что острые углы дополняют друг друга. любой острый угол равен косинусу своего дополнения.
Косинус любого острого угла равен синусу его дополнения.
Вопрос 3.
В Исследовании 1, какова связь между ∠A и ∠B с точки зрения их показателей? Найдите sin B и cos B. Как эти два значения связаны с sin A и cos A? Объясните, почему существуют эти отношения.
В ПОИСКАХ СТРУКТУРЫ
Чтобы хорошо разбираться в математике, вам нужно внимательно присматриваться, чтобы распознать закономерность или структуру.
Ответ:
Урок 9.5 Отношения синуса и косинуса
Мониторинг прогресса
Вопрос 1.
Найдите sin D, sin F, cos D и cos F. Запишите каждый ответ в виде дроби и десятичного числа, округленного до четырех знаков.
Ответ:
sin D = \(\frac { 7 }{ 25 } \)
sin F = \(\frac { 24 }{ 25 } \)
cos D = \(\frac { 24 }{ 25 } \)
cos F = \(\frac { 7 }{ 25 } \)
Объяснение:
sin D = \(\frac { EF }{ DF } \) = \(\frac { 7 }{ 25 } \ )
sin F = \(\frac { DE }{ DF } \) = \(\frac { 24 }{ 25 } \)
cos D = \(\frac { DE }{DF } \) = \(\frac { 24 }{ 25 } \)
cos F = \(\frac {EF }{DF } \) = \(\frac { 7 }{ 25 } \)
Вопрос 2.
Запишите косинус 23° через синус.
Ответ:
cos X = sin(90 – X)
cos 23° = sin (90 – 23)
= sin(67)
Итак, cos 23° = sin 67°
Вопрос 3.
Найдите значения u и t с использованием синуса и косинуса. Округлите свои ответы до десятых.
Ответ:
t = 7,2, u = 3,3
Объяснение:
sin 65 = \(\frac { t }{ 8 } \)
0,906 = \(\ frac { t }{ 8 } \)
t = 7,2
cos 65 = \(\ frac { u }{ 8 } \ )
0,422 x 8 = u
u = 3,3
Вопрос 4.
Найдите синус и косинус угла 60°.
Ответ:
sin 60° = \(\frac { √3 }{ 2 } \)
cos 60° = \(\frac { 1 }{ 2 } \)
Вопрос 5.
ЧТО ЕСЛИ?
В примере 6 угол наклона составляет 28°. Найдите расстояние x, на которое вы спускаетесь с горы до ближайшего фута.
Ответ:
sin 28° = \(\frac { 1200 }{ x } \)
x = \(\frac { 1200 }{ 0,469 } \)
x = 2558,6
Упражнение 9.5 Отношения синуса и косинуса
Проверка словарного запаса и основных понятий
Вопрос 1.
СЛОВАРЬ
Синусоида сравнивает длину ______________ с длиной _____________
Ответ:
Вопрос 2.
Какое соотношение не относится к остальным трем? Объясните свои рассуждения.
sin B
Ответ:
sin B = \(\frac { AC }{ BC } \)
cos C
Ответ:
cos C = \(\ frac { AC }{ BC } \)
tan B
Ответ:
tan B = \(\frac { AC }{ AB } \)
\(\ гидроразрыва {А С} {В С} \)
Ответ:
\(\frac{A C}{B C}\) = sin B
Мониторинг прогресса и моделирование с помощью математики
В упражнениях 3–8 найдите sin D, sin E, cos D и cos E. Запишите каждый ответ в виде дроби и десятичной дроби, округленной до четырех знаков.
Запишите каждый ответ в виде дроби и десятичной дроби, округленной до четырех знаков.
Вопрос 3.
Ответ:
Вопрос 4.
Ответ:
sin D = \(\frac { 35 }{ 37 } \)
sin E = \(\frac { 12 }{ 37 } \)
cos D = \(\frac { 12 }{ 37 } \)
cos E = \(\frac { 35 }{ 37 } \)
Вопрос 5.
Ответ:
Вопрос 6.
Ответ:
sin D = \(\frac { 36 }{ 45 } \)
sin E = \(\frac { 27 }{ 45 } \)
cos D = \(\frac { 27 }{ 45 } \)
потому что E = \(\frac { 36 }{ 45 } \)
Вопрос 7.
Ответ:
Вопрос 8.
Ответ:
sin D = \(\frac { 8 }{ 17 } \)
sin E = \(\frac { 15 }{ 17 } \)
cos D = \(\frac { 15 }{ 17 } \)
cos E = \(\frac { 8 }{ 17 } \)
В упражнениях 9 – 12 запишите выражение через косинус.
Вопрос 9.
sin 37°
Ответ:
Вопрос 10.
sin 81°
Ответ:
sin 81° = cos(90° – 81°) = cos9°
Ответ:
Вопрос 12.
sin 64°
Ответ:
sin 64° = cos(90° – 64°) = cos 26°
В упражнении 13 – 16 запишите выражение в виде условия синуса.
Вопрос 13.
cos 59°
Ответ:
Вопрос 14.
cos 42°
Ответ:
cos 42° = sin(90° – 42°) = sin 48°
2 900. Вопросы 73°
Ответ:
Вопрос 16.
cos 18°
Ответ:
cos 18° = sin(90° – 18°) = sin 72°
В упражнениях 17 – 22 найдите значение каждой переменной, используя синус и косинус. Округлите свои ответы до десятых.
Вопрос 17.
Ответ:
Вопрос 18.
Ответ:
р = 30,5, q = 14,8 p = 0,898 x 34
p = 30,5
cos 64° = \(\frac { q }{ 34 } \)
q = 0,4383 x 34
q = 14,8
Вопрос 19.
Ответ:
Вопрос 20.
Ответ:
s = 17,7, r = 19
Объяснение:
sin 43° = \(\frac { s}{26 } \)
s = 0,681 x 15 26 9
cos 43° = \(\frac { r }{ 26 } \)
r = 0,731 x 26
r = 19
Вопрос 21.
Ответ:
Ответ 22.5
5 6.7, n = 10,44
Объяснение:
sin 50° = \(\frac {8}{n} \)
0,766 = \(\frac {8}{n} \)
n = 10,44
cos 50° = \(\frac { m }{ n } \)
0,642 = \(\frac { m }{ 10,44 } \)
m = 6,7
Вопрос 23.
ОБОСНОВАНИЕ
Какие отношения равны ? Выбрать все, что подходит. Вопрос 24
sin L
Ответ:
sin L = \(\frac { 2 }{ 4 } \) = \(\frac { 1 }{ 2 } \)
cos L
Ответ:
cos L = \(\frac { 2√3 }{ 4 } \) = \(\frac { √3 }{ 2 } \)
sin J
Ответ:
sin J = \(\frac { 2 √3 }{ 4 } \) = \(\ frac { √3 }{ 2 } \)
cos J
Ответ:
cos J = \(\ frac { 2 }{ 4 } \) = \(\frac { 1 }{ 2 } \)
Вопрос 25.
АНАЛИЗ ОШИБОК
Опишите и исправьте ошибку в нахождении sin A.
Ответ:
Вопрос 26.
ПИСЬМО
Объясните, как определить, какая сторона прямоугольного треугольника прилегает к углу, а какая — гипотенузе.

Ответ:
AB примыкает к ∠A, потому что, если мы не рассматриваем гипотенузу, это единственный отрезок, связанный с углом.
Отрезок, противолежащий прямому углу, называется гипотенузой.
Последний сегмент AC называется противоположным, потому что он противоположен углу a.
Вопрос 27.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Верх горки находится на высоте 12 футов от земли и имеет угол наклона 53°. Какова длина слайда?
Ответ:
Вопрос 28.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Найдите расстояние по горизонтали, умноженное на длину эскалатора.
Ответ:
cos 41 = \(\frac { x }{ 26 } \)
0,754 = \(\frac { x }{ 26 } \)
x = 19,6 футов
Вопрос 29.
РЕШЕНИЕ ЗАДАЧИ
Вы запускаете воздушного змея с натянутой на 20 футов веревкой. Угол подъема от катушки тетивы до воздушного змея составляет 67°.
а. Нарисуйте и подпишите схему, иллюстрирующую ситуацию.
б. На каком расстоянии от земли находится кайт, если вы держите катушку на расстоянии 5 футов от земли? Опишите, как высота, на которой вы держите катушку, влияет на высоту кайта.
Ответ:
Вопрос 30.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Самолеты, которые летают на больших скоростях и на малых высотах, имеют кормовые радары, которые могут определять расстояние до препятствия и угол возвышения до вершины препятствия. Радар самолета, летящего на высоте 20 000 футов, обнаруживает башню, которая находится на расстоянии 25 000 футов. с углом подъема 1°
а. На сколько метров должен подняться самолет, чтобы пролететь над башней?
Ответ:
sin 1 = \(\frac { h }{ 25000 } \)
0,017 = \(\frac { h }{ 25000 } \)
h = 425 футов
425 футов высота подъема самолета для прохождения над башня
б. PIanes Caillot подходит к любому объекту ближе, чем на 1000 футов по вертикали. На какой высоте должен лететь самолет, чтобы пролететь над башней?
Ответ:
Если самолет в настоящее время летит на высоте 20 000 футов, ему нужно подняться примерно на 436 футов над вершиной башни и еще на 1000 футов, чтобы следовать правилам безопасности, что составляет требуемые 20 000 + 1000 + 436 = 21 436 футов.
Вопрос 31.
СПОРЫ
Ваш друг использует уравнение sin 49° = \(\frac{x}{16}\) для нахождения BC. Ваш двоюродный брат использует уравнение cos 41° = \(\frac{x}{16}\), чтобы найти BC. Кто прав? Объясните свои рассуждения.
Ответ:
Вопрос 32.
ПИСЬМО
Опишите, что вы должны знать о треугольнике, чтобы использовать коэффициент синуса, и что вы должны знать о треугольнике, чтобы использовать коэффициент косинуса
Ответ:
sin = \(\frac { противолежащая сторона }{ гипотенуза } \)
cos = \(\frac { смежная сторона }{ гипотенуза } \)
Вопрос 33.
МАТЕМАТИЧЕСКИЕ СОЕДИНЕНИЯ
Если ∆EQU равностороннее и ∆ RGT – прямоугольный треугольник с RG = 2, RT = 1 и m ∠ T = 90°, покажите, что sin E = cos G.
Ответ:
Вопрос 34.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
На подводных лодках используются гидроакустические системы , которые похожи на радарные системы, для обнаружения препятствий, системы Sonar используют звук для обнаружения объектов под водой.
а. Вы путешествуете под водой на подводной лодке. Гидроакустическая система обнаруживает айсберг на высоте 4000 метров с углом падения 34° на дно айсберга. На сколько метров должна опуститься подводная лодка, чтобы пройти под айсбергом?
Ответ:
tan 34 = \(\frac { x }{ 4000 } \)
.674 = \(\frac { x }{ 4000 } \)
x = 2696
b. Затем гидроакустическая система обнаруживает затонувший корабль на расстоянии 1500 метров впереди. с углом возвышения 19° к самой высокой части затонувшего корабля. На сколько метров должна подняться подводная лодка, чтобы пройти над затонувшим кораблем?
Ответ:
tan 19 = \(\frac { x }{ 1500 } \)
0,344 = \(\frac { x }{ 1500 } \)
x = 516 м
Вопрос 35.
РЕЗЮМЕ
Сделайте предположение о том, как можно использовать тригонометрические отношения для нахождения углов в треугольнике.
Ответ:
Вопрос 36.
КАК ВЫ ЭТО ВИДИТЕ?
Используя только данную информацию, вы бы использовали соотношение синуса или косинуса, чтобы найти длину гипотенузы? Объясните свои рассуждения.
Ответ:
sin 29 = \(\frac { 9 }{ x } \)
0,48 = \(\frac { 9 }{ x } \)
x = 18,75
Длина гипотенузы равна 18,75
Вопрос 37.
НЕСКОЛЬКО ПРЕДСТАВЛЕНИЙ
Вы стоите на скале над океаном. Вы видите парусник со своего наблюдательного пункта на высоте 30 футов над океаном.
а. Нарисуйте и обозначьте схему ситуации.
б. Составьте таблицу, показывающую угол наклона и длину линии визирования. Используйте углы 40°, 50°, 60°, 70° и 80°.
с. Нанесите на график значения, которые вы нашли в части (b), с мерами угла по оси X.
д. Предсказать длину линии визирования при угле наклона 30°.
Ответ:
Вопрос 38.
НАВОДИТ НА МЫСЛЬ
Один из следующих бесконечных рядов представляет sin x, а другой представляет cos x (где x измеряется в радианах). Какой какой? Обосновать ответ. Затем используйте каждую серию для аппроксимации синуса и косинуса \(\frac{\pi}{6}\).
(Подсказка: π = 180°; 5! = 5 • 4 • 3 • 2 • 1; Найдите значения, к которым приближаются отношения синуса и косинуса, когда мера угла приближается к нулю).
а.
Ответ:
Для x = 0
0 – \(\frac { 0³ }{ 3! } \) + \(\frac { 0⁵ }{ 5! } \) – \(\frac { 0⁷ }{ 7 !} \) + . . . = 0
sin x = x – \(\frac { x³ }{ 3! } \) + \(\ frac { x⁵ }{ 5! } \) – \(\ frac { x⁷ }{ 7! } \) + . . .
sin \(\frac {π}{6} \) = 0,5
б.
Ответ:
1 – \(\frac { 1² }{ 2! } \) + \(\frac { 1⁴ }{ 4! } \) – \(\frac { 1⁶ }{ 6! } \) + . . = 1
cos x =x1 – \(\frac { x² }{ 2! } \) + \(\frac { x⁴ }{ 4! } \) – \(\ frac { x⁶ }{ 6! } \) + . .
cos \(\frac { π }{ 6 } \) = 0,86
Вопрос 39.
КРИТИЧЕСКОЕ МЫШЛЕНИЕ
Пусть A — любой острый угол прямоугольного треугольника. Покажите, что
(a) tan A = \(\frac{\sin A}{\cos A}\) и
(b) (sin A) 2 + (cos A) 2 = 1.
Ответ :
Вопрос 40.
КРИТИЧЕСКОЕ МЫШЛЕНИЕ
Объясните, почему площадь ∆ ABC на диаграмме можно найти по формуле Площадь = \(\frac{1}{2}\) ab sin C. Затем вычислите площадь когда a = 4, b = 7 и m∠C = 40°:
Ответ:
Площадь = \(\frac{1}{2}\) ab sin C
= \(\frac{1}{2}\) (4 x 7) sin 40°
= 14 x 0,642
= 8,988
Поддержание математических знаний
Найдите значение x. Скажите, образуют ли длины сторон пифагорову тройку.
Вопрос 41.
Ответ:
Вопрос 42.
Ответ:
x = 12√2
Объяснение:
C² = A² + B²
X² = 12² + 12²
x = 144 + 144
x = 12² = 122
x = 144 + 144
x. 288
х = 12√2
Вопрос 43.
Ответ:
Вопрос 44.
Ответ:
x = 6√2
Объяснение:
C² = A² + B²
9b = x² + 3²
81 = X² +
x
. = 81 – 9
x = 6√2
9.6 Решение прямоугольных треугольников
Исследование 1
Решение специальных прямоугольных треугольников
Работайте с напарником. Используйте цифры, чтобы найти значения синуса и косинуса ∠A и ∠B. Используйте эти значения, чтобы найти меры ∠A и ∠B. Используйте программное обеспечение для динамической геометрии, чтобы проверить свои ответы.
Используйте цифры, чтобы найти значения синуса и косинуса ∠A и ∠B. Используйте эти значения, чтобы найти меры ∠A и ∠B. Используйте программное обеспечение для динамической геометрии, чтобы проверить свои ответы.
а.
Ответ:
б.
Ответ:
Исследование 2
Решение прямоугольных треугольников
Работа с партнером: Вы можете использовать калькулятор, чтобы найти меру угла, если знаете значение синуса, косинуса или тангенса правила . Используйте функцию арксинуса, арккосинуса, арктангенса 0r вашего калькулятора, чтобы аппроксимировать меры ∠A и ∠B с точностью до ближайшей десятой доли градуса. Затем используйте программное обеспечение для динамической геометрии, чтобы проверить свои ответы.
ВНИМАНИЕ К ТОЧНОСТИ
Чтобы хорошо разбираться в математике, вам необходимо точно и эффективно считать, выражая числовые ответы с точностью, соответствующей контексту задачи.
а.
Ответ:
б.
Ответ:
Сообщите свой ответ
Вопрос 3.
Зная длины сторон прямоугольного треугольника, как можно найти величины двух острых углов?
Ответ:
Грех любого угла можно вычислить отношением перпендикуляра в треугольнике к гипотенузе.
Cos любого угла можно вычислить отношением стороны основания в треугольнике к гипотенузе.
Тангенс любого угла можно рассчитать как отношение перпендикулярной стороны в треугольнике к стороне основания.
Если заданы sin, cos и tan любых углов, то углы можно легко найти, применив обратную функцию.
Вопрос 4.
Лестница, прислоненная к зданию, образует со зданием и землей прямоугольный треугольник. Катеты прямоугольного треугольника (в метрах) образуют пифагорову тройку 5-12-13. Найдите величины двух острых углов с точностью до десятых долей градуса.
Ответ:
Урок 9.6 Решение прямоугольных треугольников
Определите, какой из двух острых углов имеет заданное тригонометрическое отношение.
Вопрос 1.
Синус угла равен \(\frac{12}{13}\).
Ответ:
Sin E = \(\frac{12}{13}\)
m∠E = sin -1 (\(\frac{12}{13}\)) = 67,3°
Вопрос 2.
Тангенс угла равен \(\frac{5}{12}\)
Ответ:
tan F = \(\frac{5}{12}\)
м∠F = tan -1 (\(\frac{5}{12}\)) = 22,6°
Пусть ∠G, ∠H и ∠K — острые углы. С помощью калькулятора аппроксимируйте величины ∠G, ∠H и ∠K с точностью до десятых долей градуса.
Вопрос 3.
тангенс G = 0,43
Ответ:
∠G = инверсный тангенс 0,43 = 23,3°
Вопрос 5.
cos K = 0,94
Ответ:
∠K = обратный cos 0,94 = 19,9°
Решите прямоугольный треугольник. Округлите десятичные ответы до десятых.
Вопрос 6.
Ответ:
DE = 29, ▲ = 46,05 °, ♂ = 42,84 °
Объяснение:
C² = A² + B²
x² = 20² + 212
x² = 400 + 441
x² = 20² + 212
x² = 400 + 441
x² + 212
x = 400 + 441
x² + 212
x = 400 + 441
x². = 841
= 841
x = 29
sin D = \(\frac { 21 }{ 29 } \)
∠D = 46,05
sin E = \(\frac { 20 }{ 29 } \)
∠E = 42,84
Вопрос 7.
Ответ:
GJ = 60, ∠G = 56,09°, ∠H = 33,3°
Пояснение:
c² = a² + b²
109² = 91² + x²
x² = 1828810015 x² = 3600
x = 60
sin G = \(\frac { 91 }{ 109 } \)
∠G = 56,09
sin H = \(\frac { 60 }{ 109 } \)
∠H = 33,3
Вопрос 8.
Решите прямоугольный треугольник. Округлите десятичные ответы до десятых.
Ответ:
XY=13,82, YZ=6,69, ∠Y=37,5 } \)
XY = 13,82
sin 52 = \(\frac { YZ }{ XY } \)
0,788 = \(\ frac { YZ }{ 8,5 } \)
YZ = 6,69
sin Y = \(\frac { 8,5 }{ 13,82 } \)
∠Y = 37,5
Вопрос 9.
ЧТО ЕСЛИ?
В Примере 5 предположим, что другая ступень с граблями имеет длину 20 футов спереди назад с общим подъемом 2 фута. Находится ли уровень рейка в желаемом диапазоне?
Ответ:
x = арксинус \(\frac { 2 }{ 20 } \)
x = 5,7°
Упражнение 9.
 6. Решение прямоугольных треугольников треугольника означает найти меры всех его ________ и _______ .
6. Решение прямоугольных треугольников треугольника означает найти меры всех его ________ и _______ . Ответ:
Вопрос 2.
ПИСЬМО
Объясните, когда можно использовать тригонометрическое соотношение для нахождения длины стороны прямоугольного треугольника и когда можно использовать теорему Пифагора (теорема 9.1).
Ответ:
Тригонометрическое отношение можно использовать для нахождения длины стороны треугольника, если известна мера одного из двух острых углов, а теорему Пифагора можно использовать для нахождения длины стороны треугольника, когда мера одного длин двух сторон.
Мониторинг прогресса и моделирование с помощью математики
В упражнениях 3–6 определите, какой из двух острых углов имеет заданное тригонометрическое отношение.
Вопрос 3.
Косинус угла равен \(\frac{4}{5}\)
Ответ:
Вопрос 4.
Синус угла равен \(\frac{5}{11) }\)
Ответ:
Sin(угол) = \(\frac { противоположный }{ гипо } \)
sin A = \(\frac{5}{11}\)
Острый угол, имеющий синус угла \(\frac{5}{11}\) равно ∠A.
Вопрос 5.
Синус угла равен 0,95.
Ответ:
Вопрос 6.
Тангенс угла равен 1,5.
Ответ:
tan(угол) = \(\frac { противоположный }{ смежный } \)
1,5 = \(\frac { 18 }{ 12 } \)
tan C = 1,5
Острый угол, имеющий тангенс угла равен 1,5∠C.
В упражнениях 7–12 пусть ∠D — острый угол. Используйте калькулятор, чтобы приблизить величину ∠D к ближайшей десятой доле градуса.
ВОПРОС 7.
SIN D = 0,75
Ответ:
Вопрос 8.
SIN D = 0,19
Ответ:
SIN D = 0,19
♂ = обратный синус 0,19
T = 10,9 °
Вопрос 9002. .
COS D = 0,33
Ответ:
Вопрос 10.
COS D = 0,64
Ответ:
COS D = 0,64
↑D = обратный COS 0,64
тром = 50,2 °
Вопрос 11.
кога D = 0,28
Ответ:
Вопрос 12.
тангенс D = 0,72
Ответ:
тангенс D = 0,72
∠D = обратный тангенс 0,72
∠D = 35,8°
В упражнениях 13 – 18. решить прямоугольный треугольник. Округлите десятичные ответы до десятых.
решить прямоугольный треугольник. Округлите десятичные ответы до десятых.
Вопрос 13.
Ответ:
Вопрос 14.
Ответ:
ED = 2√65, ♂ = 59,3, ▲ = 29,7
Объяснение:
C² = 8² + 1400
x² = 64 +. 196
x² = 260
x = 2√65
sin E = \(\frac { 14} { 2√65 } \)
∠E = 59,3
sin D = \(\frac { 8 }{ 2√65 } \)
.
16² = 14² + x²
x² = 256 – 196
x² = 60
x = 2√15
sin G = \(\frac { 2√15 }{ 16 } \)
∠G = 28,9
sin J = \ (\frac { 14 }{ 16 } \)
∠J = 61
Вопрос 17.
Ответ:
Вопрос 18.
Ответ:
RT = 17,8, RS = 90,68, ∠T = 32,8
Объяснение:
sin 57 = \(\frac { 15 }{ x } \)
0,838 = \(\frac { 15 }{ x } \)
x = 17,899
RT = 17,8
cos 57 = \(\frac { x }{ 17,8 } \)
0,544 = \(\ frac { x }{ 17,8 } \)
x = 9,68
RS = 9,68
sin T = \(\ frac { 9,68 } { 17,8 } \)
∠T = 32,8
Вопрос 19.
АНАЛИЗ ОШИБОК
Опишите и исправьте ошибку в использовании обратного тригонометрического соотношения.
Ответ:
Вопрос 20.
РЕШЕНИЕ ПРОБЛЕМ
Для облегчения выгрузки глины. кузов самосвала должен быть приподнят не менее чем на 45°. Кузов самосвала длиной 14 футов поднят на 8 футов. Будет ли глина легко выливаться? Объясните свои рассуждения.
Ответ:
Угол подъема: sin x = \(\frac { 8 }{ 14 } \)
x = арксинус \(\frac { 8 }{ 14 } \) = 34,9
Глина не льется легко.
Вопрос 21.
РЕШЕНИЕ ЗАДАЧ
Вы стоите на пешеходном мосту, который находится на высоте 12 футов над озером. Вы смотрите вниз и видите утку в воде. Утка находится в 7 футах от пешеходного моста. Какой угол возвышения от утки к вам
Ответ:
Вопрос 22.
КАК ВЫ ЭТО ВИДИТЕ?
Напишите три выражения, которые можно использовать для аппроксимации меры ∠A. Какое выражение вы бы выбрали? Объяснить ваш выбор.
Какое выражение вы бы выбрали? Объяснить ваш выбор.
Ответ:
Три выражения: ∠A = обратный тангенс (\(\frac { 15 }{ 22 } \)) = 34,2°
∠A = арксинус (\(\frac { 15 }{ BA } \))
∠A = обратный потомус (\(\frac { 22 }{ BA } \))
Вопрос 23.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
В Единых федеральных стандартах доступности указано, что наклон пандуса для инвалидных колясок не может превышать 4,76. Вы хотите построить пандус с вертикальным подъемом 8 дюймов. вы хотите минимизировать горизонтальное расстояние, занимаемое пандусом. Нарисуйте схему, показывающую примерные размеры вашей рампы.
Ответ:
Вопрос 24.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Горизонтальная часть ступени называется проступью. Вертикальная часть называется подступенком. Рекомендуемое соотношение подступенка к протектору составляет 7 дюймов : 11 дюймов.
а. Найдите значение x для лестницы, построенной с использованием рекомендуемого отношения подступенка к проступи.
б. вы хотите построить лестницу менее крутую, чем лестница в части (а). Приведите пример отношения подступенка к ступеням, которое вы могли бы использовать. Найдите значение x для вашей лестницы.
Ответ:
Учитывая, что
Длина стояка = 7 в
Длина резьбы = 11 в
Соотношение = 7: 11
Возьмем углы наклона за x.
В геометрии — параллельные прямые с одинаковыми внутренними углами. Таким образом, углы наклона между стояком и резьбой равны
Tan x = подъем/резьба
Tan x = 7/11
Tan x = 0,6364
x = tan -1(0,6364)
x = 32,5 градуса.
Таким образом, значение x для этих лестниц, построенных с использованием рекомендуемого отношения подступенка к проступи, составляет 32,5 градуса.
Вопрос 25.
ИСПОЛЬЗОВАНИЕ ИНСТРУМЕНТОВ
Найдите меру ∠R, не используя транспортир. Обоснуйте свою технику.
Ответ:
Вопрос 26.
СПОРЫ
Ваш друг утверждает, что загар -1 х = \(\frac{1}{\tan x}\). Ваш друг прав? Объясните свои рассуждения.
Ваш друг прав? Объясните свои рассуждения.
Ответ:
Нет
Например,
тангенс -1 (√3) = 60
\(\frac{1}{\tan √3}\) = 33,1
ИСПОЛЬЗУЯ СТРУКТУРУ s
и в упражнении 28, решить каждый треугольник.
Вопрос 27.
∆JKM и ∆LKM
Ответ:
Вопрос 28.
∆Tus и ∆VTW
Ответ:
TS = 8,2, UT = 7.3, 6.6
ТВ = 13.2 ТВ = 13.2 ТВ = 13.2 ТВ = 13.2 ТВ = 13.2 ТВ = , ТВ = 9.6, ∠V = 46, ∠T = 42,84
Объяснение:
tan 64 = \(\frac { TS }{ 4 } \)
TS = 2,05 x 4
TS = 8,2
sin 64 = \(\frac { UT }{ 8,2 } \)
0,898 = \(\frac { UT }{ 8,2 } \)
UT = 7,3
sin T = \(\frac { 4 }{ 8,2 } \)
∠T = 28,6
TV = TS + SV
TV = 8,2 + 5 = 13,2
13,2² = TW² + 9²
TW² = 174,24 – 81
TW = 9,6
sin V = \(\frac { 9,6 }{ 13,2 } \)
∠V = 46
sin T = \(\frac { 9 }{ 13,2 } \)
∠T = 42,84
Вопрос 29.
МАТЕМАТИЧЕСКИЕ СОЕДИНЕНИЯ
Напишите выражение, с помощью которого можно найти величину острого угла, образованного каждой прямой и осью x. Затем аппроксимируйте меру угла до ближайшей десятой доли градуса.
Затем аппроксимируйте меру угла до ближайшей десятой доли градуса.
а. у = 3x
б. y = \(\frac{4}{3}\)x + 4
Ответ:
Вопрос 30.
НАВОДИТ НА МЫСЛЬ
Упростите каждое выражение. Обосновать ответ.
а. sin -1 (sin x)
Ответ:
sin -1 (sin x) = x
б. tan(tan -1 y)
Ответ:
tan(tan -1 y) = y
C. cos(cos -1 z)
Ответ:
905 cos2(cos 905 — 1
cos2(cos2) z) = z
Вопрос 31.
ОБОСНОВАНИЕ
Объясните, почему выражение sin -1 (1.2) не имеет смысла.
Ответ:
Вопрос 32.
ИСПОЛЬЗОВАНИЕ СТРУКТУРЫ
Периметр прямоугольника ABCD равен 16 сантиметрам. а отношение его ширины к длине равно 1 : 3. Отрезок BD делит прямоугольник на два равных треугольника. Найдите длины сторон и углы этих двух треугольников.
Ответ:
Периметр прямоугольника ABCD равен 16 сантиметрам
2(l + b) = 16
l + b = 8
b : l = 1 : 3
4x = 8
x = 2
l = 6, b = 2
BD = √(6² + 2²) = √40 = 2√10
sin B = \(\frac { AD }{ BD } \) = \(\ frac { 2 }{ 2√10 } \)
∠ABD = 18,4
∠CBD = 71,6
sin D = \(\frac { AB }{ BD } \) = \(\frac { 6 }{ 2√10 } \)
∠ADB = 71
∠CDB = 19
Поддержание математических знаний
Решите уравнение
Вопрос 33.
\(\frac{12}{x}=\frac{3}{2}\)
Ответ:
Вопрос 34.
\(\frac{13}{9}=\frac{ x}{18}\)
Ответ:
\(\frac{13}{9}=\frac{x}{18}\)
x = 1,44 x 18
x = 26
Вопрос 35.
\ (\frac{x}{2.1}=\frac{4.1}{3.5}\)
Ответ:
Вопрос 36.
\(\frac{5.6}{12.7}=\frac{4.9}{x}\ )
Ответ:
\(\frac{5.6}{12.7}=\frac{4.9}{x}\)
0,44 = 4,9/x
x = 11,13
9.7 Закон синусов и закон косинусов
Исследование 1
Открытие закона синусов
Работа с партнером.
а. Скопируйте и заполните таблицу для показанного треугольника. Какой вывод вы можете сделать?
Ответ:
б. Используйте программное обеспечение для динамической геометрии, чтобы нарисовать два других треугольника. Скопируйте и заполните таблицу в части (а) для каждого треугольника. Используйте полученные результаты, чтобы написать гипотезу о связи между синусом углов и длинами сторон треугольника.
СТРАТЕГИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ ИНСТРУМЕНТОВ
Чтобы хорошо разбираться в математике, вам необходимо использовать технологии для сравнения прогнозов с данными.
Ответ:
Исследование 2
Открытие закона косинусов
Работа с партнером:
a. Скопируйте и заполните таблицу для треугольника в исследовании 1 (а). Какой вывод вы можете сделать?
Ответ:
б. Используйте программное обеспечение для динамической геометрии, чтобы нарисовать два других треугольника. Скопируйте и заполните таблицу в части (а) для каждого треугольника. Используйте свои результаты, чтобы написать предположение о том, что вы наблюдаете в заполненных таблицах.
Ответ:
Сообщите свой ответ
Вопрос 3.
Что такое закон синусов и закон косинусов?
Ответ:
Закон синусов равен
sin A/a = SinB/b = sinC/c
И
a/sinA = b/sinB = c/sinC
Закон косинусов равен
a² = b² + c² -2bcCosA
x² = a² + c² – 2acCosB
x² = a² + b² – 2abCosC
Вопрос 4.
Когда бы вы использовали закон синусов для решения треугольника? Когда бы вы использовали закон косинусов, чтобы решить треугольник?
Ответ:
Заданный в любом треугольнике закон синусов можно использовать, если известны две стороны и один угол, противолежащий данной стороне (SSA), или два угла и любая сторона (AAS или ASA).
В любом треугольнике можно использовать закон косинуса, если две стороны входят в один угол сторон.
Урок 9.7 Закон синусов и Закон косинусов
Мониторинг прогресса
Используйте калькулятор, чтобы найти тригонометрическое соотношение. Округлите ответ до четырех знаков после запятой.
Вопрос 1.
тангенс 110°
Ответ:
TAN 110 ° = -2,7474
Вопрос 2.
SIN 97 °
Ответ:
SIN 97 ° = 0,9925
Вопрос 3.
COS 165 °
Ответ:
COS 165 ° = -0,9659
Найдите площадь ∆ABC с заданными длинами сторон и прилежащим к ним углом. Округлите ответ до десятых.
Вопрос 4.
м ∠ B = 60°, a = 19, c = 14
Ответ:
Площадь = 155,18
Объяснение:
Площадь = \(\frac { 1 }{ 2 } \) ac sin B
= \(\frac { 1 }{ 2 } \) (19 x 14) sin 60°
= 133 x 0,866
= 155,18
Вопрос 5.
м ∠ C = 29°, a = 38, b = 31
Ответ:
Площадь = 282,72
Объяснение:
Площадь = \(\frac { 1 }{ 2 } \) ab sin C
= \(\frac { 1 }{ 2 } \) (38 x 31) sin 29
= 598 х 0,48
= 282,72
Решите треугольник. Округлите десятичные ответы до десятых.
Вопрос 6.
Ответ:
∠C = 46,6, ∠B = 82,4, AC = 23,57
Объяснение:
Используя закон синусов
\(\frac { c }{ sin C } \) = \(\ frac { a }{ sin A } \)
\(\ frac { 17 }{ sin C } \ ) = \(\frac { 18 }{ sin 51 } \)
\(\ frac { 17 }{ sin C } \) = \(\ frac { 18 }{ 0,77 } \)
sin C = 0,7274
∠C = 46,6
∠A + ∠B + ∠C = 180
51 + 46,6 + ∠B = 180
∠B = 82,4
\(\frac {sin B} }{b} \) = \(\frac {sin A} { a } \)
\(\frac { 0,99 }{ b } \) = \(\frac { 0,77 }{ 18 } \)
b = 23,57
Вопрос 7.
Ответ:
∠B = 31,3, ∠C = 108,7, c = 23,6
Объяснение:
\(\frac { sin B }{ b } \) = \(\frac { sin A }{ a } \ )
\(\frac { sin B }{ 13 } \) = \(\ frac { sin 40 }{ 16 } \)
sin B = \(\ frac { .64 }{ 16 } \) x 13
sin B = 0,52
∠B = 31,3
∠A + ∠B + ∠C = 180
40 + 31,3 + ∠C = 180
∠C = 108,7
\(\frac { c }{ sin C } \) = \( \frac { a }{ sin A } \)
\(\ frac { c }{ sin 108.7 } \) = \(\ frac {16 }{ sin 40 } \)
c = \(\ frac {16 }{ 0,64 } \) х 0,947
c = 23,6
Решите треугольник. Округлите десятичные ответы до десятых.
Вопрос 8.
Ответ:
∠С = 66, а = 4,36, с = 8,27 = 66
\(\frac { a }{ sin A } \) = \ (\ frac { b }{ sin B } \) = \ (\ frac { c }{ sin C } \)
\ (\ frac { a }{ sin 29 } \) = \ (\ frac { 9 }{ sin 85 } \)
\ (\ frac { a }{ 0,48 } \) = \ (\ frac { 9 }{ 0,99 } \)
a = 4,36
\(\frac { b }{ sin B } \) = \ (\ frac { c }{ sin C } \)
\(\frac { 9 }{ sin 85 } \) = \(\ frac { c }{ sin 66 } \)
\(\ frac { 9 }{ 0,99 } \) = \(\ frac { c }{ Вопрос 9 70 + 81 = 180
∠A = 29
\(\frac {a}{sin A}\) = \(\frac{b}{sinB}\) = \(\frac{c}{sinC} \)
\(\frac { 10 }{ sin 29 } \) = \(\ frac { b }{ sin 70 } \)
\(\ frac { 10 }{ 0,48 } \) = \(\ frac { b { 0,93 } \)
b = 19,37
\(\frac { a }{ sin A } \) = \(\ frac { c }{ sin C } \)
\(\ frac { 10 }{ sin 29 } \) = \(\frac { c }{ sin 81 } \)
\(\frac { 10 }{ 0,48 } \) = \(\frac { c }{ 0,98 } \)
c = 20,41
Вопрос 10.
ЧТО ЕСЛИ?
В примере 5 какой длины будет мост из южной зоны для пикника в восточную зону для пикника?
Ответ:
Длина моста от Южной зоны пикника до Восточной зоны пикника составляет 188 м.
Объяснение:
\(\frac { a }{ sin A } \) = \(\ frac { b }{ sin B } \) = \(\ frac { c }{ sin C } \)
\(\ frac { c }{ sin C } \) { a }{ sin 71 } \) = \(\ frac { 150 }{ sin 49 } \)
a = 188
Решите треугольник. Округлите десятичные ответы до десятых.
Вопрос 11.
Ответ:
b = 61,3, ∠A = 46, ∠C = 46 43) cos 88
b² = 2025 + 1849 – 3870 x 0,03 = 3757,9
b = 61,3
\(\frac { sin A }{ a } \) = \(\ frac { sin B }{ b } \)
\(\ frac { sin A }{ 45 } \) = \(\ frac { sin 88 }{ 61.3 } \)
sin A = 0,72
∠A = 46
∠A + ∠B + ∠C = 180
46 + 88 + ∠C = 180
∠C = 46
a = 41,1, ∠C = 35,6, ∠B = 30,4
Объяснение:
a² = b² + c² − 2bc cos A
a² = 23² + 26² – 2(23)(26) cos 114
a² = 529 + 529 676 – 1196 x -0,406
а² = 1690,5
а = 41,1
\(\frac { sin 114 }{ 41,1 } \) = \(\ frac { sin B }{ 23 } \)
0,02 = \(\frac { sin B }{ 23 } \)
sin B = 0,507
∠B = 30,4
∠A + ∠B + ∠C = 180
114 + 30,4 + ∠C = 180
∠C 35,6
Вопрос 13.
Ответ:
∠A = 41,4, ∠B = 81,8, ∠C = 56,8
Объяснение:
(5) cos A
16 = 36 + 25 – 60 cos A
-45 = – 60 cos A
cos A = 0,75
∠A = 41,4
\(\frac { sin 41,4 }{ 4 } \) = \( \frac { sin B }{ 6 } \)
0,165 = \(\ frac { sin B }{ 6 } \)
SIN B = 0,99
TB = 81,8
секрет + ♂ + Ϫc = 180
41,4 + 81,8 + ♂ = 180
♂ = 56,8
ВОПРОС 14.
Ответ:
. , ∠A = 58,6, ∠C = 39,6
Объяснение:
a² = b² + c² − 2bc cos A
23² = 27² + 16² – 2(27)(16) cos A
529 = 729 + 256 – 864 cos A
456 = 864 cos A
cos A = 0,52
∠A = 58,6
\(\frac { sin 58,6 }{ 23 } \) = \(\ frac { sin B }{ 27 } \)
0,03 = \(\ frac { sin B }{ 27 } \)
sin B = 0,99
∠B = 81,8
∠A + ∠B + ∠C = 180
58,6 + 81,8 + ∠C = 180
∠C = 39,6
Базовое упражнение 9.7. Закон синусов и закон косинусов 9001 9001
Вопрос 1.
ПИСЬМО
Для решения треугольника какого типа вы бы использовали закон синусов или закон косинусов?
Ответ:
Вопрос 2.
СЛОВАРЬ
Какая информация вам нужна для использования закона синусов?
Ответ:
Правило синусов используется, когда даны два угла и одна сторона или даны две стороны и не включенный угол.
Мониторинг прогресса и моделирование с помощью математики
В упражнениях 3–8 используйте калькулятор, чтобы найти тригонометрическое отношение. Округлите ответ до четырех знаков после запятой.
Вопрос 3.
SIN 127 °
Ответ:
Вопрос 4.
SIN 98 °
Ответ:
SIN 98 ° = 0,9902
Вопрос 5.
COS 139 °
Ответ:
Вопрос 6.
cos 108°
Ответ:
cos 108° = -0,309
Вопрос 7.
tan 165°
Ответ:
Вопрос 8.
tan 116°
Ответ:
tan 116° = -2,0503
В упражнениях 9-12 найдите площадь треугольника. Округлите ответ до десятых.
Вопрос 9.
Ответ:
Вопрос 10.
Ответ:
Площадь = \(\frac{1}{2}\)bc sin A
Площадь = \(\frac{1}{2) }\)(28)(24) sin83
Площадь = 332,64
Вопрос 11.
Ответ:
Вопрос 12.
Ответ:
Площадь = \(\frac{1}{2}\)ab sin C
Площадь = \(\frac{1}{2}\)(15)(7) sin 96
Площадь = 51,9
В упражнениях 13 – 18. решить треугольник. Округлите десятичные ответы до десятых.
Вопрос 13.
Ответ:
Вопрос 14.
Ответ:
∠B = 38,3, ∠A = 37,7, a = 15,7
{frac B \ 5} \) = \(\frac { sin 104 }{ 25 } \)
sin B = 0,62
∠B = 38,3
∠A + ∠B + ∠C = 180
∠A + 38,3 + 104 = 180
∠A = 37,7
\(\frac { sin 37,7 }{ a } \) = \(\ frac { sin 104 }{ 25 } \)
\(\ frac { 0,61 } {a} \) = 0,0388
a = 15,7
Вопрос 15.
Ответ:
Вопрос 16.
Ответ:
TB = 65, b = 33,55, A = 24,4
Explanation:
. A + ∠B + ∠C = 180
42 + 73 + ∠B = 180
∠B = 65
\(\frac { sin B }{ b } \) = \(\ frac { sin C }{ c } \ )
\(\frac { sin 65 }{ b } \) = \(\ frac { sin 73 }{ 34 } \)
b = 33,55
\(\frac { sin A }{ a } \) = \(\ frac { sin C }{ c } \)
\(\ frac { sin 42 }{ a } \) = \(\ Frac {sin 73} {34} \)
a = 24,4
Вопрос 17.
Ответ:
Вопрос 18.
Ответ:
. :
∠A + ∠B + ∠C = 180
24 + 66 + ∠C = 180
∠C = 90
\(\frac { sin B }{ b } \) = \(\ frac { sin C }{ c } \)
\(\frac { sin 66 }{ b } \) = \(\ frac { sin 90 }{ 43 } \)
\(\frac {.91}{b} \) = 0,023
b = 39,56
\(\frac {sin A}{a} \) = \(\frac {sin C}{c} \)
\ (\frac { sin 24 }{a } \) = \(\frac { sin 90 }{ 43 } \)
\(\frac { 0,406 }{a } \) = 0,023
a = 17,6
В упражнениях 19 — 24, решить треугольник. Округлите десятичные ответы до десятых.
Вопрос 19.
Ответ:
Вопрос 20.
Ответ:
b = 29,9, ∠A = 26,1, ∠C = 15,07
Объяснение0015 b² = a² + c² – 2ac cos B
b² = 20² + 12² – 2(12)(20) cos 138
b² = 400 + 144 – 480 (-0,74)
b² = 899,2
b = 29,9
\(\ frac { sin B }{ b } \) = \ (\ frac { sin A }{ a } \)
\ (\ frac { sin 138 } 29,9 } \) = \ (\ frac { sin A } 20 } \)
\(\frac { 0,66 }{ 29,9 } \) = \(\frac { sin A }{ 20 } \)
sin A = 0,44
∠A = 26,1
\(\ frac { sin B }{ b } \) = \(\frac { sin C }{ c } \)
\(\ frac { sin 138 }{ 29,9 } \) = \(\ frac { sin C }{ 12 } \)
sin C = 0,26
↑C = 15,07
Вопрос 21.
Ответ:
Вопрос 22.
Ответ:
↑A = 107,3, ♂ = 51,6, потряно – 2ac cos B
28² = 18² + 13² – 2(18)(13) cos B
784 = 324 + 169 – 468 cos B
291 = 468 cos B
cos B = 0,62
∠B = 51,6
\(\ frac { sin C }{ c } \) = \ (\ frac { sin B }{ b } \)
\ (\ frac { sin C }{ 13 } \) = \ (\ frac { sin 51.6 } { 28 } \)
sin C = 0,36
∠C = 21,1
↑A + ♂ + ♂ = 180
51,6 + 21,1 + секрета. , ∠B = 132,1, ∠C = 24,9
Объяснение:
b² = a² + c² – 2ac cos B
5² = 12² + 13² – 2(12)(13) cos B
25 = 144 + 169 – 312 cos B
288 = 312 cos B
cos B = 0,92
∠B = 23
\(\frac { sin C }{ c } \) = \(\ frac { sin B }{ b } \)
\(\ frac { грех C }{ 13 } \) = \ (\ frac { грех 23 }{ 5 } \)
SIN C = 1,014
TC = 24,9
секрет + ♂ + ♂ = 180
23 + 24,9 + ♂ = 180
↑B = 132,1
Вопрос 25.
Анализ ошибок
и исправьте ошибка в нахождении m ∠ C.
Ответ:
Вопрос 26.
АНАЛИЗ ОШИБОК
Опишите и исправьте ошибку в нахождении m ∠ A на ∆ABC при a = 19, b = 21 и c = 11.
Ответ:
a² = b² + c² – 2bc cos A
19² = 21² + 11² – 2(21)(11) cos A
361 = 441 + 121 – 462 cosA
201 = 462 cosA
cos A = 0,43
∠A = 64,5
СРАВНЕНИЕ МЕТОДОВ
Скажите, будете ли вы использовать Закон Sines 3 в упражнении 2 27. косинусов. или теорема Пифагора (теорема 9.1) и тригонометрические соотношения для решения треугольника с заданной информацией. Объясните свои рассуждения. Затем решите треугольник.
Вопрос 27.
м ∠ A = 72°, м ∠ B = 44°, b = 14
Ответ:
Вопрос 28.
м ∠ B = 98°, м ∠ C = 37°, a = 18
Ответ:
∠A = 45, b = 25,38, c = 15,38
Пояснение:
∠A + ∠B + ∠C = 180
∠A + 98 + 37 = 180
∠A = 45
\(\frac { sin B }{ b } \) = \(\ frac { sin A }{ a } \)
\(\ frac { sin 98 }{ b } \) = \(\frac { sin 45 }{ 18 } \)
\(\ frac { 0,99 }{ b } \) = 0,039
b = 25,38
\(\ frac { sin A }{ a } \) = \(\frac { sin C }{ c } \)
\(\ frac { sin 45 }{ 18 } \) = \(\ frac { sin 37 }{ c } \)
0,039 = \( \фракция { грех 37} { с } \)
c = 15. 38
38
Вопрос 29.
м ∠ C = 65°, a = 12, b = 21
Ответ:
Вопрос 30.
м ∠ B = 90°, a = 15, c = 6
5
5
Ответ:
b = 3√29, ∠A = 66,9, ∠C = 23,1
Объяснение:
b² = a² + c²- 2ac cos B
b² = 15² + 6² – 2(15)(6) cos 90
= 225 + 36 – 180(0)
b² = 261
b = 3√29
\(\frac { sin B }{ b } \) = \(\ frac { sin A }{ a } \)
\(\ frac { sin 90 }{ 3√29 } \) = \ (\ frac { sin A }{ 15 } \)
sin A = 0,92
∠A = 66,9
∠A + ∠B + ∠C = 180
66,9 + 90 + ∠C = 180
∠C = 23,1
Вопрос 31.
м ∠ C = 40°, c = 40°, b = 36
Ответ:
Вопрос 32.
a = 34, b = 19, c = 27
Ответ:
∠B = 33,9, ∠A = 78,5, ∠C = 67,6
Объяснение c²- 2ac cos B
19² = 34² + 27²- 2(34)(27) cos B
361 = 1156 + 729 – 1836 cos B
cos B = 0,83
∠B = 33,9
\(\frac { sin 33,9 } { 19 } \) = \ (\ frac { sin A }{ 34 } \)
sin a = 0,98
♂ = 78,5
секрет + ↑B + ↑C = 180
78,5 + 33,9 + ♂ = 180
↑C = 67,6
Вопрос 33.
Моделирование с математикой
You, и ваш и ваш друг стоят на базовой линии баскетбольной площадки. Вы бросаете баскетбольный мяч своему другу, как показано на схеме. Какое расстояние между вами и вашим другом?
Ответ:
Вопрос 34.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Через долину построена зиплайн, как показано на схеме. Какова ширина w долины?
Ответ:
W = 92,5 фута
Объяснение:
W² = 25² + 84² — 2 (25) (84) COS 102
W² = 7681 — 4200 COS 102
W = 92,5 FT
ВОПРОС 35.
W = 92,5 FT
Вопрос 35.
W = 92,5 FT
. МОДЕЛИРОВАНИЕ С МАТЕМАТИКОЙ
Вы находитесь на смотровой площадке Эмпайр Стейт Билдинг и смотрите на Крайслер Билдинг. Когда вы поворачиваетесь на 145° по часовой стрелке, вы видите Статую Свободы. Вы знаете, что Крайслер-билдинг и Эмпайр-Слейт-билдинг находятся на расстоянии примерно 0,6 мили друг от друга, а Крайслер-билдинг и Статуя Свободы — примерно в 5,6 милях друг от друга. Оцените расстояние между Эмпайр Стейт Билдинг и Статуей Свободы.
Оцените расстояние между Эмпайр Стейт Билдинг и Статуей Свободы.
Ответ:
Вопрос 36.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Пизанская башня в Италии имеет высоту 183 фута и отклонена от вертикали на 4°. Найдите расстояние d по горизонтали, на котором вершина башни будет отклонена от вертикали.
Ответ:
Расстояние по горизонтали определяется по формуле тригонометрии.
Тан тета = напротив/смежный
Тета = 4
Противоположный = высота = 183 фута
Горизонтальный = смежный = а
Таким образом,
Тан 4 = 183/а
Следовательно, a = 183/tan 4
A = 2617,82 фута.
Вопрос 37.
ПРИВОДИМ АРГУМЕНТ
Ваш друг говорит, что для нахождения JK можно использовать закон синусов. Ваш двоюродный брат говорит, что закон косинусов можно использовать, чтобы найти JK. Кто прав? Объясните свои рассуждения.
Ответ:
Вопрос 38.
ОБОСНОВАНИЕ
Используйте ∆XYZ
a. Можете ли вы использовать закон синусов, чтобы решить ∆XYZ? Объясните свои рассуждения.
Можете ли вы использовать закон синусов, чтобы решить ∆XYZ? Объясните свои рассуждения.
Ответ:
Дано
y = 17, X = 64° и Y = 90°
Закон синусов можно использовать для решения треугольников, когда известны два угла и длина любой стороны.
В треугольнике XYZ даны два угла и длина одной стороны.
Следовательно, мы можем использовать закон синусов для решения ∆XYZ.
б. Можно ли использовать другой метод для решения ∆XYZ? Объясните свои рассуждения.
Ответ:
Даны два угла треугольника и одна сторона, противоположная прямоугольному углу.
sin X/YZ = sinY/XZ = sin Z/XY
m∠X = 64, m∠Y = 90, XY = 17
sin X/YZ = sinY/XZ
sin 64/YZ = sin 90/XZ
Длина участка YZ = 15,3
м∠X + m∠Y + m∠Z = 180
м∠Z = 26
Значение XY можно найти с помощью правой сторона уравнения синуса и подводных частей m∠Y = 90, m∠Z = 26 и XY = 17
sin 90/17 = sin 26/XZ
XY = 7,5
Вопрос 39.
СПОР
Ваш друг вычислил площадь треугольника по формуле A = \(\frac{1}{2}\)qr sin S и сказал, что площадь равна примерно 208,6 квадратных единиц. Ваш друг прав? Объясните свои рассуждения.
Ваш друг прав? Объясните свои рассуждения.
Ответ:
Вопрос 40.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Вы удобряете треугольный сад. Одна сторона сада имеет длину 62 фута, а другая — 54 фута. Угол, противоположный 62-футовой стороне, равен 58°.
а. Нарисуйте схему, изображающую эту ситуацию.
б. Используйте закон синусов, чтобы решить треугольник из части (а).
в. Один мешок удобрения покрывает площадь 200 квадратных футов. Сколько мешков удобрений вам понадобится, чтобы покрыть весь сад?
Ответ:
С = 47,6, А = 74,4, а = 70,4
9 мешков удобрений.
Вопрос 41.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Игрок в гольф забивает 260 ярдов на лунке длиной 400 ярдов. Выстрел на 15° от цели.
а. Каково расстояние x от мяча игрока в гольф до лунки?
б. Предположим, что игрок в гольф может попасть по мячу точно на расстояние, указанное в части (а). Каков максимальный угол θ (тета), на который мяч может отклониться от цели, чтобы приземлиться не более чем в 10 ярдах от лунки?
Ответ:
Вопрос 42.
СРАВНЕНИЕ МЕТОДОВ
Здание построено на вершине скалы высотой 300 метров. Человек, стоящий на ровной поверхности под обрывом, замечает, что угол подъема к вершине здания составляет 72°, а угол подъема к вершине обрыва — 63°.
а. На каком расстоянии человек от основания скалы?
Ответ:
б. Опишите два различных метода, которые можно использовать для определения высоты здания. Используйте один из этих методов, чтобы найти высоту здания.
Ответ:
Рассмотрим △SYZ и оценим d с помощью функции тангенса
Человек стоит на расстоянии 152,86 м от основания утеса.
Рассмотрим △XYS и оценим h + 300
tan XYZ = \(\frac { h + 300 }{ d } \)
h = 152,86 x tan 72 – 300
h = 170,45
Высота здания 170,45 м.
Вопрос 43.
МАТЕМАТИЧЕСКИЕ СОЕДИНЕНИЯ
Найдите значения x и y.
Ответ:
Вопрос 44.
КАК ВЫ ЭТО ВИДИТЕ?
Вы бы использовали закон синусов или закон косинусов, чтобы решить треугольник?
Ответ:
В любом треугольнике можно использовать закон синусов, если известны две стороны и один угол, противолежащий данной стороне (SSA), или два угла и любая сторона (AAS или ASA).
В любом треугольнике можно использовать закон косинуса, если две стороны входят в один угол сторон.
Вопрос 45.
ПЕРЕПИСАТЬ ФОРМУЛУ
A Упростите закон косинусов, если заданный угол прямой.
Ответ:
Вопрос 46.
НАВОДИТ НА МЫСЛЬ
Рассмотрим любой треугольник с длинами сторон a, b и c. Вычислите значение s, равное половине периметра треугольника. Какое измерение треугольника представлено \(\sqrt{s(s-a)(s-b)(s-c)} ?\)
Ответ:
Вопрос 47.
АНАЛИЗ СООТНОШЕНИЙ
Возникает неоднозначный случай закона синусов когда вам дана мера одного острого угла. длина одной из смежных сторон и длина стороны, противоположной этому углу, который меньше длины смежной стороны. Это приводит к двум возможным треугольникам. Используя данную информацию, найдите два возможных решения для ∆ABC
Нарисуйте схему для каждого треугольника.
(Подсказка: функция обратного синуса дает только размеры острого угла. Поэтому рассмотрим острый угол и его дополнение для ∠B.)
Поэтому рассмотрим острый угол и его дополнение для ∠B.)
a. м ∠ A = 40°, a = 13, b = 16
б. m ∠ A = 21°, a = 17, b = 32
Ответ:
Вопрос 48.
РЕЗЮМЕ
Используйте закон косинусов, чтобы показать, что мера каждого угла равностороннего треугольника равна 60. °. Объясните свои рассуждения.
Ответ:
a² = b² + c²- 2bc cos A
a² = a² + a² – 2 aa cos A
a² = 2a² coas A
cos A = 1/2
∠A = 60
Вопрос 49.
КРИТИЧЕСКОЕ МЫШЛЕНИЕ
Самолет летит в 55° к востоку от города А до города Б. расстояние 470 миль. Другой самолет летит на 7° к северу от востока из города А в город С на расстояние 890 миль. Каково расстояние между городами B и C?
Ответ:
Вопрос 50.
ПЕРЕПИСАТЬ ФОРМУЛУ
Выполните шаги, чтобы вывести формулу площади треугольника.
Площадь = \(\frac{1}{2}\)ab sin C.
а. Проведите высоту от вершины B до \(\overline{A C}\). Обозначьте высоту как h. Запишите формулу площади треугольника, используя h.
Обозначьте высоту как h. Запишите формулу площади треугольника, используя h.
Ответ:
Основание треугольника как б.
Запись площади треугольника в форме h с использованием площади треугольника.
Площадь треугольника = 1/2 × основание × высота
ΔABC = 1/2 × b × h
b. Напишите уравнение для sin C
Ответ: Нам нужно найти уравнение для sin C, если ΔABC задано со сторонами a, b, c.
в. Используя результаты пунктов (а) и (б), запишите формулу площади треугольника, не содержащего h.
Ответ:
ΔABC = 1/2 × b × h
sin C = h/a
вычисляя h,
h = a sin C
= 1/2 ab sinC
Отсюда доказано.
Вопрос 51.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Выполните шаги, чтобы использовать формулу площади треугольника для доказательства закона синусов (теорема 9.9).
а. Используйте вывод в упражнении 50, чтобы объяснить, как вывести три связанные формулы для площади треугольника.
Площадь = \(\frac{1}{2}\)bc sin A,
Площадь = \(\frac{1}{2}\)ac sin B,
Площадь = \(\frac{1}{2) }\)ab sin C
б. почему вы можете использовать формулы в части (а), чтобы написать следующее утверждение?
почему вы можете использовать формулы в части (а), чтобы написать следующее утверждение?
\(\frac{1}{2}\)bc sin A = \(\frac{1}{2}\)ac sin B = \(\frac{1}{2}\)ab sin C
c . Покажите, как переписать утверждение в части (b), чтобы доказать закон синусов. Обоснуйте каждый шаг.
Ответ:
Вопрос 52.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Используйте данную информацию для завершения двухколоночного доказательства закона косинусов (теорема 9.10).
Дана \(\overline{B D}\) высота ∆ABC.
Докажите a 2 = b 2 + c 2 – 2bc cos A
| Утверждения | Причины |
| 1. \(\overline{B D}\) — высота ∆ABC. | 1. Дано |
| 2. Треугольники ∆ADB и ∆CDB прямоугольные. | 2. _______________________ |
| 3. а 2 = (б – х) 2 + з 2 | 3. ____________________________ |
4. _______________________ _______________________ | 4. Раскройте бином. |
| 5. х 2 + ч 2 = с 2 | 5. _______________________ |
| 6. _______________________ | 6. Подстановочное свойство равенства |
| 7. cos A = \(\frac{x}{c}\) | 7. ____________________________ |
| 8. х = с cos A | 8. _______________________ |
| 9. a 2 = b 2 + c 2 – 2bc Cos A | 9. ____________________________ |
Ответ:
Поддержание математических знаний
Найдите радиус и диаметр окружности.
Вопрос 53.
Ответ:
Вопрос 54.
Ответ:
Радиус 10 дюймов, диаметр 20 дюймов.
Вопрос 55.
Ответ:
Вопрос 56.
Ответ:
Радиус равен 50 дюймам, а диаметр равен 100 дюймам. Затем скажите, образуют ли длины сторон пифагорову тройку.
Вопрос 1.
Ответ:
x = 2√34
Стороны не образуют пифагорову тройку.
Объяснение:
x² = 6² + 10²
x²= 36 + 100
x = 2√34
Вопрос 2.
Ответ:
x = 12
Стороны образуют пифагорову тройку.
Объяснение:
20² = 16²+ x²
400 = 256 + x²
x² = 144
x = 12
Вопрос 3.
Ответ:
Объяснение:
13² = 7² + x²
169 = 49 + x²
x = 2√30
Убедитесь, что длины сегментов образуют треугольник. Треугольник остроугольный, прямоугольный или тупоугольный?
Вопрос 4.
6, 8 и 9
Ответ:
9² = 81
6² + 8² = 36 + 64 = 100
9² < 6² + 8²
Итак, треугольник остроугольный
Ответ:
10² = 100
(2√2)² + (6√3)² = 8 + 108 = 116
Итак, треугольник остроугольный.
Вопрос 6.
13, 18 и 3√55
Ответ:
18² = 324
13² + (3√55)² = 169 + 495 = 664
Итак, треугольник остроугольный.
9.2 Особые прямоугольные треугольники
Найдите значение x. Запишите ответ в простейшей форме.
Вопрос 7.
Ответ:
гипотенуза = катет • √2
x = 6√2
Вопрос 8.
Ответ:
более длинный катет = более короткий катет • 0 √0 √3
x = 8,08
Вопрос 9.
Ответ:
более длинный катет = более короткий катет • √3
x = 8√3 • √3
x = 24
Затем найдите значение х.
10 вопрос (6 x 4)
x = 2√6
Вопрос 12.
Ответ:
\(\frac { RP }{ RQ } \) = \(\frac { SP }{ RS } \)
\( \frac { 9 }{ x } \) = \(\frac { 6 }{ 3 } \)
x = 3,5
Вопрос 13.
Ответ:
\(\frac { SU }{ ST } \) = \(\frac { SV }{ VU } \)
\(\frac { 16 }{ 20 } \) = \(\frac { x }{ (x – 16) } \)
4(x – 16) = 5x
x = 16
Найдите среднее геометрическое двух чисел.
Вопрос 14.
9 и 25
Ответ:
среднее значение = √(9 x 25)
= 15
Вопрос 15.
36 и 48
Ответ: 90 015 среднее значение = 90 46 √4 √3
Вопрос 16.
12 и 42
Ответ:
среднее = √(12 x 42)
= 6√14
9.4 Отношение касательных
Найдите касательные прямоугольного треугольника. Запишите каждый ответ в виде дроби и десятичной дроби, округленной до четырех знаков после запятой.
Вопрос 17.
Ответ:
tan J = \(\frac { Противоположная сторона }{ Смежная сторона } \)
tan J = \(\frac { LK }{ JK } \) = \(\frac { 11 }{ 60 } \)
tan L = \(\frac { JK }{ LK } \) = \(\frac { 60 }{ 11 } \)
Вопрос 18.
Ответ:
tan P = \(\frac { MN }{ MP } \) = \(\ frac { 35 }{ 12 } \)
tan N = \(\ frac { MP }{ MN } \) = \(\ frac { 12 }{ 35 } \)
Вопрос 19.
Ответ:
tan A = \(\frac { BC }{ AC } \) = \(\frac { 7 }{ 4√2 } \)
tan B = \(\frac { AC }{ BC } \) = \(\frac { 4√2 }{ 7 } \)
Найдите значение x. Округлите ответ до десятых. Вопрос 20
Ответ:
тангенс 25 = \(\frac { x }{ 20 } \)
0,46 x 20 = x
x = 9,2
Вопрос 22.
Ответ:
\ тангенс { 38 = \(frac 38 10 }{ х } \)
х = 12,82
Вопрос 23.
Угол между низом забора и верхушкой дерева равен 75°. Дерево в 4 годах от забора. Насколько высокое дерево? Округлите ответ до ближайшего фута.
Ответ:
tan 75 = \(\frac { x }{ 4 } \)
x = 14,92
9.5 Отношения синуса и косинуса
Найдите sin X, sin Z, cos X и cos Z. Запишите каждый ответ в виде дроби и десятичного числа, округленного до четырех знаков после запятой.
Вопрос 24.
Ответ:
sin X = \(\frac { 3 }{ 5 } \)
sin Z = \(\frac { 4 }{ 5 } \)
cos X = \(\ frac { 4 }{ 5 } \)
cos Z = \(\frac { 3 }{ 5 } \)
Вопрос 25.
Ответ:
sin X = \(\frac { 7 }{ √149 } \)
sin Z = \(\frac { 10 }{ √149 } \)
cos X = \(\frac { 10 }{ √149 } \)
cos Z = \(\frac { 7 }{ √149 } \)
Вопрос 26.
Ответ:
sin X = \(\frac { 55 }{ 73 } \)
sin Z = \(\frac { 48 }{ 73 } \)
cos X = \(\ frac { 48 }{ 73 } \)
cos Z = \(\frac { 55 }{ 73 } \)
Найдите значение каждой переменной с помощью синуса и косинуса. Округлите свои ответы до десятых.
Округлите свои ответы до десятых.
27 вопрос Вопрос 28
Вопрос 29.
Ответ:
sin 70 = \(\frac { v }{ 10 } \)
v = 9,39
cos 70 = \(\frac { w }{ 10 } \)
w = 3,42
Вопрос 30.
Напишите sin 72° по косинусу.
Ответ:
sin 72 = cos(90 – 72)
= cos 18 = 0,95
Вопрос 31.
Запишите cos 29° через синус.
Ответ:
sin 29 = cos(90 – 29)
= cos 61 = 0,48
9.6 Решение прямоугольных треугольников
Пусть ∠Q — острый угол. Используйте калькулятор, чтобы приблизить величину ∠Q к ближайшей десятой доле градуса.
Вопрос 32.
COS Q = 0,32
Ответ:
COS Q = 0,32
♂ = обратный COS 0,32
♂ = 71,3
Вопрос 33.
SIN Q = 0,91
Ответ:
SIN Q 33. = 0,91
♂ = обратный грех 0,91
♂ = 65,5
Вопрос 34.
TAN Q = 0,04
Ответ:
TAN Q = 0,04
потряно правильный треугольник. Округлите десятичные ответы до десятых.
Вопрос 35.
Ответ:
a = 5√5, ∠A = 47,7, ∠B = 42,3
Объяснение:
c² = a² + b²
15² = a² + 10²
a² = 125 A 0 5
a = 125 A 0 5
a = = \(\frac { 5√5 }{ 15 } \) = 0,74
∠A = 47,7
∠A + ∠B + ∠C = 180
47,7 + ∠B + 90 = 180
∠B = 42,3
Вопрос 36.
Ответ:
NL = 7,59, ∠L = 53, ML = 4,55
Объяснение:
cos 37 = \(\frac { 6 }{ NL } \)
NL = 7,59
∠M + ∠M + ∠L = 180
37 + 90 + ∠L = 180
∠L = 53
sin 37 = \(\frac { ML }{ 7,59 } \)
ML = 4,55
Вопрос 37.
Ответ:
XY = 17,34, ∠5 9Z0 = 4 4 ∠9Z0
Объяснение:
c² = a² + b²
25² = 18²+ b²
b² = 301
b = 17,34
sin X = \(\frac { 18 }{ 25 } \)
∠X = 46
сумма углов = 180
46 + 90 + ∠Z = 180
∠Z = 44
9.7 Закон синусов и закон косинусов
Найдите площадь ∆ABC с данными длинами сторон и прилежащим к ним углом.
Вопрос 38.
м ∠ B = 124°, a = 9, c = 11
Ответ:
Площадь = \(\frac { 1 }{ 2 } \) ac sin B
= \(\frac { 1 }{ 2 } \) (9 x 11) sin 124
= 40,59
Вопрос 39.
м ∠ A = 68°, b = 13, c = 7
Ответ:
Площадь = \(\frac { 1 } { 2 } \) bc sin A
= \(\frac { 1 }{ 2 } \) (13 x 7) sin 68
= 41,86
Вопрос 40.
м ∠ C = 79°, a = 25 b = 17
Ответ:
Площадь = \(\frac { 1 }{ 2 } \) ab sin C
= \(\frac { 1 }{ 2 } \) (25 x 17) sin 79
= 208,25
Решите ∆ABC. Округлите десятичные ответы до десятых.
Вопрос 41.
м ∠ A = 112°, a = 9, b = 4
Ответ:
∠B = 24, ∠C = 44, c = 6,76
Объяснение:
\(\frac { sin B }{ b } \) = \ (\ frac { sin A }{ a } \)
\ (\ frac { sin B }{ 4 } \) = \ (\ frac { sin 112 }{ 9 } \)
sin B = 0,408
∠B = 24
∠A + ∠B + ∠C = 180
112 + 24 + ∠C = 180
∠C = 44
\(\frac { sin 112 }{ 9 } \) = \( \фракция { грех 44} { с } \)
c = 6,76
Вопрос 42.
м ∠ 4 = 28°, м ∠ B = 64°, c = 55
Ответ:
∠C = 88, b = 49,4, a = 25,5
Объяснение:
A + ∠B + ∠C = 18028 + 64 + ∠C = 180
∠C = 88
\(\frac { sin B }{ b } \) = \(\ frac { sin C }{ c } \ )
\(\frac { sin 64 }{ b } \) = \(\ frac { sin 88 }{ 55 } \)
\(\ frac { sin 64 }{ b } \) = 0,018
b = 49,4
\(\frac { sin 28 }{ a } \) = \(\ frac { sin 88 }{ 55 } \)
a = 25,5
Вопрос 43.
м ∠ C = 48°, b = 20, c = 28
Ответ:
∠B = 31,3, ∠A = 100,7, a = 37,6
Объяснение:
\(\frac { sin B }{ b } \ ) = \(\frac { sin C }{ c } \)
\(\ frac { sin B }{ 20 } \) = \(\ frac { sin 48 }{ 28 } \)
\(\ frac { sin B }{ 20 } \) = 0,026
sin B = 0,52
∠B = 31,3
∠A + ∠B + ∠C = 180
∠A + 31,3 + 48 = 180
∠A = 100,7
\(\frac { sin 100,7 }{ a } \) = \(\frac { sin 48 }{ 28 } \)
a = 37,6
Вопрос 44.
м ∠ B = 25°, a = 8, c = 3
Ответ:
b = 5,45, ∠A = 37,5, ∠C = 117,5
Объяснение:
b² = a² + c²- 2ac cos B
b² = 8² + 3² – 2(8 x 3) cos 25 = 73 – 43,2 = 29,8
b = 5,45
\(\frac {sin A} {8} \) = \(\frac {sin 25} {5,45} \)
sin A = 0,61
∠A = 37,5
∠A + ∠ B + ∠C = 180
37,5 + 25 + ∠C = 180
∠C = 117,5
Ответ:
= 35, с = 14,72, а = 12,3
Объяснение:
∠A + ∠B + ∠C = 180
∠A + 102 + 43 = 180
∠A = 35
\(\frac { sin 102 }{ 21 } \) = \(\ frac { sin 43 }{ c } \)
0,046 = \(\frac { sin 43 }{ c } \)
c = 14,72
\(\ frac { sin 102 }{ 21 } \) = \(\ frac { sin 35 }{ a } \ Вопрос 46 = 125,19, ∠A = 43,11
Объяснение:
b² = a² + c²- 2ac cos B
3² = 10² + 12²- 2(10 x 12) cos B
9 = 100 + 144 – 240 cos B
cos B = 0,979
∠B = 11,7
a² = b² + c²- 2bc cos A
100 = 9 + 144 – 72 cos A
cos A = 0,73 ∠ 39015
∠A + ∠B + ∠C = 180
43,11 + 11,7 + ∠C = 180
∠C = 125,19
Прямоугольные треугольники и тригонометрический тест
Найдите значение каждой переменной. Округлите свои ответы до десятых.
Округлите свои ответы до десятых.
Вопрос 1.
Ответ:
sin 25 = \(\frac { t }{ 18 } \)
t = 7,5
cos 25 = \(\frac { s }{ 18 } \)
s = 16,2
Вопрос 2.
Ответ:
sin 22 = \(\frac { 6 }{ x } \)
x = 16,21
cos 22 = \(\frac { y }{ 16,21 } \)
y = 14,91
Вопрос 3.
Ответ:
tan 40 = \(\frac { k }{ 10 } \)
k = 8,3
cos 40 = \(\ frac { 10 }{ j } \)
j = 13,15
Верно, что длины отрезков образуют треугольник. Треугольник остроугольный, прямоугольный или тупоугольный?
Вопрос 4.
16, 30 и 34
Ответ:
34²= 16² + 30²
Итак, треугольник прямоугольный.
Вопрос 5.
4, √67 и 9
Ответ:
9² = 81
4² + (√67)² = 83
Итак, треугольник остроугольный
Вопрос 6.
√5. 5. и 5.5
Ответ:
5,5² = 30,25
√5² + 5² = 30
Итак, треугольник тупоугольный
Решите ∆ABC. Округлите десятичные ответы до десятых.
Вопрос 7.
Ответ:
c = 12,08, ∠A = 24,22, ∠C = 65,78
Объяснение:
tan A = \(\frac { 5 }{ 11 } \)
∠A = 24,22
c² = 11²+ 5²
c = 12,08
24,22 + 90 + ∠C = 180
∠C = 65,78
5 Вопрос 9 8,0005
Ответ:
∠B = 35,4, ∠C = 71,6, c = 17,9
Объяснение:
\(\frac { sin 73 }{ 18 } \) = \(\frac { sin B }{ 11 } \ )
sin B = 0,58
∠B = 35,4
73 + 35,4 + ∠C = 180
∠C = 71,6
\(\frac { sin 73 }{ 18 } \) = \(\frac { sin 71,6 }{ c } \)
с = 17,9
Вопрос 9.
Ответ:
BC = 4,54, ∠B = 59,3, ∠A = 30,7
Объяснение:
9,2² = 8² + x²
x = 4,54
\(\frac { sin 90 }{ 9,2 } \) = \( \frac { sin B }{ 8 } \)
sin B = 0,86
∠B = 59,3
∠A + 59,3 + 90 = 180
∠A = 30,7
Вопрос 10.
м ∠ A = 103°, b = 12, c = 24
Ответ:
a = 29, ∠B = 53,5
Объяснение:
a² = b² + c²- 2bc cos A
a² = 144 + 24² – 2(12 x 24) cos 103
a = 29
\(\frac { sin B }{ 12 } \) = \(\ frac { sin 103 }{ 29} \)
∠B = 23,5
∠C = 180 – (103 + 23,5) = 53,5
Вопрос 11.
м ∠ A = 26°, м ∠ C = 35°, b = 13
Ответ:
B = 119, a = 6,42, c = 8,5
Объяснение:
∠B + 26 + 35 = 180
∠B = 119
\(\frac { sin 119 }{ 13 } \) = \(\frac { sin 26 }{ a } \)
a = 6,42
\(\frac { sin 119 }{ 13 } \) = \(\frac { sin 35 }{ c } \)
c = 8,5
Вопрос 12.
a = 38, b = 31, c = 35
Ответ:
∠B=50,2, ∠C = 59,8, ∠A = 70
Пояснение:
b² = a² + c²- 2ac cos B
31² = 38²+ 35²- 2(35 x 38) cos B
cos B = 0,64
∠B=50,2
a² = b² + c²- 2bc cos15 A
38² = 31²+ 35²- 2(31 x 35) cos A
cos A = 0,341
∠A = 70
∠C = 59,8
Вопрос 13.
Запишите cos 53° через синус.
Ответ:
cos 53° = sin (90 – 53) = sin 37
Найдите значение каждой переменной. Запишите ответы в простейшей форме.
Вопрос 14.
Ответ:
sin 45 = \(\frac { 16 }{ q } \)
q = 22,6
cos 45 = \(\frac { r }{ q } \)
r = 16
Вопрос 15.
Ответ:
В ∆QRS m ∠ R = 57°, q = 9, s = 5. Найдите площадь ∆QRS.
Ответ:
Площадь = \(\frac { 1 }{ 2 } \) qs sin R
= \(\frac { 1 }{ 2 } \) (9 x 5) sin 57 = 18,675
Вопрос 18.
Вам даны меры обоих острых углов прямоугольного треугольника. Можно ли определить длину сторон? Объяснять.
Ответ:
№
Вопрос 19.
Вы находитесь на параде и смотрите на большой воздушный шар, парящий прямо над улицей. Вы находитесь в 60 футах от точки на улице прямо под воздушным шаром. Чтобы увидеть верхнюю часть воздушного шара, вы смотрите вверх под углом 53°. Чтобы увидеть дно воздушного шара, вы смотрите вверх под углом 29°. Оцените высоту h воздушного шара.
Ответ:
Высота воздушного шара 46 футов
Высота от земли до вершины воздушного шара представлена x.
Тригонометрическая функция:
Тан тета = противоположное/прилегающее
Тан 53 градуса = х/60
х = 60 х Тан 53 градуса.
= 79,6227
x = 79,62 фута
Высота от земли до дна воздушного шара может быть представлена как t.
Тан тета = противоположный/прилегающий
Тан 29 градусов = у/60 градусов.
Y = 60 x тангенс 90 градусов.
= 33,2585
= 33,26 фута.
Высота воздушного шара x – y
= 79,6227 – 33,2585
= 46,3642
Высота воздушного шара 46 футов.
Вопрос 20.
Вы советуете сфотографировать статую на острове Пасхи, называемую моаи. Высота моаи около 13 футов. Ваша камера стоит на штативе высотой 5 футов. Вертикальный угол обзора камеры установлен на 90°. На каком расстоянии от моаи нужно стоять, чтобы вся высота моаи была идеально обрамлена на фото?
Ответ:
Из диаграммы AB — высота статуи на острове Пасхи, а CD — высота треножника.
Угол ABC = угол DCB = 90 градусов.
AB//DC
Угол BDC = Угол ABD
УГОЛ BDC = Угол ABD x Угол ADB = BCD = 90 градусов.
Угол ADB приблизительно равен углу BCD
AB/BD = BD/DC = 13/BD = BD/5
BD² = 5 x 13 = 80
BD = квадратный корень из (80) = 4 квадратный корень из (5)
BD² = DC² + BC²
BC = квадратный корень из (BD² – DC²)
Угол BCD = 90 градусов
DC = 5
BD = 4 квадратный корень из (5)
BC = квадратный корень из ((4(квадратный корень из (5)) ²
= квадратный корень из (80 – 25)
= квадратный корень из (55)
= 7,42
Следовательно, вы можете стоять на расстоянии 7,42 фута от Моаи Таким образом, вся высота Моаи идеально обрамлена на фотографии
Прямоугольные треугольники и тригонометрия Совокупная оценка
Вопрос 1.
Размер экрана ноутбука измеряется длиной его диагонали.Хотите приобрести ноутбук с максимально большим экраном.Какой ноутбук купить?
(А)
(Б)
(В)
(Г)
Ответ:
(Б)
Объяснение:
(а) d = √9² + 12² = 15
(√) 11,25² + 20² = 22,94
(c) d = √12² + 6,75² = 13,76
(d) d = √8² + 6² = 10
Вопрос 2.
В ∆PQR и ∆SQT S находится между P и Q , T находится между R и Q, и \(\) Что должно быть верно относительно \(\overline{S T}\) и \(\overline{PR}\)? Выбрать все, что подходит.
\(\overline{ST}\) ⊥ \(\overline{PR}\) \(\overline{ST}\) || \(\overline{PR}\) ST = PR ST = \(\frac{1}{2}\)PR
Ответ:
Вопрос 3. Вопрос 4. Ответ: Вопрос 5. ____________ = ______________ sin x cos x tan x \ (\ frac {x y} {x z} \) \ (\ frac {y z} {x z} \) sin z cos z tan z \ (\ frac {X Y}{Y Z}\) \(\frac{Y Z}{X Y}\) Ответ: Вопрос 6. Вопрос 7. Вопрос 8. а. Используя длину стороны основания, высоту пирамиды и теорему Пифагора, найдите наклонную высоту AB пирамиды. Ответ: b. Найдите переменный ток. c. Назовите три возможных способа найти m ∠ 1. Затем найдите m ∠ 1,9.0015 Ответ: Добро пожаловать на курс геометрии в DRHS! На этом веб-сайте есть все документы, которые мы будем использовать для этого класса. Чтобы посмотреть видеоуроки, посетите наш канал на YouTube класса: Канал Geom DRHS на YouTube Чтобы просмотреть миллиметровую бумагу для печати, нажмите здесь: ссылка на миллиметровую бумагу Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Комментарии (-1) Кредиты: 1 Пререквизиты: Алгебра 1 Рекомендуется : 9 -е, 10 -е Тестовая подготовка: SAT, PSAT Описание: 0004 Этот курс геометрии для старших классов знакомит учащихся с основными принципами геометрии с изучением более сложных тем, таких как фракталы. Студенты учатся с помощью учебников, видео, практики, исследований и онлайн-интерактивов. Подготовка к SAT включена в ежедневные вопросы SAT по алгебре и геометрии. Студенты также будут использовать онлайн-калькулятор и сдавать экзамены, включая промежуточный и выпускной. Темы, затронутые в этом курсе, включают точки, прямые, плоскости, углы, доказательство теорем с помощью дедуктивных и индуктивных рассуждений, параллельные и перпендикулярные прямые и плоскости, отношения углов, уравнения прямых и наклонов, типы треугольников, свойства отрезков и углов, свойства конгруэнтных треугольников, многоугольников, четырехугольников, параллелограммов, ромбов, прямоугольников, квадратов, воздушных змеев, трапеций, отношения и пропорции, подобие, растяжения, теорема Пифагора и ее обращение, закон синусов, закон косинусов, свойства окружностей и их касательной линии, дуги, вписанные углы и хорды; уравнения и графики окружностей, периметр и площадь треугольников, четырехугольников, многоугольников и окружностей; площадь поверхности и объем призм, цилиндров, пирамид, конусов и сфер; Симметрия и преобразования. Материалы : транспортир, линейка, циркуль, чертежная бумага, миллиметровка Ресурсы: CK12 Geometry Flexbook, Yay Math Примечания : : Попробуйте первый учебник, попробуйте загрузить его. перезагрузка страницы. Если это не сработает, попробуйте другой браузер. Когда вы оцениваете свои ответы на контрольные вопросы, всегда подсчитывайте и записывайте, сколько из них вы ответили правильно. Не вычитайте неправильное число из полученной суммы. Каждая проблема оценивается в один балл, если не указано иное. Вы можете дать частичный зачет за задачу, состоящую из нескольких частей. Урок 1(*) (Обратите внимание, что звездочка * означает, что к этому уроку есть рабочий лист) Добро пожаловать в ваш первый день в школе! Я хотел дать вам одно важное напоминание , прежде чем вы начнете. Многие из ваших уроков ниже имеют интернет-ссылку, по которой вы можете щелкнуть. Урок 2 Урок 3 Урок 4 Урок 5 Урок 6 Урок 7 Урок 8 Урок 9 Урок 10 Урок 11 Урок 12 Урок 13 Урок 14 Урок 15* Урок 16 Урок 17 Урок 18 Урок 19* Урок 20 Урок 21 Урок 22 Урок 23* Урок 24 Урок 25 Lesson 26* Урок 27 Урок 28 Урок 29 Урок 30 Урок 31 Урок 32* Урок 33 Урок 34 Урок 35 Урок 36 Урок 37 Урок 38 Урок 39 Урок 40 Урок 41 Урок 42 Урок 43 Урок 44 Урок 45 СТОП Время для обновления табеля успеваемости и портфолио/документов. Портфолио/отчеты: В ваше портфолио вы должны включить пару ваших заданий за этот квартал. Вы также можете сделать снимок экрана графического калькулятора или другой онлайн-активности. Вот как найти свою оценку: сложите все оценки, которые вы записали за эту четверть. Сложите свои баллы и запишите это число. Разделите количество очков на возможное количество. Переместите запятую на два знака вправо. В следующем поле напишите число перед запятой (что-то между 1 и 100). Это ваш процентный балл. В следующем поле напишите свою буквенную оценку. Все, что начинается с 9, — это A. Все, что начинается с 8, — это B. Все, что начинается с 7, — это C и так далее. Если у вас все идеально, то ваша оценка 100. Это тоже пятерка. Ваша цель — получить пятерку за курс в конце года. Вернитесь и посмотрите, где вы потеряли очки. Что вы можете сделать, чтобы не потерять эти очки в следующем квартале? Урок 46(*) Урок 47 Урок 48 Урок 49 Урок 50* Урок 51 Урок 52* Урок 53* Урок 54 Урок 55 Урок 56 Урок 57* Урок 58* Урок 59 Урок 60 Урок 61 Урок 62 Урок 63 Урок 64 Урок 65 Урок 66 Lesson 67 Урок 68 Урок 69 Урок 70 Урок 71 Урок 72 Урок 73 Урок 74 Урок 75 Урок 76* Урок 77 Урок 78 Урок 79 Урок 80* Урок 81 Урок 82 Урок 83 Урок 84 Урок 85 Урок 86 Урок 87 Урок 88 Урок 89 Урок 90* СТОП Время для обновления табеля успеваемости и портфолио/документов. Портфолио/отчеты: В ваше портфолио вы должны включить пару ваших заданий за этот квартал. Вы также можете сделать снимок экрана графического калькулятора или другой онлайн-активности. Выбирайте опрятные и хорошо сохранившиеся вещи. Вот как найти свою оценку: сложите все оценки, которые вы записали за эту четверть. Разделите ваш результат на максимально возможное. Переместите запятую на два знака вправо. В следующем поле напишите число перед запятой (что-то между 1 и 100). Это ваш процентный балл. В следующем поле напишите свою буквенную оценку. Все, что начинается с 9является A. Все, что начинается с 8, является B. Все, что начинается с 7, является C и так далее. Если у вас все идеально, то ваша оценка 100. Это тоже пятерка. Ваша цель — получить пятерку за курс в конце года. Вернитесь и посмотрите, где вы потеряли очки. Что вы можете сделать, чтобы не потерять эти очки в следующем квартале? Урок 91(*) Урок 92 Урок 93 Урок 94 Урок 95 Урок 96 Урок 97 Урок 98 Урок 99 Урок 100 Урок 101 Урок 102 Урок 103 Урок 104 Урок 105 Урок 106 Урок 107 Lesson 108 Урок 109* Урок 110* Урок 111 Урок 112 Урок 113 Урок 114 Урок 115 Урок 116 Урок 117 Урок 118 Урок 119* Урок 120 Урок 121 Урок 122 Урок 123 Урок 124 Урок 125 Урок 126 Урок 127 Урок 128 Урок 129 Урок 130 Урок 131 Урок 132 Урок 133 Урок 134 Урок 135 STOP Время для обновления табеля успеваемости и портфолио/документов. Портфолио/отчеты: В ваше портфолио вы должны включить пару ваших заданий за этот квартал. Вы также можете сохранить страницу заметок из одного из видео с примечанием о том, что это такое. Выбирайте опрятные и хорошо сохранившиеся вещи. Вот как найти свою оценку: сложите все оценки, которые вы записали за эту четверть. Сложите свои баллы и запишите это число. Разделите ваш результат на максимально возможное. Переместите запятую на два знака вправо. В следующем поле напишите число перед запятой (что-то между 1 и 100). Это ваш процентный балл. В следующем поле напишите свою буквенную оценку. Все, что начинается с 9является A. Все, что начинается с 8, является B. Все, что начинается с 7, является C и так далее. Если у вас все идеально, то ваша оценка 100. Это тоже пятерка. Ваша цель — получить пятерку за курс в конце года. Урок 136*(*) Урок 137 Урок 138 Урок 139 Урок 140 Урок 141 Урок 142 Урок 143 Урок 144 Урок 145 Урок 146 Урок 147 Урок 148 Урок 149 Урок 150 Урок 151 Урок 152 Урок 153 Урок 154 Урок 155 Урок 156 Урок 157 Урок 158 Урок 159 Урок 160 Урок 161 Урок 162 Урок 163 Урок 164 Урок 165 Урок 166 Урок 167 Урок 168 Урок 169 Урок 170 Урок 171 Урок 172 Урок 173 Урок 174 Урок 175 Урок 176 Урок 177 Урок 178 Урок 179 Урок 180 СТОП Время для обновления табеля успеваемости и портфолио/документов. На этот раз вы узнаете свой общий балл, сложив и разделив свои итоги за четыре четверти. Если вы решите , вы можете получить до половины своей оценки за участие, выполняя ежедневные задания. Это будет 50 (за участие) плюс половина вашей обычной оценки за вашу общую оценку за год. Нужно подготовиться к разделу SAT по математике, но не знаете, с чего начать? Тоже бюджетно? Не беспокоиться! В этой статье мы собрали исчерпывающий список всех лучших (и бесплатных!) учебных материалов и руководств по SAT Math, доступных в настоящее время в Интернете. Примечание: Чтобы получить информацию о лучших учебных материалах для SAT, за которые вам нужно заплатить, ознакомьтесь с нашей подборкой лучших книг для подготовки к SAT. Feature Image: Alan O’Rourke/Flickr Очень важно получать учебные материалы из нужных мест. SAT — это очень специфический тест, и существует множество (много!) веб-сайтов и программ, которые, к сожалению, предлагают только некачественные ресурсы SAT. Если вы будете учиться, используя в основном некачественные материалы SAT, вы не получите четкого представления о том, как вы будете справляться в день экзамена. Подготовка к экзамену заключается в оценке и улучшении вашего текущего уровня, но вы не сможете этого сделать, если у вас возникнет ложное представление о ваших навыках, основанное на плохих учебных материалах. Таким образом, лучше отдать предпочтение официальным материалам SAT. SAT разработан Советом колледжей, и их бесплатные материалы, безусловно, являются лучшим местом для начала обучения. Отсюда вы можете перейти к программам и материалам, которые используют (или очень напоминают) официальные материалы SAT. Теперь давайте посмотрим на лучшие ресурсы, которые вы можете использовать для бесплатных официальных практических вопросов SAT по математике. Готово, готово! В этом разделе мы рассмотрим пять лучших бесплатных ресурсов, которые вы можете использовать для качественной подготовки к SAT Math. Как создатель и эмитент SAT, College Board является лучшим местом для начала сбора бесплатных учебных материалов SAT по математике. 10 официальных тренировочных тестов в настоящее время доступны в Интернете. Каждый тест поставляется с ключом ответа и подробными объяснениями ответов, которые помогут вам понять, почему вы ответили неправильно. Вы, наверное, заметили, что в приведенном выше списке отсутствуют практический тест 2 и практический тест 4. В дополнение к полноценным тестам College Board предлагает несколько практических вопросов SAT по математике (а также примеры вопросов для всех других разделов теста). Для SAT Math есть 30 вопросов, разрешенных для калькулятора, и 18 вопросов без калькулятора. Хотя это не совсем полный раздел SAT по математике, он дает вам возможность получить больше информации о той математике, которую вы увидите в день экзамена. Отвечая на каждый вопрос, старайтесь не смотреть сразу на правильные ответы. Хотя новейшие практические тесты будут наиболее полезны для вашей подготовки, вы также можете использовать любой из этих четырех старых (до 2016 г.) практических тестов SAT. Большинство математических вопросов по ним должны быть полезными — просто обратите внимание, что в наши дни геометрия менее важна, а интерпретация данных важнее. Вы могли заметить, что некоторые годы отсутствуют (например, 2005-06, 2006-07 и т. Здесь не нужно взвешивать все за и против — все ресурсы, которые мы рекомендуем, гарантированно помогут вам получить отличный результат SAT Math! Академия Хана — некоммерческая организация, партнер College Board, которая предлагает бесплатную онлайн-программу подготовки к SAT и практические вопросы. В то время как большинство вопросов взято из официальных практических материалов SAT (таких как те, которые указаны выше), другие были созданы или адаптированы с одобрения или в тандеме с самим Советом колледжей. Зарегистрируйте бесплатную учетную запись Khan Academy, чтобы получить доступ к учебным вопросам и материалам SAT, а также руководствам и видео с пояснениями, которые помогут вам в учебе. Здесь, в PrepScholar, мы предлагаем множество бесплатных ресурсов, включая подробные руководства по каждой теме SAT по математике и полную коллекцию наших лучших статей по SAT Math. Все наши руководства включают определения и пояснения, примеры того, как вы увидите тему в тесте, и реальных практических вопроса SAT с подробными объяснениями ответов. Просмотрите наши руководства по математике SAT ниже, чтобы начать! Все руководства разбиты по темам. Целые числа (базовый) Целые числа (дополнительно) Дроби, отношения и пропорции Статистика (среднее, медиана, мода) Вероятность последовательности Уравнения с одной переменной Системы уравнений Функции Очки Линии и уклоны Отражения, переводы и вращения Линии и углы Круги Треугольники полигонов Твердотельная геометрия 28 важнейших математических формул SAT, которые вы ДОЛЖНЫ знать Кроме того, у нас есть руководства по стратегии, которые помогут вам решить многочисленные математические задачи SAT: Подключение ответов Подстановка чисел Если вы найдете наши руководства и тесты полезными, вы также можете подписаться на бесплатную пятидневную пробную версию нашей программы подготовки к экзаменам. Все наши вопросы основаны на реальных вопросах теста SAT, и, хотя полная программа не бесплатна, мы гарантируем возврат ваших денег, если вы не улучшите свои результаты на 160 баллов. CrackSAT — это бесплатный неофициальный веб-сайт SAT, предлагающий официальные практические тесты SAT в формате PDF, а также множество официальных и неофициальных вопросов SAT Math. Многие вопросы по CrackSAT взяты из учебников по подготовке к SAT, написанных известными компаниями, занимающимися подготовкой к экзаменам, включая The Princeton Review и Kaplan. Несмотря на то, что неофициальные вопросы SAT, как правило, основательны, они могут сильно различаться по качеству, поэтому не полагайтесь на 9 ответов. Что особенно приятно на этом веб-сайте, так это его организация: математические вопросы доступны как в категориях с несколькими вариантами ответов, так и в виде сетки, чтобы дать вам полный спектр математических упражнений. Вы также можете просматривать задачи по понятиям (например, линейные функции, показатели степени и радикалы и т. д.). Наконец, если вы хотите попрактиковаться в математике в контексте более полных практических тестов SAT, используйте два неофициальных PDF-файла практических тестов Ivy Global (SAT Online Practice Test 1 и Practice Test 2). Эти ресурсы точно соответствуют формату SAT и очень реалистичны. Однако они не идеальны. Некоторые вопросы в математических разделах слишком просты и не так похожи на вопросы SAT, как могли бы быть. Вы собрали весь учебный материал… и что теперь? Готовы не просто читать о SAT? Тогда вам понравится бесплатная пятидневная пробная версия для нашей программы SAT Complete Prep . Наша программа SAT, разработанная и написанная экспертами PrepScholar SAT , адаптируется к вашему уровню навыков по более чем 40 поднавыкам, чтобы вы могли сосредоточить свое обучение на том, что принесет вам наибольший прирост баллов. Нажмите на кнопку ниже, чтобы попробовать! Знать, как наилучшим образом использовать учебные материалы SAT, не менее важно, чем знать, как получить к ним доступ.
На диаграмме ∆JKL ~ ∆QRS. Выберите символ, который делает каждое утверждение верным.
<=>
sin j ___________ sin q sin l ___________ cos j cos l ___________ tan q
cos s s ___________ cos j cos j ___________ sin s tan j ___________ tan q
tan l ___________ tan q ___________ cos q q sin q q
___________ cos L
Ответ:
sin j = sin q sin l = cos j cos l = tan q
cos s j cos j> sin s tan j = tan q
tan l 
Геодезист делает показанные измерения. Какова ширина реки.
tan 34 = \(\frac { AB }{ 84 } \)
AB = 56,28
Составьте как можно больше правильных уравнений.
sin X = \(\frac{Y Z}{X Z}\) = cos Z
cos X = \(\ frac{X Y}{X Z}\) = sin Z
tan x = \(\frac{Y Z}{X Y}\)
tan Z = \(\frac{X Y}{Y Z}\)
Докажите, что четырехугольник DEFG — воздушный змей.
Дано \(\overline{H E} \cong \overline{H G}\), \(\overline{EG}\) ⊥ \(\overline{D F}\)
Докажите \(\overline{FE} \cong \ overline{F G}\), \(\overline{D E} \cong \overline{D G}\)
Ответ:
Каковы координаты вершин образа ∆QRS после композиции трансформации показывают?
(А) Q’ (1, 2), R'(5, 4), S'(4, -1)
(Б) Q'(- 1, — 2), R’ (- 5, — 4), S’ (- 4, 1)
(C) Q'(3, — 2), R’ (- 1, — 4), S’ (0, 1)
(D) Q’ (-2 , 1), R'(— 4, 5), S'(1, 4)
Ответ:
Красная пирамида в Египте имеет квадратное основание. Каждая сторона основания измеряет 722 фута. Высота пирамиды составляет 343 метра.
343² = h² + 722²
h = 635,3
Ответ:
AC = 343
Возможны три варианта: sin 1, cos 1 и tan 1
tan 1 = \(\frac { 722 }{ 635.3 } \)
∠1 = 48 Математика / Геометрия
 1
1 Geometry – Easy Peasy All-in-One High School
Нашли проблему? Проверьте здесь.


 Когда вы переходите на разные интернет-страницы для своих уроков, пожалуйста, НЕ нажимайте на что-либо еще на этой странице , кроме того, что указано в инструкциях. НЕ нажимайте на рекламу или игры. НЕ нажимайте на что-либо, что приведет вас на другой веб-сайт. Просто сосредоточьтесь на своем уроке, а затем закройте это окно, и вы должны вернуться к следующему уроку. Хорошо?
Когда вы переходите на разные интернет-страницы для своих уроков, пожалуйста, НЕ нажимайте на что-либо еще на этой странице , кроме того, что указано в инструкциях. НЕ нажимайте на рекламу или игры. НЕ нажимайте на что-либо, что приведет вас на другой веб-сайт. Просто сосредоточьтесь на своем уроке, а затем закройте это окно, и вы должны вернуться к следующему уроку. Хорошо? Помните, что когда мы говорим, что что-то является 2D или 3D, буква D означает размерность. 2D-объект имеет два измерения: высоту и ширину. Трехмерный объект имеет три измерения: высоту, ширину и глубину.
Помните, что когда мы говорим, что что-то является 2D или 3D, буква D означает размерность. 2D-объект имеет два измерения: высоту и ширину. Трехмерный объект имеет три измерения: высоту, ширину и глубину.
ПРИМЕЧАНИЕ. Исправления ответов:
(Очередь проверки 3B равна -3) Нажмите и перетащите пустое место, чтобы увидеть ответ.  Остановитесь, когда доберетесь до «Далее за гранью». 1.1 Геометрия – точки, линии и плоскости Если у вас еще нет бесплатной учетной записи CK-12, вам необходимо ее создать.
Остановитесь, когда доберетесь до «Далее за гранью». 1.1 Геометрия – точки, линии и плоскости Если у вас еще нет бесплатной учетной записи CK-12, вам необходимо ее создать. 
 Углы и измерения 1.3
Углы и измерения 1.3
ПРИМЕЧАНИЕ. Исправления ответа:
(#26 — на графике есть B в неправильных координатах)
(#34 должно быть x = 12) Нажмите и перетащите в пустое место, чтобы увидеть правильный ответ  Если вы хотите попробовать их, вы можете получить дополнительный балл за любой контрольный вопрос, который вы правильно ответите. 1.4 Середины и биссектрисы.
Если вы хотите попробовать их, вы можете получить дополнительный балл за любой контрольный вопрос, который вы правильно ответите. 1.4 Середины и биссектрисы. Проработайте примеры. Остановитесь после того, как просмотрели таблицу классифицирующих фигур.
Проработайте примеры. Остановитесь после того, как просмотрели таблицу классифицирующих фигур.
ПРИМЕЧАНИЕ. Ответ № 31 неверен. Он показывает вогнутый семиугольник вместо выпуклого семиугольника.  7.
7. Сегодня вы можете пропустить вопросы очереди.
Сегодня вы можете пропустить вопросы очереди.
ПРИМЕЧАНИЕ. Исправление ответа:
(#9 — 35-й член будет 18-м нечетным. (-3)*18+12 = -42)
(#15 — шаблон для четных чисел — 14-n и схема шансов n+4.) 


(Ответ: 340)
(Ответ: 1)
ПРИМЕЧАНИЕ. Исправление ответа:
(Просмотр очереди 1: сначала прибавьте 3 к обеим сторонам, а затем разделите обе стороны на 2. x=6) 

 Используйте углы, чтобы сделать снимки. Прямо вверх это 0 и 360 градусов.
Используйте углы, чтобы сделать снимки. Прямо вверх это 0 и 360 градусов.
ПРИМЕЧАНИЕ. Исправление ответа:
(#20 — Последний шаг доказательства должен гласить: Отрезок CH — биссектриса угла ∠ACE)  (Нажмите на уравнения, а затем на график.)
(Нажмите на уравнения, а затем на график.)
ПРИМЕЧАНИЕ – Исправление ответа:
(#30 – наклон AB равен -3/5, наклон CD равен 5/3)  (Вы можете получить один дополнительный кредитный балл, если вы ответите на все вопросы правильно.)
(Вы можете получить один дополнительный кредитный балл, если вы ответите на все вопросы правильно.)
ПРИМЕЧАНИЕ. Исправления ответа:
(19. у = 22)
(33. х = 20, у = 14 1/3) 
 (возможность получения дополнительных баллов)
(возможность получения дополнительных баллов) (по 1 баллу)
(по 1 баллу)
ПРИМЕЧАНИЕ. Исправления ответов:
(ответы №12 и №14 поменяны местами)
(№18: 10) 

 Выбирайте опрятные и хорошо сохранившиеся вещи.
Выбирайте опрятные и хорошо сохранившиеся вещи.
 Убедитесь, что вы рисуете конструкции. Остановитесь на разделе постулатов SSS.
Убедитесь, что вы рисуете конструкции. Остановитесь на разделе постулатов SSS.
 5. Равнобедренные и равнобедренные треугольники
5. Равнобедренные и равнобедренные треугольники

 1.
1.
Примечание: для вопроса 13 B и C следует сказать:
б. Находится ли C на серединном перпендикуляре m? Почему или почему нет?
Находится ли C на серединном перпендикуляре m? Почему или почему нет?
в. Находится ли D на серединном перпендикуляре m? Почему или почему нет? 



 (Подсказка: если учитель говорит вам что-то конкретное, что нужно знать для теста, вы должны это изучить!)
(Подсказка: если учитель говорит вам что-то конкретное, что нужно знать для теста, вы должны это изучить!)


 Не торопитесь, читая диаграмму. Убедитесь, что вы знаете, что каждая из этих вещей меня.
Не торопитесь, читая диаграмму. Убедитесь, что вы знаете, что каждая из этих вещей меня.


ПРИМЕЧАНИЕ. Исправление ответа:
(#2 — 1:1) 
 Сложите свои баллы и запишите это число.
Сложите свои баллы и запишите это число.

ПРИМЕЧАНИЕ. Исправление ответа:
(#3 — 2,54, поскольку в дюйме 2,54 см; 2,2 — коэффициент перевода фунтов в килограммы) 

ПРИМЕЧАНИЕ. Исправление ответа:
(#20 — 3.4)
(#29 ответы меняются местами) 

ПРИМЕЧАНИЕ. Исправление ответа:
(#4A равен 6 квадратным корням из 10)
Как всегда, записывайте свою оценку как 5 минус 1 балл за каждый неправильный ответ.
(#31 – ba + ½ c²)  Будьте усердны и приложите все усилия.
Будьте усердны и приложите все усилия.
ПРИМЕЧАНИЕ. Исправление ответа
(#24 равно 0,89%) 
 5. Тангенс, синус и косинус
5. Тангенс, синус и косинус

ПРИМЕЧАНИЕ. Исправления ответа:
(угол №6 A = 82,82, угол B = 55,77, угол C = 41,41)
(угол №11 B = 65,4, угол C = 50,6)
(угол №12 A = 22, BC = 24,6, АС = 27,8)
ПРИМЕЧАНИЕ. Исправления ответов:
(#17 — 2 квадратный корень из 210)
 (Возможна дополнительная оценка)
(Возможна дополнительная оценка)

ПРИМЕЧАНИЕ. Исправления ответов:
(#5 — строка BH) 
ПРИМЕЧАНИЕ. Исправление ответа:
(ответ #9 равен 79,5)
#30 и #31 дают 12 и 8 баллов соответственно. Записывать. Проработайте примеры и проведите исследования.
Записывать. Проработайте примеры и проведите исследования.
ПРИМЕЧАНИЕ. Исправление ответа
(#23 x = 105) 


 Вернитесь и посмотрите, где вы потеряли очки. Что вы можете сделать, чтобы не потерять эти очки в следующем квартале?
Вернитесь и посмотрите, где вы потеряли очки. Что вы можете сделать, чтобы не потерять эти очки в следующем квартале?
ПРИМЕЧАНИЕ. Исправления ответов:
(№9 равен 12)
(№17 равен 76,3)
(№25 равен 796,5 )
(№35 площадь равна 135, а периметр равен 48) 
ПРИМЕЧАНИЕ. Исправление ответа:
(#9 равно 50 √3)
ПРИМЕЧАНИЕ. Исправление ответа:
(21. стороны = 6√2 и 9√2, диагонали 12, 18)
(27,3,33×5 дюймов)  (Возможны дополнительные баллы)
(Возможны дополнительные баллы)
Примечание. Исправления ответов!
(#23: 73 леденца) 
ПРИМЕЧАНИЕ. Исправления ответов:
(#15: 1188pi)
(#27: 63,59) 
ПРИМЕЧАНИЕ. Исправление ответа:
(#3: 3/2*√3)
ПРИМЕЧАНИЕ. Исправления ответов:
(№ 13 периметр равен 30,9)
(№ 14 площадь равна 295)  Вы также можете вернуться и просмотреть части главы 10. (На этот раз без доказательств.)
Вы также можете вернуться и просмотреть части главы 10. (На этот раз без доказательств.)
Примечание – Исправление ответа:
(#9 – Тест был исправлен, чтобы сказать, что нижнее число должно быть 33, а не 21. Тогда ответ будет 216 квадратный корень из 3 или приблизительно 371,12) (#8 – Это Изображение может сбивать с толку. Если бы вы использовали 8 в качестве меры внешней короткой диагонали, ответ был бы 195. Если бы вы использовали 8 в качестве меры короткой части длинной внутренней пунктирной ссылки, ответ был бы 224.) 
 (возможна дополнительная оценка)
(возможна дополнительная оценка) Вместо # 26 следует сказать: «Фермер хочет покрасить стороны BARN ».
Вместо # 26 следует сказать: «Фермер хочет покрасить стороны BARN ».
ПРИМЕЧАНИЕ. Исправление ответа:
(#12 — 832)
(#2 — v)
(#9 — 12,8)
(#25 — 1146)
(#26 — 1467,5) 
ПРИМЕЧАНИЕ – Исправления ответа:
(28: радиус равен 7, площадь равна 49π)
(30: 175π – SA боковой грани. 224π – суммарная SA конуса) 
ПРИМЕЧАНИЕ. Исправление ответа:
(№ 27 равен 14 565,29 см3) 
ПРИМЕЧАНИЕ. Исправление ответа:
(#21 равно 72√2)
ПРИМЕЧАНИЕ. Исправление ответа:
(#11 — 37,68) 
ПРИМЕЧАНИЕ. Исправления ответа:
(#20 — 47712,94)
(#26 — вычислить в дюймах при скорости плавления 2 дюйма в кубе) 
ПРИМЕЧАНИЕ. Исправление ответа:
(#3 – 36π в 3 ) 

 2. Переводы и векторы
2. Переводы и векторы
ПРИМЕЧАНИЕ. Исправления ответа:
(#19 — <6, 2>)
(#20 — <-2, 4.5 ish> График плохо читается. <-2, 5> также допустимо)
(#25 — D равно (9, 9)) 
ПРИМЕЧАНИЕ. Исправление ответа:
(#14 это (-4, -2), (2, 4), (-6, 2)) 
ПРИМЕЧАНИЕ. Исправления ответа:
(#4 — (2, -2), (-2, -4), (0, -8), (4, -6) ) 

 5, 9.1, 9.5) итоговый экзамен).
5, 9.1, 9.5) итоговый экзамен). Вы можете использовать главу, но не ответы или свои заметки. (14)
Вы можете использовать главу, но не ответы или свои заметки. (14) Полный список БЕСПЛАТНЫХ задач SAT по математике

Важность использования высококачественных математических материалов SAT
 В конечном счете, продукты и тестовые вопросы, которые не соответствуют требованиям SAT, являются пустой тратой времени.
В конечном счете, продукты и тестовые вопросы, которые не соответствуют требованиям SAT, являются пустой тратой времени. Пять лучших бесплатных ресурсов для качественной подготовки к SAT Math
#1: The College Board
 Официальный сайт предлагает полные практические тесты SAT и практические вопросы по всем разделам.
Официальный сайт предлагает полные практические тесты SAT и практические вопросы по всем разделам. Бесплатные официальные полные тренировочные тесты SAT
 Это потому, что они больше не доступны онлайн! Поскольку эти тесты были разработаны Советом колледжей, мы также включили их сюда. Имейте в виду, что вам обязательно нужно сначала пройти восемь тестов, которые есть на веб-сайте College Board.
Это потому, что они больше не доступны онлайн! Поскольку эти тесты были разработаны Советом колледжей, мы также включили их сюда. Имейте в виду, что вам обязательно нужно сначала пройти восемь тестов, которые есть на веб-сайте College Board. Бесплатная официальная практика SAT по математике
 Вместо этого запишите свои ответы на листе бумаги во время прохождения «теста». Когда закончите, обратитесь к официальным объяснениям ответа; это поможет вам понять, каковы ваши сильные и слабые стороны.
Вместо этого запишите свои ответы на листе бумаги во время прохождения «теста». Когда закончите, обратитесь к официальным объяснениям ответа; это поможет вам понять, каковы ваши сильные и слабые стороны. Старые официальные полные практические тесты SAT
 д.). Это потому что тестов за эти годы повторяет из приведенных выше. Другими словами, четыре теста, указанные выше, являются единственными бесплатными тестами SAT, доступными за последние 10 лет (исключая самые новые).
д.). Это потому что тестов за эти годы повторяет из приведенных выше. Другими словами, четыре теста, указанные выше, являются единственными бесплатными тестами SAT, доступными за последние 10 лет (исключая самые новые). #2: Академия Хана

#3: Блог PrepScholar SAT
Номера
Алгебра
Координатная геометрия
Плоская и объемная геометрия
Тригонометрия
Формулы
 Наша программа оценивает ваши текущие сильные и слабые стороны и адаптируется в зависимости от вашего прогресса. Он дает вам практические вопросы, адаптированные к вашим областям, требующим улучшения, и дает объяснения ответов на все вопросы.
Наша программа оценивает ваши текущие сильные и слабые стороны и адаптируется в зависимости от вашего прогресса. Он дает вам практические вопросы, адаптированные к вашим областям, требующим улучшения, и дает объяснения ответов на все вопросы. #4: CrackSAT.net
 6285 только это, чтобы дать вам представление о ваших математических способностях. Скорее всего, лучше использовать этот веб-сайт после того, как вы исчерпали все официальные ресурсы SAT, указанные выше.
6285 только это, чтобы дать вам представление о ваших математических способностях. Скорее всего, лучше использовать этот веб-сайт после того, как вы исчерпали все официальные ресурсы SAT, указанные выше. #5: Практические тесты Ivy Global SAT
 Также есть без пояснений к ответу, затрудняет определение того, как найти правильные ответы на математические вопросы, в которых вы ошибаетесь.
Также есть без пояснений к ответу, затрудняет определение того, как найти правильные ответы на математические вопросы, в которых вы ошибаетесь. Как эффективно использовать учебные материалы SAT по математике: 6 советов
 Эти шесть советов помогут вам достичь наивысшего результата SAT по математике в день экзамена.
Эти шесть советов помогут вам достичь наивысшего результата SAT по математике в день экзамена. №1. Пройдите полный практический тест за один присест0003 пройти полный тренировочный тест SAT
, чтобы увидеть, как вы себя поведете в день экзамена. Хотя ответить на один или два вопроса по математике может быть для вас не слишком сложно, на самом деле SAT — это марафон, и если вы не готовы, вы, скорее всего, устанете к концу. А истощение может привести к ошибкам любого!
Итак, прежде чем посвятить себя разделу SAT по математике, пройдите официальный практический тест SAT, чтобы увидеть, как ваш результат по математике вписывается в общую картину сдачи теста. Обязательно пройдите весь тест за один присест; это поможет вам развить выносливость к тестовому дню.
#2: Используйте правильное время и темп
При сдаче практических тестов SAT и любых разделов, посвященных математике, обязательно используйте те же временные ограничения, что и в день экзамена.
В приведенной ниже таблице показано, сколько времени у вас будет на каждый раздел SAT, а также сколько времени вы должны (приблизительно) потратить на каждый вопрос:
| Секция SAT | Общее время | Количество вопросов | Время на вопрос |
| Чтение | 65 минут | 52 | 75 секунд |
| Письмо и язык | 35 минут | 44 | 48 секунд |
| Математика без калькулятора | 25 минут | 20 | 75 секунд |
| Математический калькулятор | 55 минут | 38 | 87 секунд |
У вас будет около 75 секунд на вопрос в разделе «Математика без калькулятора» и 87 секунд на вопрос в разделе «Математика с калькулятором». Некоторые вопросы могут занять у вас меньше или больше времени, но продолжайте практиковаться, чтобы не тратить постоянно слишком много времени на один математический вопрос.
Некоторые вопросы могут занять у вас меньше или больше времени, но продолжайте практиковаться, чтобы не тратить постоянно слишком много времени на один математический вопрос.
Помните, что точность — это только полдела. Если вы хотите получить высокий балл по математике, вам нужно ответить на вопросы за отведенное время !
Тем не менее, не волнуйтесь, если у вас не хватит времени при сдаче первого практического теста SAT. Это совершенно нормально и дает вам отправную точку, с которой вы можете позже совершенствоваться.
#3: Анализируйте свои ошибки
Одно дело сдать тест SAT по математике, но вам также необходимо0003 просмотрите свои результаты и определите закономерности в ваших правильных и неправильных ответах. Часто ли вы неправильно отвечаете на несколько последних вопросов в каждом разделе по математике? Вам кажется, что функциональные вопросы сбивают вас с толку?
Сначала выясни, что пошло не так. Затем посмотрите, как вы можете выбрать несколько простых моментов и старательно нацеливаться на эти области в своей подготовке. (Помните, что каждый вопрос по математике, независимо от его сложности, приносит одинаковое количество баллов!)
Затем посмотрите, как вы можете выбрать несколько простых моментов и старательно нацеливаться на эти области в своей подготовке. (Помните, что каждый вопрос по математике, независимо от его сложности, приносит одинаковое количество баллов!)
#4: Нацельтесь на свои самые большие слабости
Как только вы определили закономерности в своих ошибках, пришло время копнуть глубже и изучить ваши самые большие слабости. Ваша конечная цель будет состоять в том, чтобы адаптировать свое обучение , чтобы вы могли сосредоточиться на улучшении областей, с которыми вы боретесь больше всего.
Поскольку ваша общая цель состоит в том, чтобы как можно точнее ответить на как можно большее количество вопросов, вам следует посвятить большую часть учебного времени устранению своих слабых сторон, а не повторению материала, который вы уже хорошо знаете.
Повторение знакомого материала снова и снова может помочь вам почувствовать себя продуктивным и уверенным в себе, но это не сильно повысит вашу оценку. Лучше всего сосредоточиться на своих проблемных областях, практикуясь и расширяя свою базу знаний.
Лучше всего сосредоточиться на своих проблемных областях, практикуясь и расширяя свою базу знаний.
#5: Установите расписание занятий
Не поддавайтесь искушению зубрить прямо перед тестом. У вас может быть плотный график, и вы чувствуете, что единственный вариант — подготовиться к SAT, но со временем действительно происходит улучшение. Обычно мы советуем поставить себе по крайней мере от трех до шести месяцев, чтобы подготовиться к SAT.
Если до экзамена осталось немного времени, не сдавайтесь! Независимо от того, сколько времени у вас есть на учебу, можно составить сбалансированный учебный план SAT.
Во-первых, посчитайте, сколько времени у вас есть до даты экзамена. (Например, предположим, что у вас остался месяц до экзамена.)
Затем назначьте себе не менее трех полных практических тестов (в дополнение к вашим обычным учебным материалам) и разложите их по ходу вашего учебного расписания. Если у вас есть только неделя или около того до экзамена, это, вероятно, будет невозможно. В этом случае постарайтесь выполнить хотя бы один или два тренировочных теста везде, где сможете.
Если у вас есть только неделя или около того до экзамена, это, вероятно, будет невозможно. В этом случае постарайтесь выполнить хотя бы один или два тренировочных теста везде, где сможете.
Ничто так не повторяет опыт SAT, как полный практический тест, поэтому не стоит недооценивать его важность в вашей подготовке!
#6: Никаких улучшений не видно? Получить дополнительную помощь по подготовке
Некоторые учащиеся предпочитают сдавать все экзамены SAT самостоятельно, но другие лучше справляются с небольшим руководством.
Если тема SAT просто не имеет для вас смысла или вам нужна помощь в расстановке приоритетов, то репетитор или программа подготовки к SAT (или и то, и другое!) — отличный вариант. Оба могут дать вам последний толчок, который вам нужен, чтобы оставаться сосредоточенным и максимизировать свой балл по математике SAT.
В PrepScholar мы предлагаем экспертные услуги репетиторства по SAT в дополнение к полностью настраиваемой программе подготовки к SAT. Для получения дополнительной информации прочитайте наши руководства о том, как найти лучшего репетитора по SAT и сколько вы должны потратить на репетиторство.
Для получения дополнительной информации прочитайте наши руководства о том, как найти лучшего репетитора по SAT и сколько вы должны потратить на репетиторство.
Целенаправленная и тщательная практика, отдых и уверенность: идеальный рецепт успеха SAT.
Что дальше?
Не знаете с чего начать? Взгляните на наш список всех математических тем в разделе SAT Math и определите свои слабые стороны с помощью наших отдельных руководств по SAT Math.
Хотите знать, какие самые сложные вопросы SAT Math? Мы составили список из 13 самых сложных вопросов SAT по математике, а также пояснения к каждому из них.
Укусил жук прокрастинации? Осталось время до тестового дня? Узнайте, как побороть желание откладывать дела на потом, и узнайте, как сбалансировать время для учебы.
Хотите получить идеальный результат SAT по математике? Погрузитесь в наше руководство по получению 800 баллов по математике SAT, написанное лучшим бомбардиром!
Хотите улучшить свой результат SAT на 160 баллов?
Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем ваши деньги вернутся если вы не улучшите свой результат SAT на 160 или более баллов.
Мы гарантируем ваши деньги вернутся если вы не улучшите свой результат SAT на 160 или более баллов.
Наша программа полностью онлайн, и она настраивает то, что вы изучаете, в соответствии с вашими сильными и слабыми сторонами. Если вам понравилось это руководство по математической стратегии, вам понравится и наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по отдельным навыкам, чтобы вы могли учиться наиболее эффективно. Мы также дадим вам пошаговую программу, чтобы вы никогда не запутались в том, что изучать дальше.
Воспользуйтесь 5-дневной бесплатной пробной версией:
Есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Кортни Монтгомери
Об авторе
Кортни набрала 99-й процентиль по SAT в старшей школе и окончила Стэнфордский университет со степенью в области культурной и социальной антропологии. Она увлечена тем, чтобы предоставить образование и инструменты для достижения успеха учащимся из всех слоев общества и слоев общества, поскольку она считает, что открытое образование является одним из величайших социальных уравнителей. Имеет многолетний опыт репетиторства, в свободное время пишет творческие работы.
Она увлечена тем, чтобы предоставить образование и инструменты для достижения успеха учащимся из всех слоев общества и слоев общества, поскольку она считает, что открытое образование является одним из величайших социальных уравнителей. Имеет многолетний опыт репетиторства, в свободное время пишет творческие работы.
Математика для 9 класса — EQAO
Тест по математике для 9 класса проверяет, какие математические навыки учащиеся должны усвоить к концу курса математики в 9 классе.
Проведение оценивания 9-го класса будет проходить с
- со среды, 11 января, по пятницу, 3 февраля 2023 г. Индивидуальные результаты учащихся сообщаются после того, как каждый учащийся завершит оценивание.
- Со среды, 7 июня, по среду, 28 июня 2023 г., с отчетом о результатах каждого учащегося после прохождения теста каждым учащимся.
На этой странице
Руководства пользователя для администраторов, 2021–2022
Руководства пользователя для администрирования экзамена по математике для 9 класса, 2021–2022
5 администраторы, учителя и ИТ-специалисты в школах и советах, которые участвуют в проведении оценки 9-го класса по математике. Руководства пользователя содержат рекомендации и ответы на часто задаваемые вопросы о роли учителей, администраторов и ИТ-специалистов в управлении 9-м классом.Оценка математики.
Руководства пользователя содержат рекомендации и ответы на часто задаваемые вопросы о роли учителей, администраторов и ИТ-специалистов в управлении 9-м классом.Оценка математики.
Руководства пользователя помогут
- учителям по ключевым аспектам, включая доступ к их учетным записям, управление их классами, подготовку учащихся к сессиям оценивания и администрирование официальных сессий оценивания.
- школьные администраторы в ключевых аспектах, включая доступ к своим учетным записям и навигацию по ним; управление списками учеников в своей школе, а также предстоящими сессиями оценки и учетными записями учителей; и быть основным контактным лицом для учителей.
- ИТ-команда школьных советов и представители по ключевым аспектам, включая навигацию по процессу общей технической готовности и подготовку к вариантам доступности и размещения, требованиям к пропускной способности и подключению, безопасности и протоколам разрешенного списка доменов, а также конфигурации устройств .

По техническим вопросам обращайтесь в нашу службу технической поддержки по электронной почте [email protected] или звоните по телефону 1-888-444-4017.
Образец теста
Образец теста
Этот образец онлайн-теста дает учащимся возможность ознакомиться с цифровым оцениванием и его платформой. Образец теста состоит из двух этапов, которые содержат в общей сложности 25 вопросов, оценивающих знания учащихся по новой учебной программе по математике для 9-го класса. Во время живого оценивания учащиеся пройдут два занятия, в общей сложности четыре этапа и 50 вопросов; этот тест эквивалентен одному из этих двух сеансов.
Образец теста — с полным звуковым описанием
Учащимся с нарушениями зрения могут потребоваться полные звуковые описания всех рисунков в EQAO Grade Assessment of Mathematics. Эта версия пробного теста с полным аудиоописанием дает этим учащимся возможность ознакомиться с цифровым оцениванием и его платформой. Этот образец теста содержит в общей сложности 25 вопросов, которые оценивают усвоение знаний учащимися по новой учебной программе по математике для 9-го класса. Во время живого оценивания учащиеся выполнят два занятия, в общей сложности 50 вопросов; этот тест эквивалентен одному из этих двух сеансов.
Этот образец теста содержит в общей сложности 25 вопросов, которые оценивают усвоение знаний учащимися по новой учебной программе по математике для 9-го класса. Во время живого оценивания учащиеся выполнят два занятия, в общей сложности 50 вопросов; этот тест эквивалентен одному из этих двух сеансов.
Таблицы формул и глоссарий для изучения французского языка
Математические формулы приведены в таблицах формул для справки учащимся во время оценивания. Приведены формулы периметра, площади, объема и площади поверхности для различных геометрических фигур и фигур.
- Таблица формул [PDF]
Опубликовано 09.09.21, 2021 | Пересмотрено 28.09.21 - Лист формул: крупный шрифт [PDF]
Опубликовано 21.09.2021 | Отредактировано 28.09.21
Глоссарий французского погружения [PDF]
Глоссарий французского языкового погружения содержит термины, помогающие учащимся языкового погружения в написании математических компонентов контрольных работ.
Вход для электронного оценивания
Вход для оценивания 9 класса по математике
Учащиеся, учителя и школьные администраторы могут войти в систему электронной оценки, нажав кнопку «Войти» в правом верхнем углу экрана. Войдя в систему,
- учащиеся будут иметь доступ к ресурсам. Тесты и оценки недоступны через этот логин, за исключением учащихся, использующих альтернативный доступ к специальному программному обеспечению специальных возможностей в рамках приспособления.
- учителя будут иметь доступ к своим учетным записям для управления участием своих учащихся в выборочном тесте и проведения оценки.
- школьные администраторы будут иметь доступ к своим учетным записям для управления учетными записями учителей, списками учащихся и планированием оценок.
Framework
Оценка математики для 9 класса [PDF]
Начиная с 2021–2022 учебного года, учащиеся зачисляются в 9 класс MTh2W. курс математики без потоковой передачи изучают знания и навыки, определенные в соответствии с ожиданиями, содержащимися в новой учебной программе по математике Онтарио 2021 года. Оценивание математики в 9 классе EQAO оценивает усвоение учащимися содержания этой новой учебной программы. Структура содержит подробное описание оценивания EQAO по математике для 9-го класса, в том числе то, как оценивание соотносится с учебной программой по математике Онтарио.
курс математики без потоковой передачи изучают знания и навыки, определенные в соответствии с ожиданиями, содержащимися в новой учебной программе по математике Онтарио 2021 года. Оценивание математики в 9 классе EQAO оценивает усвоение учащимися содержания этой новой учебной программы. Структура содержит подробное описание оценивания EQAO по математике для 9-го класса, в том числе то, как оценивание соотносится с учебной программой по математике Онтарио.Часто задаваемые вопросы
Вот некоторые часто задаваемые вопросы о 9 классеОценка математики.
Вернуться к началу
Honors Geometry 2015-2016
GT Geometry — это курс, предназначенный для учащихся 9-х классов, успешно сдавших экзамен по алгебре I средней школы в 7-м классе, а затем успешно завершивших алгебру II в 8-м классе с оценкой «B» или выше. Программа «Геометрия с отличием» предназначена для учащихся 10-х классов, успешно сдавших экзамен по алгебре I в средней школе в 8-м классе, а затем сдавших экзамен по алгебре с отличием II в 9-м классе. й класс на «В» или выше. Разница между GT и Honors Geometry заключается в том, что в GT учащиеся двигаются немного быстрее и решают несколько более сложные задачи.
й класс на «В» или выше. Разница между GT и Honors Geometry заключается в том, что в GT учащиеся двигаются немного быстрее и решают несколько более сложные задачи.
(Требуется рекомендация преподавателя для курсов с отличием и GT)
ВЕБ-СТРАНИЦА СТУДЕНТОВ
ВАЖНЫЕ ДАТЫ:
Программа курса по геометрии с отличием!
Обзор выпускного онлайн-экзамена
Обучение математике: видео по геометрии
MANGAHIGH.COM ВЕБ-САЙТ ДЛЯ ДОПОЛНИТЕЛЬНЫХ КРЕДИТНЫХ ИГР!!
Академия KHAN ОНЛАЙН-ОБУЧЕНИЕ
Нажмите на веб-страницу студента выше, чтобы получить доступ к полному учебнику (онлайн-версия), рабочим листам, обучающим видео и практическим тестам, а также практическим тестам.
Если вы зайдете на этот веб-сайт , вы найдете больше ресурсов, которые могут быть полезны как для учащихся, так и для родителей.
ПРОЕКТ №1 (Научная работа известного математика)
Проект № 2 (конструкции Geometer SketchPad)
Проект № 3 (Отчет о книге с оболочкой)
Проект № 4 (правый треугольный треугольный Том 3-D Рисунки)
День 1: A1 Введение в Условия и Словарной лист ( Vocab Key ) (24/24/15) A & (8/ 25/15)Б
День 2: Отдел 1,1 Условия и постулаты ( Практический лист ) (26.08.15) A & (27.08.15) B
День 3: A2 SEGRIE и Постулат линейки ( Практический рабочий лист ) (28.08.15)A и (31.08.15)B
День 4: A3 Постулат сложения углов и типы углов (1 1 Практический рабочий лист 1 01.09.15)A и (02.09.15)B
День 5: Просмотреть все материалы и завершить оценку CW #1 (9/3/15)A & (9/4/15)B
День 6: A4 Типы ракурсов и блокнот ( Типы ракурсов WS ) (9/8/15)A & (9/9 /15)B
День 7: A5 Использование формул в геометрии & A6 Формулы средней точки и расстояния & Веб-задание (9/10/15)A & (9/11/15. Практика № 1 Тест 1 900 1: Стр. 1 и Стр. 2
Практика № 1 Тест 1 900 1: Стр. 1 и Стр. 2
День 8: Обзор модуля A Test (9/15/15)A & (16/9/15)B
Просмотрите и пройдите Модульный тест A (Глава 1) (17/09/15)A & (18/9/ 15) B
День 10: Преобразования и B4 Трансформации композиции (21.09.15) A & (22.09.15) B
День 11: Симметрия и преобразования и Блок. B Преобразования (расширения) (24.09.15)A и (25.09.15)B
День 12: Завершить Блок B (9/28/15)A и (9/29/15)B
День 13: Обзор и практическое тестирование блока B (9/30/15)A и (10/1/15)B
День 14 . ) (15.10.15)A и (15.10.15)B
День 16: Раздел C 2.2 (условные заявления) (8.10.15)A и (9.10.15) Б
День 17: Завершение 2.2 Условные утверждения и Блок C (Дедуктивное рассуждение) (12.10.15)A и (13.10.15)B
День 18: Нет дневного класса (PSAT) & Оценка CW День B (14. 10.15)A и (15.10.15)B
10.15)A и (15.10.15)B
День 19: Модуль C (алгебраическое доказательство) и Модуль C (геометрическое доказательство) (19/10/ 15)A и (20.10.15)B
День 20: Блок C (двухусловные операторы) и доказательства (21.10.15)A и (22.10.15)B
День 21: Обзор для блок C Test (23.10.15) A & (26.10.15) B
День 22: Блок C Тест (Глава 2) ( 27.10.15 )A и (28.10.15)B
День 23: Подпитка (Test Boost) День (29.10.15)A и (30.10.15)B ПОСЛЕДНИЙ ДЕНЬ 1 КВАРТАЛ!
День 24: Часть D Глава 3.1 (Углы и линии) и Часть D Глава 3.2 (Углы и параллельные линии) & 5/1 (11/2/1) )Б
День 25: Часть D Глава 3.2 (Проверка с параллельными линиями) и Часть D Глава 3.3 (Параллельные линии пруфов) (4.11.15)A и (15.11.15)B
День
0 26: Оценка CW (параллельные линии/приложения) и Обзор ежеквартальной оценки № 1 линии) и Блок D Глава 3. 5 (Наклоны линий) (10.11.15)A и (11.11.15)B
5 (Наклоны линий) (10.11.15)A и (11.11.15)B Блок D Глава 3.6 (Наклоны строк и уравнений линий)
День 28: Рабочие листы для обзора для блока D и обзор для подразделения D Экзамен
День 29: Блок D Тест (Глава 3) (16.11.15)A и (17.11.15)B
День 30: Перейдите к модульному экзамену D (обзор) (18.11.15)A и (19.11.15) B
День 31: Активность с числами (теорема Пифагора) (20.11.23)A и (23.11.15)B
День 32: Экзамен по Блоку D (пересдача) (24.11.15) и (25.11.15)
День 33: 30.11.15)A и (15.12)B
День 34: Модуль F Глава 5 Раздел 7 (Теорема Пифагора) /3/15)B
День 35: Повторить теорему Пифагора и неравенства (12/4/15)A и (12/7/15)B
День 36: Раздел F Глава 5 Раздел 8 (Особые права Треугольники) (12/8/15)A и (12/9/15)B
День 37: Середина треугольника & Финиш Специальные прямоугольные треугольники (10. 12.15)A & (11.12.15)B
12.15)A & (11.12.15)B
День 38: Доказательства 10 Использование косвенных рассуждений /14/15)A и (15/12/15)B
День 39: Обзор экзамена F (16/12/15)A и (17/12/15)B
День 40: Модуль F Тест (Глава 5) (18.12.15)A и (21.12.15)B
День 41: Модуль E Глава 4.1 Именование треугольников и Модуль E Глава 4.1. Треугольники Назначение по часовой стрелке (22/12/15)A и (23/12/15)B
( Пример треугольной суммы ) ( Угол внешнего вида THM. )
Day 42: Глава 8 Раздел 2 (соотношения тригея и правые треугольники) (1/4/16) A & (1/ 5/16)B
День 43: Глава 8 Раздел 3 (Решение прямоугольных треугольников) и Глава 8 Раздел 4 (Углы возвышения) (1/6/15)A & (1/7/16) B
День 44: Обратные триггерные функции и тригонометрия единичного круга (1/8/16)A и (1/11/16)B
День 45: Общий обзор Разделы 8. 2 – 8.3 & Обзор модульного экзамена (1/12/16)A и (1/13/16)B
2 – 8.3 & Обзор модульного экзамена (1/12/16)A и (1/13/16)B
День 46: Тригонометрия) (14.01.16) A & (15.01.16) B ( Конец 2 -го квартала !!! )
День 47: Блок e Глава 4.3. Блок E Главы (4.4 и 4.5) SSS, SAS (18.01.16)A и (19.01)/16)B
День 48: Часть E Глава 4.5 AAS, ASA, HL Теорема и Доказательство конгруэнтности треугольников Рабочие листы (20.01.16)A и (21.01.16)B День 10491 .
День 51: Обзор для теста главы 4 и Тест модуля E (глава 4) (22/22/16)A и (2/19/16)B
День 51: Блок G Глава 6 Раздел 1 (свойства полигонов) (16)
День 52: Глава 6 Раздел 2 (свойства параллелограмм) ( Домашнее рук WS ) (16)
День 53: Глава 6 Раздел 3 (Условия параллелограммы) (16)
День 54: Глава 6 Раздел 4 (Специальные параллелограммы) (16)
Глава 6 Раздел 4 (Координатные доказательства)
День 55: Глава 6 Раздел 5 (Условия для специальных параллелограммов) и Глава 6 Раздел 6 (Трапеции и воздушные змеи) A и (14. 03.16)B
03.16)B
День 57: Модуль G Test (Глава 6) (15.03.16)A и (16.03.16)B
2 День 10 62:
Глава 9 Раздел 1 (Формулы для треугольников и четырехугольников мс) (3/17/16)A и (3/18/16)BДень 63: Активность Numb3rs (Площадь) (21.03.16)A и (22.03.16)B
День 64: Зона финиша и периметр четырехугольников (23.03.16)A и (24.03) 16)B
День 65: Глава 9 Раздел 2 (Формулы для окружностей и правильных многоугольников) (4/4/16)A & (4/5/16)B
День 66: Глава 9 Раздел 2 (Площади правильных многоугольников) и Глава 9 Раздел 3 (Составные фигуры) (4/6/16)A и (4/7/16)B
День 67: Глава 9Раздел 5 (Пропорции и площадь) (4/8/16)A и (4/11/16)B
День 68: Просмотр и финишная зона и периметр (4/12/16)A и (4/13) /16)B
День 69: Модуль J Экзамен (Глава 9) (14.04.16)A и (15.
 04.16)B
04.16)B День 70: 10 Глава 10 1011 0 Глава 1 (Фигуры в пространстве) и Глава 10 Раздел 3 (Формулы в трехмерном пространстве) (25.04.14)
День 71: Глава 10 Раздел 4 (Площадь поверхности призм и цилиндров) 104111 (104111) /28/14)
День 72: Глава 10 Раздел 5 (площадь поверхности конусов и пирамид) (29.04.14)
День 73: Глава 10 Раздел 6 (объем призмы и цилиндров) ( Пример ) (01.05.14)
День 74: Глава 10 Раздел 7 (Объем пирамид и конусов) & Раздел 8 (Объем и площадь поверхности сфер) (06.05.14)
День 75: Глава 10 Раздел 2 (Изометрические чертежи) (07.05.14)
День 76: Обзор объема и площади поверхности (13.05.14)
День 77: Блок k экзамен (глава 10) (5/14/14)
День 78: Глава 7 Раздел 1 (Соотношения и пропорции) и Глава 7 Раздел 2 (Сходство в многоугольниках) (18. 03.14)
03.14)
День 79: Глава 7 Глава 7 Глава 3 (Подобие треугольников) 1 1 10 10111 Раздел 4 (Свойства подобных треугольников) (24.03.14)
День 80: Оценка CW, часть I (от 7.1 до 7.3) и Глава 7, раздел 5 (Анализ реальных проблем) (26.03.14) Фактор) (27 марта 14 года)
День 82: Перейти к рабочим листам обзора глав (28 марта 2014 г.)
День 83: 14)
День 84: Глава 11 Раздел 1 (Касательные и хорды в кругах) (15.05.14)
День 85: Глава 11 Раздел 2 (Дуги и хорды) (16.05.14)
День 86: Глава 11 Раздел 3 (Площадь секторов/9/1 Длина дуги1 1 1014) )
День 87: Глава 11 Раздел 4 и 5 (углы в кругах) и градуированный CW (углы в кругах) (5/21/14)
День 88: Глава 11 Раздел 6 (Длины сегментов в кругах) (22.05.14)
День 89: Глава 11 Раздел 7 (Уравнения окружностей) и начало обзора (23. 05.14)
05.14)
День 90: Экзамен по Разделу L (Глава 11) 10 109004 (27.05.2014) День 91: Обзор для выпускного экзамена (5.06.13)
День 92 : ПЕРИОНТ 4 ВЫПУСКАЯ ЭКСПЕРТАНИЯ (6/10/13)
День 93: ПЕРИОНТ 2 Заключительный экзамен (13.06.13)
День 94: Вступительные экзамены (14.06.13)
FINAL EXAM REVIEW WORKSHEETS:
Reasoning ( ANS ), Circles ( ANS ), Area ( ANS ), Volume ( ANS ), Transformations ( ANS ), Solving Triangles ( ANS ), Similarity ( ANS ), Polygons ( ANS ), Parallel Lines ( ANS ), Segments in Triangles ( ANS ), Конгруэнтность треугольника ( ANS )
Задание Duhomework: Рабочие листы для отделки (дополнительное кредитное онлайн -задание) с должности 4/4 A и 4/5 B
Старые рабочие листы домашнего задания: 1.


 Сумма двух векторов
Сумма двух векторов