«Детская школа искусств» Мошенского муниципального района

Геометрия решебник 9 класса: ГДЗ по геометрии 9 класс от Путина: решебники

Содержание

ГДЗ по геометрии для 9 класса Солтан Г.Н.

Задачи. Решения

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453

Решения»> Вопросы. Решения

стр.12 стр.21 стр.27 стр.33 стр.38 стр.43 стр.49 стр.66 стр.75 стр.84 стр.90 стр.103 стр.107 стр.111 стр.117 стр.122 стр.139 стр.143 стр.152 стр.157 стр.161 стр.167

Практические задания.

Решения стр.22 стр.29 стр.35 стр.39 стр.45 стр.73 стр.86 стр.104 стр.113 стр.124 стр.140 стр.153

Задания для самопроверки. Решения

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53

Решения»> Приложение 2. Решения

Т1. Понятие вектора. Коллинеарные векторы

1 2 3

Т2. Сложение и вычитание векторов

1 2 3 4

Т3. Умножение вектора на число

1

Т4. Координаты вектора

1 2 3 4 5

Угол между векторами»> Т5. Угол между векторами

1 2 3 4 5

Т6. Применение векторов к решению задач

1 2 3 4 5 6 7

Т7. Преобразование плоскости. Движение

1 2 3 4 5 6 7 8 9 10

Подобие треугольников»> Т8. Подобие треугольников

1

Т9. Признаки подобия

1 2

Т10. Теорема синусов

1 2 3

Т11. Теорема косинусов

1 2 3

Т12. Углы вписанные в окружность

1 2

Свойства касательной и секущей, пересекающихся хорд окружности»> Т13. Свойства касательной и секущей, пересекающихся хорд окружности

1 2

Т14. Нахождение длин сторон и площадей правильных многоугольников

1 2

Т15. Длина окружности дуги

1 2

Т16. Площадь круга, его сектора и сегмента

1 2

Т17.

Повторение курса геометрии 9 класса 1 2 3 4 5 7

ГДЗ(дүж) решения для учебника Геометрия Солтан 9 класс 2020 KZGDZ.COM

Авторы: Солтан Г., Солтан А., Жумадилова А.

Издательство: Келешек-2030

Год: 2020

Электронный учебник

К 9 классу ученик должен знать и уметь разбираться в геометрических фигурах, их свойствах. В новом курсе предмета Геометрия девятиклассника ждут такие темы как: векторы, преобразование плоскости, решение треугольников, окружность и многоугольники. Чтобы не попасть впросак при разборе трудных упражнений, предлагаем воспользоваться решебником для учебника от автора Солтан Г., тут разобраны все задания дисциплины, приведены правильные ответы с пояснениями. Осваивать теоремы станет намного проще даже самым отстающим ребятам. С ГДЗ знания приобретают осмысленный характер, их можно применять для более сложных задач, интегрировать в смежные науки.

Повторение курса геометрии 8 класса.

Упражнение

6789101112131415171920212223242526272829

I. Векторы

1. Понятие вектора. Коллинеарные векторы

Упражнение

3334353637383941

2. Сложение и вычитание векторов

Упражнение

4345464950515253545556

3. Умножение вектора на число. Критерий коллинеарности двух векторов

Упражнение

6162636466676869707172

4. Разложение вектора по двум неколлинеарным векторам.

Упражнение

737475767778798081828384

5. Координаты вектора.

Упражнение

87889093949596979899100101

6. Угол между векторами. Скалярное произведение двух векторов.

Упражнение

103104105

106107108109110112113114115116117118119120

7. Применение векторов при решении задач

Упражнение

121122124126127128

8. Упражнения на повторение раздела «Векторы»

Упражнение

129131132133134135136138139140141142144145

Проверь себя!

Упражнение

148 3B148 4B148 5C

II. Преобразования плоскости.

9. Преобразование плоскости. Движение и его виды

Упражнение

149150151153154155157

10. Применение движений к решению задач

Упражнение

158159160161164165

11. Преобразования гомотетии и подобия, их свойства

Упражнение

166167168169170171172

12. Подобные треугольники

Упражнение

174175176177178179180181182183184185186187188189190

13.

Подобные многоугольники
Упражнение

192193194195196197

198199200

14. Применение гомотетии и подобия при решении задач.

Упражнение

202203204205206207208

15. Упражнения на повторение раздела «Преобразования плоскости»

Упражнение

209210211212213214215216217218219220221222223224

Проверь себя!

Упражнение

225 4B225 5С

III. Решение треугольников.

16. Теорема синусов

Упражнение

226227228229230231232233234235

17. Теорема косинусов

Упражнение

236237238239240241242243244245246

18. Решение треугольников

Упражнение

247248249250251253254255256257258259

19. Углы, вписанные в окружность, и их свойства

Упражнение

260262263264265266267268269

20.

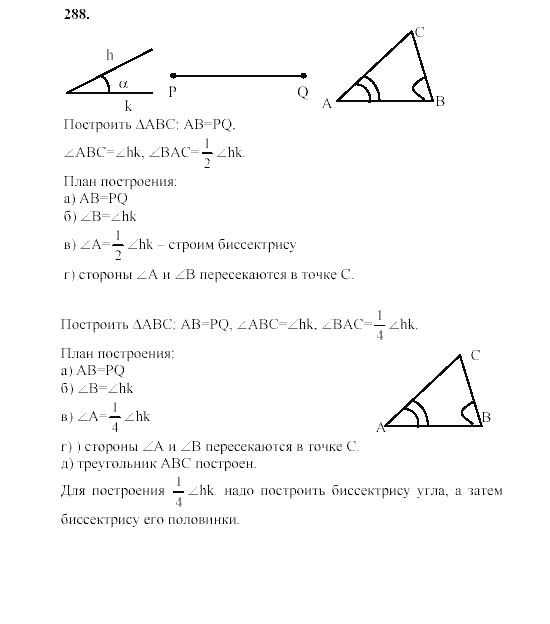Свойства касательной и секущей, пересекающихся хорд окружности
Упражнение

270271272273274275276277278279

21. Применение тригонометрии к выводу формул площадей треугольника и решению задач

Упражнение

280281282283284285286287288289290291292293294295296297298299300301302303

22. Упражнения на повторение раздела «Решение треугольников»

Упражнение

304305306307308309310311312313

Проверь себя!

Упражнение

314 4В

IV. Окружность. Многоугольники

23. Вписанные в окружность четырехугольники

Упражнение

316317318319320321

24. Описанные около окружности четырехугольники

Упражнение

322323324325326327328329330331332333334

25. Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него

Упражнение

336337338339340341342

26.

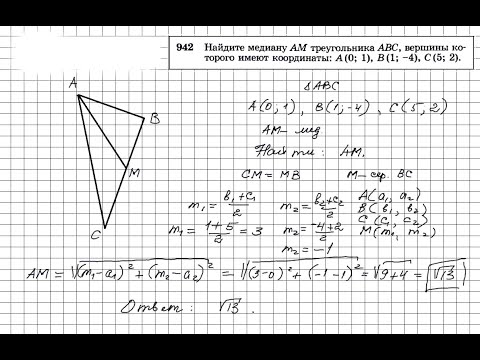Нахождение длин сторон и площадей правильных многоугольников.
Упражнение

343344345346347348349

27. Длина окружности и ее дуги

Упражнение

351352353354355356357358359360361362

363364365366367368

28. Площадь круга, его сектора и сегмента

Упражнение

370371372373374375376377378379380381382383384385

29. Упражнения на повторение раздела «Окружность. Многоугольники»

Упражнение

386387388389390391392393394395396397398399400401402403404405406407408409

Повторение курса геометрии 9 класса

Упражнение

411412413414415416417418419420421422423424425426427428430431433434435436437438439440441442443444445446

447448449450451452

К 9 классу ученик должен знать и уметь разбираться в геометрических фигурах, их свойствах. В новом курсе предмета Геометрия девятиклассника ждут такие темы как: векторы, преобразование плоскости, решение треугольников, окружность и многоугольники. Чтобы не попасть впросак при разборе трудных упражнений, предлагаем воспользоваться решебником для учебника от автора Солтан Г., тут разобраны все задания дисциплины, приведены правильные ответы с пояснениями. Осваивать теоремы станет намного проще даже самым отстающим ребятам. С ГДЗ знания приобретают осмысленный характер, их можно применять для более сложных задач, интегрировать в смежные науки.

\круг\).

  1. Ответьте на вопросы о рисунок ниже.

    1. Угол \(\hat{FOD}\) на рисунке меньше или больше прямого угла?
    2. Угол \(\hat{FOE}\) на приведенном выше рисунке меньше или больше прямого угла?

    На рисунке выше \(\text{F}\)\(\hat{\text{O}}\)\(\text{D}\) + \(\text{F}\)\( \ шляпа {\ текст {O}} \) \ (\ текст {C} \) = половина оборота = 180\(^\круг\). 9\круг\).

    1. Насколько большой \(\text{C}\)\(\шляпа{\text{M}}\)\(\text{P}\)?
    2. Объясните свои рассуждения.

  2. На рисунке ниже AMB представляет собой прямую линию и \(\text{A}\)\(\hat{\text{M}}\)\(\text{C}\) и \(\text{B}\)\(\ шляпа {\ text {M}} \) \ (\ text {C} \) равные углы.

    1. Насколько они велики углы?
    2. Откуда ты это знаешь?

    Когда одна линия образует две под равными углами там, где она встречается с другой линией, эти две линии говорят, что перпендикулярны .

    Поскольку два равных угла являются углами на прямой, их сумма равна 180°, следовательно, каждый угол составляет 90°.

  3. На рисунке ниже линии AB и CD пересекаются в точке М.

    В этой главе вы обязаны приводить веские причины для каждого заявления, которое вы делать.

    1. Похоже ли, что \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) и \(\text{B}\)\( \hat{\text{M}}\)\(\text{D}\) равны?
    2. Можете ли вы объяснить, почему они равны?
    3. Что означает \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) + \(\text{D}\)\(\hat{\text{M}}\)\(\text{A}\) равно?

      Почему ты так говоришь?

    4. Что такое \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) + \(\text{C}\)\(\шляпа{\text{M}}\)\(\text{B}\)?

      Почему ты так говоришь?

    5. Есть верно, что \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) + \(\текст{D}\)\(\шляпа{\текст{M}}\)\(\текст{A}\) = \(\текст{С}\)\(\шляпа{\текст{М}}\)\(\текст{А}\) + \(\текст{С}\)\(\шляпа{\текст{М}}\)\(\текст{В}\)
    6. Какой угол встречается на обоих стороны уравнения в (e)?
  4. Посмотрите внимательно на свой ответы на вопросы с 5(c) по 5(e).

    Теперь попробуй объяснить наблюдение в вопросе 5(а).

  5. На рисунке ниже AB и CD пересекаются в M. Образуются четыре угла. Угол CMB и угла AMD называются по вертикали напротив 9\circ\), насколько велик угол AMD?
  6. Почему так говорят?

Линии и углы

Линия, пересекающая другие линий называется секущей .

В приведенном выше шаблоне AB параллельно CD и EF \(||\) GH \(||\) KB \(||\) ЛД.

  1. Уголки a , b , c , d и e — это соответствующих углов . Сделайте соответствующие углы выглядят равными?
  2. Расследовать ли соответствующие углы равны с помощью кальки. Обведите угол, который вы хотите сравнить с другими углами, и поместите его поверх другого угла, чтобы узнать, равны ли они. Что ты заметил?
  3. Уголки f , h , j , m и n также являются соответствующими углами. Определите все остальные группы соответствующих углов в шаблон.
  4. Опишите позицию соответственных углов, которые образуются при поперечном пересекает другие линии.
  5. Ниже приведены пары чередующихся уголков : g и o ; й и с ; и к и р .

    Эти углы кажутся быть равным?

  6. Расследовать ли альтернативные углы равны с помощью кальки. След угол, который вы хотите сравнить, и поместите его поверх другого угол, чтобы узнать, равны ли они. Что ты заметил?
  7. Определить еще две пары альтернативные углы.
  8. Четко опишите относительное положение альтернативных углов, которые образуются, когда поперечная пересекает другие прямые.
  9. Вы заметили что-то о некоторых парах соответствующих углов, когда вы провели расследование в вопросе 6? Опиши себя найти.
  10. Уголки f и o ; i и q и k и s — все пары внутренние углы . Определите еще три пары совмещенные внутренние углы в узоре.

Углы одинаковые относительное положение на каждом перекрестке, где прямая линия кресты два других называются соответствующие углы .

Углы по разные стороны поперечный и между двумя другими линиями называются альтернативных углов . .

Углы на одной стороне поперечный и между двумя другими линиями называются co-interior углы . .

Углы, образованные параллельными прямыми

Соответствующие углы

Прямые AB и CD ниже никогда не пересекаются. Линии, которые никогда не пересекаются и находятся на фиксированном расстоянии от одной другие называются параллельными линиями. Мы пишем АВ \(||\) CD.

Параллельные линии имеют одинаковом направлении, то есть они образуют равный соответствующий углы с любой прямой, которая их пересекает.

Линия EF пересекает AB в G и CD в H.

EF — секущая, параллельные прямые AB и CD.

    1. Посмотрите внимательно на уголки EGA и EHC на рисунке выше. Их называют соответствующими углами . Они кажутся равными?
    2. Измерьте два угла, чтобы проверить, они равны. Что ты заметил?
  2. Предположим, что \(\text{E}\)\(\hat{\text{G}}\)\(\text{A}\) и \(\text{E}\)\(\hat{\text {H}}\)\(\text{C}\) действительно равны. Будет ли \(\text{E}\)\(\hat{\text{G}}\)\(\text{B}\) и \(\text{E}\)\(\hat{\text{ H}}\)\(\text{D}\) тоже равны? Приведите причины поддержите свой ответ.

    Когда две параллельные линии пересеченная секущей, соответствующие углы равны.

Переменные уголки

Углы \(\text{B}\)\(\hat{\text{G}}\)\(\text{F}\) и \(\text{C}\)\(\hat{ \text{H}}\)\(\text{E}\) ниже называются альтернативными углы . Они находятся на противоположных сторонах поперечной.

  1. Считаете ли вы углы AGF и DHE также следует называть альтернативными углами?
  2. Как вы думаете, альтернативный углы равны? Исследуйте, используя кальку, например вы делали ранее, или точно измерьте углы с помощью транспортир. Что вы заметили?

    При разрезании параллельных линий у секущей противоположные углы равны.

  3. Попробуйте объяснить, почему противоположные углы равны, если линии, пересекаемые поперечные параллельны, имея в виду, что соответствующие углы равны.

    Ответив на следующие вопросы, вы должны быть в состоянии увидеть, как вы можете объяснить, почему чередовать углы равны, если параллельные прямые пересечены поперечный.

  4. Уголки \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\) и \(\text{D}\)\(\hat{\text{H}}\)\(\text{F}\) на рисунке соответствующие углы?

    Что вы знаете о соответствующие углы?

    1. Что вы можете сказать о \(\text{B}\)\(\hat{\text{G}}\)\(\text{H}\) + \(\text{A}\)\( \hat{\text{G}}\)\(\text{H}\) Укажите причину.
    2. Что вы можете сказать о \(\текст{D}\)\(\шляпа{\текст{H}}\)\(\текст{G}\) + \(\text{C}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Дай причину.
    3. Правда ли, что \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\) + \(\текст{А}\)\(\шляпа{\текст{G}}\)\(\текст{Н}\) = \(\текст{D}\)\(\шляпа{\текст{H}}\)\(\текст{G}\) + \(\text{C}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Объяснять.
    4. Будет ли уравнение в (с) по-прежнему верным если вы замените угол \(\text{B}\)\(\hat{\text{G}}\)\(\text{H}\) на левая сторона с углом \(\text{C}\)\(\hat{\text{H}}\)\(\text{G}\)?
  6. Посмотрите внимательно на свой поработайте над вопросом 7 и напишите объяснение, почему чередуются углы равны, если две параллельные прямые пересечены поперечный.
    Внутренние углы

    Углы \(\text{A}\)\(\hat{\text{G}}\)\(\text{H}\) и \(\text{C}\)\(\hat{\ text{H}}\)\(\text{G}\) на рисунке ниже называются внутренние углы .

    «со-» означает вместе.

    «со-внутренний» означает на одном и том же сторона.

    Они на той же стороне поперечной.

    1. Что вы знаете о \(\text{C}\)\(\hat{\text{H}}\)\(\text{G}\) + \(\text{D}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Объяснять.
    2. Что ты знаешь о \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\) + \(\text{A}\)\(\шляпа{\text{G}}\)\(\text{H}\)? Объяснять.
    3. Что ты знаешь о \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\)+ \(\text{C}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Объяснять. 9\круг\). Другой способ сказать это состоит в том, чтобы сказать, что два внутренних угла являются дополнительными.

      Определите и назовите углы

      1. На рисунке ниже линия RF перпендикулярна AB.

        1. Является ли RF также перпендикулярным CD? Оправдывать Ваш ответ.
        2. Назовите четыре пары дополнительных углов на рисунке. В каждом случае скажите, откуда вы знаете, что углы являются дополнительными.
        3. Назовите четыре пары внутренних углов в фигура.
        4. Назовите четыре пары соответствующих углов на рисунке.
        5. Назовите четыре пары альтернативных углов в фигура.
      2. Теперь вам дано, что AB и CD на рисунке ниже параллельны.
        1. Если также указано, что РФ перпендикулярно AB, будет ли RF перпендикулярно CD? Обосновать ответ.
        2. Назовите все пары дополнительных углов на рисунке. В каждом случае скажите, откуда вы знаете, что углы являются дополнительными.
        3. Предположим, что \(\text{E}\)\(\hat{\text{G}}\)\(\text{A}\) = x. Укажите размер как можно большего числа углы на рисунке как можете, через х. Каждый раз указывайте причину Ваш ответ.

      Решение проблем

      1. Отрезки AB и CD на рисунке ниже параллельны. EF и IJ также параллельно. Отметьте эти факты на рисунке, а затем ответьте на вопросы.

        Когда вы решаете проблемы в геометрии вы можете использовать сокращенный способ написать свои причины. \circ\). 9\круг\).

        1. Найдите размеры как можно большего числа углов в рисуй, как умеешь, аргументируя.

        2. Параллельны ли EF и CD? Объясните причины ваши ответы.

      Обзор программы по математике для 9–12 классов

      Программа средней школы по математике предлагает множество курсов, которые предназначены для того, чтобы дать учащимся математические навыки и знания, необходимые для их будущего. Алгебраическое и геометрическое мышление и прикладная математика необходимы всем учащимся.

      Математическая программа средней школы включает курсы от Основы NC Math 1 до Advanced Placement (AP) Calculus AB. Разнообразие курсов предназначено для предоставления возможностей, отвечающих потребностям отдельных студентов.

      Курсы для старших классов

      • Курс профессионального обучения — Введение в математику
      • Курс профессионального обучения — NC Math 1
      • Курс профессионального обучения — Финансовый менеджмент
      • Основы NC Math 1
      • NC Math 1
      • Основы NC Math 2
      • NC Math 2
      • Honors NC Math 2
      • NC Math 3 Honors
        • 017
      • Расширенные функции и моделирование (АСМ
      • Essentials for College Math (Курс SREB Math READY)
      • Дискретная математика
      • Дискретная математика с отличием
      • Pre-Calculus — с отличием
      • Вероятность и статистика — с отличием
      • Advanced Placement (AP)

      Решение задач  и математические рассуждения  подчеркиваются в целях каждого курса математики средней школы. Развитие навыков решения задач является основной целью программы по математике. Опыт решения задач будет пронизывать обучение математике.

       

      Математическое моделирование  – важный метод, используемый для понимания абстрактных идей. Студенты будут использовать физические представления, чтобы лучше понять абстрактные математические концепции. Манипуляции для поддержки практических действий будут регулярно использоваться для обучения и оценки.

      Математические стандарты средней школы перечислены в концептуальных категориях:
      Количество и количество; Алгебра; Функции; Геометрия; Статистика и вероятность; и Моделирование.

       

      Использование калькулятора : Калькуляторы — это полезные инструменты, которые связывают учащихся с миром технологий и позволяют им продемонстрировать свое понимание сложных математических задач. Учащимся разрешается использовать графические калькуляторы в следующих тестах по математике, разработанных штатом для старших классов средней школы: Северная Каролина READY Math I End-of-Course Test; Выпускной экзамен Северной Каролины по математике II; Выпускной экзамен Северной Каролины по математике III; Выпускной экзамен Северной Каролины по продвинутым функциям и моделированию; Заключительный экзамен Северной Каролины по предварительному исчислению; Выпускной экзамен Северной Каролины по дискретной математике.

       

      Нажмите на ссылку ниже, чтобы получить доступ к самой последней версии Стандартного учебного курса Северной Каролины по математике. Инструменты поддержки    
      http://maccss.ncdpi.wikispaces.net/REVISED+High+School+Math+Standards+ 6-2016

      Нажмите здесь, чтобы получить доступ к стандартному курсу обучения

      Концептуальные категории средней школы

      Количество и количество Обзор количества и количества

    5. 7

      Математические практики

      1. Разбираться в задачах и настойчиво решать их.

      2. Рассуждать абстрактно и количественно.

      3. Придумывать жизнеспособные аргументы и критиковать рассуждения других.

      4. Модель с математикой.

      5. Стратегически используйте соответствующие инструменты.

      6. Следите за точностью.

      7. Ищите и используйте структуру.

      8. Ищите и выражайте регулярность в повторяющихся рассуждениях.

      Система действительных чисел                                    

      • Распространить свойства показателей на рациональные показатели.
      • Использование свойств рациональных и иррациональных чисел.

      Количество

      • Количественно рассуждайте и используйте единицы для решения задач.

      Комплексная система счисления

      • Выполнение арифметических операций с комплексными числами.
      • Представлять комплексные числа и их операции на комплексной плоскости.
      • Использование комплексных чисел в полиномиальных тождествах и уравнениях.

      Векторные и матричные величины

      • Представление и моделирование с помощью векторных величин.
      • Выполнение операций над векторами.
      • Выполнение операций с матрицами и использование матриц в приложениях.

      Обзор алгебры

      Математические практики

      1. Разбираться в проблемах и настойчиво решать их.

      2. Рассуждать абстрактно и количественно.

      3. Придумывать жизнеспособные аргументы и критиковать рассуждения других.

      4. Модель с математикой.

      5. Стратегически используйте соответствующие инструменты.

      6. Следите за точностью.

      7. Ищите и используйте структуру.

      8. Ищите и выражайте регулярность в повторяющихся рассуждениях.

      Просмотр структуры выражений                                    

      • Интерпретировать структуру выражений.
      • Напишите выражения в эквивалентных формах для решения задач.

      Арифметика с многочленами и рациональными выражениями

      • Выполнение арифметических операций над многочленами.
      • Понимать взаимосвязь между нулями и множителями многочленов.
      • Используйте полиномиальные тождества для решения задач.
      • Переписать рациональные выражения.

      Создание уравнений

      • Создайте уравнения, описывающие числа или отношения.

      Рассуждения с помощью уравнений и неравенств

      • Понимание решения уравнений как процесса рассуждений и объяснение рассуждений.
      • Решите уравнения и неравенства с одной переменной.
      • Решите систему уравнений.
      • Графически представлять и решать уравнения и неравенства.

      Обзор функций

      Математические практики

      1. Разбираться в проблемах и настойчиво решать их.

      2. Рассуждать абстрактно и количественно.

      3. Придумывать жизнеспособные аргументы и критиковать рассуждения других.

      4. Модель с математикой.

      5. Стратегически используйте соответствующие инструменты.

      6. Следите за точностью.

      7. Ищите и используйте структуру.

      8. Ищите и выражайте регулярность в повторяющихся рассуждениях.

      Функции интерпретации                                    

      • Понимать концепцию функции и использовать обозначения функций.
      • Интерпретировать функции, возникающие в приложениях, с точки зрения контекста.
      • Анализ функций с использованием различных представлений.

      Построение функций 

      • Построение функции, которая моделирует взаимосвязь между двумя величинами.
      • Создание новых функций из существующих.

      Линейные, квадратичные и экспоненциальные модели

      • Построение и сравнение линейных, квадратичных и экспоненциальных моделей и решение задач.
      • Интерпретируйте выражения для функций с точки зрения ситуации, которую они моделируют.

      Тригонометрические функции

      • Расширение области определения тригонометрических функций с помощью единичной окружности.
      • Моделирование периодических явлений с помощью тригонометрических функций.
      • Докажите и примените тригонометрические тождества.

      Обзор геометрии   

      Математические практики

      1. Разбираться в проблемах и настойчиво решать их.

      2. Рассуждать абстрактно и количественно.

      3. Придумывать жизнеспособные аргументы и критиковать рассуждения других.

      4. Модель с математикой.

      5. Стратегически используйте соответствующие инструменты.

      6. Следите за точностью.

      7. Ищите и используйте структуру.

      8. Ищите и выражайте регулярность в повторяющихся рассуждениях.

      Конгруэнтность                                    

      • Экспериментируйте с преобразованиями на плоскости.
      • Понять конгруэнтность в терминах жестких движений.
      • Докажите геометрические теоремы.
      • Создание геометрических конструкций.

      Сходство, прямоугольные треугольники и тригонометрия 

      • Понимание подобия с точки зрения преобразования подобия.
      • Докажите теоремы о подобии.
      • Определение тригонометрических соотношений и решение задач на прямоугольные треугольники.
      • Применение тригонометрии к обычным треугольникам.

      Круги

      • Понимать и применять теоремы о кругах.
      • Найти длины дуг и площади секторов кругов.

      Выражение геометрических свойств с помощью уравнений

      • Преобразование геометрического описания в уравнение для конического сечения.
      • Используйте координаты для алгебраического доказательства простых геометрических теорем.

      Геометрические измерения и размеры 

      • Объясните формулы объема и используйте их для решения задач.
      • Визуализация отношений между двухмерными и трехмерными объектами.

      Моделирование с помощью геометрии

      • Применение геометрических концепций в ситуациях моделирования.

      Обзор статистики и вероятностей 

      Математические практики

      1. Разбираться в проблемах и настойчиво решать их.

      2. Рассуждать абстрактно и количественно.

      3. Придумывать жизнеспособные аргументы и критиковать рассуждения других.

      4. Модель с математикой.

      5. Стратегически используйте соответствующие инструменты.

      6. Следите за точностью.

      7. Ищите и используйте структуру.

      8. Ищите и выражайте регулярность в повторяющихся рассуждениях.

      Интерпретация категорийных и количественных данных                                    

      • Обобщение, представление и интерпретация данных по одному счетчику или измеряемой переменной.
      • Обобщать, представлять и интерпретировать данные по двум категориальным и количественным переменным.
      • Интерпретация линейных моделей.

      Совершение нарушений и обоснование выводов

      • Понимание и оценка случайных процессов, лежащих в основе статистических экспериментов.
      • Делайте выводы и обосновывайте выводы на основе выборочных обследований, экспериментов и обсервационных исследований.

      Условная вероятность и правила вероятности

      • Понимание независимости и условной вероятности и их использование для интерпретации данных.

Добавить комментарий