Практические задачи по геометрии для 9-го класса
О «Практических задачах по геометрии для 9-го класса»
Практические задачи по геометрии для 9-го класса :
Здесь мы рассмотрим несколько примеров задач по геометрии для 9-го класса.
Практические задачи по геометрии для 9-го класса — практические вопросы
Вопрос 1 :
В данном случае ∠A = 64°, ∠ABC = 58°. Если BO и CO являются биссектрисами ∠ABC и ∠ACB соответственно ΔABC, найдите x° и y°
Решение:
Так как BO и CO являются биссектрисами ABC и ACB.
В треугольнике ABC 58 + 64 + В треугольнике OBC 29 + Вопрос 2 : В данном случае, если AB = 2, BC = 6, AE = 6, BF = 8, CE = 7 и CF = 7, вычислите отношение площадь четырехугольника ABDE к площади ΔCDF. Решение: Здесь у нас есть три треугольника, Δ AEC, Δ BCF и Δ BDC. Треугольник BCD, аналогичный ACE. В треугольнике AEC, AC = AB + BC = 2 + 6 = 8 см AE = 6 см и EC = 7 см a = 8, b = 6 и c = 7 Используя формулу площади разностороннего треугольника = √s(s — a) (s — b) (s — c) = √10,5(2,5) (4.5) (3.5) = √413,43 = 20,33 —-(1) В треугольнике BFC BF = 8 см , BC = 6 см, а CF = 7 см + 6 + 7)/2 = 10,5 = √s(s — a) (s — b) (s — c) = √10,5(2,5) (4,5) (3,5) = √413,43 8 = 20,33 —-(1) Треугольник BCD, аналогичный ACE. И BCF Чтобы получить длины BD и CD для треугольника BCD, мы будем использовать линейный масштабный коэффициент. Из длин AC и BC получаем LSF следующим образом: CE/CD = 8/6 7/(CD) = 8/6 42 = 8CD CD = 42/8 = 5,25 Площадь BCD : S =, (6 + 6 5,25) /2 = 8,625 A = √8. = √200,58 = 14,16 Область CDF: S = (5,25 + 7 + 2) / 2 = 2 = 2 = 2 = 7,125 A = √7,125(7,125 — 5,25) (7,125 — 7)(7,125 — 2) = √8,558 = 2,925 = 2,925 AB Площадь AB = 20,33 — 14,16 = 6,17 Отношение ABDE : CDF = 6,17 : 2,925 Приблизительно : 6 : 3 = 1 Вопрос 3 : На рисунке ABCD — прямоугольник, а EFGH — параллелограмм. Используя размеры, указанные на рисунке, какова длина d отрезка, перпендикулярного HE и FG? Вопрос 4 : В параллелограмме ABCD на прилагаемой диаграмме проведена линия DP, которая делит BC пополам в точке N и пересекает AB (продленную) в точке P. Из вершины C проводится линия CQ, которая делит сторону AD пополам в точке M и пересекает AB (продолжение) в точке Q. Прямые DP и CQ пересекаются в точке O. Покажите, что площадь треугольника QPO равна 9/8 площади параллелограмма ABCD. Решение: [QPO] = [QAM] + [PBM] + [AMONB] ——(1) [QPO] = [AMONB] + [MDC] + [NCD] — —(2) Из (2), = [AMONB] + [MDC] + [NOC] + [DOC] = [ABCD] + [DOC] Пусть [ABCD] = K = K + [DOC] [DCNM ] тоже параллелограмм. Итак, [DOC] = 1/4 [DCNM], 2[ABCD] = [DCNM] = 1/8 [ABCD] = k/8 [QPO] = K + K/8 [ [QPO] = 9k/8 ] Отсюда доказано. Мы надеемся, что после изучения материалов, приведенных выше, учащиеся поняли раздел «Практические задачи по геометрии для 9-го класса». используйте наш пользовательский поиск Google здесь. Пожалуйста, отправьте свой отзыв на [email protected] Мы всегда ценим ваши отзывы. ©Все права защищены. onlinemath5all.com Указания: В конце каждого вопроса вы можете выделить текстовую область сразу после слова «Ответ», чтобы проверить свой ответ. Если вы хотите просмотреть учебное пособие по геометрии линий и многоугольников, в котором используются несколько примеров, очень похожих на приведенные ниже вопросы (и те, что были в нескольких прошлых тестах EQAO), нажмите здесь. Вы также можете скачать копии этого документа в формате pdf и полные отработанные решения по этой ссылке. Если вы найдете ошибки, пожалуйста, прокомментируйте мой канал. Мы ценим любые отзывы. 1. Треугольник
АВС равнобедренный треугольник, в котором АС = АВ.
D, E и F — середины сторон треугольника ABC. Что из перечисленного является периметром
треугольник ДЭФ? a) 12,2 см b) 9,6 см c) 10,9 см d) 13,5 см Ответ: a Объяснение 2. Рассмотрите схему
ниже. Каково значение a + b
+ с? a) 90 o b) 180 o c) 360 o d) 540 o Answer: 360 o Explanation 3. а) г + ч = 180 o б) г = ч в) г = ч — 90 o d) g + h = 360 o Ответ: a Объяснение 4. Рассмотрите приведенную ниже диаграмму. Что из следующего всегда верно? A) x = Y B) x = y — 180 O C) x + y = 180 O D) x + y = 360 O Ответ: C 7 O . Пояснение 5. Рассмотрите схему ниже. Каково значение угла
ш? а) 77 о B) 82 O C) 93 O D) 117 O Ответ: Объяснение 6. 6. 6. двусторонний многоугольник? A) 2520 O B) 360 O C) 2340 O D) 2160 O Ответ: D 7 4. A) 120 O B) 150 O C) 90 O D) 115 O Ответ: AD 7. Каково значение у? A) 28 O B) 80 O C) 64 O D) 54 O Ответ: D . Каково значение у? A) 105 O B) 75 O C) 120 O D) 65 O . внешнего угла правильного многоугольника
показано ниже? A) 36 O B) 40 O C) 144 O D) 140 O Ответ: B 7 .0005 Углы
Углы. Рассмотрим приведенную диаграмму. Заполните таблицу ниже. Обоснуйте свои значения x и y с помощью
геометрические свойства. x = y = Answer: x = 45 o and y = 70 o Пояснение 12. Ответ: 360 o Объяснение 13. Углы и другие углы. Правильный шестиугольник имеет общую сторону с правильным пятиугольником. Сторона шестиугольника расширена и встречается
где сторона пятиугольника также расширена. Полный
таблицу ниже. Обоснуйте свои ценности для
a и b с геометрическими свойствами. a = b = Answer: a = 132 o and b = 96 Объяснение 14.
8 ( s
625 (8.625 — 6) (8,625 — 6) (8,625 — 5,25)
:
:
Геометрия линий и многоугольников Практические вопросы EQAO 9 Академический
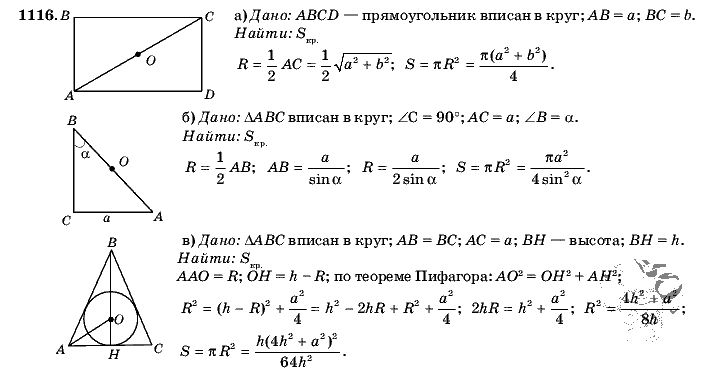Вы также можете нажать на ссылку «Пояснение», чтобы посмотреть короткое видео, объясняющее решение каждого вопроса.
Consider диаграмма ниже. Что из следующего всегда верно?
каждый внутренний угол правильного шестиугольника
(6 сторон)? Angle Measure Justification
Энгл Старз
Бенито
находит этот рисунок в старой книге. Он
только что закончил раздел геометрии в своем курсе математики в 9 классе, и он решает найти
сумма b + c + d + e + f + g. Что
это сумма? Обосновать ответ. Angle Measure Justification 