«Детская школа искусств» Мошенского муниципального района

Геометрия 9 класс задачи: Геометрия, 9 класс: уроки, тесты, задания

Содержание

Геометрия. 9 класс. Задачи ОГЭ с развёрнутым ответом. Изд. 4-е (Федор Лысенко)

Купить офлайн

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

В наличии в 2 магазинах. Смотреть на карте

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

Материал, представленный в книге, даёт возможность выработать навыки решения задач по геометрии с развёрнутым ответом второй части ОГЭ. Книга соответствует проекту демонстрационного варианта ОГЭ 2020 г., опубликованному на сайте ФИЛИ 20.08.2019.
В пособии разобраны типовые задачи повышенного и высокого уровней сложности, подобные тем, которые приведены в открытом банке заданий ОГЭ и использовались в последние годы на экзамене.
Данное пособие содержит также:
— диагностическую работу;
— необходимый для решения задач теоретический материал;
— задания базового уровня сложности для подготовки учащихся к выполнению задач первой части ОГЭ;

— примеры выполнения школьниками задач с комментариями;
— задачи для самостоятельного решения повышенного и высокого уровней сложности;
— решение всех прототипов задач.
Издание адресовано школьникам, учителям и методистам.

Описание

Характеристики

Материал, представленный в книге, даёт возможность выработать навыки решения задач по геометрии с развёрнутым ответом второй части ОГЭ. Книга соответствует проекту демонстрационного варианта ОГЭ 2020 г., опубликованному на сайте ФИЛИ 20.08.2019.
В пособии разобраны типовые задачи повышенного и высокого уровней сложности, подобные тем, которые приведены в открытом банке заданий ОГЭ и использовались в последние годы на экзамене.
Данное пособие содержит также:
— диагностическую работу;
— необходимый для решения задач теоретический материал;
— задания базового уровня сложности для подготовки учащихся к выполнению задач первой части ОГЭ;

— примеры выполнения школьниками задач с комментариями;
— задачи для самостоятельного решения повышенного и высокого уровней сложности;
— решение всех прототипов задач.
Издание адресовано школьникам, учителям и методистам.

Легион

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

1

Сделайте заказ в интернет-магазине

2

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

3

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «Геометрия. 9 класс. Задачи ОГЭ с развёрнутым ответом. Изд. 4-е» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Федор Лысенко «Геометрия.

9 класс. Задачи ОГЭ с развёрнутым ответом. Изд. 4-е» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Решение геометрических задач при подготовке к ОГЭ 9 класс | План-конспект урока по математике (9 класс):

Решение  геометрических задач при

подготовке к ОГЭ

                 Учитель математики Орлова Светлана Григорьевна

                                                      2019 г

Тип урока: Урок повторения и коррекции знаний.

Методы:

— частично-поисковый;

— системные обобщения;

— самооценка.

— элементы сингапурской методики

Цель урока: Повторить знания по теории геометрии, продолжить работу по решению геометрических задач для подготовки к ОГЭ.

  • обучающие – повторить знания по теории геометрии, продолжить работу по подготовке к ГИА. Проверка знаний и их коррекция.
  • развивающие – развивать внимание, зрительную память, логическое мышление, интуицию, математическую  речь, умение анализировать свои ошибки.
  • воспитательные – воспитывать дисциплинированность,   высокую  работоспособность и организованность, чувство патриотизма, умения проводить оценку и самооценку знаний и умений, уважение друг к другу, развивать коммуникативные компетенции.

 

Структура урока.

1°. Организационный  момент.

2°.  Повторение теоретического материала

ИНСАЙД-АУТСАЙД СЁКЛ (Inside-Outside Circle) — «внутренний и внешний круг» —

обучающая структура, в которой ученики формируют внутренний и внешний круги

и делятся своими мнениями с разными партнерами.

Теоретический материал  воспроизводится учениками  самостоятельно, каждый обучающийся по очереди играет роль учителя и ученика, педагог осуществляет так называемый «включенный контроль», слушая по очереди одного из представителей микрогруппы, оценивает их, корректирует, помогает и направляет.

Обратим внимание, что дети приучаются работать по определенному алгоритму выполнения действий по команде учителя. Выполнение алгоритма доведено до автоматизма.

3°.   Актуализация опорных знаний. Работа по готовым чертежам (модуль № 9,10, 11, 12)

4°.  Самостоятельная работа: «сималтиниусс раунд тейбл» — три члена группы выполняют письменные задания, а по окончании передают их по кругу соседу на проверку, затем сдают учителю

Индивидуально-дифференцированная работа (карточки № 1-4).

5°. Решение задач на доске и в тетради, карточка — задания на урок

70. Итог урока. Задание на дом.

8°.  Рефлексия.

Формы организации труда:

— индивидуальная;

— фронтальная;

— индивидуально-дифференцированная

-групповая

Необходимое оборудование и материалы:

  • ноутбук;
  • экран;
  • проектор;
  • слайды;
  • карточки

                                                   

                                       

                                             Ход урока

  1. Организационный момент. (2 мин.)

Ребята! У нас  сегодня гости, и от того как вы себя покажите на уроке, будет зависеть, запомнят ли они нас и захотят ли ещё к нам прийти .

Я надеюсь, что этот урок пройдёт интересно, с большой пользой для всех. Уверена, что на сегодняшнем уроке вы будете активны, внимательны и получите знания, которые пригодятся вам для успешной сдачи ОГЭ.

Тема урока: «Решение геометрических задач при подготовке к ОГЭ» (слайд 1), а девизом урока будут слова Д. Пойа: «Умение решать задачи – такое же практическое искусство, как умение плавать или бегать на лыжах. Ему можно научиться только путём подражания или упражнения» (слайд 2)

ОГЭ по геометрии включает в себя: 1.Задания тестового характера. 2.Задачи на нахождение нужных элементов. 3. Задачи на доказательство  (слайд 3)

Напомню, что в модуле  «Геометрия» нужно решить как минимум два задания. Это позволит рассчитывать выпускнику на получение удовлетворительной оценки.

  1. Чтобы быть спортсменом нужно не только быть сильным и ловким, но и хорошо знать математику. Начнем с разминки как все спортсмены. Повторим теоретический материал. (слайды 4,5,6) (8мин)  

 ИНСАЙД-АУТСАЙД СЁКЛ (Inside-Outside Circle) — «внутренний и внешний круг» —

обучающая структура, в которой ученики формируют внутренний и внешний круги

и делятся своими мнениями с разными партнерами.

Теоретический материал  воспроизводится учениками  самостоятельно, каждый обучающийся по очереди играет роль учителя и ученика, педагог осуществляет так называемый «включенный контроль», слушая по очереди одного из представителей микрогруппы, оценивает их, корректирует, помогает и направляет.

Обратим внимание, что дети приучаются работать по определенному алгоритму выполнения действий по команде учителя. Выполнение алгоритма доведено до автоматизма.

3.  Спортсмены в свою очередь тоже готовятся, усиленно тренируются и мечтают о том, чтобы одержать больше побед. А наши с вами победы – это правильно выполненные задания.

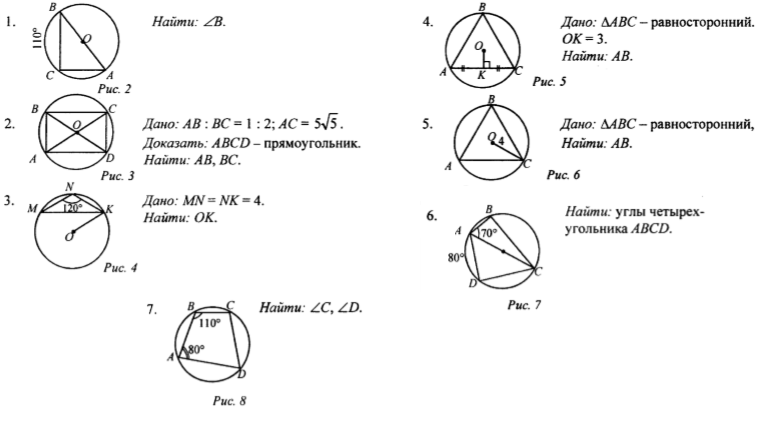
 Актуализация опорных знаний.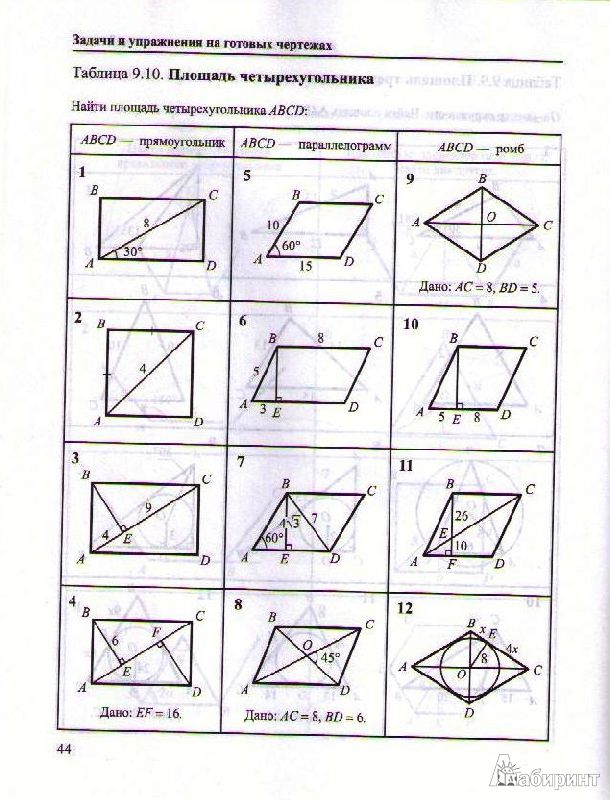 Работа по готовым чертежам  (слайды 7,8,9,11,12) (13мин)    Ответы: №9 – 74; 40; №10 – 4; 117; №11 – 15; 42; №12 – 1,2; .

  1. Самостоятельная работа. Один ученик  выполняют задание по индивидуально-дифференцированным карточкам.  Приложение 1:

«сималтиниусс раунд тейбл» — три члена группы выполняют письменные задания по карточке,  а по окончании передают их по кругу соседу на проверку, затем сдают учителю

5. Физкультминутка. Какая из картинок лишняя? (конькобежец) (слайд 10) (2мин)

Какую геометрическую фигуру описывает конькобежец, пробегая свою дистанцию? (овал)

Встаньте. Опишите овал глазами, головой, правым плечом, левым плечом, туловищем, правой ногой, левой ногой.

6. Решение задач на доске и в тетради (карточки  с заданиями  на урок) (15мин) Приложение 2

— Что является важным при решении задач?

— Знание определений, аксиом,  теорем и свойств геометрических фигур.

Задача

Задача №25

В параллелограмме ABCD точка К – середина ВС. Известно, что АК=КD, Докажите, что данный параллелограмм – прямоугольник.

Дано: ABCD – параллелограмм

BK=CK

AK=DK

Доказать: ABCD – прямоугольник

Доказательство:

1) треугольник AKD: угол1 равен углу2(как углы при основании равнобедренного треугольника)

2)  угол1 равен углу3, угол2 равен углу4(как накрест лежащие углы при параллельных прямых и секущей)

3)  треугольник АКВ равен треугольнику DKC (по двум сторонам и углу между ними)

4) угол В равен углу С(как внутренние односторонние при параллельных прямых и секущей),

5) Сумма односторонних углов равна 180°, следовательно угол В и угол С равны по 90°, то  ABCD – прямоугольник.

Молодцы! Все справились правильно с этими заданиями.

Продолжим двигаться к победе.

Дополнительно:

Задача № 24А

Биссектриса тупого угла B параллелограмма ABCD делит сторону AD в отношении 1:2, считая от вершины A. Найдите сторону AB, если полупериметр параллелограмма равен 40. (Ответ: 10)

                                                                                                                                                                                                                             

Задача № 24Б

Найдите угол ACD, если его сторона СА касается окружности, а дуга AD окружности, заключенная внутри этого угла, равна 116°. \круг\). 9\круг\).

  1. Насколько большой \(\text{C}\)\(\шляпа{\text{M}}\)\(\text{P}\)?
  2. Объясните свои рассуждения.

  • На рисунке ниже AMB представляет собой прямую линию и \(\text{A}\)\(\hat{\text{M}}\)\(\text{C}\) и \(\text{B}\)\(\ шляпа {\ text {M}} \) \ (\ text {C} \) равные углы.

    1. Насколько они велики углы?
    2. Откуда ты это знаешь?

    Когда одна линия образует две под равными углами там, где она встречается с другой линией, эти две линии говорят, что перпендикулярны .

    Поскольку два равных угла являются углами на прямой, их сумма равна 180°, следовательно, каждый угол составляет 90°.

  • На рисунке ниже линии AB и CD пересекаются в точке М.

    В этой главе вы обязаны приводить веские причины для каждого заявления, которое вы делать.

    1. Похоже ли, что \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) и \(\text{B}\)\( \hat{\text{M}}\)\(\text{D}\) равны?
    2. Можете ли вы объяснить, почему они равны?
    3. Что означает \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) + \(\text{D}\)\(\hat{\text{M}}\)\(\text{A}\) равно?

      Почему ты так говоришь?

    4. Что такое \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) + \(\text{C}\)\(\шляпа{\text{M}}\)\(\text{B}\)?

      Почему ты так говоришь?

    5. Есть верно, что \(\text{C}\)\(\hat{\text{M}}\)\(\text{A}\) + \(\текст{D}\)\(\шляпа{\текст{M}}\)\(\текст{A}\) = \(\текст{С}\)\(\шляпа{\текст{М}}\)\(\текст{А}\) + \(\текст{С}\)\(\шляпа{\текст{М}}\)\(\текст{В}\)
    6. Какой угол встречается на обоих стороны уравнения в (e)?
  • Посмотрите внимательно на свой ответы на вопросы с 5(c) по 5(e).

    Теперь попробуй объяснить наблюдение в вопросе 5(а).

  • На рисунке ниже AB и CD пересекаются в M. Образуются четыре угла. Угол CMB и угла AMD называются по вертикали напротив 9\circ\), насколько велик угол AMD?
  • Почему так говорят?

    • Линии и углы

    Линия, пересекающая другие линий называется секущей .

    В приведенном выше шаблоне AB параллельно CD и EF \(||\) GH \(||\) KB \(||\) ЛД.

    1. Уголки a , b , c , d и e — это соответствующих углов . Сделайте соответствующие углы выглядят равными?
    2. Расследовать ли соответствующие углы равны с помощью кальки. Обведите угол, который вы хотите сравнить с другими углами, и поместите его поверх другого угла, чтобы узнать, равны ли они. Что ты заметил?
    3. Уголки f , h , j , m и n также являются соответствующими углами. Определите все остальные группы соответствующих углов в шаблон.
    4. Опишите позицию соответственных углов, которые образуются при поперечном пересекает другие линии.
    5. Ниже приведены пары чередующихся уголков : g и o ; й и с ; и к и р .

      Эти углы кажутся быть равным?

    6. Расследовать ли альтернативные углы равны с помощью кальки. След угол, который вы хотите сравнить, и поместите его поверх другого угол, чтобы узнать, равны ли они. Что ты заметил?
    7. Определить еще две пары альтернативные углы.
    8. Четко опишите относительное положение альтернативных углов, которые образуются, когда поперечная пересекает другие прямые.
    9. Вы заметили что-то о некоторых парах соответствующих углов, когда вы провели расследование в вопросе 6? Опиши себя найти.
    10. Уголки f и o ; i и q и k и s — все пары внутренние углы . Определите еще три пары совмещенные внутренние углы в узоре.

    Углы одинаковые относительное положение на каждом перекрестке, где прямая линия кресты два других называются соответствующие углы .

    Углы по разные стороны поперечный и между двумя другими линиями называются альтернативных углов . .

    Углы на одной стороне поперечный и между двумя другими линиями называются co-interior углы . .

    Углы, образованные параллельными прямыми

    Соответствующие углы

    Прямые AB и CD ниже никогда не пересекаются. Линии, которые никогда не пересекаются и находятся на фиксированном расстоянии от одной другие называются параллельными линиями. Мы пишем АВ \(||\) CD.

    Параллельные линии имеют одинаковом направлении, то есть они образуют равный соответствующий углы с любой прямой, которая их пересекает.

    Линия EF пересекает AB в G и CD в H.

    EF — секущая, параллельные прямые AB и CD.

      1. Посмотрите внимательно на уголки EGA и EHC на рисунке выше. Их называют соответствующими углами . Они кажутся равными?
      2. Измерьте два угла, чтобы проверить, они равны. Что ты заметил?
    2. Предположим, что \(\text{E}\)\(\hat{\text{G}}\)\(\text{A}\) и \(\text{E}\)\(\hat{\text {H}}\)\(\text{C}\) действительно равны. Будет ли \(\text{E}\)\(\hat{\text{G}}\)\(\text{B}\) и \(\text{E}\)\(\hat{\text{ H}}\)\(\text{D}\) тоже равны? Приведите причины поддержите свой ответ.

      Когда две параллельные линии пересеченная секущей, соответствующие углы равны.

    Переменные уголки

    Углы \(\text{B}\)\(\hat{\text{G}}\)\(\text{F}\) и \(\text{C}\)\(\hat{ \text{H}}\)\(\text{E}\) ниже называются альтернативными углы . Они находятся на противоположных сторонах поперечной.

    1. Считаете ли вы углы AGF и DHE также следует называть альтернативными углами?
    2. Как вы думаете, альтернативный углы равны? Исследуйте, используя кальку, например вы делали ранее, или точно измерьте углы с помощью транспортир. Что вы заметили?

      При разрезании параллельных линий у секущей противоположные углы равны.

    3. Попробуйте объяснить, почему противоположные углы равны, если линии, пересекаемые поперечные параллельны, имея в виду, что соответствующие углы равны.

      Ответив на следующие вопросы, вы должны быть в состоянии увидеть, как вы можете объяснить, почему чередовать углы равны, если параллельные прямые пересечены поперечный.

    4. Уголки \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\) и \(\text{D}\)\(\hat{\text{H}}\)\(\text{F}\) на рисунке соответствующие углы?

      Что вы знаете о соответствующие углы?

      1. Что вы можете сказать о \(\text{B}\)\(\hat{\text{G}}\)\(\text{H}\) + \(\text{A}\)\( \hat{\text{G}}\)\(\text{H}\) Укажите причину.
      2. Что вы можете сказать о \(\текст{D}\)\(\шляпа{\текст{H}}\)\(\текст{G}\) + \(\text{C}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Дай причину.
      3. Правда ли, что \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\) + \(\текст{А}\)\(\шляпа{\текст{G}}\)\(\текст{Н}\) = \(\текст{D}\)\(\шляпа{\текст{H}}\)\(\текст{G}\) + \(\text{C}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Объяснять.
      4. Будет ли уравнение в (с) по-прежнему верным если вы замените угол \(\text{B}\)\(\hat{\text{G}}\)\(\text{H}\) на левая сторона с углом \(\text{C}\)\(\hat{\text{H}}\)\(\text{G}\)?
    6. Посмотрите внимательно на свой поработайте над вопросом 7 и напишите объяснение, почему чередуются углы равны, если две параллельные прямые пересечены поперечный.
      Внутренние углы

      Углы \(\text{A}\)\(\hat{\text{G}}\)\(\text{H}\) и \(\text{C}\)\(\hat{\ text{H}}\)\(\text{G}\) на рисунке ниже называются внутренние углы .

      «со-» означает вместе.

      «со-внутренний» означает на одном и том же сторона.

      Они на той же стороне поперечной.

      1. Что вы знаете о \(\text{C}\)\(\hat{\text{H}}\)\(\text{G}\) + \(\text{D}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Объяснять.
      2. Что ты знаешь о \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\) + \(\text{A}\)\(\шляпа{\text{G}}\)\(\text{H}\)? Объяснять.
      3. Что ты знаешь о \(\текст{B}\)\(\шляпа{\текст{G}}\)\(\текст{H}\)+ \(\text{C}\)\(\шляпа{\text{H}}\)\(\text{G}\)? Объяснять. 9\круг\). Другой способ сказать это состоит в том, чтобы сказать, что два внутренних угла являются дополнительными.

        Определите и назовите углы

        1. На рисунке ниже линия RF перпендикулярна AB.

          1. Является ли RF также перпендикулярным CD? Оправдывать Ваш ответ.
          2. Назовите четыре пары дополнительных углов на рисунке. В каждом случае скажите, откуда вы знаете, что углы являются дополнительными.
          3. Назовите четыре пары внутренних углов в фигура.
          4. Назовите четыре пары соответствующих углов на рисунке.
          5. Назовите четыре пары альтернативных углов в фигура.
        2. Теперь вам дано, что AB и CD на рисунке ниже параллельны.
          1. Если также указано, что РФ перпендикулярно AB, будет ли RF перпендикулярно CD? Обосновать ответ.
          2. Назовите все пары дополнительных углов на рисунке. В каждом случае скажите, откуда вы знаете, что углы являются дополнительными.
          3. Предположим, что \(\text{E}\)\(\hat{\text{G}}\)\(\text{A}\) = x. Укажите размер как можно большего числа углы на рисунке как можете, через х. Каждый раз указывайте причину Ваш ответ.

        Решение проблем

        1. Отрезки AB и CD на рисунке ниже параллельны. EF и IJ также параллельно. Отметьте эти факты на рисунке, а затем ответьте на вопросы.

          Когда вы решаете проблемы в геометрии вы можете использовать сокращенный способ написать свои причины. \circ\). 9\круг\).

          1. Найдите размеры как можно большего числа углов в рисуй, как умеешь, аргументируя.

          2. Параллельны ли EF и CD? Объясните причины ваши ответы.

        Модуль 3-Координатная геометрия — MYP Math 9 Расширенный

        : Уравнение прямой 8E
      4. 9 1-12: Графические линии из уравнений 8F
      5. 10 5-12: Нахождение уравнения прямой 8G
      6. 11 6-12: Обзор Desmos, викторина
      7. 12 12-12: Итоговый обзор и викторины 904 1579 904 Расстояние между двумя точками 8A.1

        Цель урока: Я смогу найти расстояние между двумя точками на числовой плоскости.

        • Разминка: Найдите длину недостающих сторон.


        • Верните и просмотрите Раздел 2 Экзаменационный лист

        • Notes on Number Plane and Distance between two points 8A.1

        • Problem Set:

        8. Содержание

        1. 1 7-11: Расстояние между двумя точками 8A.1
        2. 2 8-11: The Distance Formula 8A.2
        3. 3 14-11: Midpoint 8B
        4. 4 16-11: Gradient of a line 8C.1
        5. 5 17-11 : Исследование параллельных и перпендикулярных линий; Уравнение градиента 8C.2
        6. 6 21-11: Параллельные и перпендикулярные линии 8D
        7. 7 24-11: Уравнение прямой 8E. 1
        8. 8 
         Page  Exercise  Number  Letter
         149  8A.1  1 pick 3 
            2  pick 3 
            3  All 

        • Homework Watch Video and take notes on 8A. 2 The Distance Formula
        • YouTube Video

        8-11: The Distance Formula 8A .2

        Цель урока: Я смогу найти расстояние между двумя точками, используя формулу расстояния.

        • Разминка: Полиция получает сообщение о том, что дом в H(1,2) ограблен. На место прибыли сотрудники полиции ближайшей к дому станции. Если полиция находится в A(-7,5), B(7,8) и C(6,-5), какую полицию должен ожидать владелец.
        • Вопросы по конспектам, домашнее задание. Имеет ли значение, какую точку вы выберете как 1 или 2?
        • Problem Set:
        2
         Page Exercise   Number Letter 
         150 8A.2  1  pick 4 
         151   2  в, г
        3 а, б
        4
        152 6 ВСЕ
        .
      8. YouTube Video

        9. 14-11: Средняя точка 8B

        Цель урока: Я смогу использовать формулу средней точки, чтобы найти средние или конечные точки.


        • Вопросы по домашнему заданию/заметкам.

        • Исследование для этого модуля: Суммативное: Исследовательская работа. Как была «открыта» тригонометрия и чем так знаменита теорема Пифагора. Исследуйте реальные применения тригонометрии в различных областях помимо математики.

          • Сегодня посмотрите, какие интересные факты мы можем найти о Пифагоре и его знаменитой теореме, пост на адлете P , https://padlet.com/lburge2/zhjbihc3cjcu
          • Я опубликую больше информации, включая рубрику, в будущее в этом исследовательском документе.
        • Problem Set: 

        •  Page  Exercise Number   Letter
           153  8B 2  a,c,e,g,i 
               3 a,c 
               4 pick 1 
               7 a,b 

        • Смотрите видео и делайте заметки на Gradient 8C

          Видео на YouTube

        16-11: Градиент линии от Gosonal: я могу найти градиент 8C.1

        график и вычислить градиент по двум точкам.

        • Разминка: M — середина [PQ]. Найдите координаты Q, если:
          • P равно (-1, 0) и M равно (0, -5)
          • M равно (-1, 3) и P равно (-1/2, 0)
        • Вопросы по домашнему заданию.
        • Практика на доске с градиентами.
        • Problem Set:
           Page Exercise   Number Letter 
           156 8C.1  1-5   All

        • No notes, review notes on уравнение градиента 8C.2.
        • Расследование следующего класса.

        17-11: Исследование параллельных и перпендикулярных линий; Уравнение градиента 8C.

        2

        Цель урока: Я смогу определить взаимосвязь между параллельными и перпендикулярными линиями и их градиентами.

        • Разминка: Найдите градиент отрезка, соединяющего (1, 3) и (4, -2). Это должно быть сделано с помощью формулы градиента, вы можете проверить на графике.
        • Самостоятельное расследование.
        • Набор задач:
          Страница Упражнение Номер Письмо
          157 8C.2  2  pick 4 
              3  All 
              4  All 
          158    7  All 
          159 8 Все

        21-11: Parallel & Perpendiul их градиент; использовать эту информацию для решения геометрических задач на декартовой плоскости.

        • Разминка: рассмотрите точки A(1, 0), B(2, 4) и C(5, 1) и постройте график на картезианской плоскости.
          • Докажите, что треугольник ABC равнобедренный.
          • Найдите середину M отрезка [BC].
          • Используйте градиенты, чтобы показать, что [AM] и [BC] перпендикулярны.
          • Проиллюстрируйте три приведенных выше решения на наборе осей.
        • Из исследования вы должны были обнаружить, что:
          • линии параллельны тогда и только тогда, когда они имеют равный градиент .
          • линии перпендикулярны тогда и только тогда, когда их градиенты являются отрицательными обратными величинами .
        • Викторина по расстоянию, средней точке и градиенту.
        • Problem Set:
           Page Exercise  Number  Letters 
           161  8D  1  All
               2  All
               3  All
               5  All
               8  All

        • Homework: Watch video and делать заметки по Уравнению прямой 8E (Будет размещен после школы)

        24-11: Уравнение прямой 8E.

        1

        Цель урока: Я смогу идентифицировать уравнение прямой как градиент- форма перехвата или общая форма и преобразование общей формы в форму перехвата градиента.

        • Рассмотрим точки A(-1, 0), B(1, 4) и C(3, 2) и построим график на декартовой плоскости.
          • Докажите, что треугольник ABC равнобедренный.
          • Найдите середину M отрезка [BC].
          • Используйте градиенты, чтобы показать, что [AM] и [BC] перпендикулярны.
          • Проиллюстрируйте три приведенных выше решения на наборе осей.
        • Сдайте исследование, обсудите результаты всем классом.
        • Тест на возврат: Необходимо внести исправления.
          • Исправления должны быть сделаны на отдельном листе бумаги, НЕ на оригинальном тесте. Работа должна быть сделана!
          • Любая пропущенная проблема должна быть исправлена.
          • Заявление о непонимании и какую логику нужно исправить.
          • Прикреплен к исходному экзамену, сдан в следующем классе.
        • Примечания к уравнению линии.
        • Problem Set: 
           Page # Exercise  Number  Letter 
           163  8E.1  1  all
               2  a,e,i
               3 a,d 
               4 pick 3 

        • Homework: Notes on Equation линии 8E
        • Видео на YouTube

        30-11: Уравнение линии 8E

        Цель урока: я буду в состоянии определять форму уравнения линии и преобразовывать формы с помощью алгебры.

        • Разминка: Укажите градиент и точку пересечения линии по оси y, а затем напишите уравнение в общей форме.
          • y = -6x-1
          • y = (4x-5)/8
        • Вопрос по домашнему заданию или заметкам?
        • Problem Set: 
           Page Exercise  Number  Letter 
           164  8E.2  1  a,c
               2 a,c 
              3  a,c,d 
              4  pick 3 
               5  a,b
          .
        • Смотреть видео и делать заметки о построении линий из уравнений 8F
        • видео на YouTube

        1-12: построение линий из уравнений 8F

        когда задано в градиентном перехвате или в общей форме.

        • Разминка:
        • Практика построения графиков на белой доске.
        • Problem Set
           Page Exercise   Number  letter 
           166  8F.1  1  b,d,e,g
               2 б, д, д, г
          3 Все
          0515 All
          8F.2 1 A, B, G, H

        • .

        5-12: Нахождение уравнения прямой 8G

        Цель урока: Я смогу найти уравнение прямой по ее графику.

        • Разминка: начертите следующие два уравнения и укажите одну точку на прямой, которая не является точкой пересечения x или y.
          • y=2/3x-2
          • x=-2
          • 2x-16y=-32
          • y=1/2
        • Вопросы к домашнему заданию 8f или заметки по нахождению уравнений прямой.
        • Викторина следующего класса по уравнениям линий и графикам.
        • 9052 9052.

          6-12: Обзор Desmos, викторина

          Цель урока: Я выявлю свои сильные и слабые стороны в графических линиях и поищу стратегии для улучшения моего понимания.

          • РАЗМИНКА: Перейдите в Desmos и начните строить графики.

            Добавить комментарий

            ©2024 «Детская школа искусств» Мошенского муниципального района
           Page Exercise  Number  letter 
           167 8G  1  pick 3 
               2 pick 2 
           168   3  pick 2 
              4  a
           169    5  a, c
          7 B, C, F
          170 A, B, E, A, B, E,