Описание УМК Геометрия. Атанасян Л.С. И др. (7-9) — Группа компаний «Просвещение»
Авторы: Л.С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.
Самая популярная линия учебников по геометрии переиздавалась более 20 раз и, по-прежнему, не потеряла своей актуальности.
В состав УМК входят:
- учебник Л.С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. Геометрия. 7-9 классы
- рабочая программа
- рабочие тетради
- дидактические материалы
- самостоятельные и контрольные работы
- тематические тесты
- пособие для учителя
- задачи по геометрии
Учебник соответствуют Федеральному государственному образовательному стандарту основного общего образования. В учебнике много оригинальных приёмов изложения, которые используются из-за стремления сделать учебник доступным и одновременно строгим. Большое внимание уделяется тщательной формулировке задач, нередко приводится несколько решений одной и той же задачи.
Задания, имеющие электронную версию, отмечены специальным знаком. Добавлены темы рефератов, исследовательские задачи, список рекомендуемой литературы.
Рабочие тетради содержат большое количество чертежей и помогут легко и быстро усвоить материал.
Дидактические материалы включают самостоятельные, контрольные работы, работы на повторение и математические диктанты в нескольких вариантах и различного уровня сложности.
Самостоятельные и контрольные работы даны в виде разрезных карточек.
Тематические тесты предназначены для оперативной проверки знаний и подготовки к государственной итоговой аттестации.
В пособии для учителей сформулированы основные требования к учащимся, даны методические рекомендации по проведению уроков, решены наиболее сложные задачи из учебника, даны карточки для устного опроса, примерное планирование материала.
Приложение к учебнику на электронном носителе содержит анимации, позволяющие лучше понять доказательства теорем; тренажёры, помогающие научиться решать основные типовые задачи; тесты, позволяющие ученикам проверить свои знания; интерактивные модели, позволяющие экспериментально изучить свойства геометрических фигур; справочные материалы, помогающие решать задачи.
Особенности линии:
- доступное изложение теоретического материала
- обширный задачный материал
- возможность организации индивидуальной работы
Авторы: Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.
Основной идеей УМК является сочетание наглядности и строгой логики.
В состав УМК входят:
- Учебник Л.С. Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углублённый уровни) 10-11 классы
- рабочая тетрадь;
- дидактические материалы;
- пособия «Готовимся к ЕГЭ»;
- поурочные разработки.
Учебник соответствует Федеральному государственному образовательному стандарту среднего (полного) общего образования. В учебнике реализован принцип преемственности с традициями российского образования в области геометрии. При изложении теоретического материала соблюдается систематичность, последовательность изложения.
Учебник позволяет обеспечить вариативность, дифференцированность и другие принципы обучения. Его характеризует хорошо подобранная система задач, включающая типовые задачи к каждому параграфу, дополнительные задачи к каждой главе и задачи повышенной трудности. Красочное оформление поможет учащимся лучше усвоить стереометрический материал.
Рабочая тетрадь предназначена для работы учащихся на уроке. Задания, включающие большое количество чертежей, помогут легко усвоить новый материал.
Дидактические материалы содержат самостоятельные и контрольные работы, работы на повторение и математические диктанты в нескольких вариантах, а также задачи повышенной трудности и примерные задачи к экзамену. Большая вариативность представленных в пособии работ позволяет учителю на любом уровне отобрать необходимые задания.
В пособиях «Готовимся к ЕГЭ» в справочной форме приводятся и иллюстрируются на изображениях многогранников и тел вращения основные геометрические сведения.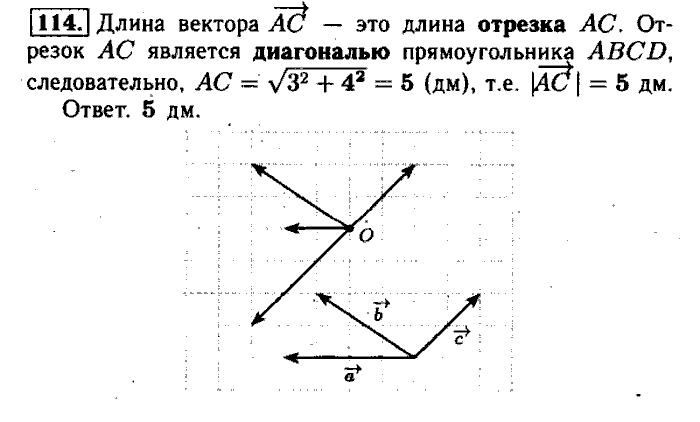
В книги включены задачи, решение которых направленно на неформальное восприятие теоретического материала.
В пособии для учителей «Поурочные разработки» сформулированы основные требования к учащимся, даны методические рекомендации по проведению уроков и распределению задач, самостоятельные и контрольные работы, карточки для устного опроса, примерное тематическое планирование в трех вариантах в зависимости от количества учебных часов, решены сложные задачи учебника и предложены дополнительные.
Особенности линии УМК:
- возможность использования на базовом и углублённом уровнях;
- доступность изложения материала, сочетающаяся с достаточной строгостью, краткостью, схематичностью.
ГДЗ по геометрии решебник
ГДЗ / Решебник: Геометрия
7 класс
Геометрия Тесты к учебнику Атанасяна
7 класс
Фарков А.В.
Геометрия Тесты
7 класс
Звавич Л.И.
Геометрия Тесты
7 класс
Фарков А.
В.
Геометрия Контрольно-измерительные материалы
7 класс
Гаврилова А.С.
Геометрия Дидактические материалы
7 класс
Зив Б.Г., Мейлер В.М
Геометрия 7-9 класс
7 класс
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Позняк Э.Г., Юдина И.И.
Геометрия 7-11 класс
7 класс
Погорелов А.В.
8 класс
Геометрия Тесты к уч. Атанасяна
8 класс
Звавич Л.И., Потоскуев Е.В.
Геометрия Тесты
8 класс
Фарков А.В.
Геометрия Контрольно-измерительные материалы
8 класс
Гаврилова Н.Ф.
Геометрия 7-9 класс
7 класс
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Позняк Э.Г., Юдина И.И.
Геометрия 7-11 класс
7 класс
Погорелов А.В.
Геометрия 7-9 класс
8 класс
Погорелов А.В.
9 класс
Геометрия Тесты к уч. Погорелова
9 класс
Фарков А.В.
Геометрия Тесты к уч. Атанасяна
9 класс
Фарков А.
В.
Геометрия Контрольно-измерительные материалы
9 класс
Рурукин А.Н.
Геометрия 7-9 класс
7 класс
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Позняк Э.Г., Юдина И.И.
Геометрия 7-11 класс
7 класс
Погорелов А.В.
10 класс
Геометрия Рабочая тетрадь
10 класс
Глазков Ю.А., Бутузов В.Ф.
Геометрия 7-11 класс
7 класс
Погорелов А.В.
11 класс
Геометрия Рабочая тетрадь
11 класс
Бутузов В.Ф., Глазков Ю.А.
Геометрия 7-11 класс
7 класс
Погорелов А.В.
Не придуман еще такой предмет, чтобы при его изучении у школьников не возникало сложностей. В основном, одним из самых трудных для детского восприятия считается геометрия. Первые изученные темы покажутся не такими то и сложными, но в дальнейшем для решения заданий все равно придется прибегнуть за помощью к ГДЗ по геометрии.
Как правило, проблемы начинают проявляться тогда, когда доходит дело до решения задач на доказательство теорем.
При хорошем запоминании теоретического материала и правильном применении таких сборников с ответами на практике позволит не только вовремя справляться с любыми заданиями, но и закреплять изученный материал более качественно.
Решебники по геометрии развивают интеллектуальные способности и подготавливают учащихся к более сложным темам. Подобные пособия формируют умения правильно отбирать нужный материал. В таких сборниках все ответы учитывают уровень подготовки ребят, соответственно, предлагаемые решенные задания рассчитаны и на базовый, и на повышенный уровень. При сопоставлении готовых верных решений главное понимать, что данные издания не спасают, а предоставляют достоверную вспомогательную информацию.
Планиметрия. Пособие для углубленного изучения математики. Когда учиться в удовольствие
Бутузов Валентин Федорович
На кафедре работает 55 преподавателей и научных сотрудников, в том числе 13 профессоров и 19 доцентов, 17 сотрудников кафедры являются докторами наук и 36 кандидатами наук.
Бутузов Валентин Федорович
начальник отдела
Бутузов Валентин Федорович родился 23 ноября 1939г. в Москве в семье служащих. Отец, Бутузов Федор Григорьевич (1909-1975), техник-строитель, мать, Бутузова (Кураева) Анастасия Владимировна (1912-1994) окончила художественное училище и много лет работала руководителем сельского клуба. В 1957 г. В.Ф.Бутузов с золотой медалью окончил Сухаревскую среднюю школу (Краснополянский район Московской области) и поступил на физфак МГУ им. М.В. Ломоносов. По ее окончании в 1963 г. был принят в аспирантуру. На выбор специальности и формирование научных интересов большое влияние оказали профессора и преподаватели кафедры математики физического факультета А.Н. Тихонов, А.Г. Свешников, А.Б. Васильев, П.С. Моденов. В 1966 Окончил аспирантуру, защитил кандидатскую диссертацию. кандидатскую диссертацию «Асимптотика решений некоторых задач для интегро-дифференциальных уравнений с малым параметром в производных» и был принят на работу на кафедру математики физического факультета.
С 1981 г. работает профессором (ученое звание профессора утверждено в 1982 г.), с 1993 г. — заведующий кафедрой математики физического факультета МГУ.
С 1979 г. В.Ф.Бутузов вместе с коллегами принимает активное участие в создании новых школьных учебников по геометрии. В 1988 г. эти учебники (для 7–9 и 10–11 классов) заняли 1-е место на Всесоюзном конкурсе школьных учебников. В настоящее время в них учатся десятки миллионов школьников России и стран СНГ. Под его редакцией были написаны, выдержали несколько изданий и переведены на английский и испанский языки два учебника по высшей математике для вузов.
Бутузов В.Ф. награжден медалями «За трудовое отличие» (1986 г.) и «В память 850-летия Москвы» (1997 г.), знаками «Отличник народного образования» (1985 г.) и «Почетный работник высшей профессиональной Образование Российской Федерации» (1999). Лауреат Ломоносовской премии МГУ за педагогическую деятельность (1993), лауреат Ломоносовской премии МГУ I степени за научную деятельность (2003).
Подготовил 12 кандидатов наук, трое его учеников стали докторами наук. В соавторстве с проф. А. Б. Васильевой он написал четыре монографии по асимптотическим методам в теории сингулярных возмущений.
Основные работы:
- Асимптотические разложения решений сингулярно возмущенных уравнений. М., Наука, 1973 (совм. с А.Б. Васильевой).
- Асимптотические методы в теории сингулярных возмущений. М., Высшая школа, 1990 (совместно с А.Б. Васильевой).
- Математический анализ в вопросах и заданиях. М., Высшая школа, 1-е издание, 1984; М., Физматлит, 4-е изд.
, 2001 г. (совместно с Н.Ч. Крутицкой, Г.Н. Медведевым, А.А. Шишкиным). - Геометрия 7-9 (учебник для общеобразовательных учреждений).М., Просвещение, 1-е издание, 1990; 15-е издание, 2005 г. (совместно с Л.С. Атанасяном, С.Б. Кадомцевым, Е.Г. Позняком, И.И. Юдиной).
- Геометрия 10-11 (учебник для общеобразовательных учреждений).М., Просвещение, 1-е издание, 1992; 11-е издание, 2005 г. (совместно с Л.С. Атанасяном, С.Б. Кадомцевым, Л.С. Киселевой, Е.Г. Позняк).
, 2001 г. (совместно с Н.Ч. Крутицкой, Г.Н. Медведевым, А.А. Шишкиным).Очень часто ученики седьмого класса обращаются к книгам такого формата, чтобы справиться с огромным количеством задач по геометрии. Прежде чем начать пользоваться этими каталогами, лучше ознакомиться с основной информацией о них и о том, какую пользу они могут принести.
Изучаем пользу, которую дают компьютерщики по геометрии
Детские психологи уже доказали положительное влияние на личность ребенка, работая с такими консультантами как готовые домашние задания. В первую очередь родители заботятся о здоровье своего ребенка, и мы тоже об этом подумали.
Используя ГДЗ по геометрии на нашем сайте, семиклассник не будет вынужден сидеть за домашним заданием до ночи, и сможет выспаться в соответствии с нормами для своего возраста.
Также уверенность в правильности ответов на домашние задания избавит от стресса, который испытывает ученик, выступая с результатами своей работы перед классом. Кроме того, не менее важным преимуществом использования учебников типа ГДЗ по геометрии Атанасяна 7 класс является подготовка ребенка к самостоятельной жизни.
Например, когда ответы на задачу не совпадают с данными, которые предлагают решатели, учащийся сможет проследить за ходом решения упражнения и самостоятельно найдет допущенную в нем ошибку. Отличный результат и высокую успеваемость приносит сотрудничество только с правильными лицами, принимающими решения в геометрии Атанасяна. С появлением нашего портала ВИПГДЗ вам больше не нужно тратить свое время на поиск качественных книг такого формата. Просто посетите наш образовательный ресурс.
сайт дает семиклассникам только правильные решения
Наш портал ВИПГДЗ очень выгодно отличается от других сайтов подобного типа. Все дело в том, что он дает огромное количество неоспоримых преимуществ своим пользователям. Во-первых, вам не нужно беспокоиться о плате за использование 7-х классов на наших страницах, ведь вся учебная литература предоставляется абсолютно бесплатно.
Также мы уверены, что вас приятно впечатлит широкий выбор книг по геометрии, которые предлагает сайт. Среди других преимуществ нашего ресурса выделяется возможность не только просматривать каталоги онлайн, но и скачивать их на компьютер или другой современный гаджет.
Зная, что родители и дети — личности нового поколения, мы подумали, что мобильная версия нашего сайта, сайт им понравится, и создали ее. Теперь вы можете пользоваться всеми преимуществами ответов по геометрии в любое время, просто добавив наш ресурс в закладки.
Вместе с нашим сайтом вы поймете, насколько интересным и беззаботным может быть процесс выполнения домашнего задания по геометрии в 7 классе!
Когда учиться весело
Учиться может быть легко и интересно.
В основе этого лежит выбор правильного руководства по обучению. Таким верным напарником без проблем станет учебник по геометрии 7 класс (Бутузов, Прасолов, Кадомцев). Она способствует качественному усвоению знаний детьми и помогает им добиться колоссальных успехов. Крайне удобно работать с этим каталогом на нашем Вклассе онлайн.
Используем материалы и решаем задачи
У нас лучшее пособие по геометрии, которое принесет в жизнь детей много приятных сюрпризов. Нам чрезвычайно удобно работать с этим учебником для седьмого класса. Никаких барьеров на этом пути мы не ставили. Все материалы на ресурсе открыты в любое время суток, и для начала сотрудничества с ними регистрация не требуется. Наши учебники бесплатны и их легко просматривать.
Большое влияние учебника на Вклассе
Учебники больше любых других справочников влияют на детей. Все дело в том, что благодаря этим книгам восьмиклассники легко изучают геометрию. С пособиями они получают самые важные знания по предмету, которые показаны в доступной форме.
Они легко смогут изучить их, чтобы использовать в практических целях в будущем. Это принесет отличные оценки в учебе и станет спутником в успешном будущем.
Внутренняя часть книги
Желая учиться на 5+, студенты постоянно работают с квалифицированным учебником на нашем ресурсе. Этот справочник отличается правильной структурой и содержит только актуальную учебную информацию, которая есть в школьной программе. Это учебное пособие 2010 г. включает широкий спектр тем: Окружность, Треугольники и другие. Они подали основные правила дисциплины.
Планиметрия. Пособие для углубленного изучения математики / В.Ф. Бутузов, С.Б. Кадомцев, Е.Г. Позняк, С.А. Шестаков, И.И. Юдина. — М., 2005. — 488 с.
В этом руководстве систематизировано изложение углубленного курса планиметрии. Наряду с основными геометрическими сведениями, включенными в стандартную школьную программу по геометрии, имеется много дополнительного материала, расширяющего и углубляющего основные сведения.
Стиль изложения, принятый в пособии, заметно отличается от традиционного: теорема есть доказательство. В ряде случаев авторы не формулируют заранее теоремы и аксиомы, а ищут их формулировки вместе с читателем. Такой подход объясняется стремлением авторов дать представление о том, как устроена математика и как работают математики.
В книге большое внимание уделено геометрии Лобачевского, кривым постоянной ширины, изопериметрическим задачам, доказан ряд замечательных теорем планиметрии.
Пособие предназначено для учащихся, проявляющих живой интерес к математике, а также всех, кого привлекает красота геометрии. Может использоваться на занятиях с углубленным изучением математики, в работе математических кружков и факультативов, служить основным учебником в школах физико-математического профиля.
ОГЛАВЛЕНИЕ
Предисловие ………………………………………… 3
Глава 1. Исходная геометрическая информация …………………. 6
§ 1.
Точки, прямые, отрезки …………….. ………. 6
§2. Измерение отрезков и углов …………………. 17
§3. Перпендикулярные и параллельные прямые ……………. 25
Глава 2. Треугольники …………………………… ……. 37
§ 1. Треугольники и их виды …………………. 37
§2. Равнобедренный треугольник ……………………. 43
§3. Отношения между сторонами и углами треугольника ……. 46
§4. Признаки равенства треугольников ………………………….. 52
§5. Признаки равенства прямоугольных треугольников ………. 68
§6. Задания на построение ………………………….. 79
Глава 3. Параллельные прямые ……… ……………. 101
§1. Аксиома параллельных прямых …………………. 101
§2. Свойства параллельных прямых …………………. 119
Глава 4. Дополнительная информация о треугольниках …… 127
§1. Сумма углов треугольника. Средняя линия треугольника .
….. 127
§2. Четыре замечательные точки треугольника ……………. 139
Глава 5. Многоугольники …………………. ……. 150
§1. Выпуклый многоугольник ………………………….. 150
§2. Четырехугольники ……………………………….. 168
Глава 6. Площадь ……. ………………………….. 180
§1. Эквивалентные полигоны …………………. 180
§ 2. Понятие площади ……………………………….. 188
§3. Площадь треугольника…………………………….. 197
§4. Формула Герона и ее приложения …………………. 210
§5. Теорема Пифагора ………………………….. 213
Глава 7. Подобные треугольники ……. …………….. 219
§1. Признаки подобия треугольников …………………. 219
§2. Применение подобия для доказательства теорем и решения задач. . 230
§3. Задания на построение ……………………………….. 245
§4.
О чудесных точках треугольника ……………. 255
Глава 8. Окружность ……………… …………… 260
§1. Свойства окружности ……………………………….. 260
§2. Углы, связанные с окружностью …………………. 268
Глава 9. Векторы ……………. ………………. 285
§1. Сложение векторов ………………………….. 285
§ 2. Умножение вектора на число …………………. 292
Глава 10. Координатный метод ……. …………….. 298
§ 1. Координаты точек и векторов ………………….. .. 298
§2. Уравнения прямой и окружности ……………………………….. 304
§3. Радикальная ось и радикальный центр окружностей ………. 309
§4. Гармонические четверки точек …………………. 317
Глава 11. Тригонометрические соотношения в треугольнике. Скалярное произведение векторов …………………. 324
§ 1. Отношения между сторонами и углами треугольника .
…… 324
§2. Использование тригонометрических формул для решения геометрических задач ………………………….. 331
§3. Скалярное произведение векторов …………………. 339
Глава 12. Правильные многоугольники. Длина и площадь …… 347
§1. Правильные многоугольники …………………. 347
§2. Длина ……………………………….. 355
§3. Площадь ……………………………….. 363
Глава 13. Геометрические преобразования …………….. 374
§1. Движение ……………………………….. 374
§2. Центральное подобие ……………………………….. 386
§3. Инверсия ……………………………….. 396
Приложение 1. Снова о цифрах *. ……………………… 414
Приложение 2. Снова о геометрии Лобачевского ………… ….. 430
М.: Физматлит, 2005. — 488с.
В этом руководстве систематизировано изложение углубленного курса планиметрии.
Наряду с основными геометрическими сведениями, включенными в стандартную школьную программу по геометрии, имеется много дополнительного материала, расширяющего и углубляющего основные сведения. Стиль изложения, принятый в пособии, заметно отличается от традиционного: теорема есть доказательство. В ряде случаев авторы не формулируют заранее теоремы и аксиомы, а ищут их формулировки вместе с читателем. Такой подход объясняется стремлением авторов дать представление о том, как устроена математика и как работают математики.
В книге значительное внимание уделено геометрии Лобачевского, кривым постоянной ширины, изопериметрическим задачам, доказан ряд замечательных теорем планиметрии.
Пособие предназначено для учащихся, проявляющих живой интерес к математике, а также всех, кого привлекает красота геометрии. Может использоваться на занятиях с углубленным изучением математики, в работе математических кружков и факультативов, служить основным учебником в школах физико-математического профиля.
Формат: pdf
Размер: 7.7 Мб
Смотреть, скачать: диск.гугл
Предисловие 3
Глава 1. Исходная геометрическая информация 6
§ 1. Точки, линии, отрезки 6
1. Точка ( 6). 2. Прямая (б). 3. Балка и сегмент (9). 4. Несколько задач A0). 5. Угол А3). б. Полуплоскость А4).
§2. Измерение отрезков и углов 17
7. Равенство геометрических фигур A7). 8. Сравнение отрезков и углов A7). 9. Середина отрезка и биссектриса угла A8). 10. Измерьте отрезки и углы A9). 11. О числах B0).
§3. Перпендикулярные и параллельные линии 25
12. Перпендикулярные линии B5). 13. Признаки параллельности двух прямых Б8). 14. Практические приемы построения параллельных прямых С1). 15. Есть ли квадрат? С2). 16. Заключительные замечания C4).
Глава 2. Треугольники 37
§ 1. Треугольники и их виды 37
17. Треугольник С7). 18. Внешний угол треугольника С8).
19.
Классификация треугольников С9). 20. Медианы, биссектрисы и высоты треугольника D0).
§2. Равнобедренный треугольник 43
21. Теорема об углах равнобедренного треугольника D3).
22. Знак равнобедренного треугольника D3). 23. Теорема о высоте равнобедренного треугольника D4).
§3. Отношения между сторонами и углами треугольника 46
24. Теорема о соотношениях между сторонами и углами треугольника D6). 25. Обратные теоремы D7). 26. Неравенство треугольника D9).
§4. Признаки равенства треугольников 52
27. Три признака равенства треугольников E2). 28. Существуют ли другие признаки равенства треугольников? Е6). 29. Признаки равенства треугольников по медианам, биссектрисам и высотам F1).
§5. Признаки равенства прямоугольных треугольников 68
30. Пять признаков равенства прямоугольных треугольников F8).
31. Средний перпендикуляр к сегменту. Осевая симметрия G2).
32. Расстояние от точки до линии G5). 33.
Свойство биссектрисы угла G5). 34. Теорема о пересечении биссектрис треугольника G7).
§6. Building Challenges 79
35. Окружность. Центральная симметрия G9). 36. Взаимное расположение линии и окружности (81). 37. Окружность, вписанная в треугольник (84). 38. Взаимное расположение двух окружностей (85). 39. Построение треугольника по трем сторонам (88).
40. Основные проблемы строительства (91). 41. Еще несколько задач на построение треугольника (94).
Глава 3. Параллельные линии 101
§ 1. Аксиома параллельных прямых 101
42. Аксиомы A01). 43. Основные понятия A02). 44. Система аксиом планиметрии 45. Два следствия из аксиом А08).
46. О теоремах А09). 48. Аксиома параллельных прямых A14).
49. О пятом постулате Евклида А16). 50. Еще раз о существовании квадрата A17).
§2. Свойства параллельных прямых 119
51. Расстояние между параллельными прямыми A19). 52. Еще один способ построения параллельных линий А20).
53. Задания для корпуса А21).
Глава 4. Дополнительная информация о треугольниках 127
§1. Сумма углов треугольника. Средняя линия треугольника 127
54. Задача о разрезании треугольника A27). 55. Сумма углов треугольника А29). 56. Средняя линия треугольника А34). 57. Теорема Фалеса A34). 58. Неожиданный факт A36).
§2. Четыре замечательные точки треугольника 139
59. Теорема о пересечении средних перпендикуляров к сторонам треугольника A39). 60. Окружность, описанная около треугольника A41). 61. Теорема о пересечении высот треугольника А42). 62. Размышления о точке пересечения медиан треугольника A43). 63. Теорема о пересечении медиан треугольника А45).
Глава 5. Полигоны 150
§ 1. Выпуклый многоугольник 150
64. Ломаная А50). 65. Полигон А52). 66. Выпуклый многоугольник A58). 67. Выпуклая линия А61). 68. Замкнутая линия A62). 69. Замкнутая выпуклая линия А63). 70. Вписанный многоугольник A64). 71. Описанный многоугольник A66).
§2. Четырехугольники 168
72. Свойство диагоналей выпуклого четырехугольника A68).
73. Характеристика рисунка A70). 74. Параллелограмм A70). 75. Теоремы Вариньона и Гаусса A72). 76. Прямоугольник, ромб и квадрат А73). 77. Трапеция А76).
Глава 6. Зона 180
§ 1. Равнозначные многоугольники 180
78. Задания на вырезание многоугольников A80). 79. составные полигоны A83). 80. Разрезание квадрата на неравные квадраты A85).
§2. Понятие площади 188
81. Измерение площади многоугольника А88). 82. Площадь произвольной фигуры А93).
§3. Площадь треугольника 197
84. Квадраты прямоугольника, параллелограмма и треугольника A97). 85. Изометрические многоугольники A98). 86. Евклидов метод B00). 87. Две теоремы об отношении площадей треугольников В01). 88. Две теоремы о биссектрисах треугольника B03). 89. Признак равенства треугольников по двум сторонам и биссектрисе, проведенной из одной вершины B04).
§4.
Формула Герона и ее применение 210
90. Формула Герона B10). 91. Теорема о медиане B11). 92. Формула биссектрисы треугольника B12).
§5. Теорема Пифагора 213
93. Обобщенная теорема Пифагора B13). 94. Задача о разрезании квадратов Б15).
Глава 7. Подобные треугольники 219
§ 1. Признаки подобия треугольников 219
95. Подобие и равенство треугольников Б19). 96. Другие признаки подобия треугольников B22). 97. Тригонометрические функции Б24).
§2. Применение подобия для доказательства теорем и решения задач. . 230
98. Обобщенная теорема Фалеса B30). 99. Следствие из обобщенной теоремы Фалеса B32). 100. Теорема о пропорциональных прямых в треугольнике B35). 101. Теорема Чева B37).
102. Теорема Менелая B41).
§3. Building Challenges 245
103. Среднее геометрическое B45). 104. Среднее арифметическое, среднее гармоническое и среднее квадратичное для двух сегментов B46). 105. Метод подобия B47).
§4. О чудесных точках треугольника 255
106. О высотах треугольника B55). 107. О биссектрисах треугольника B57). 108. Еще две точки связаны с треугольником B58).
Глава 8. Круг 260
§ 1. Свойства окружности 260
109. Характеристическое свойство окружности B60). ПО. Задания для сборки Б60). 111. Кривые постоянной ширины B63).
§2. Окружные углы 268
112. Вписанные углы B68). 113. Углы между хордами и секущими B71). 114. Угол между касательной и хордой B72). 115. Теорема о квадратном касательном B73). 116. Теорема Паскаля B75).
117. Вписанные окружности треугольника B76).
Глава 9. Векторы 285
§ 1. Сложение векторов 285
118. Сонаправленные векторы B85). 119. Равенство векторов B88). 120. Сумма векторов B89).
§2. Умножение вектора на 292
121. Произведение вектора на число B92). 122. Несколько задач Б94).
Глава 10. Координатный метод 298
§ 1.
Координаты точек и векторов 298
123. Координатная ось B98). 124. Прямоугольная система координат B99). 125. Координаты вектора C00). 126. Длина вектора и расстояние между двумя точками C02). 127. Теорема Стюарта C02).
§2. Уравнения прямой и окружности 304
128. Перпендикулярные векторы C04). 129. Уравнение прямой C05). 130. Уравнение окружности C06).
§3. Радикальная ось и радикальный центр окружностей 309
131. Радикальная ось двух окружностей C09). 132. Расположение радикальной оси относительно окружностей С11). 133. Радикальный центр трех окружностей C13). 134. Теорема Брианшона C15).
§4. Гармонические четверки точек 317
135. Примеры гармонических четверок (С17). 136. Полар С20).
137. Четырехугольник С21). 138. Построение касательной по одной линейке C22).
Глава 11. Тригонометрические соотношения в треугольнике. Скалярное произведение векторов 324
§1. Отношения между сторонами и углами треугольника 324
139.
Синус и косинус двойного угла C24). 140. Тригонометрические функции произвольных углов С25). 141. Формулы литья C25). 142. Другая формула площади треугольника — C26).
143. Теорема синусов C27). 144. Теорема косинусов C28).
§2. Использование тригонометрических формул для решения геометрических задач 331
145. Синус и косинус суммы и разности углов С31). 146. Теорема Морли С33). 147. Площадь четырехугольника С35). 148. Площади вписанных и описанных четырехугольников С37).
§3. Скалярное произведение векторов 339
149. Угол между векторами C39). 150. Определение и свойства скалярного произведения векторов C41). 151. Теорема Эйлера С43). 152. Теорема Лейбница C44).
Глава 12. Правильные многоугольники. Длина и площадь 347
§ 1. Правильные многоугольники 347
153. Равносторонние и равносторонние многоугольники C47).
154. Построение правильных многоугольников C50).
§2. Длина 355
155. Окружность C55).
156. Длина линии C57).
§ 3. Площадь 363
158. Площадь фигуры С63). 159. Первый замечательный предел — С65). 160. Изопериметрическая задача C67).
Глава 13. Геометрические преобразования 374
§ 1. Движения 374
161. Осевая симметрия C74). 162. Движение С75). 163. Использование движений при решении задач С77).
§2. Центральное подобие 386
164. Свойства центрального подобия C86). 165. Теорема Наполеона C88). 166. Задача Эйлера C89). 167. Директ Симеон C92).
§3. Инверсия 396
168. Определение инверсии C96). 169. Основные свойства инверсии C98). 170. Теорема Птолемея D01). 171. Формула Эйлера D02). 172. Круги Аполлония D02). 173. Круги Аполлония нужны даже флибустьерам D05). 174. Теорема Фейербаха D07). 175. Задача Аполлония D08).
Приложение 1. Снова о цифрах * 414
176. Неотрицательные действительные числа D14). 177. Сравнение неотрицательных действительных чисел D17). 178. Сложение неотрицательных действительных чисел D17).
179. Умножение положительных действительных чисел D18). 180. Отрицательные вещественные числа D19). 181. Точная верхняя грань D20).
182. Теорема Вейерштрасса D21). 183. Двоичная форма записи числа D21). 184. О взаимном расположении линии и окружности D23). 185. Об измерении углов D26). 186. О взаимном расположении двух окружностей D27).
Приложение 2. Еще раз о геометрии Лобачевского 430
Ответы и инструкции 437
Наша ноутбука 471
Индекс 473
Индекс 474
Из предисловия:
Это целесообразны интерес к математике, и предназначен в первую очередь для занятий с углубленным изучением математики, для математических кружков и факультативов. Он состоит из 13 глав, соответствующих главам учебника «Геометрия 7-9Атанасян Л.С., Бутузова В.Ф., Кадомцева С.Б., Позняк Е.Г., Юдина И.И. (Москва: Просвещение, 1990 и последующие издания). При этом пособие является полностью автономным, что позволяет использовать его как на тех занятиях, где геометрия преподается в других учебниках и в качестве основного учебника в школах физико-математического профиля.
Следует отметить, что стиль изложения, принятый в пособии, отличается от традиционного: доказательством является теорема.В ряде случаев мы не заранее формулировать теоремы и аксиомы, но искать их формулировки вместе с читателем.Такой подход объясняется стремлением авторов дать представление о том, как устроена математика и как работают математики.
Пособие, наряду с основными геометрическими сведениями, входящими в стандартную школьную программу по геометрии, содержит большой дополнительный материал, расширяющий и углубляющий основные сведения. В частности, значительное внимание уделяется теории параллельных прямых и дается представление о связанной с ней геометрии Лобачевского.
В каждой главе по мере изложения теоретического материала даются задачи с решениями, иллюстрирующие применение тех или иных утверждений. К каждому параграфу главы даны задания для самостоятельной работы, снабженные ответами и указаниями. Самые сложные задания и разделы отмечены звездочкой. Также имеется предметный указатель, облегчающий навигацию в книге.