Русский язык и литература Жанпейс У. 9 класс 2019 Упражнение 16 ГДЗ(дүж) решебник KZGDZ.COM
Раздел IV. Реальность и фантазия 40-42. «Жизнь -это море!». Ч.Т. Айтматов «Легенда о рогатой матери-оленихе» («Белый пароход») . Стр 171. Упражнение 16
← Предыдущий Следующий →
Раздел I. Культура народов мира
1. Феномен культуры. Стр 6.
Упражнение
1234567891011
2. Мир казахов. Стр 11.
Упражнение
123456789101112
3. Общение и культура. Стр 17.
Упражнение
1234567891011
4. Национальная культура — это национальная память народа. Стр 22.
Упражнение
12345678910
5. «Первый поэт казахов» Абай Кунанбаев «Слова назидания. Семнадцатое слово» . Стр 27.
Упражнение
123456781011
6.
«Русский сын казахского народа» В.Р. Гундарев «На земле Абая» . Стр 35.Упражнение
123456
7. Исповедь поэта М. Шаханов «Четыре матери» . Стр 28.
Упражнение
1234567
8. Необычные традиции, обычаи и праздники народов мира. Стр 43.
Упражнение
123456789
Раздел II. Природные ресурсы планеты Земля
9-10. Гармония человека и природы. К. Паустовский «Мещёрская сторона». Стр 50.
Упражнение
123
456789101112
11-12. Человеком надо стать. Т. Айтматов «Плаха» . Стр 57.
Упражнение
13456789
13-14. Малая родина. B. Распутин «Прощание с Матёрой» . Стр 64.
Упражнение
23457
15. Живопись в поэзии. C. Сейфуллин «Кокшетау» . Стр70.
Упражнение
1234567
16-17.
Праздники планеты Земля. Стр 76.Упражнение
1234567891011
18-19 Природа — открытая книга. Стр 83.
Упражнение
123456789101112131415
20-21 «Экос» значит дом. Стр 90.
Упражнение
134567891011
Раздел III. История и личность
23. Научный стиль Аннотация. Тезисы. Научная статья. Стр 106.
Упражнение
123456789
24-25. Певец свободы. A.С. Пушкин «Узник» . Стр 111.
Упражнение
123456
78910111213
26. Подвиг Пушкина. Тезисный план. Стр 119.
Упражнение
1234567
27-29. «Береги честь смолоду». A. С. Пушкин «Капитанская дочка» . Стр 123.
Упражнение
3578910111213141516171819202122232425262728293032333435
30-31.
«Книга памяти». М. Шаханов «Отрарская поэма о побежденном победителе, или Просчёт Чингисхана» . Стр 142.Упражнение
123456891011121314
32-35. «Вершина казахской литературы». М.О. Ауәзов «Путь Абая» . Стр 148.
Упражнение
1234567891011
36-37. «Щедрая доля». A. Кекилбаев «Плеяды — созвездие надежды» . Стр 157.
Упражнение
1345678910111213
14
38-39. Поэт и гражданин. A. Байтурсынов «Главный поэт казахов» . Стр 166.
Упражнение
1234567891011
Раздел IV. Реальность и фантазия
40-42. «Жизнь -это море!». Ч.Т. Айтматов «Легенда о рогатой матери-оленихе» («Белый пароход») . Стр 171.
Упражнение
1234567891011121415161718192021
43. «Солнце — это цветок». Р. Брэдбери «Всё лето в один день» . Стр 184.
Упражнение
1234567891011
ГДЗ Физика 9 класс Очень старое издание
Авторы:Очень старое издание
Тип:учебник
Нужно другое издание?
Какой номер надо решить?
§1. Материальная точка. Система отсчёта
§2. Перемещение
§3. Определение координаты движущегося тела
§4. Перемещение при прямолинейном равномерном движении
§5. Прямолинейное равноускоренное движение
§6. Скорость прямолинейного равноускоренного движения
§7. Перемещение тела при прямолинейном равноускоренном движении
§8. Перемещение тела при прямолинейном равноускоренном движении без начальной скорости
§9. Относительность движения
§10. Инерциальные системы отсчёта
§11. Второй закон Ньютона
§12. Третий закон Ньютона
§13. Свободное падение тел
§14.
Движение тела, брошенного вертикально вверх. Невесомость
§15. Закон всемирного тяготения
§16. Ускорение свободного падения на Земле
§18. Прямолинейное и криволинейное движени
§19. Движение тела по окружности с постоянной по модулю скоростью
§20. Искусственные спутники Земли
§21. Импульс тела. Закон сохранения импульса
§22. Реактивное движение. Ракеты
§23. Вывод закона сохранения механической энергии
§24. Колебательное движение
§25. Свободные колебания. Колебательные системы. Маятник
§26. Величины, характеризующие колебательное движение
§27. Гармонические колебания
§28. Затухающие колебания
§29. Вынужденные колебания
§30. Резонанс
§31. Распространение колебаний в среде. Волны
§32. Продольные и поперечные волны
§33. Длина волны. Скорость распространения волн
§34. Источники звука. Звуковые колебания
§35. Высота и тембр звука
§36. Громкость звука
§37. Распространение звука
§38.
Звуковые волны. Скорость звука
§39. Отражение звука. Эхо
§40. Звуковой резонанс
§41. Интерференция звука
§42. Магнитное поле и его графическое изображение
§43. Неоднородное и однородное магнитное поле
§44. Направление тока и направление линий его магнитного поля
§45. Обнаружение магнитного поля по его действию на электрический ток. Правило
§46. Индукция магнитного поля
§47. Магнитный поток
§48. Явление электромагнитной индукции
§49. Направление индукционного тока. Правило Ленца
§50. Явление самоиндукции
§51. Получение и передача переменного электрического тока. Трансформатор
§52. Электромагнитное поле
§53. Электромагнитные волны
§54. Конденсатор
§55. Колебательный контур. Получение электромагнитных колебаний
§56. Принципы радиосвязи и телевидения
§57. Интерференция света
§58. Электромагнитная природа света
§59. Преломление света. Физический смысл показателя преломления
§60.
Дисперсия света. Цвета тел
§61. Спектрограф и спектроскоп
§62. Типы оптических спектров
§63. Спектральный анализ
§64. Поглощение и испускание света атомами. Происхождение линейчатых спектров
§65. Радиоактивность как свидетельство сложного строения атомов
§66. Модели атомов. Опыт Резерфорда
§67. Радиоактивные превращения атомных ядер
§68. Экспериментальные методы исследования частиц
§69. Открытие протона
§70. Открытие нейтрона
§71. Состав атомного ядра. Массовое число. Зарядовое число
§72. Ядерные силы
§73. Энергия связи. Дефект масс
§74. Деление ядер урана
§75. Цепная реакция
§76. Ядерный реактор. Преобразование внутренней энергии атомных ядер в электрическую энергию
§77. Атомная энергетика
§78. Биологическое действие радиации. Закон радиоактивного распада
§79. Термоядерная реакция
Топовые ГДЗ по другим предметам
- Учебник
- Учебник
- Учебник
- Учебник
- Контурные
- Учебник
- Учебник
- Учебник
- Контрольные
- Дидактич.
org/Book»>Учебник© 2021 Copyright. Все права защищены. Правообладатель SIA Ksenokss.
Адрес: 1069, Курземес проспект 106/45, Рига, Латвия.
Тел.: +371 29-851-888 E-mail: [email protected]
Научные и технологические решения для класса 9 Science Chapter 16
- Решения для учебников
- Класс 9
- Наука
- наследственность и изменчивость
Научные и технологические решения Решения для класса 9 по естественным наукам Глава 16 «Наследственность и изменчивость» представлены здесь с простыми пошаговыми пояснениями.
Страница № 193:
Вопрос 1:
Дополните следующие предложения, выбрав подходящие слова из скобок.
(Наследование, половое размножение, бесполое размножение, хромосомы, ДНК, РНК, ген)
а. Наследственные признаки передаются от родителей к потомкам с помощью …………, поэтому их называют структурными и функциональными единицами наследственности.
б. Организмы, образуемые .
……….., имеют незначительные вариации.
в. Компонент, находящийся в ядрах клеток и несущий наследственные признаки, называется ………….
d. Хромосомы в основном состоят из ………….
e. Организмы, произведенные с помощью …………, показывают большие различия.
Ответ:
а. Наследственные признаки передаются от родителей потомству с помощью гена , поэтому их называют структурными и функциональными единицами наследственности.
б. Организмы, произведенные бесполое размножение имеют незначительные вариации.
с. Компонент, находящийся в ядрах клеток и несущий наследственные признаки, называется хромосомой .
д. Хромосомы в основном состоят из ДНК .
эл. Организмы, полученные в результате полового размножения , демонстрируют значительные различия.
Страница № 193:
Вопрос 2:
Объясните следующее.
а. Объясните моногибридное потомство Менделя с помощью какого-либо одного скрещивания.
б. Объясните соотношение дигибридов Менделя с помощью любого скрещивания.
в. Различают моногибридное и дигибридное скрещивание.
д. Правильно ли избегать проживания с человеком, страдающим генетическим заболеванием?
Ответ:
а. Моногибридное скрещивание — это скрещивание двух родителей, имеющих одну пару контрастных признаков; например, если скрестить растение гороха с желтой оболочкой с растением гороха с зеленой оболочкой, то в поколении F1 все растения дадут желтые семена.
б. Дигибридное скрещивание — это скрещивание двух родителей, которые имеют две пары контрастных признаков, например, растение с круглыми и желтыми семенами скрещивают с растением с зелеными и морщинистыми семенами.
в.
| Моногибридный кросс | Дигибридный кросс |
| Скрещивание, в котором задействована только одна пара контрастных признаков, называется моногибридным скрещиванием.  | Скрещивание, в котором участвуют только две пары контрастных признаков, известно как дигибридное скрещивание. |
| Моногибридное скрещивание полезно для определения доминирования генов. | Дигибридное скрещивание полезно при изучении ассортимента потомства.
|
| пример — помесь высокого и карликового растения | пример — скрещивание высокого растения с красными цветками и карликового растения с белыми цветками |
д. Нет, неправильно избегать проживания с человеком, страдающим генетическим заболеванием. Генетические нарушения не являются инфекционными заболеваниями, которые могут передаваться людям, вступающим в контакт с людьми с генетическими нарушениями. Генетические нарушения вызываются изменениями в последовательностях ДНК, которые могут передаваться от одного поколения к другому только при определенных обстоятельствах.
Скорее, мы должны поддерживать и принимать людей с такими расстройствами, чтобы они могли жить нормальной жизнью.
Страница № 193:
Вопрос 3:
Своими словами отвечает на следующие вопросы.
а. Что понимается под термином «хромосома». Объясните его виды.
б. Опишите строение молекулы ДНК.
в. Выскажите свое мнение о применении ДНК-дактилоскопии.
д. Объясните строение, функции и типы РНК.
эл. Почему необходимо, чтобы люди сдавали кровь на анализ перед вступлением в брак?
Ответ:
а. Хромосомы представляют собой нитевидные структуры, встречающиеся в ядре всех живых клеток. Хромосомы делятся на четыре типа в зависимости от положения центромеры.
(1) Метацентрические хромосомы: В этих хромосомах центромера находится посередине, что дает начало двум равным плечам.
(2) Субметацентрические хромосомы: В субметацентрических хромосомах центромера находится немного в стороне от средней области.
В результате у него одна рука немного длиннее другой.
(3) Акроцентрические хромосомы: В акроцентрических хромосомах центромера расположена близко к концу хромосомы. В результате у него одна рука очень длинная, а другая очень короткая.
(4) Телоцентрические хромосомы: В телоцентрических хромосомах центромера находится на терминальном конце. В результате хромосома имеет только одно плечо.
б. ДНК представляет собой очень большую одиночную молекулу, также называемую макромолекулой. Он имеет структуру двойной спирали, похожую на лестницу, которая закручена с обоих концов. Молекула ДНК состоит из основных материалов, называемых нуклеотидами, и каждый нуклеотид состоит из трех компонентов:
- Сахар
- Фосфатные группы
Сахара и фосфаты расположены вдоль.
- Азотистые основания присоединены к сахару изнутри, что простирается до соединения водородной связи и комплементарного азотистого основания из другой нити.
Азотистые основания:
- Аденин(А)
- Гуанин(Г)
- Цитозин(С)
- Тимин(Т)
Адинин образует пары с тимином с двумя водородными связями. Гуанин образует пары с цитозином тремя водородными связями.
Во время интерфазы клеточного цикла молекулы ДНК удваиваются для их равного распределения в дочерних клетках во время митоза. Двойная спираль открывается на одном конце, освобождает две нити, и из них формируются новые нити.
в. Отпечатки пальцев ДНК — это метод сравнения последовательностей ДНК любых двух людей. 99,9% последовательностей оснований у всех людей идентичны. Именно оставшиеся 0,1% делают каждого человека уникальным.
Снятие отпечатков пальцев ДНК применяется следующим образом:
- Отпечатки пальцев ДНК
широко используются в криминалистике, поскольку ДНК каждой ткани человека имеет одинаковую степень полиморфизма.
- Отпечатки пальцев ДНК
составляют основу тестирования на отцовство, поскольку ребенок наследует полиморфизм от обоих родителей.
- Может использоваться для изучения эволюции и генетического разнообразия в популяции.
д. Нуклеотид РНК состоит из трех основных компонентов: азотистого основания, сахара рибозы и фосфатной группы.
• Рибозный сахар и фосфаты образуют основу полинуклеотидной цепи с азотистыми основаниями, связанными с частью сахара и выступающими из основы.
• Присутствуют два типа азотистых оснований, т. е. пурины (аденин и гуанин) и пиримидины (цитозин и урацил).
• Азотистое основание связано с сахаром рибозой через N-гликозидные связи с образованием нуклеозида (например, аденозина, гуанозина или цитидина и уридина).
• Фосфатная группа связана с 5′-ОН нуклеозида посредством фосфоэфирной связи с образованием соответствующего нуклеотида.
• Каждый нуклеотидный остаток имеет дополнительную группу -ОН, присутствующую в 2′-положении рибозы.
• Многие нуклеотиды связаны друг с другом 3′-5′ фосфодиэфирными связями, образуя полинуклеотидную цепь.
• Конец цепи со свободной фосфатной группой на 5′-конце рибозного сахара называется 5′-концом, а другой конец цепи со свободной 3′-ОН группой на рибозном сахаре называется называется 3′-концом полинуклеотидной цепи.
Существует 3 типа РНК:
1. мРНК (информационная РНК) – служит матрицей для синтеза белка. ДНК транскрибируется с образованием мРНК, которая, в свою очередь, транслируется с образованием белка.
2. тРНК (транспортная РНК) — приносит аминокислоты во время трансляции и считывает генетический код.
3. рРНК (рибосомная РНК) — это рабочие столы трансляции. Они играют структурную и каталитическую роль во время трансляции.
эл. Людям необходимо сдавать кровь перед браком, потому что генетические нарушения передаются только при репродукции. Если носитель/больной генетическим заболеванием женится на человеке, который также является носителем/страдающим этим заболеванием, есть вероятность, что это заболевание будет передано потомству.
Чтобы предотвратить эту передачу, люди должны сдать кровь на анализ до брака, чтобы узнать, являются ли они носителями какого-либо генетического заболевания.
Номер страницы 193:
Вопрос 4:
Напишите краткую заметку по каждому из них.
а. Синдром Дауна
б. Моногенные заболевания
c. Серповидноклеточная анемия: симптомы и лечение.
Ответ:
а. Синдром Дауна: Синдром Дауна возникает из-за наличия дополнительной копии хромосомы 21 (трисомия 21). Это было первое обнаруженное и описанное хромосомное заболевание у человека. Общее число хромосом у людей, страдающих синдромом Дауна, достигает 47. У больного низкий рост, маленькая, круглая голова, морщинистый язык, частично открытый рот, складка на ладонях, врожденный порок сердца и умственная отсталость.
б. Моногенные расстройства: Моногенные расстройства — это генетические нарушения, вызванные мутацией в одном гене. Эта мутация может присутствовать на одной или обеих хромосомах.
Некоторыми примерами моногенных заболеваний являются серповидноклеточная анемия, муковисцидоз, поликистоз почек и т. д.
c. Серповидноклеточная анемия: Серповидноклеточная анемия представляет собой аутосомно-связанный рецессивный признак, проявляющийся изменением формы эритроцитов с двояковогнутого диска на серповидную при низком напряжении кислорода. Это результат замены ГАГ на ГУГ, что приводит к замене Глу на Вал в шестом положении цепи бета-глобина гемоглобина. Он характеризуется низким уровнем гемоглобина и другими симптомами анемии, такими как утомляемость и раздражительность, отеки рук и ног, боли в суставах, постоянная субфебрильная температура и т. д.
Специального лечения серповидноклеточной анемии не существует, доступные методы лечения обеспечивают симптоматическое облегчение симптомов, связанных с этим заболеванием.
Страница № 193:
Вопрос 5:
Как взаимосвязаны элементы в группах A, B и C?
| А | В | С |
| 44+ХХУ | Бледная кожа, белые волосы |
| Диабет | 45+Х | Мужчины бесплодны |
| Альбинизм | Митохондриальное заболевание | Женщины бесплодны |
| Синдром Тернера | Полигенное расстройство | Это нарушение возникает во время развития зиготы.  |
| Синдром Клайнфельтера | Моногенное расстройство | Влияние на уровень глюкозы в крови |
Ответ:
| А | В | С |
| Наследственная оптическая нейропатия Лебера | митохондриальное заболевание | Это нарушение возникает во время развития зиготы. |
| Диабет | Полигенное расстройство | Влияние на уровень глюкозы в крови |
| Альбинизм | Моногенное расстройство | Бледная кожа, белые волосы |
| синдром Тернера | 45+Х | Женщины бесплодны |
| Синдром Клайнфельтера | 44+ХХУ | Мужчины бесплодны |
Страница № 193:
Вопрос 6:
Заполнение пропусков на основе заданного соотношения.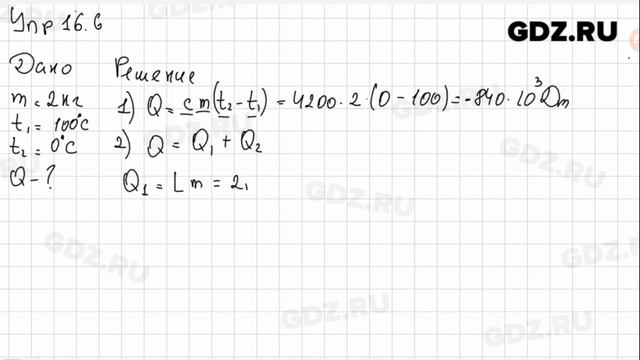
а. 44+X:Синдром Тернера: :44+XXY:- ………..
б. 3:1 Моногибрид: : 9:3:3:1 : ………….
c. Женщины : Синдром Тернера : : Мужчины : …….
Ответ:
a. 44+X:Синдром Тернера: :44+XXY:- Синдром Клайнфельтера
b. 3:1 Моногибрид: : 9:3:3:1 : Дигибридный кросс
c. Женщины : синдром Тернера : : Мужчины : Синдром Клайнфельтера
Страница № 193:
Вопрос 7:
Заполните приведенную ниже древовидную диаграмму в зависимости от типов наследственных заболеваний.
Ответ:
Селина Краткий курс 9 Математика Глава 16 Теоремы о площади Упражнение 16B Решения
Реклама
Selina Concise Class 9 Math Chapter 16 Теоремы о площади Упражнение 16B РешенияУПРАЖНЕНИЕ – 16B
(Q1) Покажите, что:
(1) (i) Диагональ делит параллелограмм на два равновеликих треугольника.
(ii) Отношение площадей двух треугольников одинаковой высоты равно отношению их оснований.
(iii) Отношение площадей двух треугольников на одном основании равно отношению их высот.
Решение:
(i) Доказательство:
В △ADC и △ABC
∠DAC = ∠BCA (альтернативные внутренние углы)
AC = AC (общая сторона)
∠DCA = ∠BAC2 ∴11 900 △ADC ≅ △ABC (по углу-стороне-углу (ASA))
Тогда площадь (△ADC) = площадь (△ABC)
(ii) Доказательство:
Площадь (△ABD) = 1/ 2 × BD × AE —— (i)
Площадь (△ADC) = 1/2 × CD × AE ——- (ii)
Из уравнения (i) и (ii),
Площадь (△ABD) /площадь (△ADC) = (1/2×BD×AE)/(1/2×CD×AE)
Площадь (△ABD)/площадь (△ADC) = m/n (следовательно доказано)
(iii) Доказательство:
Площадь (△ADB) = 1/2 × AB × DF —– (i)
Площадь (△ACB) = 1/2 × AB × CE —– (ii)
Уравнение (i), разделенное на уравнение (ii), ((i) ÷ (ii))
Площадь (△ADB)/ площадь (△ACB) = (1/2×AB×DF)/(1/2×AB×CE)
Площадь (△ADB)/площадь (△ACB) = DF/CE (отсюда доказано)
(Q2) На данном рисунке; AD — это медиана △ABC, а E — только точка на медиане AD.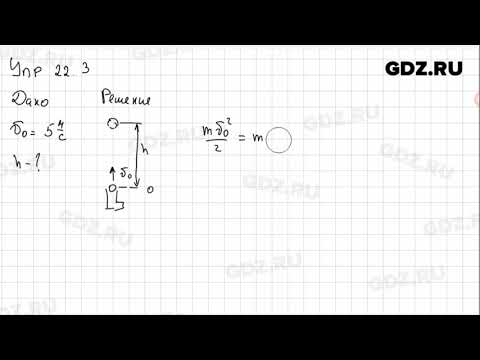
Докажите, что площадь (△ABE) = площадь (△ACE)
Решение:
Дано: AD является медианой.
Доказательство:
Площадь (△ABE) = площадь (△ACE)
Доказательство: В △ABC,
Площадь (△ABD) = площадь (△ACD) —– (i)
В △BEC,
Площадь (△BED) = площадь (△CED) —– (ii)
Уравнение вычитания (i) и (ii),
Площадь (△ABD) – площадь (△BED) = площадь (△ACD) – площадь (△CED)
Площадь (△ABE) = площадь (△ACE) (отсюда доказано)
(Q3) На рисунке к вопросу 2, если E является серединой медианы AD, то докажите, что:
Площадь (△ABE) = 1/4 площади (△ABC).
Решение:
Если E — середина медианы AD.
Доказать:
Площадь (△ABE) = 1/4 площади (△ABC)
В △ABC,
Площадь (△ABD) = площадь (△ACD) —– (i)
В △BEC , площадь (△BED) = площадь (△CED) —– (ii)
В △ABD,
Площадь (△ABE) = площадь (△BED) —– (iii)
Из уравнения (i), (ii) и (iii),
Площадь (△ABE) = площадь (△BED) = площадь (△CBD) = площадь (△ACE)
= x единица измерения 2
Теперь площадь (△ABC) = площадь (△ABE) + площадь (△BED) + площадь (△CED) + площадь (△ACE)
= x + x + x + x
Площадь (△ABC) = 4x
1/4 площади (△ABC) = x
1/4 площади (△ABC) = площадь (△ABE) (отсюда доказано)
(Q4) ABCD — параллелограмм, P и Q — середины сторон AB и AD соответственно.
Докажите, что площадь треугольника APQ = 1/8 площади параллелограмма ABCD.
Решение:
Дан параллелограмм ABCD, P и Q — середины сторон AB и AD.
Чтобы доказать:
Площадь (△APQ) = 1/8 площади (ABCD)
Доказательство:
Площадь (ABCD) = площадь (△ABD) + площадь (△BCD)
Площадь (ABCD) = площадь (△ABD) + площадь (△ABD)
Площадь (ABCD) = 2 площади (△ABD) —- (i)
Кроме того, площадь (△BDP) = площадь (△ACP) —— (ii)
Теперь площадь (ABCD) = 2 [площадь (△BDP) + площадь (△ADP)] [из уравнения (i)]
Площадь (ABCD) = 4 области (△ADP)
Площадь (ABCD) = 4 [область (△APQ) + площадь (△QDP)
Площадь (ABCD) = 4 [область (△APQ) + площадь ( △APQ)] [площадь APQ = площадь QD]
Площадь (ABCD) = 8 площади (△APQ)
1/8 площади (ABCD) = площадь (△APQ) (следовательно доказано)
(Q5) Основание BC треугольника △ABC делится в точке D так, что BD = 1/2 DC.
Докажите, что площадь △ABD = 1/3 площади △ABC.
Решение:
Дано:
Чтобы доказать:
Площадь (△ABD) = 1/3 площади (△ABC)
Доказательство: BD = 1/2 DC
BD/DC = 1/3
, BD = 1x и CD = 2x
Площадь (△ABD) = 1/2 × BD × AE —– (i)
Площадь (△ABC) = 1/2 × BC × AE —— (ii)
Разделить уравнение (i) на (ii), ((i) ÷ (ii))
Площадь (△ABD)/площадь (△ABC) = (1/2×BD×AE)/(1/2×BC× AE)
Площадь(△ABD)/площадь(△ABC) = BD/BC
Площадь(△ABD)/площадь(△ABC) = x/3x
Площадь (△ABD) = 1/3 площади (△ABC) (Отсюда доказано)
(Q6) В параллелограмме ABCD точка P лежит в DC. Так что DP:PC = 3:2. Если площадь △DPB = 30 кв. см, найдите параллелограмм ABCD.
Решение:
Дано:
DP/PC = 3/2
Площадь (△DPB) = 30 см 2
3 Найти: 90
Найти: площадь (△DBP)/площадь(△BPC) = 3/2
30/площадь(△BPC) = 3/2
30×2/3 = площадь (△BPC)
10×2 = площадь (△BPC)
20 = площадь (△BPC)
Теперь площадь (△BDC) = 30+20
= 50 см 2
Следовательно, площадь (ABCD) = 2 × 50
= 100 см 2
(Q7) ABCD такая, что параллельна ECBC и AE пересекает CD в точке F.
Если площадь (△DFB) = 30 см 2 , найдите площадь параллелограмма.
Дано:
Площадь (△DFB) = 30 см 2
Найти: площадь (ABCD) =?
Решение:
в △ ADF и △ ECF
↑FAD = потряс (альтернативные внутренние углы)
AD = CE (∵ DED)
.
∴ △ADF ≅ △ECF (по углу-стороне-углу (ASA)
DF = FC (по CPCTC)
In △DBC,
Площадь (△DBF) = площадь (△FBC) = 30° { потому что BF медиана}
Тогда площадь (△DBC) = 30 + 30
= 60 см 2
Следовательно, площадь (ABCD) = 2 × площадь (△DBC)
= 2 × 60
= 0604 см 2 9 1204 1204 см
(Q8) На следующем рисунке показан треугольник ABC, в котором P, Q и R являются серединами сторон AB, BC и CA соответственно. S — середина PQ.
Докажите, что: Площадь (△ABC) = 8×площадь (△QSB)
Решение:
P, Q и R — середины сторон AB, BC и CA соответственно S — середины сторон PQ.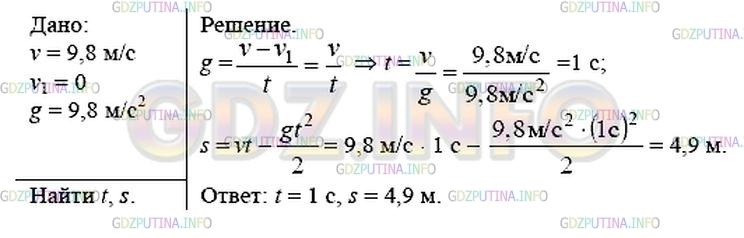
Доказательство: Площадь (△ABC) = 8 площади (△QSB)
Доказательство: RQ параллельная AP (RQ||AP) (по теореме о средней точке)
AR параллельная QP (AR||QP)
Тогда APQR — параллелограмм.
Площадь (△APR) = площадь (△PQR) —– (i)
Аналогично, площадь (△QRG) = площадь (PQR) —– (ii)
Площадь (△PQR) = площадь (△QBP) —- (iii)
Из уравнения (i), (ii) и (iii),
Площадь (△QRC) = площадь (△PQR) = площадь (△QBP) = площадь (△APR) = x единица
Теперь площадь (△ABC) = площадь (△APR) + площадь (△QRC) + площадь (△PQR) + площадь (△QBP)
Площадь (△ABC) = x + x + x + x
Площадь (△ABC) = 4x
Площадь (△ABC) = 4 площади (△QBP)
Площадь (△ABC) = 4 [площадь (△BQS) + площадь (△BPS)]
= 4 [2 площадь (△QSB)]
Площадь (△ABC) = 8 площадь (△QSB) (отсюда доказано)
Вот ваше решение Selina Concise Class 9Математика Глава 16 Теоремы для областей Упражнение 16B
Дорогой студент, Я ценю ваши усилия и тяжелую работу, которую вы все приложили..jpg)