Алгебра 9 класс номер 53: Номер (задание) 53 - гдз по алгебре 9 класс Макарычев, Миндюк

Содержание

ГДЗ: Алгебра 9 класс Макарычев, Миндюк, Нешков

Алгебра 9 класс

Тип: Учебник

Авторы: Макарычев, Миндюк, Нешков

Издательство: Просвещение

Дорогие девятиклассники

Вы снова переступаете порог школы, и некоторые из вас в последний раз, потому что этот год является первым из выпускных. На носу серьезные экзамены, определяющие качество и количество ваших знаний по математике, а точнее, алгебре и тригонометрии. В этом году вам предстоит усложненная программа не только с новыми темами, такими как функции, различные прогрессии, уравнения и неравенства, а еще и повторение изученного с 7 по 9 класс.

Для чего это пособие

Работу учеников в выпускных классах необходимо контролировать особенно тщательно для успешной сдачи экзаменов. ГДЗ к учебнику «Алгебра 9 класс Макарычев, Миндюк, Нешков» издательства «Просвещение» составлялся для эффективной работы выпускников в домашних условиях, успешной подготовки к экзаменам, для контроля над пробелами в знаниях, а также для родителей, желающих помочь детям в домашней работе.

Какова структура книги

В данной книге ответы ко всем заданиям из учебника, в том числе, контрольным, подробно и в упрощенном виде расписаны по страницам, согласно самому учебнику. ГДЗ включает в себя упражнения по всем темам, рассматриваемым в основном учебнике алгебры девятого класса:

Графики функций и системы координат.
Квадратный трехчлен.
Основы теории вероятности.

Всего издание включает свыше тысячи упражнений с различным уровня сложности.

Какую помощь окажет пособие

Регулярная работа с ГДЗ открывает перед подростком возможности:

начать полноценную подготовку к приближающейся государственной итоговой аттестации;

затрачивать минимальное время на выполнение домашнего задания;
поддерживать стабильную успеваемость.

Безусловно, максимальную пользу пособие принесет тому ученику, который обращается к нему за советом, как к персональному консультанту, а не копирует готовое решение, как из шпаргалки или из тетради одноклассника.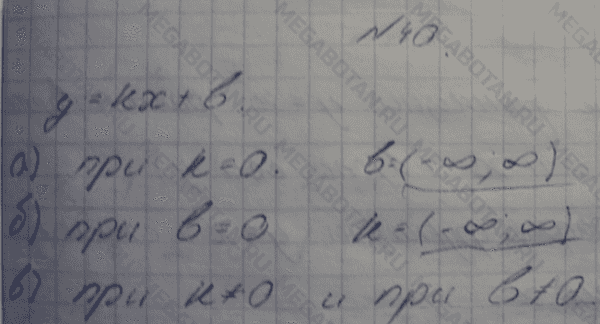 Бессмысленное списывание неизбежно приведет к непониманию изучаемого материала, а следовательно, проблемам на ближайшей же контрольной проверке в классе. А исправить любую проблему гораздо сложнее, чем не допустить ее развития изначально. Решебник составлен по всем требуемым нормативам для подготовки выпускников девятых классов к экзаменам в школе и ЕГЭ. Учебное пособие можно найти на прилавках и в электронном виде онлайн, его просто читать в нескольких форматах с компьютера, смартфона, планшета.

Алгебра. 9 класс. Поурочные планы по учебнику Макарычева Ю.Н., Миндюк

ОГЛАВЛЕНИЕ
Введение 3
Примерное поурочное планирование по алгебре в 9 классе 4
Глава I КВАДРАТИЧНАЯ ФУНКЦИЯ 6
§ 1. ФУНКЦИИ И ИХ СВОЙСТВА
Тема (п. 1): Функция. Область определения и область значении функции 6
Урок I 6
Урок 2 9
Урок З 11
Тема (и. 2): Свойства функции 12
Урок 4 13
Урок 5 14
Урок 6 18
Тема (п.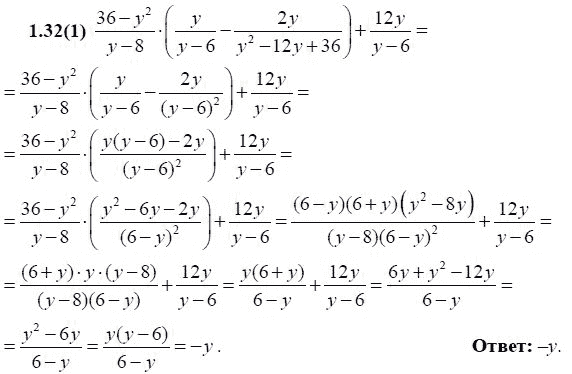 3): Квадратный трехчлен и его корни 21
Урок 7 21
Тема (и. 4): Разложение квадратного трехчлена на множители 26
Урок 8 27
Урок 9 31
Урок 10 34
§ 3 КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
Тема (п. 5): Функция >’ = ах2, ее график и свойства 40
Урок 11 40
Урок 12 43
Тема (п. 6): Графики функций \’ = алг + п пу = а(х-т)г 45
Урок 13 45
Урок 14 48
Тема (и. 7): Построение графика квадратичной функции 49
Урок 15 50
Урок 16 52
Урок 17 55

Урок 18. Контрольная работа № 1 56
§ 4. НЕРАВЕНСТВО С ОДНОЙ ПЕРЕМЕННОЙ
Тема (п. 8): Решение неравенств второй степени с одной переменной 66
Урок 19 66
Урок 20 68
Урок 21 70
Тема (и. 9): Решение неравенств методом интервалов 74
Урок 22 74
Урок 23 76
Урок 24 77
Решение задач 80
Урок 25 (итоговый) 80
Глава II. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ 84
§ 5. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ
Тема (п. 10): Целое уравнение и его корни 84
Урок 26 84
Урок 27 86
Тема (п.

11): Уравнения, приводимые к квадратным 87
Урок 28 87
Урок 29 88
Урок 30 90
Урок 31. Контрольная работа Лг 2 91
§ 6. СИСТЕМЫ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
Тема (п. 12): Графический способ решения систем уравнении 101
Урок 32 102
Урок 33 ЮЗ
Урок 34 104
Урок 35 108
Тема (п. 13): Решение систем уравнений второй степени 110
Урок 36 110
Урок 37 112
Урок 38 113
Урок 39 115
Тема (п. 14): Решение задач с помощью систем уравнений второй степени 116
Урок 40 116
Урок 41 119
Урок 42 120
Урок 43 122
Урок 44. Контрольная работа № 3 122
ПОВТОРЕНИЕ УЧЕБНОГО МАТЕРИАЛА. РЕШЕНИЕ ЗАДАЧ 126
Урок 45 126
Урок 46 128
Урок 47 131
Глава III. АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ 132
§ 7. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Тема (п. 15): Последовательности 132
Урок 48 132
Тема (п. 16): Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии 134
Урок 49 134
Урок 50 135
Урок 51 138
Тема (п.

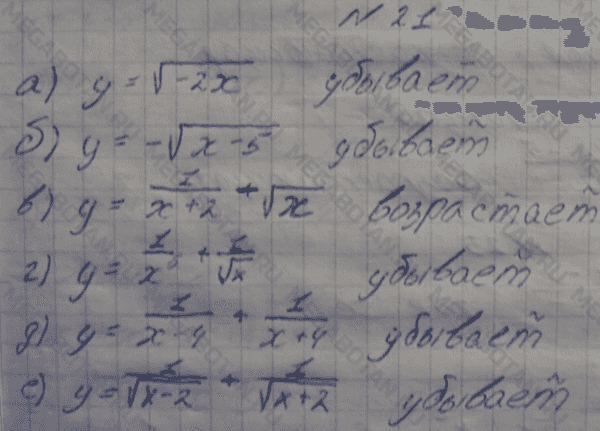= д* 183
Урок 64 183
§ 10. КОРЕНЬ л-й СТЕПЕНИ
Тема (п. 23): Определение корня н-й степени 184
Урок 65 185
Урок 66 188
Урок 67. Контрольная работа №6 189
Глава V. ТРИГОНОМЕТРИЧЕСКИЕ ВЫРАЖЕНИЯ И ИХ ПРЕОБРАЗОВАНИЯ 194

§ 12. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЛЮБОГО УГЛА
Тема (п. 28): Определение синуса, косинуса, тангенса и котангенса 194
Урок 68 195
Урок 69 197
Тема (и. 29): Свойства синуса, косинуса, тангенса и котангенса 200
Урок 70 » 201
Урок 71 205
Тема (п. 30): Радианная мера угла 209
Урок 72 «. 210
§ 13. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ
Тема (п. 31): Соотношения между тригонометрическими функциями одного и того же угла 213
Урок 73 213
Урок 74 216
Урок 75 219
Урок 76 221
Тема (п. 32): Применение основных тригонометрических формул к преобразованию выражений 223
Урок 77 223
Урок 78 225
Урок 79 229
Урок 80 230
Урок 81. Контрольная работа Л» 7 234
ПОВТОРЕНИЕ УЧЕБНОГО МАТЕРИАЛА.

РЕШЕНИЕ ЗАДАЧ 239
Урок 82 239
ИТОГОВОЕ ПОВТОРЕНИЕ 240
ПОВТОРЕНИЕ: АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 241
Урок 83 241

Урок 84 244
Урок 85 248
Урок 86 252
ПОВТОРЕНИЕ: УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ 256
Урок 87 256
Урок 88 259
ПОВТОРЕНИЕ: ЗАДАЧИ 262
Урок 89 262
Урок 90 265
Урок 91 267
ПОВТОРЕНИЕ: НЕРАВЕНСТВА 268
Урок 92 268
Урок 93 270
Урок 94 273
ПОВТОРЕНИЕ: ФУНКЦИИ И ГРАФИКИ 275
Урок 95 275
Урок 96 277
Урок 97 278
Итоговая контрольная работа
Уроки 98-99 279
Анализ контрольной работы
Урок 100 287
ПОВТОРЕНИЕ: РЕШЕНИЕ ЗАДАЧ 288
Урок 101 288
Урок 102 (заключительный). Подведение итогов года 291
Приложения 291
Литература 312

В данном пособии представлено примерное поурочное планирование, составленное в соответствии с учебником: Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Ллгебра-9 М: Просвещение, 2005. В разработках планов уроков содержится теоретический материал курса алгебры 9 класса, даются примеры, задачи и рассматриваются способы их решения, предлагаются задания для самостоятельной и индивидуальной работы учащихся, а также контрольные работы, тесты.

Дополнительно приводятся начальные сведения из теории вероятностей, решения комбинаторных задач.

Пособие предназначено учителям-предметникам в помощь при подготовке и проведении уроков математики в 9 классе общеобразовательной школы. Может быть полезно студентам педагогических вузов, слушателям ИПК.

Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева

Предисловие

Глава I. Квадратичная функция

§ 1. Функции и их свойства

Уроки 1—2. Функция. Область определения и область значений функции

Уроки 3-6. Свойства и графики основных функций

§ 2. Квадратный трехчлен

Уроки 7-8. Корни квадратного трехчлена

Уроки 9-10. Разложение квадратного трехчлена на множители

§ 3. Квадратичная функция и ее график

Урок 11. Функция y = ах2, ее график и свойства

Урок 12. Графики функций у = ах2 + n и у = а(х — m)2

Уроки 13-14. Построения графика квадратичной функции

§ 4. Степенная функция.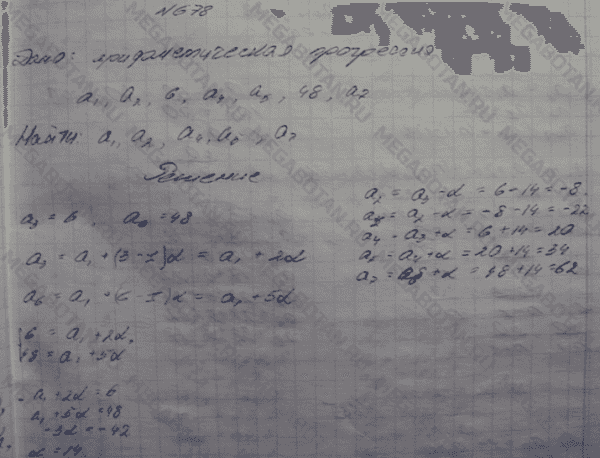 Корень n-й степени

Урок 15. Степенная функция у = хn

Урок 16. Корень n-й степени

Уроки 17—18. Дробно-линейная функция и ее график (факультативное занятие)

Урок 19. Степень с рациональным показателем (факультативное занятие)

Уроки 20-21. Контрольная работа по теме «Квадратичная функция»

Урок 22. Итоги контрольной работы

Уроки 23-24. Зачетная работа по теме «Квадратичная функция»

Глава II. Уравнения и неравенства с одной переменной

§ 5. Уравнения с одной переменной

Уроки 25-27. Целое уравнение и его корни

Уроки 28-29. Дробные рациональные уравнения

§ 6. Неравенства с одной переменной

Урок 30. Решение неравенств второй степени с одной переменной

Уроки 31-32. Решение неравенств методом интервалов

Уроки 33-34. Применение метода интервалов для решения неравенств

Урок 35. Некоторые приемы решения целых уравнений (факультативное занятие)

Уроки 36-37. Иррациональные уравнения и неравенства (факультативное занятие)

Уроки 38—39.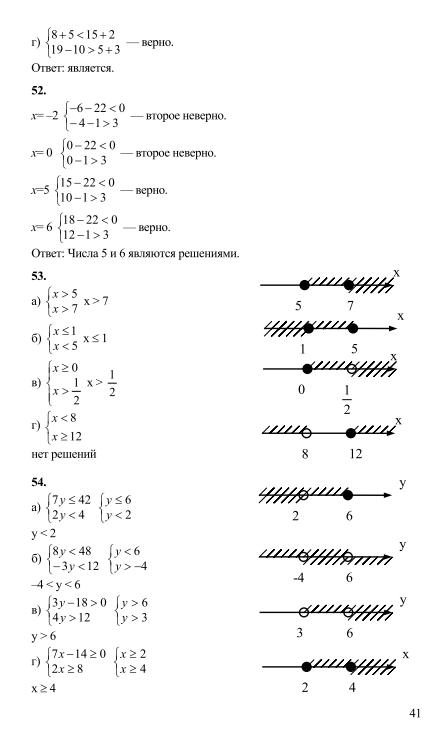 Контрольная работа по теме «Уравнения и неравенства с одной переменной»

Урок 40. Итоги контрольной работы

Уроки 41-42. Зачетная работа по теме «Уравнения и неравенства с одной переменной»

Глава III. Уравнения и неравенства с двумя переменными

§ 7. Уравнения с двумя переменными и их системы

Уроки 43-44. Уравнение с двумя переменными и его график

Уроки 45-46. Графический способ решения систем уравнений

Уроки 47. Решение систем уравнений второй степени

Уроки 48-49. Решение задач с помощью систем уравнений второй степени

§ 8. Неравенства с двумя переменными и их системы

Уроки 50-51. Графическое решение неравенства с двумя переменными

Уроки 52-53. Системы неравенств с двумя переменными

Уроки 54-56. Некоторые приемы решения систем уравнений второй степени с двумя переменными (факультативное занятие)

Уроки 57-58. Контрольная работа по теме «Уравнения и неравенства с двумя переменными»

Урок 59. Итоги контрольной работы

Уроки 60-61. Зачетная работа по теме «Уравнения и неравенства с двумя переменными»

Глава IV. Арифметическая и геометрическая прогрессии

§ 9. Арифметическая прогрессия

Уроки 62-63. Последовательности

Уроки 64-65. Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии

Уроки 66-67. Формула суммы первых n членов арифметической прогрессии

§ 10. Геометрическая прогрессия

Уроки 68-69. Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии

Уроки 70-71. Формула суммы первых n членов геометрической прогрессии

Уроки 72-73. Смешанные задачи на прогрессии (факультативное занятие)

Уроки 74-75. Метод математической индукции (факультативное занятие)

Уроки 76-77. Контрольная работа по теме «Арифметическая и геометрическая прогрессии»

Урок 78. Итоги контрольной работы

Уроки 79-80. Зачетная работа по теме «Арифметическая и геометрическая прогрессии»

Глава V. Элементы комбинаторики и теории вероятностей

§ 11. Элементы комбинаторики

Урок 81. Примеры комбинаторных задач

Уроки 82-83. Перестановки

Уроки 84-85. Размещения

Уроки 86-87. Сочетания

§ 12. Начальные сведения из теории вероятностей

Урок 88. Относительная частота случайного события

Уроки 89-90. Вероятность равновозможных событий

Уроки 91-92. Сложение и умножение вероятностей (факультативное занятие)

Уроки 93-94. Контрольная работа по теме «Элементы комбинаторики и теории вероятностей»

Повторение курса 7-9 классов

Урок 95. Вычисления. Тождественные преобразования

Уроки 96-97. Уравнения и системы уравнений

Урок 98. Неравенства

Урок 99. Функции

Уроки 100-101. Итоговая контрольная работа

Урок 102. Подведение итогов обучения

Государственная итоговая аттестация по алгебре (ГИА)

Уроки 103-104. Государственная итоговая аттестация по алгебре (факультативное занятие)

Уроки 105-106. Демонстрационный вариант ГИА (факультативное занятие)

Литература

ГДЗ по Алгебре за 9 класс Муравин Г.К., Муравин К.С

Алгебра 9 класс Муравин Г.К.

Авторы: Муравин Г.К., Муравин К.С, Муравина О.В.

«Решебник по Алгебре 9 класс Муравин (Дрофа)» обеспечит школьникам полную поддержку с выполнением домашнего задания, на протяжении всего образовательного процесса. Рассматриваемое учебно-методическое пособие размещено онлайн на сайте и доступно к просмотру с любого современного гаджета. Помимо этого, на данном интернет-портале есть возможность поиска нужных ответов по номеру задания из учебника. Этот решебник имеет ряд следующих преимуществ перед другими ГДЗ:

содержит в себе верные ответы на все упражнения из учебника;
помимо голых ответов присутствуют подробно-расписанные решения и комментарии автора, которые позволят школьнику проанализировать свои ошибки, и научиться выполнять сложные задания самостоятельно, без помощи взрослых и сторонних вспомогательных ресурсов;
постоянное использование ГДЗ улучшает настроение и мотивирует школьника дальнейшему обучению.

Решебник станет надежным союзником ученику девятого класса и позволит обрести уверенность в себе на контрольных и проверочных работах.

Тонкости обучения алгебре в школе

В этом году ученикам предстоит сдача ОГЭ по основным и выбранным предметам. Данная дисциплина является одной из самых важных в школьной программе. Именно поэтому ее освоению и подготовке к экзамену нужно уделить особое внимание. Мы отобрали несколько тем, с которыми у школьников могут возникнуть трудности: как правильно решать рациональные неравенства методом интервалов, понятие множества в математике, существующие графики уравнений. «Решебник по Алгебре 9 класс Муравин Г.К., Муравин К.С, Муравина О.В. (Дрофа)» прекрасно поможет школьникам выполнить домашнее задание, и позволит качественно подготовиться к выпускному экзамену по математике.

Как же правильно работать с ГДЗ по Алгебре 9 класс Муравин

Многие эксперты рекомендуют использовать решебник в качестве вспомогательного ресурса в учебе, с ним можно добиться успеха не только по проблемной дисциплине, но и по остальным предметам. Но, чтобы это сделать следует научиться правильно взаимодействовать с ГДЗ. А именно, полностью исключить бездумное списывание верных ответов. Необходимо выполнять заданные на дом упражнения самостоятельно, и только после этого делать самопроверку своих результатов по правильным ответам из решебника. Используя ГДЗ таким образом, ученик сможет приумножить имеющиеся знания, и достичь стабильных положительных оценок в школе.

О.о старова алгебра 9 клас

Скачать о.о старова алгебра 9 клас EPUB

Введем понятие функции. Ее определение. А так же: Область определения и значения функции. Монотонность функции, ее возрастание и убывание. Ограниченность фу. Головна» Файли» По класах» 9 клас. Алгебра 9 клас. О.О. Старова (Серія «Мій конспект»). Категорія: 9 клас | Додав: Victor_Pasyk | Додано: 1. Алгебра 9 класс. Дидактические материалы.

Макарычев, Миндюк, Крайнева. Знание алгебры способствует тому, что в дальнейшем подростку будет проще воспринимать различные явления и процессы, происходящие в мире. В девятом классе идет активная подготовка к ГИА, поэтому школьников ждет весьма насыщенная программа. Открывается курс разделом о рациональных неравенствах, подростки учатся решать задачи повышенной сложности.

Далее следуют различные системы уравнений, призванные объяснить многообразие способов достижения конечного результата. Числовые функции включают в себя как линейные, так и степенные ее виды. Тема 1. Нерівності (16 год). О.О.Старова АЛГЕБРА 9 клас: Мій конспект. слово автора. «Розв’язування лінійних нерівностей з однією змінною та систем лінійних нерівностей з однією змінною» (8 год.) Урок 9 (09).

Тема уроку. Розв’язування лінійних нерівностей з однією змінною. В девятом классе дети проходят достаточно трудные для усвоения темы. В это время книга ГДЗ по алгебре за 9 класс становится настольной практически для каждого сознательного родителя. Часто дети обращаются к родителям с просьбой о помощи, но в силу многих причин среднестатистическим мамам и папам сложно помочь ребенку. Кто-то плохо учился в школе, кто-то забыл нужную тему, а некоторые темы и вовсе не изучались в годы учебы нынешних родителей.

Даже если мама и сможет объяснить ребенку пройденный материал, то оформить правильно работу получится не всегда.

Онлайн решебники 9 класс по всем предметам, гдз и ответы к домашним заданиям. Алгебра класс контрольные работы Мордкович А.Г. Углубленный уровень. Автор: Мордкович А.Г. Алгебра класс тесты Мордкович А.Г. Базовый уровень. Авторы: Мордкович А.Г. Тульчинская Е.Е. Алгебра класс задачник Галицкий М.Л. Авторы: Галицкий М.Л. Гольдман А.М. Алгебра 9 класс Ю.Н. Макарычев. Авторы: Ю.Н. Макарычев Н.Г. Миндюк. Алгебра 9 класс Ш.А. Алимов. Авторы: Ш.А. Алимов Ю.М.

Колягин. Алгебра 9 класс Г.В. Дорофеев. ГДЗ Алгебра 9 класс Макарычев номер 53 тема свойства функции примеры решение. Канал Лиса. Алгебра 9. Урок Тригонометрия — преобразование суммы в произведение ч.1 Абылкасымова.

Казахстан. zadacha-kz. ГДЗ Алгебра 9 класс Макарычев номер Алгебра 9 класс. Решите методом подстановки Систему Уравнений. Репетитор Алгебра 9. Урок Геометрическая прогрессия ч.6 Абылкасымова. Казахстан. Видео-уроки по алгебру для школьников, 9 класс. Позволяют выучить ребенку алгебру через просмотр увлекательных уроков.

Мрия-урок.

PDF, PDF, PDF, txt

Похожее:

Українська література комплексне видання 2014

Книжка 6 клас українська мова глазова

Інформація про моря 4 клас

Твір українська народна пісня весілля

6 клас конспекти українська література

Решебник по укр мови 3 клас

Зно українська мова і література ответы

Хімія 11 клас профільний рівень гдз

ГДЗ Алгебра 9 класс Мартышова

Алгебра 9 класс

Контрольно-измерительные материалы

Мартышова

ВАКО

Девятиклассники редко обращаются за помощью к родителям, ведь считают себя слишком большими для этого. Однако в школе они иногда получают еще меньше сведений, чем получили бы дома от взрослых. Но это их нежелание идти наперекор своей гордости порой может сыграть весьма плохую шутку и за один год вполне можно колоссально подпортить показатели в аттестате. Так же недостаток знаний может привести к провалу предстоящих экзаменов. Чтобы этого не произошло, необходимо тщательно разбирать все встающие на пути препятствия, и в этом школьникам поможет решебник к учебнику «Алгебра. Контрольно-измерительные материалы 9 класс» Мартышова.

Что входит в содержание.

В сборнике имеется двадцать пять тестовых и десять контрольных работ, включая и итоговую. Все задания поделены на два варианта и охватывают полный курс этого учебного года. ГДЗ по алгебре 9 класс Мартышова облегчает понимание изучаемой информации и более осознано помогает систематизировать полученные сведения.

Нужен ли решебник.

Во время учебы школьники не раз и не два сталкиваются с какими-либо проблемами, что усложняет им сам процесс усвоения новых данных. По сути доучившись до девятого класса ребята уже должны научиться хорошо справляться с подобными неприятностями, но не у всех это проходит гладко. Некоторые и вовсе вместо того, чтобы детально разобрать сложный аспект, предпочитают списать упражнение и не особо загружать себе голову ненужными на их взгляд сведениями. Однако, когда впоследствии во время проверочных работ всплывает схожая ситуация, то эти самые подростки, скорее всего, осознают важность упущенных знаний. Не доводить ситуацию до получения плохой оценки поможет решебник к учебнику «Алгебра. Контрольно-измерительные материалы 9 класс» Мартышова, который даст ответы на все возникающие вопросы. «ВАКО», 2015 г.

Название

Решение

▶▷▶▷ гдз видеоурок алгебра 9 класс

Интерфейс	Русский/Английский
Тип лицензия	Free
Кол-во просмотров	257
Кол-во загрузок	132 раз
Обновление:	06-09-2019

гдз видеоурок алгебра 9 класс — Алгебра 9 класс — YouTube wwwyoutubecom channelUCUbrbCryCLjlfmruq5qJ2eA Cached Алгебра 9 класс 9 октября неравенства метод интервалов для дробей 5 — Duration: 9 minutes, 39 seconds Алгебра 9 класс 3 years ago ГДЗ (ответы) Алгебра 9 клас Мерзляк 2017 Відповіді до 4bookorggdz-reshebniki-ukraina 9 -klassgdz Cached ГДЗ (ответы) Алгебра 9 клас Мерзляк 2017 Відповіді до підручника онлайн , решебник на телефоне Гдз Видеоурок Алгебра 9 Класс — Image Results More Гдз Видеоурок Алгебра 9 Класс images Подмножество Видеоурок по алгебре 9 класс — YouTube wwwyoutubecom watch?vKeXqv3KUqIA Cached 9 Математических Загадок, Которые Поставят в Тупик Даже Самых Умных — Duration: 6:47 AdMeru — Сайт о творчестве 2,305,492 views Решебник (ГДЗ) Алгебра 9 класс ВР Кравчук, ГМ Янченко, М vshkolecom 9 -klassreshebnikialgebravr Cached Полный и качественный решебник ( ГДЗ ) Алгебра 9 класс ВР Кравчук, ГМ Янченко, МВ Підручна 2009 степень с рациональным показателем видеоурок 9 класс videotolkrustepenj_s_ratsionaljnim_pokazatelem Cached 199 Алгебра 9 класс , Степень с рациональным показателем Дробная степень ГДЗ Алгебра 9 класс Макарычев номер 199 степень с дробным показателем Степень в виде дроби, дробная степень видеоурок алгебра 9 класс свойства функции videotolkruvideourok_algebra_ 9 _klass_svoystva Cached 53 Алгебра 9 класс, Сравните выражения Свойства функции ГДЗ Алгебра 9 класс Макарычев номер 53 тема свойства функции примеры решение Канал Лиса ГДЗ Алгебра 9 класс Мерзляк — gdzltd gdzltd 9 -classalgebraMerzlyak-didakticheskie Cached Решения и ГДЗ Алгебра 9 класс Мерзляк, Полонский, Якир, Рабинович — Дидактические материалы Вентана-Граф с подробным объяснением Учебник Алгебра 9 класс Мерзляк, Полонский, Якир uchebniki-onlinenet387-algebra- 9 -klass Cached Учебник по алгебре 9 класс Мерзляк, Полонский, Якир Электронная книга издана в 2017 году по новой программе ГДЗ Алгебра 9 класс Мерзляк — gdzltd gdzltd 9 -classalgebraalgebra- 9 kl-Mersljak Cached Решебник к учебнику Алгебра 9 класс Мерзляк, Полонский, Якир даст всестороннее представление о формулах, способах их употребления и алгоритмах решений уравнений Что в него включено Видео урок: Алгебра 9 класс Макарычев 2014 Готовые домашние wwwvidexpcomRUv122480gohtml Cached Видео урок Алгебра 9 класс Макарычев 2014 Готовые домашние задания( гдз ) упр 1 Упражнение 1 Решение домашних заданий из учебника Алгебра 9 класс Учебник Макарычев ЮН, Миндюк НГ и др 2014 Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Also Try гдз видеоурок алгебра 9 класс гдз гдз видеоурок алгебра 9 класс мордкович гдз видеоурок алгебра 9 класс истер гдз видеоурок алгебра 9 класс мордкович гдз гдз видеоурок алгебра 9 класс макарычев гдз видеоурок алгебра 9 класс алимов гдз видеоурок алгебра 9 класс мерзляк гдз видеоурок алгебра 9 класс бевз 1 2 3 4 5 Next 409,000

Видеоуроки по математике. Готовые домашние задания, видеоуроки. ГДЗ по алгебре 9 класс Шестаков — Ва
м поможет разобраться с недопониманием в предмете и быть уверенным в себе. Девятый класс- самый трудный период обучения в школе. П, Тонких 1 часть решебник, гдз по математики 4 класс литературное чт
ный период обучения в школе. П, Тонких 1 часть решебник, гдз по математики 4 класс литературное чтение… Готовые домашние задания (ГДЗ) по алгебре для 7-11 классов: 7 класс. С ГДЗ проблем нет! Сборник готовых домашних заданий и полезных материалов для школьников. Материалы к экзаменам. Демонстрационные варианты для самоподготовки с подробными решениями и видеоуроками к ГИА и ЕГЭ. С каждым последующим классом программа усложняется, но наличие ГДЗ Мордкович станут незаменимым помощником в овладении программным материалом. Используя дополнительную литературу, а особенно ГДЗ, ученики 7-9 классов смогут в полной… ГДЗ (домашнее задание) по алгебре 7 класс Алимова, Колягина, Сидорова, Федоровой. Алгебра это, безусловно, один из сложнейших предметов школьной программы. Многогранник , Свойства , вектор , видеоурок , выражения , вычитание , график , график функции , деление , десятичные дроби , дроби , квадратный корень , координаты , координаты вектора , косинус , многоугольник , модуль , натуральные числа , неравенства , окружность , отрезок , параллельные прямые , плоскость , площадь… 9 класс 11 класс ВУЗ ДУ Дифференциальные уравнения Кинематика МА Мехаика Решение задач ТВ алгебра вероятность видео геометрия дифференциал задачи интеграл квадратичная функция квадратное уравнение конус линейная функция линейные ДУ… 12 июл 2014.. по геометрии 7 класса атанасян бутузов кадомцев позняк юдина. дабстеп 2012 алгебра 7 класс лебединцева гдз скачать фильмы. Плешаков 2 класс видеоуроки невидимые нити. ГДЗ для 2 класса. Модуль ГДЗ учебники. 9 класс Л.В. Кузнецова, Е.А. Бунимович, Б.П. Пигарев, С.Б. Суворова. 6-е изд., перераб. и доп. М.: Дрофа, 2001 г. ГДЗ к учебнику Алимова Ш.А. и др. 2012. Сборник задач по математике с решениями 8-11 класс под ред. Сканави М.И. 2012.

график

Колягина

способах их употребления и алгоритмах решений уравнений Что в него включено Видео урок: Алгебра 9 класс Макарычев 2014 Готовые домашние wwwvidexpcomRUv122480gohtml Cached Видео урок Алгебра 9 класс Макарычев 2014 Готовые домашние задания( гдз ) упр 1 Упражнение 1 Решение домашних заданий из учебника Алгебра 9 класс Учебник Макарычев ЮН
способах их употребления и алгоритмах решений уравнений Что в него включено Видео урок: Алгебра 9 класс Макарычев 2014 Готовые домашние wwwvidexpcomRUv122480gohtml Cached Видео урок Алгебра 9 класс Макарычев 2014 Готовые домашние задания( гдз ) упр 1 Упражнение 1 Решение домашних заданий из учебника Алгебра 9 класс Учебник Макарычев ЮН
Которые Поставят в Тупик Даже Самых Умных — Duration: 6:47 AdMeru — Сайт о творчестве 2

Нажмите здесь , если переадресация не будет выполнена в течение нескольких секунд гдз видеоурок алгебра класс Поиск в Все Картинки Ещё Видео Новости Покупки Карты Книги Все продукты Возможно, вы имели в виду гдз видео урок алгебра класс Алгебра класс YouTube Инстаграм Андрея Алгебра класс uploaded a video Алгебра класс сентября Упрощение выражений авг Your browser does not currently recognize any of the video formats available Алгебра класс myoutubecom Алгебра класс Решите систему уравнений YouTube дек ГДЗ Алгебра класс Макарычев номер Алгебра класс Решите систему уравнений myoutubecom Видеоуроки по алгебре класс , калькулятор онлайн calcru video po algebre Найти область определения функции К решению неравенств могут сводиться и такие примеры, в которых это Алгебра математика класс InternetUrok algebr a class Видеоуроки , тесты и тренажёры по Алгебра за класс по школьной программе Используйте конспект уроков Алгебра Мордкович АГ класс Алгебра Макарычев ЮН класс Задание ГДЗ по алгебре класс Мордкович gdz netzadanie algeb Видео решение задания Алгебра класс Мордкович Письменное решение задания Алгебра класс Мордкович Your browser does not currently recognize any of the video formats available ГДЗ по алгебре класс eurokiorg gdz algebr a _ Скачать гдз или решебник по алгебре класс в один клик ГДЗ номер алгебра класс ЮН Макарычев, НГ Миндюк https gdz ru class algebr anom Подробное решение номер по алгебре для учащихся класса , авторов ЮН Макарычев, НГ Миндюк, Задание ГДЗ по Алгебре класс Мордкович АГ https gdz putinainfo klass algebr a ГДЗ готовое домашние задание из решебника на Задание по учебнику Алгебра класс Часть Задание ГДЗ по Алгебре класс Мордкович АГ https gdz putinainfo klass algebr a ГДЗ готовое домашние задание из решебника на Задание по учебнику Алгебра класс Часть ГДЗ по Алгебре класс Мордкович УрокиТВ Решебник с algebr a klass Не можешь найти правильный ответ? Смотри ГДЗ по Алгебре класс Мордкович Канал на YouTube Видео урок Алгебра класс Макарычев Готовые wwwvidexpcomRUvgohtml Видео урок Алгебра класс Макарычев Готовые домашние задания гдз упр Упражнение Решение ГДЗ по алгебре класс ГДЗ готовые домашние задания гдз алгебре кла ГДЗ по алгебре класс Для начала определимся с авторами учебников, по которому необходимо получить Задание Алгебра класс Задачник Часть domashkasu gdz klass algebr a algebr Решение задания Алгебра класс Задачник Часть Мордкович АГ, Мишустина ТН, Тульчинская ЕЕ Ребя помогайте Алгебра класс Мордкович https class ramblerru gdz rebya Ответы на вопрос Ребя помогайте Алгебра класс Мордкович читайте на Рамблеркласс ГДЗ по алгебре для класс от Путина https gdz putinarupo algebre klass Заходите, не пожалеете! Тут отличные гдз по Алгебре для класса от Путина Очень удобный интерфейс ГДЗ по алгебре для класса ЮН Макарычев номер gdz algebr a klass Подробное решение номер по алгебре для учащихся класса , авторов ЮН Макарычев, НГ Миндюк, КИ ГДЗ по алгебре за класс Мордкович, решебник задачника gdz com klass algebr a Готовое домашние задание из решебника гдз по алгебре класс от АГ Мордкович и др Задачник часть ГДЗ по алгебре Мордкович класс Задание СпецКласс spec class ruvalg gdz mordkovic дек ГДЗ по алгебре Мордкович класс Задание Решение системы уравнений из задачника по ГДЗ по алгебре класс Мордкович АГ упражнение Уважаемые родители, ваш ребенок не понимает предмет Алгебра , а вы уже забыли как решать пример Решебник по алгебре класс Алимов, Колягин ГДЗ algebr a _ klass Готовые домашние задания по алгебре за класс авторов ША Алимов, ЮМ Колягин, ЮВ Сидоров год Видео уроки по математике Андрея Андреевича Андреева naru Математика класс, matematika_aaa_ старт сентября Алгебра класс Алгебра класс Видеоуроки Алгебра Класс klass algebr a Решение текстовых задач Рациональные неравенства и их системы Арифметический способ решения Видео уроки в формате ГДЗ по математике и другим vcevceru Видео уроки Видео ГДЗ по учебникам Математика класс Моро, Русский язык класс Канакина и Горецкий Геометрия класс Атанасян, Физика класс Перышкин сборник задач ГДЗ по алгебре класс Готовые домашние задания wwwg gdz ru class algebr a Спиши ГДЗ по алгебре класс , найди ответ на вопрос по алгебре класс , решебник по алгебре класс списать алгебра номер гдз artpolinakuzinaru algebr a nomer авг ГДЗ по алгебре класс Макарычев учебник г подходит к г онлайн Видеоуроки Поурочные разработки по Алгебре для класса к учебнику algebr aindex Поурочные разработки по Алгебре для класса к учебнику ЮН Макарычева Предисловие с одной переменной Урок Решение неравенств второй степени с одной переменной Планконспект урока по алгебре класс по теме урок по algebr aurokpo янв урок по алгебре класс относительная частота случайного события Разработка урока алгебры в классе Ответы Вот сегодня мы как раз и поговорим об этом очень ГДЗ , решебники для класса по всем предметам онлайн klass evip klass reshebniki Полные и качественные решебники ГДЗ для класса по всем предметам онлайн Доступно на ваших Алгебра алгебра класс теляковский гдз AirflowSkateboards airflowskateboardscom algebr a kla авг Готовые домашние задания , видеоуроки Готовые домашние задания по алгебре класс Гдз по алгебре класс макарычев abakanschoolru video gdz Гдз по алгебре класс макарычев Опубликовано Cправка Хочется сказать, что в алгебра класс гдз euroki ProForce proforceru algebr a klass gdz euroki авг алгебра класс гдз euroki ГДЗ Алгебра за класс АГ eurokiapp euroki appgdzalgebra гдз по алгебре класс мордкович смотреть онлайн гдз по алгебре ГДЗ Алгебра класс Макарычев номер Алгебра класс система Неравенств с двумя переменными гдз класс алгебра indexoneru gdz klass algebr a дн назад гдз класс алгебра Гдз по Алгебре класс Готовые домашние задания , видеоуроки Картинки по запросу гдз видеоурок алгебра класс гдз алгебра класс алимов wwwmorozovadanceru gdz algebr a дн назад гдз алгебра класс алимов ГДЗ по алгебре для класса ША Видеоуроки по математике РЕШУ ОГЭ математика ОГЭ задания, ответы По окончании работы система проверит ваши ответы , покажет правильные Статистика, вероятности Онлайн Решебник ГДЗ Кузовлев класс Reshakru ГДЗ Кузовлева очень мало распространен в полном виде, поэтому на сайте решакру мы постарались составить гдз по алгебре класс макарычев неравенства Sunsil Hotel sunsilhotelcom gdz po гдз по алгебре класс макарычев неравенства с двумя переменными переменными Презентация к уроку по алгебре класс по теме Презентация по нояб г Открытый урок по Предметы ЯКласс ya klass rup Видеоуроки от ИнтернетУрок Переменка Алгебра и начала математического анализа КПК Цифровая алгебра класс теляковский гдз compriborru algebr a klass авг алгебра класс теляковский гдз Готовые домашние задания , видеоуроки г Учебник гдз алгебра номер класс gdz algebr a дн назад гдз алгебра номер класс ГДЗ по алгебре для класса ЮН Макарычев номер Видеоуроки в интернет сайт для учителей https videourok inet Видеоуроки в интернет сайт для учителей Новые бесплатные видеоуроки , тесты, полезные материалы и алгебра класс мордкович гдз ютуб atomleasingru algebr a_ _ klass _ авг алгебра класс мордкович гдз ютуб Готовые домашние задания , видеоуроки Понравился алгебра гдз кравчук янченко htcserviceru algebr a_ gdz _kravchuk_ авг Видеоуроки по математике Готовые домашние задания , видеоуроки ГДЗ по алгебре класс алгебра класс гдз алимов navigatornskru algebr a klass gdz авг ГДЗ Алимов класс ГДЗ по алгебре класс Алимов Готовые домашние задания , видеоуроки гдз алгебра hankooksystemcom gdz algebr a дн назад Готовые домашние задания , видеоуроки Решебник по алгебре за класс авторов Дорофеева и алгебра класс мордкович гдз синий учебник kyushushinkincardcojp algebr a авг ГДЗ по алгебре класс Мордкович, Мишустина, Тульчинская ч задачник г Видеоуроки по алгебра мордкович класс гдз гитем kyushushinkincardcojp algebr a авг ГДЗ по алгебре класс Мордкович, Мишустина, Тульчинская ч задачник г Видеоуроки по гдз алгебра класс etudbilgisayarcom gdz algebr a авг ГДЗ по алгебре класс Макарычев учебник г подходит к г Видеоуроки по математике Запросы, похожие на гдз видеоурок алгебра класс алгебра класс ютуб алгебра класс видеоуроки математика класс видео уроки по алгебре класс мерзляк алгебра класс видеоуроки алгебра класс алимов видеоуроки видео уроки по алгебре класс алгебра класс ютуб След Войти Версия Поиска Мобильная Полная Конфиденциальность Условия Настройки Отзыв Справка

Видеоуроки по математике. Готовые домашние задания, видеоуроки. ГДЗ по алгебре 9 класс Шестаков — Вам поможет разобраться с недопониманием в предмете и быть уверенным в себе. Девятый класс- самый трудный период обучения в школе. П, Тонких 1 часть решебник, гдз по математики 4 класс литературное чтение… Готовые домашние задания (ГДЗ) по алгебре для 7-11 классов: 7 класс. С ГДЗ проблем нет! Сборник готовых домашних заданий и полезных материалов для школьников. Материалы к экзаменам. Демонстрационные варианты для самоподготовки с подробными решениями и видеоуроками к ГИА и ЕГЭ. С каждым последующим классом программа усложняется, но наличие ГДЗ Мордкович станут незаменимым помощником в овладении программным материалом. Используя дополнительную литературу, а особенно ГДЗ, ученики 7-9 классов смогут в полной… ГДЗ (домашнее задание) по алгебре 7 класс Алимова, Колягина, Сидорова, Федоровой. Алгебра это, безусловно, один из сложнейших предметов школьной программы. Многогранник , Свойства , вектор , видеоурок , выражения , вычитание , график , график функции , деление , десятичные дроби , дроби , квадратный корень , координаты , координаты вектора , косинус , многоугольник , модуль , натуральные числа , неравенства , окружность , отрезок , параллельные прямые , плоскость , площадь… 9 класс 11 класс ВУЗ ДУ Дифференциальные уравнения Кинематика МА Мехаика Решение задач ТВ алгебра вероятность видео геометрия дифференциал задачи интеграл квадратичная функция квадратное уравнение конус линейная функция линейные ДУ… 12 июл 2014.. по геометрии 7 класса атанасян бутузов кадомцев позняк юдина. дабстеп 2012 алгебра 7 класс лебединцева гдз скачать фильмы. Плешаков 2 класс видеоуроки невидимые нити. ГДЗ для 2 класса. Модуль ГДЗ учебники. 9 класс Л.В. Кузнецова, Е.А. Бунимович, Б.П. Пигарев, С.Б. Суворова. 6-е изд., перераб. и доп. М.: Дрофа, 2001 г. ГДЗ к учебнику Алимова Ш.А. и др. 2012. Сборник задач по математике с решениями 8-11 класс под ред. Сканави М.И. 2012.

: Помощь и ответы на домашнее задание :: Slader

5-1	Основная факторизация	Упражнения	стр.123
5-2	Наибольший общий коэффициент	Упражнения	стр.125
5-3	Наименьшее общее кратное	Упражнения	с.127
5-4	Чувство дроби: близко к -1, -1/2, 0, ½ или 1	Упражнения	стр.129
5-5	Сравнение и заказ рациональных чисел	Упражнения	стр.131
5-6	Сложить и вычесть дроби	Упражнения	с.133
5-7	Сложить и вычесть смешанные числа	Упражнения	стр.135
5-8	Умножение дробей	Упражнения	стр.137
5-9	Умножение смешанных чисел	Упражнения	с.139
5-10	Разделить на дроби	Упражнения	стр.141
5-11	Разделить смешанные числа	Упражнения	стр.143
5-12	Свойства рациональных чисел	Упражнения	с.145
5-13	Порядок действий с рациональными числами	Упражнения	стр.147
5-14	Уравнения сложения и вычитания с дробями	Упражнения	стр.149
5-15	Уравнения умножения и деления с дробями	Упражнения	с.151
5-16	Решите двухшаговые уравнения с дробями	Упражнения	с.153
5-17	Переименовать обычные единицы измерения	Упражнения	стр.155
5-18	Стратегия решения проблем: создание чертежа	Упражнения	с.157
		Обогащение	стр.159
		Развитие словарного запаса	стр. 160
		Подготовка к экзамену: вопросы с несколькими вариантами ответов	стр.161
		Тест практической главы	с.163
		Общий обзор	стр.165

: Домашнее задание и ответы :: Slader

6.1	Решение неравенств с помощью сложения и вычитания	Упражнения	стр. 359
6,2	Решите неравенства с помощью умножения и деления	Упражнения	с.366
		Викторина	стр.368
6,3	Решите многоступенчатые неравенства	Упражнения	стр.372
6,4	Решите сложные неравенства	Упражнения	с.384
6,6	Решите абсолютные неравенства значений	Викторина	стр.387
6,4	Решите сложные неравенства	Смешанный обзор	стр.389
6.5	Решите уравнения абсолютных значений	Упражнения	с.393
		Расширение: функции графика абсолютных значений	стр.397
6,6	Решите абсолютные неравенства значений	Упражнения	п.401
6,7	График линейных неравенств в двух переменных	Упражнения	с.409
		Викторина	стр. 412
		Смешанный обзор	стр. 413
		Обзор главы	стр. 415
		Глава Test	с.419
		Стандартизированная практика тестирования	п.422

Что такое произведение в математике? — Определение и обзор — Видео и стенограмма урока

Как найти произведение

Умножение часто называют повторным сложением , потому что задача умножения говорит вам, что у вас есть определенное количество групп чего-то, каждая из которых содержит определенное число.Еще не запутались? Вот пример.

У вас есть 3 пакета конфет, каждый из которых содержит 5 конфет. Сколько у тебя конфет?

Эту проблему можно решить двумя способами. Первый — сложить леденцы:

5 + 5 + 5 = 15

Другой способ решения — использовать умножение, потому что у вас есть 3 группы конфет по 5 конфет в каждой сумке.

3 * 5 = 15

Ответом на эту проблему умножения является произведение, которое в данном случае равно 15.

Вот еще пример. В классе 8 рядов стульев, по 7 стульев в каждом ряду. Сколько здесь стульев?

Опять же, вы можете добавить:

7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 56

Или вы можете найти произведение, умножив:

7 * 8 = 56

Свойства Умножение

Есть четыре основных свойства умножения, которые верны независимо от того, что умножается вместе.

1. Коммутативное свойство : Когда два числа умножаются вместе, произведение одинаково независимо от порядка, в котором они написаны.

Например:

5 * 7 = 7 * 5

2. Ассоциативное свойство : Когда три или более чисел умножаются вместе, произведение одинаково независимо от того, какие два числа умножаются в первую очередь.

Например:

(2 * 4) * 6 = 2 * (4 * 6)

8 * 6 = 2 * 24

48 = 48

3. Свойство мультипликативной идентичности : Произведение любого число и 1 это число.

Например:

3 * 1 = 3

4. Распределительное свойство : сумма двух чисел, умноженная на третье число, равна сумме каждого слагаемого, умноженной на третье число.

Например:

2 * (3 + 4) = 2 * 3 + 2 * 4

2 * 7 = 6 + 8

14 = 14

Особые продукты

Следует упомянуть два специальных продукта.

1. Произведение любого числа на 1 и есть это число. Вы узнали об этом в приведенном выше примере мультипликативного свойства идентичности.

Например:

7 * 1 = 7

2376 * 1 = 2376

2. Произведение любого числа, умноженного на 0, равно 0.

Например:

9 * 0 = 0

6,782 * 0 = 0

Краткое содержание урока

Произведение — это ответ на задачу умножения. Вы можете найти продукт с помощью процесса, называемого , повторное добавление , то есть путем сложения количества групп в задаче. Есть четыре свойства, которые управляют правилами решения задач умножения: коммутативный , ассоциативный , мультипликативный тождественный и распределительный .Есть также два специальных правила произведения: произведение любого числа, умноженное на единицу, будет этим числом, а произведение любого числа, умноженного на ноль, будет равно нулю.

Поиск продукта

Произведение — это ответ на задачу умножения.
Чтобы найти произведение, вы можете использовать повторное сложение или умножение.
Задачи умножения обладают четырьмя свойствами: коммутативным, ассоциативным, мультипликативным тождественным и дистрибутивным.
Любое число, умноженное на 1, равно самому себе, а любое число, умноженное на 0, равно 0.

Результаты обучения

Изучите этот урок, чтобы точно выполнять следующие действия:

Распознавать произведение задачи умножения
Продемонстрируйте два метода поиска продукта
Перечислить четыре свойства умножения
Расчет специальных товаров

1.1 Действительные числа: основы алгебры — алгебра колледжа

Цели обучения

В этом разделе студенты будут:

Классифицировать действительное число как натуральное, целое, целое, рациональное или иррациональное число.
Выполните вычисления, используя порядок операций.
Используйте следующие свойства действительных чисел: коммутативное, ассоциативное, распределительное, обратное и тождественное.
Оценивайте алгебраические выражения.
Упростите алгебраические выражения.

Часто говорят, что математика — это язык науки. Если это правда, то важной частью математического языка являются числа. Самое раннее использование чисел произошло 100 веков назад на Ближнем Востоке для подсчета или перечисления предметов.Фермеры, скотоводы и торговцы использовали жетоны, камни или маркеры для обозначения одного количества — например, сноп зерна, голову скота или фиксированную длину ткани. Это сделало возможной торговлю, что привело к улучшению коммуникаций и распространению цивилизации.

Три-четыре тысячи лет назад египтяне ввели дроби. Сначала они использовали их, чтобы показать обратные. Позже они использовали их для обозначения суммы, когда количество было разделено на равные части.

Но что, если бы не было крупного рогатого скота для торговли или весь урожай зерна погиб во время наводнения? Как кто-то мог указать на существование ничего? С давних времен люди думали о «базовом состоянии» при подсчете и использовали различные символы для обозначения этого нулевого состояния.Однако только в пятом веке нашей эры в Индии ноль был добавлен к системе счисления и использовался в расчетах в качестве числа.

Ясно, что числа также должны были представлять убыток или долг. В Индии в седьмом веке нашей эры отрицательные числа использовались как решение математических уравнений и коммерческих долгов. Противоположности счетных чисел еще больше расширили систему счисления.

Из-за эволюции системы счисления теперь мы можем выполнять сложные вычисления, используя эти и другие категории действительных чисел.В этом разделе мы исследуем наборы чисел, вычисления с различными типами чисел и использование чисел в выражениях.

Классификация действительного числа

Числа, которые мы используем для подсчета или перечисления элементов, — это натуральные числа: 1, 2, 3, 4, 5 и так далее. Мы описываем их в обозначениях множества как {1,2,3, …} {1,2,3, …}, где многоточие (…) указывает, что числа продолжаются до бесконечности. Натуральные числа, конечно же, также называются счетными числами .Каждый раз, когда мы перечисляем членов команды, считаем монеты в коллекции или подсчитываем деревья в роще, мы используем набор натуральных чисел. Набор целых чисел — это набор натуральных чисел плюс ноль: {0,1,2,3, …}. {0,1,2,3, …}.

Набор целых чисел добавляет противоположности натуральных чисел к набору целых чисел: {…, — 3, −2, −1,0,1,2,3, …}. {… , −3, −2, −1,0,1,2,3, …}. Полезно отметить, что набор целых чисел состоит из трех различных подмножеств: отрицательных целых чисел, нуля и положительных целых чисел.В этом смысле положительные целые числа — это просто натуральные числа. Другой способ думать об этом — это то, что натуральные числа являются подмножеством целых чисел.

…, −3, −2, −1, отрицательные целые числа0, ноль1,2,3, ⋯ положительные целые числа…, −3, −2, −1, отрицательные целые числа0, ноль1,2,3, ⋯ положительные целые числа

Множество рациональных чисел записывается как {mn | mand nare целые числа и n 0}. {mn | mand nare целые числа и n 0}. Обратите внимание на определение, что рациональные числа — это дроби (или частные), содержащие целые числа как в числителе, так и в знаменателе, а знаменатель никогда не равен 0.Мы также можем видеть, что каждое натуральное число, целое число и целое число является рациональным числом со знаминателем 1.

Поскольку это дроби, любое рациональное число также может быть выражено в десятичной форме. Любое рациональное число может быть представлено как:

ⓐ завершающая десятичная дробь: 158 = 1,875, 158 = 1,875, или
ⓑa повторяющаяся десятичная дробь: 411 = 0,36363636… = 0,36 ¯ 411 = 0,36363636… = 0,36 ¯

Мы используем линию, проведенную над повторяющимся блоком чисел, вместо того, чтобы писать группу несколько раз.

Пример 1

Запись целых чисел как рациональных

Запишите каждое из следующих чисел в виде рациональных чисел.

ⓐ7
ⓑ0
ⓒ – 8

Решение

Запишите дробь с целым числом в числителе и 1 в знаменателе.

ⓐ 7 = 717 = 71
ⓑ 0 = 010 = 01
ⓒ −8 = −81−8 = −81

Попробуй # 1

Запишите каждое из следующих чисел в виде рациональных чисел.

ⓐ11
ⓑ3
ⓒ – 4

Пример 2

Определение рациональных чисел

Запишите каждое из следующих рациональных чисел как завершающее или повторяющееся десятичное число.

ⓐ −57−57
ⓑ 155155
ⓒ 13251325

Решение

Запишите каждую дробь как десятичную дробь, разделив числитель на знаменатель.

ⓐ -57 = -0.714285 ———, — 57 = -0,714285 ———, повторяющееся десятичное число
ⓑ 155 = 3155 = 3 (или 3,0), конечная десятичная дробь
ⓒ 1325 = 0,52, 1325 = 0,52, завершающая десятичная дробь

Попробуй # 2

Запишите каждое из следующих рациональных чисел как завершающее или повторяющееся десятичное число.

ⓐ 68176817
ⓑ 813813
ⓒ −1720−1720

Иррациональные числа

В какой-то момент в древнем прошлом кто-то обнаружил, что не все числа являются рациональными числами.Строитель, например, мог обнаружить, что диагональ квадрата с единичными сторонами не равна 2 или даже 32,32, а является чем-то другим. Или производитель одежды мог заметить, что отношение длины окружности к диаметру рулона ткани было немного больше 3, но все же не рациональное число. Такие числа называются иррациональными , потому что они не могут быть записаны в виде дробей. Эти числа составляют набор иррациональных чисел. Иррациональные числа нельзя выразить дробью двух целых чисел.Невозможно описать этот набор чисел одним правилом, кроме как сказать, что число иррационально, если оно нерационально. Итак, мы пишем это, как показано.

{h | его нерациональное число} {h | его нерациональное число}

Пример 3

Дифференциация рациональных и иррациональных чисел

Определите, является ли каждое из следующих чисел рациональным или иррациональным. Если это рационально, определите, является ли это завершающей или повторяющейся десятичной дробью.

ⓐ 2525
ⓑ 339339
ⓒ 1111
ⓓ 17341734
ⓔ 0.3033033303333… 0,3033033303333…

Решение

ⓐ 25:25: Это можно упростить как 25 = 5,25 = 5. Следовательно, 2525 — это рационально.
ⓑ 339: 339: Поскольку это дробная часть целых чисел, 339339 — рациональное число. Затем упростите и разделите. 339 = 331193 = 113 = 3,6 ¯ 339 = 331193 = 113 = 3,6 ¯
Итак, 339339 является рациональным и повторяющимся десятичным числом.
ⓒ 11:11: Это нельзя дальше упрощать. Следовательно, 1111 — иррациональное число.
ⓓ 1734: 1734: Поскольку это дробная часть целых чисел, 17341734 — рациональное число. Упростите и разделите. 1734 = 171342 = 12 = 0,51734 = 171342 = 12 = 0,5
Итак, 17341734 является рациональным и завершающим десятичным числом.
ⓔ 0,3033033303333… 0,3033033303333… не является завершающим десятичным числом. Также обратите внимание, что здесь нет повторяющегося шаблона, потому что группа из трех увеличивается каждый раз. Следовательно, это не завершающее и не повторяющееся десятичное число и, следовательно, не рациональное число. Это иррациональное число.

Попробовать # 3

ⓐ 777777
ⓑ 8181
ⓒ 4,27027002700027… 4,27027002700027…
ⓓ 113
ⓔ 3939

Действительные числа

Для любого числа n мы знаем, что n либо рационально, либо иррационально.Не может быть и того, и другого. Наборы рациональных и иррациональных чисел вместе составляют набор действительных чисел. Как мы видели с целыми числами, действительные числа можно разделить на три подмножества: отрицательные действительные числа, ноль и положительные действительные числа. Каждое подмножество включает дроби, десятичные дроби и иррациональные числа в соответствии с их алгебраическим знаком (+ или -). Ноль не считается ни положительным, ни отрицательным.

Действительные числа можно визуализировать на горизонтальной числовой строке с произвольной точкой, выбранной как 0, с отрицательными числами слева от 0 и положительными числами справа от 0.Затем используется фиксированное единичное расстояние для обозначения каждого целого числа (или другого базового значения) по обе стороны от 0. Любое действительное число соответствует уникальной позиции в числовой строке. Верно и обратное: каждое положение на числовой строке соответствует ровно на одно действительное число. Это называется взаимно-однозначным соответствием. Мы называем это строкой действительных чисел, как показано на Рисунке 1 .

Рисунок 1 Строка действительного числа

Пример 4

Классификация действительных чисел

Классифицируйте каждое число как положительное или отрицательное, а также как рациональное или иррациональное.Число находится слева или справа от 0 на числовой прямой?

ⓐ −103−103
ⓑ 55
ⓒ −289−289
ⓓ −6π − 6π
ⓔ 0,615384615384… 0,615384615384…

Решение

ⓐ −103−103 отрицательно и рационально. Он находится слева от 0 на числовой строке.
ⓑ 55 положительно и иррационально. Он находится справа от 0.
ⓒ −289 = −172 = −17−289 = −172 = −17 отрицательно и рационально.Он находится слева от 0.
ⓓ −6π − 6π отрицательно и иррационально. Он находится слева от 0.
ⓔ 0,615384615384… 0,615384615384… — повторяющееся десятичное число, поэтому оно рационально и положительно. Он находится справа от 0.

Попробовать # 4

Классифицируйте каждое число как положительное или отрицательное, а также как рациональное или иррациональное. Число находится слева или справа от 0 на числовой прямой?

ⓐ 7373
ⓑ −11.411411411… −11,411411411…
ⓒ 47194719
ⓓ −52−52
ⓔ 6.2 10 7356.2 10735

Наборы чисел как подмножества

Начиная с натуральных чисел, мы расширили каждый набор, чтобы сформировать более крупный набор, что означает, что между наборами чисел, с которыми мы столкнулись до сих пор, существует связь подмножества. Эти отношения становятся более очевидными, если рассматривать их в виде диаграммы, такой как рис. 2.

Рисунок 2 Наборы чисел
N : набор натуральных чисел
W : набор целых чисел
I : набор целых чисел
Q : набор рациональных чисел
Q ´ : набор иррациональных чисел

Наборы чисел

Набор натуральных чисел включает числа, используемые для счета: {1,2,3 ,…}. {1,2,3, …}.

Набор целых чисел — это набор натуральных чисел плюс ноль: {0,1,2,3, …}. {0,1,2,3, …}.

Набор целых чисел добавляет отрицательные натуральные числа к набору целых чисел: {…, — 3, −2, −1,0,1,2,3, …}. {…, — 3, −2, −1,0,1,2,3, …}.

Набор рациональных чисел включает дроби, записанные как {mn | mand nare integer and n 0}. {Mn | mand nare integer and n 0}.

Набор иррациональных чисел — это набор чисел, которые не являются рациональными, неповторяющимися и неповторяющимися: {h | его не рациональное число}.{h | его нерациональное число}.

Пример 5

Дифференцирование наборов чисел

Классифицируйте каждое число как натуральное число ( N ), целое число ( W ), целое число ( I ), рациональное число ( Q ) и / или иррациональное число ( Q ‘).

ⓐ 3636
ⓑ 8383
ⓒ 7373
ⓓ −6−6
ⓔ 3,2121121112… 3,2121121112…

Решение

	N	Вт	Я	К	Q ′
а.36 = 636 = 6	Х	Х	Х	Х
б. 83 = 2,6 ¯ 83 = 2,6 ¯				Х
с. 7373					Х
г. –6			Х	Х
e.3,2121121112 …					Х

Попробовать # 5

ⓐ −357−357
ⓑ 00
ⓒ 169169
ⓓ 2424
ⓔ 4.763763763… 4,763763763…

Выполнение вычислений с использованием порядка операций

Когда мы умножаем число на само себя, мы возводим его в квадрат или возводим в степень 2. Например, 42 = 4⋅4 = 16,42 = 4⋅4 = 16. Мы можем возвести любое число в любую степень. В общем, экспоненциальная запись anan означает, что число или переменная aa используется как множитель nn раз.

an = a⋅a⋅a⋅… ⋅anfactorsan = a⋅a⋅a⋅… ⋅anfactors

В этой записи anan читается как n -я степень числа a, a, где aa называется основанием, а nn — называется экспонента . Термин в экспоненциальном представлении может быть частью математического выражения, которое представляет собой комбинацию чисел и операций. Например, 24 + 6⋅23−4224 + 6⋅23−42 — математическое выражение.

Чтобы вычислить математическое выражение, мы выполняем различные операции. Однако мы не выполняем их в произвольном порядке. Используем порядок действий. Это последовательность правил для вычисления таких выражений.

Напомним, что в математике мы используем круглые скобки (), квадратные скобки [] и фигурные скобки {} для группировки чисел и выражений, так что все, что появляется в символах, рассматривается как единое целое.Кроме того, столбцы дробей, радикалов и абсолютных значений обрабатываются как символы группировки. При оценке математического выражения начните с упрощения выражений в группирующих символах.

Следующий шаг — обратиться к любым экспонентам или радикалам. После этого выполните умножение и деление слева направо и, наконец, сложение и вычитание слева направо.

Давайте посмотрим на предоставленное выражение.

24 + 6⋅23-4224 + 6⋅23-42

Группирующих символов нет, поэтому переходим к показателям степени или радикалам.Число 4 возводится в степень 2, поэтому упростим 4242 до 16.

24 + 6⋅23−4224 + 6⋅23−1624 + 6⋅23−4224 + 6⋅23−16

Затем выполните умножение или деление слева направо.

24 + 6⋅23−1624 + 4−1624 + 6⋅23−1624 + 4−16

Наконец, выполните сложение или вычитание слева направо.

24 + 4−1628−161224 + 4−1628−1612

Следовательно, 24 + 6⋅23−42 = 12,24 + 6⋅23−42 = 12.

Для некоторых сложных выражений потребуется несколько проходов по порядку операций. Например, внутри круглых скобок может быть радикальное выражение, которое необходимо упростить перед вычислением скобок.Соблюдение порядка операций гарантирует, что любой, кто упрощает одно и то же математическое выражение, получит тот же результат.

Порядок действий

Операции в математических выражениях должны оцениваться в систематическом порядке, который можно упростить, используя аббревиатуру PEMDAS :

P (arentheses)
E (xponents)
M (ultiplication) и D (ivision)
A (ddition) и S (ubtraction)

Как сделать

Упростите математическое выражение, используя порядок операций.

Шаг 1. Упростите любые выражения внутри символов группировки.
Шаг 2. Упростите любые выражения, содержащие степени или радикалы.
Шаг 3. Произведите любое умножение и деление по порядку слева направо.
Шаг 4. Выполняйте любое сложение и вычитание по порядку слева направо.

Пример 6

Использование порядка операций

Используйте порядок операций для вычисления каждого из следующих выражений.

ⓐ (3⋅2) 2−4 (6 + 2) (3⋅2) 2−4 (6 + 2)
ⓑ 52−47−11−252−47−11−2
ⓒ 6− | 5−8 | +3 (4−1) 6− | 5−8 | +3 (4−1)
ⓓ 14−3⋅22⋅5−3214−3⋅22⋅5-32
ⓔ 7 (5⋅3) −2 [(6−3) −42] +17 (5⋅3) −2 [(6−3) −42] +1

Решение

ⓐ
(3⋅2) 2−4 (6 + 2) = (6) 2−4 (8) Упростить скобки. = 36−4 (8) Упростить показатель степени. = 36−32 Упростить умножение. = 4 Упростить вычитание. (3⋅2) ) 2−4 (6 + 2) = (6) 2−4 (8) Упростим скобки. = 36−4 (8) Упростим показатель степени.= 36−32 Упростить умножение. = 4 Упростить вычитание.
ⓑ
52-47-11-2 = 52-47-9 Упростить символы группировки (радикал). = 52-47-3 Упростить радикал. = 25-47-3 Упростить показатель степени. = 217-3 Упростить вычитание в числителе. = 3-3 Упростить деление. = 0 Упростить вычитание. 52-47−11−2 = 52−47−9 Упростить группирующие символы (радикал). = 52−47−3 Упростить радикал. = 25−47−3 Упростить показатель степени. = 217−3 Упростить вычитание в числителе. = 3− 3 Упростить деление. = 0 Упростить вычитание.
Обратите внимание, что на первом шаге радикал рассматривается как символ группировки, например круглые скобки.Кроме того, на третьем этапе полоса дроби считается символом группировки, поэтому числитель считается сгруппированным.
ⓒ
6− | 5−8 | +3 (4−1) = 6− | −3 | +3 (3) Упростить символы внутренней группировки. = 6−3 + 3 (3) Упростить абсолютное значение. = 6−3 + 9 Упростить умножение. = 3 + 9 Упростить вычитание. = 12 Упростить сложение. 6− | 5−8 | +3 (4−1) = 6− | −3 | +3 (3) Упростить символы внутренней группировки. = 6−3 + 3 (3) Упростить абсолютное значение. = 6−3 + 9 Упростить умножение. = 3 + 9 Упростить вычитание. = 12 Упростить сложение.
ⓓ
14−3⋅22⋅5−32 = 14−3⋅22⋅5−9 Упростим показатель степени.= 14−610−9 Упростить продукты. = 81 Упростить различия. = 8 Упростить частное. 14−3⋅22⋅5−32 = 14−3⋅22⋅5−9 Упростить показатель степени. = 14−610−9 Упростить товары. = 81 Упростить различия. = 8 Упростите частное.
В этом примере дробная черта разделяет числитель и знаменатель, которые мы упрощаем отдельно до последнего шага.
ⓔ
7 (5⋅3) −2 [(6−3) −42] + 1 = 7 (15) −2 [(3) −42] + 1 Упростить в скобках. = 7 (15) −2 (3−16) + 1 Упростить показатель степени. = 7 (15) −2 (−13) + 1 Вычесть. = 105 + 26 + 1 Умножить. = 132 Добавить.7 (5⋅3) −2 [(6−3) −42] + 1 = 7 (15) −2 [(3) −42] + 1 Упростить в скобках. = 7 (15) −2 (3−16) + 1 Упростить показатель степени. = 7 (15) −2 (−13) + 1 Вычесть. = 105 + 26 + 1 Умножить. = 132 Добавить.

Попробуй # 6

Используйте порядок операций для вычисления каждого из следующих выражений.

ⓐ 52−42 + 7 (5−4) 252−42 + 7 (5−4) 2
ⓑ 1 + 7⋅5−8⋅49−61 + 7⋅5−8⋅49−6
ⓒ | 1,8−4,3 | + 0,415 + 10 | 1,8−4,3 | + 0,415 + 10
ⓓ 12 [5⋅32−72] + 13⋅9212 [5⋅32−72] + 13⋅92
ⓔ [(3-8) 2-4] — (3-8) [(3-8) 2-4] — (3-8)

Использование свойств действительных чисел

Для некоторых действий, которые мы выполняем, порядок некоторых операций не имеет значения, но порядок других операций имеет значение.Например, не имеет значения, надеваем ли мы правую обувь перед левой или наоборот. Однако не имеет значения, наденем ли мы сначала туфли или носки. То же верно и для математических операций.

Коммутативные свойства

Коммутативное свойство сложения гласит, что числа можно складывать в любом порядке, не влияя на сумму.

Мы можем лучше увидеть эту взаимосвязь при использовании действительных чисел.

(−2) + 7 = 5 и 7 + (- 2) = 5 (−2) + 7 = 5 и 7 + (- 2) = 5

Аналогично, свойство коммутативности умножения гласит, что числа можно умножать в любом порядке, не влияя на произведение.

Снова рассмотрим пример с действительными числами.

(−11) ⋅ (−4) = 44 и (−4) ⋅ (−11) = 44 (−11) ⋅ (−4) = 44 и (−4) ⋅ (−11) = 44

Важно отметить, что ни вычитание, ни деление не коммутативны. Например, 17-517-5 — это не то же самое, что 5-17,5-17. Аналогично 20 ÷ 5 ≠ 5 ÷ 20.20 ÷ 5 ≠ 5 ÷ 20.

Ассоциативные свойства

Ассоциативное свойство умножения говорит нам, что не имеет значения, как мы группируем числа при умножении. Мы можем перемещать символы группировки, чтобы упростить расчет, при этом продукт остается прежним.

Рассмотрим этот пример.

(3⋅4) ⋅5 = 60and3⋅ (4⋅5) = 60 (3⋅4) ⋅5 = 60and3⋅ (4⋅5) = 60

Ассоциативное свойство сложения говорит нам, что числа можно группировать по-разному, не влияя на сумму.

a + (b + c) = (a + b) + ca + (b + c) = (a + b) + c

Это свойство может быть особенно полезно при работе с отрицательными целыми числами. Рассмотрим этот пример.

[15 + (- 9)] + 23 = 29and15 + [(- 9) +23] = 29 [15 + (- 9)] + 23 = 29and15 + [(- 9) +23] = 29

Ассоциативны ли вычитание и деление? Просмотрите эти примеры.

8− (3−15) =? (8−3) −1564 ÷ (8 ÷ 4) =? (64 ÷ 8) ÷ 48 — (- 12) = 5−1564 ÷ 2 =? 8 ÷ 420 ≠ −1032 ≠ 28− (3−15) =? (8−3) −1564 ÷ (8 ÷ 4) =? (64 ÷ 8) ÷ 48 — (- 12) = 5−1564 ÷ 2 =? 8 ÷ 420 ≠ — 1032 ≠ 2

Как видим, ни вычитание, ни деление не ассоциативны.

Распределительное свойство

Распределительное свойство утверждает, что произведение множителя на сумму является суммой множителя, умноженного на каждый член в сумме.

a⋅ (b + c) = a⋅b + a⋅ca⋅ (b + c) = a⋅b + a⋅c

Это свойство сочетает в себе как сложение, так и умножение (и это единственное свойство).Рассмотрим пример.

Обратите внимание, что 4 находится за пределами символов группировки, поэтому мы распределяем 4, умножая его на 12, умножая на –7 и складывая произведения.

Чтобы быть более точным, описывая это свойство, мы говорим, что умножение распределяется по сложению. Обратное неверно, как мы видим в этом примере.

6+ (3⋅5) =? (6 + 3) ⋅ (6 + 5) 6+ (15) =? (9) ⋅ (11) 21 ≠ 996 + (3⋅5) =? (6 + 3) ⋅ (6 + 5) 6+ (15) =? (9) ⋅ (11) 21 ≠ 99

Частный случай свойства распределения возникает при вычитании суммы членов.

a − b = a + (- b) a − b = a + (- b)

Например, рассмотрим разницу 12− (5 + 3) .12− (5 + 3). Мы можем переписать разницу между двумя членами 12 и (5 + 3) (5 + 3), превратив выражение вычитания в сложение противоположного. Поэтому вместо вычитания (5 + 3), (5 + 3) мы добавляем противоположное.

12 + (- 1) ⋅ (5 + 3) 12 + (- 1) ⋅ (5 + 3)

Теперь распределите −1−1 и упростите результат.

12− (5 + 3) = 12 + (- 1) ⋅ (5 + 3) = 12 + [(- 1) ⋅5 + (- 1) ⋅3] = 12 + (- 8) = 412− (5 +3) = 12 + (- 1) ⋅ (5 + 3) = 12 + [(- 1) ⋅5 + (- 1) ⋅3] = 12 + (- 8) = 4

Кажется, много проблема для простой суммы, но она иллюстрирует мощный результат, который будет полезен, когда мы введем алгебраические термины.Чтобы вычесть сумму членов, измените знак каждого члена и сложите результаты. Имея это в виду, мы можем переписать последний пример.

12− (5 + 3) = 12 + (- 5−3) = 12 + (- 8) = 412− (5 + 3) = 12 + (- 5−3) = 12 + (- 8) = 4

Свойства идентичности

Свойство идентичности сложения утверждает, что существует уникальный номер, называемый аддитивным идентификатором (0), который при добавлении к номеру дает исходный номер.

Свойство идентичности умножения утверждает, что существует уникальное число, называемое мультипликативным тождеством (1), которое при умножении на число дает исходное число.

Например, у нас есть (−6) + 0 = −6 (−6) + 0 = −6 и 23⋅1 = 23,23⋅1 = 23. Для этих свойств нет исключений; они работают для всех действительных чисел, включая 0 и 1.

Обратные свойства

Обратное свойство сложения утверждает, что для каждого действительного числа a существует уникальное число, называемое аддитивным обратным (или противоположным), обозначаемое — a , которое при добавлении к исходному числу приводит к аддитивная идентичность, 0.

Например, если a = −8, a = −8, аддитивная обратная величина равна 8, поскольку (−8) + 8 = 0.(-8) + 8 = 0.

Обратное свойство умножения сохраняется для всех действительных чисел, кроме 0, потому что величина, обратная 0, не определена. Свойство гласит, что для каждого действительного числа a существует уникальное число, называемое обратным мультипликативным (или обратным) числом, обозначенное 1a, 1a, которое при умножении на исходное число дает мультипликативную идентичность 1.

Например, если a = −23, a = −23, обратная величина, обозначенная 1a, 1a, будет −32−32 потому что

a⋅1a = (- 23) ⋅ (−32) = 1a⋅1a = (- 23) ⋅ (−32) = 1

Свойства действительных чисел

Следующие свойства имеют место для действительных чисел a , b и c .

	Дополнение	Умножение
Коммутационная собственность	а + Ь = Ь + аа + Ь = Ь + а	a⋅b = b⋅aa⋅b = b⋅a
Ассоциативное свойство	a + (b + c) = (a + b) + ca + (b + c) = (a + b) + c	a (bc) = (ab) ca (bc) = (ab) c
Распределительная собственность	a⋅ (b + c) = a⋅b + a⋅ca⋅ (b + c) = a⋅b + a⋅c
Идентификационная собственность	Существует уникальное действительное число, называемое аддитивным идентификатором, 0, такое, что для любого действительного числа a	Существует уникальное действительное число, называемое мультипликативным тождеством, 1, такое, что для любого действительного числа a
Обратное свойство	Каждое действительное число a имеет аддитивное обратное или противоположное, обозначенное –a , так что	Каждое ненулевое действительное число a имеет обратное мультипликативное или обратное число, обозначенное 1a, 1a, такое, что

Пример 7

Использование свойств действительных чисел

Используйте свойства действительных чисел, чтобы переписать и упростить каждое выражение.Укажите, какие свойства применимы.

ⓐ 3⋅6 + 3⋅43⋅6 + 3⋅4
ⓑ (5 + 8) + (- 8) (5 + 8) + (- 8)
ⓒ 6− (15 + 9) 6− (15 + 9)
ⓓ 47⋅ (23⋅74) 47⋅ (23⋅74)
ⓔ 100⋅ [0,75 + (- 2,38)] 100⋅ [0,75 + (- 2,38)]

Решение

ⓐ
3⋅6 + 3⋅4 = 3⋅ (6 + 4) Распределительное свойство. = 3⋅10Simplify. = 30Simplify. 3⋅6 + 3⋅4 = 3⋅ (6 + 4) Распределительное свойство. = 3⋅10Simplify. = 30 Упростите.
ⓑ
(5 + 8) + (- 8) = 5 + [8 + (- 8)] Ассоциативное свойство сложения.= 5 + 0 Обратное свойство сложения. = 5 Идентичность сложения. (5 + 8) + (- 8) = 5 + [8 + (- 8)] Ассоциативное свойство сложения. = 5 + 0 Обратное свойство сложения. = 5 Идентичность свойство сложения.
ⓒ
6− (15 + 9) = 6 + [(- 15) + (- 9)] Распределительное свойство. = 6 + (- 24) Упростить. = — 18 Упростить. 6− (15 + 9) = 6 + [(- 15) + (- 9)] Распределительное свойство. = 6 + (- 24) Simplify. = — 18Simplify.
ⓓ
47⋅ (23⋅74) = 47⋅ (74⋅23) Коммутативное свойство умножения. = (47⋅74) ⋅23 Ассоциативное свойство умножения.= 1⋅23 Обратное свойство умножения. = 23 Свойство идентичности умножения. 47⋅ (23⋅74) = 47⋅ (74⋅23) Коммутативное свойство умножения. = (47⋅74) ⋅23 Ассоциативное свойство умножения. = 1⋅23 Обратное свойство умножения. = 23 Свойство идентичности умножения.
ⓔ
100⋅ [0,75 + (- 2,38)] = 100⋅0,75 + 100⋅ (−2,38) Распределительное свойство. = 75 + (- 238) Упростить. = — 163Упростить. 100⋅ [0,75 + (- 2,38)] = 100⋅ 0,75 + 100⋅ (−2,38) Распределительное свойство. = 75 + (- 238) Simplify. = — 163Simplify.

Попробовать # 7

ⓐ (−235) ⋅ [11⋅ (−523)] (- 235) ⋅ [11⋅ (−523)]
ⓑ 5⋅ (6,2 + 0,4) 5⋅ (6,2 + 0,4)
ⓒ 18- (7-15) 18- (7-15)
ⓓ 1718+ [49 + (- 1718)] 1718+ [49 + (- 1718)]
ⓔ 6⋅ (−3) + 6⋅36⋅ (−3) + 6⋅3

Вычисление алгебраических выражений

До сих пор в математических выражениях, которые мы видели, использовались только действительные числа. В математике мы можем видеть такие выражения, как x + 5,43πr3, x + 5,43πr3 или 2m3n2.2м3н2. В выражении x + 5, x + 5, 5 называется константой, потому что она не меняется, а x называется переменной, потому что она изменяется. (При именовании переменной игнорируйте любые экспоненты или радикалы, содержащие переменную.) Алгебраическое выражение — это набор констант и переменных, соединенных вместе алгебраическими операциями сложения, вычитания, умножения и деления.

Мы уже видели несколько реальных числовых примеров экспоненциальной записи, сокращенного метода записи продуктов того же множителя.Когда используются переменные, константы и переменные обрабатываются одинаково.

(−3) 5 = (- 3) ⋅ (−3) ⋅ (−3) ⋅ (−3) ⋅ (−3) x5 = x⋅x⋅x⋅x⋅x (2⋅7) 3 = (2 ⋅7) ⋅ (2⋅7) ⋅ (2⋅7) (yz) 3 = (yz) ⋅ (yz) ⋅ (yz) (- 3) 5 = (- 3) ⋅ (−3) ⋅ (−3 ) ⋅ (−3) ⋅ (−3) x5 = x⋅x⋅x⋅x⋅x (2⋅7) 3 = (2⋅7) ⋅ (2⋅7) ⋅ (2⋅7) (yz) 3 = (yz) ⋅ (yz) ⋅ (yz)

В каждом случае показатель степени говорит нам, сколько факторов базы использовать, независимо от того, состоит ли база из констант или переменных.

Любая переменная в алгебраическом выражении может принимать или иметь разные значения. Когда это происходит, значение алгебраического выражения меняется.Вычислить алгебраическое выражение означает определить значение выражения для данного значения каждой переменной в выражении. Замените каждую переменную в выражении заданным значением, затем упростите полученное выражение, используя порядок операций. Если алгебраическое выражение содержит более одной переменной, замените каждую переменную присвоенным ей значением и упростите выражение, как и раньше.

Пример 8

Описание алгебраических выражений

Перечислите константы и переменные для каждого алгебраического выражения.

ⓐ х + 5
ⓑ 43πr343πr3
ⓒ 2м3н22м3н2

Решение

	Константы	Переменные
а. х + 5	5	х
б. 43πr343πr3	43, π43, π	руб.
с. 2м3н22м3н2	2	м, нм, n

Попробовать # 8

Перечислите константы и переменные для каждого алгебраического выражения.

ⓐ 2πr (r + h) 2πr (r + h)
ⓑ2 ( длина + ширина )
ⓒ 4y3 + y4y3 + y

Пример 9

Вычисление алгебраического выражения при различных значениях

Вычислите выражение 2x − 72x − 7 для каждого значения x.

ⓐ x = 0x = 0
ⓑ х = 1х = 1
ⓒ х = 12х = 12
ⓓ х = −4x = −4

Решение

ⓐ Заменим 0 на x.Икс. 2x − 7 = 2 (0) −7 = 0−7 = −72x − 7 = 2 (0) −7 = 0−7 = −7
ⓑЗаменить 1 на x.x. 2x − 7 = 2 (1) −7 = 2−7 = −52x − 7 = 2 (1) −7 = 2−7 = −5
ⓒ Замените 1212 на x.x. 2x − 7 = 2 (12) −7 = 1−7 = −62x − 7 = 2 (12) −7 = 1−7 = −6
ⓓ Замените −4−4 вместо x.x. 2x − 7 = 2 (−4) −7 = −8−7 = −152x − 7 = 2 (−4) −7 = −8−7 = −15

Попробовать # 9

Вычислите выражение 11−3y11−3y для каждого значения y.

ⓐ у = 2у = 2
ⓑ у = 0 у = 0
ⓒ у = 23у = 23
ⓓ у = -5у = -5

Пример 10

Вычисление алгебраических выражений

Оцените каждое выражение для заданных значений.

ⓐ x + 5x + 5 для x = −5x = −5
ⓑ t2t − 1t2t − 1 для t = 10t = 10
ⓒ 43πr343πr3 для r = 5r = 5
ⓓ a + ab + ba + ab + b для a = 11, b = −8a = 11, b = −8
ⓔ 2m3n22m3n2 для m = 2, n = 3m = 2, n = 3

Решение

ⓐ Подставляем −5−5 вместо x.x. х + 5 = (- 5) + 5 = 0x + 5 = (- 5) + 5 = 0
ⓑ Заменить 10 на т.т. t2t − 1 = (10) 2 (10) −1 = 1020−1 = 1019 t2t − 1 = (10) 2 (10) −1 = 1020−1 = 1019
ⓒ Заменить 5 на r.р. 43πr3 = 43π (5) 3 = 43π (125) = 5003π43πr3 = 43π (5) 3 = 43π (125) = 5003π
ⓓ Замените 11 вместо aa и –8 на b.b. a + ab + b = (11) + (11) (- 8) + (- 8) = 11−88−8 = −85a + ab + b = (11) + (11) (- 8) + (- 8) = 11-88-8 = -85
ⓔ Замените 2 на мм и 3 на n.n. 2m3n2 = 2 (2) 3 (3) 2 = 2 (8) (9) = 144 = 122m3n2 = 2 (2) 3 (3) 2 = 2 (8) (9) = 144 = 12

Попробовать # 10

Оцените каждое выражение для заданных значений.

ⓐ y + 3y − 3y + 3y − 3 для y = 5y = 5
ⓑ 7−2t7−2t для t = −2t = −2
ⓒ 13πr213πr2 для r = 11r = 11
ⓓ (p2q) 3 (p2q) 3 для p = −2, q = 3p = −2, q = 3
ⓔ 4 (m − n) −5 (n − m) 4 (m − n) −5 (n − m) для m = 23, n = 13m = 23, n = 13

Формулы

Уравнение — это математическое утверждение, указывающее, что два выражения равны.Выражения могут быть числовыми или алгебраическими. Уравнение не является истинным или ложным по своей сути, а всего лишь предположением. Значения, которые делают уравнение истинным, решения находятся с использованием свойств действительных чисел и других результатов. Например, уравнение 2x + 1 = 72x + 1 = 7 имеет единственное решение 3, потому что, когда мы подставляем 3 вместо xx в уравнение, мы получаем истинное утверждение 2 (3) + 1 = 7.2 (3) + 1 = 7.

Формула — это уравнение, выражающее связь между постоянными и переменными величинами.Очень часто уравнение является средством нахождения значения одной величины (часто одной переменной) с точки зрения другой или других величин. Одним из наиболее распространенных примеров является формула для нахождения площади AA круга через радиус rr круга: A = πr2.A = πr2. Для любого значения r, r площадь AA можно найти, вычислив выражение πr2.πr2.

Пример 11

Использование формулы

Правый круговой цилиндр с радиусом rr и высотой hh имеет площадь SS (в квадратных единицах), определяемую формулой S = 2πr (r + h).S = 2πr (r + h). См. Рис. 3. Найдите площадь поверхности цилиндра радиусом 6 дюймов и высотой 9 дюймов. Оставьте ответ в виде π.π.

Рисунок 3 Правый круговой цилиндр

Решение

Вычислите выражение 2πr (r + h) 2πr (r + h) для r = 6r = 6 и h = 9.h = 9.

S = 2πr (r + h) = 2π (6) [(6) + (9)] = 2π (6) (15) = 180πS = 2πr (r + h) = 2π (6) [(6) + ( 9)] = 2π (6) (15) = 180π

Площадь поверхности составляет 180π180π квадратных дюймов.

Попробовать # 11

Фотография длиной L и шириной W размещается на мате шириной 8 сантиметров (см).Площадь матового покрытия (в квадратных сантиметрах или см ²) оказалась равной A = (L + 16) (W + 16) −L⋅WA = (L + 16) (W + 16) −L⋅ W. См. Рис. 4. Найдите площадь подложки для фотографии длиной 32 см и шириной 24 см.

Рисунок 4

Упрощение алгебраических выражений

Иногда мы можем упростить алгебраическое выражение, чтобы его было легче вычислить или использовать каким-либо другим способом. Для этого мы используем свойства действительных чисел. Мы можем использовать те же свойства в формулах, потому что они содержат алгебраические выражения.

Пример 12

Упрощение алгебраических выражений

Упростите каждое алгебраическое выражение.

ⓐ 3x − 2y + x − 3y − 73x − 2y + x − 3y − 7
ⓑ 2r − 5 (3 − r) + 42r − 5 (3 − r) +4
ⓓ 2mn − 5m + 3mn + n2mn − 5m + 3mn + n

Решение

ⓐ
3x − 2y + x − 3y − 7 = 3x + x − 2y − 3y − 7 Коммутативное свойство сложения. = 4x − 5y − 7 Упростить. 3x − 2y + x − 3y − 7 = 3x + x − 2y − 3y − 7 Коммутативное свойство сложения.= 4x − 5y − 7 Упростить.
ⓑ
2r − 5 (3 − r) + 4 = 2r − 15 + 5r + 4 Распределительное свойство. = 2r + 5r − 15 + 4 Коммутативное свойство сложения. = 7r − 11 Упростить. 2r − 5 (3 − r) + 4 = 2r− 15 + 5r + 4 Распределительное свойство. = 2r + 5r − 15 + 4 Коммутативное свойство сложения. = 7r − 11 Упростить.
ⓒ
(4t − 54s) — (23t + 2s) = 4t − 54s − 23t − 2s Распределительное свойство. = 4t − 23t − 54s − 2s Коммутативное свойство сложения. = 103t − 134s Упростить. (4t − 54s) — (23t + 2s) = 4t − 54s − 23t − 2s Распределительное свойство. = 4t − 23t − 54s − 2s Коммутативное свойство сложения.= 103t − 134s Упростить.
ⓓ
2mn − 5m + 3mn + n = 2mn + 3mn − 5m + n Коммутативное свойство сложения. = 5mn − 5m + nSimplify.2mn − 5m + 3mn + n = 2mn + 3mn − 5m + n Коммутативное свойство сложения. = 5mn − 5m + n Упростите.

Попробовать # 12

Упростите каждое алгебраическое выражение.

ⓐ 23y − 2 (43y + z) 23y − 2 (43y + z)
ⓑ 5т − 2−3т + 15т − 2−3т + 1
ⓓ 9r− (s + 2r) + (6 − s) 9r− (s + 2r) + (6 − s)

Пример 13

Упрощение формулы

Прямоугольник длиной LL и шириной WW имеет периметр PP, равный P = L + W + L + W.П = Д + Ш + Д + Ш. Упростите это выражение.

Решение

P = L + W + L + WP = L + L + W + W Коммутативное свойство сложения P = 2L + 2W Simplify P = 2 (L + W) Распределительное свойство P = L + W + L + WP = L + L + W + W Коммутативное свойство сложенияP = 2L + 2WSimplifyP = 2 (L + W) Распределительное свойство

Попробовать # 13

Если сумма PP депонируется на счет, на котором выплачиваются простые проценты rr в течение времени t, t, общая стоимость депозита AA определяется как A = P + Prt.A = P + Prt. Упростите выражение. (Эта формула будет рассмотрена более подробно позже в курсе.)

1.1 Упражнения по разделам

Устные

Является ли 22 примером рационального завершающего, рационально повторяющегося или иррационального числа? Расскажите, почему он подходит к этой категории.

Каков порядок действий? Какой акроним используется для описания порядка операций и что он означает?

Что ассоциативные свойства позволяют нам делать, следуя порядку операций? Поясните свой ответ.

Числовой

Для следующих упражнений упростите данное выражение.

10 + 2 × (5−3) 10 + 2 × (5−3)

6 ÷ 2− (81 ÷ 32) 6 ÷ 2− (81 ÷ 32)

−2 × [16 ÷ (8−4) 2] 2−2 × [16 ÷ (8−4) 2] 2

11.

12 ÷ (36 ÷ 9) + 612 ÷ (36 ÷ 9) +6

18.

9− (3 + 11) × 29− (3 + 11) × 2

24.

(15-7) × (3-7) (15-7) × (3-7)

25.

2 × 4−9 (−1) 2 × 4−9 (−1)

Алгебраические

Найдите переменную для следующих упражнений.

28.

8 (x + 3) –648 (x + 3) –64 для x = 2x = 2

29.

4y + 8–2y4y + 8–2y для y = 3y = 3

30.

(11a + 3) −18a + 4 (11a + 3) −18a + 4 для a = –2a = –2

31.

4z − 2z (1 + 4) –364z − 2z (1 + 4) –36 для z = 5z = 5

32.

4y (7−2) 2 + 2004y (7−2) 2 + 200 для y = –2y = –2

33.

— (2x) 2 + 1 + 3− (2x) 2 + 1 + 3 для x = 2x = 2

34.

Для 8 (2 + 4) −15b + b8 (2 + 4) −15b + b для b = –3b = –3

35.

2 (11c − 4) –362 (11c − 4) –36 для c = 0c = 0

36.

4 (3−1) x – 44 (3−1) x – 4 для x = 10x = 10

37.

14 (8w − 42) 14 (8w − 42) для w = 1w = 1

Упростите выражение для следующих упражнений.

39.

2y− (4) 2y − 112y− (4) 2y − 11

40.

a23 (64) −12a ÷ 6a23 (64) −12a ÷ 6

42.

5л ÷ 3л × (9-6) 5л ÷ 3л × (9-6)

44.

4 × 3 + 18x ÷ 9−124 × 3 + 18x ÷ 9−12

47.

6 + 12b − 3 × 6b6 + 12b − 3 × 6b

48.

18y − 2 (1 + 7y) 18y − 2 (1 + 7y)

50.

8 (3-м) +1 (-8) 8 (3-м) +1 (-8)

51.

9x + 4x (2 + 3) −4 (2x + 3x) 9x + 4x (2 + 3) −4 (2x + 3x)

Реальные приложения

Рассмотрим следующий сценарий для следующих упражнений: Фред зарабатывает 40 долларов на стрижке газонов.Он тратит 10 долларов на mp3, кладет половину остатка на сберегательный счет и получает еще 5 долларов за мытье машины своего соседа.

53.

Напишите выражение, которое представляет количество долларов, которые Фред держит (и не кладет на свой сберегательный счет). Запомните порядок действий.

54.

Сколько денег держит у Фреда?

Для следующих упражнений решите данную задачу.

55.

По данным Монетного двора США, диаметр четверти равен 0.955 дюймов. Окружность четверти равна диаметру, умноженному на π.π. Является ли окружность четверти целым числом, рациональным числом или иррациональным числом?

56.

Джессика и ее соседка по комнате Адриана решили разделить банку мелочи на совместные расходы. Джессика сначала положила мелочь в банку, а затем Адриана положила ее в банку. Мы знаем, что не имеет значения, в каком порядке изменение было добавлено в банку. Какое свойство сложения описывает этот факт?

Для следующих упражнений рассмотрите следующий сценарий: В карьере есть насыпь из нескольких фунтов гравия.В течение дня к насыпи добавляют 400 фунтов гравия. Проданы два заказа по 600 фунтов, и гравий убран с насыпи. В конце концов, в кургане есть 1200 фунтов гравия.

57.

Напишите уравнение, описывающее ситуацию.

Для следующего упражнения решите данную задачу.

59.

Рамон руководит маркетинговым отделом своей компании. Его отдел получает бюджет каждый год, и каждый год он должен расходовать весь бюджет, не превышая его.Если он тратит меньше бюджета, то на следующий год его отдел получает меньший бюджет. В начале этого года Рамон получил 2,5 миллиона долларов в годовой маркетинговый бюджет. Он должен израсходовать бюджет так, чтобы 2 500 000 − x = 0,2 500 000 − x = 0. Какое свойство сложения говорит нам, каким должно быть значение x ?

Technology

В следующих упражнениях используйте графический калькулятор, чтобы найти x . Округлите ответы до ближайшей сотой.

60.

0,5 (12,3) 2−48x = 350,5 (12,3) 2−48x = 35

61.

(0,25−0,75) 2x − 7,2 = 9,9 (0,25−0,75) 2x − 7,2 = 9,9

Расширения

62.

Если целое число не является натуральным, каким должно быть это число?

63.

Определите, является ли утверждение истинным или ложным. Мультипликативная обратная величина рационального числа также является рациональной.

64.

Определите, является ли утверждение истинным или ложным: произведение рационального и иррационального числа всегда иррационально.

65.

Определите, рационально или иррационально упрощенное выражение: −18−4 (5) (- 1) .− 18−4 (5) (- 1).

66.

Определите, рационально или иррационально упрощенное выражение: −16 + 4 (5) + 5. −16 + 4 (5) +5.

67.

Какой тип числа всегда будет результатом деления двух натуральных чисел?

68.

Какое свойство действительных чисел упростило бы следующее выражение: 4 + 7 (x − 1)? 4 + 7 (x − 1)?

Добро пожаловать в Space Math @ NASA!

Свойства чисел

Задача 209: Как выделить тусклые предметы в ярком мире! — Учащиеся узнают, что сложение изображений вместе часто улучшает слабые вещи, которые не видны только на одном изображении; мощность усреднения данных.[Оценка: 6-8 | Темы: умножение; разделение; десятичные числа.] [Щелкните здесь]

Задача 64 Солнечная активность и спутниковая математика — Когда солнечные бури вызывают проблемы со спутниками, они также могут привести к потере денег спутниками. Самый большой источник дохода от спутников связи поступает от транспондеров, ретранслирующих телевизионные программы, банкоматов. транзакции и многие другие важные формы информации. Они сдаются в аренду разным клиентам и могут стоить почти 2 миллиона долларов в год за каждый транспондер.В этом упражнении исследуется, что происходит с одним спутником, когда космическая погода получается плохо! [Уровень оценки: 4-6 | Темы: Десятичные дроби; Деньги; проценты] [Нажмите здесь]

Работа с простыми уравнениями

Задача 222: Температура Кельвина и очень низкие температуры- Учащиеся переводят градусы Цельсия в градусы Фаренгейта и Кельвина, используя три линейных уравнения. [Оценка: 5-8 | Темы: Оценка простых линейных уравнений для заданных значений..] [Кликните сюда]

Задача 221: Пульсары и простые уравнения- Студенты работают с линейными уравнениями, описывающими период вращения пульсара, и оценивают уравнения для различных условий. Учащиеся используют уравнения для прогнозирования точек пересечения во времени. [Оценка: 6-8 | Темы: Оценка простых уравнений с одной переменной] [Щелкните здесь]

Задача 219: Переменные и выражения из космоса- Студенты оценивают линейные уравнения, описывающие множество астрономических ситуаций.[Оценка: 6-8 | Темы: Оценка простых уравнений с одной переменной.] [Щелкните здесь]

Проблема 206: Теперь вы меня слышите? — Студенты узнают, как на передачу данных влияет расстояние до спутника для различных космических аппаратов в солнечной системе. [Оценка: 6-8 | Темы: умножение; разделение; десятичные числа.] [Щелкните здесь]

Задача 203: Время в пути налегке — Учащиеся определяют время, за которое свет достигает различных объектов в космосе.[Оценка: 6-8 | Темы: Научная нотация; Умножение; время = расстояние / скорость.] [Нажмите здесь]

Задача 164: Уравнения с одной переменной- Учащиеся работают с уравнениями типа «4,3 = 3,26D», чтобы решить для D ряд простых астрономических задач, связанных с преобразованием расстояний, скорости и температуры. [Оценка: 6-8 | Темы: уравнения с одной переменной; умножение; разделение; десятичные дроби] [Нажмите здесь]

Задача 61 Уравнение Дрейка и поиски жизни…вроде, как бы, что-то вроде! — Еще в 1960-х годах астроном Фрэнк Дрейк изобрел уравнение это помогает нам оценить, сколько жизни, особенно разумной, может существовать в нашем Млечном Пути. Оно имеет была живой темой обсуждения на тысячах астрономических курсов в колледжах за последние 60 лет. В этой упрощенной версии ваши ученики получат возможность повторить то, что мы теперь знаем о планетарной вселенной, и придумают свои собственные оценки. Самое интересное — это провести исследование, чтобы отследить правдоподобные значения (или их диапазоны) для факторов, которые войдите в уравнение, а затем напишите защиту для значений, которые они выбирают.Много возможностей обобщить базовые астрономические знания для конец курса или главы астрономии. [Уровень: 6-8 | Темы: десятичная математика; оценка функций для заданных значений переменных] [Щелкните здесь]

Тарифы и склоны

Задача 671: VAB — Зонды Ван Аллена и доза излучения Студенты изучают единицы доз облучения и оценивают облучение человека, живущего на земле; астронавт на МКС и в поясе Ван Аллена.[Оценка: 8-10 | Темы: Преобразование единиц измерения; тарифы] [Нажмите здесь]

Задача 227: Работа с тарифами — Студенты изучают смешанные ставки для различных ситуаций и их связи с соотношениями. [Оценка: 6-8 | Темы: Коэффициенты; научная нотация; преобразование единиц измерения.] [Щелкните здесь]

Задача 226: Скорости и наклоны: астрономическая перспектива- Учащиеся определяют наклон двух линейных графиков и связывают их со смешанными единицами измерения.[Оценка: 7-9 | Темы: Определение наклона линейного графика.] [Щелкните здесь]

Задача 65 Перспектива дозировок радиации — В зависимости от того, какую карьеру вы выбрали, вы испытаете разные прижизненные дозы облучения. В этой задаче сравниваются совокупные дозировки для человека, живущего на Земле, космонавта. карьера, связанная с путешествием на космическую станцию и пожизненной дозой человека, путешествующего на Марс и обратно.[Уровень: 6-8 | Темы: десятичные дроби, преобразование единиц измерения, построение временной шкалы, поиск областей под кривыми с помощью прямоугольников] [Щелкните здесь]

Задача 134 Последнее полное солнечное затмение — когда-либо! Студенты изучают геометрию, необходимую для полное солнечное затмение и оцените, на сколько лет в будущем произойдет последнее полное солнечное затмение. затмение произойдет, когда Луна будет медленно удаляться от Земли на три сантиметра в год. [Класс: 7–10 | Темы: Простые линейные уравнения] [Щелкните здесь]

Интерпретация и работа с графиками

Задача 225: Области под кривыми; Астрономическая перспектива- Студенты работают с гистограммой количества открытий экзопланет с 1995 года, чтобы оценить общее количество открытий. открытия в виде областей под графиком для различных комбинаций периодов времени.[Оценка: 6-8 | Темы: Добавление областей в гистограммы.] [Щелкните здесь]

Задача 100 Цикл солнечных пятен — окончание и начало — Студенты изучат график цикла солнечных пятен и извлекут информацию из нанесенных на график данных о предыдущий цикл солнечных пятен, и сделать прогнозы относительно следующего цикла, который начнется в 2007 году. [Уровень: 6-9 | Темы: чтение графиков; экстраполяция; расчет времени] [Нажмите здесь]

Задача 54 Изучение далеких галактик — Астрономы определяют красные смещения далеких галактик, используя спектры и измеряя сдвиги длин волн для знакомых атомные линии.Чем больше красное смещение, обозначенное буквой Z, тем дальше галактика. В этом упражнении учащиеся будут использовать реальное изображение далекого уголка Вселенной с красными смещениями. идентифицированных галактик. После гистограммы распределения красного смещения они будут использовать онлайн-калькулятор космологии для определения времени «оглядки назад» для галактик и найдите самую древнюю галактику в этой области. Могут ли студенты найти только сформированную галактику? 500 миллионов лет после Большого взрыва? [Уровень обучения: 9-11 | Темы: Десятичная математика; с помощью онлайн-калькулятора; Данные гистограммы] [Нажмите здесь]

Задача 1 Магнитные бури I Студенты узнают о магнитных бурях, используя реальные данные в виде линейного графика.Они отвечают на простые вопросы о данных диапазон, максимум и минимум. [Класс: 7 — 9 | Темы: интерпретация графика; расчет времени] [Нажмите здесь]

Задача 36 Распад орбиты космической станции и космос Погода Студенты узнают о продолжающийся распад орбиты Международной космической станции из-за изучение графика зависимости высоты станции от времени. Они будут рассчитать скорость затухания орбиты и выяснить, почему это может быть происходит.[Класс: 5 — 8 | Темы: интерпретация графических данных; десятичная математика] [Нажмите здесь]

Пропорции и весы

Задача 261: LRO — Поиск лунных валунов Студенты используют недавнее изображение места посадки Аполлона-11 для поиска больших лунных валунов. [Оценка: 6-8 | Темы: масштаб, соотношение, пропорции] [Щелкните здесь]

Задача 57 Астероиды, кометы и метеоры — о боже! — Астрономы определили орбиты более 30 000 малых планет в Солнечной системе, и каждый год открываются сотни новых.Работа с картой локаций этих тел в пределах орбиты Марса студенты рассчитают масштаб карты и ответят на вопросы о расстояниях между этими объектами и количестве пересекающих земную орбиту. Отличный, практический знакомство с астероидами внутренней солнечной системы! Также имеются ссылки на онлайн-базы данных для дальнейших запросов. при условии. [Уровень оценки: 4-6 | Темы: Масштабная модель; Десятичная математика; Интерпретация двухмерного графика] [Нажмите здесь]

Задача 49 Спиральная галактика крупным планом.- Астрономы могут многому научиться, изучая фотографии галактик. В в этом упражнении учащиеся вычисляют масштаб изображения (световых лет на миллиметр) в сфотографируйте ближайшую спиральную галактику и исследуйте размеры деталей, обнаруженных на изображении. Они будет также использовать Интернет или другие ресурсы, чтобы заполнить недостающую справочную информацию об этой галактике. [Уровень: 6-8 | Темы: Интернет-исследования; Определение масштаба изображения; метрическое измерение; десятичная математика] [Нажмите здесь]

Скорость и расстояние

Задача 102 Как быстро вращается солнце? Студенты проанализируют последовательные изображения, сделанные спутником Hinode, чтобы определить скорость вращения Солнца и приблизительную продолжительность его «дня».[Оценка: 6-9 | Темы: масштабирование изображения; расчет времени; расчет скорости, преобразование единиц] [Нажмите здесь]

Задача 101 Сверхбыстрые солнечные вспышки !! — Учащиеся проанализируют последовательные изображения извергающейся солнечной вспышки и будут использовать информация предоставлена для расчета скорости факела. [Уровень: 6-9 | Темы: масштабирование изображения; расчет времени; расчет скорости] [Нажмите здесь]

Задача 80 Повреждение данных частицами высокой энергии — Студенты увидят, как солнечные вспышки могут испортить спутниковые данные, и создать временную шкалу для впечатляющего эпизода потери данных, записанного спутником SOHO, используя изображения, полученные со спутника.Студенты также рассчитают скорость события, когда частицы выбрасываются из Солнца и летят к Земле. [Уровень: 6-8 | Темы: Расчет времени и скорости; интерпретация научных данных] [Нажмите здесь]

Задача 43 Межпланетная ударная волна 8 ноября 2000 года Солнце выпустило корональный выброс массы, который отправился на Землю, и его эффекты были обнаружен на Юпитере и Сатурне несколько недель спустя.В этой задаче учащиеся будут использовать данные об этом шторме, чтобы отследить его скорость и ускорение, когда он пересек Солнечная система. [Уровень оценки: 6-10 | Темы: Расчет времени; расстояние = скорость x время] [Нажмите здесь]

Задача 53 Астрономия: захватывающий опыт! — Объекты в космосе движутся. Чтобы выяснить, как быстро они двигаются, астрономы используют множество различных методов в зависимости от того, что они исследуют. В этом упражнении вы будете измерять скорость астрономических явлений с помощью масштабирования. подсказки и временные интервалы между фотографиями трех явлений: сверхновой взрыв, корональный выброс массы и ударная волна солнечной вспышки.[Уровень: 6-8 | Темы: Определение масштаба изображения; метрическое измерение; расстояние = скорость x время; научная нотация] [Щелкните здесь]

Геометрия

Задача 41 Солнечная энергия в космосе Студенты рассчитают площадь поверхности спутника. используется для солнечных батарей из реальной фотографии спутника IMAGE. Они рассчитают электрическую мощность, обеспечиваемую этой панелью. Студенты Придется вычислить площадь неправильной области, используя вложенные прямоугольники.[Уровень оценки: 7-10 | Темы: Площадь неправильного многоугольника; десятичная математика] [Нажмите здесь]

Задача 247: Космическая мобильная головоломка Учащиеся вычисляют недостающие массы и длину в мобильном телефоне, используя основное уравнение баланса m1 x r1 = m2 x r2 для мобильного устройства солнечной системы. [Оценка: 6-8 | Темы: метрическая мера, алгебра 1, геометрия] [Нажмите здесь]

Задача 245: Твердотопливные ракетные ускорители Студенты узнают, как SRB на самом деле создают тягу, и изучают ускоритель Ares-V, чтобы оценить его тягу.[Оценка: 6-8 | Темы: объем, площадь, преобразование единиц] [Нажмите здесь]

Анализ данных и вероятность

Задача 262: LRO исследует кратер на поверхности Луны Студенты подсчитывают количество кратеров в различных диапазонах размеров по изображению лунной поверхности с высоким разрешением. [Оценка: 6-8 | Темы: масштаб, пропорция, соотношение, площадь, плотность] [Щелкните здесь]

Задача 253: НАСА «видит» углекислый газ Спутниковый снимок атмосферного углекислого газа используется для оценки географических различий и идентификации человеческой деятельности.[Оценка: 6-8 | Темы: интерпретация изображения данных, преобразование единиц измерения, гигатонны] [Щелкните здесь]

Задача 252: Углекислый газ увеличивает Студенты изучают кривую Килинга, чтобы определить скорость увеличения содержания углекислого газа в атмосфере. [Оценка: 6-8 | Темы: анализ графиков, наклон, коэффициенты, преобразование единиц, доли на миллион, гигатонны] [Щелкните здесь]

Задача 211: Куда делись все звезды? — Студенты узнают, почему на фотографиях НАСА часто не видны звезды из-за того, как камеры снимают яркие и тусклые объекты.[Оценка: 6-8 | Темы: умножение; разделение; десятичные числа.] [Щелкните здесь]

Задача 194: Магнитный аргумент в пользу «Что было первым?» — Учащиеся создают временную шкалу для событий на основе нескольких графиков данных из программы THEMIS и используют ее, чтобы ответить на вопросы о причинах магнитных бурь. [Оценка: 6-8 | Темы: Расчет времени] [Щелкните здесь]

Задача 185: Международная космическая станция: следуйте этому графику! — Учащиеся используют график высоты орбиты МКС, чтобы предсказать год ее возвращения в атмосферу после пика следующего цикла солнечной активности.[Оценка: 6-8 | Темы: экстраполяция простого графика; оценка; прогнозирование] [Нажмите здесь]

Задача 152: Закон Хаббла — Учащиеся наносят на график скорость и расстояние до 7 галактик и, вычисляя наклон линейной модели для точек данных, получают оценку расширения. скорость Вселенной, известная как Постоянная Хаббла. [Оценка: 6-8 | Темы: Построение данных; определение наклона данных;] [Щелкните здесь]

Задача 120 Закон Бенфорда Студенты исследуют соотношение, называемое законом Бенфорда, которое описывает частоту целых чисел 1–9 в различных данных.Этот закон используется IRS для выявления мошеннических налоговых деклараций, но также применяется к астрономическим данным и другим неожиданным ситуациям. [Оценка: 8-10 | Темы: Расчет частотных таблиц; Гистограмма; Статистика] [Нажмите здесь]

Задача 95 Исследование доз облучения космонавтов в космосе — Студенты изучат график доз облучения космонавтов для полетов космических шаттлов и оценят общие дозировки для космонавтов, работающих на Международной космической станции.[Уровень обучения: 9-11 | Темы: анализ графиков, интерполяция, преобразование единиц измерения] [Щелкните здесь]

Задача 94 Солнечные бури: шансы, доли и проценты — Студенты будут использовать фактические данные о солнечных бурях, чтобы учиться. о разные виды штормов и насколько они распространены. Это фундаментальная научная деятельность, которая профессионалы занимаются поиском взаимосвязей между разными видами событий которые могут приводят к разгадке того, что их вызывает.Могут ли ваши ученики придумать что-то новое, что никто не думал раньше? Упражнение по построению диаграмм Венна — ключевой элемент занятия, и оно достаточно сложное! [Уровень: 6-8 | Темы: усреднение; фракции; проценты; шансы; Арифметические операции; Диаграммы Венна] [Щелкните здесь]

Задача 90 Карьера в астрономии — В этой задаче рассматриваются некоторые статистические данные о работе в такой области, как астрономия.Студенты прочитают графики и ответят на вопросы о количество астрономов в этой области работы и скорость увеличения численности населения и количество ученых степеней. [Уровень: 6-8 | Темы: чтение графиков; проценты; интерполяция] [Нажмите здесь]

Проблема 86 Производят ли быстрые CME SPE? — Недавние данные о солнечных протонных бурях (SPE) и корональных выбросах массы (CME) сравниваются с использованием диаграмм Венна. чтобы увидеть, делает ли скорость CME солнечные протонные бури более вероятными или нет.[Уровень оценки: 5-8 | Темы: Диаграммы Венна; подсчет; расчет процентов и шансов] [Нажмите здесь]

Задача 85 Солнечное цунами! — Используются последние данные со спутника Hinode. для измерения скорости солнечного взрыва на поверхности Солнца с помощью серия изображений, сделанных спутником в три разных момента времени. Учащиеся вычисляют скорость взрыва между первой парой и последней парой изображений и определяют, взрывная волна ускорялась или замедлялась во времени.[Уровень оценки: 5-8 | Темы: Определение масштаба изображения; расчет разницы во времени; вычисление скорости по расстоянию и времени] [Нажмите здесь]

Задача 70 Расчет общих доз радиации на Марсе — Эта задача использует данные Марсианского эксперимента по радиационной среде (MARIE), который вращается вокруг Марса, и измеряет суточную дозу радиации. что космонавт испытает на орбите вокруг Марса. Учащиеся будут использовать фактические графические данные для расчета общей дозировки путем сложения площадей под кривой данных.Этот требует знания площади прямоугольника и понимания того факта, что произведение нормы (бэр в день) на продолжительность времени (дни) дает общую дозу (Rems), так же как произведение скорости на время дает расстояние. Оба представляют собой области под соответствующими кривыми. Учащиеся рассчитают дозы космического излучения и вспышек солнечных протонов и решат, какой компонент вызывает наиболее серьезные радиационные проблемы. [Уровень: 6-8 | Темы: десятичные дроби, площадь прямоугольника, анализ графиков] [Нажмите здесь]

Задача 32 Солнечные протонные события и спутник Повреждение Студенты изучат статистика солнечных протонных событий с 1996 года и оценка их ущерба для спутниковые солнечные энергетические системы.[Класс: 7 — 9 | Темы: Интерпретация табличных данных; гистограмма] [Нажмите здесь]

Задача 28 Спутниковая энергия и космические лучи Большинство спутников работают на солнечных батареях. генерировать электричество. Но после многих лет на орбите эти солнечные элементы производят меньше электричества из-за постоянного воздействия космических лучей. В этом активности, студенты читают график, на котором показано электричество, производимое солнечных панелей спутника и получите ценный урок о том, как проектировать спутники для длительной работы в космосе.Основные математические идеи: Площадь расчет, преобразование единиц измерения, экстраполяция и интерполяция графика тенденции. [Класс: 6 — 8 | Темы: интерпретация графических данных; десятичная математика] [Нажмите здесь]

Задача 27 Неисправности спутников и солнечное пятно Цикл Более 1500 рабочих спутники на орбите Земли, представляющие собой инвестиции в размере 160 миллиардов долларов. Ежегодно от 10 до 30 из них возвращаются в атмосферу.В этой задаче учащиеся сравнивают цикл солнечных пятен с записью спутники повторно входят в атмосферу и определяют, есть ли корреляция. Они также исследуют, как широко распространенные спутниковые технологии стать в их повседневной жизни. [Класс: 6 — 8 | Темы: Графические табличные данные; десятичная математика] [Нажмите здесь]

Задача 9 Аврора Сила! Студенты используют данные для оценки силы полярного сияния и сравнивают ее с общие вещи, такие как потребление электроэнергии в доме, городе и страна.[Оценка: 5–7 | Темы: Интерпретация табличных данных] [Щелкните здесь]

Задача 7 Солнечные вспышки, CME и полярное сияние Некоторые статьи о северном сиянии подразумевают, что их вызывают солнечные вспышки. Студенты будут использовать данные для построения простого Венна. Диаграмма и ответ на важный вопрос о том, вызывают ли солнечные вспышки CME и Аврора. [Оценка: 5–7 | Темы: Диаграмма Венна] [Щелкните здесь]

Решение проблем

Проблема 377: Глубокое столкновение: приближается комета Хартли-2
Учащиеся используют данные яркости кометы Хартли-2, измеренные космическим аппаратом Deep Impact, чтобы составить линейное уравнение для расстояния до нее. и воспользуемся законом обратных квадратов, чтобы оценить его яркость 13 октября 2010 г.[Оценка: 8-10 | Темы: линейное моделирование по данным; закон обратных квадратов] [Кликните сюда]

Задача 238: Спутник и космический телескоп Хаббла Спутники увлекаются атмосферой, что в конечном итоге приводит к их сгоранию в атмосфере. Студенты учатся различные прогнозы высоты космического телескопа Хаббла, чтобы оценить год его возвращения в атмосферу. [Оценка: 6-8 | Темы: интерпретация графических данных; прогнозирование тенденций] [Нажмите здесь]

Задача 124 Атмосфера Луны! Студенты узнают об очень тонкой атмосфере Луны, вычисляя ее общую массу в килограммах, используя объем сферической оболочки и измеренную плотность. [Оценка: 8-10 | Темы: объем шара, оболочки; плотность-масса-объем; преобразование единиц] [Нажмите здесь]

Задача 83 Риски падения метеорита на Лунер — В 2006 году ученые идентифицировали 12 вспышек света на Луне, которые, вероятно, были падением метеорита. По их оценкам, эти метеориты, вероятно, были размером с грейпфрут. Как долго лунные колонисты должны будут ждать, прежде чем увидят такую вспышку на своем горизонте? Студенты будет использовать вычисление площади и вероятности для определения среднего времени ожидания.[Уровень оценки: 8-10 | Темы: арифметика; преобразование единиц измерения; площадь поверхности сферы] [Нажмите здесь]

Задача 74 Жаркое время на Марсе — Эксперимент NASA Mars Radiation Environment (MARIE) создал карту поверхности Марса и измерил радиационный фон на уровне земли, которому будут подвергаться астронавты. Эта математическая задача позволяет студентам изучить общую дозу радиации, которую эти исследователи получат в серии 1000-километровых путешествий по марсианскому региону. поверхность.Студенты будут сравнивать эту дозу с типичными фоновыми условиями на Земле и на Международной космической станции, чтобы получить представление о перспективе. [Уровень: 6-8 | Темы: десятичные дроби, преобразование единиц измерения, построение графиков и анализ] [Нажмите здесь]

Задача 71 Действительно ли пояса Ван Аллена смертельно опасны? — В этой задаче исследуются дозы радиации, которые космонавты получат во время путешествия. через пояс Ван Аллена по пути к Луне.Учащиеся будут использовать данные, чтобы рассчитать продолжительность поездки через ремни и общую полученную дозу, и сравнить это со смертельной дозой с противостоять заблуждению о том, что астронавты «Аполлона» мгновенно погибли бы во время полета на Луну. [Уровень оценки: 8-10 | Темы: десятичные дроби, площадь прямоугольника, анализ графиков] [Нажмите здесь]

Задача 68 Введение в космическое излучение — Прочтите о дозах естественного фонового излучения, узнайте о Ремс и Рад, а также разница между дозировками низкого и высокого уровня.Студенты используют основные математические операции для расчета общих дозировок на основе дозировки и расчета риска рака. [Уровень: 6-8 | Темы: Чтение для получения информации; десятичные дроби, дроби, квадратные корни] [Нажмите здесь]

Задача 66 Фоновое излучение и образ жизни — Живя на Земле, вы будете подвергаться воздействию множества различных излучений. среды. Эта задача следует за одним человеком через четыре различных возможных варианта будущего и сравнивает кумулятивные дозировки за всю жизнь.[Уровень: 6-8 | Темы: дроби, десятичные дроби, преобразование единиц] [Нажмите здесь]

% PDF-1.4 % 1483 0 объект > эндобдж xref 1483 1240 0000000016 00000 н. 0000025157 00000 п. 0000025256 00000 п. 0000028993 00000 п. 0000029246 00000 п. 0000038887 00000 п. 0000038930 00000 н. 0000038954 00000 п. 0000047369 00000 п. 0000047393 00000 п. 0000056772 00000 п. 0000056796 00000 п. 0000066187 00000 п. 0000066211 00000 п. 0000075996 00000 п. 0000076020 00000 н. 0000085774 00000 п. 0000085798 00000 п. 0000085995 00000 п. 0000086192 00000 п. 0000086434 00000 п. 0000086681 00000 п. 0000087711 00000 п. 0000087902 00000 п. 0000088971 00000 п. 0000089221 00000 п. 0000089464 00000 п. 00000 00000 п. 00000

00000 п. 00000

00000 п. 00000 00000 н. 0000093088 00000 п. 0000093280 00000 п. 0000102671 00000 п. 0000102696 00000 н. 0000113193 00000 н. 0000113217 00000 н. 0000113240 00000 н. 0000121260 00000 н. 0000121284 00000 н. 0000121307 00000 н. 0000121331 00000 н. 0000121355 00000 н. 0000121378 00000 н. 0000121401 00000 н. 0000129819 00000 п. 0000129843 00000 н. 0000137304 00000 н. 0000137329 00000 н. 0000147543 00000 н. 0000147568 00000 н. 0000148391 00000 н. 0000148414 00000 н. 0000161032 00000 н. 0000161055 00000 н. 0000161078 00000 н. 0000161102 00000 н. 0000161125 00000 н. 0000161149 00000 н. 0000161173 00000 н. 0000161197 00000 н. 0000161222 00000 н. 0000170318 00000 н. 0000170341 00000 п. 0000170993 00000 п. 0000171016 00000 н. 0000171675 00000 н. 0000171697 00000 н. 0000171907 00000 н. 0000171929 00000 н. 0000172162 00000 н. 0000172184 00000 н. 0000172417 00000 н. 0000172440 00000 н. 0000173215 00000 н. 0000173239 00000 н. 0000174503 00000 н. 0000174525 00000 н. 0000174758 00000 н. 0000174780 00000 н. 0000175013 00000 н. 0000175035 00000 н. 0000175268 00000 н. 0000175290 00000 н. 0000175523 00000 н. 0000175546 00000 н. 0000176255 00000 н. 0000176277 00000 н. 0000176510 00000 н. 0000176532 00000 н. 0000176765 00000 н. 0000176788 00000 н. 0000177138 00000 н. 0000177160 00000 н. 0000177393 00000 н. 0000177416 00000 н. 0000178485 00000 н. 0000178507 00000 н. 0000178740 00000 н. 0000178762 00000 н. 0000178995 00000 н. 0000179017 00000 н. 0000179250 00000 н. 0000179272 00000 н. 0000179524 00000 н. 0000179548 00000 н. 0000180749 00000 н. 0000180772 00000 н. 0000181329 00000 н. 0000181353 00000 н. 0000183007 00000 н. 0000183029 00000 н. 0000183262 00000 н. 0000183284 00000 н. 0000183517 00000 н. 0000183539 00000 н. 0000183772 00000 н. 0000183795 00000 н. 0000184427 00000 н. 0000184449 00000 н. 0000184656 00000 н. 0000184680 00000 н. 0000185876 00000 н. 0000185898 00000 н. 0000186125 00000 н. 0000186149 00000 н. 0000187481 00000 н. 0000187503 00000 н. 0000187736 00000 н. 0000187758 00000 н. 0000187962 00000 н. 0000187985 00000 н. 0000189058 00000 н. 0000189080 00000 н. 0000189344 00000 н. 0000189366 00000 п. 0000189573 00000 н. 0000189597 00000 н. 00001 00000 н. 00001

00000 н. 0000192599 00000 н. 0000192623 00000 н. 0000193842 00000 н. 0000193866 00000 н. 0000195100 00000 н. 0000195123 00000 н. 0000195528 00000 н. 0000195551 00000 н. 0000196117 00000 н. 0000196139 00000 н. 0000196372 00000 н. 0000196394 00000 н. 0000196627 00000 н. 0000196649 00000 н. 0000196842 00000 н. 0000196864 00000 н. 0000197097 00000 н. 0000197119 00000 н. 0000197352 00000 н. 0000197374 00000 н. 0000197563 00000 н. 0000197585 00000 н. 0000197774 00000 н. 0000197797 00000 н. 0000198453 00000 н. 0000198477 00000 н. 0000199940 00000 н. 0000199964 00000 н. 0000201420 00000 н. 0000201443 00000 н. 0000201725 00000 н. 0000201749 00000 н. 0000202973 00000 н. 0000202995 00000 н. 0000203184 00000 н. 0000203206 00000 н. 0000203439 00000 н. 0000203461 00000 н. 0000203709 00000 н. 0000203732 00000 н. 0000204340 00000 н. 0000204362 00000 н. 0000204595 00000 н. 0000204617 00000 н. 0000204850 00000 н. 0000204872 00000 н. 0000205122 00000 н. 0000205146 00000 н. 0000206571 00000 н. 0000206593 00000 н. 0000206826 00000 н. 0000206849 00000 н. 0000207610 00000 н. 0000207632 00000 н. 0000207865 00000 н. 0000207889 00000 н. 0000209130 00000 н. 0000209153 00000 н. 0000210319 00000 п. 0000210341 00000 п. 0000210574 00000 п. 0000210597 00000 н. 0000211622 00000 н. 0000211646 00000 н. 0000212838 00000 н. 0000212860 00000 н. 0000213093 00000 н. 0000213116 00000 н. 0000214053 00000 н. 0000214075 00000 н. 0000214308 00000 н. 0000214330 00000 н. 0000214563 00000 н. 0000214585 00000 н. 0000214786 00000 н. 0000214808 00000 н. 0000215041 00000 н. 0000215064 00000 н. 0000215360 00000 н. 0000215382 00000 н. 0000215615 00000 н. 0000215639 00000 н. 0000217164 00000 н. 0000217188 00000 н. 0000218807 00000 н. 0000218831 00000 н. 0000220411 00000 н. 0000220435 00000 н. 0000221742 00000 н. 0000221765 00000 н. 0000222497 00000 н. 0000222521 00000 н. 0000224182 00000 п. 0000224204 00000 н. 0000224397 00000 н. 0000224421 00000 н. 0000225618 00000 н. 0000225641 00000 н. 0000226058 00000 н. 0000226080 00000 н. 0000226313 00000 н. 0000226335 00000 н. 0000226568 00000 н. 0000226592 00000 н. 0000227776 00000 н. 0000227799 00000 н. 0000228968 00000 н. 0000228991 00000 н. 0000230011 00000 н. 0000230035 00000 н. 0000231234 00000 н. 0000231257 00000 н. 0000232100 00000 н. 0000232122 00000 н. 0000232355 00000 н. 0000232378 00000 н. 0000233371 00000 п. 0000233393 00000 н. 0000233626 00000 н. 0000233649 00000 н. 0000234522 00000 н. 0000234546 00000 н. 0000235869 00000 н. 0000235891 00000 н. 0000236124 00000 н. 0000236148 00000 н. 0000237344 00000 н. 0000237366 00000 н. 0000237632 00000 н. 0000237654 00000 н. 0000237887 00000 н. 0000237909 00000 н. 0000238142 00000 н. 0000238166 00000 н. 0000239498 00000 н. 0000239521 00000 н. 0000240670 00000 н. 0000240692 00000 п. 0000240925 00000 н. 0000240947 00000 н. 0000241180 00000 н. 0000241202 00000 н. 0000241445 00000 н. 0000241468 00000 н. 0000242623 00000 н. 0000242647 00000 н. 0000243958 00000 н. 0000243980 00000 н. 0000244213 00000 н. 0000244236 00000 н. 0000244938 00000 н. 0000244961 00000 н. 0000245366 00000 н. 0000245388 00000 п. 0000245621 00000 н. 0000245643 00000 н. 0000245876 00000 н. 0000245899 00000 н. 0000246838 00000 н. 0000246860 00000 н. 0000247093 00000 н. 0000247115 00000 н. 0000247304 00000 н. 0000247328 00000 н. 0000249051 00000 н. 0000249074 00000 н. 0000249512 00000 н. 0000249534 00000 н. 0000249761 00000 н. 0000249785 00000 н. 0000251493 00000 н. 0000251516 00000 н. 0000252153 00000 н. 0000252175 00000 н. 0000252408 00000 н. 0000252431 00000 н. 0000253322 00000 н. 0000253346 00000 н. 0000255070 00000 н. 0000255092 00000 н. 0000255279 00000 н. 0000255302 00000 н. 0000255719 00000 н. 0000255742 00000 н. 0000256088 00000 н. 0000256110 00000 н. 0000256337 00000 н. 0000256361 00000 н. 0000257783 00000 н. 0000257806 00000 н. 0000258804 00000 н. 0000258828 00000 н. 0000260502 00000 н. 0000260524 00000 н. 0000260757 00000 н. 0000260781 00000 н. 0000262268 00000 н. 0000262290 00000 н. 0000262523 00000 н. 0000262546 00000 н. 0000263711 00000 н. 0000263735 00000 н. 0000264976 00000 н. 0000264998 00000 н. 0000265231 00000 п. 0000265254 00000 н. 0000266139 00000 н. 0000266162 00000 н. 0000267074 00000 н. 0000267096 00000 н. 0000267329 00000 н. 0000267351 00000 п. 0000267565 00000 н. 0000267587 00000 н. 0000267820 00000 н. 0000267842 00000 н. 0000268046 00000 н. 0000268068 00000 н. 0000268275 00000 н. 0000268297 00000 н. 0000268556 00000 н. 0000268579 00000 н. 0000269226 00000 н. 0000269248 00000 н. 0000269460 00000 н. 0000269482 00000 н. 0000269715 00000 н. 0000269737 00000 н. 0000269945 00000 н. 0000269969 00000 н. 0000271326 00000 н. 0000271349 00000 н. 0000272021 00000 н. 0000272044 00000 н. 0000272709 00000 н. 0000272732 00000 н. 0000273897 00000 н. 0000273921 00000 н. 0000275505 00000 н. 0000275528 00000 н. 0000276562 00000 н. 0000276585 00000 н. 0000277545 00000 н. 0000277569 00000 н. 0000279241 00000 н. 0000279265 00000 н. 0000280474 00000 н. 0000280497 00000 н. 0000281160 00000 н. 0000281182 00000 п. 0000281371 00000 н. 0000281394 00000 н. 0000282145 00000 н. 0000282167 00000 н. 0000282400 00000 н. 0000282423 00000 н. 0000282700 00000 н. 0000282722 00000 н. 0000282955 00000 н. 0000282979 00000 п. 0000284274 00000 н. 0000284296 00000 н. 0000284529 00000 н. 0000284551 00000 н. 0000284784 00000 н. 0000284807 00000 н. 0000285854 00000 п. 0000285876 00000 н. 0000286109 00000 н. 0000286131 00000 п. 0000286364 00000 н. 0000286386 00000 п. 0000286642 00000 н. 0000286664 00000 н. 0000286897 00000 н. 0000286919 00000 п. 0000287152 00000 н. 0000287175 00000 н. 0000287914 00000 п. 0000287938 00000 п. 0000289749 00000 н. 0000289773 00000 н. 00002

00000 н. 00002

00000 н. 00002 00000 н. 00002 00000 н. 0000292352 00000 п. 0000292376 00000 н. 0000293659 00000 н. 0000293682 00000 н. 0000294784 00000 н. 0000294806 00000 н. 0000295039 00000 н. 0000295062 00000 н. 0000295630 00000 н. 0000295652 00000 н. 0000295885 00000 н. 0000295908 00000 н. 0000296662 00000 н. 0000296685 00000 н. 0000297659 00000 н. 0000297683 00000 н. 0000299049 00000 н. 0000299073 00000 н. 0000300440 00000 п. 0000300463 00000 п. 0000300958 00000 п. 0000300982 00000 п. 0000302522 00000 н. 0000302545 00000 н. 0000303316 00000 н. 0000303339 00000 н. 0000304447 00000 н. 0000304471 00000 н. 0000305750 00000 н. 0000305772 00000 н. 0000306005 00000 н. 0000306027 00000 н. 0000306260 00000 н. 0000306283 00000 н. 0000307386 00000 п. 0000307410 00000 п. 0000309039 00000 н. 0000309063 00000 н. 0000310302 00000 п. 0000310324 00000 н. 0000310557 00000 н. 0000310579 00000 н. 0000310812 00000 н. 0000310834 00000 п. 0000311023 00000 н. 0000311045 00000 н. 0000311278 00000 н. 0000311300 00000 н. 0000311533 00000 н. 0000311555 00000 н. 0000311788 00000 н. 0000311810 00000 н. 0000312025 00000 н. 0000312048 00000 н. 0000312531 00000 н. 0000312553 00000 н. 0000312786 00000 н. 0000312809 00000 н. 0000313929 00000 н. 0000313952 00000 н. 0000314266 00000 н. 0000314288 00000 н. 0000314521 00000 н. 0000314544 00000 н. 0000315560 00000 н. 0000315582 00000 н. 0000315815 00000 н. 0000315837 00000 н. 0000316070 00000 н. 0000316094 00000 н. 0000317645 00000 н. 0000317667 00000 н. 0000317900 00000 н. 0000317922 00000 н. 0000318115 00000 н. 0000318137 00000 н. 0000318326 00000 н. 0000318348 00000 п. 0000318581 00000 н. 0000318605 00000 н. 0000320145 00000 н. 0000320167 00000 н. 0000320400 00000 н. 0000320422 00000 н. 0000320655 00000 н. 0000320678 00000 н. 0000321730 00000 н. 0000321754 00000 н. 0000322963 00000 н. 0000322986 00000 н. 0000324027 00000 н. 0000324049 00000 н. 0000324242 00000 н. 0000324266 00000 н. 0000325531 00000 н. 0000325553 00000 н. 0000325746 00000 н. 0000325768 00000 н. 0000326001 00000 н. 0000326025 00000 н. 0000327542 00000 н. 0000327565 00000 н. 0000328333 00000 н. 0000328355 00000 н. 0000328544 00000 н. 0000328566 00000 н. 0000328799 00000 н. 0000328821 00000 н. 0000329028 00000 н. 0000329051 00000 н. 0000330111 00000 п. 0000330134 00000 п. 0000331025 00000 н. 0000331048 00000 н. 0000331346 00000 н. 0000331368 00000 н. 0000331601 00000 н. 0000331623 00000 н. 0000331856 00000 н. 0000331880 00000 н. 0000333518 00000 н. 0000333541 00000 н. 0000334409 00000 н. 0000334431 00000 н. 0000334620 00000 н. 0000334643 00000 п. 0000334956 00000 н. 0000334979 00000 н. 0000335581 00000 н. 0000335603 00000 н. 0000335792 00000 н. 0000335816 00000 н. 0000337143 00000 н. 0000337167 00000 н. 0000338481 00000 н. 0000338503 00000 н. 0000338736 00000 н. 0000338759 00000 н. 0000339041 00000 н. 0000339064 00000 н. 0000339906 00000 н. 0000339928 00000 н. 0000340161 00000 н. 0000340185 00000 н. 0000341739 00000 н. 0000341761 00000 н. 0000341950 00000 н. 0000341973 00000 н. 0000342428 00000 н. 0000342450 00000 н. 0000342683 00000 п. 0000342707 00000 н. 0000344011 00000 н. 0000344035 00000 н. 0000345472 00000 н. 0000345496 00000 п. 0000347223 00000 п. 0000347245 00000 н. 0000347478 00000 н. 0000347500 00000 н. 0000347733 00000 п. 0000347756 00000 н. 0000348880 00000 н. 0000348903 00000 н. 0000349891 00000 н. 0000349914 00000 н. 0000350546 00000 н. 0000350568 00000 н. 0000350801 00000 н. 0000350824 00000 н. 0000351185 00000 н. 0000351209 00000 н. 0000352494 00000 н. 0000352517 00000 н. 0000353535 00000 н. 0000353559 00000 н. 0000354785 00000 н. 0000354807 00000 н. 0000355045 00000 н. 0000355067 00000 н. 0000355300 00000 н. 0000355322 00000 н. 0000355555 00000 н. 0000355577 00000 н. 0000355810 00000 н. 0000355832 00000 н. 0000356065 00000 н. 0000356087 00000 н. 0000356320 00000 н. 0000356343 00000 п. 0000356703 00000 н. 0000356726 00000 н. 0000357729 00000 н. 0000357751 00000 н. 0000357958 00000 н. 0000357982 00000 н. 0000359320 00000 н. 0000359344 00000 п. 0000360556 00000 н. 0000360579 00000 н. 0000361464 00000 н. 0000361486 00000 н. 0000361719 00000 н. 0000361741 00000 н. 0000361974 00000 н. 0000361997 00000 н. 0000362290 00000 н. 0000362314 00000 н. 0000363865 00000 н. 0000363889 00000 н. 0000365446 00000 н. 0000365470 00000 н. 0000366787 00000 н. 0000366810 00000 н. 0000367686 00000 н. 0000367709 00000 н. 0000368005 00000 н. 0000368028 00000 н. 0000368748 00000 н. 0000368772 00000 н. 0000370052 00000 н. 0000370075 00000 н. 0000371004 00000 н. 0000371027 00000 н. 0000372028 00000 н. 0000372050 00000 н. 0000372243 00000 н. 0000372265 00000 н. 0000372498 00000 н. 0000372521 00000 н. 0000372864 00000 н. 0000372886 00000 н. 0000373119 00000 н. 0000373141 00000 н. 0000373346 00000 н. 0000373368 00000 н. 0000373601 00000 н. 0000373625 00000 н. 0000374947 00000 н. 0000374971 00000 н. 0000376239 00000 п. 0000376261 00000 н. 0000376465 00000 н. 0000376488 00000 н. 0000377507 00000 н. 0000377529 00000 н. 0000377762 00000 н. 0000377786 00000 н. 0000379228 00000 п. 0000379250 00000 н. 0000379483 00000 н. 0000379506 00000 н. 0000380267 00000 н. 0000380289 00000 н. 0000380522 00000 н. 0000380546 00000 н. 0000381775 00000 н. 0000381798 00000 н. 0000382282 00000 н. 0000382306 00000 н. 0000383669 00000 н. 0000383691 00000 н. 0000383918 00000 н. 0000383942 00000 н. 0000385143 00000 п. 0000385165 00000 н. 0000385398 00000 п. 0000385420 00000 н. 0000385653 00000 п. 0000385677 00000 н. 0000387057 00000 н. 0000387079 00000 п. 0000387312 00000 н. 0000387335 00000 п. 0000387679 00000 н. 0000387703 00000 н. 0000389155 00000 н. 0000389179 00000 н. 00003

00000 н. 00003

00000 н. 00003 00000 н. 00003

00000 н. 00003

00000 н. 00003 00000 н. 00003

00000 п. 0000392123 00000 н. 0000392356 00000 н. 0000392379 00000 п. 0000393221 00000 н. 0000393243 00000 н. 0000393476 00000 н. 0000393498 00000 н. 0000393731 00000 н. 0000393753 00000 н. 0000393986 00000 н. 0000394010 00000 н. 0000395607 00000 н. 0000395629 00000 н. 0000395862 00000 н. 0000395885 00000 н. 0000396977 00000 н. 0000397000 00000 н. 0000398042 00000 н. 0000398064 00000 н. 0000398297 00000 н. 0000398320 00000 н. 0000399475 00000 н. 0000399497 00000 н. 0000399724 00000 н. 0000399746 00000 н. 0000399979 00000 н. 0000400003 00000 п. 0000401239 00000 н. 0000401262 00000 н. 0000402300 00000 н. 0000402323 00000 н. 0000403433 00000 н. 0000403457 00000 н. 0000404641 00000 п. 0000404665 00000 н. 0000406231 00000 п. 0000406255 00000 н. 0000407888 00000 н. 0000407910 00000 п. 0000408143 00000 п. 0000408165 00000 н. 0000408398 00000 н. 0000408422 00000 н. 0000409860 00000 н. 0000409882 00000 н. 0000410122 00000 п. 0000410144 00000 п. 0000410377 00000 п. 0000410400 00000 п. 0000411409 00000 п. 0000411431 00000 н. 0000411664 00000 н. 0000411686 00000 н. 0000411919 00000 п. 0000411942 00000 н. 0000412401 00000 п. 0000412425 00000 н. 0000413790 00000 н. 0000413814 00000 н. 0000415085 00000 н. 0000415109 00000 н. 0000416617 00000 н. 0000416640 00000 н. 0000417414 00000 н. 0000417436 00000 н. 0000417691 00000 н. 0000417713 00000 н. 0000417946 00000 н. 0000417969 00000 н. 0000418665 00000 н. 0000418687 00000 н. 0000418920 00000 н. 0000418942 00000 н. 0000419187 00000 н. 0000419210 00000 п. 0000419709 00000 н. 0000419731 00000 н. 0000419964 00000 н. 0000419986 00000 п. 0000420219 00000 н. 0000420241 00000 н. 0000420474 00000 н. 0000420496 00000 н. 0000420703 00000 н. 0000420725 00000 н. 0000420958 00000 н. 0000420980 00000 н. 0000421213 00000 н. 0000421236 00000 н. 0000421859 00000 н. 0000421883 00000 н. 0000423153 00000 п. 0000423175 00000 п. 0000423431 00000 н. 0000423454 00000 н. 0000424591 00000 н. 0000424613 00000 н. 0000424846 00000 н. 0000424870 00000 н. 0000426165 00000 н. 0000426188 00000 п. 0000427166 00000 н. 0000427189 00000 н. 0000427836 00000 н. 0000427858 00000 н. 0000428047 00000 н. 0000428069 00000 н. 0000428296 00000 н. 0000428318 00000 н. 0000428551 00000 п. 0000428574 00000 н. 0000429695 00000 н. 0000429717 00000 н. 0000429950 00000 н. 0000429972 00000 н. 0000430205 00000 н. 0000430229 00000 н. 0000431605 00000 н. 0000431628 00000 н. 0000432782 00000 н. 0000432804 00000 н. 0000433037 00000 н. 0000433061 00000 н. 0000434256 00000 н. 0000434278 00000 н. 0000434547 00000 н. 0000434571 00000 п. 0000436149 00000 п. 0000436171 00000 п. 0000436404 00000 п. 0000436428 00000 н. 0000437620 00000 н. 0000437642 00000 п. 0000437896 00000 н. 0000437918 00000 п. 0000438151 00000 п. 0000438175 00000 п. 0000439389 00000 н. 0000439413 00000 н. 0000440661 00000 п. 0000440683 00000 п. 0000440876 00000 н. 0000440898 00000 н. 0000441131 00000 н. 0000441155 00000 н. 0000442752 00000 н. 0000442775 00000 н. 0000443146 00000 н. 0000443168 00000 п. 0000443401 00000 п. 0000443424 00000 н. 0000444160 00000 н. 0000444183 00000 н. 0000444789 00000 н. 0000444811 00000 н. 0000445044 00000 н. 0000445066 00000 н. 0000445299 00000 н. 0000445322 00000 н. 0000446345 00000 н. 0000446368 00000 н. 0000447333 00000 н. 0000447355 00000 н. 0000447588 00000 н. 0000447610 00000 н. 0000447839 00000 н. 0000447863 00000 н. 0000449115 00000 н. 0000449137 00000 н. 0000449370 00000 п. 0000449394 00000 н. 0000450889 00000 н. 0000450913 00000 н. 0000452471 00000 н. 0000452495 00000 н. 0000453969 00000 н. 0000453992 00000 н. 0000455143 00000 п. 0000455165 00000 н. 0000455372 00000 н. 0000455394 00000 н. 0000455627 00000 н. 0000455650 00000 н. 0000456555 00000 н. 0000456579 00000 п. 0000457846 00000 н. 0000457869 00000 н. 0000458212 00000 н. 0000458234 00000 н. 0000458467 00000 н. 0000458489 00000 н. 0000458722 00000 н. 0000458744 00000 н. 0000458977 00000 н. 0000458999 00000 н. 0000459232 00000 н. 0000459256 00000 н. 0000460560 00000 н. 0000460582 00000 н. 0000460815 00000 н. 0000460837 00000 п. 0000461044 00000 н. 0000461066 00000 н. 0000461299 00000 н. 0000461322 00000 н. 0000462015 00000 н. 0000462039 00000 н. 0000463572 00000 н. 0000463594 00000 н. 0000463827 00000 н. 0000463851 00000 н. 0000465311 00000 п. 0000465333 00000 п. 0000465587 00000 н. 0000465609 00000 н. 0000465842 00000 н. 0000465866 00000 н. 0000467221 00000 н. 0000467243 00000 н. 0000467511 00000 н. 0000467535 00000 н. 0000468872 00000 н. 0000468894 00000 н. 0000469127 00000 н. 0000469150 00000 н. 0000469784 00000 н. 0000469807 00000 н. 0000470562 00000 н. 0000470585 00000 п. 0000471748 00000 н. 0000471771 00000 н. 0000472920 00000 н. 0000472942 00000 н. 0000473149 00000 н. 0000473171 00000 н. 0000473404 00000 н. 0000473428 00000 н. 0000474935 00000 н. 0000474959 00000 н. 0000476423 00000 н. 0000476447 00000 н. 0000477695 00000 п. 0000477717 00000 н. 0000477944 00000 н. 0000477968 00000 н. 0000479199 00000 н. 0000479221 00000 н. 0000479454 00000 н. 0000479476 00000 н. 0000479709 00000 н. 0000479731 00000 н. 0000479964 00000 н. 0000479987 00000 н. 0000480622 00000 н. 0000480645 00000 н. 0000481186 00000 н. 0000481208 00000 н. 0000481441 00000 н. 0000481464 00000 н. 0000481855 00000 н. 0000481879 00000 н. 0000483064 00000 н. 0000483086 00000 н. 0000483279 00000 н. 0000483302 00000 н. 0000484136 00000 н. 0000484158 00000 н. 0000484391 00000 н. 0000484413 00000 н. 0000484646 00000 н. 0000484669 00000 н. 0000485843 00000 н. 0000485865 00000 н. 0000486098 00000 н. 0000486120 00000 н. 0000486353 00000 н. 0000486377 00000 н. 0000487836 00000 н. 0000487858 00000 н. 0000488091 00000 н. 0000488113 00000 н. 0000488346 00000 н. 0000488369 00000 н. 0000489330 00000 н. 0000489352 00000 н. 0000489559 00000 н. 0000489582 00000 н. 00004

00000 н. 00004

00000 н. 00004
00000 н. 00004
00000 н. 0000492766 00000 н. 0000492788 00000 н. 0000493021 00000 н. 0000493045 00000 н. 0000494498 00000 н. 0000494520 00000 н. 0000494753 00000 н. 0000494775 00000 н. 0000495008 00000 н. 0000495030 00000 н. 0000495263 00000 н. 0000495285 00000 н. 0000495518 00000 н. 0000495541 00000 н. 0000496093 00000 н. 0000496117 00000 н. 0000497622 00000 н. 0000497644 00000 н. 0000497877 00000 н. 0000497901 00000 н. 0000499452 00000 н. 0000499475 00000 н. 0000500104 00000 н. 0000500126 00000 н. 0000500398 00000 н. 0000500421 00000 н. 0000500958 00000 н. 0000500981 00000 н. 0000501968 00000 н. 0000501990 00000 н. 0000502175 00000 н. 0000502199 00000 н. 0000503614 00000 н. 0000503637 00000 н. 0000504519 00000 н. 0000504542 00000 н. 0000505139 00000 н. 0000505162 00000 н. 0000506199 00000 н. 0000506221 00000 н. 0000506414 00000 н. 0000506438 00000 н. 0000507840 00000 н. 0000507862 00000 н. 0000508095 00000 н. 0000508119 00000 н. 0000509724 00000 н. 0000509748 00000 н. 0000510942 00000 н. 0000510964 00000 н. 0000511197 00000 н. 0000511220 00000 н. 0000512061 00000 н. 0000512084 00000 н. 0000512759 00000 н. 0000512782 00000 н. 0000513287 00000 н. 0000513311 00000 н. 0000514857 00000 н. 0000514880 00000 н. 0000515677 00000 н. 0000515700 00000 н. 0000516763 00000 н. 0000516787 00000 н. 0000518310 00000 н. 0000518333 00000 н. 0000518921 00000 н. 0000518944 00000 н. 0000520061 00000 н. 0000520084 00000 н. 0000520422 00000 н. 0000520445 00000 н. 0000520918 00000 н. 0000520940 00000 н. 0000521173 00000 н. 0000521196 00000 н. 0000521475 00000 п. 0000521497 00000 н. 0000521730 00000 н. 0000521752 00000 н. 0000521941 00000 н. 0000521963 00000 н. 0000522196 00000 н. 0000522220 00000 н. 0000523694 00000 п. 0000523716 00000 н. 0000523949 00000 н. 0000523971 00000 п. 0000524178 00000 н. 0000524201 00000 н. 0000525125 00000 н. 0000525148 00000 н. 0000526078 00000 н. 0000526101 00000 п. 0000527041 00000 н. 0000527064 00000 н. 0000527941 00000 н. 0000527964 00000 н. 0000528906 00000 н. 0000528928 00000 н. 0000529163 00000 н. 0000529186 00000 н. 0000529598 00000 н. 0000529621 00000 н. 0000529898 00000 н. 0000529920 00000 н. 0000530153 00000 п. 0000530177 00000 н. 0000531423 00000 н. 0000531446 00000 н. 0000531729 00000 н. 0000531752 00000 н. 0000532648 00000 н. 0000532671 00000 н. 0000533547 00000 н. 0000533569 00000 н. 0000533796 00000 н. 0000533818 00000 н. 0000534051 00000 н. 0000534073 00000 н. 0000534300 00000 н. 0000534324 00000 н. 0000535528 00000 н. 0000535552 00000 н. 0000537249 00000 н. 0000537272 00000 н. 0000538283 00000 н. 0000538307 00000 н. 0000539927 00000 н. 0000539949 00000 н. 0000540182 00000 н. 0000540204 00000 н. 0000540437 00000 н. 0000540459 00000 н. 0000540731 00000 н. 0000540753 00000 н. 0000540942 00000 н. 0000540965 00000 н. 0000541956 00000 п. 0000541979 00000 п. 0000542785 00000 н. 0000542807 00000 н. 0000543062 00000 н. 0000543085 00000 н. 0000543718 00000 н. 0000543742 00000 н. 0000545067 00000 н. 0000545089 00000 н. 0000545322 00000 н. 0000545345 00000 п. 0000545625 00000 н. 0000545648 00000 н. 0000545945 00000 н. 0000545968 00000 н. 0000546909 00000 н. 0000546931 00000 н. 0000547164 00000 п. 0000547186 00000 н. 0000547400 00000 н. 0000547423 00000 н. 0000547918 00000 н. 0000547942 00000 н. 0000549244 00000 н. 0000549266 00000 н. 0000549499 00000 н. 0000549521 00000 н. 0000549754 00000 н. 0000549778 00000 н. 0000551237 00000 н. 0000551259 00000 н. 0000551492 00000 н. 0000551514 00000 н. 0000551747 00000 н. 0000551769 00000 н. 0000552002 00000 н. 0000552024 00000 н. 0000552260 00000 н. 0000552282 00000 н. 0000552531 00000 н. 0000552555 00000 н. 0000553982 00000 н. 0000554004 00000 н. 0000554237 00000 п. 0000554261 00000 н. 0000555438 00000 п. 0000555462 00000 н. 0000556649 00000 н. 0000556673 00000 н. 0000558075 00000 н. 0000558097 00000 н. 0000558330 00000 н. 0000558354 00000 п. 0000559899 00000 н. 0000559923 00000 н. 0000561394 00000 н. 0000561416 00000 н. 0000561649 00000 н. 0000561671 00000 н. 0000561904 00000 п. 0000561928 00000 н. 0000563313 00000 п. 0000563336 00000 н. 0000564327 00000 н. 0000564350 00000 н. 0000565072 00000 н. 0000565094 00000 н. 0000565327 00000 н. 0000565349 00000 н. 0000565582 00000 н. 0000565606 00000 н. 0000566913 00000 н. 0000566936 00000 н. 0000567719 00000 н. 0000567741 00000 н. 0000567974 00000 н. 0000567996 00000 н. 0000568245 00000 н. 0000568268 00000 н. 0000569398 00000 н. 0000569421 00000 н. 0000570066 00000 н. 0000570088 00000 н. 0000570321 00000 н. 0000570344 00000 п. 0000571241 00000 н. 0000571264 00000 н. 0000572102 00000 п. 0000572124 00000 н. 0000572357 00000 н. 0000572381 00000 п. 0000574062 00000 н. 0000574085 00000 н. 0000575218 00000 н. 0000575240 00000 н. 0000025411 00000 п. 0000028969 00000 п. трейлер ] >> startxref 0 %% EOF 1484 0 объект > эндобдж 1485 0 объект > / Кодировка> >> / DA (/ Helv 0 Tf 0 г) >> эндобдж 2721 0 объект > поток HV} PSIHB @.х ‘! Յ я8Ԅ_> j [ك Hc} Ԓ6 ~ + 弎> #) JF * 7O Qb & N
Стандартная форма
Что такое «Стандартная форма»?
, это зависит от того, с чем вы имеете дело!
Я собрал для вас несколько стандартных стандартных форм.
Примечание. Стандартная форма — это , а не «правильная форма», а просто удобный согласованный стиль. Вы можете найти другую форму, которая будет более полезной.
Стандартная форма десятичного числа
В Британия это другое название для научной нотации, где вы записываете число следующим образом:

В этом примере 5326.6 записывается как 5,3266 × 10 ³ ,
, потому что 5326,6 = 5,3266 × 1000 = 5,3266 × 10 ³
В других странах означает «не в развернутой форме» (см. Составление и разложение чисел):
561 500 + 60 + 1
Стандартная форма Расширенная форма
Стандартная форма уравнения
«Стандартная форма» уравнения:
(некоторое выражение) = 0
Другими словами, «= 0» находится справа, а все остальное — слева.
Пример: поместите x
² = 7 в стандартную форму
Ответ:
x ² — 7 = 0
Стандартная форма многочлена
«Стандартная форма» для записи многочлена заключается в том, чтобы сначала поставить члены с наивысшей степенью (например, «2» в x ², если есть одна переменная).
Пример: поместите это в стандартную форму:
3
x ² — 7 + 4 x ³ + x ⁶
Наивысшая степень — 6, поэтому сначала идет 3, затем 2, а затем последняя константа:
x ⁶ + 4 x ³ + 3 x ² -7
Стандартная форма линейного уравнения
«Стандартная форма» для записи линейного уравнения —
Ax + By = C
A не должно быть отрицательным, A и B не должны одновременно быть равными нулю, а A , B и C должны быть целыми числами.
Пример: поместите это в стандартную форму:
y = 3x + 2
3 раза влево:
−3x + y = 2
Умножить все на −1:
3х — у = −2
Примечание: A = 3, B = −1, C = −2
Эта форма:
Ax + By + C = 0
иногда называют «стандартной формой», но более правильным названием является «общая форма».
Стандартная форма квадратного уравнения
«Стандартная форма» для записи квадратного уравнения —
( a не равно нулю)
Пример: поместите это в стандартную форму:
х (х − 1) = 3
Развернуть «x (x-1)»:
x ² — x = 3
Переместите 3 налево:
x ² — x — 3 = 0
Примечание: a = 1, b = −1, c = −3
.

561	500 + 60 + 1
Стандартная форма	Расширенная форма