Страница не найдена
Новости
28 июн
В России выступили с предложением предоставить школьникам из экономически неблагополучных семей специальные сертификаты для оплаты курсов по подготовке к ЕГЭ. Об этом говорится в обращении Анны Маркс, директора Института прогрессивного образования, к министру просвещения страны Сергею Кравцову. Копия соответствующего документа есть в распоряжении RT.
25 июн
В Севастополе десять выпускников сдали Единый госэкзамен на 100 баллов.
Новые школьные здания будут построены в 23 районах Москвы до конца 2021 года, заявил заммэра по вопросам градостроительной политики и строительства Андрей Бочкарёв.
25 июн
Главной темой всероссийского выпускного, организованного Министерством просвещения, стал Год науки и технологий.
25 июн
Губернатор Московской области Андрей Воробьёв поздравил выпускников областных школ с окончанием учёбы.25 июн
Заммэра Москвы по вопросам экономической политики и имущественно-земельных отношений Владимир Ефимов сообщил, что в столице сделали бесплатным снятие запрета на строительство образовательных учреждений.
25 июн
Президент России Владимир Путин поздравил выпускников школ и пожелал им в полной мере реализовать свои таланты.
Алгебра. 9 класс. Задачник. Мордкович А.Г., и др.
Основная особенность задачника — система упражнений, тщательно выстроенная по степени нарастания трудности. Названия параграфов задачника и учебника идентичны. Учебник и задачник прошли широкую экспериментальную проверку в школах России.ОГЛАВЛЕНИЕ (12-е изд., 2010)
Предисловие для учителя 3
Задачи на повторение 5
Глава 1. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ
§ 1. Линейные и квадратные неравенства 13
§ 2. Рациональные неравенства 16
Рациональные неравенства 16
§ 3. Множества и операции над ними 21
§ 4. Системы рациональных неравенств 25
Домашняя контрольная работа № 1 31
Глава 2. СИСТЕМЫ УРАВНЕНИЙ
§ 6. Основные понятия 34
§ 7. Системы уравнений как математические модели реальных ситуаций 46
Домашняя контрольная работа № 2 53
Глава 3. ЧИСЛОВЫЕ ФУНКЦИИ
§ 8. Определение числовой функции. Область определения, область значений функции 57
§ 9. Способы задания функций 62
§ 10. Свойства функций 70
§ 11. Четные и нечетные функции 73
§ 12. Функции у = хп(пе N), их свойства и графики 79
§ 13. Функции у = х~» (п е N), их свойства и графики 84
§ 14. Функция у = 3[х, ее свойства и график 88
Домашняя контрольная работа № 3 91
Глава 4. ПРОГРЕССИИ
§ 15. Числовые последовательности 93
§ 16. Арифметическая прогрессия 98
§ 17.
 Геометрическая прогрессия 108
Геометрическая прогрессия 108Домашняя контрольная работа № 4 118
§ 18. Комбинаторные задачи 120
§19. Статистика — дизайн информации 125
§ 20. Простейшие вероятностные задачи 131
§ 21. Экспериментальные данные и вероятности событий 135
Домашняя контрольная работа № 5 140
Итоговое повторение 142
Ответы 205
Опять двойка по математике…Почему девятиклассники провалили экзамен? | ОБРАЗОВАНИЕ
Что-то не ладится в школьном королевстве. В немилость попала сама царица наук. В нашем округе четверть девятиклассников провалили ОГЭ по математике, получив за испытание «неуд». Хорошо, что экзамен можно пересдать в резервные дни.
«Детей вогнали в стресс»
По информации департамента образования Югры в 2019 году с первой попытки ОГЭ по математике не сдали порядка 20% девятиклассников. В 2020-м из-за пандемии экзамен был отменён.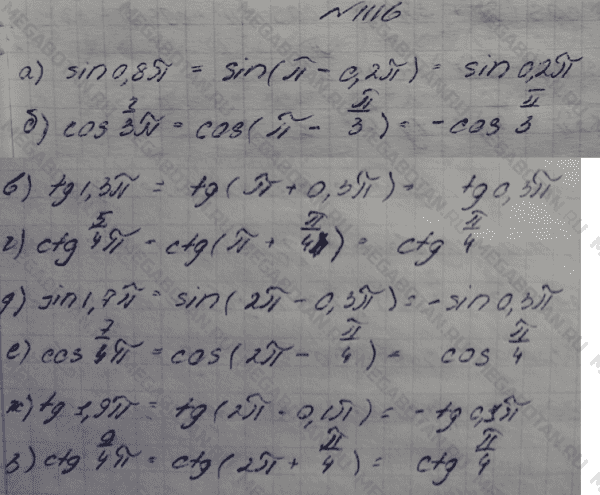 В этом году число «неудов» по математике выросло до 25%, а в отдельных школах округа до 50%. В Сургуте первую попытку провалили 1700 человек! Конечно, подводить окончательные итоги рано. 16 июня ребята имели возможность пересдать экзамен. Ещё один резервный день — 2 июля. Но вопрос, почему возникают такие проблемы, остаётся.
В этом году число «неудов» по математике выросло до 25%, а в отдельных школах округа до 50%. В Сургуте первую попытку провалили 1700 человек! Конечно, подводить окончательные итоги рано. 16 июня ребята имели возможность пересдать экзамен. Ещё один резервный день — 2 июля. Но вопрос, почему возникают такие проблемы, остаётся.
«Зачем нужен этот аналог ЕГЭ в девятом классе? Детям по 15 лет, они ещё не понимают важность образования в современном мире, а мы их вгоняем в такой стресс, постоянно напоминая, что за провал на экзамене им светит только работа дворника. А куда смотрят родители, вспомните, как воспитывали нас?» – вопрошает вартовчанка Анна Захарова в соцсетях. Есть версия, что причина провала кроется в трудных задачах.
«В этом году включено дополнительное задание по геометрии, которая всегда являлась предметом повышенной сложности. Такая ситуация типична для всей России», – объясняет директор департамента образования Нижневартовска Инна Святченко. С этим согласен руководитель департамента образования Югры Алексей Дренин. Но лишь отчасти. По его мнению, на низком уровне подготовки к ОГЭ мог сказаться и «дистант».
С этим согласен руководитель департамента образования Югры Алексей Дренин. Но лишь отчасти. По его мнению, на низком уровне подготовки к ОГЭ мог сказаться и «дистант».
«Удалёнушка» виновата?
В Югре, как и по всей стране, дети заканчивали 2020 учебный год на удалёнке. С осени школы стали практиковать смешанный формат обучения и только в начале этого года вернулись к привычному режиму работы. По сути, дети почти полгода обучались дистанционно.
«На плачевные результаты по ОГЭ повлиял, прежде всего, дистанционный формат обучения. Невыполненные или списанные домашние задания, невыученные уроки… Очно ты всегда видишь глаза ученика и готов прийти на помощь, а на удалёнке на первый план выходит отношение к учёбе ребёнка и его родителей, понимание, что здесь и сейчас вершится будущее. А такого понимания у большинства просто нет», – сетует учитель математики из Ханты-Мансийска Ирина Курковская и добавляет, что несовершенство школьной программы тоже сыграло свою роль.
«Образовательный уровень учеников, переходящих из начальной школы в среднюю, с каждым годом падает. Слишком перегружена программа, дети не могут сразу адаптироваться к 5 классу, поэтому возникают трудности. Классы нужно разделять по успеваемости учащихся. Кто-то усваивает материал быстро, а с кем-то приходится долго заниматься», – говорит педагог.
С этим мнением согласна и учитель начальных классов Марина Коробцова: «Уровень знаний начал падать 6-7 лет назад, когда сменили программу. Причин, конечно, нам не объяснили. Некоторые учителя втихушку продолжают обучать детей по учебнику Петерсон. Ведь начальная школа – это фундамент всех знаний». Речь идёт об учебнике Людмилы Петерсон для 1-4 классов. В 2014 году он не прошёл государственную экспертизу и был исключён из школьной программы. Эксперт Российской академии образования Любовь Ульяхина сочла, что «содержание учебника не способствует формированию патриотизма»…
В моде гуманитарии?
Между тем есть в округе и школы, в которых каверзные задачки ОГЭ ученики как семечки щелкают. Например, гимназия «Лаборатория Салахова». Недавно эта школа вошла в топ-200 лучших общеобразовательных учреждений России, которые занимаются подготовкой абитуриентов для технических вузов страны. Откуда такой успех?
Например, гимназия «Лаборатория Салахова». Недавно эта школа вошла в топ-200 лучших общеобразовательных учреждений России, которые занимаются подготовкой абитуриентов для технических вузов страны. Откуда такой успех?
 Уже в младших классах детям преподают наглядную геометрию и математическое конструирование. Скоро в гимназии появится собственный кванториум.
Уже в младших классах детям преподают наглядную геометрию и математическое конструирование. Скоро в гимназии появится собственный кванториум.«Важна роль учителя: заинтересовать, правильно донести информацию, мотивировать».
Удивительно, но математика, похоже, в принципе теряет популярность. «Два-три года назад у нас стали востребованными гуманитарные специальности: филология, журналистика, лингвистика. Молодые люди поступают на эти направления с высокими баллами по ЕГЭ. Сдавать математику тут не требуется», – говорит ректор Югорского госуниверситета Роман Кучин
 Определите, сколько открыток было подписано за девятый день, если вся работа была выполнена за 16 дней».
Определите, сколько открыток было подписано за девятый день, если вся работа была выполнена за 16 дней».ЗНО з математики складали немотивовані вступники – Освіта.UA
У Центрі вважають, що частка учасників не мала намірів використовувати результати для вступу |
В Українському центрі оцінювання якості освіти вважають, що цьогорічні результати ЗНО з математики, які отримали вступники до вишів, пояснюються тим, що значна частка абітурієнтів не мала намірів використовувати цей результат для вступу.
Про це йдеться у коментарі УЦОЯО з приводу обговорення у суспільстві результатів ЗНО з математики, за результатами якого 31 % учасників тестування не змогли набрати понад 9 тестових балів з 67 можливих.
Водночас в Українському центрі оцінювання якості освіти наголошують, що встановлений пороговий бал для тесту ЗНО з математики є адекватним.
«Пороговий бал з математики 2021 року адекватний і дає змогу відсікти найменш підготовлених вступників, які не будуть у змозі навчатися в закладах вищої освіти, де математика є визначальною», – повідомляють в УЦОЯО.
Також в УЦОЯО, посилаючись на думку експертів, наголошують, що завдання сертифікаційної роботи з математики є посильними для здобувачів повної загальної середньої освіти.
«Окрім цього, в зошитах із тестовими завданнями було розміщено довідкові матеріали (зокрема, формули), на які під час виконання завдань могли спиратися учасники», – зазначають у Центрі.
Разом з тим, в Українському центрі оцінювання якості освіти не стали стверджувати, що результати з математики цьогорічних учасників ЗНО значно погіршилися, мотивуючи свої висновки тим, що не всі учасники цьогорічного ЗНО з математики потребували результату, необхідного для вступу до закладів вищої освіти.
«Очевидно, що значна частка випускників вибрала тестування з математики, попри відсутність намірів використовувати результат для вступу», – вважають в Українському центрі оцінювання якості освіти.
Як відомо, тест профільного рівня з математики, результати якого необхідно надати до приймальних комісій, містив 34 завдання, за виконання яких учасник мав можливість отримати 67 балів.
Пороговий бал тесту був встановлений на рівні 10 тестових балів. Мінімальний поріг тесту не змогли подолати 31 % вступників до закладів вищої освіти.
Для того, щоб оцінити рівень складності тесту та встановлений експертами мінімальний поріг за його виконання, можна пройти тест з математики 2021 року на платформі ЗНО-ОНЛАЙН.
ТЕСТ ЗНО 2021 РОКУ З МАТЕМАТИКИ
Освіта.ua
22.06.2021
Упрощение алгебраических выражений
Распределительная собственность
Свойства действительных чисел важны в нашем изучении алгебры, потому что переменная — это просто буква, представляющая действительное число. В частности, распределительное свойство: для любых вещественных чисел a , b и c , a (b + c) = ab + ac или (b + c) a = ba + ca. заявляет, что для любых действительных чисел a , b и c ,
Это свойство применяется при упрощении алгебраических выражений. Чтобы продемонстрировать, как это используется, мы упростим 2 (5−3) двумя способами и получим тот же правильный результат.
Чтобы продемонстрировать, как это используется, мы упростим 2 (5−3) двумя способами и получим тот же правильный результат.
Конечно, если содержание круглых скобок можно упростить, сделайте это в первую очередь. С другой стороны, если содержание круглых скобок не может быть упрощено, умножьте каждый член в круглых скобках на множитель вне скобок, используя свойство распределения. Применение дистрибутивного свойства позволяет умножать и убирать круглые скобки.
Пример 1: Упростить: 5 (7y + 2).
Решение: Умножьте 5 раз каждый член в круглых скобках.
Ответ: 35лет + 10
Пример 2: Упростить: −3 (2×2 + 5x + 1).
Решение: Умножьте −3 на каждый из коэффициентов членов в круглых скобках.
Ответ: −6×2−15x − 3
Пример 3: Упростить: 5 (−2a + 5b) −2c.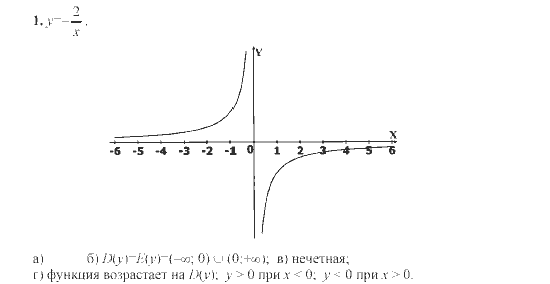
Решение: Примените свойство распределения, умножив на 5 только термины, сгруппированные в круглых скобках.
Ответ: −10a + 25b − 2c
Поскольку умножение коммутативно, мы также можем записать свойство распределения следующим образом: (b + c) a = ba + ca.
Пример 4: Упростить: (3x − 4y + 1) ⋅3.
Решение: Умножьте каждый член в скобках на 3.
Ответ: 9x − 12y + 3
Деление в алгебре часто обозначается чертой дроби, а не символом (÷). А иногда бывает полезно переписать выражения, включающие разделение как продукты:
Переписывание алгебраических выражений как продуктов позволяет нам применять свойство распределенности.
Пример 5: Разделить: 25×2−5x + 105.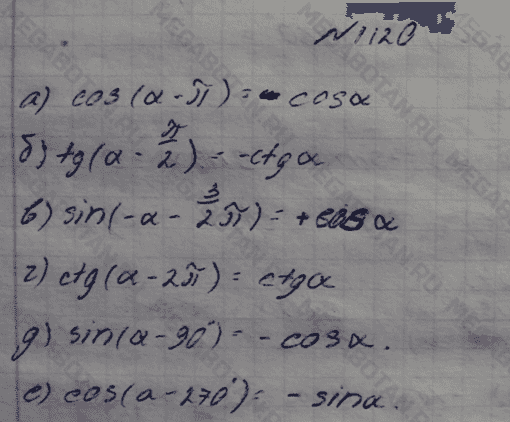
Решение: Сначала обработайте это как 15-кратное выражение в числителе, а затем распределите.
Альтернативное решение: Думайте о 5 как о общем знаменателе и разделите каждый член в числителе на 5:
Ответ: 5×2 − x + 2
Мы обсудим разделение алгебраических выражений более подробно по мере прохождения курса.
Попробуй! Упростить: 13 (−9x + 27y − 3).
Ответ: −3x + 9y − 1
Объединение одинаковых терминов
Термины с одинаковыми переменными частями называются как термины. Если алгебраическое выражение содержит похожие термины, примените свойство распределения следующим образом:
Другими словами, если переменные части терминов в точности совпадают с , то мы можем складывать или вычитать коэффициенты, чтобы получить коэффициент одного члена с той же переменной частью. Этот процесс называется объединением схожих терминов. Добавление или вычитание схожих терминов в алгебраическом выражении для получения одного члена с той же самой переменной частью. Например,
Этот процесс называется объединением схожих терминов. Добавление или вычитание схожих терминов в алгебраическом выражении для получения одного члена с той же самой переменной частью. Например,
Обратите внимание, что переменные коэффициенты и их показатели не меняются. Комбинирование похожих терминов таким образом, чтобы выражение не содержало других похожих терминов, называется упрощением выражения. Процесс объединения похожих терминов до тех пор, пока выражение не перестанет содержать похожие термины.. Используйте эту идею, чтобы упростить алгебраические выражения с помощью нескольких одинаковых терминов.
Пример 6: Упростить: 3a + 2b − 4a + 9b.
Решение: Определите похожие термины и объедините их.
Ответ: −a + 11b
В предыдущем примере перестановка терминов обычно выполняется мысленно и не отображается в представлении решения.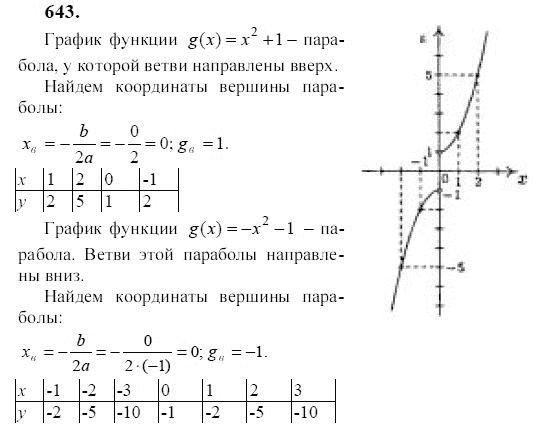
Пример 7: Упростить: x2 + 3x + 2 + 4×2−5x − 7.
Решение: Определите похожие термины и сложите соответствующие коэффициенты.
Ответ: 5×2−2x − 5
Пример 8: Упростить: 5x2y − 3xy2 + 4x2y − 2xy2.
Решение: Не забудьте оставить переменные множители и их показатели неизменными в итоговом комбинированном члене.
Ответ: 9x2y − 5xy2
Пример 9: Упростить: 12a − 13b + 34a + b.
Решение: Чтобы сложить дробные коэффициенты, используйте эквивалентные коэффициенты с общими знаменателями для каждого подобного члена.
Ответ: 54a + 23b
Пример 10: Упростить: −12x (x + y) 3 + 26x (x + y) 3.
Решение: Рассмотрим переменную часть как x (x + y) 3. Тогда в этом выражении есть два одинаковых члена с коэффициентами −12 и 26.
Ответ: 14x (x + y) 3
Попробуй! Упростить: −7x + 8y − 2x − 3y.
Ответ: −9x + 5y
Распределительная собственность и подобные термины
При упрощении нам часто придется комбинировать одинаковые термины после применения свойства распределения. Этот шаг соответствует порядку операций: умножение перед сложением.
Пример 11: Упростить: 2 (3a − b) −7 (−2a + 3b).
Решение: Распределите 2 и −7, а затем объедините одинаковые члены.
Ответ: 20a − 23b
В приведенном выше примере важно отметить, что вы можете убрать скобки и собрать похожие термины, потому что вы умножаете вторую величину на −7, а не только на 7. Чтобы правильно применить свойство распределения, представьте это как добавление — В 7 раз больше заданного количества, 2 (3a − b) + (- 7) (- 2a + 3b).
Чтобы правильно применить свойство распределения, представьте это как добавление — В 7 раз больше заданного количества, 2 (3a − b) + (- 7) (- 2a + 3b).
Попробуй! Упростить: −5 (2x − 3) + 7x.
Ответ: −3x + 15
Часто мы встречаем алгебраические выражения вроде + (a + b) или — (a + b).Как мы видели, на самом деле подразумевается, что коэффициенты равны +1 и -1 соответственно, и, следовательно, свойство распределения применяется с использованием +1 или -1 в качестве множителя. Умножьте каждый член в скобках на следующие множители:
Это приводит к двум полезным свойствам:
Пример 12: Упростить: 5x — (- 2×2 + 3x − 1).
Решение: Умножьте каждый член в круглых скобках на -1, а затем объедините похожие члены.
Ответ: 2×2 + 2x + 1
При распределении отрицательного числа все знаки в круглых скобках изменятся. Обратите внимание, что 5x в приведенном выше примере — это отдельный термин; следовательно, свойство распределения на него не распространяется.
Обратите внимание, что 5x в приведенном выше примере — это отдельный термин; следовательно, свойство распределения на него не распространяется.
Пример 13: Упростить: 5−2 (x2−4x − 3).
Решение: Порядок операций требует, чтобы мы умножали перед вычитанием.Следовательно, распределите −2, а затем объедините постоянные члены. Вычитание 5–2 сначала приводит к неверному результату, как показано ниже:
Ответ: −2 x 2 + 8 x + 11
Осторожно
Стоит повторить, что вы должны соблюдать порядок операций : умножение и деление перед сложением и вычитанием!
Попробуй! Упростить: 8−3 (−x2 + 2x − 7).
Ответ: 3×2−6x + 29
Пример 14: Вычтем 3x − 2 из удвоенного количества −4×2 + 2x − 8.
Решение: Сначала сгруппируйте каждое выражение и обработайте каждое как количество:
Затем определите ключевые слова и переведите их в математическое выражение.
Наконец, упростите полученное выражение.
Ответ: −8×2 + x − 14
Основные выводы
- Свойства действительных чисел применимы к алгебраическим выражениям, потому что переменные — это просто представления неизвестных действительных чисел.
- Объединяйте одинаковые термины или термины с одной и той же переменной частью, чтобы упростить выражения.
- Используйте свойство распределенности при умножении сгруппированных алгебраических выражений: a (b + c) = ab + ac.
- Рекомендуется применять свойство распределения только тогда, когда выражение внутри группировки полностью упрощено.

- После применения свойства распределения удалите скобки, а затем объедините любые похожие термины.
- При упрощении всегда используйте порядок операций.
Тематические упражнения
Часть A: Распределительная собственность
Умножить.
1. 3 (3x − 2)
2. 12 (−5y + 1)
3. −2 (х + 1)
4. 5 (а-б)
5. 58 (8x − 16)
6. −35 (10x − 5)
7.(2x + 3) ⋅2
8. (5x − 1) ⋅5
9. (−x + 7) (- 3)
10. (−8x + 1) (- 2)
11. — (2a − 3b)
12. — (х − 1)
13. 13 (2x + 5)
14. −34 (y − 2)
15. −3 (2a + 5b − c)
16. — (2y2−5y + 7)
17. 5 (y2−6y − 9)
5 (y2−6y − 9)
18. −6 (5×2 + 2x − 1)
19. 7×2− (3x − 11)
20.- (2a − 3b) + с
21. 3 (7×2−2x) −3
22. 12 (4a2−6a + 4)
23. −13 (9y2−3y + 27)
24. (5×2−7x + 9) (- 5)
25. 6 (13×2−16x + 12)
26. −2 (3×3−2×2 + x − 3)
27. 20x + 30y − 10z10
28. −4a + 20b − 8c4
29. 3×2−9x + 81−3
30. −15y2 + 20y − 55
Переведите следующие предложения в алгебраические выражения, а затем упростите.
31. Упростим дважды выражение 25×2−9.
32. Упростим выражение, противоположное выражению 6×2 + 5x − 1.
33. Упростим произведение 5 и x2−8.
34. Упростим произведение −3 и −2×2 + x − 8.
Часть B: Объединение одинаковых терминов
Упростить.
35. 2х − 3х
36. −2a + 5a − 12a
37.10лет − 30−15лет
38. 13x + 512x
39. −14x + 45 + 38x
40. 2x − 4x + 7x − x
41. −3y − 2y + 10y − 4y
42. 5x − 7x + 8y + 2y
43. −8α + 2β − 5α − 6β
44. −6α + 7β − 2α + β
45. 3x + 5−2y + 7−5x + 3y
46. –y + 8x − 3 + 14x + 1 − y
47. 4xy − 6 + 2xy + 8
48. −12ab − 3 + 4ab − 20
49.13x − 25y + 23x − 35y
50. 38a − 27b − 14a + 314b
51. −4×2−3xy + 7 + 4×2−5xy − 3
52. x2 + y2−2xy − x2 + 5xy − y2
53. x2 − y2 + 2×2−3y
54. 12×2−23y2−18×2 + 15y2
55. 316a2−45 + 14a2−14
56. 15y2−34 + 710y2−12
57. 6x2y − 3xy2 + 2x2y − 5xy2
6x2y − 3xy2 + 2x2y − 5xy2
58. 12x2y2 + 3xy − 13x2y2 + 10xy
59. −ab2 + a2b − 2ab2 + 5a2b
60.m2n2 − mn + mn − 3m2n + 4m2n2
61. 2 (x + y) 2 + 3 (x + y) 2
62,15 (x + 2) 3−23 (x + 2) 3
63. −3x (x2−1) + 5x (x2−1)
64,5 (x − 3) −8 (x − 3)
65. −14 (2x + 7) +6 (2x + 7)
66. 4xy (x + 2) 2−9xy (x + 2) 2 + xy (x + 2) 2
Часть C: Смешанная практика
Упростить.
67,5 (2x − 3) +7
68. −2 (4y + 2) −3y
69.5x − 2 (4x − 5)
70. 3- (2х + 7)
71. 2x− (3x − 4y − 1)
72. (10y − 8) — (40x + 20y − 7)
73. 12y − 34x− (23y − 15x)
74. 15a − 34b + 315a − 12b
75,23 (x − y) + x − 2y
76. −13 (6x − 1) +12 (4y − 1) — (- 2x + 2y − 16)
−13 (6x − 1) +12 (4y − 1) — (- 2x + 2y − 16)
77. (2×2−7x + 1) + (x2 + 7x − 5)
78. 6 (−2×2 + 3x − 1) + 10×2−5x
79. — (x2−3x + 8) + x2−12
80.2 (3a − 4b) +4 (−2a + 3b)
81. −7 (10x − 7y) −6 (8x + 4y)
82,10 (6x − 9) — (80x − 35)
83. 10−5 (x2−3x − 1)
84. 4 + 6 (y2−9)
85. 34x− (12×2 + 23x − 75)
86. −73×2 + (- 16×2 + 7x − 1)
87. (2y2−3y + 1) — (5y2 + 10y − 7)
88. (−10a2 − b2 + c) + (12a2 + b2−4c)
89. −4 (2×2 + 3x − 2) +5 (x2−4x − 1)
90. 2 (3×2−7x + 1) −3 (x2 + 5x − 1)
91.x2y + 3xy2− (2x2y − xy2)
92. 3 (x2y2−12xy) — (7x2y2−20xy + 18)
93. 3−5 (ab − 3) +2 (ba − 4)
94. −9−2 (xy + 7) — (yx − 1)
95. −5 (4α − 2β + 1) +10 (α − 3β + 2)
−5 (4α − 2β + 1) +10 (α − 3β + 2)
96,12 (100α2−50αβ + 2β2) −15 (50α2 + 10αβ − 5β2)
Переведите следующие предложения в алгебраические выражения, а затем упростите.
97. В чем разница между 3x − 4 и −2x + 5?
98.Вычтем 2x − 3 из 5x + 7.
99. Вычтем 4x + 3 из удвоенного количества x − 2.
100. Вычтем трижды величину −x + 8 из 10x − 9.
Часть D. Темы дискуссионной доски
101. Нужно ли нам распределительное свойство для деления, (a + b) ÷ c? Объяснять.
102. Нужно ли нам отдельное распределительное свойство для трех членов, a (b + c + d)? Объяснять.
103. Объясните, как вычесть одно выражение из другого.Приведите несколько примеров и продемонстрируйте важность порядка, в котором выполняется вычитание.
104. Учитывая алгебраическое выражение 8−5 (3x + 4), объясните, почему вычитание 8−5 не является первым шагом.
105. Можно ли применить свойство распределенности к выражению 5 (abc)? Объясните, почему или почему нет, и приведите несколько примеров.
106. Как проверить, правильно ли вы упростили выражение? Приведите несколько примеров.
ответов
1: 9x − 6
3: −2x − 2
5: 5х − 10
7: 4x + 6
9: 3x − 21
11: −2a + 3b
13: 23x + 53
15: −6a − 15b + 3c
17: 5y2−30y − 45
19: 7×2−3x + 11
21: 21×2−6x − 3
23: −3y2 + y − 9
25: 2×2 − x + 3
27: 2x + 3y − z
29: −x2 + 3x − 27
31: 50×2−18
33: 5×2-40
35: −x
37: −5y − 30
39: 18x + 45
41: y
43: -13α-4β
45: −2x + y + 12
47: 6xy + 2
49: х-у
51: −8xy + 4
53: 3×2 − y2−3y
55: 716a2−2120
57: 8x2y − 8xy2
59: 6a2b − 3ab2
61: 5 (х + у) 2
63: 2x (x2−1)
65: −8 (2x + 7)
67: 10х − 8
69: −3x + 10
71: −x + 4y + 1
73: −1120x − 16y
75: 53x − 83y
77: 3×2−4
79: 3x − 20
81: −118x + 25y
83: −5×2 + 15x + 15
85: −12×2 + 112x + 75
87: −3y2−13y + 8
89: −3×2−32x + 3
91: −x2y + 4xy2
93: −3ab + 10
95: -10α − 20β + 15
97: 5x − 9
99: −2x − 7
Решайте приложения с линейными неравенствами — элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Решите приложения с линейными неравенствами
Решение приложений с линейными неравенствами
Многие жизненные ситуации требуют от нас решения проблемы неравенства.-reshenie-30.12.jpg) Фактически, приложения неравенства настолько распространены, что мы часто даже не осознаем, что занимаемся алгеброй. Например, сколько галлонов бензина можно заправить в машину за? 20? Доступна ли аренда квартиры? Есть ли достаточно времени перед уроком, чтобы пойти пообедать, съесть его и вернуться? Сколько денег должен стоить праздничный подарок каждому члену семьи, не выходя за рамки бюджета?
Фактически, приложения неравенства настолько распространены, что мы часто даже не осознаем, что занимаемся алгеброй. Например, сколько галлонов бензина можно заправить в машину за? 20? Доступна ли аренда квартиры? Есть ли достаточно времени перед уроком, чтобы пойти пообедать, съесть его и вернуться? Сколько денег должен стоить праздничный подарок каждому члену семьи, не выходя за рамки бюджета?
Метод, который мы будем использовать для решения приложений с линейными неравенствами, очень похож на тот, который мы использовали при решении приложений с уравнениями.Мы прочитаем задачу и убедимся, что все слова понятны. Затем мы определим, что мы ищем, и назначим переменную для его представления. Мы сформулируем проблему в одном предложении, чтобы облегчить перевод в неравенство. Затем решим неравенство.
Эмма получила новую работу и ей придется переехать. Ее ежемесячный доход составит 5265 евро. Чтобы иметь право снимать квартиру, ежемесячный доход Эммы должен быть как минимум в три раза больше, чем арендная плата. На какую самую высокую арендную плату будет претендовать Эмма?
На какую самую высокую арендную плату будет претендовать Эмма?
Решение
| Шаг 1.Прочтите задачу. | |
| Шаг 2. Определите , что мы ищем. | самая высокая арендная плата Эмма будет претендовать на |
| Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества. | Сдам в аренду. |
| Шаг 4. Переведите в неравенство. Сначала напишите предложение, которое дает информацию, чтобы найти его. | Ежемесячный доход Эммы должен быть как минимум в три раза больше арендной платы. |
| Шаг 5. Решите неравенство. Помните, имеет то же значение, что и. | |
| Шаг 6. Проверьте ответ в проблеме и убедитесь, что он имеет смысл. Максимальная арендная плата в размере 1755 фунтов стерлингов кажется разумной для дохода в размере 5625 фунтов стерлингов.  | |
| Шаг 7. Ответьте на вопрос полным предложением. | Максимальная арендная плата составляет 1755 евро. |
Алан загружает поддон ящиками по 45 фунтов каждая.Поддон может безопасно выдержать не более 900 фунтов. Сколько ящиков он может безопасно загрузить на поддон?
Ящиков может быть не более 20.
На лифте в многоквартирном доме Йехира есть табличка, на которой указано, что максимальный вес составляет 2100 фунтов. Если средний вес одного человека составляет 150 фунтов, сколько людей могут безопасно пользоваться лифтом?
В лифте могут безопасно ездить до 14 человек.
Иногда приложение требует, чтобы решением было целое число, но алгебраическое решение неравенства не является целым числом.В этом случае мы должны округлить алгебраическое решение до целого числа. Контекст приложения будет определять, округлять ли мы в большую или меньшую сторону. Чтобы проверить подобные приложения, мы округлим наш ответ до числа, с которым легко вычислить, и убедимся, что это число делает неравенство истинным.
Dawn выиграла мини-грант в размере 4000 фунтов стерлингов на покупку планшетных компьютеров для своего класса. Таблетки, которые она хотела бы купить, стоят 254,12 евро каждый, включая налоги и доставку. Какое максимальное количество планшетов может купить Dawn?
У Энджи есть 20 фунтов, которые она может потратить на коробки из-под сока для дошкольного пикника сына.Каждая упаковка коробки сока стоит 2,63 евро. Какое максимальное количество пакетов она может купить?
Даниэль хочет удивить свою девушку днём рождения в её любимом ресторане. Это будет стоить 42,75 фунтов стерлингов на человека за ужин, включая чаевые и налог. Его бюджет на вечеринку составляет 500 фунтов стерлингов. Какое максимальное количество людей может присутствовать на вечеринке Дэниел?
Пит работает в компьютерном магазине. Его еженедельная заработная плата будет либо фиксированной, либо 925 фунтов стерлингов, либо 500 фунтов стерлингов плюс 12% от общей суммы продаж.Сколько должны быть его общие продажи, чтобы его вариант с переменной оплатой превысил фиксированную сумму в 925?
Решение
| Шаг 1. Прочтите проблему. | |
| Шаг 2. Определите , что мы ищем. | — общий объем продаж, необходимых для того, чтобы его вариант переменной оплаты превысил фиксированную сумму в 925 | фунтов стерлингов.
| Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества. | Пусть общий объем продаж. |
| Шаг 4. Переведите . Напишите предложение, которое дает информацию, чтобы найти его. Перевести в неравенство. Не забудьте, что преобразовать процент в десятичное число. | |
| Шаг 5. Решите неравенство. | |
| Шаг 6. Проверьте ответ в проблеме и убедитесь, что он имеет смысл. Если округлить общий объем продаж до 4000 фунтов стерлингов, то получится , что больше, чем 925 фунтов стерлингов. | |
| Шаг 7. Ответьте на вопрос полным предложением. | Общий объем продаж должен быть более 3541,67 евро. |
Тиффани только что закончила колледж, и ее новая работа будет приносить ей 20 000 евро в год плюс 2% от всех продаж. Она хочет зарабатывать не менее 100 000 евро в год. При каком общем объеме продаж она сможет достичь своей цели?
Кристиану предложили новую работу с оплатой 24 000 евро в год плюс 3% от продаж.При каком общем объеме продаж эта новая работа будет платить больше, чем его текущая работа, за которую платят 60 000 фунтов стерлингов?
У Серджио и Лизет очень ограниченный бюджет на отпуск. Они планируют арендовать автомобиль у компании, которая взимает 75 фунтов стерлингов в неделю плюс 0,25 фунтов стерлингов за милю. Сколько миль они могут проехать, не выходя за рамки своего бюджета? 200?
Решение
| Шаг 1. Прочтите проблему. | |
| Шаг 2. Определите , что мы ищем. | — количество миль, которое Серхио и Лизет могут преодолеть |
| Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества. | Пусть количество миль. |
| Шаг 4. Переведите . Напишите предложение, которое дает информацию, чтобы найти его. Перевести в неравенство. | ? 75 плюс 0,25 количества миль меньше или равно 200? |
| Шаг 5.Решите неравенство. | |
| Шаг 6. Проверьте ответ в проблеме и убедитесь, что он имеет смысл. Да,. | |
| Шаг 7. Напишите предложение, которое отвечает на вопрос. | Серджио и Лизет могут проехать 500 миль, не выходя из бюджета. |
для Талейши стоит 28,80 фунтов стерлингов в месяц плюс 0,20 фунтов стерлингов за текстовое сообщение. Сколько текстовых сообщений она может использовать, а ее ежемесячный счет за телефонные разговоры не превышает 50 фунтов стерлингов?
не более 106 текстовых сообщений
Счет за отопление Рамина составляет 5 фунтов стерлингов.42 в месяц плюс 1,08 евро за терм. Сколько термосов может использовать Рамин, если он хочет, чтобы его счет за отопление составлял максимум 87,50?
Общая цель большинства предприятий — получение прибыли. Прибыль — это деньги, которые остаются после вычета расходов из заработанных денег. В следующем примере мы найдем количество работ, которые мелкий бизнесмен должен выполнять каждый месяц, чтобы получать определенную прибыль.
Elliot занимается обслуживанием ландшафтов.Его ежемесячные расходы составляют 1100 фунтов стерлингов. Если он берет 60 фунтов за работу, сколько работ он должен сделать, чтобы получать прибыль не менее 4000 фунтов в месяц?
У Калеба есть бизнес по присмотру за домашними животными. Он заряжает 32 евро в час. Его ежемесячные расходы составляют 2 272 евро. Сколько часов он должен работать, чтобы получать прибыль не менее 800 фунтов стерлингов в месяц?
Фелисити занимается каллиграфией. Она берет 2,50 евро за приглашение на свадьбу. Ее ежемесячные расходы составляют 650 фунтов стерлингов. Сколько приглашений она должна написать, чтобы получать прибыль не менее 2800 фунтов стерлингов в месяц?
минимум 1380 приглашений
Иногда жизнь усложняется! Есть много ситуаций, когда несколько количеств вносят вклад в общие расходы.Когда мы решаем подобные проблемы, мы должны учитывать все индивидуальные расходы.
У лучшей подруги Бренды свадьба по назначению, мероприятие продлится 3 дня. У Бренды есть сбережения в размере 500 фунтов стерлингов, и она может зарабатывать 15 фунтов в час присмотра за детьми. Она рассчитывает заплатить 350 фунтов стерлингов за перелет, 375 фунтов стерлингов за еду и развлечения и 60 фунтов стерлингов за ночь за свою долю в гостиничном номере. Сколько часов она должна сидеть с ребенком, чтобы иметь достаточно денег, чтобы оплатить поездку?
Решение
| Шаг 1.Прочтите задачу. | |
| Шаг 2. Определите , что мы ищем. | количество часов, которые Бренда должна присматривать за детьми |
| Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества. | Пусть количество часов. |
| Шаг 4. Переведите . Напишите предложение, которое дает информацию, чтобы найти его. Перевести в неравенство. | Расходы должны быть меньше или равны доходу. Стоимость авиабилета плюс стоимость еды и развлечений и счет за гостиницу должны быть меньше или равны сбережениям плюс сумме заработка за услуги няни. |
| Шаг 5. Решите неравенство. | |
| Шаг 6. Проверьте ответ в проблеме и убедитесь, что он имеет смысл. Подставляем в неравенство 27. | |
| Шаг 7.Напишите предложение, которое отвечает на вопрос. | Бренда должна присматривать за детьми не менее 27 часов. |
Малик планирует 6-дневную поездку на летние каникулы. У него есть сбережения в размере 840 фунтов стерлингов, и он зарабатывает 45 фунтов в час за репетиторство. Поездка обойдется ему в 525 фунтов стерлингов за перелет, 780 фунтов стерлингов за питание и осмотр достопримечательностей и 95 фунтов стерлингов за ночь в отеле. Сколько часов он должен заниматься репетитором, чтобы хватило денег на поездку?
Хосуэ хочет отправиться в 10-дневное путешествие следующей весной.Ему это будет стоить 180 фунтов стерлингов за бензин, 450 фунтов стерлингов за еду и 49 фунтов стерлингов за ночь в мотеле. У него есть сбережения в размере 520 фунтов стерлингов, и он может заработать 30 фунтов стерлингов за уборку снега на проезжей части. Сколько проездов он должен прорыть, чтобы иметь достаточно денег, чтобы заплатить за поездку?
Упражнения по разделам
Практика ведет к совершенству
Решение приложений с линейными неравенствами
В следующих упражнениях решите.
Мона планирует вечеринку по случаю дня рождения сына, ее бюджет составляет 285 фунтов стерлингов.Плата за посещение Fun Zone составляет 19 евро за ребенка. Сколько детей она может иметь на вечеринке и оставаться в рамках своего бюджета?
Карлос просматривает апартаменты с тремя своими друзьями. Они хотят, чтобы ежемесячная арендная плата не превышала 2360 фунтов стерлингов. Если соседи по комнате поровну распределяют арендную плату между четырьмя из них, какова максимальная арендная плата, которую каждый из них будет платить?
Водное такси имеет максимальную нагрузку 1800 фунтов. Если средний вес одного человека составляет 150 фунтов, сколько людей могут безопасно ездить на водном такси?
Марсела записывается на уроки в колледже, стоимость которых составляет 105 фунтов стерлингов за единицу.Сколько единиц она может взять, чтобы максимальная стоимость составила 1365 фунтов стерлингов?
Арлин получила подарочную карту на 20 евро для кофейни. Ее любимый напиток со льдом стоит 3,79 фунтов стерлингов. Какое максимальное количество напитков она может купить по подарочной карте?
Тиган любит играть в гольф. В следующем месяце он заложил 60 фунтов стерлингов на тренировочное поле. Каждый раз, когда он идет, это стоит 10,55 фунтов за ведро с мячиками. Какое максимальное количество раз он может посещать тренировочное поле в следующем месяце?
Joni продает кухонные фартуки онлайн за 32 фунта стерлингов.50 каждый. Сколько фартуков ей нужно продать в следующем месяце, если она хочет заработать не менее 1000?
Райан взимает со своих соседей 17,50 фунтов стерлингов за мытье машины. Сколько машин он должен помыть следующим летом, если его цель — заработать не менее 1500?
Кешаду платят 2400 фунтов в месяц плюс 6% от его продаж. Его брат зарабатывает 3300 евро в месяц. На какой общий объем продаж ежемесячная зарплата Кешада будет выше, чем месячная зарплата его брата?
Кимуен нужно зарабатывать 4150 фунтов стерлингов в месяц, чтобы оплачивать все свои расходы.Ее работа приносит ей 3 475 евро в месяц плюс 4% от общего объема продаж. Каков минимальный общий объем продаж Кимуен, чтобы она могла оплатить все свои расходы?
Андре предложили работу начального уровня. Компания предлагала ему 48 000 фунтов стерлингов в год плюс 3,5% от его общих продаж. Андре знает, что средняя заработная плата за эту работу составляет 62 000 фунтов стерлингов. Каким должен быть общий объем продаж Андре, чтобы его зарплата была не меньше средней заработной платы за эту работу?
Наталья рассматривает два предложения о работе.На первой работе ей платили 83 тысячи евро в год. Второй будет платить ей 66 500 фунтов стерлингов плюс 15% от общего объема продаж. Каким должен быть ее общий объем продаж, чтобы ее зарплата по второму предложению была выше, чем по первому?
Счет за воду Джейка составляет 24,80 фунта в месяц плюс 2,20 фунта за кубический фут (сто кубических футов) воды. Какое максимальное количество ccf может использовать Джейк, если он хочет, чтобы его счет был не более 60 фунтов стерлингов?
Стоимость тарифного планаКиёши составляет 17,50 фунтов стерлингов в месяц плюс 0,15 фунтов стерлингов за текстовое сообщение. Какое максимальное количество текстовых сообщений может использовать Киёси, чтобы телефонный счет не превышал 56 фунтов стерлингов.50?
Тарифный планМарлона стоит 49,99 фунтов стерлингов в месяц плюс 5,49 фунтов стерлингов за первый просмотр фильма. Сколько фильмов он сможет посмотреть в первый раз, если он хочет, чтобы его ежемесячный счет составлял максимум 100 фунтов стерлингов?
Келлен хочет снять банкетный зал в ресторане для детского душа своей кузины. Ресторан стоит 350 евро за банкетный зал плюс 32,50 евро на человека за обед. Сколько людей может принять Келлен в душе, если она хочет, чтобы максимальная стоимость была 1500 фунтов?
Мошде ведет парикмахерский бизнес из своего дома.Она берет 45 фунтов за стрижку и укладку. Ее ежемесячные расходы составляют 960 фунтов стерлингов. Она хочет иметь возможность вкладывать не менее 1200 евро в месяц на свой сберегательный счет, чтобы открыть собственный салон. Сколько «стилей и стилей» она должна сделать, чтобы сэкономить не менее 1200 евро в месяц?
Noe устанавливает и настраивает программное обеспечение на домашних компьютерах. Он берет 125 евро за работу. Его ежемесячные расходы составляют 1600 фунтов стерлингов. Сколько рабочих мест он должен отработать, чтобы получить прибыль не менее 2400 фунтов стерлингов?
Кэтрин — личный повар.Она берет 115 фунтов за обед на четырех человек. Ее ежемесячные расходы составляют 3150 евро. Сколько обедов для четырех человек она должна продать, чтобы получить прибыль не менее 1900?
Мелисса делает ожерелья и продает их в Интернете. Она берет 88 фунтов за ожерелье. Ее ежемесячные расходы составляют 3745 евро. Сколько ожерелий она должна продать, если хочет получить прибыль не менее 1650 фунтов стерлингов?
Пять чиновников студенческого самоуправления хотят пойти на съезд штата. Им это будет стоить 110 фунтов стерлингов за регистрацию, 375 фунтов стерлингов на транспорт и питание и 42 фунта стерлингов на человека в отеле.На сберегательный счет студенческого самоуправления заложено 450 фунтов стерлингов. Остальные деньги они могут заработать на мойке машин. Если они берут 5 фунтов за машину, сколько машин они должны помыть, чтобы иметь достаточно денег для оплаты поездки?
Сезар планирует 4-дневную поездку, чтобы навестить своего друга в колледже в другом штате. Это будет стоить ему 198 фунтов стерлингов за авиаперелет, 56 фунтов стерлингов за проезд на местном транспорте и 45 фунтов стерлингов в день на питание. У него 189 евро сбережений, и он может заработать 35 евро с каждой стриженой лужайки.Сколько газонов нужно косить, чтобы на поездку хватило денег?
Алонзо работает мастером по ремонту автомобилей. Он берет 175 евро за машину. Он планирует переехать из родительского дома и снять свою первую квартиру. Ему нужно будет заплатить 120 фунтов стерлингов за регистрационный взнос, 950 фунтов стерлингов за залог, а также арендную плату за первый и последний месяцы из расчета 1140 фунтов стерлингов в месяц. У него есть сбережения в размере 1810 евро. Сколько машин нужно собрать, чтобы иметь достаточно денег на аренду квартиры?
Ын-Кён работает репетитором и зарабатывает 60 евро в час.У нее 792 евро сбережений. Она планирует отпраздновать годовщину своих родителей. Она хочет пригласить 40 гостей. Вечеринка обойдется ей в 1520 евро за еду и напитки и 150 евро за фотографа. Она также окажет услугу каждому из гостей, и каждая услуга будет стоить 7,50 фунтов стерлингов. Сколько часов она должна заниматься репетитором, чтобы денег на вечеринку хватило?
Повседневная математика
Максимальная нагрузка на сцену В 2014 году обрушилась сцена средней школы в Фуллертоне, Калифорния, когда 250 учеников вышли на сцену для финала музыкальной постановки.Пострадали два десятка студентов. Сцена могла выдержать максимум 12 750 фунтов. Если предполагается, что средний вес студента составляет 140 фунтов, каково максимальное количество студентов, которые могут безопасно выйти на сцену?
Максимальный вес лодки В 2004 году водное такси затонуло в гавани Балтимора, и пять человек утонули. Водное такси имело максимальную вместимость 3500 фунтов (25 человек при среднем весе 140 фунтов). Средний вес 25 человек в водном такси, когда оно затонуло, составлял 168 фунтов на человека.Каким должно быть максимальное количество людей с таким весом?
Свадебный бюджет Адель и Уолтер нашли идеальное место для своего свадебного приема. Стоимость составляет 9850 евро за до 100 гостей, плюс 38 евро за каждого дополнительного гостя. Сколько гостей может принять участие, если Адель и Уолтер хотят, чтобы общая стоимость была не более 12 500?
Бюджет душа Пенни планирует детский душ для своей невестки. Стоимость ресторана до 25 человек составляет 950 евро, плюс 31 евро.95 за каждого дополнительного гостя. Сколько гостей может присутствовать, если Пенни хочет, чтобы общая стоимость не превышала 1500 фунтов?
Письменные упражнения
Найдите свой телефонный счет за последний месяц и почасовую зарплату, которую вам платят на работе. (Если у вас нет работы, используйте почасовую зарплату, которую вы реально получали бы, если бы у вас была работа.) Подсчитайте количество рабочих часов, которые вам понадобятся, чтобы заработать хотя бы достаточно денег для оплаты телефонного счета, написав соответствующее неравенство, а затем его решение.
Узнайте, сколько единиц у вас осталось после этого семестра для достижения вашей цели в колледже, и оцените количество единиц, которое вы можете сдавать в каждом семестре в колледже. Подсчитайте количество терминов, которые вам понадобятся для достижения вашей цели в колледже, написав соответствующее неравенство и затем решив его.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Упражнения на повторение главы 3
3.1 Использование стратегии решения проблем
Подходите к проблемам со словами с позитивным отношением
В следующих упражнениях поразмышляйте о своем подходе к задачам со словами.
Как изменилось ваше отношение к решению словесных задач в результате работы над этой главой? Объяснять.
Помогла ли вам стратегия решения задач решать текстовые задачи в этой главе? Объяснять.
Используйте стратегию решения проблем с Word
В следующих упражнениях решайте, используя стратегию решения задач для текстовых задач.Не забудьте написать полное предложение, чтобы ответить на каждый вопрос.
Три четверти присутствующих на концерте — дети. Если на концерте 87 детей, сколько всего человек на концерте?
В группе девять саксофонистов. Количество саксофонистов на один меньше, чем в два раза больше, чем тубистов. Найдите количество игроков на тубе.
Решите проблемы с числами
В следующих упражнениях решите каждую задачу с числовыми словами.
Сумма числа и тройки равна сорок одному. Найдите номер.
Дважды разница числа и десяти равна пятидесяти четырем. Найдите номер.
Одно число на девять меньше другого. Их сумма отрицательная — двадцать семь. Найдите числа.
Одно число на одиннадцать больше другого. Если их сумма увеличится на семнадцать, результат будет 90. Найдите числа.
Одно число на два больше, чем в четыре раза больше другого. Их сумма — найти числа.
Сумма двух последовательных целых чисел — это Найти числа.
Найдите три последовательных целых числа, сумма которых равна
.Найдите три последовательных четных целых числа, сумма которых равна 234.
Найдите три последовательных нечетных целых числа, сумма которых равна 51.
У Кодзи на сберегательном счету 5 502 евро. Это на 30 фунтов меньше, чем в шесть раз больше суммы на его текущем счете. Сколько денег у Кодзи на его текущем счете?
3.2 Решить процент приложений
Перевод и решение основных процентных уравнений
В следующих упражнениях переведите и решите.
Какое число составляет 67% от 250?
300% от 82 — какое число?
12,5% от какого числа 20?
72 — это 30% от какого числа?
Какой процент от 125 составляет 150?
127,5 — это какой процент от 850?
Процент решения
В следующих упражнениях решите.
Счет за обед Дино составил 19,45 фунтов стерлингов. Он хотел оставить 20% от суммы счета в качестве чаевых. Сколько должны быть чаевые?
Реза был очень болен и потерял 15% своего первоначального веса. Он похудел на 27 фунтов. Каков был его первоначальный вес?
Долорес купила детскую кроватку на распродаже за 350 фунтов стерлингов. Цена продажи составила 40% от первоначальной цены. Какова была первоначальная цена детской кроватки?
Джейден зарабатывает 2680 фунтов стерлингов в месяц. Он платит 938 евро в месяц за аренду. Какой процент его ежемесячной зарплаты идет на аренду?
Найти процент увеличения и процента уменьшения
В следующих упражнениях решите.
Годовая зарплата Энджела увеличена с 55 400 до 56 785 фунтов стерлингов. Найдите процент увеличения.
Ежемесячный счет на бензинRowena упал с 83,75 фунтов стерлингов в прошлом месяце до 56,95 фунтов стерлингов в этом месяце. Найдите процент уменьшения.
Решение простых процентных заявок
В следующих упражнениях решите.
Уинстон положил 3294 евро на банковский счет с процентной ставкой 2,6%. Сколько процентов было заработано за 5 лет?
Мойра заняла 4500 фунтов стерлингов у деда, чтобы оплатить первый год обучения в колледже.Три года спустя она выплатила 4500 фунтов стерлингов плюс 243 фунта стерлингов. Какая была процентная ставка?
В выписке по кредиту на холодильник Хайме сказано, что он заплатит 1026 фунтов стерлингов в виде процентов за 4-летний кредит под 13,5%. Сколько Хайме занял, чтобы купить холодильник?
За 12 лет облигация с доходностью 6,35% принесла 7 620 фунтов стерлингов. Какова была основная сумма облигации?
Решать заявки со скидкой или наценкой
В следующих упражнениях найдите продажную цену.
Первоначальная цена сумочки составляла 84 евро. Кэрол купила его на распродаже за 21 евро.
Мариан хочет купить журнальный столик стоимостью 495 фунтов стерлингов. На следующей неделе журнальный столик будет продаваться со скидкой 149 евро.
В следующих упражнениях найдите сумму скидки и ⓑ продажную цену.
Эммет купил пару туфель на распродаже со скидкой 40% от первоначальной цены 138 фунтов стерлингов.
Анастасия купила на распродаже платье со скидкой 75% от первоначальной цены 280 фунтов стерлингов.
В следующих упражнениях найдите ⓐ сумму скидки и ⓑ ставку дисконтирования. (При необходимости округлите до ближайшей десятой процента.)
Зак купил для своего офиса принтер, который продавался за 380 фунтов стерлингов. Первоначальная цена принтера составляла 450 фунтов стерлингов.
Лейси купила пару ботинок на распродаже за 95 фунтов стерлингов. Первоначальная цена ботинок составляла 200 фунтов стерлингов.
В следующих упражнениях найдите сумму наценки и ⓑ прейскурантную цену.
Нга и Лорен купили сундук на блошином рынке за 50 фунтов стерлингов.Они переработали его, а затем добавили наценку 350%.
Карли купила воду в бутылках по цене 0,24 фунта за бутылку в дисконтном магазине. Она добавила наценку 75%, прежде чем продавать их на футбольном матче.
3.3 Приложения для решения смеси
Решите проблемы с монетами
В следующих упражнениях решите каждую задачу с монетами.
У Фрэнси 4,35 евро в десятицентовых монетах. Количество десятицентовиков на пять больше, чем количество четвертей. Сколько у нее каждой монеты?
У Скотта? 0.39 пенсов и пятак. Количество пенни в восемь раз больше, чем монета. Сколько у него каждой монеты?
У Полетт есть купюры номиналом 5 и 10 евро по 140 евро. Количество купюр? 10 на один меньше, чем вдвое, количества купюр? 5. Сколько у нее каждого?
шесть? 5 векселей, 11? 10 векселей
У Ленни 3,69 фунта в пенни, десять центов и четвертаки. Количество пенни на три больше, чем количество монет. Количество четвертей вдвое больше, чем десятицентовик.Сколько у него каждой монеты?
Решение проблем со словами о билетах и штампах
В следующих упражнениях решите каждую проблему со словом билета или штампа.
Церковный обед сделал? 842. Взрослые билеты стоят 10 евро, детские — 6 евро. Количество детей было на 12 больше, чем в два раза больше взрослых. Сколько было продано каждого билета?
Билеты на баскетбольный матч стоят 2 евро для студентов и 5 евро для взрослых. Количество студентов было на три меньше, чем количество взрослых, более чем в 10 раз.Общая сумма денег от продажи билетов составила 619 евро. Сколько было продано каждого билета?
На концерт джаз-бэнда было продано125 билетов на общую сумму 1022 евро. Студенческие билеты стоят 6 евро каждый, а общие входные билеты — 10 евро. Сколько билетов каждого вида было продано?
Однажды днем в аквапарке было продано 525 билетов на общую сумму 13 545 евро. Детские билеты стоят 19 евро, взрослые — 40 евро. Сколько билетов каждого вида было продано?
Ана потратила? 4.06 покупка штампов. Количество купленных марок номиналом 0,41 фунта было на пять больше, чем марок номиналом 0,26 фунта стерлингов. Сколько штук каждого она купила?
три марки 0,26, восемь марок 0,41
Юми потратила 34,15 евро на покупку марок. Количество купленных марок по 0,56 фунта было в 10 раз меньше, чем количество марок по 0,41 фунта. Сколько штук каждого она купила?
Решение проблем со смешанными словами
В следующих упражнениях решите каждую задачу на смешанные слова.
Marquese делает 10 фунтов сухой смеси из изюма и орехов.Изюм стоит 3,45 фунтов за фунт, а орехи — 7,95 фунтов за фунт. Сколько фунтов изюма и сколько фунтов орехов должен использовать Маркез для приготовления смеси для троп, чтобы стоить ему 6,96 фунтов за фунт?
2,2 фунта изюма, 7,8 фунта орехов
Эмбер хочет выложить плитку на кухонную плиту. Ей понадобится 36 квадратных футов плитки. Она будет использовать основные плитки, которые стоят 8 фунтов за квадратный фут, и декоративные плитки, которые стоят 20 фунтов за квадратный фут. Сколько квадратных футов каждой плитки она должна использовать, чтобы общая стоимость фартука составила 10 фунтов за квадратный фут?
У Шона есть 15 000 фунтов стерлингов для инвестиций.Часть из них она вложит в фонд, который выплачивает 4,5% годовых, а остальное — в депозитный сертификат, по которому выплачивается 1,8% годовых. Сколько ей следует инвестировать в каждый счет, если она хочет получать 4,05% годовых от общей суммы?
? 12 500 при 4,5%, 2500? При 1,8%
Энрике взял взаймы 23 500 евро на покупку автомобиля. Он платит своему дяде 2% годовых на 4500 фунтов стерлингов, которые он взял у него в долг, а на оставшуюся часть он платит банку 11,5% годовых. Какую среднюю процентную ставку он платит на общую сумму 23 500? (Округлите ответ до ближайшей десятой процента.)
3.4 Решение геометрических приложений: треугольники, прямоугольники и теорема Пифагора
Решение приложений с использованием свойств треугольника
В следующих упражнениях решите, используя свойства треугольника.
Размеры двух углов треугольника — 22 и 85 градусов. Найдите размер третьего угла.
Детская площадка в торговом центре представляет собой треугольник с периметром 48 футов. Длина двух сторон составляет 19 футов и 14 футов.Какова длина третьей стороны?
Треугольный дорожный знак имеет основание 30 дюймов и высоту 40 дюймов. Какая у него площадь?
Какова высота треугольника площадью 67,5 квадратных метров с основанием 9 метров?
Один угол треугольника больше наименьшего угла. Самый большой угол — это сумма других углов. Найдите размеры всех трех углов.
Размер одного угла прямоугольного треугольника Какова мера других углов треугольника?
Размер наименьшего угла в прямоугольном треугольнике меньше, чем размер следующего большего угла.Найдите размеры всех трех углов.
Периметр треугольника 97 футов. Одна сторона треугольника на одиннадцать футов больше самой маленькой стороны. Третья сторона на шесть футов больше, чем вдвое меньшая сторона. Найдите длины всех сторон.
Используйте теорему Пифагора
В следующих упражнениях используйте теорему Пифагора, чтобы найти длину гипотенузы.
В следующих упражнениях используйте теорему Пифагора, чтобы найти длину недостающей стороны.При необходимости округлите до ближайшей десятой.
В следующих упражнениях решите. При необходимости с точностью до десятых долей.
Серджио нужно прикрепить провод, чтобы прикрепить антенну к крыше своего дома, как показано на рисунке. Антенна 8 футов высотой, а у Серджио 10 футов провода. Как далеко от основания антенны можно прикрепить провод?
Сеонг строит стеллажи в своем гараже. Полки имеют ширину 36 дюймов и высоту 15 дюймов.Он хочет прикрепить диагональную скобу к спине, чтобы стабилизировать полки, как показано. Какой длины должна быть скобка?
Решение приложений с использованием свойств прямоугольника
В следующих упражнениях решите, используя свойства прямоугольника.
Длина прямоугольника составляет 36 футов, а ширина — 19 футов. Найдите область ⓐ периметра ⓑ.
ⓐ 110 футов ⓑ 684 кв. Футов
Тротуар перед домом Кэти имеет форму прямоугольника шириной четыре фута и длиной 45 футов.Найдите область ⓐ периметра ⓑ.
Площадь прямоугольника 2356 квадратных метров. Длина 38 метров. Какая ширина?
Ширина прямоугольника 45 сантиметров. Площадь составляет 2700 квадратных сантиметров. Какая длина?
Длина прямоугольника на 12 см больше ширины. Периметр 74 см. Найдите длину и ширину.
Ширина прямоугольника в три раза больше его длины более чем в два раза. По периметру 96 дюймов. Найдите длину и ширину.
3.5 Решение приложений с равномерным движением
Решение приложений с равномерным движением
В следующих упражнениях решите.
Гейб едет из Сакраменто в Реддинг, это занимает у него 2,2 часа. Эльза преодолевает такое же расстояние за 2 часа. Скорость Эльзы на семь миль в час выше скорости Гейба. Найдите скорость Гейба и скорость Эльзы.
Луэллен и Трейси встретились в ресторане на дороге между Чикаго и Нэшвиллом.Луэллен покинул Чикаго и ехал 3,2 часа в сторону Нэшвилла. Трейси покинула Нэшвилл и ехала 4 часа в сторону Чикаго со скоростью на одну милю в час быстрее, чем скорость Луэллена. Расстояние между Чикаго и Нэшвиллом составляет 472 мили. Найдите скорость Луэллен и скорость Трейси.
Два автобуса отправляются из Амарилло одновременно. Автобус из Альбукерке направляется на запад по I-40 со скоростью 72 мили в час, а автобус из Оклахома-Сити направляется на восток по I-40 со скоростью 78 миль в час.Сколько часов им понадобится, чтобы разойтись на 375 миль?
Кайл греб на своей лодке против течения 50 минут. Ему потребовалось 30 минут, чтобы плыть обратно вниз по течению. Его скорость вверх по течению на две мили в час меньше, чем скорость вниз по течению. Найдите скорость Кайла вверх и вниз по потоку.
В 6:30 Девон вышла из дома и ехала на велосипеде по ровной дороге до 7:30. Потом она начала кататься в гору и ехала до 8:00. Всего она проехала 15 миль. Ее скорость на ровной дороге была на три мили в час выше, чем при подъеме в гору.Найдите скорость Девон на ровной дороге и в гору.
ровная дорога 11 миль / ч, подъём 8 миль / ч
Энтони ехал из Нью-Йорка в Балтимор, расстояние 192 мили. Он уехал в 3:45, и движение было загружено до 5:30. Движение было слабым, и он прибыл в 7:30. Его скорость в легком транспортном потоке была на четыре мили в час больше, чем в два раза быстрее, чем в плотном потоке. Узнайте скорость движения Энтони в условиях интенсивного и легкого движения.
3.6 Решение приложений с линейными неравенствами
Решение приложений с линейными неравенствами
В следующих упражнениях решите.
Еженедельный бюджет Джулианны на питание для ее семьи составляет 231 евро. Если она планирует выделять одинаковую сумму на каждый из семи дней недели, какова максимальная сумма, которую она может тратить на еду каждый день?
Рохелио пишет акварелью. Он получил подарочную карту на 100 фунтов стерлингов в магазин товаров для искусства и хочет использовать ее для покупки холстов. Каждый холст стоит 10,99 евро. Какое максимальное количество холстов он может купить по подарочной карте?
Бриане предложили работу продавцом в другом городе.Предложение было за 42 500 фунтов стерлингов плюс 8% от общего объема продаж. Чтобы переезд окупился, Бриана должна иметь годовую зарплату не менее 66 500 фунтов стерлингов. Какой должна быть сумма ее продаж, чтобы она переехала?
Автомобиль Рене обходится ей в 195 фунтов в месяц плюс 0,09 фунтов за милю. Сколько миль может проехать Рене, чтобы ее ежемесячные расходы на машину не превышали 250 фунтов стерлингов?
Коста — бухгалтер. Во время налогового сезона он взимает 125 евро за простую налоговую декларацию. Его расходы на покупку программного обеспечения, аренду офиса и рекламу составляют 6000 фунтов стерлингов.Сколько налоговых деклараций он должен сделать, если он хочет получить прибыль не менее 8000?
Дженна планирует 5-дневный курортный отпуск с тремя своими друзьями. Это будет стоить ей 279 фунтов стерлингов за авиаперелет, 300 фунтов стерлингов за еду и развлечения и 65 фунтов стерлингов в день за ее долю в отеле. Она накопила 550 фунтов стерлингов на свой отпуск и может зарабатывать 25 фунтов в час в качестве ассистента в фотостудии своего дяди. Сколько часов она должна работать, чтобы иметь достаточно денег на отпуск?
Все множители чисел 1-100
Ниже приведен список или диаграмма всех множителей чисел от 1 до 100 .Вы можете использовать этот ресурс, чтобы быстро найти все множители первых ста (100) элементов набора счетных чисел.
Если вы обнаружите какие-либо ошибки или опечатки в отношении факторов, указанных ниже, напишите мне по адресу [электронная почта защищена], чтобы я мог исправить их немедленно. Спасибо!
Если вам нужно узнать, как найти все множители числа, ознакомьтесь с моим уроком «Выявление всех множителей числа».
Факторы каждого числа от 1 до 100
Коэффициент 1: 1
Факторы 2: 1, 2
Факторы 3: 1, 3
Коэффициент 4: 1, 2, 4
Коэффициент 5: 1, 5
Факторы 6: 1, 2, 3, 6
Факторы 7: 1, 7
Факторы 8: 1, 2, 4, 8
Факторы 9: 1, 3, 9
Множители 10: 1, 2, 5, 10
Факторы 11: 1, 11
Факторы 12: 1, 2, 3, 4, 6, 12
Факторы 13: 1, 13
Множители 14: 1, 2, 7, 14
Факторы 15: 1, 3, 5, 15
Факторы 16: 1, 2, 4, 8, 16
Факторы 17: 1, 17
Факторы 18: 1, 2, 3, 6, 9, 18
Факторы 19: 1, 19
Факторы 20: 1, 2, 4, 5, 10, 20
Факторы 21: 1, 3, 7, 21
Факторы 22: 1, 2, 11, 22
Факторы 23: 1, 23
Факторы 24: 1, 2, 3, 4, 6, 8, 12, 24
Факторы 25: 1, 5, 25
Факторы 26: 1, 2, 13, 26
Факторы 27: 1, 3, 9, 27
Факторы 28: 1, 2, 4, 7, 14, 28
Факторы 29: 1, 29
Факторы 30: 1, 2, 3, 5, 6, 10, 15, 30
Факторы 31: 1, 31
Факторы 32: 1, 2, 4, 8, 16, 32
Факторы 33: 1, 3, 11, 33
Факторы 34: 1, 2, 17, 34
Факторы 35: 1, 5, 7, 35
Факторы 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Факторы 37: 1, 37
Факторы 38: 1, 2, 19, 38
Факторы 39: 1, 3, 13, 39
Факторы 40: 1, 2, 4, 5, 8, 10, 20, 40
Факторы 41: 1, 41
Факторы 42: 1, 2, 3, 6, 7, 14, 21, 42
Факторы 43: 1, 43
Коэффициенты 44: 1, 2, 4, 11, 22, 44
Факторы 45: 1, 3, 5, 9, 15, 45
Факторы 46: 1, 2, 23, 46
Коэффициенты 47: 1, 47
Факторы 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Факторы 49: 1, 7, 49
Факторы 50: 1, 2, 5, 10, 25, 50
Факторы 51: 1, 3, 17, 51
Факторы 52: 1, 2, 4, 13, 26, 52
Факторы 53: 1, 53
Факторы 54: 1, 2, 3, 6, 9, 18, 27, 54
Факторы 55: 1, 5, 11, 55
Факторы 56: 1, 2, 4, 7, 8, 14, 28, 56
Факторы 57: 1, 3, 19, 57
Факторы 58: 1, 2, 29, 58
Факторы 59: 1, 59
Факторы 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Факторы 61: 1, 61
Факторы 62: 1, 2, 31, 62
Факторы 63: 1, 3, 7, 9, 21, 63
Факторы 64: 1, 2, 4, 8, 16, 32, 64
Факторы 65: 1, 5, 13, 65
Факторы 66: 1, 2, 3, 6, 11, 22, 33, 66
Коэффициенты 67: 1, 67
Факторы 68: 1, 2, 4, 17, 34, 68
Факторы 69: 1, 3, 23, 69
Факторы 70: 1, 2, 5, 7, 10, 14, 35, 70
Факторы 71: 1, 71
Факторы 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Факторы 73: 1, 73
Множители 74: 1, 2, 37, 74
Факторы 75: 1, 3, 5, 15, 25, 75
Факторы 76: 1, 2, 4, 19, 38, 76
Факторы 77: 1, 7, 11, 77
Факторы 78: 1, 2, 3, 6, 13, 26, 39, 78
Факторы 79: 1, 79
Факторы 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Факторы 81: 1, 3, 9, 27, 81
Факторы 82: 1, 2, 41, 82
Факторы 83: 1, 83
Факторы 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Факторы 85: 1, 5, 17, 85
Факторы 86: 1, 2, 43, 86
Факторы 87: 1, 3, 29, 87
Факторы 88: 1, 2, 4, 8, 11, 22, 44, 88
Факторы 89: 1, 89
Факторы 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Факторы 91: 1, 7, 13, 91
Факторы 92: 1, 2, 4, 23, 46, 92
Факторы 93: 1, 3, 31, 93
Коэффициенты 94: 1, 2, 47, 94
Коэффициенты 95: 1, 5, 19, 95
Факторы 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
Коэффициенты 97: 1, 97
Факторы 98: 1, 2, 7, 14, 49, 98
Факторы 99: 1, 3, 9, 11, 33, 99
Факторы 100: 1, 2, 4, 5, 10, 20, 25, 50, 100
Возможно, вас заинтересует:
Нахождение всех множителей числа с помощью метода радуги
Кратные числа 1-100
Математика, часть I Решения для класса 9 по математике Глава 3
Страница № 39:
Вопрос 1:
Укажите, являются ли данные алгебраические выражения многочленами? Оправдывать.
(i) y + 1y (ii) 2-5 x (iii) x2 + 7x + 9 (iv) 2m-2 + 7m — 5 (v) 10
Ответ:
В алгебраическом выражении, если степени переменных являются целыми числами, тогда алгебраическое выражение является многочленом.
(i)
y + 1y = y + y-1
Здесь одна из степеней y равна −1, что не является целым числом. Итак, y + 1y — это , а не полином.
(ii)
2-5 x = 2-5×12
Здесь степень x равна 12, что не является целым числом.Итак, 2-5 x — это , а не многочлен.
(iii)
x2 + 7x + 9
Здесь степени переменной x равны 2, 1 и 0, которые являются целыми числами. Итак, x2 + 7x + 9 — многочлен.
(iv)
2m-2 + 7m — 5
Здесь одна из степеней m равна −2, что не является целым числом. Итак, 2m-2 + 7m — 5 — это , а не полином.
(v)
10 = 10 × 1 = 10 x 0
Здесь степень x равна 0, что является целым числом.Итак, 10 — это многочлен (или постоянный многочлен).
Страница № 39:
Вопрос 2:
Запишите коэффициент при м 3 в каждом заданном полиноме.
(i) м 3 (ii) -3 2 + m — 3 м3 (iii) -23 м3 — 5 м2 + 7 м — 1
Ответ:
(i)
Коэффициент м 3 = 1
(ii)
-3 2 + m — 3 м3
Коэффициент м 3 = -3
(iii)
-23 м3 — 5м2 + 7м — 1
Коэффициент м 3 = -23
Страница № 39:
Вопрос 3:
Запишите многочлен в формате x , используя данную информацию.
(i) Моном со степенью 7
(ii) Биномиальное со степенью 35
(iii) Трехчлен со степенью 8
Ответ:
(i) Многочлен, содержащий только один член, называется одночленом. Кроме того, наивысшая степень переменной в полиноме называется степенью полинома.
3 x 7 — одночлен от x со степенью 7.
(ii) Многочлен, состоящий только из двух членов, называется биномом.Кроме того, наивысшая степень переменной в полиноме называется степенью полинома.
2 x 35 + 1 — это бином от x со степенью 35.
(iii) Полином, состоящий только из трех членов, называется трехчленом. Кроме того, наивысшая степень переменной в полиноме называется степенью полинома.
5 x 8 + 6 x 4 + 7 x — трехчлен от x со степенью 8.
Страница № 40:
Вопрос 4:
Напишите степень заданных многочленов.
(i) 5 (ii) x ° (iii) x2 (iv) 2 m10 — 7 (v) 2p — 7 (vi) 7y — y3 + y5 (vii) xyz + xy — z (viii) m3n7 — 3m5n + Мин
Ответ:
Наивысшая степень переменной в полиноме одной переменной называется степенью полинома.Кроме того, наибольшая сумма степеней переменных в каждом члене многочлена от более чем одной переменной является степенью многочлена.
(i)
5 = 5 × 1 = 5×0
Степень многочлена 5 равна 0.
(ii)
Степень многочлена x 0 равна 0.
(iii)
Степень многочлена x 2 равна 2.
(iv)
Степень многочлена 2m10-7 равна 10.
(v)
Степень многочлена 2p-7 равна 1.
(vi)
Степень полинома 7y-y3 + y5 равна 5.
(vii)
Сумма степеней переменных в полиноме xyz + xy-z равна 1 + 1 + 1 = 3 и 1 + 1 = 2.
Степень многочлена xyz + xy-z равна 3.
(viii)
Сумма степеней переменных многочлена m3n7-3m5n + mn равна 3 + 7 = 10, 5 + 1 = 6 и 1 + 1 = 2.
Степень многочлена m3n7-3m5n + mn равна 10.
Страница № 40:
Вопрос 5:
Классифицируйте следующие многочлены как линейные, квадратичные и кубические многочлены.
(i) 2 x 2 + 3 x + 1 (ii) 5p (iii) 2y — 12 (iv) m3 + 7m2 + 52m — 7 (v) a2 (vi) 3r3
Ответ:
(i)
Степень многочлена 2 x 2 + 3 x + 1 равна 2.
Итак, многочлен 2 x 2 + 3 x + 1 равен квадратичный многочлен.
(ii)
Степень многочлена 5 p равна 1.
Итак, многочлен 5 p является линейным многочленом.
(iii)
Степень многочлена 2y-12 равна 1.
Итак, многочлен 2y-12 является линейным многочленом.
(iv)
Степень многочлена m3 + 7m2 + 52m-7 равна 3.
Итак, многочлен m3 + 7m2 + 52m-7 является кубическим многочленом.
(v)
Степень многочлена a 2 равна 2.
Итак, многочлен a 2 является квадратичным многочленом.
(vi)
Степень многочлена 3 r 3 равна 3.
Итак, многочлен 3 r 3 является кубическим многочленом.
Страница № 40:
Вопрос 6:
Запишите следующие многочлены в стандартной форме.
(i) м3 + 3 + 5m (ii) -7y + y5 + 3y3 — 12 + 2y4 — y2
Ответ:
Многочлен, записанный в возрастающей или убывающей степени своей переменной, называется стандартной формой полинома.
(i)
Данный многочлен равен м 3 + 3 + 5 м .
Стандартная форма многочлена: 3 + 5 m + m 3 или m 3 + 5 m + 3.
(ii)
Данный многочлен равен -7y + у5 + 3у3-12 + 2у4-у2.
Стандартная форма многочлена y5 + 2y4 + 3y3-y2-7y-12 или -12-7y-y2 + 3y3 + 2y4 + y5.
Страница № 40:
Вопрос 7:
Запишите следующие многочлены в форме коэффициентов.
(i) x3 — 2 (ii) 5y (iii) 2m4 — 3m2 + 7 (iv) -23
Ответ:
(i)
x3-2 = x3 + 0x2 + 0x-2
Коэффициент формы многочлена (1, 0, 0, −2).
(ii)
5 y = 5 y + 0
Коэффициент формы многочлена (5, 0).
(iii)
2m4-3m2 + 7 = 2m4 + 0m3-3m2 + 0m + 7
Коэффициент формы многочлена (2, 0, −3, 0, 7).
(iv)
Коэффициент полинома -23 равен -23.
Страница № 40:
Вопрос 8:
Запишите многочлены в виде индекса.
(i) (1, 2, 3) (ii) (5, 0, 0, 0, -1) (iii) (-2, 2, — 2, 2)
Ответ:
(i)
Коэффициент формы многочлена (1, 2, 3).
Следовательно, индексная форма многочлена равна x 2 + 2 x + 3.
(ii)
Коэффициент формы многочлена (5, 0, 0, 0, −1) .
Следовательно, индексная форма полинома равна 5 x 4 + 0 x 3 + 0 x 2 + 0 x — 1 или 5 x 4 — 1.
(iii)
Коэффициент формы многочлена (−2, 2, −2, 2).
Следовательно, индексная форма полинома равна −2 x 3 + 2 x 2 −2 x + 2.
Страница № 40:
Вопрос 9:
Напишите соответствующие многочлены в квадратах.
Ответ:
Страница № 43:
Вопрос 1:
Используйте указанные буквы, чтобы написать ответ.
(i) В деревне Лат растут деревья ‘ a ’. Если количество деревьев увеличивается каждый год на « b », то сколько деревьев будет через « x » лет?
(ii) Для парада в каждом ряду и учеников, и формируется такой ряд x . Тогда сколько всего студентов придет на парад?
(iii) Разряд десятков и единиц двузначного числа равен m и n соответственно.Напишите многочлен, представляющий двузначное число.
Ответ:
(i)
Начальное количество деревьев в деревне = a
Увеличение количества деревьев каждый год = b
∴ Количество деревьев в деревне через x лет
= Начальное число деревьев в деревне + Увеличение количества деревьев каждый год × x
= a + bx
Таким образом, количество деревьев через x лет составляет a + bx .
(ii)
Количество студентов в каждой строке = y
Количество строк = x
∴ Общее количество студентов в параде = Количество студентов в каждой строке × Количество строк = y × x = yx = xy
Таким образом, всего на парад xy студентов.
(iii)
Цифра в разряде десятков = м
Цифра в разряде единиц = n
∴ Двухзначное число = Цифра в разряде десятков × 10 + Цифра в разряде единиц = м × 10 + n = 10 m + n
Таким образом, многочлен, представляющий двузначное число, равен 10 m + n .
Страница № 43:
Вопрос 2:
Сложите заданные многочлены.
(i) x3 — 2×2 — 9; 5×3 + 2x + 9 (ii) — 7м4 + 5м3 + 2; 5м4 — 3м3 + 2м2 + 3м — 6 (iii) 2y2 + 7y + 5; 3лет + 9; 3 года 2 — 4 года — 3
Ответ:
(i)
x3-2×2-9 + 5×3 + 2x + 9 = x3 + 5×3-2×2 + 2x-9 + 9 = 6×3-2×2 + 2x
(ii)
-7m4 + 5m3 + 2 + 5m4-3m3 + 2м2 + 3м-6 = -7м4 + 5м4 + 5м3-3м3 + 2м2 + 3м + 2-6 = -2м4 + 2м3 + 2м2 + 3м-6 + 2
(iii)
2y2 + 7y + 5 + 3y + 9 + 3y2-4y-3 = 2y2 + 3y2 + 7y + 3y-4y + 5 + 9-3 = 5y2 + 6y + 11
Страница № 43:
Вопрос 3:
Вычтите второй многочлен из первого.
(i) x2 — 9x + 3; -19x + 3 + 7×2 (ii) 2ab2 + 3a2b — 4ab; 3ab -8ab2 + 2a2b
Ответ:
(i)
x2-9x + 3 —19x + 3 + 7×2 = x2-9x + 3 + 19x-3-7×2 = x2-7×2-9x + 19x + 3-3 = -6×2 + 10x
(ii )
2ab2 + 3a2b-4ab-3ab-8ab2 + 2a2b = 2ab2 + 3a2b-4ab-3ab + 8ab2-2a2b = 2ab2 + 8ab2 + 3a2b-2a2b-4ab-3ab = 10ab2 + a2b-7ab
Страница № 43:
Вопрос 4:
Умножьте заданные многочлены.
(i) 2x; x2 — 2x — 1 (ii) x5 — 1; x3 + 2×2 + 2 (iii) 2y + 1; y2 — 2y3 + 3y
Ответ:
(i)
2xx2 -2x-1 = 2x × x2 + 2x × -2x + 2x × -1 = 2×3-4×2-2x
(ii)
x5-1 × x3 + 2×2 + 2 = x5x3 + 2×2 + 2-1×3 + 2×2 + 2 = x8 + 2×7 + 2×5-x3-2×2-2
(iii)
2y + 1 × y2-2y3 + 3y = 2yy2-2y3 + 3y + 1y2-2y3 + 3y = 2y3-4y4 + 6y2 + y2-2y3 + 3y = -4y4 + 2y3-2y3 + 6y2 + y2 + 3y = -4y4 + 7y2 + 3y
Страница № 43:
Вопрос 5:
Разделите первый многочлен на второй и запишите ответ в виде «Дивиденд = Делитель × Частное + Остаток».
(i) x3 — 64; x — 4 (ii) 5×5 + 4×4 — 3×3 + 2×2 + 2; х2 — х
Ответ:
(i)
x3-64 = x3 + 0x2 + 0x-64
Используя метод деления в столбик,
Дивиденд = делитель × частное + остаток
∴x3-64 = x-4 × x2 + 4x + 16 +0
(ii)
5×5 + 4×4-3×3 + 2×2 + 2 = 5×5 + 4×4-3×3 + 2×2 + 0x + 2
Используя метод деления в столбик,
Дивиденд = Делитель × Частное + Остаток
∴ 5×5 + 4×4-3×3 + 2×2 + 2 = x2-x × 5×3 + 9×2 + 6x + 8 + 8x + 2
Страница № 43:
Вопрос 6:
Запишите информацию в форме алгебраического выражения и упростите.
Имеется прямоугольная ферма длиной 2a2 + 3b2 метра и шириной (a2 + b2) метра. Фермер использовал квадратный участок фермы для постройки дома. Сторона участка составляла (a2 — b2) метр. Какова площадь оставшейся части фермы?
Ответ:
Длина прямоугольной фермы = (2 a 2 + 3 b 2 ) м
Ширина прямоугольной фермы = ( a 2 + b 2 ) м
Сторона квадратного участка = ( a 2 — b 2 ) m
∴ Площадь остальной части фермы
= Общая площадь фермы — Площадь квадратного участка
= Длина прямоугольной фермы × Ширина прямоугольной фермы — (Сторона квадратного участка) 2
= (2 a 2 + 3 b 2 ) × ( a 2 + b 2 ) — ( a 2 — b 2 ) 2
= 2 a 2 ( a 2 90 b252 + 2 ) + 3 b 2 ( a 2 + b 2 ) — ( a 4 + b 4 -2 a 2 b 2 )
= 2 a 4
a2 + 2 2 b 2 + 3 a 2 b 2 + 3 b 4 — a 4 —55 2
56 a 2 b 2 = 2 a 4 — a 4 + 2 a 2 b 2 9025 2 b 2 + 2 a 2 b 2 + 3 b 4 — b 4
= (
55 a 7
а 2 б 2 + 2 б 4 ) m 2 Таким образом, площадь оставшейся части фермы составляет ( a 4 + 7 a 2 b 2 + 2 b 4 ) м 2 .
Страница № 46:
Вопрос 1:
Разделите каждый из следующих многочленов методом синтетического деления, а также на
. метод линейного деления. Напишите частное и остаток. (i) 2m2 — 3m + 10 ÷ m — 5 (ii) x4 + 2×3 + 3×2 + 4x + 5 ÷ x + 2 (iii) y3 — 216 ÷ y — 6
(iv) 2×4 + 3×3 + 4x — 2×2 ÷ x + 3 (v) x4 — 3×2 — 8 ÷ x + 4 (vi) y3 — 3y2 + 5y — 1 ÷ y — 1
Ответ:
(i)
Синтетическое подразделение:
Дивиденд = 2м2-3м + 10
Делитель = m-5
Противоположно -5 = 5
Коэффициент формы частного является (2, 7) .
∴ Частное = 2 м + 7 и остаток = 45
Линейный метод:
2м2-3м + 10 = 2мм-5 + 10м-3м + 10 = 2мм-5 + 7м-5 + 35 + 10 = m-5 × 2m + 7 + 45
(ii)
Синтетическое подразделение:
Дивиденд = x4 + 2×3 + 3×2 + 4x + 5
Делитель = x + 2
Напротив 2 = −2
Коэффициент формы частного является (1, 0, 3, −2).
∴ Частное = x 3 + 3 x — 2 и остаток = 9
Линейный метод:
x4 + 2×3 + 3×2 + 4x + 5 = x3x + 2 + 3xx + 2-6x + 4x + 5 = x3x + 2 + 3xx + 2-2x + 5 = x3x + 2 + 3xx + 2-2x + 2 + 4 + 5 = x + 2 × x3 + 3x-2 + 9
(iii)
Синтетическое подразделение:
Дивиденд = y3-216 = y3 + 0y2 + 0y-216
Делитель = y-6
Противоположно −6 = 6
Коэффициент формы частного является (1, 6, 36).
∴ Частное = y 2 + 6 y + 36 и остаток = 0
Линейный метод:
y3-216 = y2y-6 + 6y2-216 = y2y-6 + 6yy-6 + 36y-216 = y2y-6 + 6yy-6 + 36y-6 + 216-216 = y2y-6 + 6yy-6 + 36y-6 = y-6 × y2 + 6y + 36
(iv)
Синтетическое подразделение :
Дивиденд = 2×4 + 3×3 + 4x-2×2 = 2×4 + 3×3-2×2 + 4x + 0
Делитель = x + 3
Напротив 3 = −3
Коэффициент формы частного является ( 2, −3, 7, −17).
∴ Частное = 2 x 3 — 3 x 2 + 7 x -17 и остаток = 51
Линейный метод:
2×4 + 3×3-2×2 + 4x = 2x3x + 3-6×3 + 3×3-2×2 + 4x = 2x3x + 3-3x2x + 3 + 9×2-2×2 + 4x = 2x3x + 3-3x2x + 3 + 7xx + 3-21x + 4x = 2x3x + 3-3x2x + 3 + 7xx + 3-17x + 3 + 51 = x + 3 × 2×3-3×2 + 7x-17 + 51
(v)
Синтетическое подразделение:
Дивиденд = x4-3×2-8 = x4 + 0x3-3×2 + 0x-8
Делитель = x + 4
Противоположно 4 = −4
Коэффициент формы частного является (1, −4, 13, −52).
∴ Частное = x 3 — 4 x 2 + 13 x — 52 и остаток = 200
Линейный метод:
x4-3×2-8 = x3x + 4-4×3 -3×2-8 = x3x + 4-4x2x + 4 + 16×2-3×2-8 = x3x + 4-4x2x + 4 + 13xx + 4-52x-8 = x3x + 4-4x2x + 4 + 13xx + 4-52x + 4 + 208-8 = x + 4 × x3-4×2 + 13x-52 + 200
(vi)
Синтетическое подразделение:
Дивиденд = y3-3y2 + 5y-1
Делитель = y-1
Напротив −1 = 1
Коэффициент формы частного является (1, −2, 3).
∴ Частное = лет 2 -2 лет + 3 и остаток = 2
Линейный метод:
y3-3y2 + 5y-1 = y2y-1 + y2-3y2 + 5y-1 = y2y-1-2yy-1-2y + 5y-1 = y2y-1-2yy-1 + 3y-1 + 3-1 = y-1 × y2-2y + 3 + 2
Страница № 48:
Вопрос 1:
Для x = 0 найдите значение многочлена x2 — 5x + 5.
Ответ:
Пусть px = x2-5x + 5.
∴p0 = 02-5 × 0 + 5 = 0-0 + 5 = 5
Следовательно, для x = 0 значение полинома равно 5.
Страница № 48:
Вопрос 2:
Если py = y2 — 32y + 1, найти p 32.
Ответ:
py = y2-32y + 1
∴p32 = 322-32 × 32 + 1 = 18-18 + 1 = 1
Страница № 48:
Вопрос 3:
Если pm = m3 + 2m2 — m + 10, то pa + p-a =?
Ответ:
pm = m3 + 2m2-m + 10
∴pa = a3 + 2a2-a + 10….. (1)
Также,
pa = -a3 + 2-a2 — a + 10
⇒pa = -a3 + 2a2 + a + 10 ….. (2)
Сложение (1) и (2) получаем
pa + pa = a3 + 2a2-a + 10 + -a3 + 2a2 + a + 10 = a3-a3 + 2a2 + 2a2-a + a + 10 + 10 = 4a2 +20
∴pa + pa = 4a2 + 20
Страница № 48:
Вопрос 4:
Если py = 2y3 — 6y2 — 5y + 7, найти p2.
Ответ:
py = 2y3-6y2-5y + 7
∴p2 = 2 × 23-6 × 22-5 × 2 + 7 = 16-24-10 + 7 = -11
Страница № 53:
Вопрос 1:
Найдите значение полинома 2x — 2×3 + 7, используя заданные значения x.
(i) x = 3 (ii) x = -1 (iii) x = 0
Ответ:
Пусть px = 2x-2×3 + 7.
(i)
p3 = 2 × 3-2 × 33 + 7 = 6-2 × 27 + 7 = 6-54 + 7 = -41
Таким образом, значение полинома для x = 3 равно −41 .
(ii)
p-1 = 2 × -1-2 × -13 + 7 = -2-2 × -1 + 7 = -2 + 2 + 7 = 7
Таким образом, значение полинома для x = −1 равно 7.
(iii)
p0 = 2 × 0-2 × 03 + 7 = 0-0 + 7 = 7
Таким образом, значение полинома для x = 0 равно 7.
Страница № 53:
Вопрос 2:
Для каждого из следующих многочленов найдите p1, p0 и p-2.
(i) px = x3 (ii) py = y2 -2y + 5 (iii) px = x4 -2×2 — x
Ответ:
(i)
пикселей = x3∴p1 = 13 = 1p0 = 03 = 0p-2 = -23 = -8
(ii)
py = y2-2y + 5∴p1 = 12-2 × 1 + 5 = 1-2 + 5 = 4p0 = 02-2 × 0 + 5 = 0-0 + 5 = 5p-2 = -22-2 × -2 + 5 = 4 + 4 + 5 = 13
(iii)
пикселей = x4-2×2-x∴p1 = 14-2 × 12-1 = 1-2-1 = -2p0 = 04-2 × 02-0 = 0-0-0 = 0p-2 = -24-2 × -22 —2 = 16-2 × 4 + 2 = 16-8 + 2 = 10
Страница № 53:
Вопрос 3:
Если значение полинома m3 + 2m + a равно 12 для m = 2, найдите значение a .
Ответ:
Пусть pm = m3 + 2m + a
Для m = 2, p (2) = 12.
∴23 + 2 × 2 + a = 12⇒8 + 4 + a = 12⇒12 + a = 12⇒a = 12-12 = 0
Таким образом, значение a равно 0.
Страница № 53:
Вопрос 4:
Для полинома mx2 -2x + 3, если p-1 = 7, найдите m.
Ответ:
Пусть px = mx2-2x + 3.
∴p-1 = 7⇒m × -12-2 × -1 + 3 = 7⇒m + 2 + 3 = 7⇒m = 7-5 = 2
Таким образом, значение m равно 2.
Страница № 53:
Вопрос 5:
Разделите первый многочлен на второй и найдите остаток, используя теорему о множителях.
(i) x2 — 7x +9; (x + 1) (ii) 2×3 — 2×2 + ax — a; (X — a) (iii) 54м3 + 18м2 -27м + 5; (М — 3)
Ответ:
(i)
По синтетическому разделению:
Дивиденд = x2-7x + 9
Делитель = x + 1
Противоположность 1 = -1
Коэффициент формы частного является (1 , −8).
∴ Частное = x — 8
Остаток = 17
По теореме об остатке:
Пусть px = x2-7x + 9.
Делитель = x + 1
По теореме об остатках
Остаток = p (−1) = -12-7 × -1 + 9 = 1 + 7 + 9 = 19
(ii)
По синтетическому разделению:
Дивиденд = 2×3-2×2 + ax-a
Делитель = x — a
Напротив — a = a
Коэффициент формы частного равно (2, 2 a -2, 2 a 2 — a ).
∴ Частное = 2 x 2 + (2 a -2) x + 2 a 2 — a
Остаток = 2 a 3 — a 2 — a
По теореме об остатке:
Пусть px = 2×3-2×2 + ax-a.
Делитель = x — a
По теореме об остатках
Остаток = p ( a ) = 2 × a3-2 × a2 + a × aa = 2a3-2a2 + a2-a = 2a3-a2-a
(iii)
По синтетическому подразделению:
Дивиденд = 54м3 + 18м2-27м + 5
Делитель = м — 3
Напротив −3 = 3
Коэффициентная форма частного (54, 180, 513).
∴ Частное = 54 x 2 + 180 x + 513
Остаток = 1544
По теореме об остатках:
Пусть pm = 54m3 + 18m2-27m + 5.
Делитель = м — 3
По теореме об остатках
Остаток = p (3) = 54 × 33 + 18 × 32-27 × 3 + 5 = 54 × 27 + 18 × 9-27 × 3 + 5 = 1458 + 162-81 + 5 = 1544
Страница № 53:
Вопрос 6:
Если многочлен y3 — 5y2 + 7y + m разделен на y + 2, а остаток равен 50, найдите значение m.
Ответ:
Пусть py = y3-5y2 + 7y + m.
Когда полином делится на ( y + 2), остаток равен 50. Это означает, что значение полинома при y = −2 равно 50.
По теореме об остатках
Остаток = p (−2) = 50
∴-23-5 × -22 + 7 × -2 + m = 50⇒-8-5 × 4-14 + m = 50⇒-8-20-14 + m = 50⇒-42 + m = 50⇒m = 50 + 42 = 92
Таким образом, значение m равно 92.
Страница № 53:
Вопрос 7:
Используйте теорему о множителях, чтобы определить, является ли x + 3 множителем x 2 + 2 x — 3 или нет.
Ответ:
Пусть p ( x ) = x 2 + 2 x — 3.
Делитель = x + 3
∴p-3 = -32 + 2 × -3- 3 = 9-6-3 = 0
Итак, по теореме множителей ( x + 3) является множителем x 2 + 2 x — 3.
Страница № 53:
Вопрос 8:
Если ( x — 2) является множителем x3 — mx2 + 10x — 20, тогда найдите значение m .
Ответ:
Пусть px = x3-mx2 + 10x-20.
Принято, что ( x — 2) является множителем px = x3-mx2 + 10x-20.
∴p2 = 0⇒23-m × 22 + 10 × 2-20 = 0⇒8-4m + 20-20 = 0⇒8-4m = 0⇒4m = 8⇒m = 2
Таким образом, значение м — 2.
Страница № 53:
Вопрос 9:
Используя теорему о факторах в следующих примерах, определите, является ли q ( x ) фактором p ( x ) или нет.
(i) px = x3 — x2 — x — 1, qx = x — 1
(ii) px = 2×3 — x2 -45, qx = x — 3
Ответ:
(i)
пикселей = x3-x2-x-1
Делитель = qx = x-1
∴p1 = 13-12-1-1 = 1-1-1-1 = -2
Поскольку p (1) ≠ 0, поэтому по теореме множителей qx = x-1 равно , а не множителю полинома px = x3-x2-x-1.
(ii)
пикселей = 2×3-x2-45
Делитель = qx = x-3
∴p3 = 2 × 33-32-45 = 2 × 27-9-45 = 54-54 = 0
Итак, по теореме о множителях qx = x-3 является множителем многочлена px = 2×3-x2-45.
Страница № 53:
Вопрос 10:
Если ( x 31 + 31) делится на ( x + 1), найдите остаток.
Ответ:
Пусть p ( x ) = x 31 + 31.
Делитель = x + 1
По теореме об остатках имеем
Остаток = p (−1) = (−1) 31 + 31 = −1 + 31 = 30
Таким образом, остаток при делении ( x 31 + 31) на ( x + 1) равен 30.
Страница № 53:
Вопрос 11:
Покажите, что m -1 является множителем m 21 — 1 и m 22 — 1.
Ответ:
Пусть p ( м ) = м 21 — 1 и q ( м ) = м 22 — 1.
Делитель = м — 1
Теперь
p (1) = (1) 21 — 1 = 1 — 1 = 0
Следовательно, по теореме о множителях ( m — 1) множитель равен p ( m ). ) = м 21 — 1.
Кроме того,
q (1) = (1) 22 — 1 = 1 — 1 = 0
Следовательно, теорема о факторах ( m — 1) является множителем q ( м ) = м 22 — 1.
Следовательно, ( м — 1) является множителем м 21 — 1 и м 22 — 1.
Страница № 53:
Вопрос 12:
Если x — 2 и x — 12 являются множителями многочлена nx 2 -5 x + m , то покажите, что m = n = 2
Ответ:
Пусть p ( x ) = nx 2 -5 x + m .
При условии, что ( x -2) и x-12 являются множителями полинома p ( x ) = nx 2 -5 x + m .
∴ По теореме множителей p (2) = 0 и p12 = 0.
p2 = 0⇒n × 22-5 × 2 + m = 0⇒4n-10 + m = 0⇒4n + m = 10 ….. 1
Также
p12 = 0⇒n122-5 × 12 + m = 0⇒n4 + m = 52⇒n + 4m = 10 ….. 2
Из (1) и (2) имеем
4 n + m = n + 4 м
⇒ 4 n — n = 4 м — м
⇒ 3 n = 3 м
⇒ n = м Расстановка
n = м в (1), имеем 4 м + м = 10
⇒ 5 м = 10
⇒ м = 2
∴ n = м = 2
Страница № 53:
Вопрос 13:
(i) Если px = 2 + 5x, то p2 + p-2 — p1.
(ii) px = 2×2 — 53x + 5, затем p53.
Ответ:
(i)
пикселей = 2 + 5x∴p2 = 2 + 5 × 2 = 2 + 10 = 12p-2 = 2 + 5 × -2 = 2-10 = -8p1 = 2 + 5 × 1 = 2 + 5 = 7
∴p2 + p-2-p1 = 12 + -8-7 = 12-8-7 = 12-15 = -3
(ii)
пикселей = 2×2-53x + 5
∴p53 = 2 × 532-53 × 53 + 5 = 2 × 75-25 × 3 + 5 = 150-75 + 5 = 80
Страница № 54:
Вопрос 1:
Найдите множители полиномов, указанных ниже.
(i) 2 x 2 + x — 1
(ii) 2 м 2 + 5 м — 3
(iii) 12 x 2 + 61 x + 77
(iv) 3 y 2 -2 y -1
(v) 3×2 + 4x + 3
(vi) 12×2-3x + 4
Ответ:
(i)
2×2 + x-1 = 2×2 + 2x-x-1 = 2xx + 1-1x + 1 = x + 12x-1
(ii)
2m2 + 5m-3 = 2m2 + 6m-m- 3 = 2 мм + 3-1 м + 3 = м + 32 м-1
(iii)
12×2 + 61x + 77 = 12×2 + 28x + 33x + 77 = 4x3x + 7 + 113x + 7 = 3x + 74x + 11
(iv )
3y2-2y-1 = 3y2-3y + y-1 = 3yy-1 + 1y-1 = y-13y + 1
(v)
3×2 + 4x + 3 = 3×2 + 3x + x + 3 = 3xx + 3 + 1x + 3 = x + 33x + 1
(vi)
12×2-3x + 4 = 12×2-2x-x + 4 = 12xx-4-1x-4 = x-412x-1
Страница № 55:
Вопрос 2:
Разложите следующие многочлены на множители.
(i) ( x 2 — x ) 2 — 8 ( x 2 — x ) + 12
(ii) ( x — 5) 2 — (5 x — 25) — 24
(iii) ( x 2 — 6 x ) 2 — 8 ( x 2 — 6 x + 8) — 64
(iv) ( x 2 -2 x + 3) ( x 2 -2 x + 5) — 35
(v) ( y + 2) ( y — 3) ( y + 8) ( y + 3) + 56
(vi) ( y 2 + 5 y ) ( y 2 + 5 y — 2 ) — 24
(vii) ( x — 3) ( x — 4) 2 ( x — 5) — 6
Ответ:
(i)
( x 2 — x ) 2 — 8 ( x 2 — x ) + 12
Пусть x 2 — x z .
∴x2-x2-8×2-x + 12 = z2-8z + 12 = z2-6z-2z + 12 = zz-6-2z-6 = z-6z-2
= x2-x-6×2-x-2 Заменить z = x2-x = x2-3x + 2x-6×2-2x + x-2 = xx-3 + 2x-3xx-2 + 1x-2 = x-3x + 2x-2x + 1
(ii)
( x — 5) 2 — (5 x — 25) — 24
= ( x — 5) 2 — 5 ( x — 5) — 24
Пусть x — 5 = z .
∴x-52-5x-5-24 = z2-5z-24 = z2-8z + 3z-24 = zz-8 + 3z-8 = z-8z + 3
= x-5-8x-5 + 3 Заменить z = x-5 = x-13x-2
(iii)
( x 2 -6 x ) 2 -8 ( x 2 -6 x + 8) — 64
= ( x 2 — 6 x ) 2 — 8 ( x 2 — 6 x ) — 64-64
= ( x 2 — 6 x ) 2 — 8 ( x 2 — 6 x ) — 128
Пусть x 2 — 6 x = z .
∴x2-6×2-8×2-6x-128 = z2-8z-128 = z2-16z + 8z-128 = zz-16 + 8z-16 = z-16z + 8
= x2-6x-16×2-6x + 8 Заменить z = x2-6x = x2-8x + 2x-16×2-4x-2x + 8 = xx-8 + 2x-8xx-4-2x-4 = x-8x + 2x-4x-2
(iv )
( x 2 -2 x + 3) ( x 2 -2 x + 5) — 35
Пусть x 2 -2 x = z .
∴x2-2x + 3×2-2x + 5-35 = z + 3z + 5-35 = z2 + 5z + 3z + 15-35 = z2 + 8z-20 = z2 + 10z-2z-20
= zz + 10 -2z + 10 = z + 10z-2 = x2-2x + 10×2-2x-2 Заменить z = x2-2x
(v)
( y + 2) ( y -3) ( y + 8) ( y + 3) + 56
= ( y + 2) ( y + 3) ( y + 8) ( y -3) + 56
= ( y 2 + 5 y + 6) ( y 2 + 5 y -24) + 56
Let y 2 + 5 y = z .
∴y2 + 5y + 6y2 + 5y-24 + 56 = z + 6z-24 + 56 = z2-18z-144 + 56 = z2-18z-88
= z2-22z + 4z-88 = zz-22 + 4z -22 = z-22z + 4 = y2 + 5y-22y2 + 5y + 4 Заменить z = y2 + 5y
= y2 + 5y-22y2 + 4y + y + 4 = y2 + 5y-22yy + 4 + 1y + 4 = y2 + 5y-22y + 4y + 1
(vi)
( y 2 + 5 y ) ( y 2 + 5 y -2) — 24
Let y 2 + 5 y = z .
∴y2 + 5yy2 + 5y-2-24 = zz-2-24 = z2-2z-24 = z2-6z + 4z-24 = zz-6 + 4z-6 = z-6z + 4
= y2 + 5y -6y2 + 5y + 4 Заменить z = y2 + 5y = y2 + 6y-y-6y2 + 4y + y + 4 = yy + 6-1y + 6yy + 4 + 1y + 4 = y + 6y-1y + 4y + 1
(vii)
( x — 3) ( x — 4) 2 ( x — 5) — 6
= ( x — 3) ( x — 5) ( x -4) 2 -6
= ( x 2 -8 x + 15) ( x 2 -8 x + 16) — 6
Пусть x 2 — 8 x = z .
∴x2-8x + 15×2-8x + 16-6 = z + 15z + 16-6 = z2 + 31z + 240-6 = z2 + 31z + 234
= z2 + 18z + 13z + 234 = zz + 18 + 13z + 18 = z + 18z + 13 = x2-8x + 18×2-8x + 13 Заменить z = x2-8x
Страница № 55:
Вопрос 1:
Напишите правильный альтернативный ответ на каждый из следующих вопросов.
(i) Что из следующего является многочленом?
(A) xy (B) x2 — 3x (C) x-2 + 7 (D) 2×2 + 12 (ii) Какова степень многочлена 7?
(A) 12 (B) 5 (C) 2 (D) 0
(iii) Какова степень полинома 0?
(A) 0 (B) 1 (C) undefined (D) любое действительное число (iv) Какова степень многочлена 2 x 2 + 5 x 3 + 7?
(A) 3 (B) 2 (C) 5 (D) 7
(v) Какова форма коэффициента у x3 — 1?
(A) (1, — 1) (B) (3, -1) (C) (1, 0, 0, -1) (D) (1, 3, — 1)
(vi) p ( x) = x2 — 77x + 3, тогда p77 =?
(A) 3 (B) 77 (C) 42 7 + 3 (D) 497
(vii) Когда x = — 1, каково значение полинома 2 x 3 + 2 x ?
(A) 4 (B) 2 (C) -2 (D) -4
(viii) Если x-1, каков множитель полинома 3×2 + mx, тогда найдите значение m .
(A) 2 (B) -2 (C) -3 (D) 3
(ix) Умножение ( x 2 -3) (2 x — 7x 3 + 4) и напишите степень продукта.
(A) 5 (B) 3 (C) 2 (D) 0
(x) Что из следующего является линейным многочленом?
(А) x + 5
(В) x 2 + 5
(К) x 3 + 5
(Д) x 4 + 5
Ответ:
(i)
В алгебраическом выражении, если степени переменных являются целыми числами, тогда алгебраическое выражение является полиномом.
В выражении 2×2 + 12 степень переменной x равна 2, то есть целому числу. Итак, выражение 2×2 + 12 — многочлен.
Следовательно, правильный ответ — вариант (D).
(ii)
7 = 7 × 1 = 7×0
Степень полинома 7 равна 0.
Следовательно, правильный ответ — вариант (D).
(iii)
Степень полинома 0 не определена.
Следовательно, правильный ответ — вариант (С).
(iv)
Наивысшая степень переменной в полиноме называется степенью полинома.
Степень полинома 2 x 2 + 5 x 3 + 7 равна 3.
Следовательно, правильный ответ — вариант (A).
(v)
x3-1 = x3 + 0x2 + 0x-1
Коэффициент формы многочлена x3-1 равен (1, 0, 0, −1).
Следовательно, правильный ответ — вариант (С).
(vi)
пикселей = x2-77x + 3
∴p77 = 772-77 × 77 + 3 = 343-343 + 3 = 3
Следовательно, правильный ответ — вариант (А).
(vii)
Пусть p ( x ) = 2 x 3 + 2 x
∴ p (−1) = 2 × (−1) 3 + 2 × (−1) = 2 × (−1) — 2 = −2 — 2 = −4
Таким образом, значение полинома при x = −1 равно −4.
Следовательно, правильный ответ — вариант (D).
(viii)
Пусть p ( x ) = 3 x 2 + mx .
( x — 1) — коэффициент p ( x ).
∴ p (1) = 0
⇒ 3 × (1) 2 + м × 1 = 0
⇒ 3 + м = 0
⇒ м = −3
Следовательно, правильный ответ — вариант (С).
(ix)
x2-32x-7×3 + 4 = x22x-7×3 + 4-32x-7×3 + 4 = 2×3-7×5 + 4×2-6x + 21×3-12 = -7×5 + 2×3 + 21×3 + 4×2-6x-12 = -7×5 + 23×3 + 4×2-6x-12
Таким образом, степень полученного многочлена равна 5.
Следовательно, правильный ответ — вариант (А).
(x)
Многочлен первой степени называется линейным многочленом.
Таким образом, многочлен x + 5 является линейным многочленом.
Следовательно, правильный ответ — вариант (А).
Страница № 56:
Вопрос 2:
Напишите степень полинома для каждого из следующих значений.
(i) 5 + 3 x 4 (ii) 7 (iii) ax 7 + bx 9 ( a , b — константы.)
Ответ:
Наивысшая степень переменной в полиноме от одной переменной называется степенью полинома.
(i)
Степень многочлена 5 + 3 x 4 равна 4.
(ii)
7 = 7 × 1 = 7 x 0
Степень постоянного многочлена 7 равно 0.
(iii)
Степень полинома ax 7 + bx 9 равна 9.
Страница № 56:
Вопрос 3:
Запишите следующие многочлены в стандартной форме.
(i) 4 x 2 + 7 x 4 — x 3 — x + 9
(ii) p + 2 p 3 + 10 p 2 + 5 p 4 -8
Ответ:
Многочлен, записанный в возрастающей или убывающей степени своей переменной, называется стандартной формой полинома.
(i)
Данный полином равен 4 x 2 + 7 x 4 — x 3 — x + 9.
Стандартная форма многочлена 7 x 4 — x 3 + 4 x 2 — x + 9 или 9 — x + 4 x 2 — x 3 + 7 x 4 .
(ii)
Данный полином равен p + 2 p 3 + 10 p 2 + 5 p 4 — 8.
Стандартная форма полинома: 5 p 4 + 2 p 3 + 10 p 2 + p -8 или −8 + p + 10 p 2 + 2 п. 3 + 5 п 4 .
Страница № 56:
Вопрос 4:
Запишите следующий многочлен в форме коэффициентов.
(i) x 4 + 16 (ii) м 5 + 2 м 2 + 3 м + 15
Ответ:
(i)
x4 + 16 = x4 + 0x3 + 0x2 + 0x + 16
Следовательно, данный полином в форме коэффициентов равен (1, 0, 0, 0, 16).
(ii)
m5 + 2m2 + 3m + 15 = m5 + 0m4 + 0m3 + 2m2 + 3m + 15
Следовательно, данный полином в форме коэффициентов равен (1, 0, 0, 2, 3, 15).
Страница № 56:
Вопрос 5:
Запишите индексную форму многочлена, используя переменную x из его коэффициента.
(i) (3, -2, 0, 7, 18)
(ii) (6, 1, 0, 7)
(iii) (4, 5, -3, 0)
Ответ:
(i)
Коэффициент формы многочлена (3, −2, 0, 7, 18).
Следовательно, индекс полинома равен 3 x 4 -2 x 3 + 0 x 2 + 7 x + 18 или 3 x 4 — 2 x 3 + 7 x + 18.
(ii)
Коэффициент формы многочлена (6, 1, 0, 7).
Следовательно, индекс полинома равен 6 x 3 + x 2 + 0 x + 7 или 6 x 3 + x 2 + 7.
(iii)
Коэффициент формы многочлена (4, 5, −3, 0).
Следовательно, индекс полинома равен 4 x 3 + 5 x 2 — 3 x + 0 или 4 x 3 + 5 x 2 — 3 х .
Страница № 56:
Вопрос 6:
Добавьте следующие полиномы.
(i) 7 x 4 -2 x 3 + x + 10; 3 x 4 + 15 x 3 + 9 x 2 -8 x + 2
(ii) 3 p 3 q + 2 p 2 q + 7; 2 p 2 q + 4 pq -2 p 3 q
Ответ:
(i)
7×4-2×3 + x + 10 + 3×4 + 15×3 + 9×2-8x + 2 = 7×4 + 3×4-2×3 + 15×3 + 9×2 + x-8x + 10 + 2 = 10×4 + 13×3 + 9×2-7x + 12
(ii)
3p3q + 2p2q + 7 + 2p2q + 4pq-2p3q = 3p3q-2p3q + 2p2q + 2p2q + 4pq + 7 = p3q + 4p2q + 4pq + 7
Страница № 56:
Вопрос 7:
Вычтите второй многочлен из первого.
(i) 5 x 2 -2 y + 9; 3 x 2 + 5 y -7 (ii) 2 x 2 + 3 x + 5; х 2 -2 х + 3
Ответ:
(i)
5×2-2y + 9-3×2 + 5y-7 = 5×2-2y + 9-3×2-5y + 7 = 5×2-3×2-2y-5y + 9 + 7 = 2×2-7y + 16
(ii )
2×2 + 3x + 5-x2-2x + 3 = 2×2 + 3x + 5-x2 + 2x-3 = 2×2-x2 + 3x + 2x + 5-3 = x2 + 5x + 2
Страница № 56:
Вопрос 8:
Умножьте следующие многочлены.
(i) ( м 3 -2 м + 3) ( м 4 -2 м 2 + 3 м + 2)
(ii) (5 м 3 -2) ( м 2 — м + 3)
Ответ:
(i)
м3-2м + 3м4-2м2 + 3м + 2 = м3м4-2м2 + 3м + 2-2мм4-2м2 + 3м + 2 + 3м4-2м2 + 3м + 2 = м7-2м5 + 3м4 + 2м3- 2m5 + 4m3-6m2-4m + 3m4-6m2 + 9m + 6 = m7-2m5-2m5 + 3m4 + 3m4 + 2m3 + 4m3-6m2-6m2-4m + 9m + 6 = m7-4m5 + 6m4 + 6m3-12m2 + 5м + 6
(ii)
5м3-2м2-м + 3 = 5м3м2-м + 3-2м2-м + 3 = 5м5-5м4 + 15м3-2м2 + 2м-6
Страница № 56:
Вопрос 9:
Разделите многочлен 3 x 3 — 8 x 2 + x + 7 на x — 3, используя синтетический метод, и запишите частное и остаток.
Ответ:
Дивиденд = 3×3-8×2 + x + 7
Делитель = x-3
Противоположность −3 = 3
Коэффициент формы частного является (3, 1, 4).
∴ Частное = 3 x 2 + x + 4 и остаток = 19
Страница № 56:
Вопрос 10:
Для которого значение м , x + 3 является множителем полинома x 3 -2 mx + 21?
Ответ:
Пусть px = x3-2mx + 21.
( x + 3) — множитель полинома px = x3-2mx + 21.
∴p-3 = 0⇒-33-2m × -3 + 21 = 0⇒-27 + 6m + 21 = 0⇒6m-6 = 0⇒6m = 6⇒m = 1
Таким образом, значение м — 1.
Страница № 56:
Вопрос 11:
На конец 2016 года население сел Ковад, Варуд, Чихали составляет 5 x 2 -3 y 2 , 7 y 2 + 2 xy и 9 x 2 + 4 xy соответственно.На начало 2017 года x 2 + xy — y 2 , 5 xy и 3 x 2 + xy человек из каждой из трех деревень соответственно пошел учиться в другую деревню, тогда какова общая численность населения этих трех деревень?
Ответ:
Общая численность населения трех деревень
= 5×2-3y2 + 7y2 + 2xy + 9×2 + 4xy = 5×2 + 9×2-3y2 + 7y2 + 2xy + 4xy = 14×2 + 4y2 + 6xy
Общее количество человек, переехавших в другую деревню на образование
= x2 + xy-y2 + 5xy + 3×2 + xy = x2 + 3×2-y2 + xy + 5xy + xy = 4×2-y2 + 7xy
∴ Оставшаяся общая численность населения трех деревень = Общая численность населения трех деревень — Всего количество человек, которые отправились в другую деревню для получения образования
= 14×2 + 4y2 + 6xy-4×2-y2 + 7xy = 14×2 + 4y2 + 6xy-4×2 + y2-7xy = 14×2-4×2 + 4y2 + y2 + 6xy-7xy = 10×2 + 5y2-xy
Таким образом, оставшаяся общая численность населения этих трех деревень составляет 10 x 2 + 5 y 2 — xy .
Страница № 56:
Вопрос 12:
Полиномы bx 2 + x + 5 и bx 3 -2 x + 5 делятся на полином x -3, а остатки равны m и n соответственно. Если m — n = 0, то найдите значение b .
Ответ:
Пусть px = bx2 + x + 5 и qx = bx3-2x + 5.
Остаток от деления px = bx2 + x + 5 на ( x — 3) составляет м .
По теореме об остатке
Остаток = p3 = m
∴b × 32 + 3 + 5 = m⇒m = 9b + 8 ….. 1
Остаток при делении qx = bx3-2x + 5 by ( x — 3) равно n .
По теореме об остатках
Остаток = q3 = n
∴b × 33-2 × 3 + 5 = n⇒n = 27b-6 + 5⇒n = 27b-1 ….. 2
Теперь,
mn = 0⇒9b + 8-27b-1 = 0 Используя 1 и 2⇒9b-27b + 8 + 1 = 0⇒-18b + 9 = 0⇒-18b = -9⇒b = -9-18 = 12
Таким образом, значение b равно 12.
Страница № 56:
Вопрос 13:
Упростить
(8 м 2 + 3 м -6) — (9 м -7) + (3 м 2 -2 м + 4)
Ответ:
8м2 + 3м-6-9м-7 + 3м2-2м + 4 = 8м2 + 3м-6-9м + 7 + 3м2-2м + 4 = 8м2 + 3м2 + 3м-9м-2м-6 + 7 + 4 = 11м2-8м + 5
Страница № 56:
Вопрос 14:
Какой многочлен нужно вычесть из x 2 + 13 x + 7, чтобы получить многочлен 3 x 2 + 5 x -4?
Ответ:
Пусть p ( x ) будет полиномом, который нужно вычесть из x 2 + 13 x + 7, чтобы получить полином 3 x 2 + 5 x — 4.
∴ ( x 2 + 13 x + 7) — p ( x ) = 3 x 2 + 5 x — 4
⇒ p ( x ) = ( x 2 + 13 x + 7) — (3 x 2 + 5 x -4)
⇒ p ( x ) = x 2 + 13 x + 7-3 x 2 -5 x + 4
⇒ p ( x ) = x 2 — 3
51 x
2 + 13 x -5 x + 7 + 4 ⇒ p ( x ) = −2 x 2 + 8 x + 11
Таким образом, требуемый полином равен −2 x 2 + 8 x + 11.
Страница № 56:
Вопрос 15:
Какой многочлен нужно добавить к 4 m + 2 n + 3, чтобы получить многочлен 6 m + 3 n + 10?
Ответ:
Требуемый полином может быть получен путем вычитания полинома 4 m + 2 n + 3 из 6 m + 3 n + 10.
∴ Требуемый многочлен
= (6 m + 3 n + 10) — (4 m + 2 n + 3)
= 6 m + 3 n + 10 — 4 м — 2 n — 3
= 6 м — 4 м + 3 n — 2 n + 10 — 3
= 2 м + n + 7
Таким образом, полином 2 m + n + 7 нужно добавить к 4 m + 2 n + 3, чтобы получить полином 6 m + 3 n + 10.
Просмотреть решения NCERT для всех глав класса 9
Перевод слов в алгебраическое уравнение и решение
Результаты обучения
- Преобразование операторов в алгебраические уравнения, включающие сложение, вычитание, умножение и деление
Перевод словосочетаний в алгебраические уравнения
Помните, что уравнение имеет знак равенства между двумя алгебраическими выражениями.Итак, если у нас есть предложение, в котором говорится, что две фразы равны, мы можем перевести его в уравнение. Мы ищем ключевые слова, которые означают, что равно . Вот некоторые слова, которые переводятся как знак равенства:
- равно
- совпадает с
- это
- дает
- было
- будет
Может быть полезно поставить рамку вокруг , равного словам в предложении, чтобы помочь вам сосредоточиться на каждой фразе отдельно.Затем переведите каждую фразу в выражение и напишите их по обе стороны от знака равенства.
Мы попрактикуемся в переводе словесных предложений в алгебраические уравнения. Некоторые из предложений будут базовыми числовыми фактами без каких-либо переменных. Некоторые предложения можно преобразовать в уравнения с переменными. Сейчас основное внимание уделяется просто переводу слов в алгебру.
пример
Переведите предложение в алгебраическое уравнение: сумма [латекс] 6 [/ латекс] и [латекс] 9 [/ латекс] составляет [латекс] 15 [/ латекс].
Решение
Слово равно говорит нам, что знак равенства находится между 9 и 15.
Найдите слово (слова) «равно». Напишите знак =. Переведите слова слева от равно слов в алгебраическое выражение. Переведите слова справа от , равного слову, в алгебраическое выражение.
пример
Переведите предложение в алгебраическое уравнение: произведение [латекс] 8 [/ латекс] и [латекс] 7 [/ латекс] есть [латекс] 56 [/ латекс].
Показать решение Решение
Расположение слова — говорит нам, что знак равенства находится между 7 и 56.
Найдите слово (слова) «равно». Напишите знак =. Переведите слова слева от равно слов в алгебраическое выражение. Переведите слова справа от , равного слову, в алгебраическое выражение.
пример
Переведите предложение в алгебраическое уравнение: двойная разница между [латексом] x [/ латексом] и [латексом] 3 [/ латексом] дает [латекс] 18 [/ латекс].
Показать решение Решение
Найдите слово (слова) «равно». Распознать ключевые слова: дважды; разница…. и… . Дважды означает два раза. Перевести.
Перевести в уравнение и решить
А теперь давайте попрактикуемся переводить предложения в алгебраические уравнения и затем решать их. Мы будем решать уравнения, используя свойства равенства вычитания и сложения.
пример
Переведите и решите: Три больше, чем [latex] x [/ latex], равно [latex] 47 [/ latex].
Показать решение Решение
Три больше чем х равно [латекс] 47 [/ латекс]. Перевести. [латекс] x + 3 = 47 [/ латекс] Вычтем [латекс] 3 [/ латекс] из обеих частей уравнения. [латекс] x + 3 \ color {red} {- 3} = 47 \ color {red} {- 3} [/ latex] Упростить. [латекс] x = 44 [/ латекс] Мы можем проверить. Пусть [latex] x = 44 [/ latex]. [латекс] x + 3 = 47 [/ латекс] [латекс] 44 + 3 = 47 [/ латекс] [латекс] 47 = 47 [/ латекс]
Итак, [latex] x = \ text {} 44 [/ latex] — это решение.
пример
Переведите и решите: Разница между [latex] y [/ latex] и [latex] 14 [/ latex] составляет [latex] 18 [/ latex].
Показать решение Решение
Разница между и и [латексом] 14 составляет 18 [/ латекс]. Перевести. [латекс] y-14 = 18 [/ латекс] Добавьте [латекс] 14 [/ латекс] с обеих сторон. [латекс] y-14 \ color {red} {+ 14} = 18 \ color {red} {+ 14} [/ latex] Упростить. [латекс] y = 32 [/ латекс] Мы можем проверить. Пусть [latex] y = 32 [/ latex]. [латекс] y-14 = 18 [/ латекс] [латекс] 32-14 = 18 [/ латекс] [латекс] 18 = 18 [/ латекс]
Итак, [латекс] y = 32 [/ latex] — это решение.
В следующем видео мы покажем больше примеров того, как перевести уравнение в слова и решить. Обратите внимание, что это отличается от письменных примеров на этой странице, потому что мы начинаем с математического уравнения, а затем переводим его в слова.
Расмус — Математика, Простые числа и делимость, Урок 1.
Расмус — Математика, Простые числа и делимость, Урок 1. — с 7. по 9. класс. 2004 Rasmus ehf Простые числа
Печать
Prime
числа и делимость
Урок 1.
прайм
число — это целое число больше 1, которое можно разделить только само по себе и
1. Наименьшее простое число — 2,
3, 5, 7, 11, 13, 17, 19 и 23. Число 2 — единственное четное простое число.
номер.
Пример:
7 = 1 7 Число 7 имеет всего два фактора: 1 и сам. 11 = 1 11 Число 11 имеет только два фактора: 1 и сам.
композитный
числа: составное число имеет более двух факторов.
Составные числа можно разбить на простые множители.
Пример:
6
= 2 3 2
и 3 — простые числа. 20
= 2 25 2
и 5 — простые числа. 35
= 5 7 5
и 7 — простые числа.
Prime
факторы: Найдите
простые множители 30.
30
= 2 35 простые множители 30 — это числа 2, 3 и 5.
- Начните с наименьшего простого числа, которое
фактор 30.Разделите на 2, чтобы получить множитель 15.
- Теперь используйте наименьшее простое число, которое
множитель 15. Разделите на 3, чтобы получить множитель 5, который также является простым числом.
Вы
также можно найти простые множители целого числа, нарисовав множитель
дерево. 30
= 2 35
Делимость
номеров:
Вы можете использовать
Сито Эратосфена в
найти простые числа.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103
Все
четные числа делятся на 2. Если
сумму цифр номера можно разделить на 3
, число делится на 3
.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103
Если
последние 2 цифры числа можно разделить на 4, число делится на
4. Пример: 1 12 4 = 28 и 12 4 =
3
Если
число заканчивается на 0 или 5, оно делится на 5.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103
Если
Число можно разделить на 2 и 3, оно делится на 6. Эти
числа делятся на 7.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103
Эти
числа делятся на 8. Если
сумму цифр номера можно разделить на 9
, число делится на 9
. Пример: 54 9
= 6 5 + 4
= 9
Первые 27 простых чисел показаны желтым цветом в таблице ниже.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103
Вы можете
найдите эти простые числа, вычеркнув кратные 2, 3, 5 и 7
(кроме себя) на графике.
Попрактикуйтесь в этих методах, а затем пройдите тест 1 на Prime
числа.
Пс. Не забудьте использовать контрольный список, чтобы отслеживать
твоя работа.
1.6: Решение уравнений сложением и вычитанием
Начнем с определения переменной.
Переменная
Переменная — это символ (обычно буква), обозначающий значение, которое может варьироваться.
Далее мы продолжим определение уравнения.
Уравнение
Уравнение — это математическое утверждение, которое уравнивает два математических выражения.
Ключевым отличием математического выражения от уравнения является наличие знака равенства. Так, например,
2 + 3 [5 — 4 · 2], x2 + 2x — 3 и x + 2y + 3
— математические выражения (два из которых содержат переменные), а
3 + 2 (7-3) = 11, x + 3 = 4 и 3x = 9
— это уравнения.Обратите внимание, что каждое из уравнений содержит знак равенства, а выражения — нет.
Далее у нас есть определение решения уравнения.
Что значит быть решением
Решение уравнения — это числовое значение, которое удовлетворяет уравнению. То есть, когда переменная в уравнении заменяется решением, получается истинное утверждение.
Пример 1
Покажите, что 3 является решением уравнения x + 8 = 11.
Решение
Заменим 3 вместо x в данном уравнении и упростим.
\ [\ begin {array} {rlrl} {x + 8} & {= 11} & {} & {\ textcolor {red} {\ text {Данное уравнение. }}} \\ {3 + 8} & {= 11} & {} & {\ textcolor {red} {\ text {Substitute} 3 \ text {for} x.}} \\ {11} & {= 11 } & {} & {\ textcolor {red} {\ text {Упростите обе стороны. }}} \ end {array} \ nonumber \]
Поскольку левая и правая части последней строки равны, это показывает, что когда в уравнении подставляется 3 вместо x, получается истинное утверждение.Следовательно, 3 является решением уравнения.
Упражнение
Покажите, что 27 является решением уравнения x — 12 = 15
Пример 2
Является ли 23 решением уравнения 4 = y -11?
Решение
Заменим 23 вместо y в данном уравнении и упростим.
\ [\ begin {array} {ll} {4 = y-11} & {\ textcolor {red} {\ text {Данное уравнение. }}} \\ {4 = 23-11} & {\ textcolor {red} {\ text {Substitute} 23 \ text {for} y}} \\ {4 = 12} & {\ textcolor {red} {\ text {Упростите обе стороны.}}} \ end {array} \ nonumber \]
Поскольку левая и правая части последней строки не равны , это показывает, что когда 23 заменяется на на в уравнении, получается ложное утверждение. Следовательно, 23 — это , а не как решение уравнения.
Упражнение
Является ли 8 решением 5 = 12 — y ?
- Ответ
№
Эквивалентные уравнения
Начнем с определения эквивалентных уравнений.
Эквивалентные уравнения
Два уравнения эквивалентны, если они имеют один и тот же набор решений.
Пример 3
Эквивалентны ли уравнения x + 2 = 9 и x = 7?
Решение
Число 7 — единственное решение уравнения x + 2 = 9. Аналогично, 7 — единственное решение уравнения x = 7. Следовательно, x + 2 = 9 и Ответ: № x = 7 имеют одинаковые наборы решений и эквивалентны.
Упражнение
Эквивалентны ли уравнения x = 4 и x + 8 = 3?
- Ответ
№
Пример 4
Являются ли уравнения x 2 = x и x = 1 эквивалентными?
Решение
При осмотре уравнение x 2 = x имеет два решения: 0 и 1.С другой стороны, уравнение x = 1 имеет единственное решение, а именно 1. Следовательно, уравнения x 2 = x и x = 1 не имеют одинаковых наборов решений и равны не эквивалент .
Упражнение
Эквивалентны ли уравнения x = 2 и x 2 = 2 x ?
- Ответ
№
Операции, производящие эквивалентные уравнения
Есть много операций, которые производят эквивалентные операции.В этом разделе мы рассмотрим два: сложение и вычитание.
Добавление одинаковой величины к обеим сторонам уравнения
Добавление одного и того же количества к обеим сторонам уравнения не меняет набор решений. То есть, если
\ [a = b, \ nonumber \]
, а затем прибавление c к обеим сторонам уравнения дает эквивалентное уравнение
\ [a + c = b + c. \ Nonumber \]
Посмотрим, работает ли это так, как рекламируется. Рассмотрим уравнение x — 4 = 3.Судя по осмотру, 7 — единственное решение уравнения. Теперь давайте прибавим 4 к обеим сторонам уравнения, чтобы увидеть, эквивалентно ли полученное уравнение x — 4 = 3.
\ [\ begin {array} {rlrl} {x-4} & {= 3} & {} & {\ textcolor {red} {\ text {Данное уравнение. }}} \\ {x-4 + 4} & {= 3 + 4} & {} & {\ textcolor {red} {\ text {Добавьте 4 к обеим сторонам уравнения.}}} \\ {x} & {= 7} & {} & {\ textcolor {red} {\ text {Упростите обе части уравнения. }}} \ end {array} \ nonumber \]
Число 7 — единственное решение уравнения x = 7.Таким образом, уравнение x = 7 эквивалентно исходному уравнению x — 4 = 3 (они имеют одинаковые решения).
Важный момент
Добавление одинаковой суммы к обеим частям уравнения не меняет его решения.
Также факт, что вычитание одной и той же величины из обеих частей уравнения дает эквивалентное уравнение.
Вычитание одинаковой величины из обеих сторон уравнения
Вычитание одной и той же величины из обеих частей уравнения не меняет набор решений.То есть, если
\ [a = b, \ nonumber \]
, затем вычитание c из обеих частей уравнения дает эквивалентное уравнение
\ [a — c = b — c. \ Nonumber \]
Давайте также посмотрим, работает ли это так, как рекламируется. Рассмотрим уравнение
\ [x + 4 = 9. \ nonumber \]
Судя по осмотру, 5 — единственное решение уравнения. Теперь давайте вычтем 4 из обеих частей уравнения, чтобы увидеть, эквивалентно ли полученное уравнение x + 4 = 9.
\ [\ begin {array} {rlrl} {x + 4} & {= 9} & {} & {\ textcolor {red} {\ text {Данное уравнение. }}} \\ {x + 4-4} & {= 9-4} & {} & {\ textcolor {red} {\ text {Вычтите 4 из обеих частей уравнения. }}} \\ {x} & {= 5} & {} & {\ textcolor {red} {\ text {Упростите обе части уравнения. }}} \ end {array} \ nonumber \]
Число 5 — единственное решение уравнения \ (x = 5 \). Таким образом, уравнение \ (x = 5 \) эквивалентно исходному уравнению \ (x + 4 = 9 \) (они имеют одинаковые решения).
Важный момент
Вычитание одинаковой суммы из обеих частей уравнения не меняет его решения.
Письмо по математике
При решении уравнений соблюдайте следующие правила, чтобы аккуратно организовать свою работу:
1. Одно уравнение в строке . Значит, не стоит так устраивать свою работу:
\ [x + 3 = 7 \ quad x + 3-3 = 7-3 \ quad x = 4 \ nonumber \]
Это три уравнения на прямой. Лучше расположите свою работу по одному уравнению в строке следующим образом:
\ [\ begin {align} x + 3 & = 7 \\ x + 3-3 & = 7-3 \\ x & = 4 \ end {align} \ nonumber \]
2. Сложить и вычесть в строке. Не делайте этого:
\ [\ begin {array} {r} x -7 & = & 12 \\ +7 & & & + 7 \\ \ hline x & = & 19 \ end {array} \ nonumber \]
Вместо этого добавьте 7 к обеим сторонам уравнения «inline».
\ [\ begin {align} x-7 & = 12 \\ x-7 + 7 & = 12 + 7 \\ x & = 19 \ end {align} \ nonumber \]
Заворачивать и распаковывать
Предположим, вы упаковываете подарок для кузины. Вы выполняете следующие шаги по порядку.
- Положите подарочную бумагу.
- Оберните ленту.
- Наденьте декоративный бант.
Когда мы дарим упакованный подарок нашему двоюродному брату, он вежливо разворачивает подарок, «отменяя» каждый из наших трех шагов в обратном порядке.
- Снимите декоративный бант.
- Снимите ленту.
- Снимите подарочную бумагу.
Эта, казалось бы, легкомысленная упаковка и разворачивание подарка содержит очень сильные математические идеи.Рассмотрим математическое выражение \ (x + 4 \). Чтобы оценить это выражение при конкретном значении x , мы должны начать с заданного значения x , затем
- прибавить 4.
Предположим, мы начали с числа 7. Если мы прибавим 4, мы получим следующий результат: 11.
Теперь, как бы мы «развернули» этот результат, чтобы вернуться к нашему исходному числу? Начнем с нашего результата, затем
- Вычесть 4.
То есть, мы возьмем наш результат сверху, 11, затем вычтем 4, что вернет нас к нашему исходному числу, а именно 7.
Сложение и вычитание как обратные операции
Два чрезвычайно важных наблюдения:
Сумма, обратная сложению, — это вычитание. Если мы начнем с числа x и прибавим число к , то вычитание на из результата вернет нас к исходному числу x . В символах,
\ [x + a — a = x. \ Nonumber \]
Обратным вычитанием является сложение. Если мы начнем с числа x и вычтем число на , то добавление к результату вернет нас к исходному числу x .В символах,
\ [x — a + a = x. \ Nonumber \]
Пример 5
Решите \ (x — 8 = 10 \) для x .
Решение
Чтобы отменить эффект вычитания 8, мы добавляем 8 к обеим частям уравнения.
\ [\ begin {align} x-8 = 10 & \ textcolor {red} {\ text {Исходное уравнение. }} \\ x-8 + 8 = 10 + 8 & \ textcolor {red} {\ text {Добавьте 8 к обеим сторонам уравнения. }} \\ x = 18 & \ textcolor {red} {\ text {Слева добавление «отменяет» эффект}} \\ & \ textcolor {red} {\ text {вычитания 8 и возвращает} x.\ text {Справа}} \\ & \ textcolor {красный} {10 + 8 = 18.} \ end {выравнивается} \ nonumber \]
Следовательно, решение уравнения равно 18.
Чек
Для проверки подставьте решение 18 в исходное уравнение.
\ [\ begin {align} x — 8 = 10 & \ textcolor {red} {\ text {Исходное уравнение. }} \\ 18 — 8 = 10 & \ textcolor {red} {\ text {Заменить 18 на} x. } \\ 10 = 10 & \ textcolor {red} {\ text {Упростите обе стороны. }} \ конец {выровнено} \ nonumber \]
Тот факт, что последняя строка нашей проверки является истинным утверждением, гарантирует, что 18 является решением x — 8 = 10.
Упражнение
Решите \ (x + 5 = 12 \) для x .
- Ответ
7.
Пример 6
Решите \ (11 = y + 5 \) для г.
Решение
Чтобы отменить эффект добавления 5, мы вычитаем 5 из обеих частей уравнения.
\ [\ begin {align} 11 = y + 5 & \ textcolor {red} {\ text {Исходное уравнение. }} \\ 1 — 5 = y + 5 — 5 & \ textcolor {red} {\ text {Вычтите 5 из обеих частей уравнения.}} \\ 6 = y & \ textcolor {red} {\ text {Справа вычитание «отменяет» эффект}} \\ & \ textcolor {red} {\ text {добавления 5 и возвращает} y. \ text {Слева}} \\ & \ textcolor {red} {11 — 5 = 6.} \ end {align} \ nonumber \]
Следовательно, решение уравнения — 6.
Чек
\ [\ begin {align} 11 = y + 5 & \ textcolor {red} {\ text {Исходное уравнение. }} \\ 11 = 6 + 5 & \ textcolor {red} {\ text {Заменить 6 на} y.} \\ 11 = 11 & \ textcolor {red} {\ text {Упростите обе стороны. }} \ конец {выровнено} \ nonumber \]
Тот факт, что последняя строка нашей проверки является истинным утверждением, гарантирует, что 6 является решением 11 = y + 5.
Упражнение
Решите \ (y — 8 = 11 \) для y .
- Ответ
\ (y = 19. \)
Проблемы со словами
Решение проблемы со словом должно включать в себя каждый из следующих шагов.
Требования к решению проблем Word
- Настройка словаря переменных . Вы должны сообщить своим читателям, что представляет собой каждая переменная в вашей проблеме. Это можно сделать несколькими способами:
- Такие утверждения, как «Пусть P представляет периметр прямоугольника».
- Пометка неизвестных значений переменными в таблице.
- Обозначение неизвестных величин на эскизе или диаграмме.
- Установите уравнение .Каждое решение проблемы со словом должно включать тщательно составленное уравнение, которое точно описывает ограничения в постановке задачи.
- Решите уравнение . Вы всегда должны решать уравнение, заданное на предыдущем шаге.
- Ответьте на вопрос . Этот шаг легко упустить из виду. Например, в задаче может задаваться вопрос о возрасте Джейн, но решение вашего уравнения дает возраст сестры Джейн, Лиз. Убедитесь, что вы ответили на исходный вопрос, заданный в задаче.Ваше решение должно быть записано в предложении с соответствующими единицами.
- Оглянуться назад . Важно отметить, что этот шаг не означает, что вы должны просто проверить свое решение в своем уравнении. В конце концов, возможно, что ваше уравнение неверно моделирует ситуацию проблемы, поэтому у вас может быть действительное решение неправильного уравнения. Важный вопрос: «Имеет ли ваш ответ смысл на основе слов в исходной постановке проблемы».
Проведем тест-драйв этим требованиям.
Пример 7
На четыре больше определенного числа равно 12. Найдите число.
Решение
В нашем решении мы внимательно рассмотрим каждый шаг «Требования к решению проблем Word».
1. Настройка словаря переменных . Мы можем удовлетворить это требование, просто заявив: «Пусть x представляет определенное число».
2. Установите уравнение . «На четыре больше, чем определенное число равно 12» становится
. \ [\ begin {align} \ colorbox {cyan} {4} & \ text {more than} & \ colorbox {cyan} {определенное число} & \ text {is} & \ colorbox {cyan} {12} \ \ 4 & + & x & = & 12 \ end {выровнено} \ nonumber \]
3. Решите уравнение . Чтобы «отменить» сложение, вычтите 4 из обеих частей уравнения.
\ [\ begin {align} 4 + x = 12 & \ textcolor {red} {\ text {Исходное уравнение.}} \\ 4 + x — 4 = 12-4 & \ textcolor {red} {\ text {Вычесть 4 с обеих сторон уравнения. }} \\ x = 8 & \ textcolor {red} {\ text {Слева вычитание 4 «отменяет» эффект}} \\ & \ textcolor {red} {\ text {добавления 4 и возвращает} x. \ text {Справа}} \\ & \ textcolor {красный} {12 — 4 = 8.} \ конец {выровнено} \ nonumber \]
4. Ответить на вопрос . Номер 8.
5. Оглянуться назад . Удовлетворяет ли решение 8 словам исходной задачи? Нам сказали, что «на четыре больше, чем определенное число — 12». Итак, на четыре больше, чем на 8, будет 12, так что наше решение правильное.
Упражнение
12 больше определенного числа равно 19. Найдите число.
- Ответ
7
Пример 8
Амели снимает 125 долларов со своего сберегательного счета.Из-за вывода средств текущий баланс на ее счету составляет 1200 долларов. Каков был исходный баланс на счете до вывода средств?
Решение
В нашем решении мы внимательно рассмотрим каждый шаг требования для решения проблем Word .
1. Создайте словарь переменных. Мы можем удовлетворить это требование, просто заявив: «Пусть B представляет исходный баланс на счете Амели».
2. Установите уравнение . Мы можем описать ситуацию словами и символами.
\ [\ begin {align} \ colorbox {cyan} {Исходный баланс} & \ text {minus} & \ colorbox {Вывод средств Амели} & \ text {is} & \ colorbox {cyan} {Текущий баланс} \\ B & — & 125 & = & 1200 \ end {выровнено} \ nonumber \]
3. Решите уравнение . Чтобы «отменить» вычитание, добавьте 125 к обеим частям уравнения.
\ [\ begin {align} B — 125 = 1200 & \ textcolor {red} {\ text {Исходное уравнение.}} \\ B — 125 + 125 = 1200 + 125 & \ textcolor {red} {\ text {Добавьте 125 к обеим сторонам уравнения. }} \\ B = 1325 & \ textcolor {red} {\ text {Слева добавление 125 «отменяет» эффект}} \\ & \ textcolor {red} {\ text {вычитания 125 и возвращает} B. \ text {Справа}} \\ & \ textcolor {красный} {1200 + 125 = 1325.} \ end {выравнивается} \ nonumber \]
4. Ответить на вопрос . Первоначальный баланс составлял 1325 долларов.
5. Оглянуться назад . Удовлетворяет ли решение за 1325 долларов словам исходной задачи? Обратите внимание, что если Амели снимет с этого баланса 125 долларов, новый баланс составит 1200 долларов.Значит, решение правильное.
Упражнение
Фред снимает со своего счета 230 долларов, уменьшая свой баланс до 3500 долларов. Каков был его первоначальный баланс?
- Ответ
$ 3730
Пример 9
Периметр треугольника 114 футов. Две стороны треугольника имеют размеры 30 футов и 40 футов соответственно. Найдите размер третьей стороны треугольника.
Решение
В нашем решении мы внимательно рассмотрим каждый шаг требования для решения проблем Word .
1. Создайте словарь переменных. Когда речь идет о геометрии, мы можем создать наш словарь переменных, пометив тщательно построенную диаграмму. Помня об этом, мы рисуем треугольник, затем маркируем его известные и неизвестные стороны и его периметр.
Из рисунка видно, что x представляет длину неизвестной стороны треугольника. На рисунке также представлена информация, необходимая для решения. 2. Составьте уравнение. Мы знаем, что периметр треугольника находится путем нахождения суммы трех его сторон; прописью и символами,
\ [\ begin {align} \ colorbox {cyan} {Perimeter} & \ text {is} & \ colorbox {cyan} {First Side} & \ text {plus} & \ colorbox {cyan} {Second Side} & \ текст {плюс} & \ colorbox {голубой} {Третья сторона} \\ 114 & = & x & + & 30 & + & 40 \ end {align} \ nonumber \]
Упростите правую часть, добавив 30 и 40; я.е., \ (30 + 40 = 70 \).
\ [114 = x + 70 \ nonumber \]
3. Решите уравнение. Чтобы «отменить» добавление 70, вычтите 70 из обеих частей уравнения.
\ [\ begin {align} 114 = x + 70 & \ textcolor {red} {\ text {Наше уравнение. }} \\ 114 — 70 = x + 70 — 70 & \ textcolor {red} {\ text {Вычтите 70 с обеих сторон. }} \\ 44 = x & \ textcolor {red} {\ text {Справа вычитание 70 «отменяет» эффект}} \\ & \ textcolor {red} {\ text {добавления 70 и возвращает} x .\ text {Слева}} \\ & \ textcolor {red} {114 — 70 = 44.} \ end {align} \ nonumber \]
4. Ответить на вопрос . Неизвестная сторона треугольника составляет 44 фута.
5. Оглянуться назад . Удовлетворяет ли решение 44 фута словам исходной задачи? Нам сказали, что периметр составляет 114 футов, а две стороны имеют длину 30 и 40 футов соответственно. Мы обнаружили, что третья сторона имеет длину 44 фута. Теперь, сложив три стороны, 30+ 40+ 44 = 114, что равно периметру в 114 футов.Ответ работает!
Упражнение
Периметр четырехугольника 200 метров. Если три стороны имеют размер 20, 40 и 60 метров, какова длина четвертой стороны.
- Ответ
80 метров
Упражнения
Какие из чисел, следующих за данным уравнением, в упражнениях 1-12 являются решениями данного уравнения? Поддержите свой ответ работой, аналогичной показанной в примерах 1 и 2.
1. х — 4 = 6; 10, 17, 13, 11
2. х — 9 = 7; 17, 23, 19, 16
3. х + 2 = 6; 5, 11, 7, 4
4. х + 3 = 9; 6, 9, 7, 13
5. х + 2 = 3; 8, 1, 4, 2
6. х + 2 = 5; 10, 3, 6, 4
7. х — 4 = 7; 12, 11, 18, 14
8. х — 6 = 7; 13, 16, 20, 14
9. х + 3 = 4; 8, 4, 2, 1
10. х + 5 = 9; 5, 11, 7, 4
11. х — 6 = 8; 17, 21, 14, 15
12. х — 2 = 9; 11, 14, 12, 18
В упражнениях 13-52 решите данное уравнение относительно x .
13. х + 5 = 6
14. х + 6 = 19
15. 5 = 4 + x
16. 10 = 8 + x
17. 13 + x = 17
18. 7+ x = 15
19. 9+ x = 10
20. 14 + х = 17
21. 19 = х — 3
22. 2 = х — 11
23. х — 18 = 1
24. х — 20 = 8
25. х — 3 = 11
26. х — 17 = 18
27. 2+ x = 4
28. 1+ x = 16
29. х — 14 = 12
30.х — 1 = 17
31. х + 2 = 8
32. х + 11 = 14
33,11 + х = 17
34,11 + х = 18
35. х + 13 = 17
36. х + 1 = 16
37,20 = 3 + х
38. 9 = 3 + х
39,20 = 8 + х
40. 10 = 3 + х
41,3 = х — 20
42,13 = х — 15
43. х + 16 = 17
44. х + 6 = 12
45,5 = х — 6
46. 10 = х — 7
47.18 = х — 6
48,14 = х — 4
49,18 = 13 + х
50,17 = 5 + х
51. х — 9 = 15
52. х — 11 = 17
53. 12 меньше определенного числа равно 19. Найдите число.
54. 19 меньше определенного числа равно 1. Найдите число.
55. Треугольник имеет периметр 65 футов. Он также имеет две стороны размером 19 футов и 17 футов соответственно. Найдите длину третьей стороны треугольника.
56.Треугольник имеет периметр 55 футов. Он также имеет две стороны размером 14 футов и 13 футов соответственно. Найдите длину третьей стороны треугольника.
57. Берт вносит депозит на счет, имеющий остаток в 1900 долларов. После депозита новый баланс на счете составляет 8050 долларов. Найдите сумму депозита.
58. Дэйв вносит депозит на счет с балансом 3500 долларов. После депозита новый баланс на счете составляет 4600 долларов. Найдите сумму депозита.
59. 8 больше определенного числа равно 18. Найдите число.
60. На 3 больше определенного числа будет 19. Найдите число.
61. Мишель снимает 120 долларов со своего банковского счета. В результате баланс нового аккаунта составляет 1000 долларов США. Найдите баланс счета перед выводом.
62. Мерси снимает 430 долларов со своего банковского счета. В результате баланс нового аккаунта составляет 1200 долларов. Найдите баланс счета перед выводом.
63. Выкупа .В период с января по март прошлого года 650 000 домов получили уведомление о отчуждении права выкупа. Между первыми тремя месяцами этого года было 804 000 уведомлений о потере права выкупа. Насколько увеличилось количество уведомлений о потере права выкупа дома? Associated Press Times-Standard 22.04.09
64. Цена дома . Согласно данным экономического индекса Гумбольдта экономического факультета Государственного университета имени Гумбольдта, средняя цена на жилье в США упала на 1500 долларов за последний месяц до 265 000 долларов. Какова была средняя цена дома до падения цен?
65. Беспилотный аэродромный аппарат . Беспилотный дрон Global Hawk компании Northrup Grumman может летать на высоте 65 000 футов, что на 40 000 футов выше, чем беспилотный самолет NASA Ikhana. Насколько высоко может летать Ихана?
66. Tribal Land . Племя Юрок имеет возможность купить 47 000 акров земли, чтобы увеличить территорию своих предков. Первая фаза будет включать 22 500 акров в водоразделах Каппель и Пекман. На втором этапе планируется засеять посевными площадями в районе Блю-Крик. Сколько гектаров можно купить на втором этапе? Times-Standard 15.04.09
ответы
1.10
3. 4
5. 1
7. 11
9. 1
11. 14
13. 1
15. 1
17. 4
19. 1
21. 22
23. 19
25. 14
27. 2
29. 26
31. 6
33. 6
35. 4
37,17
39. 12
41,23
43. 1
45,11
47. 24
49.5
51. 24
53,31
55. 29
57. $ 6150
59. 10
61. $ 1120
63,154 000
65.
Синтетическое подразделение:
(ii)
Синтетическое подразделение:
(iii)
Синтетическое подразделение:
(iv)
Синтетическое подразделение :
(v)
Синтетическое подразделение:
(vi)
Синтетическое подразделение:
Пусть px = x2-5x + 5.
py = y2-32y + 1
pm = m3 + 2m2-m + 10
∴pa + pa = 4a2 + 20
py = 2y3-6y2-5y + 7
Пусть px = 2x-2×3 + 7.
p3 = 2 × 3-2 × 33 + 7 = 6-2 × 27 + 7 = 6-54 + 7 = -41
Таким образом, значение полинома для x = 3 равно −41 .
p-1 = 2 × -1-2 × -13 + 7 = -2-2 × -1 + 7 = -2 + 2 + 7 = 7
Таким образом, значение полинома для x = −1 равно 7.
p0 = 2 × 0-2 × 03 + 7 = 0-0 + 7 = 7
Таким образом, значение полинома для x = 0 равно 7.
(i)
пикселей = x3∴p1 = 13 = 1p0 = 03 = 0p-2 = -23 = -8
(ii)
py = y2-2y + 5∴p1 = 12-2 × 1 + 5 = 1-2 + 5 = 4p0 = 02-2 × 0 + 5 = 0-0 + 5 = 5p-2 = -22-2 × -2 + 5 = 4 + 4 + 5 = 13
(iii)
пикселей = x4-2×2-x∴p1 = 14-2 × 12-1 = 1-2-1 = -2p0 = 04-2 × 02-0 = 0-0-0 = 0p-2 = -24-2 × -22 —2 = 16-2 × 4 + 2 = 16-8 + 2 = 10
Пусть pm = m3 + 2m + a
Таким образом, значение a равно 0.
Пусть px = mx2-2x + 3.
Таким образом, значение m равно 2.
По синтетическому разделению:
По синтетическому разделению:
По синтетическому подразделению:
Пусть py = y3-5y2 + 7y + m.
Таким образом, значение m равно 92.
Пусть p ( x ) = x 2 + 2 x — 3.
Пусть px = x3-mx2 + 10x-20.
Таким образом, значение м — 2.
(i)
пикселей = x3-x2-x-1
пикселей = 2×3-x2-45
Пусть p ( x ) = x 31 + 31.
Пусть p ( м ) = м 21 — 1 и q ( м ) = м 22 — 1.
Пусть p ( x ) = nx 2 -5 x + m .
Также
Из (1) и (2) имеем
(i)
пикселей = 2 + 5x∴p2 = 2 + 5 × 2 = 2 + 10 = 12p-2 = 2 + 5 × -2 = 2-10 = -8p1 = 2 + 5 × 1 = 2 + 5 = 7
∴p2 + p-2-p1 = 12 + -8-7 = 12-8-7 = 12-15 = -3
пикселей = 2×2-53x + 5
∴p53 = 2 × 532-53 × 53 + 5 = 2 × 75-25 × 3 + 5 = 150-75 + 5 = 80
(i) 2 x 2 + x — 1
(i)
2×2 + x-1 = 2×2 + 2x-x-1 = 2xx + 1-1x + 1 = x + 12x-1
(ii)
2m2 + 5m-3 = 2m2 + 6m-m- 3 = 2 мм + 3-1 м + 3 = м + 32 м-1
(iii)
12×2 + 61x + 77 = 12×2 + 28x + 33x + 77 = 4x3x + 7 + 113x + 7 = 3x + 74x + 11
(iv )
3y2-2y-1 = 3y2-3y + y-1 = 3yy-1 + 1y-1 = y-13y + 1
(v)
3×2 + 4x + 3 = 3×2 + 3x + x + 3 = 3xx + 3 + 1x + 3 = x + 33x + 1
(vi)
12×2-3x + 4 = 12×2-2x-x + 4 = 12xx-4-1x-4 = x-412x-1
(i) ( x 2 — x ) 2 — 8 ( x 2 — x ) + 12
(ii) ( x — 5) 2 — (5 x — 25) — 24
(iii) ( x 2 — 6 x ) 2 — 8 ( x 2 — 6 x + 8) — 64
(iv) ( x 2 -2 x + 3) ( x 2 -2 x + 5) — 35
(v) ( y + 2) ( y — 3) ( y + 8) ( y + 3) + 56
(vi) ( y 2 + 5 y ) ( y 2 + 5 y — 2 ) — 24
(vii) ( x — 3) ( x — 4) 2 ( x — 5) — 6
(i)
( x 2 — x ) 2 — 8 ( x 2 — x ) + 12
Пусть x 2 — x z .
∴x2-x2-8×2-x + 12 = z2-8z + 12 = z2-6z-2z + 12 = zz-6-2z-6 = z-6z-2
= x2-x-6×2-x-2 Заменить z = x2-x = x2-3x + 2x-6×2-2x + x-2 = xx-3 + 2x-3xx-2 + 1x-2 = x-3x + 2x-2x + 1
(ii)
( x — 5) 2 — (5 x — 25) — 24
= ( x — 5) 2 — 5 ( x — 5) — 24
Пусть x — 5 = z .
∴x-52-5x-5-24 = z2-5z-24 = z2-8z + 3z-24 = zz-8 + 3z-8 = z-8z + 3
= x-5-8x-5 + 3 Заменить z = x-5 = x-13x-2
(iii)
( x 2 -6 x ) 2 -8 ( x 2 -6 x + 8) — 64
= ( x 2 — 6 x ) 2 — 8 ( x 2 — 6 x ) — 64-64
= ( x 2 — 6 x ) 2 — 8 ( x 2 — 6 x ) — 128
Пусть x 2 — 6 x = z .
∴x2-6×2-8×2-6x-128 = z2-8z-128 = z2-16z + 8z-128 = zz-16 + 8z-16 = z-16z + 8
= x2-6x-16×2-6x + 8 Заменить z = x2-6x = x2-8x + 2x-16×2-4x-2x + 8 = xx-8 + 2x-8xx-4-2x-4 = x-8x + 2x-4x-2
( x 2 -2 x + 3) ( x 2 -2 x + 5) — 35
Пусть x 2 -2 x = z .
∴x2-2x + 3×2-2x + 5-35 = z + 3z + 5-35 = z2 + 5z + 3z + 15-35 = z2 + 8z-20 = z2 + 10z-2z-20
= zz + 10 -2z + 10 = z + 10z-2 = x2-2x + 10×2-2x-2 Заменить z = x2-2x
(v)
( y + 2) ( y -3) ( y + 8) ( y + 3) + 56
= ( y + 2) ( y + 3) ( y + 8) ( y -3) + 56
= ( y 2 + 5 y + 6) ( y 2 + 5 y -24) + 56
Let y 2 + 5 y = z .
∴y2 + 5y + 6y2 + 5y-24 + 56 = z + 6z-24 + 56 = z2-18z-144 + 56 = z2-18z-88
= z2-22z + 4z-88 = zz-22 + 4z -22 = z-22z + 4 = y2 + 5y-22y2 + 5y + 4 Заменить z = y2 + 5y
= y2 + 5y-22y2 + 4y + y + 4 = y2 + 5y-22yy + 4 + 1y + 4 = y2 + 5y-22y + 4y + 1
(vi)
( y 2 + 5 y ) ( y 2 + 5 y -2) — 24
Let y 2 + 5 y = z .
∴y2 + 5yy2 + 5y-2-24 = zz-2-24 = z2-2z-24 = z2-6z + 4z-24 = zz-6 + 4z-6 = z-6z + 4
= y2 + 5y -6y2 + 5y + 4 Заменить z = y2 + 5y = y2 + 6y-y-6y2 + 4y + y + 4 = yy + 6-1y + 6yy + 4 + 1y + 4 = y + 6y-1y + 4y + 1
(vii)
( x — 3) ( x — 4) 2 ( x — 5) — 6
= ( x — 3) ( x — 5) ( x -4) 2 -6
= ( x 2 -8 x + 15) ( x 2 -8 x + 16) — 6
Пусть x 2 — 8 x = z .
∴x2-8x + 15×2-8x + 16-6 = z + 15z + 16-6 = z2 + 31z + 240-6 = z2 + 31z + 234
= z2 + 18z + 13z + 234 = zz + 18 + 13z + 18 = z + 18z + 13 = x2-8x + 18×2-8x + 13 Заменить z = x2-8x
(A) 12 (B) 5 (C) 2 (D) 0
(A) 3 (B) 2 (C) 5 (D) 7
(A) (1, — 1) (B) (3, -1) (C) (1, 0, 0, -1) (D) (1, 3, — 1)
(A) 3 (B) 77 (C) 42 7 + 3 (D) 497
(A) 4 (B) 2 (C) -2 (D) -4
(A) 2 (B) -2 (C) -3 (D) 3
(A) 5 (B) 3 (C) 2 (D) 0
(i)
В алгебраическом выражении, если степени переменных являются целыми числами, тогда алгебраическое выражение является полиномом.
7 = 7 × 1 = 7×0
Степень полинома 0 не определена.
Наивысшая степень переменной в полиноме называется степенью полинома.
x3-1 = x3 + 0x2 + 0x-1
пикселей = x2-77x + 3
Пусть p ( x ) = 2 x 3 + 2 x
Пусть p ( x ) = 3 x 2 + mx .
x2-32x-7×3 + 4 = x22x-7×3 + 4-32x-7×3 + 4 = 2×3-7×5 + 4×2-6x + 21×3-12 = -7×5 + 2×3 + 21×3 + 4×2-6x-12 = -7×5 + 23×3 + 4×2-6x-12
Таким образом, степень полученного многочлена равна 5.
Многочлен первой степени называется линейным многочленом.
Наивысшая степень переменной в полиноме от одной переменной называется степенью полинома.
Степень многочлена 5 + 3 x 4 равна 4.
7 = 7 × 1 = 7 x 0
Степень полинома ax 7 + bx 9 равна 9.
Многочлен, записанный в возрастающей или убывающей степени своей переменной, называется стандартной формой полинома.
Данный полином равен 4 x 2 + 7 x 4 — x 3 — x + 9.
Стандартная форма многочлена 7 x 4 — x 3 + 4 x 2 — x + 9 или 9 — x + 4 x 2 — x 3 + 7 x 4 .
Данный полином равен p + 2 p 3 + 10 p 2 + 5 p 4 — 8.
(i)
x4 + 16 = x4 + 0x3 + 0x2 + 0x + 16
m5 + 2m2 + 3m + 15 = m5 + 0m4 + 0m3 + 2m2 + 3m + 15
(i)
Коэффициент формы многочлена (3, −2, 0, 7, 18).
Коэффициент формы многочлена (6, 1, 0, 7).
Коэффициент формы многочлена (4, 5, −3, 0).
(i)
7×4-2×3 + x + 10 + 3×4 + 15×3 + 9×2-8x + 2 = 7×4 + 3×4-2×3 + 15×3 + 9×2 + x-8x + 10 + 2 = 10×4 + 13×3 + 9×2-7x + 12
(ii)
3p3q + 2p2q + 7 + 2p2q + 4pq-2p3q = 3p3q-2p3q + 2p2q + 2p2q + 4pq + 7 = p3q + 4p2q + 4pq + 7
(i)
5×2-2y + 9-3×2 + 5y-7 = 5×2-2y + 9-3×2-5y + 7 = 5×2-3×2-2y-5y + 9 + 7 = 2×2-7y + 16
(ii )
2×2 + 3x + 5-x2-2x + 3 = 2×2 + 3x + 5-x2 + 2x-3 = 2×2-x2 + 3x + 2x + 5-3 = x2 + 5x + 2
(ii) (5 м 3 -2) ( м 2 — м + 3)
(i)
м3-2м + 3м4-2м2 + 3м + 2 = м3м4-2м2 + 3м + 2-2мм4-2м2 + 3м + 2 + 3м4-2м2 + 3м + 2 = м7-2м5 + 3м4 + 2м3- 2m5 + 4m3-6m2-4m + 3m4-6m2 + 9m + 6 = m7-2m5-2m5 + 3m4 + 3m4 + 2m3 + 4m3-6m2-6m2-4m + 9m + 6 = m7-4m5 + 6m4 + 6m3-12m2 + 5м + 6
(ii)
5м3-2м2-м + 3 = 5м3м2-м + 3-2м2-м + 3 = 5м5-5м4 + 15м3-2м2 + 2м-6
Коэффициент формы частного является (3, 1, 4).
Пусть px = x3-2mx + 21.
Таким образом, значение м — 1.
Общая численность населения трех деревень
= 5×2-3y2 + 7y2 + 2xy + 9×2 + 4xy = 5×2 + 9×2-3y2 + 7y2 + 2xy + 4xy = 14×2 + 4y2 + 6xy
Общее количество человек, переехавших в другую деревню на образование
= x2 + xy-y2 + 5xy + 3×2 + xy = x2 + 3×2-y2 + xy + 5xy + xy = 4×2-y2 + 7xy
∴ Оставшаяся общая численность населения трех деревень = Общая численность населения трех деревень — Всего количество человек, которые отправились в другую деревню для получения образования
= 14×2 + 4y2 + 6xy-4×2-y2 + 7xy = 14×2 + 4y2 + 6xy-4×2 + y2-7xy = 14×2-4×2 + 4y2 + y2 + 6xy-7xy = 10×2 + 5y2-xy
Таким образом, оставшаяся общая численность населения этих трех деревень составляет 10 x 2 + 5 y 2 — xy .
Пусть px = bx2 + x + 5 и qx = bx3-2x + 5.
Остаток при делении qx = bx3-2x + 5 by ( x — 3) равно n .
Теперь,
mn = 0⇒9b + 8-27b-1 = 0 Используя 1 и 2⇒9b-27b + 8 + 1 = 0⇒-18b + 9 = 0⇒-18b = -9⇒b = -9-18 = 12
Таким образом, значение b равно 12.
8м2 + 3м-6-9м-7 + 3м2-2м + 4 = 8м2 + 3м-6-9м + 7 + 3м2-2м + 4 = 8м2 + 3м2 + 3м-9м-2м-6 + 7 + 4 = 11м2-8м + 5
Пусть p ( x ) будет полиномом, который нужно вычесть из x 2 + 13 x + 7, чтобы получить полином 3 x 2 + 5 x — 4.
Требуемый полином может быть получен путем вычитания полинома 4 m + 2 n + 3 из 6 m + 3 n + 10.
Слово равно говорит нам, что знак равенства находится между 9 и 15.
Расположение слова — говорит нам, что знак равенства находится между 7 и 56.
Простые числа
простые множители 30 — это числа 2, 3 и 5.
Вы можете использовать Сито Эратосфена в найти простые числа.
| 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
| 32 | 33 | 34 | 35 | 36 | 37 |
| 38 | 39 | 40 | 41 | 42 | 43 |
| 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 |
| 56 | 57 | 58 | 59 | 60 | 61 |
| 62 | 63 | 64 | 65 | 66 | 67 |
| 68 | 69 | 70 | 71 | 72 | 73 |
| 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 |
| 86 | 87 | 88 | 89 | 90 | 91 |
| 92 | 93 | 94 | 95 | 96 | 97 |
| 98 | 99 | 100 | 101 | 102 | 103 |
| 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
| 32 | 33 | 34 | 35 | 36 | 37 |
| 38 | 39 | 40 | 41 | 42 | 43 |
| 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 |
| 56 | 57 | 58 | 59 | 60 | 61 |
| 62 | 63 | 64 | 65 | 66 | 67 |
| 68 | 69 | 70 | 71 | 72 | 73 |
| 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 |
| 86 | 87 | 88 | 89 | 90 | 91 |
| 92 | 93 | 94 | 95 | 96 | 97 |
| 98 | 99 | 100 | 101 | 102 | 103 |
| 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
| 32 | 33 | 34 | 35 | 36 | 37 |
| 38 | 39 | 40 | 41 | 42 | 43 |
| 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 |
| 56 | 57 | 58 | 59 | 60 | 61 |
| 62 | 63 | 64 | 65 | 66 | 67 |
| 68 | 69 | 70 | 71 | 72 | 73 |
| 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 |
| 86 | 87 | 88 | 89 | 90 | 91 |
| 92 | 93 | 94 | 95 | 96 | 97 |
| 98 | 99 | 100 | 101 | 102 | 103 |
| 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
| 32 | 33 | 34 | 35 | 36 | 37 |
| 38 | 39 | 40 | 41 | 42 | 43 |
| 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 |
| 56 | 57 | 58 | 59 | 60 | 61 |
| 62 | 63 | 64 | 65 | 66 | 67 |
| 68 | 69 | 70 | 71 | 72 | 73 |
| 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 |
| 86 | 87 | 88 | 89 | 90 | 91 |
| 92 | 93 | 94 | 95 | 96 | 97 |
| 98 | 99 | 100 | 101 | 102 | 103 |
Пример: 1 12 4 = 28 и 12 4 = 3
| 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
| 32 | 33 | 34 | 35 | 36 | 37 |
| 38 | 39 | 40 | 41 | 42 | 43 |
| 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 |
| 56 | 57 | 58 | 59 | 60 | 61 |
| 62 | 63 | 64 | 65 | 66 | 67 |
| 68 | 69 | 70 | 71 | 72 | 73 |
| 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 |
| 86 | 87 | 88 | 89 | 90 | 91 |
| 92 | 93 | 94 | 95 | 96 | 97 |
| 98 | 99 | 100 | 101 | 102 | 103 |
| 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
| 32 | 33 | 34 | 35 | 36 | 37 |
| 38 | 39 | 40 | 41 | 42 | 43 |
| 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 |
| 56 | 57 | 58 | 59 | 60 | 61 |
| 62 | 63 | 64 | 65 | 66 | 67 |
| 68 | 69 | 70 | 71 | 72 | 73 |
| 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 |
| 86 | 87 | 88 | 89 | 90 | 91 |
| 92 | 93 | 94 | 95 | 96 | 97 |
| 98 | 99 | 100 | 101 | 102 | 103 |
| 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
| 32 | 33 | 34 | 35 | 36 | 37 |
| 38 | 39 | 40 | 41 | 42 | 43 |
| 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 |
| 56 | 57 | 58 | 59 | 60 | 61 |
| 62 | 63 | 64 | 65 | 66 | 67 |
| 68 | 69 | 70 | 71 | 72 | 73 |
| 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 |
| 86 | 87 | 88 | 89 | 90 | 91 |
| 92 | 93 | 94 | 95 | 96 | 97 |
| 98 | 99 | 100 | 101 | 102 | 103 |
| 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
| 32 | 33 | 34 | 35 | 36 | 37 |
| 38 | 39 | 40 | 41 | 42 | 43 |
| 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 |
| 56 | 57 | 58 | 59 | 60 | 61 |
| 62 | 63 | 64 | 65 | 66 | 67 |
| 68 | 69 | 70 | 71 | 72 | 73 |
| 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 |
| 86 | 87 | 88 | 89 | 90 | 91 |
| 92 | 93 | 94 | 95 | 96 | 97 |
| 98 | 99 | 100 | 101 | 102 | 103 |
Пример: 54 9 = 6 5 + 4 = 9
| 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
| 32 | 33 | 34 | 35 | 36 | 37 |
| 38 | 39 | 40 | 41 | 42 | 43 |
| 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 |
| 56 | 57 | 58 | 59 | 60 | 61 |
| 62 | 63 | 64 | 65 | 66 | 67 |
| 68 | 69 | 70 | 71 | 72 | 73 |
| 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 |
| 86 | 87 | 88 | 89 | 90 | 91 |
| 92 | 93 | 94 | 95 | 96 | 97 |
| 98 | 99 | 100 | 101 | 102 | 103 |
| 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
| 32 | 33 | 34 | 35 | 36 | 37 |
| 38 | 39 | 40 | 41 | 42 | 43 |
| 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 |
| 56 | 57 | 58 | 59 | 60 | 61 |
| 62 | 63 | 64 | 65 | 66 | 67 |
| 68 | 69 | 70 | 71 | 72 | 73 |
| 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 |
| 86 | 87 | 88 | 89 | 90 | 91 |
| 92 | 93 | 94 | 95 | 96 | 97 |
| 98 | 99 | 100 | 101 | 102 | 103 |
Пс. Не забудьте использовать контрольный список, чтобы отслеживать твоя работа.
№
№
№
7.
\ (y = 19. \)
- Такие утверждения, как «Пусть P представляет периметр прямоугольника».
- Пометка неизвестных значений переменными в таблице.
- Обозначение неизвестных величин на эскизе или диаграмме.
7
$ 3730
80 метров

