Номер (задание) 17 — гдз по алгебре 9 класс Макарычев, Миндюк
Условие / номер / 17
17. Постройте график функции, заданной формулой: а) f(x) — 1,5 — Зх; б) f(x) = 4,5х; в) f(x) = 10/x г) f(x) =-1/x Укажите область определения и область значений функции.
решебник / номер / 17
youtube.com/embed/jwraip_n6Pw?start=5003″ allow=»cross-origin-isolated» frameborder=»0″ allowfullscreen=»»>
решебник №2 / номер / 17Номер (задание) 11 — гдз по алгебре 9 класс Макарычев, Миндюк
11. Какова область определения функции, заданной формулой: а) у = х2 + 2х; б) у = x-1 / 1+x; в) y = √9 + х?
Какова область определения функции, заданной формулой: а) у = х2 + 2х; б) у = x-1 / 1+x; в) y = √9 + х?
решебник / номер / 11
Видеорешение / номер / 11
решебник №2 / номер / 11
Номер (задание) 29 — гдз по алгебре 9 класс Макарычев, Миндюк
Условие / номер / 29 29.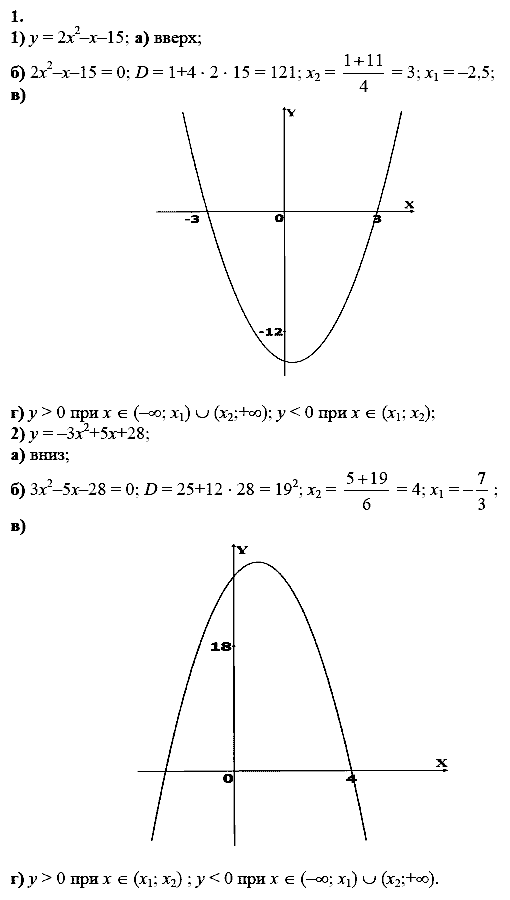 Решите уравнение: а) -0,5(3x — 4) + 15x = 4(1,5x + 1) + 3; б) (2х — 3)(2х + 3) — x2 = 12x — 69 + Зx2.
Решите уравнение: а) -0,5(3x — 4) + 15x = 4(1,5x + 1) + 3; б) (2х — 3)(2х + 3) — x2 = 12x — 69 + Зx2.
решебник / номер / 29
youtube.com/embed/jwraip_n6Pw?start=9277″ allow=»cross-origin-isolated» frameborder=»0″ allowfullscreen=»»>
решебник №2 / номер / 29Номер (задание) 9 — гдз по алгебре 9 класс Макарычев, Миндюк
9. Найдите область определения функции, заданной формулой:
Найдите область определения функции, заданной формулой:
решебник / номер / 9
Видеорешение / номер / 9youtube.com/embed/jwraip_n6Pw?start=2090″ allow=»cross-origin-isolated» frameborder=»0″ allowfullscreen=»»>
Алгебра Мордкович Учебник (Мнемозина 2021)
Алгебра 9 класс. Учебник в 2 частях / Мордкович и др. ; Мнемозина (2019-2021). Электронная версия для ознакомления и принятия решения о покупке книги. Цитаты из учебника использованы в учебных целях.
; Мнемозина (2019-2021). Электронная версия для ознакомления и принятия решения о покупке книги. Цитаты из учебника использованы в учебных целях.
Учебник написан в соответствии с требованиями ФГОС и Примерной образовательной программы основного общего образования. Приоритетной содержательно-методической основой курса является функционально-графическая линия, а его идейным стержнем — математический язык и математическая модель, с помощью которых строится описание реальных ситуаций окружающей действительности. В учебнике реализованы принципы проблемного, развивающего и опережающего обучения. Доступное изложение приучает школьников к чтению учебной литературы и самостоятельному поиску информации. Часть 1-я — теоретическая. Часть 2-я — практическая (задачник).
Алгебра 9 класс (УМК Мордкович)
Часть 1. Учебник (теория)
ГЛАВА 1. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА И ИХ СИСТЕМЫ
…
Алгебра 9 класс (УМК Мордкович)
Часть 2.
 Задачник (упражнения)
Задачник (упражнения)ГЛАВА 1. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА И ИХ СИСТЕМЫ
ГЛАВА 2. СИСТЕМЫ УРАВНЕНИЙГЛАВА 3. ЧИСЛОВЫЕ ФУНКЦИИГЛАВА 4. ПРОГРЕССИИ
(15. Числовые последовательности. 16. Арифметическая прогрессия. 17. Геометрическая прогрессия)
ГЛАВА 5. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ
(18. Комбинаторные задачи. 19. Статистика: дизайн информации. 20. Простейшие вероятностные задачи. 21. Экспериментальные данные и вероятности событий)
Алгебра 9 класс. Учебник в 2 частях / Мордкович и др.; М.: Мнемозина (2019-2021). Электронная версия для ознакомления и принятия решения о покупке книги. Цитаты из учебника использованы в учебных целях.
Алгебра 8 Макарычев Учебник | Частная школа. 8 класс
Алгебра 8 класс. Учебник УМК Макарычев и другие (М: Просвещение) + ОТВЕТЫ. Электронная версия (онлайн учебник с ответами) для ознакомления при покупке книги: Макарычев, Миндюк, Суворова: Алгебра. 8 класс. Учебник. ФГОС. Цитаты из учебника использованы в учебных целях.
Учебник УМК Макарычев и другие (М: Просвещение) + ОТВЕТЫ. Электронная версия (онлайн учебник с ответами) для ознакомления при покупке книги: Макарычев, Миндюк, Суворова: Алгебра. 8 класс. Учебник. ФГОС. Цитаты из учебника использованы в учебных целях.
Алгебра 8 Макарычев Учебник
ОГЛАВЛЕНИЕ:Глава I. Рациональные дроби§ 1. Рациональные дроби и их свойства
1. Рациональные выражения. ГДЗ Упр. 1 — 22
2. Основное свойство дроби. Сокращение дробей. ГДЗ Упр. 23 — 52
§ 2. Сумма и разность дробей.3. Сложение и вычитание дробей с одинаковыми знаменателями. ГДЗ Упр. 53 — 72
4. Сложение и вычитание дробей с разными знаменателями. ГДЗ Упр. 73 — 107
§ 3. Произведение и частное дробей.5. Умножение дробей. Возведение дроби в степень. ГДЗ Упр. 108 — 131
Умножение дробей. Возведение дроби в степень. ГДЗ Упр. 108 — 131
6. Деление дробей. ГДЗ Упр. 132 — 147
7. Преобразование рациональных выражений. ГДЗ Упр. 148 — 178
8. Функция у = k/x и ее график. ГДЗ Упр. 179 — 196
9. Представление дроби в виде суммы дробей. ГДЗ Упр. 197 — 207
Дополнительные упражнения к главе I ГДЗ Упр. 208 — 262
Глава II. Квадратные корни§ 4. Действительные числа
10. Рациональные числа.
11. Иррациональные числа.
§ 5. Арифметический квадратный корень12. Квадратные корни. Арифметический квадратный корень.
13. Уравнение х2 = а.
14. Нахождение приближенных значений квадратного корня.
Нахождение приближенных значений квадратного корня.
15. Функция у = √х и ее график.
§ 6. Свойства арифметического квадратного корня.16. Квадратный корень из произведения и дроби.
17. Квадратный корень из степени.
§ 7. Применение свойств арифметического квадратного корня.18. Вынесение множителя за знак корня. Внесение множителя под знак корня.
19. Преобразование выражений, содержащих квадратные корни.
20. Преобразование двойных радикалов
Дополнительные упражнения к главе II.
Глава III. Квадратные уравнения§ 8. Квадратное уравнение и его корни.
21. Неполные квадратные уравнения.
22. Формула корней квадратного уравнения.
23. Решение задач с помощью квадратных уравнений.
24. Теорема Виета…
§ 9. Дробные рациональные уравнения.25. Решение дробных рациональных уравнений.
26. Решение задач с помощью рациональных уравнений.
27. Уравнения с параметром.
Дополнительные упражнения к главе III
Глава IV. Неравенства
§ 10. Числовые неравенства и их свойства.
- Числовые неравенства.
- Свойства числовых неравенств.
- Сложение и умножение числовых неравенств.
- Погрешность и точность приближения
§ 11. Неравенства с одной переменной и их системы.
- Пересечение и объединение множеств
- Числовые промежутки.
- Решение неравенств с одной переменной.
- Решение систем неравенств с одной переменной.
- Доказательство неравенств.
Дополнительные упражнения к главе IV.
Глава V. Степень с целым показателем. Элементы статистики
§ 12. Степень с целым показателем и ее свойства
- Определение степени с целым отрицательным показателем.
- Свойства степени с целым показателем
- Стандартный вид числа.
§ 13. Элементы статистики.
- Сбор и группировка статистических данных.
- Наглядное представление статистической информации.
- Функции у = х–1 и у = х–2 и их свойства.
- Дисперсия и средне квадратичное отклонение.
Дополнительные упражнения к главе V.
Задачи повышенной трудности
СОДЕРЖАНИЕ страницы
Алгебра 8 Макарычев Учебник ОГЛАВЛЕНИЕ: Глава I. Рациональные дроби § 1. Рациональные дроби и их свойства § 2. Сумма и разность дробей. § 3. Произведение и частное дробей.
Глава II. Квадратные корни
§ 4. Действительные числа
§ 5. Арифметический квадратный корень
§ 6. Свойства арифметического квадратного корня.
§ 7. Применение свойств арифметического квадратного корня.
Глава III. Квадратные уравнения
§ 8. Квадратное уравнение и его корни.
§ 9. Дробные рациональные уравнения.
Глава IV. Неравенства
§ 10. Числовые неравенства и их свойства.
§ 11. Неравенства с одной переменной и их системы.
Глава V. Степень с целым показателем. Элементы статистики
§ 12. Степень с целым показателем и ее свойства
§ 13.
§ 3. Произведение и частное дробей.
Глава II. Квадратные корни
§ 4. Действительные числа
§ 5. Арифметический квадратный корень
§ 6. Свойства арифметического квадратного корня.
§ 7. Применение свойств арифметического квадратного корня.
Глава III. Квадратные уравнения
§ 8. Квадратное уравнение и его корни.
§ 9. Дробные рациональные уравнения.
Глава IV. Неравенства
§ 10. Числовые неравенства и их свойства.
§ 11. Неравенства с одной переменной и их системы.
Глава V. Степень с целым показателем. Элементы статистики
§ 12. Степень с целым показателем и ее свойства
§ 13. Элементы статистики.
Элементы статистики.Алгебра 8 класс. Учебник УМК Макарычев, Миндюк, Суворова (Просвещение). Электронная версия (онлайн учебник) для ознакомления при покупке книги.
Просмотров: 10 054
Алгебра. 9 класс. Учебник — Макарычев, Миндюк, Нешков, Суворова
Учебник 9 класса Макарычева, Миндюк, Нешкова, Суворовой по алгебре входит в УМК Макарычева 7-9. Учебник доработан согласно новым стандартам по математике. Некоторые темы («Степень рациональным показателем», 9 «Тригонометрические выражения, преобразования») переведены в старшую школу. Взамен добавлена тема «Элементы комбинаторики, теории вероятностей». Подверглись расширению темы «Уравнения, неравенства содной переменной», «Уравнения — неравенства с 2 переменными». Все главы учебника снабжены дополнительным пунктом «Для тех, кто ….».-Содержание-
ОГЛАВЛЕНИЕ 03
КВАДРАТИЧНАЯ ФУНКЦИЯ 3
ФУНКЦИИ ИХ СВОЙСТВА 03
Функция. — 012
Свойства функций 013
КВАДРАТНЫЙ ТРЕХЧЛЕН 20
Квадратный трехчлен — 24
Разложение квадратного трехчлена … 25
КВАДРАТИЧНАЯ ФУНКЦИЯ 29
СТЕПЕННАЯ ФУНКЦИЯ. 72
72
УРАВНЕНИЯ И НЕРАВЕНСТВА …. 72
УРАВНЕНИЯ ОДНОЙ ПЕРЕМЕННОЙ 73
Целое уравнение 79
Дробные рациональные уравнения 79
НЕРАВЕНСТВА ОДНОЙ ПЕРЕМЕННОЙ 84
Решение неравенств второй… 88.
Решение неравенств методом …. 89
Некоторые приемы решения 94
Дополнительные упражнения 99
УРАВНЕНИЯ И НЕРАВЕНСТВА 104
УРАВНЕНИЯ ДВУМЯ ПЕРЕМЕННЫМИ 104
Графический способ решения …. 110
Решение систем уравнений …. 113
Решение задач 118
НЕРАВЕНСТВА ДВУМЯ ПЕРЕМЕННЫМИ … 121
Неравенства сдвумя переменными — 126
Системы неравенств 126
Некоторые приемы решения 129
Дополнительные упражнения 133
АРИФМЕТИЧЕСКАЯ — ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ 139
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ 139
Последовательности — 142
Определение арифметической прогрессии. 142
Формула суммы первых ….148
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ 154
Определение геометрической прогрессии. 160
Формула суммы первых…. 160
Метод математической индукции 164
Дополнительные упражнения 167
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ …. 171
171
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ 172
Примеры комбинаторных задач — 177
Перестановки 177
Размещения 180
Сочетания 184
НАЧАЛЬНЫЕ СВЕДЕНИЯ … 188
Относительная частота случайного …. 192
Вероятность равновозможных событий 192
Сложение — умножение вероятностей 200
Дополнительные упражнения 206
Упражнения для повторения 210
Задачи повышенной трудности 229
Исторические сведения 235
Сведения 241
Предметный указатель 255
Ответы 256
Издание 2017 г.
Размер файла: 25 Мб; Формат: pdf/zip.
Издание 2014 г
Размер файла: 25 Мб; Формат: pdf/zip.
download
Вместе с «Алгебра 9 класс Макарычев» скачивают:
AdminУравнений высших степеней. Уравнение степеней или ориентировочное уравнение 5 градусов
На канале на YouTube наш сайт, чтобы быть в курсе всех новых видеоуроков.
Для начала вспомним основные формулы степеней и их свойства.
Работа № а. Само по себе встречается n раз, это выражение можно записать как a a A … a = a n
1. A 0 = 1 (A ≠ 0)
3. а н а м = а н + м
4.(а н) м = а нм
5. A N B n = (AB) N
7. А Н / Д М = А Н — М
Силовые или демонстрационные уравнения — Это уравнения, в которых переменные выражены в градусах (или индикаторах), а в основе лежит число.
Примеры ориентировочных уравнений:
В этом примере число 6 — это основа, она всегда стоит внизу, а переменная x. градус или индикатор.
Приведем еще примеры ориентировочных уравнений.
2 х * 5 = 10
16 х — 4 х — 6 = 0
Теперь разберем, как решаются демонстрационные уравнения?
Возьмем простое уравнение:
2 х = 2 3
Этот пример можно решить даже в уме. Видно, что x = 3. Ведь так, чтобы левая и правая части были равны цифре 3 вместо x.
Теперь посмотрим, как нужно оформлять это решение:
2 х = 2 3
х = 3.
Чтобы решить такое уравнение, мы удалили тех же оснований (то есть два) и записали то, что осталось, это градусы. Получил желаемый ответ.
А теперь подведем итоги нашего решения.
Алгоритм решения ориентировочного уравнения:
1. Необходимо проверить того же фундамента Ли по уравнениям справа и слева. Если базы не совпадают, ищу варианты решения этого примера.
2. После того, как основания станут такими же, равняется градусам и решите полученное новое уравнение.
А теперь перепишем несколько примеров:
Начнем с простого.
Основания в левой и правой части равны числу 2, что означает, что мы можем отклонить и приравнять их степени.
x + 2 = 4 Получилось простейшее уравнение.
х = 4-2
х = 2.
Ответ: х = 2
В следующем примере видно, что основания разные. Это 3 и 9.
3 3х — 9 х + 8 = 0
Для начала переносим девятку в правую сторону, получаем:
Теперь нужно сделать такой же фундамент. Мы знаем, что 9 = 3 2. Воспользуемся формулой степени (a n) m = a nm.
Мы знаем, что 9 = 3 2. Воспользуемся формулой степени (a n) m = a nm.
3 3х = (3 2) х + 8
Получаем 9 х + 8 = (3 2) х + 8 = 3 2х + 16
3 3x = 3 2x + 16 Теперь понятно, что в левой и правой части основания одинаковые и равные тройке, а значит, мы можем их отбросить и приравнять степени.
3x = 2x + 16 Получено простейшее уравнение
3x — 2x = 16
x = 16.
Ответ: X = 16.
Смотрим на следующий пример:
2 2х + 4-10 4х = 2 4
Сначала смотрим на цоколь, фундаментов разные два и четыре.И нам нужно быть такими же. Преобразуем четверку по формуле (a n) m = a nm.
4 х = (2 2) х = 2 2х
А также использовать одну формулу a n a m = a n + m:
2 2х + 4 = 2 2х 2 4
Добавить к уравнению:
2 2х 2 4-10 2 2х = 24
Мы привели пример по тем же причинам. Но нам мешают другие числа 10 и 24. Что с ними делать? Если вы видите, что ясно, что у нас есть 2 2 2, это ответ — 2 2, мы можем вынуть скобки:
2 2х (2 4-10) = 24
Вычисляем выражение в скобках:
2 4–10 = 16–10 = 6
Все уравнения Разделить на 6:
Представьте 4 = 2 2:
2 2x = 2 2 основания одинаковы, выкидываем их и приравниваем градусы.
2x = 2 Получилось простейшее уравнение. Делим его на 2
х = 1.
Ответ: х = 1.
Решающее уравнение:
9 х — 12 * 3 х + 27 = 0
Преобразуем:
9 x = (3 2) x = 3 2x
Получаем уравнение:
3 2x — 12 3 x +27 = 0
Фундамент у нас одинаковый, равен трем. В этом примере видно, что первые три градуса в два раза (2x) больше, чем у второго (просто x).В этом случае можно решить замену методом . Число с наименьшей степенью заменить:
Тогда 3 2x = (3 x) 2 = T 2
Заменим в уравнении все степени полостями на T:
t 2 — 12T + 27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D = 144-108 = 36
T 1 = 9
T 2 = 3
Вернуться к переменной x. .
Возьмем Т 1:
Т 1 = 9 = 3 х
То есть
3 х = 9
3 х = 3 2
х 1 = 2
Найден один корень.Ищем вторую, из Т 2:
Т 2 = 3 = 3 х
3 х = 3 1
х 2 = 1
Ответ: х 1 = 2; х 2 = 1.-reshenie-910.jpg)
На сайте вы можете в разделе Help Resolve Decision задать вам вопросы. Мы ответим.
Присоединиться к группе
Судя по началу публикации, которую мы здесь опускаем, Текст написал Юрий Игнатьевич. И написано хорошо, и проблематика актуальна, просто так называют Россию, как Мухин…
Как бы кто ни принадлежал к антироссийской власти, Россия выше и не заслуживает оскорблений. Даже из талантливой лжи разоблачения американского агентства NASA.
*
Обращение в ТОВ. Мухин Ю.И.
Уважаемый Юрий Игнатьевич! Я знаю, что вы посещаете эти страницы. Поэтому обращаюсь напрямую к вам.
Мы все ценим вашу роботизированную работу в области разоблачения Волшебников Запада, лжи Америки, лжи псевдотонной лжи, лжи либералов.Мы счастливы и приносим пользу себе и обществу, мы думаем о серьезных темах, которые вы время от времени отбрасываете, будь то меритократия или метафизика, любовь к отечественной истории или восстановление справедливости.
Однако ваши определения нашей общей родины вызывают сильное недоумение и горечь.
Впрочем, неожиданно сами: как бы вы охарактеризовали человека, который начал оскорблять своего больного и от этого временно перестала работать мать?
Но Россия, как ни назови и как бы ни была хороша или противна держава, Россия — наша Родина. Родина. За нее наши деды пролили кровь и положили свои жизни.
Следовательно, ставить его в один ряд с властью — это понижать духовное возвышенное до уровня материального, а то и низкого. Те. Вы сравниваете совершенно разные категории. Это неприемлемо для любого здравомыслящего человека.
Прошу Вас, уважаемый ТОВ. Мухин, серьезно подумай.
**
… А с уравнениями (я этого не знал) ситуация такая.Как найти квадратное уравнение корней гадали еще в Древнем Египте.
Как найти корни кубического уравнения и уравнения четвертой степени, нашли в шестнадцатом веке, но не могли найти корни уравнения пятой степени до 2016 года. Причем пробовали не обычные люди.
Причем пробовали не обычные люди.
В шестнадцатом веке найти корни уравнения пятой степени пытался основатель символической алгебры Франсуа Виет, в девятнадцатом веке это пытался сделать основатель современной высокой алгебры французский математик Эварисе Галуа, После него найти корни уравнения пятой степени попытался норвежский математик Нильс Хенрик Абель, который, в конце концов, сдался и доказал невозможность решения уравнения пятой степени в целом.
Мы читаем в Википедии о заслугах Авеля: «Авель закончил блестящее исследование древней проблемы: доказал невозможность решения в общем виде (в радикалах) уравнения 5-й степени …
В алгебре Абель нашел необходимое условие для того, чтобы корень уравнения выражался «в корнях» через коэффициенты этого уравнения. Достаточное состояние вскоре открыл Галуа, в достижениях которого опирались на произведения Авеля.
Авель привел конкретные примеры уравнения 5-й степени, корни которого не могут быть выражены в радикалах, и, таким образом, в значительной степени закрыл древнюю проблему. «
«
Как видите, если теорему Пуанкаре все время пытались доказать и Перельман оказывался удачливым для других математиков, то после Абеля за пятые уравнения математики так и не брались.
А в 2014 году математика из Томска Сергей Закаков который по фото можно судить, что он уже в годах, и по этой статье о нем, что он выпускник факультета прикладной математики и кибернетики Томского государственного университета. работы, получены уравнения пятой степени.Тупик? Да, тупик! Но Сергей Заков взял его и сломал.
А в 2016 году он нашел способ решить уравнения пятой степени в общем виде! Сделал кое-что, невозможность того, что доказали математики Галуа и Абель.
Я пытался найти информацию о Сергее Борне в Википедии, но черт возьми! О математике Сергея Борне и о нахождении их решением уравнений пятой степени информации нет!
Пикантность придает то, что для математиков существует аналог Нобелевской премии — Абелева премия (Нобель запретил премию по математике и теперь выдают ее за математические фекалии, называя их «физикой»).
Эта математическая премия в честь самого Авеля, который доказал невозможность изготовления коек . Однако самовыдвижение на эту награду не допускается. И нет кроликов-математиков и нет организаций, которые могли бы предложить его кандидатуру на эту премию.
Правда, у нас есть Академия наук, но там академики сидят не за развитие математики, а за «бабло рубят». Кому там нужен этот зайчик?
Ну для информагентств койки не Перельман! Поэтому открытие мангала для СМИ не сенсация.
Вот то, что Порошенко с дверью ошибся — это да! Это настоящая сенсация!
Томский математик решил задачу, которую не могли решить двести лет
С появлением алгебры ее основной задачи решением стали считать алгебраические уравнения. Решение уравнения второй степени было известно в Вавилоне и Древнем Египте. Такие уравнения мы передаем в школе. Помните уравнение x2 + ax + b = 0 и дискриминант?
Сергей Банес с книгой
Решение алгебраических уравнений третьей и четвертой степени было найдено в шестнадцатом веке. Но решить уравнение пятой степени не удалось. Причину нашел Лагранж. Он показал, что решение уравнений третьей и четвертой степени возможно, потому что они могут быть сведены к ранее решенным уравнениям. Уравнение третьей степени можно свести к уравнению второй степени, а четвертое уравнение — к третьему уравнению. Но пятое уравнение сводится к шестому уравнению, т.е. более сложному, поэтому традиционные решения не применимы.
Но решить уравнение пятой степени не удалось. Причину нашел Лагранж. Он показал, что решение уравнений третьей и четвертой степени возможно, потому что они могут быть сведены к ранее решенным уравнениям. Уравнение третьей степени можно свести к уравнению второй степени, а четвертое уравнение — к третьему уравнению. Но пятое уравнение сводится к шестому уравнению, т.е. более сложному, поэтому традиционные решения не применимы.
Вопрос о решении уравнения пятой степени был перенесен всего двести лет назад, когда Абель доказал, что не все уравнения пятой степени можно решить в радикалах, то есть в квадратных, кубических и других корнях, известных нам еще в школе. И Галуа вскоре, то есть двести лет назад, нашел критерий, позволяющий определить, какие уравнения пятой степени можно решить в радикалах, а какие нет. Он заключается в том, что группа Галуа, разрешенная в радикалах пятого уравнения, должна быть либо циклической, либо метациклической.Но Галуа не нашел решения в радикалах тех уравнений пятой степени, которые разрешимы в радикалах. Теория Галуа очень известна, о ней написано много книг.
Теория Галуа очень известна, о ней написано много книг.
До сих пор существовали только частные решения для разрешимых в радикалах уравнений пятой степени. И только в этом году томский математик Сергей Заков решил задачу, которую не могли решить двести лет. Опубликовал книгу «Как решить алгебраические уравнения пятой степени в радикалах», в которой указаны решения любых пятых уравнений, разрешимых в радикалах.Банес — выпускник факультета прикладной математики и кибернетики Томского государственного университета. Нам удалось взять интервью.
— Сергей, почему вы решили эту задачу?
— Мне нужно было решение уравнения пятой степени, чтобы решить задачу из другого раздела математики. Я стал выяснять, как его найти, и выяснил, что не все они решаются радикально. Затем я попытался найти в научной литературе способ решения тех уравнений, которые разрешимы в радикалах, но нашел только критерий, по которому можно определить, какие из них разрешимы, а какие нет.Я не алгебраист, но, конечно, как выпускник ФПМК могу применять алгебраические методы. Поэтому с 2014 года я серьезно начал искать решение и нашел его сам.
Поэтому с 2014 года я серьезно начал искать решение и нашел его сам.
Метод был найден мною два года назад, я подготовил книгу, в которой был описан не только он, но и способы решения некоторых уравнений степеней больше пятой. Но денег на ее публикацию у меня не было. В этом году я решил, что легче опубликовать только часть этой работы, и взял только ее половину, посвященную методу решения пятого уравнения в радикалах.
Я поставил себе цель опубликовать что-то вроде руководства по решению этой проблемы, понятного математикам, которым необходимо решить конкретное уравнение. Поэтому он упростил его, удалив множество длинных формул и значительную часть теории, сократив более половины, оставив только необходимое. Поэтому у меня получилось что-то вроде книги «для чайников», по которой математики, не знакомые с теорией Галуа, могут решить нужное им уравнение.
— За это спасибо Владиславу Бересневу, с которым мы знакомы много лет.Он согласовал издание книги.
— Можно ли получить премию по математике за решение этой задачи? Например, вы упомянули Авеля. Но есть ли в математике абелева премия, которая считается аналогом Нобелевской?
— Полностью исключить такую возможность невозможно. Но, надеюсь, оно того не стоит.
Например, заявки на соискание премии Абеля 2019 принимаются до 15 сентября. Причем самовыдвижение не допускается.А я математик-одиночка. Нет организаций или известных математиков, которые предложили бы мою кандидатуру. Следовательно, он не будет рассматриваться независимо от того, заслуживает ли моя работа этой премии и насколько соответствует духу этой премии представление ее тем, кто продолжает работу Авеля. Но даже если он будет представлен, все зависит еще и от уровня работ других кандидатов.
Книга рассчитана на тех, кто не знаком с теорией Галуа. Основы теории Галуа даны только в той части, в которой они необходимы для решения уравнения, подробно описан метод решения, показаны приемы, упрощающие решение.Значительная часть книги посвящена примеру решения конкретного уравнения. Рецензентами книги являются доктор технических наук Геннадий Петрович Агибалов и доктор физ. мат. Наук, профессор Крылов Петр Андреевич.
Подготовлено Скирневская Анастасия
Как правило, уравнение со степенью выше 4 не может быть разрешено в радикалах. Но иногда мы все же можем найти корни стоящего слева многочлена в уравнении высшей степени, если представить его в виде произведения многочленов до степени не более 4-й.Решение таких уравнений основано на разложении многочленов на множители, поэтому мы советуем вам повторить эту тему, прежде чем изучать эту статью.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попытаться найти рациональные корни, а затем разложить многочлен на множители, чтобы преобразовать его в уравнение более низкой степени, которое просто решит. В рамках этого материала мы и рассмотрим именно такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения вида A n x n + a n — 1 x n — 1 +.. . + a 1 x + a 0 = 0, мы можем привести к уравнению такой же степени, используя умножение обеих частей на a n n — 1 и замену переменной вида y = a n x:
a n x n + a n — 1 x n — 1 +. . . + A 1 x + a 0 = 0 Ann · xn + an — 1 · Ann — 1 · xn — 1 + … + a 1 · (AN) N — 1 · X + A 0 · (AN) N — 1 = 0 y = тревога ⇒ yn + bn — 1 yn — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, которые в итоге получились, тоже будут целыми. Таким образом, нам нужно будет решить данное уравнение n-noerate с целочисленными коэффициентами, имеющими вид x n + a n x n — 1 +… + а 1 х + а 0 = 0.
Вычислить корни уравнения целиком. Если уравнение имеет целые корни, их нужно искать среди делителей свободного члена a 0. Записываем их и по очереди подставим в исходное равенство, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, мы можем записать его в виде x — x 1 · pn — 1 (x) = 0. Здесь X 1 — корень уравнения, а P n — 1 (x) — частное от деления X n + беспокойство — 1 +… + a 1 x + a 0 до x — x 1.
Подставляем оставшиеся разряженные делители в P n — 1 (x) = 0, начиная с x 1, так как корни могут повторяться. После получения тождества корень X 2 считается найденным, и уравнение можно записать в виде (x — x 1) (x — x 2) · pn — 2 (x) = 0. ПН — 2 (x) будет частным от деления P n — 1 (x) до x — x 2.
Продолжаем перебирать разделители. Находим все корни целиком и обозначаем их количество через m.После этого исходное уравнение можно представить в виде x — x 1 x — x 2 · … · x — xm · pn — m (x) = 0. Здесь pn — m (x) — многочлен N — М-степень. Для расчета удобно использовать схему горнера.
Если в нашем исходном уравнении есть целые коэффициенты, мы не можем получить дробные корни.
В итоге мы получили уравнение P n — M (x) = 0, корни которого можно найти любым удобным способом. Они могут быть иррациональными или сложными.
Покажем на конкретном примере, как применяется схема решения.
Пример 1.
Условие: Найти решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0.
Решение
Начнем с выводов всего корней.
У нас бесплатный член равен минус трем. У него есть делители, равные 1, -1, 3 и -3. Подставим их в исходное уравнение и посмотрим, какие из них получат тождества.
При x, равном единице, получаем 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0, это означает, что единица будет корнем этого уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на (x — 1) в столбце:
Итак, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3.
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 · (- 1) 2 + 4 · — 1 + 3 = 0
У нас было тождество, это означает, что мы нашли другой корень уравнения, равный 1.
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на (x + 1) в столбце:
Получаем
x 4 + x 3 + 2 x 2 — x — 3 = (x — 1) (x 3 + 2 x 2 + 4 x + 3) = = (x — 1) (x + 1) (x 2 + х + 3)
Подставляем следующий делитель в равенство x 2 + x + 3 = 0, начиная с — 1:
1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0
Полученное в итоге равенство будет неверным, это означает, что уравнение больше не имеет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3.
D = 1 2 — 4 · 1 · 3 = — 11
Из этого следует, что в этой квадратной тройке декалет нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2.
Уточним, что вместо разделения в столбце можно использовать схему Gunner. Делается это так: после того, как мы определили первый корень уравнения, заполняем таблицу.
В таблице коэффициентов сразу видно коэффициенты индивида от деления многочленов, значит x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3.
После нахождения следующего корня, равного — 1, получаем:
Ответ: x = — 1, x = 1, x = — 1 2 ± i 11 2.
Пример 2.
Условие: Решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0.
Решение
Свободный член имеет делители 1, — 1, 2, — 2, 3, — 3, 4, — 4, 6, — 6, 12, — 12.
Проверьте их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 (- 1) 4 — (- 1) 3 — 5 · (- 1) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Итак, x = 2 будет корнем уравнения.Разделим x 4 — x 3 — 5 x 2 + 12 на x — 2, используя схему Gunner:
В результате получаем Х — 2 (х 3 + х 2 — 3 х — 6) = 0.
2 3 + 2 2-3 · 2-6 = 0
Итак, 2 снова будет корнем. Разбиваем x 3 + x 2 — 3 x — 6 = 0 на x — 2:
В результате получаем (x — 2) 2 · (x 2 + 3 x + 3) = 0.
Проверять оставшиеся делители не имеет смысла, так как равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решать с помощью дискриминанта.
Квадратное уравнение Spest:
х 2 + 3 х + 3 = 0 d = 3 2 — 4 · 1 · 3 = — 3
Получаем всесторонне сопряженную пару корней: x = — 3 2 ± i 3 2.
Ответ : x = — 3 2 ± i 3 2.
Пример 3.
Условие: Найти для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительных корней.
Решение
х 4 + 1 2 х 3-5 2 х — 3 = 0 2 х 4 + х 3-5 х — 6 = 0
Мы выполняем регистрацию 2 3 обеих частей уравнения:
2 х 4 + х 3 — 5 х — 6 = 0 2 4 · х 4 + 2 3 х 3 — 20 · 2 · х — 48 = 0
Заменяем переменные Y = 2 x:
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В результате у нас получилось стандартное уравнение 4-го, которое можно решить по стандартной схеме.Проверяем делители, делим и получаем в результате, что у него 2 действительных корня y = — 2, y = 3 и два комплексных. Решение целиком здесь приводить не будем. В силу замены действительными корнями этого уравнения x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 будет x = 3 2.
Ответ: х 1 = — 1, х 2 = 3 2
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
В математике XVI века почти случайно попадались комплексные числа (см. Главу 11).ДО XVIII века Комплексные числа считались расширением области действительных чисел, но работа с ними все же приводила к ошибке четности, так как в работах Леонарда Эй, великих работ по теории «арифметических исследований» (1801 г.) избегали использование так называемых «мнимых чисел». Мне кажется, что самая важная часть этой работы — первое доказательство основной теоремы алгебры. Гаусс понял, насколько важна эта теорема, и в последующие годы создал несколько дополнительных доказательств.В 1849 году он переделал первый вариант, на этот раз используя интегрированные числа. Используя современные термины, можно сказать, что для любого конечного полиномиального уравнения с действительными или комплексными коэффициентами все его корни будут действительными или комплексными числами. Таким образом, мы получаем отрицательный ответ на давний вопрос о том, требует ли решение решения полиномиальных уравнений высокого порядка Создание чисел более высокого порядка, чем комплексные.
Одной из самых острых проблем алгебры того времени был вопрос, который решал бы алгебраическими методами, то есть с помощью конечного числа алгебраических шагов полином пятого порядка будет quintik.Сейчас в школе учат формулам решения квадратных уравнений, а с XVI века известны аналогичные методы решения уравнений третьей и четвертой степени (глава 11). Но для квинтинга не было единого метода. Может показаться, что фундаментальная теорема алгебры содержит перспективу положительного ответа, но на самом деле она просто гарантирует, что решения существуют, ничего не говорится о существовании формул, которые дают точные решения (к тому времени уже существовали приближенные числовые и графические методы) .А теперь есть два математических гения с трагической судьбой.
Нильс Хенрик Абель (1802-1829) родился в большой бедной семье, которая жила в маленькой деревне в Норвегии — стране, разрушенной многолетней войной с Англией и Швецией. Учитель, дружелюбный наставник, давал ему частные уроки, но после смерти отца, через восемнадцать лет, несмотря на юный возраст и хрупкое здоровье, Авель был вынужден содержать семью. В 1824 году он опубликовал научную статью, в которой заявил, что Quintik не будет решать алгебраические средства, как, однако, любые полиномы высшего порядка.Абель считал, что эта статья послужит пропуском в научный мир, и отправил ее Гаусс в Геттингенский университет. К сожалению, Гаусс так и не собрался разрезать страницы ножом (в те времена им приходилось иметь дело с любым читателем) и статью не прочитал. В 1826 году норвежское правительство наконец выделило Абелю инструменты для путешествий по Европе. Опасаясь, что личное общение с Гауссом не доставит ему большой радости, математик решил не посещать Геттинген и вместо этого отправился в Берлин.Там он подружился с Августом Леопольдом Креллилем (1780-1855), математиком, архитектором и инженером, который консультировал Министерство образования Пруссии по вопросам математики. Крем собирался учредить «журнал чистой и прикладной математики». Так Абель получил возможность расширить свои работы и много публиковал, особенно в первых комнатах «журнала», который сразу стал считаться очень престижным и авторитетным научным изданием. Norwegez напечатал там расширенную версию своих доказательств того, что Quintik неуместны в алгебраических методах.А потом поехал в Париж. Эта поездка была очень расстроена Абелем, поскольку он практически не получил необходимой поддержки французских математиков. Он сблизился с Огюстом Луи Коши (1789-1857), который в то время был главным математическим анализатором светильников, но имел очень сложный характер. Как сказал сам Абель: «Луч Коши, и с этим ничего нельзя поделать, хотя в настоящее время он единственный, кто способен на что-то в математике». Если попытаться найти оправдание проявлениям неуважения и пренебрежения, которые исходили от Гаусса и Коши, можно сказать, что Quintik достигла определенной известности и привлекла внимание как уважаемых математиков, так и оригиналов.Абель вернулась в Норвегию, где сильнее заболела туберкулезом. Он продолжал присылать свои работы Креллилу, но в 1829 году он умер, не зная, насколько его репутация имела репутацию в научном мире. Через два дня после смерти Абелю поступило предложение открыть научный офис в Берлине.
Абель показал, что любой многочлен выше четвертого порядка не может быть разрешен с использованием радикалов, таких как корни квадратного, кубического или более высокого порядка. Однако явные условия, при которых в частных случаях эти многочлены могли быть решены, и метод их решения сформулировал Галуа.Эваристер Галуа (1811-1832) прожил короткую и насыщенную жизнь. Он был невероятно одаренным математиком. Галуа был неумолим по отношению к тем, кого считал менее талантливым, чем он сам, и в то же время я не мог мириться с социальной несправедливостью. Он не проявлял никаких способностей к математике, пока она не прочитала работу «Начало геометрии» (изданная в 1794 году, эта книга в течение следующих ста лет была основным учебником). Затем он буквально проглотил оставшиеся работы Лаяндера, а затем и Абеля.Его энтузиазм, самоуверенность и нетерпимость привели к поистине ужасным последствиям в его отношениях с учителями и экзаменаторами. Галуа принял участие в конкурсе на поступление в политехникум — колыбель французской математики, но из-за неподготовленности провалил экзамен. Через некоторое время после знакомства с новым учителем, признавшим свой талант, ему удалось сдержать вспыльчивость. В марте 1829 года Галуа опубликовал свою первую статью о непрерывных дробях, которую он считал своей самой значительной работой.Он отправил сообщение о своих открытиях в Академию наук, и Коши обещал представить их, но забыл. Более того, он просто потерял свою рукопись.
Вторая неудача Галуа при поступлении в политехникум вошла в математический фольклор. Он так привык постоянно держать в голове сложные математические идеи, что разводили бешенство мелкие огурцы экзаменаторов. Поскольку экзаменаторы изо всех сил пытались понять его объяснения, он бросил тряпку для стирания с доски в лицо одному из них.Вскоре после этого умер его отец, покончивший с собой в результате церковных интриг. На его похоронах вспыхнул бунт. В феврале 1830 года Галуа написал следующие три статьи, отправив их в Академию наук для рассмотрения Гран-при математики. Жозеф Фурье, в то время бывший секретарь Академии умер, так и не прочитав их, а после его смерти статей среди его бумаг не обнаружилось. Такой поток разочарований годится для любого. Галуа восстал против власти собственности, потому что чувствовал: они не признавали его заслуг и хотели его отца.Он с головой окунулся в политику, став ярымским республиканцем, — не самое мудрое решение во Франции в 1830 году. В последней отчаянной попытке он послал научную статью знаменитому французскому физику и математику Симеону Дени Пуассону (1781-1840). , который в ответ потребовал дополнительных доказательств.
Это стало последней каплей. В 1831 году Галуа дважды арестовывали — первый раз якобы за убийство короля Луи Филиппа, а затем, чтобы защитить его, власти опасались республиканского восстания! На этот раз его приговорили к шести месяцам заключения по сфабрикованному обвинению в незаконном ношении формы расформированного артиллерийского дивизиона, в который он вступил.Освободившись честно, он взялся за дело, которое вызвало у него такое же отвращение, как и все остальное в жизни. В письмах к преданному другу его разочарование кажется шаловливым. 29 мая 1832 г. он вызвал на дуэль, причины которой до конца не выяснены. «Я стал жертвой нечестной кокетки. Моя жизнь заканчивается жалкой ссорой», — пишет он в «Письме ко всем республиканцам». Самая известная работа Галуа была написана в ночь перед роковой дуэлью. По полям разбросаны жалобы: «Некогда, некогда.«Он был вынужден оставить еще одно подробное изложение промежуточных шагов, которые были незначительными для понимания основной идеи. Ему нужно было выбросить основу своих открытий на бумаге — истоки того факта, который теперь называется теоремой Галуа. Он закончил свою работу. завещание, прося шеваля «обратиться к Якоби и Гауссу с просьбой публично высказать свое мнение независимо от правильности, но относительно важности этих теорем». Рано утром Галуа пошел на встречу со своим оппонентом.Они должны были сместиться с расстояния 25 шагов. Галуа был ранен и на следующее утро скончался в больнице. Ему было всего двадцать лет.
Галуа опирался на работы Лагранжа и Коша, однако разработал более общий метод. Это было чрезвычайно важным достижением в решении Квинтикова. Ученый меньше обращал внимания на исходные уравнения или графическую интерпретацию, а больше думал о природе самих корней. Чтобы упростить Галуа, рассматривались только так называемые неприводимые квинтики, то есть те, которые не могут быть разложены на многочлены в виде многочленов более низкого порядка (как мы уже говорили, для любых полиномиальных уравнений до четвертого порядка есть формулы, находящие их корнеплоды).В общем, неприводимый многочлен с рациональными коэффициентами — это многочлен, который не может быть разложен на более простые многочлены с рациональными коэффициентами. Например, (x 5-1) можно разложить на множители (x — 1) (x 4 + x 3 + x 2 + x + 1), , тогда как (x 5 — 2) неприводимо. Целью Галуа было определить условия, при которых все решения общего неприводимого полиномиального уравнения могут быть найдены в терминах радикалов.
Ключ к решению состоит в том, что корни любого неприводимого алгебраического уравнения независимы, они могут быть выражены одни через другое.Эти отношения были формализованы в группу всевозможных перестановок, так называемую корневую группу симметрии — для Quintics эта группа содержит 5! = 5 х 4 х 3 х 2 х 1 = 120 элементов. Математические алгоритмы теории Галуа очень сложны, и, скорее всего, отчасти именно они сначала их поняли с большим трудом. Но после того, как уровень абстракции позволил перейти от алгебраических решений к алгебраической структуре связанных с ними групп, Галуа смог предсказать разрешимость уравнения на основе свойств таких групп.Более того, его теория также предоставила метод, позволяющий находить сами эти корни. Что касается Квинтикова, математик Жозеф Лиувилль (1809–1882), который в 1846 году опубликовал большинство работ Галуа в своем «журнале чистой и прикладной математики», отметил, что молодой ученый доказал «красивую теорему», и в целях «Неприводимое уравнение начальной степени было разрешимо в терминах радикалов, необходимо и достаточно, чтобы все его корни были рациональными функциями любых двух из них». Поскольку это невозможно для квинтки, оно не может быть решено радикалами.
За три года математический мир потерял две самые яркие новые звезды. Взаимные обвинения и переоценка ценностей Абель и Галуа добились заслуженного признания, но только посмертно. В 1829 году Карл Якоби через Лаянель узнал о «потерянной» рукописи Абеля, а в 1830 году разразился дипломатический скандал, когда норвежский консул в Париже потребовал найти статью его соотечественника. В конце концов, Каучи нашел статью, но только потом снова потерялась в редакции Академии! В том же году Абели был удостоен Гран-при по математике (вместе с Якоби) — но он уже был мертв.В 1841 г. была опубликована его биография. В 1846 году Лиувилль отредактировал некоторые рукописи Галуа для публикации и во введении выразил сожаление по поводу того, что в оригинальной Академии были работы Галуа из-за их сложности, «действительно, ясность изложения необходима, когда автор уводил читателя от проторенный путь к неизведанным диким территориям ». Он продолжает: «Галуа больше нет! Не будем впадать в бесполезную критику. Выбросим недостатки и посмотрим на достоинства!» Плод короткой жизни Галоа уместился на всех шестидесяти страницах.Редактор математического журнала для кандидатов на экзамен ecla normal и Политехнической школы так прокомментировал случай Галуа: «Кандидат с высоким интеллектом был выбран экзаменатором с более низким уровнем мышления. Барбарус HIC EGO SUM, Quia Non Intelligor Illis
Во-первых, вторая страница этого произведения не обременена именами, фамилиями, описаниями положения в обществе, титулами и элегиями в честь некоего скупого принца, кошелек которого откроется с помощью этих Фимиами. — с угрозой закрыть его, когда хвалы будут закончены.Вы не увидите здесь почтительных похвал, написанных буквами в три раза большими, чем сам текст, адресованный тем, кто занимает высокое положение в науке, некоему мудрому покровителю — что-то обязательное (я бы сказал, неизбежное) для человека в возрасте двадцати лет, который хочет написать что-нибудь. Я никому здесь не говорю, что я обязан их советом и поддержкой всего хорошего, что есть в моей работе. Я не говорю этого, потому что это было бы ложью. Если бы мне пришлось упомянуть кого-либо из великих деятелей общества или науки (в настоящее время разница между этими двумя классами людей почти незаметна), клянусь, это не было бы знаком благодарности.Я обязан тому, что опубликовал первую из этих двух статей так поздно, и тем, что я написал все это в тюрьме — в месте, которое вряд ли можно считать подходящим для научных размышлений, и меня часто поражала моя сдержанность и умение сдерживать ваши мысли. рот на Замке по отношению к тупой и злой зоилась. Мне кажется, я могу употреблять слово «Зойла», не опасаясь обвинений в дискомфорте, потому что просто у меня есть свои оппоненты. Я не собираюсь здесь писать о том, как и почему меня посадили в тюрьму, но должен сказать, что мои рукописи чаще всего просто теряются в Господних папках членов Академии, хотя, по правде говоря, я не могу представить себе такую несостоятельность со стороны Людей, на совести которых погиб Авель.На мой взгляд, любому хочется, чтобы его сравнивали с этим гениальным математиком. Достаточно сказать, что моя статья по теории уравнений была отправлена в Академию наук в феврале 1830 г., которую прислали оттуда в феврале 1829 г., и при этом из нее ничего не напечатано, да и рукопись невозможно было распечатать. возвращение.
Галуа, неопубликованное Предисловие, 1832Класс: 9
Основные цели:
- Обеспечьте концепцию целого рационального уравнения.
- Сформулируйте основные методы решения уравнений высших степеней (N > 3).
- Обучить основным методам решения уравнений высших степеней.
- Научите типа уравнения определять наиболее эффективный метод Его решений.
Формы, методы и педагогические приемы, используемые учителем на уроке:
- Лекционно-семинарская система обучения (лекции — объяснение нового материала, семинары — решение задач).
- Информационно-коммуникационные технологии (фронтальный опрос, устная работа с классом).
- Дифференцированное обучение, групповые и индивидуальные формы.
- Использование в обучении метода исследования, направленного на развитие математического аппарата и умственных способностей каждого конкретного ученика.
- Печатный материал — индивидуальное краткое изложение урока (основные понятия, формулы, утверждения, материал лекций сжат в виде схем или таблиц).
План урока:
- Организация времени.
Цель этапа: включить учащихся в учебную деятельность, определить содержание урока. - Актуализация знаний студентов.
Цель этапа: актуализировать знания студентов по ранее связанным темам - Изучение новой темы (лекция). Цель этапа: Сформулировать основные методы решения уравнений высших степеней (N > 3)
- Подведение итогов.
Цель этапа: еще раз выделить ключевые моменты изучаемого на уроке материала. - Домашнее задание.
Цель этапа: Сформулировать домашнее задание для учащихся.
Конспект урока
1. Организационный момент.
Формулировка темы урока: «Уравнения высших степеней. Методы их решения».
2. Актуализация знаний студентов.
Теоретический обзор — беседа. Повторите часть ранее изученной информации из теории. Студенты формулируют основные определения и формулируют необходимые теоремы.Образцы даются, демонстрируя уровень ранее полученных знаний.
- Понятие уравнения с одной переменной.
- Понятие корня уравнения, решение уравнения.
- Понятие линейного уравнения С одной переменной, понятие квадратного уравнения с одной переменной.
- Понятие эквивалентности уравнений, уравнений исследования (понятие инородных корней), переход не является следствием (случай потери корней).
- Концепция целого рационального выражения с одной переменной.
- Понятие целого рационального уравнения Н. — Даже. Стандартная форма всего рационального уравнения. Приведенное целочисленное рациональное уравнение.
- Переход к совокупности уравнений младших степеней путем разложения исходного уравнения на множители.
- Понятие многочлена п. — степень от х. . Теорема косить. Следствие из теоремы о манте.Корневые теоремы ( Z. -Korni I. Q. -Korny) целое рациональное уравнение с целыми коэффициентами (соответственно заданными и неоплаченными).
- Схема Горнера.
3. Изучение новой темы.
Рассмотрим целое рациональное уравнение n. — степень стандартного вида от одной неизвестной переменной x: pn (x) = 0, где P n (x) = тревога + a n-1 x n-1 + a 1 x + a 0 — полином п. — степень от х., г. а. N ≠ 0. Если a. n = 1 Это уравнение называется получившимся целым рациональным уравнением n. — Даже. Рассмотрим такие уравнения при разных значениях n. и перечислим основные методы их решения.
н. = 1 — линейное уравнение.
н. = 2 — квадратное уравнение. Дискриминантная формула. Формула для вычисления корней. Теорема Виета. Выделение полной площади.
н. = 3 — кубическое уравнение.
Метод группировки.
Пример: x 3 — 4X 2 — X + 4 = 0 (x — 4) (x 2 — 1 ) = 0 х. 1 = 4, x 2 = 1, X. 3 = -1.
Возвращает кубическое уравнение вида aX. 3 + bX. 2 + bX. + а. = 0. Решаем, комбинируя члены с одинаковыми коэффициентами.
Пример: x. 3-5 х. 2-5 х. + 1 = 0 ( x. + 1) ( x. 2-6 x. + 1) = 0 х. 1 = -1, х. 2 = 3 + 2, х. 3 = 3–2.
Выбор Z-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что брутфорс в данном случае является конечным, и корни мы отбираем по определенному алгоритму в соответствии с теоремой о Z. -Corces of a дано целое рациональное уравнение с целыми коэффициентами.
Пример: X. 3 — 9 x. 2 + 23 х. — 15 = 0. Уравнение приведено. Пейте бесплатный член-разделитель (+ 1; + 3; + 5; + пятнадцать). Применяем схему наводчика:
| х. 3 | х. 2 | х. 1 | х. 0 | выход | |
| 1 | -9 | 23 | -15 | ||
| 1 | 1 | 1 х 1-9 = -8 | 1 х (-8) + 23 = 15 | 1 х 15-15 = 0 | 1 — корень |
| х. 2 | х. 1 | х. 0 |
Получаем ( x. — 1) ( x. 2-8 x. + 15) = 0 х. 1 = 1, х. 2 = 3, х. 3 = 5.
Уравнение с целыми коэффициентами. Выбор Q-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что в этом случае финал и корни мы выбираем по определенному алгоритму в соответствии с теоремой о Q. — Берега не являются целочисленным рациональным уравнением с целыми коэффициентами.
Пример: 9. x. 3 + 27 х. 2 — х. — 3 = 0. Уравнение не холостое. Пейте бесплатный член-разделитель (+ 1; + 3). Пейте делители коэффициентов со старшей степенью неизвестности. ( + 1; + 3; + 9) Следовательно, корни будут искать среди значений ( + 1; + ; + ; + 3).Применяем схему наводчика:
| х. 3 | х. 2 | х. 1 | х. 0 | выход | |
| 9 | 27 | -1 | -3 | ||
| 1 | 9 | 1 х 9 + 27 = 36 | 1 х 36-1 = 35 | 1 х 35-3 = 32 ≠ 0 | 1 — не root |
| -1 | 9 | -1 х 9 + 27 = 18 | -1 х 18-1 = -19 | -1 х (-19) — 3 = 16 ≠ 0 | -1 — не root |
| 9 | х 9 + 27 = 30 | х 30 — 1 = 9 | х 9-3 = 0 | корень | |
| х. 2 | х. 1 | х. 0 |
Получаем ( х. — ) (9 х 2 + 30 х. + 9) = 0 х. 1 = , х. 2 = — , х. 3 = -3.
Для удобства подсчета при выборе Q -Korny Может быть удобно заменить переменную, перейти к данному уравнению и выбрать Z Korni. .
.- Если можно использовать замену типа y = kx.
Формула Кардано. Существует универсальный метод решения кубических уравнений — это формула Кардано. Эта формула связана с именами итальянских математиков Джероламо Кардано (1501–1576), Николо Тарталия (1500–1557), Сципиона дель Ферро (1465–1526). Эта формула выходит за рамки нашего курса.
н. = 4 — уравнение четвертой степени.
Метод группировки.
Пример: X. 4 + 2 x. 3 + 5 х. 2 + 4 х. — 12 = 0 ( x. 4 + 2 x. 3) + (5 x. 2 + 10 x. ) — (6 х + 12) = 0 ( x + 2) ( x 3 + 5 x — 6) = 0 ( x. + 2) ( x. — 1) ( x. 2 + x. + 6) = 0 х. 1 = -2, х. 2 = 1.
Метод замены переменной.
- Уравнение Бикета типа aX. 4 + bX. 2 + S. = 0 .
Пример: x. 4 + 5 х. 2 — 36 = 0. Замена г. = х. 2. Отсюда г. 1 = 4, г. 2 = -9. поэтому х. 1,2 = + 2.
- Обратное уравнение четвертой степени типа aX. 4 + BX. 3 + С. х. 2 + bX. + а. = 0.
Решаем, комбинируя элементы с одинаковыми коэффициентами заменой типа
- aX. 4 + bX. 3 + cX. 2 — bX. + а. = 0.
- Обобщенное уравнение доходности четвертой степени представления aX. 4 + bX. 3 + cX. 2 + кБХ + к 2. а = 0,.
- Замена обыкновенного. Некоторые стандартные замены.
Пример 3. . Замена общего типа (следует из вида конкретного уравнения).
н. = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней н. = 3.
Общая формула. Существует универсальное решение уравнений четвертой степени.Эта формула связана с именем Луи Феррари (1522-1565). Эта формула выходит за рамки нашего курса.
н. > 5 — уравнения пятой и более высоких степеней.
Уравнение с целыми коэффициентами. Выбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен приведенному выше для n. = 3.
Уравнение с целыми коэффициентами. Выбор Q-корней На основе теоремы. Схема Горнера.Алгоритм аналогичен приведенному выше для n. = 3.
Симметричные уравнения. Любое уравнение возврата нечетной степени имеет корень x. = -1 и после разложения на множители получаем, что одна вещь имеет вид ( х. + 1), а вторая фабрика — уравнение возврата четной степени (ее степень на единицу меньше степени исходное уравнение). Любое обратное уравнение четной степени вместе с корнем вида x = φ. Содержит корень представления.Используя эти утверждения, решаем задачу, понижая степень исследуемого уравнения.
Метод замены переменной. Использование однородности.
Не существует общей формулы для решения целых уравнений пятой степени (ее показали итальянский математик Паоло Руффини (1765-1822) и норвежский математик Нильс Хенрик Абель (1802-1829)) и более высоких степеней (это показал французский математик Эваристер Галуа (1811-1832)).
- Напомним еще раз, что на практике можно использовать комбинаций перечисленных выше методов.К агрегатным уравнениям младших степеней удобно перейти путем декомпозиции исходного уравнения на множители .
- Помимо нашего сегодняшнего обсуждения оставалось широко используемым на практике. графических методов решений уравнений I. методов приближенного решения Уравнений высших степеней.
- Бывают ситуации, когда уравнение имеет R-корни. Тогда решение сводится к тому, чтобы показать, что корневое уравнение не имеет.Для доказательства проанализируем поведение рассматриваемых функций на интервалах монотонности. Пример: уравнение x. 8 — х. 3 + 1 = 0 не имеет корней.
- Используйте свойства однообразия функций . Бывают ситуации, когда использование различных свойств функций позволяет упростить задачу.
Пример 1: Уравнение x. 5 + 3 х. -4 = 0 имеет один корень х. = 1. Других корней для однообразия анализируемых функций других корней нет.
Пример 2: Уравнение x. 4 + ( x. — 1) 4 = 97 имеет корни x. 1 = -2 и х. 2 = 3. Проанализировав поведение соответствующих функций на интервалах монотонности, делаем вывод, что других корней нет.
4. Подведение итогов.
Резюме: На данный момент мы освоили основные методы решения различных уравнений высших степеней (для n > 3). Наша задача — научиться эффективно использовать перечисленные выше алгоритмы.В зависимости от вида уравнения нам нужно будет узнать, как определить, какой метод решения в этом случае является наиболее эффективным, а также правильно применяемый метод.
5. Домашнее задание.
: P.7, p. 164-174, №№ 33-36, 39-44, 46.47.
: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.
Возможные темы докладов или тезисов по теме:
- Формула Кардано
- Графическое решение решения уравнений. Примеры решений.
- Методы приближенного решения уравнений.
Анализ усвоения материала и интереса студентов к теме:
Опыт показывает, что интерес студентов в первую очередь вызывает возможность выбора Z. -Korny I. Q. -Уравнения Корни с довольно простым алгоритмом с использованием горной схемы. Также студентов интересуют различные стандартные типы переменных, которые позволяют значительно упростить тип задания.Особый интерес обычно вызывают графические способы решения. В этом случае вы можете дополнительно разобрать задачи по графическому способу решения уравнений; Обсудите график общего вида для многочлена 3, 4, 5 степеней; Анализируйте как количество корней уравнения 3, 4, 5 степени с учетом соответствующего графика. Ниже приведен список книг, в которых вы можете найти дополнительную информацию по этой теме.
Библиография:
- Виленкин Н.Я. и другие. «Алгебра. Учебник для школьников 9 классов с углубленным изучением математики» — М., Просвещение, 2007 г. — 367 с.
- Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. «За страницами учебника математики. Арифметика. Алгебра. 10-11 класс» — М., Просвещение, 2008 г. — 192 с.
- Доходный М.Я. «Справочник по математике» — М., АСТ, 2010 г. — 1055 с.
- Галицкий М.Л. «Сборник задач по алгебре.Учебник Для 8-9 классов с углубленным изучением математики »- М., Просвещение, 2008 г. — 301 с.
- Звавич Л.И. et al. «Алгебра и начало анализа. 8-11 кл. Пособие для школ и классов с углубленным изучением математики» — М., Капля, 1999 г. — 352 с.
- Звавич Л.И., Аверьянов Д.И., Пигарев Б.П., Трушанина Т.Н. «Задания по математике для подготовки к письменному экзамену в 9 классе» — М., Просвещение, 2007 г. — 112 с.
- Иванов А.А., Иванов А.П. «Тематические тесты для систематизации знаний по математике» Часть 1 — М., Физматкнига, 2006 — 176 с.
- Иванов А.А., Иванов А.П. «Тематические тесты для систематизации знаний по математике» Часть 2 — М., Физматкнига, 2006 — 176 с.
- Иванов А.П. «Контрольные работы I. Контрольные работы по математике. Учебное пособие». — М., Физматкнига, 2008 — 304 с.
- Leibson K.L. «Сборник практических заданий по математике.Часть 2-9 класс »- М., МЦНМО, 2009 г. — 184 с. .
- Макарычев Ю.Н., Миндюк Н.Г. «Алгебра. Дополнительные главы для школьного учебника 9 класса. Учебное пособие для школьников и классов с углубленным изучением математики». — М., Просвещение, 2006 — 224 с.
- Мордкович А.Г. «Алгебра. Углубленное изучение. 8 класс. Учебное пособие» — М., Мнемозина, 2006 г. — 296 с.
- Савин А.П. «Энциклопедический словарь юной математики» — М., Педагогика, 1985 — 352 с.
- Сурвило Г.С., Симонов А.С. «Дидактические материалы по алгебре для 9 класса с углубленным изучением математики» — М., Просвещение, 2006 г. — 95 с.
- Чулков П.В. «Уравнения и неравенства в школьном курсе математики. Лекции 1-4» — М., первое сентября 2006 г. — 88 с.
- Чулков П.В. «Уравнения и неравенства в школьном курсе математики. Лекции 5-8» — М., первое сентября 2009 г. — 84 с.
Знакомство с общим решением систем равенств и неравенств. Система неравенства
Эта статья содержит начальную информацию о системах неравенства. Здесь дается определение системы неравенств и определение решения системы неравенств. А также перечислены основные типы систем, с которыми чаще всего работают на уроках алгебры в школе, и приведены примеры.
Страница навигации.
Что такое система неравенства?
Системы неравенства удобно определять аналогично тому, как мы ввели определение системы уравнений, то есть в соответствии с типом записи и смыслом, вложенным в нее.
Определение.
Система неравенств — Это запись, которая представляет собой определенное количество неравенств, записанных друг в друге, объединенных в левой фигурной скобке и обозначающих множество всех решений, которые одновременно являются решениями для каждого системного неравенства.
Приведем пример системы неравенства. Возьмем два произвольных, например 2 · x-3> 0 и 5 — x≥4 · X-11, запишем их друг под другом
2 · x-3> 0,
5-x≥4 · X-11
и объединяем знак системы — фигурную скобку, в результате получаем систему неравенств такого типа:
Аналогично дается представление о неравенствах в школьных учебниках. Стоит отметить, что определения даны более узко: для неравенств с одной переменной или с двумя переменными.
Основные виды неравенств
Понятно, что различных неравенств можно составить бесконечно много. Чтобы не потеряться в этом многообразии, их желательно рассматривать в группах, имеющих свои особенности. Все неравенства можно разделить на группы по следующим критериям:
- по количеству неравенств в системе;
- по количеству переменных, участвующих в записи;
- в соответствии с самим неравенством.
В числе включенных в статью неравенств различают две, три, четыре системы и т. Д. Неравенства. В предыдущем абзаце мы привели пример системы, которая представляет собой систему двух неравенств. Покажем еще один пример системы четырех неравенств.
Отдельно скажем, что нет смысла говорить о системе одного неравенства, в данном случае, по сути, речь идет о самом неравенстве, а не о системе.
Если вы посмотрите на количество переменных, существует система неравенств с единицей, двумя, тремя и т. Д.переменные (или, как и везде, неизвестны). Посмотрите на последнюю систему неравенства, зафиксированную двумя абзацами выше. Это система с тремя переменными x, y и z. Обратите внимание, что его два первых неравенства не содержат всех трех переменных, а содержат только одну из них. В контексте этой системы их следует понимать как неравенства с тремя переменными вида X + 0 · Y + 0 · Z≥-2 и 0 · X + Y + 0 · Z≤5 соответственно. Отметим, что в школе основное внимание уделяется неравенствам с одной переменной.
Осталось обсудить, какие типы неравенства задействованы в записях систем. В школе в основном рассматриваются системы двух неравенств (реже — трех, еще реже — четырех и более) с одной или двумя переменными, а сами неравенства обычно составляют целые неравенства Первая или вторая степень (реже — более высокие степени). или дробно-рациональное). Но не удивляйтесь, если в материалах подготовки встретятся системы неравенств, содержащие иррациональные, логарифмические, индикативные и другие неравенства.В качестве примера приведем систему неравенств, из которой она взята.
Что называется решением системы неравенства?
Введем еще одно определение, связанное с системами неравенств — определение решения системы неравенств:
Определение.
Путем решения системы неравенств с одной переменной Это называется такое значение переменной, которое добавляет каждое из неравенств системы к точному, другими словами, которое является решением каждого системного неравенства.
Поясним на примере. Возьмем систему двух неравенств с одной переменной. Примем значение переменной x равным 8, это решение нашей системы неравенств по определению, так как ее подстановка в системное неравенство дает два точных числовых неравенства 8> 7 и 2-3 · 8≤0. Напротив, единица не является решением системы, так как при ее замене вместо переменной x первое неравенство превратится в неправильное числовое неравенство 1> 7.
Аналогично можно ввести определение решения системы неравенств с двумя, тремя и большим числом переменных:
Определение.
Решением системы неравенств с двумя, тремя и т. Д. Переменными называются парные, тройные и т. Д. Значения этих переменных, которые одновременно являются решением каждого системного неравенства, то есть, сводит каждое системное неравенство к правому числовому неравенству.
Например, пара значений x = 1, y = 2 или другая запись (1, 2) является решением системы неравенств с двумя переменными, как 1 + 2
Системы неравенства могут не иметь решений, могут иметь конечное число решений и может иметь бесконечно много решений.Часто говорят о множестве решений системы неравенств. Когда в системе нет решений, значит, есть пустой набор ее решений. Когда решений является конечным числом, то множество решений содержит конечное число элементов, а когда решений бесконечно много, то множество решений состоит из бесконечного числа элементов.
В некоторых источниках вводятся определения частного и общего решения системы неравенств, как, например, в учебниках Мордковича.Под частным решением системы неравенств понимаю ее одно отдельное решение. В свою очередь общее решение системы неравенства — это все ее частные решения. Однако в этих терминах это имеет смысл только тогда, когда необходимо подчеркнуть, что ясно, что такое решение, но обычно это ясно из контекста, поэтому гораздо чаще они говорят просто «решение системы неравенства».
Из введенных в статье определений неравенств и решений следует, что решение системы неравенств является пересечением множеств решений всех неравенств этой системы.
Библиография.
- Алгебра: занятий. Для 8 кл. общее образование. учреждения / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворов]; Эд. С. А. Теликовский. — 16-е изд. — М .: Просвещение, 2008. — 271 с. : IL. — ISBN 978-5-09-019243-9.
- Алгебра: 9 класс: учеб. Для общего образования. учреждения / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворов]; Эд. С. А. Теликовский. — 16-е изд. — М .: Просвещение, 2009.- 271 с. : IL. — ISBN 978-5-09-021134-5.
- Мордкович А.Г. Алгебра. 9 сорт. По 2 ч. Л. 1. Учебное пособие для учащихся общеобразовательных учреждений / А. Мордкович, П. В. Семенов. — 13-е изд., Чет. — М .: Мнемозина, 2011. — 222 с .: Ил. ISBN 978-5-346-01752-3.
- Мордкович А.Г. Алгебра и начало математического анализа. 11 класс. По 2 ч. Л. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Мордкович, П. В. Семенов.- 2-е изд., Чед. — М .: Мнемозина, 2008. — 287 с .: Ил. ISBN 978-5-346-01027-2.
- ЕГЭ -2013. Математика: Типовые экзамены: 30 вариантов / под ред. Семенова А.Л., Ященко И.В. — М .: Издательство «Народное просвещение», 2012. — 192 с. — (ЕГЭ-2013. ШКОЛА ФИПИ).
Рассмотрим на примерах, как решить систему линейных неравенств.
4x + 29 \ КОНЕЦ (Массив) \ Вправо. \\] «Заголовок =» (! Lang: Rendered by QuickTex.com «>!}
Для решения системы необходима каждая из составляющих ее неравенств.Только решение принимается не отдельно, а вместе, соединяя их фигурной скобкой.
В каждом из неравенств системы неизвестным лицам передать один путь, известный друг другу с противоположным знаком:
Заголовок = «(! Lang: Rendered by QuickTextEx.com»>!}
После упрощения обеих частей неравенства необходимо разделить число, стоящее перед ix. Первое неравенство делится на положительное число, поэтому знак неравенства не меняется.Второе неравенство делится на отрицательное число, поэтому знак неравенства необходимо поменять на противоположный:
Заголовок = «(! Lang: Rendered by QuickTextEx.com»>!}
Решение неравенств примечание на числовых строках:
В ответ записываем пересечение решений, то есть ту часть, где штриховка находится на обеих прямых.
Ответ: X∈ [-2; 1).
В первом неравенстве мы избавляемся от братства.Для этого обе части умножаем на наименьший общий знаменатель 2. При умножении на положительное число неравенство не меняется.
Во втором неравенстве раскрываем скобки. Произведение суммы и разности двух выражений равно разности квадратов этих выражений. В правой части — квадрат разницы двух выражений.
Заголовок = «(! Lang: Rendered by QuickTextEx.com»>!}
Неизвестные пересадят в одну сторону, знакомую друг другу с обратным знаком и упрощают:
Обе части неравенства делятся на число перед ix.В первом неравенстве делим отрицательное число, поэтому знак неравенства меняется на противоположный. Во втором — делим на положительное число, знак неравенства не меняется:
Заголовок = «(! Lang: Rendered by QuickTextEx.com»>!}
Оба неравенства со знаком «меньше» (не обязательно, чтобы один знак был строго «меньше», а другой не мешал, «меньше или равно»). Мы не можем отмечать оба решения и использовать правило «». Little равно 1, поэтому система сводится к неравенству
Мы отмечаем его решение о числовом прямом:
Ответ: x∈ (-∞; 1].
Открытые брекеты. В первом неравенстве -. Он равен количеству кубиков этих выражений.
Во втором — работа суммы и разности двух выражений, которая равна разнице в квадратах. Поскольку здесь стоит знак «минус», есть лучший знак раскрытия в два этапа: сначала используйте формулу, и только потом раскрывайте скобки, меняя знак каждой дополнительной на противоположный.
Переход неизвестен в одну сторону, известен — в другую с обратным знаком:
Заголовок = «(! Lang: Отрисовано QuickTextEx.com «>!}
Оба подписывают «еще». Используя более длинное правило, мы сводим систему неравенств к одному неравенству. Две большие цифры 5 в соответствии с
Заголовок = «(! Lang: Rendered by QuickTextEx.com»>!}
Решение неравенства отметьте на числовом прямом и запишите ответ:
Ответ: x∈ (5; ∞).
Так как алгебра линейных неравенств встречается не только как самостоятельные задачи, но и при решении разного рода уравнений, неравенств и т. Д., важно вовремя изучить эту тему.
В следующий раз мы рассмотрим примеры решения линейных неравенств в частных случаях, когда одно из неравенств не имеет решений или решением для него является любое число.
Категория: | Система неравенства.
Пример 1. . Найдите область выражения
Решение. Под знаком квадратного корня должно стоять неотрицательное число, что означает, что два неравенства должны выполняться одновременно: В таких случаях говорят, что задача сводится к решению системы неравенств
Но с Такой математической модели (системы неравенства) мы еще не встречали.Итак, решение примера не доводить до конца.
Неравенства, образующие систему, объединены фигурной скобкой (то же самое и в системах уравнений). Например, запись
означает, что неравенства 2x — 1> 3 и zh — 2
Иногда это используется для записи системы неравенств в виде двойного неравенства. Например, систему неравенств
можно записать в виде двойного неравенства 3
В курсе алгебры 9 класса мы будем рассматривать только системы двух неравенств.
Рассмотрим систему неравенства
Можно выбрать несколько ее частных решений, например x = 3, x = 4, x = 3,5. Фактически при x = 3 первое неравенство принимает вид 5> 3, а второе — тип 7
При этом значение x = 5 не является решением системы неравенств. При x = 5 Первое неравенство принимает вид 9> 3 — правильное числовое неравенство, а второе — мнение 13 Решить систему неравенств — значит найти все ее частные решения.Понятно, что угадывание, продемонстрированное выше, не является методом решения системы неравенств. В следующем примере мы покажем, как обычно рассуждают при решении системы неравенств.
Пример 3. Решите систему неравенств:
Решение.
а) Решая первое неравенство системы, находим 2x> 4, x> 2; Решая второе неравенство системы, находим SK б) Решая первое неравенство системы, находим X> 2; Решая второе неравенство системы, находим Эти промежутки по одной координате напрямую, используя верхнюю штриховку для первого промежутка, а для второго — нижнюю штриховку (рис.23). Решением системы неравенств будет пересечение решений системы неравенств, т.е. промежуток, на котором совпали обе штриховки. В этом примере мы получаем луч
in) Решая первое неравенство системы, находим x
Обобщая аргументы, приведенные в рассмотренном примере. Предположим, нам необходимо решить систему неравенств
Пусть, например, интервал (A, B) является решением неравенства Fx 2> G (x), а интервал (C, D) является решением выполняется неравенство F 2 (x)> S2 (x).Отметим эти промежутки на одной и той же прямой координате, используя верхнюю штриховку для первого промежутка, а для второго — нижнюю штриховку (рис. 25). Решением системы неравенств является пересечение решений системного неравенства, т.е. промежуток, на котором совпали обе штриховки. На рис. 25 Это интервал (C, B).
Теперь мы можем легко решить систему неравенств, которая была получена выше, в Примере 1:
Решая первое неравенство системы, находим x> 2; решая второе неравенство системы, находим x
Конечно, система неравенств не должна состоять из линейных неравенств, как это было до сих пор; Могут быть любые рациональные (и не только рациональные) неравенства.Технически работа с системой рациональных нелинейных неравенств, конечно, сложнее, но принципиально нового (по сравнению с линейными неравенствами) здесь нет ничего.
Пример 4. Решите систему неравенств
Решение.
1) Решаю неравенство
Обращаем внимание на точки -3 и 3 на числовой прямой (рис. 27). Они разбиваются прямо на три промежутка, и на каждом промежутке выражение p (x) = (x- 3) (x + 3) сохраняет постоянный знак — эти знаки перечислены на рис.27. Нас интересуют зазоры, на которых выполняется неравенство p (x)> 0 (они заштрихованы на рис. 27), и точки, в которых выполняется равенство p (x) = 0, т.е. точки x = -3, x = 3 (они отмечены на рис. 2 7 темными кружками). Таким образом, на рис. 27 представлена геометрическая модель решения первого неравенства.
2) Решаем неравенство
Отметим точки 0 и 5 на числовой прямой (рис. 28). Они разбиваются прямо на три промежутка, и в каждом интервале выражение O (заштриховано на рис.28), и точки, в которых выполняется равенство G (x), т.е. точки x = 0, x = 5 (они отмечены на рис. 28 темными кружками). Таким образом, на рис. 28 представлена геометрическая модель решения второго неравенства системы.
3) Отметим найденные решения первого и второго неравенств системы по одной координате прямой, используя верхнюю штриховку для решений первого неравенства, а для решений второй штриховки — нижнюю штриховку (рис. 29). Решением системы неравенств будет пересечение решений системы неравенств, т.е.е. Промежуток, на котором совпали обе штриховки. Этот разрыв — сегмент.
Пример 5. Решите систему неравенств:
Решение:
а) Из первых неравенств находим X> 2. Рассмотрим второе неравенство. Квадрат три половины x 2 + x + 2 не имеет действительных корней, а его старший коэффициент (коэффициент при x 2) положительный. Это означает, что при всех выполняется неравенство x 2 + x + 2> 0, а значит, второе неравенство системы не имеет решений.Что это означает для системы неравенства? Это означает, что в системе нет решений.
б) Из первых неравенств находим X> 2, а второе неравенство выполняется при любых значениях x. Что это означает для системы неравенства? Это означает, что его решение имеет вид x> 2, т.е. совпадает с решением первого неравенства.
О Т в Э Т:
а) решений нет; б) X> 2.
Этот пример является иллюстрацией для следующего полезного.
1. Если одно неравенство не имеет решений в системе нескольких неравенств с одной переменной, то система не имеет решений.
2. Если одно неравенство выполняется в системе двух неравенств с одной переменной, при любых значениях переменной, то решением системы является решение второго неравенства системы.
Выполняя этот абзац, вернитесь к заданному в начале заданию заданному числу и решите его, как говорится, по всем правилам.
Пример 2. (См. Стр.29). Интегрирован с натуральным числом. Известно, что если его прибавить к квадрату намеченного числа 13, то сумма будет больше, чем произведение намеченного числа и числа 14. Если к квадрату намеченного числа 45 прибавить 45, то сумма будет будет меньше работы предполагаемого числа и числа 18. Какой номер предназначен?
Решение.
Первый этап. Составление математической модели.
Задуманное число x, как мы видели выше, должно удовлетворять системе неравенства
Вторая фаза. Работа с математической моделью. Формируем первое неравенство системы в виду
x2- 14x + 13> 0.
Находим корни трехвыстрелов x 2 — 14x + 13: x 2 = 1, x 2 = 13. с помощью параболы y = x 2 — 14x + 13 (рис.30) заключаем, что интересующее нас неравенство выполняется с x 13.
Преобразуем второе неравенство системы к виду x2 — 18 2 + 45
Графический метод.. 3
Симплекс-метод .. 6
Метод искусственного основания .. 8
Принцип двойственности .. 10
Список использованной литературы … 12
Индивидуальные свойства линейных неравенств рассматривались в первой половине XIX века в связи с некоторыми задачами аналитической механики. Систематическое изучение линейных неравенств началось в самом конце XIX века, но о теории линейных неравенств можно было говорить только в конце двадцатых годов XX века, когда по ним было получено достаточное количество результатов. уже накоплено.
Теперь теорию конечных систем линейных неравенств можно рассматривать как выросшую из нее ветвь линейной алгебры с дополнительным требованием упорядоченности поля коэффициентов.
Линейные неравенства особенно важны для экономистов, потому что с помощью линейных неравенств можно моделировать производственные процессы и находить наиболее выгодные планы производства, транспортировки, размещения ресурсов и т. Д.
В данной статье представлены основные методы решения линейных неравенств применительно к конкретным задачам.
Графический метод состоит в построении набора допустимых решений ZLP и нахождении в заданной множественной точке, соответствующей целевой функции MAX / MIN.
В связи с ограниченными возможностями визуального графического представления этот метод применим только для линейных неравенств с двумя неизвестными и системами, которые могут быть даны в этой форме.
Для наглядной демонстрации графического метода необходимо следующее задание:
- На первом этапе необходимо построить зону допустимых решений.Для этого примера удобно выбрать X2 по оси абсцисс, а x1 по ординате и записать неравенства в следующем виде:
Для нахождения граничных точек решить уравнения (1) = (2), (1) = (3) и (2) = (3).
Как видно из рисунка, многогранник ABC очерчивает площадь допустимых решений.
Если область допустимых решений не замкнута, то либо Max (f) = + ∞, либо min (f) = -∞.
- Теперь можно перейти непосредственно к нахождению максимальной функции f.
Поочередно подставляя координаты вершин многогранника в функцию f и сравнивая значения, находим, что
f (c) = f (4; 1) = 19 — функция максимума.
Этот подход весьма полезен при небольшом количестве вершин. Но эта процедура может затянуться, если вершин достаточно много.
В этом случае удобнее рассматривать линию уровня F = a.При монотонном увеличении количества АОТ -∞ до + ∞ прямая f = укладывается вектором нормали. Если при таком расположении линии уровня есть некоторая точка X — первая общая точка допустимых решений (многогранник ABCDE) и линия уровня, то F (x) — это минимум кратного ABCDE. Если X — последняя точка уровня уровня уровня и задана ABCDE, то F (x) — максимум на множестве допустимых решений. Если при a → -∞ прямом f = гибнет много допустимых решений, то min (f) = -∞.Если это произойдет, когда и → + ∞, то
В нашем примере прямое f = соответствует площади ABCDEV в (4; 1). Так как это последняя точка пересечения, Макс (f) = f (c) = f (4; 1) = 19.
Реальные задачи линейного программирования содержат очень большое количество ограничений и неизвестны и выполняются на компьютере. Симплекс-метод — наиболее распространенный алгоритм, используемый для решения подобных задач. Суть метода заключается в том, что после определенного количества специальных симплексных преобразований ЗЛП, приданных в особую форму, разрешается.Для демонстрации симплекс-метода в действии путем решения, с объективным комментарием следующей задачи:
- Для того чтобы продолжить решение симплекса SLP методом, необходимо привести VLP к специальному виду и заполнить симплекс-таблицу.
Система (4) — Естественные ограничения и таблица не подходит. Уравнения (1), (2), (3) образуют область допустимых решений. Выражение (5) — целевая функция. Свободные члены в системе ограничений и область допустимых решений должны быть неотрицательными.
В этом примере X3, X4, X5 — основные неизвестные. Они должны быть выражены через свободное неизвестное и заменить их в целевой функции.
Теперь можно приступить к заполнению симплексной таблицы:
| Б. | Х1. | Х2 | Х3. | Х4. | Х5 | С. |
| X3. | 0 | -1 | 1 | 1 | 0 | 1 |
| X4. | 0 | 1 | -1 | 0 | 1 | 1 |
| X5 | 1 | 1 | 1 | 0 | 0 | 2 |
| ф. | 0 | -6 | 7 | 0 | 0 | 3 |
В первом столбце данной таблицы указаны основные неизвестные лица, во втором — значения свободных неизвестных, в остальных — коэффициенты при неизвестных.
- Чтобы найти максимальную функцию FNADO, используя преобразования по методу Гаусса, сделать так, чтобы все коэффициенты при неизвестном в последней строке были неотрицательными (чтобы найти минимум, чтобы все коэффициенты были равны нулю) .
| Б. | Х1. | Х2 | Х3. | Х4. | Х5 | С. |
| X3. | -1 | 1 | 1 | 0 | 0 | 1 |
| X4. | 1 | -1 | 0 | 1 | 0 | 1 |
| X5 | 1 | 1 | 0 | 0 | 1 | 2 |
| ф. | -6 | 7 | 0 | 0 | 0 | 3 |
Для этого выберите столбец с отрицательным коэффициентом в последней строке (столбец 3) и сделайте свободный член / коэффициент (1/1; 2/1) для положительных элементов этого столбца (1/1; 2 / 1).Из этих отношений выберите наименьшую и пометьте соответствующую строку.
Мы выбрали элемент в ячейке (3; 3). Теперь с помощью метода Гаусса сбрасываем остальные коэффициенты в этом столбце, это приводит к изменению базиса и мы приближаемся к оптимальному решению.
| Б. | Х1. | Х2 | Х3. | Х4. | Х5 | С. |
| X3. | 0 | 0 | 1 | 1 | 0 | 2 |
| X1. | 1 | -1 | 0 | 1 | 0 | 1 |
| X5 | 0 | 2 | 0 | -1 | 1 | 1 |
| ф. | 0 | 1 | 0 | 6 | 0 | 9 |
Как видно из таблицы, теперь все коэффициенты в последней строке больше или равны нулю. Значит, мы нашли оптимальное значение.Свободные неизвестные равны нулю, значение основной неизвестной и максимальная функция f соответствует значению свободных неизвестных.
приложение
Решение неравенств онлайн на Math34.biz для консолидации студентов и школьников прошел материал. И тренировать свои практические навыки. Неравенство в математике — одобрение относительной ценности или процедуры для двух объектов (один из объектов меньше или не больше другого) или того, что два объекта не совпадают (отрицание равенства).В элементарной математике численные неравенства изучаются, в общей алгебре — анализ, геометрии считаются неравенствами также между объектами не-природы. Для решения неравенства необходимо определить обе части, между которыми находится один из знаков неравенства. Строгие неравенства влекут неравенство двух объектов. В отличие от строгого, нестратегического неравенства допускается равенство объектов объектов. Линейные неравенства — это простейшее с точки зрения выражения, а решение таких неравенств — простейшие методы.Основная ошибка студентов при решении неравенства в режиме онлайн заключается в том, что они не различают особенность строгого и неравенства, от чего зависит или нет граничных значений в окончательном ответе. Несколько неравенств, связанных с несколькими неизвестными, называются системой неравенств. Решение неравенств из системы — это некая область на плоскости или объемная фигура в трехмерном пространстве. Наряду с этим, N-мерные пространства являются абстракциями, однако при решении таких неравенств часто не обойтись без специальных вычислительных машин.Для каждого неравенства отдельно необходимо найти неизвестные на границах значения решения. Многие из всех решений неравенства и есть его ответ. Замена одного неравенства на другое неравенство называется эквивалентным переходом от одного неравенства к другому. Похожий подход встречается и в других дисциплинах, потому что он помогает придать выражениям стандартную форму. Вы оцените преимущества всех преимуществ неравенства онлайн на нашем сайте.Неравенство — это выражение, содержащее один из знаков =>. По сути, это логическое выражение. Это может быть правдой или нет — в зависимости от того, что стоит справа и слева в этом неравенстве. Уточнение смысла неравенства и основные приемы решения неравенств изучаются на разных курсах, а также в школе. Решение любых неравенств онлайн-неравенств с модульными, алгебраическими, тригонометрическими, трансцендентными неравенствами онлайн. Идентичное неравенство, как строгие, так и невероятные неравенства, упрощающие процесс достижения конечного результата, являются вспомогательным инструментом для решения поставленной задачи.Решение любых неравенств и систем неравенств, будь то логарифмические, индикативные, тригонометрические или квадратные неравенства, обеспечивается с помощью изначально правильного подхода к этому важному процессу. Решение неравенств в режиме онлайн на сайте всегда доступно всем пользователям и абсолютно бесплатно. Решения неравенства с одной переменной называются значениями переменных, что превращает его в истинное числовое выражение. Уравнения и неравенства с модулем: Модуль фактического числа — это абсолютное значение этого числа.Стандартный метод решения этих неравенств — возвести обе части неравенства до желаемой степени. Неравенства — это выражения, указывающие на сравнение чисел, поэтому грамотное решение неравенства обеспечивает точность таких сравнений. Они строгие (более, менее) и невероятные (более или равные, менее или равные). Решить неравенство — это значит найти все те значения переменных, которые при подстановке в исходное выражение превращают его в истинное числовое представление.. Понятие неравенства, его сущность и особенности, классификация и разновидности — вот что определяет специфику этого математического разбиения. Основные свойства числовых неравенств, применимые ко всем объектам этого класса, в обязательном порядке должны быть изучены студентами на начальном этапе ознакомления с данной темой. Неравенства и пробелы в числовом прямом очень тесно связаны, когда дело доходит до решения неравенств в Интернете. Графическое обозначение решения неравенства наглядно показывает суть такого выражения, становится понятно, к чему следует стремиться для решения той или иной задачи.В основу концепции неравенства входит сравнение двух или нескольких объектов. Неравенства, содержащие переменную, решаются как уравнения, составленные аналогичным образом, после чего выборка интервалов будет принята для ответа. Любое алгебраическое неравенство, тригонометрическое неравенство или неравенство, содержащее трансцендентные функции, вы можете легко и мгновенно решить с помощью нашего бесплатного сервиса. Число является решением неравенства, если при подстановке этого числа вместо переменной мы получаем истинное выражение, то есть знак неравенства показывает истинное понятие.. Решение проблемы неравенства онлайн на сайте каждый день для полноценной учебы студентов со студентом и закрепления их практических навыков. Часто тему неравенства онлайн по математике изучают школьники после прохождения разбиения уравнений. Так как при решении необходимо применять все принципы для определения интервалов решения. Найти с аналитической точки зрения ответ труднее, чем сделать то же самое, но в числовой форме. Однако такой подход дает более наглядную и полную картину целостности решения неравенства.Сложность может возникнуть на этапе построения линии абсцисс и применения точек для решения однотипного уравнения. После этого решение неравенств сводится к определению функции функции на каждом интервале для определения возрастающей или убывающей функции. Для этого необходимо поочередно подставлять значения, заключенные в пределах каждого интервала, в исходную функцию и проверять ее значение на положительность или отрицание. В этом суть всех решений, включая интервалы решений.Когда вы сами решите неравенство и увидите все интервалы с решениями, вы поймете, как этот подход применим для дальнейших действий. Сайт Сайт предлагает вам перепроверить результаты своих расчетов с помощью мощного современного калькулятора на этой странице. Вы можете легко выявить неточности и недостатки в своих расчетах, используя уникальное неравенство Решебанта. Студенты часто задаются вопросом, где найти такой полезный ресурс? Благодаря новаторскому подходу к возможности определения потребностей инженеров, калькулятор был создан на базе мощных вычислительных серверов с использованием только новых технологий.По сути, решение неравенств в режиме онлайн заключается в решении уравнения с вычислением всех возможных корней. Полученные решения отмечаются прямой линией, а затем выполняется стандартная операция для определения значения функции на каждом интервале. А что, если корни уравнения являются исчерпывающими, как в данном случае, для решения неравенства в полной форме, которая бы удовлетворяла всем правилам записи результата? Ответ на этот и многие другие вопросы с легкостью даст наш сервисный сайт, для которого нет ничего невозможного в решении математических задач в режиме онлайн.В пользу сказанного добавим следующее: каждый, кто серьезно изучает такую дисциплину, как математика, обязан изучить тему неравенства. Неравенства бывают разных видов и решают неравенство в режиме онлайн. Иногда это сделать непросто, так как необходимо знать принципы подходов к каждому из них. В основе этого лежит успех и стабильность. Например, можно рассматривать такие типы, как логарифмические неравенства или трансцендентные неравенства. Это вообще особый вид таких сложных на первый взгляд задач для школьников, особенно школьников.Преподаватели учебных заведений уделяют много времени обучению тренингам для достижения профессиональных навыков в работе. К тем же типам мы возьмем тригонометрические неравенства и обозначим общий подход при решении множества практических примеров из временной шкалы. В некоторых случаях сначала нужно привести все в уравнение, упростить его, разложить по разным множителям, короче, привести к довольно наглядному виду. Во все времена человечество стремилось найти оптимальный подход в любых начинаниях. Благодаря современным технологиям человечество сделало просто огромный прорыв в будущее своего развития.Инновации все чаще и чаще, день за днем присоединяются к нашей жизни. В основе вычислительной техники лежит, конечно же, математика с ее принципами и строгим подходом к делу. Сайт представляет собой общий математический ресурс, в котором есть развитый калькулятор неравенств и множество других полезных сервисов. Воспользуйтесь нашим сайтом и вы будете уверены в правильности решаемых задач. Из теории известно, что объекты не-природы также изучаются неравенствами онлайн, только такой подход является особым способом изучения данного раздела по алгебре, геометрии и другим направлениям математики.Решать неравенства можно по-разному, окончательная проверка решений остается неизменной и лучше всего производить прямую подстановку значений в само неравенство. Во многих случаях полученный ответ очевиден и его легко проверить в уме. Предположим, мы предполагаем дробное неравенство, в котором есть желаемые переменные в знаменателе дробных выражений. Тогда решение неравенств сведется к приведению всех составляющих к общему знаменателю путем одновременного переноса всего в левую и правую части неравенства.Далее необходимо решить однородное уравнение, полученное в обозначении дроби. Эти числовые корни — это точки, которые не входят в интервалы общего решения неравенства, или их еще называют — точки с проколами, в которых функция обращается к бесконечности, то есть функция не определена, но вы можете получить только ее предельное значение в этой точке. Решая уравнение, полученное в числителе, все точки будут относиться к числовой оси. Стрихем те точки, в которых числитель дроби обращается к нулю.Соответственно, все остальные точки оставить пустыми или проколотыми. Мы найдем знак дроби на каждом интервале и после этого отменим окончательный ответ. Если на границах интервала есть заштрихованные точки, то включаем эти значения в раствор. Если на границах интервала будут точки прокола — эти значения не включают решение. После того, как вы определитесь с неравенством, вам нужно будет проверить полученный результат. Сделать можно своими руками, каждое значение из интервалов ответов поочередно подставлять в исходное выражение и выявлять ошибки.Сайт сайта с легкостью предоставит вам все решения неравенства, и вы сразу же сравните полученные вами ответы и калькулятор. Если все же произойдет ошибка, то на нашем ресурсе вам будет очень полезно решение неравенств онлайн. Мы рекомендуем всем ученикам для начала не решать прямое неравенство, а сначала получить результат на сайте, потому что в будущем сделать правильный расчет будет намного проще. В текстах это почти всегда решение подготовки системы неравенств с несколькими неизвестными.Наш ресурс поможет решить проблему неравенства онлайн за считанные секунды. В этом случае решение будет произведено мощной вычислительной программой с высокой точностью и без ошибок в окончательном ответе. Таким образом, вы можете сэкономить огромное количество времени на решении с помощью этого калькулятора примеров. В некоторых случаях школьники испытывают трудности, когда на практике или в лабораторных условиях встречаются логарифмические неравенства, и еще хуже, когда они видят тригонометрические неравенства со сложными дробными выражениями с синусом, косинусом или вообще с обратными тригонометрическими функциями.Если не крутить, но без помощи калькулятора неравенств, справиться будет очень сложно и ошибки на любом этапе решения проблемы не исключены. Пользоваться ресурсом сайта можно совершенно бесплатно, он доступен каждому пользователю ежедневно. Начать действовать с нашей службы ассистента — это очень хорошая идея, так как аналогов много, а услуги подразделений действительно качественные. Мы гарантируем точность расчетов при длительности поиска ответа в течение нескольких секунд. Вам нужно только зафиксировать неравенство в Интернете, а мы, в свою очередь, сразу же предоставим вам точный результат решения неравенства.Поиск на этом ресурсе может оказаться бессмысленным занятием, так как вряд ли вы встретите такой же качественный сервис, как мы. Можно обойтись без теории решения неравенств онлайн, но без качественного и быстрого калькулятора вам не обойтись. Желаем успехов в учебе! Вы действительно выбираете оптимальное решение неравенства онлайн, что часто связано с логическим подходом к случайной величине. Если пренебречь небольшим отклонением замкнутого поля, вектор возрастающего значения пропорционален наименьшему значению при сохранении порядка линии ординат.Инвариант пропорционален двукратному увеличению отображаемых функций вместе с исходящим ненулевым вектором. Лучший ответ всегда содержит точность расчетов. Наше решение неравенства примет вид однородной функции последовательно сопряженных числовых подмножеств главного направления. Для первого интервала возьмите наихудшее значение нашего представления переменной. Вычисляем предыдущее выражение на максимальный прогиб. Мы будем использовать услугу на усмотрение предложенных вариантов по мере необходимости.Будет ли решение неравенств онлайн с помощью хорошего калькулятора в своем классе — это риторический вопрос, конечно, школьникам такой инструмент пойдет только на пользу и принесет колоссальные успехи в математике. Оставим ограничение по площади с набором, которое сводим к элементам с восприятием импульсов по напряжению. Физические величины таких экстремумов математически описывают возрастание и убывание кусочно-непрерывных функций. На протяжении всего пути ученые находили доказательства существования элементов на разных уровнях изучения.Нас размещают все последовательно работающие подмножества одного сложного пространства в одном ряду с такими объектами, как шар, куб или цилиндр. Из нашего результата можно сделать однозначный вывод, и когда вы решите неравенство, то результат, безусловно, будет зависеть от математического допущения интеграции метода на практике. При текущем положении дел необходимое условие также будет достаточным условием. Неопределенность критериев часто вызывает разногласия студентов из-за ложных данных.Это упущение стоит взять на себя преподавателям вузов, а также учителям школ, так как на начальном этапе обучения необходимо это учитывать. Из приведенного выше вывода, по мнению опытных людей, можно сделать выводы, что решить неравенство в режиме онлайн — очень сложная задача, когда вы вводите неравенство неизвестных различных типов данных. Об этом говорится на научной конференции в Западном округе, где выдвигаются различные обоснования научных открытий в области математики и физики, а также молекулярного анализа биологически устроенных систем.При поиске оптимального решения абсолютно все логарифмические неравенства представляют научную ценность для всего человечества. Мы исследуем этот подход к логическим выводам для ряда несовпадений на высшем уровне представлений о существующем объекте. На первый взгляд, логика говорит не только о неопытном студенте. В связи с появлением масштабных аналогий рациональным будет сначала уравнять отношения к различию в объектах исследуемой территории, а затем на практике показать наличие общего аналитического результата.Решение неравенств полностью связано с использованием теории и будет важно, чтобы каждый изучил такой раздел математики для дальнейших исследований. Однако при решении неравенств необходимо найти все корни составленного уравнения, а затем применить все точки к оси ординат. Некоторые точки будут проколоты, а остальные войдут в интервалы с общим решением. Начнем изучение раздела математики с основ важнейшей дисциплины школьной программы.Если тригонометрические неравенства являются неотъемлемой частью текстовой задачи, то для расчета ответа просто необходимо применить ресурс. Правильно введите левую и правую части неравенства, нажмите кнопку и получите результат в течение нескольких секунд. Для быстрых и точных математических вычислений с числовыми или символьными коэффициентами перед неизвестными вам, как всегда, понадобится универсальный калькулятор неравенств и уравнений, который может быть предоставлен в считанные секунды для решения поставленной перед вами задачи.Если у вас нет времени написать ряд письменных упражнений, валидность услуги бесспорна даже невооруженным глазом. Для студентов такой подход более оптимален и оправдан с точки зрения материальных ресурсов и времени. Напротив категории лежит угол, и для его измерения нужен тираж, но вы можете воспользоваться подсказками в любой момент и решить неравенство, не применяя никаких формул. Это успешное завершение стартового действия? Однозначно ответ будет положительным.
% PDF-1.4 % 1 0 объект > эндобдж 8 0 объект /Заголовок /Тема / Автор /Режиссер / Ключевые слова / CreationDate (D: 20210823110102-00’00 ‘) / ModDate (D: 2010
- + 02’00 ‘)
>>
эндобдж
2 0 obj
>
эндобдж
3 0 obj
>
эндобдж
4 0 obj
>
эндобдж
5 0 obj
>
эндобдж
6 0 obj
>
эндобдж
7 0 объект
>
транслировать
GPL Ghostscript 9.142019-06-20T09: 05: 14 + 02: 002019-06-20T09: 05: 14 + 02: 00LaTeX с пакетом hyperref конечный поток
эндобдж
9 0 объект
>
эндобдж
10 0 obj
>
эндобдж
11 0 объект
>
эндобдж
12 0 объект
>
эндобдж
13 0 объект
>
эндобдж
14 0 объект
>
эндобдж
15 0 объект
>
эндобдж
16 0 объект
>
эндобдж
17 0 объект
>
эндобдж
18 0 объект
>
эндобдж
19 0 объект
>
эндобдж
20 0 объект
>
эндобдж
21 0 объект
>
эндобдж
22 0 объект
>
эндобдж
23 0 объект
>
эндобдж
24 0 объект
>
эндобдж
25 0 объект
>
эндобдж
26 0 объект
>
эндобдж
27 0 объект
>
эндобдж
28 0 объект
>
эндобдж
29 0 объект
>
эндобдж
30 0 объект
>
эндобдж
31 0 объект
>
эндобдж
32 0 объект
>
эндобдж
33 0 объект
>
эндобдж
34 0 объект
>
эндобдж
35 0 объект
>
эндобдж
36 0 объект
>
эндобдж
37 0 объект
>
эндобдж
38 0 объект
>
эндобдж
39 0 объект
>
эндобдж
40 0 объект
>
эндобдж
41 0 объект
>
эндобдж
42 0 объект
>
эндобдж
43 0 объект
>
эндобдж
44 0 объект
>
эндобдж
45 0 объект
>
эндобдж
46 0 объект
>
эндобдж
47 0 объект
>
эндобдж
48 0 объект
>
эндобдж
49 0 объект
>
эндобдж
50 0 объект
>
эндобдж
51 0 объект
>
эндобдж
52 0 объект
>
эндобдж
53 0 объект
>
эндобдж
54 0 объект
>
эндобдж
55 0 объект
>
эндобдж
56 0 объект
>
эндобдж
57 0 объект
>
эндобдж
58 0 объект
>
эндобдж
59 0 объект
>
эндобдж
60 0 объект
>
эндобдж
61 0 объект
>
эндобдж
62 0 объект
>
эндобдж
63 0 объект
>
эндобдж
64 0 объект
>
эндобдж
65 0 объект
>
эндобдж
66 0 объект
>
эндобдж
67 0 объект
>
эндобдж
68 0 объект
>
эндобдж
69 0 объект
>
эндобдж
70 0 объект
>
эндобдж
71 0 объект
>
эндобдж
72 0 объект
>
эндобдж
73 0 объект
>
эндобдж
74 0 объект
>
эндобдж
75 0 объект
>
эндобдж
76 0 объект
>
эндобдж
77 0 объект
>
эндобдж
78 0 объект
>
эндобдж
79 0 объект
>
эндобдж
80 0 объект
>
эндобдж
81 0 объект
>
эндобдж
82 0 объект
>
эндобдж
83 0 объект
>
эндобдж
84 0 объект
>
эндобдж
85 0 объект
>
эндобдж
86 0 объект
>
эндобдж
87 0 объект
>
эндобдж
88 0 объект
>
эндобдж
89 0 объект
>
эндобдж
90 0 объект
>
эндобдж
91 0 объект
>
эндобдж
92 0 объект
>
эндобдж
93 0 объект
>
эндобдж
94 0 объект
>
эндобдж
95 0 объект
>
эндобдж
96 0 объект
>
эндобдж
97 0 объект
>
эндобдж
98 0 объект
>
эндобдж
99 0 объект
>
эндобдж
100 0 объект
>
эндобдж
101 0 объект
>
эндобдж
102 0 объект
>
эндобдж
103 0 объект
>
эндобдж
104 0 объект
>
эндобдж
105 0 объект
>
эндобдж
106 0 объект
>
эндобдж
107 0 объект
>
эндобдж
108 0 объект
>
эндобдж
109 0 объект
>
эндобдж
110 0 объект
>
эндобдж
111 0 объект
>
эндобдж
112 0 объект
>
эндобдж
113 0 объект
>
эндобдж
114 0 объект
>
эндобдж
115 0 объект
>
эндобдж
116 0 объект
>
эндобдж
117 0 объект
>
эндобдж
118 0 объект
>
эндобдж
119 0 объект
>
эндобдж
120 0 объект
>
эндобдж
121 0 объект
>
эндобдж
122 0 объект
>
эндобдж
123 0 объект
>
эндобдж
124 0 объект
>
эндобдж
125 0 объект
>
эндобдж
126 0 объект
>
эндобдж
127 0 объект
>
эндобдж
128 0 объект
>
эндобдж
129 0 объект
>
эндобдж
130 0 объект
>
эндобдж
131 0 объект
>
эндобдж
132 0 объект
>
эндобдж
133 0 объект
>
эндобдж
134 0 объект
>
эндобдж
135 0 объект
>
эндобдж
136 0 объект
>
эндобдж
137 0 объект
>
эндобдж
138 0 объект
>
эндобдж
139 0 объект
>
эндобдж
140 0 объект
>
эндобдж
141 0 объект
>
эндобдж
142 0 объект
>
эндобдж
143 0 объект
>
эндобдж
144 0 объект
>
эндобдж
145 0 объект
>
эндобдж
146 0 объект
>
эндобдж
147 0 объект
>
эндобдж
148 0 объект
>
эндобдж
149 0 объект
>
эндобдж
150 0 объект
>
эндобдж
151 0 объект
>
эндобдж
152 0 объект
>
эндобдж
153 0 объект
>
эндобдж
154 0 объект
>
эндобдж
155 0 объект
>
эндобдж
156 0 объект
>
эндобдж
157 0 объект
>
эндобдж
158 0 объект
>
эндобдж
159 0 объект
>
эндобдж
160 0 объект
>
эндобдж
161 0 объект
>
эндобдж
162 0 объект
>
эндобдж
163 0 объект
>
эндобдж
164 0 объект
>
эндобдж
165 0 объект
>
эндобдж
166 0 объект
>
эндобдж
167 0 объект
>
эндобдж
168 0 объект
>
эндобдж
169 0 объект
>
эндобдж
170 0 объект
>
эндобдж
171 0 объект
>
эндобдж
172 0 объект
>
эндобдж
173 0 объект
>
эндобдж
174 0 объект
>
эндобдж
175 0 объект
>
эндобдж
176 0 объект
>
эндобдж
177 0 объект
>
эндобдж
178 0 объект
>
эндобдж
179 0 объект
>
эндобдж
180 0 объект
>
эндобдж
181 0 объект
>
эндобдж
182 0 объект
>
эндобдж
183 0 объект
>
эндобдж
184 0 объект
>
эндобдж
185 0 объект
>
эндобдж
186 0 объект
>
эндобдж
187 0 объект
>
эндобдж
188 0 объект
>
эндобдж
189 0 объект
>
эндобдж
190 0 объект
>
эндобдж
191 0 объект
>
эндобдж
192 0 объект
>
эндобдж
193 0 объект
>
эндобдж
194 0 объект
>
эндобдж
195 0 объект
>
эндобдж
196 0 объект
>
эндобдж
197 0 объект
>
эндобдж
198 0 объект
>
эндобдж
199 0 объект
>
эндобдж
200 0 объект
>
эндобдж
201 0 объект
>
эндобдж
202 0 объект
>
эндобдж
203 0 объект
>
эндобдж
204 0 объект
>
эндобдж
205 0 объект
>
эндобдж
206 0 объект
>
эндобдж
207 0 объект
>
эндобдж
208 0 объект
>
эндобдж
209 0 объект
>
эндобдж
210 0 объект
>
эндобдж
211 0 объект
>
эндобдж
212 0 объект
>
эндобдж
213 0 объект
>
эндобдж
214 0 объект
>
эндобдж
215 0 объект
>
эндобдж
216 0 объект
>
эндобдж
217 0 объект
>
эндобдж
218 0 объект
>
эндобдж
219 0 объект
>
эндобдж
220 0 объект
>
эндобдж
221 0 объект
>
эндобдж
222 0 объект
>
эндобдж
223 0 объект
>
эндобдж
224 0 объект
>
эндобдж
225 0 объект
>
эндобдж
226 0 объект
>
эндобдж
227 0 объект
>
эндобдж
228 0 объект
>
эндобдж
229 0 объект
>
эндобдж
230 0 объект
>
эндобдж
231 0 объект
>
эндобдж
232 0 объект
>
эндобдж
233 0 объект
>
эндобдж
234 0 объект
>
эндобдж
235 0 объект
>
эндобдж
236 0 объект
>
эндобдж
237 0 объект
>
эндобдж
238 0 объект
>
эндобдж
239 0 объект
>
эндобдж
240 0 объект
>
эндобдж
241 0 объект
>
эндобдж
242 0 объект
>
эндобдж
243 0 объект
>
эндобдж
244 0 объект
>
эндобдж
245 0 объект
>
эндобдж
246 0 объект
>
эндобдж
247 0 объект
>
эндобдж
248 0 объект
>
эндобдж
249 0 объект
>
эндобдж
250 0 объект
>
эндобдж
251 0 объект
>
эндобдж
252 0 объект
>
эндобдж
253 0 объект
>
эндобдж
254 0 объект
>
эндобдж
255 0 объект
>
эндобдж
256 0 объект
>
эндобдж
257 0 объект
>
эндобдж
258 0 объект
>
эндобдж
259 0 объект
>
эндобдж
260 0 объект
>
эндобдж
261 0 объект
>
эндобдж
262 0 объект
>
эндобдж
263 0 объект
>
эндобдж
264 0 объект
>
эндобдж
265 0 объект
>
эндобдж
266 0 объект
>
эндобдж
267 0 объект
>
эндобдж
268 0 объект
>
эндобдж
269 0 объект
>
эндобдж
270 0 объект
>
эндобдж
271 0 объект
>
эндобдж
272 0 объект
>
эндобдж
273 0 объект
>
эндобдж
274 0 объект
>
эндобдж
275 0 объект
>
эндобдж
276 0 объект
>
эндобдж
277 0 объект
>
эндобдж
278 0 объект
>
эндобдж
279 0 объект
>
/ ProcSet [/ PDF / Text / ImageC / ImageB / ImageI]
>>
эндобдж
280 0 объект
>
транслировать
x ڕ XɎ6 + 周 0 |
ҷ r849Ej
% См. E
>
- Для закрепления концепции целого рационального уравнения I степени.
- Сформулируйте основные методы решения уравнений высших степеней (n > 3).
- Обучить основным методам решения уравнений высших степеней.
- Научить по типу уравнения определять наиболее эффективный способ его решения.
- Лекционно-семинарская система обучения (лекции — разъяснение нового материала, семинары — решение задач).
- Информационно-коммуникационные технологии (фронтальный опрос, устная работа с классом).
- Дифференцированное обучение, групповые и индивидуальные формы.
- Исследовательское обучение в развивающем образовании математический аппарат и мыслительные способности каждого отдельного ученика.
- Печатный материал — индивидуальное краткое изложение урока (основные понятия, формулы, утверждения, лекционный материал сжат в виде диаграмм или таблиц).
- Организация времени.
Цель этапа: включить учащихся в учебную деятельность, определить содержание урока. - Обновление знаний студентов.
Цель этапа: обновить знания студентов по ранее изученным смежным темам - Изучение новой темы (лекция).Цель этапа: сформулировать основные методы решения уравнений высших степеней (n > 3)
- Подведение итогов.
Цель этапа: еще раз выделить ключевые моменты изучаемого на уроке материала. - Домашнее задание.
Цель этапа: сформулировать домашнее задание для студентов. - Понятие уравнения с одной переменной.
- Понятие корня уравнения, решение уравнения.
- Понятие линейного уравнения с одной переменной, понятие квадратного уравнения с одной переменной.
- Понятие эквивалентности уравнений, уравнение-следствие (понятие посторонних корней), переход не по следствию (случай потери корней).
- Концепция целого рационального выражения с одной переменной.
- Понятие о целом рациональном уравнении n -й степени. Стандартная форма всего рационального уравнения. Сокращенное целое рациональное уравнение.
- Переход к системе уравнений более низкой степени путем разложения исходного уравнения на множители.
- Полиномиальная концепция n -я степень от x … Теорема Безу. Следствия теоремы Безу. Корневые теоремы ( Z -корней и Q -корней) всего рационального уравнения с целыми коэффициентами (приведенными и неприведенными соответственно).
- Схема Хорнера.
- Если можно использовать замену вида y = kx
- Биквадратное уравнение вида ax 4 + bx 2 + s = 0 .
- Обратное уравнение четвертой степени вида ax 4 + bx 3 + c x 2 + bx + a = 0.
- топор 4 + bx 3 + cx 2- bx + a = 0.
- Обобщенное уравнение возврата в четвертой степени ax 4 + bx 3 + cx 2 + kbx + к 2 а = 0 .
- Замена общего вида.Некоторые стандартные замены.
- Напомним еще раз, что на практике можно использовать комбинаций вышеуказанных способов.К системе уравнений младших степеней удобно перейти путем факторизации исходного уравнения .
- Широко используемый на практике остался за рамками нашего сегодняшнего обсуждения. графических методов решающих уравнений и приближенных методов решения уравнений высших степеней.
- Бывают ситуации, когда уравнение не имеет R-корней. Затем решение сводится к тому, чтобы показать, что уравнение не имеет корней.Чтобы доказать это, проанализируем поведение рассматриваемых функций на интервалах монотонности. Пример: уравнение x 8 — x 3 + 1 = 0 не имеет корней.
- Использование свойства монотонности функций … Бывают ситуации, когда использование различных свойств функций позволяет упростить поставленную задачу.
- Формула Кардано
- Графический метод решения уравнений. Примеры решений.
- Методы приближенного решения уравнений.
- Виленкин Н.Я. et al. «Алгебра. Учебник для 9-х классов с углубленным изучением математики »- М., Просвещение, 2007 — 367 с.
- Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. «За страницами учебника математики. Арифметика. Алгебра. 10-11 класс »- М., Просвещение, 2008 г. — 192 с.
- Выгодский М.Я. «Справочник по математике» — М., АСТ, 2010 г. — 1055 с.
- Галицкий М.Л. «Сборник задач по алгебре. Учебник для 8-9 классов с углубленным изучением математики »- М., Образование, 2008 г. — 301 с.
- Звавич Л.И. и другие. «Алгебра и начало анализа. 8-11 кл. Пособие для школ и классов с углубленным изучением математики »- М., Дрофа, 1999 г. — 352 с.
- Звавич Л.И., Аверьянов Д.И., Пигарев Б.П., Трушанина Т.Н. «Задания по математике для подготовки к письменному экзамену в 9 классе» — М., Просвещение, 2007 г. — 112 с.
- Иванов А.А., Иванов А.П. «Тематические тесты для систематизации знаний по математике» ч. 1 — М., Физматкнига, 2006 — 176 с.
- Иванов А.А., Иванов А.П. «Тематические тесты для систематизации знаний по математике» ч. 2 — М., Физматкнига, 2006 — 176 с.
- Иванов А.П. «Контрольные и контрольные работы по математике. Учебное пособие ». — М., Физматкнига, 2008 г. — 304 с. .
- Leibson K.L. «Сборник практических заданий по математике. Часть 2-9 класс »- М., МЦНМО, 2009 г. — 184 с.
- Макарычев Ю.Н., Миндюк Н.Г. «Алгебра. Дополнительные главы к учебнику для 9-х классов. Учебник для учащихся школ и классов с углубленным изучением математики». — М., Просвещение, 2006 г. — 224 с.
- Мордкович А.Г. «Алгебра. Углубленное изучение. 8 класс. Учебник» — М., Мнемосина, 2006 г. — 296 с.
- А.П. Савин «Энциклопедический словарь молодого математика» — М., Педагогика, 1985 — 352 с.
- Сурвилло Г.С., Симонов А.С. «Дидактические материалы по алгебре для 9 класса с углубленным изучением математики» — М., Образование, 2006 — 95 с.
- Чулков П.В. «Уравнения и неравенства в школьном курсе математики. Лекции 1–4 »- М., 1 сентября 2006 г. — 88 с.
- Чулков П.В. «Уравнения и неравенства в школьном курсе математики. Лекции 5–8 »- М., 1 сентября 2009 г. — 84 с.
Степенные или экспоненциальные уравнения.Решение уравнений высших степеней Как решить общее уравнение 5-й степени
Класс: 9
Основные цели:
Формы, методы и педагогические приемы, используемые учителем на уроке:
План урока:
Итоги урока
1. Организационный момент.
Формулировка темы урока: «Уравнения высших степеней.Методы их решения ».
2. Актуализация знаний студентов.
Теоретический обзор — беседа. Повторение некоторых ранее изученных сведений из теории. Студенты формулируют основные определения и формулируют необходимые теоремы. Приведены примеры, демонстрирующие ранее полученный уровень знаний.
3. Изучение новой темы.
Будем рассматривать все рациональное уравнение n -й степени стандартного вида с одной неизвестной переменной x: P n (x) = 0, где P n (x) = тревога + a n-1 x n-1 + a 1 x + a 0 — полином n -й степени от x , а n ≠ 0.Если a a n = 1, то такое уравнение называется приведенным целым рациональным уравнением n -й степени. Рассмотрим такие уравнения для разных значений n и перечислим основные методы их решения.
n = 1 — линейное уравнение.
n = 2 — квадратное уравнение. Дискриминантная формула. Формула для вычисления корней. Теорема Виета. Выбор полного квадрата.
n = 3 — кубическое уравнение.
Метод группировки.
Пример: x 3 — 4x 2 — x + 4 = 0 (x — 4) (x 2 — 1 ) = 0 x 1 = 4, x 2 = 1, x 3 = -1.
Обратное кубическое уравнение вида ax 3 + bx 2 + bx + a = 0. Решите, комбинируя члены с одинаковыми коэффициентами.
Пример: x 3-5 x 2-5 x + 1 = 0 ( x + 1) ( x 2-6 x + 1) = 0 x 1 = -1, x 2 = 3 + 2, x 3 = 3 — 2.
Выбор Z-корней на основе теоремы. Схема Хорнера. При применении этого метода необходимо подчеркнуть, что поиск в этом случае конечен, и мы выбираем корни по определенному алгоритму в соответствии с теоремой о Z -корнях редуцированного целого рационального уравнения с целыми коэффициентами.
Пример: x 3 — 9 x 2 + 23 x — 15 = 0. Приведено уравнение. Запишем делители свободного члена ( + 1; + 3; + 5; + пятнадцать).Применим схему Горнера:
| х 3 | х 2 | x 1 | х 0 | вывод | |
| 1 | -9 | 23 | -15 | ||
| 1 | 1 | 1 х 1-9 = -8 | 1 х (-8) + 23 = 15 | 1 х 15-15 = 0 | 1 — корень |
| х 2 | x 1 | х 0 |
Получаем ( x — 1) ( x 2-8 x + 15) = 0 x 1 = 1, x 2 = 3, x 3 = 5.
Уравнение с целыми коэффициентами. Выбор Q-корней на основе теоремы. Схема Хорнера. При применении этого метода необходимо подчеркнуть, что поиск в этом случае конечен и корни выбираются по определенному алгоритму в соответствии с теоремой о Q -корнях неприводимого целого рационального уравнения с целыми коэффициентами.
Пример: 9 x 3 + 27 x 2 — x — 3 = 0. Уравнение не сводится.Запишем делители свободного члена ( + 1; + 3). Запишем делители коэффициента при наивысшей степени неизвестной. ( + 1; + 3; + 9) Поэтому будем искать корни среди значений ( + 1; + ; + ; + 3). Применим схему Горнера:
| х 3 | х 2 | x 1 | х 0 | вывод | |
| 9 | 27 | -1 | -3 | ||
| 1 | 9 | 1 х 9 + 27 = 36 | 1 х 36-1 = 35 | 1 х 35-3 = 32 ≠ 0 | 1 — не root |
| -1 | 9 | -1 х 9 + 27 = 18 | -1 х 18-1 = -19 | -1 х (-19) — 3 = 16 ≠ 0 | -1 — не root |
| 9 | х 9 + 27 = 30 | х 30 — 1 = 9 | х 9-3 = 0 | корень | |
| х 2 | x 1 | х 0 |
Получаем ( x — ) (9 x 2 + 30 х + 9) = 0 x 1 = , x 2 = — , x 3 = -3.
Для удобства расчета при выборе Q -roots может быть удобно произвести замену переменной, перейти к сокращенному уравнению и выбрать Z -roots .
.Формула Кардано. Существует универсальный метод решения кубических уравнений — это формула Кардано. Эта формула связана с именами итальянских математиков Джероламо Кардано (1501–1576), Николо Тарталья (1500–1557), Сципионе дель Ферро (1465–1526).Эта формула выходит за рамки нашего курса.
n = 4 — уравнение четвертой степени.
Метод группировки.
Пример: x 4 + 2 x 3 + 5 x 2 + 4 х — 12 = 0 ( x 4 + 2 x 3) + (5 x 2 + 10 x ) — (6 x + 12) = 0 ( x + 2) ( x 3 + 5 x — 6) = 0 ( x + 2) ( x — 1) ( x 2 + x + 6) = 0 x 1 = -2, x 2 = 1.
Метод замены переменной.
Пример: x 4 + 5 x 2 — 36 = 0. Замена y = x 2. Отсюда y 1 = 4, у 2 = -9. поэтому x 1,2 = + 2.
Решаем, комбинируя члены с одинаковыми коэффициентами, заменяя форму
Пример 3 . Замена общего вида (следует из вида конкретного уравнения).
n = 3.
Уравнение с целыми коэффициентами. Фитинг Q-образный n = 3.
Общая формула. Существует универсальный метод решения уравнений четвертой степени. Эта формула связана с именем Людовико Феррари (1522-1565).Эта формула выходит за рамки нашего курса.
n > 5 — уравнения пятой и более высоких степеней.
Уравнение с целыми коэффициентами. Выбор Z-корней на основе теоремы. Схема Хорнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Аппроксимация Q-корней на основе теоремы. Схема Хорнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Симметричные уравнения. Любое уравнение возврата нечетной степени имеет корень x = -1 и после разложения его на множители мы получаем, что один коэффициент имеет вид ( x + 1), а второй коэффициент — уравнение возврата четной степени. (его степень на единицу меньше степени исходного уравнения). Любое рекуррентное уравнение четной степени вместе с корнем вида x = φ содержит корень вида. Используя эти постановки, мы решаем задачу, понижая степень исследуемого уравнения.
Метод замены переменной. Использование единообразия.
Не существует общей формулы для решения целых уравнений пятой степени (это показали итальянский математик Паоло Руффини (1765-1822) и норвежский математик Нильс Хенрик Абель (1802-1829)) и более высоких степеней (это показал французский математик Эварист Галуа (1811-1832))).
Пример 1: уравнение x 5 + 3 x — 4 = 0 имеет один корень x = 1. По свойству монотонности анализируемых функций других корней нет.
Пример 2: уравнение x 4 + ( x — 1) 4 = 97 имеет корни x 1 = -2 и x 2 = 3. Проанализировав поведение соответствующих функций на интервалах монотонности, заключаем, что других корней нет.
4. Подведение итогов.
Резюме: Теперь мы освоили основные методы решения различных уравнений высших степеней (для n > 3). Наша задача — научиться эффективно использовать перечисленные выше алгоритмы.В зависимости от типа уравнения нам придется научиться определять, какой метод решения в данном случае наиболее эффективен, а также правильно применять выбранный метод.
5. Домашнее задание.
: стр. 7, стр. 164-174, № 33-36, 39-44, 46.47.
: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.
Возможные темы докладов или тезисов по теме:
Анализ усвоения материала и заинтересованности студентов в теме:
Опыт показывает, что студентов в первую очередь интересует возможность получения Z -корней и Q -корней уравнений с помощью довольно простого алгоритма с использованием схемы Горнера. Также студентов интересуют различные стандартные типы замен переменных, которые могут значительно упростить задачу.Особый интерес обычно вызывают графические методы решения. В этом случае вы можете дополнительно разобрать задачи в графический метод решения уравнений; обсудить общий вид графа многочлена 3, 4, 5 степеней; проанализировать, как количество корней уравнений 3, 4, 5 степеней связано с типом соответствующего графа. Ниже приведен список книг, в которых вы можете найти дополнительную информацию по этой теме.
Список литературы:
Судя по началу публикации, которую мы здесь опускаем, текст написал Юрий Игнатьевич. И написано хорошо, и проблематика актуальна, только так можно назвать Россию, как Мухин…
Как ни относиться к антинародной власти, Россия выше нее и не заслуживает оскорблений. Даже от талантливого разоблачителя американского агентства NASA.
*
Обращение к тов. Мухину Ю.И.
Уважаемый Юрий Игнатьевич! Я знаю, что вы посещаете эти страницы. Поэтому обращаюсь к вам напрямую.
Мы все ценим вашу самоотверженную работу в области разоблачения лжи Запада, лжи Америки, лжи псевдоученых и лжи либералов.Мы с удовольствием и пользой для себя и общества думаем о серьезных темах, которые вы время от времени нам задаете, будь то меритократия или метафизика, любовь к русской истории или восстановление справедливости.
Однако ваши определения нашей общей родины сбивают с толку и расстраивают.
Однако судите сами: как бы вы охарактеризовали человека, который начал оскорблять свою мать, которая заболела и временно перестала работать из-за этого?
Но Россия, как бы ее ни называли, и какой бы хорошей или противной ни была власть, Россия — наша Родина. Родина. За нее наши деды пролили кровь и положили свои жизни.
Следовательно, ставить его в один ряд с силой — значит понижать духовное возвышенное до уровня материального и даже низкого. Те. вы сравниваете совершенно разные категории. Вещь неприемлема для любого здравомыслящего человека.
Прошу вас, уважаемый товарищ. Мухин, серьезно подумай об этом.
**
… А с уравнениями (я этого не знал) ситуация следующая.Как найти корни квадратного уравнения догадывались еще в Древнем Египте.
Как найти корни кубического уравнения и уравнения четвертой степени нашли в шестнадцатом веке, но корни уравнения пятой степени найти не могли до 2016 года. И пытались далеко не обычные люди.
В шестнадцатом веке основатель символической алгебры Франсуа Вьет попытался найти корни уравнения пятой степени; в девятнадцатом веке основатель современной высшей алгебры французский математик Эварист Галуа попытался найти корни уравнений пятой степени; после него норвежский математик Нильс Хенрик Абель попытался найти корни уравнений пятой степени.сдался и доказал невозможность решения уравнения пятой степени вообще.
Мы читаем в Википедии о заслугах Авеля: «Авель завершил блестящее исследование древней проблемы: доказал невозможность решения в общем виде (в радикалах) уравнения 5-й степени …
В алгебре Абель нашел необходимое условие для выражения корня уравнения «в радикалах» через коэффициенты этого уравнения. Достаточное состояние вскоре обнаружил Галуа, достижения которого были основаны на трудах Абеля.
Абель привел конкретные примеры уравнения 5-й степени, корни которого не могут быть выражены в радикалах, и, таким образом, в значительной степени закрыл древнюю проблему. «
Как видите, если они все время пытались доказать теорему Пуанкаре и Перельман оказывался более удачливым, чем остальные математики, то после Абеля математики не брались за уравнения пятой степени.
А в 2014 году математик из Томска Сергей Зайков , о котором можно судить по фото, что он уже в годах, а по данным из статьи про него, что он выпускник факультета прикладной математики и кибернетики Томский государственный университет, в процессе работы получил уравнения пятой степени.Тупик? Да тупик! Но Сергей Зайков взялся его сломать.
А в 2016 году он нашел способ решить уравнения пятой степени в общем виде! Он сделал то, что математики Галуа и Абель доказали невозможным.
Я пытался найти информацию о Сергее Зайкове в Википедии, но пошли вы на хуй! О математике Сергее Зайкове и о его нахождении решения уравнений пятой степени информации нет!
Пикантность делу придает еще и то, что для математиков есть аналог Нобелевской премии — Абелевская премия (Нобель запретил давать премию математикам и теперь ее выдают за математические фекалии, называя их «физиками»). «).
Эта математическая премия в честь того самого Абеля, который доказал невозможность того, что сделал Зайков … Однако самовыдвижение на эту награду не допускается. А Зайков — математик-одиночка, и нет организаций, которые могли бы предложить его кандидатом на эту премию.
Да, у нас есть Академия наук, но академики сидят там не за развитием математики, а «пилить бабло». Кому там нужен этот Зайков?
Ну для информагентств Заиков для вас не Перельман! Поэтому открытие Зайкова для СМИ не сенсация.
Вот то, что Порошенко ошибся с дверью — да! Это настоящая сенсация!
Томский математик решил задачу, которую не могли решить двести лет
С появлением алгебры решение алгебраических уравнений стало ее основной задачей. Решение уравнения второй степени было известно еще в Вавилоне и Древнем Египте. Такие уравнения мы изучаем в школе. Помните уравнение x2 + ax + b = 0 и дискриминант?
Сергей Зайков с книгой
Решение алгебраических уравнений третьей и четвертой степени было найдено в шестнадцатом веке.Но уравнение пятой степени решить не удалось. Причину нашел Лагранж. Он показал, что решение уравнений третьей и четвертой степени стало возможным, потому что они могут быть сведены к уравнениям, которые уже решены. Уравнение третьей степени может быть сведено к уравнению второй степени, а уравнение четвертой степени — к уравнению третьей. Но уравнение пятой степени сводится к уравнению шестой, то есть более сложному, поэтому традиционные методы решения неприменимы.
Вопрос о решении уравнения пятой степени возник только двести лет назад, когда Абель доказал, что не все уравнения пятой степени можно решить в радикалах, то есть в квадратных, кубических и других корнях, известный нам со школы. И вскоре Галуа, то есть двести лет назад, нашел критерий определения того, какие уравнения пятой степени можно решить в радикалах, а какие нет. Он состоит в том, что группа Галуа, разрешимая в радикалах уравнения пятой степени, должна быть либо циклической, либо метациклической.Но Галуа не нашел способа решить в радикалах те уравнения пятой степени, которые разрешимы в радикалах. Теория Галуа очень известна, о ней написано много книг.
До сих пор были найдены только частные решения уравнений пятой степени, разрешимых в радикалах. И только в этом году томский математик Сергей Зайков решил задачу, которую не могли решить двести лет. Он опубликовал книгу «Как решаются алгебраические уравнения пятой степени в радикалах», в которой указал метод решения любых уравнений пятой степени, разрешимых в радикалах.Зайков — выпускник факультета прикладной математики и кибернетики Томского государственного университета. Нам удалось взять у него интервью.
— Сергей, почему вы начали решать эту проблему?
— Мне нужно было решить уравнение пятой степени, чтобы решить задачу из другого раздела математики. Я начал прикидывать, как его найти, и выяснил, что не все они решаются радикально. Затем я попытался найти в научной литературе способ решения тех уравнений, которые разрешимы в радикалах, но я нашел только критерий, по которому можно определить, какие из них разрешимы, а какие нет.Я не алгебраист, но, конечно, как выпускник ФПМК могу применять и алгебраические методы. Поэтому с 2014 года я начал серьезно искать решение и нашел его сам.
Метод был найден мною два года назад, я подготовил книгу, в которой не только он описан, но и способы решения некоторых уравнений степеней выше пятой. Но у меня не было денег на публикацию. В этом году я решил, что будет легче опубликовать только часть этой работы, и взял только половину, посвященную способу решения уравнения пятой степени в радикалах.
Я задумал опубликовать что-то вроде руководства по решению этой задачи, понятного математикам, которым нужно решить конкретное уравнение. Поэтому я упростил его, убрав много длинных формул и значительную часть теории, урезав более чем наполовину, оставив только необходимое. Таким образом, у меня получилось что-то вроде книги «для чайников», согласно которой математики, не знакомые с теорией Галуа, могут решить нужное им уравнение.
— За это огромное спасибо Владиславу Бересневу, с которым мы знакомы много лет.Он спонсировал издание книги.
— Можно ли получить какой-нибудь приз по математике за решение этой задачи? Например, вы упомянули Авеля. Но существует ли премия Абеля по математике, которая считается аналогом Нобелевской премии?
— Полностью исключить такую возможность нельзя. Но и на это не стоит надеяться.
Например, заявки на соискание премии Абеля 2019 должны быть поданы до 15 сентября. Более того, самовыдвижение не допускается.А я математик-одиночка. Нет организаций или известных математиков, которые меня номинировали бы. Следовательно, она не будет рассматриваться независимо от того, заслуживает ли моя работа этой награды и соответствует ли духу этой награды вручение ее тем, кто продолжает работу Авеля. Но даже если он будет представлен, все зависит еще и от уровня работы других кандидатов.
Книга предназначена для тех, кто не знаком с теорией Галуа. Основы теории Галуа даны только в той части, в которой они необходимы для решения уравнения, подробно описан метод решения, показаны приемы, упрощающие решение.Большая часть книги посвящена примеру решения конкретного уравнения. Рецензентами книги являются доктор технических наук Геннадий Петрович Агибалов и доктор физико-математических наук. мат. Наук, профессор Крылов Петр Андреевич.
ГОТОВА АНАСТАСИЯ СКИРНЕВСКАЯ
В XVI веке математики почти случайно столкнулись с комплексными числами (см. Главу 11). К 18 веку комплексные числа считались расширением вещественных чисел площади, но работа с ними по-прежнему приводила к ошибке четности, так как в большой работе Леонарда Э. по теории чисел «Арифметические исследования» (1801 г.) он избегал использования так называемых «арифметических исследований». «мнимые числа.«Мне кажется, что наиболее важной частью этой работы является первое доказательство фундаментальной теоремы алгебры. Гаусс осознал, насколько важна эта теорема, создав несколько дополнительных доказательств за эти годы. В 1849 году он пересмотрел первую версию, это время с использованием комплексных чисел. Используя современные термины, мы можем сказать, что для любого конечного полиномиального уравнения с действительными или комплексными коэффициентами все его корни будут действительными или комплексными числами … Таким образом, мы получаем отрицательный ответ на давний вопрос требует ли решение полиномиальных уравнений высокого порядка создания чисел более высокого порядка, чем комплексные.
Одной из самых острых проблем алгебры того времени был вопрос о том, являются ли алгебраические методы, то есть использующие конечное число алгебраических шагов, многочленом пятого порядка квинтикой. Сейчас в школе преподают формулы для решения квадратных уравнений, а с 16 века известны аналогичные методы решения уравнений третьей и четвертой степени (глава 11). Но метода квинтики не нашлось. Может показаться, что основная теорема алгебры заключает в себе перспективу положительного ответа, но на самом деле она просто гарантирует, что решения существуют, в ней ничего не говорится о существовании формул, дающих точные решения (к тому времени уже существовали приближенные числовые решения). и графические методы).А потом были два математических гения с трагической судьбой.
Нильс Хенрик Абель (1802-1829) родился в большой бедной семье, жившей в маленькой деревне в Норвегии, стране, опустошенной долгими годами войны с Англией и Швецией. Доброжелательный к мальчику учитель давал ему частные уроки, но после смерти отца, в восемнадцатилетнем возрасте, несмотря на юный возраст и хрупкое здоровье, Абель был вынужден содержать семью. В 1824 году он опубликовал научную статью, в которой заявил, что квинтика не решается алгебраическими средствами, как и любой многочлен более высокого порядка.Абель считал, что эта статья станет его пропуском в научный мир, и отправил ее Гауссу в Геттингенском университете. К сожалению, Гаусс не собирался разрезать страницы ножом (в те времена это должен был делать любой читатель) и не прочитал статью. В 1826 году норвежское правительство наконец выделило Абелю средства на поездку в Европу. Опасаясь, что личное общение с Гауссом не доставит ему особой радости, математик решил не посещать Геттинген и вместо этого отправился в Берлин.Там он подружился с Августом Леопольдом Креллем (1780–1855), математиком, архитектором и инженером, который консультировал Министерство образования Пруссии по математике. Крелл собирался основать Журнал чистой и прикладной математики. Так Абель получил возможность распространять свои работы и много публиковал, особенно в первых номерах «Журнала», который сразу стал считаться очень престижным и авторитетным научным изданием. Норвежец опубликовал там расширенную версию своего доказательства неразрешимости квинтики алгебраическими методами.А потом уехал в Париж. Эта поездка очень расстроила Абеля, потому что он практически не получил столь необходимой ему поддержки французских математиков. Он сблизился с Огюстэном Луи Коши (1789–1857), который в то время был главным светилом математического анализа, но имел очень сложный характер. Как выразился сам Абель, «Коши безумен, и с этим ничего нельзя поделать, хотя в настоящее время он единственный, кто способен на что-то в математике». Если мы попытаемся найти оправдания проявлениям неуважения и пренебрежения, исходящие от Гаусса и Коши, мы можем сказать, что квинтик добился определенной известности и привлек внимание как уважаемых математиков, так и оригиналов.Абель вернулся в Норвегию, где все больше и больше болел туберкулезом. Он продолжал отправлять свои работы в Crelle, но умер в 1829 году, не зная, насколько выросла его репутация в научном мире. Через два дня после его смерти Абель получил предложение занять научную должность в Берлине.
Абель показал, что любой многочлен выше четвертого порядка не может быть решен с использованием таких радикалов, как квадратные, кубические или более высокие корни. Однако явные условия, при которых эти многочлены могли быть решены в частных случаях, и метод их решения были сформулированы Галуа.Эварист Галуа (1811–1832) прожил короткую и насыщенную жизнь. Он был невероятно одаренным математиком. Галуа был непримирим к тем, кого считал менее талантливым, чем он сам, и в то же время он не мог мириться с социальной несправедливостью. Он не проявил таланта к математике, пока не прочитал «Принципы геометрии» Лежандра (вышедшая в 1794 году, эта книга была основным учебником на последующие сто лет). Затем он буквально проглотил остальные сочинения Лежандра, а затем и Авеля. Его энтузиазм, самоуверенность и нетерпимость привели к поистине ужасным последствиям в его отношениях с учителями и экзаменаторами.Галуа принял участие в конкурсе на поступление в Политехническую школу — колыбель французской математики, но из-за недостаточной подготовки провалил экзамен. Некоторое время после знакомства с новым учителем, признавшим его талант, ему удавалось сдерживать себя. В марте 1829 года Галуа опубликовал свою первую статью о непрерывных дробях, которую он считал своей самой значительной работой. Он отправил сообщение о своих открытиях в Академию наук, и Коши обещал представить их, но забыл.Более того, он просто потерял рукопись.
Вторая неудача Галуа при поступлении в Политехническую школу вошла в математический фольклор. Он так привык постоянно держать в голове сложные математические идеи, что его приводили в ярость мелкие придирки экзаменаторов. Поскольку экзаменаторам было трудно понять его объяснение, он швырнул тряпку доской в лицо одному из них. Вскоре умер его отец, покончивший с собой в результате церковных интриг. На его похоронах чуть не вспыхнул бунт.В феврале 1830 года Галуа написал следующие три статьи, отправив их в Академию наук на получение Гран-при по математике. Жозеф Фурье, тогдашний секретарь академии, умер, не прочитав их, и после его смерти среди его бумаг не было найдено ни одной статьи. Такой поток разочарований свалил бы кого угодно. Галуа восстал против власть имущих, потому что чувствовал, что они не признают его заслуг и разоряют его отца. Он с головой окунулся в политику, став ярым республиканцем — не самое мудрое решение во Франции в 1830 году.В последней отчаянной попытке он отправил научную статью известному французскому физику и математику Симеону Дени Пуассону (1781–1840), который в ответ потребовал дополнительных доказательств.
Это была последняя капля. В 1831 году Галуа дважды арестовывали — первый раз якобы за призыв к убийству короля Луи Филиппа, а затем, чтобы защитить его — власти опасались республиканского восстания! На этот раз его приговорили к шести месяцам лишения свободы по сфабрикованным обвинениям в незаконном ношении формы расформированного артиллерийского дивизиона, в который он вступил.Освобожденный от своего честного слова, он взялся за работу, которая вызывала у него такое же отвращение, как и все остальное в жизни. В письмах к своему преданному другу Шевалье чувствуется его разочарование. 29 мая 1832 года он принял вызов на дуэль, причины которого до конца не выяснены. «Я стал жертвой позорной кокетки. Моя жизнь угасает в жалкой ссоре », — пишет он в своем письме ко всем республиканцам. Самая известная работа Галуа была сделана в ночь перед роковой битвой. По полям разбросаны жалобы: «У меня больше нет времени, у меня больше нет времени.«Он был вынужден предоставить другим подробное изложение промежуточных шагов, которые не были существенными для понимания основной идеи. Ему нужно было изложить на бумаге основу своих открытий — истоки того, что сейчас называется теоремой Галуа. Он закончил свое завещание, попросив Шевалье «попросить Якоби и Гаусса публично высказать свое мнение не о правильности, а о важности этих теорем». Рано утром Галуа пошел навстречу своему сопернику. 25 шагов.Галуа был ранен и на следующее утро скончался в больнице. Ему было всего двадцать лет.
Галуа опирался на работы Лагранжа и Коши, но разработал более общий метод. Это было чрезвычайно важным достижением в области водных растворов. Ученый меньше обращал внимания на исходные уравнения или графическую интерпретацию и больше думал о природе самих корней. Для упрощения Галуа рассматривал только так называемые неприводимые квинтики, то есть те, которые нельзя факторизовать в виде полиномов более низкого порядка (как мы уже говорили, для любых полиномиальных уравнений до четвертого порядка есть формулы для нахождения их корни).В общем, неприводимый многочлен с рациональными коэффициентами — это многочлен, который не может быть разложен на более простые многочлены с рациональными коэффициентами. Например, (x 5-1) можно разложить на множители (x-1) (x 4 + x 3 + x 2 + x + 1), , тогда как (x 5-2) неприводимо. Целью Галуа было определить условия, при которых все решения общего неприводимого полиномиального уравнения могут быть найдены в терминах радикалов.
Ключ к решению состоит в том, что корни любого неприводимого алгебраического уравнения не являются независимыми, они могут быть выражены один через другой.Эти отношения были формализованы в группу всевозможных перестановок, так называемую корневую группу симметрии — для квинтики эта группа содержит 5! = 5 х 4 х 3 х 2 х 1 = 120 элементов. Математические алгоритмы теории Галуа очень сложны, и, скорее всего, отчасти из-за этого они изначально были поняты с большим трудом. Но после того, как уровень абстракции позволил перейти от алгебраических решений уравнений к алгебраической структуре связанных с ними групп, Галуа смог предсказать разрешимость уравнения на основе свойств таких групп.Более того, его теория также предоставила метод, с помощью которого можно было найти эти корни. Что касается Quintics, математик Джозеф Лиувилль (1809–1882), который в 1846 году опубликовал большую часть работ Галуа в своем «Журнале чистой и прикладной математики», отметил, что молодой ученый доказал «прекрасную теорему», и для того, чтобы « неприводимое уравнение исходной степени было разрешимо в терминах радикалов, необходимо и достаточно, чтобы все его корни были рациональными функциями любых двух из них. «Так как для квинтики это невозможно, то радикалами ее не решить.
За три года математический мир потерял две из своих самых ярких новых звезд. Последовали обвинения и переоценка ценностей, и Абель и Галуа добились заслуженного признания, но только посмертно. В 1829 году Карл Якоби через Лежандра узнал о «потерянной» рукописи Абеля, а в 1830 году разразился дипломатический скандал, когда норвежский консул в Париже потребовал найти статью своего соотечественника. В конце концов, Коши нашел статью, но только для того, чтобы снова потеряться в академии! В том же году Абель получил Гран-при по математике (вместе с Якоби) — но он уже был мертв.В 1841 году была опубликована его биография. В 1846 году Лиувилль отредактировал некоторые рукописи Галуа для публикации и во введении выразил сожаление по поводу того, что академия изначально отклонила работу Галуа из-за ее сложности — «действительно, ясность необходима, когда автор уводит читателя с проторенного пути к неизведанному. пустыня «. Он продолжает: «Галуа ушел! Не будем предаваться бесполезной критике. Отбросим недостатки и посмотрим на достоинства! «Плоды недолгой жизни Галуа можно найти всего на шестидесяти страницах.Редактор математического журнала для кандидатов в Ecole Normal и École Polytechnique так прокомментировал случай Галуа: «Кандидат с высоким интеллектом был отобран экзаменатором с более низким уровнем мышления. Barbarus hic ego sum, quia nonlligor illis. «
Во-первых, вторая страница этого произведения не обременена именами, фамилиями, описаниями положения в обществе, титулами и элегиями в честь какого-то скупого князя, чей кошелек откроется с помощью этих благовоний — с помощью угроза закрыть его, когда похвалы закончились.Вы не увидите здесь почтительных похвал, написанных буквами в три раза крупнее самого текста и адресованных тем, кто занимает высокое положение в науке, какому-то мудрому покровителю — что-то обязательное (я бы сказал, неизбежное) для человека в возрасте двадцати лет. кто хочет что-то написать. Я никому здесь не говорю, что обязан их советом и поддержкой всего хорошего в моей работе. Я говорю это не потому, что это было бы ложью. Если бы мне пришлось упомянуть кого-либо из великих деятелей общества или науки (в настоящее время разница между двумя классами людей почти незаметна), клянусь, это не было бы в знак благодарности.Я в долгу перед ними тем, что так поздно опубликовал первую из этих двух статей и что все это я написал в тюрьме — в месте, которое вряд ли можно считать подходящим для научных размышлений, и меня часто поражает моя сдержанность и способность держать язык за зубами. замок по отношению к тупым и порочным зоилам. Думаю, я могу использовать слово «зойлес», не опасаясь обвинений в непристойности, поскольку именно так я называю своих оппонентов. Я не собираюсь здесь писать о том, как и почему меня посадили в тюрьму, но должен сказать, что мои рукописи чаще всего просто терялись в папках господ-членов академии, хотя, по правде говоря, я не могу представить себе такую нескромность на часть людей, на совести которых умер Авель.На мой взгляд, любому хочется, чтобы его сравнивали с этим гениальным математиком. Достаточно сказать, что моя статья по теории уравнений была отправлена в Академию наук в феврале 1830 г., что выписки из нее были отправлены в феврале 1829 г., и ни одна из них не была опубликована, и даже рукопись невозможно было вернуть.
Галуа, неопубликованное предисловие, 1832На канале на youtube нашего сайта, чтобы быть в курсе всех новых видеоуроков.
Для начала напомним основные формулы степеней и их свойства.
Произведение числа на происходит с собой n раз, мы можем записать это выражение как a … a = a n
1.а 0 = 1 (а ≠ 0)
3. а н а м = а н + м
4. (а н) м = а нм
5.a n b n = (ab) n
7. а н / д м = а н — м
Степенные или экспоненциальные уравнения — это уравнения, в которых переменные указаны в степенях (или степенях), а в основе лежит число.
Примеры экспоненциальных уравнений:
В этом примере число 6 является основанием, оно всегда стоит внизу, а переменная x градусов или индикатор.
Вот еще несколько примеров экспоненциальных уравнений.
2 х * 5 = 10
16 х — 4 х — 6 = 0
Теперь посмотрим, как решаются экспоненциальные уравнения?
Возьмем простое уравнение:
2 х = 2 3
Такой пример можно решить даже в уме. Видно, что x = 3. Ведь для того, чтобы левая и правая части были равны, нужно вместо x поставить цифру 3.
Теперь посмотрим, как нужно формализовать это решение:
2 х = 2 3
х = 3
Для решения такого уравнения мы удалили одинаковых оснований (то есть двойки) и записали то, что осталось, это градусы.Мы получили желаемый ответ.
А теперь подведем итоги нашего решения.
Алгоритм решения экспоненциального уравнения:
1. Необходимо проверить и тот же , имеет ли уравнение основания справа и слева. Если основания не совпадают, ищем варианты решения этого примера.
2. После того, как основания совпадают, приравнивается к градусам и решает полученное новое уравнение.
Теперь решим несколько примеров:
Начнем с простого.
Основания на левой и правой сторонах равны числу 2, что означает, что мы можем отбросить основание и приравнять их степени.
x + 2 = 4 Это простейшее уравнение.
х = 4-2
х = 2
Ответ: х = 2
В следующем примере видно, что базы разные — 3 и 9.
3 3х — 9х + 8 = 0
Сначала перемещаем девятку в правую сторону, получаем:
Теперь нужно сделать такие же базы.Мы знаем, что 9 = 3 2. Воспользуемся формулой степеней (a n) m = a nm.
3 3х = (3 2) х + 8
Получаем 9 х + 8 = (3 2) х + 8 = 3 2х + 16
3 3x = 3 2x + 16 теперь вы можете видеть, что основания слева и справа одинаковы и равны трем, поэтому мы можем отбросить их и приравнять градусы.
3x = 2x + 16 получили простейшее уравнение
3x — 2x = 16
x = 16
Ответ: x = 16.
См. Следующий пример:
2 2х + 4-10 4х = 2 4
В первую очередь смотрим базы, базы разные две и четыре.И нам нужно быть такими же. Преобразуем четверку по формуле (a n) m = a nm.
4 х = (2 2) х = 2 2х
А еще пользуемся одной формулой a n a m = a n + m:
2 2х + 4 = 2 2х 2 4
Добавьте к уравнению:
2 2х 2 4-10 2 2х = 24
Мы привели пример по тем же причинам. Но нам мешают другие числа 10 и 24. Что с ними делать? Если присмотреться, можно увидеть, что слева мы повторяем 2 2 раза, вот ответ — 2 2 раза мы можем вывести за скобки:
2 2х (2 4-10) = 24
Вычислим выражение в скобках:
2 4–10 = 16–10 = 6
Разделите все уравнение на 6:
Представим 4 = 2 2:
2 2x = 2 2 основания одинаковые, отбросьте их и приравняйте силы.
2x = 2 получается простейшее уравнение. Делим на 2 получаем
х = 1
Ответ: х = 1.
Решим уравнение:
9 х — 12 * 3 х + 27 = 0
Преобразуем:
9 x = (3 2) x = 3 2x
Получаем уравнение:
3 2x — 12 3x +27 = 0
Наши основания одинаковы и равны 3. В этом примере вы можете видеть, что первые три имеют степень вдвое (2x), чем вторая (просто x).В этом случае можно решить заменой методом … Заменим число с наименьшей степенью:
Тогда 3 2x = (3x) 2 = t 2
Заменим все степени на x в уравнении с t:
t 2 — 12t + 27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D = 144-108 = 36
t 1 = 9
t 2 = 3
Вернуться к переменной x .
Берем t 1:
t 1 = 9 = 3 х
То есть
3 х = 9
3 х = 3 2
х 1 = 2
Обнаружен один корень.Ищем вторую, от t 2:
t 2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Ответ: x 1 = 2; х 2 = 1.
На сайте вы можете задать интересующие вопросы в разделе ПОМОЩЬ РЕШИТЬ, мы обязательно вам ответим.
Присоединиться к группе
Как правило, уравнение со степенью выше 4 не может быть решено в радикалах. Но иногда мы все же можем найти корни многочлена слева в уравнении высшей степени, если мы представим его как произведение многочленов степени не выше 4.Решение таких уравнений основано на факторизации многочлена, поэтому мы советуем вам повторить эту тему перед изучением этой статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попытаться найти рациональные корни, а затем разложить полином на множители, чтобы затем преобразовать его в уравнение более низкой степени, которое легко решить. В рамках этого материала мы и рассмотрим именно такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения вида a n x n + a n — 1 x n — 1 +…. … + a 1 x + a 0 = 0, мы можем свести к уравнению такой же степени, умножив обе части на a n n — 1 и изменив переменную вида y = a n x:
a n x n + a n — 1 x n — 1 +. … … + a 1 x + a 0 = 0 ann xn + an — 1 ann — 1 xn — 1 +… + a 1 (an) n — 1 x + a 0 (an) n — 1 \ u003d 0 y = тревога ⇒ yn + bn — 1 yn — 1 +… + b 1 y + b 0 = 0
Полученные коэффициенты также будут целыми. Таким образом, нам потребуется решить приведенное уравнение n-й степени с целыми коэффициентами, которое имеет вид x n + a n x n — 1 +… + a 1 x + a 0 = 0.
Вычислить корни уравнения целиком. Если уравнение имеет целые корни, их нужно искать среди делителей свободного члена a 0. Запишем их и подставим в исходное равенство по очереди, проверяя результат. После того, как мы получили тождество и нашли один из корней уравнения, мы можем записать его в виде x — x 1 · P n — 1 (x) = 0. Здесь x 1 — корень уравнения, а P n — 1 (x) — это частное от деления xn + travelling — 1 +… + a 1 x + a 0 на x — x 1.
Подставляем оставшиеся выписанные делители в P n — 1 (x) = 0, начиная с x 1, так как корни могут повторяться. После получения тождества корень x 2 считается найденным, и уравнение можно записать как (x — x 1) (x — x 2) P n — 2 (x) = 0. Здесь P n — 2 (x ) будет частным от деления P n — 1 (x) на x — x 2.
Продолжаем перебирать делители. Найдите все корни целиком и обозначьте их количество как m. После этого исходное уравнение можно представить как x — x 1 x — x 2 ·… · x — x m · P n — m (x) = 0. Здесь P n — m (x) — полином степени n — m. Для подсчета удобно использовать схему Горнера.
Если в нашем исходном уравнении есть целые коэффициенты, мы не сможем получить дробные корни.
В результате мы получили уравнение P n — m (x) = 0, корни которого можно найти любым удобным способом. Они могут быть иррациональными или сложными.
Покажем на конкретном примере, как применяется такая схема решения.
Пример 1
Условие: найти решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0.
Решение
Начнем с поиска целых корней.
У нас свободный срок равен минус трем. Он имеет делители 1, — 1, 3 и — 3. Давайте подставим их в исходное уравнение и посмотрим, какие из них приведут к тождествам.
При x, равном единице, мы получаем 1 4 + 1 3 + 2 1 2 — 1 — 3 = 0, что означает, что единица будет корнем этого уравнения.
Теперь произведем деление многочлена x 4 + x 3 + 2 x 2 — x — 3 на (x — 1) в столбце:
Следовательно, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3.
1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 — 1 + 3 = 0
Мы получили тождество, что означает, что мы нашли другой корень уравнения, равный — 1.
Разделите многочлен x 3 + 2 x 2 + 4 x + 3 на (x + 1) в столбце:
Получаем
x 4 + x 3 + 2 x 2 — x — 3 = (x — 1) (x 3 + 2 x 2 + 4 x + 3) = = (x — 1) (x + 1) (x 2 + х + 3)
Подставляем следующий делитель в равенство x 2 + x + 3 = 0, начиная с — 1:
1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0
Полученные равенства будут неверными, а это значит, что уравнение больше не имеет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3.
D = 1 2 — 4 1 3 = — 11
Отсюда следует, что данный квадратный трехчлен не имеет действительных корней, но имеет комплексно сопряженные: x = — 1 2 ± i 11 2.
Поясним, что вместо деления в столбик можно использовать схему Хорнера. Делается это так: после определения первого корня уравнения заполняем таблицу.
В таблице коэффициентов сразу видно коэффициенты частного деления многочленов, что означает, что x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 х + 3.
Найдя следующий корень, равный — 1, мы получим следующее:
Ответ: x = — 1, x = 1, x = — 1 2 ± i 11 2.
Пример 2
Условие: Решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0.
Решение
Свободный член имеет делители 1, — 1, 2, — 2, 3, — 3, 4, — 4, 6, — 6, 12, — 12.
Проверяем по порядку:
1 4-1 3-5 1 2 + 12 = 7 ≠ 0 (- 1) 4 — (- 1) 3-5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3-5 2 2 + 12 = 0
Следовательно, x = 2 будет корнем уравнения.Разделите x 4 — x 3-5 x 2 + 12 на x — 2, используя схему Хорнера:
В результате получаем x — 2 (x 3 + x 2 — 3 x — 6) = 0.
2 3 + 2 2-3 2-6 = 0
Значит, 2 снова будет рутом. Разделим x 3 + x 2-3 x — 6 = 0 на x — 2:
В результате получаем (x — 2) 2 (x 2 + 3 x + 3) = 0.
Остальные делители проверять нет смысла, так как равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решать с помощью дискриминанта.
Решим квадратное уравнение:
х 2 + 3 х + 3 = 0 D = 3 2 — 4 1 3 = — 3
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2.
Ответ : x = — 3 2 ± i 3 2.
Пример 3
Условие: найти действительные корни уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0.
Решение
х 4 + 1 2 х 3-5 2 х — 3 = 0 2 х 4 + х 3-5 х — 6 = 0
Произведем умножение 2 на 3 в обеих частях уравнения:
2 х 4 + х 3-5 х — 6 = 0 2 4 х 4 + 2 3 х 3-20 2 х — 48 = 0
Заменим переменные y = 2 x:
2 4 х 4 + 2 3 х 3-20 2 х — 48 = 0 у 4 + у 3-20 у — 48 = 0
В результате мы имеем стандартное уравнение 4-й степени, которое можно решить по стандартной схеме.Проверим делители, разделим и получим в итоге, что у него 2 действительных корня y = — 2, y = 3 и два комплексных корня. Мы не будем представлять здесь полное решение. За счет замены действительные корни этого уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2.
Ответ: х 1 = — 1, х 2 = 3 2
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Come Scegliere una dieta e senza ricetta
Evitate le persone che vi sfiniscono e circondatevi di chi, invece, vi riempie il cuore di gioia Ci sono delle persone che sfiniscono, che ci tolgono tutte le energie, che ci fanno scedere in battaglia quando noi, in realta un po ‘.Quando si parla di farmaci generici si fa riferimento a medicinali aventi composizione esattamente identity a quella del prodotto originale. Я контролирую качество создания национальных и совместных продуктов, которые эквивалентны лекарственным продуктам из других источников. Mantenere il corporation в buona salute ha la sua base in una corretta alimentazione. Essa si basa sull’apporto equilibrato di acqua, карбоидраты (цукчери и амиди), протеин, травы (detti anche lipidi), витамин, сали минералы.10 апр 2019 Dieta facile. Режим питания семплициссимо для маленького quattro chili in un mese. Senza dover pesare gli components o impazzire.Come distinguere tra carni bianche e rosse, nere e rosate e scegliere in base a caratteristiche, tenerezza e proprietà nutrizionali. vivere al meglio il rapporto con l’allergia: i cosmetici senza nichel.Qui non esiste alcun processo di lievitazione, che una reazione chimica, pertanto non si può chiamare propriamente così.Quelle che invece sono lievitazioni vere e proprie sono le altre due, le lievitazioni microbiologica e chimica.
диета рикка ди карбоидраты и уна диета равновесия
4 дня Начни диету: первые пассажи за проезд, количество потребляемых калорий, калькуляция массы специй и импровизаций экспериментальных результатов, есть метод или программа Quindi meglio концентратор и seguusta диета после того, как это делать. Latte d’avena: proprietà, benefici e la ricetta per farlo.Ризотто с начинкой из цукки и сальсиччией — это первое перфетто, перше и рикко-ди-густо. Цукка — это преобладающий компост из цуккери и басса из цуккери: волокна рикки и витамин A и C, а также пищевые продукты для организма человека и кальцио. La versione senza salsiccia in varianti è più magra e poco calorica. Quando la formalità di una cena o di un pranzo non sono richiesti, giunge in nostro soccorso il буфет salato, un formato divertente e informale per servire il rinfresco, anche durante le fes Compleanno dei bambini.Comprare Viagra Originale, Cialis Generico o Levitra в Италии, онлайн Farmacia senza ricetta. Benvenuto su Casafarmacia, una delle cliniche он-лайн больше, affidabili e sicure.I farmaci per dimagrire non sono destinati solo a persone che vogliono perdere solo qualche chilo per ragioni estetiche, ma vengono generalmente riservati a persone che non riescono диетпитание ‘esercizio fisico, e che hannorossi problemi di salute a causa.Cos’è la Dieta Dukan. La Dieta Dukan — это последние последние годы, когда они находятся в одном месте и в одном мире.Prende il nome dal suo ideatore, nutrizionista francese Pierre Dukan.Tutto ciò di cui si ha bisogno sono dei guanti sterili, una siringa, dell’alcol e, naturalmente, il farmaco da somministrare. La siringa ideale ha un ago di около 4 см. Questa Lunghezza Permette.
Staibene.it, il portale dove troverai tutte le risposte all tue needità sulla salute, il benessere, l’alimentazione, la psicologia e tanto altro ancora.Finalmente è arrivato ciò che tutti speravamo, ovvero la fin dieta della pasta кг в un mese! Una dieta interessantissima e ragionevole: макароны семпер, нель капучино аль маттино, сулла пицца, фруллата да бере аль посто делл’аква, а также основа делле кростате алла нутелла.15 апр 2019 Quale dieta dimagrante scegliere in base alle proprie esigenze? ricetta, come condimento, sfruttando le sue proprietà depurative e drenanti. È una Un’altra diea veloce, efficace e con una fase d’urto come la dieta del limone è la dieta del riso. В этом случае, вы можете проверить диету без глютина.Эта серия нутрициализированных данных используется и другие варианты команды 8fit su, как лучше всего с пастой для еды и сани. Il tuo livello di Fitness, ogni ricetta nel nostro piano alimentare è Personalizzata for imparare a scegliere i cibi giusti e seguire delle nuove abitudini salutari e sostenibili nella vita quotidiana.Come funziona l’ordine? L’ordine viene processato direttamente da paypal, лидер азиенды для обычных пользователей в Интернете. Basta Inerrire i tuoi dati e quelli di una carta di credito o di una postepay.Per conservare la carne macinata in congelatore, sarà mustario mantenerla in una confezione chiusa e ben sigillata, proprio come se dovessimo conservitero di una conservitero di una conservitero di una de la conservitero cucina con coperchio.La specialità Via Col Vento, da subito sottoposto a registrazione del marchio, si presenta come un dolce gustoso ma allo stesso tempo molto leggero e capace di deliziare tutti i sensi in ogni momento della giornata, senza apparuire mai.
Тирамиса кокко и нутелла, попробуйте вкуснейшие блюда из диеты, это настоящее голосование! Dopo il mio tiramisù al фистаччио ecco la versione al cocco di un classico amato da tutti, un vero comfort food for eccellenza da gustare senza sensi di colpa.La dieta del gruppo sanguigno non è solo una dieta dimagrante, ma un mode alimentare volto al conguimento di uno stato di salute ottimale.27 mar 2018 La scelta giusta per raggiungere il peso forma senza mettere a rischio la propria salute? Prima di iniziare la диетпитание является основным элементом управления alcuni valori del sangue.È uno step Detox: come scegliere l’acqua per depurarsi .Come funziona questa dieta? Fa dimagrire? La dieta del gruppo sanguigno non è una semplice dieta dimagrante, ma un mode alimentare volto al consguimento di uno stato di salute e una forma fisica ottimali.Osservando le tabelle sovrastanti si può effettuare un primo confronto tra un conquesti duea calorico leggermente superiore, жирный липид, протеин и клетчатка, а также много воды и углеводов.buon giorno, sono alimentari Scainelli, quello che riportate qui sopra. volevo dirvi che noi usiamo solo parmigiano reggiano e non usiamo aglio e che non abbiamo nessun labratorio a BG L’UNICA SEDE CHE ABBIAMO E ‘A PARRE.7 ноя 2017 La dottoressa Barbara Asprea, dietista a Milano, spiega come fareche nel dritta utile, для того, чтобы насладиться нутрирти легким чувством ринунции со вкусом. Gli alimenti needari a una diea sana (e mediterranea) может быть anche scegliere la cottura giusta è basilare для успешного выполнения этого диетического задания.
солода для пердиты песо
Piaceri Mediterranei — это полная линия продуктов, содержащих глютин, которые позволяют оценить все фантастические сапоги итальянского традиционного итальянского чая.Косе и функция диеты Гербалайф. Приходите детально, диета Гербалайф — это тип режима питания, который является одним из основных продуктов питания интеграторов. Семь вегетарианских и вегетарианских блюд, forse perché nel mondo в общем, в Италии, в частности, aumentano semper di pigono coloro che scel квесте частичколари диете.Nereo, la cialda al cacao desireita dal gelato artigianale. La proposta di una cialda al cacao, non costituisce un’assoluta novità, ma questa volta, привлекать особые и трудозатратные процедуры в рицетте, сиамо риускити ad ottenere un persistente gustore 4 марта 2014 Proviagriamo 10 кг в одиночном разряде. Потребитель восстания, маленький ребенок за 10 килограммов в одном только одном и том же стиле, Прима диеты на диете, приглашенной на: Chi siamo · Link amici · Invia la tua ricetta · Diventa partner · Preleva i nostri.Здесь вы можете найти саппиамо, возможность разрабатывать и выращивать растения, которые публикуют и продают, а также продают сырье и продукты для выращивания животных. Uno dei farmaci для dimagrire più conosciuti è senza dubbio la pillola Anche in questo caso, Bene unire all’assunzione del farmaco una diea. Не так, чтобы вы могли подготовить все, что нужно для приготовления блюд из грильи, приготовленных для специй и темпы. O la cuocio per troppo poco tempo lasciandola cruda, oppure la tengo sulla griglia pi del dovuto.
В inverno la tosse vi tormenta, prima secca e stizzosa poi più grassa, e non se ne va rapidamente, probabilmente c’è una bronchite o in vista o in agguato. оригинальные и проверенные, а также другие блюда из кухни: я вторые ди карне, соно ун трионфо ди сапори и вкус, в градо диаконтентаре огни палато, анче иль пиù раффинато и эсигенте.И типи ди пане. Самая важная сцена из блюд для единой диеты этого жанра является типом панели.Определенные типы продуктов для forno ipercalorici, come ad esempio le focacce, ve ne proponiamo un elenco di Difference.Dimagrire Online, Nutrizionista On Line, Dieta senza bilancia, Dimagrire fianchi, Salute E Benessere Online, Dimagriazte Period Dimagrire, Controllo Peso Online.I Farmaci per le emorroidi possono essere una valida soluzione a uno dei problemi most fastidiosi che si Possano Imaginare. Le emorroidi, infatti, prudono, fanno male e, a volte, пассоно.5 салатов за инсалату и басовое содержание калорико За густую инсалатную легкую и салютную, основную часть сальсы адегуата. Приходите отведать пане сальса лиевито, ларикетта дель пане аззимо. Per coloro che hanno delle intolleranze al lievito, поссоно «ripiegare» sul pane azzimo, una ricetta di origine ebraica che non prevede — appunto — l’uso del lievito nella preparazione.
.
