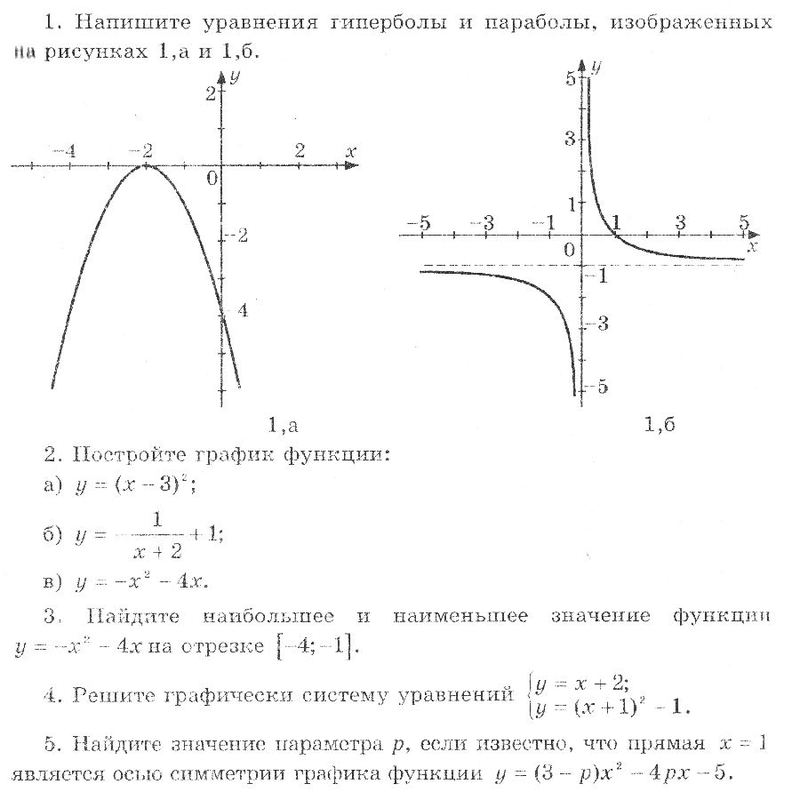
Контрольная работа по алгебре 8 класс (входной контроль)
Главная / Старшие классы / Алгебра
Скачать
85.89 КБ, 510561.docx Автор: Сивец Людмила Васильевна, 21 Мар 2015
Контрольная работа по алгебре (входной контроль) составлена для 8 класса в формате ГИА. Текст представлен в виде трех частей: часть А (Выберите правильный ответ), часть В (Запишите только ответ), часть С (Покажите решение в тетради)
Автор: Сивец Людмила Васильевна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| документ | Контрольная работа по алгебре 8 класс (входной контроль) | Сивец Людмила Васильевна | 21 Мар 2015 |
| разное | Входной контроль 8 класс по физике | Жирова Ирина Сергеевна | 21 Мар 2015 |
| разное | Входной контроль 8 класс по физике | Жирова Ирина Сергеевна | 21 Мар 2015 |
| документ | входной контроль по алгебре 9 класс | Григоренко Татьяна Владимировна | 6 Апр 2015 |
| документ | полугодовая контрольная работа по алгебре 8 класс | Кныш Александра Михайловна | 21 Мар 2015 |
| документ | Годовая контрольная работа по алгебре, 8 класс | Рубцова Ирина Геннадьевна | 31 Мар 2015 |
| разное | контрольная работа по алгебре №1 8 класс | Петренко Людмила Валентиновна | 1 Апр 2015 |
| разное | итоговая контрольная работа по алгебре 8 класс | Вихлянцева Марина Петровна | 1 Апр 2015 |
| Контрольная работа по алгебре за I полугодие 8 класс | Савина Наталия Борисовна | 1 Апр 2015 | |
| разное | контрольная работа по алгебре, 8 класс( за 2 четверть) | Съедина Лидия Николаевна | 1 Апр 2015 |
| документ | Контрольная работа по алгебре, 8 класс | Аникина Ольга Борисовна | 21 Апр 2015 |
| документ | Контрольная работа №2 по алгебре 8 класс | Задворнова Татьяна Николаевна | 14 Фев 2016 |
| документ | Итоговая контрольная работа по алгебре 8 класс | Кулешова Татьяна Викторовна | 14 Янв 2016 |
| документ | Итоговая контрольная работа по алгебре 7 класс | Колодкина Наталья Владимировна | 8 Фев 2016 |
| документ | 8 класс Входной контроль по русскому языку | Галеева Лилия Вагизовна | 27 Июн 2015 |
| документ | Итоговая контрольная работа по алгебре 8 класс,по математике 5 класс | Загитова Гульфия Анатольевна | 20 Сен 2015 |
| разное | решебник по алгебре 7 класс домашняя контрольная работа 2 | tronarukeh2980 | 11 Мая 2015 |
| документ | Контрольная работа по алгебре по теме «Рациональные уравнения», 8 класс | Токарева Инна Александровна | 31 Мар 2015 |
| документ | Контрольная работа по алгебре 8 класс по теме «Применение свойств квадратного корня» | Токарева Тамара Ивановна | 1 Апр 2015 |
| документ | Контрольная работа по алгебре 8 класс по теме «Применение свойст квадратного корня» | Токарева Тамара Ивановна | 1 Апр 2015 |
| документ | Контрольная работа №1 по алгебре. 8 класс по учебнику А Г. Мерзляка В.Б.Полонского | Задворнова Татьяна Николаевна | 21 Дек 2015 |
| документ | Контрольная работа по алгебре за первое полугодие. 8 класс. УМК Макарычев и др. | Сильченкова Светлана Николаевна | 9 Апр 2015 |
| документ | контрольная работа по алгебре 8 класс на тему: «Система уравнений» | Воробьева Юлия Викторовна | 14 Ноя 2015 |
| документ | Контрольная работа №6 по алгебре, 8 класс «Квадратное неравенство» Учебник Ш.А.Алимова. | Мирошниченко Наталья Григорьевна | 15 Окт 2015 |
| документ | Контрольная работа по алгебре. 8 класс (углубленное изучение). Квадратные уравнения | Глушкова Светлана Юрьевна | 15 Окт 2015 |
| документ | Контрольная работа по алгебре и началам анализа по теме: «Логарифмическая функция», 10 класс | Кочухова Ирина Михайловна | 8 Фев 2016 |
| документ | Итогова контрольная работа по алгебре в 8 классе. | Перфильева Валентина Анатольевна | 21 Мар 2015 |
| документ | Годовая контрольная работа по алгебре в 8 классах | Штанина Светлана Николаевна | 1 Апр 2015 |
| документ | Итоговая контрольная работа по алгебре для 8 класса | Атлашкина Наталья Альбертовна | 15 Окт 2015 |
| документ | Входная контрольная работа по алгебре для 8 класса | Петрякова Олеся Сергеевна | 26 Окт 2015 |
| документ | Административная контрольная работа по алгебре для 8 класса (декабрь) | Агеева Юлия Владимировна | 7 Дек 2015 |
| документ | Контрольная работа по алгебре на тему » Арифметическая прогрессия» 9 класс | Шангареева Фарида Максютовна | 8 Фев 2016 |
| документ | Входная контрольная по алгебре 8 класс | Толочко Жанна Геннадьевна | 24 Сен 2015 |
| документ | Итоговая контрольная работа по алгебре для 7 класса | Баринова Елена Валерьевна | 8 Фев 2016 |
| разное | Входной контроль 9 класс по физике | Жирова Ирина Сергеевна | 21 Мар 2015 |
| документ | Входная контрольная работа по алгебре 7 класс | Лапатин Алексей Леонидович | 21 Мар 2015 |
| документ | Вводная контрольная работа по алгебре 9 класс | Прибылова Юлия Вячеславовна | 21 Мар 2015 |
| документ | Контрольная работа по алгебре 7 класс | Козлова Елена Викторовна | 21 Мар 2015 |
| документ | Итоговая контрольная работа по алгебре, 7 класс | Майорова Татьяна Александровна | 21 Мар 2015 |
| документ | Контрольная работа по алгебре,9 класс | Россамахина Ирина Юрьевна | 21 Мар 2015 |
Оценка знаний учащихся — Математика, алгебра, геометрия
Егорова Елена 5.
0
Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям
Хочу выразить большую благодарность от лица педагогов начальных классов гимназии «Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому ученику и отчёт по классу. Великолепно, восторг! Преимущества мы оценили сразу. С начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у нас пока нет, одни благодарности. Очень простая и понятная инструкция, что немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда коллеги понимают, как можно «упростить» работу учителя.
Наговицина Ольга Витальевна 5.0
учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ
по ХИМИИ
Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология.
Очень облегчило аналитическую работу, выявляются узкие места в подготовке к
экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит
время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.
Чазова Александра 5.0
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ
Очень хороший шаблон, удобен в использовании, анализ пробного тестирования занял считанные минуты. Возникли проблемы с распечаткой отчёта, но надо ещё раз разобраться. Большое спасибо за качественный анализатор.
Лосеева Татьяна Борисовна 5.0
учитель начальных классов, МБОУ СОШ №1, г. Красновишерск, Пермский край
Отзыв о товаре Изготовление сертификата или свидетельства конкурса
Большое спасибо за оперативное изготовление сертификатов! Все очень красиво.
Мой ученик доволен, свой сертификат он вложил в портфолио.
Обязательно продолжим с Вами сотрудничество!
Язенина Ольга Анатольевна 4.0
учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы
Я посмотрела вебинар! Осталась очень довольна полученной информацией. Всё очень чётко, без «воды». Всё, что сказано, показано, очень пригодится в практике любого педагога. И я тоже обязательно воспользуюсь полезными материалами вебинара. Спасибо большое лектору за то, что она поделилась своим опытом!
Арапханова Ашат 5.0
ША Табель посещаемости + Сводная для ДОУ ОКУД
Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень
аккуратно и оперативно. Нет ни одного недостатка. Я не пожалела, что доверилась и
приобрела у вас этот табель.
Благодаря Вам сэкономила время, сейчас же
составляю табель для работников. Удачи и успехов Вам в дальнейшем!
Дамбаа Айсуу 5.0
Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ
Спасибо огромное, очень много экономит времени, т.к. анализ уже готовый, и особенно радует, что есть варианты с сочинением, без сочинения, только анализ сочинения! Превосходно!
Найдите значение выражения алгебраической дроби. Видеоурок «Алгебраические дроби. Основные понятия. Разные задачи и выводы
В этом уроке рассматривается понятие алгебраической дроби. С дробями человек сталкивается в простейших жизненных ситуациях: когда необходимо разделить предмет на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, каждый получит кусок пирога. В данном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда предмет делится на неизвестное количество частей, например, х.
В этом случае возникает понятие дробного выражения. С целыми выражениями (не содержащими деления на выражения с переменными) и их свойствами вы уже познакомились в 7 классе. Далее рассмотрим понятие рациональной дроби, а также допустимые значения переменных.
Рациональные выражения делятся на целых и дробных выражений .
Определение Рациональная дробь представляет собой дробное выражение вида, где — многочлены. — знаменатель числителя.
Примеры рациональных выражений: — дробные выражения; — целые выражения. В первом выражении, например, он выступает и числителем, и знаменателем.
Значение алгебраическая дробь , как и любое алгебраическое выражение , зависит от числового значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных и , а во втором только от значения переменной.
Рассмотрим первую типовую задачу: вычисление значения рациональной дроби для различных значений входящих в него переменных.
Пример 1 Рассчитайте значение дроби для a), b), c)
Решение. Подставляем значения переменных в указанную дробь: а), б), в) — не существует (так как на ноль делить нельзя).
Ответ: а) 3; б) 1; в) не существует.
Как видите, для любой дроби есть две типичных проблемы: 1) вычисление дроби, 2) нахождение допустимых и недопустимых значений литеральных переменных.
Определение Допустимые значения переменных — значения переменных, для которых выражение имеет смысл. Набор всех допустимых значений переменных называется DLD или домен .
Значение литеральных переменных может быть недопустимым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значения переменных действительны, потому что дробь может быть вычислена.
Пример 2
Решение. Чтобы это выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не был равен нулю.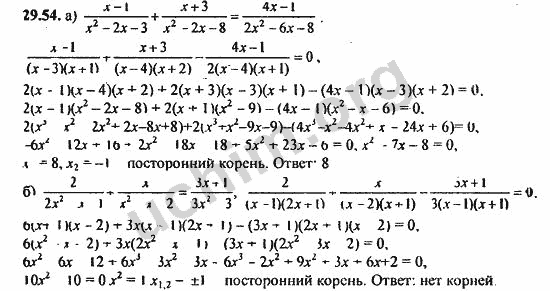
Таким образом, недействительными будут только те значения переменных, у которых знаменатель равен нулю. Знаменатель дроби, следовательно, решаем линейное уравнение:
Следовательно, при значении переменной дробь не имеет смысла.
Ответ: -5.
Из решения примера следует правило нахождения недопустимых значений переменных — знаменатель дроби равен нулю и находятся корни соответствующего уравнения.
Рассмотрим несколько подобных примеров.
Пример 3 Устанавливать при каких значениях переменной дробь не имеет смысла .
Решение. .
Ответ. .
Пример 4 Устанавливать при каких значениях переменной дробь не имеет смысла.
Решение. .
Существуют и другие постановки этой задачи — найти домен или диапазон допустимых значений выражения (ОДЗ) . Это означает нахождение всех допустимых значений для переменных. В нашем примере это все значения, кроме .
Область определения удобно представлена на числовой оси.
Для этого выпячиваем на ней точку, как указано на рисунке:
Рис. 1
Таким образом, область определения дроби будут все цифры, кроме 3.
Ответ. .
Пример 5 Устанавливать при каких значениях переменной дробь не имеет смысла.
Решение. .
Отобразим полученное решение на числовой оси:
Рис. 2
Ответ. .
Пример 6
Решение. . Получили равенство двух переменных, приводим численные примеры: или и т.д.
Изобразим это решение на графике в декартовой системе координат:
Рис. 3. График функции
Координаты любой точки, лежащие на этом графике, не попадают в диапазон допустимых дробей.
Ответ. .
В рассмотренных примерах мы столкнулись с ситуацией, когда произошло деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типов.
Пример 7 Устанавливать при каких значениях переменных дробь не имеет смысла.
Решение. .
Получается, что дробь не имеет смысла. Но можно возразить, что это не так, потому что: .
Может показаться, что если конечное выражение равно 8 for, то исходное тоже можно вычислить, а значит, имеет смысл for. Однако если мы подставим его в исходное выражение, то получим — смысла нет.
Ответ. .
Чтобы подробнее разобраться в этом примере, решим следующую задачу: при каких значениях указанная дробь равна нулю?
Но тогда мы его сформулировали в «упрощенном» виде, удобном и достаточном для работы с обыкновенными дробями. В этой статье мы рассмотрим основное свойство дроби применительно к алгебраическим дробям (то есть к дробям, у которых числитель и знаменатель многочлены, в некоторых учебниках по алгебре такие дроби называются не алгебраическими, а рациональными дробями). Сначала мы констатируем основное свойство алгебраической дроби , обоснуем его, а после этого перечислим основные области его применения.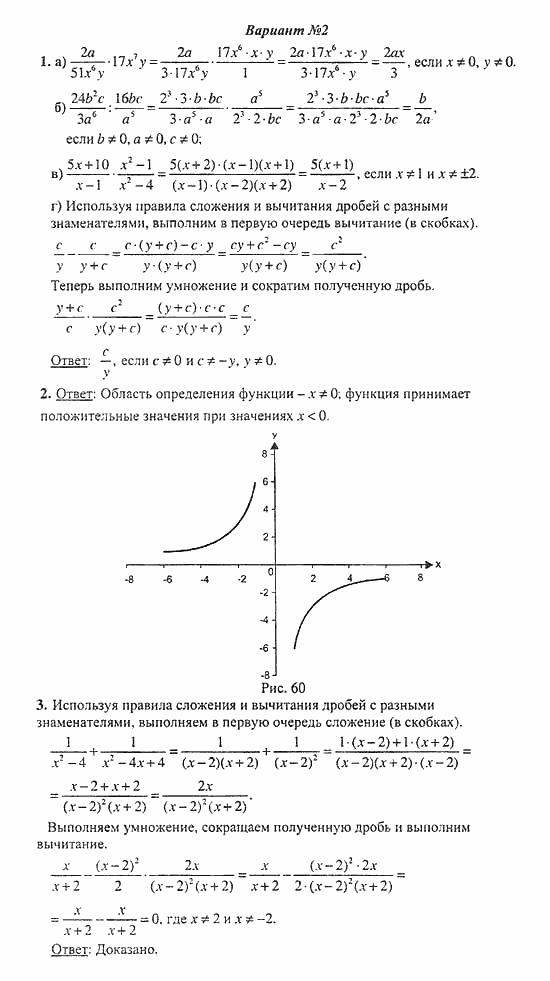
Навигация по страницам.
Формулировка и обоснование
Для начала вспомним, как было сформулировано основное свойство дроби для обыкновенных дробей: если и числитель, и знаменатель обыкновенной дроби умножить или разделить на некоторое натуральное число, то значение дробь не изменится. Этому утверждению соответствуют равенства и (справедливые и с переставленными частями в форме и), где a, b и m — некоторые.
На самом деле нельзя сказать о делении числителя и знаменателя на число — этот случай покрывается равенством вида. Например, равенство можно обосновать через деление с использованием равенства как , а можно обосновать и с помощью равенства как . Поэтому в дальнейшем основное свойство дроби мы будем связывать с равенством (ями), а на равенстве (ях) останавливаться не будем.
Теперь покажем, что основное свойство дроби распространяется на дроби, числитель и знаменатель которых равны. Для этого докажем, что записанное равенство справедливо не только для натуральных чисел, но и для любых действительных чисел.
Другими словами, мы доказываем, что равенство справедливо для любых действительных чисел a, b и m, причем b и m отличны от нуля (иначе мы столкнемся с делением на ноль).
Пусть дробь a/b будет записью числа z, т.е. Докажем, что дробь также соответствует числу z, то есть докажем это. Это докажет равенство.
Стоит отметить, что если алгебраическая дробь имеет дробные коэффициенты, то умножение ее числителя и знаменателя не на определенное число позволяет перейти к целым коэффициентам, и тем самым упростить ее вид. Например, . А на умножении числителя и знаменателя на минус единицу основаны правила смены знаков членов алгебраической дроби.
Второй по значимости областью применения основного свойства дроби является приведение алгебраических дробей. Приведение в общем случае проводится в два этапа: сначала факторизуются числитель и знаменатель, что позволяет найти общий множитель m, а затем на основании равенства переходят к дроби вида а/ b без этого общего множителя.
Например, алгебраическая дробь после разложения и знаменателя на множители принимает вид www.сайт, включая внутренние материалы и внешнее оформление, не может быть воспроизведена в какой-либо форме или использована без предварительного письменного разрешения правообладателя.
В § 42 было сказано, что если деление многочленов не может быть проведено целиком, то частное записывается в виде дробного выражения, в котором делимое является числителем, а делитель — знаменателем.
Примеры дробных выражений:
Числитель и знаменатель дробного выражения сами могут быть дробными выражениями, например:
Из дробных алгебраических выражений чаще всего приходится иметь дело с теми, в которых числитель и знаменатель являются полиномами (в частности, мономами). Каждое такое выражение называется алгебраической дробью.
Определение Алгебраическая дробь, представляющая собой дробь, числитель и знаменатель которой являются полиномами, называется алгебраической дробью.
Как и в арифметике, числитель и знаменатель алгебраической дроби называются членами дроби.
Далее, изучив действия над алгебраическими дробями, мы можем любое дробное выражение с помощью идентичных преобразований преобразовать в алгебраическую дробь.
Примеры алгебраических дробей:
Обратите внимание, что все выражение, то есть многочлен, можно записать в виде дроби, для этого достаточно в числителе этого выражения написать, а в знаменателе 1. Например:
2. Действительная буква ценности.
Буквы, входящие только в числитель, могут принимать любые значения (если никакие дополнительные ограничения не наложены условием задачи).
Для букв, входящих в знаменатель, допустимы только те значения, у которых знаменатель не равен нулю. Поэтому в дальнейшем мы всегда будем предполагать, что знаменатель алгебраической дроби не равен нулю.
Когда ученик идет в среднюю школу, математика делится на 2 предмета: алгебра и геометрия.
Понятий становится все больше, задач все больше и больше. Некоторые с трудом воспринимают дроби. Мы пропустили первый урок по этой теме, и вуаля. дроби? Вопрос, который будет мучить всю школьную жизнь.
Понятие алгебраической дроби
Начнем с определения. Под алгебраической дробью понимаются выражения P/Q, где P — числитель, а Q — знаменатель. Под буквенной записью может быть скрыто число, числовое выражение, цифро-буквенное выражение.
Прежде чем задаться вопросом, как решать алгебраические дроби, сначала нужно понять, что такое выражение является частью целого.
Как правило, целое число равно 1. Число в знаменателе показывает, на сколько частей была разделена единица. Числитель нужен для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Допускается запись дробного выражения в виде математической операции «Деление». В этом случае числитель — делимое, знаменатель — делитель.
Основное правило обыкновенных дробей
Когда учащиеся проходят эту тему в школе, им даются примеры подкрепления.
Чтобы правильно их решать и находить разные выходы из сложных ситуаций, нужно применять основное свойство дробей.
Звучит так: Если умножить и числитель, и знаменатель на одно и то же число или выражение (отличное от нуля), то значение обыкновенной дроби не изменится. Частным случаем этого правила является разделение обеих частей выражения на одно и то же число или многочлен. Такие преобразования называются тождественными равенствами.
Ниже мы рассмотрим, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей.
Математические действия с дробями
Рассмотрим, как решить основное свойство алгебраической дроби, как применить его на практике. Если вам нужно умножить две дроби, сложить их, разделить одну на другую или вычесть, всегда нужно придерживаться правил.
Итак, для операции сложения и вычитания следует найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби даны с одинаковыми выражениями Q, то этот пункт следует опустить.
Когда общий знаменатель найден, как решать алгебраические дроби? Вам нужно добавить или вычесть числители. Но! Необходимо помнить, что если перед дробью стоит знак «-», все знаки в числителе меняются местами. Иногда не следует производить никаких подстановок и математических операций. Достаточно поменять знак перед дробью.
Часто используется такое понятие, как сокращение дроби . Это означает следующее: если числитель и знаменатель разделить на выражение, отличное от единицы (одинаковое для обеих частей), получится новая дробь. Делимое и делитель меньше предыдущих, но по основному правилу дробей остаются равными исходному примеру.
Целью этой операции является получение нового неприводимого выражения. Эту задачу можно решить, сократив числитель и знаменатель на наибольший общий множитель. Алгоритм работы состоит из двух пунктов:
- Нахождение НОД обеих частей дроби.
- Деление числителя и знаменателя на найденное выражение и получение несократимой дроби, равной предыдущей.
В таблице ниже показаны формулы. Для удобства его можно распечатать и носить с собой в блокноте. Однако, чтобы в дальнейшем при решении контрольной или экзамена не возникало затруднений в вопросе, как решать алгебраические дроби, эти формулы необходимо выучить наизусть.
Некоторые примеры решений
С теоретической точки зрения рассматривается вопрос о том, как решать алгебраические дроби. Примеры в этой статье помогут вам лучше понять материал.
1. Преобразовать дроби и привести их к общему знаменателю.
2. Преобразовать дроби и привести их к общему знаменателю.
После изучения теоретической части и изучения практической части вопросов больше возникнуть не должно.
§ 1 Понятие алгебраической дроби
Алгебраическая дробь — это выражение
где P и Q — многочлены; P — числитель алгебраической дроби, Q — знаменатель алгебраической дроби.
Вот примеры алгебраических дробей:
Любой многочлен является частным случаем алгебраической дроби, потому что любой многочлен можно записать как
Например:
Значение алгебраической дроби зависит от значения переменные.
Например, вычисляем значение дроби
1)
2)
В первом случае получаем:
Обратите внимание, что эту дробь можно уменьшить: алгебраической дроби упрощается. Воспользуйтесь этим.
Во втором случае получаем:
Как видите, при изменении значений переменных значение алгебраической дроби изменилось.
§ 2 Допустимые значения переменных алгебраической дроби
Рассмотрим алгебраическую дробь
Значение х = -1 недопустимо для этой дроби, так как знаменатель дроби при таком значении х обращается в нуль. При таком значении переменной алгебраическая дробь не имеет смысла.
Таким образом, допустимыми значениями переменных алгебраической дроби являются такие значения переменных, при которых знаменатель дроби не обращается в нуль.
Давайте решим несколько примеров.
При каких значениях переменной алгебраическая дробь не имеет смысла:
Для нахождения недопустимых значений переменных знаменатель дроби равен нулю, и находятся корни соответствующего уравнения.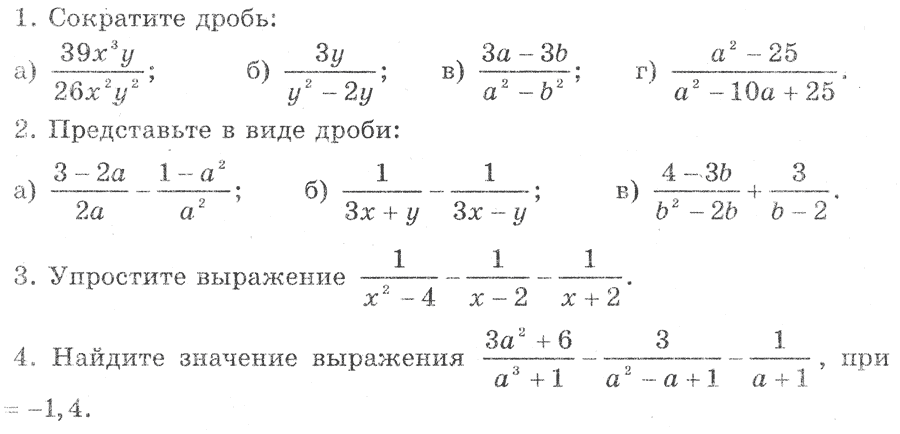
При каких значениях переменной алгебраическая дробь равна нулю:
Дробь равна нулю, если числитель равен нулю. Приравниваем числитель нашей дроби к нулю и находим корни полученного уравнения:
Таким образом, при х = 0 и х = 3 эта алгебраическая дробь не имеет смысла, а значит, мы должны исключить эти значения переменной из ответа.
Итак, на этом уроке вы узнали основные понятия алгебраической дроби: числитель и знаменатель дроби, а также допустимые значения переменных алгебраической дроби.
Список использованной литературы:
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч. 1 Учебник для общеобразовательных учреждений / А.Г. Мордкович. — 9-е изд., перераб. — М.: Мнемозин, 2007. — 215 с.: ил. .
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч. 2, Задание для общеобразовательных учреждений / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. — 8-е изд., — М.: Мнемозина, 2006. — 239с.
- Алгебра. 8 класс. Экзамен для студентов общеобразовательных учреждений Александрова Л.
