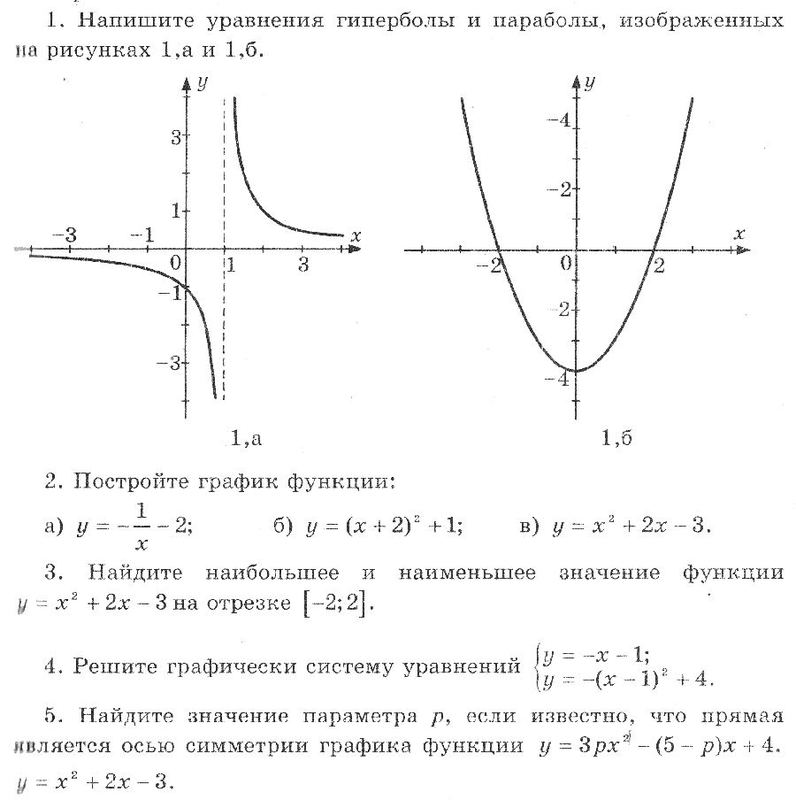
ГДЗ контрольная работа / №3 / Вариант 1 5 алгебра 8 класс дидактические материалы Жохов, Макарычев – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
ГДЗ контрольная работа / №3 / Вариант 1 5 алгебра 8 класс дидактические материалы Жохов, Макарычев
ГДЗ по Алгебре за 8 класс Дидактические материалы Жохов , Макарычев, Миндюк . Как правило, в восьмом классе школьникам необходимо успеть многое освоить, в особенности это касается такой сложной науки, как алгебра . Контрольные работы . № 1 . Вариант 1 .
Авторы : Жохов В .И ., Макарычев Ю .Н ., Миндюк Н .Г . Издательство: Просвещение .
Жохов В .И ., Макарычев Ю .Н ., Миндюк Н .Г . Решебник (ГДЗ ) по Алгебре за 8 (восьмой ) класс дидактические материалы авторы: Жохов , Макарычев, Миндюк издательство Просвещение, год .
• материал из этого сборника ГДЗ по алгебре за 8 класс дидактические материалы Жохов подобран в соответствии с предоставляемыми ГДЗ к дидактическим материалам по алгебре за 8 класс Звавич Л . И . можно посмотреть здесь . Самостоятельные работы . Вариант 1 .
И . можно посмотреть здесь . Самостоятельные работы . Вариант 1 .
Если у вас нет денег на репетиторов, не хватает времени, сил или компетенции для помощи своему чаду с уроками, лучшим вариантом будет воспользоваться онлайн-пособием ГДЗ по алгебре за 8 класс «Дидактические материалы » авторов Жохов В .И ., Макарычев, Миндюк .
ГДЗ > Алгебра > 8 класс > Дидактические материалы по алгебре 8 класс Жохов , Макарычев, Миндюк Просвещение . В методичке доходчиво изложен весь школьный курс за восьмой класс , что позволяет школьнику самостоятельно подготовиться к тестовым работам .
Дидактические материалы » Жохов , Макарычев , Миндюк с решениями (ГДЗ) . Алгебра 8 Контрольные Макарычев Ю .Н . + ОТВЕТЫ . Задачи контрольных работ из учебного пособия Представленные ниже контрольные работы в 2-х вариантах ориентированы на учебник . .
Решебник к учебнику «Алгебра 8 класс Дидактические материалы Жохов , Макарычев, Миндюк ГДЗ выполняет именно такую работу – помогает исправить отставание в предмете ребятам В ГДЗ Жохова школьная программа по алгебре за восьмой класс изложена столь . .
.
Алгебра 8 Макарычев Контрольная 3 . Контрольная работа № 3 по алгебре в 8 классе по учебнику Макарычева . Алгебра 8 Макарычев Контрольная 3 и Ответы . Цитаты из учебного пособия: «Алгебра 8 класс . Дидактические материалы / В .И . Жохов , Ю .Н . Макарычев, Н .Г . .
Учебник «Алгебра 8 класс дидактические материалы Жохов , Макарычев, Миндюк» контрольными работами в четырех вариантах; итоговое повторение всех тем Благодаря детальному изложению материала в «ГДЗ по Алгебре 8 класс дидактические материалы . .
Алгебра Дидактические материалы Жохов В .И ., Макарычев Ю .Н ., Миндюк Н .Г . 8 класс . Контрольные работы . К-1 А . Вариант 1 .
Дидактические материалы по Алгебре 8 класс В .И . Жохов , Ю .Н . Макарычев . Дидактические материалы , предоставленные Жоховым и Макарычевым, полностью соответствуют современным требованиям министерства образования и пробуждают у ребенка . .
Алгебра . 8 класс . Дидактические материалы . СОДЕРЖАНИЕ Предисловие 3 Самостоятельные работы 7 Вариант I — Вариант II 56 Контрольные работы 106 Итоговое повторение по темам . к учебнику под редакцией С . А . Теляковского … .
к учебнику под редакцией С . А . Теляковского … .
Дидактические материалы по алгебре для 8 класса . Самостоятельные работы . Вариант I . Контрольные работы . ’ Алгебра -8 ’’ под редакцией Жохова , отлично подойдет для людей, которые хотят изучать алгебру, аи даже заменит настоящего репетитора, что ограничит вас от . .
Дидактические материалы — Жохов В .И ., Макарычев Ю .Н ., Миндюк Н .Г . cкачать в PDF . Пособие содержит упражнения для самостоятельных работ , которые носят обучающий характер, а также тексты контрольных работ и задания для проведения школьных математических . .
ГДЗ по Алгебре за 8 класс Дидактические материалы Жохов , Макарычев, Миндюк . Как правило, в восьмом классе школьникам необходимо успеть многое освоить, в особенности это касается такой сложной науки, как алгебра . Контрольные работы . № 1 . Вариант 1 .
Авторы : Жохов В .И ., Макарычев Ю .Н ., Миндюк Н .Г . Издательство: Просвещение .
Жохов В .И ., Макарычев Ю .Н ., Миндюк Н . Г . Решебник (ГДЗ ) по Алгебре за 8 (восьмой ) класс дидактические материалы авторы: Жохов , Макарычев, Миндюк издательство Просвещение, год .
Г . Решебник (ГДЗ ) по Алгебре за 8 (восьмой ) класс дидактические материалы авторы: Жохов , Макарычев, Миндюк издательство Просвещение, год .
• материал из этого сборника ГДЗ по алгебре за 8 класс дидактические материалы Жохов подобран в соответствии с предоставляемыми ГДЗ к дидактическим материалам по алгебре за 8 класс Звавич Л .И . можно посмотреть здесь . Самостоятельные работы . Вариант 1 .
Если у вас нет денег на репетиторов, не хватает времени, сил или компетенции для помощи своему чаду с уроками, лучшим вариантом будет воспользоваться онлайн-пособием ГДЗ по алгебре за 8 класс «Дидактические материалы » авторов Жохов В .И ., Макарычев, Миндюк .
ГДЗ > Алгебра > 8 класс > Дидактические материалы по алгебре 8 класс Жохов , Макарычев, Миндюк Просвещение . В методичке доходчиво изложен весь школьный курс за восьмой класс , что позволяет школьнику самостоятельно подготовиться к тестовым работам .
Дидактические материалы » Жохов , Макарычев , Миндюк с решениями (ГДЗ) . Алгебра 8 Контрольные Макарычев Ю .Н . + ОТВЕТЫ . Задачи контрольных работ из учебного пособия Представленные ниже контрольные работы в 2-х вариантах ориентированы на учебник . .
Алгебра 8 Контрольные Макарычев Ю .Н . + ОТВЕТЫ . Задачи контрольных работ из учебного пособия Представленные ниже контрольные работы в 2-х вариантах ориентированы на учебник . .
Решебник к учебнику «Алгебра 8 класс Дидактические материалы Жохов , Макарычев, Миндюк ГДЗ выполняет именно такую работу – помогает исправить отставание в предмете ребятам В ГДЗ Жохова школьная программа по алгебре за восьмой класс изложена столь . .
Алгебра 8 Макарычев Контрольная 3 . Контрольная работа № 3 по алгебре в 8 классе по учебнику Макарычева . Алгебра 8 Макарычев Контрольная 3 и Ответы . Цитаты из учебного пособия: «Алгебра 8 класс . Дидактические материалы / В .И . Жохов , Ю .Н . Макарычев, Н .Г . .
Учебник «Алгебра 8 класс дидактические материалы Жохов , Макарычев, Миндюк» контрольными работами в четырех вариантах; итоговое повторение всех тем Благодаря детальному изложению материала в «ГДЗ по Алгебре 8 класс дидактические материалы . .
Алгебра Дидактические материалы Жохов В . И ., Макарычев Ю .Н ., Миндюк Н .Г . 8 класс . Контрольные работы . К-1 А . Вариант 1 .
И ., Макарычев Ю .Н ., Миндюк Н .Г . 8 класс . Контрольные работы . К-1 А . Вариант 1 .
Дидактические материалы по Алгебре 8 класс В .И . Жохов , Ю .Н . Макарычев . Дидактические материалы , предоставленные Жоховым и Макарычевым, полностью соответствуют современным требованиям министерства образования и пробуждают у ребенка . .
Алгебра . 8 класс . Дидактические материалы . СОДЕРЖАНИЕ Предисловие 3 Самостоятельные работы 7 Вариант I — Вариант II 56 Контрольные работы 106 Итоговое повторение по темам . к учебнику под редакцией С . А . Теляковского … .
Дидактические материалы по алгебре для 8 класса . Самостоятельные работы . Вариант I . Контрольные работы . ’ Алгебра -8 ’’ под редакцией Жохова , отлично подойдет для людей, которые хотят изучать алгебру, аи даже заменит настоящего репетитора, что ограничит вас от . .
Дидактические материалы — Жохов В .И ., Макарычев Ю .Н ., Миндюк Н .Г . cкачать в PDF . Пособие содержит упражнения для самостоятельных работ , которые носят обучающий характер, а также тексты контрольных работ и задания для проведения школьных математических . .
.
ГДЗ страница 23 география 8 класс тетрадь-экзаменатор Барабанов
ГДЗ повторение 36 алгебра 10‐11 класс Колмогоров, Абрамов
ГДЗ страница 15 география 8 класс рабочая тетрадь Ким, Марченко
ГДЗ unit 3 136 английский язык 11 класс Enjoy English Биболетова, Трубанева
ГДЗ часть 2 Данилов (страница) 4 окружающий мир 3 класс рабочая тетрадь Данилов, Кузнецова
ГДЗ часть 1. страница 7 математика 2 класс Башмаков, Нефедова
ГДЗ задание 1002 математика 5 класс Никольский, Потапов
ГДЗ §27. Безлесные зоны на юге России / Вопросы в конце параграфа 4 география 8 класс Баринова
ГДЗ упражнение / упражнение 17 8 физика 10 класс Мякишев, Буховцев
ГДЗ контрольные работы / КР-5 / подготовительный вариант 5 алгебра 8 класс дидактические материалы Феоктистов
ГДЗ глава 5 / параграф 2 / упражнение 20 математика 5 класс Козлов, Никитин
ГДЗ самостоятельные работы / СР-21 / вариант 1 3 алгебра 8 класс дидактические материалы Феоктистов
ГДЗ упражнение 566 русский язык 5 класс Разумовская, Львова
ГДЗ вправа 444 математика 5 класс Истер
ГДЗ номер 468 математика 5 класс Дорофеев, Шарыгин
ГДЗ страница 21 история 7 класс тетрадь-тренажёр Данилов, Лукутин
ГДЗ Учебник 2019 / часть 2 386 (1236) математика 5 класс Виленкин, Жохов
ГДЗ упражнение 474 геометрия 9 класс Мерзляк, Полонский
ГДЗ страница 82 немецкий язык 5 класс рабочая тетрадь Wunderkinder Яцковская
ГДЗ страница 45 биология 9 класс рабочая тетрадь Пономарева, Панина
ГДЗ вариант 1 183 математика 5 класс дидактические материалы Мерзляк, Полонский
ГДЗ параграф 1 1. 15 геометрия 8 класс Мерзляк, Поляков
15 геометрия 8 класс Мерзляк, Поляков
ГДЗ § 1 обществознание 6 класс рабочая тетрадь Хромова, Кравченко
ГДЗ самостоятельная работа / вариант 2 39 математика 5 класс дидактические материалы Чесноков, Нешков
ГДЗ задание 109 информатика 5 класс рабочая тетрадь Босова, Босова
ГДЗ параграф § 32 история 5 класс Михайловский
ГДЗ упражнение 501 русский язык 7 класс Львова, Львов
ГДЗ ГЛАВА 1 / 6. Wir prüfen, was wir schon können. (Мы повторяем то, что уже умеем.) 15 немецкий язык 9 класс Бим, Садомова
ГДЗ часть 2 231 математика 1 класс Истомина
ГДЗ номер 36 алгебра 7 класс Макарычев, Миндюк
ГДЗ параграф 8 8.24 алгебра 8 класс задачник Мордкович, Александрова
ГДЗ упражнение 1078 алгебра 10 класс Колягин, Ткачева
ГДЗ вариант 3 158 геометрия 8 класс дидактические материалы Мерзляк, Полонский
ГДЗ § 47. Вторая война Рима с Карфагеном 2 история 5 класс Вигасин, Годер
ГДЗ страница 33 английский язык 5 класс Starlight Student’s book Баранова, Эванс
ГДЗ вариант 1 109 геометрия 7 класс дидактические материалы Мерзляк, Полонский
ГДЗ § 1 6 обществознание 7 класс рабочая тетрадь Хромова, Скворцова
ГДЗ часть 2. страница 60 математика 2 класс Дорофеев, Миракова
страница 60 математика 2 класс Дорофеев, Миракова
ГДЗ unit 1 / section 8 1 английский язык 5 класс рабочая тетрадь Биболетова, Денисенко
ГДЗ упражнение 533 алгебра 7 класс Муравин, Муравин
ГДЗ страница 67 окружающий мир 3 класс проверочные работы Плешаков, Плешаков
ГДЗ тема 1 (задание) 1 география 10 класс рабочая тетрадь Максаковский
ГДЗ упражнение 323 русский язык 7 класс Разумовская, Львова
ГДЗ 3 глава 3.65 химия 8 класс задачник Кузнецова, Левкин
ГДЗ Учебник 2019 / часть 1 47 (47) математика 5 класс Виленкин, Жохов
ГДЗ страница 95 английский язык 9 класс forward Вербицкая, Маккинли
ГДЗ самостоятельная работа / вариант 7 С-8 геометрия 7 класс дидактические материалы Зив, Мейлер
ГДЗ упражнение 550 математика 5 класс сборник задач и упражнений Гамбарин, Зубарева
ГДЗ часть 1. страница 135 математика 2 класс Дорофеев, Миракова
ГДЗ по географии 5‐6 класс Лобжанидзе Решебник
Гольдич Дидактические Материалы 7 Класс ГДЗ
Решебник По Чтению 4 Класс Тетрадь
ГДЗ По Русскому 9 Класс Загоровская Учебник
ГДЗ По Русскому 9 Класс Пичугов Ангелина
Гдз По Англ 7
ГДЗ решебник Алгебра за 8 класс Потапов (Дидактические материалы) «Просвещение»
Самостоятельная работа №1.
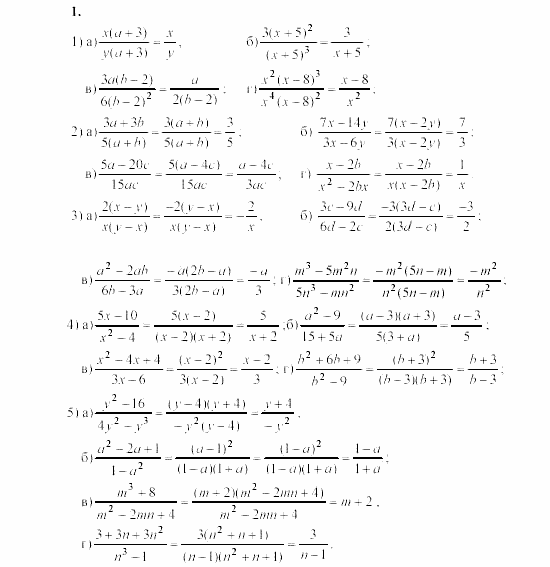 Вариант 1123456
Вариант 1123456Самостоятельная работа №1. Вариант 2
123456Самостоятельная работа №1. Вариант 3
123456Самостоятельная работа №1. Вариант 4
123456Самостоятельная работа №2. Вариант 1
1234Самостоятельная работа №2. Вариант 2
1234Самостоятельная работа №2. Вариант 3
1234Самостоятельная работа №2. Вариант 4
1234Самостоятельная работа №3. Вариант 1
123456Самостоятельная работа №3. Вариант 2
123456Самостоятельная работа №3. Вариант 3
123456Самостоятельная работа №3. Вариант 4
123456Самостоятельная работа №4. Вариант 1
123456Самостоятельная работа №4. Вариант 2
123456Самостоятельная работа №4. Вариант 3
123456Самостоятельная работа №4. Вариант 4
123456Самостоятельная работа №5. Вариант 1
12345Самостоятельная работа №5. Вариант 2
12345Самостоятельная работа №5. Вариант 3
12345Самостоятельная работа №5. Вариант 4
12345Самостоятельная работа №6.
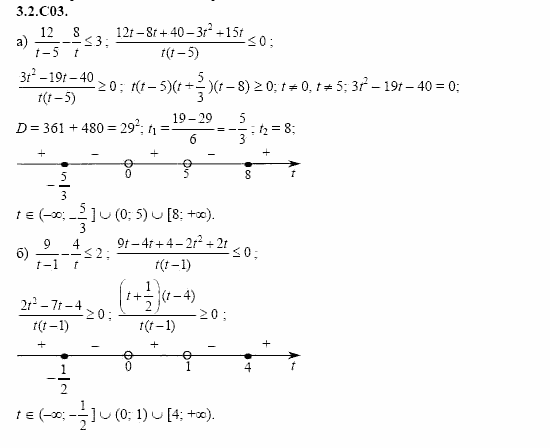 Вариант 112345
Вариант 112345Самостоятельная работа №6. Вариант 2
12345Самостоятельная работа №6. Вариант 3
12345Самостоятельная работа №6. Вариант 4
12345Самостоятельная работа №7. Вариант 1
1234Самостоятельная работа №7. Вариант 2
1234Самостоятельная работа №7. Вариант 3
1234Самостоятельная работа №7. Вариант 4
1234Самостоятельная работа №8. Вариант 1
1234Самостоятельная работа №8. Вариант 2
1234Самостоятельная работа №8. Вариант 3
1234Самостоятельная работа №8. Вариант 4
1234Самостоятельная работа №9. Вариант 1
123Самостоятельная работа №9. Вариант 2
123Самостоятельная работа №9. Вариант 3
123Самостоятельная работа №9. Вариант 4
123Самостоятельная работа №10. Вариант 1
1234Самостоятельная работа №10. Вариант 2
1234Самостоятельная работа №10. Вариант 3
1234Самостоятельная работа №10. Вариант 4
1234Самостоятельная работа №11. Вариант 1
12345Самостоятельная работа №11.
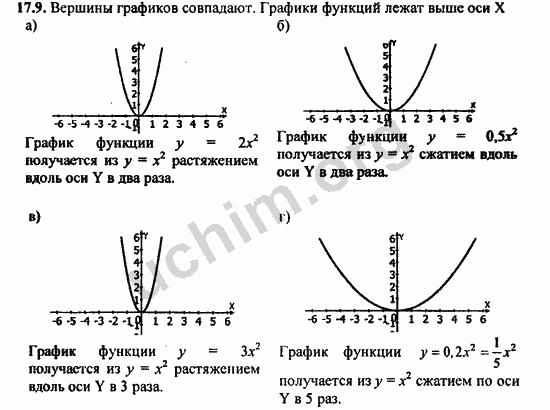 Вариант 212345
Вариант 212345Самостоятельная работа №11. Вариант 3
12345Самостоятельная работа №11. Вариант 4
12345Самостоятельная работа №12. Вариант 1
1234Самостоятельная работа №12. Вариант 2
1234Самостоятельная работа №12. Вариант 3
1234Самостоятельная работа №12. Вариант 4
1234Самостоятельная работа №13. Вариант 1
1234Самостоятельная работа №13. Вариант 2
1234Самостоятельная работа №13. Вариант 3
1234Самостоятельная работа №13. Вариант 4
1234Самостоятельная работа №14. Вариант 1
123456Самостоятельная работа №14. Вариант 2
123456Самостоятельная работа №14. Вариант 3
123456Самостоятельная работа №14. Вариант 4
123456Самостоятельная работа №15. Вариант 1
12345Самостоятельная работа №15. Вариант 2
12345Самостоятельная работа №15. Вариант 3
12345Самостоятельная работа №15. Вариант 4
12345Самостоятельная работа №16. Вариант 1
1234Самостоятельная работа №16.
 Вариант 21234
Вариант 21234Самостоятельная работа №16. Вариант 3
1234Самостоятельная работа №16. Вариант 4
1234Самостоятельная работа №17. Вариант 1
12345Самостоятельная работа №17. Вариант 2
12345Самостоятельная работа №17. Вариант 3
12345Самостоятельная работа №17. Вариант 4
12345Самостоятельная работа №18. Вариант 1
123Самостоятельная работа №18. Вариант 2
123Самостоятельная работа №18. Вариант 3
123Самостоятельная работа №18. Вариант 4
123Самостоятельная работа №19. Вариант 1
1234Самостоятельная работа №19. Вариант 2
1234Самостоятельная работа №19. Вариант 3
1234Самостоятельная работа №19. Вариант 4
1234Самостоятельная работа №20. Вариант 1
12345Самостоятельная работа №20. Вариант 2
12345Самостоятельная работа №20. Вариант 3
12345Самостоятельная работа №20. Вариант 4
12345Самостоятельная работа №21. Вариант 1
123Самостоятельная работа №21.
 Вариант 2123
Вариант 2123Самостоятельная работа №21. Вариант 3
123Самостоятельная работа №21. Вариант 4
123Самостоятельная работа №22. Вариант 1
12Самостоятельная работа №22. Вариант 2
12Самостоятельная работа №22. Вариант 3
12Самостоятельная работа №22. Вариант 4
12Самостоятельная работа №23. Вариант 1
12Самостоятельная работа №23. Вариант 2
12Самостоятельная работа №23. Вариант 3
12Самостоятельная работа №23. Вариант 4
12Самостоятельная работа №24. Вариант 1
1234Самостоятельная работа №24. Вариант 2
1234Самостоятельная работа №24. Вариант 3
1234Самостоятельная работа №24. Вариант 4
1234Самостоятельная работа №25. Вариант 1
123Самостоятельная работа №25. Вариант 2
123Самостоятельная работа №25. Вариант 3
123Самостоятельная работа №25. Вариант 4
123Самостоятельная работа №26. Вариант 1
12345Самостоятельная работа №26. Вариант 2
12345Самостоятельная работа №26.
 Вариант 312345
Вариант 312345Самостоятельная работа №26. Вариант 4
12345Самостоятельная работа №27. Вариант 1
1234Самостоятельная работа №27. Вариант 2
1234Самостоятельная работа №27. Вариант 3
1234Самостоятельная работа №27. Вариант 4
1234Самостоятельная работа №28. Вариант 1
1234Самостоятельная работа №28. Вариант 2
1234Самостоятельная работа №28. Вариант 3
1234Самостоятельная работа №28. Вариант 4
1234Контрольная работа №1. Вариант 1
12345Контрольная работа №1. Вариант 2
12345Контрольная работа №1. Вариант 3
12345Контрольная работа №1. Вариант 4
12345Контрольная работа №2. Вариант 1
123456Контрольная работа №2. Вариант 2
123456Контрольная работа №2. Вариант 3
123456Контрольная работа №2. Вариант 4
123456Контрольная работа №3. Вариант 1
12345Контрольная работа №3. Вариант 2
12345Контрольная работа №3. Вариант 3
12345Контрольная работа №3.
 Вариант 412345
Вариант 412345Контрольная работа №4. Вариант 1
12345Контрольная работа №4. Вариант 2
12345Контрольная работа №4. Вариант 3
12345Контрольная работа №4. Вариант 4
12345Контрольная работа №5. Вариант 1
12345Контрольная работа №5. Вариант 2
12345Контрольная работа №5. Вариант 3
12345Контрольная работа №5. Вариант 4
12345Контрольная работа №6. Вариант 1
12345Контрольная работа №6. Вариант 2
12345Контрольная работа №6. Вариант 3
12345Контрольная работа №6. Вариант 4
12345Контрольная работа №7. Вариант 1
123456Контрольная работа №7. Вариант 2
123456Контрольная работа №7. Вариант 3
123456Контрольная работа №7. Вариант 4
123456Похожие ГДЗ Алгебра 8 класс
Алгебра 8 классУчебникНикольский, Потапов«Просвещение»
Алгебра 8 классТематические тестыМГУ — школеЧулков, Струков«Просвещение»
Самостоятельная работа №1. Вариант 1: 1
◄ Предыдущий
Следующий ►
Условие
Решение
◄ Предыдущий
Следующий ►
закрытьГДЗ и решебники
Материалы контрольных работ Алгебра 8 класс (Ю.
 Н. Макарычев) — контрольная работа 8 класс
Н. Макарычев) — контрольная работа 8 классСкачать 0.79 Mb.
|
Подборка по базе: Практическая работа №3 (часть 2).doc, Самостоятельная работа №2.docx, план конспект 8 класс.docx, Практическая работа № 2_ «Анализ с позиции системно-деятельностн, Самостоятельная работа №4.doc, Самостоятельная работа №7.pdf, Самостоятельная работа 3.4.1.docx, Практическая работа №1.  doc, практическая работа 1 (Кеда, Кхань) (1).docx, КВН 2 КЛАСС.docx doc, практическая работа 1 (Кеда, Кхань) (1).docx, КВН 2 КЛАСС.docx1 2 3 4 5 6 7 Примерные материалы контрольных работ Алгебра 8 класс (Ю.Н. Макарычев) Вариант 1. 1. Сократите дробь: 2. Представьте в виде дроби: 3. Найдите значение выражения при 4. Упростить выражение: Контрольная работа №1. 8 класс. Вариант 2. 1. Сократите дробь: 2. Представьте в виде дроби: 3. Найдите значение выражения при 4. Упростить выражение: Контрольные работы по алгебре в 8 Вариант 1. 1. Сократите дробь: 2. Представьте в виде дроби: 3. Найдите значение выражения при 4. Упростить выражение: Контрольная работа №1. 8 класс. Вариант 2. 1. Сократите дробь: 2. Представьте в виде дроби: 3. Найдите значение выражения при 4. Упростить выражение: Контрольная работа №2. 8 класс. Рациональные выражения. 1 вариант. 1. Представьте выражение в виде дроби: 3. Докажите, что при всех значениях значение выражения не зависит от . Контрольная работа №2. 8 класс. Рациональные выражения. 2 вариант. 1. Представьте выражение в виде дроби: 3. Докажите, что при всех значениях значение выражения не зависит от . Контрольная работа №2. 8 класс Рациональные выражения. 1 вариант. 1. Представьте выражение в виде дроби: 3. Докажите, что при всех значениях значение выражения не зависит от . Рациональные выражения. 2 вариант. 1. Представьте выражение в виде дроби: 3. Докажите, что при всех значениях значение выражения не зависит от . Контрольная работа №3. 8 класс. 1 вариант. 1. Вычислите: а) б) в) 2. Найдите значение выражения: а) 3. Решить уравнения: а) 4. Упростить выражение: а) 5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число 6. 1. Вычислите: а) б) в) 2. Найдите значение выражения: а) 3. Решить уравнения: а) 4. Упростить выражение: а) 5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число 6. Имеет ли корни уравнение 1. Вычислите: а) б) в) 2. Найдите значение выражения: а) 3. Решить уравнения: а) 4. Упростить выражение: а) 5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число 6. Имеет ли корни уравнение 2 вариант. 1. Вычислите: а) б) в) 2. Найдите значение выражения: а) 3. Решить уравнения: а) 4. Упростить выражение: а) 5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число 6. Имеет ли корни уравнение Контрольная работа № 4. 1. Упростите выражение: 2. Сравните: 3. Сократите дробь: 4. Освободитесь от иррациональности в знаменателе: 5. Докажите, что значение выражения есть число рациональное. 1. Упростите выражение: 2. Сравните: 3. Сократите дробь: 4. Освободитесь от иррациональности в знаменателе: 5. Докажите, что значение выражения есть число рациональное. Контрольная работа № 4. 8 класс. 1. Упростите выражение: 2. Сравните: 3. Сократите дробь: 4. Освободитесь от иррациональности в знаменателе: 5. Докажите, что значение выражения есть число рациональное. 1. Упростите выражение: 2. Сравните: 3. Сократите дробь: 4. Освободитесь от иррациональности в знаменателе: 5. Докажите, что значение выражения есть число рациональное. Контрольная работа №5. Квадратные уравнения. 1 вариант. 1. Решите уравнения: 2. Периметр прямоугольника 20 см. Найдите его стороны, если известно, что площадь прямоугольника 24см². 3. В уравнении один из корней равен -9. Найдите другой корень и коэффициент p. Контрольная работа №5. 8 класс. Квадратные уравнения. 2 вариант. 1. Решите уравнения: 2. Периметр прямоугольника 30 см. Найдите его стороны, если известно, что площадь прямоугольника 36см². 3. В уравнении один из корней равен -7. Найдите другой корень и коэффициент q. Контрольная работа №5. 8 класс. Квадратные уравнения. 1 вариант. 1. Решите уравнения: 2. Периметр прямоугольника 20 см. Найдите его стороны, если известно, что площадь прямоугольника 24см². 3. В уравнении один из корней равен -9. Найдите другой корень и коэффициент p. Контрольная работа №5. Квадратные уравнения. 2 вариант. 1. Решите уравнения: 2. Периметр прямоугольника 30 см. Найдите его стороны, если известно, что площадь прямоугольника 36см². 3. В уравнении один из корней равен -7. Найдите другой корень и коэффициент q. Контрольная работа №6. 8 класс. 1 вариант. 1. Решить уравнение: а) б) 2. Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В? 1. Решить уравнение: а) б) 2. Катер прошел 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему понадобилось бы, если бы он шел 18 км по озеру. 1 вариант. 1. Решить уравнение: а) б) 2. Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В? 1. Решить уравнение: а) б) 2. Катер прошел 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему понадобилось бы, если бы он шел 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч? Контрольная работа №7. 8 класс. 1 вариант. 1. Докажите неравенство: 2. Известно, что . 3. Известно, что . Оцените: 4. Оцените периметр и площадь прямоугольника со сторонами см и см, если известно, что 5. К каждому из чисел 2, 3, 4 и 5 прибавили одно и тоже число . Сравните произведение крайних членов получившейся последовательности с произведением средних членов. 1. Докажите неравенство: 2. Известно, что . Сравните: 3. Известно, что . Оцените: 4. Оцените периметр и площадь прямоугольника со сторонами см и см, если известно, что 5. К каждому из чисел 6, 5, 4 и 3 прибавили одно и тоже число . Сравните произведение крайних членов получившейся последовательности с произведением средних членов. 1. Докажите неравенство: 2. Известно, что . Сравните: 3. Известно, что . Оцените: 4. Оцените периметр и площадь прямоугольника со сторонами см и см, если известно, что 5. 1. Докажите неравенство: 2. Известно, что . Сравните: 3. Известно, что . Оцените: 4. Оцените периметр и площадь прямоугольника со сторонами см и см, если известно, что 5. К каждому из чисел 6, 5, 4 и 3 прибавили одно и тоже число . Сравните произведение крайних членов получившейся последовательности с произведением средних членов. 1 2 3 4 5 6 7 |
Math Placement Policy & Algebra 1 Руководство по завершению для средней и старшей школы
Connecting Waters Math Placement Policy & Algebra 1 Руководство по завершению для средней и старшей школы
Эта политика описывает использование местных и государственных данных, чтобы гарантировать, что все учащиеся 9-12 классов, которые не учатся по математике на уровне своего класса, получают надзор и поддержку от Эффективного педагога (EE) для подготовки и демонстрации знаний по алгебре 1.
Учащиеся, не продемонстрировавшие знаний по стандартам математики 8, должны будут иметь надзор за EE для курсовой работы Pre-Algebra или Algebra 1. Это можно сделать несколькими способами:
- a-g Algebra 1 (CMS или утвержденный поставщик a-g (Apex),
- Интенсивный курс CMS с квалифицированным инструктором по математике (EE) с использованием утвержденной высококачественной учебной программы, соответствующей стандартам, которая была создана для обеспечения дополнительной поддержки.
Каждый из вышеперечисленных вариантов может предложить различный уровень учебной поддержки и темпа, как указано ниже. ES должны тесно сотрудничать со своими учащимися и их семьями, чтобы определить наилучший вариант для каждого учащегося.
Кроме того, учащиеся, работающие выше уровня своего класса (в средних 6-8 классах) для прохождения Алгебры 1, также должны иметь EE Надзор, как указано ниже.
Учащиеся 9-х классов, показавшие уровень владения стандартами для 8-х классов (подтвержденный CAASPP и/или iReady), могут пройти курс алгебры 1 под наблюдением назначенного им ES, используя утвержденную учебную программу, которая соответствует стандартам штата или превосходит их, как указано ниже.
- SB359: (Закон о приеме на работу по математике от 2015 г.): «Успеваемость учащихся по математике важна для подготовки учащихся к поступлению в колледж и их будущей карьере, особенно карьере в области естественных наук, технологий, инженерии и математики (STEM). . Попадание на соответствующие курсы математики имеет решающее значение для ученика в средние и старшие классы. Поступление ученика в 9-й класс на курс математики является важным перекрестком для его или ее будущего успеха в учебе. Неправильное размещение в последовательности математических курсов создает ряд барьеров и приводит к тому, что ученики менее конкурентоспособны при поступлении в колледжи, в том числе при поступлении в Калифорнийский государственный университет и Калифорнийский университет».
- Калифорнийский закон о распределении учащихся по математике от 2015 г. требует, чтобы руководящие советы или органы местных образовательных агентств (LEA), которые обслуживают учащихся, поступающих в девятый класс, и которые еще не сделали этого, приняли «справедливую, объективную и прозрачную политику распределения по математике» до начало 2016-2017 учебного года.

- Систематически принимает во внимание многочисленные объективные показатели успеваемости учащихся;
- Включает как минимум одну контрольную точку в течение первого месяца учебного года, чтобы обеспечить точное зачисление и позволить переоценить индивидуальный прогресс учащегося;
- Требуется ежегодная проверка данных о размещении учеников, чтобы гарантировать, что учащиеся не задерживаются непропорционально на основании их расы, этнической принадлежности, пола или социально-экономического положения;
- Требуется отчет о результатах ежегодного экзамена местного агентства по образованию своему руководящему совету или органу
- Предлагает четкую и своевременную помощь каждому учащемуся и его или ее родителю или законному опекуну, который сомневается в размещении учащегося.
- Калифорнийский закон о распределении учащихся по математике от 2015 г. требует, чтобы руководящие советы или органы местных образовательных агентств (LEA), которые обслуживают учащихся, поступающих в девятый класс, и которые еще не сделали этого, приняли «справедливую, объективную и прозрачную политику распределения по математике» до начало 2016-2017 учебного года.
- AB220: Кроме того, в Законе о собрании 220 говорится: «.
 .. до того, как учащийся получит аттестат об окончании средней школы, учащийся должен пройти по крайней мере один курс или комбинацию двух курсов, необходимых для получения диплома, который соответствует или превышает строгость алгебры I или математики I, что соответствует стандартам содержания, принятым государственным советом. Законопроект будет предусматривать, что учащийся, который завершает курсовую работу, которая соответствует или превышает стандарты содержания для алгебры I, принятые советом штата, считается выполнившим требование об окончании школы. Законопроект также освобождает от обязательных выпускных экзаменов по алгебре I или математике I тех учеников, которые до зачисления в 9-й класс, прошел курс алгебры I или математики I или курсы математики равной строгости, которые соответствуют стандартам содержания, принятым советом штата ».
.. до того, как учащийся получит аттестат об окончании средней школы, учащийся должен пройти по крайней мере один курс или комбинацию двух курсов, необходимых для получения диплома, который соответствует или превышает строгость алгебры I или математики I, что соответствует стандартам содержания, принятым государственным советом. Законопроект будет предусматривать, что учащийся, который завершает курсовую работу, которая соответствует или превышает стандарты содержания для алгебры I, принятые советом штата, считается выполнившим требование об окончании школы. Законопроект также освобождает от обязательных выпускных экзаменов по алгебре I или математике I тех учеников, которые до зачисления в 9-й класс, прошел курс алгебры I или математики I или курсы математики равной строгости, которые соответствуют стандартам содержания, принятым советом штата ».- Навыки алгебры не только необходимы для окончания средней школы, но и являются ключевыми для поступления на курсы высшей математики.
 Поэтому важно, чтобы учащиеся продемонстрировали владение алгеброй, если курс будет пройден в раннем возрасте (до школы). Кроме того, учащиеся, получившие зачет по курсу, должны соответствовать стандартам, указанным выше, или превосходить их.
Поэтому важно, чтобы учащиеся продемонстрировали владение алгеброй, если курс будет пройден в раннем возрасте (до школы). Кроме того, учащиеся, получившие зачет по курсу, должны соответствовать стандартам, указанным выше, или превосходить их. - Департамент образования Калифорнии напоминает нам, что:
- Стандарты алгебры I можно и нужно преподавать всем учащимся, в том числе учащимся с ограниченными возможностями. Этим учащимся должен быть предоставлен доступ к общеобразовательной программе, чтобы вооружить их практическими жизненными навыками, которые им понадобятся для достижения успеха в 21 веке. Они могут быть не в состоянии завершить курс за стандартное время, и им может потребоваться более одного класса для завершения курса обучения. Кроме того, им могут понадобиться практические способы демонстрации навыков и компетенций, например, с помощью манипулятивных средств и с помощью калькуляторов. Им также могут потребоваться дополнительные учебные материалы, отвечающие их потребностям в обучении.
 Тем не менее, важно обеспечить, чтобы Всем учащимся была предоставлена возможность доступа к стандартам общеобразовательной программы.
Тем не менее, важно обеспечить, чтобы Всем учащимся была предоставлена возможность доступа к стандартам общеобразовательной программы. - В прошлом многие учащиеся направлялись в базовый курс математики общего или коррекционного уровня, что ограничивало их возможности пройти Алгебру I, критический курс начального уровня. Чтобы гарантировать, что учащиеся из групп риска пройдут обучение по такому важному курсу, как алгебра I, ES может потребоваться помощь в разработке учебного плана и инструкций, отвечающих потребностям их учащихся.
- Стандарты алгебры I можно и нужно преподавать всем учащимся, в том числе учащимся с ограниченными возможностями. Этим учащимся должен быть предоставлен доступ к общеобразовательной программе, чтобы вооружить их практическими жизненными навыками, которые им понадобятся для достижения успеха в 21 веке. Они могут быть не в состоянии завершить курс за стандартное время, и им может потребоваться более одного класса для завершения курса обучения. Кроме того, им могут понадобиться практические способы демонстрации навыков и компетенций, например, с помощью манипулятивных средств и с помощью калькуляторов. Им также могут потребоваться дополнительные учебные материалы, отвечающие их потребностям в обучении.
- Навыки алгебры не только необходимы для окончания средней школы, но и являются ключевыми для поступления на курсы высшей математики.
- AB705: Кроме того, Закон о собрании 705 – это законопроект, подписанный губернатором 13 октября 2017 года и вступивший в силу 1 января 2018 года. Законопроект требует, чтобы район муниципального колледжа или колледж максимизировал вероятность того, что учащийся завершить курсовую работу на уровне перевода по английскому языку и математике в течение одного года и использовать при распределении учащихся на курсы английского языка и математики один или несколько из следующих параметров: курсовая работа в средней школе, оценки в средней школе и средний балл в средней школе.
 Поскольку на уровне колледжа предлагается меньше коррекционных курсов, еще более важно, чтобы учащиеся заканчивали обучение на этих курсах.
Поскольку на уровне колледжа предлагается меньше коррекционных курсов, еще более важно, чтобы учащиеся заканчивали обучение на этих курсах.
Начиная со средней школы, учащиеся, как правило, выбирают разные пути в своем математическом образовании, при этом продвинутые учащиеся могут по-прежнему пройти Алгебру 1 в средней школе, что направит их на путь к завершению Математического анализа в старшей школе. Ниже приведены лишь некоторые из приемлемых сценариев последовательности курсов по математике в средних и старших классах.
- Имейте в виду, что учащиеся младше среднего школьного возраста получают зачеты только в том случае, если они соответствуют критериям, изложенным в этих правилах: Правила школьного возраста и требования к выпускным экзаменам по алгебре перечислены ниже.
- Учащиеся, окончившие математические курсы уровня алгебры 1 или выше в средних школах ES, должны пройти « Курсы, которые посещают учащиеся, проходящие типовое обследование возраста HS » Несовершеннолетние учащиеся, потерявшие место, будут переведены на соответствующий курс.

Требования к выпускным экзаменам по алгебре будут выполнены учащимися средней школы ТОЛЬКО в том случае, если они:
- Выполнили и сдали экзамен на C- или выше a-g Алгебра 1 с утвержденным экзаменом по математике EE и тестом на готовность к геометрии.
- AWR должны отражать курсовую работу, которую выполняет студент. Если учащийся изучает алгебру, название курса основного соглашения должно быть a-g Algebra, а AWR должны быть выполнены. Кредит средней школы не будет выдан.
- Пройти курс алгебры 1 в средней школе CA, аккредитованной .
- Подтвердить через a-g Алгебра 2.
Примечание. Учащиеся, выполняющие General Algebra 1 в средней школе, не не соответствовали требованиям к выпускному делу, если только они не проверяют алгебру 1 с A-G Алгебра 2.
- . будет рекомендован курс их преподавателем ES и/или математикой 8-го класса после рассмотрения нескольких показателей данных, основанных на некоторых или всех следующих показателях:
- Курс 8 класса и успеваемость учащихся по этому курсу
- Балл по математике CAASPP 8-го класса
- Результаты диагностики I-Ready
- ES также могут проконсультироваться со своим консультантом, специалистом по математике и/или директором по учебной программе и оценке, если это необходимо.
- Диагностическая оценка iReady #1 будет завершена в течение первых 2 недель в школе для всех 9учащиеся й класса. iReady Diagnostic #3 можно использовать, если вернувшиеся восьмиклассники завершили оценку в предыдущем весеннем семестре.
- Для продвинутых учащихся 9-х классов, изучающих курс выше Алгебры 1, будет проведена проверка записей, чтобы обеспечить надлежащее зачисление в углубленную курсовую работу; учащиеся, не сдавшие соответствующие тесты на готовность, будут сдавать их в течение первого учебного месяца.

- ES учащихся 9-х классов определят рекомендацию по зачислению на основе вышеупомянутых критериев, а ES рассмотрят рекомендацию по зачислению с родителями во время первого собрания по учету успеваемости.
- Родители могут оспорить рекомендацию школы, попросив свой ES скорректировать размещение на курсе по своему усмотрению.
- Группа данных CWCS будет ежегодно дезагрегировать данные о зачислении учащихся 9-х классов по математике и предоставлять результаты администрации.
- Данные будут дезагрегированы по признаку расы, этнической принадлежности, пола и социально-экономического положения.
- Годовой отчет будет представлен Правлению CWCS.
Требования к выпускным экзаменам по алгебре по алгебре 1 Окончены в средней школе:
Требования к выпускным экзаменам по алгебре будут выполнены учащимися средней школы ТОЛЬКО в том случае, если они:
- 2 и 3 Учащиеся, которые не набрали по крайней мере 3 балла «Соответствует стандартам» или «4 балла выше стандарта» в CAASPP для 8-го класса или на уровне класса по диагностике I-Ready, могут НЕ сдавать общую алгебру 1) или интенсивную алгебру 1 с CWCS с использованием соответствующий учебный план, как указано ниже.
- Пройти курс алгебры 1 в аккредитованной средней школе
- Пройти курс алгебры 1 в общественном колледже или у одобренного онлайн-провайдера a-g
- Завершить и сдать экзамен по алгебре a-g 2 (CWCS или другая аккредитованная средняя школа)

- Примечание: любые курсы, на которые не распространяется вышеуказанная политика, должны быть одобрены Департаментом методического обучения (т. е.: кредит от школ за пределами США)
В соответствии с уставом школы учащиеся CWCS должны использовать учебную программу, которая позволит учащимся соответствовать требованиям Основных общегосударственных стандартов. Все стандарты должны быть включены в выбранную учебную программу. Все учащиеся относятся к первому уровню пирамиды RtI. Уровень 1 предлагает учебные стратегии, основанные на исследованиях, и должен включать сильную основную учебную программу. Если учащиеся не используют учебную программу, согласованную со стандартами, они рискуют получить «пробелы» в своем обучении, подвергая их риску дальнейшего отставания от своих сверстников. Все учащиеся, получившие кредит по алгебре 1, должны выбрать один из следующих вариантов ниже, чтобы обеспечить соответствие требованиям AB220.
Если учащиеся не используют учебную программу, согласованную со стандартами, они рискуют получить «пробелы» в своем обучении, подвергая их риску дальнейшего отставания от своих сверстников. Все учащиеся, получившие кредит по алгебре 1, должны выбрать один из следующих вариантов ниже, чтобы обеспечить соответствие требованиям AB220.
Учащиеся, получившие кредит a-g по алгебре 1 или a-g по математике 1, должны использовать утвержденный учебник в CWCS Course Outline.
Варианты курса «Общая алгебра 1» (доступны только для учащихся 9-го класса на уровне или выше):- Принятая государством программа учебника «Алгебра 1» или «Математика 1» или
- Согласованная со стандартами программа учебника по алгебре 1 или математике 1 с опубликованным объемом и согласованием последовательности с Калифорнийскими общими базовыми стандартами; или
- Учебная программа по алгебре 1 или математике 1 с одним из следующих соответствующих заполненных понятий и навыков рассматривает дополнительные рабочие тетради.
 ES должен будет подтвердить завершение следующего варианта рабочей книги: .
ES должен будет подтвердить завершение следующего варианта рабочей книги: .
- Базовая алгебра 1 от Houghton Mifflin
- Common Core Coach, алгебра I от Triumph Learning
- Алгебра 1. Общая основная практика и решение задач, Прентис Холл
Примечание. Дополнительная рабочая тетрадь «Концепции и навыки» должна быть заполнена полностью, если специалист по математике не получил одобрение с согласованием. ES должны собирать по крайней мере 1 образец в каждый период обучения из вышеупомянутого стандартного дополнения после его завершения для документации и хранить в личном деле учащегося.
- Другие варианты учебных программ могут быть представлены специалисту по математике для рассмотрения и возможного утверждения. Материалы должны включать полное оглавление, объем и последовательность, а также минимум 3 примера уроков из учебника. Важно помнить, что многие популярные учебные программы для отстающих учащихся НЕ соответствуют или не превосходят стандарты содержания, если они используются в качестве отдельной основной учебной программы.
 Сюда входят такие учебные программы, как Acellus, AGS Algebra, Teaching Textbooks Algebra и Math-U-See Algebra, которые не соответствуют текущим стандартам контента CA Algebra 1.
Сюда входят такие учебные программы, как Acellus, AGS Algebra, Teaching Textbooks Algebra и Math-U-See Algebra, которые не соответствуют текущим стандартам контента CA Algebra 1.
Интенсивная алгебра 1 Варианты (доступны для учащихся младшего уровня, которым требуется дополнительная поддержка):
- Интенсивная алгебра CMS 1: Это двухгодичный курс, который проводится три дня в неделю. Будет предоставлена обширная поддержка и поддержка, а также дифференцированные задания и оценки для студентов.
- APEX CTV: Учащиеся могут пройти годичный или двухлетний курс Apex Algebra 1.
Дополнительное руководство
Дополнительные рекомендации по обеспечению всеобщего доступа к обучению математике см. в Основах математики для государственных школ Калифорнии, от детского сада до двенадцатого класса.
Настройка уравнений | Алгебраические уравнения
w3.org/1999/xhtml»> В этой главе вы узнаете чтобы найти числа, которые делают некоторые утверждения верными. Заявление относительно неизвестного числа называется уравнением. Когда мы работаем, чтобы выяснить, какое число сделает уравнение верным, мы говорим, что мы решить уравнение. Число, которое делает уравнение верным, равно называется решением уравнения. 9х = 8\]\(х + 3 = 11\) верно если \(х=8\), но ложно, если \(x = 3\).
Когда мы ищем число или числа, которые делают уравнение верным, мы говорим, что решим уравнение . Например, \(x = 4\) является решением уравнения \(2x + 8\), потому что оно делает \(2x +8\) истинным. (Проверьте: \(2 \times 4 = 8\)
Ищем числа, чтобы сделать утверждение верным
- Следующие утверждения
правда или ложь? Обосновать ответ.
93 = 8\), если \(х = -2\)
- \(3x = -6\), если \(x = -3\)
- \(3x = 1\), если \(x = 1\)
- \(6x + 5 = 47\), если \(x = 7\)
 Показывать
ваше рассуждение.
Показывать
ваше рассуждение.- Число, умноженное на 10, равно 80.
- Прибавьте к числу 83 и получите 100.
- Разделите число на 5 и получите 4.
- Умножьте число на 4 и получите 20.
- Дважды число равно 100.
- Число, возведенное в степень 5, равно 32.
- Число, возведенное в степень 4, равно -81.
- Пятнадцать раз число 90.
- 93 добавляется к числу -3.
- Половина числа равна 15.
Пример: \(4 +x = 23\). Четыре плюс число равно двадцати трем. Номер 19.
- \(8x = 72\)
\( \frac{2x}{5} = 2 \)
\( 2x+ 5 = 21\)
\(12 + 9x = 30\)
\(30 — 2x = 40\)
\(5x + 4 = 3x+ 10\)
Решение уравнений методом проверки
Ответ на виду
- Под таблицей приведены семь уравнений. Используйте таблицу, чтобы
выяснить, для какого из заданных значений \(х\) будет
верно, что левая часть уравнения равна
справа.

Вы можете прочитать решения уравнение из таблицы.
\(х\)
-3
-2
-1
0
1
2
3
4
\(2x + 3\)
-3
-1
1
3
5
7
9
11
\(х + 4\)
1
2
3
4
5
6
7
8
\(9 -х\)
12
11
10
9
8
7
6
5
\(3x -2\)
-11
-8
-5
-2
1
4
7
10
\(10x -7\)
-37
-27
-17
-7
3
13
23
33
\(5x+3\)
-12
-7
-2
3
8
13
18
23
\(10 — 3x\)
19
16
13
10
7
4
1
-2
- \(2x + 3 = 5x + 3\)
- \(5х + 3 = 9 — х\)
- \(2x + 3 = x+4\)
- \(10x -7 = 5x + 3\)
- \(3x -2 = x+4\)
- \(9 -х = 2х + 3\)
- \(10 -3x = 3x — 2\)
- \(2x + 3 = 5x + 3\)
Два или более уравнений могут иметь одно и то же решение. Например, \(5x = 10\) и \(x + 2 = 4\) имеют одно и то же решение; \(x = 2\) является решением обоих уравнений.
Например, \(5x = 10\) и \(x + 2 = 4\) имеют одно и то же решение; \(x = 2\) является решением обоих уравнений.
Два уравнения называются эквивалентными , если они имеют одинаковые решение.
- Какое из уравнений в
вопрос 1 имеют те же решения? Объяснять.
- Заполните приведенную ниже таблицу. затем
ответьте на следующие вопросы.
Вы также можете выполнить поиск по сужение возможного решения уравнения.
\(х\)
0
5
10
15
20
25
30
35
40
\(2x + 3\)
\(3x -10\)
- Можете ли вы найти решение
для \(2x + 3 = 3x — 10\) в таблице?
- Что происходит со значениями
из \(2x + 3\) и \(3x — 10\) при увеличении \(x\)? Делать
они становятся больше или меньше?
- Есть ли точка, в которой значение
\(3x — 10\) становится больше или меньше значения
\(2x + 3\) при увеличении значения \(x\)? Если так,
между какими \(x\)-значениями это происходит?
Эта точка, где два выражения равны, называется безубыточностью пункт .

- Теперь, когда вы сузили круг поиска
возможное решение может быть, попробуйте другие возможные значения для
\(x\), пока не найдете
для какого значения \(x\) утверждение \(2x + 3 = 3x — 10\) верно.
«Поиск» решения уравнение с помощью таблиц или путем сужения до возможное решение называется решение от осмотр .
- Можете ли вы найти решение
для \(2x + 3 = 3x — 10\) в таблице?
Другие примеры
Поиск и проверка решений
- Какое решение для
уравнения ниже?
- \(х — 3 = 4\)
- \(х + 2 = 9\)
- \(3x = 21\)
- \(3x + 1 = 22\)
- \(х — 3 = 4\)
Когда определенный номер
решения уравнения мы говорим, что число удовлетворяет уравнению. Например, \(х=4\)
удовлетворяет уравнению \(3x=12\), потому что \(3 \times 4 =
12\).
Например, \(х=4\)
удовлетворяет уравнению \(3x=12\), потому что \(3 \times 4 =
12\).
- Выберите номер в скобках, который
удовлетворяет уравнению. Объяснить ваш выбор.
- \(12x = 84\) {5; 7; 10; 12}
\( \frac{84}{x} = 12\) {-7; 0; 7; 10}
\(48 = 8k + 8\) {-5; 0; 5; 10}
\(19 — 8m = 3\) {-2; -1; 0; 1; 2}
\(20 = 6у — 4\) {3; 4; 5; 6}
92 = 9\) {1; 2; 3; 4}
- \(12x = 84\) {5; 7; 10; 12}
- \(м + 8 = 100\)
- \( 80 = х + 60 \)
- \(26 — к = 0 \)
- \(105 \умножить на 0\)
- \(к\умножить на 10 = 10\)
- \(5x = 100\)
- \( \frac{15}{t} = 5 \)
- \( 3 = \frac{t}{5} \)
 Проверить свои ответы.
Проверить свои ответы.- \(12х+14=50\)
- \(100 = 15м + 25\)
- \( \frac{100}{x} =20\)
- \( 7м + 5 = 40\)
- \(2x + 8 = 10\)
- \(3x + 10 = 31\)
- \(-1 + 2x = -11\)
- \(2 + \frac{x}{7} = 5\)
- \(100 = 64 + 9x\)
- \( \frac{2x}{6}= 4\)
Использование материалов для учителей математики IM 6–12 для расширения доступа к математике на уровне класса
Ванесса Серрахоглу и Даниэль Сиболд, сертифицированные инструкторы IM® Как преподаватели могут действовать в соответствии с этими убеждениями при преподавании и обучении с помощью IM 6–12 Math™ для создания учебных сообществ и опыта, в котором каждый учащийся знает, использует и получает удовольствие от математики? Illustrative Mathematics (IM) считает, что каждый учащийся заслуживает доступа к математике на уровне своего класса. Этот пост является первым в серии из трех, в которых мы стремимся помочь учителям Мы с нетерпением ждем от вас информации о том, что перекликается с вашим собственным опытом и как эта серия может помочь вам в дальнейшем обучении. Каждый урок IM начинается с того, что приглашает учащихся на уроки математики. Затем упражнения позволяют учащимся глубоко погрузиться в концепции. Наконец, учитель сотрудничает со студентами, чтобы закрепить и применить обучение в рамках синтеза деятельности, синтеза урока и заминки. Каждый учащийся может изучать математику на уровне своего класса при тщательном и целенаправленном планировании. Как мы можем улучшить доступ учащихся к математическому содержанию на каждом уроке? Какие учебные возможности уже записаны в материалах для учителей? Давайте проанализируем урок, чтобы выяснить это. Сбалансированное уравнение (8 класс, Раздел 4: Линейные уравнения и линейные системы) направлен на достижение следующих целей обучения: Эти цели направлены на достижение 8.EE.C: Анализ и решение линейных уравнений и пар одновременных линейных уравнений. Как учащиеся должны достичь этих целей? Один из способов узнать, как учащиеся достигают учебных целей урока, — это изучить заминку. Учащиеся могут: Итак, как урок настраивает учащихся на успех в заминке и направляет их к достижению целей обучения? Все начинается с приглашения учащихся на урок математики с упражнения 2. Что вы заметили? Что вам интересно? [из 8 класса, Раздел 4, Урок 2: Упражнение 2.1] Эта визуальная основа для проверки равновесия может улучшить доступ к более абстрактным представлениям (диаграммы вешалок, затем уравнения) позже в этом уроке и разделе. Во время этой разминки и на протяжении всего урока учащиеся будут использовать 3 когнитивные функции — концептуальную обработку, визуально-пространственную обработку и речь — для достижения целей обучения. Например, они могут полагаться на концептуальную обработку Почему это важно? Существует восемь способов мышления, называемых когнитивными функциями, которые, как было установлено, являются неотъемлемой частью изучения математики. Бродески и др. (2002). Инструментарий стратегий доступности для математики. Центр развития образования. Когда мы даем нашим ученикам математическую задачу, мы просим их думать одним или несколькими из этих способов. Когда когнитивные функции, задействованные в задании, соответствуют сильным сторонам учащихся, они могут с большей готовностью и успешно выполнять задание. С другой стороны, когда одна или несколько когнитивных функций представляют собой проблему для учащихся, учащиеся могут столкнуться с препятствиями в обучении и выполнении задания. В этом случае учителя могут использовать учебные возможности и стратегии, предлагаемые на каждом уроке IM 6–12 Math™, чтобы предоставить альтернативные способы доступа к задаче, не подрывая ее когнитивных требований. (Расширение доступа учащихся к математике является одним из ключевых обязательств Руководства по универсальному дизайну для обучения, изложенного на веб-сайте cast. После разминки «Уведомление и удивление» учащиеся приступают к Упражнению 2.2: Подвешивание кубиков. Цель этого задания состоит в том, чтобы учащиеся поняли и объяснили, почему они могут складывать или вычитать выражения из каждой части уравнения и при этом сохранять равенство, даже если значения этих выражений неизвестны. [из 8 класса, Раздел 4, Урок 2: Упражнение 2.2] В следующем упражнении, Упражнении 2.3: Дополнительные подвесные блоки, учащиеся имеют возможность решить еще две задачи с вешалками и написать уравнения для каждой вешалки. [из 8 класса, Раздел 4, Урок 2: Упражнение 2.3] Мы снова можем заметить, что когнитивные функции обработки понятий и визуально-пространственной обработки задействованы. Что это может означать для студентов? Если концептуальная и визуально-пространственная обработка данных окажутся сильными познавательными силами учащихся, они могут с радостью выполнять эту задачу, когда возятся с важными математическими понятиями. Давайте сосредоточимся на вешалке А. Как мы можем упростить ее, чтобы учащиеся занимались одним и тем же обучением? Есть ли способ упростить его, чтобы ученики также получали тот же ответ, что и их одноклассники? Основываясь на предложенной стратегии обучения, мы могли бы упростить вешалку А несколькими способами, как показано ниже: Какой из этих вариантов может расширить доступ учащихся к математике, привлечь внимание к когнитивным функциям в игре и достичь целей обучения? урока? Давайте вспомним вторую учебную цель урока: Поймите, что добавление и удаление одинаковых предметов с каждой стороны диаграммы вешалки или умножение и деление предметов с каждой стороны вешалки на одинаковое количество — это движения, которые удерживают вешалку в равновесии. Почему бы не использовать упрощенную вешалку для всех? Оригинальная вешалка предвещает будущие уроки, на которых учащиеся добавляют или вычитают константы (кружки) и переменные (квадраты) из обеих частей уравнения. Использование упрощенной вешалки может соответствовать сегодняшним целям, но это может повлиять на общий прогресс обучения по устройству. Необходимо проявлять большую осторожность при создании приспособлений для расширения доступа. Учителя руководствуются этим убеждением, когда мы проводим обучение с помощью IM 6–12 Math™, потому что IM построила учебную программу непосредственно на основе стандартов. IM также считает, что каждый студент может понять и решить проблемы, а также имеет ценный и блестящий опыт и идеи. Один из способов, которым учителя могут действовать в соответствии с этими убеждениями, — это использовать учебные возможности и стратегии, предлагаемые на каждом уроке.
Учителя руководствуются этим убеждением, когда мы проводим обучение с помощью IM 6–12 Math™, потому что IM построила учебную программу непосредственно на основе стандартов. IM также считает, что каждый студент может понять и решить проблемы, а также имеет ценный и блестящий опыт и идеи. Один из способов, которым учителя могут действовать в соответствии с этими убеждениями, — это использовать учебные возможности и стратегии, предлагаемые на каждом уроке.

 1: разминка «Висячие носки». Эта разминка предназначена для того, чтобы активизировать мышление учащихся о балансе и равенстве.
1: разминка «Висячие носки». Эта разминка предназначена для того, чтобы активизировать мышление учащихся о балансе и равенстве. Разминка вызывает троих из восьми.
Разминка вызывает троих из восьми. org.)
org.) С другой стороны, если эти когнитивные функции представляют собой проблему для учащихся, у нас, учителей, есть возможность расширить доступ учащихся к концептуальной и визуально-пространственной обработке, чтобы они тоже могли испытать радость и уверенность при работе с математикой задачи. После прочтения встроенной учебной поддержки нам нужно принять некоторые учебные решения. Рассмотрим некоторые из этих вариантов.
С другой стороны, если эти когнитивные функции представляют собой проблему для учащихся, у нас, учителей, есть возможность расширить доступ учащихся к концептуальной и визуально-пространственной обработке, чтобы они тоже могли испытать радость и уверенность при работе с математикой задачи. После прочтения встроенной учебной поддержки нам нужно принять некоторые учебные решения. Рассмотрим некоторые из этих вариантов. Если мы выберем вариант 1, мы лишим учащихся возможности возиться с добавлением или удалением одинаковых предметов с вешалки. Итак, как повлияет на обучение, если мы выберем варианты 2 или 3? Мы признаем, что оба варианта 2 и 3 позволяют учащимся возиться с добавлением или удалением одинаковых предметов с вешалки, давая учащимся возможность укрепить свою способность усваивать понимание. При ближайшем рассмотрении мы видим, что вариант 3 дает то же значение для синего квадрата, что и коллеги, работающие с исходной вешалкой. Вариант 3 будет способствовать развитию чувства общности в классе.
Если мы выберем вариант 1, мы лишим учащихся возможности возиться с добавлением или удалением одинаковых предметов с вешалки. Итак, как повлияет на обучение, если мы выберем варианты 2 или 3? Мы признаем, что оба варианта 2 и 3 позволяют учащимся возиться с добавлением или удалением одинаковых предметов с вешалки, давая учащимся возможность укрепить свою способность усваивать понимание. При ближайшем рассмотрении мы видим, что вариант 3 дает то же значение для синего квадрата, что и коллеги, работающие с исходной вешалкой. Вариант 3 будет способствовать развитию чувства общности в классе.




 Имеет ли корни уравнение
Имеет ли корни уравнение  8 класс.
8 класс. 8 класс.
8 класс. 8 класс.
8 класс. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч?
Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч? Сравните:
Сравните: К каждому из чисел 2, 3, 4 и 5 прибавили одно и тоже число . Сравните произведение крайних членов получившейся последовательности с произведением средних членов.
К каждому из чисел 2, 3, 4 и 5 прибавили одно и тоже число . Сравните произведение крайних членов получившейся последовательности с произведением средних членов.
 .. до того, как учащийся получит аттестат об окончании средней школы, учащийся должен пройти по крайней мере один курс или комбинацию двух курсов, необходимых для получения диплома, который соответствует или превышает строгость алгебры I или математики I, что соответствует стандартам содержания, принятым государственным советом. Законопроект будет предусматривать, что учащийся, который завершает курсовую работу, которая соответствует или превышает стандарты содержания для алгебры I, принятые советом штата, считается выполнившим требование об окончании школы. Законопроект также освобождает от обязательных выпускных экзаменов по алгебре I или математике I тех учеников, которые до зачисления в 9-й класс, прошел курс алгебры I или математики I или курсы математики равной строгости, которые соответствуют стандартам содержания, принятым советом штата ».
.. до того, как учащийся получит аттестат об окончании средней школы, учащийся должен пройти по крайней мере один курс или комбинацию двух курсов, необходимых для получения диплома, который соответствует или превышает строгость алгебры I или математики I, что соответствует стандартам содержания, принятым государственным советом. Законопроект будет предусматривать, что учащийся, который завершает курсовую работу, которая соответствует или превышает стандарты содержания для алгебры I, принятые советом штата, считается выполнившим требование об окончании школы. Законопроект также освобождает от обязательных выпускных экзаменов по алгебре I или математике I тех учеников, которые до зачисления в 9-й класс, прошел курс алгебры I или математики I или курсы математики равной строгости, которые соответствуют стандартам содержания, принятым советом штата ». Поэтому важно, чтобы учащиеся продемонстрировали владение алгеброй, если курс будет пройден в раннем возрасте (до школы). Кроме того, учащиеся, получившие зачет по курсу, должны соответствовать стандартам, указанным выше, или превосходить их.
Поэтому важно, чтобы учащиеся продемонстрировали владение алгеброй, если курс будет пройден в раннем возрасте (до школы). Кроме того, учащиеся, получившие зачет по курсу, должны соответствовать стандартам, указанным выше, или превосходить их. Тем не менее, важно обеспечить, чтобы Всем учащимся была предоставлена возможность доступа к стандартам общеобразовательной программы.
Тем не менее, важно обеспечить, чтобы Всем учащимся была предоставлена возможность доступа к стандартам общеобразовательной программы. Поскольку на уровне колледжа предлагается меньше коррекционных курсов, еще более важно, чтобы учащиеся заканчивали обучение на этих курсах.
Поскольку на уровне колледжа предлагается меньше коррекционных курсов, еще более важно, чтобы учащиеся заканчивали обучение на этих курсах.

 ES должен будет подтвердить завершение следующего варианта рабочей книги:
ES должен будет подтвердить завершение следующего варианта рабочей книги: Сюда входят такие учебные программы, как Acellus, AGS Algebra, Teaching Textbooks Algebra и Math-U-See Algebra, которые не соответствуют текущим стандартам контента CA Algebra 1.
Сюда входят такие учебные программы, как Acellus, AGS Algebra, Teaching Textbooks Algebra и Math-U-See Algebra, которые не соответствуют текущим стандартам контента CA Algebra 1. 
