Арифметический способ решения задач на смеси и сплавы. Алгебра. 8-й класс
Задачи, которые мы будем решать, относятся к традиционным задачам математики. Они охватывают большой круг ситуаций: смешение товаров разной цены, жидкостей с различным содержанием соли, кислот разной концентрации, сплавление металлов с различным содержанием некоторого металла. Когда-то они имели исключительно практическое значение. В настоящее время эти задачи часто встречаются в тестах на выпускных экзаменах и на вступительных экзаменах в вузы.
Мы рассмотрим задачи на смешение, которые можно решить не только алгебраически, то есть с помощью уравнения, но и арифметическим способом.
Для успешной работы нам понадобится повторить основные понятия этой темы.
Ход урока
I. Фронтальная работа с классом.
1. Сформулируйте определение концентрации.
(Слайд 1)
(Концентрация вещества в смеси – это часть, которую составляет масса вещества в смеси от массы смеси) Нахождение части от целого.
Концентрация вещества может быть указана и числом и %.
2. Объясните значение высказываний:
(Слайд 2)
а) Концентрация раствора 3 %;
(В 100 г раствора содержится 3 г вещества).
в) Молоко имеет 1,5 % жирности;
(В100 г молока содержится 1,5 г жира).
с) золотое кольцо имеет 583 пробу?
(В1 г кольца содержит 583 миллиграмма золота).
Сколько сахара содержится в 200 г 10%- го сахарного сиропа?
Теперь давайте попробуем решить устно несколько задач.
3. К одной части сахара прибавили 4 части воды. Какова концентрация полученного раствора?
(1: 5 ·100 = 20 %)
(Слайд 3)
4. Килограмм соли растворили в 9 л воды. Какова концентрация раствора?
(1 : 10 ·100 = 10%)
(Слайд 4)
II. Решение задач
Конечно, вы понимаете, что не все задачи можно решить устно. Следующую задачу мы решим с вами с помощью уравнения.
Следующую задачу мы решим с вами с помощью уравнения.
№1. В каких пропорциях нужно смешать раствор 50 % и 70 % кислоты, чтобы получить раствор 65 % кислоты?
(Слайд 5)
Для решения задачи я попрошу вас заполнить таблицу, которая находится у вас на столе.
|
Концентрация |
Масса раствора ( г ) |
Масса кислоты ( г ) |
I раствор |
|
|
|
IIраствор |
|
|
|
смесь |
|
|
|
(Слайд 6)
Заполняем 1-й столбик. Здесь мы указываем концентрацию растворов.
Здесь мы указываем концентрацию растворов.
Заполняем 2-й столбик. Здесь мы указываем массу каждого раствора. Предположим, что первого раствора нужно взять х г, а второго у г. Считаем, что при смешении нет потерь массы, то есть масса смеси равна сумме масс смешиваемых растворов.
Тогда масса смеси будет (х + у) г.
Теперь заполним 3-й столбик. Найдем количество чистой кислоты в 1-ом растворе. Это 0,5х г, во втором растворе 0,7у г, а в смеси будет 0,65(х + у) г кислоты.
По условию задачи составим и решим уравнение.
(Слайд 7)
0,65 (х + у) = 0,5 х + 0,7 у,
65 х – 50 х = 70 у – 65 у,
15 х = 5 у,
3 х = 1 у,
х : у = 1 : 3.
Нужно взять: 1 часть раствора 50% кислоты и 3 части раствора 70% кислоты
Ответ: 50% раствора кислоты -1 часть, 70% раствора кислоты — 3 части.
А теперь я хочу предложить вам схему решения этой задачи арифметическим методом, который позволяет решить ее практически устно. Запишем концентрацию каждого раствора кислоты и концентрацию смеси так:
Вычислим, на сколько концентрация первого раствора кислоты меньше, чем концентрация смеси и на сколько концентрация второго раствора кислоты больше, чем концентрация смеси и запишем результат по линиям:
(Слайд 8)
Таким образом, 5 частей нужно взять 50% раствора кислоты и 15 частей 70% раствора кислоты, то есть отношение взятых частей .
Вовсе не случайно в старые времена отношение масс смешиваемых вещей находили таким образом. Но вряд ли все ученики, получавшие правильные ответы описанным способом, понимали тогда смысл выполняемых действий.
Докажем справедливость этого способа.
В каких пропорциях нужно смешать растворы а % и b % кислот, чтобы получить раствор с % кислоты?
Заполним вторую таблицу.
(Слайд 9)
|
|
Концентрация |
Масса раствора (г) |
Масса кислоты (г) |
I раствор |
|
|
|
II раствор |
|
|
|
смесь |
|
|
|
Заполняем 1-й столбик. Здесь мы указываем концентрацию растворов.
Здесь мы указываем концентрацию растворов.
Заполняем 2-й столбик. Здесь мы указываем массу каждого раствора. Предположим, что первого раствора нужно взять х г, а второго у г. Считаем, что при смешении нет потерь массы, то есть масса смеси равна сумме масс смешиваемых растворов.
Тогда масса смеси будет (х + у) г.
Теперь заполним 3-й столбик. Найдем количество чистой кислоты в 1-м растворе. Это 0,01·ах г, во втором растворе 0,01·bу г, а в смеси будет 0,01·c(х + у) г кислоты.
Составим и решим уравнение
(Слайд 10)
0,01·c(х + у) = 0,01·ах + 0,01·bу,
cx +cy = ax + by
х(с – а) = у(b – c),
Заполним схему, учитывая, что а < c < b.
Теперь понятно, почему эта схема давала правильные результаты.
Давайте применим этот способ для решения задач.
№2. В каких пропорциях нужно сплавить золото 375 пробы с золотом 750 пробы, чтобы получить золото 500 пробы?
(Слайд 11)
Итак составляем схему.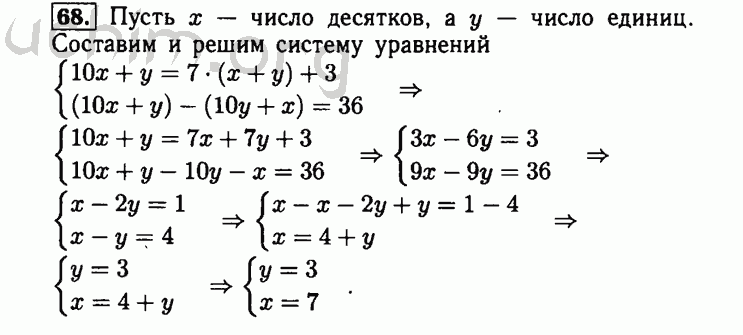
(Слайд 12)
Чтобы получить золото 500 пробы нужно взять: 2 части золота 375 пробы и 1 часть золота750 пробы.
Решим следующую задачу.
№3. Морская вода содержит 5 % соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5 %?
(Слайд 13)
(Слайд 14)
Нужно взять 7 частей пресной воды и 3 части морской воды. По условию нам известно, что морской воды 30 кг и это 3 части нового раствора. Значит на одну часть приходится 10 кг. Следовательно 7частей пресной воды – это 70 кг.
Ответ: нужно добавить 70 кг пресной воды.
А теперь я попрошу вас составить задачу на смешение и решить ее алгебраическим способом. (Самостоятельная работа). Какие это могут быть задачи? На смешение товаров разной цены, жидкостей с различным содержанием соли, кислот разной концентрации, сплавление металлов с различным содержанием некоторого металла.
Подведем итог урока. Сегодня мы познакомились с алгебраическим способом решения задач на смешение. Конечно, не все задачи можно решить этим способом, но я думаю, что вам интересно было познакомиться с ним. Дома еще раз осмыслить способ решения и я думаю, что на уроках в 9 классе при подготовке к итоговой аттестации вы успешно примените этот способ.
Онлайн-олимпиада Фоксфорда для школьников 1-11 классов
с 1 ноября по 1 декабря
Испытайте свои силы перед ВсОШ и получите бонусы от вузов-партнёров
УчаствоватьЯ учитель
Что вас ждёт
второй уровень можно проходить даже тем, кто не участвовал в первом
задачки как на ВсОШ
Проверьте свои силы на заданиях уровня всероссийских и перечневых олимпиад – узнайте, насколько вы круты!
призы и подарки
Участвуйте в розыгрыше набора мерча от «Фоксфорда». Получайте грамоты, дипломы и подарки от «ЛитРеса».
онлайн-рейтинг
Участвуйте в личном и командном зачёте: узнайте, какое место вы и ваша школа занимаете в нашей олимпиадной таблице.
Как устроена наша олимпиада
В зависимости от предмета и класса у вас будет от 1 до 3,5 часов на решение заданий.
русский язык
математика
информатика
биология
Физика
английский язык
Базовый
1 уровень
с 21 сентября по 21 октября
проверьте свою смекалку на прочность — убедитесь, что олимпиады не только для гениев
завершён
Продвинутый
2 уровень
с 1 ноября по 1 декабря
бросьте вызов своим знаниям — с заданиями от составителей всероссийских и вузовских олимпиад
Участвовать
идёт сейчас
Призы и подарки
всем участникам
- скидки на учёбу в «Фоксфорде»
- электронная книга от «ЛитРес»
- розыгрыш 10 наборов мерча от нашей школы
победителям
- именной диплом
- бесплатный годовой курс «Фоксфорда» на выбор
- бонусы от вузов-партнёров
учителям
- сертификат организатора
- розыгрыш MacBook
- бесплатный курс повышения квалификации на выбор
Участвовать
Бонусы от партнёров
Зачисление на заключительный этап олимпиады
«Миссия выполнима.
 Твое призвание — финансист!»
Твое призвание — финансист!»i
Кто претендует
Ученики 9-11 классов — победители и призёры 2 уровня олимпиады «Фоксфорда»
По предметам
- математика
- информатика
- английский язык
Зачисление на заключительный этап олимпиады
«Политехническая олимпиада»
i
Кто претендует
Ученики 9-11 классов — победители и призёры 2 уровня олимпиады «Фоксфорда»
По предметам
- математика
- информатика
- физика
Баллы в компетенциях конкурса цифровых портфолио «Талант НТО»
«Программирование на Python» и «Программирование на C/C++»
i
Кто претендует
Ученики 8-11 классов — победители и призёры 1 и 2 уровня олимпиады «Фоксфорда»
По предметам
- математика
- информатика
онлайн-школа «фоксфорд»
Поможем усвоить все правила, теоремы, законы на практике — и подготовиться к олимпиадам любого уровня!
базовые курсы
освежите свои знания по школьным предметам, разберите темы, которые не поняли на уроках, – и оценки в школе станут выше!
Скопируйте и примените в корзине
Выбрать курсы
профильные программы
начните изучать любимые предметы углублённо, разберите темы, которых нет в школьной программе, и подготовьтесь к олимпиадам любой сложности
Скопируйте и примените в корзине
Выбрать курсы
второй уровень олимпиады завершится через
11
часов
5
минут
Класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
ПредметРусскийМатематикаБиологияФизикаИнформатикаАнглийский язык
Ой! Что-то пошло не так. Попробуйте еще раз
Попробуйте еще раз
Готово!
Вы — участник олимпиады
Мы сообщим вам условия розыгрыша призов и напомним о старте 1 и 2 уровня по почте или телефону, который вы указали
Правила проведения олимпиады
Расскажите про олимпиаду друзьям
Решения NCERT для класса 8 по математике Глава 9 Алгебраические выражения и тождества
- Математика для класса 8 Алгебраические выражения и тождества Упражнение 9.1
- Класс 8. Математические алгебраические выражения и тождества. Упражнение 9.2
- Класс 8 Математические алгебраические выражения и тождества Упражнение 9.3
- Класс 8 Математические алгебраические выражения и тождества Упражнение 9.4
- Класс 8. Математические алгебраические выражения и тождества. Упражнение 9.5
- Алгебраические выражения и тождества Класс 8 Дополнительные вопросы
Решения NCERT для класса 8 по математике Глава 9 Алгебраические выражения и тождества Упражнение 9. 1
1
Упр. 9.1 Класс 8 по математике Вопрос 1.
Определите термины и их коэффициенты для каждого из следующих выражений.
(I) 5xyz 2 — 3ZY
(II) 1 + x + x 2
(III) 4x 2 Y 2 — 4x 2 Y 2 Z 2 + Z 3 + Z 3 + Z 3 + + Z 3 2 + Z 3 2 Y 2 . 2
(iv) 3 – pq + qr – rp
(v) \(\frac { x}{ 2 }\) + \(\frac { y }{ 2 }\) – xy
(vi) 0.3a – 0.6ab + 0.5b
Решение:
Упр. 9.1 Класс 8 Математика Вопрос 2.
Классифицируйте следующие многочлены как одночлены, двучлены и трехчлены. Какие многочлены не подходят ни к одной из этих трех категорий?
х + у, 1000, х + х 2 + х 3 + х 4 , 7 + у + 5х, 2у – 3у 2 , 2у – 3у 2 90 52 3 90 + 4у – 4y + 3xy, 4z – 15z 2 , ab + bc + cd + da, pqr, p 2 q + pq 2 , 2p + 2q
Решение:
Упр. 9.1 Класс 8 по математике Вопрос 3.
9.1 Класс 8 по математике Вопрос 3.
Добавьте следующее:
(i) ab – bc, bc – ca, ca – ab
(ii) a – b + ab , b – c + bc, c – a + ac
(iii) 2p 2 q 2 – 3pq + 4, 5 + 7pq – 3p 2 q 2
(iv) l
2 +
- 3 2 2 q 2
- Решения NCERT для класса 8 по математике
- Решения NCERT для науки класса 8
- Решения NCERT для социальных наук класса 8
- Решения NCERT для английского языка 8 класса
- Решения NCERT для английского Honeydew класса 8
- Решения NCERT для английского языка 8 класса It So Happened
- Решения NCERT для класса 8, хинди
- Решения NCERT для класса 8 на санскрите
- Решения NCERT
(iv) m 2 , m 2 + n 2 , n 2 + l 2 , 2lm + 2mn + 2nl
Решение:
(i) Дано: ab – abca, bc –c
У нас есть
(ab – bc) + (bc – ca) + (ca – ab) (сложение всех терминов)
= ab – bc + bc – ca + ca – ab
= (ab – ab) + (bc – bc) + (ca – ca) (Собирая одинаковые термины вместе)
= 0 + 0 + 0
= 0
(ii) Дано:
a – b + ab, b – c + bc, c – a + ac
We have (a – b + ab) + (b – c + bc) + (c – a + ac) (сложение всех терминов)
= a – b + ab + b – c + bc + c – a + ac
= (a – a) + (b – b) + (c – c) + ab + bc + ac (собирая все подобные термины вместе)
= 0 + 0 + 0 + ab + bc + ac
= ab + bc + ac
(iii) Дано:
2p 2 q 2 – 3pq + 4, 5 + 7pq – 3p 2 q 2
, мы имеем
(добавление столбца)
(IV) Дано: L 2 + M 2 , M 2 + N 2 , N 2 + L 2 , 2LM + 2MN + + 2MN + 2MN + 2MN + 2MN + 2MN + 2MN + 2MN + 2MN + 2. nl
nl
Расставив одинаковые члены в одном столбце, мы получим
Таким образом, сумма данных выражений равна 2(l 2 + m 2 + n 2 + lm + mn + nl)
Упражнение 9.1, класс 8, математика, вопрос 4.
(a) Вычтите 4a – 7ab + 3b + 12 из 12a – 9ab3 + 5b
(6) Вычесть 3xy + 5yz – 7zx из 5xy – 2yz – 2zx + 10xyz
(c) Вычесть 4p 2 q – 3pq + 5pq 2 – 8p + 7q – 10 из 18 – 3p – 11q –q 2pq 2 + 5p 2 q
Решение:
(a) Упорядочив одинаковые члены по столбцам, мы получим
[Замените знаки всех членов младших выражений, а затем добавьте]
(b) Располагая одинаковые термины по столбцам, мы имеем
[Заменим знаки всех членов нижних выражений и затем прибавим]
(c) Расположив одинаковые термины по столбцам, мы получим
[Заменим Признаки всех условий более низких выражений, а затем добавить]
Условия являются p 2 Q — 7pq 2 + 8pq — 18q + 5p + 20
 Учебный материал
Учебный материалРешения NCERT для математики класса 8, глава 9 в формате PDF на 2022–2023 годы.
Решения NCERT для математики класса 8 Глава 9в формате PDF на 2022-2023 гг. Решения NCERT для математики класса 8 Глава 9 АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ И ИДЕНТИЧНОСТИ Упражнение 9.1, Упражнение 9.2, Упражнение 9.3, Упражнение 9.4 и Упражнение 9.5 на английском и хинди Среда обновлена для новой академической сессии 2022-23. Загрузите Прашнавали 9.1, Прашнавали 9.2, Прашнавали 9.3, Прашнавали 9.4 и Прашнавали 9. 5 на хинди Medium для изучения онлайн или в формате PDF для бесплатной загрузки для автономного использования. Решения NCERT 2022-23 обновлены для новой академической сессии 2022-2023 на основе обновленных книг NCERT. Варианты загрузки для хинди и английского Medium NCERT Solutions приведены ниже.
5 на хинди Medium для изучения онлайн или в формате PDF для бесплатной загрузки для автономного использования. Решения NCERT 2022-23 обновлены для новой академической сессии 2022-2023 на основе обновленных книг NCERT. Варианты загрузки для хинди и английского Medium NCERT Solutions приведены ниже.
NCERT Solutions for Class 8 Maths Chapter 9
| Class: 8 | Mathematics |
| Chapter 9: | Algebraic Expressions and Identities |
Class 8 Maths Chapter 9 Solutions
Класс 8 Математика Глава 9 Алгебраические выражения и тождества Все упражнения на английском языке, а также на языке хинди приведены ниже для загрузки в формате PDF. Все решения сделаны правильно с учетом последней учебной программы CBSE 2022-23.
Класс 8 Математические упражнения 9.1 Решения в видео
Класс 8 Математические упражнения 9. 1. Решения в видео
1. Решения в видео
Класс 8 Математические упражнения 9.1
класс 8 Математические упражнения 9.1
Class 8 Maths. Математическое упражнение 8 класса 9.2 Решение
Математическое упражнение 9 класса 9.2 Объяснение
Математическое упражнение 9 класса 9.3 Решения в видео
Класс 8 Математические упражнения 9. 3 Решения в видео
3 Решения в видео
Класс 8 Математические упражнения 9.3. Объяснение
класс 8 Математические упражнения 9.4. 9.4 Объяснение
Математическое упражнение 8 класса 9.5 Решения в видео
Математическое упражнение 8 класса 9.5 Решение
Математическое упражнение 9 класса 92]
= 6400 – 4
= 6396
В главе 9 «Алгебраические выражения и тождества» мы должны узнать о фундаментальных терминах, таких как множители, коэффициенты, мономиальные, биномиальные, трехчленные и все другие многочлены, подобные и отличные термины в алгебраическом выражение, сложение и вычитание выражений, отбрасывая одинаковые термины.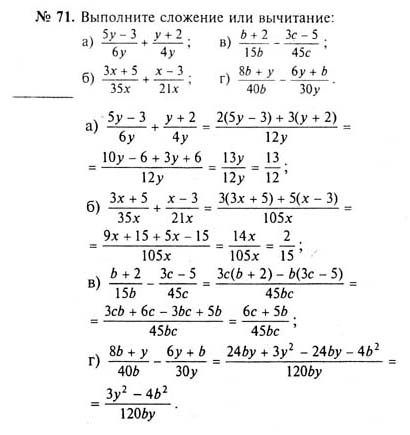


 Твое призвание — финансист!»
Твое призвание — финансист!»