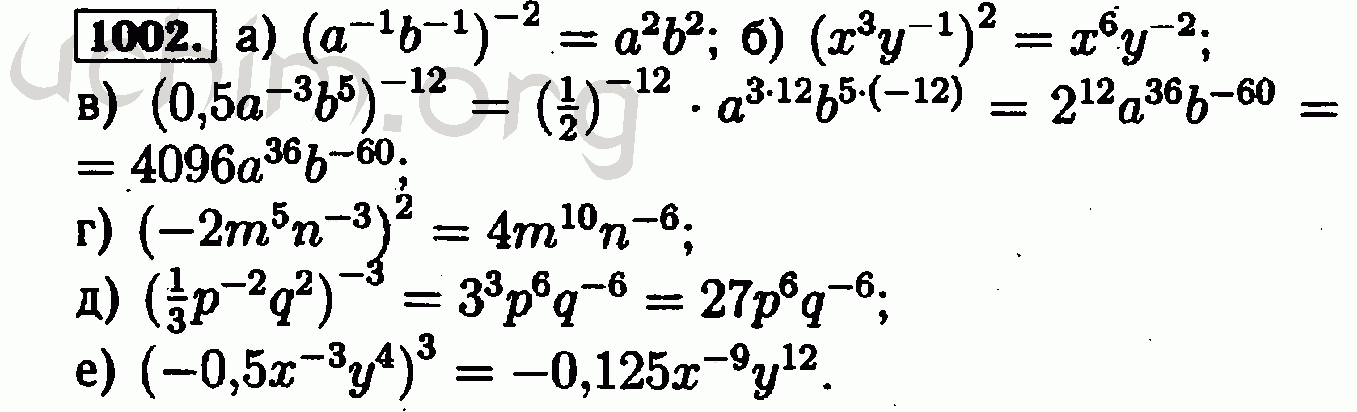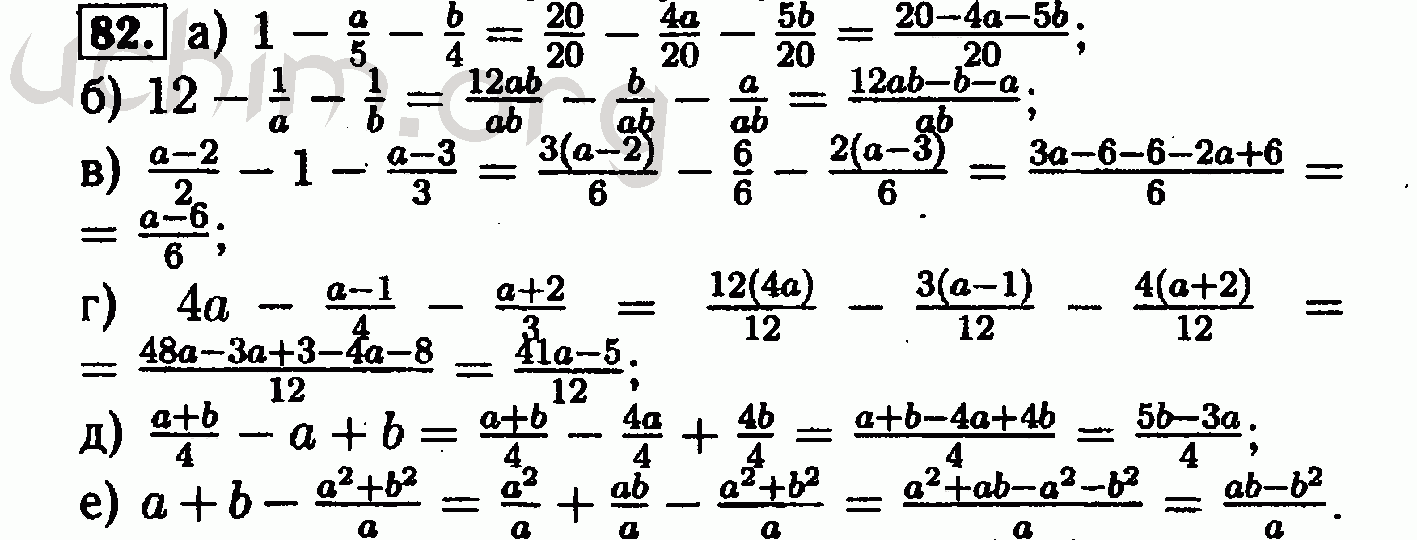Решеба ру по алгебре 8 класс: Решебник по Алгебре 8 класс (Арефьева) – Решеба

ГДЗ Решебник Алгебра 8 класс Учебник «Народная асвета» Арефьева, Пирютко.

ГДЗ Решебник Алгебра 8 класс Учебник «Народная асвета» Арефьева, Пирютко.

Алгебра 8 классУчебникАрефьева, Пирютко«Народная асвета»

Зачастую обучение в школе проходит не так гладко, как хотелось бы большинству родителей. Да это и не удивительно, учитывая сложность учебной программы. Поэтому учащимся может весьма пригодится решебник к учебнику «Алгебра 8 класс Учебник, авторы: Арефьева, Пирютко» от издательства Народная асвета, которое входит в серии УМК «». В сборнике подробно приводятся решения всех заданий, которые так же сопровождаются условиями.

ГДЗ «Алгебра 8 класс Учебник, авторы: Арефьева, Пирютко» поможет преодолеть множество трудностей в ходе обучения:

• дополнить и углубить свои познания;
• разобраться в мельчайших аспектах предмета Алгебра;
• исправить допущенные ошибки;
• повысить успеваемость.

Делитесь решением с друзьями, оставляйте комментарии — они помогают нам становится лучше!

Глава1.

Задания123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402

Глава1.

Я проверяю свои знания12345678910

Глава1. Практическая математика

123Глава1. Исследовательское задание

Глава1. Готовимся к олимпиаде

12

Глава 2. Задания

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244

Глава 2. Я проверяю свои знания

12345678910

Глава 2. Практическая математика

12345Глава 2. Исследовательское задание

Глава 2. Готовимся к олимпиаде

123

Глава 3. Задания

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237

Глава 3.

Я проверяю свои знания12345678910

Глава 3. Практическая математика

1234

Глава 3. Исследовательское задание

12

Глава 3. Готовимся к олимпиаде

12

Глава 4. Задания

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116

Глава 4. Я проверяю свои знания

12345678910

Глава 4. Практическая математика

12Глава 4. Исследовательское задание

Глава 4. Готовимся к олимпиаде

12

Повторение

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112

Вопросы к параграфу

1234567891011121314151617181920

Глава1. Задания: 1

Предыдущее

Следующее

Условие

Решение

Предыдущее

Следующее

закрыть

ГДЗ и решебники

Мордкович.

Решебник по алгебре 8 класс

• формат exe
• размер 4.42 МБ
• добавлен 30 ноября 2010 г.

Решебник по Алгебре 8 класс Мордкович — даёт правильные решения по данному предмету. Помогает ученикам 7го класса, которые не знаю данный предмет.

Смотрите также

• формат pdf
• размер 8.82 МБ
• добавлен 24 апреля 2011 г.

Домашняя работа (ГДЗ) (решебник) по алгебре за 9 класс к задачнику «Алгебра 9 кл. А. Г. Мордкович и др. М.: «Мнемозина», 2008-2010 годов издания. «

• формат djvu, pdf
• размер 29.88 МБ
• добавлен 24 апреля 2011 г.

Первое издание сборника датировано 1996 годом, и до 2000 года он выходил в 1-й редакции. Впоследствии сборник был переработан и дополнен, и с 2000 года выходит во 2-й редакции. В архиве: 1) Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы, 9 класс. Л. В. Кузнецова, Е. А. Бунимович, Б. П. Пигарев, С. Б. Суворова. — М.: Дрофа, 2008, 2-я редакция, 192 страницы. 2) Сборник заданий для проведения письменного экза…

• формат exe
• размер 3.11 МБ
• добавлен 30 ноября 2010 г.

Решебник даёт правильные решения по данному предмету. Помогает ученикам 9-го класса, которые не знают данный предмет.rn

• формат pdf
• размер 1.62 МБ
• добавлен 08 января 2010 г.

Учебно-практическое пособие. Страниц ч.1. 247 и ч.2. 45. к задачнику «Алгебра. 7 класс: Задачник для общеобразоват. учреждений. — 3-е изд., доработ. » А. Г. Мордкович и др. VI.: «Мнемозина», 2000 г. Часть I и 2.

• формат djvu, pdf
• размер 5.01 МБ
• добавлен 08 января 2010 г.

Учебное пособие. Страниц 251+984. к задачнику «Алгебра и начала анализа. Задачник для 10-11 кл. общеобразовательных учреждений Л. Г. Мордкович. Л. О. Депищева. Т. Д. Корешкова. Т. Н. Мишустина, Е. Е. Тульчинская — VI.: «Мнемозина». 2001 г. »

• формат pdf
• размер 1.87 МБ
• добавлен 26 ноября 2009 г.

Предлагаемое учебное пособие содержит подробное решение заданий к задачнику «Алгебра и начала анализа. Задачник для 10-11 кл. общеобразовательных учреждений А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова, Т. Н. Мишустина, Е. Е. Тульчинская — М. : 2001 г. » Пособие адресовано в первую очередь школьникам, испытывающим трудности в решении задач по алгебре, а также их родителям для проверки уровня готовности ученика к контрольным работам. 251 с.

• формат pdf
• размер 2.32 МБ
• добавлен 02 января 2011 г.

4-е изд. учебно-методическое пособие. — Экзамен, 2009. — 129 с. Серия: Решебник Качество: Отсканированные страницы В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Математика: 5 кл.: учеб. для общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 8-е изд. стер. — М.: Мнемозина, 2006». Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости. ..

Mathematical Mindset Algebra — YouCubed

Этот 4-недельный учебный модуль, который мы разработали, может быть использован для ознакомления с алгебраическими понятиями в любом классе. Он основан на алгебраических исследованиях, показывающих, что учащимся полезнее изучать алгебру, изучая рост паттернов, где переменная представляет номер случая и может варьироваться, прежде чем изучать «нахождение x». Когда студенты начинают изучать алгебру, находя x, они приходят к выводу, что переменная представляет собой одно число и не меняется. Позже, когда им нужно понять, что переменные могут варьироваться, они сталкиваются с концептуальным барьером, и многие так и не преодолевают этот барьер. Мы рекомендуем учащимся сначала узнать о росте паттернов и увидеть, что алгебра может быть полезна для описания роста. Позже, когда они сталкиваются с ситуациями, когда переменная представляет собой одно пропущенное число, они видят в этом подмножество своего более широкого знания о переменных, и путаницы не возникает. Подробный обзор исследований по обучению алгебре см. в Kieran, (2013).

Вторая цель нашей учебной программы — научить учащихся тому, что алгебра — это инструмент для решения задач. Студенты научатся исследовать различные функции, которые они изучают визуально, численно, графически, физически и алгебраически. Студенты будут обобщать, представлять, моделировать, описывать и интерпретировать отношения между двумя величинами. Они также будут различать линейный, квадратичный, кубический и экспоненциальный рост в рамках нескольких представлений.

Третья цель нашей учебной программы — помочь учащимся развить более сильное чувство числа, поскольку многие ученики не сдают алгебру не потому, что алгебра сложна, а потому, что им не хватает прочной основы в смысле числа (Gray & Tall, 1994; Boaler, 2016). . В наших занятиях по чувству чисел учащиеся узнают, как адаптировать числа и использовать символы группировки, которые помогут им понимать и использовать алгебраические выражения.

В течение 4-х недель учащиеся получат возможность установить важные мозговые связи, так как они познают алгебру различными способами, формами и представлениями.

Ссылки и дополнительная литература.

Боалер, Дж. (2016) Математическое мышление: Раскрытие потенциала учащихся с помощью творческой математики, вдохновляющих сообщений и инновационного обучения. Джосси-Басс/Уайли: Чаппакуа, Нью-Йорк.

Грей, Э. и Д. Толл (1994). «Двойственность, двусмысленность и гибкость: «процептивный» взгляд на простую арифметику». Journal for Research in Mathematics Education 25 (2): 116-140.

Киран, К. (1992). Изучение и преподавание школьной алгебры. В Д. А. Гроувс (ред.), Справочник по исследованиям в области преподавания и обучения математике: проект Национального совета учителей математики  (стр. 390–419). Нью-Йорк, штат Нью-Йорк, Англия: Macmillan Publishing Co, Inc.

Мейсон Дж. (1996) Выражение общности и корней алгебры. В: Бернарц Н., Киран К., Ли Л. (ред.) Подходы к алгебре. Библиотека математического образования, том 18. Springer, Дордрехт.

Шенфельд, А. и Аркави, А. (1988) О значении переменной. Учитель математики, 420-427.

Томпсон, П. В., МакКаллум, В., Харел, Г., Блэр, Р., Дэнс, Р., и Нолан, Э. (2007). Промежуточная алгебра. В Алгебра: ворота в технологическое будущее.

Решение простых уравнений

При решении простого уравнения думайте об уравнении как о балансе, где знак равенства (=) является точкой опоры или центром. Таким образом, если вы делаете что-то с одной частью уравнения, вы должны сделать то же самое с другой стороной. Выполняя одно и то же действие с обеими сторонами уравнения (скажем, добавляя по 3 к каждой стороне), уравнение остается сбалансированным.

Решение уравнения – это процесс получения искомого или решения по одну сторону знака равенства, а всего остального по другую. Вы действительно сортируете информацию. Если вы решаете для x , вы должны получить x  с одной стороны.

Уравнения сложения и вычитания

Некоторые уравнения включают только сложение и/или вычитание.

Пример 1

Найдите x .

x + 8 = 12

Чтобы решить уравнение x + 8 = 12, вы должны получить x отдельно с одной стороны. Следовательно, вычтите 8 с обеих сторон.

Чтобы проверить свой ответ, просто подставьте его в уравнение:

 

Пример 2

Найдите y .

г  – 9 = 25

Чтобы решить это уравнение, вы должны получить

y отдельно с одной стороны. Поэтому прибавьте 9 к обеим сторонам.

Для проверки просто замените y на 34:

 

Пример 3

Найдите x .

x + 15 = 6

Чтобы решить, вычтите 15 с обеих сторон.

Для проверки просто замените x на –9 :

.

 

Обратите внимание, что в каждом вышеприведенном случае используются противоположные операции  ; то есть, если в уравнении есть сложение, вы вычитаете из каждой стороны.

Уравнения умножения и деления

Некоторые уравнения включают только умножение или деление. Обычно это происходит, когда переменная уже находится в одной части уравнения, но есть либо более одной переменной, например 2 x , либо часть переменной, например

.

или

Таким же образом, как при сложении или вычитании, вы можете умножать или делить обе части уравнения на одно и то же число  , если оно не равно нулю , и уравнение не изменится.

Пример 4

Найдите x .

3  x  = 9

Разделите каждую часть уравнения на 3.

Для проверки замените x на 3:

 

Пример 5

Найдите y .

Чтобы решить, умножьте каждую сторону на 5.

Для проверки замените y на 35:

 

Пример 6

Найдите x .

Чтобы решить, умножьте каждую сторону на .

Или без отмены

 

Обратите внимание, что слева вы обычно не пишете, потому что оно всегда сокращается до 1  x или x .

Комбинации операций

Иногда для решения уравнения приходится использовать более одного шага. В большинстве случаев сначала выполните шаг сложения или вычитания. Затем, отсортировав переменные с одной стороны, а числа с другой, умножьте или разделите, чтобы получить только одну из переменных (то есть переменную без номера или 1 перед ней):  x , а не 2 x ).

Пример 7

Найдите x .

2 x + 4 = 10

Вычтите 4 с обеих сторон, чтобы получить 2 x отдельно с одной стороны.

Затем разделите обе стороны на 2, чтобы получить x .

Для проверки подставьте свой ответ в исходное уравнение:

 

Пример 8

Найдите x .

5x  – 11 = 29

Добавьте 11 с обеих сторон.

Разделите каждую сторону на 5.

Для проверки замените x на 8:

 

Пример 9

Найдите x .

Вычтите 6 с каждой стороны.

Умножить каждую сторону на .

Для проверки замените x на 9:

Пример 10

Решите для и .

Добавьте 8 с обеих сторон.

Умножить каждую сторону на .

Для проверки замените y на -25:

Пример 11

Найдите x .

3 x + 2 = x + 4

Вычесть 2 с обеих сторон (то же самое, что добавить -2).

Вычесть x с обеих сторон.

Обратите внимание, что 3  x  –  x  равно 3  x  – 1  x .

Разделите обе части на 2.

Для проверки замените x на 1:

 

Пример 12

Найдите y .

5 y  + 3 = 2 y  + 9

Вычесть 3 с обеих сторон.

Вычтите 2  y  с обеих сторон.

Разделите обе части на 3.

Для проверки замените y на 2:

 

Иногда вам нужно упростить каждую сторону (объединить одинаковые термины) перед тем, как начать процесс сортировки.

Пример 13

 Найти x .

3 x + 4 + 2 = 12 + 3

Во-первых, упростите каждую сторону.

Вычтите 6 с обеих сторон.

Разделите обе части на 3.

Для проверки замените x на 3:

Пример 14

Найдите x .

4 x + 2 x + 4 = 5 x + 3 + 11

Упростите каждую сторону.

6 x + 4 = 5 x + 14

Вычесть 4 с обеих сторон.

Вычтите 5 x с обеих сторон.