Тесты по Математике для 8 класса
Тесты по Математике для 8 классаАнглийский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP — доступ
- Предметы »
- Математика »
- 8 класс
для 8 класса
1 класс
2 класс
3 класс
4 класс
5 класс
6 класс
7 класс
8 класс
9 класс
10 класс
11 класс
В данном каталоге представлены интерактивные компьютерные тесты по «Математике» для 8 класса. Любой тест, который находится на нашем портале, можно загрузить и использовать на своем локальном компьютере, либо решать и проверять ответы прямо на сайтеТест: Вписанные и описанные окружности
Проверка значений по теме «Вписанные и описанные окружности».
Математика 8 класс | Автор: Голубев Дмитрий Игоревич | ID: 17440 | Дата: 9.9.2022
Тест: Симметрия
Показать знания осевой и центральной смметрии
Математика 8 класс | Автор: Кивва В.Е. | ID: 17439 | Дата: 9.9.2022
Тест: Решение рациональных уравнений
Математика 8 класс | Автор: Бексяк А. Ю. | ID: 17438 | Дата: 9.9.2022
Тест: Квадратные уравнения №10
Тест содержит десять вопросов. Проверка умений решать квадратные уравнения.
Математика 8 класс | Автор: Олейникова М.В. | ID: 17436 | Дата: 9.9.2022
Тест: Иррациональные и тригонометрические уравнения
Цель теста проверить знания учащихся, умение находить корни иррациональных и тригонометрических уравнений.
Математика 8 класс | Автор: Афанасьев Даниил Максимович | ID: 17435 | Дата: 8.9.2022
Тест: Диаграммы
Освоение основных видов диаграмм
Математика 8 класс | Автор: Кивва В.Е. | ID: 17434 | Дата: 8.9.2022
Тест: Четырехугольник и его свойства
Математика 8 класс | Автор: Конобеева Марина Олеговна | ID: 17433 | Дата: 8. 9.2022
9.2022
Тест: Анализ геометрических высказываний
выполните тест, читая внимательно задания
Математика 8 класс | Автор: Бочкарева Татьяна | ID: 17432 | Дата: 8.9.2022
Тест: Решение неполных квадратных уравнений №2
Математика 8 класс | Автор: Рабова Т.В., Овчарова Л.А. | ID: 17431 | Дата: 8.9.2022
Тест: Четырехугольник
Для успешного усвоения учащимися геометрического материала целесообразно проводить диктанты. Работу можно применять:при проведении урока по геометрии, систематизации и закреплении знаний учащихся для проверки знаний учащихся по теме «Четырехугольник». Задается пять вопросов. Проверку правильности выполнения заданий диктанта надо организовать после его завершения. Оценка выставляется по количеству выполненных заданий.
Математика 8 класс | Автор: Иванова Нина Николаевна | ID: 16840 | Дата: 7.4.2022
Страница 1 из 18
© TestEdu.ru 2013-2023
E-mail администратора: [email protected]
Тесты по алгебре Корни (8 класс) онлайн
Последний раз тест пройден более 24 часов назад. Для учителя
Для учителя
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Вычислитe
4
3
5
15
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 2 из 10
Вычислитe
0,4
0,04
0,02
0,16
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 3 из 10
Выберите число, которое может принимать а в выражении
4
3,1
-5
15
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 4 из 10
Вычислитe
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 5 из 10
Упростите выражение
-1
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 6 из 10
Вычислите
9,1
2,9
89,9
8,9
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 7 из 10
Вычислитe
225
15
25
30
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 8 из 10
Вычислитe
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 9 из 10
Упростите выражение
1
2
0
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 10 из 10
Вычислитe
7
1
49
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Доска почёта
Чтобы попасть сюда — пройдите тест.
Тест по алгебре «Квадратные корни» представляет собой десять заданий разного уровня сложности, которые надо сначала выполнить, а затем среди предложенных найти правильный ответ. Задания помогают подготовиться к итоговому или тематическому контролю в школе, а также могут быть полезны старшеклассникам, готовящимся к сдаче ЕГЭ.
Тест онлайн вы найдете на нашем сайте.
Рейтинг теста
3.9
Средняя оценка: 3.9
Всего получено оценок: 3380.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
8 класс | Математика | Iowa Department of Education
В 8-м классе учебное время должно быть сосредоточено на трех важнейших областях: (1) формулировка и обоснование выражений и уравнений, включая моделирование ассоциации двумерных данных с линейным уравнением, а также решение линейных уравнений и систем линейных уравнений.
- Учащиеся используют линейные уравнения и системы линейных уравнений для представления, анализа и решения различных задач. Учащиеся узнают уравнения для пропорций (y/x = m или y = mx) как специальные линейные уравнения (y = mx + b), понимая, что константа пропорциональности (m) — это наклон, а графики — это линии, проходящие через начало координат. Они понимают, что наклон (m) линии представляет собой постоянную скорость изменения, так что если входные данные или координата x изменяются на величину A, выходные данные или координата y изменяются на величину m·A. Учащиеся также используют линейное уравнение для описания связи между двумя величинами в двумерных данных (например, между размахом рук и ростом учащихся в классе).

Учащиеся стратегически выбирают и эффективно реализуют процедуры для решения линейных уравнений с одной переменной, понимая, что при использовании свойств равенства и концепции логической эквивалентности они сохраняют решения исходного уравнения. Учащиеся решают системы двух линейных уравнений с двумя переменными и связывают системы с парами прямых на плоскости; они пересекаются, параллельны или являются одной и той же линией. Учащиеся используют линейные уравнения, системы линейных уравнений, линейные функции и свое понимание наклона линии для анализа ситуаций и решения проблем.
- Учащиеся усваивают понятие функции как правила, которое назначает каждому входу ровно один выход.
 Они понимают, что функции описывают ситуации, когда одна величина определяет другую. Они могут переводиться между представлениями и частичными представлениями функций (отмечая, что табличные и графические представления могут быть частичными представлениями), и они описывают, как аспекты функции отражаются в различных представлениях.
Они понимают, что функции описывают ситуации, когда одна величина определяет другую. Они могут переводиться между представлениями и частичными представлениями функций (отмечая, что табличные и графические представления могут быть частичными представлениями), и они описывают, как аспекты функции отражаются в различных представлениях. - Учащиеся используют идеи о расстоянии и углах, их поведении при перемещении, вращении, отражении и расширении, а также идеи о конгруэнтности и сходстве для описания и анализа двухмерных фигур и решения задач. Учащиеся показывают, что сумма углов в треугольнике есть угол, образованный прямой линией, и что различные конфигурации линий порождают подобные треугольники из-за углов, образующихся при пересечении параллельных прямых секущей. Учащиеся понимают формулировку теоремы Пифагора и ее обратной формы, а также могут объяснить, почему теорема Пифагора верна, например, путем разложения квадрата двумя разными способами. Они применяют теорему Пифагора для нахождения расстояний между точками на координатной плоскости, для нахождения длин и для анализа многоугольников.

Система счисления (8.NS)
Знайте, что есть нерациональные числа, и аппроксимируйте их рациональными числами. (8.NS.A)
- Знайте, что числа, не являющиеся рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число. (8.NS.A.1) (ДОК 1)
- Используйте рациональные приближения иррациональных чисел, чтобы сравнить размер иррациональных чисел, расположить их приблизительно на диаграмме числовых линий и оценить значение выражений (например, π2). Например, усекая десятичное разложение √2, покажите, что √2 находится между 1 и 2, затем между 1,4 и 1,5, и объясните, как продолжить, чтобы получить более точные приближения.
 (8.НС.А.2) (ДОК 1,2)
(8.НС.А.2) (ДОК 1,2)
Выражения и уравнения (8.EE)
Работа с радикалами и целыми показателями. (8.EE.A)
- Знать и применять свойства целочисленных показателей степени для создания эквивалентных числовых выражений. Например, 32 × 3–5 = 3–3 = 1/33 = 1/27. (8.EE.A.1) (DOK 1)
- Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x2 = p и x3 = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что √2 иррационально. (8.EE.A.2) (ДОК 1)
- Используйте числа, выраженные в виде одной цифры, умноженной на целую степень числа 10, для оценки очень больших или очень малых величин и для выражения того, во сколько раз одно больше другого. Например, оцените население Соединенных Штатов как 3 × 108, а население мира как 7 × 109 и определите, что население мира более чем в 20 раз больше. (8.
 EE.A.3) (DOK 1,2)
EE.A.3) (DOK 1,2) - Выполнение операций с числами, выраженными в экспоненциальном представлении, включая задачи, в которых используется как десятичное, так и экспоненциальное представление. Используйте научные обозначения и выбирайте единицы соответствующего размера для измерения очень больших или очень малых величин (например, используйте миллиметры в год для распространения по морскому дну). Интерпретировать научную нотацию, созданную технологией. (8.EE.A.4) (ДОК 1,2)
Понимать связи между пропорциональными отношениями, линиями и линейными уравнениями. (8.EE.B)
- График пропорциональных соотношений, интерпретируя удельную скорость как наклон графика. Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график «расстояние-время» с уравнением «расстояние-время», чтобы определить, какой из двух движущихся объектов имеет большую скорость. (8.EE.B.5) (ДОК 1,2,3)
- Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для прямой, проходящей через начало координат, и уравнение y = mx + b для прямой, пересекающей вертикальную ось в точке b.
 (8.EE.B.6) (ДОК 1,2,3)
(8.EE.B.6) (ДОК 1,2,3)
Анализ и решение линейных уравнений и пар одновременных линейных уравнений. (8.EE.C)
- Решение линейных уравнений с одной переменной.
- Приведите примеры линейных уравнений с одной переменной с одним решением, бесконечным числом решений или без решений. Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данное уравнение в более простые формы, пока не получится эквивалентное уравнение вида x = a, a = a или a = b (где a и b — разные числа).
- Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием свойства дистрибутивности и сбора подобных членов. (8.EE.C.7) (DOK 1,2)
- Анализ и решение пар одновременных линейных уравнений.
- Поймите, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, потому что точки пересечения удовлетворяют обоим уравнениям одновременно.

- Решите системы двух линейных уравнений с двумя переменными алгебраически и оцените решения, построив уравнения в виде графика. Решите простые случаи путем проверки. Например, 3x + 2y = 5 и 3x + 2y = 6 не имеют решения, потому что 3x + 2y не может быть одновременно 5 и 6.
- Решите реальные и математические задачи, ведущие к двум линейным уравнениям с двумя переменными. Например, зная координаты двух пар точек, определите, пересекает ли прямая, проходящая через первую пару точек, прямую, проходящую через вторую пару. (8.EE.C.8) (ДОК 1,2,3)
Функции (8.F)
Определение, оценка и сравнение функций. (8.F.A)
- Поймите, что функция — это правило, которое назначает каждому входу ровно один выход. График функции представляет собой набор упорядоченных пар, состоящих из входа и соответствующего выхода. (8.Ф.А.1) (ДОК 1,2)
- Сравните свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесными описаниями).
 Например, если дана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения. (8.Ф.А.2) (ДОК 1,2)
Например, если дана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения. (8.Ф.А.2) (ДОК 1,2) - Интерпретировать уравнение y = mx + b как определяющее линейную функцию, график которой представляет собой прямую линию; приведите примеры функций, которые не являются линейными. Например, функция A = s2, задающая площадь квадрата как функцию длины его стороны, не является линейной, поскольку ее график содержит точки (1,1), (2,4) и (3,9), которые равны не по прямой. (8.F.A.3) (ДОК 1,2)
Используйте функции для моделирования отношений между величинами. (8.F.B)
- Построить функцию для моделирования линейной зависимости между двумя величинами. Определить скорость изменения и начальное значение функции по описанию зависимости или по двум значениям (x, y), в том числе прочитать их из таблицы или из графика. Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.
 (8.Ф.Б.4) (ДОК 1,2,3)
(8.Ф.Б.4) (ДОК 1,2,3) - Качественно описать функциональную связь между двумя величинами, анализируя график (например, где функция возрастает или убывает, линейна или нелинейна). Нарисуйте график, демонстрирующий качественные характеристики функции, описанной словесно. (8.Ф.Б.5) (ДОК 1,2,3)
Геометрия (8.G)
Понимание конгруэнтности и подобия с помощью физических моделей, прозрачных пленок или программного обеспечения для геометрии. (8.G.A)
- Проверить экспериментально свойства вращения, отражения и перемещения:
- Линии превращаются в прямые, а отрезки прямых в отрезки одинаковой длины.
- Углы принимают за углы одной и той же меры.
- Параллельные линии превращаются в параллельные. (8.G.A.1) (ДОК 2)
- Понять, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.
 (8.Г.А.2) (ДОК 1,2)
(8.Г.А.2) (ДОК 1,2) - Описать эффект расширения, перемещения, поворота и отражения двухмерных фигур с использованием координат. (8.Г.А.3) (ДОК 1,2)
- Понять, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними. (8.Г.А.4) (ДОК 1,2)
- Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников. Например, расположите три копии одного и того же треугольника так, чтобы сумма трех углов представляла собой линию, и приведите аргумент в терминах секущей, почему это так. (8.Г.А.5) (ДОК 1,2,3)
Понять и применить теорему Пифагора. (8.G.B)
 (8.G.B.6) (ДОК 2,3)
(8.G.B.6) (ДОК 2,3)Решайте реальные и математические задачи на объем цилиндров, конусов и сфер. (8.G.C)
Статистика и вероятность (8.SP)
Исследовать закономерности связи в двумерных данных. (8.СП.А)
- Построение и интерпретация точечных диаграмм для данных двумерных измерений для исследования закономерностей связи между двумя величинами. Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная связь, линейная связь и нелинейная связь. (8.СП.А.1) (ДОК 1,2,3)
- Знайте, что прямые линии широко используются для моделирования отношений между двумя количественными переменными.
 Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии. (8.СП.А.2) (ДОК 1,2)
Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии. (8.СП.А.2) (ДОК 1,2) - Используйте уравнение линейной модели для решения задач в контексте данных двумерных измерений, интерпретируя наклон и точку пересечения. Например, в линейной модели для биологического эксперимента интерпретируйте наклон 1,5 см/ч как означающий, что дополнительный час солнечного света каждый день связан с дополнительными 1,5 см высоты взрослого растения. (8.СП.А.3) (ДОК 1,2)
- Поймите, что закономерности ассоциации также можно увидеть в двумерных категориальных данных, отображая частоты и относительные частоты в двусторонней таблице. Постройте и интерпретируйте двустороннюю таблицу, обобщающую данные по двум категориальным переменным, собранным у одних и тех же субъектов. Используйте относительные частоты, рассчитанные для строк или столбцов, чтобы описать возможную связь между двумя переменными.




 Они понимают, что функции описывают ситуации, когда одна величина определяет другую. Они могут переводиться между представлениями и частичными представлениями функций (отмечая, что табличные и графические представления могут быть частичными представлениями), и они описывают, как аспекты функции отражаются в различных представлениях.
Они понимают, что функции описывают ситуации, когда одна величина определяет другую. Они могут переводиться между представлениями и частичными представлениями функций (отмечая, что табличные и графические представления могут быть частичными представлениями), и они описывают, как аспекты функции отражаются в различных представлениях.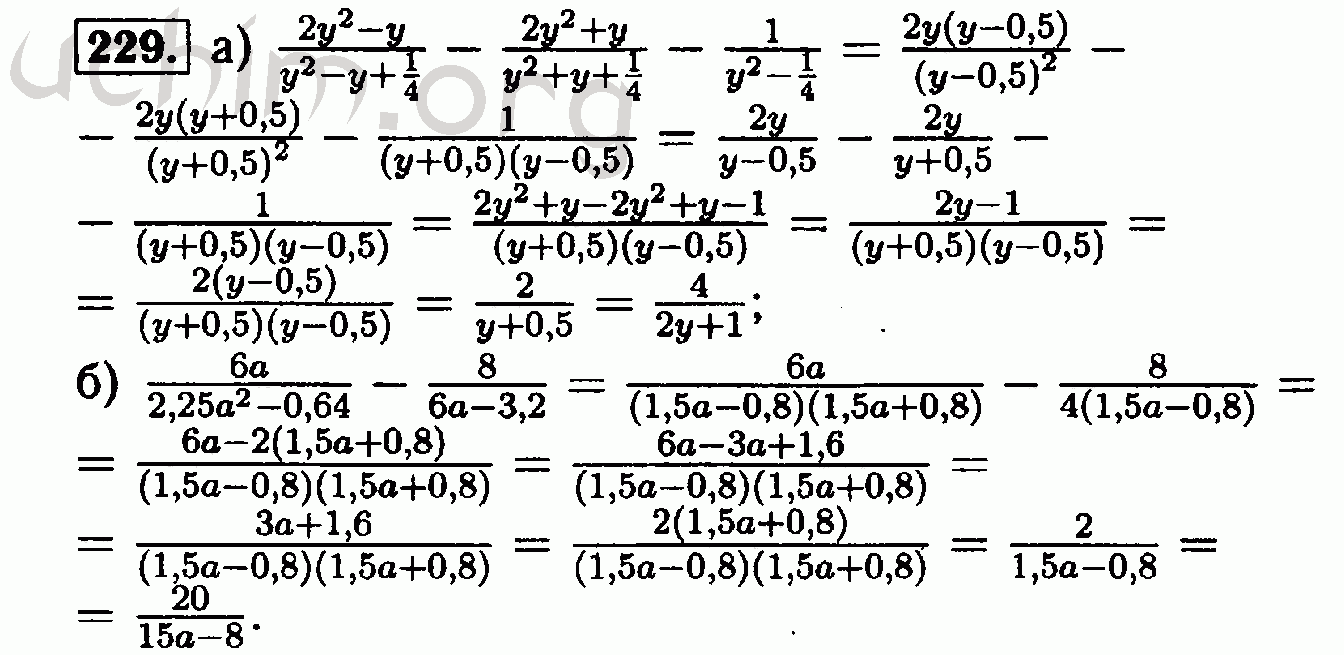
 (8.НС.А.2) (ДОК 1,2)
(8.НС.А.2) (ДОК 1,2) EE.A.3) (DOK 1,2)
EE.A.3) (DOK 1,2) (8.EE.B.6) (ДОК 1,2,3)
(8.EE.B.6) (ДОК 1,2,3)
 Например, если дана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения. (8.Ф.А.2) (ДОК 1,2)
Например, если дана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения. (8.Ф.А.2) (ДОК 1,2) (8.Ф.Б.4) (ДОК 1,2,3)
(8.Ф.Б.4) (ДОК 1,2,3) (8.Г.А.2) (ДОК 1,2)
(8.Г.А.2) (ДОК 1,2) Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии. (8.СП.А.2) (ДОК 1,2)
Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии. (8.СП.А.2) (ДОК 1,2)