Контрольные работы алгебра 8 класс А.Г.Мерзляк
- 1
- Войти
- Зарегистрироваться / Создать сайт
Курсы для аттестации учителей от 800 ₽ (72 часа). Документы об окончании по почте БЕСПЛАТНО…
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Выбрать материалы
Скидки до 50 %
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Категории пользователя
Методические пособия по математике (132)
Контрольные работы (129)
материалы ОГЭ (1059)
проекты учащихся (37)
проекты учащихся (24)
классный час (70)
материалы ЕГЭ (780)
материалы ЕГЭ (167)
Подготовка к олимпиадам (106)
экзамены (3)
Занимательная математика (7)
урок (22)
Журнал Математика (10)
Задание № 18 С параметром и с решением из ЕГЭ (73)
Задания ЕГЭ № 15 с решением.
Задание № 16 из ЕГЭ с решением (100)
ЕГЭ база (10)
тесты по стереометрии 11 класс (9)
Контрольные работы 5 класс А.Г. Мерзляк (8)
Вязание (1)
Планиметрия 10 класс. (27)
Контрольные работы алгебра 8 класс А.Г.Мерзляк (14)
Сад и огород (3)
контрольные работы геометрия 8 кл Мерзляк А.
Г. (7)
Контрольные работы алгебра 9 класс А.Г.Мерзляк (12)
Работа с классом (27)
контрольные работы алгебра 10 класс Ю.М. Колягин (35)
Нормативные документы (4)
Варианты ЕГЭ с сайта А.Ларина (305)
математика ОГЭ варианты с сайта Ларина А. (58)
Решение заданий № 16 из егэ с сайта А .Ларина (10)
Решение заданий № 17 из егэ с сайта А .
Ларина (118)
Решение заданий № 14 из егэ с сайта А .Ларина (122)
Задание № 11 решение текстовых задач ЕГЭ с сайта Ларина (84)
Презентации по наглядной геометрии (27)
Решения олимпиады Фоксфорд, Физтех (7)
Решение задания № 19 из ЕГЭ (105)
ВПР для классов 6-8 (6)
Алгебра-11 А.Г. Мерзляк Решения (17)
Алгебра -10 А.
Г. Мерзляк Решения (6)
Геометрия 10-11 А.Г. Мерзляк решения (7)
Алгебра 8 к-4 в.3 Мерзляк А.Г. угл. …
Категория: Алгебра
22.11.2021 21:55 324 1
Алгебра 8 к-4 в.4 Мерзляк А.Г. угл. …
Категория: Алгебра
22.11.2021 21:40 134 0
Алгебра 8 к-4 в.2 Мерзляк А.Г. угл. …
Категория: Алгебра
22.
11.2021 20:57
181
0
Категория: Алгебра
21.11.2021 20:34 172 0
Контрольная работа № 2 по теме Умножение и деление рациональных дробей. …
Категория: Алгебра
26.10.2021 05:56 386 13
Входная контрольная работа по алгебре в 8 классе -1 .
..
Категория: Алгебра
26.09.2021 06:11 1716 5
Контрольная работа №2 Основное свойство рациональной дроби Сложение и вычитание рациональных дробей …
Категория: Алгебра
06.10.2019 17:28 8867 75
8 класс алгебра Мерзляк А.Г. Итоговая контрольная работа. …
Категория: Алгебра
20.07.2019 12:35 4515 102
a-8-k-6_Уравнения, сводящиеся к квадратным.
А.Г.Мерзляк …
Категория: Алгебра
20.07.2019 12:19 1091 66
a-8-k-5_Квадратные уравнения. Теорема Виета. А.Г.Мерзляк …
Категория: Алгебра
20.07.2019 12:18 1167 52
КР Алгебра 8 класс Мерзляк
Контрольная работа №1
Основное свойство рациональной дроби.
Сложение и вычитание рациональных дробей.
Вариант 1
1. При каких значениях переменной имеет смысл выражение ?
2.
Сократите
дробь:
1) ; 2) ; 3) ; 4)
3. Выполните вычитание:
1) ; 3)
2) ; 4)
4. Упростите выражение:
1) ; 2) .
5. Известно, что . Найдите значение выражения:
1) ; 2) .
6. Постройте график функции .
Контрольная работа №1
Основное свойство рациональной дроби.
Сложение и вычитание рациональных дробей.
Вариант 2
1. При каких значениях переменной имеет смысл выражение ?
2. Сократите дробь:
1) ; 2) ; 3) ; 4)
3. Выполните вычитание:
1) ; 3)
2) ; 4)
4. Упростите выражение:
1) ; 2) .
5. Известно, что . Найдите значение выражения:
1) ; 2) .
6. Постройте график функции .
Контрольная работа №1
Основное
свойство рациональной дроби.
Сложение и вычитание рациональных дробей.
Вариант 3
1. При каких значениях переменной имеет смысл выражение ?
2. Сократите дробь:
1) ; 2) ; 3) ; 4)
3. Выполните вычитание:
1) ; 3)
2) ; 4)
4. Упростите выражение:
1) ; 2) .
5. Известно, что . Найдите значение выражения:
1) ; 2) .
6. Постройте график функции .
Контрольная работа №1
Основное свойство рациональной дроби.
Сложение и вычитание рациональных дробей.
Вариант 4
1. При каких значениях переменной имеет смысл выражение ?
2. Сократите дробь:
1) ; 2) ; 3) ; 4)
3. Выполните вычитание:
1) ; 3)
2) ; 4)
4.
Упростите
выражение:
1) ; 2) .
5. Известно, что . Найдите значение выражения:
1) ; 2) .
6. Постройте график функции .
Контрольная работа №2
Умножение и деление рациональных дробей.
Тождественные преобразования рациональных выражений.
Вариант 1
1. Выполните действия:
1) ; 3) ;
2) ; 4) .
2. Упростите выражение:
1) ; 2) .
3. Доказать тождество .
4. Известно, что . Найдите значение выражения .
Контрольная работа №2
Умножение и деление рациональных дробей.
Тождественные
преобразования рациональных выражений.
Вариант 2
1. Выполните действия:
1) ; 3) ;
2) ; 4) .
2. Упростите выражение:
1) ; 2) .
3. Доказать тождество .
4. Известно, что . Найдите значение выражения .
Контрольная работа №2
Умножение и деление рациональных дробей.
Тождественные преобразования рациональных выражений.
Вариант 3
1. Выполните действия:
1) ; 3) ;
2) ; 4) .
2. Упростите выражение:
1) ; 2) .
3. Доказать тождество .
4. Известно, что . Найдите значение выражения .
Контрольная работа №2
Умножение и деление рациональных дробей.
Тождественные
преобразования рациональных выражений.
Вариант 4
1. Выполните действия:
1) ; 3) ;
2) ; 4) .
2. Упростите выражение:
1) ; 2) .
3. Доказать тождество .
4. Известно, что . Найдите значение выражения .
Контрольная работа №3
Рациональные уравнения. Степень с целым отрицательным
показателем. Функция и её график
Вариант 1
1. Решите уравнение:
1) ; 2).
2. Запишите в стандартном виде число:
1) ; 2) .
3. Представьте в виде степени с основанием выражение:
1) ; 2) ; 3) .
4. Упростите выражение .
5. Найдите значение выражения:
1) ; 2) .
6. Преобразуйте
выражение так, чтобы оно не
содержало степеней с отрицательными показателями.
7. Вычислите:
1) ; 2) .
8. Решите графически уравнение .
9. Порядок числа равен , а порядок числа равен . Каким может быть порядок значения выражения:
1) ; 2) ?
Контрольная работа №3
Рациональные уравнения. Степень с целым отрицательным
показателем. Функция и её график
Вариант 2
1. Решите уравнение:
1) ; 2).
2. Запишите в стандартном виде число:
1) ; 2) .
3. Представьте в виде степени с основанием выражение:
1) ; 2) ; 3) .
4. Упростите выражение .
5. Найдите значение выражения:
1) ; 2) .
6. Преобразуйте выражение так, чтобы оно не содержало степеней с отрицательными показателями.
7. Вычислите:
1) ; 2) .
8. Решите графически уравнение .
9. Порядок числа равен , а порядок числа равен . Каким может быть порядок значения выражения:
1) ; 2) ?
Контрольная работа №3
Рациональные уравнения. Степень с целым отрицательным
показателем. Функция и её график
Вариант 3
1. Решите уравнение:
1) ; 2).
2. Запишите в стандартном виде число:
1) ; 2) .
3. Представьте в виде степени с основанием выражение:
1) ; 2) ; 3) .
4. Упростите выражение .
5. Найдите значение выражения:
1) ; 2) .
6. Преобразуйте выражение так, чтобы оно не содержало степеней с отрицательными показателями.
7. Вычислите:
1) ; 2) .
8. Решите
графически уравнение .
9. Порядок числа равен , а порядок числа равен . Каким может быть порядок значения выражения:
1) ; 2) ?
Контрольная работа №3
Рациональные уравнения. Степень с целым отрицательным
показателем. Функция и её график
Вариант 4
1. Решите уравнение:
1) ; 2).
2. Запишите в стандартном виде число:
1) ; 2) .
3. Представьте в виде степени с основанием выражение:
1) ; 2) ; 3) .
4. Упростите выражение .
5. Найдите значение выражения:
1) ; 2) .
6. Преобразуйте выражение так, чтобы оно не содержало степеней с отрицательными показателями.
7. Вычислите:
1) ; 2) .
8. Решите графически уравнение .
9. Порядок
числа равен , а порядок числа равен .
Каким может быть
порядок значения выражения:
1) ; 2) ?
Контрольная работа №4
Квадратные корни.
Вариант 1
1.Найдите пересечение и объединение множеств A и B, где A – множество делителей числа 20, B – множество делителей числа 64.
2.Найдите значение выражений:
1) 3) ;
2) ; 4) .
3.Решите уравнение:
1) ; 2) ; 3) ; 4) .
4.Упростите выражение:
1) ; 3) ;
2) ; 4) .
5.Сравните числа:
1) ; 2) .
6.Сократите дробь:
1) ; 2) ; 3) .
7.Освободитесь от иррациональности в знаменателе дроби:
1) ; 2)
.
8.Вынесите множитель из-под знака корня:
1) ; 3) ;
2) ; 4) .
9.Упростите выражение .
Контрольная работа №4
Квадратные корни.
Вариант 2
1. Найдите пересечение и объединение множеств A и B, где A – множество делителей числа 54, B – множество делителей числа 63.
2.Найдите значение выражений:
1) 3) ;
2) ; 4) .
3.Решите уравнение:
1) ; 2) ; 3) ; 4) .
4.Упростите выражение:
1) ; 3) ;
2) ; 4) .
5.Сравните числа:
1) ; 2) .
6.
Сократите дробь:
1) ; 2) ; 3) .
7.Освободитесь от иррациональности в знаменателе дроби:
1) ; 2) .
8.Вынесите множитель из-под знака корня:
1) ; 3) ;
2) ; 4) .
9.Упростите выражение .
Контрольная работа №4
Квадратные корни.
Вариант 3
1.Найдите пересечение и объединение множеств A и B, где A – множество делителей числа 40, B – множество делителей числа 32.
2.Найдите значение выражений:
1) 3) ;
2) ; 4) .
3.Решите уравнение:
1) ; 2) ; 3) ; 4) .
4.Упростите выражение:
1) ; 3) ;
2) ; 4)
.
5.Сравните числа:
1) ; 2) .
6.Сократите дробь:
1) ; 2) ; 3) .
7.Освободитесь от иррациональности в знаменателе дроби:
1) ; 2) .
8.Вынесите множитель из-под знака корня:
1) ; 3) ;
2) ; 4) .
9.Упростите выражение .
Контрольная работа №4
Квадратные корни.
Вариант 4
1.Найдите пересечение и объединение множеств A и B, где A – множество делителей числа 28, B – множество делителей числа 42.
2.Найдите значение выражений:
1) 3) ;
2) ; 4) .
3.Решите уравнение:
1) ; 2) ; 3) ; 4) .
4.Упростите выражение:
1) ; 3) ;
2) ; 4) .
5.Сравните числа:
1) ; 2) .
6.Сократите дробь:
1) ; 2) ; 3) .
7.Освободитесь от иррациональности в знаменателе дроби:
1) ; 2) .
8.Вынесите множитель из-под знака корня:
1) ; 3) ;
2) ; 4) .
9.Упростите выражение .
Контрольная работа №5
Квадратные уравнения. Теорема Виета.
Вариант 1
1. Решите уравнение:
уравнение имеет два корня. 8. Постройте график функции |
1.
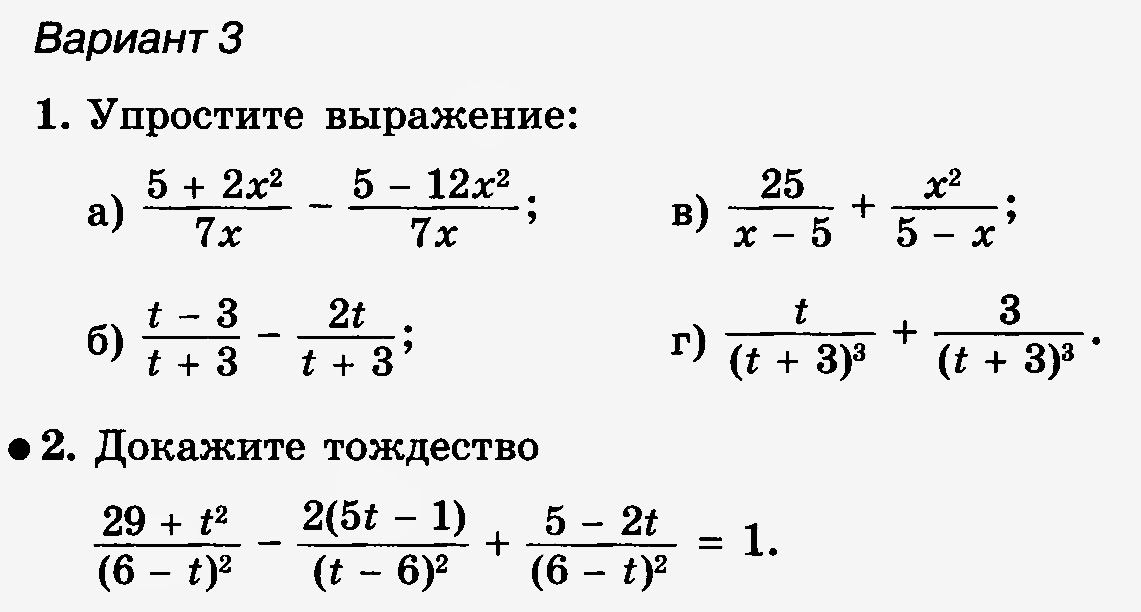6 Рациональные выражения — Алгебра колледжа 2eЦели обучения
В этом разделе вы:
- Упрощать рациональные выражения.
- Умножение рациональных выражений.
- Разделить рациональные выражения.
- Сложение и вычитание рациональных выражений.
- Упростите сложные рациональные выражения.
Кондитерская имеет фиксированные затраты в размере 280$280 в неделю и переменные затраты в размере 9$9 за коробку выпечки. Затраты магазина в неделю в пересчете на х, х, количество изготовленных коробок, составляют 280+9.х.280+9х. Мы можем разделить затраты в неделю на количество изготовленных коробок, чтобы определить стоимость коробки выпечки.
280+9xx280+9xx
Обратите внимание, что результатом является полиномиальное выражение, деленное на второе полиномиальное выражение. В этом разделе мы рассмотрим частные полиномиальные выражения.
Упрощение рациональных выражений
Частное двух полиномиальных выражений называется рациональным выражением.
Мы можем применять свойства дробей к рациональным выражениям, например, упрощая выражения, исключая общие множители из числителя и знаменателя. Для этого нам сначала нужно разложить как числитель, так и знаменатель. Начнем с показанного рационального выражения.
х2+8х+16х2+11х+28х2+8х+16х2+11х+28
Мы можем разложить числитель и знаменатель, чтобы переписать выражение.
(х+4)2(х+4)(х+7)(х+4)2(х+4)(х+7)
Тогда мы можем упростить это выражение, убрав общий множитель (x+4).(x+4).
х+4х+7х+4х+7
Как
Дано рациональное выражение, упростите его.
- Разложите числитель и знаменатель на множители.
- Отменить любые общие факторы.
Пример 1
Упрощение рациональных выражений
Упростить x2-9×2+4x+3.×2-9×2+4x+3.
Решение
(x+3)(x−3)(x+3)(x+1)Разложить на множители числитель и знаменатель.
x−3x+1Отменить общий множитель(x+3).(x+3)(x−3 )(x+3)(x+1)Разложить на множители числитель и знаменатель.x−3x+1Отменить общий множитель (x+3).
Анализ
Мы можем отменить общий множитель, потому что любое выражение, деленное само на себя, равно 1.
вопросы и ответы
Можно ли отменить термин x2x2 в примере 1?
Нет. Коэффициент — это выражение, которое умножается на другое выражение. Член x2x2 не является фактором числителя или знаменателя.
Попробуй это #1
Упростить x-6×2-36.x-6×2-36.
Умножение рациональных выражений
Умножение рациональных выражений работает так же, как и умножение любых других дробей. Мы умножаем числители, чтобы найти числитель произведения, а затем умножаем знаменатели, чтобы найти знаменатель произведения.
Перед умножением полезно разложить числители и знаменатели на множители так же, как мы это делали при упрощении рациональных выражений. Нам часто удается упростить произведение рациональных выражений.
Как
Даны два рациональных выражения, умножьте их.
- Разложите числитель и знаменатель на множители.
- Умножить числители.
- Умножить знаменатели.
- Упростить.
Пример 2
Умножение рациональных выражений
Умножение рациональных выражений и представление произведения в простейшей форме:
x2+4x−53x+18⋅2x−1x+5×2+4x−53x+18⋅2x−1x+5
Решение
(x+5)(x−1)3(x+6)⋅(2x−1)(x+5)Разложить на множители числитель и знаменатель.(x+5)(x−1)(2x−1)3 (x+6)(x+5)Умножить числители и знаменатели.(x+5)(x−1)(2x−1)3(x+6)(x+5)Отменить общие множители для упрощения.
(x− 1)(2x−1)3(x+6) (x+5)(x−1)3(x+6)⋅(2x−1)(x+5) Разложите числитель и знаменатель на множители (x+5). )(x−1)(2x−1)3(x+6)(x+5)Умножение числителей и знаменателей.(x+5)(x−1)(2x−1)3(x+6)(x +5)Отменить общие множители для упрощения.(x−1)(2x−1)3(x+6)
Попробуй это #2
Умножьте рациональные выражения и покажите произведение в простейшей форме:
x2+11x+30×2+5x+6⋅x2+7x+12×2+8x+16×2+11x+30×2+5x+6⋅x2+7x+12×2+8x+16
Разделение рациональных выражений
Деление рациональных выражений работает так же, как и деление других дробей. Чтобы разделить рациональное выражение на другое рациональное выражение, умножьте первое выражение на обратную величину второго. Используя этот подход, мы перепишем 1x÷x231x÷x23 как произведение 1x⋅3×2,1x⋅3×2. Как только выражение деления было переписано как выражение умножения, мы можем умножать, как делали это раньше.
1x⋅3×2=3x31x⋅3×2=3×3
Как
Даны два рациональных выражения, разделите их.
- Перепишите как первое рациональное выражение, умноженное на обратную величину второго.
- Разложите числители и знаменатели на множители.
- Умножить числители.
- Умножить знаменатели.
- Упростить.
Пример 3
Деление рациональных выражений
Разделение рациональных выражений и выражение частного в простейшей форме:
2×2+x−6×2−1÷x2−4×2+2x+12×2+x−6×2−1÷x2−4×2+2x+1
Решение
2×2+x−6×2−1⋅x2+2x+1×2−4 Переписать как умножение.(2x−3)(x+2)(x+1)(x−1)⋅(x+1)2(x+2) )(x−2)Коэффициент.(2x−3)(x+2)(x+1)2(x+1)(x−1)(x+2)(x−2)Умножить.(2x−3 )(x+1)(x−1)(x−2)Отменить общие множители для упрощения.2×2+x−6×2−1⋅x2+2x+1×2−4Переписать как умножение.(2x−3)(x+2) (x+1)(x−1)⋅(x+1)2(x+2)(x−2)Коэффициент.(2x−3)(x+2)(x+1)2(x+1) (x−1)(x+2)(x−2)Умножить.(2x−3)(x+1)(x−1)(x−2)Отменить общие множители для упрощения.
Попробуй это #3
Разделить рациональные выражения и выразить частное в простейшей форме:
9×2−163×2+17x−28÷3×2−2x−8×2+5x−149×2−163×2+17x−28÷3×2−2x−8×2+5x−14
Сложение и вычитание рациональных выражений
Сложение и вычитание рациональных выражений работает так же, как сложение и вычитание числовых дробей. Чтобы сложить дроби, нам нужно найти общий знаменатель. Рассмотрим пример сложения дробей.
524+140=25120+3120=28120=730524+140=25120+3120=28120=730
Мы должны переписать дроби, чтобы они имели общий знаменатель, прежде чем мы сможем складывать. Мы должны делать то же самое при сложении или вычитании рациональных выражений.
Самый простой в использовании общий знаменатель — это наименьший общий знаменатель, или LCD. LCD — это наименьшее кратное, общее для знаменателей. Чтобы найти LCD двух рациональных выражений, мы факторизуем выражения и перемножаем все различные множители. Например, если факторизованные знаменатели были (x+3)(x+4)(x+3)(x+4) и (x+4)(x+5),(x+4)(x+5) , тогда ЖК-экран будет (x+3)(x+4)(x+5).(x+3)(x+4)(x+5).
Как только мы найдем ЖК, нам нужно умножить каждое выражение на форму 1, что изменит знаменатель на ЖК. Нам нужно будет умножить выражение со знаменателем (x+3)(x+4)(x+3)(x+4) на x+5x+5x+5x+5, а выражение со знаменателем (x +4)(x+5)(x+4)(x+5) на x+3x+3. x+3x+3.
Как
Даны два рациональных выражения, сложите или вычтите их.
- Разложите числитель и знаменатель на множители.
- Найдите на ЖК-дисплее выражения.
- Умножьте выражения на форму 1, которая меняет знаменатели на LCD.
- Сложите или вычтите числители.
- Упростить.
Пример 4
Добавление рациональных выражений
Добавление рациональных выражений:
5x+6y5x+6y
Решение
Сначала нам нужно найти ЖК-дисплей. В этом случае ЖК-дисплей будет xy.xy. Затем мы умножаем каждое выражение на соответствующую форму 1, чтобы получить xyxy в качестве знаменателя для каждой дроби.
5x⋅yy+6y⋅xx5yxy+6xxy5x⋅yy+6y⋅xx5yxy+6xxy
Теперь, когда выражения имеют одинаковый знаменатель, мы просто складываем числители, чтобы найти сумму.
6x+5yxy6x+5yxy
Анализ
Умножение на yyyy или xxxx не изменяет значение исходного выражения, поскольку любое число, деленное само на себя, равно 1, а умножение выражения на 1 дает исходное выражение.
Пример 5
Вычитание рациональных выражений
Вычесть рациональные выражения:
6×2+4x+4-2×2-46×2+4x+4-2×2-4
Решение
6(x+2)2−2(x+2)(x−2)Коэффициент.6(x+2)2⋅x−2x−2−2(x+2)(x−2)⋅x+ 2x+2Умножьте каждую дробь, чтобы получить LCD в качестве знаменателя.6(x−2)(x+2)2(x−2)−2(x+2)(x+2)2(x−2)Multiply.6x− 12−(2x+4)(x+2)2(x−2)Применить распределительное свойство.4x−16(x+2)2(x−2)Вычесть.4(x−4)(x+2)2 (x−2)Упрощение.6(x+2)2−2(x+2)(x−2)Коэффициент.6(x+2)2⋅x−2x−2−2(x+2)(x −2)⋅x+2x+2Умножьте каждую дробь, чтобы получить LCD в качестве знаменателя.6(x−2)(x+2)2(x−2)−2(x+2)(x+2)2(x− 2) Умножить.6x−12−(2x+4)(x+2)2(x−2)Применить распределительное свойство. 4x−16(x+2)2(x−2)Вычесть.4(x−4) (x+2)2(x−2)Упростить.
вопросы и ответы
Должны ли мы использовать ЖК-дисплей для сложения или вычитания рациональных выражений?
Нет. Подойдет любой общий знаменатель, но проще всего использовать ЖК-дисплей.
Попробуй это #4
Вычтите рациональные выражения: 3x+5-1x-3,3x+5-1x-3.
Упрощение сложных рациональных выражений
Комплексное рациональное выражение — это рациональное выражение, которое содержит дополнительные рациональные выражения в числителе, знаменателе или в обоих. Мы можем упростить сложные рациональные выражения, переписав числитель и знаменатель как отдельные рациональные выражения и разделив их. Сложное рациональное выражение a1b+ca1b+c можно упростить, переписав числитель как дробь a1a1 и объединив выражения в знаменателе как 1+bcb. 1+bcb. Затем мы можем переписать выражение как задачу на умножение, используя обратную величину знаменателя. Получаем a1⋅b1+bc,a1⋅b1+bc, что равно ab1+bc.ab1+bc.
Как
Дано сложное рациональное выражение, упростите его.
- Объедините выражения в числителе в одно рациональное выражение путем сложения или вычитания.
- Объединить выражения в знаменателе в одно рациональное выражение путем сложения или вычитания.
- Перепишите как числитель разделить на знаменатель.
- Переписать как умножение.
- Умножить.
- Упростить.
Пример 6
Упрощение сложных рациональных выражений
Упрощение: y+1xxyy+1xxy .
Решение
Начните с объединения выражений в числителе в одно выражение.
y⋅xx+1x Умножить на xx, чтобы получить LCD в качестве знаменателя. xyx+1xxy+1x Добавить числители.y⋅xx+1x Умножить на xx, чтобы получить LCD в качестве знаменателя.xyx+1xxy+1x Добавить числители.
Теперь числитель — это единственное рациональное выражение, а знаменатель — это единственное рациональное выражение.
xy+1xxyxy+1xxy
Мы можем переписать это как деление, а затем умножение.
xy+1x÷xyxy+1x⋅yxПереписать как умножение.y(xy+1)x2Умножить.xy+1x÷xyxy+1x⋅yxПереписать как умножение.y(xy+1)x2Умножить.
Попробуй это #5
Упрощение: xy-yxyxy-yxy
вопросы и ответы
Всегда ли можно упростить сложное рациональное выражение?
Да. Мы всегда можем переписать сложное рациональное выражение как упрощенное рациональное выражение.
1.6 Секционные упражнения
Устный
1.
Как можно использовать факторинг для упрощения рациональных выражений?
2.
Как с помощью ЖК-дисплея объединить два рациональных выражения?
3.
Скажите, верно или нет следующее утверждение, и объясните, почему: Вам нужно найти ЖК только при сложении или вычитании рациональных выражений.
Алгебраический
Для следующих упражнений упростите рациональные выражения.
4.
x2-16×2-5x+4×2-16×2-5x+4
5.
у2+10у+25у2+11у+30у2+10у+25у2+11у+30
6.
6а2-24а+246а2-246а2-24а+246а2-24
7.
9b2+18b+93b+39b2+18b+93b+3
8.
м-12м2-144м-12м2-144
9.
2×2+7x-44×2+2x-22×2+7x-44×2+2x-2
10.
6×2+5x-43×2+19x+206×2+5x-43×2+19x+20
11.
а2+9а+18а2+3а-18а2+9а+18а2+3а-18
12.
3c2+25c-183c2-23c+143c2+25c-183c2-23c+14
13.
12n2-29n-828n2-5n-312n2-29n-828n2-5n-3
В следующих упражнениях умножьте рациональные выражения и выразите произведение в простейшей форме.
14.
x2-x-62×2+x-6⋅2×2+7x-15×2-9×2-x-62×2+x-6⋅2×2+7x-15×2-9
15.
c2+2c−24c2+12c+36⋅c2−10c+24c2−8c+16c2+2c−24c2+12c+36⋅c2−10c+24c2−8c+16
16.
2d2+9d−35d2+10d+21⋅3d2+2d−213d2+14d−492d2+9d−35d2+10d+21⋅3d2+2d−213d2+14d−49
17.
10h3-9h-92h3-19h+24⋅h3-16h+645h3-37h-2410h3-9h-92h3-19h+24⋅h3-16h+645h3-37h-24
18.
6b2+13b+64b2-9⋅6b2+31b-3018b2-3b-106b2+13b+64b2-9⋅6b2+31b-3018b2-3b-10
19.
2d2+15d+254d2−25⋅2d2−15d+2525d2−12d2+15d+254d2−25⋅2d2−15d+2525d2−1
20.
6×2-5x-5015×2-44x-20⋅20×2-7x-62×2+9x+106×2-5x-5015×2-44x-20⋅20×2-7x-62×2+9х+10
21.
t2-1t2+4t+3⋅t2+2t-15t2-4t+3t2-1t2+4t+3⋅t2+2t-15t2-4t+3
22.
2n2−n−156n2+13n−5⋅12n2−13n+34n2−15n+92n2−n−156n2+13n−5⋅12n2−13n+34n2−15n+9
23.
36×2−256×2+65x+50⋅3×2+32x+2018×2+27x+1036×2−256×2+65x+50⋅3×2+32x+2018×2+27x+10
Для следующих упражнений разделите рациональные выражения.
24.
3y2-7y-62y2-3y-9÷y2+y-22y2+y-33y2-7y-62y2-3y-9÷y2+y-22y2+y-3
25.
6п2+п-128п2+18п+9÷6п2-11п+42п2+11п-66п2+п-128п2+18п+9÷6п2-11п+42п2+11п-6
26.
q2-9q2+6q+9÷q2-2q-3q2+2q-3q2-9q2+6q+9÷q2-2q-3q2+2q-3
27.
18d2+77d−1827d2−15d+2÷3d2+29d−449d2−15d+418d2+77d−1827d2−15d+2÷3d2+29d−449d2−15d+4
28.
16×2+18x-5532×2-36x-11÷2×2+17x+304×2+25x+616×2+18x-5532×2-36x-11÷2×2+17x+304×2+25x+6
29.
144b2-2572b2-6b-10÷18b2-21b+536b2-18b-10144b2-2572b2-6b-10÷18b2-21b+536b2-18b-10
30.
16а2-24а+94а2+17а-15÷16а2-94а2+11а+616а2-24а+94а2+17а-15÷16а2-94а2+11а+6
31.
22y2+59y+1012y2+28y−5÷11y2+46y+824y2−10y+122y2+59y+1012y2+28y−5÷11y2+46y+824y2−10y+1
32.
9×2+3x-203×2-7x+4÷6×2+4x-10×2-2x+19×2+3x-203×2-7x+4÷6×2+4x-10×2-2x+1
В следующих упражнениях сложите и вычтите рациональные выражения, а затем упростите.
33.
4x+10y4x+10y
34.
122q-63p122q-63p
35.
4а+1+5а-34а+1+5а-3
36.
с+23-с-44с+23-с-44
37.
у+3у-2+у-3у+1у+3у-2+у-3у+1
38.
х-1х+1-2х+32х+1х-1х+1-2х+32х+1
39.
3zz+1+2z+5z−23zz+1+2z+5z−2
40.
4pp+1−p+14p4pp+1−p+14p
41.
хх+1+уу+1хх+1+уу+1
Для следующих упражнений упростите рациональное выражение.
42.
6y-4xy6y-4xy
43.
2а+7бб2а+7бб
44.
x4-p8px4-p8p
45.
3а+b62b3a3а+b62b3а
46.
3x+1+2x-1x-1x+13x+1+2x-1x-1x+1
47.
аб-баа+бабаб-баа+баб
48.
2×3+4x7x22x3+4x7x2
49.
2cc+2+c-1c+12c+1c+12cc+2+c-1c+12c+1c+1
50.
xy-yxxy+yxxy-yxxy+yx
Реальные приложения
51.
Бренда укладывает плитку на пол в ванной. Площадь пола 15×2-8x-715×2-8x-7 футов 2 . Площадь одной плитки равна x2−2x+1ft2.x2−2x+1ft2. Чтобы найти необходимое количество плиток, упростите рациональное выражение: 15×2−8x−7×2−2x+1,15×2−8x−7×2−2x+1.
52.
Площадь двора Лицзюаня составляет 25×2−62525×2−625 футов 2 . Участок дерна имеет площадь x2−10x+25×2−10x+25 футов 2 . Разделите две области и упростите, чтобы найти, сколько кусков дерна нужно Лицзюань, чтобы покрыть ее двор.
53.
Элрой хочет замульчировать свой сад. Его сад x2+18x+81×2+18x+81 ft 2 . Один мешок мульчи покрывает x2−81×2−81 ft 2 . Разделите выражения и упростите, чтобы найти, сколько мешков мульчи нужно Элрою для мульчирования своего сада.
Расширения
Для следующих упражнений выполните данные операции и упростите.
54.
x2+x-6×2-2x-3⋅2×2-3x-9×2-x-2÷10×2+27x+18×2+2x+1×2+x-6×2-2x-3⋅2×2-3x-9×2-x-2÷ 10×2+27x+18×2+2x+1
55.
3y2-10y+33y2+5y-2⋅2y2-3y-202y2-y-15y-43y2-10y+33y2+5y-2⋅2y2-3y-202y2-y-15y-4
56.
4а+12а-3+2а-32а+34а2+9а4а+12а-3+2а-32а+34а2+9а
57.
x2+7x+12×2+x−6÷3×2+19x+288×2−4x−24÷2×2+x−33×2+4x−7×2+7x+12×2+x−6÷3×2+19x+288×2−4x−24÷ 2×2+x-33×2+4x-7
рациональных выражений
Выражение, представляющее собой отношение двух многочленов:
Это как дробь, но с многочленами.
Другие примеры:
| x 3 + 2x − 1 6x 2 | 2x + 9 x 4 − x 2 |
Также
| 1 2 − х 2 | Верхний полином «1», что нормально. |
| 2x 2 + 3 | Да, это так! Как можно было бы написать: 2x 2 + 3 1 |
Но не
| 2 − √(x) 4 − x | вершина не является полиномом (не допускается квадратный корень переменной) | |
1 − х 1 − 1/х | 1/x не допускается в многочлене |
В целом
Рациональная функция — это отношение двух многочленов P(x) и Q(x), подобное этому
f(x) = P(x) Q(x)
За исключением того, что Q(x) не может быть нулем (и везде, где Q(x)=0 не определено)
Нахождение корней рациональных выражений
«Корень» (или «ноль») — это когда выражение равно нулю : |
Чтобы найти корни рационального выражения нам нужно только найти корни верхний полином , пока Rational Expression находится в «самых низких терминах».
Так что же означает «самые низкие условия»?
Самые низкие условия
Что ж, дробь находится в наименьшем выражении, когда верхний и нижний множители не имеют общих делителей.
Пример: дроби
2 6 , а не в наименьшем выражении,
, так как 2 и 6 имеют общий делитель «2»
Но:
1 3 равно в наименьшем выражении,
, так как 1 и 3 не имеют общих делителей
Аналогично, Rational Expression находится в наименьших терминах, когда верхний и нижний не имеют общих делителей.
Пример: Rational Expressions
x 3 +3x 2 2x равно , а не в наименьшем выражении,
как x и 2 х 3 +3x 3x
имеют общий делитель «x»
Но
x 2 +3x 2 равно в наименьшем выражении,
как x 2 +3x и 2 не имеют общих делителей
Итак, чтобы найти корни рационального выражения:
- Привести рациональное выражение к наименьшим терминам,
- Затем найдите корни верхнего многочлена
Как найти корни? Прочтите «Решение полиномов», чтобы узнать, как это сделать.
Правильное против Неправильного
| Дроби могут быть правильными и неправильными: |
| (В «Неправильном» нет ничего плохого, это просто другой тип) |
И аналогично:
Rational Expression также может быть правильным или неправильным !
Но что делает многочлен больше или меньше?
Степень!
Для полинома с одной переменной Степень является наибольшим показателем этой переменной.
Примеры степени:
| 4x | Степень равна 1 (переменная без показателя степени фактически имеет показатель степени 1) | |
| 4x 3 − x + 3 | Степень 3 (наибольшая степень x) |
Вот как узнать, является ли рациональное выражение правильным или неправильным :
Правильно: степень верха меньше степени низа.
| Правильный: | 1 х + 1 | градусов (вверху) < градусов (внизу) |
Другой пример: x x 3 − 1
Неправильно: степень верхней части больше или равна степени нижней.
| Неправильный: | х 2 − 1 х + 1 | градусов (вверху) ≥ градусов (внизу) |
Другой пример: 4x 3 − 3 5x 3 + 1
Если полином неправильный, мы можем упростить его с помощью Polynomial Long Division
Асимптоты
Рациональные выражения могут иметь асимптоты ( линия , к которой приближается кривая, стремясь к бесконечности):
Пример: (х
2 -3х)/(2х-2)График (x 2 -3x)/(2x-2) имеет:
|
Рациональное выражение может иметь:
- любое количество вертикальных асимптот,
- только ноль или одна горизонтальная асимптота,
- только ноль или одна косая (наклонная) асимптота
Нахождение горизонтальных или наклонных асимптот
Их довольно легко найти. ..
… но это зависит от степени верхнего полинома против нижнего .
Тот, у кого больше степень, будет расти быстрее.
Точно так же, как «Правильный» и «Неправильный», но на самом деле есть четыре возможных случая, показаны ниже.
(я показываю тестовое значение x=1000 для каждого случая, просто чтобы показать, что происходит)
Давайте рассмотрим каждый из этих примеров по очереди:
Степень верха
Меньше Чем низНижний многочлен будет доминировать, а в нуле находится горизонтальная асимптота.
Пример: f(x) = (3x+1)/(4x
2 +1)Когда x равно 1000:
f(1000) = 3001/4000001 = 0,00075…
И по мере увеличения x f(x) приближается к 0
Степень верха
равна низу Ни один из них не доминирует . .. асимптота задается старшими членами каждого многочлена.
Пример: f(x) = (3x+1)/(4x+1)
Когда x равно 1000:
f(1000) = 3001/4001 = 0,750…
И как x становится больше, f(x) приближается к 3/4
Почему 3/4? Потому что «3» и «4» являются «старшими коэффициентами» каждого полинома
.
Члены расположены в порядке от наибольшего к наименьшему показателю
(Технически 7 — константа, но здесь их все проще рассматривать как коэффициенты.)
Способ простой:
Разделите старший коэффициент верхнего полинома на старший коэффициент нижнего полинома.
Вот еще пример:
Пример: f(x) = (8x
3 + 2x 2 − 5x + 1)/(2x 3 + 15x + 2)Степени равны (оба имеют степень 3)
Просто взгляните на старшие коэффициенты каждого полинома:
- Вершина равна 8 (из 8x 3 )
- Нижний 2 (из 2x 3 )
Таким образом, существует горизонтальная асимптота 8/2 = 4
Степень Верхнего
1 Больше Чем Нижнего Это частный случай: имеется наклонная асимптота , и нам нужно найти уравнение прямой.
Чтобы вычислить это, используйте полиномиальное длинное деление: разделите верх на низ, чтобы найти частное (оставшуюся часть игнорируйте).
Пример: f(x) = (3x
2 +1)/(4x+1)Степень вершины равна 2, а степень основания равна 1, поэтому будет наклонная асимптота
Нам нужно разделить 3x 2 +1 на 4x+1 с помощью полиномиального длинного деления:
Игнорируя остаток, получаем решение (из вершины длинного деления):
Асимптота линия : 3 4 x − 3 16
Верхний угол равен
Более чем на 1 больше НижнийКогда верхний полином больше 1 степени выше нижнего полинома, нет ни горизонтальной, ни наклонной асимптоты .
Пример: f(x) = (3x
3 +1)/(4x+1)Степень верха равна 3, а степень низа равна 1.
Вершина больше 1 градуса выше основания, поэтому нет горизонтальной или наклонной асимптоты .