ГДЗ Дорофеев Контрольная работа 2
Админ
Алгебра 8 класс. ГДЗ Дорофеев Контрольная работа 2 «Степень с целым показателем» (4 варианта, три уровня сложности). Решения и ответы на контрольные работы из пособия для 8 класса (Кузнецова, Минаева, Рослова, Суворова) — М. : Просвещение.
Вернуться к Списку контрольных работ (ОГЛАВЛЕНИЕ).
Алгебра 8 класс. УМК Дорофеев Контрольная работа № 2. Вариант 1
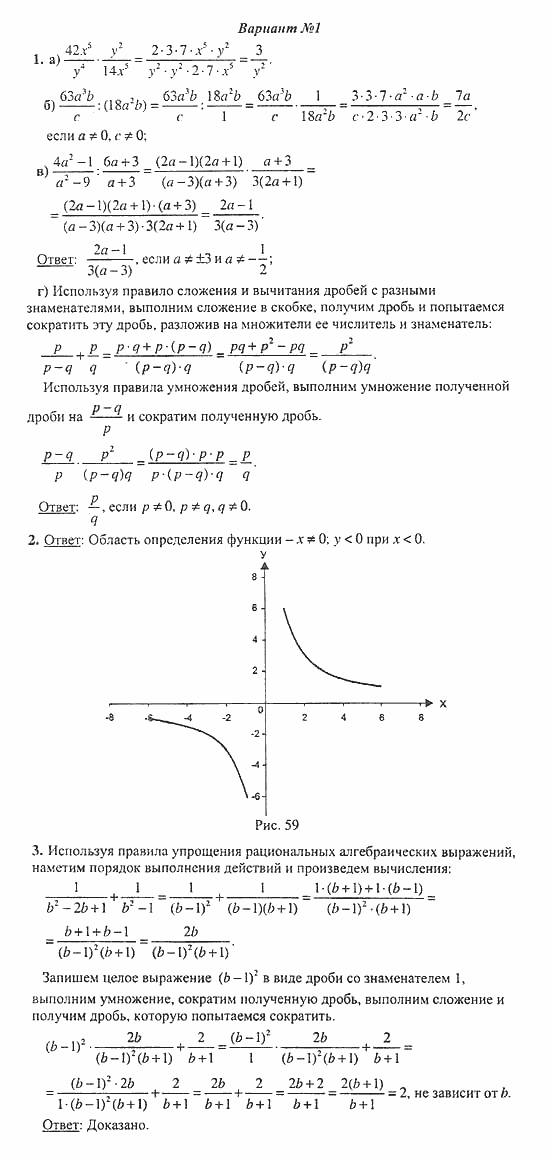
Решения и Ответы на Вариант 1
Контрольная работа № 2. Вариант 2
Решения и Ответы на Вариант 2
Контрольная работа № 2. Вариант 3
Решения и Ответы на Вариант 3
 Вариант 4
Вариант 4Решения и Ответы на Вариант 4
Алгебра 8 класс. УМК ДорофеевКонтрольная работа № 2. Вариант 1
Степень с целым показателем (КР Кузнецова)
- Вычислите: 5–3; (–4)–2; (2/3)–1; (0,34)0.
- Запишите число 21,0376 в виде суммы разрядных слагаемых.
- а) Диаметр молекулы азота равен 3,7 • 10–7 мм. Выразите эту величину в микрометрах и запишите её десятичной дробью (1 мм = 1000 мкм).
б) Расстояние от Венеры – одной из планет Солнечной системы – до Солнца равно 1,08 • 108 км. Выразите это расстояние в млн км. - Упростите выражение: а) 2ах–1 • а–3x4; б) (a–3b4)/(a–5b–2).
- Представьте выражение в виде степени с основанием х:
a) (x–8x10)/x4; б) (x–6/x–8)–3.
- Найдите значение выражения 25–4 • 58.
- Сравните (1,8 • 10–3) • (2 • 10–4) и 3,6 • 10–8.
- Найдите значение выражения 2–10 • 16–3 • (1/4)–10.
- Расположите в порядке возрастания числа (2/3)–4; 2/3; (3/2)–4; (3/2)0.
- Сократите дробь (25 • 15n)/(3n–2 • 5n+2).
Дополнительное задание
*11. Сравните а2 и а–2, если известно, что 0 < а < 1. Запишите свои рассуждения. Приведите конкретный пример, иллюстрирующий ваш вывод.
Решения и Ответы на Вариант 1
Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ заданий в тетради
Контрольная работа № 2. Вариант 2
Вверх
Решения и Ответы на Вариант 2Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ заданий в тетради
Контрольная работа № 2.
 Вариант 3
Вариант 3Вверх
Решения и Ответы на Вариант 3Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ заданий в тетради
Контрольная работа № 2. Вариант 4
Вверх
Решения и Ответы на Вариант 4Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ заданий в тетради
Вверх
Вы смотрели: Алгебра 8 класс. ГДЗ Дорофеев Контрольная работа 2 «Степень с целым показателем» (4 варианта, три уровня сложности). Решения и ответы на контрольные работы из пособия для 8 класса (Кузнецова, Минаева, Рослова, Суворова)
Какие умения проверяются:
- находить значения степеней с целым отрицательным показателем;
- записывать числа в виде суммы разрядных слагаемых с использованием целых степеней числа 10;
- использовать запись в стандартном виде больших и малых чисел, являющихся результатом измерения различных объектов и процессов в окружающем мире; выполнять действия с числами, записанными в стандартном виде;
- применять свойства степеней для преобразования выражений, содержащих степени с целым показателем;
- применять преобразование выражений, содержащих степени с целым показателем, для решения различных задач.

Вернуться к Списку контрольных работ (ОГЛАВЛЕНИЕ).
Просмотров: 43 993
АлгебраконтрольныеКонтрольные работы 8 класса по алгебре | Тест по алгебре (8 класс):
Контрольные работы по алгебре в 8 классе
Контрольная работа №1. 8 класс.
Вариант 1.
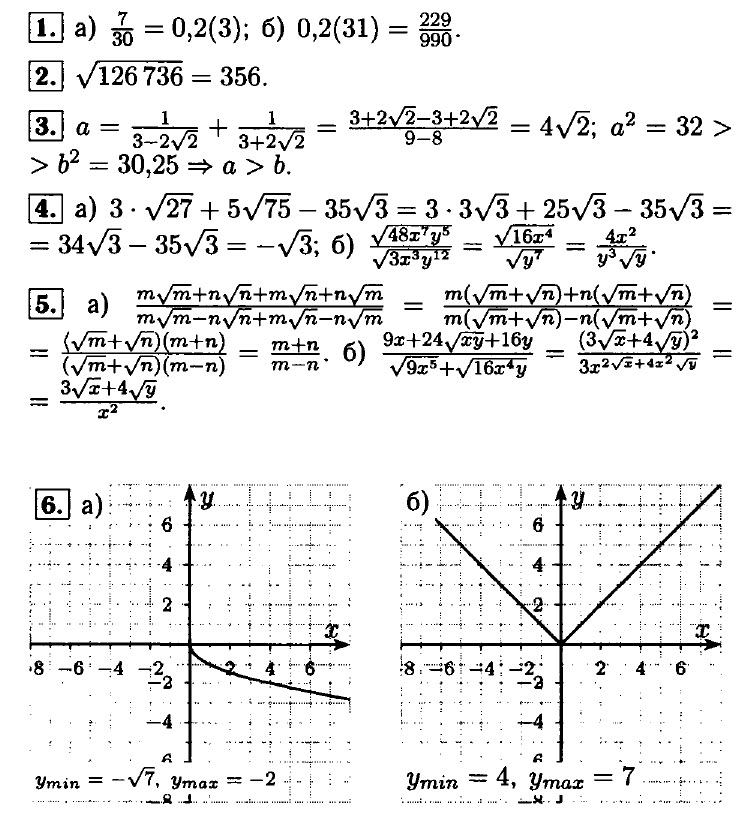
1. Сократите дробь:
2. Представьте в виде дроби:
3. Найдите значение выражения при
4. Упростить выражение:
Контрольная работа №1. 8 класс.
Вариант 2.
1. Сократите дробь:
2. Представьте в виде дроби:
3. Найдите значение выражения при
4. Упростить выражение:
Контрольная работа №2. 8 класс.
Рациональные выражения.
1 вариант.
1. Представьте выражение в виде дроби:
2. Постройте график функции . Какова область определения функции? При каких значениях функция принимает отрицательные значения?
3. Докажите, что при всех значениях значение выражения не зависит от .
Контрольная работа №2. 8 класс.
Рациональные выражения.
2 вариант.
1. Представьте выражение в виде дроби:
2. Постройте график функции . Какова область определения функции? При каких значениях функция принимает отрицательные значения?
3. Докажите, что при всех значениях значение выражения не зависит от .
Контрольная работа №3. 8 класс.
1 вариант.
1. Вычислите: а) б) в)
2. Найдите значение выражения:
а)
3. Решить уравнения: а)
4. Упростить выражение: а)
5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число
6. Имеет ли корни уравнение
2 вариант.
1. Вычислите: а) б) в)
2. Найдите значение выражения:
а)
3. Решить уравнения: а)
4. Упростить выражение: а)
5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число
6. Имеет ли корни уравнение
Контрольная работа № 4
1 вариант.
1. Упростите выражение:
2. Сравните:
3. Сократите дробь:
4. Освободитесь от иррациональности в знаменателе:
5. Докажите, что значение выражения есть число рациональное.
2 вариант.
1. Упростите выражение:
2. Сравните:
3. Сократите дробь:
4. Освободитесь от иррациональности в знаменателе:
5. Докажите, что значение выражения есть число рациональное.
Контрольная работа №5. 8 класс.
Квадратные уравнения.
1 вариант.
1. Решите уравнения:
2. Периметр прямоугольника 20 см. Найдите его стороны, если известно, что площадь прямоугольника 24см².
3. В уравнении один из корней равен -9. Найдите другой корень и коэффициент p.
Контрольная работа №5. 8 класс.
Квадратные уравнения.
2 вариант.
1. Решите уравнения:
2. Периметр прямоугольника 30 см. Найдите его стороны, если известно, что площадь прямоугольника 36см².
3. В уравнении один из корней равен -7. Найдите другой корень и коэффициент q.
Найдите другой корень и коэффициент q.
Контрольная работа №6. 8 класс.
1 вариант.
1. Решить уравнение: а) б)
2. Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В?
2 вариант.
1. Решить уравнение: а) б)
2. Катер прошел 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему понадобилось бы, если бы он шел 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч?
Контрольная работа №7. 8 класс.
1 вариант.
1. Докажите неравенство:
2. Известно, что . Сравните:
3. Известно, что . Оцените:
4. Оцените периметр и площадь прямоугольника со сторонами см и см, если известно, что
Оцените периметр и площадь прямоугольника со сторонами см и см, если известно, что
5. К каждому из чисел 2, 3, 4 и 5 прибавили одно и тоже число . Сравните произведение крайних членов получившейся последовательности с произведением средних членов.
Контрольная работа №7. 8 класс.
2 вариант.
1. Докажите неравенство:
2. Известно, что . Сравните:
3. Известно, что . Оцените:
4. Оцените периметр и площадь прямоугольника со сторонами см и см, если известно, что
5. К каждому из чисел 6, 5, 4 и 3 прибавили одно и тоже число . Сравните произведение крайних членов получившейся последовательности с произведением средних членов.
Math Placement Policy & Algebra 1 Руководство по завершению для средней и старшей школы
Connecting Waters Math Placement Policy & Algebra 1 Руководство по завершению для средней и старшей школы
Эта политика описывает использование местных и государственных данных, чтобы гарантировать, что все учащиеся 9-12 классов, которые не учатся по математике на уровне своего класса, получают надзор и поддержку от Эффективного педагога (EE) для подготовки и демонстрации знаний по алгебре 1.
Учащиеся, которые не продемонстрировали уровень владения математикой по стандарту 8, должны будут иметь контроль EE за курсовой работой Pre-Algebra или Algebra 1. Это можно сделать несколькими способами:
- a-g Algebra 1 (CMS или утвержденный поставщик a-g (Apex),
- Интенсивный курс CMS с квалифицированным инструктором по математике (EE) с использованием утвержденной высококачественной учебной программы, соответствующей стандартам, которая была создана для обеспечения дополнительной поддержки.
Каждый из вышеперечисленных вариантов может предложить различный уровень учебной поддержки и темпа, как указано ниже. ES должны тесно сотрудничать со своими учащимися и их семьями, чтобы определить наилучший вариант для каждого учащегося.
Кроме того, учащиеся, работающие выше уровня своего класса (в средних 6-8 классах) для прохождения Алгебры 1, также должны иметь EE Надзор, как указано ниже.
Учащиеся 9-х классов, показавшие уровень владения стандартами для 8-х классов (подтвержденный CAASPP и/или iReady), могут пройти курс алгебры 1 под наблюдением назначенного им ES, используя утвержденную учебную программу, которая соответствует стандартам штата или превосходит их, как указано ниже.
- SB359: (Закон о приеме на работу по математике от 2015 г.): «Успеваемость учащихся по математике важна для подготовки учащихся к поступлению в колледж и их будущей карьере, особенно карьере в области естественных наук, технологий, инженерии и математики (STEM). . Попадание на соответствующие курсы математики имеет решающее значение для ученика в средние и старшие классы. Поступление ученика в 9-й класс на курс математики является важным перекрестком для его или ее будущего успеха в учебе. Неправильное размещение в последовательности математических курсов создает ряд барьеров и приводит к тому, что ученики менее конкурентоспособны при поступлении в колледжи, в том числе при поступлении в Калифорнийский государственный университет и Калифорнийский университет».
- Калифорнийский закон о распределении учащихся по математике от 2015 г. требует от руководящих советов или органов местных образовательных агентств (LEA), которые обслуживают учащихся, поступающих в девятый класс, и которые еще не сделали этого, принять «справедливую, объективную и прозрачную политику распределения предметов по математике» до начало 2016-2017 учебного года.

- Систематически принимает во внимание многочисленные объективные показатели успеваемости учащихся;
- Включает как минимум одну контрольную точку в течение первого месяца учебного года, чтобы обеспечить точное зачисление и позволить переоценить индивидуальный прогресс учащегося;
- Требуется ежегодная проверка данных о размещении учеников, чтобы гарантировать, что учащиеся не задерживаются непропорционально на основании их расы, этнической принадлежности, пола или социально-экономического положения;
- Требуется отчет о результатах ежегодного экзамена местного агентства по образованию своему руководящему совету или органу
- Предлагает четкую и своевременную помощь каждому учащемуся и его или ее родителю или законному опекуну, который сомневается в размещении учащегося.
- Калифорнийский закон о распределении учащихся по математике от 2015 г. требует от руководящих советов или органов местных образовательных агентств (LEA), которые обслуживают учащихся, поступающих в девятый класс, и которые еще не сделали этого, принять «справедливую, объективную и прозрачную политику распределения предметов по математике» до начало 2016-2017 учебного года.
- AB220: Кроме того, в Законе о собрании 220 говорится: «.
 .. до того, как учащийся получит аттестат об окончании средней школы, учащийся должен пройти по крайней мере один курс или комбинацию двух курсов, необходимых для получения диплома, который соответствует или превышает строгость алгебры I или математики I, что соответствует стандартам содержания, принятым государственным советом. Законопроект будет предусматривать, что учащийся, который завершает курсовую работу, которая соответствует или превышает стандарты содержания для алгебры I, принятые советом штата, считается выполнившим требование об окончании школы. Законопроект также освобождает от обязательных выпускных экзаменов по алгебре I или математике I тех учеников, которые до зачисления в 9-й класс, прошел курс алгебры I или математики I или курсы математики равной строгости, которые соответствуют стандартам содержания, принятым советом штата ».
.. до того, как учащийся получит аттестат об окончании средней школы, учащийся должен пройти по крайней мере один курс или комбинацию двух курсов, необходимых для получения диплома, который соответствует или превышает строгость алгебры I или математики I, что соответствует стандартам содержания, принятым государственным советом. Законопроект будет предусматривать, что учащийся, который завершает курсовую работу, которая соответствует или превышает стандарты содержания для алгебры I, принятые советом штата, считается выполнившим требование об окончании школы. Законопроект также освобождает от обязательных выпускных экзаменов по алгебре I или математике I тех учеников, которые до зачисления в 9-й класс, прошел курс алгебры I или математики I или курсы математики равной строгости, которые соответствуют стандартам содержания, принятым советом штата ».- Навыки алгебры не только необходимы для окончания средней школы, но и являются ключевыми для поступления на курсы высшей математики.
 Поэтому важно, чтобы учащиеся продемонстрировали владение алгеброй, если курс будет пройден в раннем возрасте (до школы). Кроме того, учащиеся, получившие зачет по курсу, должны соответствовать стандартам, указанным выше, или превосходить их.
Поэтому важно, чтобы учащиеся продемонстрировали владение алгеброй, если курс будет пройден в раннем возрасте (до школы). Кроме того, учащиеся, получившие зачет по курсу, должны соответствовать стандартам, указанным выше, или превосходить их. - Департамент образования Калифорнии напоминает нам, что:
- Стандарты алгебры I можно и нужно преподавать всем учащимся, в том числе учащимся с ограниченными возможностями. Этим учащимся должен быть предоставлен доступ к общеобразовательной программе, чтобы вооружить их практическими жизненными навыками, которые им понадобятся для достижения успеха в 21 веке. Они могут быть не в состоянии завершить курс за стандартное время, и им может потребоваться более одного класса для завершения курса обучения. Кроме того, им могут понадобиться практические способы демонстрации навыков и компетенций, например, с помощью манипулятивных средств и с помощью калькуляторов. Им также могут потребоваться дополнительные учебные материалы, отвечающие их потребностям в обучении.
 Тем не менее, важно обеспечить, чтобы Всем учащимся была предоставлена возможность доступа к стандартам общеобразовательной программы.
Тем не менее, важно обеспечить, чтобы Всем учащимся была предоставлена возможность доступа к стандартам общеобразовательной программы. - В прошлом многие учащиеся направлялись в базовый курс математики общего или коррекционного уровня, что ограничивало их возможности пройти Алгебру I, критический курс начального уровня. Чтобы гарантировать, что учащиеся из групп риска пройдут обучение по такому важному курсу, как алгебра I, ES может потребоваться помощь в разработке учебного плана и инструкций, отвечающих потребностям их учащихся.
- Стандарты алгебры I можно и нужно преподавать всем учащимся, в том числе учащимся с ограниченными возможностями. Этим учащимся должен быть предоставлен доступ к общеобразовательной программе, чтобы вооружить их практическими жизненными навыками, которые им понадобятся для достижения успеха в 21 веке. Они могут быть не в состоянии завершить курс за стандартное время, и им может потребоваться более одного класса для завершения курса обучения. Кроме того, им могут понадобиться практические способы демонстрации навыков и компетенций, например, с помощью манипулятивных средств и с помощью калькуляторов. Им также могут потребоваться дополнительные учебные материалы, отвечающие их потребностям в обучении.
- Навыки алгебры не только необходимы для окончания средней школы, но и являются ключевыми для поступления на курсы высшей математики.
- AB705: Кроме того, Закон о собрании 705 – это законопроект, подписанный губернатором 13 октября 2017 года и вступивший в силу 1 января 2018 года. Законопроект требует, чтобы район муниципального колледжа или колледж максимизировал вероятность того, что учащийся завершить курсовую работу на уровне перевода по английскому языку и математике в течение одного года и использовать при распределении учащихся на курсы английского языка и математики один или несколько из следующих параметров: курсовая работа в средней школе, оценки в средней школе и средний балл в средней школе.
 Поскольку на уровне колледжа предлагается меньше коррекционных курсов, еще более важно, чтобы учащиеся заканчивали обучение на этих курсах.
Поскольку на уровне колледжа предлагается меньше коррекционных курсов, еще более важно, чтобы учащиеся заканчивали обучение на этих курсах.
Начиная со средней школы, учащиеся, как правило, выбирают разные пути в своем математическом образовании, при этом продвинутые учащиеся могут по-прежнему пройти Алгебру 1 в средней школе, что направит их на путь к завершению Математического анализа в старшей школе. Ниже приведены лишь некоторые из приемлемых сценариев последовательности курсов по математике в средних и старших классах.
- Имейте в виду, что учащиеся младше среднего школьного возраста получают зачеты только в том случае, если они соответствуют критериям, изложенным в этих правилах: Правила школьного возраста и требования к выпускным экзаменам по алгебре перечислены ниже.
- Учащиеся, окончившие математические курсы уровня алгебры 1 или выше в средних школах ES, должны пройти « Курсы, которые посещают учащиеся, проходящие типовое обследование возраста HS » Несовершеннолетние учащиеся, потерявшие место, будут переведены на соответствующий курс.

Требования к выпускным экзаменам по алгебре будут выполнены учащимися средней школы ТОЛЬКО в том случае, если они:
- Выполнили и сдали экзамен на C- или выше a-g Алгебра 1 с утвержденным экзаменом по математике EE и тестом на готовность к геометрии.
- AWR должны отражать курсовую работу, которую выполняет студент. Если учащийся изучает алгебру, название курса основного соглашения должно быть a-g Algebra, а AWR должны быть выполнены. Кредит средней школы не будет выдан.
- Пройти курс алгебры 1 в средней школе CA, аккредитованной .
- Подтвердить через a-g Алгебра 2.
Примечание. Учащиеся, выполняющие General Algebra 1 в средней школе, не не соответствовали требованиям к выпускному делу, если только они не проверяют алгебру 1 с A-G Алгебра 2.
- . будет рекомендован курс их преподавателем ES и/или математикой 8-го класса после рассмотрения нескольких показателей данных, основанных на некоторых или всех следующих показателях:
- Курс 8 класса и успеваемость учащихся по этому курсу
- Балл по математике CAASPP 8-го класса
- Результаты диагностики I-Ready
- ES также могут проконсультироваться со своим консультантом, специалистом по математике и/или директором по учебной программе и оценке, если это необходимо.
- Диагностическая оценка iReady #1 будет завершена в течение первых 2 недель в школе для всех 9учащиеся й класса. iReady Diagnostic #3 можно использовать, если вернувшиеся восьмиклассники завершили оценку в предыдущем весеннем семестре.
- Для продвинутых учащихся 9-х классов, изучающих курс выше Алгебры 1, будет проведена проверка записей, чтобы обеспечить надлежащее зачисление в углубленную курсовую работу; учащиеся, не сдавшие соответствующие тесты на готовность, будут сдавать их в течение первого учебного месяца.

- ES учащихся 9-х классов определят рекомендацию по зачислению на основе вышеупомянутых критериев, а ES рассмотрят рекомендацию по зачислению с родителями во время первого собрания по учету успеваемости.
- Родители могут оспорить рекомендацию школы, попросив свой ES скорректировать размещение на курсе по своему усмотрению.
- Группа данных CWCS будет ежегодно дезагрегировать данные о зачислении учащихся 9-х классов по математике и предоставлять результаты администрации.
- Данные будут дезагрегированы по признаку расы, этнической принадлежности, пола и социально-экономического положения.
- Годовой отчет будет представлен Правлению CWCS.
Требования к выпускным экзаменам по алгебре по алгебре 1 Окончены в средней школе:
Требования к выпускным экзаменам по алгебре будут выполнены учащимися средней школы ТОЛЬКО в том случае, если они:
- 2 и 3 Учащиеся, которые не набрали по крайней мере 3 балла «Соответствует стандартам» или «4 балла выше стандарта» в CAASPP для 8-го класса или на уровне класса по диагностике I-Ready, могут НЕ сдавать общую алгебру 1) или интенсивную алгебру 1 с CWCS с использованием соответствующий учебный план, как указано ниже.
- Пройти курс алгебры 1 в аккредитованной средней школе
- Пройти курс алгебры 1 в общественном колледже или у одобренного онлайн-провайдера a-g
- Завершить и сдать экзамен по алгебре a-g 2 (CWCS или другая аккредитованная средняя школа)

- Примечание: любые курсы, на которые не распространяется вышеуказанная политика, должны быть одобрены Департаментом методического обучения (т. е.: кредит от школ за пределами США)
В соответствии с уставом школы учащиеся CWCS должны использовать учебную программу, которая позволит учащимся соответствовать требованиям Основных общегосударственных стандартов. Все стандарты должны быть включены в выбранную учебную программу. Все учащиеся относятся к первому уровню пирамиды RtI. Уровень 1 предлагает учебные стратегии, основанные на исследованиях, и должен включать сильную основную учебную программу. Если учащиеся не используют учебную программу, согласованную со стандартами, они рискуют получить «пробелы» в своем обучении, подвергая их риску дальнейшего отставания от своих сверстников. Все учащиеся, получившие кредит по алгебре 1, должны выбрать один из следующих вариантов ниже, чтобы обеспечить соответствие требованиям AB220.
Если учащиеся не используют учебную программу, согласованную со стандартами, они рискуют получить «пробелы» в своем обучении, подвергая их риску дальнейшего отставания от своих сверстников. Все учащиеся, получившие кредит по алгебре 1, должны выбрать один из следующих вариантов ниже, чтобы обеспечить соответствие требованиям AB220.
Учащиеся, получившие кредит a-g по алгебре 1 или a-g по математике 1, должны использовать утвержденный учебник в CWCS Course Outline.
Варианты курса «Общая алгебра 1» (доступны только для учащихся 9-го класса на уровне или выше):- Принятая государством программа учебника «Алгебра 1» или «Математика 1» или
- Согласованная со стандартами программа учебника по алгебре 1 или математике 1 с опубликованным объемом и согласованием последовательности с Калифорнийскими общими базовыми стандартами; или
- Учебная программа по алгебре 1 или математике 1 с одним из следующих соответствующих заполненных понятий и навыков рассматривает дополнительные рабочие тетради.
 ES должен будет подтвердить завершение следующего варианта рабочей книги: .
ES должен будет подтвердить завершение следующего варианта рабочей книги: .
- Базовая алгебра 1 от Houghton Mifflin
- Common Core Coach, алгебра I от Triumph Learning
- Алгебра 1. Общая основная практика и решение задач, Прентис Холл
Примечание. Дополнительная рабочая тетрадь «Концепции и навыки» должна быть заполнена полностью, если специалист по математике не получил одобрение с согласованием. ES должны собирать по крайней мере 1 образец в каждый период обучения из вышеуказанного стандартного приложения после его завершения для документации и хранить в личном деле учащегося.
- Другие варианты учебных программ могут быть представлены специалисту по математике для рассмотрения и возможного утверждения. Материалы должны включать полное оглавление, объем и последовательность, а также минимум 3 примера уроков из учебника. Важно помнить, что многие популярные учебные программы для отстающих учащихся НЕ соответствуют или не превосходят стандарты содержания, если они используются в качестве отдельной основной учебной программы.
 Сюда входят такие учебные программы, как Acellus, AGS Algebra, Teaching Textbooks Algebra и Math-U-See Algebra, которые не соответствуют текущим стандартам контента CA Algebra 1.
Сюда входят такие учебные программы, как Acellus, AGS Algebra, Teaching Textbooks Algebra и Math-U-See Algebra, которые не соответствуют текущим стандартам контента CA Algebra 1.
Интенсивная алгебра 1 Варианты (доступны для учащихся младшего уровня, которым требуется дополнительная поддержка):
- Интенсивная алгебра CMS 1: Это двухгодичный курс, который проводится три дня в неделю. Будет предоставлена обширная поддержка и поддержка, а также дифференцированные задания и оценки для студентов.
- APEX CTV: Учащиеся могут пройти годичный или двухлетний курс Apex Algebra 1.
Дополнительные рекомендации
Дополнительные рекомендации по обеспечению всеобщего доступа к обучению математике см. в Основах математики для государственных школ Калифорнии, от детского сада до двенадцатого класса.
Часто задаваемые вопросы по средней школе
Какова последовательность курсов для средних и старших классов?
Чем курсы CCSS Math 8 и CCSS Algebra 1 отличаются от старого курса Algebra 1?
Могут ли учащиеся пропустить CCSS Math 8 и перейти сразу к CCSS Algebra 1?
Смогут ли учащиеся сдавать AP Calculus в старшей школе?
Почему ученики не могут ускориться в средней школе?
Какова последовательность курсов для средних и старших классов? | Это последовательность курсов, принятая Советом по образованию SFUSD в феврале 2014 года. Последовательность математических курсов SFUSD обеспечивает прочную основу для средних классов, которая не только помогает всем учащимся успешно выполнить требование UC «c», но и готовит их к математике в колледже. Наличие одной основной последовательности обеспечивает целенаправленность и согласованность по мере того, как школы и учителя внедряют CCSS-M, и поддерживает равенство, создавая путь для всех учащихся к изучению точных математических знаний. Точки принятия решения указывают, где учащиеся и их семьи могут выбирать различные варианты курса в зависимости от своих целей. Различные варианты обучения в старших классах представлены на нашей странице Путеводители по математике в старших классах . Узнайте больше о нашей последовательности вторичных курсов. |
Чем курсы CCSS Math 8 и CCSS Algebra 1 отличаются от старого курса Algebra 1? | Стандарты, которые определяли курс алгебры 1 в соответствии со старыми стандартами Калифорнии, теперь разделены между курсом CCSS Math 8 и курсом CCSS Algebra 1, как показано ниже. |
Могут ли учащиеся пропустить CCSS Math 8 и перейти сразу к CCSS Algebra 1? | Нет. CCSS Math 8 представляет новый обширный материал по математике, и это не тот курс, который можно пропустить. Содержание последовательности курсов средних классов (CCSS Math 6, CCSS Math 7 и CCSS Math 8) имеет важное значение для подготовки учащихся как к CCSS Algebra 1, так и к CCSS Geometry в старшей школе. Авторы Common Core разработали намеренную вертикальную связь алгебраических и геометрических тем от классов K–8 до средней школы. CCSS Algebra 1 основывается на содержании, которое учащиеся изучают в CCSS Math 8, и не повторяет содержание CCSS Math 8. CCSS Algebra 1 также намного более строгий, чем старая CA Algebra 1. 9-классники SFUSD автоматически помещаются в SFUSD 9курс математики для 1-го класса, CCSS Algebra 1. Однако некоторые учащиеся прошли курс алгебры 1 за пределами SFUSD до 9-го класса. Если ваш ребенок будет поступать в 9-й класс и завершил или завершает годичный курс алгебры 1 либо в своей средней школе, либо в аккредитованной средней школе или колледже, и он желает быть рассмотренным для после поступления в CCSS Geometry в 9-м классе они могут получить право на прохождение Math Validation Test (MVT). Содержание курса и поставщики должны быть проверены и одобрены SFUSD, чтобы иметь право на участие. Курсы оцениваются после того, как абитуриенты отправят документацию о своей курсовой работе. |
Смогут ли учащиеся сдавать AP Calculus в старшей школе? | Да, удвоив или сжав курсы в старшей школе. Из-за существенного характера всех курсов CCSS учащиеся больше не могут ускориться в математике, пропустив курс. Последовательность средних курсов включает в себя возможность ускориться в старшей школе, сжав CCSS Algebra 2 с предварительным исчислением в годичный курс. Другой вариант — удвоить количество занятий по математике в течение одного года старшей школы. Вы можете увидеть графическое представление различных вариантов на странице Путеводители по математике в средней школе . В зависимости от того, какие учащиеся старших классов посещают, у них есть один из следующих возможных вариантов (1, 2 или 3) для перехода к программе AP Calculus в старшем классе. Вариант 1:
, если ученик по желанию станет для участия в AP Calculus , если студент по желанию. год без курса компрессии, есть два варианта, которые включают в себя «удвоение» и один вариант, который включает интенсивный курс летней геометрии между 9 и 10 классами. Вариант 2:
Вариант 3:
В любом из вариантов 2 или 3 выше, геометрия — это курс, который может быть объединен с другим курсом, поскольку содержание геометрии зависит от математики CCSS Grade 8, а не от алгебры 1, а алгебра 2 не слишком зависит от содержания геометрии. |




 .. до того, как учащийся получит аттестат об окончании средней школы, учащийся должен пройти по крайней мере один курс или комбинацию двух курсов, необходимых для получения диплома, который соответствует или превышает строгость алгебры I или математики I, что соответствует стандартам содержания, принятым государственным советом. Законопроект будет предусматривать, что учащийся, который завершает курсовую работу, которая соответствует или превышает стандарты содержания для алгебры I, принятые советом штата, считается выполнившим требование об окончании школы. Законопроект также освобождает от обязательных выпускных экзаменов по алгебре I или математике I тех учеников, которые до зачисления в 9-й класс, прошел курс алгебры I или математики I или курсы математики равной строгости, которые соответствуют стандартам содержания, принятым советом штата ».
.. до того, как учащийся получит аттестат об окончании средней школы, учащийся должен пройти по крайней мере один курс или комбинацию двух курсов, необходимых для получения диплома, который соответствует или превышает строгость алгебры I или математики I, что соответствует стандартам содержания, принятым государственным советом. Законопроект будет предусматривать, что учащийся, который завершает курсовую работу, которая соответствует или превышает стандарты содержания для алгебры I, принятые советом штата, считается выполнившим требование об окончании школы. Законопроект также освобождает от обязательных выпускных экзаменов по алгебре I или математике I тех учеников, которые до зачисления в 9-й класс, прошел курс алгебры I или математики I или курсы математики равной строгости, которые соответствуют стандартам содержания, принятым советом штата ». Поэтому важно, чтобы учащиеся продемонстрировали владение алгеброй, если курс будет пройден в раннем возрасте (до школы). Кроме того, учащиеся, получившие зачет по курсу, должны соответствовать стандартам, указанным выше, или превосходить их.
Поэтому важно, чтобы учащиеся продемонстрировали владение алгеброй, если курс будет пройден в раннем возрасте (до школы). Кроме того, учащиеся, получившие зачет по курсу, должны соответствовать стандартам, указанным выше, или превосходить их. Тем не менее, важно обеспечить, чтобы Всем учащимся была предоставлена возможность доступа к стандартам общеобразовательной программы.
Тем не менее, важно обеспечить, чтобы Всем учащимся была предоставлена возможность доступа к стандартам общеобразовательной программы.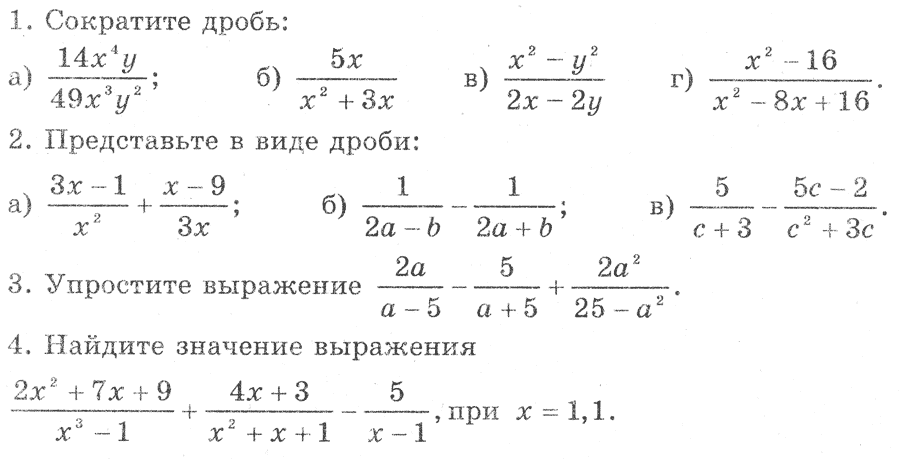 Поскольку на уровне колледжа предлагается меньше коррекционных курсов, еще более важно, чтобы учащиеся заканчивали обучение на этих курсах.
Поскольку на уровне колледжа предлагается меньше коррекционных курсов, еще более важно, чтобы учащиеся заканчивали обучение на этих курсах.

 ES должен будет подтвердить завершение следующего варианта рабочей книги:
ES должен будет подтвердить завершение следующего варианта рабочей книги: Сюда входят такие учебные программы, как Acellus, AGS Algebra, Teaching Textbooks Algebra и Math-U-See Algebra, которые не соответствуют текущим стандартам контента CA Algebra 1.
Сюда входят такие учебные программы, как Acellus, AGS Algebra, Teaching Textbooks Algebra и Math-U-See Algebra, которые не соответствуют текущим стандартам контента CA Algebra 1.  Курсы CCSS Math 8 и CCSS Algebra 1 также включают материалы из более продвинутых курсов средней школы и концепции, которые ранее не преподавались в средней школе по математике, особенно статистика.
Курсы CCSS Math 8 и CCSS Algebra 1 также включают материалы из более продвинутых курсов средней школы и концепции, которые ранее не преподавались в средней школе по математике, особенно статистика. Он предполагает, что учащиеся уже работали с линейными уравнениями и функциями, а затем расширяет их изучение нелинейных функций, включая квадратичные и экспоненциальные функции — темы, которые были введены в Алгебра 2 в прошлом. CCSS Algebra 1 также уделяет большое внимание статистике и применению алгебраических инструментов для решения сложных реальных задач.
Он предполагает, что учащиеся уже работали с линейными уравнениями и функциями, а затем расширяет их изучение нелинейных функций, включая квадратичные и экспоненциальные функции — темы, которые были введены в Алгебра 2 в прошлом. CCSS Algebra 1 также уделяет большое внимание статистике и применению алгебраических инструментов для решения сложных реальных задач.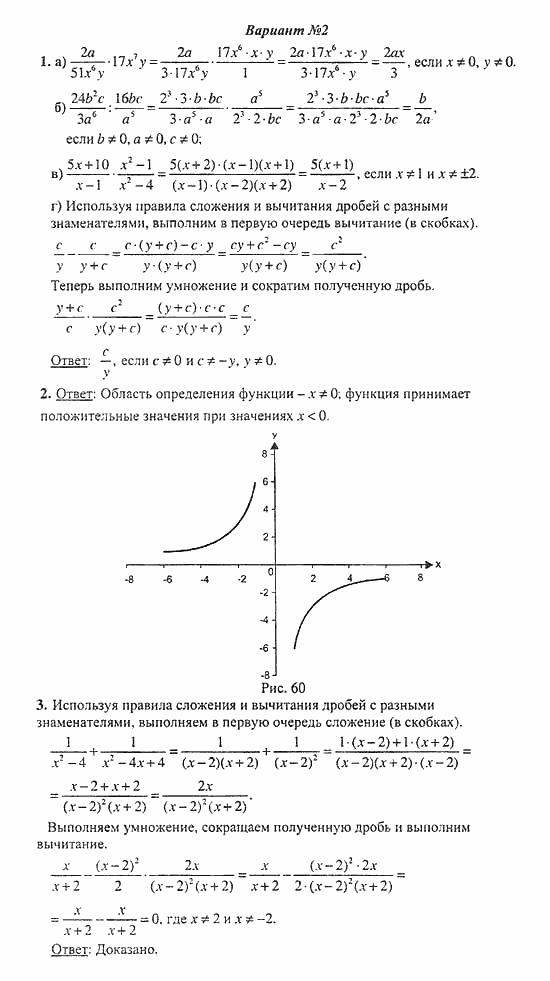 Этот тест не требуется; только студенты, которые хотят изучать геометрию на первом курсе, должны ее сдавать.
Этот тест не требуется; только студенты, которые хотят изучать геометрию на первом курсе, должны ее сдавать. 
