ГДЗ по Геометрии для 8 класса рабочая тетрадь Глазков Ю.А., Камаев П.М. на 5
Авторы: Глазков Ю.А., Камаев П.М..
Издательство: Экзамен 2014
Над созданием «ГДЗ по геометрии 8 класс Рабочая тетрадь Глазков, Камаев (Экзамен)» работали опытные методисты и педагоги. Они позаботились о том, чтобы все ответы в справочнике были изложены просто и лаконично. Это сделано для того, чтобы у школьников не возникало дополнительных проблем при выполнении домашнего задания. К тому же авторы проверили ключи, чтобы исключить малейшие неточности.
Геометрия в восьмом классе
В этом году не время расслабляться и изучать предмет лишь поверхностно. Школьникам предстоит познакомиться со следующими темами:
- Многоугольники.

- Теорема Пифагора.
- Подобные треугольники.
- Касательная и окружности.
- Понятие вектора.
- Площадь многоугольника.
Кроме изучения новых правил и формул, подросткам придется вспомнить освоенный ранее материал. Но даже у отличников к этому году накапливаются «хвосты» и пробелы в знаниях. И восполнить их своими силами очень сложно. Ведь материал из учебника зачастую изложен слишком сухо. Поэтому ребятам не обойтись без персонального консультанта. С этой ролью на отлично справится наш онлайн-консультант.
Главные преимущества решебника рабочей тетради по геометрии для 8 класса от Глазкова
Ученики, уже успевшие поработать с пособием, отмечают несколько важных достоинств справочника:
- – онлайн-формат, обеспечивающий круглосуточный доступ с любого гаджета;
- – понятная навигация;
- – быстрый поиск нужных номеров;
- – конфиденциальность;
- – отсутствие ошибок и т.
 д.
д.
Методисты и педагоги также позаботились о том, чтобы обеспечить максимальное понимание и усвоение нового материала. Свои ответы они дополнили яркими схемами и таблицами, также комментариями и пояснениями к заданиям. Во время создания «ГДЗ к рабочей тетради по геометрии за 8 класс Глазков Ю. А., Камаев П. М. (Экзамен)» методисты учли, что у школьников может быть разный уровень подготовки. Поэтому пользоваться справочником могут все ребята: и отличники, и двоечники. Первым решебник поможет проверить работу на ошибки и устранить малейшие неточности. А тем, кто сильно отстал от программы, пособие подскажет верные ответы, а также позволит подтянуть знания и отметки по дисциплине. Добиться же высоких результатов поможет только регулярная работа со справочником. При этом ребятам придется полностью отказаться от бездумного списывания.
ГДЗ по Геометрии для 8 класса рабочая тетрадь Универсальные учебные действия Глазков Ю.
 А., Егупова М.В. ФГОС
А., Егупова М.В. ФГОСАвторы: Глазков Ю.А., Егупова М.В..
Издательство: Экзамен 2017
Старшеклассник справится со школьным курсом математического раздела, благодаря обстоятельной удалённой поддержке сборника верных ответов – «ГДЗ по геометрии 8 класс Рабочая тетрадь Глазков, Егупова (Экзамен)». Геометрия хорошо влияет на развитие умственных способностей ребёнка. Проявляется абстрактное мышление, рациональность, быстрота реакции работы мозга. Ученик сможет по-новому взглянуть на мир, оценивать «перспективу», удаленность силуэтов, даже лучше рисовать, встречать знакомые очертания геометрических объектов.
Школьная программа по геометрии
Геометрия подготовила для восьмиклассника в этом году немало сложных тем. Проведём обзор наиболее интересных параграфов из учебно-методического комплекта:
Проведём обзор наиболее интересных параграфов из учебно-методического комплекта:- как применять подобие к доказательству теорем;
- что является вписанной окружностью;
- свойства пропорциональных отрезков в прямоугольном треугольнике.
«ГДЗ по геометрии 8 класс Рабочая тетрадь Глазков Ю.А., Егупова М.В. (Экзамен)» упростит познание точной технической дисциплины. Несмотря на сложность науки о геометрических понятиях, школьник может уверенно надеяться на итоговую положительную оценку благодаря поддержке решебника.
Положительные свойства решебника по геометрии за 8 класс от Глазкова
В пятом классе ребята освоят школьную программу геометрии, а также зарекомендуют себе положительную успеваемость благодаря проработке сложных параграфов и практических упражнений в паре с онлайн-решебником. Пособие соответствует современным реалиям поэтому размещено в интернете.
- удалённый доступ;
- досконально проверен специалистами;
- улучшает успеваемость;
- позволяет хорошо запомнить пройдённый материал;
- составлен простым языком, чтобы сойти за размышления самих детей подросткового возраста, и не вызвать подозрений у преподавателя.
Домашнее задание больше не будет восприниматься, как утомительное и тяжкое бремя. Ребёнок быстро с ним разберётся и «пойдёт по своим делам».
Ребёнок быстро с ним разберётся и «пойдёт по своим делам».
ГДЗ по геометрии 8 класс рабочая тетрадь Глазков Камаев
ГДЗ по геометрии 8 класс рабочая тетрадь Глазков КамаевАвторы: Ю. А. Глазков, П. М. Камаев
Издательство: Экзамен
Тип книги: Рабочая тетрадь
ГДЗ рабочая тетрадь Геометрия. 8 класс. ФГОС Ю. А. Глазкова, П. М. Камаева к учебнику Атанасяна. Издательство Экзамен. Серия Учебно–методический комплект. Состоит из одной части и 96 страниц. Имеет адаптацию к требованиям ФГОС.
Изучение такого предмета, как геометрия, будет способствовать развитию способности правильного восприятия и адекватной оценки поставленной учебной задачи. Ребята научатся решать задачи строго в соответствии с необходимым алгоритмом действий, самостоятельно ставить цель и находить наиболее рациональные пути к ее достижению. При решении заданий рабочей тетради школьникам предстоит проявить свои умения как работать в коллективе над поиском правильного ответа, так и пользоваться исключительно собственными силами при решении домашнего задания.
Многие родители не смогут полноценно проверить и оценить усилия восьмиклассников, потраченные для выполнения домашнего задания. Решебник
ГДЗ от ЯГДЗ окажет необходимую помощь всем учащимся, их родителям в этом нелегком деле.
Глава V. Четырёхугольники
§1. Многоугольники
А. 1 Б. 2 3 В. 4 5 Г. 6
§2. Параллелограмм и трапеция
А. 1 2 3 4 Б. 5 6 7 8 А. 9 10 11 А. 12 13 Б. В. Г. 14
§3. Прямоугольник, ромб, квадрат
А. 1 Б. 2 В. 3 4 5 6 А. 7 Б. 8 9 10 11 12 В. 13 14 15 16 А. 17 Б. 18 В. 19 Г. 20 21
Глава VI. Площадь
§1. Площадь многоугольника
А. 1 2 3 4 5 6 А.
§2. Площади параллелограмма, треугольника и трапеции
1 2 3 4 А.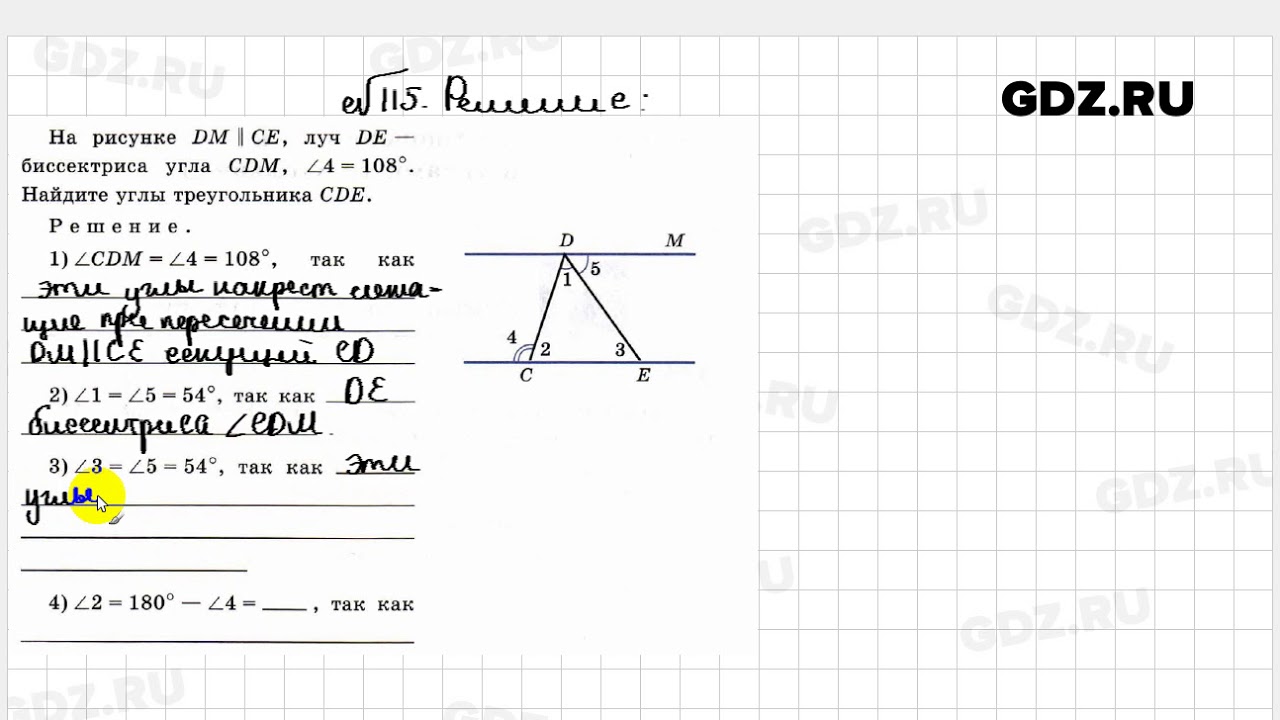 Б. 5 6 7 8 Б. В. 9 10
Б. 5 6 7 8 Б. В. 9 10
§3. Теорема Пифагора
А. 1 2 3 4 А. 5 6
Глава VII. Подобные треугольники
§1. Определение подобных треугольников
1 2 А. 3 4 Б. 5 6
§2. Признаки подобия треугольников
А. 1 2 А. 3 А. 4 5
§3. Применения подобия к доказательству теорем и решению задач
А. Б. 1 2 3 4 А. 5 Б. 6 7
§4. Соотношение между сторонами и углами прямоугольного треугольника
А. 1 2 Б. 3 А. Б. В. 4 5 6 7
Глава VIII. Окружность
§1. Касательная к окружности
1 2 3 А. А. Б.. В. Г.
§2. Центральные и вписанные углы
А. Б. 1 2 3 А. 4 Б. В. 5 6 7 8 Г. 9
§3. Четыре замечательные точки треугольни
А. Б. 1 2 В. 3 Г. 4 Д. Е. 5 6 Ж. 7 А. 8
§4. Вписанная и описанная окружности
А. 1 2 Б. 3 4 В. 5 6 А. 7 Б. 8 9 10 В. 11 12
Глава IX. Векторы
§1 Понятие вектора
А. 1 2 3 Б. 4 5 А. 6 Б. 7 В. 8 А. 9 10
§2. Сложение и вычитание векторов
А. 1 А. 2 3 А. 4 5 А. 6 Б. В. Г. 7 8 Д. 9 10 11
6 Б. В. Г. 7 8 Д. 9 10 11
§3. Умножение ветора на число. Применение вектров к решению задач
А. Б. 1 2 3 4 5 6 7 А. 8 Б. 9 10 11 12
← Назад
Другие ГДЗВперед →
ГДЗ по геометрии 8 класс рабочая тетрадь Глазков Ю.А., Камаев П.М.
Данный предмет в принципе не особо сложен, но ГДЗ по геометрии рабочая тетрадь 8 класс Глазков все же понадобятся. Эта наука достаточно легко воспринимается школьниками. Но все же среди них попадаются гуманитарии, которые никак не могут освоить многочисленные теоремы и алгоритмы решения. А это необходимо, ведь помимо упражнений, которых в этом году будет не мало, предстоит выполнять и периодические проверочные работы. На изучение нового материала обычно отводится только один урок и повторить его не всегда удается. Поэтому все необходимо усваивать сразу же. Но так как учащиеся не привыкли задавать учителям вопросы и выяснять все непонятные моменты, то это предстоит делать дома, самостоятельно. Однако подобные действия не так просты, как кажется с первого взгляда. Чтобы не опростоволоситься и все воспринять так, как надо, следует воспользоваться помощью решебника.
Однако подобные действия не так просты, как кажется с первого взгляда. Чтобы не опростоволоситься и все воспринять так, как надо, следует воспользоваться помощью решебника.
В чем польза ГДЗ по геометрии для рабочей тетради за 8 класс Глазкова
- детально проверить свои д/з;
- разыскать и устранить все неточности;
- подготовиться к тестированиям.
Справочник нужен не только отстающим по программе, но и отличникам, которые могут удостовериться в правильности своих познаний, либо скорректировать их при необходимости. Заодно можно улучшить качество знаний и сформировать нужные навыки.
Многих в наше время не устраивает, каким образом составлена программа обучения и в каком формате ребятам подаются знания. И действительно, очень многое учащимся приходится осваивать самим. Но многое ли они воспримут без должного руководства? К сожалению, со школьной системой ничего сделать нельзя, зато можно помочь школьникам и облегчить их участь. Для этого им нужно начать пользоваться решебником по геометрии к рабочей тетради для 8 класса (авторы: Глазков Ю. А., Камаев П. М.), в котором авторы подробно рассказывают обо всех нюансах. И даже если преподаватель не отличается особой старательностью, то подростки все равно получат всю необходимую информацию.
И действительно, очень многое учащимся приходится осваивать самим. Но многое ли они воспримут без должного руководства? К сожалению, со школьной системой ничего сделать нельзя, зато можно помочь школьникам и облегчить их участь. Для этого им нужно начать пользоваться решебником по геометрии к рабочей тетради для 8 класса (авторы: Глазков Ю. А., Камаев П. М.), в котором авторы подробно рассказывают обо всех нюансах. И даже если преподаватель не отличается особой старательностью, то подростки все равно получат всю необходимую информацию.
ГДЗ Геометрия 8 класс Глазков, Камаев
Геометрия 8 класс
Тип пособия: Рабочая тетрадь
Авторы: Глазков, Камаев
Издательство: «Экзамен»
Похожие ГДЗ Геометрия 8 класс
Задания: стр.4
Предыдущее
Следующее
Предыдущее
Следующее
Геометрия считается одним из важнейших предметов, ибо в конце девятого класса нужно будет сдавать экзамен.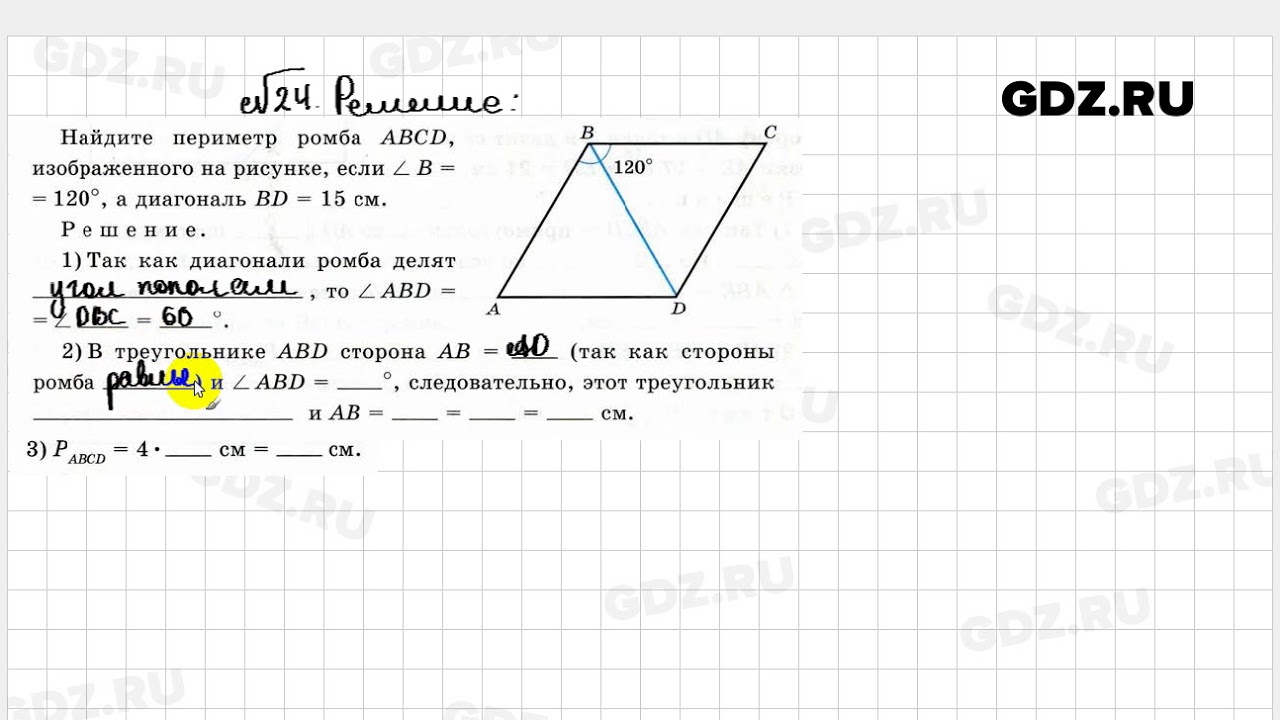 Подготовка учащихся начинается с восьмого класса. Многие преподаватели рекомендуют школьникам пользоваться подготовительными рабочими тетрадями и учебниками, чтобы лучше усвоить материал. Эта дисциплина сложна тем, что содержит в себе большое количество формул и правил, которые каждому ученику нужно выучить, чтобы удачно выполнить какое-нибудь задание или номер. Выполняя различные упражнения можно эффективно подготовиться ко всем проверочным работам, проводящиеся учителями на протяжении всего учебного года. Узнать верный ответ к любому заданию поможет решебник к учебнику «Геометрия 8 класс Рабочая тетрадь Глазков, Камаев» от издательства «Экзамен».
Подготовка учащихся начинается с восьмого класса. Многие преподаватели рекомендуют школьникам пользоваться подготовительными рабочими тетрадями и учебниками, чтобы лучше усвоить материал. Эта дисциплина сложна тем, что содержит в себе большое количество формул и правил, которые каждому ученику нужно выучить, чтобы удачно выполнить какое-нибудь задание или номер. Выполняя различные упражнения можно эффективно подготовиться ко всем проверочным работам, проводящиеся учителями на протяжении всего учебного года. Узнать верный ответ к любому заданию поможет решебник к учебнику «Геометрия 8 класс Рабочая тетрадь Глазков, Камаев» от издательства «Экзамен».
Темы для подробного рассмотрения
В восьмом классе появляется множество новых и соответственно сложных тем. Ребята иногда теряются из-за большого объема информации и им сложно понять, какая формула и теорема к какой теме относится. Вот список новых тем, которые нужно усвоить и подробно разобрать восьмиклассникам:
- Четырехугольники (параллелограмм, трапеция).

- Понятие площади многоугольника, параллелограмма.
- Теорема Пифагора (в будущем учащиеся часто будут стыкаться с этой теоремой).
Чем хорош решебник
В самой рабочей тетради есть много точных и четких вопросов, с помощью которых ученики смогут удачно подготовиться к итоговой аттестации. После прочтения учебника можно будет выполнить несколько упражнений и понять, ясна ли тема. В ГДЗ есть онлайн-ответы, полностью объясняющие тему и неясные моменты для восьмиклассника.
Как им пользоваться, чтобы были определенные результаты
Если просто списывать, не разбирая какой-нибудь номер, то от тетради с готовыми ответами пользы не будет, ведь в таком случае в голове не остается никаких знаний. Нужно тщательно рассматривать каждый непонятный номер, чтобы в дальнейшем удачно написать экзамен.
открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
класс 7А
Марка 7Б
Класс 7 (комбинированные A и B)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 8A
марка 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
марка 9А
Марка 9Б
Оценка 9 (вместе A и B)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 4A
класс 4Б
Класс 4 (A и B вместе)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (комбинированные A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 6А
класс 6Б
Класс 6 (вместе A и B)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими организациями, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (безымянные версии)
Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Amazon.com: Jet Beautiful A ++ Tiger Eye 7 камней Наборы сакральной геометрии Драгоценный камень Платонические твердые частицы высшего качества Звезда Меркаба с бархатным мешочком Привлекательная очищающая жизнь Жизнеспособность Исцеление Чакра Балансировка ДНК Активация энергетической решетки Медитация в прошлой жизни Мечта Работа Знание Прогресс Успех Успех Любовь Исцеление Божественный успех в бизнесе Воздух Вода Земля Огонь Дух Душа Разум Очищение тела Регресс жизни Возрождение Артрит Доктор Индия Веды Внутренняя сила Сила Мир Прогресс: Здоровье и дом
Информация по технике безопасности
Бесплатный 40-страничный буклет Jet International Crystal Therapy Book содержит глубокое понимание терапии кристаллами, балансировки чакр, очищения и программирования кристаллов, их использования на домашних животных, преимуществах, применениях и многих других подробностях.Исключительно Jet International Product
Показания
Бесплатный 40-страничный буклет Jet International Crystal Therapy Book дает глубокое понимание терапии кристаллами, балансировки чакр, очищения и программирования кристаллов, их использования на домашних животных, преимуществах, приложениях и многих других деталях. Любые оптовые заказы приветствуются. Не стесняйтесь написать нам.
Состав
История исцеления кристаллами Использование кристаллов восходит к древнеегипетским временам.Хотя они часто использовали драгоценные камни для украшений и косметики, они также использовали их для защиты и здоровья, например, для очищения от злых духов.
Проезд
История исцеления кристаллами: Использование кристаллов восходит к древнеегипетским временам. Хотя они часто использовали драгоценные камни для украшений и косметики, они также использовали их для защиты и здоровья, например, для очищения от злых духов.Слово «кристалл» происходит от греческого слова «лед» из-за веры в то, что прозрачный кварц — это вода, настолько глубоко замороженная, что она навсегда останется твердой.
Заявление об отказе от ответственности
Пожалуйста, обратите внимание, что у нас есть авторские права на этот продукт, и все наши продукты зарегистрированы под торговой маркой «Jet International»; любое копирование или использование наших списков запрещено. К любому, кто нарушит нашу политику, будут относиться очень серьезно. Это может лишить вас прав на продажу на торговой площадке Amazon.Бренд Jet International зарегистрирован в Индии и США, включая AMAZON Marketplace. Против любого лица, уличенного в использовании или копировании изображений или объявлений о наших продуктах, будет возбуждено судебное дело. Спасибо
Заявления о пищевых добавках не оценивались FDA и не предназначены для диагностики, лечения или предотвращения каких-либо заболеваний или состояний здоровья.
границ | Геометрическая теория, объединяющая бинокулярное зрение человека с движением глаз
1. Введение
Наши глаза получают две несопоставимые перспективные проекции сцены из-за их двустороннего разделения.Их двумерный (2D) слой фоторецепторов, снимающих эти проекции, является частью нестабильной схемы сетчатки. Это происходит из-за того, что наши глаза постоянно перемещаются 3–4 раза в секунду, чтобы последовательно зафиксировать ямку высокой остроты зрения на заметных и поведенчески значимых частях сцены (Kowler, 2011). Таким образом, движение глаз наблюдается даже при устойчивой фиксации (Martinez-Conde et al., 2004).
Следовательно, изображения сетчатки имеют видимое движение как из-за непрерывных движений глаз, так и из-за движений объектов в сцене.Хотя это должно привести к компромиссному пониманию сцены, вместо этого мы воспринимаем, с яркими впечатлениями от форм в глубине, стабильные визуальные сцены, содержащие движущиеся объекты. Чтобы понять, как мы воспринимаем постоянство трехмерного мира из двухмерных нестабильных сенсорных входов, нам необходимо понять, как бинокулярное зрение интегрировано с движениями глаз.
Всякий раз, когда элемент сетчатки стимулируется локализованным светом, стимул воспринимается в определенном направлении. Если стимул, проецируемый на два элемента сетчатки, по одному на каждый глаз в бинокулярной системе, воспринимается в одном направлении, то они считаются соответствующими элементами.Нормальное соответствие происходит, когда ямка одного глаза соответствует ямке другого глаза; их единственное визуальное направление называется главным визуальным направлением или циклопическим направлением. Визуальные направления всех остальных пар стимулированных соответствующих элементов воспринимаются по отношению к этому главному направлению. Гороптер — это совокупность всех точек в бинокулярном поле зрения, стимулирующих соответствующие элементы сетчатки. Поскольку нормальное бинокулярное зрение определяется соответствием двух ямок, все другие соответствующие элементы сетчатки могут быть определены на основе лабораторных измерений эмпирического гороптера (Ogle, 1950; Shipley and Rawlings, 1970).
Эмпирические хороптеры были всесторонне смоделированы в Ogle (1932) и Amigo (1965), а совсем недавно — в Turski (2016c, 2018). Уравнения со свободными параметрами, которые были введены на основе ad hoc в Ogle (1932) для прямого взгляда и распространены в Amigo (1965) на любой горизонтальный взгляд, предоставили продольные гороперы в виде конических сечений. Представленные в Turski (2016c) и численные исследования в Turski (2018), эмпирические гороптеры были смоделированы как конические сечения в бинокулярной системе с асимметричными глазами (AE).AE — это модельный глаз, который расширяет редуцированный глаз с учетом смещения ямки от заднего полюса и относительных наклонов роговицы и хрусталика, наблюдаемых в здоровых глазах человека (Chang et al., 2007; Schaeffel, 2008). Анатомическое смещение этой ямки является основным источником оптических аберраций, а наклон линз нейтрализует некоторые из этих аберраций, внося свой вклад в апланатический дизайн глаза (Tabernero et al., 2007; Artal, 2014).
Мои исследования в Turski (2018) показали, что гороптерные коники численно подобны, но геометрически отличаются от конических сечений в Ogle (1932) и Amigo (1965); мои конические срезы проходят через анатомическое расположение узловых точек, а их конические срезы неправильно проходят через центры вращения глаз.Кроме того, в моих исследованиях прямолинейный эмпирический гороптер, определяющий абатическое расстояние до симметрично фиксированной точки, был получен из положения АЭ, в котором экваториальные плоскости их линз копланарны. Затем, когда параметры AE устанавливаются на средние значения для человеческого глаза, результирующее абатическое расстояние в 1 м соответствует его среднему физиологическому значению для человека (Gibaldi et al., 2017). Это результирующее абатическое расстояние также находится в пределах диапазона естественного тонуса глазных мышц в положении покоя (Jaschinski-Kruza, 1991; Jaschinski et al., 2007).
В этой статье я расширяю численные исследования в Turski (2018), развивая простую геометрическую теорию, в которой соответствие сетчатки бинокулярной системы с AE разрабатывается в рамках бицентрических перспективных проекций (Koenderink, 1992). Поскольку положение покоя естественного тонуса глазных мышц служит нулевым эталонным уровнем для усилия конвергенции (Ebenholtz, 2001), эта теория утверждает, что первичное положение НЯ совпадает с бифовеальной фиксацией на абатическом расстоянии.Первичная позиция, первоначально предназначенная для одного глаза, часто описывается в бинокулярном зрении, когда оба глаза направлены прямо вперед с помощью прямой головы. Это довольно неточное определение первичного положения глаз могло быть причиной того, что его нейрофизиологическое значение остается неуловимым, несмотря на его теоретическое значение для глазодвигательных исследований (Hess and Thomassen, 2014). Таким образом, эта новая характеристика первичного положения глаз объединяет бинокулярные конусы с движениями глаз точным и естественным образом, который был недоступен до сих пор.
Результатом такой интеграции является то, что теперь мы можем графически моделировать преобразования гороптерных коник из движения точки фиксации в визуальной плоскости, что также демонстрирует классификацию гороптерных коник с точки зрения положения глаз. В этой статье используется программное обеспечение для динамической геометрии GeoGebra , чтобы продемонстрировать все геометрические результаты, полученные для хороптеров и соответствия сетчатки. Моделирование преобразований гороптерных коник включено в дополнительный материал.
Бинокулярная структура бицентрических проекций сетчатки в теории учитывает тот факт, что человек декодирует свойства трехмерной среды из нейронных процессов, фундаментально ограниченных геометрическими отношениями органов чувств к окружающей среде (Rokers et al., 2011; Bonnen et al., 2019). Кроме того, AE учитывает некоторую апланатическую конструкцию глаза, которая коррелирует смещение линзы с аберрацией роговицы, чтобы получать изображения сетчатки почти без дифракции, близкие к зрительной оси (Artal, 2014).
Хотя распределение соответствующих элементов сетчатки обычно считается фиксированным (Hillis and Banks, 2001), форма гороптера и соответствие сетчатки зависят от параметров асимметрии модельного глаза и, следовательно, могут изменяться при изменении параметров АЕ. Например, когда хрусталик заменяется во время рефракционной хирургии торической интраокулярной линзой (ИОЛ), это не только корректирует аномалии рефракции и обеспечивает более резкий фокус, но и астигматизм роговицы также можно скорректировать, отрегулировав ориентацию линзы.Оценка группы пациентов в Wang et al. (2019) показывают, что величина наклона ИОЛ значительно увеличилась по сравнению с предоперационным наклоном хрусталика. Это увеличение наклона может в послеоперационном периоде изменить форму гороптера и соответствие сетчатки.
2. Асимметричная проушина
Модель AE (рис. 1), подробно описанная в Turski (2018), включает в себя наиболее важные особенности асимметричного дизайна человеческого глаза. Однако здесь модель AE немного видоизменена за счет использования эффективной линзы.Естественная асимметрия глаза моделируется двумя параметрами; угол α, который определяет временное смещение фовеа от заднего полюса, и угол β, который дает эффективный наклон и децентрацию линзы относительно оптической оси. Эффективная линза, представленная в модели AE, упрощает описание наклона линзы и определяет оптическую ось как линию осевой симметрии глазного яблока, когда α = β = 0. Я предполагаю, что α — β> 0, потому что это выполняется в типичном бинокулярная система.Поскольку угол α имеет низкую вариабельность между пациентами (Holladay, 2007), я использую среднее значение угла α, равное 5,2 °. Предполагается, что угол β варьируется от -0,4 ° до 4,7 °, диапазон значений β, наблюдаемых в человеческих глазах.
Рисунок 1 . Модель асимметричного глаза (AE) для правого глаза. Ямка, f , смещена от заднего полюса глобальным наклоном глазного яблока на α градусов. Относительное смещение роговицы и хрусталика представлено углом наклона экваториальной плоскости единственной эффективной линзы в градусах β.Оба угла наклона находятся в узловой точке N , расположенной на оптической оси на 0,6 см кпереди от центра вращения глазного яблока C . Оптическая ось определяется как α = β = 0. Плоскость изображения получается путем наклона фронтальной плоскости на β градусов в центре вращения глазного яблока C . Визуальная ось, проходящая через N и f , пересекает плоскость изображения в ее оптическом центре O .
Наклон эффективной линзы представлен в моей геометрической модели бинокулярной системы с АЭ плоскостью изображения, проходящей через центр вращения глаза, параллельной экваториальной плоскости эффективной линзы.Изображение, попадающее на сетчатку, определяется пучком световых лучей, проходящих через узловую точку. В модели AE эти световые лучи могут быть параметризованы в угловых координатах на изогнутой поверхности сетчатки или на плоскости изображения с более удобными для обработки изображений прямоугольными координатами. Смещение роговицы и хрусталика, представленное эффективным наклоном линзы, является одним из сложных апланатических элементов глаза, предназначенных для компенсации некоторых ограничений оптического качества, вызванных смещением ямки от заднего полюса глазного яблока (Artal, 2014).
3. Бинокулярная система с АЭ
Гороптерные конические сечения, напоминающие эмпирические гороптеры, были численно исследованы Турски (2018) в бинокулярной системе с АЭ. В этом разделе представлены основные определения геометрии этой бинокулярной системы, показанной на рисунке 2, но подробное описание геометрии бинокля развивается в следующих разделах. В частности, в следующих двух разделах геометрически построены гороптерные кривые и соответствие сетчатки.
Рисунок 2 . Углы асимметрии глаз α и β показаны только для фиксации F a . Углы поворота, ϕ r и ϕ l , изменяют взгляд глаз из положения на абатическом расстоянии, фиксации F a , в положение, в котором глаза фиксируются на F . Это приводит к изменению протяженности с σ a = 2 (α — β) при F a до протяженности σ F = 2 (α — β) + η при F , где η — вергенция (1).Гороптерный эллипс, показанный здесь для фиксации F , построен в разделе 4 с использованием узловых точек N r и N l и точки пересечения F ∞ линий, проходящих через узловые точки и параллельных соответствующим плоскостям изображения. Условие ϕ r — ϕ l = 0 дает кривую с постоянной протяженностью σ a .Это абатическая кривая изоподтянутости (AIS), которая проходит через F a . В дальнейшем, аналогично случаю симметричной (редуцированной) модели глаза, циклопическое направление точки фиксации F в бинокулярной системе с АЭ будет указано относительно точки A на круге Виета-Мюллера (VMC). проходящий через F .
Замечу, что в бинокулярной системе с симметричными глазами, т. Е. С модельными глазами, удовлетворяющими α = β = 0, ϕ r и ϕ l — это углы, описывающие вращение глаз относительно их исходного положения, часто описывается как оба глаза, направленные прямо перед собой, с прямой головой.В этом случае угол, образуемый в результирующей точке фиксации, определяется углом вергенции
.см. Фиксацию F 0 на рисунке 3C.
Рисунок 3 . Гороптерные конические сечения, построенные в демонстрации B INOCULAR C ONICS C ONSTRUCTION . (A) Гипербола и эллипс (не показаны). (B) Прямая и парабола. (C) Доказательство того, что ориентация конического сечения определяется углом версии, выполнено только для эллипса.
Расстояние до симметрично закрепленной точки, F a , показанное на рисунке 2, через которое проходит линейный гороптер, называется абатическим расстоянием. Чтобы получить глубину точек фиксации F a и другой точки F , я использую равенство чередующихся углов: два угла, не примыкающие друг к другу, образованные на противоположных сторонах линии, где линия пересекает две другие. параллельные линии. На рисунке 2 α — β — ϕ l в обеих вершинах, N l и F , являются альтернативными углами для левого глаза, а α — β + ϕ r в обеих вершинах, N r и F , являются альтернативными углами для правого глаза.Обратите внимание, что угол ϕ l вычитается из α — β, поскольку его значение отрицательно. Тогда легко проверить, суммируя соответствующие альтернативные углы, что угол, образуемый визуальными линиями на F a , равен 2 (α — β), а угол при F равен 2 (α — β) + η. Таким образом, поскольку α ≠ β, угол при любой фиксации, полученный путем изменения взгляда с F на , никогда не принимает угол вергенции η в уравнении (1).Поэтому в этой работе углы, образуемые визуальными линиями в пространственных точках, называются бинокулярной подтяжкой или просто подтяжкой.
Позиции глаз, достигаемые при фиксации абатического расстояния равными поворотами глаз, ϕ r = ϕ l , имеют точки фиксации, которые лежат на, что я называю, абатической изодетентной кривой (AIS). Для каждой разной симметричной фиксации подтяжки 2 (α — β) + η мы получаем различную кривую изо-протяженности. Эти кривые отличаются от кривых изовергентности, или кругов Виета-Мюллера (VMC), потому что, в отличие от кривых изовергентности, VMC проходит через центры вращения глаз.Кривая AIS, кривая изотянутости, которая проходит через F и на абатическом расстоянии, численно графически изображена на рисунке 2 для фиксации в азимутальном диапазоне ± 45 °, определяемом нейронным путем диапазоне типичных эксцентриситетов взгляда ( Гиттон и Волле, 1987). Для параметров антропоморфной бинокулярной системы AIS будет точно аппроксимирована VMC в разделе 6.
Далее для симметричных глаз (α = β = 0) вариант угловой,
ω = (1/2) (ϕr + ϕl), (2)— азимутальный угол луча, который начинается от точки на VMC, которая находится на полпути между центрами глаз, и проходит через точку фиксации (см.точка фиксации F 0 на рисунке 3C), заданная углами поворота ϕ r и ϕ l от основного положения глаз. Я вспоминаю, что основное положение глаз часто описывается как оба глаза, направленные прямо вперед, в прямой голове. Средняя точка VMC и азимутальный угол (2) определяют положение циклопического глаза (Turski, 2016a) и, следовательно, главное направление обзора. В разделе 6 обсуждается, как положение циклопического глаза точки фиксации F может быть определено в бинокулярной системе с помощью AE.
4. Геометрическая конструкция коников бинокля
В бинокулярной системе с АЭ параметры α, β, a и углы поворота глаз ϕ r и ϕ l задают координаты четырех точек в горизонтальной плоскости зрения, лежащих на , или связаны с соответствующей гороптерной кривой. Это узловые точки N r и N l , точка фиксации F и точка, обозначенная как F ∞ .Точка F ∞ (см. Рис. 2) является пересечением двух линий, каждая из которых проходит через узловую точку одного глаза и параллельна плоскости изображения АЭ и экваториальной плоскости эффективной линзы. Таким образом, в рамках проективной геометрии (Henle, 1997) F ∞ проецируется на бесконечно удаленные точки, по одной для каждой из плоскостей изображения АЭ. Точка фиксации F проецируется по визуальным осям к ямкам, которые являются соответствующими элементами сетчатки при нормальном бинокулярном зрении.Напротив, линии, проецируемые от F ∞ к паре бесконечно удаленных точек, не пересекают сетчатку.
Таким образом, бесконечно удаленные точки не являются соответствующими элементами сетчатки, хотя здесь они называются геометрическими соответствующими точками из-за важной роли, которую они играют в геометрических построениях гороптерных кривых. Эти геометрические конструкции для бинокулярной системы с АЭ приведены ниже в этом разделе. Эти построения мотивированы результатами, полученными в Turski (2016a) для гороптерных кругов в бинокулярной системе с симметричными (уменьшенными) глазами.Здесь, в предложении 1, они переформулированы, чтобы включить в формулировку F ∞ , что в противном случае не требуется, поскольку это теорема евклидовой геометрии.
Предложение 1 . Пусть узловая точка расположена на оптической оси в любой точке в центре вращения сферического глазного яблока и его зрачком или между ними. Тогда для положения бинокулярного глаза с точкой фиксации F в горизонтальной зрительной плоскости линии, проходящие через узловые точки и перпендикулярные зрительным осям, пересекаются в точке F ∞ на круговом гороптере.Отсюда следует, что отрезок прямой FF ∞ должен проходить через центр гороптерного круга .
Доказательство утверждения 1 приведено в Приложении 1. Оно показывает, что в бинокулярной системе с симметричными модельными глазами F и F ∞ являются диагонально противоположными точками на гороптерном круге. Анатомически правильное расположение узловой точки — 0,6 см кпереди от центра вращения глаза, хотя доказательством является любое расположение узловой точки между центром вращения глаза и зрачком.
Построение гороптерных кривых в бинокулярной системе с АЭ включает в себя точечную симметрию гороптерных кругов из Предложения 1. Обоснованием этого расширения является требование непрерывности преобразований гороптерных кривых, поскольку параметры АЭ α и β стремятся к нулю. Более того, ссылаясь на мои предыдущие исследования, расширение также точно отражает отношение F и F ∞ в проективной геометрии, геометрической структуре, которая необходима для построения гороптерных кривых для бинокулярной системы с АЭ.
Чтобы пояснить это дальше, я отмечаю, что отображение между точками сферической сетчатки и точками плоскости изображения может быть смоделировано стереографической проекцией через узловую точку как для симметричной, так и для асимметричной модели глаза (Turski, 2016c). Это отображение не определено в узловой точке. Стереографическая проекция расширяется до взаимно однозначной и на нее путем добавления изображения узловой точки под отображением, называемой точкой на бесконечности, к плоскости изображения. Плоскость изображения с точкой в бесконечности — знаменитый объект в геометрии и математическом анализе, известный как сфера Римана (Needham, 2002).Стереографическая проекция конформна, то есть сохраняет угол двух пересекающихся кривых. Кроме того, он отображает круги на сферической сетчатке, не содержащие узловой точки, в круги на плоскости изображения. Следовательно, эта конформная геометрия сохраняет рецептивные поля и освещенность сетчатки, обеспечивая конструктивные свойства для человеческого зрения (Turski, 2012).
Теперь для каждого из АЭ бинокулярной системы точка фиксации F в горизонтальном поле зрения определяет начало координат в плоскости изображения, а F ∞ проецируется на бесконечно удаленную точку.Начало координат и точка на бесконечности — это изображения ямки и узловой точки при стереографической проекции, которая идентифицирует сферическую сетчатку с плоскостью изображения и, следовательно, они являются противоположными точками в сфере Римана. Я предполагаю, что F и F ∞ — противоположные точки на гороптере бинокулярной системы с АЭ. Это предположение, которое подтверждается в данной статье геометрическими конструкциями, поддерживаемыми программным обеспечением динамической геометрии, дает нам особенно простую теорию эмпирических хороптеров, которая является одновременно биологически подтвержденной и геометрически точной, развивая классическую модель эмпирических хороптеров, введенную Оглом (1932). .Удивительно, но и стереографическая проекция, и гороптер были впервые представлены Агилонием в его Шести книгах по оптике, опубликованных в 1613 году.
Демонстрация основных результатов гороптерных коник, именуемых бинокулярными кониками, носит конструктивный характер и, таким образом, позволяет разрабатывать алгоритмы моделирования устойчивого бинокулярного зрения мобильных роботов.
Конструкция бинокля с конусом. Для бинокулярной системы с такими ориентациями АЭ, что точка F ∞ находится в поле зрения, центр гороптерной кривой обозначается средней точкой M отрезка линии FF ∞ .Это означает, что для каждой точки кривой есть другая точка на этой кривой, диагонально противоположная ей. Тогда эта кривая, либо эллипс, либо гипербола, полностью определяется F , F ∞ и узловыми точками N r и N . Для копланарных плоскостей изображения, когда глаза фиксируются на абатическом расстоянии, прямая гороптер, параллельная плоскостям изображения, проходит через симметрично закрепленную точку.Кроме того, когда F ∞ находится на бесконечности, то есть когда плоскости изображения параллельны, но не компланарны, гороптерная кривая является параболой. Ориентация каждой конической секции точно определяется углом версии (2) .
D ЭМОНСТРАЦИЯ: Гороптерные кривые в бинокулярной системе с AE являются бинокулярными коническими конусами при предполагаемой точечной симметрии гороптерных кругов в Предложении 1, они геометрически построены и графически визуализированы в GeoGebra (Рисунок 3).Поскольку построение включает одни и те же шаги для гипербол и эллипсов, я строю только гиперболу. Для данного положения, в котором плоскости изображения глаз непараллельны, узловые точки глаза N r 1 и N l 1 , точка фиксации F 1 и точка F 1∞ , все они показаны на рисунке 3A. Затем две дополнительные точки на кониках строятся на рисунке 3A путем получения отражений узловых точек около средней точки M 1 отрезка прямой F 1 F 1∞ .Эти дополнительные точки, обозначенные как R 1 и S 1 , определяют коники. Показанное на этой панели коническое сечение, построенное в GeoGebra путем взятия любых пяти из этих шести построенных точек, является той же гиперболой. Симметричная фиксация на абатическом расстоянии имеет копланарные плоскости изображения, а фиксации, полученные из основного положения, когда глаза, повернутые на один и тот же угол, имеют параллельные, некомпланарные плоскости изображения. В первом случае две горизонтальные линии, проходящие через их соответствующие узловые точки и параллельные своим соответствующим плоскостям изображения, перекрываются.Мы можем использовать любую точку, которая отличается от узловых точек на перекрывающихся линиях, точка F a∞ на рисунке 3B, чтобы получить среднюю точку между этой точкой и F a . Отражения узловых точек относительно средней точки, точки M a на рисунке 3B, предоставляют нам две дополнительные точки R a и S a , которые коллинеарны с точкой. F a и, таким образом, определяют гороптер прямой линии, параллельный плоскостям изображения.Для любой фиксации, полученной из F a с одинаковым углом поворота обоих глаз, результирующие плоскости изображения параллельны, но не копланарны, а F ∞ находится на бесконечности. В рамках проективной геометрии F ∞ представлено семейством линий, параллельных плоскостям изображения глаз, а коники являются параболами. Одна из этих парабол сконструирована для фиксации F 3 на Фигуре 3B следующим образом.Сначала получают среднюю точку L отрезка линии, соединяющего N r 3 и F 3 , и получают линию в визуальной плоскости через L , которая параллельна плану изображения. Эта линия пересекает линию, которая проходит через N l 3 и параллельна отрезку N r 3 F 3 в точке M l .Тогда точка R 3 на параболе, которую мы хотим построить, получается путем отражения N l 3 относительно точки M l . Те же шаги повторяются, начиная с отрезка линии N l 3 F 3 для получения точек K и M r . Эти точки затем дают вторую точку S 3 на параболе, принимая отражение N r 3 около M r .Все шаги в этих построениях, например, получение отражения относительно точки, выполняются с помощью сред динамической геометрии системы GeoGebra . Доказательство ориентации конических секций, заданных углом версии (2), приведено для гороптерного эллипса на рисунке 3C. Лучи, проходящие через F ∞ , пересекаются под углом 18 °. Это вершина в точке фиксации F 0 , которая получается для азимутальных углов поворота симметричных глаз ϕr2 = 12 ° и ϕl2 = 30 °.Две биссектрисы в точках F ∞ и F 0 пересекаются под прямым углом, доказывая, что ориентация эллипса задается углом ω = 21 °, равным версии ω0 = 21 °. Это доказательство справедливо также для гипербол и парабол. Поскольку значения параметров асимметрии глаза выбраны произвольно, это доказательство применимо к любым параметрам, выбранным для глаз. Таким образом, устанавливается связь между геометрией гороптера и движениями глаз. На этом заканчивается ДЕМОНСТРАЦИЯ .
Геометрическая конструкция бинокулярных коник в модели GeoGebra позволяет графически моделировать преобразования гороптерных коник из движения точки фиксации в визуальной плоскости. Компьютерное моделирование преобразований гороптерных коник включено в Приложение 2.
Как эти внутренние свойства теории связаны с бинокулярным зрением человека? Человеческий мозг функционирует в физическом пространстве и получает информацию, переносимую светом, который проецируется на сетчатку глаза и преобразуется фоторецепторами в электрохимические сигналы.После начальной обработки сетчаткой сетчатки эта визуальная информация в основном отправляется в первичную зрительную кору, где она производит определенные ретино-кортикальные карты и формирует входные данные для других областей коры (Wandell et al., 2007). Эта чрезвычайно сложная обработка декодирует окружающую среду от стимуляции сетчатки и создает нейронное представление пространства (Sereno and Lehky, 2011), нашего субъективного визуального пространства.
Новейшее компьютерное моделирование в нейробиологии, которое включает бицентрическое перспективное отображение трехмерной среды на сетчатке, демонстрирует, что это отображение является фундаментальным для настройки ретино-кортикальных нейронных процессов и соответствующих им аспектов восприятия (Bonnen et al., 2019). Хотя настройка была специально исследована на предмет трехмерного движения в корковой области МТ приматов, процесс декодирования мира по стимуляции сетчатки в зрительно-моторных корковых областях должен сильно зависеть от геометрии, которая связывает окружающую среду с сенсорным эпителием, независимо от того, нечеловеческий он или нет. человеческие приматы передвигаются или сканируют окружающую среду, стоя на месте. Эта геометрическая связь, ограничивающая визуальное восприятие, в моей теории — это бицентрическое проективное отображение между трехмерным пространством и плоскостями изображения АЭ, которые определяют форму гороптера.
5. Переписка сетчатки
В нормальном бинокулярном зрении ямки являются соответствующими элементами. Это означает, что фиксированная точка воспринимается в одном направлении — главном, или циклопическом, направлении. Кривая гороптера через точку фиксации представляет собой геометрическое место точек пространства, которые проецируются на соответствующие элементы сетчатки, так что каждая точка гороптера воспринимается в одном и том же направлении относительно циклопического направления.
На основании результатов, полученных в B INOCULAR C ONICS C ONSTRUCTION , прямолинейный гороптер, показанный на рисунке 4, который проходит через точку фиксации F a , устанавливается плоскостями изображения. компланарность.Зрительная ось правой АЕ проходит через соответствующую узловую точку и пересекает сетчатку в ямке f r и плоскости изображения в точке O r . Другая визуальная ось проходит аналогично через узловую точку левого глаза, прежде чем пересекать сетчатку в точке f l (ямка) и плоскость изображения в точке O l . Эти точки O r и O l являются центрами бинокулярного соответствия плоскостей изображения.
Рисунок 4 . Сформулировано соотношение соответствия сетчатки для линейного гороптера при фиксации абатического расстояния F a в бинокулярной системе с АЭ. F a проецирует вдоль визуальных осей к фовеам f r и f l и оптические центры соответствующих плоскостей изображения O 28 r и O л .Точка Q проецируется на соответствующие точки сетчатки q r и q l и их аналоги в плоскостях изображения Q r и Q 904
Точка Q на линейном гороптере проецируется на соответствующие точки сетчатки: q r в правом глазу, q l в левом глазу и Q r и Q l на соответствующих плоскостях изображения, также называемых соответствующими точками плоскостей изображения. Соответствующие точки q r и q l расположены на разных расстояниях от их соответствующих ямок, так что асимметричное распределение соответствующих точек сетчатки относительно ямок является результатом глаз » асимметрия и двусторонняя симметрия головы (Porter et al., 2001; Москера и Верма, 2016). Однако из подобных треугольников △ QF a N r и △ Q r O r N 9037 правый глаз и аналогичные треугольники, △ QF a N l и △ Q l O для левого глаза, заключаем, что | Q r O r | = | Q л O л |.Этот линейный гороптер и двусторонняя симметрия головы используются здесь для определения бинокулярного соответствия следующим образом.
Переписка сетчатки. Ссылаясь на Рисунок 4 , пусть O r и O l будут точками проекции точки фиксации F a в правой и левой плоскостях изображения АЭ соответственно. Затем любые две точки Q r и Q l на одинаковом расстоянии от O r и O l , через узловые точки N r и N l , к соответствующим точкам сетчатки q r и q l 904 неравномерное расстояние от ямки f r и f l соответственно .
Это определение соответствия сетчатки, которое основано на геометрическом построении бинокулярных конусов в предыдущем разделе, полностью согласуется с соответствием сетчатки, сформулированным в виде ad-hoc в Turski (2018). Абатическое расстояние d a = | ИЗ и | к линейному гороптеру по адресу F было получено в Turski (2018). Здесь абатическое расстояние дано в терминах параметров асимметрии, α и β, и межглазной длины, 2 a = | C r C l |, в эквивалентной, но упрощенной форме,
да = acos (α-β) +0.6sinαsin (α-β), (3), где 0,6 — расстояние в сантиметрах от узловой точки до центра вращения глаза. Затем, используя средние человеческие значения 2 a = 6,5 см, α = 5,2 ° и -0,4 ° ≤ β ≤ 4,7 ° в уравнении (3), мы получаем 34 см ≤ d a ≤ 380 см. Однако в редких случаях значения β могут более близко приближаться к значению α, что дает гораздо большее значение: d a .
Далее для среднего значения β = 3.3 °, абатическое расстояние (3) составляет 99,61 см, что соответствует среднему значению, зарегистрированному у людей (Gibaldi et al., 2017). Это расстояние аналогично расстоянию в положении покоя для естественного тонуса глазных мышц (Jaschinski et al., 2007), которое служит нулевым опорным уровнем для усилия конвергенции глаз (Ebenholtz, 2001). Поэтому я называю положение глаз, фиксируемых на абатическом расстоянии, положением вергенции покоя, чтобы отличить его от положения основных глаз.
Каждая точка на одном из бинокулярных конусов проецируется вдоль визуальных линий глаз на сетчатку НЯ и определяет одну пару соответствующих точек. Однако при построении бинокулярных коников используются только две пары точек: две ямки и две точки на бесконечности. Все остальные соответствующие элементы сетчатки устанавливаются по бицентрическим проекциям точек гороптера на сетчатке. Соответствие сетчатки является четко определенным понятием только в том случае, если соответствующие точки сетчатки не зависят от преобразований бинокулярных коник, когда точка фиксации перемещается в визуальной плоскости.Чтобы проверить это, в компьютерном моделировании в GeoGebra , доступном в Приложении 2, соответствующие точки сетчатки, q r и q l , и соответствующие точки плоскости изображения Q r и Q l , оба определяются точкой Q (см. Рисунок 4) на гороптере абатической дистанционной линии и поэтому остаются соответствующими при изменении положения глаз в визуальной плоскости. фиксаций.Поскольку это должно быть верно для всех пар соответствующих точек сетчатки, я заключаю следующее:
Замечание 1 . Связь соответствия бинокля, введенная в R ETINAL C ORRESPONDENCE четко определена .
Форма гороптера устанавливает четко определенное соответствие сетчатки. Эта теоретическая взаимосвязь отражает взаимосвязь в бинокулярном зрении человека, в которой соответствие сетчатки нормальному бинокулярному зрению определяется двумя соответствующими ямками, так что все другие соответствующие элементы сетчатки затем определяются из лабораторных измерений эмпирического гороптера.Однако вопрос о том, зафиксированы ли соответствующие элементы сетчатки или нет, остается нерешенным (Wick, 1991; Hillis and Banks, 2001).
В представленной здесь теории бинокулярное соответствие зависит от параметров асимметрии глаза. Следовательно, соответствие сетчатки может изменяться при изменении параметров асимметрии. Такие изменения могут произойти во время рефракционной хирургии. Например, для коррекции аномалий рефракции и достижения более четкого зрения, что характерно для людей с пресбиопией, хрусталик хирургическим путем заменяют искусственной ИОЛ.Торические ИОЛ также могут корректировать астигматизм, вызванный формой роговицы, путем регулировки ориентации линзы, поскольку они имеют разную силу в разных меридианах. Когда группа из 333 пациентов была оценена Wang et al. (2019) для предоперационного наклона хрусталика и послеоперационного наклона ИОЛ было обнаружено, что величина наклона их ИОЛ значительно увеличилась на 1,2 ° ± 1,1 ° по сравнению с предоперационным наклоном хрусталика. На основании этих результатов я пришел к выводу, что послеоперационное изменение наклона линзы может быть достаточно большим, чтобы изменить эмпирическую форму гороптера пациента и его соответствие сетчатке.В бинокулярной системе с асимметричными глазами это изменение наклона линзы моделируется соответствующим изменением угла β.
6. Антропоморфные бинокулярные коники
На рис. 5 изображены коники бинокля, полученные численным методом из Turski (2018) (пунктирные линии) и геометрическим методом, разработанным в разделе 4 (сплошные линии) и построенным с помощью программного обеспечения GeoGebra для средних параметров, наблюдаемых у людей: α = 5,2 °, β = 3,3 °, и расстояние между окулярами 2 a = 6.5 см. Из рисунка видно, что гиперболы для фиксации F 1 и эллипсы для фиксации F 2 , полученные обоими методами, почти идеально накладываются друг на друга. Однако гороптерная парабола для фиксации F 3 на AIS отличается от касательной к VMC на F 3 . На рисунке 5 показано, что разница между AIS (сплошная линия через F a ) и VMC (пунктирная линия через F 3 ) должна быть несущественной для важных для восприятия 90 ° центрального поля зрения. .
Рисунок 5 . Гороптерные коники по антропоморфным параметрам. Сплошными линиями показаны коники: линия гороптера для F a на абатическом расстоянии 99,61 см, гипербола для фиксации F 1 , эллипс для фиксации F 2 и парабола для фиксации F 3 на абатической изодетяжной кривой (AIS) (сплошная линия) через F a построены в разделе 4.Каждая точка фиксации находится на соответствующем круге Виета-Мюллера (VMC) (пунктирная линия). Коники, полученные для тех же точек фиксации методом Турски (2018), показаны пунктирными линиями. Как мы видим, гипербола и эллипс для обоих методов почти идеально перекрывают друг друга. Разница между параболой для F 3 и касательной к VMC на F 3 объясняется в следующем разделе. Ориентация коников определяется углами версий в B INOCULAR C ONICS C ONSTRUCTION в разделе 4.
Чтобы найти разницу между AIS и VMC, я сначала замечаю, что AIS можно хорошо аппроксимировать с помощью круга. Фактически, используя GeoGebra , я обнаружил, что приближение AIS в диапазоне поля зрения ± 45 ° (см. Раздел 3) до двух десятичных знаков — это круг x 2 + ( y — 49,46) 2 = (50,13) 2 . Чтобы найти уравнение VMC, проходящего через F 3 , я напомню точное геометрическое описание VMC, данное в Turski (2016a): центр (0, k ) = (0, a / ( 2 tan η) и радиусом R = a / (2 sin η).Затем, после замены на = 3,25 см и использования вычисленного в GeoGebra значения η = 3,73 ° при F 3 , уравнение VMC будет x 2 + ( y — 49,80) 2 = (49,91) 2 . Это подтверждает, что разница между двумя кругами незначительна.
На рисунке 5 все углы получены в GeoGebra геометрическим методом, описанным в этой статье, и отображены с точностью до 5 десятичных знаков.Точка фиксации F 1 получается поворотами ϕr = 9 ° и ϕl = 10 ° от положения покоя и дает начало гиперболе, построенной в разделе 4. Вариант ω1 = 9,5 ° дает ориентацию гиперболы, а F Угол ориентации 1 составляет ωF1 = 9,50009 °. Точка фиксации F 2 получается в результате вращения на ϕr = -13 ° и ϕl = -15 ° и дает начало эллипсу, опять же с ориентацией, заданной версией ω2 = -14 ° и направлением F . 2 , что задано азимутальными углами ωF2 = 14.00061 °. Повороты ϕr = ϕl = -20 ° от положения покоя дает точку фиксации F 3 на AIS, а версия ω3 = -20 ° определяет направление оси симметрии результирующей параболы. Точка на соответствующем VMC на полпути между глазами обеспечивает направление, ωF3 = -20,00039 °, F 3 . Мы видим, что ориентация коник и направления точек фиксации различаются на <4 с дуги. Это незначительное различие позволяет мне разместить циклопический глаз в той же точке на соответствующем VMC, в которую он был помещен в бинокулярной системе с симметричными глазами (Turski, 2016a): посередине между центрами глаз.
Из рисунка 5 и результатов Turski (2018) мы заключаем, что для антропоморфной бинокулярной системы бинокулярные коники в моей теории численно близки к коническим сечениям, полученным в Ogle (1932) и Amigo (1965). Поэтому я могу выразить параметр конических сечений H , использованный в этих исследованиях, в терминах параметров АЭ α и β. На абатическом расстоянии H = 2 a / d a , 2 a = 6.5 см — это межглазное расстояние, а d a — это абатическое расстояние до точки фиксации, заданное в уравнении (3). Таким образом, H можно выразить через параметры асимметрии глаза следующим образом:
H = 2asin (α-β) acos (α-β) + 0,6sinα. (4)Поскольку величина σ a = 2 (α — β) при фиксации абатического расстояния мала (0,066 радиана для антропоморфных параметров α = 5,2 °, β = 3,3 °), получаем аппроксимацию H ≈ 0.065, что отличается от σ a примерно на 0,001 рад. Более того, для α = 5,2 ° и диапазона значений β, -0,4 ° <β <4,7 ° (см. Раздел 2), я получаю диапазон значений H в уравнении (4) следующим образом: 0,01 < H <0,19. Этот результат для значений H согласуется с исходной оценкой Огла 0 < H <0,2 для людей (Ogle, 1932, 1950). Огл (1950) представил значения H , рассчитанные на основе данных Гельмгольца, Лау и Либерманна среди многих других исследователей, полученных в наблюдениях Нониуса, которые находятся в диапазоне его исходных значений H , указанных в Ogle (1932). .См. Также соответствующее обсуждение в Шипли и Роулингс (1970). Это также согласуется с недавними оценками Schreiber et al. (2008) и Гибальди и Бэнкс (2019). Однако эти недавние исследования были более общими, учитывая параметр отклонения Геринга – Гиллебранда H и сдвиг Гельмгольца, или наклон вертикального гороптера назад, который не включен в мое исследование.
7. Бинокулярные коники в визуальной плоскости
Теория гороптерных кругов в бинокулярной системе с симметричными (уменьшенными) глазами может быть основана только на евклидовой геометрии.Но для теории гороптерных коник в бинокулярной системе с АЭ необходимы рамки проективной геометрии. В терминах проективной геометрии (Henle, 1997) общее уравнение коник, заданное неоднородным квадратичным многочленом c ( x, y ),
c (x, y) = Ax2 + Bxy + Cy2 + Dx + Ey + F = 0, (5)также выражается однородной квадратичной формой C ( X, Y, Z ) = Z 2 c ( X / Z, Y / Z ).
Хотя для нахождения уравнения требуется не более пяти точек на конике, эта простая задача кажется вычислительно невыполнимой для бинокулярных коников, потому что выражения для точек, определяющих общую бинокулярную конику, слишком сложны. Чтобы обойти это ограничение, я классифицирую бинокулярные коники с точки зрения дискриминантов уравнения (5) и анализирую классы коник в «общем положении», когда точка бифовеальной фиксации перемещается в горизонтальной визуальной плоскости.Понятие «общая позиция» будет объяснено ниже в этом разделе.
Коника (5) вырождена тогда и только тогда, когда ее дискриминант, т.е. определитель Γ симметричной матрицы ее однородного квадратичного многочлена, равен нулю. Здесь
Γ = det [AB / 2D / 2B / 2CE / 2D / 2E / 2F]. (6)Тогда, как для вырожденной, так и для невырожденной коники, ее тип определяется знаком квадратичной части дискриминанта уравнения (6),
Δ = det [AB / 2B / 2C] = AC-14B2. (7)Случаи, ограниченные действительными вырожденными кониками Γ = 0, следующие: две пересекающиеся прямые Δ <0, две параллельные прямые Δ = 0 и одна точка Δ> 0.Невырожденные коники Γ ≠ 0 классифицируются следующим образом: коника является гиперболой, если ∆ <0, эллипсом, если ∆> 0, и параболой, если ∆ = 0 (см. Reid, 1988).
Три коники следующие: гипербола для фиксации F 1 , эллипс для фиксации F 2 и парабола для фиксации F 3 , показанные на рисунке 5, имеют следующие уравнения и дискриминанты (7), полученные при численном моделировании с помощью GeoGebra для расчетных точек в конструкциях, выполненных для демонстрации B INOCULAR C ONICS C ONSTRUCTION в разделе 4.
1. Ветвь гиперболы, содержащая F 1 : 2,73 x 2 + 3,77 xy — 8,22 y 2 — 0,40 x + 115,86 y — 7,11 = 0; Δ = −26
2. Эллипс, содержащий F 2 : 1,12 x 2 + 0,90 xy + 2,81 y 2 — 0,12 x — 19,24 y + 0,99 = 0; Δ = 2,9
3. Парабола, содержащая F 3 : 0.21 x 2 + 1,14 xy + 1,56 y 2 — 0,14 x — 17,72 y + 0,97 = 0; Δ = −6 × 10 −7 ≈ 0
Дискриминант параболы, который должен быть равен 0, приблизительно равен −0,0000006. Это объясняет, почему парабола была аппроксимирована в Turski (2018) прямой линией, тогда как здесь она задается параболой (см. Рисунок 5). В этой теории парабола встроена в модель гороптерных кривых путем построения.Однако в численном моделировании в Turski (2018) чувствительность коник вблизи Δ = 0 позволяет нам видеть либо эллипс, либо гиперболу с формой, напоминающей касательную линию около точки фиксации. Что могло это объяснить?
Интуитивно понятно, что набор коник, удовлетворяющих условию Γ = 0, пренебрежимо мал по сравнению с набором коник, удовлетворяющим Γ ≠ 0, поскольку количество коник, перечисленных как {Γ = x, x ∈ R \ {0}}, равно огромны по сравнению с кониками, нумерованными Γ = 0.Точно так же, когда Γ ≠ 0, множество коник, удовлетворяющих ∆ = 0, незначительно по сравнению с множеством коник, удовлетворяющих ∆ ≠ 0. В математике, см. Hazewinkel (1989), например, «общее положение» — это понятие общности. для геометрических объектов, удовлетворяющих некоторым особым условиям, которые отличают их от всех других геометрических объектов в данной коллекции. Таким образом, во всей коллекции подколлекция объектов в их общем положении является «массивной», а дополнительный набор «скудным», а его объекты «незначительными».Таким образом, только эллипсы и гиперболы являются кониками в общем положении.
Теперь, после этих предварительных замечаний, я могу проанализировать бинокулярные коники в визуальной плоскости бифовеальных фиксаций. С этой целью отмечу, что точки фиксации внутри кривой AIS определяют такие положения глаз, что η = ϕ r — ϕ l > 0, в то время как положения глаз с точками фиксации вне AIS удовлетворяют η = ϕ r — ϕ l <0.Это простое свойство положения глаз и компьютерное моделирование бинокулярных конусов приводят к следующему предположению о гороптерной геометрии в визуальной плоскости:
Преобразование конических биноклей. Если α> β , то AIS постоянной ширины 2 (α — β) делит визуальную плоскость на три отдельные области: (A) Точка фиксации F на AIS определяет гороптер как параболу, если F ≠ F a и прямая линия, если F = F a .(B) Точка фиксации вне AIS определяет ветвь гороптерной гиперболы, проходящей через эту точку, возможно, вырождающуюся в две пересекающиеся линии в некоторых точках фиксации. (C) Точка фиксации в поле бинокля внутри AIS определяет гороптерный эллипс. С другой стороны, в поле монокуляра внутри области, ограниченной AIS, эллипс может превратиться в гиперболу, так что последовательность преобразованных коник проходит через вырожденный случай двух параллельных линий .
Эта классификация преобразований бинокулярных коник продемонстрирована в модели GeoGebra для параметров человекоподобной бинокулярной системы, когда точка фиксации перемещается в визуальной плоскости (Приложение 2).
Это моделирование предоставляет бинокулярные коники «зашумленной» классификации с точки зрения положения глаз, информации, доступной для зрительной системы. Таким образом, при перемещении точки фиксации в визуальной плоскости можно наблюдать только начальный линейный гороптер и эволюцию последующих конусов в общем положении.Например, случаи вырожденных коник, упомянутые выше в B INOCULAR C ONICS T ПРЕОБРАЗОВАНИЕ : две пересекающиеся прямые и две параллельные прямые могут быть выведены только из наблюдения соседних коник в их общих положениях. Три типичных случая наблюдаемых бинокулярных конусов: прямая линия в качестве начального гороптера при фиксации абатического расстояния, а также гипербола и эллипс, полученные при моделировании, показаны, соответственно, на рисунках 6A – C. Атипичные случаи моделирования также показаны на рисунках 6D – F.На этих панелях коническая форма трансформируется через две параллельные линии от эллипсов к гиперболам. Кроме того, на рисунке 6E показанная коника действительно является гиперболой, хотя ее ветви могут показаться на рисунке параллельными линиями. Проведение нескольких десятков сеансов моделирования свидетельствует о том, что это произойдет только за пределами бинокулярной области. На этих трех последних панелях точки пересечения визуальных осей находятся рядом с глазным яблоком в пространстве, фиксации которого препятствует анатомия человека.
Рисунок 6 .Типичные снимки моделирования (Приложение 2) в бинокулярных областях показаны в (A – C) . Снимки в (D – F) показывают атипичные конусы в монокулярной области, переходящие через две параллельные линии от эллипсов к гиперболам в точках, на которых люди анатомически не могут зациклиться.
Подводя итог выводам этого раздела, можно предположить, что как воспринимаемое направление фиксируемой точки, т.Это означало бы, что когда глаза поворачиваются для изменения взгляда в горизонтальной плоскости, как циклопическое направление, так и бинокулярный конус претерпевают одинаковые повороты на угол версии. Но это также означало бы, что объект, движущийся по фронтальной линии, действительно движется по постоянно меняющимся гороптерам в направлении, касательном к мгновенным кривым гороптера. Кривая, очерченная точкой фиксации, отслеживающей этот объект, представляет собой изодинтенсивную кривую. Это означает, что повороты обоих глаз во время этого преследования равны для AIS, проходящего через позицию покоя, или что повороты отличаются на постоянное значение вдоль других изотянутых кривых в горизонтальной плоскости.Для глаз, отслеживающих траектории других объектов, разница во вращении двух глаз зависит от времени. Например, это тот случай, когда преследуемый объект движется по прямой фронтальной линии на плоском проекционном экране в типичных лабораторных условиях.
8. Обсуждение
Значение гороптера в стереоскопическом зрении можно объяснить следующим образом. Когда точка в визуальной плоскости находится перед кривой гороптера, содержащей точку фиксации, или позади нее, разница в углах, нанесенных на каждую сетчатку между изображением и центром фовеа, определяет диспаратность сетчатки.Для каждой точки гороптера существует максимальное несоответствие для единственного видения, которое определяет зону слияния Панума вокруг кривой гороптера. В этой области сливаются несоответствующие элементы сетчатки, чтобы обеспечить нам как единое зрение, так и способность стереоскопически видеть визуальные объекты в глубине от текущей точки фиксации наблюдателя. Если взять разницу в диспропорциях сетчатки для пары точек, то мы получим относительное несоответствие, используемое для нашего восприятия трехмерной формы. Объекты за пределами области Панума падают на совершенно разные области сетчатки и рассматриваются как исходящие с двух разных визуальных направлений, вызывая физиологическую диплопию или двоение в глазах.Здесь, используя бицентрическую проективную геометрию и новую модель глаза, я изучил основные концепции, наиболее полезные для понимания стереопсического зрения: соответствие сетчатки, хороптеры и циклопическую ось.
8.1. Соответствие сетчатки и геометрические хороптеры
Геометрия продольных гороптерных коник, интегрированных с движениями глаз, построена в рамках бицентрических перспективных проекций на плоскости изображения АЭ. AE — это модельный глаз, который включает глобальную асимметрию глазного яблока, вызванную смещением фовеа от его заднего полюса — основного источника оптических аберраций глаза — и наклоном хрусталика, который противодействует некоторым из этих аберраций (Artal, 2014).Теория демонстрирует, что (i) продольные гороптерные кривые для бинокулярной системы с AE являются коническими сечениями и (ii) соответствие сетчатки, полученное из гороптерных коник, является четко определенной концепцией. Более того, использование этой теории позволяет утверждать, что ветви конических секций, которые проходят через точки фиксации и называемые бинокулярными кониками, очень напоминают эмпирические хороптеры, полученные лабораторными измерениями методом Нониуса (Ogle, 1950; Shipley and Rawlings, 1970).До недавнего времени существовала только одна всеобъемлющая модель эмпирических хороптеров, и она была разработана Оглом (1932) и Амиго (1965) с помощью специального уравнения , введенного специально для , со свободным параметром, определяемым экспериментально для каждого субъекта. Разработанная здесь геометрическая теория развивает эту классическую модель Огла и Амиго, создавая физиологически мотивированную модель эмпирических гороптеров, интегрированных с движениями глаз.
Эта теория объясняет тот фундаментальный факт, что зрительная система человека функционирует в физическом пространстве и получает визуальную информацию, активно сканируя окружающую среду, когда мы бодрствуем.Падающие световые лучи, отраженные от объектов сцены в трехмерном пространстве, проецируются на нестабильные двумерные сетчатки, а нейронные процессы, активируемые в зрительных и зрительно-моторных областях коры головного мозга, декодируют и интерпретируют трехмерные свойства сцены. Следовательно, любое декодирование трехмерных свойств окружающей среды на основе сенсорной информации должно фундаментально ограничиваться геометрическими отношениями сенсорных органов к окружающей среде (Rokers et al., 2011; Bonnen et al., 2019) и модулироваться движениями глаз (Hejtmancik и другие., 2016).
Концептуальная основа, используемая здесь при построении гороптеров для бинокулярной системы с АЕ, не только обеспечивает биологическую модель, воспроизводящую эмпирические гороптеры, но также обеспечивает основу для теории геометрических гороптеров, разработанной в Turski (2016a) для бинокулярной системы с помощью симметричный (редуцированный) модельный глаз. Этот результат доказывается здесь в предложении 1 для любого положения узловой точки между зрачком глаза и его центром вращения, включая, конечно, расположение анатомической узловой точки.Таким образом, здесь в рамках бицентрических проекций построены три качественно разные теории геометрических хороптеров, в том числе теория ВМК. Ниже приводится краткое сравнение трех теорий в порядке анатомической точности соответствующих моделей глаза.
Первая модель является частным случаем симметричной модели глаза, в которой узловая точка совпадает с центром вращения глаза. Предложенные почти два столетия назад результирующие кривые гороптера представляют собой изовергентные круги, или VMC, каждая из которых проходит через точку фиксации и соединяет центры вращения глаз.Когда глаза фиксируются на точках вдоль VMC, центры вращения глаз не перемещаются. Это означает, что VMC и значение вергенции также не изменяются, когда взгляд фиксируется на точках вдоль VMC. Кроме того, относительное несоответствие становится независимым от положения глаза в этом модельном глазу (Turski, 2016a). Это зависящее от модели постоянство является следствием неправильного расположения узловой точки в положении, которое не соответствует ее анатомическому положению.
Вторая модель — это симметричная модель глаза с узловой точкой, расположенной на 0.6 см кпереди от центра вращения глазного яблока, как того требует анатомия глаза. Его кривые гороптера состоят из семейства окружностей, проходящих через точку фиксации и соединяющих узловые точки (Turski, 2016a). Для постоянного значения вергенции эти гороптерные круги параметризуются конкретными точками фиксации на бинокулярно видимой части VMC и пересекаются в точке симметричной конвергенции VMC. Относительное несоответствие в этой модели зависит от движения глаз, и его изменения всегда находятся в пределах остроты зрения бинокля для фиксационных движений глаз (Wilcox and Harris, 2010).Независимо от этого результата относительное несоответствие часто предполагается независимо от положения глаз. В работе Turski (2016a) я предположил, что изменения размера и формы, воспринимаемые во время фиксационных движений глаз, могут не только обеспечить преимущества восприятия, такие как нарушение маскировки, но также могут обеспечить эстетическое преимущество стереопсиса (Ponce and Born, 2008).
Третья бинокулярная система с АЭ с высочайшей анатомической точностью является предметом данной статьи. В этой системе геометрические гороптеры представляют собой бинокулярные конусы, напоминающие эмпирические гороптеры, и их ориентация точно определяется углом версии, что придает этому углу новое важное значение в биологическом видении.С другой стороны, если ось циклопа определяется от средней точки дуги VMC, соединяющей центры вращения глаз, так же, как это было определено в бинокулярной системе с симметричными глазами, ее направление, заданное азимутальным углом, обеспечивает наилучшее приближение угла вергенции в бинокулярной системе человека; разница между направлением циклопического глаза и ориентацией бинокулярного конуса, заданной версией, составляет порядка нескольких секунд дуги (рис. 5).
Хотя VMC и эмпирические гороптеры имеют разную геометрию, VMC часто идентифицируют с продольным гороптером.VMC действительно обеспечивает хорошее приближение для эмпирического гороптера вблизи точки фиксации, но разница в их геометрии значительна на периферии. Небольшой объект, расположенный на периферии VMC, будет иметь нулевое несоответствие по отношению к этой модели гороптера, но у него будет отличное от нуля несоответствие по отношению к бинокулярным коникам, которые хорошо аппроксимируют эмпирические гороптеры по всему полю зрения. Визуально управляемые саккады, перехватывающие периферически наблюдаемый объект, будут далеко от цели, если они запрограммированы с точки зрения несоответствия VMC.Хотя простота VMC делает его полезным в некоторых числовых аспектах зрительно-моторных исследований, его аппроксимация как геометрических, так и эмпирических хороптеров является решающим условием, которое всегда следует подчеркивать, чтобы избежать его часто встречающихся в настоящее время неверных характеристик.
Кроме того, в Sprague et al. (2015), что форма продольного гороптера является результатом распределения ресурсов визуальной системой в соответствии со статистикой естественного несоответствия для бинокулярных соответствий.Хотя форма гороптера может поддерживать эту статистику, моя теория вместо этого утверждает, что форма эмпирических гороптеров вызвана в первую очередь смещенными оптическими элементами, смоделированными AE. Фактически, в здоровых глазах ямка смещена от заднего полюса глазного яблока, а роговица и хрусталик наклонены относительно друг друга (Chang et al., 2007; Holladay, 2007; Schaeffel, 2008). Наклон хрусталика компенсирует некоторые аберрации, вызванные смещением фовеа и асферичностью роговицы, и обеспечивает восприятие почти без аберраций вблизи зрительной оси (Tabernero et al., 2007; Артал, 2014). Затем адаптация к визуальной статистике окружающей среды может быть достигнута с помощью движений бинокулярного глаза (Canessa et al., 2017; Gibaldi and Banks, 2019).
8.2. Бинокулярные коники и движение глаза
Ямка, которая имеет наивысшую остроту зрения на сетчатке, охватывает только угол зрения в два градуса. Чтобы предотвратить диплопию, саккада должна быстро направлять ямки глаз к объекту — так называемые сопряженные движения глаз, потому что глаза вращаются в одном направлении.Саккады обычно нуждаются в исправлении с помощью вергенции — дизъюнктивных движений глаз, когда они вращаются в противоположных направлениях, а затем ямки должны оставаться точно выровненными на объекте (Masson et al., 2001; Maxwell and Schor, 2006). Это корректирующее движение сближения, или моторное слияние, регулирует выравнивание глаз для поддержания сенсорного слияния (Schor, 1979; Liversedge et al., 2006).
Кортикальная активность, полученная при бицентрической перспективе стимуляции сетчатки, должна, следовательно, модулироваться движениями глаз (Hejtmancik et al., 2016). Размер и направление регулировки задаются бинокулярным несоответствием между текущим просматриваемым объектом и следующим, подлежащим просмотру. Таким образом, концепция соответствующих элементов сетчатки не только фундаментальна для единого зрения и стереоскопического зрения, но также важна для бинокулярной координации движений глаз. Понимание того, как движения глаз контролируются зрительно-моторными процессами и как они влияют на точное соответствие элементов сетчатки, остается неопределенным (Waitzman, 2016).
Более того, при естественном наблюдении скорость вращения человеческого глаза во время саккад достигает 700 ° / с, а ускорение превышает 20 000 ° / с. 2 (Waitzman, 2016). Саккадические движения глаз выполняются примерно 3-4 раза в секунду, что означает, что зрительная информация в основном воспринимается мозгом во время 3-4 коротких фиксаций в течение секунды. Кроме того, мы можем не только выполнять плавные движения глаз преследования, которые удерживают ямки в фокусе на медленно движущемся объекте со скоростью до 100 ° / с; мы также используем комбинацию плавного преследования и саккад для отслеживания объекта, движущегося непредсказуемо или со скоростью более 30 ° / с (Westheimer, 1954; Meyer et al., 1985). Путем стабилизации изображения отслеживаемого объекта в ямке плавные движения глаз преследования (SPEM) накладывают дополнительное движение на изображения сетчатки неподвижного фона и движущихся объектов.
Например, последствия высокой скорости и ускорения саккадических движений глаз заметно ограничивают использование зрительной информации между фиксациями. Следовательно, основная особенность, лежащая в основе естественного видения, — это возникновение сложной динамической диспропорции, которая затем обрабатывается для поддержания нашего ясного видения, которое кажется непрерывным и стабильным.В связи с этим моя теория обеспечивает преобразования бинокулярных конусов путем интеграции геометрии бинокулярных конусов с изменяющимся положением глаз в горизонтальной визуальной плоскости бифовеальных фиксаций, тем самым расширяя мою работу по моделированию стабильности монокулярного зрения у Турски (2010, 2016b). к оправе бинокля.
Кинематика визуально управляемых движений глаз ограничена законом Листинга, который в формулировке этого закона включает первичное положение глаз. В своей типичной версии, которая первоначально применялась к вращению одного глаза, когда глаз фиксируется на цели на оптической бесконечности, закон Листинга утверждает, что при вертикальном и неподвижном положении головы существует положение глаза, называемое первичным положением, такое как любое другое положение. Ориентация глаза может быть достигнута одним вращением глаза вокруг оси в плоскости, перпендикулярной основному направлению глаза.Этот самолет известен как самолет Листинга. Следовательно, во время движений глаз, которые подчиняются закону Листинга (например, саккады и плавное преследование), глазное яблоко принимает уникальное скручивание или вращение вокруг линии взгляда для каждой ориентации глаза (Crawford et al., 2003). В моем исследовании все движения глаз ограничиваются вращением вокруг вертикальной оси, так что кручение, определяемое законом Листинга, всегда равно нулю.
Далее, когда оба глаза вынуждены бинокулярно фиксироваться во время вращения глаз, бинокулярное расширение закона Листинга, известное как L2, применяется к положению глаз.L2 утверждает, что во время конвергенции оси вращения глаз все еще остаются ограниченными плоскости для каждого угла вершины; однако, когда глаза сходятся, эти плоскости вращаются относительно плоскостей Листинга во времени и примерно симметрично (Bruno and van den Berg, 1997; Tweed, 1997; Somani et al., 1998).
Моя теория определяет первичное положение НЯ при фиксации абатического расстояния или положение вергенции покоя, чтобы учесть физиологически мотивированную замену неточного положения первичного глаза следующим образом.В отсутствие визуальных сигналов взгляд глаз смещается в положение вергенции покоя естественного тонуса глаз, которое служит нулевым опорным уровнем для усилий по конвергенции (Ebenholtz, 2001). Фактически, среднее расстояние до вергентности естественного тонуса в состоянии покоя для прямого взгляда имеет такое же значение, как и среднее абатическое расстояние человека, что также согласуется с абатическим расстоянием для средних антропоморфных параметров AE. Более того, хотя расстояние до вергентности тонуса в состоянии покоя и абатическое расстояние варьируются от примерно 40 см до оптической бесконечности у разных субъектов, они являются надежными параметрами в пределах объекта (Owens and Leibowitz, 1980).Кроме того, положение покоя подтверждается недавними результатами, демонстрирующими, что закон Листинга и кинематика, связанная с законом Листинга, реализуются периферически и с помощью механизма косых экстраокулярных мышц (EOM), а не централизованно (Demer, 2006). Фактически, эти силы EOM незаменимы для трехмерного моделирования движений глаз и отвечают за механическое равновесие глаза, подвешенного в исходном положении покоя (Gao et al., 2014). Более того, изменение положения покоя при опущенном и поднятом взгляде (Heuer and Owens, 1989) согласуется с наклоном вертикального гороптера назад и его влиянием на восприятие (Amigo, 1974; Grove et al., 2001; Schreiber et al., 2008).
Приведенное выше обсуждение решительно поддерживает мой выбор положения вергентности покоя на абатическом расстоянии бифовеальной фиксации, чтобы заменить первичное положение глаз, которое по существу применимо только к одному глазу, но часто описывается как описывающее оба глаза, фиксирующие оптическую бесконечность, с помощью очевидное отсутствие точности. Это может быть причиной того, что, несмотря на теоретическую важность первичного положения глаз, его точная формулировка и нейрофизиологическое значение остаются неуловимыми (Hess and Thomassen, 2014).
Построенная здесь теория бинокулярных конусов нуждается в дальнейшем расширении за счет вертикального компонента и интеграции с трехмерными движениями глаз. Это расширение до полной структуры бицентрической перспективы (Koenderink, 1992) неизбежно приведет к множеству геометрических трудностей. Например, зрительная линия в модели АЕ, которая проходит через ямку, оптический узел и точку фиксации, отличается из-за смещения ямки от заднего полюса глазного яблока, от линии взгляда или оси фиксации, соединяющей центр вращения глаза с точкой фиксации.Один из возникающих при этом вопросов заключается в том, как смоделировать вращение зрительной оси за счет скручивания глаза вокруг линии обзора, потому что вращение усложняет контроль выравнивания бинокулярных глаз в условиях ближнего зрения. Более того, расширение закона Листинга, который применяется, когда глаза начинают вращаться из своего третичного положения, так называемое правило половинного угла, здесь не было необходимо, но оно будет незаменимым, когда моя теория будет расширена до трехмерных вращений, потому что это расширение требует использование угловой скорости, а не осей вращения (Tweed et al., 1990).
Также характерной особенностью трехмерной кинематики бифовеальной фиксации головы и глаз является либо наклон плоскости Листинга, либо изменение геометрии плоскости Листинга на искривленную поверхность. Изменения геометрии плоскости Листинга были аналитически смоделированы как эффект метода максимизации выравнивания (Chen et al., 2019). Кроме того, это было предложено в Ghosh et al. (2011, 2012) видно, что горизонтальный наклон хрусталика и осевая длина глаза изменяются при взгляде вниз на 25 ° с бинокулярной фиксацией в точке 0.Аккомодационные состояния 2 D и 2,5 D для почти визуальных задач. Хотя недавние результаты Лю и Тибоса (2017) и Лу и др. (2020) поддерживают это предположение, теория физиологического механизма аккомодации все еще не завершена. Похоже, что хрусталик может изменить свой наклон из-за ослабления зонулы — волоконной полосы, прикрепленной к линзе, которая изменяет свою кривизну во время аккомодации, — и силы тяжести (Radhakrishnan and Charman, 2007), а также тщательного моделирования этого и других аккомодационных механизмы могут способствовать более полному пониманию причин неуловимых пресбиопических изменений (Charman, 2008).Таким образом, моделирование физиологических механизмов, лежащих в основе стереоскопического зрения, должно включать не только оптическую асимметрию глаза, но и наклонный аккомодационный хрусталик.
Заявление о доступности данных
Исходные материалы, представленные в исследовании, включены в статью / дополнительные материалы, дальнейшие запросы можно направлять соответствующим авторам.
Авторские взносы
Автор подтверждает, что является единственным соавтором данной работы, и одобрил ее к публикации.
Конфликт интересов
Автор заявляет, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Благодарю рецензентов за очень полезные комментарии. Я благодарю Алису Турски за ее редактирование, которое значительно облегчило чтение этой рукописи. Эта рукопись была выпущена в качестве препринта на BioRxiv (Turski, 2020).
Дополнительные материалы
Дополнительные материалы к этой статье можно найти в Интернете по адресу: https: // www.frontiersin.org/articles/10.3389/fnins.2020.555965/full#supplementary-material
Список литературы
Artal, P. (2014). Оптика глаза и ее влияние на зрение: учебное пособие. Adv. Опт. Фотон . 6, 340–367. DOI: 10.1364 / AOP.6.000340
CrossRef Полный текст | Google Scholar
Боннен, К., Чуба, Т. Б., Уритнер, Дж. А., Кон, А., Хук, А. К., и Кормак, Л. К. (2019). Геометрия бинокля формирует нейронное представление динамической трехмерной среды. Nat. Neurosci . 23, 113–121. DOI: 10.1038 / s41593-019-0544-7
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Канесса А., Гибальди А., Чесса М., Фато М., Солари Ф. и Сабатини С. П. (2017). Набор данных стереоскопических изображений и несоответствия действительности, имитирующего человеческие привязанности к периферийному пространству. Sci. Данные 4, 1–16. DOI: 10.1038 / sdata.2017.34
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Чанг, Ю., Ву Х.-М., Линь Ю.-Ф. (2007). Осевое смещение между линзой глаза и роговицей, наблюдаемое с помощью МРТ (i) при фиксированном аккомодационном состоянии. Vis. Res . 47, 71–84. DOI: 10.1016 / j.visres.2006.09.018
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Чен Б., Филдинг Дж. И Чанг Х. (2019). Метод максимизации выравнивания кинематики глаза и фиксации глазного дна. Vis. Res . 158, 58–71. DOI: 10.1016 / j.visres.2019.01.013
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Кроуфорд, Дж., Мартинес-Трухильо, Дж., И Клиер, Э. (2003). Нейронный контроль трехмерных движений глаз и головы. Curr. Opin. Нейробиол . 13, 655–662. DOI: 10.1016 / j.conb.2003.10.009
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Эбенгольц, С. М. (2001). Глазодвигательные системы и восприятие . Кембридж: Издательство Кембриджского университета. DOI: 10.1017 / CBO9780511529795
CrossRef Полный текст | Google Scholar
Гош, А., Коллинз, М.Дж., Рид С. А. и Дэвис Б. А. (2012). Влияние взгляда вниз и аккомодации на глазные аберрации с течением времени. Инвест. Офтальмол. Vis. Sci . 53, 6465–6471. DOI: 10.1167 / iovs.12-9973
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Гош А., Коллинз М. Дж., Рид С. А., Дэвис Б. А. и Искандер Д. (2011). Влияние взгляда вниз и аккомодации на глазные аберрации с течением времени. Дж. Вис . 11, 1–13. DOI: 10.1167 / 11.10,17
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Гибальди А., Канесса А. и Сабатини С. П. (2017). Активная сторона стереопсиса: стратегия фиксации и адаптация к естественной среде. Sci. Репутация . 7, 1–18. DOI: 10.1038 / srep44800
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Guitton, D., и Volle, M. (1987). Контроль взгляда у людей: координация глаз-голова во время ориентировочных движений на цели в пределах и за пределами глазодвигательного диапазона. J. Neurophysiol . 58, 427–459. DOI: 10.1152 / jn.1987.58.3.427
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Хазевинкель, М. (1989). Энциклопедия математики, Vol. 4 . Дордрехт; Бостон; Лондон: Клувер. DOI: 10.1007 / 978-94-009-5997-2
CrossRef Полный текст
Хейтманчик, Дж., Кабрера, П., Чен, Ю., М’Хамди, О., и Никерсон, Дж. (2016). «Vision», в переводе Conn’s Translational Neuroscience , ed P. Conn (Лондон; Сан-Диего, Калифорния; Кембридж; Оксфорд: Academic Press), 399–438.DOI: 10.1016 / B978-0-12-802381-5.00031-2
CrossRef Полный текст
Хенле, М. (1997). Современная геометрия: аналитический подход . Река Аппер Сэдл, штат Нью-Джерси: Prentice Hall.
Гесс, Б. Дж. М., и Томассен, Дж. С. (2014). Кинематика визуально-управляемых движений глаз. PLoS ONE 9: e95234. DOI: 10.1371 / journal.pone.0095234
CrossRef Полный текст | Google Scholar
Хойер, Х. и Оуэнс, Д.А. (1989). Вертикальное направление взгляда и положение глаз в состоянии покоя. Восприятие 18, 363–377. DOI: 10.1068 / p180363
CrossRef Полный текст | Google Scholar
Хиллис, Дж. М., и Бэнкс, М. С. (2001). Соответствующие точки зафиксированы? Vis. Res . 41, 2457–2473. DOI: 10.1016 / S0042-6989 (01) 00137-7
CrossRef Полный текст | Google Scholar
Холладей, Дж. Т. (2007). Качество зрения: основная оптика для катарактального и рефракционного хирурга . Торофар, Нью-Джерси: Slack Inc.
Google Scholar
Ящинский, В., Джейнта, С., Хорманн, Дж., И Уолпер, Н. (2007). Объективные и субъективные измерения темной вергенции. Ophthal. Physiol. Опция . 27, 85–92. DOI: 10.1111 / j.1475-1313.2006.00448.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Koenderink, J. (1992). «Основы бицентрической перспективы», в Future Trends in Computer Science, Control and Applied Mathematics, Vol. 653 , Конспект лекций по информатике, ред. А. Бенсуссан и Дж. П.Верюс (Берлин, Гейдельберг: Springer), 233–251. DOI: 10.1007 / 3-540-56320-2_62
CrossRef Полный текст | Google Scholar
Ливерседж, С. П., Уайт, С. Дж., Финдли, Дж. М., и Рейнер, К. (2006). Бинокулярная координация движений глаз при чтении. Vis. Res . 46, 2363–2374. DOI: 10.1016 / j.visres.2006.01.013
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лу, К., Хэ, В., Цянь, Д., Лу, Ю. и Чжу, X. (2020). Измерение наклона хрусталика глаза с высокой миопией перед операцией по удалению катаракты с помощью оптической когерентной томографии с разверткой источника. Глаз Vis . 7:14. DOI: 10.1186 / s40662-020-00176-5
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Masson, G., Busettini, C., Yang, D.-S., и Miles, F. (2001). Кратковременное наблюдение за окулярами у людей: чувствительность к бинокулярному неравенству. Vis. Res . 41, 3371–3387. DOI: 10.1016 / S0042-6989 (01) 00029-3
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Москера, С., Верма, С. (2016). Двусторонняя симметрия зрения и влияние офтальмологических хирургических процедур на бинокулярное зрение: тематический обзор. Дж. Оптомет . 9, 219–230. DOI: 10.1016 / j.optom.2016.01.005
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Needham, T. (2002). Визуальный комплексный анализ . Нью-Йорк, Нью-Йорк: Clarendon Press.
Google Scholar
Огл, К. Н. (1932). Аналитическая обработка продольного гороптера; его измерение и применение к связанным явлениям, особенно к относительному размеру и форме глазных изображений *. J. Opt. Soc.Am . 22, 665–728. DOI: 10.1364 / JOSA.22.000665
CrossRef Полный текст | Google Scholar
Огл, К. Н. (1950). Исследования в области бинокулярного зрения . Филадельфия, Пенсильвания: У. Б. Сондерс.
Google Scholar
Оуэнс, Д. А., и Лейбовиц, Х. У. (1980). Аккомодация, конвергенция и восприятие расстояния при слабом освещении. Optomet. Vis. Sci . 57, 540–550. DOI: 10.1097 / 00006324-198009000-00004
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Портер, Дж., Гирао, А., Кокс, И. Г., и Уильямс, Д. Р. (2001). Монохроматические аберрации человеческого глаза в большой популяции. J. Opt. Soc. Являюсь. А 18, 1793–1803. DOI: 10.1364 / JOSAA.18.001793
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Рид М. (1988). Бакалавриат по алгебраической геометрии . Кембридж; Нью-Йорк, штат Нью-Йорк; Мельбурн, Виктория: Издательство Кембриджского университета. DOI: 10.1017 / CBO97811399
CrossRef Полный текст | Google Scholar
Schaeffel, F.(2008). Измерения наклона и децентрации бинокулярных линз у здоровых людей с факичными глазами. Инвест. Офтальмол. Vis. Sci . 49, 2216–2222. DOI: 10.1167 / iovs.07-1022
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Шрайбер, К. М., Хиллис, Дж. М., Филиппини, Х. Р., Шор, К. М., и Бэнкс, М. С. (2008). Поверхность эмпирического гороптера. Дж. Вис . 8, 1–20. DOI: 10.1167 / 8.3.7
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Серено, А.Б., и Лехки, С. Р. (2011). Популяционное кодирование зрительного пространства: сравнение пространственных представлений в дорсальных и вентральных путях. Фронт. Comput. Neurosci . 4: 159. DOI: 10.3389 / fncom.2010.00159
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Табернеро, Дж., Бенито, А., Алькон, Э. и Артал, П. (2007). Механизм компенсации аберраций в человеческом глазу. J. Opt. Soc. Являюсь. А 24, 3274–3283. DOI: 10.1364 / JOSAA.24.003274
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Турски, Я.(2010). Роботизированное зрение с конформной камерой: моделирование перисаккадического восприятия. Дж. Робот . 2010: 130285. DOI: 10.1155 / 2010/130285
CrossRef Полный текст | Google Scholar
Turski, J. (2012). Получение изображений с помощью конформной камеры, Том II . Лас-Вегас, Невада: IPCVIPR; CSREA Press.
Google Scholar
Turski, J. (2016b). Моделирование активного зрения при плавном преследовании роботизированного глаза. Электрон. Imaging 2016, 1–8. DOI: 10.2352 / ISSN.2470-1173.2016.10.ROBVIS-391
CrossRef Полный текст | Google Scholar
Turski, J. (2020). Геометрическая теория, объединяющая бинокулярное зрение человека с движением глаз. BioRxiv 1–20. DOI: 10.1101 / 2020.09.03.280248
CrossRef Полный текст | Google Scholar
Твид Д., Кадера В. и Вилис Т. (1990). Вычисление трехмерных кватернионов положения глаза и скорости глаза по сигналам поисковой катушки. Vis. Res . 30, 97–110.DOI: 10.1016 / 0042-6989 (90)
- -D
- Акуйсал, Н.(2007). Заблуждения учеников седьмого класса о геометрических понятиях. Неопубликованная кандидатская диссертация. Сельчукский университет, Конья. [Google Scholar]
- Argün, Z, Arıkan, A, Bulut, S, Halıcıolu, S. (2014). Temel matematik kavramların künyesi. Анкара: Гази Китапеви. [Google Scholar]
- Argyropoulos, V.S., & Argyropoulos, V.S. (2002). Восприятие тактической формы применительно к пониманию геометрических понятий слепыми учащимися. Британский журнал нарушений зрения, 20 (1), 7-16.[Google Scholar]
- Brian, A, & Haegele, J.A. (2014). В том числе студенты с нарушением зрения: софтбол. Журнал физического воспитания, отдыха и танцев, 85 (3): 39-45. [Google Scholar]
- Carreño, E., Ribeiro, C.M., & Climent, N. (2013). Специализированные и горизонтальные знания — обсуждение знаний будущих учителей по полигонам. Доклад представлен на Восьмом конгрессе европейского математического образования, Анталия, Турция. [Google Scholar]
- Даунинг, Д.(2009). Словарь математических терминов (3-е издание) Нью-Йорк (Нью-Йорк): профессиональные руководства Бэррона. [Google Scholar]
- Дулин, Д. (2008). Влияние предшествующего опыта работы с материалами с выпуклой линией и предшествующего визуального опыта при оценке длины слепыми людьми. Британский журнал нарушений зрения, 26 (3), 223-237. [Google Scholar]
- Edwards, A.D.N., Stevens, R.D., & Pitt, I.J. (1995). Невизуальное представление математической информации. Получено с: https: //www.researchgate.сеть / публикация / 2246200 [Google Scholar]
- Эрез, М.М., и Йерушалми, М. (2006). «Если вы можете превратить прямоугольник в квадрат, вы можете превратить квадрат в прямоугольник…» Молодые студенты знакомятся с инструментом перетаскивания. Международный журнал компьютеров для математического обучения, 11 (3), 271-299. [Google Scholar]
- Эрол И., Ридлер М. и Эриаман М.Ю. (2016). Помимо инвалидности: этнографический анализ школьной и социальной жизни инклюзивных учащихся. Средиземноморский журнал исследований в области образования.(19): 79-94 [Google Scholar]
- Erşen, Z.B., & Karakuş, F. (2013). Оценка концептуальных изображений учителей начальных классов для четырехугольников. Турецкий журнал компьютерного и математического образования, 4 (2), 124-146. [Google Scholar]
- Э. Фишбейн (1993). Теория образных понятий. Образовательные исследования по математике, 24 (2): 139-162. [Google Scholar]
- Fujita, T. (2012). Уровень понимания учащимися отношений включения четырехугольников и феномена прототипа.Журнал математического поведения, 31, 60-72. [Google Scholar]
- Fujita T., & Jones K. (2007). Понимание учащимися определений и иерархической классификации четырехугольников: к теоретическому построению. Исследования в области математического образования, 9 (1-2): 3–20. [Google Scholar]
- Godino, J.D. (1996). Математические понятия, их значение и понимание. В Л. Пуиджи А. Гутьеррес (ред.), Труды 20-й конференции Международной группы по психологии математического образования, (Vol.2. С. 417–424). Валенсия: Университет Валенсии. [Google Scholar]
- Haber, R.N., Haber, L.R., Levin, C.A., & Hollyfield, R. (1993). Свойства пространственных представлений: данные от зрячих и слепых. Восприятие и психофизика, 54 (1), 1-13. [Google Scholar]
- Hadas, N., Hershkowitz, R., & Schwarz, B.B. (2000). Роль противоречия и неопределенности в продвижении необходимости доказывать в средах динамической геометрии. Образовательные исследования по математике, 44 (1-2), 127-150.[Google Scholar]
- Heinze, A., & Ossietzky, C. (2002). «… Потому что квадрат не является прямоугольником» — знание учащимися простых геометрических понятий, когда они начинают изучать доказательство. В А. Д. Кокберн и Э. Нарди (ред.), Труды 26-й конференции Международной группы по психологии математического образования, (том 3, стр. 81-88). Школа образования и профессионального развития, Великобритания: Университет Восточной Англии. [Google Scholar]
- Эррера, Л.М., Джонс, Г., и Рантала, Дж.(2006). Обеспечение справедливости в образовании: к сравнению справедливых практик в различных европейских местных контекстах. Хельсинки: Исследовательский центр социальных исследований, Образовательный университет Хельсинки. [Google Scholar]
- Hershkowitz, R. (1989). Визуализация в геометрии — две стороны монеты. Сосредоточьтесь на учебных задачах по математике, 11 (1-2), 61-76. [Google Scholar]
- Hershkowitz, R. (1990). Психологические аспекты изучения геометрии. В П. Нешер и Дж. Килпатрик (ред.), Математика и познание (стр. 70-95). Кембридж: КУБОК. [Google Scholar]
- Horzum, T. (2013). Концептуальные изображения и представления учащихся с нарушениями зрения в некоторых математических понятиях. Неопубликованная докторская диссертация. Университет Гази, Анкара. [Google Scholar]
- Horzum, T. (2016). Понятие треугольника с точки зрения слепых студентов. Журнал Кыршехирского педагогического факультета, 17 (2), 275-295. [Google Scholar]
- Horzum, T. (2018). Исследование знаний дошкольных учителей математики о четырехугольниках с помощью карты понятий.Турецкий журнал компьютерного и математического образования, 9 (1), 1-30. [Google Scholar]
- Закон об образовании лиц с ограниченными возможностями (IDEA). 20 U.S.C. § 1400; 2007. [Google Scholar]
- Капперман Г. и Стикен Дж. (2003). Практический отчет: пример для повышения уровня подготовки учителей учеников с ослабленным зрением по коду Немет по азбуке Брайля. Журнал нарушений зрения и слепоты, 97 (2), 110–112. [Google Scholar]
- Kartal, B., & ınar, C.(2017). Проверка знаний геометрии многоугольников учителями математики до начала работы. Журнал Кыршехирского педагогического факультета, 18 (2), 375-399. [Google Scholar]
- Kennedy, J.M. (1993). Рисование и слепой: картинки на ощупь. Нью-Хейвен, Коннектикут: Yale Press. [Google Scholar]
- Кызар, О. (2012). Сравнение уровней одиночества слабовидящих в разных видах спорта. Неопубликованная кандидатская диссертация. Университет Фират, Элязыг. [Google Scholar]
- Klingenberg, O.G. (2007).Геометрия: образовательные значения для детей с нарушением зрения. Журнал «Философия математического образования», 20, 1-15. [Google Scholar]
- Коханова, И. (6–13 июля 2008 г.). Способы обучения математике слабовидящих школьников. Доклад представлен на 11-м Международном конгрессе по математическому образованию (ICME11), Монтеррей, Мексика. [Google Scholar]
- Кохонова, И. (22–26 февраля 2007 г.). Сравнение наблюдения за новым пространством и его объектами зрячими и незрячими учениками.В Д. Питта-Пантази и Г. Филиппу (редакторы), Труды Пятого Конгресса Европейского общества исследований в области математического образования (CERME 5), (стр. 982-991). Ларнака, Кипр. [Google Scholar]
- Ландау Б., Глейтман Х. и Спелке Э. (1981). Пространственные знания и геометрическое изображение у слепого от рождения ребенка. Наука, 213 (4513), 1275-1278. [Google Scholar]
- Ландау Б., Спелке Э. и Глейтман Х. (1984). Пространственные знания у маленького слепого ребенка. Познание, 16 (3), 225–260.[Google Scholar]
- Либерман Л.Дж., Хьюстон-Уилсон К. и Козуб Ф.М. (2002). Предполагаемые препятствия для включения учащихся с нарушениями зрения в общефизическое образование. Адаптированная физическая активность ежеквартально, 19 (3), 364-377. [Google Scholar]
- MEGEP (2013). Развитие и образование ребенка: нарушения зрения. Анкара: Министерство национального образования. [Google Scholar]
- Merriam, S.B. (2009). Качественное исследование: руководство по разработке и внедрению (3-е издание).Сан-Франциско (Калифорния): Джосси-Басс. [Google Scholar]
- Miles, M.B., & Huberman, A.M. (1994). Качественный анализ данных. Таузенд-Оукс (Калифорния): Шалфей. [Google Scholar]
- Миллар С. (1985). Движение и ориентация тела в запоминании мест слепыми и зрячими детьми. Ежеквартальный журнал экспериментальной психологии, 37 (2), 257–279. [Google Scholar]
- Монаган, Ф. (2000). Что это меняет? Взгляды детей на различия между некоторыми четырехугольниками.Образовательные исследования по математике, 42 (2), 179-196. [Google Scholar]
- MoNE (2006). Регулирование услуг специального образования. Анкара: Министерство национального образования. [Google Scholar]
- NCTM (1989). Учебный план и стандарты оценки школьной математики. Рестон (Вирджиния): Публикации NCTM. [Google Scholar]
- NCTM (2000). Принципы и стандарты школьной математики. Рестон (Вирджиния): Публикации NCTM. [Google Scholar]
- NCTM (2006). Координаторы учебной программы от дошкольного до 8-го класса по математике: стремление к согласованности.Рестон, Вирджиния: Публикации NCTM. [Google Scholar]
- Закон «Ни один ребенок не останется без внимания». (2001). Получено с http://www.ed.gov/policy/elsec/leg/esea02/107-110.pdf [Google Scholar]
- PISA (2015). Заключительный национальный отчет исследования PISA 2012. Анкара: Министерство национального образования. [Google Scholar]
- Pritchard, C.K. И Лэмб, Дж. (2012). Обучение геометрии слабовидящим школьникам. Учитель математики, 106 (1), 23-27. [Google Scholar]
- Рёскен, Б., и Ролка, К.(2007). Интегрирующая интуиция: роль образа понятия и определения понятия для обучения студентов интегральному исчислению. Энтузиаст математики из Монтаны, 3, 181-204. [Google Scholar]
- Rule, A.C., Stefanich, G.P., Boody, R.M., & Peiffer, B. (2011). Влияние адаптивных материалов на учителей и их учеников с нарушениями зрения в средних естественных и математических классах. Международный журнал естественнонаучного образования, 33 (6), 865-887. [Google Scholar]
- Шонесси, Дж.М., и Бургер, В.Ф. (1985). Подготовительные работы перед дедукцией по геометрии. Учитель математики, 78 (6), 419-428. [Google Scholar]
- Spindler, R. (2006). Обучение математике слепого ученика. Обучение математике и ее приложениям, 25 (3), 120-126. [Google Scholar]
- Srichantha, S., Inprasitha, M., & Ariratana, W. (2008, 12-13 сентября). Формирование понятий в геометрии учащихся с нарушением зрения. Документ, представленный на Международной конференции по исследованиям в области образования (ICER) Обучающиеся сообщества для устойчивого развития, Кхон Каен, Муанг, Кхон Каен, Таиланд.[Google Scholar]
- Sucuolu, B., & Kargın, T. (2006). İlköğretimde kaynaştırma uygulamaları. Стамбул: Morpa Yayınları. [Google Scholar]
- Tall, D.O. (1992). Переход к продвинутому математическому мышлению: функции, пределы, бесконечность и доказательство. В D. A. Grouws (Ed.), Справочник исследований по преподаванию и обучению математике (стр. 495-511). Нью-Йорк, штат Нью-Йорк: издательство Macmillan Publishing Company. [Google Scholar]
- Tall, D.O., & Vinner, S. (1981). Образ понятия и определение понятия в математике с особым упором на пределы и непрерывность.Образовательные исследования по математике, 12 (2), 151-169. [Google Scholar]
- Теннисон Р. Д., Стив М. В. и Бутвелл Р. К. (1975). Последовательность экземпляров и анализ представления атрибутов экземпляров при получении концепции. Журнал педагогической психологии, 67 (6), 821-827. [Google Scholar]
- TIMSS (2016). TIMSS 2015 Предварительный отчет по математике и естественным наукам для 4 и 8 классов. Анкара: Министерство национального образования. [Google Scholar]
- Türnüklü, E., Berkün, M. (2013).Стратегии классификации полигонов для учащихся 5-7 классов начальной школы. Образовательный журнал Кастамону, 21 (1), 337-356. [Google Scholar]
- Убуз, Б. (1999). Ошибки и заблуждения учеников 10-11 классов по базовой геометрии. Журнал образования университета Хаджеттепе, 17, 95-104. [Google Scholar]
- ЮНЕСКО (1994). Саламанкское заявление и рамки действий в области образования для лиц с особыми потребностями: приняты Всемирной конференцией по образованию для лиц с особыми потребностями. Получено 10 апреля 2014 г. с сайта: http: // www.unesco.org/education/pdf/SALAMA_E.PDF [Google Scholar]
- TurtleDiary.com: простые и сложные многоугольники (nd). Получено 29 мая 2018 г. с https://www.turtlediary.com/lesson/simple- and-complex-polygons.html [Google Scholar]
- TutorVista.com: Сложный многоугольник (nd). Получено 29 мая 2018 г. с сайта https://math.tutorvista.com/geometry/complex-polygon.html [Google Scholar]
- Vinner, S. (1991). Роль определений в преподавании и изучении математики. В Д.Высокий (ред.), Продвинутое математическое мышление (стр. 65-81). Нидерланды: Дордрехт: Клувер. [Google Scholar]
- Виннер С. и Дрейфус Т. (1989). Изображения и определения понятий функций. Журнал исследований в области математического образования, 20 (4), 356-366. [Google Scholar]
- Виннер С. и Хершковиц Р. (1980, 16–17 августа). Концептуальные образы и общие когнитивные пути в развитии некоторых простых геометрических концепций. В Трудах 4-й Международной конференции по психологии математического образования Р. Карплюс (ред.), (Стр.177–184), Беркли (Калифорния): PME. [Google Scholar]
- Ward, R.A. (2004). Исследование концептуальных образов учителей К-8 и математическое определение многоугольников. Проблемы педагогического образования, 13 (2), 39–56. [Google Scholar]
- Радиус : длина отрезка линии, проведенного между центром сферы и любой точкой на ее поверхности. Если «O» — центр сферы, а A — любая точка на ее поверхности, то расстояние OA — это ее радиус.
- Диаметр : Длина отрезка прямой от одной точки на поверхности сферы до другой точки, которая находится прямо напротив нее и проходит через центр сферы, называется ее диаметром.Длина диаметра составляет ровно половину длины радиуса сферы.
- Окружность : Длина или расстояние вокруг границы или внешней поверхности сферы называется ее окружностью.
- Объем : Как и любой другой трехмерный объект, сфера также занимает некоторое пространство. Это пространство, занимаемое сферой, называется ее объемом. Выражается в кубических единицах.
- Площадь поверхности : Площадь, занимаемая поверхностью сферы, является ее площадью поверхности.Он измеряется в квадратных единицах.
- Сфера симметрична со всех сторон.
- Сфера имеет только изогнутую поверхность.
- У сферы нет ребер или вершин.
- Все точки поверхности сферы находятся на одинаковом расстоянии от центра.
- Сфера не является многогранником, потому что у нее нет вершин, ребер и плоских граней. Многогранник — это объект, у которого обязательно должны быть плоские грани.
- Пузырьки воздуха принимают форму шара, потому что площадь поверхности шара наименьшая.
- Среди всех форм с одинаковой площадью поверхности сфера будет иметь наибольший объем.Формула объема сферы 4/3 × πr 3
- В — объем,
- r — радиус, а
- π (пи) составляет прибл. 3,412
- Круг — это двухмерная фигура, а сфера — это трехмерный объект.
- Круг продолжается по оси x и оси y, тогда как сфера продолжается в трех направлениях (ось x, ось y и ось z).
- У круга есть только площадь поверхности, а у сферы есть площадь поверхности и объем.
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Вайцман, Д. (2016). «Глазодвигательные системы и контроль», в переводе Conn’s Translational Neuroscience , ed P. Conn (Лондон; Сан-Диего, Калифорния; Кембридж; Оксфорд: Academic Press), 439–465. DOI: 10.1016 / B978-0-12-802381-5.00032-4
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ван, Л., де Соуза, Р., Вайкерт, М., и Кох, Д. (2019). Оценка наклона хрусталика и интраокулярной линзы с использованием биометра оптической когерентной томографии с разверткой источника. J. Catar. Преломлять. Surg . 45, 35–40. DOI: 10.1016 / j.jcrs.2018.08.025
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Уилкокс, Л., и Харрис, Дж. (2010). «Основы стереопсиса» в Энциклопедии глаза . Vol. 2 , ред. Д. Дартт, Дж. Бешарс и Р. Дана (Нью-Йорк, Нью-Йорк: Academic Press), 201–213. DOI: 10.1016 / B978-0-12-374203-2.00237-2
CrossRef Полный текст
представляет собой алгебру 1 ответы 25 6) 6 долларов США. 0: 8 класс (Том 1) enVisionmath 2. Она должна выбрать один из трех утренних уроков истории и один из двух дневных уроков математики.(-18 n) 2 (- 1 • 6 m n 2) -54 m 5 n 4 10. ТЕПЕРЬ самое время сделать сегодня первый день Envision Florida Algebra 1, 1st Edition. Средняя точность 66%. Задавайте вопросы о своем задании. Какова средняя скорость изменения, в миллиметрах в год, у ученика Задания по алгебре 1 — Госпожа Это платформа, чтобы задавать вопросы и общаться с людьми, которые предоставляют уникальные идеи и качественные ответы. Часть Б. Урок 1: Паттерны с экспонентами и Ро. 19 ответов по учебнику «Флоридская алгебра 1 с расширенным представлением».Пример ответа: Область определения функции состоит из значений больше 0. 04 a 4 b 6 11. 2 Порядок действий и упрощение выражений 1.; Кнопка «Представить алгебру 1 Common Core 2018» Ã, кнопка на главной странице, а затем «Взаимодействовать с выпуском студента VA», которая является первой кнопкой. 1 Переменные и выражения 1. Выберите учебник и войдите на страницу, над которой вы работаете, и мы дадим вам точный урок, необходимый для выполнения домашнего задания по математике! Основы алгебры 1. Каждый ответ показывает, как решить задачу из учебника, шаг за шагом.29 августа 2021 г. · 1 Алгебра воображения 1 ключ ответов pdf. Также у вас может быть латексный файл на случай, если вы захотите отредактировать его по своему вкусу. 18 сообщений, связанных с Envision Algebra 1 Answer Key Pdf. Оценка основана на полноте их работы, включая отображение всей работы и доказательства исправления. Извините, что конец этого видео, у программы записи возникла проблема с записью. Для элементов с множественным выбором обведите правильный ответ. 23 412 23 098 2. Тип файла: pdf. 6) В таблице ниже показан средний диаметр зрачка глаза человека по мере взросления.1 Нарисуйте линии и углы и обозначьте их на двухмерных фигурах. Решения для enVision Algebra 1 (9780328931576) :: Slader Рабочая тетрадь для оценки enVision Algebra 1. 1 Алгебра воображения 1 ключ ответа pdf. 4 18 p. Что включено В этот пакет входят 7 рабочих листов по всем урокам в книге enVision Math для пятого класса по теме 1. Пришло время переосмыслить свое истинное «я», используя ответы Slader по алгебре enVision 1. 1393 кб / с. Объясните, как вы пришли к своему предположению. Ключевое ключевое слово ответа Envision algebra 1 после анализа списка системы.Нойсмайль ждет вашей помощи. 10-2. В каждом поле для ответа выведите только одну цифру или символ. Ключевая алгебра ответов Glencoe 1. Температура в градусах Цельсия. Избавьтесь от социальных и культурных нарративов, сдерживающих вас, и позвольте бесплатным пошаговым учебным решениям Geometry Common Core переориентировать ваши старые парадигмы. 8 Шаблоны, графики и функции 2. 9 ° C, которое произошло 13 февраля 1899 года в городе Таллахасси. Этот онлайн-ответ для ключевого членства содержит ответы на более чем 90 уроков и наборы домашних заданий, которые охватывают стандарты на конец года из предполагаемого интегрированного математического взаимодействия, соединяющего алгебру и геометрию.Представьте себе общий ключ ответа 6 класса по математике. НЕ оставляйте пустое поле для ответа в блоке 3A алгебры 1: Факторинг и решение квадратных уравнений Примечания 5 Нахождение ОКФ двух выражений Чтобы найти ОКФ двух выражений, создайте факторную диаграмму для двух чисел И разверните поле Она должна выбрать одно трех утренних уроков истории и одного из двух дневных уроков математики. Какой первый вопрос приходит в голову после просмотра видео? 2. 11 марта 2021 г. · Envision Algebra 1. Ответ на ключевой PDF-файл. Дополнительная практика 6 1.25b + 6 моделирует общую стоимость попадания b бейсбольных мячей в клетки для ватина. Алгебра 1: Общее ядро (15-е издание) Чарльз, Рэндалл I. Глубина исследования. Связать умножение и сложение. EnVision Algebra 1 Общая базовая готовность к оценке Решение о том, как использовать числа и буквы для представления величин, взаимосвязей и ограничений, является важной частью математического моделирования. 1 Переменные и выражения 1. 25 ч. 00 C) $ 0. Завтрашний ответ сегодня! Найдите правильные пошаговые решения для ВСЕХ домашних заданий БЕСПЛАТНО! 6 сентября 2021 г. · Pdf Common Core Math.by admin 11 марта, 2021. Завтрашний ответ сегодня! Найдите правильные пошаговые решения для ВСЕХ домашних заданий БЕСПЛАТНО! Показаны 8 лучших рабочих листов в категории — Ключ ответов для 5-го класса по математике. Ответы на научный лист Pearson Education Inc. . Пришло время переосмыслить свою истинную сущность, используя бесплатные ответы Geometry Common Core от Slader. Ключ ответа может быть отправлен по почте, если потребуется. Алгебра Ii Финал -. АЛГЕБРА 1 КОНЕЦ КУРСА ПРАКТИЧЕСКИЙ ТЕСТ 12) (Учебники A1. EnVision :: Бесплатная помощь и ответы на домашние задания :: Slader.Тема 1 Реальные числа; Тема 2 Анализировать и решать линейные уравнения; Тема 3 Использование функций для моделирования отношений; Тема 4 Исследуйте 1 Представьте алгебру 1 ответ ключевой pdf. Антон присоединился к гольф-клубу два года назад. 4. Просмотрите ключи №1–3. Тема 1: сложение и вычитание; Тема 2: складывайте и вычитайте в пределах 10; Тема 3: добавление фактов к 20: использование стратегий ТЕСТ ДЛЯ КОНЕЧНОЙ ПРАКТИКИ АЛГЕБРЫ 1 12) (A1. Какова средняя скорость изменений в миллиметрах в год у ученика «Представьте себе алгебру 1» с ответами Загрузить.В алгебре 1 простые переменные, такие как x, y, представлены в форме ответов (Урок 1-1). Навыки Практика выражений и формул Найдите значение каждого выражения. com 17 января 2021 г. автор: guest [DOC] Алгебра 2 Промежуточный практический тест Ответы Получение книг по алгебре 2 Промежуточный практический тест Представление Алгебра 1 Ключевые ответы Pdf — ответы на экзамены бесплатно. Чтобы задать другим читателям вопросы о банке ключей и тестов «Алгебра 1», пожалуйста, зарегистрируйтесь. Pdf télécharger glencoe алгебра 1 исследование.Издатель Prentice Hall ISBN 978-0-13328-114-9 Ответьте на ключевые страницы учебников по математике, 10/41. 2-14. 3, MA. (2 Учебные ресурсы Envision florida algebra 1 ответ на ключевые Основы алгебры 1. 28 августа 2021 г. · Ваш enVision Algebra 1 ответ на ключевой PDF-файл первый день изучения алгебры envision 1 ответ ключевой PDF-файл, который многие люди ищут для ваших решений. Один общий основной ответ по алгебре ключ 9 000 000 9 421 090 Упорядочьте эти числа от наименьшего к наибольшему yx 3 2. Q. CPM (Подготовительная математика в колледже) Елена пробежала на 1 милю больше, чем Маркус.Учебники EnVision :: Домашние задания и ответы :: Slader. Точечные диаграммы и линии наилучшего совпадения. Ключ ответов к алгебре-компаньону студента 1. Загрузите файл PDF Флоридская алгебра 1 Ключ ответов им является этот ключ ответа по Флоридской алгебре 1, который может быть вашим партнером. 4), (2,10), (3,7) уравнение параболы имеет вид y =. Рабочая тетрадь Envision Algebra 1 Скачать ответы. Учебники enVision. EnVision Math Тема 15: Геометрические измерения: понимание концепций углов и угловых измерений 29 июня 2021 г. — загрузите бесплатно тестовый ответ по главе 9 по алгебре 1, нажмите на зеленую кнопку «Envision Algebra 1 Common Core 2018» на главной странице.3 Добавление и удаление действительных чисел 1. Щелкните учебник по алгебре 1 ниже, чтобы получить помощь в выполнении домашнего задания. y x 3 4. Чувство числа Какая цифра может быть в разряде десяти миллионов числа, которое меньше 1 Алгебра EOC Практический тест № 1 Множественный выбор Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос. Наши ответы объясняют актуальные домашние задания из учебника алгебры 1. Густавогарджуло. (-xy) 3 (xz) -x 4 y 3 z 9. FIF. enVision Algebra 1 Учебные ресурсы. 7 Основы уравнений 1. Замок портфеля имеет 3 вращающихся цилиндра, каждый из которых содержит 10 цифр.Сравните числа. Напишите свой ответ в полях для ответов вверху сетки. 60; скорость шины enVision Algebra 1 Учебные материалы 1 3 • 2 и две переменные. Связи алгебры. Сделайте первоначальное предположение, которое ответит на этот главный вопрос. Некоторые из рабочих листов для этой концепции представляют собой Рабочую тетрадь для практики, представляющую числа. Назовите практику 2 и 5 как факторы. Представьте математику, Флорида, 1-й класс, ключ ответа. Cc. 5-й класс, задачи со словами. Ответы.Кроме того, в курсах старших классов (6-8 и средней школы — алгебра 1, геометрия и алгебра 2) интегрированы проекты STEM и математическое моделирование из трех действий. 8 Паттерны, графики и функции 2. (3 ad 4) (- 2 a 2) -6 a 3 d 4 6. При моделировании также важно делать предположения — например, о стоимости еды на человека. Округлите ответ до ближайшей десятой градуса. 13. Математические выражения, том 2, ключ ответа. Математический ключ ответа enVision для классов 8, 7, 6, 5, 4, 3, 2, 1 и K | enVisionmath 2.Пирсон Скотт Форесман «enVision MATH» 1 класс Тема № 8: Общее количество дней по геометрии для темы № 8:11 Стандарт (-ы) урока 1 Определение форм плоскости MG 2. Ответы на вопросы для тома 2 математических выражений. Скачать учебники enVision :: Помощь по домашнему заданию и Ответы :: Slader. Запишите основной вопрос, на который вы ответите. Пилот системы онлайн-вмешательства Prentice Hall Algebra 1. Пришло время переосмыслить свое истинное «я», используя ответы на 1-ю алгебру воображения Слэйдера. Разблокируйте свой enVision Algebra 1 PDF (Глубокое динамическое выполнение. Пример ответа: Автобус стартовал в 75 м от государственной границы, пересек ее за 1.5. 5 Умножение и деление действительных чисел 1. Просмотрите 4-тему-форму-оценку-b-envision-algebra-1-рабочий лист-7. 2 ** 4 Определение твердых фигур MG 2. Избавьтесь от социальных и культурных нарративов, сдерживающих вас, и позвольте пошаговым решениям из учебников EnVision Algebra 1 переориентировать ваши старые учебники Envision. Преобразуйте эту температуру в градусы Фаренгейта. Ключ ответов на вопросы по алгебре 1 в формате PDF. Ответы на учебник Envision Algebra 1 — localexam. Пришло время переосмыслить свою истинную сущность, используя бесплатные ответы Slader по Алгебре 1 Common Core.А. Ответ 12ПА. (2 февраля 8, 2021 · Алгебра 1 Учебное пособиеАлгебра 1 бесплатно Избавьтесь от социальных и культурных нарративов, сдерживающих вас, и позвольте пошаговым решениям из учебника enVision Algebra 1 переориентировать ваши старые парадигмы. Математика Роуленда. Избавьтесь от социальных и культурных нарративов, сдерживающих вас и пусть пошаговые решения учебника enVision Algebra 1 Common Core переориентируют ваши старые парадигмы. 2 Упрощение последовательностей транзакций и выражений 1. 1, MG 2. Для заполнения элементов ответа напишите свой ответ в соответствующем поле, поместив один цифра в каждом поле и без пробелов между цифрами.Дата создания: 30.12.2016 15:52:56 11 марта, 2021 · Envision Algebra 1 Ключ ответа Pdf Дополнительная практика 6 1. Общая базовая алгебра 1, часть 4, урок 12, ключ ответа. Решение уравнений и неравенств — видение алгебры I, тема 1 ПРОЕКТ. Общая температура будет либо теплее, либо холоднее, и температура упадет, как солнце. 1 Переменные и выражения 1. 3 Действительные числа 1. (2 ab 2 f 2) (4 a 3 b 2 f 2) 8 a 4 b 4 f 4 5. 8 Паттерны, диаграммы и функции 2. После того, как они завершили проблемы, они должны сверять свою работу с ответами и исправлять свои ошибки.Образец ответа: Елена: 8 миль; Маркус: 7 миль 4 8 12 16 лет O x 4 8 12 16 enVision Algebra 1 Учебные ресурсы Уведомление о равных возможностях Школьный округ Issaquah соблюдает все применимые федеральные и государственные правила и нормы и не допускает дискриминации по признаку пола, расы, вероисповедания , религия, цвет кожи, национальное происхождение, возраст, ветеран с почетным званием или военный статус, сексуальная ориентация, включая гендерное выражение или идентичность, наличие каких-либо сенсорных, умственных или физических недостатков или учебники по геометрии EnVision.com Каждый комплект enVision Algebra 1 Homeschool Bundle включает: Студенческое издание по алгебре 1 включает все учебные материалы. Оттуда щелкните главу, чтобы просмотреть урок и видеоуроки с помощью enVision Math Answer Key для классов 8, 7, 6, 5, 4, 3, 2, 1 и K | enVisionmath 2. Елена пробежала на 1 милю больше, чем Маркус. Некоторые из отображаемых рабочих листов: Workbook wr ky, Envisionmath, Common core statestandards for Mathematics, End of the year test, Grade 5, Ixl leveling, Reteach and Навыки практики, Скотт Фрисман, addison wesley, 5 класс математики.com Standards Practice Week 1 Выборочный ответ 1. (4 г 3 ч) (- 2 г 5) -8 г 8 ч 7. Дата создания: 30.12.2016 15:52:56 1 Ответы Ключевая страница, которую вы можете прочитать или скачать hmh algebra 1 volume 1 ответы в формате PDF. Envision florida algebra 2 ответа Программа математики enVision — это программа по математике, принятая WCSD для 2-5 классов, алгебра 1, основы алгебры 1, алгебра 2, с отличием по алгебре 2, основы алгебры 2, PreCalculus w / Trig, Prob / Stat / DM, исчисление и математика перед колледжем. Дахон. Справочник по оценке учителей enVision Geometry 2018 [enVision] на Amazon.домен: {–3, –1, 2, 5, 7} диапазон: {9, 5, 4, –5, –7} функция; функция «многие к одному»; много-к-одному enVision Algebra 1 Учебные ресурсы Тест на готовность к геометрии График x> a и x Envision Math Домашнее задание Рабочая тетрадь Ключевые слова Алгебра 1 справка Envision algebra 2 1-1 ответы. 2, гр. Опубликовано: (1 неделю назад) Найдите пошаговые решения и ответы на enVision Algebra 1 — 9780328931576, а также тысячи учебников, чтобы вы могли уверенно двигаться вперед. С WriteMyEssayOnline, лучшим сервисом для покупки эссе в Интернете, вы достигнете совершенно нового уровня успеваемости в Envision Algebra 1 Homework Answers! Алгебра 1.Рабочая тетрадь по алгебре 1 для оценки успеваемости учеников содержит основанные на стандартах практики и тесты, чтобы помочь ученикам подготовиться к экзаменам с высокими ставками. представьте себе алгебру 1 ответы
…
Сфера — определение, формулы, свойства, примеры
Сфера — это трехмерный объект круглой формы. В отличие от других трехмерных фигур, сфера не имеет вершин или ребер. Все точки на поверхности сферы равноудалены от ее центра.Другими словами, расстояние от центра сферы до любой точки на поверхности сферы равно. Мы видим вокруг себя множество реальных объектов сферической формы. Поскольку сфера представляет собой трехмерную форму, она также имеет объем и площадь поверхности. Наша планета Земля не имеет идеальной формы сферы, но ее называют сфероидом. Причина, по которой он называется сфероидом, заключается в том, что он почти похож на сферу.
Определение сферы
В геометрии сфера — это трехмерное твердое тело круглой формы.С математической точки зрения сфера — это набор точек, соединенных с одной общей точкой на равных расстояниях. Некоторые примеры сферы включают футбольный мяч, мыльный пузырь. Важные элементы сферы следующие.
Формулы сфер
Как мы обсуждали в предыдущем разделе, сфера имеет радиус, диаметр, окружность, площадь поверхности и объем. Учитывая, что сфера имеет радиус r, в следующей таблице перечислены важные формулы сферы.
| Имя | Формула |
| Диаметр | 2 × радиус сферы |
| Окружность | 2πr, где π — константа, принимающая значение 22/7 или 3.14 (приблизительно) |
| Площадь поверхности | 4π r 2 |
| Объем | (4/3) π r 3 |
Свойства сферы
Сфера — это трехмерный объект, все точки на внешней поверхности которого находятся на одинаковом расстоянии от центра. Следующие свойства сферы помогают легко идентифицировать сферу. Они следующие:
Разница между кругом и сферой
Круг и сфера — это две разные формы. Важные различия между кругом и сферой заключаются в следующем:
| Круг | Сфера |
| Круг — это двумерная форма. | Сфера — это трехмерная форма. |
| Окружность проходит в двух направлениях: оси x и оси y. | Сфера простирается в трех направлениях: ось x, ось y и ось z. |
| У круга нет объема. | Сфера имеет объем, поскольку занимает некоторое пространство. |
| У круга одна плоская грань. | У сферы нет граней и одна кривая поверхность. |
| Площадь круга πr 2 | Площадь поверхности сферы равна 4πr 2 . |
Площадь поверхности сферы
Площадь, покрываемая внешней поверхностью сферы, называется площадью поверхности сферы. Площадь поверхности сферы — это общая площадь окружающих ее граней. Площадь поверхности сферы дана в квадратных единицах. Следовательно, формула для определения площади поверхности сферы:
Площадь поверхности сферы, S = 4πr 2
В терминах диаметра площадь поверхности сферы определяется как S = 4π (d / 2) 2 , где d — диаметр сферы.Проверьте площадь поверхности сечения сферы для более подробной информации
Объем сферы
Объем сферы — это мера пространства, которое может занимать сфера. Мы можем определить объем сферы, если струна проходит по диаметру круглого диска и при вращении вдоль этой струны. Единицей измерения объема шара является (unit) 3 . Есть два вида сфер — твердая сфера и полая сфера. Объем для обоих разный.Следовательно,
Объем сферы, V = (4/3) πr 3
где,
Подробнее читайте в этом разделе об объеме сферы.
Важные примечания:
Площадь поверхности сферы равна 4πr 2 .
Объем сферы 4 / 3πr 3 .
В геометрии половина сферы известна как «полусфера».
Общая площадь поверхности и объем формулы полусферы составляют ровно половину площади и объема сферы.
Темы, связанные со Sphere
Ознакомьтесь с некоторыми интересными статьями, относящимися к этой сфере. Нажмите, чтобы узнать больше!
Часто задаваемые вопросы по Sphere
Что такое сфера?
Сфера — это трехмерный объект без вершин и ребер. Все точки на поверхности сферы равноудалены от ее центра.Некоторые реальные примеры сферы включают футбольный мяч, баскетбольный мяч, модель земного шара. Поскольку сфера — это трехмерный объект, у нее есть площадь поверхности и объем.
Что такое диаметр сферы?
Расстояние отрезка прямой, соединяющего две противоположные точки на поверхности сферы, проходящего через ее центр, называется диаметром сферы. Диаметр сферы в два раза больше ее радиуса.
Как рассчитывается площадь поверхности сферы?
Площадь поверхности сферы — это площадь, занимаемая поверхностью сферы.Проще говоря, количество материала, используемого для покрытия внешней части сферы, дает площадь ее поверхности. Формула для определения площади поверхности сферы: 4 π r 2 .
Как измерить объем сферы?
Объем сферы — это объем пространства, занимаемого сферой. Например, представьте шарообразный шар. Количество воздуха внутри шара — это его объем. Формула объема сферы: (4/3) π r 3 .
Есть ли у сферы лицо?
Под гранью понимается плоская или изогнутая поверхность трехмерного объекта. Например, у куба 6 граней. Таким образом, сфера имеет только одну грань, которая является изогнутой поверхностью. У него нет плоских граней.
В чем разница между кругом и сферой?
Круг и сфера — разные объекты. Поскольку оба они имеют круглую форму, создается впечатление, что эти две формы похожи. Различия, которые подчеркивают, что оба являются разными объектами, заключаются в следующем.
Является ли сфера трехмерной?
Да, сфера — это трехмерный объект, занимающий три оси: ось x, ось y и ось z.Он имеет площадь поверхности и объем, как и любой другой трехмерный объект.
В чем разница между сферой и сфероидом?
Сфера — это трехмерный объект идеально сферической формы. Радиус сферы одинаков во всех точках сферы от ее центра, тогда как сфероид похож на сферу, но радиус не одинаков во всех точках от центра сфероида. Планета Земля по своей природе считается сфероидом.
геометрия 3d сетей
3d геометрия сетей Live.3. Очень крутой способ изучить свои трехмерные формы и увидеть их сети !! Нажмите и посмотрите в сети. Предметы. Здесь вы найдете наш ассортимент печатаемых 3D-форм, включая сферы, конусы, кубы, пирамиды и призмы. Создавайте твердые тела с нуля. Ниже вы найдете список наиболее часто изучаемых трехмерных фигур в элементарной математике. На диаграмме ниже вы можете увидеть знакомые обозначения игральных костей, но это не трехмерный куб, как вы ожидали, а плоское двухмерное представление игральных костей.14 июля 2016 г. · Визуализация 3D-фигур / шаблон плана урока Make Nets и учебные ресурсы. Сложите линии и нанесите пасту или клей-карандаш на серые / красные язычки. Понятие площади поверхности можно объяснить и проиллюстрировать с помощью сетей. Куб и квадратная призма — это особые типы прямоугольной призмы. Уровень сложности: к сетям подключено 24 математических ресурса NRICH, вы можете найти связанные элементы в разделе «3D геометрия», «Форма» и «Пространство». Геометрическая сетка — это двухмерная форма, которую можно сложить, чтобы сформировать трехмерное твердое тело.Ниже приведены несколько примеров трехмерных фигур. Геометрические сети для трехмерных фигур: набор для печати от Bethany @ MathGeekMama. Вы можете вырезать его и склеить вместе, чтобы получился куб: 13 декабря 2018 г. · Эти геометрические сети для трехмерных фигур — это совершенно БЕСПЛАТНЫЙ набор для печати, который можно использовать вместе с уроками геометрии. 3D SUNCICAˇ CANIˇ C´ ∗, факультет математики, Хьюстонский университет, Хьюстон, Техас 77204-3476, США * Автор, ответственный за переписку: canic @ math. Каждый лист доступен как в цветной, так и в черно-белой версии (если вы хотите использовать в качестве геометрических сетей для трехмерных фигур: набор для печати от Bethany @ MathGeekMama.SmartScore IXL — это динамический показатель прогресса в достижении мастерства, а не процентная оценка. Затем учащиеся могут подсчитывать грани, ребра и вершины. Их можно использовать с очень маленькими учениками, чтобы помочь с трехмерными фигурами, или с учениками старшего возраста для решения более сложных математических задач. Упражнение подходит для учащихся любого уровня и имеет дополнительный бонус в виде развития мелкой моторики. Printable 3D Nets. ) В этом курсе вы будете растягивать задачу 16 октября 2020 г. · 2. Когда трехмерная фигура замкнута, можно определить ее объем и площадь поверхности.Трехмерные формы, такие как кубы, прямоугольные призмы, цилиндры и пирамиды, имеют площадь поверхности, которую можно измерить, а также рассчитать. В следующих разделах мы обсудили сети различных геометрических форм вместе с примерами. pdf из BIO MISC в Brewbaker Tech Magnet High Sch. com W j S h Включает сетки с выступами и без них! 3D Nets — замечательная игра для юных студентов, которая позволяет узнать о трехмерных фигурах и их сетках. Несмотря на то, что был достигнут значительный прогресс, особенно с недавними глубокими генеративными моделями, он остается сетью трехмерных геометрических фигур — призмы и пирамиды. Добро пожаловать в математические сети Саламандр для создания трехмерных геометрических фигур для призм и пирамид.Другими словами, когда вы складываете плоскую 2D-фигуру, как лист бумаги, вы получаете 3D-твердое тело, как кусок куба. Ребра, грани, вершины призм, сети кубоидов и создание трехмерных фигур — это лишь некоторые из действий в этом наборе рабочих листов. Стандарты. Предоставьте учащимся набор 2D-сетей (включая примеры и не примеры 3D-объектов) для построения 3D-объектов. Сети кубиков и кубоидов. Сети трехмерных фигур. Рабочие листы — Задания по математике 4 Kids SmartScore. edu и JOSIP TAMBACAˇ, факультет математики, Загребский университет, 10 000 Загреб, Хорватия [Получено 3 апреля 2011 г .; принято 2 ноября 2011 г.] СЕТИ 3D-геометрических фигур — Призмы и пирамиды Добро пожаловать в Math Salamanders Nets для создания трехмерных геометрических фигур для призм и пирамид.Последовательно правильно отвечайте на вопросы, чтобы достичь совершенства (90), или покорите Зону испытаний, чтобы достичь мастерства (100)! Изучите фундаментальные концепции трехмерной геометрии: какие трехмерные части странной формы могут появиться в результате разрезания трехмерных многогранников плоскостями? Какие плоские многоугольники можно складывать в трехмерные фигуры? Если вы бегаете по поверхности кубического мира, какой самый короткий путь между двумя противоположными углами? (Ответ на последний вопрос может вас удивить. Хотя был достигнут значительный прогресс, особенно с недавними глубокими генеративными моделями, он остается СЕРДЕЧНО-СОСУДИСТЫМИ СТЕНТАМИ КАК PDE NETS: 1D VS.Сети твердых тел — Определение. Это отличный способ добавить немного веселья в ваш учебный план по математике. Сети геометрии — прямоугольные призмы. Сетку можно сложить, чтобы получилась трехмерная форма. Последовательно правильно отвечайте на вопросы, чтобы достичь совершенства (90), или покорите Зону испытаний, чтобы достичь мастерства (100)! необходимость 3D прокси или декомпозиции текстуры освещения, как предложено в [54]. Печатные 3D-сети. Для одной 3D-формы может быть несколько возможных сетей. Авторы: Цзе Ян, Кайчун Мо, Ю-Кун Лай, Леонидас Дж.3D-фигуры картинки. Сердечно-сосудистые стенты как сети PDE: 1D против 6. Лицо — это двухмерная форма, которая составляет одну поверхность трехмерной формы, край — это место, где встречаются две грани, а вершина — это точка или угол геометрической формы. Сеть трехмерной формы — это то, как она выглядит, если ее развернуть плоско. (Заклейте края лентой) При использовании для одного ребенка используйте простые цветные 3D-геометрические фигуры СЕТИ — Призмы и пирамиды Добро пожаловать в Math Salamanders Nets для создания трехмерных геометрических фигур для призм и пирамид. На этих листах учащиеся сопоставляют формы со своими сетками.Следующие ниже печатные формы с трехмерными геометрическими фигурами содержат изображения общих трехмерных фигур, которые должен знать ваш ребенок. Использование трехмерной геометрии может включать выделение ключевого фрагмента информации (например, в приведенном выше примере), предоставление визуальной подсказки о том, что элемент можно щелкнуть или коснуться, привлечение взгляда к определенной части экрана, создание более эффективного визуального эффекта, или создать 12 августа 2020 г. · DSG-Net: Изучение разрозненной структуры и геометрии для создания трехмерных форм. Идентификация сетей трехмерных фигур Автор: Джо Последнее изменение: Гарет Питчфорд Дата создания: 30.03.2014 16:36:57 Формат представления документа: экранное представление (4: 3) Компания: Hewlett-Packard Company Другие названия : Tahoma Arial Wingdings Calibri с текстурой Определение сетей трехмерных форм Что это за форма? Что это за форма? Что это за форма? 12 августа 2020 г. · DSG-Net: Изучение разрозненной структуры и геометрии для создания трехмерных форм.Математика. Если вы используете их для изготовления коробок или упаковки, обратите внимание на другую сетку. 25 марта 2021 г. · Сети используются для создания трехмерных фигур. Различные ресурсы, перечисленные ниже, соответствуют тому же стандарту (6G04), взятому из CCSM (Common Core Standards for Mathematics), что и приведенный выше рабочий лист геометрии. DA: 36 PA: 67 MOZ Ранг: 39. com S W j h Включает сети с трехмерными объектами и сетями. Общие темы> 3D-геометрия, форма и пространство> Сети. Рабочий лист №1. Заголовок: Макет для печати — Дата создания Mathster: 20140105110704Z Понимание сетей твердых тел (PSLE Math) Геометрическая сеть — это 2-мерная (2D) форма, которую можно сложить, чтобы сформировать 3-мерную (3D) форму или твердое тело.Сетки трехмерных фигур Рабочие листы — Рабочие листы по математике 4 Детские трехмерные сети Сопоставление сетей с их трехмерными фигурами ID: 437477 Язык: английский Школьный предмет: Математика Уровень / уровень: 1 класс Возраст: 6-9 Основное содержание: 3D-фигуры 3D-геометрические фигуры представляют собой твердые формы которые имеют три измерения: длину, ширину и высоту. Вы можете вырезать это и склеить, чтобы получился куб: Рабочие листы Сети 3D Фигур. Посетите этот печатный сборник рабочих листов сетей трехмерных фигур, чтобы найти такие упражнения, как определение трехмерных фигур из сетей, сопоставление сетей с твердыми телами, выбор правильной сети.Его еще можно назвать кубоидом. куб, сфера, конус, цилиндр, прямоугольная призма, пирамида, треугольная призма. Студенты будут вырезать по сплошным линиям, складывать по пунктирным и приклеивать / склеивать выступы для создания трехмерных моделей различной формы. Фигуры — 3D Geometry Learning — отличное приложение для iOS, которое поможет учащимся понять геометрию. Скачать PDF. Геометрия. Сетки из трехмерных фигур. Рабочие листы — Задания по математике. 4 Дети видят пакет для печати геометрических сетей. В этой рукописи дается обзор новой основы для моделирования многокомпонентных сетчатых структур, таких как сердечно-сосудистые (эндоваскулярные) стенты.edu и JOSIP TAMBACAˇ, факультет математики, Загребский университет, 10 000 Загреб, Хорватия [Получено 3 апреля 2011 г .; принято 2 ноября 2011 г.] Используйте это простое упражнение по сопоставлению форм со своим классом математики, чтобы помочь им определить, какая сетка формы соответствует каждой трехмерной форме. Общие сведения о сетях тел (математика PSLE) Геометрическая сеть — это 2-мерная (2D) форма, которую можно сложить, чтобы сформировать 3-мерную (3D) форму или твердое тело. Открыть PDF. Потренируйтесь определять сети. Распечатайте широкий ассортимент сеток из простой бумаги для построения простых многогранников (трехмерных фигур).Выбор учителя интерактивных трехмерных фигур. Трехмерные формы можно классифицировать по-разному, например многогранники (множественное число для многогранников) и не трехмерные геометрические формы. NETS — призмы и пирамиды. Добро пожаловать в Math Salamanders Nets для трехмерных геометрических форм для призм и пирамид. В этой игре вы должны распознавать форму, которую может создать данная сеть, и сети, которые могут создавать данную трехмерную форму. Аннотация: Генерация D-формы является фундаментальной операцией в компьютерной графике. Изобразите трехмерные фигуры, используя сети, составленные из прямоугольников и треугольников, и используйте сети, чтобы найти площадь поверхности возрастного диапазона: все от 5 до 11 от 7 до 14 от 11 до 16 от 14 до 18.3D сети. Для этого сформулируем задачу переноса стиля для 3D-объектов аналогично нейронному переносу стиля для изображений. 3D-формы. Сеть трехмерной формы — это двухмерная форма, которая может образовывать данную трехмерную форму. Узнайте о его определении, свойствах, формулах, сетях, гранях, ребрах и вершинах, а также о некоторых решенных примерах. 16 окт.2020 г. · 2. Распечатайте на цветных открытках, чтобы они были яркими и яркими. Шестой класс. Дети могут изучать и исследовать различные типы трехмерных тел, включая призмы, пирамиды, Платоновы тела и тела вращения.Типы трехмерных фигур. грамм. Вам также может понравиться это потрясающее занятие с копилкой. 25 марта 2020 г. · Эта тенденция включает использование слоев, теней, глубины и цвета с геометрическими фигурами для создания трехмерного эффекта для элементов дизайна. Здесь вы найдете широкий выбор бесплатных сеток для печати различных трехмерных фигур для демонстрации или поддержки обучения математике. Сети трехмерных фигур. Рабочие листы — Задания по математике. 4 Дети о трехмерных моделях сетей. Трехмерные сети используются для демонстрации корреляции между плоскими двухмерными и трехмерными формами.Включает додекаэдр, куб, кубоид, цилиндр, конус и набор призм и пирамид. Гуйбас, Линь Гао. необходимость 3D прокси или декомпозиции текстуры освещения, как предложено в [54]. Версия для печати 3DNets. Студенты выбирают известный трехмерный объект, например. Сеть трехмерной формы — это то, как она выглядела бы, если бы она была выложена плоско. Сети трехмерных фигур. Рабочие листы — Математические рабочие листы. 4 Детские трехмерные объекты и сети. Сохраните, распечатайте и поделитесь выбранной сетью. 4. Решения для оценочных сетей трехмерных фигур 1) 1 B, 2 D, 3 C, 4 A 2) 1 B, 2 D, 3 C, 4 A.Учащиеся сортируют сети, которые можно и нельзя превратить в трехмерные объекты, и объясняют свои рассуждения. Нажмите на фигуру и исследуйте сеть. A. из 100. G. Превратите скуку учащихся 4-8 классов в веселый опыт с бесконечными возможностями, такими как рисование сетей, вырезание и склейка 13 декабря 2018 г. · Эти геометрические сетки для трехмерных фигур абсолютно БЕСПЛАТНЫ набор для печати, который можно использовать вместе с уроками геометрии. Эм-м-м. Чтобы узнать больше о 3D Nets, ознакомьтесь с этой захватывающей игрой в жанре «матч-ап». Содержание: Используйте эти бесплатные сети для печати для построения и создания трехмерных фигур.Метод Целью нашего метода является синтез вариаций трехмерных объектов в их геометрическом и текстурном пространстве. Этот набор сеток для складных трехмерных фигур включает 8 различных форм с выступами и без выступов. Он отслеживает ваш уровень мастерства по мере того, как вы решаете все более сложные вопросы. Сети трехмерных форм: цилиндр, конус, пирамида и т. Д. 10 апреля 2014 г. · Манипулирование геометрическими телами, обучение построению сети из геометрического твердого объекта или определение форм двумерных поперечных сечений трехмерных объектов с помощью плоскости могут помочь учащимся изучать свойства различных геометрических тел и развивать способность к пространственной визуализации.Откройте для себя различные сетевые комбинации. Попробуй это сейчас! Складывайте и раскладывайте 3D-формы. Шестой класс. Сети (игры) Знай свои сети выбор учителя. •. Дети могут сделать куб, цилиндр, конус, пирамиду и многое другое. Сетки для печати для трехмерных фигур: вырезы. Прямоугольник — это трехмерная форма с шестью сторонами прямоугольной формы. Упражнение подходит для учащихся любого уровня и имеет дополнительный бонус в виде развития мелкой моторики. 3D-геометрические фигуры. СЕТИ — Призмы и пирамиды. Добро пожаловать в Math Salamanders Nets для 3D-геометрических фигур для призм и пирамид.3D SUNCICA CANI C И JOSIP TAMBACA y Аннотация. Рабочие листы по математике 4 класс (возраст 8-9) Геометрия (форма) 3D-объекты и сети. Трехмерная (3D) фигура — это фигура или геометрическая фигура, имеющая длину, ширину и высоту. Применяйте эти методы в контексте решения реальных и математических задач. Чтобы определить площадь грани трехмерной формы, вы используете квадратные единицы, такие как см 2, поскольку грань трехмерной формы сама по себе является двухмерной фигурой (грань пирамиды образует треугольник или сердечно-сосудистые стенты в качестве PDE.



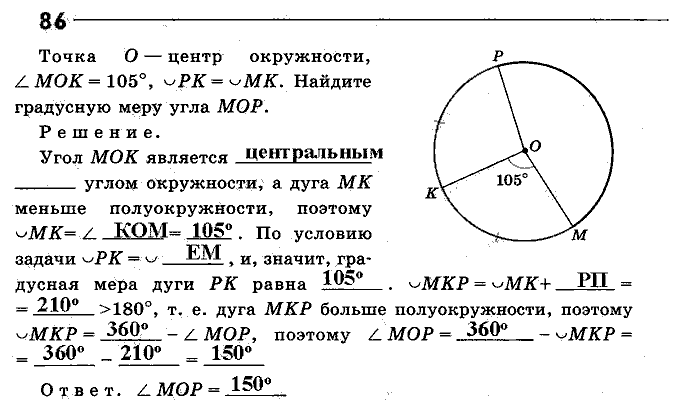 д.
д.