Гаврилова геометрия контрольно измерительные материалы 8 класс: ГДЗ Геометрия 8 класс Гаврилова Контрольно-измерительные

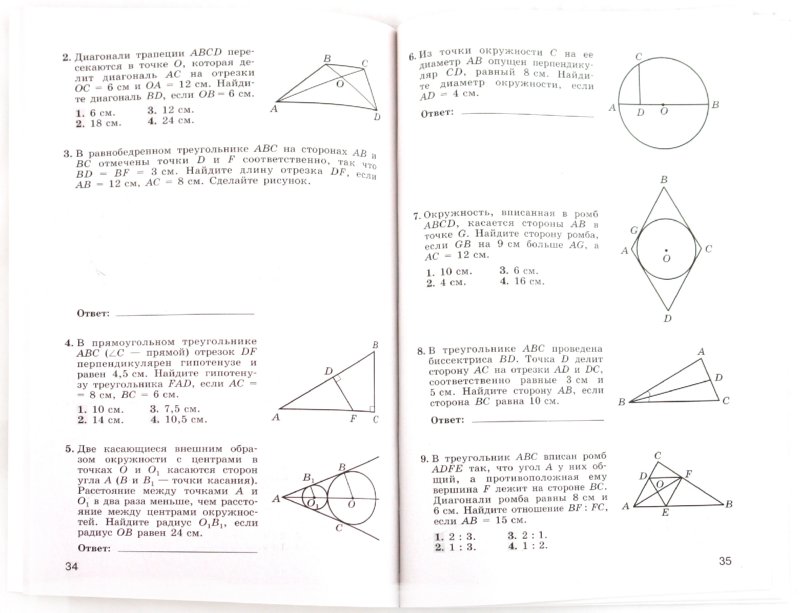
ГДЗ Геометрия 8 класс Гаврилова Контрольно-измерительные

Подробные решения по геометрии за 8 класс авторы Гаврилова

Геометрия – одна из самых важных дисциплин в школьной программе. Изучение данного предмета необходимо для освоения полного курса образования. Но у многих детей она вызывает массу проблем: запоминание формул, теорем, нахождение площадей и периметров. Эти сложности ставят ребенка в тяжелое положение. Поэтому на помощь пришли специалисты и разработали * гдз по геометрии контрольно-измерительные материалы за 8 класс Гаврилова ** — замечательное подспорье, которое будет служить верным другом и помощником. У школьников больше не будет проблем в решении самых сложных заданий, если он станет обращаться к данному ресурсу ежедневно.

Для кого решебник играет важную роль в процессе освоения предмета?

Справочник ** онлайн ответы к контрольно-измерительным материалам по геометрии для 8 класса автора Гавриловой ** не то используют ежедневно, но и любят:

• восьмиклассники, которые заняты в различных спортивных секциях, так как у них и так мало времени. Это отличная альтернатива различным дополнительным пособникам, а также репетиторам. Не нужно тратить драгоценное время на поездки к преподавателю после школьных занятий;
• школьники, которые не хотят просить помощи у родителей в подготовке домашних заданий. Намного удобнее самостоятельно разобраться со сложными и непонятными заданиями;
• педагоги, предпочитающие не тратить время зря. Поскольку проверка множества самостоятельных, контрольных и проверочных работ занимает много времени, которое можно потратить с пользой для себя и учеников. Например, можно подготовить интерактивный урок;
• родители, у которых ненормированный или скользящий график работы. Не всегда они могут вникнуть в материал, объяснить его, чтобы помочь ребёнку выполнить домашнее задание;
• ученики, активно участвующие в олимпиадах, конкурсах по геометрии. Для них это ещё одна проверка знаний, ведь они хотят получить больше знаний, чтобы повысить итоговую оценку;
• дети, обучающиеся на домашнем или дистанционном обучении. Они смогут ещё раз вникнуть, изучить или повторить материал.
• ребята, которые по разным обстоятельствам пропустили изучение материала. Для быстрого усвоения тем, они могут с лёгкостью использовать данный ресурс.

Безусловные преимущества применения готовых заданий в школе

Систематическое применение быстрых решений к контрольно-измерительным материалам по геометрии за 8 класс Гавриловой принесет только положительный результат. Ведь сегодня найти ответ даже на самую сложную школьную задачу или задание можно легко и быстро. Преимущества применения таковы:

• они круглосуточно доступны в любое время дня и ночи с любого устройства;
  • поднимают самооценку школьников;
• экономят время не только школьникам, но и родителям и педагогам;
• проясняют самые сложные и невыполнимые задания;
• помогают подготовиться к конкурсам и олимпиадам;
• не просто дают правильный ответ, но и предоставят весь путь действий и решений;
• помогают родителям в объяснении материала и проверке сложных домашних заданий;
• удобный интерфейс;
• не требует регистрации;
• имеют только актуальные ответы и решения;
• учат самостоятельно анализировать и делать выводы.

Использование готовых домашних заданий для современных учащихся не является исключением из правил, это скорее обычная практика. Благодаря создателям еуроки ГДЗ школьникам станет легче учиться.

Гаврилова Н.Ф. Контрольно-измерительные материалы. Геометрия 8 класс ОНЛАЙН

Избранное / Математика / Математика для учителей и преподавателей / Математика для школьников / Сборники заданий по математике / Учебники, пособия, рабочие тетради по математике

22.08.201328.05.2020

Контрольно-измерительные материалы. Геометрия: 8 класс / Сост. Н.Ф. Гаврилова. — М.: ВАКО, 2011. -96 с. — (Контрольно-измерительные материалы).
В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для 8 класса. Тесты тематически сгруппированы, соответствуют требованиям школьной программы. Структура КИМов аналогична структуре тестов в формате ЕГЭ, что позволит постепенно подготовить учащихся к работе с подобным материалом. В конце пособия предложены тексты самостоятельных и контрольных работ, а также ключи к тестам.
Издание адресовано учителям, школьникам и их родителям.
Содержание
От составителя…………………………………..3
Тест 1. Многоугольники……………………………6
Тест 2. Параллелограмм……………………………8
Тест 3. Трапеция………………………………..10
Тест 4. Прямоугольник. Ромб. Квадрат……………….12
Тест 5. Обобщение темы «Четырехугольники»………….14
Тест 6. Четырехугольники (теоретический)……………18
Тест 7. Площадь многоугольника. Площадь прямоугольника….20
Тест 8. Площадь параллелограмма, ромба и треугольника… 22
Тест 9. Площадь трапеции…………………………24
Тест 10. Теорема Пифагора………………………..26
Тест 11. Обобщение темы «Площадь»………………..28
Тест 12. Площадь (теоретический)…………………..32
Тест 13. Определение подобных треугольников…………34
Тест 14. Признаки подобия треугольников…………….36
Тест 15. Применение подобия при решении задач………38
Тест 16. Соотношения между сторонами и углами прямоугольного треугольника……40
Тест 17. Обобщение темы «Подобные треугольники»……42
Тест 18. Подобные треугольники (теоретический)………46
Тест 19. Касательная к окружности………………….48
Тест 20. Центральные и вписанные углы………………50
Тест 21. Четыре замечательные точки окружности………52
Тест 22. Вписанные и описанные окружности………….54
Тест 23. Обобщение темы «Окружность»……………..56
Тест 24. Окружность (теоретический)………………..60
Тест 25. Итоговый по программе 8 класса……………..62
ПРИЛОЖЕНИЯ
Самостоятельные работы………………………….66
Контрольные работы……………………………..78
Ключи к тестам…………………………….. ….84
Ответы к самостоятельным работам………………….89
Ответы к контрольным работам…………………….92

ТегиГаврилова геометрияГаврилова кимы по геометриикимы по геометрии для 8 классаКонтрольно-измерительные материалыКонтрольно-измерительные материалы для 8 классаконтрольно-измерительные материалы по геометриичитать онлайн

Геометрия и измерение — проект «Подключенная математика»

Естественные и искусственные объекты окружающего нас мира очерчены, поддерживаются и украшаются бесконечным разнообразием геометрических форм. Главной целью модулей в разделе Connected Mathematics 3 (CMP3) «Геометрия и измерения» является развитие понимания учащимися связей между формой и функцией обычных форм. Например, треугольники обеспечивают структурную устойчивость фермам моста, потому что они являются жесткими фигурами. Шестиугольники — это распространенная форма декоративной плитки из-за их множества симметрий и того факта, что их можно использовать для покрытия плоских поверхностей без нахлеста или зазоров. Строители используют 3-4-5 треугольников для проверки перпендикулярности каркаса, потому что каждый такой треугольник должен быть прямоугольным.

В разделе «Геометрия и измерения» имеется шесть модулей, а также связи с темами «Геометрия и измерения» во многих модулях других направлений контента. Основными задачами направления являются:

• Расширить понимание и навыки геометрических измерений периметра и площади многоугольников и кругов, а также площади поверхности и объема прямых призм, цилиндров, конусов и сфер;
• Развивать понимание сходства и соответствия геометрических фигур, используя как концепции преобразований, так и условия, связанные с измерениями сторон и углов, для установления этих отношений;
• Разработка связей пропорциональности между линейными, площадными и объемными измерениями для подобных фигур;
• Расширение понимания построения координатных графиков до четырех квадрантов; и
• Разработайте теорему Пифагора для прямоугольных треугольников и связанную с ней формулу расстояния для точек на координатной сетке.

Процессы обучения, направленные на достижение каждой из этих широких целей, описаны в следующих разделах.

Расширение знаний и навыков с помощью геометрических измерений

Учащиеся шестого класса, скорее всего, знают, как найти площадь прямоугольника и объем прямоугольной призмы. Модуль «Покрытие и окружение » для шестого класса рассматривает основные идеи периметра, площади и объема, но расширяет основную идею покрытия (и заполнения) фигуры копиями единицы длины (отрезка), площади (квадрата) или объем (куб) несколькими способами. Во-первых, он выделяет и помогает учащимся увидеть разницу между периметром и площадью, задавая вопрос: «Каковы размеры прямоугольника с фиксированным периметром и максимальной площадью?» и «Каковы размеры прямоугольника с фиксированной площадью и минимальным периметром?» Например, на следующем изображении показаны два прямоугольника площадью 16 квадратных единиц, но с разными периметрами.

Область ABCD = 16 квадратных единиц площадь EFGH = 16 квадратных единиц Периметр ABCD = 16 единиц Периметр EFGH = 20 единиц

Второе, покрытие и окружение . Использует принцип, который может быть порезан. на части и собирать в новые формы без изменения площади, чтобы логически разработать формулы площади треугольников и параллелограммов. Этот принцип проиллюстрирован ниже.

Площадь параллелограмма слева равна сумме двух площадей, трапеции и треугольника. Площадь прямоугольника справа также является суммой тех же двух площадей. В обоих случаях A = bh квадратных единиц. Учащиеся связывают геометрическую идею, площадь с алгебраической идеей, отношениями.

Наконец, Покрытие и окружение закладывает основу для расчета объема в любой призме, подчеркивая тот факт, что такую ​​призму можно рассматривать как стопку из нескольких слоев единичных кубов и что количество таких кубов в каждой стопке равно на площадь основания призмы.

Те же самые общие принципы измерения применяются в Классе 7 Раздел Наполнение и упаковка . Filling and Wrapping расширяет возможности вычисления площади и объема для кругов, многоугольных призм, цилиндров, конусов и сфер. В каждом случае учащиеся распространяют основные идеи, которые очень хорошо применимы к прямоугольным фигурам, на аппроксимацию других, более сложных фигур. Площадь круга аппроксимируется путем покрытия круга квадратами радиуса, как показано здесь.

Площадь и длина окружности соединены рассечением. Окружность внизу разрезана на восемь секторов, а затем эти сектора переставлены так, чтобы получился примерный параллелограмм. По мере того, как мы делим круг на все больше и больше секторов, основание параллелограмма приближается к половине окружности 9.0003 C окружности, а высота параллелограмма приближается к радиусу r окружности. Площадь параллелограмма примерно равна 0,5Cr или 0,5(2π r ) r или π r ² .

А объем цилиндра рассчитывается по принципу «площадь основания умножить на высоту», введенному с прямоугольными призмами. Площадь поверхности и объем цилиндров, конусов и сфер пересмотрены в «Скажи это с помощью символов» для 8 класса.

Для 7 класса, Формы и конструкции рассматривает и расширяет измерение углов. Несколько проблем приводят к фундаментальным результатам о мерах углов в многоугольниках: вывод формулы для внешних и внутренних угловых мер любого многоугольника и развитие отношений между мерами углов, образованных пересекающимися прямыми и параллельными прямыми, пересекаемыми секущими. В совокупности эти расширения понятий и навыков измерения закладывают прочную основу для развития понятий подобия и соответствия в 7 и 8 классах9.0005

Развитие понимания конгруэнтности и подобия

С неформальной точки зрения две геометрические фигуры считаются конгруэнтными, если они имеют одинаковую форму и размер. Две фигуры называются подобными, если они имеют одинаковую форму, но, возможно, разные по размеру. Есть по крайней мере два стандартных способа сделать это неформальное понимание математически точным: один статический, а другой динамический.

Стандартный способ установить конгруэнтность для фигур, подобных двум треугольникам, состоит в том, чтобы сказать, что существует соответствие между вершинами фигур, при котором соответствующие пары сторон и углов равны по размеру. Более динамичный подход к конгруэнтности состоит в том, чтобы сказать, что существует сохраняющее расстояние преобразование (отражение, вращение, перенос или скользящее отражение), которое отображает одну фигуру точно поверх другой.

Статический критерий сходства говорит, что два треугольника подобны, если существует соответствие между вершинами, такое что соответствующие углы равны по мере и отношения длин соответствующих сторон равны. Более динамичный, но математически эквивалентный подход к сходству начинается с концепции преобразований растяжения и коэффициентов масштабирования. Например, расширение с масштабным коэффициентом ³ / ₂ и центральной точкой P сопоставляет каждую точку X с точкой изображения X’, , так что PX’ = ³ / ₂ PX. Тогда две геометрические фигуры подобны с масштабным коэффициентом k , если существует некоторая комбинация преобразований растяжения и жесткого движения, которая отображает одну фигуру точно поверх другой.

Как со статической, так и с динамической точки зрения в конце концов нужно получить ответы на вопрос: «Какая минимальная информация о сторонах и углах двух фигур (особенно треугольников) гарантирует, что они конгруэнтны или подобны?» Для конгруэнтности треугольников есть несколько знакомых критериев: наиболее распространенными являются сторона-угол-сторона, сторона-сторона-сторона и угол-сторона-угол. Для подобия треугольников есть сравнимые результаты. Например, два треугольника подобны, если отношения длин соответствующих сторон одинаковы или отношения двух пар сторон равны и углы между ними равны по размеру. Для подобия есть еще один критерий, подчеркивающий значение измерения углов: два треугольника подобны, если существует соответствие между вершинами, так что соответствующие углы равны по мере. На самом деле этот критерий может быть установлен с конгруэнтностью только двух пар соответствующих углов (поскольку постоянная сумма углов 180 ° в каждом треугольнике заставляет третью пару углов быть конгруэнтной).

Развитие конгруэнтности и сходства в CMP3 делает упор на более динамичный подход посредством преобразований, и начинается с концептуально более богатой концепции сходства. Модуль 7 класса «Растягивание и сжатие » вовлекает учащихся в различные практические действия по расширению, которые растягивают и уменьшают размер простых фигур (и связаны с функциями увеличения и уменьшения копировальных аппаратов). Этот опыт показывает, как изменяется размер, но не форма расширенных фигур, и как размеры углов сохраняются при преобразованиях подобия.

История конгруэнтности и подобия, начатая несколько неформально и визуально в Формы и конструкции и Растяжение и сжатие , завершается в главе 8 класса Бабочки, вертушки и обои , в которой динамика (включая трансформации) и статические подходы объединяются и применяются к множеству стандартных задач.

Развить пропорциональные соединения подобных фигур

В Растяжение и сжатие , учащихся просят сравнить отношения длин сторон в подобных фигурах, чтобы дать визуальную основу для пропорциональных рассуждений. Затем сравнение периметров и площадей подобных фигур вводит принципиально важный вопрос: «Как масштабные коэффициенты расширения связаны с изменениями периметра и площади фигур?» Общий принцип, согласно которому линейные размеры изменяются на коэффициент расширения k , а площади изменяются на k ² , пересматривается и расширяется в последующих задачах измерения. В Заполнение и упаковка В 7 классе учащиеся обнаруживают, что если объемную фигуру увеличить в масштабе k , объем изменится в k ³ коэффициенте.

Расширение знаний о координатных методах и теореме Пифагора

Повсеместное использование компьютерных инструментов для графических задач, таких как архитектурное черчение, роботизированное производство и производство фильмов, сделало координатные методы в геометрии фундаментальными навыками для многих современных рабочих. Эта тенденция отражена в задачах CCSSM по математике для средних классов и в модулях геометрии CMP3, которые соответствуют этим ожиданиям.

Первый блок 6-го класса, Prime Time , просит учеников построить пары факторов, чтобы найти визуальную закономерность в этих числах. Связанное задание в Покрытие и окружение просит учащихся показать шаблоны длины и ширины, которые дают постоянную площадь, но другой периметр, и постоянный периметр, но другую площадь. Эти связи с алгебраическими отношениями переменных снова исследуются в разделе «Переменные и шаблоны» , где основное внимание уделяется выражениям и функциям в разделе «Алгебра и функции». Переменные и закономерности и Подчеркните отрицательное в начале 7 класса расширьте графическое представление на все четыре квадранта.

Учащиеся умеют находить расстояния в координатных сетках, используя неформальные методы из раздела Покрытие и окружение и формальные методы из раздела В поисках Пифагора . Последний модуль развивает теорему Пифагора и стандартную формулу расстояния. Кроме того, в В поисках Пифагора учащиеся разрабатывают уравнение окружности, геометрическую идею, выраженную алгебраически. Координаты и формула расстояния снова сходятся в Бабочки, вертушки и обои , чтобы разработать правила координат для преобразований конгруэнтности и подобия.

Connections

В духе Connected Mathematics эти геометрические идеи и методы применяются и улучшаются при работе над задачами во многих других модулях. Наиболее заметная и мощная связь геометрии и измерений с другими направлениями учебной программы CMP3 — это взаимодействие концепций рационального числа и пропорциональности в разделе «Числа и операции» со сходством. Однако, поскольку подход CMP3 к алгебре делает упор на функциональные отношения между количественными переменными, геометрические методы построения координатных графиков также занимают видное место в каждом модуле алгебры. Эта визуализация взаимосвязей между переменными также занимает центральное место в нашей разработке темы математического моделирования в анализе данных, а модели областей обеспечивают мощную поддержку работы с дробями, десятичными знаками и вероятностью. Наконец, концепции геометрии и измерения в CMP3 предоставляют бесценные визуальные ресурсы для решения проблем и абстрактных рассуждений обо всех аспектах математики.

Точное измерение углов и расстояний до модели

Что отличает цельную конструкцию и дизайн от M.C. Оптическая иллюзия Эшера? Точные измерения.

В SketchUp инструмент «Рулетка», инструмент «Транспортир» и поле «Измерения» позволяют точно моделировать:

• С помощью инструмента «Рулетка» () можно измерить расстояние и установить точные направляющие линии или направляющие точки.

  Примечание: Направляющие линии и направляющие точки — временные пунктирные линии, используемые в качестве направляющих для точного рисования. Они не мешают правильной геометрии.

• Инструмент Транспортир () позволяет измерять углы и устанавливать точную направляющую линию под углом.
• Вы можете включить функцию «Создать направляющую» в инструментах «Рулетка» и «Транспортир», нажав Ctrl в Windows или Command на Mac, чтобы включить или выключить ее.
• Вы можете привязать функциональность инструмента к оси, нажав соответствующую клавишу со стрелкой до или во время работы.
• Поскольку вы используете практически любой инструмент в SketchUp, поле «Измерения» ожидает принятия точного значения.

Помимо этих инструментов, вы также можете сочетать советы из этой статьи с небольшими математическими расчетами, чтобы точно оценить высоту здания.

Содержание

1. Измерение расстояния
2. Измерение угла
3. Редактирование направляющих линий
4. Скрытие и удаление направляющих линий
5. Точная оценка высоты здания
6. Краткий справочник по блоку измерений

Измерение расстояния

Инструмент «Рулетка» может измерять расстояние, создавать направляющие или отображать координаты вдоль оси. Вот где вы найдете рулетку в интерфейсе SketchUp:

• Панель инструментов «Начало работы»
• Строительная панель инструментов
• Панель инструментов «Большой набор инструментов»
• Меню инструментов в строке меню
• Палитра инструментов (macOS)

Совет: При выбранном инструменте «Рулетка» вы можете сразу увидеть длину линии или площадь лица. Наведите курсор рулетки на линию или грань, и вы увидите расстояние или площадь в поле «Измерения».

Чтобы измерить геометрию или установить направляющую линию, выполните следующие действия:

Примечание: Хорошее правило, которое следует запомнить; Вы будете использовать конечные точки для создания Guide Points , вы можете создать Guide Lines , используя средние точки, линии или грани.

1. Выберите инструмент
   Рулетка () или нажмите клавишу T .

   Примечание. По умолчанию инструмент «Рулетка» создает направляющие линии и направляющие точки по мере измерения. Знак плюс появляется рядом с курсором рулетки в режиме создания направляющих (). Если вы хотите просто измерить расстояние между двумя точками, не создавая направляющую, вы можете нажать Ctrl (Microsoft Windows) или Option (macOS). Знак «плюс» рядом с инструментом «Измерить» в этом режиме исчезает. Этот режим будет сохраняться до тех пор, пока вы не переключите инструменты.

2. Щелкните начальную точку вашего измерения. Если вам нужно выбрать конечную или среднюю точку, механизм логического вывода SketchUp поможет вам найти ее. Чтобы создать направляющую линию, щелкните линию, которая должна быть параллельна направляющей линии.
3. Переместите курсор в нужном направлении. Когда вы перемещаете мышь, временная линия измерительной ленты со стрелками на каждом конце растягивается от начальной точки, как показано на рисунке.

   Совет: Вот несколько советов, которые помогут вам перемещать курсор рулетки в трехмерном пространстве:

   • Линия измерительной ленты меняет цвет, чтобы соответствовать цветам оси, когда она параллельна какой-либо оси. На рисунке вы видите измерительную ленту, выровненную по красной оси.
   • Нажмите кнопку направления во время измерения, чтобы заблокировать ось. стрелка вверх блокирует синюю ось, стрелка влево блокирует зеленую ось, а стрелка вправо блокирует красную ось. Рядом с курсором вы увидите уведомление о том, что вывод заблокирован.
   • В поле «Измерения» динамически отображается длина измерительной ленты.
4. Нажмите Esc , если вам нужно начать сначала.
   
5. (необязательно) Чтобы создать направляющую, нажмите Ctrl (Microsoft Windows) или Option (macOS). Рядом с курсором рулетки ().
6. Щелкните в конечной точке вашего измерения. Расстояние от начальной точки отображается в поле Измерения. Если вы нажали Ctrl на предыдущем шаге, направляющая линия появится в виде пунктирной линии, уходящей в бесконечное трехмерное пространство (по крайней мере, в вашей модели). На следующем рисунке направляющие линии отмечают расстояние в 3 фута от внутренних стен. (Информацию о маркировке расстояний в вашей модели см. в разделе Добавление текста к модели.)
7. (необязательно) Чтобы переместить направляющую линию на точное расстояние от начальной точки, введите число и единицу измерения, а затем нажмите . Введите .

Примечание: Если вы измерите расстояние без создания направляющей, а затем введете значение, SketchUp спросит, хотите ли вы изменить размер модели. Подробнее см. в разделе Масштабирование модели или частей модели.

Совет: При измерении от конечной точки и создании направляющей SketchUp создает направляющую точку, как показано на рисунке. Направляющая точка представляет собой конечную пунктирную линию, тогда как направляющая линия бесконечна.

Измерение угла

Измерьте угол, если вы хотите воспроизвести этот угол в другом месте модели или создать план, например, для проекта деревообработки. Чтобы измерить угол или создать наклонные направляющие линии, используйте инструмент «Транспортир».

Инструмент «Транспортир» () находится в нескольких разных частях интерфейса SketchUp:

• Панель инструментов построения
• Панель инструментов «Большой набор инструментов»
• Меню инструментов
• Палитра инструментов (macOS)

В видео показано, как измерять углы и устанавливать направляющие с помощью инструмента Транспортир. Шаги, которые проведут вас через этот процесс, прочитаны в оставшейся части этого раздела.

Чтобы измерить угол и создать наклонную направляющую линию, выполните следующие действия:

1. Выберите инструмент Транспортир (). Курсор изменится на транспортир. Центральная точка зафиксирована на курсоре.
2. Нажмите, чтобы установить вершину угла, который вы хотите измерить. (См. выноску 1 на рисунке.) Если вам нужно зафиксировать ориентацию, нажмите и удерживайте кнопку 9.0093 Shift перед нажатием кнопки.

   Совет: Когда вы нажимаете и удерживаете клавишу Shift, чтобы заблокировать/ограничить плоскость вращения, вы можете нажать Alt (Microsoft Windows> или Command (macOS), чтобы вывести транспортир из предполагаемой плоскости. Угол транспортира изменится. остается угол исходной плоскости, но теперь вы можете перемещать транспортир, чтобы вывести другую геометрию.

3. Щелкните там, где начинается угол, который вы хотите измерить. (См. выноску 2 на рисунке.)

   Совет: Вы можете щелкнуть и перетащить от вершины к первой точке, чтобы определить ось вращения. Это особенно полезно, если вам нужно повернуть вокруг оси, которая не находится на красной, зеленой или синей плоскостях. Нажмите Esc в любой момент, чтобы начать сначала.

4. Переместите курсор, чтобы измерить угол. (См. выноску 3 на рисунке.)

   Совет: Вот несколько советов, которые помогут вам найти правильное измерение угла:

   • При перемещении курсора угол динамически появляется в поле Измерения.
   • Когда курсор находится близко к транспортиру, угол привязывается к делениям транспортира, что указывает на шаг в 15 градусов. Когда ваш курсор находится дальше от центра транспортира, вы можете измерить угол более точными измерениями.
5. Нажмите, чтобы установить наклонную направляющую линию.
6. (Необязательно) Введите значение и нажмите . Введите , чтобы изменить угол направляющей линии (относительно начальной линии). Вы можете ввести десятичное значение, например 9009.3 34.1 или наклон, такой как 1:6 . Изменяйте это значение столько раз, сколько хотите, пока не сделаете другой выбор или не выберете другую команду.

Примечание. SketchUp поддерживает угловую точность до 0,1 градуса.

Редактирование направляющих линий

Чтобы изменить направление направляющей линии или направляющей точки, вы можете переместить или повернуть их. Подробности см. в разделах «Перемещение объектов» и «Отражение и вращение».

Примечание: Размер направляющей линии изменить нельзя, так как длина направляющих линий бесконечна.

Скрытие и стирание направляющих линий

Направляющие линии обычно создаются как временное вспомогательное средство для построения части модели. Сохранение слишком большого количества направляющих линий в модели может снизить точность логического вывода SketchUp и производительность отображения, поэтому вы можете скрыть направляющие линии во время работы или удалить все направляющие линии после завершения создания 3D-модели.

Чтобы скрыть направляющие линии, вы можете использовать любой из следующих методов:

• С помощью инструмента Выбрать (), выберите одну или несколько направляющих, а затем выберите Правка > Скрыть .
• Щелкните выбранную направляющую или направляющие в контексте и выберите Скрыть в появившемся меню, как показано на рисунке.

Чтобы снова сделать скрытые направляющие видимыми, выберите Правка > Показать и выберите параметр в подменю Показать.

При удалении направляющих линий они полностью удаляются и никогда не возвращаются. Вот несколько способов удаления направляющих:

• С помощью инструмента Select (), выберите одну или несколько направляющих, а затем выберите Правка > Удалить .
• Щелкните направляющую в контексте и выберите Стереть в появившемся меню.
• Щелкните направляющую линию инструментом Ластик ().
• Выберите Правка > Удалить направляющие , чтобы стереть все направляющие в текущем контексте.

Точная оценка высоты здания

Если вы не знаете высоту существующего здания, которое пытаетесь смоделировать, вот несколько методов, которые вы можете использовать, чтобы сделать обоснованное предположение:

• Подсчет повторяющихся единиц.
• Сделать снимок с объектом известной высоты
• Используйте тригонометрию.

Когда вы будете готовы выдавить контур здания до нужной высоты, убедитесь, что вы находитесь в представлении ISO, выбрав Camera > Standard Views > Iso . Затем используйте инструмент Push/Pull (), чтобы выдавить ваше здание в 3D и ввести точную высоту вашего здания.

Метод 1: подсчет повторяющихся единиц

Часто здания строятся из кирпича, блоков или других модульных строительных материалов. Измерьте высоту одной единицы, подсчитайте общее количество единиц на фасаде и умножьте, чтобы получить приблизительную общую высоту.

Этот метод также работает для целых уровней здания. Если вы можете измерить один уровень на фасаде вашего здания, вы можете умножить его на общее количество уровней, чтобы получить приблизительное общее измерение.

Способ 2. Сфотографируйте объект с известной высотой

Когда вы фотографируете здание, которое планируете смоделировать, включите в фотографию что-то (или кого-то), чью высоту вы знаете.

Совет: Вот несколько советов по оценке высоты здания с помощью этого метода:

• Счетчик или человек хорошо работают.
• Расположите свое «известное количество» как можно ближе к зданию для точности.
• Делайте снимок как можно дальше, чтобы свести к минимуму вертикальные искажения.

Вы можете использовать программу для редактирования фотографий, чтобы оценить высоту вашего здания на основе объекта (или человека), включенного в фотографию.

Метод 3. Используйте простую тригонометрию

Выполнив несколько простых измерений, можно с некоторой точностью оценить рост. Взгляните на рисунок ниже. Все, что вам нужно знать, это:

1. Ваше расстояние от здания
2. Высота вашего глаза
3. Угол между землей и верхом здания

Используйте эту формулу для расчета высоты здания:

Высота = (tan(угол) x расстояние) + высота глаз

Например, если расстояние до здания 25 метров, угол 37 градусов , а высота глаз 1,75 метра, формула будет выглядеть так:

 Высота = tan(37) x 25м + 1,75м

= 0,75355 х 25 м + 1,75 м

= 20,6 м
 

Примечание: На вашем калькуляторе кнопка загара вычисляет тангенс угла.

Краткий справочник по блоку измерений

В этом разделе вы найдете таблицы со всеми значениями, которые принимает блок измерений, в зависимости от используемого инструмента. Помните, что после использования инструмента вы можете просто ввести значение и нажать Enter . Вам не нужно щелкать в поле «Измерения». Кроме того, пока вы не внесете еще одно изменение в свою модель или не выберете другой инструмент, вы можете продолжать вводить значения, изменяющие ваше действие.

Указание единиц измерения

В следующей таблице показано, как указать единицы измерения. Если вы не укажете единицы, SketchUp использует единицы в вашем шаблоне. Чтобы просмотреть или изменить единицы измерения по умолчанию, выберите Window > Model Info и выберите Units на боковой панели слева.

Блок	Как указать	Пример
Дюймы	номер + “	10”
Ножки	номер +’	10’
Миллиметры	номер + мм	10 мм
Сантиметры	номер + см	10см
Метры	номер + м	10 м

Создание массивов

Массив упорядочивает геометрию по линии (линейный массив ) или вокруг точки (радиальный массив ). Массив создается при копировании геометрии с помощью инструмента «Перемещение» или инструмента «Поворот». В следующей таблице перечислены все модификаторы, которые вы можете использовать при создании массивов.

Тип массива	Как указать	Пример	Расстояние
Внешний	число + х	3x	Равное расстояние оригинала и исходной копии
Внешний	номер + *	3*	Равное расстояние оригинала и исходной копии
Внутренний	номер +/	3/	Равное расстояние между оригиналом и исходной копией

Ввод значений измерений для конкретного инструмента

Сразу после использования инструмента вы можете ввести точные значения, которые отображаются в поле Измерения. Значения, которые вы можете ввести, зависят от инструмента.

Примечание: Точный формат разделителя списка может различаться в зависимости от региональных настроек вашего компьютера.