ГДЗ Геометрия 7 класс Мерзляк, Полонский, Якир
Геометрия 7 класс
Учебник
Мерзляк, Полонский, Якир
Вентана-Граф
Довольно часто происходит ситуация, когда школьники сначала легко осваивают новый предмет, а затем дойдя до определенной точки, как будто упираются в стену непонимания. С большой долей вероятности происходит это потому, что какие-то нюансы во время прохождения начального материала были все же упущены. Ни одна точная наука не терпит халатности, как следствие это может обернуться плохими оценками. Поэтому внимательность — одна из важнейших критериев при учебе. А если все же какая-то тема осталась недопонятой и начинаются трудности при выполнении упражнений, всегда можно использовать решебник к учебнику «Геометрия 7 класс» Мерзляк, Полонский, Якир.
Содержание пособия
Сборник включает в себя двадцать два параграфа и в целом имеет семьсот сорок четыре упражнения. Так же здесь приведены вопросы к параграфам и задания для самопроверки.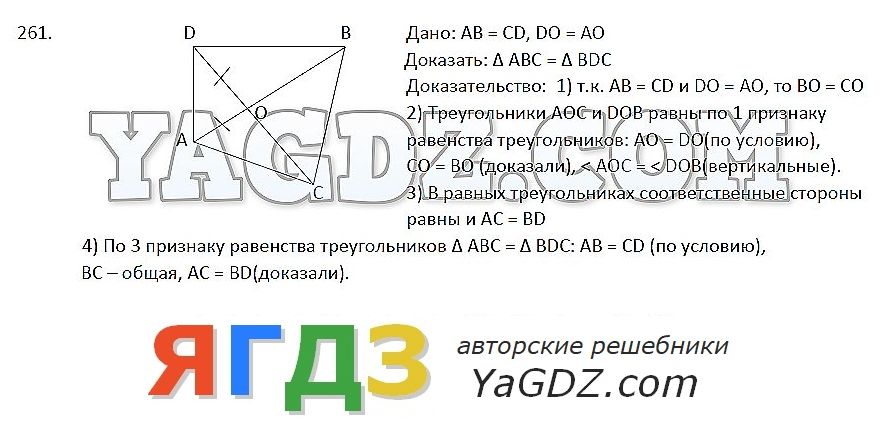
Стоит ли им пользоваться
Данный предмет таит в себе много подводных камней и скрытых водоворотов, что делает его изучение совершенно непредсказуемым. С виду простой он тем не менее вызывает порой много вопросов. Так и же и задачи могут содержать в себе не только прямые действия, но и добавочные, так что они тоже требуют внимательности со стороны учащихся. Поэтому не зря говорят, что данный предмет развивает не только логику, но и интуицию. Чего уж точно не терпит эта наука, так это спешки, на которой и зиждется вся современная школьная программа. Не лишним в такой обстановке будет иметь под рукой решебник к учебнику «Геометрия 7 класс» Мерзляк, где отражены все аспекты и полностью раскрыта тематика предмета.
Геометрия 7 класс Мерзляк А.Г. Полонский В.Б. Якир М.С.
Оглавление
От авторов 3
Что изучает геометрия? 6
Глава 1. Простейшие геометрические фигуры и их свойства
§ 1. Точки и прямые 9
§ 2. Отрезок и его длина 13
§ 3. Луч. Угол. Измерение углов 20
§ 4. Смежные и вертикальные углы 29
§ 5. Перпендикулярные прямые 34
§ 6. Аксиомы 38
Из истории геометрии 40
Задание № 1 «Проверьте себя» в тестовой форме 42
Итоги главы 1 43
Глава 2. Треугольники
§ 7. Равные треугольники. Высота, медиана, биссектриса треугольника 46
§ 8. Первый и второй признаки равенства треугольников 53
§ 9. Равнобедренный треугольник и его свойства 61
§ 10. Признаки равнобедренного треугольника 67
§11. Третий признак равенства треугольников 72
§ 12. Теоремы 75
Задание № 2 «Проверьте себя» в тестовой форме 80
Итоги главы 2 82
Глава 3. Параллельные прямые. Сумма углов треугольника
§ 14.
 Признаки параллельности двух прямых 88
Признаки параллельности двух прямых 88Пятый постулат Евклида 95
§ 15. Свойства параллельных прямых 96
§ 16. Сумма углов треугольника 102
§ 17. Прямоугольный треугольник 111
§ 18. Свойства прямоугольного треугольника 116
Задание № 3 «Проверьте себя» в тестовой форме 120
Итоги главы 3 121
Глава 4. Окружность и круг. Геометрические построения
§ 19. Геометрическое место точек. Окружность и круг 124
§ 20. Некоторые свойства окружности. Касательная к окружности 131
§ 21. Описанная и вписанная окружности треугольника 137
§ 22. Задачи на построение 144
§ 23. Метод геометрических мест точек в задачах на построение 153
Из истории геометрических построений 158
Задание № 4 «Проверьте себя» в тестовой форме 160
Итоги главы 4 161
Дружим с компьютером 164
Проектная работа 170
Упражнения для повторения курса 7 класса 173
Ответы и указания к упражнениям 181
Ответы к заданиям «Проверьте себя» в тестовой форме 186
Алфавитно-предметный указатель 187
Происхождение математических терминов 189
Учителю 191
Учебник предназначен для изучения геометрии в 7 классе общеобразовательных организаций. В нём предусмотрена уровневая дифференциация, позволяющая формировать у школьников познавательный интерес к математике. Учебник входит в систему учебно-методических комплектов «Алгоритм успеха». Содержание учебника соответствует федеральному государственному образовательному стандарту основного общего образования (2010 г.).
В нём предусмотрена уровневая дифференциация, позволяющая формировать у школьников познавательный интерес к математике. Учебник входит в систему учебно-методических комплектов «Алгоритм успеха». Содержание учебника соответствует федеральному государственному образовательному стандарту основного общего образования (2010 г.).
Учебники Геометрия 7 класс А. Г. Мерзляк, В. Б. Полонский, М. С. Якир 2015
На какие блоки разделен учебник по геометрии для 7 класса А.Г. Мерзляк
Учебник по геометрии для 7 класса А.Г. Мерзляк, В.Б. Полонский, М.С. Якир 2015 состоит из нескольких разделов. Каждый раздел поделен на параграфы, а параграфы — поделены на пункты. В каждом пункте есть теоретический материал, которые нужно будет прочесть и запомнить и практические задачи, которые необходимо будет выполнить.
Курсив и шрифты
Курсивом и жирным шрифтом в учебнике выделены правила, термины и определения, которые нужно запомнить.
Как решать задачи
В учебнике после теоретического материала есть примеры выполнения практических заданий по новой теме. Эти примеры можно использовать в качестве образа для решения однотипных заданий.
Эти примеры можно использовать в качестве образа для решения однотипных заданий.
Работаем дома
В каждом пункте есть задания, предназначенные для самостоятельной работы дома, однако нужно учесть, что приступать к работе над этими заданиями следует только после ознакомления с теоретическим материалом.
Специальная рубрика
В учебнике есть необычная рубрика, которая называется «Наблюдайте, рисуйте, конструируйте, фантазируйте». В этой рубрике собраны задачи, для решения которых понадобится здравый смысл, логика и умение мыслить.
Учебник по геометрии для 7 класса, А.Г. Мерзляк — почему это работает
Несмотря на то, что в седьмом классе у учеников уже достаточно серьезные нагрузки и порой разобраться в домашнем задании под силу далеко не всем родителям, проверить уровень подготовки школьника с помощью учебника по геометрии для 7 класса, А.Г. Мерзляк 2015 проще простого. Уникальность издания А.Г. Мерзляк, учебник по геометрии для 7 класса, 2015 заключается в том, что этот учебник не требует дополнительных затрат и при отсутствии печатного экземпляра учебника по геометрии для 7 класса, А. Г. Мерзляк 2015, можно зайти на сайт и открыть онлайн-версию учебника для 7 класса по геометрии, А.Г. Мерзляк 2015.
Г. Мерзляк 2015, можно зайти на сайт и открыть онлайн-версию учебника для 7 класса по геометрии, А.Г. Мерзляк 2015.
Учебник по геометрии — это просто и быстро
Издание А.Г. Мерзляк, учебник по геометрии для 7 класса, 2015 — это уникальная методическая разработка, в которой вы сможете найти доходчивые, понятные объяснения ко всем темам по геометрии за 7 класс. С помощью учебника по геометрии для 7 класса, А.Г. Мерзляк 2015 школьники смогут не только проверить правильность выполнения того или иного упражнения, но и самостоятельно освоят новые темы.
Учебник по геометрии учит школьников думать
Учебник по геометрии для 7 класса, А.Г. Мерзляк 2015 — это книга, которая поможет школьникам сэкономить не только время, но и деньги. Однако, самое главное — учебник по геометрии для 7 класса, А.Г. Мерзляк 2015 учит школьников думать, мыслить логически и не бояться ошибиться. Работая с изданием А.Г. Мерзляк, учебник по геометрии для 7 класса, 2015 дети смогут по-настоящему разобраться в азах геометрии и поймут, что это действительно интересный и увлекательный предмет. Еще одно преимущество учебника для 7 класса по геометрии, А.Г. Мерзляк 2015 заключается в том, что для того, чтобы разобраться в том, как правильно выполнить задание, не нужно покупать дорогостоящие книги. Достаточно внимательно изучить новый материал, изложенный в учебнике для 7 класса по геометрии, А.Г. Мерзляк 2015 и на примере выполнения однотипных заданий, закрепить полученные знания.
Еще одно преимущество учебника для 7 класса по геометрии, А.Г. Мерзляк 2015 заключается в том, что для того, чтобы разобраться в том, как правильно выполнить задание, не нужно покупать дорогостоящие книги. Достаточно внимательно изучить новый материал, изложенный в учебнике для 7 класса по геометрии, А.Г. Мерзляк 2015 и на примере выполнения однотипных заданий, закрепить полученные знания.
(PDF) Семантическое чтение в обучении математике и математике
100
Семантическое чтение в обучении математике и математике
Асланбек Назиев
Рязанский государственный университет, Рязань, Российская Федерация
Улица Свободы, 46, Рязанская область, Рязанская область , Россия, 3
Телефон: +7 491 297-15-15
Реферат
Автор уже публиковал одну статью о семантическом чтении в обучении математике (Назиев,
2014 ).Статья содержала короткие инструкции о том, что такое семантическое чтение, и несколько более или менее простых примеров
применения семантического чтения в школьной алгебре, геометрии, вероятности и исчислении. В
В
этой статье мы дадим более наглядное определение семантического чтения и несколько более сложных
и, мы надеемся, более интересных примеров.
Наша работа связана с результатами в области искусственного интеллекта (Гарридо, 2017). Важным предметом
в искусственном интеллекте является автоматическое (или механическое) доказательство теорем, и, в частности,
доказательство теорем механической геометрии (Chou, 1988).Развитие этой последней области показало
свидетельств того, что для того, чтобы проводить доказательства геометрических теорем механически, мы должны строго следовать
некоторым правилам и аксиомам (Chou, 1988). Это основная цель нашей статьи — показать, насколько важно в математике
, а не только в искусственном интеллекте, строго следовать аксиомам, определениям и теоремам, то есть
, чтобы читать их семантически.
Ключевые слова: обучение математике, семантическое чтение, кванторы, квадратичный трехчлен,
Архимед, Зенон.
1. Семантическое чтение: определение и первые примеры
Чтобы найти правильный подход к определению понятия семантического чтения, нам поможет следующее изречение великого математика
:
Математика — это искусство называть разные вещи с тем же именем ».
(Анри Пуанкаре)
Обратите внимание, что каждый речевой акт соединяет две стороны: отправителя (говорящего, писателя) и получателя
(слушателя, читателя).Отправитель называет разные вещи одним и тем же именем, но это не означает, что
получатель автоматически видит эти разные вещи с одним и тем же именем. Он должен быть готов и способен
на это. Таким образом, для наших целей следует уточнить приведенную выше цитату Х. Пуанкаре:
Математика — это искусство называть разные вещи одним и тем же именем в сочетании с
— искусство видеть разные вещи за одним и тем же именем.
Обратите внимание, что если одно и то же имя называет разные вещи, то каждое сообщение, в контексте
, в которое включено это имя, неизбежно сообщает о разных вещах, то есть несет в себе разные значения
. Таким образом, искусство называть одним и тем же именем разные вещи должно иметь продолжение в искусстве
Таким образом, искусство называть одним и тем же именем разные вещи должно иметь продолжение в искусстве
видеть в одном и том же сообщении разные значения.
Теперь в целом понятно, что нужно называть смысловым чтением.
Семантическое чтение — это искусство обнаружения в читаемом всем разнообразии содержащихся в нем значений
и извлечения из него смысла, наиболее точно соответствующего решаемой задаче
.
ЗАМЕЧАНИЯ.1) Семантическое чтение — это искусство. По этой причине мы не можем обучать семантическому чтению. Вы
можете научить ремеслу, но не искусству. Искусство можно освоить, только изучая образцы,
имитируя и улучшая их. По этой причине как в нашей предыдущей работе, так и в предлагаемой сейчас имеется
Remote Sensing | Бесплатный полнотекстовый | Оценка изображений RGB и мультиспектральных беспилотных летательных аппаратов (БПЛА) для высокопроизводительного фенотипирования и прогнозирования урожайности в селекции ячменя
3.
 1. Определение высоты купола Корреляции HEI CHM и HEI GT по всем датам показаны на рисунке 3. В трех средах HAL, IPK и MER корреляции 0,82, 0,89 и 0,91 были достигнуты, в результате общая корреляция r = 0,87 с использованием квантиля графика 95% CHM. Более того, Рисунок 3 и Рисунок S3 демонстрируют, что максимальная высота была достигнута до MAT. Как известно у ячменя, при созревании колосья начинают наклоняться и, таким образом, их высота уменьшается.Несмотря на в первую очередь сильную корреляцию, БПЛА в целом недооценил HEI GT , как это показано на рисунке S3. Использование квантиля графика 95% CHM показывает наименьшие абсолютные отклонения от HEI GT . Недостатком использования квантиля графика 95% CHM для оценки роста было то, что изолированные и вертикально растущие растения на участках генотипов, где произошло полегание, приводили к завышению общей высоты участка. Это вызвало более низкую корреляцию с данными HEI GT , что можно увидеть на позднем периоде сбора данных в HAL и IPK (Рисунок S3).
1. Определение высоты купола Корреляции HEI CHM и HEI GT по всем датам показаны на рисунке 3. В трех средах HAL, IPK и MER корреляции 0,82, 0,89 и 0,91 были достигнуты, в результате общая корреляция r = 0,87 с использованием квантиля графика 95% CHM. Более того, Рисунок 3 и Рисунок S3 демонстрируют, что максимальная высота была достигнута до MAT. Как известно у ячменя, при созревании колосья начинают наклоняться и, таким образом, их высота уменьшается.Несмотря на в первую очередь сильную корреляцию, БПЛА в целом недооценил HEI GT , как это показано на рисунке S3. Использование квантиля графика 95% CHM показывает наименьшие абсолютные отклонения от HEI GT . Недостатком использования квантиля графика 95% CHM для оценки роста было то, что изолированные и вертикально растущие растения на участках генотипов, где произошло полегание, приводили к завышению общей высоты участка. Это вызвало более низкую корреляцию с данными HEI GT , что можно увидеть на позднем периоде сбора данных в HAL и IPK (Рисунок S3). Это усложняет простое автоматическое обнаружение заселенных участков, и в некоторых случаях может потребоваться ручная проверка путем просмотра изменений информации CHM на всем графике. Кроме того, отдельные моменты времени показали большие различия в коэффициентах корреляции между HEI CHM. и HEI GT в диапазоне от r = 0,09 в HAL на 104 DAS до r = 0,93 в MER на 68 DAS и в HAL на 89 DAS, что показано на рисунке S3.Для прямого статистического сравнения в смысле разведения ( повторяемость и соответствие ассоциаций генотипов) между традиционным и новым методом фенотипирования, была сформирована подмножество набора данных HEI CHM (HEI CHMred ), которое было сокращено до 107 идентичных участков набора данных HEI GT .Повторяемость HEI CHM, HEI CHMred и HEI GT на рисунке S4 продемонстрировала одинаковые тенденции между отдельными временными точками с высокими значениями до R² = 0,98 почти на протяжении всего вегетационного периода.
Это усложняет простое автоматическое обнаружение заселенных участков, и в некоторых случаях может потребоваться ручная проверка путем просмотра изменений информации CHM на всем графике. Кроме того, отдельные моменты времени показали большие различия в коэффициентах корреляции между HEI CHM. и HEI GT в диапазоне от r = 0,09 в HAL на 104 DAS до r = 0,93 в MER на 68 DAS и в HAL на 89 DAS, что показано на рисунке S3.Для прямого статистического сравнения в смысле разведения ( повторяемость и соответствие ассоциаций генотипов) между традиционным и новым методом фенотипирования, была сформирована подмножество набора данных HEI CHM (HEI CHMred ), которое было сокращено до 107 идентичных участков набора данных HEI GT .Повторяемость HEI CHM, HEI CHMred и HEI GT на рисунке S4 продемонстрировала одинаковые тенденции между отдельными временными точками с высокими значениями до R² = 0,98 почти на протяжении всего вегетационного периода. До SHO повторяемость была низкой и начинала увеличиваться с ростом высоты вокруг SHO, чтобы найти максимум и выйти на плато в HEA, пока не началось созревание, и повторяемость снова не уменьшилась. Следует подчеркнуть, что HEI CHM в целом показал лучшую повторяемость, чем HEI GT и HEI CHMred , за исключением поздних стадий развития растений в HAL, где HEI GT показал немного лучшую повторяемость (Рисунок S4).Воспроизводимость HEI CHMred незначительно колебалась и была в той же шкале, что и HEI GT даже в тех точках, где высота купола, измеренная в полевых условиях, была явно недооценена БПЛА (например, HAL на 89, 95 DAS, IPK на 104, 111 DAS, MER на 84, 90 DAS). На рисунке S4 показана повторяемость трех признаков, которые представляют результаты анализа кривой роста, ставшего возможным благодаря фенотипированию БПЛА. Таким образом, необработанные HEI CHM были сглажены (Рисунок S1) для определения фаз гомогенного роста и определения скорости роста в пределах однородного роста.
До SHO повторяемость была низкой и начинала увеличиваться с ростом высоты вокруг SHO, чтобы найти максимум и выйти на плато в HEA, пока не началось созревание, и повторяемость снова не уменьшилась. Следует подчеркнуть, что HEI CHM в целом показал лучшую повторяемость, чем HEI GT и HEI CHMred , за исключением поздних стадий развития растений в HAL, где HEI GT показал немного лучшую повторяемость (Рисунок S4).Воспроизводимость HEI CHMred незначительно колебалась и была в той же шкале, что и HEI GT даже в тех точках, где высота купола, измеренная в полевых условиях, была явно недооценена БПЛА (например, HAL на 89, 95 DAS, IPK на 104, 111 DAS, MER на 84, 90 DAS). На рисунке S4 показана повторяемость трех признаков, которые представляют результаты анализа кривой роста, ставшего возможным благодаря фенотипированию БПЛА. Таким образом, необработанные HEI CHM были сглажены (Рисунок S1) для определения фаз гомогенного роста и определения скорости роста в пределах однородного роста. Увеличение скорости роста (HEI GRi ) произошло между 59–85 DAS в HAL, 34–61 в MER и 62–83 DAS в IPK. Снижение скорости роста (HEI GRd ) было между 85–120 DAS в Галле, 61–103 DAS в MER и 83–111 DAS в IPK.
Увеличение скорости роста (HEI GRi ) произошло между 59–85 DAS в HAL, 34–61 в MER и 62–83 DAS в IPK. Снижение скорости роста (HEI GRd ) было между 85–120 DAS в Галле, 61–103 DAS в MER и 83–111 DAS в IPK.От умеренной до высокой повторяемости этих параметров в диапазоне от R 2 = 0,59 для HEI GRd в IPK до R 2 = 0,98 для HEI GRi в HAL, показывают, что фенотипические вариации могут быть объяснены генотипом и, следовательно, могут использоваться в разведении.Моделирование вузов с течением времени на основе фенотипирования БПЛА показало надежные результаты, поэтому параметры GR были интегрированы в модель оценки урожайности.
Последующий тест Даннета для выявления статистически значимых ассоциаций генотипов для всех признаков ВУЗа выявил большое количество S42IL, которые значительно отличаются от Скарлетт (рисунок S5). Наибольшие значимые различия были обнаружены между SHO и HEA во всех средах, где разница в росте была наибольшей, поскольку не применялся регулятор роста растений и не происходило полегания в течение этого периода. В целом, набор данных HEI CHM достиг наивысшей значимости, и в течение периода измерения постоянно обнаруживалось несколько линий. Для сравнения, сокращенные наборы данных HEI GT и HEI CHMred показали менее значимые результаты, что показывает большое преимущество фенотипирования БПЛА, которое может охватывать больший размер выборки. Кроме того, те же самые линии со значительным HEI могут быть обнаружены для рассчитанных параметров роста и для HEI MAX . Опять же, HEI GRi , который представляет период роста вузов и, следовательно, время между SHO и HEA, показал наивысшее значение.
В целом, набор данных HEI CHM достиг наивысшей значимости, и в течение периода измерения постоянно обнаруживалось несколько линий. Для сравнения, сокращенные наборы данных HEI GT и HEI CHMred показали менее значимые результаты, что показывает большое преимущество фенотипирования БПЛА, которое может охватывать больший размер выборки. Кроме того, те же самые линии со значительным HEI могут быть обнаружены для рассчитанных параметров роста и для HEI MAX . Опять же, HEI GRi , который представляет период роста вузов и, следовательно, время между SHO и HEA, показал наивысшее значение.3.2. Растительный покров
Растительный покров (VCOV) был определен с использованием как RGB, так и мультиспектральных изображений для сравнения двух методов. Для определения генотипов ранней прорастания были использованы отдельные временные точки VCOV для сглаживания (рис. S2) и последующего извлечения параметров роста. Оценка VCOV по изображениям RGB привела к более высокой согласованности между последовательными полетами с более поздним насыщением и меньшим количеством выбросов (рис. S2), что обеспечило более надежный набор данных по сравнению со значениями VCOV, определенными с помощью мультиспектральных изображений.Значения VCOV для набора мультиспектральных данных оказались более низкого качества из-за большего разброса и частоты выбросов. В MER VCOV показал наибольшую вариативность для обоих методов определения, но, тем не менее, по всем наборам данных можно увидеть, что среднее значение S42IL для генеральной совокупности немного выше, чем у Scarlett. Неточности могут быть устранены путем сглаживания кривой роста и при этом учитываются тенденции роста. быть идентифицированным. Для выявления быстрорастущих генотипов данные сглаженного растительного покрова (VCOV , сглаженный ) были использованы для оценки параметров роста VCOV GRi и VCOV 90 .Расчетная повторяемость показывает различия между средами (Рисунок S6). По всем признакам VCOV наивысшая повторяемость R 2 = 0,94 была оценена в HAL в 81 DAS по изображениям RGB.
S2), что обеспечило более надежный набор данных по сравнению со значениями VCOV, определенными с помощью мультиспектральных изображений.Значения VCOV для набора мультиспектральных данных оказались более низкого качества из-за большего разброса и частоты выбросов. В MER VCOV показал наибольшую вариативность для обоих методов определения, но, тем не менее, по всем наборам данных можно увидеть, что среднее значение S42IL для генеральной совокупности немного выше, чем у Scarlett. Неточности могут быть устранены путем сглаживания кривой роста и при этом учитываются тенденции роста. быть идентифицированным. Для выявления быстрорастущих генотипов данные сглаженного растительного покрова (VCOV , сглаженный ) были использованы для оценки параметров роста VCOV GRi и VCOV 90 .Расчетная повторяемость показывает различия между средами (Рисунок S6). По всем признакам VCOV наивысшая повторяемость R 2 = 0,94 была оценена в HAL в 81 DAS по изображениям RGB. Кроме того, в HAL, и особенно в IPK, можно было обнаружить высокую и стабильную повторяемость (R 2 = 0,47–0,94) с течением времени. В некоторых случаях более высокая повторяемость была обнаружена с необработанными данными VCOV, а в некоторых случаях со сглаженными данными VCOV, которые не выявляют последовательной тенденции.Тем не менее, MER показал самую низкую повторяемость (R 2 = 0–0,36). Повторяемость параметров роста VCOV GRi и VCOV 90 была того же порядка величины, что и повторяемость в отдельные дни измерения, так что имело смысл, за исключением MER, провести тест Даннета для выявления значимых ассоциаций генотипов на основе сглаженных данных VCOV . Тест Даннета выявил одну значительную линию в HAL и в IPK на основе мультиспектрального определения VCOV , сглаженного и трех значимых линий на основе определения RGB, для VCOV , сглаженного только в IPK (Рисунок S6).К сожалению, нет перекрытия значимых линий на сайтах или в наборах данных, хотя уменьшение p-значений некоторых линий указывает на те же тенденции.
Кроме того, в HAL, и особенно в IPK, можно было обнаружить высокую и стабильную повторяемость (R 2 = 0,47–0,94) с течением времени. В некоторых случаях более высокая повторяемость была обнаружена с необработанными данными VCOV, а в некоторых случаях со сглаженными данными VCOV, которые не выявляют последовательной тенденции.Тем не менее, MER показал самую низкую повторяемость (R 2 = 0–0,36). Повторяемость параметров роста VCOV GRi и VCOV 90 была того же порядка величины, что и повторяемость в отдельные дни измерения, так что имело смысл, за исключением MER, провести тест Даннета для выявления значимых ассоциаций генотипов на основе сглаженных данных VCOV . Тест Даннета выявил одну значительную линию в HAL и в IPK на основе мультиспектрального определения VCOV , сглаженного и трех значимых линий на основе определения RGB, для VCOV , сглаженного только в IPK (Рисунок S6).К сожалению, нет перекрытия значимых линий на сайтах или в наборах данных, хотя уменьшение p-значений некоторых линий указывает на те же тенденции.
3.3. Прогноз урожайности
Измеренная урожайность участка была целевым значением моделирования урожайности и показана на Рисунке 4. Самые высокие урожаи были обнаружены в IPK, со средней урожайностью 4,43 кг / 7,5 м 2 (59,1 ц / га) , затем идут MER с 4,01 кг / 7,5 м 2 (53,5 ц / га) и HAL с 3,73 кг / 7,5 м 2 (49.7 ц / га). HAL показал самый высокий коэффициент вариации с CV = 0,27, за ним следовали MER с CV = 0,16 и IPK с CV = 0,12. Чтобы максимально точно предсказать урожайность графика, были протестированы три различных подхода. Далее описаны только результаты моделей GLM, а результаты соответствующих RF-моделей, которые, как правило, отражают одни и те же тенденции, включены в рисунок S. 7. В подходе 1 линейная регрессия урожайности участков на основе одного признака и единственная временная точка выявила сильные различия в прогностической эффективности между отдельными чертами и временными точками (рис. 5а).Для рисунка 5a были выбраны два виртуальных прибора с наивысшими значениями r 2 для среды и набора данных изображений, которые были нанесены на график для всех сред, в результате чего были получены четыре и пять виртуальных приборов для наборов данных мультиспектральных изображений и изображений RGB, соответственно. Наивысшие значения r 2 набора данных RGB были обнаружены во всех трех средах незадолго до MAT с r 2 = 0,55, r 2 = 0,37 и r 2 = 0,21 в HAL, MER и IPK, соответственно. (Рисунок 5а, г). В наборе мультиспектральных данных высокие значения r 2 были обнаружены как вокруг HEA, так и незадолго до MAT, которые были того же порядка величины, что и в наборе данных RGB, за исключением высокой предсказательной силы мультиспектральных данных на 47 DAS в MER.HAL обычно имел самые высокие значения r², а IPK — самые низкие. В некоторых случаях r 2 увеличивалось после осадков, особенно в наборе мультиспектральных данных, например, на HAL 61 DAS, IPK 70 DAS и 92 DAS и в MER 84 DAS. В подходе 2 прогнозы урожайности одновременно включали ряд RGB , мультиспектральные и морфологические признаки (HEI и VCOV) в один момент времени. Прогностическая сила увеличилась, но все еще оставалась подверженной значительным колебаниям между временными точками (рис.
Наивысшие значения r 2 набора данных RGB были обнаружены во всех трех средах незадолго до MAT с r 2 = 0,55, r 2 = 0,37 и r 2 = 0,21 в HAL, MER и IPK, соответственно. (Рисунок 5а, г). В наборе мультиспектральных данных высокие значения r 2 были обнаружены как вокруг HEA, так и незадолго до MAT, которые были того же порядка величины, что и в наборе данных RGB, за исключением высокой предсказательной силы мультиспектральных данных на 47 DAS в MER.HAL обычно имел самые высокие значения r², а IPK — самые низкие. В некоторых случаях r 2 увеличивалось после осадков, особенно в наборе мультиспектральных данных, например, на HAL 61 DAS, IPK 70 DAS и 92 DAS и в MER 84 DAS. В подходе 2 прогнозы урожайности одновременно включали ряд RGB , мультиспектральные и морфологические признаки (HEI и VCOV) в один момент времени. Прогностическая сила увеличилась, но все еще оставалась подверженной значительным колебаниям между временными точками (рис. 5b). Кривые точности прогноза между RGB и набором мультиспектральных данных показали аналогичные колебания в диапазоне между r 2 = 0.03 и r 2 = 0,6. Наибольшая точность прогноза была обнаружена на всех 3 участках в последней трети вегетационного периода и достигла значений r 2 = 0,6, r 2 = 0,5 и r 2 = 0,29 на изображениях RGB в HAL, MER. и ИПК соответственно (рис. 5б, г). RMSE противоречит r 2 и колеблется от 0,51 кг / участок в HAL (89 DAS, RGB) до 0,28 в IPK (92 DAS, Multi), что соответствует ошибке 13,7% и 6,3% соответственно. Подход 3 включал все признаки и временные точки одновременно для моделирования урожайности участка.При таком подходе точность прогноза увеличивалась с каждым дополнительным днем измерений и явно превышала точность прогноза в конце вегетационного периода по сравнению со вторым подходом (рис. 6). Точность прогнозов всех моделей оценки урожайности в целом показывала асимптотическую тенденцию.
5b). Кривые точности прогноза между RGB и набором мультиспектральных данных показали аналогичные колебания в диапазоне между r 2 = 0.03 и r 2 = 0,6. Наибольшая точность прогноза была обнаружена на всех 3 участках в последней трети вегетационного периода и достигла значений r 2 = 0,6, r 2 = 0,5 и r 2 = 0,29 на изображениях RGB в HAL, MER. и ИПК соответственно (рис. 5б, г). RMSE противоречит r 2 и колеблется от 0,51 кг / участок в HAL (89 DAS, RGB) до 0,28 в IPK (92 DAS, Multi), что соответствует ошибке 13,7% и 6,3% соответственно. Подход 3 включал все признаки и временные точки одновременно для моделирования урожайности участка.При таком подходе точность прогноза увеличивалась с каждым дополнительным днем измерений и явно превышала точность прогноза в конце вегетационного периода по сравнению со вторым подходом (рис. 6). Точность прогнозов всех моделей оценки урожайности в целом показывала асимптотическую тенденцию. Однако время и уровень точности прогнозов различались между средами и наборами данных изображений. Тенденции в точности прогнозов между средами и наборами данных RGB и мультиспектральных данных были сохранены из подхода 2, но на более высоком уровне.Высокие значения r 2 были также обнаружены незадолго до MAT и достигли самого высокого значения в HAL с r 2 = 0,82, за которым следовали r 2 = 0,65 в MER и r 2 = 0,55 в IPK. Тем не менее, высокие значения r 2 в HAL имели более высокое RMSE, чем MER или IPK. Погрешность регрессионных моделей набора мультиспектральных данных составляла от 0,24 до 0,39 кг / участок (6,4–10,4%) в HAL, от 0,27 до 0,35 кг / участок (6,7–8,7%) в MER и от 0,26 до 0,33. кг / участок (≙5.9–7,5%) в ИПК. RMSE регрессионных моделей на основе RGB варьировалось в HAL от 0,23 до 0,45 кг на участок (6,1–12,1%), в MER от 0,24 до 0,32 кг на участок (6,1–8,0%) и в IPK от 0,23 до 0,33 кг. / участок (≙5,2–7,6%). Абсолютная ошибка оценки была наименьшей в IPK, несмотря на более низкое значение r 2 , потому что CV измеренной урожайности самый низкий (Рисунок 4).
Однако время и уровень точности прогнозов различались между средами и наборами данных изображений. Тенденции в точности прогнозов между средами и наборами данных RGB и мультиспектральных данных были сохранены из подхода 2, но на более высоком уровне.Высокие значения r 2 были также обнаружены незадолго до MAT и достигли самого высокого значения в HAL с r 2 = 0,82, за которым следовали r 2 = 0,65 в MER и r 2 = 0,55 в IPK. Тем не менее, высокие значения r 2 в HAL имели более высокое RMSE, чем MER или IPK. Погрешность регрессионных моделей набора мультиспектральных данных составляла от 0,24 до 0,39 кг / участок (6,4–10,4%) в HAL, от 0,27 до 0,35 кг / участок (6,7–8,7%) в MER и от 0,26 до 0,33. кг / участок (≙5.9–7,5%) в ИПК. RMSE регрессионных моделей на основе RGB варьировалось в HAL от 0,23 до 0,45 кг на участок (6,1–12,1%), в MER от 0,24 до 0,32 кг на участок (6,1–8,0%) и в IPK от 0,23 до 0,33 кг. / участок (≙5,2–7,6%). Абсолютная ошибка оценки была наименьшей в IPK, несмотря на более низкое значение r 2 , потому что CV измеренной урожайности самый низкий (Рисунок 4).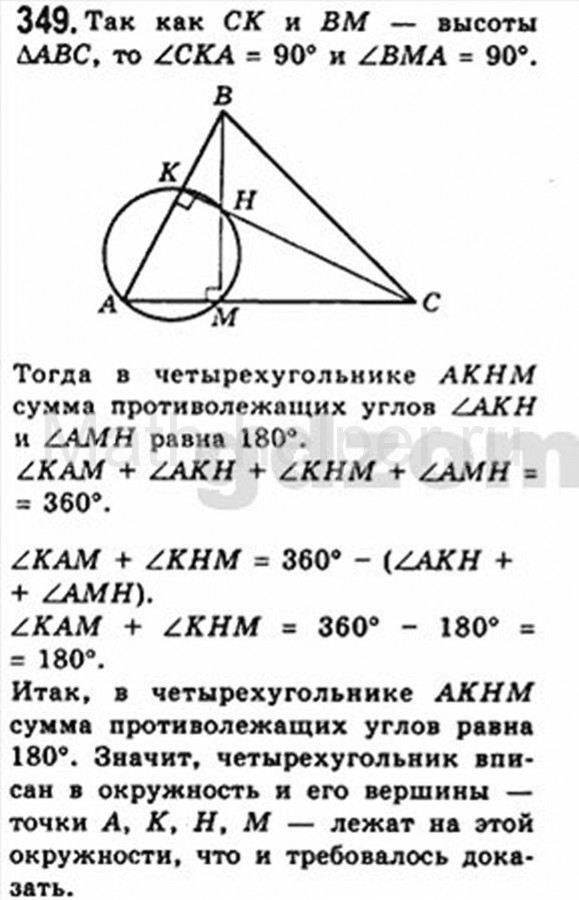 Хотя IPK имеет самое низкое значение r 2 , абсолютная ошибка оценки наименьшая, потому что CV измеренной урожайности наименьшая (рис. 4).Чтобы получить более глубокое понимание того, какие черты были выбраны для прогнозирования урожайности (подход 3), размеры эффекта черт были извлечены и визуализированы на Рисунке 7 и перечислены в Таблице S6. Таким образом, VI были сгруппированы в соответствии с таблицей 2. Это показывает важность групп признаков для оценки урожайности с течением времени и выявления общих тенденций. Например, в наборе данных RGB важность HEI и VCOV сначала увеличивается, а затем уменьшается в течение вегетационного периода. ВП, классифицированные по пигментам, по-видимому, играют большую роль в оценке урожайности в разных средах и наборах данных в начале вегетационного периода, чем в конце.Таблица S6 показывает, что с увеличением размера набора данных в течение вегетационного периода количество признаков, выбранных с помощью прогнозной модели, также увеличивалось, в то время как влияние каждого отдельного оценщика на признак уменьшалось.
Хотя IPK имеет самое низкое значение r 2 , абсолютная ошибка оценки наименьшая, потому что CV измеренной урожайности наименьшая (рис. 4).Чтобы получить более глубокое понимание того, какие черты были выбраны для прогнозирования урожайности (подход 3), размеры эффекта черт были извлечены и визуализированы на Рисунке 7 и перечислены в Таблице S6. Таким образом, VI были сгруппированы в соответствии с таблицей 2. Это показывает важность групп признаков для оценки урожайности с течением времени и выявления общих тенденций. Например, в наборе данных RGB важность HEI и VCOV сначала увеличивается, а затем уменьшается в течение вегетационного периода. ВП, классифицированные по пигментам, по-видимому, играют большую роль в оценке урожайности в разных средах и наборах данных в начале вегетационного периода, чем в конце.Таблица S6 показывает, что с увеличением размера набора данных в течение вегетационного периода количество признаков, выбранных с помощью прогнозной модели, также увеличивалось, в то время как влияние каждого отдельного оценщика на признак уменьшалось. Поскольку производительность прогнозирования во всех средах со временем увеличивалась, очевидно, что диверсификация выбранных характеристик улучшила производительность прогнозирования. Однако эта взаимосвязь кажется ограниченной, поскольку в конце вегетационного периода количество выбранных признаков для модели продолжало увеличиваться, в то время как значения r 2 оставались неизменными.Интересно, что информация о высоте растительного покрова (HEI) важна для прогнозирования урожайности в наборе данных RGB, начиная с самого начала (Рисунок 7), и, более того, для моделирования были выбраны высоты растительного покрова на всех этапах разработки, а не только самая последняя высота растительного покрова, особенно в HAL (Таблица S6). Напротив, в MER и IPK, где высота растительного покрова в конце вегетационного периода демонстрировала минимальные отклонения из-за применения регуляторов роста, ранняя информация о высоте (с большей изменчивостью) была выбрана для прогнозирования урожайности до конца.
Поскольку производительность прогнозирования во всех средах со временем увеличивалась, очевидно, что диверсификация выбранных характеристик улучшила производительность прогнозирования. Однако эта взаимосвязь кажется ограниченной, поскольку в конце вегетационного периода количество выбранных признаков для модели продолжало увеличиваться, в то время как значения r 2 оставались неизменными.Интересно, что информация о высоте растительного покрова (HEI) важна для прогнозирования урожайности в наборе данных RGB, начиная с самого начала (Рисунок 7), и, более того, для моделирования были выбраны высоты растительного покрова на всех этапах разработки, а не только самая последняя высота растительного покрова, особенно в HAL (Таблица S6). Напротив, в MER и IPK, где высота растительного покрова в конце вегетационного периода демонстрировала минимальные отклонения из-за применения регуляторов роста, ранняя информация о высоте (с большей изменчивостью) была выбрана для прогнозирования урожайности до конца. VCOV был вторым морфологическим признаком, извлеченным из изображений БПЛА, и был включен как в наборы данных RGB, так и в мультиспектральные данные, как определено различными методами. Признак был фенотипирован очень рано в вегетационный период и все еще присутствовал почти во всех моделях урожайности в разных средах и наборах данных (рис. 7). В HAL VCOV на 55 DAS часто появлялся в моделях доходности, в MER на 34 и 40 DAS и в IPK на 42 и 49 DAS. Оценки VCOV были особенно высокими в наборе данных RGB, превышая 30% в модели доходности 47 DAS в MER.В наборе данных RGB сумма оценок VCOV достигла максимума в ранних моделях урожайности вокруг SHO. Однако следует учитывать, что на данный момент точность прогноза еще не достигла максимума. В наборе мультиспектральных данных VCOV играла меньшую роль, но, тем не менее, была обнаружена в моделях урожайности на протяжении всего вегетационного периода с постоянными оценками VCOV от 2% до 14% без заметного максимума за вегетационный период. Тем не менее, спектральная информация представляет собой самую большую процент оценок.
VCOV был вторым морфологическим признаком, извлеченным из изображений БПЛА, и был включен как в наборы данных RGB, так и в мультиспектральные данные, как определено различными методами. Признак был фенотипирован очень рано в вегетационный период и все еще присутствовал почти во всех моделях урожайности в разных средах и наборах данных (рис. 7). В HAL VCOV на 55 DAS часто появлялся в моделях доходности, в MER на 34 и 40 DAS и в IPK на 42 и 49 DAS. Оценки VCOV были особенно высокими в наборе данных RGB, превышая 30% в модели доходности 47 DAS в MER.В наборе данных RGB сумма оценок VCOV достигла максимума в ранних моделях урожайности вокруг SHO. Однако следует учитывать, что на данный момент точность прогноза еще не достигла максимума. В наборе мультиспектральных данных VCOV играла меньшую роль, но, тем не менее, была обнаружена в моделях урожайности на протяжении всего вегетационного периода с постоянными оценками VCOV от 2% до 14% без заметного максимума за вегетационный период. Тем не менее, спектральная информация представляет собой самую большую процент оценок. При моделировании урожайности на основе набора мультиспектральных данных эта доля составляет в среднем 91,2% по средам и временным точкам. С одной стороны, отдельные полосы и VI (простые отношения и нормализованные VI) показали высокие эффекты, зависящие от среды. В MER, например, NDWI (содержание воды VI) продемонстрировал большое влияние в диапазоне 7,4-20,2% за весь вегетационный период и, таким образом, имел решающее значение для прогноза урожайности (Таблица S6). Однако в других средах этот VI вряд ли играл роль.
При моделировании урожайности на основе набора мультиспектральных данных эта доля составляет в среднем 91,2% по средам и временным точкам. С одной стороны, отдельные полосы и VI (простые отношения и нормализованные VI) показали высокие эффекты, зависящие от среды. В MER, например, NDWI (содержание воды VI) продемонстрировал большое влияние в диапазоне 7,4-20,2% за весь вегетационный период и, таким образом, имел решающее значение для прогноза урожайности (Таблица S6). Однако в других средах этот VI вряд ли играл роль. VOG (пигмент VI) показал более сильные эффекты в HAL и IPK до последних моделей урожайности и, казалось, был менее взвешенным в MER и не проявлялся в последних трех моделях урожайности. С другой стороны, PSSRa (пигмент VI) и индекс REP (Physiology VI) казались менее зависящими от среды, так как производительность была одинаковой на разных сайтах, причем PSSRa показывал более высокие оценки, чем REP. В моделях урожайности, основанных на наборе данных RGB, оценки спектральной информации имели более низкую релевантность — в среднем 75,5% по средам и временным точкам по сравнению с набором мультиспектральных данных. Три отдельные полосы, а также шесть рассчитанных значений ВИ были одинаково важны для моделей урожайности.
Три отдельные полосы, а также шесть рассчитанных значений ВИ были одинаково важны для моделей урожайности.
 Эффективность прогнозирования модели GLM увеличилась до r 2 = 0,73, приближаясь к модели RF (r 2 = 0.75), но опять же не было очевидного сильного повышения прогнозирующей способности из слияния данных (рисунок S7d). Другим критерием точности прогнозирования был расчет повторяемости, который проводился с прогнозируемыми значениями и истинным урожаем (YLD GT). , измерено в полевых условиях). Рисунок S8 показывает, что наивысшая повторяемость на сегодняшний день может быть рассчитана на стабильно высоком уровне в IPK. Повторяемость прогнозируемой урожайности показала небольшое изменение в течение вегетационного периода от R 2 = 0.81 (42 DAS) до R 2 = 0,91 (70 DAS) мультиспектрального и R 2 = 0,85 (49 DAS) до R 2 = 0,95 (62 DAS) набора данных RGB, но не достигли высокая повторяемость R 2 = 0,96 данных YLD GT . Для HAL и MER были рассчитаны значительно более низкие значения повторяемости: от 2 = 0,07 до 2 = 0,56 с тенденцией к увеличению в течение вегетационного периода.
Эффективность прогнозирования модели GLM увеличилась до r 2 = 0,73, приближаясь к модели RF (r 2 = 0.75), но опять же не было очевидного сильного повышения прогнозирующей способности из слияния данных (рисунок S7d). Другим критерием точности прогнозирования был расчет повторяемости, который проводился с прогнозируемыми значениями и истинным урожаем (YLD GT). , измерено в полевых условиях). Рисунок S8 показывает, что наивысшая повторяемость на сегодняшний день может быть рассчитана на стабильно высоком уровне в IPK. Повторяемость прогнозируемой урожайности показала небольшое изменение в течение вегетационного периода от R 2 = 0.81 (42 DAS) до R 2 = 0,91 (70 DAS) мультиспектрального и R 2 = 0,85 (49 DAS) до R 2 = 0,95 (62 DAS) набора данных RGB, но не достигли высокая повторяемость R 2 = 0,96 данных YLD GT . Для HAL и MER были рассчитаны значительно более низкие значения повторяемости: от 2 = 0,07 до 2 = 0,56 с тенденцией к увеличению в течение вегетационного периода. Воспроизводимость данных YLD GT также была на низком уровне: R 2 = 0.66 в HAL и R 2 = 0,57 в MER. Последующее исследование ассоциации генотипов, проведенное с прогнозируемой урожайностью на основе подхода 3 с накоплением данных, подтвердило результаты анализа повторяемости. В HAL и MER, основанный на данных YLD GT , тест Даннета выявил только линию S42IL-143 со значительным отличием урожайности от Scarlett, в то время как с смоделированными данными урожайности не было обнаружено никаких значимых линий (Таблица S7). Таким образом, на Рисунке S9 показаны только результаты полевых испытаний Даннетта в IPK.Всего в IPK в данных YLD GT было обнаружено девять значимых линий. В наборе мультиспектральных данных было обнаружено 9 значимых линий в 11 моделях, созданных за вегетационный период, но только 6 линий совпали с найденными в наборе данных YLD GT . Это означает, что три оставшиеся строки S42 были ложноположительными.
Воспроизводимость данных YLD GT также была на низком уровне: R 2 = 0.66 в HAL и R 2 = 0,57 в MER. Последующее исследование ассоциации генотипов, проведенное с прогнозируемой урожайностью на основе подхода 3 с накоплением данных, подтвердило результаты анализа повторяемости. В HAL и MER, основанный на данных YLD GT , тест Даннета выявил только линию S42IL-143 со значительным отличием урожайности от Scarlett, в то время как с смоделированными данными урожайности не было обнаружено никаких значимых линий (Таблица S7). Таким образом, на Рисунке S9 показаны только результаты полевых испытаний Даннетта в IPK.Всего в IPK в данных YLD GT было обнаружено девять значимых линий. В наборе мультиспектральных данных было обнаружено 9 значимых линий в 11 моделях, созданных за вегетационный период, но только 6 линий совпали с найденными в наборе данных YLD GT . Это означает, что три оставшиеся строки S42 были ложноположительными. Ложные срабатывания S24IL_105, S24IL_121 и S24IL_138 были обнаружены только между началом и средней фазой вегетационного периода (49-83 DAS).Кроме того, важные линии S42IL-111, S42IL-126 и S42IL-176 из набора данных YLD GT были ложноотрицательными, которые не могли быть подтверждены смоделированными данными урожайности в любой момент времени. Результаты теста Даннета, основанного на прогнозе урожайности набора данных RGB, выявили 12 значимых линий по 12 моделям, с четырьмя ложноположительными линиями (S24IL_103, S24IL_105, S24IL_121, S24IL_138) и 1 ложноотрицательной линией (S42IL_111), в результате чего получилось 7 перекрывающиеся линии с YLD GT .Сравнение прогнозируемой урожайности с YLD GT показало, что отсутствие разницы в расчетной урожайности между ложноотрицательными результатами и сортом Скарлетт было связано с переоценкой прогнозируемой урожайности ложноотрицательных результатов (Таблица S8). Например, доходность линии S24IL_111 была переоценена даже для двух наборов данных, хотя линия показала очень сильный отрицательный эффект в наборе данных YLD GT .
Ложные срабатывания S24IL_105, S24IL_121 и S24IL_138 были обнаружены только между началом и средней фазой вегетационного периода (49-83 DAS).Кроме того, важные линии S42IL-111, S42IL-126 и S42IL-176 из набора данных YLD GT были ложноотрицательными, которые не могли быть подтверждены смоделированными данными урожайности в любой момент времени. Результаты теста Даннета, основанного на прогнозе урожайности набора данных RGB, выявили 12 значимых линий по 12 моделям, с четырьмя ложноположительными линиями (S24IL_103, S24IL_105, S24IL_121, S24IL_138) и 1 ложноотрицательной линией (S42IL_111), в результате чего получилось 7 перекрывающиеся линии с YLD GT .Сравнение прогнозируемой урожайности с YLD GT показало, что отсутствие разницы в расчетной урожайности между ложноотрицательными результатами и сортом Скарлетт было связано с переоценкой прогнозируемой урожайности ложноотрицательных результатов (Таблица S8). Например, доходность линии S24IL_111 была переоценена даже для двух наборов данных, хотя линия показала очень сильный отрицательный эффект в наборе данных YLD GT .
Сборник приложений БПЛА для точного земледелия
Панайотис Радоглу-Грамматикис получил диплом (5 лет) кафедры.инженера по информатике и телекоммуникациям, инженерный факультет Университета Западной Македонии, Греция, в 2016 году. В настоящее время он является доктором философии. студент того же факультета. Его основные исследовательские интересы лежат в области информационной безопасности и в основном сосредоточены на обнаружении вторжений, исследовании уязвимостей и прикладной криптографии. В настоящее время он работает научным сотрудником в Университете Западной Македонии в национальных и европейских исследовательских проектах.
Панайотис Саригианнидис — доцент кафедры информатики и телекоммуникаций Университета Западной Македонии, Козани, Греция, с 2016 года.Он получил степень бакалавра наук. и к.т.н. степени в области компьютерных наук Университета Аристотеля в Салониках, Салоники, Греция, в 2001 и 2007 годах, соответственно. Он опубликовал более 130 статей в международных журналах, на конференциях и в разделах книг. Он принимал участие в нескольких национальных, европейских и международных проектах. В настоящее время он является координатором проекта h3020 SPEAR: Secure and PrivatE smArt gRid (h3020-DS-SC7-2017) и операционной программы MARS: sMart fArming with dRoneS (конкурентоспособность, предпринимательство и инновации). главный исследователь проекта h3020 SDN-microSENSE: SDN-microgrid reSilient Electrical eNergy SystEm (h3020-SU-DS-2018) и Erasmus + KA2 ARRANGE-ICT: партнерство для решения мегатенденций в сфере ИКТ (сотрудничество для инноваций и обмена благами). Практики).Его исследовательские интересы включают телекоммуникационные сети, Интернет вещей и безопасность сетей. Он является членом IEEE и участвует в редакционных советах различных журналов.
Он опубликовал более 130 статей в международных журналах, на конференциях и в разделах книг. Он принимал участие в нескольких национальных, европейских и международных проектах. В настоящее время он является координатором проекта h3020 SPEAR: Secure and PrivatE smArt gRid (h3020-DS-SC7-2017) и операционной программы MARS: sMart fArming with dRoneS (конкурентоспособность, предпринимательство и инновации). главный исследователь проекта h3020 SDN-microSENSE: SDN-microgrid reSilient Electrical eNergy SystEm (h3020-SU-DS-2018) и Erasmus + KA2 ARRANGE-ICT: партнерство для решения мегатенденций в сфере ИКТ (сотрудничество для инноваций и обмена благами). Практики).Его исследовательские интересы включают телекоммуникационные сети, Интернет вещей и безопасность сетей. Он является членом IEEE и участвует в редакционных советах различных журналов.
Томас Лагкас получил докторскую степень в области компьютерных наук в Университете Аристотеля в Салониках, Греция, в 2006 году. Он является старшим преподавателем (доцент) Международного факультета Университета Шеффилда — Колледжа CITY, в котором он работает с 2012 года. Он является директором по исследованиям Департамента компьютерных наук и руководителем направления исследований в области ИКТ в Исследовательском центре Юго-Восточной Европы с 2017 года.Его исследовательские интересы лежат в области IoT-коммуникаций и распределенных архитектур, сетей беспроводной связи, QoS в управлении доступом к среде передачи, мобильной мультимедийной связи, энергосбережения / обеспечения справедливости для распределения ресурсов в беспроводных широкополосных сетях с кооперативными датчиками, а также в гибридных оптоволоконных сетях. -Беспроводные сети, мониторинг данных электронного здравоохранения, системы 5G, летающие специальные сети, безопасность связи и компьютерные образовательные технологии с более чем 60 публикациями в ряде широко известных международных научных журналов и конференций.Он является членом IEEE и ACM, а также членом Академии высшего образования Великобритании.
Он является старшим преподавателем (доцент) Международного факультета Университета Шеффилда — Колледжа CITY, в котором он работает с 2012 года. Он является директором по исследованиям Департамента компьютерных наук и руководителем направления исследований в области ИКТ в Исследовательском центре Юго-Восточной Европы с 2017 года.Его исследовательские интересы лежат в области IoT-коммуникаций и распределенных архитектур, сетей беспроводной связи, QoS в управлении доступом к среде передачи, мобильной мультимедийной связи, энергосбережения / обеспечения справедливости для распределения ресурсов в беспроводных широкополосных сетях с кооперативными датчиками, а также в гибридных оптоволоконных сетях. -Беспроводные сети, мониторинг данных электронного здравоохранения, системы 5G, летающие специальные сети, безопасность связи и компьютерные образовательные технологии с более чем 60 публикациями в ряде широко известных международных научных журналов и конференций.Он является членом IEEE и ACM, а также членом Академии высшего образования Великобритании.
Иоаннис Д. Москолиос родился в Афинах, Греция, в 1976 году. Он получил степень Dipl.-Eng. степень в области электротехники и вычислительной техники Университета Патры, Патры, Греция, в 1999 г., степень магистра наук. степень в области космических технологий и спутниковой связи Лондонского университетского колледжа, Великобритания, в 2000 году и докторская степень.Степень доктора наук в области электротехники и вычислительной техники Университета Патры в 2005 году. С 2005 по 2009 год он был научным сотрудником лаборатории проводной связи, кафедра электротехники и вычислительной техники Университета Патры. С 2009 по 2013 год он был преподавателем кафедры телекоммуникационных наук и технологий Университета Пелопоннеса, Триполис, Греция. С 2013 по 2018 год он был доцентом кафедры информатики и телекоммуникаций Университета Пелопоннеса, Триполис, Греция.
Текущий URL, files / file / agroforestry% 20book.pdf , не соответствует ни одному из них.
Вы видите эту ошибку, потому что у вас DEBUG = True в
ваш файл настроек Django. Измените это на False и Django
отобразит стандартную страницу 404.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.

- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в cookie-файлах может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Как перевести к общему знаменателю. Приведение дроби к наименьшему общему знаменателю: правило, примеры решений
Схема приведения к общему знаменателю
- Необходимо определить, каким будет наименьшее общее кратное для знаменателей дробей.Если вы имеете дело со смешанным или целым числом, то вы должны сначала превратить его в дробь, а только потом определить наименьшее общее кратное. Чтобы преобразовать целое число в дробь, нужно записать само число в числитель, а единицу — в знаменатель. Например, цифра 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратилось в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых чисел и 3/5 в виде дроби = 8×5 + 3/5 = 43/5.

- После этого необходимо найти дополнительный коэффициент, который определяется делением NOZ на знаменатель каждой дроби.
- Последний шаг — умножить дробь на дополнительный коэффициент.
Важно помнить, что приведение к общему знаменателю нужно не только для сложения или вычитания. Чтобы сравнить несколько дробей с разными знаменателями, также нужно сначала привести каждую из них к общему знаменателю.
Общий знаменатель дробей
Чтобы понять, как привести дробь к общему знаменателю, необходимо разобраться в некоторых свойствах дробей.Итак, важным свойством приведения к НОЗ является равенство дробей. Другими словами, если числитель и знаменатель дроби умножить на число, то получится дробь, равная предыдущей. В качестве примера возьмем следующий пример. Чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, вам нужно сделать следующее:
- Сначала найдите наименьшее общее кратное знаменателей. В этом случае для чисел 9 и 6 НОК равно 18.

- Определите дополнительные коэффициенты для каждой фракции. Это делается следующим образом. Делим НОК на знаменатель каждой дроби, в результате получаем 18: 9 = 2 и 18: 6 = 3. Эти числа будут дополнительными множителями.
- Вносим в НОЗ две фракции. Когда вы умножаете дробь на число, вам нужно умножить и числитель, и знаменатель. Дробь 5/9 может быть умножена на дополнительный коэффициент 2, в результате чего получится дробь, равная этой — 10/18.То же самое проделываем со второй дробью: умножаем 5/6 на 3, получаем 15/18.
Как видно из приведенного выше примера, обе дроби были приведены к наименьшему общему знаменателю. Чтобы окончательно разобраться, как найти общий знаменатель, нужно освоить еще одно свойство дробей. Он заключается в том, что числитель и знаменатель дроби можно сократить одним и тем же числом, которое называется общим делителем. Например, 12/30 можно уменьшить до 2/5, разделив его на общий делитель — число 6.
Как перевести дроби к общему знаменателю
Если у общих дробей одинаковые знаменатели, то говорят, что эти дроби сводятся к общему знаменателю .
Пример 1
Например, дроби $ \ frac (3) (18) $ и $ \ frac (20) (18) $ имеют одинаковый знаменатель. Говорят, что у них общий знаменатель $ 18. Дроби $ \ frac (1) (29) $, $ \ frac (7) (29) $ и $ \ frac (100) (29) $ также имеют тот же знаменатель.Говорят, что у них общий знаменатель 29 долларов.
Если дроби имеют разные знаменатели, то их можно привести к общему знаменателю. Для этого нужно умножить их числители и знаменатели на определенные дополнительные множители.
Пример 2
Как привести две дроби $ \ frac (6) (11) $ и $ \ frac (2) (7) $ к общему знаменателю.
Решение.
Умножим дроби $ \ frac (6) (11) $ и $ \ frac (2) (7) $ на дополнительные множители $ 7 $ и $ 11 $, соответственно, и приведем их к общему знаменателю $ 77 $:
$ \ frac (6 \ cdot 7) (11 \ cdot 7) = \ frac (42) (77)
долл. США$ \ frac (2 \ cdot 11) (7 \ cdot 11) = \ frac (22) (77) $
Таким образом, приведение дробей к общему знаменателю называется умножением числителя и знаменателя этих дробей. дополнительными множителями, которые в результате позволяют получить дроби с одинаковыми знаменателями.
дополнительными множителями, которые в результате позволяют получить дроби с одинаковыми знаменателями.
Общий знаменатель
Определение 1
Любое положительное общее кратное всех знаменателей некоторого набора дробей называется общим знаменателем .
Другими словами, общим знаменателем данных дробей является любое натуральное число, которое можно разделить на все знаменатели данных дробей.
Определение подразумевает бесконечный набор общих знаменателей данного набора дробей.
Пример 3
Найдите общие знаменатели дробей $ \ frac (3) (7) $ и $ \ frac (2) (13) $.
Решение .
Эти дроби имеют знаменатели 7 и 13 долларов соответственно. Положительные общие мультипликаторы 2 и 5 долларов равны 91, 182, 273, 364 доллара и т. Д.
Любое из этих чисел может быть общим знаменателем дробей $ \ frac (3) (7) $ и $ \ frac (2) (13) $.
Пример 4
Определите, можно ли привести дроби $ \ frac (1) (2) $, $ \ frac (16) (7) $ и $ \ frac (11) (9) $ к общему знаменателю $ 252 $.
Решение.
Чтобы определить, как привести дробь к общему знаменателю 252 доллара, необходимо проверить, является ли число 252 доллара общим кратным знаменателям 2, 7 и 9 долларов. Для этого делим число 252 $ на каждый знаменатель:
$ \ frac (252) (2) = 126, $ $ \ frac (252) (7) = 36 $, $ \ frac (252) (9) = 28 $.
Число 252 доллара делится на все знаменатели, т.е. является общим кратным 2, 7 и 9 долларов.Следовательно, данные дроби $ \ frac (1) (2) $, $ \ frac (16) (7) $ и $ \ frac (11) (9) $ могут быть сведены к общему знаменателю $ 252 $.
Ответ: можно.
Наименьший общий знаменатель
Определение 2
Среди всех общих знаменателей данных дробей можно выделить наименьшее натуральное число, которое называется наименьший общий знаменатель .
Поскольку НОК является наименьшим положительным общим знаменателем данного набора чисел, то НОК знаменателей данных дробей является наименьшим общим знаменателем этих дробей.
Следовательно, чтобы найти наименьший общий знаменатель дробей, необходимо найти НОК знаменателей этих дробей.
Пример 5
Даны дроби $ \ frac (4) (15) $ и $ \ frac (37) (18) $. Найдите их наименьший общий знаменатель.
Решение .
Знаменатели этих дробей — 15 и 18 долларов. Найдите наименьший общий знаменатель как НОК чисел 15 и 18 долларов. Для этого используем разложение чисел на простые множители:
$ 15 = 3 \ cdot 5 $, 18 $ = 2 \ cdot 3 \ cdot 3 $
$ LCM (15, 18) = 2 \ cdot 3 \ cdot 3 \ cdot 5 = 90 $.
Ответ: 90 $.
Правило приведения дробей к наименьшему общему знаменателю
Чаще всего при решении задач по алгебре, геометрии, физике и т.д. принято приводить обыкновенные дроби к наименьшему общему знаменателю, а не к какому-либо общему знаменателю.
Алгоритм :
- Используя НОК знаменателей данных дробей, найдите наименьший общий знаменатель.
- 2. Вычислить дополнительный коэффициент для заданных фракций.
 Для этого найденный наименьший общий знаменатель необходимо разделить на знаменатель каждой дроби. Полученное число будет дополнительным множителем этой дроби.
Для этого найденный наименьший общий знаменатель необходимо разделить на знаменатель каждой дроби. Полученное число будет дополнительным множителем этой дроби. - Умножьте числитель и знаменатель каждой дроби на найденный дополнительный множитель.
Пример 6
Найдите наименьший общий знаменатель дробей $ \ frac (4) (16) $ и $ \ frac (3) (22) $ и сведите к нему обе дроби.
Решение.
Воспользуемся алгоритмом приведения дробей к наименьшему общему знаменателю.
Вычислите наименьшее общее кратное 16 и 22 долларов:
Разобьем знаменатели на простые множители: $ 16 = 2 \ cdot 2 \ cdot 2 \ cdot 2 $, $ 22 = 2 \ cdot 11 $.
$ LCM (16, 22) = 2 \ cdot 2 \ cdot 2 \ cdot 2 \ cdot 11 = 176 $.
Рассчитаем дополнительные множители для каждой дроби:
$ 176 \ div 16 = 11 $ — для дроби $ \ frac (4) (16) $;
$ 176 \ div 22 = 8 $ — для дроби $ \ frac (3) (22) $.
Умножьте числители и знаменатели дробей $ \ frac (4) (16) $ и $ \ frac (3) (22) $ на дополнительные множители $ 11 $ и $ 8 $ соответственно. Получаем:
$ \ frac (4) (16) = \ frac (4 \ cdot 11) (16 \ cdot 11) = \ frac (44) (176)
долл. США$ \ frac (3) (22) = \ frac (3 \ cdot 8) (22 \ cdot 8) = \ frac (24) (176) $
Обе дроби сводятся к наименьшему общему знаменателю 176 $.
Ответ: $ \ frac (4) (16) = \ frac (44) (176) $, $ \ frac (3) (22) = \ frac (24) (176) $.
Иногда, чтобы найти наименьший общий знаменатель, необходимо провести серию трудоемких вычислений, которые могут не оправдать цель решения проблемы. В этом случае вы можете использовать самый простой способ — привести дроби к общему знаменателю, который является произведением знаменателей этих дробей.
Общий знаменатель дробей
Дроби И имеют одинаковые знаменатели. Говорят, у них общий знаменатель и 25. Дроби и имеют разные знаменатели, но их можно привести к общему знаменателю, используя основное свойство дробей.Для этого находим число, которое делится на 8 и 3, например 24. Сокращаем дроби до знаменателя 24, для этого умножаем числитель и знаменатель дроби на , дополнительный множитель 3. Дополнительный множитель обычно записывается слева над числителем:
Умножьте числитель и знаменатель дроби на дополнительный коэффициент 8:
Приведем дроби к общему знаменателю. Чаще всего в результате дроби получается наименьший общий знаменатель, который является наименьшим общим кратным знаменателя дроби.Поскольку НОК (8, 12) = 24, то дроби можно свести к знаменателю 24. Найдите дополнительные множители дробей: 24: 8 = 3, 24:12 = 2. Тогда
К общему знаменателю можно привести несколько дробей.
Пример. Приведем дроби к общему знаменателю. Поскольку 25 = 5 2, 10 = 2 5, 6 = 2 3, то НОК (25, 10, 6) = 2 3 5 2 = 150.
Найдем дополнительные множители дробей и приведем их к знаменателю 150:
Сравнение дробей
На рис.4.7 показан отрезок AB длиной 1. Он разделен на 7 равных частей … Отрезок AC имеет длину, а отрезок AD — длину.
Длина сегмента AD больше, чем длина сегмента AC, т.е. дробь больше дроби
Из двух дробей с общим знаменателем дробь с большим числителем больше, т. Е.
Например, или
Для сравнения любых двух дробей их приводят к общему знаменателю, а затем применяется правило сравнения дробей с общим знаменателем.
Пример. Сравнить дроби
Решение. НОК (8, 14) = 56. Тогда Поскольку 21> 20, то
Если первая дробь меньше второй, а вторая меньше третьей, то первая меньше третьей.
Доказательство. Пусть даны три дроби. Приведем их к общему знаменателю. Пусть после этого они имеют вид Поскольку первая дробь меньше
второй, то r
Дробь называется правильной , если ее числитель меньше знаменателя.
Дробь называется неправильной , если ее числитель больше или равен знаменателю.
Например, дроби правильные, а дроби неправильные.
Правильная дробь меньше 1, а неправильная дробь больше или равна 1.
В этом уроке мы рассмотрим приведение дробей к общему знаменателю и решим задачи по этой теме. Дадим определение понятию общего знаменателя и дополнительного множителя, напомним взаимно простые числа… Определим понятие наименьшего общего знаменателя (LCN) и решим ряд задач, чтобы найти его.
Тема: Сложение и вычитание дробей с разными знаменателями
Урок: Преобразование дробей к общему знаменателю
Повторение. Главное свойство фракции.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, получится равная дробь.
Например, числитель и знаменатель дроби можно разделить на 2. Получаем дробь. Эта операция называется дробным сокращением. Вы можете выполнить и обратное преобразование, умножив числитель и знаменатель дроби на 2. В этом случае они говорят, что мы уменьшили дробь до нового знаменателя. Число 2 называется дополнительным фактором.
Выход. Дробь может быть уменьшена до любого знаменателя, кратного знаменателю данной дроби.Чтобы привести дробь к новому знаменателю, ее числитель и знаменатель умножаются на дополнительный множитель.
1. Довести дробь до знаменателя 35.
35 делится на 7, то есть 35 делится на 7 без остатка. Это означает, что это преобразование возможно. Найдем дополнительный фактор. Для этого делим 35 на 7. Получаем 5. Умножаем числитель и знаменатель исходной дроби на 5.
2.Приведем дробь к знаменателю 18.
Найдем дополнительный коэффициент. Для этого делим новый знаменатель на исходный. Получаем 3. Умножаем числитель и знаменатель этой дроби на 3.
3. Довести дробь до знаменателя 60.
Разделив 60 на 15, мы получим дополнительный множитель. Это 4. Умножьте числитель и знаменатель на 4.
4. Довести дробь до знаменателя 24
В простых случаях приведение к новому знаменателю выполняется в уме.Допускается указывать только дополнительный множитель вне скобок справа и над исходной дробью.
Дробь может быть уменьшена до знаменателя 15, а дробь может быть уменьшена до знаменателя 15. У дробей также есть общий знаменатель 15.
Общим знаменателем дробей может быть любое общее кратное их знаменателям. Для простоты дроби дают наименьший общий знаменатель. Он равен наименьшему общему кратному знаменателей этих дробей.
Пример. Привести дробь и к наименьшему общему знаменателю.
Сначала найдите наименьшее общее кратное знаменателей этих дробей. Это число 12. Давайте найдем дополнительный множитель для первой и второй дробей. Для этого мы делим 12 на 4 и на 6. Три — это дополнительный множитель для первой дроби, а два — для второй. Приведем дроби к знаменателю 12.
Мы привели дроби к общему знаменателю, то есть нашли равные им дроби, имеющие одинаковый знаменатель.
Правило. Чтобы привести дроби к наименьшему общему знаменателю, нужно
Сначала найдите наименьшее общее кратное знаменателей этих дробей, оно будет их наименьшим общим знаменателем;
Во-вторых, разделите наименьший общий знаменатель на знаменатели этих дробей, то есть найдите дополнительный множитель для каждой дроби.
В-третьих, умножьте числитель и знаменатель каждой дроби на ее дополнительный множитель.
а) Уменьшить дробь и до общего знаменателя.
Наименьший общий знаменатель равен 12. Дополнительный множитель для первой дроби равен 4, а для второй — 3. Приведем дроби к знаменателю 24.
б) Уменьшить дробь и к общему знаменателю.
Наименьший общий знаменатель — 45. Деление 45 на 9 на 15 дает 5 и 3 соответственно. Довести дроби до знаменателя 45.
в) Сократить дробь и к общему знаменателю.
Общий знаменатель равен 24. Дополнительные множители равны 2 и 3 соответственно.
Иногда бывает трудно найти в устной форме наименьшее общее кратное для знаменателей этих дробей. Затем общий знаменатель и дополнительные множители находятся с использованием разложения на простые множители.
Приведите дробь и к общему знаменателю.
Разложим числа 60 и 168 на простые множители. Давайте запишем разложение 60 и сложим недостающие множители 2 и 7 из второго разложения.Умножьте 60 на 14, чтобы получить общий знаменатель 840. Дополнительный коэффициент для первой дроби равен 14. Дополнительный коэффициент для второй дроби равен 5. Приведите дроби к общему знаменателю 840.
Библиография
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и другие. Математика 6. — М .: Мнемосина, 2012.
.2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6. класс — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
.4. Рурукин А.Н., Чайковский И.В. Задания по курсу математики 5-6 класс. — ЗШ МИФИ, 2011.
.5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Учебное пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
.6. Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы… Библиотека учителя математики. — Просвещение, 1989.
.Вы можете скачать книги, перечисленные в п. 1.2. этого урока.
Домашнее задание
Виленкин Н.Я., Жохов В.И., Чесноков А.С. и другие. Математика 6. — М .: Мнемосина, 2012. (см. Ссылку 1.2)
Домашнее задание: # 297, # 298, # 300.
Прочие назначения: 270, 290
В этой статье объясняется, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель.Даны определения, дано правило приведения дробей к общему знаменателю, рассмотрены практические примеры.
Что такое сокращение общего знаменателя?
У обыкновенных дробей числитель вверху и знаменатель внизу. Если дроби имеют одинаковый знаменатель, говорят, что их приводят к общему знаменателю. Например, дроби 11 14, 17 14, 9 14 имеют одинаковый знаменатель 14. Другими словами, они приводятся к общему знаменателю.
Если дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю с помощью простых действий.Для этого нужно умножить числитель и знаменатель на определенные дополнительные множители.
Очевидно, что дроби 4 5 и 3 4 не приводятся к общему знаменателю. Для этого нужно привести их к знаменателю 20 с помощью дополнительных множителей 5 и 4. Как именно это сделать? Умножим числитель и знаменатель 4 5 на 4, а числитель и знаменатель 3 4 на 5. Вместо дробей 4 5 и 3 4 мы получим 16 20 и 15 20 соответственно.
Общий знаменатель дробей
Приведение дробей к общему знаменателю — это умножение числителей и знаменателей дробей на такие множители, что в результате получаются идентичные дроби с одинаковым знаменателем.
Общий знаменатель: определение, примеры
Какой общий знаменатель?
Общий знаменатель
Общим знаменателем дробей является любое положительное число, являющееся общим кратным всех данных дробей.
Другими словами, общим знаменателем набора дробей будет натуральное число, которое без остатка делится на все знаменатели этих дробей.
Диапазон натуральных чисел бесконечен, и поэтому, по определению, каждый набор обыкновенных дробей имеет бесконечный набор общих знаменателей.Другими словами, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Общий знаменатель для нескольких дробей легко найти, используя определение. Пусть есть дроби 1 6 и 3 5. Общим знаменателем дробей является любое положительное общее кратное 6 и 5. Эти положительные общие кратные равны 30, 60, 90, 120, 150, 180, 210 и так далее.
Рассмотрим пример.
Пример 1. Общий знаменатель
Можно ли привести дробь 1 3, 21 6, 5 12 к общему знаменателю, равному 150?
Чтобы узнать, так ли это, нужно проверить, является ли 150 общим кратным для знаменателей дробей, то есть для чисел 3, 6, 12.Другими словами, число 150 должно делиться на 3, 6, 12 без остатка. Проверим:
150 ÷ 3 = 50, 150 ÷ 6 = 25, 150 ÷ 12 = 12, 5
Следовательно, 150 не является общим знаменателем этих дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из набора общих знаменателей набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель
Наименьший общий знаменатель дробей — это наименьшее число среди всех общих знаменателей этих дробей.
Наименьший общий делитель данного набора чисел — это наименьшее общее кратное (НОК). НОК всех знаменателей дробей является наименьшим общим знаменателем этих дробей.
Как найти наименьший общий знаменатель? Его поиск сводится к нахождению наименьшего общего кратного дробей. Возьмем пример:
Пример 2. Найдите наименьший общий знаменатель
Найдите наименьший общий знаменатель для дробей 1 10 и 127 28.
Ищем НОК номеров 10 и 28.Разложим их на простые множители и получим:
10 = 2 5 28 = 2 2 7 H O K (15, 28) = 2 2 5 7 = 140
Как привести дроби к наименьшему общему знаменателю
Есть правило, объясняющее, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
Правило приведения дробей к общему знаменателю
- Найдите наименьший общий знаменатель дробей.
- Найдите дополнительный множитель для каждой дроби.Чтобы найти множитель, вам нужно разделить наименьший общий знаменатель на знаменатель каждой дроби.
- Умножьте числитель и знаменатель на найденный дополнительный множитель.
Рассмотрим применение этого правила на конкретном примере.
Пример 3. Приведение дробей к общему знаменателю
Есть дроби 3 14 и 5 18. Приведем их к наименьшему общему знаменателю.
Как правило, сначала мы находим НОК знаменателей дробей.
14 = 2 7 18 = 2 3 3 H O K (14, 18) = 2 3 3 7 = 126
Рассчитываем дополнительные коэффициенты для каждой дроби. Для 3 14 дополнительный множитель 126 ÷ 14 = 9, а для дроби 5 18 дополнительный множитель будет 126 ÷ 18 = 7.
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
3 9 14 9 = 27 126, 5 7 18 7 = 35 126.
Приведение нескольких дробей к наименьшему общему знаменателю
Согласно рассмотренному правилу к общему знаменателю можно привести не только пары дробей, но и большее их количество.
Приведем еще один пример.
Пример 4. Приведение дробей к общему знаменателю
Сократите дроби 3 2, 5 6, 3 8 и 17 18 до наименьшего общего знаменателя.
Рассчитаем НОК знаменателей. Находим НОК трех и более чисел:
H O C (2, 6) = 6 H O C (6, 8) = 24 H O C (24, 18) = 72 H O C (2, 6, 8, 18) = 72
Для 3 2 дополнительный множитель 72 ÷ 2 = 36, для 5 6 дополнительный множитель 72 ÷ 6 = 12, для 3 8 дополнительный множитель 72 ÷ 8 = 9, наконец, для 17 18 дополнительный множитель 72 ÷ 18 = 4.
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
3 2 36 = 108 72 5 6 12 = 60 72 3 8 9 = 27 72 17 18 4 = 68 72
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Скачать демо-версию. Варианты демонстрации ОГЭ (ГИА) по математике
18.02.202121.08.2017 на официальном сайте ФИПИ опубликованы документы, регулирующие структуру и содержание KIM USE 2018 (демонстрационная версия OGE).ФИПИ приглашает экспертные и профессиональные сообщества принять участие в обсуждении проектов материалов экспертизы на 2018 год.
Демо-версии ОГЭ 2018 на русском языке с ответами и критериями оценки
В КИМ ОГЭ в 2018 году на русском языке изменений по сравнению с 2017 годом не произошло.
Всего заданий — 15; из них по типам заданий: с кратким ответом — 13; с развернутым ответом — 2; по уровню сложности: В — 14; IN 1.
Максимальный начальный балл — 39
Общее время выполнения работы 235 минут.
Описание структуры и содержания CMM 2018
Каждая версия CMM состоит из трех частей и включает 15 задач, различающихся по форме и уровню сложности.
Часть 1 — краткое содержание (задание 1).
Часть 2 (задания 2-14) — задания с кратким ответом. В экзаменационной работе предлагаются следующие типы заданий с кратким ответом:
— задания открытого типа на запись самостоятельно сформулированного короткого ответа;
— задания на выбор и запись одного правильного ответа из предложенного списка ответов.
Часть 3 (альтернативное задание 15) — это открытое задание с подробным ответом (эссе), в котором проверяется способность составить собственное утверждение на основе прочитанного текста.
Условия экзамена
К экзамену по русскому языку не допускаются специалисты-филологи. Организатором экзамена должен быть учитель, не преподающий русский язык и литературу. Использование единой инструкции к экзамену позволяет обеспечить соблюдение единых условий без привлечения к организации экзамена лиц со специальным образованием по данному предмету.
Порядок сдачи экзамена ОГЭ 2018 по русскому языку в 9 классе.
Получив пакет с экзаменационными материалами, испытуемые подписывают все листы или бланки, на которых они будут выполнять задания. Подписанные листы или бланки складываются в правильном порядке на рабочем месте испытуемых и заполняются ими во время экзамена.
Тестируемые сначала слушают исходный текст. При чтении текста экзаменуемым разрешается делать пометки в черновике. После второго чтения текста испытуемые кратко излагают его в письменной форме.Для воспроизведения текста презентации используется аудиозапись.
Затем студенты знакомятся с текстом для чтения, который предоставляется каждому из них в распечатанном виде. Испытуемым предлагается выполнить задания, связанные с содержательным и лингвистическим анализом прочитанного текста.
Во время тестирования при выполнении всех частей работы испытуемые имеют право пользоваться орфографическим словарем.
Задание с развернутым ответом проверяется специалистами по русскому языку, прошедшими специальную подготовку по проверке заданий государственной итоговой аттестации.
Основное общее образование
Линия УМК А.Г. Мерзляк. Алгебра (7-9) (базовая)
Математика
Демовариант, кодификатор и спецификация ОГЭ 2020 по математике с официального сайта ФИПИ.Загрузите демо-версию OGE 2020 вместе с кодификатором и спецификацией по ссылке ниже:
Основные изменения в новой демке
В КИМ добавлен новый блок практических заданий 1-5.
График ОГЭ по математике в 2020 году
На данный момент известно, что Минобразования и Рособрнадзор опубликовали проект расписания НГЭ для общественного обсуждения.Ориентировочные даты экзаменов по математике основной волны: 9 июня, резервные дни 24, 25, 30 июня.
Скоро мы поговорим о предстоящем ЕГЭ на нашем YouTube-канале и в прямом эфире.
Выпускникам 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практические задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики. «.Представлены задания разного уровня сложности. В конце книги даются ответы, которые помогут в отслеживании и оценке знаний, навыков и умений. Материалы пособия могут быть использованы для систематического повторения изученного материала и обучения выполнению заданий разного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а студентам — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», состоящих из двух частей: базового уровня (часть 1), продвинутого и высокого уровня (часть 2). Всего в работе 26 задач, из них 20 задач базового уровня, 4 задачи продвинутого уровня и 2 задачи высокого уровня. Модуль «Алгебра» содержит 17 задач: в части 1 — 14 задач; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 задач: в 1 части — 6 задач; в части 2 — 3 задания. На экзаменационную работу по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Упражнение 1
Найдите значение выражения
Решение
Ответ: 0,32.
Решение
Так как время составляет 5,62 секунды, эталон девушки на «4» не выполнен, однако это время не превышает 5,9 секунды. — эталон оценки «3». Следовательно, его оценка — «3».
Ответ: 3.
Решение
Первое число больше 11, поэтому оно не может быть числом A.Обратите внимание, что точка A расположена на второй половине отрезка, что означает, что она определенно больше 5 (из-за масштаба координатной линии). Так что это не номер 3) и не номер 4). Обратите внимание, что число удовлетворяет неравенству:
Ответ: 2.
Назначение 4
Найдите значение выражения
Решение
По свойству арифметического квадратного корня (при a ≥ 0, b ≥ 0) имеем:
Ответ: 165.
Решение
Для ответа на этот вопрос достаточно определить цену деления по горизонтальной и вертикальной осям. По горизонтальной оси одна выемка составляет 0,5 км, по вертикальной — 20 мм. r.s. Следовательно, давление 620 мм. r.s. достигается на высоте 1,5 км.
Ответ: 1,5.
Назначение 6
Решите уравнение x 2 + x — 12 = 0.
Если в вашем уравнении более одного корня, запишите в ответ наибольший корень.
Решение
Воспользуемся формулой для корней квадратного уравнения
Откуда x 1 = –4, x 2 = 3.
Ответ: 3.
Назначение 7
Стоимость проезда в электропоезде 198 руб. Студентам предоставляется скидка 50%. Сколько будет стоить проезд для 4 взрослых и 12 школьников?
Решение
Студенческий билет будет стоить 0.5198 = 99 руб. Это означает, что проезд для 4 взрослых и 12 школьников обойдется в
.4198 + 12 99 = 792 + 1188 = 1980.
Ответ: 1980.
Решение
Утверждения 1) и 2) можно считать правильными, поскольку области, соответствующие белкам и углеводам, занимают примерно 36% и 24% всей части круговой диаграммы. В то же время из диаграммы видно, что жиры занимают менее 16% всей диаграммы, и поэтому утверждение 3) неверно, как и утверждение 4) неверно, так как жиры, белки и углеводы составляют большую часть. диаграммы в их совокупности.
Ответ: 12 или 21.
Назначение 9
На тарелке одинаковые пироги: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирог. Найдите вероятность того, что в пироге останутся яблоки.
Решение
Вероятность события в классическом определении — это отношение количества благоприятных исходов к общему количеству возможных исходов:
В данном случае количество всех возможных исходов равно 4 + 8 + 3 = 15.Количество благоприятных исходов — 3. Следовательно,
Ответ: 0,2.
Установите соответствие между графиками функций и формулами, которые их определяют.
Решение
Первый график, очевидно, соответствует параболе, общее уравнение которой:
y = ax 2 + bx + c .
Следовательно, это формула 1). Второй график соответствует гиперболе, общее уравнение которой:
Следовательно, это формула 3).Остается третий график, который является графиком прямой пропорциональности:
y = kx .
Это формула 2).
Ответ: 132.
Назначение 11
В последовательности чисел первое число — 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.
Решение
Задача касается арифметической прогрессии с первым членом a 1 = 6 и разностью d = 4.Формула общего члена
a n = a 1 + d · ( n — 1) = 6 + 414 = 62.
Ответ: 62.
Решение
Вместо того, чтобы сразу подставлять числа в это выражение, мы сначала упростим его, записав в виде рациональной дроби:
Ответ: 1,25.
Задача 13
Чтобы преобразовать значение температуры из Цельсия в Фаренгейт, используйте формулу t F = 1,8 t C + 32, где t C — температура в градусах Цельсия, t F — температура в градусах Фаренгейта.Сколько градусов по Фаренгейту составляет –25 градусов по Цельсию?
Решение
Подставьте значение -25 в формулу
т F = 1,8 · (–25) + 32 = –13
Ответ: –13.
Укажите решение системы неравенств
Решение
Решая данную систему неравенств, получаем:
Следовательно, решением системы неравенств является отрезок [–4; –2.6], что соответствует рисунку 2).
Ответ: 2.
Решение
Фигура, показанная на рисунке, представляет собой прямоугольную трапецию. Средняя опора — это не что иное, как средняя линия трапеции, длина которой рассчитывается по формуле
., где а , b — длина баз. Составим уравнение:
б = 2,5.
Ответ: 2,5.
В равнобедренном треугольнике ABC с основанием AS внешний угол при вершине C равен 123 °. Найдите угол ВЫ … Ответьте в градусах.
Решение
Треугольник ABC равнобедренный, поэтому угол ВАС равен углу ICA … А вот угол ICA — смежный с углом 123 °. Следовательно,
∠ ВАС = ∠ ICA = 180 ° — 123 ° = 57 °.
Ответ: 57 °.
Найдите длину хорды окружности радиуса 13, если расстояние от центра окружности до хорды равно 5.
Решение
Рассмотрим треугольник AOB (см. Рисунок).
Он равнобедренный ( ООО = ОВ ) и НЕ по его высоте (его длина равна по условию 5). Следовательно, IS HE — это медиана по свойству равнобедренного треугольника и AN = HB … Найдите AN из прямоугольного треугольника ANO по теореме Пифагора:
Следовательно, AB = 2 AN = 24.
Ответ: 24.
Найдите площадь трапеции, показанную на рисунке.
Решение
Нижнее основание трапеции — 21. Воспользуемся формулой для площади трапеции
.Ответ: 168.
Найдите тангенс острого угла, показанного на рисунке.
Решение
Выберите прямоугольный треугольник (см. Рисунок).
Касательная — это отношение противоположной ветви к соседней, отсюда находим
Ответ: 2.
Какие из следующих утверждений верны?
1) Через точку, не лежащую на заданной линии, вы можете провести линию, параллельную этой линии.
2) Треугольник со сторонами 1, 2, 4 существует.
3) У любого параллелограмма два равных угла.
Решение
Первое утверждение — аксиома параллельной прямой. Второе утверждение неверно, поскольку неравенство треугольника не выполняется для отрезков длиной 1, 2, 4 (сумма длин любых двух сторон меньше длины третьей стороны)
1 + 2 = 3> 4.
Верно третье утверждение — в параллелограмме противоположные углы равны.
Ответ: 13 или 31.
Часть 2
Решите уравнение x 4 = (4 x — 5) 2.
Решение
Используя формулу для разности квадратов, исходное уравнение приводится к виду:
( x 2 — 4 x + 5) ( x 2 + 4 x — 5) = 0,
Уравнение x 2-4 x + 5 = 0 не имеет корней ( D
x 2 + 4 x — 5 = 0
имеет корни −5 и 1.
Ответ: −5; 1.
Рыбак в 5 часов утра на моторной лодке отправился от причала против течения реки, через некоторое время бросил якорь, ловил рыбу 2 часа и вернулся обратно в 10 часов утра. тот же день.Как далеко он плыл от причала, если скорость реки 2 км / ч, а собственная скорость лодки 6 км / ч?
Решение
Пусть рыболов отплывет на расстояние, равное с. … Время, в течение которого он проплыл этот путь, равно часам (потому что против течения скорость лодки составляет 4 км / ч). Время, которое он затратил на обратный путь, равно часам (так как скорость катера по течению 8 км / ч). Общее время с учетом парковки — 5 часов.Составим и решим уравнение:
Ответ: 8 километров.
Решение
Область рассматриваемой функции содержит все действительные числа, кроме чисел –2 и 3.
Упростим форму аналитической зависимости, вычленив числитель дроби:
Таким образом, график этой функции представляет собой параболу
y = x 2 + x — 6,
с двумя «проколотыми» точками, абсциссы которых равны –2 и 3.Построим этот граф. Координаты вершины параболы
(–0,5; –6,25).
Прямой y = c имеет ровно одну общую точку с графиком, либо когда он проходит через вершину параболы, либо когда он пересекает параболу в двух точках, одна из которых пробита. Координаты «проколотых» точек
(−2; −4) и (3; 6). поэтому c = –6,25, c = –4 или c = 6.
Ответ : c = –6,25; c = –4; с = 6.
В прямоугольном треугольнике ABC прямой угол ИЗ известны катеты: AS = 6, Солнце = 8. Найдите медиану СК этого треугольника.
Решение
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине. следовательно
Ответ: 5.
В параллелограмме ABCD точка E — середина стороны AB … Известно, что EC = ED … Докажите, что данный параллелограмм — прямоугольник.
Решение
Рассмотрим треугольники EBC и AED. Они равны с трех сторон. Действительно, AE = EB , ED = EC (по условию), AD = BC (противоположные стороны параллелограмма). Следовательно, A = ∠ B , но сумма смежных углов в параллелограмме равна 180 °, поэтому ∠ A = 90 ° и ABCD — прямоугольник.
Основание AS равнобедренный треугольник ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения сторон треугольника и касается основания AS … Найдите радиус круга, вписанного в треугольник. треугольник ABC .
Решение
Пусть будет O, — это центр этой окружности, а Q — центр окружности, вписанной в треугольник ABC .
Начиная с точки ПРО , равноудаленной от сторон угла ∠СВА , поскольку она лежит на его биссектрисе.При этом на биссектрисе угла ∠СВА лежит точка Q и в то же время, в силу свойств равнобедренного треугольника, эта биссектриса является как срединой, так и высотой треугольника ABC . … Из этих соображений легко вывести, что рассматриваемые круги касаются в одной точке M , точке касания M окружности делят AC пополам и OQ перпендикулярно AC .
Проведем лучи AQ и AO … Нетрудно понять, что AQ и AO являются биссектрисами смежных углов, а значит, угол OAQ прямой. Из прямоугольного треугольника OAQ получаем:
AM 2 = MQ · MO .
Следовательно,
Модуль «Алгебра»
1 … Найдите значение выражения
2. В таблице приведены нормативы бега на 30 метров для учащихся 9 класса.
Какую оценку получит девушка, пробежав это расстояние за 5,62 секунды?
1) отметка «5» 2) отметка «4»
3) отметка «3» 4) стандарт не соблюдается
3 … На координатной линии отмечена точка A … Известно, что она соответствует одному из четырех чисел ниже.
Какое из чисел соответствует точке И ?
1) 2) 3) 4)
4 … Найдите значение выражения
5 … График показывает взаимосвязь между атмосферным давлением и высотой.По горизонтальной оси отложена высота над уровнем моря в километрах, по вертикальной оси — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление составляет 620 миллиметров ртутного столба. Дайте свой ответ в километрах.
6. Решите уравнение. Если в вашем уравнении более одного корня, запишите самый большой корень в своем ответе.
7. Стоимость проезда в электропоезде 198 руб. Студентам предоставляется скидка 50%.Сколько будет стоить проезд для 4 взрослых и 12 школьников?
8. На диаграмме показано содержание питательных веществ в сушеных белых грибах.
Какие из следующих утверждений верны?
1) В 1000 граммах грибов содержится около 360 г жира.
2) 1000 граммов грибов содержат около 240 граммов углеводов.
3) 1000 граммов грибов содержат примерно 140 граммов белка.
4) 1000 граммов грибов содержат примерно 500 г жиров, белков и углеводов.
В ответ запишите номера выбранных операторов без пробелов, запятых и других дополнительных символов.
9. На тарелке одинаковые пироги: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирог. Найдите вероятность того, что в пироге останутся яблоки.
10. Установите соответствие между графиками функций и формулами, которые их определяют.
11. В последовательности чисел первое число — 6, а каждое следующее больше предыдущего на 4.Найдите пятнадцатое число.
12. Найдите значение выражения в.
13. Чтобы преобразовать температуру из Цельсия в Фаренгейт, используйте формулу, где — температура в градусах Цельсия, — температура в градусах Фаренгейта. Сколько градусов по Фаренгейту составляет -25 градусов по Цельсию?
14. Укажите решение системы неравенств
15. Скатная крыша устанавливается на трех вертикальных опорах, основания которых расположены на одной прямой.Средняя опора стоит посередине между малой и большой опорами (см. Рис.). Высота малой опоры 1,7 м, высота средней опоры 2,1 м. Найдите высоту большой опоры. Дайте свой ответ в метрах.
16 … В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123 °. Найдите угол ВЫ … Ответьте в градусах.
17 … Найдите длину хорды окружности с радиусом 13 см, если расстояние от центра окружности до хорды составляет 5 см. Ответьте в см.
18. Найдите площадь трапеции, показанную на рисунке.
19 … Найдите тангенс острого угла, показанного на рисунке.
20 … Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной линии, вы можете провести линию, параллельную этой линии.
2) Треугольник со сторонами 1, 2, 4 существует.
3) У любого параллелограмма два равных угла.
В ответ запишите номера выбранных операторов без пробелов, запятых и других дополнительных символов.
Модуль «Алгебра»
21 … Решите уравнение
22 … Рыбак в 5 часов утра на моторной лодке отправился от причала против течения реки, через некоторое время бросил якорь, ловил рыбу 2 часа и вернулся обратно в 10 часов утра. утром того же дня.Как далеко он плыл от причала, если скорость течения реки 2 км / ч, а собственная скорость лодки 6 км / ч?
23 … Постройте график функции и определите, при каких значениях линия имеет ровно одну общую точку с графиком.
Модуль «Геометрия»
24 … В прямоугольном треугольнике ABC прямой угол C катеты известны: AC = 6, BC = 8. Найдите медиану CK этого треугольника.
25 … В параллелограмме ABCD точка E — середина стороны AB … Известно, что EC = ED … Докажите, что данный параллелограмм является прямоугольником.
26 … Основание AC равнобедренный треугольник ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC … Найти радиус круг вписан в треугольник ABC .
Ответы| 1 | 0,32 |
| 2 | 3 |
| 3 | 2 |
| 4 | 165 |
| 5 | 1,5 |
| 6 | 3 |
| 7 | 1980 г. |
| 8 | 12; 21 |
| 9 | 0,2 |
| 10 | 132 |
| 11 | 62 |
| 12 | 1,25 |
| 13 | -13 |
| 14 | 2 |
| 15 | 2,5 |
| 16 | 57 |
| 17 | 24 |
| 18 | 168 |
| 19 | 2 |
| 20 | 13; 31 |
| 21 | -5; 1 |
| 22 | 8 километров |
| 23 | -6,25; -4; 6 |
| 24 | 5 |
| 25 | |
| 26 | 4,5 |
На официальном сайте ФИПИ представлены документы, определяющие состав и содержание контрольно-измерительных материалов главного государственного экзамена по математике в 2020 году.Демо-версия представлена пока как проект. По сравнению с экзаменом за последний учебный год, есть существенные изменения, пожалуйста, внимательно изучите этот вариант. Вот черновик Демонстрационной версии ОГЭ 2020 по математике с комментариями в удобной для обучения и подготовки форме.
В отличие от прошлого года, в экзаменационной работе явно не выделяются модули «Алгебра» и «Геометрия», однако условие успешной сдачи экзамена — как минимум из двух правильно решенных задач по геометрии — остается в силе.
Добавлен блок практических заданий. Эти задачи решаются на основе не только знаний по математике, но и исходя из разумных практических соображений.
Все задания, как и раньше, разделены на две части. Часть 1 содержит 20 задач с кратким ответом, часть 2 содержит 6 задач с подробным ответом.
В задачах первой части проверяются только ответы, которые нужно перенести в специальную форму. Все необходимые расчеты, преобразования выполняются на чертеже.Записи в проекте, а также в тексте контрольно-измерительных материалов при оценке работы не учитываются. Вторая часть требует записи полного решения проблемы. Задания можно выполнять в любом порядке. Переписывать условие задачи не нужно, достаточно указать номер задачи.
Также не забывайте, что содержание базового экзамена для 11 класса существенно перекликается с ОГЭ для девятого класса, потому что за первые 9 лет изучения математики вы выучили больше, чем вы можете сделать за оставшиеся два года.Используйте все ссылки и комментарии, , чтобы найти материалы, необходимые для подготовки к экзамену.
Внимание:
тренажер устроен следующим образом.1) Синее поле — поле состояния задачи. Белая область рядом со словом «Ответ» — это, по сути, кнопка, на которую вы нажимаете, чтобы увидеть правильный ответ. Если вы еще не решили демоверсию, то, прежде чем нажимать кнопку, попробуйте получить ответ самостоятельно и сравните его с заведомо правильным.
2) Оранжевое поле — поле для комментариев, ссылки на другие страницы сайта или на задания ЕГЭ.
Кнопки срабатывают после полной загрузки страницы.
Часть 1
Внимательно прочтите текст и выполните задания 1–5.
На плане изображено домохозяйство по адресу: s. Авдеево, 3-й Поперечный переулок, д. 13 (сторона каждой клетки на плане 2 м). Участок прямоугольной формы. Въезд и выезд через одни ворота.
При въезде на участок справа от ворот баня, а слева гараж, обозначенный на плане цифрой 7.Площадь, занимаемая гаражом, составляет 32 квадратных метра. м.
Жилой дом находится в глубине территории. Кроме гаража, жилого дома и бани, на участке есть сарай (подсобное помещение), расположенный рядом с гаражом, и построенная на территории огорода теплица (огород обозначен цифрой 2). Перед жилым домом — яблоневые насаждения.
Все дорожки в пределах участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м × 1 м.Между баней и гаражом 64 кв.м, вымощена такой же плиткой.
Дом подведено электричество. Есть магистральный газ.
Вы можете увидеть это на отдельной странице сайта.
1. Для объектов, указанных в таблице, определите, какими номерами они обозначены на плане. Заполните таблицу, перенесите в форму ответа последовательность из четырех чисел.
Ответ: ______.
2. Тротуарная плитка продается упаковками по 4 штуки.Сколько пачек плитки понадобилось, чтобы выложить все дорожки и территорию перед гаражом?
Ответ: ______.
3. Найдите площадь, занимаемую жилым домом. Ответьте в квадратных метрах.
Ответ: ______.
4. Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками на прямой) в метрах.
Ответ: ______.
5. Хозяин планирует устроить в жилом доме зимнее отопление.Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о потреблении газа, электроэнергии и их стоимости приведены в таблице.
Рассмотрев оба варианта, собственник решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости установки газового и электрического отопления?
Ответ: ______.
6. Найдите значение выражения
1 _ 4 + 0,07.
Ответ: ______.
7. Точка A отмечена на координатной линии.
Известно, что оно соответствует одному из четырех чисел ниже.
Какому из чисел соответствует точка A?
1) 181 ___ 16 2) √37__ 3) 0,6 4) 4
Ответ: ______.
8. Найдите значение выражения √45 __ √605 ___ .
Ответ: ______.
9. Решите уравнение x 2 + x — 12 = 0 .
Если в вашем уравнении более одного корня, запишите самый большой корень в своем ответе.
Ответ: ______.
10. На тарелке одинаковые пироги: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирог. Найдите вероятность того, что в пироге останутся яблоки.
Ответ: ______.
11. Установите соответствие между графиками функций и формулами, которые их определяют.
1) y = x 2 2) y = x _ 2 3) y = 2 _ х
В таблице под каждой буквой укажите соответствующий номер.
12. В последовательности чисел первое число — 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.
Ответ: ______.
13. Найдите значение выражения
9 b + 5 a — 9 b 2 ______ b
при a = 9, b = 36.Ответ: ______.
14. Чтобы преобразовать значение температуры из градусов Цельсия в градусы Фаренгейта, используйте формулу t F = 1,8 t C + 32, Где t C, — температура в градусах Цельсия, t F — температура в градусах Фаренгейта.Сколько градусов по Фаренгейту составляет -25 градусов по Цельсию?
Ответ: ______.
15. Укажите решение системы неравенств
Ответ: ______.
16. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123º. Найдите угол ВЫ … Ответьте в градусах.
Ответ: ______.
17. Найдите длину хорды окружности радиуса 13, если расстояние от центра окружности до хорды равно 5.
Ответ: ______.
18. Найдите площадь трапеции, показанную на рисунке.
Ответ: ______.
19. Найдите тангенс острого угла, показанного на рисунке.
Ответ: ______.
20. Какие из следующих утверждений верны?
1) Через точку, не лежащую на заданной линии, вы можете провести линию, параллельную этой линии.
2) Треугольник со сторонами 1, 2, 4 существует.
3) У любого параллелограмма два равных угла.
В ответ запишите номера выбранных операторов без пробелов, запятых и других дополнительных символов.
Ответ: ______.
Часть 2
При выполнении задач этой части вам нужно будет записать полное решение проблемы на отдельном листе. И оценивать будет именно решение, краткий ответ здесь уже не актуален. Поэтому белое поле после текста задачи — это всего лишь кнопка для просмотра решения, рекомендованного авторами варианта.Не спешите его нажимать, если вы не пытались решить проблему самостоятельно.
Первые три задания второй части относятся к алгебре.
21. Решите уравнение x 4 = (4 x — 5) 2.
Ответ: ______
Решение.
Исходное уравнение сводится к форме: ( x 2-4 x + 5) ( x 2 + 4 x — 5) = 0.
Уравнение x 2-4 x + 5 = 0
не имеет корней.
Уравнение x 2 + 4 x — 5
имеет корни −5 и 1.
Ответ: −5; 1.
22. В 5 часов утра рыбак отплыл на моторной лодке от причала против течения реки, через некоторое время бросил якорь, ловил рыбу 2 часа и вернулся обратно в 10 часов утра. тот же день. Как далеко он плыл от причала, если скорость реки 2 км / ч, а собственная скорость лодки 6 км / ч?
Ответ: ______.
Решение.
Пусть требуется расстояние x км. Скорость лодки при движении против течения — 4 км / ч, при движении по течению — 8 км / ч. Время, необходимое лодке, чтобы добраться от пункта отправления до пункта назначения и обратно, составляет ( x /4 + x /8) часов. Из постановки задачи следует, что это время равно 3 часам. Составим уравнение:
x _ 4 + x _ 8 = 3.
Решая уравнение, получаем x = 8.
Ответ: 8 километров.
23. Постройте функциональный график
y = x 4-13 x 2 + 36 _____________. ( x — 3) ( x + 2)
И определите, при каких значениях из по прямой y = c имеет ровно одну общую точку с графиком.
Ответ: ______.
Решение.
Выносим за скобки числитель дроби:
x 4-13 x 2 + 36 = ( x 2-4) ( x 2-9) = ( x -2) ( x + 2) ( x — 3) ( x + 3).
Когда x ≠ −2 и x ≠ 3 функция принимает следующий вид: y = ( x — 2) ( x + 3) = x 2 + x — 6
, его график представляет собой параболу, из которой выкалываются точки (−2; −4) и (3; 6).
Прямая y = c имеет ровно одну общую точку с графиком, либо когда она проходит через вершину параболы, либо когда она пересекает параболу в двух точках, одна из которых пробита. Вершина параболы имеет координаты (−0,5; −6,25). поэтому c = −6,25, c = −4 или c = 6.
Ответ: c = −6,25; c = — 4; c = 6.
Технические условия
Контрольно-измерительные материалы для проведения
в 2018 году основного государственного экзамена
математика
1.Назначение КИМ ОГЭ — для оценки уровня общего образования по математике выпускников 9 классов общеобразовательных организаций с целью проведения государственной итоговой аттестации выпускников. Результаты экзамена могут быть использованы при зачислении учащихся в классы общеобразовательной школы.
ОГЭ проводится в соответствии с Федеральным законом Российской Федерации от 29 декабря 2012 г. № 273-ФЗ «Об образовании в Российской Федерации».
2.Документы, определяющие содержание CMM
Содержание экзаменационной работы ОГЭ определяется на основании Федерального компонента государственного стандарта основного общего образования по математике (приказ Минобрнауки России от 05.03.2004 № 1089 «Об утверждении федеральный компонент государственных образовательных стандартов начального, общего, основного общего и среднего (полного) общего образования »).
Кроме того, в экзаменационной работе отражены концептуальные положения Федерального государственного образовательного стандарта основного общего образования (Приказ Минобрнауки России от 17.07.2012).12.2010 № 1897 «Об утверждении Федерального государственного образовательного стандарта основного общего образования»). КИМ разрабатываются с учетом того, что результатом освоения основной образовательной программы основного общего образования должна быть математическая компетентность выпускников, т.е. они должны: овладевать знаниями и деятельностью, характерными для математики; узнать, как трансформировать знания и их применение в учебных и внешкольных ситуациях; сформировать качества, присущие математическому мышлению, а также овладеть математической терминологией, ключевыми понятиями, методами и приемами.
3. Подходы к выбору содержания, разработке структуры КИМ
Структура КИМ ОГЭ отвечает цели построения системы дифференцированного обучения математике в современной школе. Дифференциация обучения направлена на решение двух задач: формирование у всех учащихся базовой математической подготовки, составляющей функциональную основу общего образования, и одновременное создание условий, способствующих получению частью учащихся подготовки повышенного уровня. , достаточного для активного использования математики в процессе дальнейшего обучения, особенно при ее изучении.в средней школе на профильном уровне.
В целях обеспечения эффективности проверки усвоения основных понятий курса математики, умения применять математические знания и решать практические задачи, а также с учетом наличия в практике основной школы Как при раздельном преподавании предметов математического цикла, так и при преподавании интегрированного курса математики в экзаменационной работе выделяются два модуля: «Алгебра и геометрия».
4. Связь экзаменационной модели ОГЭ с КИМ экзамена
Содержательное единство государственной итоговой аттестации по курсу основной и средней школы обеспечивается едиными подходами к разработке кодификаторов элементов содержания и требований к уровню подготовки выпускников по математике. Оба кодификатора базируются на разделе «Математика» Федерального компонента государственного общеобразовательного стандарта.
5.Характеристики состава и состава CMM
Работа состоит из двух модулей: «Алгебра» и «Геометрия». Каждый модуль состоит из двух частей, соответствующих базовой и расширенной проверкам.
При проверке базовой математической компетентности учащиеся должны продемонстрировать владение базовыми алгоритмами, знание и понимание ключевых элементов содержания (математические концепции, их свойства, методы решения задач и т. Д.), Способность использовать математические обозначения, применять знания для решения математические задачи, которые не ограничиваются непосредственным применением алгоритма, а также применяют математические знания в простейших практических ситуациях.
Части 2 модулей «Алгебра» и «Геометрия» направлены на проверку владения материалом на продвинутом уровне. Их цель — дифференцировать успешных школьников по уровням подготовки, выявить наиболее подготовленную часть выпускников, составляющую потенциальный контингент профильных классов. Эти части содержат задания повышенного уровня сложности из различных разделов курса математики. Все задачи требуют записи решений и ответов.Задания расположены по возрастающей сложности — от относительно простых до сложных, требующих свободного владения материалом и высокого уровня математической культуры.
Модуль «Алгебра» содержит 17 заданий: в 1-й части — 14 заданий; в части 2 — 3 задания.
Модуль «Геометрия» содержит 9 заданий: в 1 части — 6 заданий; в части 2 — 3 задания.
Всего в работе 26 задач, из них 20 задач базового уровня, 4 задачи продвинутого уровня и 2 задачи высокого уровня.
.



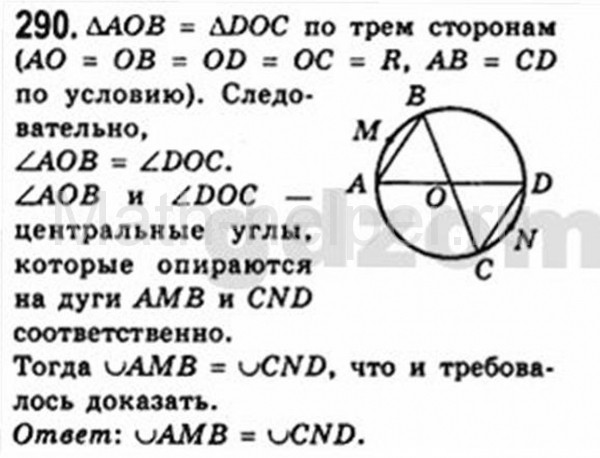
 Для этого найденный наименьший общий знаменатель необходимо разделить на знаменатель каждой дроби. Полученное число будет дополнительным множителем этой дроби.
Для этого найденный наименьший общий знаменатель необходимо разделить на знаменатель каждой дроби. Полученное число будет дополнительным множителем этой дроби.