Электронная рабочая тетрадь по алгебре для 7 класса, онлайн версия
Описание
| ОПИСАНИЕ | ОТЗЫВЫ | ХАРАКТЕРИСТИКИ | ОПЛАТА и ДОСТАВКА |
Электронная рабочая тетрадь «Алгебра, 7 класс» предназначена для учителей и учащихся 7 классов школ, лицеев, гимназий. Тетрадь представляет собой электронный тренажер, предназначенный для выработки и закрепления знаний и умений по предмету, а также для промежуточной аттестации учащихся в ходе электронных четвертных работ. Рабочая тетрадь состоит из интерактивных заданий, проверка которых производится автоматически – компьютером.
Рабочая тетрадь входит в состав интерактивного мультимедийного учебно-методического комплекса «Облако знаний»; результаты работы с рабочей тетрадью хранятся на облачном сервере проекта. Используя свою учетную запись и пин-код, активирующий доступ к курсу, учащийся может работать с курсом из любого места, с любого компьютерного устройства и в любое время.
Для работы с электронным приложением необходим доступ в Интернет по каналу со скоростью передачи данных не менее 64 кБ/с на одного пользователя. При отсутствии доступа в интернет пользователь не сможет авторизироваться, следовательно у него не будет доступа к купленным материалам.
Содержание курса соответствует федеральному государственному образовательному стандарту начальной школы и примерной программе по окружающему миру общеобразовательных учреждений России.
Содержание электронной рабочей тетради
1 Рациональные числа.
1.1. Натуральные числа.
1.1.1 Натуральные числа и действия с ними.
1.1.2. Простые и составные числа.
1.1.3. Делимость чисел.
1.2. Степень с натуральным показателем.
1.2.1. Степень числа.
1.2.2. Свойства степени с натуральным показателем.
1.2.3. Свойства степени с натуральным показателем.
1.3.1. Обыкновенные дроби.
1.3.2. Разложение обыкновенной дроби в конечную десятичную.
1.3.3. Периодические десятичные дроби.
2. Алгебраические выражения.
2.1. Одночлены.
2.1.1. Числовые и буквенные выражения. Понятие одночлена.
2.1.2. Сложение и вычитание одночленов.
2.1.3. Умножение и деление одночленов.
2.1.4. Возведение одночлена в степень.
2.1.5. Стандартный вид одночлена.
2.1.6. Подобные одночлены.
2.2. Многочлены.
2.2.1. Понятие многочлена.
2.2.2. Стандартный вид многочленов.
2.2.3. Сложение и вычитание многочленов.
2.2.4. Умножение многочлена на одночлен.
2.2.5. Умножение многочленов.
2.2.6. Целые выражения.
2.3. Формулы сокращенного умножения.
2.3.2. Квадрат разности.
2.3.3. Выделение полного квадрата.
2.3.4. Разность квадратов.
2.
3.5. Сумма кубов.2.3.6. Разность кубов.
2.3.7. Куб суммы.
2.3.8. Куб разности.
2.3.9. Применение формул сокращенного умножения.
2.3.10. Разложение многочлена на множители.
2.4. Алгебраические дроби.
2.4.1. Свойства алгебраических дробей.
2.4.2. Приведение алгебраических дробей к общему знаменателю.
2.4.3. Арифметические действия над алгебраическими дробями.
2.4.4. Рациональные выражения.
2.4.5. Равенство рациональных выражений.
2.5. Степень с целым показателем.
2.5.1. Степень с целым показателем.
2.5.2. Понятие степени с целым показателем.
2.5.3. Свойства степени с целым показателем.
2.5.4. Стандартный вид числа.
3. Простейшие функции.
3.1. Функции и их графики.
3.1.1. Координатная прямая и координатная плоскость.
3.1.2. Понятие функции.
3.1.3. График функции.
3.2. Линейная функция.
3.2.1. График линейного уравнения с двумя переменными.
3.2.2. Линейная функция и ее график.
3.2.3. Прямая пропорциональность.
3.2.4. Взаимное расположение графиков линейных функций.
3.3. Функция y = x2.
3.3.1. Функция y = x2 и её свойства.
3.3.2. Графическое решение уравнений.
В рабочей тетради по каждому параграфу учебной программы представлены 3–8 интерактивных заданий. Помимо этого тетрадь содержит тематические контрольные работы, в которых обобщается и проверяется материал по разделам, пройденным в течение учебной четверти.
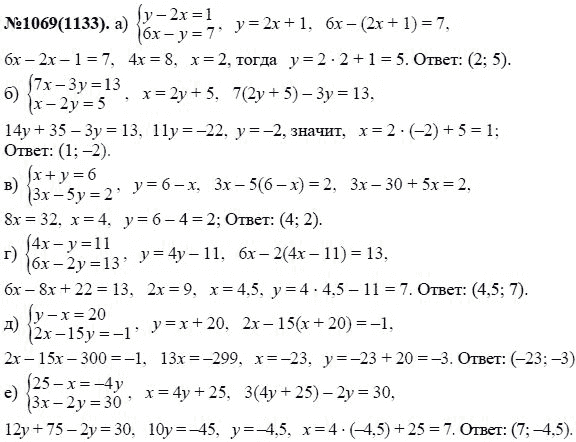
Перечень контрольных работ
- Рациональные числа.
- Одночлены и многочлены.
- Формулы сокращенного умножения и действия с алгебраическими дробями.
- Степень с целым показателем. Простейшие функции.
Видеоролик
Этот ролик демонстрирует принцип работы электронных рабочих тетрадей на основе облачных технологий (в нем показаны рабочие тетради по математике, физике, истории и географии)
Комплектация электронной рабочей тетради по алгебре для 7 класса»
– Для ПК
Плеер «Облако знаний» cкачать (8,2 Мб)
Тренажёр по предмету.
Индивидуальная лицензия (пин-код доступа) или лицензия на образовательное учреждение.
– Для iPad и Android
Плеер «Облако знаний» cкачать (161,0 Мб)
Тренажёр по предмету.
– Для систем дистанционного образования (СДО)
Тренажёр по предмету в формате SCORM 2004 (ZIP-архив). Выдается отдельно после оплаты.
Лицензия на образовательное учреждение.
- Операционная система Microsoft Windows 7/8/10.
- 100 Мб свободного дискового пространства на 1 тренажер.
- Устройство для чтения CD или DVD-дисков.
- Разрешение экрана – 1024 на 768 пикселей.
- Веб-браузер Microsoft Internet Explorer 11.
- Доступ в Интернет по каналу со скоростью передачи данных не менее 64 Кб/с на одного пользователя. При отсутствии доступа в интернет пользователь не сможет авторизироваться, следовательно у него не будет доступа к купленным материалам.
- Компьютерное устройство: персональный компьютер или ноутбук (процессор Pentium 4 или выше; не менее 512 Мб оперативной памяти; не менее 31 Мб памяти на жёстком диске) или планшетный компьютер под управлением ОС Android или iPad.
Доступ в интернет требуется для работы плеера. Он необходим для следующих операций:
- при регистрации пользователей,
- при аутентификации пользователей,
- при работе с журналом успеваемости,
- при работе с закладками,
- при передачи результатов работы с контентом на сервер,
- при работе с контентом.
Оплата и доставка
– Методы оплаты
Вы можете выбрать наиболее удобный для Вас способ оплаты. Интернет-магазин «Интеграл» предлагает Вам следующие варианты оплаты:
- Банковские карты.
- Интернет-банкинг – онлайн платежи.
- Терминалы оплаты.
- Банковские переводы.
- Электронные деньги.
Более подробнее о методах оплаты.
– Доставка
Электронная доставка бесплатная. Электронный ключ или ключ активации высылается на e-mail заказчика после оплаты.
На текущий момент мы не пересылаем покупателям коробочные версии или программы, записанные на CD или DVD носителях.
По всем вопросам обращайтесь на наш контактный e-mail: [email protected].
Отзывы покупателей о программе
«Приведено много теоретических и практических вопросов, которые помогут закрепить пройденный материал. Задания очень интересные и разнообразные. Ребята с удовольствием и выполняют в классе. В целом, очень хорошая рабочая тетрадь. Рекомендую.»
«Использую эту рабочую тетрадь уже давно, почти 4 года. Тетрадь позволяет выявлять недостатки и пробелы в знаниях и своевременно их устранять. Прекрасно работает в дополнении с учебником.»
ГДЗ по Алгебре за 7 класс Рабочая тетрадь Минаева С.С., Рослова Л.О.
Алгебра 7 класс Минаева С.С. рабочая тетрадь
Авторы: Минаева С.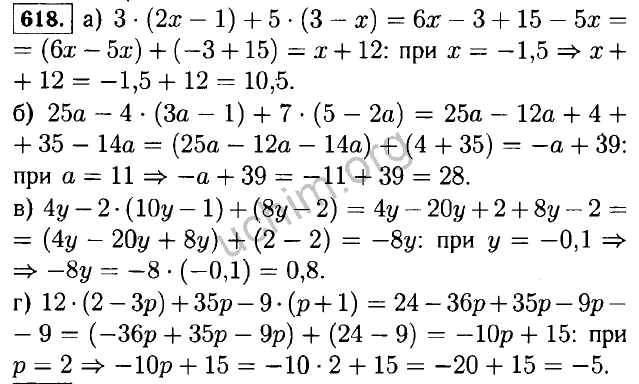
С., Рослова Л.О.
Семиклассники сталкиваются с серьёзной и неожиданной для себя проблемой: они не успевают подготовиться по всем предметам даже к текущим урокам, не говоря уже о контрольных. Домашних заданий стало намного больше, но самое главное – повысился уровень их сложности. В младших классах огромную роль играет всесторонняя поддержка родителей. Но алгебра – это именно та наука, которую забывает любой взрослый без постоянного повторения и практического применения. Но темы столь разнообразны и сложны, что самостоятельно разобраться в них удаётся даже не каждому отличнику. И тогда на помощь ученикам приходит персональный репетитор, который каждую минуту может подсказать верное решение – «ГДЗ по алгебре 7 класс рабочая тетрадь Минаева, Рослова (Просвещение)».
Консультант в точных науках – РТ
К сожалению, изучать алгебру не просто трудно. Возникает ещё и достаточно серьёзная психологическая проблема: многие выпускники на следующий день после сдачи финального экзамена никогда в своей жизни не вспомнят о существовании логарифмов и функций.
Семикласснику это понятно, результат – отношение к этому предмету как к лишней и крайне сложной науке. Но она является неизбежной дисциплиной на любом экзамене, поэтому желание школьника обойти алгебру ничего не меняет. Но существует способ сократить время на подготовку к урокам и при этом повысить уровень знаний достаточно для того, чтобы не опасаться никакого экзамена, – поддержка виртуального помощника, готового разъяснить любой непонятный момент: «ГДЗ к рабочей тетради по алгебре за 7 класс Минаева С. С., Рослова Л. О. (Просвещение)».
Что содержится в пособии
Авторы предлагают вниманию семиклассника 255 упражнений различного уровня сложности, которые помогут разобраться во всех разделах основного учебника алгебры для текущего года и заложить твёрдые знания по всем темам:
- Дроби и проценты.
- Прямая и обратная пропорциональность.
- Уравнения.
- Координаты и графики.
- Свойства степени с натуральным показателем.
- Многочлены.
Самостоятельное выполнение всех упражнений пособия позволит не только закрепить знания по всем темам, но и развить чёткое логическое мышление.
Как работаем с онлайн-решебником рабочей тетради по алгебре для 7 класса от Минаевой
С самых первых уроков алгебры ученик должен не забывать верный способ работы с решебником:
- проверять по ГДЗ не только правильность, но и стиль оформления решений;
- если собственный ответ отличается от варианта задачника, нужно исправлять ошибки, не подглядывая в него.
Следует всегда помнить: готовые домашние задания – это не шпаргалка, а личный консультант.
Скорость, расстояние и время — алгебра среднего уровня
Глава 8. Рациональные выражения
Задачи расстояния, скорости и времени являются стандартным применением линейных уравнений. При решении этих задач используйте соотношение скорость (скорость или скорость) умножить на время равно расстояние .
[латекс]r\cdot t=d[/латекс]
Например, предположим, что человек должен был двигаться со скоростью 30 км/ч в течение 4 часов. Чтобы найти общее расстояние, умножьте скорость на время или (30 км/ч) (4 ч) = 120 км.
Проблемы, которые нужно решить здесь, будут иметь несколько шагов больше, чем описано выше. Поэтому, чтобы систематизировать информацию в задаче, используйте таблицу. Пример базовой структуры таблицы ниже:
| Кто или что | Ставка | Время | Расстояние |
|---|---|---|---|
Третий столбец, расстояние, всегда будет заполняться путем перемножения столбцов скорости и времени. Если указано общее расстояние обоих людей или поездок, поместите эту информацию в столбец расстояния. Теперь используйте эту таблицу, чтобы настроить и решить следующие примеры.
Джоуи и Наташа начинают с одной точки и идут в противоположных направлениях. Джоуи идет на 2 км/ч быстрее, чем Наташа. Через 3 часа расстояние между ними 30 км. С какой скоростью шел каждый?
| Кто или что | Ставка | Время | Расстояние |
|---|---|---|---|
| Наташа | [латекс]г[/латекс] | [латекс]\текст{3 ч}[/латекс] | [латекс]\текст{3 ч}(р)[/латекс] |
| Джои | [латекс]r + 2[/латекс] | [латекс]\текст{3 ч}[/латекс] | [латекс]\текст{3 ч}(г + 2)[/латекс] |
Расстояние, пройденное обоими, составляет 30 км. Следовательно, нужно решить уравнение:
[латекс]\begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \\ 3r&+&3r&+&6&=&30 \\ &&&-&6&&-6 \ \ \hline &&&&\dfrac{6r}{6}&=&\dfrac{24}{6} \\ \\ &&&&&r&=&4 \text{ км/ч} \end{array}[/latex]
Это означает, что Наташа ходит со скоростью 4 км/ч, а Джои ходит со скоростью 6 км/ч.
Ник и Хлоя покинули свой лагерь на каноэ и поплыли вниз по течению со средней скоростью 12 км/ч. Они развернулись и пошли обратно вверх по течению со средней скоростью 4 км/ч. Всего поездка заняла 1 час. Через сколько времени отдыхающие развернулись вниз по течению?
| Кто или что | Ставка | Время | Расстояние |
|---|---|---|---|
| Нижестоящий | [латекс]\текст{12 км/ч}[/латекс] | [латекс]т[/латекс] | [латекс]\текст{12 км/ч} (т)[/латекс] |
| Восходящий поток | [латекс]\текст{4 км/ч}[/латекс] | [латекс](1 — т)[/латекс] | [латекс]\текст{4 км/ч} (1 — т)[/латекс] |
Расстояние, пройденное вниз по течению, равно расстоянию, которое они прошли вверх по течению. Таким образом, уравнение, которое нужно решить:
[латекс]\begin{array}{rrlll} 12(t)&=&4(1&-&t) \\ 12t&=&4&-&4t \\ +4t&&&+&4t \\ \ hline \dfrac{16t}{16}&=&\dfrac{4}{16}&& \\ \\ t&=&0.
25&& \end{массив}[/latex]
Это означает, что туристы плыли вниз по течению 0,25 часа и 0,75 часа плыли обратно.
Терри выезжает из дома на велосипеде со скоростью 20 км/ч. Через 6 часов Салли уезжает на скутере, чтобы догнать его, двигаясь со скоростью 80 км/ч. Сколько времени ей понадобится, чтобы догнать его?
| Кто или что | Ставка | Время | Расстояние |
|---|---|---|---|
| Терри | [латекс]\текст{20 км/ч}[/латекс] | [латекс]т[/латекс] | [латекс]\текст{20 км/ч}(т)[/латекс] |
| Салли | [латекс]\текст{80 км/ч}[/латекс] | [латекс](т — \текст{6 ч})[/латекс] | [латекс]\текст{80 км/ч}(т — \текст {6 ч})[/латекс] |
Расстояние, пройденное обоими, одинаково. Следовательно, нужно решить уравнение:
[латекс]\begin{array}{rrrrr} 20(t)&=&80(t&-&6) \\ 20t&=&80t&-&480 \\ -80t&&-80t&& \\ \ hline \dfrac{-60t}{-60}&=&\dfrac{-480}{-60}&& \\ \\ t&=&8&& \end{array}[/latex]
Это означает, что Терри едет 8 часов, а Салли нужно всего 2 часа, чтобы его догнать.
Во время 130-километровой поездки автомобиль двигался со средней скоростью 55 км/ч, а затем снизил скорость до 40 км/ч до конца пути. Поездка заняла 2,5 часа. Сколько времени автомобиль ехал со скоростью 40 км/ч?
| Кто или что | Ставка | Время | Расстояние |
|---|---|---|---|
| Пятьдесят пять | [латекс]\текст{55 км/ч}[/латекс] | [латекс]т[/латекс] | [латекс]\текст{55 км/ч}(т)[/латекс] |
| Сорок | [латекс]\текст{40 км/ч}[/латекс] | [латекс](\текст{2,5 ч}-т)[/латекс] | [латекс]\текст{40 км/ч}(\текст{2,5 ч}-т)[/латекс] |
Расстояние, пройденное обоими, составляет 30 км. Таким образом, уравнение, которое нужно решить:
[латекс]\begin{array}{rrrrrrr} 55(t)&+&40(2,5&-&t)&=&130 \\ 55t&+&100&-&40t&=&130 \\ & -&100&&&&-100 \\ \hline &&&&\dfrac{15t}{15}&=&\dfrac{30}{15} \\ \\ &&&&t&=&2 \end{массив}[/latex]
Это означает, что время движения со скоростью 40 км/ч составило 0,5 часа.
Задачи расстояния, времени и скорости имеют несколько вариаций, в которых неизвестные смешиваются между расстоянием, скоростью и временем. Как правило, они включают решение задачи, в которой общее пройденное расстояние используется для равного некоторому расстоянию, или задачи, в которой расстояния, пройденные обеими сторонами, одинаковы. Эти задачи на расстояние, скорость и время будут рассмотрены позже в этом учебнике, где для их решения требуются квадратичные решения.
Для вопросов с 1 по 8 найдите уравнения, необходимые для решения задач. Не решить.
- A находится в 60 км от B. Автомобиль в A отправляется в B со скоростью 20 км/ч в то же время, что автомобиль в B отправляется в A со скоростью 25 км/ч. Сколько времени пройдет, прежде чем автомобили встретятся?
- Два автомобиля находятся на расстоянии 276 километров друг от друга и одновременно начинают двигаться навстречу друг другу. Они едут со скоростями, отличающимися на 5 км/ч. Если они встретятся через 6 ч, найдите скорость каждого из них.
- Два поезда, отправившиеся с одной станции, движутся в противоположных направлениях. Они едут со скоростями 25 и 40 км/ч соответственно. Если они стартуют одновременно, как скоро расстояние между ними составит 195 километров?
- Два курьера на велосипедах, Джерри и Сьюзен, едут в противоположных направлениях. Если Джерри едет со скоростью 20 км/ч, то с какой скоростью должна ехать Сьюзен, если через 5 часов их разделяет 150 километров?
- Пассажирский и товарный поезд одновременно отправляются навстречу друг другу из двух точек, удаленных друг от друга на 300 километров. Если скорость пассажирского поезда превышает скорость товарного поезда на 15 км/ч и они встречаются через 4 часа, то какой должна быть скорость каждого из них?
- Два автомобиля двинулись в одно и то же время в противоположных направлениях из одной и той же точки. Их скорости составляли 25 и 35 км/ч соответственно. Через сколько часов расстояние между ними составило 180 км?
- Мужчина, имея в своем распоряжении 10 часов, совершил экскурсию на велосипеде, выезжая со скоростью 10 км/ч и возвращаясь пешком со скоростью 3 км/ч. Найдите расстояние, которое он проехал.
- Человек идет со скоростью 4 км/ч. Какое расстояние он может пройти за город и вернуться обратно на тележке, движущейся со скоростью 20 км/ч, если он должен вернуться домой через 3 часа с момента старта?
Найдите расстояние, которое он проехал.Решите вопросы с 9 по 22.
- Мальчик уезжает из дома на автомобиле со скоростью 28 км/ч и возвращается обратно со скоростью 4 км/ч. Поездка туда и обратно занимает 2 часа. Как далеко он едет?
- Моторная лодка выходит из гавани и плывет со средней скоростью 15 км/ч к острову. Средняя скорость на обратном пути 10 км/ч. На каком расстоянии от гавани находился остров, если в общей сложности путешествие заняло 5 часов?
- Семья ехала на курорт со средней скоростью 30 км/ч, а затем возвращалась по той же дороге со средней скоростью 50 км/ч. Найдите расстояние до курорта, если общее время в пути составило 8 часов.
- В рамках своей летной подготовки пилот-курсант должен был долететь до аэропорта, а затем вернуться. Средняя скорость до аэропорта составила 90 км/ч, а средняя скорость обратно – 120 км/ч. Найдите расстояние между двумя аэропортами, если общее время полета составило 7 часов.
- Сэм начинает движение со скоростью 4 км/ч из лагеря на 2 часа раньше Сью, которая едет со скоростью 6 км/ч в том же направлении. Через сколько часов Сью догонит Сэма?
- Человек едет со скоростью 5 км/ч. Через 6 часов другой человек стартует с того же места, что и первый, со скоростью 8 км/ч. Когда второй человек догонит первого?
- Моторная лодка выходит из гавани и плывет со средней скоростью 8 км/ч к маленькому острову. Два часа спустя каютный катер выходит из той же гавани и движется со средней скоростью 16 км/ч к тому же острову. Через сколько часов после отплытия катер с каютами будет рядом с моторной лодкой?
- Бегун на длинные дистанции стартовал с дистанции со средней скоростью 6 км/ч. Через час второй бегун начал тот же маршрут со средней скоростью 8 км/ч. Через какое время после старта второго бегуна он догонит первого бегуна?
- Два человека едут в противоположных направлениях со скоростью 20 и 30 км/ч в одно и то же время и из одного и того же места. Через сколько часов расстояние между ними будет 300 км?
- Два поезда отправляются в одно и то же время из одного и того же места и едут в противоположных направлениях. Если скорость одного из них на 6 км/ч больше, чем скорость другого, и через 4 часа расстояние между ними составляет 168 км, какова скорость каждого из них?
- Два велосипедиста стартовали из одной точки и едут в противоположных направлениях. Один велосипедист едет в два раза быстрее другого. Через три часа их разделяет 72 километра. Найдите скорость каждого велосипедиста.
- Два маленьких самолета вылетают из одной точки и летят в противоположных направлениях. Первый самолет летит на 25 км/ч медленнее второго. Через два часа расстояние между самолетами составляет 430 километров. Найдите скорость каждого самолета.
- Во время 130-километровой поездки автомобиль ехал со средней скоростью 55 км/ч, а затем до конца пути снизил скорость до 40 км/ч. В общей сложности дорога заняла 2,5 часа. Какое время автомобиль ехал со скоростью 40 км/ч?
- Бегущий со средней скоростью 8 м/с, спринтер добежал до конца дорожки, а затем вернулся к исходной точке со средней скоростью 3 м/с. Спринтеру потребовалось 55 с, чтобы добежать до конца дорожки и вернуться назад. Найдите длину дорожки.
Средняя скорость до аэропорта составила 90 км/ч, а средняя скорость обратно – 120 км/ч. Найдите расстояние между двумя аэропортами, если общее время полета составило 7 часов.
Через сколько часов расстояние между ними будет 300 км?
Какое время автомобиль ехал со скоростью 40 км/ч?Ключ ответа 8.8
Словесные задачи «Расстояние» | Purplemath
Другие примеры
Purplemath
Что такое задача на «расстояние»?
Словесные задачи на «расстояние», часто также называемые задачами на «равномерную скорость», включают в себя что-то, движущееся с некоторой фиксированной и устойчивой («равномерной») скоростью («скорость», «скорость» или «скорость») или же движущееся с какая-то средняя скорость.
Всякий раз, когда вы читаете задачи на «как быстро», «как далеко» или «как долго», вы должны думать об уравнении расстояния, d = rt , где d обозначает расстояние, r обозначает скорость (постоянную или среднюю), а t обозначает время.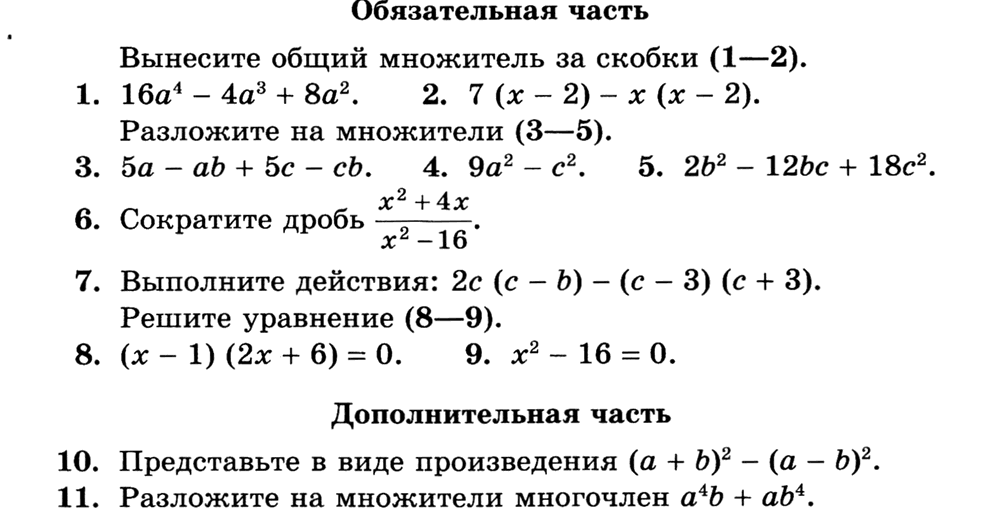
Содержание продолжается ниже
MathHelp.com
Проблемы со словами о расстоянии
Убедитесь, что единицы времени и расстояния совпадают с единицами скорости. Например, если они дают вам скорость в футах в секунду, то ваше время должно быть в секундах, а ваше расстояние должно быть в футах. Иногда они пытаются обмануть вас, используя неправильные единицы измерения, и вы должны уловить это и преобразовать в правильные единицы измерения.
Если вам интересно, этот тип упражнения требует, чтобы скорость была фиксированной и постоянной (то есть неизменной), чтобы работала формула d = rt . Единственный способ справиться со скоростью, которая может меняться, — это взять среднюю скорость за рассматриваемое время или расстояние. Работа непосредственно с изменяющимися скоростями будет чем-то, с чем вы столкнетесь в исчислении, так как это требует исчисления (или более продвинутых) методов.
В чем разница между фиксированной скоростью и средней скоростью?
Упражнение с фиксированной скоростью — это упражнение, в котором машина, скажем, всегда движется ровно шестьдесят миль в час; за три часа машина проедет 180 миль.
Упражнение на среднюю скорость — это упражнение, в котором автомобиль, скажем, в среднем разгоняется до сорока миль в час, но это среднее значение включает различные скорости, относящиеся к светофорам, шоссе и проселочным дорогам; за три часа машина прошла 120 миль, хотя скорость машины была непостоянной. Большинство упражнений, которые вы увидите, будут упражнениями с фиксированной скоростью, но, очевидно, они не очень «реальны». Это упрощение, которое они делают, чтобы сделать ситуацию возможной, используя только алгебраические методы.
Каков пример постановки и решения словесной задачи «расстояние»?
- 555-мильное 5-часовое путешествие на самолете было выполнено на двух скоростях. В первой части пути средняя скорость составляла 105 миль в час. Затем усилился попутный ветер, и оставшуюся часть пути самолет летел со средней скоростью 115 миль в час. Сколько времени самолет летел с каждой скоростью?
Существует метод подготовки и решения этих упражнений, с которым я впервые столкнулся задолго до того, как действительно выполнял их в классе.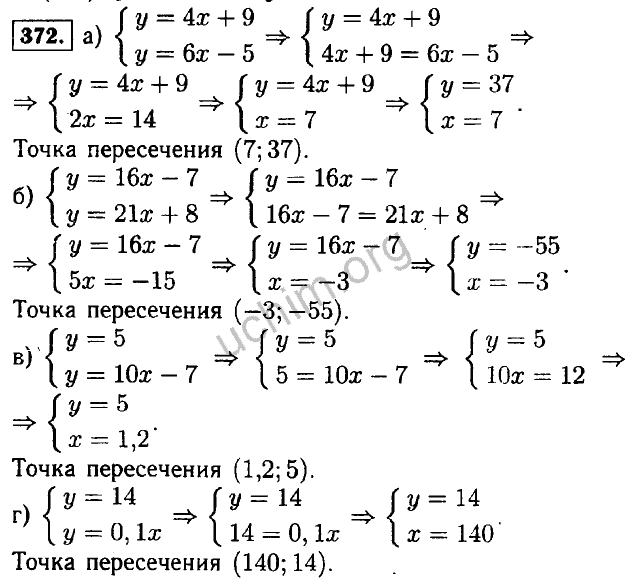
Но, как только меня познакомили с ним, я переключился, потому что это так намного проще.
Сначала я настроил сетку, столбцы которой были помечены переменными из формулы «расстояние», а строки были помечены задействованными «частями»:
В первой части самолет преодолел некоторое расстояние. Я не знаю, сколько, поэтому мне понадобится переменная для этого неизвестного значения. Я буду использовать переменную, которую они мне дали в уравнении расстояния:
Они дали мне скорость или скорость для этой части, поэтому я добавлю это в свою таблицу:
Во время этой первой части самолет некоторое время летал, но я не знаю, сколько времени это было. Поэтому мне нужна переменная для этого неизвестного значения; Я буду использовать переменную из уравнения расстояния:
Во второй части самолет преодолел оставшуюся часть общего расстояния. Я не знаю точное расстояние, которое было пройдено во время этой второй части, но я знаю, что это было «сколько бы ни осталось от 555 миль после того, как первые d миль были пройдены в первой части».
была оставлена после того, как [какая-то сумма] была изъята» выражается вычитанием: я беру сумму, о которой уже позаботились, и вычитаю ее из того, что было общей суммой. Добавляя это к моей таблице, я получаю:
Мне дали скорость или скорость для второй части, и я могу использовать то же самое «Сколько осталось?» строительство для того, чтобы было время для этой второй части. Итак, теперь моя таблица выглядит так:
Для строки «итого» я прибавляю (или беру информацию из отчета об упражнении):
Почему я не прибавляю в столбце «ставка»? Потому что я не могу добавлять ставки! В этом упражнении добавление скоростей показало бы, что средняя скорость за всю поездку составляет 105 + 115 = 220 миль в час. Но очевидно, что это не имеет смысла.
Гениальность этого табличного метода настройки заключается в том, что теперь я могу создавать уравнения из строк и столбцов. В этом упражнении есть несколько способов продолжить. Я буду работать с уравнением «расстояние», чтобы создать выражения для расстояний, пройденных в каждой части.
Умножая поперек, первая строка говорит мне, что расстояние, пройденное в первой части полета, было:
Расстояние 1-й части: 105 t вторая часть полета составила:
Вторая часть расстояния: 115(5 − t )
Я могу сложить эти два выражения частичного расстояния и установить их равными известному общему расстоянию:
105 t + 115(5 − t ) = 555
Это уравнение с одной переменной, которое я могу решить:
105 t + 115(5 − t ) = 555
105 т + 575 — 115 т = 555
575 — 10 т = 555
20 = 10 т
2 = t
Оглядываясь назад на свою таблицу, я вижу, что я определил t как время, которое самолет провел в воздухе на первой части своего пути. Оглядываясь назад на исходное упражнение, я вижу, что они хотят знать время, которое самолет провел на каждой из двух скоростей.
Теперь у меня есть время для первой части полета; время было два часа. В упражнении говорилось, что вся поездка длилась пять часов, поэтому вторая часть должна была занять три часа (получено путем вычитания времени первой части из общего времени). Они не запрашивали частичные расстояния, так что у меня есть вся необходимая информация. Мой ответ:
первая часть: 2 часа
вторая часть: 3 часа
Когда я устанавливал свое уравнение, я упомянул, что есть несколько способов действовать. Каков был другой путь? Я мог бы использовать таблицу, чтобы создать выражение для каждого из двух неполных значений времени, добавить, установить результат равным заданной сумме и решить для переменной d . Поскольку уравнение расстояния d = rt , то выражения для неполных времен будут созданы путем решения уравнения для т =. Моя работа выглядела бы так:
t = d / r
первая часть: d /105
вторая часть: (555
6 d 6 d добавление: d / 105 + (555 − d )/115 = 5 Оглядываясь назад на свою таблицу, я бы увидел, что это дает мне расстояние, пройденное за первую половину полета. Есть три вещи, которые, я надеюсь, вы усвоили из приведенного выше примера. (1) Использование таблицы или сетки для отслеживания того, что вы делаете, может быть невероятно полезным. (2) Важно четко определить ваши переменные, чтобы вы знали (к концу), что вы имели в виду (еще в начале), чтобы вы могли правильно применить свои результаты. (3) Вы должны всегда проверять исходное упражнение, чтобы быть уверенным, что отвечаете на вопрос, который они действительно задали. (Мое значение расстояния, найденное выше, правильное, но не то, что они просили.) Но самое главное вот что: НИКОГДА НЕ ПЫТАЙТЕСЬ ДОБАВЛЯТЬ ЦЕНЫ! Подумайте об этом: если вы едете со скоростью 20 миль в час по одной улице и со скоростью 40 миль в час по другой улице, значит ли это, что вы в среднем едете со скоростью 60 миль в час? Конечно, нет. Могу ли я хотя бы усреднить ставки? Если бы я ехал со скоростью 20 миль в час в течение одного часа, а затем ехал бы со скоростью 60 миль в час в течение двух часов, то я бы проехал 140 миль за три часа, или чуть меньше 47 миль в час. Но 47 — это не среднее между 20 и 60. Как видите, реальная математика, используемая для решения этого типа упражнений, часто довольно проста. Это настройка, это сложная часть. Ниже приведены еще несколько примеров, но только с показанной настройкой. Попробуйте свои силы в решении и нажмите на ссылки, чтобы получить всплывающие окна, из которых можно проверить свои уравнения и решения. Я начну обычным способом, настроив свою таблицу: Я пометил свои строки, чтобы было ясно, как они относятся к упражнению. Для летной части пути я буду использовать конструкцию «сколько осталось» вместе с заданной скоростью, чтобы заполнить вторую строку. Я также заполню итоги. Первая строка дает мне уравнение d = 30 t . Вторая строка более беспорядочна, что дает мне уравнение: 150 − d = 60(3 − t ) Отсюда я могу пойти разными путями; Думаю, я решу это второе уравнение для переменной d , а затем приравняю результаты друг к другу. 150 − d = 60(3 − t ) Приравнивая эти два выражения для d , я получаю: 30 t = 150 − 50 6 t 0 Решите для т ; интерпретировать значение; сформулируйте окончательный ответ. Оба автомобиля проехали одинаковое количество времени. Значения автомобиля выражаются в терминах значений автобуса, поэтому я буду использовать переменные для неизвестных автобуса, а затем определю автомобиль в терминах переменных автобуса. Это дает мне: (Как оказалось, на этот раз мне не понадобится строка «всего».) Это не очень полезно. Вторая строка дает мне: d = 2 r Я буду использовать второе уравнение, чтобы упростить первое уравнение, подставив «2 r » из второго уравнения вместо « d » в первом уравнении. Затем я решу уравнение для значения « r ». Наконец, мне нужно будет интерпретировать это значение в контексте упражнения, а затем я дам окончательный ответ.
23 д + 11 655 — 21 д = 12 075
2 d = 420
d = 210
Оглядываясь назад на упражнение, я бы увидел, что им нужно время, а не расстояние. Таким образом, я бы вычислил время для первой части, а затем сделал вычитание, чтобы найти время для второй части. В моей работе было бы больше шагов, но мой ответ был бы таким же.
Теперь мне нужно заполнить строки. Как и раньше, я не знаю ни расстояния, ни времени на участке, где ехал руководитель, поэтому я буду использовать переменные для этих неизвестных вместе с заданной скоростью.
150 − 60(3 − t ) = d 
