ГДЗ по Обществознанию для 7 класса рабочая тетрадь Соболева О.Б. на 5
ГДЗ по Обществознанию для 7 класса рабочая тетрадь Соболева О.Б. на 5Часто ищут
- Русский язык 7 класс
- Авторы: М.М. Разумовская, С.И. Львова, В.И. Капинос, П.А. Леканта
- Издательство: Дрофа 2014-2020
- Английский язык 7 класс Рабочая тетрадь Starlight Углубленный уровень
- Авторы: Баранова К.
 М., Дули Д., Эванс В., Копылова В., Мильруд Р.
М., Дули Д., Эванс В., Копылова В., Мильруд Р. - Издательство: Просвещение 2017
- Английский язык 7 класс Рабочая тетрадь Инновационная школа
- Авторы: Комарова Ю.А., Ларионова И.В., Билсборо К., Билсборо С.
- Издательство: Русское слово 2016
- История 7 класс Школа 2100
- Авторы: Данилов Д.
 Д., Лисейцев Д.В., Павлова Н.С., Рогожкин В.А.
Д., Лисейцев Д.В., Павлова Н.С., Рогожкин В.А. - Издательство: Баласс 2015
- Русский язык 7 класс Школа 2100
-
- Издательство: Баласс 2016
- Русский язык 7 класс
- Авторы: М.
 Т. Баранов, Т.А. Ладыженская, Л.А. Тростенцова
Т. Баранов, Т.А. Ладыженская, Л.А. Тростенцова - Издательство: Просвещение 2015-2022
- Немецкий язык 7 класс Horizonte
- Авторы: Аверин М.М., Джин Ф., Рорман Л.
- Издательство: Просвещение 2016
- Алгебра 7 класс Углубленный уровень
- Авторы: Ю.
 Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов
Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов - Издательства: Просвещение, Мнемозина 2013, 2019
- Химия 7 класс Рабочая тетрадь
- Авторы: О.С. Габриелян, Г.А. Шипарева
- Издательство: Дрофа 2015
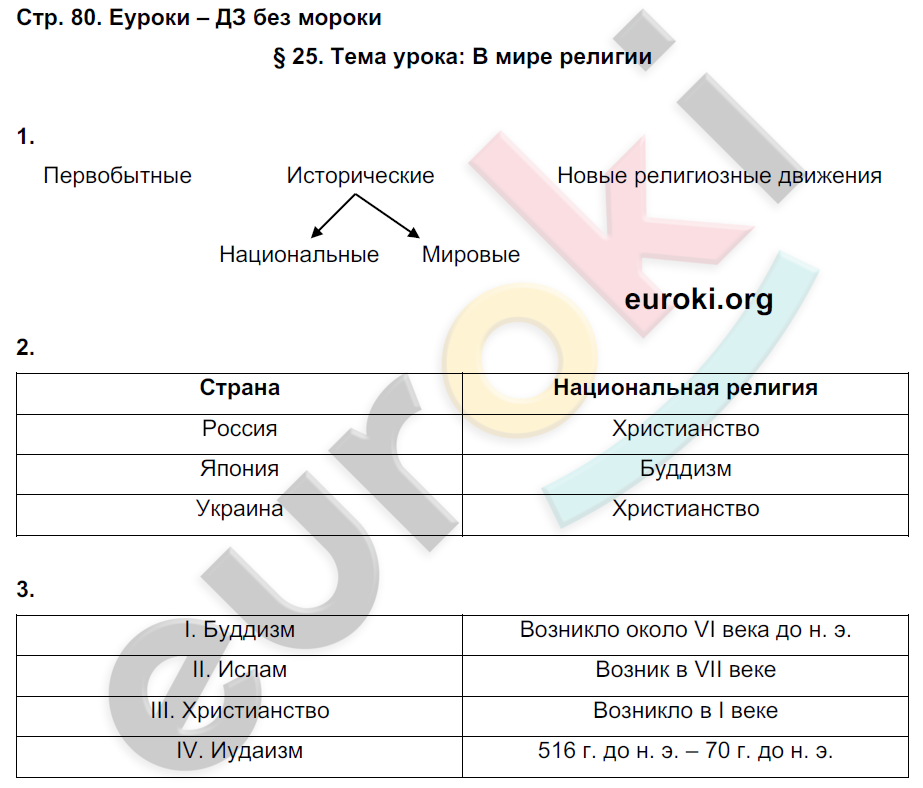
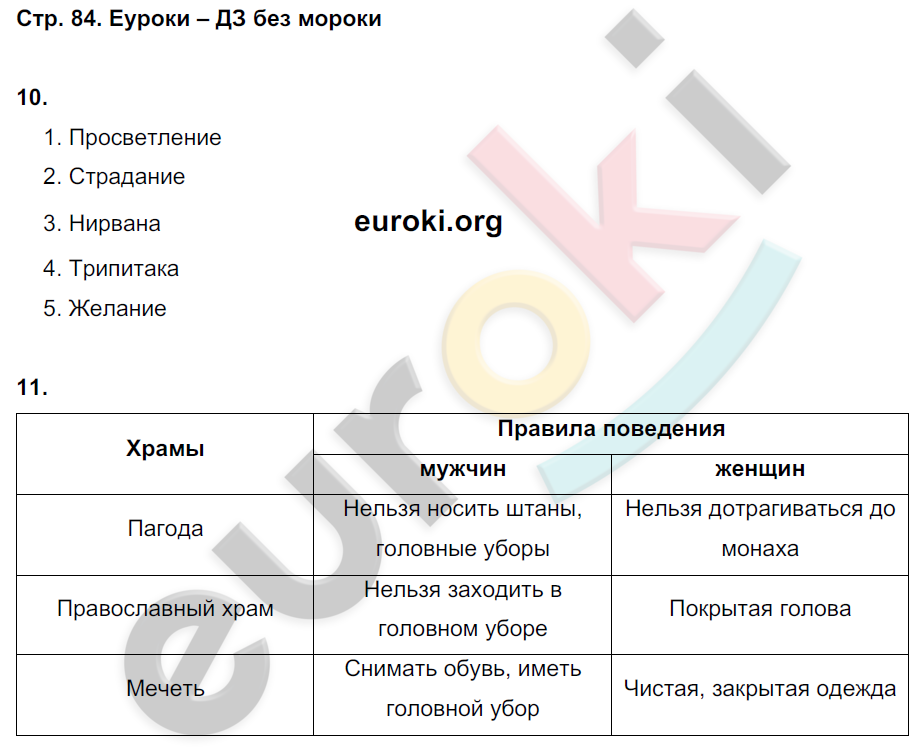
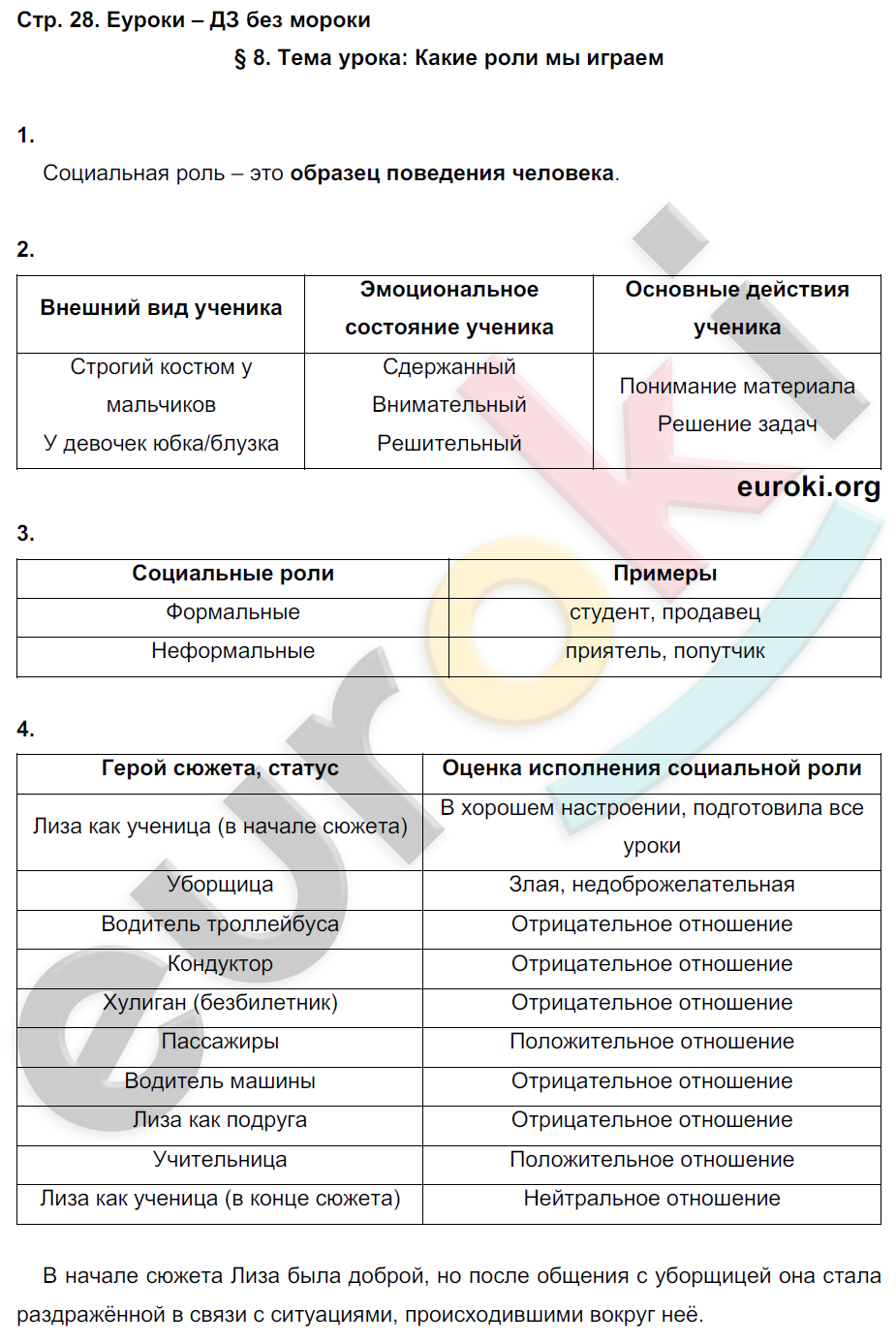
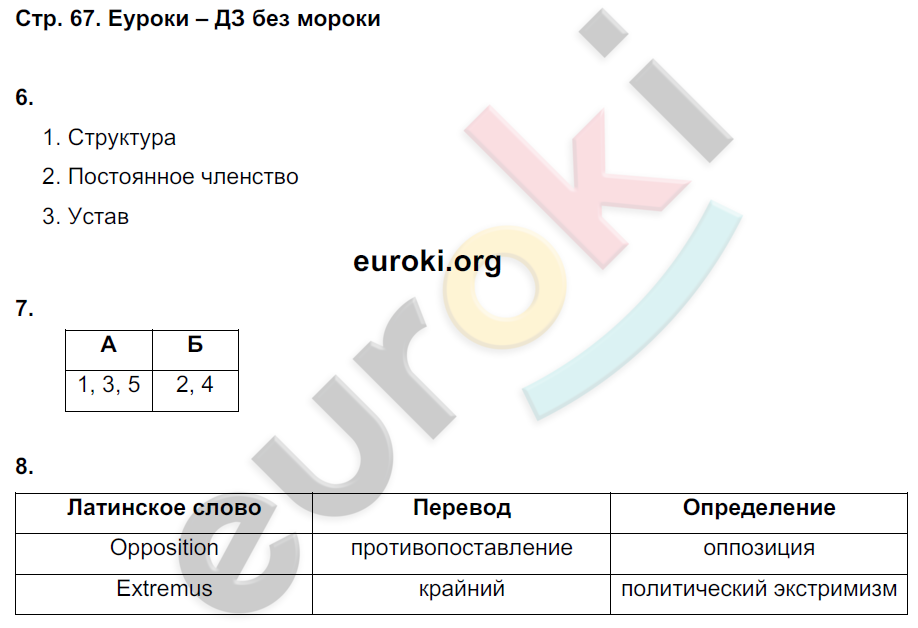
ГДЗ страница 80 обществознание 8 класс рабочая тетрадь Соболева, Воронцов – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
ГДЗ страница 80 обществознание 8 класс рабочая тетрадь Соболева, Воронцов
Подробное решение страница № 80 по обществознанию рабочая тетрадь для учащихся 8 класса Алгоритм успеха , авторов Соболева , Воронцов 2019 . ГДЗ по обществознанию 8 класс Соболева рабочая тетрадь страница — 80 .
ГДЗ по обществознанию 8 класс Соболева рабочая тетрадь страница — 80 .
Решебник по обществознанию за 8 класс авторы Соболева , Воронцов издательство Изображения обложек учебников приведены на страницах данного сайта исключительно в ГДЗ рабочая тетрадь по обществознанию 8 класс Соболева , Воронцов Вентана-Граф .
Подробный решебник (ГДЗ ) по Обществознанию за 8 (восьмой ) класс рабочая тетрадь — готовый ответ страница — 80 . Авторы учебника: Соболева , Воронцов . Издательство: Вентана-граф 2019 .
Обществоведение 8 класс . Рабочая тетрадь . Соболева , Воронцов . Вентана-Граф . Решебник к учебнику «Обществоведение 8 класс рабочая тетрадь Соболева , Воронцова » от издательства «Вентана-Граф» содержит множество ответов на все задания и упражнения .
авторы: Соболева О .Б ., Воронцов А .В . ГДЗ по обществознанию 8 класс рабочая тетрадь , авторы: , Соболева О .Б ., Воронцов А .В ., Вентана-граф 2020-2021 год .
Бесплатный решебник (ГДЗ ) к рабочей тетради по обществознанию за 8 класс , авторы: Соболева О . Б ., Воронцов А .В . авторы: Соболева О .Б ., Воронцов А .В . Страницы тетради .
Б ., Воронцов А .В . авторы: Соболева О .Б ., Воронцов А .В . Страницы тетради .
Обществознание . 8 кл . Рабочая тетрадь . (ФГОС) купить в Москве, интернет-магазин KnigiToday . Обществознание . 8 кл . Рабочая тетрадь . (ФГОС) с доставкой можно по телефону 8 (800) 201 07 36 . 8 класс . Автор . Соболева О .Б ., Воронцов А .В . Издательство .
8 класс . Рабочая тетрадь . Автор . Соболева О .Б ., Воронцов А .В . Серия . Линия УМК Соболевой . Обществознание (5-9) . Содержит вопросы и задания , составленные в соответствии с материалами учебника (авторы О .Б . Соболева, В .Н . Чайка), что существенно . .
Гдз и решебник Обществоведение 8 класс Соболева , Воронцов — Рабочая тетрадь . Также обществоведение знакомит восьмиклассников с историческими и социальными реалиями нашего общества, предлагая начальные сведения из области уголовного права, социальных структур . .
Данные гдз книг и тетрадей помогут вам проверить выполненное домашние задание . ГДЗ Путина инфо незаменимый сайт родителям, для контроля ДЗ своих детей . ГДЗ по обществознанию 8 класс Хромова рабочая тетрадь . (голосов: 77, в среднем: 4,01 из 5) .
ГДЗ по обществознанию 8 класс Хромова рабочая тетрадь . (голосов: 77, в среднем: 4,01 из 5) .
Соболева О . Б ., Воронцов А . В . Школьный класс . 8 . Количество страниц . 96 . Год издания . 2020 . Автор . Соболева О . Б . Тип обложки .
Авторы: Соболева О .Б ., Воронцов А .В . Выполнения заданий за 8 класс по Обществознанию Соболева О .Б ., Воронцов А .В . рабочая тетрадь , от издательства: Вентана-граф 2019 ФГОС , не простое занятие, поэтому ГДЗ поможем Вам сверить ответы к заданиям .
Книга Соболева О .Б . «, Воронцов А .В . Обществознание . 8 класс . Рабочая тетрадь » — купить сегодня c доставкой и гарантией по выгодной цене . Соболева О .Б . «, Воронцов А .В . Обществознание . 8 класс . Рабочая тетрадь»: характеристики, фото, магазины поблизости на . .
Здесь вы найдете рабочая тетрадь по Обществознанию 8 класса авторы: Соболева О .Б ., Воронцов А .В ., от издательства ГДЗ содержит все ответы на вопросы и поможет Вам правильно выполнить домашнее задание . ГДЗ к учебнику по обществознанию за 8 класс . .
ГДЗ к учебнику по обществознанию за 8 класс . .
8 класс . Соболева О .Б ., Воронцов А .В . 2020 Возврат денежных средств Клиенту осуществляется в течение 5-7 рабочих дней . Товар должен быть возвращен в полной комплектации, со всеми упаковками и наклейками, в непоношенном/неиспользованном виде .
Подробное решение страница № 80 по обществознанию рабочая тетрадь для учащихся 8 класса Алгоритм успеха , авторов Соболева , Воронцов 2019 . ГДЗ по обществознанию 8 класс Соболева рабочая тетрадь страница — 80 .
Решебник по обществознанию за 8 класс авторы Соболева , Воронцов издательство Изображения обложек учебников приведены на страницах данного сайта исключительно в ГДЗ рабочая тетрадь по обществознанию 8 класс Соболева , Воронцов Вентана-Граф .
Подробный решебник (ГДЗ ) по Обществознанию за 8 (восьмой ) класс рабочая тетрадь — готовый ответ страница — 80 . Авторы учебника: Соболева , Воронцов . Издательство: Вентана-граф 2019 .
Обществоведение 8 класс . Рабочая тетрадь . Соболева , Воронцов . Вентана-Граф . Решебник к учебнику «Обществоведение 8 класс рабочая тетрадь Соболева , Воронцова » от издательства «Вентана-Граф» содержит множество ответов на все задания и упражнения .
Рабочая тетрадь . Соболева , Воронцов . Вентана-Граф . Решебник к учебнику «Обществоведение 8 класс рабочая тетрадь Соболева , Воронцова » от издательства «Вентана-Граф» содержит множество ответов на все задания и упражнения .
авторы: Соболева О .Б ., Воронцов А .В . ГДЗ по обществознанию 8 класс рабочая тетрадь , авторы: , Соболева О .Б ., Воронцов А .В ., Вентана-граф 2020-2021 год .
Бесплатный решебник (ГДЗ ) к рабочей тетради по обществознанию за 8 класс , авторы: Соболева О .Б ., Воронцов А .В . авторы: Соболева О .Б ., Воронцов А .В . Страницы тетради .
Обществознание . 8 кл . Рабочая тетрадь . (ФГОС) купить в Москве, интернет-магазин KnigiToday . Обществознание . 8 кл . Рабочая тетрадь . (ФГОС) с доставкой можно по телефону 8 (800) 201 07 36 . 8 класс . Автор . Соболева О .Б ., Воронцов А .В . Издательство .
8 класс . Рабочая тетрадь . Автор . Соболева О .Б ., Воронцов А .В . Серия . Линия УМК Соболевой . Обществознание (5-9) . Содержит вопросы и задания , составленные в соответствии с материалами учебника (авторы О . Б . Соболева, В .Н . Чайка), что существенно . .
Б . Соболева, В .Н . Чайка), что существенно . .
Гдз и решебник Обществоведение 8 класс Соболева , Воронцов — Рабочая тетрадь . Также обществоведение знакомит восьмиклассников с историческими и социальными реалиями нашего общества, предлагая начальные сведения из области уголовного права, социальных структур . .
Данные гдз книг и тетрадей помогут вам проверить выполненное домашние задание . ГДЗ Путина инфо незаменимый сайт родителям, для контроля ДЗ своих детей . ГДЗ по обществознанию 8 класс Хромова рабочая тетрадь . (голосов: 77, в среднем: 4,01 из 5) .
Соболева О . Б ., Воронцов А . В . Школьный класс . 8 . Количество страниц . 96 . Год издания . 2020 . Автор . Соболева О . Б . Тип обложки .
Авторы: Соболева О .Б ., Воронцов А .В . Выполнения заданий за 8 класс по Обществознанию Соболева О .Б ., Воронцов А .В . рабочая тетрадь , от издательства: Вентана-граф 2019 ФГОС , не простое занятие, поэтому ГДЗ поможем Вам сверить ответы к заданиям .
Книга Соболева О . Б . «, Воронцов А .В . Обществознание . 8 класс . Рабочая тетрадь » — купить сегодня c доставкой и гарантией по выгодной цене . Соболева О .Б . «, Воронцов А .В . Обществознание . 8 класс . Рабочая тетрадь»: характеристики, фото, магазины поблизости на . .
Б . «, Воронцов А .В . Обществознание . 8 класс . Рабочая тетрадь » — купить сегодня c доставкой и гарантией по выгодной цене . Соболева О .Б . «, Воронцов А .В . Обществознание . 8 класс . Рабочая тетрадь»: характеристики, фото, магазины поблизости на . .
Здесь вы найдете рабочая тетрадь по Обществознанию 8 класса авторы: Соболева О .Б ., Воронцов А .В ., от издательства ГДЗ содержит все ответы на вопросы и поможет Вам правильно выполнить домашнее задание . ГДЗ к учебнику по обществознанию за 8 класс . .
8 класс . Соболева О .Б ., Воронцов А .В . 2020 Возврат денежных средств Клиенту осуществляется в течение 5-7 рабочих дней . Товар должен быть возвращен в полной комплектации, со всеми упаковками и наклейками, в непоношенном/неиспользованном виде .
ГДЗ часть 2. упражнение 137 русский язык 4 класс рабочая тетрадь Климанова, Бабушкина
ГДЗ часть 1 7 русский язык 3 класс Каленчук, Чуракова
ГДЗ unit 2 7 английский язык 9 класс Enjoy English Биболетова, Бабушис
ГДЗ часть 1 / что узнали. чему научились / задания на страницах 69-73 20 математика 4 класс Моро, Бантова
чему научились / задания на страницах 69-73 20 математика 4 класс Моро, Бантова
ГДЗ номер 47 биология 9 класс рабочая тетрадь Пасечник, Швецов
ГДЗ упражнение 582 русский язык 3 класс Рамзаева
ГДЗ § 27 4 алгебра 8 класс задачник Мордкович, Звавич
ГДЗ часть 1 77 окружающий мир 3 класс Плешаков, Крючкова
ГДЗ часть 1. задание 174 математика 3 класс рабочая тетрадь Захарова, Юдина
ГДЗ номер 649 алгебра 9 класс Макарычев, Миндюк
ГДЗ по математике 4 класс рабочая тетрадь Устный счет Рудницкая Решебник
ГДЗ страница 30 немецкий язык 5 класс рабочая тетрадь Wunderkinder Яцковская
ГДЗ вариант 4. тест 30 математика 6 класс тематические тесты Чулков, Шершнев
ГДЗ § 5. Металлургия. География черной металлургии 1 география 9 класс Дронов, Баринова
ГДЗ природа Земли 37 география 7 класс мой тренажёр Николина
ГДЗ страница 75 история 6 класс рабочая тетрадь Кочегаров
ГДЗ § 39 16 алгебра 8 класс задачник Мордкович, Звавич
ГДЗ упражнение 192 русский язык 4 класс Соловейчик, Кузьменко
ГДЗ §21 21. 22 алгебра 10‐11 класс Учебник, Задачник Мордкович, Семенов
22 алгебра 10‐11 класс Учебник, Задачник Мордкович, Семенов
ГДЗ часть 1. упражнение 186 русский язык 4 класс Полякова
ГДЗ unit 3 / lesson 6 3 английский язык 6 класс рабочая тетрадь Кузовлев, Лапа
ГДЗ страница 15 английский язык 5 класс рабочая тетрадь Комарова, Ларионова
ГДЗ самостоятельная работа №2 / вариант 2 5 алгебра 7 класс дидактические материалы, к учебнику Мордкович Попов
ГДЗ номер 949 математика 5 класс Дорофеев, Шарыгин
ГДЗ вариант 1 113 алгебра 9 класс дидактические материалы Мерзляк, Полонский
ГДЗ вправа 44 алгебра 8 класс Кравчук, Пидручна
ГДЗ номер 488 алгебра 9 класс Алимов, Колягин
ГДЗ часть 2 114 математика 4 класс ИстоминаБ
ГДЗ упражнение 238 русский язык 7 класс Львова, Львов
ГДЗ упражнение 32 русский язык 7 класс рабочая тетрадь Ларионова
ГДЗ тетрадь 1 86 математика 5 класс рабочая тетрадь Лебединцева, Беленкова
ГДЗ Song Sheets / Module 7 2 английский язык 11 класс spotlight Эванс, Дули
ГДЗ § / § 21 11 математика 4 класс Муравин, Муравина
ГДЗ вправа 615 математика 5 класс Истер
ГДЗ часть 2 19 информатика 4 класс Горячев, Горина
ГДЗ номер 1359 математика 6 класс Мерзляк, Полонский
ГДЗ глава 2 / подготовка к экзамену 17 алгебра 10 класс дидактические материалы Шабунин, Ткачева
ГДЗ упражнение 707 русский язык 7 класс Львова, Львов
ГДЗ страница 56 география 7 класс рабочая тетрадь Румянцев, Ким
ГДЗ § 13 13. 16 физика 7 класс задачник Генденштейн, Кирик
16 физика 7 класс задачник Генденштейн, Кирик
ГДЗ § 20 20.45 алгебра 8 класс Мерзляк, Поляков
ГДЗ упражнение 61 алгебра 9 класс Мерзляк, Полонский
ГДЗ страница 11 история 6 класс рабочая тетрадь Артасов, Данилов
ГДЗ упражнение 13 русский язык 9 класс Бархударов, Крючков
ГДЗ урок 33 литература 6 класс рабочая тетрадь Соловьева
ГДЗ часть 1 / страница 34 1 математика 1 класс Моро, Волкова
ГДЗ unit 8 / vocabulary activator 1 английский язык 10 класс рабочая тетрадь forward Вербицкая, Уайт
ГДЗ самостоятельная работа / вариант 1 272 математика 6 класс дидактические материалы Чесноков, Нешков
ГДЗ часть №1 / номер 72 русский язык 2 класс Канакина, Горецкий
ГДЗ тест 6. вариант 2 русский язык 11 класс контрольно-измерительные материалы Егорова
ГДЗ По Математике 6 Класс 629
ГДЗ Горецкий 2 Кл
Решебник Русский Язык В П Канакина
ГДЗ Русский Язык 4 Класс Упражнение 24
ГДЗ упражнение 701 русский язык 5 класс Ладыженская, Баранов
Математика | Бесплатный полнотекстовый | Существование решения и управляемость нелинейной дробно-интегро-дифференциальной системы с запаздыванием соболевского типа 2,3,4,5,6,7]).
 Проблемы управляемости для различных видов динамических систем изучались несколькими авторами (см. [8,9,10,11,12,13,14,15]) и ссылками в них. Таким образом, динамические системы должны трактоваться более слабым понятием управляемости, а именно приближенной управляемостью (см. [16,17,18,19,20,21]). Однако до настоящего времени не сообщалось о работе по нулевой управляемости нелинейной интегро-дифференциальной системы с дробным запаздыванием соболевского типа с импульсным условием порядка 1
Проблемы управляемости для различных видов динамических систем изучались несколькими авторами (см. [8,9,10,11,12,13,14,15]) и ссылками в них. Таким образом, динамические системы должны трактоваться более слабым понятием управляемости, а именно приближенной управляемостью (см. [16,17,18,19,20,21]). Однако до настоящего времени не сообщалось о работе по нулевой управляемости нелинейной интегро-дифференциальной системы с дробным запаздыванием соболевского типа с импульсным условием порядка 12. Предварительные занятия
Пусть L(X) — банахово пространство всех ограниченных линейных операторов из X в X, снабженное нормой ∥·∥L(X), и пусть C(J,X) — банахово пространство всех непрерывных функций из J в X. X с нормой ∥·∥C(J,X).
Основные аксиомы относительно β следующие:
- (A)
Если x:(−∞,T]→X,T>0 — непрерывная функция на J и x0∈β, то для любого t∈ J выполняются следующие условия:
- (i)
xtentaβ,
- (II)
∥x (T) ∥x≤h∥xt∥β,
- (III)
∥xt∥ββдель. K(t)sup{∥x(s)∥X:0≤s≤t}+N(t)∥x0∥β,
, где H≥0 — константа, K:[0,+∞) →[0,+∞) непрерывна, N(·):[0,+∞)→[0,+∞) локально ограничена и K(·), N(·) не зависят от x(·).
- (B)
Для функции x(·) в (A) t→xt является непрерывной функцией при t∈[0,T].
- (К)
Пространство β заполнено.
Для получения наших результатов предположим, что абстрактная дробно-интегро-дифференциальная задача
имеет ассоциированный q-резольвентный оператор ограниченного линейного оператора (Rq(t))t≥0 на X.
Операторы A:D(A)⊂X→X и µ:D(µ)⊂X→X удовлетворяют условию следующие гипотезы:
- (I)
A и µ — замкнутые линейные операторы,
- (II)
D(µ)⊂D(A) и µ биективен,
- (III)
µ−1:X→D(µ) непрерывна.
Здесь из (I) и (II) вместе с теоремой о замкнутом графике следует ограниченность линейного оператора Aµ−1:X→X. Кроме того, Aµ−1 порождает сильно непрерывную полугруппу связанных линейных операторов в X.
В этой статье мы рассмотрели следующие условия.
(P1) Оператор Aµ−1:D(Aµ−1)⊂X→X является замкнутым линейным оператором с плотным в X [D(Aµ−1)].
Пусть q∈(1,2). Для некоторого ϕ0∈(0,π2] для каждого ϕ<ϕ0 существует положительная константа c0=c0(ϕ) такая, что λ∈ρ(Aµ−1) для каждого λ∈∑0,q,ν={λ ∈C;λ≠0,|arg(λ)|
∥A1(t)x∥≤b0(t)∥x∥ для всех t>0 и x∈D(A). Более того, оператор
A1˜:∑0,π2→L([D(A)],X) имеет аналитическое продолжение на ∑0,ν такое, что
∥A1˜(λ)x∥ ≤∥A1˜(λ)∥∥x∥ для всех x∈D(A) и ∥A1˜(λ)∥=O(1λ) при |λ|→∞.

(P3) Существуют плотное в [D(A)] подпространство D⊆D(A) и положительная константа c1 такие, что A(D)⊆D(A),A1˜(λ)(D) ⊆D(A) и
∥AA1˜(λ)x∥≤c1∥x∥ для каждого x∈D для всех λ∈∑0,ν.
Для τ>0 и θ∈(π2,ν) тогда ∑τ,θ={λ∈C;λ≠0,|λ|>τ,|arg(λ)|<θ}.
Для Γτ,θ,Γτ,θi,i=1,2,3 пути
Определим теперь семейство операторов (Rq(t))t≥0 посредством
3. Существование решения
В этом разделе мы исследуем существование мягкого решения соболевского типа интегро-дифференциального уравнения дробного порядка с конечным импульсивные состояния в следующем виде:
где состояние x принимает значения в банаховом пространстве X,A, µ и (γ(t))t∈J — замкнутые линейные операторы на X,cD0q представляют производную Капуто порядка q∈(1,2). Для установления В результате нам понадобятся следующие гипотезы: Кроме того, существует константа LS>0 такая, что ∥ϱ(s)∥≤LS Мы хотим доказать, что оператор ψ имеет неподвижную точку. Сначала покажем, что ψ отображает Br в себя. Для x∈Br, Таким образом, ψ отображает Br в себя. Далее докажем, что ψ является сжатием на Br Для m,n∈Br получаем Тогда ψ — сжимающее отображение на Br. Далее мы докажем, что ψ вполне непрерывна. ∞ Поскольку функции γ,F и G непрерывны, т. е. при n→∞ выполняются следующие условия: Следовательно, ψ непрерывна. Далее мы покажем, что (ψx)(t) эквинепрерывна на J для любого x∈Br. Пусть 0 Известно, что правая часть (5) стремится к нулю при ϵ→0. Следовательно, (ψx)(t) вполне непрерывна на J. По теореме о неподвижной точке ψ имеет единственную неподвижную точку x(t) на J. Следовательно, система (3) имеет единственное мягкое решение на J. Установим набор достаточных условий приближенной управляемости дробно-дифференциального уравнения с импульсным запаздыванием в следующем виде: где функция управления u(·)∈L2(J,U), банахово пространство допустимых функций управления, где U банахово пространство, а B линейный ограниченный оператор из U в X. Для изучения приближенной управляемости для системы (6), введем следующую линейно-дробную дифференциальную систему: Определим операторы, связанные с (6), следующим образом: Пусть x(T,x0,u) — значение состояния (6) в терминальном состоянии T, соответствующее управлению u и начальному значению x0. Для установления результата нам понадобится следующее дополнение. Мы хотим доказать, что оператор ψ* имеет неподвижную точку. Тогда эта неподвижная точка является мягким решением системы (6). Покажем, что ψ* отображает Br в себя, x∈Br, Таким образом, ψ* отображает Br в себя. Далее, для x,y∈Br получаем Это означает, что Тогда ψ* является сжимающим отображением и, следовательно, существует единственная неподвижная точка x∈Br такая, что ψ*x(t)=x(t). Следовательно, любая неподвижная точка ψ* является мягким решением (6) на J. F:J×X×X→X,G:J×X→X равномерно ограничены, а резольвентный оператор Rq и компактные операторы Sq , то система (6) приближенно управляема на J. В этом разделе мы исследуем точную нулевую управляемость дробно-нелинейного дифференциального уравнения системы (6). Для изучения точной нулевой управляемости уравнения (6) рассмотрим дробно-линейную систему связанные с системой (6). Определим оператор L0Tu=∫0Tµ−1Sq(T−s)Bu(s)ds:L2(J,U)→X,u∈L2(J,U), где L0Tu имеет ограниченный обратный оператор (L0) −1 со значениями в L2(J,U)/ker(L0T) и N0T(x0,F,G)=µ−1Rq(T)x0+∫0Tµ−1Sq(T−s)[G(s) +F(s)]ds:X×L2(J,U)→X. В этом разделе нам понадобится следующее предположение. Теперь мы можем сформулировать и доказать наши основные результаты. Шаг 1 . Управление u(·)=−H(x0,F,G) ограничено на Br. Действительно, Шаг 2 . Существуют r>0 такие, что φ переводит Br в себя. Если x(t)∈Br,t∈[0,T], имеем Следовательно, φ отображает Br в себя. Шаг 3 . Докажем непрерывность (φx)(t) на J для любого x∈X. Пусть 0 Ясно, что из непрерывности операторов Rq и Sq правая часть (15) стремится к нулю при ϵ→0. Следовательно, (φx)(t) непрерывна на [0,T]. Шаг 4 . Докажем, что (φx)(t) — сжатие на X. Пусть x,y∈X для t∈(0,T] фиксированы, тогда Следовательно, φ является сужением на C(J,X). По теореме Банаха о неподвижной точке φ имеет единственную неподвижную точку. Следовательно, система (6) является точной нуль-управляемой на J. Рассмотрим следующее уравнение в частных производных с дробным запаздыванием дробного порядка: cD0qt[v(t,x)−vxx(t,x)+K1(t−τ,v(t−τ,x))]=∂2∂x2v(t,x)+ξ(t,x )+K2(t−τ,v(t−τ,x))+∫0t(t−s)2e−ρ(t−s)∂2∂x2v(s,x)ds,0≤x≤π, t∈J,v(t,0)=v(t,π)=0,t∈J,v(t,x)=ϕ(t,x),t∈J,0≤x≤πv(tk+, х)−v(tk−,x)=Ikv(tk,x),k=1,2,…m, (16) где cD0qt — дробная производная Капуто порядка 1 где каждая область D(A) и D(µ) задается {v∈X:v,vx абсолютно непрерывны, vxx∈X,v(0)=v(π)=0}. Тогда A и μ можно записать соответственно как: Оператор Aµ−1 является самосопряженным и имеет собственные значения λn=−n2π2,n∈N с соответствующими нормированными собственными векторами en(ξ)=2sin(nπξ). Определим ограниченный оператор B:U→X как Bu=χ(t,y),0≤y≤π,u∈U. Кроме того, мы определяем следующие функции: Кроме того, Теперь условия (h2)–(h4) и (H5) выполнены. Следовательно, все условия теорем 2 и 3 выполнены и Таким образом, уравнение в частных производных с дробным запаздыванием с импульсным условием (16) приближенно управляемо на J. В работе была рассмотрена нелинейная интегро-дифференциальная система с дробным запаздыванием типа Соболева с импульсным условием. Перейти к основному содержанию Скачать книгу PDF Неравенства Харди на однородных группах Скачать книгу PDF Департамент математики Имперского колледжа Лондона, Великобритания; Кафедра математики: анализа, логики и дискретной математики, Гентский университет, Гент, Бельгия; Школа математических наук Лондонского университета королевы Марии, Лондон, Великобритания Посмотреть публикации автора Вы также можете искать этого автора в
пабмед
Google Scholar Кафедра математики, Назарбаев Университет, Астана, Казахстан Посмотреть публикации автора Вы также можете искать этого автора в
пабмед
Google Scholar Представляет пошаговое руководство по методам основных функциональных неравенств с точки зрения однородных групп Фолланда и Штейна (Ли), а также для приложений таких методов. Направлен на сбор идей, лежащих в основе неравенств типа Харди для общих однородных групп, в форме, доступной для всех, кто имеет базовый уровень понимания анализа Обеспечивает автономное освещение элементов традиционного и современного анализа однородных групп Ли и не требует предыдущего знания теории Ли Подробный отчет о последних разработках в области анизотропных функциональных неравенств и их связи с потенциальными и другими свойствами операторов Часть серии книг: Прогресс в математике (PM, том 327) 52 тыс. обращений 45
Цитаты 4
Альтметрика ‘)
var head = document. Страницы i-xvi PDF Страницы 1-10Открытый доступ PDF Страницы 11-70Открытый доступ PDF Страницы 71-127Открытый доступ PDF Страницы 129-189Открытый доступ PDF Страницы 191-235Открытый доступ PDF Страницы 237-269Открытый доступ PDF Страницы 271-329Открытый доступ PDF Страницы 331-372Открытый доступ PDF Страницы 373-388Открытый доступ PDF Страницы 389-403Открытый доступ PDF Страницы 405-450Открытый доступ PDF Страницы 451-500Открытый доступ PDF Страницы 501-543Открытый доступ PDF Страницы 545-571 PDF Наверх Эта книга с открытым доступом содержит подробное рассмотрение неравенств Харди и близких к ним тем с точки зрения однородных групп Фолланда и Штейна (Ли). Место, где встречаются неравенства Харди и однородные группы, представляет собой прекрасную область математики, связанную со многими другими предметами. При описании общей теории Харди, Реллиха, Каффарелли-Кона-Ниренберга, Соболева и других неравенств в контексте общих однородных групп авторы особое внимание уделяют специальному классу стратифицированных групп. Эта монография является лауреатом Премии Феррана Суньера и Балагера 2018 года, престижной награды за книги описательного характера, представляющие последние разработки в активной области исследований в области математики. Как можно засвидетельствовать как обладатель такой награды, это жизненно важный вклад в аналитическую литературу не только потому, что в ней представлен подробный отчет о последних достижениях в этой области, но и потому, что книга доступна для всех с базовым уровнем знаний. понимания анализа. Студенты бакалавриата и магистратуры, а также исследователи из любой области математических и физических наук, связанных с анализом функциональных неравенств или анализом однородных групп, найдут этот текст полезным для углубления своего понимания. Наверх История xt:(−∞,0]→X, заданная формулой xt(θ)=x(t+θ), принадлежит некоторому абстрактному фазовому пространству β, определенному позже, F,G и Ik — соответствующие функции, 0
История xt:(−∞,0]→X, заданная формулой xt(θ)=x(t+θ), принадлежит некоторому абстрактному фазовому пространству β, определенному позже, F,G и Ik — соответствующие функции, 0
4. Приближенная управляемость
 Обозначим через R(T,x0)=x(T,x0,u):u∈L2(J,U) множество достижимости системы (6) в терминальный момент времени T, ее замыкание в X обозначим через R(T, x0)¯
Обозначим через R(T,x0)=x(T,x0,u):u∈L2(J,U) множество достижимости системы (6) в терминальный момент времени T, ее замыкание в X обозначим через R(T, x0)¯ 5.
 Точная нулевая управляемость
Точная нулевая управляемость
6. Приложение
7. Выводы
 Используя дробное исчисление и теоремы о неподвижной точке с резольвентным оператором, мы доказали существование мягкого решения для нелинейной интегро-дифференциальной системы с дробным запаздыванием соболевского типа с импульсным условием. Кроме того, установлены необходимые условия приближенной управляемости и нулевой управляемости нелинейной интегро-дифференциальной системы с дробным запаздыванием соболевского типа с импульсным условием. В конце мы предоставили пример в дробном интегро-частном дифференциальном уравнении, чтобы проиллюстрировать наши результаты.
Используя дробное исчисление и теоремы о неподвижной точке с резольвентным оператором, мы доказали существование мягкого решения для нелинейной интегро-дифференциальной системы с дробным запаздыванием соболевского типа с импульсным условием. Кроме того, установлены необходимые условия приближенной управляемости и нулевой управляемости нелинейной интегро-дифференциальной системы с дробным запаздыванием соболевского типа с импульсным условием. В конце мы предоставили пример в дробном интегро-частном дифференциальном уравнении, чтобы проиллюстрировать наши результаты. Неравенства Харди на однородных группах: 100 лет неравенств Харди
Авторы:
 Кроме того, в этой книге показано, что эти методы иногда дают новые результаты даже в классических (евклидовых) случаях
Кроме того, в этой книге показано, что эти методы иногда дают новые результаты даже в классических (евклидовых) случаях Секции
 getElementsByTagName(«head»)[0]
var script = document.createElement(«сценарий»)
script.type = «текст/javascript»
script.src = «https://buy.springer.com/assets/js/buybox-bundle-abe5f44a67.js»
script.id = «ecommerce-scripts-» + метка времени
head.appendChild (скрипт)
var buybox = document.querySelector(«[data-id=id_»+ метка времени +»]»).parentNode
var сейчас = новая дата().getTime()
вар начало = 1650956400000
вар конец = 1652338800000
var isMeasuringTime = сейчас > начать && сейчас -1
;[].slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) {
var toggle = option.querySelector(priceNS + «.buying-option-price»)
var form = option.querySelector(«.форма-варианта-покупки»)
var priceInfo = option.
getElementsByTagName(«head»)[0]
var script = document.createElement(«сценарий»)
script.type = «текст/javascript»
script.src = «https://buy.springer.com/assets/js/buybox-bundle-abe5f44a67.js»
script.id = «ecommerce-scripts-» + метка времени
head.appendChild (скрипт)
var buybox = document.querySelector(«[data-id=id_»+ метка времени +»]»).parentNode
var сейчас = новая дата().getTime()
вар начало = 1650956400000
вар конец = 1652338800000
var isMeasuringTime = сейчас > начать && сейчас -1
;[].slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) {
var toggle = option.querySelector(priceNS + «.buying-option-price»)
var form = option.querySelector(«.форма-варианта-покупки»)
var priceInfo = option. querySelector(priceNS + «.price-info»)
если (allOptionsInitiallyCollapsed || узкаяBuyboxArea && индекс > 0) {
toggle.setAttribute («ария-расширенная», «ложь»)
form.hidden = «скрытый»
priceInfo.hidden = «скрытый»
} еще {
переключить.щелчок()
}
})
}
начальное состояниеОткрыть()
если (window.buyboxInitialized) вернуть
window.buyboxInitialized = истина
initKeyControls()
если (window.fetch && isMeasuringTime) {
var свернутый = buybox.querySelector(«.buying-option.expanded») === ноль
var metricsAppendix = «»
metricsAppendix += «&discount=» + (buybox.querySelector(«.
querySelector(priceNS + «.price-info»)
если (allOptionsInitiallyCollapsed || узкаяBuyboxArea && индекс > 0) {
toggle.setAttribute («ария-расширенная», «ложь»)
form.hidden = «скрытый»
priceInfo.hidden = «скрытый»
} еще {
переключить.щелчок()
}
})
}
начальное состояниеОткрыть()
если (window.buyboxInitialized) вернуть
window.buyboxInitialized = истина
initKeyControls()
если (window.fetch && isMeasuringTime) {
var свернутый = buybox.querySelector(«.buying-option.expanded») === ноль
var metricsAppendix = «»
metricsAppendix += «&discount=» + (buybox.querySelector(«. Цена-кампания-покупки-варианта»).className.indexOf(«со скидкой») !== -1).toString()
metricsAppendix += «&metricsGroup=» + кампанияPricesMetricsGroup
metricsAppendix += «&collapsed=» +collapsed.toString()
window.fetch(«https://test-buckets.springer.com/log?v3&time=» + сейчас + приложение metrics)
.затем (функция (разрешение) {
вернуть рез.текст()
})
.поймать (функция () {
})
}
})()
Цена-кампания-покупки-варианта»).className.indexOf(«со скидкой») !== -1).toString()
metricsAppendix += «&metricsGroup=» + кампанияPricesMetricsGroup
metricsAppendix += «&collapsed=» +collapsed.toString()
window.fetch(«https://test-buckets.springer.com/log?v3&time=» + сейчас + приложение metrics)
.затем (функция (разрешение) {
вернуть рез.текст()
})
.поймать (функция () {
})
}
})() Содержание (13 глав)
Искать в книге Front Matter
Введение
Глава 1 Анализ однородных групп
Глава 2.
 Неравенства Харди на однородных группах
Неравенства Харди на однородных группах Глава 3. Неравенства типа Реллиха, Каффарелли–Кона–Ниренберга и Соболева
Глава 4. Дробные неравенства Харди
Глава 5.
 Интегральные неравенства Харди на однородных группах
Интегральные неравенства Харди на однородных группах Глава 6 Горизонтальные неравенства в стратифицированных группах
Глава 7 Неравенства Харди–Реллиха и фундаментальные решения
Глава 8.
 Геометрические неравенства Харди на стратифицированных группах
Геометрические неравенства Харди на стратифицированных группах Глава 9Соотношения неопределенностей на однородных группах.
Глава 10 Функциональные пространства на однородных группах
Глава 11 Элементы потенциальной теории стратифицированных групп
Глава 12.
 Неравенства Харди и Реллиха для сумм квадратов векторных полей
Неравенства Харди и Реллиха для сумм квадратов векторных полей Back Matter
Об этой книге
 В этой среде теория неравенств Харди запутанным образом переплетается со свойствами сублапласианов и субэллиптических уравнений в частных производных. Эти темы составляют ядро этой книги, и они дополняются дополнительными, тесно связанными темами, такими как принципы неопределенности, функциональные пространства на однородных группах, теория потенциала для стратифицированных групп и теория потенциала для общих сумм квадратов Хёрмандера и их фундаментальных решений. .
В этой среде теория неравенств Харди запутанным образом переплетается со свойствами сублапласианов и субэллиптических уравнений в частных производных. Эти темы составляют ядро этой книги, и они дополняются дополнительными, тесно связанными темами, такими как принципы неопределенности, функциональные пространства на однородных группах, теория потенциала для стратифицированных групп и теория потенциала для общих сумм квадратов Хёрмандера и их фундаментальных решений. .
Ключевые слова
Отзывы
“Эта книга посвящена неравенствам Харди и им подобным, неравенствам Реллиха, Соболева, Каффарелли-Кона-Ниренберга на однородных группах Ли. … Книга представляет собой хорошо написанную исчерпывающую монографию по предмету. Он также содержит богатую библиографию». (Лешек Скшипчак, zbMATH 1428.22011, 2020)
Наверх
Авторы и филиалы
Департамент математики Имперского колледжа Лондона, Великобритания; Кафедра математики: анализа, логики и дискретной математики, Гентский университет, Гент, Бельгия; Школа математических наук Лондонского университета королевы Марии, Лондон, Великобритания
Михаил Ружанский
Кафедра математики, Назарбаев Университет, Астана, Казахстан
Дурвудхан Сураган
Наверх
Об авторах
Майкл Ружански — профессор чистой математики Имперского колледжа Лондона.
Дурвудхан Сураган — доцент кафедры математики Назарбаев Университета.
Наверх
Наверх
Скачать книгу PDF
‘)
var head = document.getElementsByTagName(«head»)[0]
var script = document.createElement(«сценарий»)
script.type = «текст/javascript»
script.src = «https://buy.springer.com/assets/js/buybox-bundle-abe5f44a67.js»
script.id = «ecommerce-scripts-» + метка времени
head.appendChild (скрипт)
var buybox = document.querySelector(«[data-id=id_»+ метка времени +»]»).parentNode
var сейчас = новая дата().getTime()
вар начало = 1650956400000
вар конец = 1652338800000
var isMeasuringTime = сейчас > начать && сейчас -1
;[]. slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) {
var toggle = option.querySelector(priceNS + «.buying-option-price»)
var form = option.querySelector(«.форма-варианта-покупки»)
var priceInfo = option.querySelector(priceNS + «.price-info»)
если (allOptionsInitiallyCollapsed || узкаяBuyboxArea && индекс > 0) {
toggle.setAttribute («ария-расширенная», «ложь»)
form.hidden = «скрытый»
priceInfo.hidden = «скрытый»
} еще {
переключить.щелчок()
}
})
}
начальное состояниеОткрыть()
если (window.buyboxInitialized) вернуть
window.buyboxInitialized = истина
initKeyControls()
если (window.
slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) {
var toggle = option.querySelector(priceNS + «.buying-option-price»)
var form = option.querySelector(«.форма-варианта-покупки»)
var priceInfo = option.querySelector(priceNS + «.price-info»)
если (allOptionsInitiallyCollapsed || узкаяBuyboxArea && индекс > 0) {
toggle.setAttribute («ария-расширенная», «ложь»)
form.hidden = «скрытый»
priceInfo.hidden = «скрытый»
} еще {
переключить.щелчок()
}
})
}
начальное состояниеОткрыть()
если (window.buyboxInitialized) вернуть
window.buyboxInitialized = истина
initKeyControls()
если (window.


 М., Дули Д., Эванс В., Копылова В., Мильруд Р.
М., Дули Д., Эванс В., Копылова В., Мильруд Р. Д., Лисейцев Д.В., Павлова Н.С., Рогожкин В.А.
Д., Лисейцев Д.В., Павлова Н.С., Рогожкин В.А. Т. Баранов, Т.А. Ладыженская, Л.А. Тростенцова
Т. Баранов, Т.А. Ладыженская, Л.А. Тростенцова Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов
Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов