ГДЗ Биология 7 класс Тихонова Рабочая тетрадь
Авторы:Тихонова, Романова
Изд-во:Русское Слово
Вид УМК:рабочая тетрадь
Серия:Инновационная школа
Найди ответ по номеру страницы
Топовые ГДЗ по другим предметам
- Учебник
- Учебник
- Учебник
- Учебник
- Учебник
- Учебник
- Учебник
- Учебник
- Контурные
- Учебник
Подробные решения по биологии за 7 класс авторы Тихонова, Романова
Как известно, ни один урок биологии не обходится без записи в рабочей тетради. Так уж принято, что к учебнику обязательно должно прилагаться специализированное печатное издание, в котором автор припас для школьников множество вопросов и заданий по самым разным темам. Для того чтобы домашнее задание не превращалось в рутину, учителя настоятельно рекомендуют применять гдз по биологии рабочая тетрадь за 7 класс Тихонова при выполнении домашнего задания. Занимаясь с решебником по несколько часов в неделю, школьник сможет заметно подтянуть свои познания по пропущенным, или просто сложным темам, для разбора которых ранее пришлось бы ходить на занятия к репетитору.
Так уж принято, что к учебнику обязательно должно прилагаться специализированное печатное издание, в котором автор припас для школьников множество вопросов и заданий по самым разным темам. Для того чтобы домашнее задание не превращалось в рутину, учителя настоятельно рекомендуют применять гдз по биологии рабочая тетрадь за 7 класс Тихонова при выполнении домашнего задания. Занимаясь с решебником по несколько часов в неделю, школьник сможет заметно подтянуть свои познания по пропущенным, или просто сложным темам, для разбора которых ранее пришлось бы ходить на занятия к репетитору.
Для кого сборник ответов к тетради играет важную роль в процессе освоения предмета?
К числу тех, для кого подробные решения к рабочей тетради по биологии 7 класс авторов Тихоновой, Романовой будут максимально полезны во время учебного процесса, можно отнести:
- школьников, переведенных на дистанционное обучение. Без разъяснений учителя, только по учебнику, довольно сложно понять суть большинства тем, не говоря уже о сложных процессах жизнедеятельности живых организмов.
 С решебником под рукой это будет сделать проще;
С решебником под рукой это будет сделать проще; - восьмиклассников, повторяющих прошлые темы в первые недели обучения. Достаточно взять тетрадь с решебником, чтобы освежить в памяти всё то, что учил в прошлом году. Самоанализ дает хороший прирост к навыкам списывания и конспектирования, так как учит школьника запоминать то, что они читает и пишет;
- родителей, для которых сборник гдз – это единственный вариант быстро разобраться с домашкой ребенка. Помочь ответить на вопрос, решить кроссворд, выполнить тестовое задание, да и просто проверить то, как семиклассник выполнил упражнения, всё это сделать намного проще с подсказками авторов-составителей УМК;
- учителей, которым нужно ускорить процесс проверки домашнего задания. Особенно это актуально доя тестов и заданий, в которых используются «ключи» или числовые значения. Достаточно открыть ответы и сравнить их с теми, что написали ученики и не придется разбираться в пунктах и обозначениях.
Явные плюсы применения готовых ответов к рабочей тетради по биологии 7 класс (авторы Тихонова, Романова)
Многие родители всё еще выступают против решебников, обвиняя их составителей в том, что дети бездумно списывают задания. Но разве будут авторы учебника делать что-то просто так? Конечно, нет! Несомненно, ответы на еуроки ГДЗ имеют ряд явных плюсов:
Но разве будут авторы учебника делать что-то просто так? Конечно, нет! Несомненно, ответы на еуроки ГДЗ имеют ряд явных плюсов:
- решения и их оформление соответствуют требованиям, представленным в школах и лицеях;
- удобная система поиска помогает найти ответ в пару кликов, достаточно знать номер страницы и задания;
- материал подан грамотно и лаконично, чтобы школьник мог его быстро усвоить даже во время переписывания в тетрадь;
- подсказки доступны круглосуточно, можно смотреть сайт с телефона и с компьютера.
Потому не стоит запрещать семикласснику пользоваться решебником. В его возрасте как раз пора научиться работать с разной информацией, правильно пользоваться подсказками и самостоятельно готовиться к предстоящим урокам. Эти навыки будут незаменимы в старших классах и пригодятся на всех уроках.
ГДЗ 7 класс — решебники онлайн для 7 класса
| » ГДЗ 7 класс загрузка. М.П. Бойко І.Ю. Сліпчук Ф.Я. Божинова, О.О. Кірюхіна О.Д. Карп’юк, А.В. Павлюк С.В. Мясоєдова С.І. Сотникова Г. М. Янченко, В. Р. Кравчук А.Г. Мерзляк, В.Б. Полонський, Ю.М. Рабінович, М.С. Якір А.С. Марченко, О. В. Сасіна, В. В. Уліщенко В.А. Солопенко, А.А. Ворон Н.В. Бондаренко, А.В. Ярмолюк В. Ф. Жовтобрюх На страницах нашего сайта вы найдете решебники и ГДЗ для 7 класса. Зачем необходим решебник для 7 класса? Даже если ваш ребенок учится на отлично, он не всегда с первого раза правильно усваивает учебный материал. Это ведет к появлению множества ошибок при выполнении домашней работы. При попытке помочь разобраться с новой темой родители сталкиваются с определенными трудностями. Учеба далеко позади и некоторые простейшие алгоритмы решения благополучно забыты. Что делать? Открываем решебник для 7 класса на нашем сайте и легко находим правильный ответ. Конечно, во всем главное соблюдение чувства меры. Не стоит прибегать к помощи ГДЗ там, где ученик самостоятельно способен справиться с заданными примерами и задачами. ГДЗ за 7 класс помогут вам и вашему ребенку добиться высоких показателей в учебе. Умение самостоятельно справляться с трудностями – лучшая школа для ребенка. Даже если вас нет рядом, с помощью ГДЗ юный ученик сможет выйти из трудного положения. Для подготовки к очередной школьной олимпиаде решебник для 7 класса просто необходим. Занимаясь с решебником, что важно, вы получаете не только готовые ответы, но и алгоритм решения, что развивает мышление и повышает эрудицию в выбранном предмете. Заходите на наш ресурс и повышайте качество выполняемых домашних работ. Используя ГДЗ и решебники в своем обучении, вы сможете избежать массы ненужных ошибок. |
NCERT Solutions for Class 7 Math Chapter 4
Страница № 81:
Вопрос 1:
Заполните последний столбец таблицы.
С. № | Уравнение | Значение | Скажите, выполняется ли уравнение. (Да/Нет) |
(и) | х + 3 = 0 | х = 3 | — |
(ii) | х + 3 = 0 | х = 0 | — |
(iii) | х + 3 = 0 | х = — 3 | — |
(iv) | х — 7 = 1 | х = 7 | — |
(в) | х — 7 = 1 | х = 8 | — |
(ви) | 5 х = 25 | х = 0 | — |
(vii) | 5 х = 25 | х = 5 | — |
(viii) | 5 х = 25 | х = — 5 | — |
(икс) | м = − 6 | — | |
(х) | м = 0 | — | |
м = 6 | — |
Ответ:
(i) x + 3 = 0
L. H.S. = x + 3
H.S. = x + 3
Положив x = 3,
L.H.S. = 3 + 3 = 6 ≠ RHS
∴ Нет, уравнение не выполняется.
(ii) х + 3 = 0
Л.Х.С. = x + 3
Положив x = 0,
L.H.S. = 0 + 3 = 3 ≠ R.H.S.
∴ Нет, уравнение не выполняется.
(iii) x + 3 = 0
Л.В.С. = x + 3
Положив x = −3,
LHS = — 3 + 3 = 0 = RHS
∴ Да, уравнение выполнено.
(iv) x − 7 = 1
L.H.S. = x − 7
Поставив x = 7,
L.H.S. = 7 — 7 = 0 ≠ RHS
∴ Нет, уравнение не выполняется.
(v) x − 7 = 1
L.H.S. = x − 7
Положив x = 8,
LHS = 8 — 7 = 1 = RHS
∴ Да, уравнение выполнено.
(vi) 5 x = 25
Л.В.С. = 5 x
Положив x = 0,
L.H.S. = 5 × 0 = 0 ≠ RHS
∴ Нет, уравнение не выполняется.
(vii) 5 x = 25
Л. В.С. = 5 x
В.С. = 5 x
Положив x = 5,
L.H.S. = 5 × 5 = 25 = правая сторона
∴ Да, уравнение выполнено.
(viii) 5 x = 25
Л.В.С. = 5 x
Положив x = −5,
L.H.S. = 5 × (−5) = −25 ≠ RHS
∴ Нет, уравнение не выполняется.
(икс) знак равно 2
Л.Х.С. знак равно
Поставив м = −6,
Д. В. С. = ≠ Р.Х.С.
∴Нет, уравнение не выполняется.
(х) знак равно 2
Л.Х.С. знак равно
Поставив м = 0,
L.H.S. знак равно ≠ Р.Х.С.
∴Нет, уравнение не выполняется.
(xi) знак равно 2
Л.Х.С. знак равно
Положив м = 6,
Л.В.С. знак равно = R.H.S.
∴ Да, уравнение выполнено.
Страница № 81:
Вопрос 2:
Проверить, является ли значение, указанное в скобках, решением данного уравнения:
(a) n + 5 = 19 ( n = 1) (b) 7 n + 5 = 19 ( n = − 2)
(c) 7 n + 5 = 19 ( n = 2) (d) 4 p − 3 = 13 ( p = 1)
6 (
7 9) 4 p − 3 = 13 ( p = − 4) (f) 4 p − 3 = 13 ( p = 0)
Ответ:
(a) n + 9( n = 1)
Ввод n = 1 в левую сторону,
n + 5 = 1 + 5 = 6 ≠ 19
As L.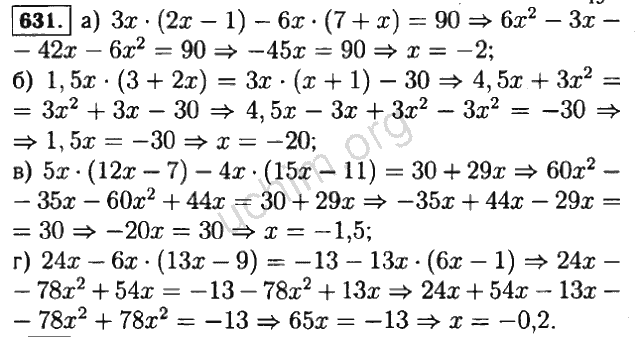 H.S. ≠ R.H.S.,
H.S. ≠ R.H.S.,
Следовательно, n = 1 не является решением данного уравнения, n + 5 = 19.
Помещение n = −2 в LHS,
7 n + 5 = 7 × (−2) + 5 = −14 + 5 = −9 ≠ 19
As L.H.S. ≠ RHS,
Следовательно, n = −2 не является решением данного уравнения, 7 n + 5 = 19.
(c) 7 n + 5 = 19 ( n = 2)
Положив 3n 4 = 2 слева,
7 n + 5 = 7 × (2) + 5 = 14 + 5 = 19 = справа
Как L.H.S. = R.H.S.,
Следовательно, n = 2 является решением данного уравнения, 7 n + 5 = 19.
(d) 4 p − 3 = 13 ( p
Положение p = 1 в левой плоскости,
4 p — 3 = (4 × 1) — 3 = 1 ≠ 13
As данное уравнение, 4 p − 3 = 13.
(e) 4 p − 3 = 13 ( p = −4)
Помещение p = −4 в L.H.S.,
4 9 — 3 = 4 × (-4) — 3 = — 16 — 3 = -19 ≠ 13
Как Л.Х.С. ≠ RHS,
≠ RHS,
Следовательно, p = −4 не является решением данного уравнения, 4 p − 3 = 13.
(f) 4 p − 3 = 13 ( p = 0)
Помещение p = 0 в Л.С.,
− 3 p4 × 0) − 3 = −3 ≠ 13
Как L.H.S. ≠ R.H.S.,
Следовательно, p = 0 не является решением данного уравнения, 4 p − 3 = 13.
Стр. метод ошибки:
(i) 5 p + 2 = 17 (ii) 3 м − 14 = 4
Ответ:
(i) 5 p + 2 = 17
Положив p = 1 в Л.С.,
(5 × 1) + .2 = .7.
Вставка p = 2 в левой стороне,
(5 × 2) + 2 = 10 + 2 = 12 ≠ в правой стороне.
Ввод p = 3 в Л.С.С.,
(5 × 3) + 2 = 17 = П.С.
Следовательно, p = 3 является решением данного уравнения.
(ii) 3 м − 14 = 4
Укладка м = 4,
(3 × 4) — 14 = -2 ≠ П.С.
Укладка м = 5,
(3 × 5) − 14 = 1 ≠ П. С.
С.
Укладка м = 6,
(3 × 6) − 14 = 18 − 14 = 4 = R.H.S.
Следовательно, м = 6 является решением данного уравнения.
Страница № 81:
Вопрос 4:
Напишите уравнения для следующих утверждений:
(i) Сумма чисел x и 4 равна 9.
(ii) 2 вычесть из y равно 8.
(iii) Десять раз a равно 70.
(iv) Число b , разделенное на 5, дает 6.
(v) Три четверти t 1
3 равно
(vi) Семь раз m плюс 7 дает 77.
(vii) Четвертая часть числа x минус 4 дает 4.
(viii) Если из 6 умножить на 6 , вы получите 60.
(ix) Если вы прибавите 3 к одной трети z , вы получите 30.
Ответ:
(i) x + 4 =
(ii) y — 2 = 8
(iii) 10 A = 70
(iv)
(v)
666 (vi) Семь раз по м равно 7 м .
7 м + 7 = 77
(vii) Четвертая часть числа x равна .
(viii) Шесть раз y равно 6 y .
6 y − 6 = 60
(ix) Одна треть от z есть .
Видео Решение простых уравнений (Страница: 81 , Q.No.: 4)
NCERT Решение для 7 класса математики — простые уравнения 81 , Вопрос 4
Страница № 81:
Вопрос 5:
Написать следующие уравнения в формулярных формах:
(i) p + 4 = 15 (ii) m − 7 = 3
(iii) 2 m = 7 (iv)
(v) (vi ) 3 p + 4 = 25
(vii) 4 p − 2 = 18 (viii)
Ответ:
(i) Сумма p и 4 равна 15.
(ii) 7 вычитается из m равно 3.
(iii) Удвоенное число m равно 7.
(iv) Одна пятая от м равна 3.
(v) Три пятых от м равна 6.
(vi) Три раза числа p , при добавлении к 4 дает 25
(vii) Когда 2 вычитается из четырех раз числа p , получается 18.
(viii) Когда 2 прибавляется к половине числа p , это дает 8.
Страница № 82:
Вопрос 6:
Составьте уравнение для следующих случаев:
(i) Ирфан говорит, что у него 7 шариков больше, чем в пять раз больше, чем у Пармита. . У Ирфана 37 шариков. (Возьмем м за число шариков Пармита.)
(ii) Отцу Лакшми 49 лет. Он на 4 года старше, чем в три раза старше Лакшми. (Примите возраст Лакшми равным х лет.)
(iii) Учитель сообщает классу, что самая высокая оценка, полученная ученицей в ее классе, равна удвоенной самой низкой отметке плюс 7. Наивысшая оценка равна 87. (Возьмите самый низкий балл должен быть l .)
(iv) В равнобедренном треугольнике угол при вершине вдвое больше угла при основании. (Пусть угол при основании равен b в градусах. Помните, что сумма углов треугольника равна 180 градусам.)
Ответ:
(i) Пусть у Пармита м шариков.
5 × Количество шариков у Пармита + 7 = Количество шариков у Ирфана старый.
3 × возраст Лакшми + 4 = возраст отца Лакшми
2 × Самые низкие баллы + 7 = Высшие баллы
2 × l + 7 = 87
2 l + 7 = 87
(iv) Два угла равнобедренного треугольника равны.
Пусть угол основания равен b .
Угол вершины = 2 × угол основания = 2 B
Сумма всех внутренних углов A Δ = 180 °
B + B + 2 B = 180 °
4 B = 180 °
. Простые и уравнения для простого решения для простого решения для простого решения. (Страница: 82 , Q.No.: 6)
NCERT Решение для класса 7 по математике — простые уравнения 82 , Вопрос 6
Номер страницы 86:
Вопрос 1:
Дайте сначала шаг, который вы будете использовать для разделения переменной, а затем решить уравнение:
(а) х + 1 = 0 (б) х + 1 = 0 (в) х — 1 = 5
(г) х + 6 = 2 (д) у — 4 = — 7 (е) у — 4 = 4
(ж) у + 4 = 4 (h) y + 4 = − 4
Ответ:
(a) x − 1 = 0
Прибавив 1 к обеим частям данного уравнения, мы получим
х — 1 + 1 = 0 + 1
х = 1
(б) х + 1 = 0
Вычитая 1 из обеих частей данного уравнения, мы получаем
х + 1 — 1 = 0 — 1
х = -1
(в) х — 1 = 5
Прибавив 1 к обеим частям данного уравнения, мы получим
х — 1 + 1 = 5 + 1
х = 6
(г) х + 6 = 2
Вычитая 6 из обеих частей данного уравнения, мы получаем
х + 6 — 6 = 2 — 6
х = −4
(д) у − 4 = −7
Прибавив 4 к обеим частям данного уравнения, мы получим
г — 4 + 4 = — 7 + 4
г = −3
(е) г − 4 = 4
Прибавив 4 к обеим частям данного уравнения, мы получим
у — 4 + 4 = 4 + 4
у = 8
(г) у + 4 = 4
Вычитая 4 из обеих частей данного уравнения, мы получаем
г + 4 — 4 = 4 — 4
г = 0
(ч) г + 4 = −4
Вычитая 4 из обеих частей данного уравнения, мы получаем
г + 4 — 4 = — 4 — 4
y = −8
Номер страницы 86:
Вопрос 2:
Дайте сначала шаг, который вы будете использовать для разделения переменной, а затем решить уравнение:
(а) 3 л = 42 (б) (в)
(г) 4 х = 25 (д) 8 у = 36 (е)
(ж) (ч) 20 т = − 10
Ответ:
(а) 3 l = 42
Разделив обе части данного уравнения на 3, получим
л = 14
(б)
Умножая обе части данного уравнения на 2, получаем
б = 12
(в)
Умножив обе части данного уравнения на 7, получим
р = 28
(г) 4 х = 25
Разделив обе части данного уравнения на 4, получим
х =
(д) 8 у = 36
Разделив обе части данного уравнения на 8, получим
г =
(ж)
Умножая обе части данного уравнения на 3, получаем
(г)
Умножая обе части данного уравнения на 5, получаем
(ч) 20 т = −10
Разделив обе части данного уравнения на 20, получим
Страница № 86:
Вопрос 3:
Укажите шаги, которые вы будете использовать для разделения переменной, а затем решите уравнение: 7 = 17 (в)
(г)
Ответ:
(a) 3 n − 2 = 46
Прибавив 2 к обеим частям данного уравнения, получим Разделив обе части данного уравнения на 3, получим
n = 16
(b) 5 m + 7 = 17
Вычтя 7 из обеих частей данного уравнения, получим 9000 5 м + 7 — 7 = 17 — 7
5 м = 10
Разделив обе части данного уравнения на 5, получим
(c)
Умножив обе части данного уравнения на 3, получим
Разделив обе части данного уравнения на 20, получим получаем
(d)
Умножив обе части данного уравнения на 10, получим
Разделив обе части данного уравнения на 3, получим
Страница № 86:
Вопрос 4:
Решите следующие уравнения:
(а) 10 р = 100 (б) 10 р + 10 = 100 (в)
(г) (д) (е) 3 с = − 9
(г) 3 с + 12 = 0 (h) 3 с = 0 (i) 2 q = 6
(j) 2 q − 6 = 0 (k) 2 q + 6 = 0 (l) 2 q + 6 = 12
Ответ:
(a) 10 p = 100
(б) 10 р + 10 = 100
10 р + 10 — 10 = 100 — 10
10 р = 90
(в)
(г)
(д)
(е) 3 с = −9
(г) 3 с + 12 = 0
3 с + 12 − 12= 0 − 12
3 с = −12
(ч) 3 с = 0
(i) 2 q = 6
(к) 2 q − 6 = 0
2 q − 6 + 6 = 0 + 6
2 q = 6
(к) 2 кв + 6 = 0
2 q + 6 — 6 = 0 — 6
2 q = −6
(левый) 2 q + 6 = 12
2 q + 6 — 6 = 12 — 6
2 q = 6
Страница № 89:
Вопрос 1:
Решите
следующие уравнения.
(а) (б) 5 т + 28 = 10 (в)
(г) (д) (е)
(ж) (з) 6 z + 10 = − 2 (i)
(j)
Ответ:
(a)
(Транспонирование к R.H.S.)
Разделив обе части на 2,
(б) 5 т + 28 = 10
5 t = 10 − 28 = −18 (перенос 28 в правую сторону)
Разделив обе части на 5,
(в)
(Транспонирование 3 по правой стороне)
Умножение обеих сторон на 5,
a = −1 × 5 = −5
(г)
(Транспонирование 7 по правой стороне)
Умножение обеих сторон на 4,
q = −8
(д)
Умножение обеих сторон на 2,
5 х = -10 х 2 = -20
Разделив обе части на 5,
(ж)
Умножение обеих сторон на 2,
Разделив обе части на 5,
(г)
(Транспонирование справа)
Разделив обе части на 7,
(ч) 6 z + 10 = −2
6 z = − 2 − 10 = −12 (перенос 10 в
R. H.S.)
H.S.)
Разделив обе части на 6,
(и)
Умножение обеих сторон на 2,
Разделив обе части на 3,
(к)
(Транспонирование −5 до правой стороны)
Умножение обеих сторон на 3,
2 б = 8 × 3 = 24
Разделив обе части на 2,
б = знак равно 12
Страница № 89:
Вопрос 2:
Решите следующие уравнения.
(а) 2 ( х + 4) = 12 (б) 3 ( н — 5) = 21
(в) 3 ( н − 5) = − 21 (d) −4 (2 + x ) = 8
(e) 4(2 − х ) = 8
Ответ:
(а) 2 ( х + 4) = 12
Разделив обе части на 2,
x = 6 − 4 = 2 (перенос 4 в правую сторону)
(b) 3 ( n − 5) = 21
Разделив обе части на 3,
n = 7 + 5 = 12 (перенос −5 в правую сторону)
(c) 3 ( n − 5) = −21
Разделив обе части на 3,
n = − 7 + 5 = −2 (перенос −5 в
П. С.С.)
С.С.)
(г) −4 (2 + х ) = 8
Разделив обе стороны на −4,
x = − 2 − 2 = −4 (перенос 2 в правую сторону)
(e) 4 (2 − х ) = 8
Разделив обе части на 4,
2 − х = 2
− x = 2 − 2 (Транспонирование 2 в правую сторону)
− х = 0
х = 0
Страница № 89:
Вопрос 3:
Решите следующие уравнения.
(а) 4 = 5 ( р — 2) (б) — 4 = 5 ( р — 2)
(в) 16 = 4 + 3 ( t + 2) (г) 4 + 5 ( р — 1) = 34
(д) 0 = 16 + 4 ( м − 6)
Ответ:
(а) 4 = 5 ( стр − 2)
Разделив обе части на 5,
(б) − 4 = 5 ( р — 2)
Разделив обе части на 5,
(в) 16 = 4 + 3 ( т + 2)
16 − 4 = 3 ( t + 2) (Перенос 4 в левую сторону)
12 = 3 ( т + 2)
Разделив обе части на 3,
4 = т + 2
4 − 2 = t (Транспонирование 2 в левую сторону)
2 = т
(г) 4 + 5 ( п — 1) = 34
5 ( p — 1) = 34 — 4 = 30 (перенос 4 в правую сторону)
Разделив обе части на 5,
p = 6 + 1 = 7 (перенос −1 в правую сторону)
(e) 0 = 16 + 4 ( м − 6)
0 = 16 + 4 м − 24
0 = −8 + 4 м
4 м = 8 (перенос −8 в левую сторону)
Разделив обе части на 4,
м = 2
Страница № 89:
Вопрос 4:
(a) Конструкция 3 уравнения начинающиеся с х = 2
(б) Конструкция 3 уравнения, начинающиеся с x = − 2
Ответ:
(a) x = 2
Умножение с обеих сторон на 5,
5 x = 10 (i)
Вычитание 3 с обеих сторон,
5 x − 3 = 10 − 3
5 х − 3 = 7 (ii)
Разделение обе стороны на 2,
(b) x = −2
Вычитание 2 с обеих сторон,
х − 2 = − 2 − 2
x − 2 = −4 (i)
Опять же, x = −2
Умножение на 6,
6 × х = -2 х 6
6 х = −12
Вычитание 12 с обеих сторон,
6 x − 12 = − 12 − 12
6 x − 12 = −24 (ii)
Добавление 24 на обе стороны,
6 x − 12 + 24 = − 24 + 24
6 x + 12 = 0 (iii)
Страница № 91:
Вопрос 1:
Составьте уравнения и решите их, чтобы найти неизвестные числа в таблице. следующие случаи:
следующие случаи:
а) прибавьте число от 4 до 8 раз; вы получаете 60.
(b) Одна пятая числа минус 4 дает 3.
в) Если я возьму три четверти числа и прибавлю к нему 3, то получу 21.
(d) Когда я вычел 11 из удвоенного числа, в результате получилось 15.
д) Мунна вычитает из 50 тетрадей в три раза больше, чем у него. находит результат равным 8.
(f) Ибенхаль загадывает число. Если она прибавит к нему 19 и поделит суммируй на 5, она получит 8.
(ж) Анвар загадывает число. Если он отнимет 7 у из число, результат 23.
Ответ:
(a) Пусть число будет х .
8 умноженное на это число = 8 x
8 x + 4 = 60
8 х = 60 − 4 (Транспонирование 4 в правую сторону)
8 x = 56
Разделение обе стороны на 8,
(б) Пусть число будет х .
Одна пятая этого числа =
(Транспонирование от −4 до правой)
Умножение с обеих сторон на 5,
(c) Пусть число будет х .
Три четверти этого числа =
(Транспонирование 3 до R.H.S.)
Умножение
с обеих сторон по 4,
Разделение с обеих сторон на 3,
(d) Пусть число будет х .
Дважды этого числа = 2 x
2 x − 11 = 15
2 x = 15 + 11 (преобразование −11 в правую сторону)
2 x = 26
Разделение с обеих сторон по 2,
x = 13
(e) Пусть число книги должны быть x .
Трижды количество книг = 3 x
50 − 3 х = 8
− 3 x = 8 −50 (перенос 50 в правую сторону)
−3 х = −42
Разделение с обеих сторон на −3,
(f) Пусть число будет х .
Умножение с обеих сторон по 5,
x + 19 = 40
х = 40 − 19 (перенос 19 в правую сторону)
x = 21
(г) Пусть число будет х .
этого числа =
Умножение обе стороны на 2,
Разделение с обеих сторон на 5,
Страница № 91:
Вопрос 2:
Решите следующее:
(a) Учитель сообщает классу, что самая высокая оценка, полученная учеником в ее классе, в два раза выше самой низкой оценки плюс 7. Самый высокий балл 87. Какой самый низкий балл?
(б) В равнобедренном треугольнике углы при основании равны. Угол при вершине равен 40°. Чему равны углы при основании треугольника? (Помните, сумма трех углов треугольника равна 180°).
(c) Сачин набрал в два раза больше очков, чем Рахул. Вместе их пробеги не дотянули до двух столетий. Сколько пробежек сделал каждый?
Ответ:
(a) Пусть наименьший результат будет l .
2 × самые низкие оценки + 7 = самые высокие оценки
2 L + 7 = 87
2 L = 87 — 7 (транспозирование с 7 до R.H.S.). на 2,
Таким образом, наименьший балл равен 40.
(b) Пусть углы при основании равны b .
Сумма всех внутренних углов треугольника равна 180°.
B + B + 40 ° = 180 °
2 B + 40 ° = 180 °
2 B = 180º — 40º = 140º (перевод 40º до R.H.S. на 2,
Следовательно, углы при основании треугольника равны 70º.
(c) Пусть счет Рахула будет x .
Следовательно, оценка Сачина = 2 x
Оценка Рахула + Оценка Сачина = 200 — 2
2 x + x = 198
3 x = 198
Divider Divider Divider на S -Siesdes на 3, 3, 3 x = 198
Дидиционирование оба Стоя 3, 3, 3 x = 198
.
x = 66
Оценка Рахула = 66
Оценка Сачина = 2 × 66 = 132 7 математика — простые уравнения 91 , Вопрос 2
Страница № 91:
Вопрос 3:
Решите следующее:
(i) Ирфан говорит, что у него на 7 шариков больше, чем в пять раз больше, чем у Пармита. У Ирфана 37 шариков. Сколько шариков у Пармита?
У Ирфана 37 шариков. Сколько шариков у Пармита?
(ii) Отцу Лакшми 49 лет. Он на 4 года старше, чем в три раза старше Лакшми. Сколько лет Лакшми?
(iii) Жители Сундарграма посадили деревья в деревенском саду. Некоторые из деревьев были плодовыми деревьями. Количество неплодовых деревьев в два и более раза превышало количество плодовых деревьев. Сколько плодовых деревьев было посажено, если неплодовых было посажено 77?
Ответ:
(i) Пусть шарики Пармита равны x .
5 умноженное на количество шариков у Пармита = 5 x
5 x + 7 = 37
5 x = 37 − 7 = 30 ,
Следовательно, у Пармита 6 шариков.
(ii) Пусть возраст Лакшми будет х года.
3 × возраст Лакшми + 4 = возраст ее отца
3 x + 4 = 49
3 x = 49 — 4 (транспонирование от 4 до R.H.S.)
3 x = 45
Разделив обе стороны на 3,
x = 15
, поэтому
x = 15
, поэтому
x = 15
x = 15
x = 15
. Лакшми 15 лет.
Лакшми 15 лет.
(iii) Пусть количество фруктовых деревьев равно x .
3 × количество фруктовых деревьев + 2 = количество неплодовых деревьев
3 x + 2 = 77
3 x = 77 − 2 (перенос 2 в правую сторону)
3 x = 75
Разделив обе части уравнения на 3,
x = 25
Следовательно, количество фруктовых деревьев равно 25. , Q.No.: 3)
NCERT Решение для класса 7 по математике — простые уравнения 91 , Вопрос 3
Номер страницы 92:
Вопрос 4:
Решите следующую загадку:
Я число,
Скажи мою личность!
Возьми меня семь раз больше
И добавь пятьдесят!
Чтобы достичь тройного века
Вам нужно еще сорок!
Ответ:
Пусть число будет х .
(7 x + 50) + 40 = 300
7 x + 90 = 300
7 x = 300 — 90 (перенос 90 к р.Х. Разделив обе части на 7,
x = 30
Следовательно, число равно 30.
Решение линейных уравнений: с Пареном; «Все x», «No x» Soln’s
Add/SubtractTimes/DivideMulti-StepZero/No/All Sol’n
Purplemath
В этом уроке мы сначала попрактикуемся в решении линейных уравнений, содержащих скобки. Их решение потребует умножения и упрощения, прежде чем приступить к фактическому процессу решения. Если вам не нравятся скобки, сначала изучите. Тогда возвращайся сюда.
Затем мы рассмотрим два странных вида решений: «нет решения» и решение «все 9».2233 x «. В первом случае процесс решения заканчивается бессмыслицей, а во втором — тривиально верным утверждением. запутать. Но я бы поставил хорошие деньги, что по крайней мере одно из этих уравнений будет в следующем тесте, а еще одно, вероятно, в финальном. Так что изучите и сделайте пометку сейчас, чтобы просмотреть уравнения «нет решения» и все- x решение» уравнений перед следующим экзаменом.
Содержание продолжается ниже
MathHelp.com
Решение уравнений со скобками
После того, как вы изучите основы решения линейных уравнений, ваш учебник и преподаватель начнут предлагать вам упражнения, в которых используются скобки, которые обычно необходимо сначала упрощенный (или «расширенный», что означает, что вы умножили, а затем упростили результат).
Решить 9 = 3(5
x — 2)
Во-первых, я должен умножить через круглые скобки в правой части. Затем я могу действовать обычным образом:
Тогда мое решение:
x = 1
Сначала я упрощу левую часть; тогда решу обычным способом. Я хочу быть осторожным, когда беру отрицания через круглые скобки. Если у меня возникнут проблемы с отслеживанием знаков «минус», я поставлю «1» перед скобками.
Тогда мое решение:
x = 8
Это уравнение имеет скобки с обеих сторон уравнения. Я должен быть уверен, что 7 и 6 проходят через соответствующие скобки.
После того, как я упростил обе стороны, я переместил меньший из двух переменных терминов (то есть «35 x » в левую часть), чтобы гарантировать, что у моего результирующего переменного члена не будет знака «минус» на нем. . Это не «правило», но оно определенно облегчает мою жизнь. И мой окончательный ответ:
И мой окончательный ответ:
x = −8
Для уравнений со скобками не торопитесь и запишите все ваших шага, как я сделал выше. Не пытайтесь сделать все в своей голове.
Решите 3 (
х — 2) = 6
Во-первых, мне нужно умножить в левой части, проведя 3 через—
Минуточку… В этом уравнении я действительно могу избавиться от 3, разделив, потому что 6 на правая часть делится на 3. На самом деле мне не нужно распределять для этого конкретного уравнения. Вместо:
3(х — 2) = 6
——— —
3 3
х — 2 = 2
+2 +2
———-
x = 4
Тогда мое решение:
x = 4
Если бы я не заметил, что могу начать с деления, я все равно получил бы в конце концов правильный ответ. Но если можно разделить, давая себе для работы меньшие числа, мне нравится этим пользоваться. Это упрощение встречается не часто, но постарайтесь не закрывать на это глаза, когда оно всплывает несколько раз.
Это упрощение встречается не часто, но постарайтесь не закрывать на это глаза, когда оно всплывает несколько раз.
Я начну с умножения на каждую из скобок (знак «минус» слева и 2 справа). Затем я соединю одинаковые термины, упрощу и решу:
Тогда мой ответ:
x = 1
Не забывайте: никогда не бывает причин быть неуверенным в своем решении линейного уравнения. , потому что вы всегда можете проверить свой ответ. Смысл значения решения в том, что именно значение x делает уравнение верным. Итак, чтобы проверить свой ответ, вы снова подставляете значение решения к исходному уравнению и убеждаетесь, что уравнение «работает» с этим значением. Например, в последнем упражнении выше моим решением было 9.2233 x = 1. Чтобы проверить свое решение, я подставлю свое значение в левую (левую) и правую части (правую) исходного уравнения и удостоверюсь, что обе стороны дают одно и то же число. .
13 — (2 x + 2) = 2( x + 2) + 3 x
Левая сторона: 13 — (2[1] + 2)
= 13 — (2 + 2) = 13 − 4 = 9
Правая ось: 2([1] + 2) + 3[1]
= 2(3) + 3 = 6 + 3 = 9
Две части уравнения оцениваются одинаково значение, так что решение «проверил», и я теперь знай что мой ответ правильный
Кстати, по возможности надо стараться проверять свои ответы при сдаче тестов. После того, как вы ответили на все вопросы (при условии, что у вас осталось немного времени), вернитесь и вставьте свои решения обратно в исходный вопрос. Если ваше решение данного вопроса «проверено», значит, вы правильно ответили на этот вопрос. Если он не проходит проверку, то у вас есть шанс исправить свою ошибку до того, как вы сдадите тест.
После того, как вы ответили на все вопросы (при условии, что у вас осталось немного времени), вернитесь и вставьте свои решения обратно в исходный вопрос. Если ваше решение данного вопроса «проверено», значит, вы правильно ответили на этот вопрос. Если он не проходит проверку, то у вас есть шанс исправить свою ошибку до того, как вы сдадите тест.
Вам также может понадобиться решить линейные уравнения с вложенными скобками .
Прежде чем я смогу решить, мне нужно упростить. Сначала упростим левую часть:
2[3 x + 4(3 − x )]
2[3 x + 4(3) + 4(− x ) ]
2 [3 x + 12-4 x ]
2 [12- x ]
24-2 x
. Затем я упростите правую достаточную сторону:
66
. Затем я упростите правую достаточную сторону:
69 3(5 — 4 x ) — 11
3(5) + 3(-4 x ) — 11
15 — 12 x — 11
4 — 12
x
4 Теперь я упростил обе стороны уравнения, я могу перейти к решению.
24 — 2x = 4 — 12x
+12x +12x
——————-
24 + 10х = 4
-24 -24
—————
10x = -20
— —
10 10
x = -2
Итак, мой окончательный ответ:
x = -2
Мой первый шаг будет заключаться в упрощении каждой части этого уравнения, работая изнутри наружу. Я начну с левой стороны:
3[ x — 2(3 x — 4)] + 15
3[ x — 6 x + 8] + 15
3[−5 x + 8] + 15−15 x + 24 + 15
−15 x + 39
Тогда я упрощу правую часть:
5 — [2 x — (3 + x )] — 11
5 — [2 x — 3 — x ] — 11
— 4 x 9223] 11
5 − x + 3 − 11
− x − 3
Упростив каждую сторону, я могу перейти к решению. Мое упрощенное уравнение:
-15 x + 39 = — x — 3
числа вокруг, чтобы закончить решение.


 С решебником под рукой это будет сделать проще;
С решебником под рукой это будет сделать проще; ..
..

