Поиск материала «Алгебра. 7 класс. Дидактические материалы. Феоктистов И.Е. 2009» для чтения, скачивания и покупки
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Алгебра. 7 класс. Дидактические материалы к учебнику…
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Пособие содержит комментарии для учителя и примерное поурочное планирование. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс. Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
11klasov.
 net
net - 7 класс. Алгебра. Дидактические материалы. Методические…
Алгебра. Дидактические материалы. Методические рекомендации. Феоктистов И.Е. Последние записи: «Всё сдал!» — онлайн сервис помощи студентам. ЕГЭ 2023 Математика. Открыт прием заявок на Конкурс молодых международников.. Алгебра. 7кл. Дидактич. мат.
vk.com
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.ru
- Алгебра. 7 класс. Дидактические материалы к учебнику…
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Пособие содержит комментарии для учителя и примерное поурочное планирование.
 Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс. Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс. Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.cdnpdf.com
- Феоктистов И. Е. Алгебра, 7 класс: дидактические материалы…
https://www.mathedu.ru/text/feoktistov_algebra_7_klass_didakticheskie_materialy_2009/. © «Математическое образование», 2006—2023. Феоктистов И. Е. Алгебра, 7 класс: дидактические материалы, методические рекомендации.
www.mathedu.ru
- Алгебра. 7 класс. Дидактические материалы к учебнику…
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики.

www.at.alleng.org
- Авторы: Феоктистов | Контрольные
Алгебра 9 Контрольные Макарычев — это ОТВЕТЫ на контрольные работы с повышенным уровнем математической подготовки из пособия для учащихся «Алгебра 9 класс. Дидактические материалы / И.Е. Феоктистов — М.: Мнемозина», которое используется в комплекте с учебником «Алгебра 9 класс. Углубленное изучение» авторов: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. … ЧИТАТЬ ДАЛЕЕ.
xn—-ctbjbygnbgbvgs4kna.xn--p1ai - Алгебра. 7 класс.
 Дидактические материалы — Звавич…
Дидактические материалы — Звавич…7 класс. Дидактические материалы — Звавич Л.И., Кузнецова Л.В., Суворова С.Б. Пособие содержит упражнения для самостоятельных работ, которые носят обучающий характер, а также тексты контрольных работ и задания для проведения школьных математических олимпиад. Рубрика: Алгебра / 7 класс. Автор: Звавич Л.И., Кузнецова Л.В., Суворова С.Б. Год: 2019. Для учеников: 7 класс. Язык учебника: Русский.
11klasov.net
- Алгебра. 7 класс. Дидактические материалы. Методические…
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Пособие содержит комментарии для учителя и примерное поурочное планирование. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И.

alleng.net
- Алгебра 7 Макарычев (углубленное) — КОНТРОЛЬНЫЕ РАБОТЫ
Контрольные работы по алгебре 7 класс (угл.) Алгебра 7 Макарычев (углубленное изучение математики) — это цитаты контрольных работ в 2-х вариантах из пособия для учащихся «Алгебра 7 класс. Дидактические материалы / И.Е. Феоктистов — М.: Мнемозина, 2009», которое используется в комплекте с учебником «Алгебра 7
При постоянном использовании контрольных работ в 7 классе с углубленным изучением математики рекомендуем купить книгу: Илья Феоктистов: Алгебра. 7 класс. Дидактические материалы. Методические рекомендации.
algeomath.ru
- Алгебра. 7 класс. Дидактические материалы к учебнику.
 ..
..Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Пособие содержит комментарии для учителя и примерное поурочное планирование. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс. Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
psschool.ru
- Название: Алгебра. 7 класс. Дидактические материалы…
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Пособие содержит комментарии для учителя и примерное поурочное планирование. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю.
 Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс. Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс. Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.www.psyoffice.ru
- Алгебра: 7 класс. Дидактический материал. | Bookwinx
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю.Н. Макарычева, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
bookwinx.ru
- Алгебра 7 Макарычев (углубленное) | КОНТРОЛЬНЫЕ РАБОТЫ
Алгебра 7 Макарычев (углубленное изучение математики)».
 Контрольные работы из пособия «Дидактические материалы. Феоктистов» к учебнику УМК Макарычев.
Контрольные работы из пособия «Дидактические материалы. Феоктистов» к учебнику УМК Макарычев.При постоянном использовании контрольных работ в 7 классе с углубленным изучением математики рекомендуем купить книгу: Илья Феоктистов: Алгебра. 7 класс. Дидактические материалы.
xn—-ctbjbygnbgbvgs4kna.xn--p1ai
- Скачать Алгебра. 7 класс. Дидактические материалы.
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю.Н.Макарычева, Н.Г.Миндюк, К.Н.Нешкова, И.Е.Феоктистова «Алгебра. 7 класс» (М. : Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
cepheusbook.
 info
info - Феоктистов И.Е.: Алгебра: 7 класс. Дидактический материал.
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю.Н. Макарычева, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
fb2lib.ru
- Феоктистов И.Е.: Алгебра: 7 класс. Дидактический материал.
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю.
 Н. Макарычева, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
Н. Макарычева, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.fb2lib.ru
- Дидактические материалы по алгебре: 7 класс
СКАЧАТЬ djvu PDF Читать онлайн
co8a.ru
- алгебра. 7 класс. дидактические материалы. методические…
7 класс. дидактические материалы. методические рекомендации. феоктистов и.е.- книгу скачать. М.: 2009. — 166 с. Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Пособие содержит комментарии для учителя и примерное поурочное планирование. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю.
 Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс (М. : Мнемозина).
Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс (М. : Мнемозина).advice-me.ru
- ГДЗ: Алгебра 7 класс Феоктистов — Дидактический материал
Что изучают на уроках алгебры семиклассники. Как узконаправленная самостоятельная дисциплина – алгебра появляется именно в седьмом после разделения математики на неё и геометрию. Наука продолжает арифметический курс, готовит ребят к освоению более сложных тем в будущем. Также приобретённые знания пригодятся для обретения финансовой грамотности и планирования во взрослом возрасте. Но вернёмся в седьмой класс, проведем обзор некоторых параграфов из теоретической части учебно-методического комплекта
gdzbezmoroki.com
- Алгебра 7 Макарычев (углубленное) | КОНТРОЛЬНЫЕ РАБОТЫ
Алгебра 7 Макарычев (углубленное изучение математики)».
 Контрольные работы из пособия «Дидактические материалы. Феоктистов» к учебнику УМК Макарычев.
Контрольные работы из пособия «Дидактические материалы. Феоктистов» к учебнику УМК Макарычев.При постоянном использовании контрольных работ в 7 классе с углубленным изучением математики рекомендуем купить книгу: Илья Феоктистов: Алгебра.
xn--b1agatflbfbtgq5jm.xn--p1ai
- ГДЗ по Алгебре 7 класс дидактические материалы Феоктистов
ГДЗ дидактические материалы по алгебре 7 класс Феоктистов выполняют роль онлайн-помощника. Здесь собраны подробные решения с объяснениями и попутными комментариями ко всем заданиям из основной книги. Пособие представляет собой онлайн-решебник, который доступен в интернете с любого устройства.
Как использовать ГДЗ по алгебре за седьмой класс для дидактических материалов Феоктистова (Углубленный уровень). Онлайн-решебник – это не просто шпаргалка, в умелых руках он является ценным обучающим инструментом.

gdz.moda
- Феоктистов И.Е. Алгебра. 7 класс. Дидактические материалы.
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Пособие содержит комментарии для учителя и примерное поурочное планирование. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс (М. : Мнемозина).
www.studmed.ru
- Феоктистов И.Е.: Алгебра: 7 класс. Дидактический материал.
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю.
 Н. Макарычева, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
Н. Макарычева, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.www.fb2archive.ru
- Л. И. Звавич Л. В. Кузнецова С. Б. Суворова ПРОСВЕЩЕНИ
Л. В. Кузнецова. С. Б. Суворова. АЛГЕБРА дидактические материалы. класс. 17-е издание. Москва.
УДК 372.8:512 ббк 74.262.21. Звавич Л. И. Алгебра. Дидактические материалы.
ege-ok.ru
- ГДЗ 7 класс Алгебра Дидактические материалы Феоктистов И. Е.
Точные и бесплатные ответы от автора И. Е. Феоктистова помогают школьнику в 7 классе разобраться в различных темах по алгебре. Решебник представлен в онлайн-форме, не надо скачивать. Удобно, что есть все ответы на задания различного уровня и формата, которые собраны в дидактические материалы.
 Для поиска нужного ответа внедрен поиск по разделам.
Для поиска нужного ответа внедрен поиск по разделам.gdzdo.ru
- ГДЗ по Алгебре 7 класс: дидактические материалы Феоктистов
Готовые домашнии задания по Алгебре за 7 класс — решение заданий к дидактическим материалам Феоктистов Мнемозина- решебники и ГДЗ ко всем учебникам и рабочим тетрадям.
mne5.ru
- Илья Феоктистов: Алгебра. 7 класс. Дидактические материалы.
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением материала. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (М: Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.

www.labirint.ru
- Феоктистов, Илья Евгеньевич — Алгебра. 7 класс… — Search RSL
1# $a Феоктистов, Илья Евгеньевич. 245. 00 $a Алгебра. 7 класс $h [Текст] : $b дидактические материалы, методические рекомендации $c И. Е. Феоктистов. 250. ## $a 5-е изд., стер.
search.rsl.ru
- Скачать бесплатно Алгебра. 7 класс. Дидактические материалы…
Алгебра. 7 класс. Дидактические материалы — Звавич Л.И., Кузнецова Л.В., Суворова С.Б. cкачать в PDF. Пособие содержит упражнения для самостоятельных работ, которые носят обучающий характер, а также тексты контрольных работ и задания для проведения школьных математических олимпиад.
fizikadlyvas.net
- Алгебра. 7 класс.
 Дидактические материалы. Методические…
Дидактические материалы. Методические…Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
www.chitai-gorod.ru
- Алгебра 7 класс. Углубленный уровень. Дидактические…
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю.Н.Макарычева, Н.Г.Миндюк, К.Н.Нешкова, И.Е.Феоктистова «Алгебра.
 7 класс» (М. : Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
7 класс» (М. : Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.www.roslit.ru
- Алгебра. 7 класс. Дидактические материалы. Методические…
Дидактические материалы предназначены для проверки знаний учащихся 7-го класса с углубленным изучением математики. Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю.Н. Макарычева, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
My-shop.ru
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Алгебра. 7 класс. Дидактические материалы. Феоктистов И.Е. 2009»
7 класс. Дидактические материалы. Феоктистов И.Е. 2009»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 17 млн ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
Семинар в Дагштуле 15301: Проблема удовлетворения ограничений: сложность и аппроксимация
Проблема удовлетворения ограничений , или сокращенно CSP,
обеспечивает объединяющую основу, в которой можно выразить,
естественным образом широкий спектр вычислительных задач, связанных с отображениями и назначениями, включая выполнимость, раскрашиваемость графов и системы уравнений. Фреймворк CSP возник 25-30 лет назад независимо друг от друга в области искусственного интеллекта, теории баз данных и теории графов, под тремя разными обличьями, и был реализован только в конце 19 века.90-х, что на самом деле это разные грани одной и той же фундаментальной проблемы. В настоящее время CSP широко используется в теоретической информатике, будучи математическим объектом с очень богатой структурой, который обеспечивает отличную лабораторию как для методов классификации, так и для алгоритмических методов, в то время как в ИИ и более прикладных областях информатики эта структура широко рассматривается как универсальный и эффективный способ моделирования и решения множества реальных проблем, таких как планирование и составление графиков, проверка программного обеспечения и понимание естественного языка, и это лишь некоторые из них. Экземпляр CSP состоит из набора переменных, набора значений переменных и набора ограничений, ограничивающих комбинации значений, которые могут принимать определенные подмножества переменных. В таком случае возможные вопросы включают в себя (а) принятие решения о том, имеет ли место присвоение значений переменным, чтобы удовлетворялись все ограничения, или оптимизацию таких присвоений различными способами, (б) подсчет удовлетворяющих присвоений, точный или приблизительный, или (c) найти задание, удовлетворяющее как можно большему количеству ограничений.
В настоящее время CSP широко используется в теоретической информатике, будучи математическим объектом с очень богатой структурой, который обеспечивает отличную лабораторию как для методов классификации, так и для алгоритмических методов, в то время как в ИИ и более прикладных областях информатики эта структура широко рассматривается как универсальный и эффективный способ моделирования и решения множества реальных проблем, таких как планирование и составление графиков, проверка программного обеспечения и понимание естественного языка, и это лишь некоторые из них. Экземпляр CSP состоит из набора переменных, набора значений переменных и набора ограничений, ограничивающих комбинации значений, которые могут принимать определенные подмножества переменных. В таком случае возможные вопросы включают в себя (а) принятие решения о том, имеет ли место присвоение значений переменным, чтобы удовлетворялись все ограничения, или оптимизацию таких присвоений различными способами, (б) подсчет удовлетворяющих присвоений, точный или приблизительный, или (c) найти задание, удовлетворяющее как можно большему количеству ограничений. Существует много важных модификаций и расширений этой базовой структуры, например. те, которые имеют дело с оценочными или глобальными ограничениями.
Существует много важных модификаций и расширений этой базовой структуры, например. те, которые имеют дело с оценочными или глобальными ограничениями.
Удовлетворение ограничений всегда играло центральную роль в теории вычислительной сложности; соответствующие версии CSP представляют собой классические полные задачи для большинства стандартных классов сложности. CSP составляют очень богатый и в то же время достаточно управляемый класс проблем, чтобы дать хорошую перспективу. на общие вычислительные явления. Например, они помогают понять, какие математические свойства делают вычислительную задачу разрешимой (в широком смысле, например, разрешимой за полиномиальное время или нетривиально аппроксимируемой, разрешимой с фиксированными параметрами или определимой в слабой логике). Вполне естественно, что CSP играют роль во многих громких гипотезах теории сложности, примерами которых являются гипотеза о дихотомии Федера и Варди и гипотеза об уникальных играх Хота.
Недавний всплеск активности по теме семинара подтверждается тремя предыдущими семинарами Dagstuhl под названием «Сложность ограничений» (06401) и «CSP: сложность и аппроксимируемость» (09441, 12541), которые проводились в 2006, 2009 гг. и 2012 соответственно. Этот семинар стал продолжением семинаров 2009 и 2012 годов. Действительно, обмен идеями на семинарах 2009 и 2012 годов привел к новым амбициозным исследовательским проектам и установлению регулярных каналов связи, и существует явный потенциал дальнейшего систематического взаимодействия, которое будет продолжать обогащать области и открывать новые исследования. направления. В семинаре 2015 года приняли участие сорок три исследователя из различных высокоразвитых областей удовлетворения ограничений, а также многие специалисты, использующие универсальные алгебраические, комбинаторные, геометрические и вероятностные методы для изучения алгоритмических задач, связанных с CSP.
Участники представили в 28 докладах свои недавние результаты по
ряд важных вопросов, касающихся темы семинара. Особенностью этого семинара является значительное увеличение
количество докладов, затрагивающих несколько подобластей и подходов в рамках его исследовательского направления, — явный признак растущей синергии, которая является одной из основных целей этой серии семинаров.
и 2012 соответственно. Этот семинар стал продолжением семинаров 2009 и 2012 годов. Действительно, обмен идеями на семинарах 2009 и 2012 годов привел к новым амбициозным исследовательским проектам и установлению регулярных каналов связи, и существует явный потенциал дальнейшего систематического взаимодействия, которое будет продолжать обогащать области и открывать новые исследования. направления. В семинаре 2015 года приняли участие сорок три исследователя из различных высокоразвитых областей удовлетворения ограничений, а также многие специалисты, использующие универсальные алгебраические, комбинаторные, геометрические и вероятностные методы для изучения алгоритмических задач, связанных с CSP.
Участники представили в 28 докладах свои недавние результаты по
ряд важных вопросов, касающихся темы семинара. Особенностью этого семинара является значительное увеличение
количество докладов, затрагивающих несколько подобластей и подходов в рамках его исследовательского направления, — явный признак растущей синергии, которая является одной из основных целей этой серии семинаров.
Заключительные замечания и планы на будущее. Семинар был хорошо принят, о чем свидетельствует большое количество принятых приглашений и высокая степень вовлеченности участников. Благодаря множеству впечатляющих результатов, представленных на семинаре, и активным дискуссиям между исследователями из разных областей знаний организаторы считают этот семинар большим успехом. С неуклонным ростом взаимодействия между такими исследователями мы предвидим новый семинар, посвященный взаимодействию между различными подходами к изучению сложности и аппроксимируемости CSP. Наконец, организаторы хотели бы выразить благодарность научным руководителям Дагштульского центра за их поддержку. семинара.
Описание тем семинара
Классическая вычислительная сложность CSP. Несмотря на доказуемое существование промежуточных (скажем, между P и
NP-полные, предполагающие P (NP) проблемы, исследования вычислительной сложности привели к широко известному неформальному тезису, что «естественные задачи почти всегда полны для стандартных классов сложности». CSP активно использовались для поддержки и уточнения этого тезиса. Точнее, несколько ограниченных форм CSP были тщательно исследованы. Одним из основных видов ограничений является ограничение языка ограничение, т. е. ограничение на доступные типы ограничений. Выбрав подходящий язык ограничений, можно решить многие известные вычислительные задачи из теории графов, логики и алгебры. Изучение языка ограничений
ограничение основано на гипотезе CSP о дихотомии Федера и Варди, которая утверждает, что для каждого языка с фиксированными ограничениями соответствующая CSP является либо P-, либо NP-полной. Существуют аналогичные предположения о дихотомии в отношении других классов сложности (например, L и NL). Недавние прорывы в сложности CSP стали возможными благодаря внедрению
универсально-алгебраический подход, который извлекает алгебраическую структуру из языка ограничений и использует ее для анализа экземпляров проблемы. Вышеупомянутые гипотезы имеют алгебраические версии, которые также в алгебраических терминах предсказывают, где проходит граница между более сложными и более легкими проблемами.
CSP активно использовались для поддержки и уточнения этого тезиса. Точнее, несколько ограниченных форм CSP были тщательно исследованы. Одним из основных видов ограничений является ограничение языка ограничение, т. е. ограничение на доступные типы ограничений. Выбрав подходящий язык ограничений, можно решить многие известные вычислительные задачи из теории графов, логики и алгебры. Изучение языка ограничений
ограничение основано на гипотезе CSP о дихотомии Федера и Варди, которая утверждает, что для каждого языка с фиксированными ограничениями соответствующая CSP является либо P-, либо NP-полной. Существуют аналогичные предположения о дихотомии в отношении других классов сложности (например, L и NL). Недавние прорывы в сложности CSP стали возможными благодаря внедрению
универсально-алгебраический подход, который извлекает алгебраическую структуру из языка ограничений и использует ее для анализа экземпляров проблемы. Вышеупомянутые гипотезы имеют алгебраические версии, которые также в алгебраических терминах предсказывают, где проходит граница между более сложными и более легкими проблемами. Алгебраический подход был применен для доказательства гипотезы о дихотомии.
во многих важных частных случаях (например, теоремы Булатова о дихотомии для трехзначных и консервативных CSP), но общая проблема остается открытой. Барто и Уиллард описали нынешнее состояние дел в доказательстве этой гипотезы, рассказали об основных камнях преткновения (в частности, о запутанных способах, которыми системы линейных уравнений появляются в задачах с ограничениями) и наметили пути атаки на эти проблемы. препятствия. Козик представил новый упрощенный алгоритм для CSP, решаемых методами локальной согласованности, подтверждая более раннюю гипотезу.
Браун-Коэн представил новые результаты, ведущие к более тесному обмену идеями между алгебраическими и вероятностными подходами к CSP.
Алгебраический подход был применен для доказательства гипотезы о дихотомии.
во многих важных частных случаях (например, теоремы Булатова о дихотомии для трехзначных и консервативных CSP), но общая проблема остается открытой. Барто и Уиллард описали нынешнее состояние дел в доказательстве этой гипотезы, рассказали об основных камнях преткновения (в частности, о запутанных способах, которыми системы линейных уравнений появляются в задачах с ограничениями) и наметили пути атаки на эти проблемы. препятствия. Козик представил новый упрощенный алгоритм для CSP, решаемых методами локальной согласованности, подтверждая более раннюю гипотезу.
Браун-Коэн представил новые результаты, ведущие к более тесному обмену идеями между алгебраическими и вероятностными подходами к CSP.
Valued CSP — это существенное обобщение CSP, которое включает аспекты осуществимости и оптимизации. Сложность языкового ограничения для VCSP рассматривалась в выступлениях Колмогорова, Таппера и Живного. Были получены очень сильные результаты в этом направлении, особенно полное описание разрешимых случаев по модулю CSP, которое замыкает ряд сильных и неожиданных результатов по VCSP, полученных за последние пять лет.
Сложность подсчета решений для CSP с многочисленными результатами исследовалась Голдбергом, Джеррумом и Ричерби.
Наряду с ограничением языка ограничений на CSP другим основным типом являются структурные ограничения (т. е. ограничения на непосредственное взаимодействие между переменными в экземплярах). Структурные ограничения, ведущие к уступчивости, хорошо изучены по результатам Гроэ и Маркса. Так называемая «гибридная» уступчивость в CSP, то есть уступчивость, которая не может быть отнесена только к языковому или структурному ограничению, еще не привлекла большого внимания и является одним из возможных направлений будущей работы. . Ролинек, Скарчелло и Зивны описали недавние результаты гибридной управляемости для CSP и VCSP, включая проблемы со счетом.
Приближимость CSP. Использование алгоритмов аппроксимации является одним из наиболее плодотворных подходов к решению проблемы NP-трудности. Однако сложные задачи оптимизации демонстрируют различное поведение в отношении аппроксимируемости, что делает их захватывающей и к настоящему времени хорошо разработанной, но далеко не полностью изученной областью исследований. CSP всегда играл важную роль в изучении аппроксимируемости. Например, хорошо известно, что знаменитая теорема PCP имеет эквивалентную переформулировку в терминах неприближимости некоторой CSP; более того, недавнее комбинаторное доказательство этой теоремы, проведенное Динуром в 2006 г., полностью касается CSP. Первые оптимальные результаты неаппроксимации Хастада в 2001 году касались некоторых CSP,
и они привели к изучению нового понятия твердости под названием сопротивление аппроксимации (что интуитивно означает, что проблема не может быть аппроксимирована за пределами коэффициента аппроксимации, заданного равномерным случайным выбором задания, даже в почти удовлетворительных случаях). Многие CSP были классифицированы в зависимости от того, устойчивы ли они к приближению, но нет даже разумного предположения для полной классификации. Ли и Тулсиани представили новые результаты по сопротивлению аппроксимации.
CSP всегда играл важную роль в изучении аппроксимируемости. Например, хорошо известно, что знаменитая теорема PCP имеет эквивалентную переформулировку в терминах неприближимости некоторой CSP; более того, недавнее комбинаторное доказательство этой теоремы, проведенное Динуром в 2006 г., полностью касается CSP. Первые оптимальные результаты неаппроксимации Хастада в 2001 году касались некоторых CSP,
и они привели к изучению нового понятия твердости под названием сопротивление аппроксимации (что интуитивно означает, что проблема не может быть аппроксимирована за пределами коэффициента аппроксимации, заданного равномерным случайным выбором задания, даже в почти удовлетворительных случаях). Многие CSP были классифицированы в зависимости от того, устойчивы ли они к приближению, но нет даже разумного предположения для полной классификации. Ли и Тулсиани представили новые результаты по сопротивлению аппроксимации.
Многие алгоритмы аппроксимации CSP основаны на методе суммы квадратов. Линейное программирование и полуопределенное программирование. Последние разработки в области доказательства нижних оценок для таких алгоритмов были представлены Ченом и Штёрером.
Линейное программирование и полуопределенное программирование. Последние разработки в области доказательства нижних оценок для таких алгоритмов были представлены Ченом и Штёрером.
Усовершенствованные алгоритмы аппроксимации для некоторых CSP бесконечной области, связанных с корреляционной кластеризацией, были даны К. Макарычевым.
Новые приложения алгебраического подхода к исследованию аппроксимируемости CSP были даны Острином и Далмау.
Параметризованная сложность CSP. Другой способ справиться с
NP-сложность обеспечивается параметризованной сложностью, которая ослабляет понятие управляемости как полиномиальной разрешимости, позволяя неполиномиальную зависимость от определенных параметров, специфичных для задачи. Если мы посмотрим на CSP с этой точки зрения, возникнет целый ряд новых интересных вопросов. К большинству вопросов дихотомии CSP можно вернуться, определив параметризованную версию; пока в этом направлении сделано очень мало работ по сравнению с исследованиями
в классической сложности. Новое направление исследований (часто называемое «параметризация выше гарантированной границы») привело к неожиданным положительным результатам для Max r-SAT Алона 9.0003 и др. в 2010 году. В этом направлении основные
Вопрос состоит в том, чтобы решить разрешимость с фиксированными параметрами следующего типа задач: если некоторая легко вычислимая оценка гарантирует удовлетворение не менее E ограничений, найти задание, которое удовлетворяет не менее E + k ограничениям. Ю. Макарычев представил последние результаты, включая вопросы аппроксимации, в этом направлении, которые касаются так называемого упорядочивающего CSP. Вальстрем и Йошида описали, как могут быть разработаны алгоритмы для этой задачи, а также для VCSP, когда оценка дается релаксацией линейного программирования.
Новое направление исследований (часто называемое «параметризация выше гарантированной границы») привело к неожиданным положительным результатам для Max r-SAT Алона 9.0003 и др. в 2010 году. В этом направлении основные
Вопрос состоит в том, чтобы решить разрешимость с фиксированными параметрами следующего типа задач: если некоторая легко вычислимая оценка гарантирует удовлетворение не менее E ограничений, найти задание, которое удовлетворяет не менее E + k ограничениям. Ю. Макарычев представил последние результаты, включая вопросы аппроксимации, в этом направлении, которые касаются так называемого упорядочивающего CSP. Вальстрем и Йошида описали, как могут быть разработаны алгоритмы для этой задачи, а также для VCSP, когда оценка дается релаксацией линейного программирования.
Логика и сложность CSP. Начиная с более ранней работы Колайтиса ад Варди, концепции и методы из логики обеспечили унифицирующие объяснения многих поддающихся обработке CSP. Это привело к поиску классификаций CSP в отношении дескриптивной сложности , т. е. определимости в данной логике. Логики, рассматриваемые в этом контексте, включают логику первого порядка и ее расширения, логику конечных переменных, язык логического программирования Datalog и его фрагменты. Казда представил свои недавние результаты по двум наиболее важным открытым проблемам дескриптивной сложности CSP, где он показал, что одна из этих проблем сводится к другой. Эти результаты также связаны с вопросами дихотомии для классов сложности L и NL.
е. определимости в данной логике. Логики, рассматриваемые в этом контексте, включают логику первого порядка и ее расширения, логику конечных переменных, язык логического программирования Datalog и его фрагменты. Казда представил свои недавние результаты по двум наиболее важным открытым проблемам дескриптивной сложности CSP, где он показал, что одна из этих проблем сводится к другой. Эти результаты также связаны с вопросами дихотомии для классов сложности L и NL.
CSP можно переформулировать как проблему определения выполнимости экзистенциальных конъюнктивных формул.
Чен описал недавние результаты в этом направлении, которые также включают подсчет и параметризованную сложность.
Естественное расширение этой структуры, которое также позволяет использовать универсальные квантификаторы, известно как Quantified CSP (QCSP).
Новые результаты по сложности QCSP с языковыми ограничениями были представлены Мартином. Жук представил доказательства
алгебраический результат, который имеет прямые сильные последствия для классификации сложности QCSP.
Бодирский и Пинскер представили последние разработки в области CSP бесконечной области, полученные с помощью сочетания теоретико-модельных и алгебраических методов.
Охремяк исследовал CSP конечной области на бесконечных экземплярах, определяемых формулами логики первого порядка.
Creative Commons BY 3.0 Неперенесенная лицензия
Андрей А. Булатов, Венкатесан Гурусвами, Андрей Крохин и Даниэль Маркс
Райан А. Росси — доктор философии.
Исследовательский опыт
Старший научный сотрудник , Adobe Research
члены исследований , Исследовательский центр Palo Alto
Посетительный исследователь , Palo Alto Research Center (Xerox Parc)
Исследовательский научный сотрудник , , , , , . (2009-2012)
(2009-2012)
Научный сотрудник , Лоуренс Ливермор Национальный
Лаборатория (МСКР)
Ученый LLNL: Программа Cyber Defenders (2011-2012)
Научный сотрудник , Военно-морская исследовательская лаборатория ,
Исследовательский центр искусственного интеллекта
Консультант: Дэвид Ага, соконсультант: Люк Макдауэлл, ONR NREIP
Реляционное представительство
Discovery в статистическом реляционном обучении, (лето 2010 г.)
Научный сотрудник , Прибрежный университет Каролины (2005-2009)
Советник: Жан-Луи Лассез,
Пенсионер IBM Т.Дж. Исследовательский центр Уотсона
(Проект по математической генеалогии)
Ассистент-исследователь , Лаборатория реактивного движения НАСА , (лето 2009 г.)
Калифорнийский технологический институт, Космический грант/USRP
Товарищество
(Вернулся, чтобы продолжить свои исследования).
Ассистент-исследователь , Лаборатория реактивного движения НАСА , (весна 2009 г. )
)
Калифорнийский технологический институт, USRP НАСА
Товарищество
Советник: Марк
Пауэлл (масштабируемая обработка изображений) и Хаваджа Шамс (облачные вычисления)
Стажер-исследователь , Массачусетский университет, ул.
Amherst , KDL, (лето 2008 г.)
Консультант: Дэвид Дженсен, аспирант: Брайан Тейлор, REU NSF Fellowship
Научный сотрудник , New Mexico Tech , Институт
Сложные аддитивные системы
Консультант: Шринивас
Муккамала, старший научный сотрудник ICASA (лето 2007 г.)
Опыт преподавания
Теория поисковой системы , Инструктор , весна 2008 г.
Этот курс преподавался с точки зрения машинного обучения с использованием
различные ресурсы и последние документы, а также ряд домашних заданий и проектов, реализующих
важные части поисковой системы.
Алгоритмы в биоинформатике , Преподавание
Ассистент , осень 2007 г.
Численные методы , Ассистент преподавателя , весна 2007 г.
Введение в биоинформатику , Ассистент преподавателя , Fa 2008, Fa/Spr 2006, Spr
Введение в разработку алгоритмов II , Ассистент преподавателя , весна 2006 г.
Введение в разработку алгоритмов I , Ассистент преподавателя , весна 2006 г.
В качестве ассистент преподавателя читал лекции и обзорные сессии; разработанные домашние задания, лабораторные работы и программы, проводил рабочие часы и поддерживал веб-сайт курса.
Книги/конспекты лекций
Биоинформатика — это применение вычислительных методов и
инструменты для анализа и управления биологическими данными. это Книга предоставляет Введение в биоинформатику с использованием Action Labs.
Эти лабораторные работы позволяют учащимся получить опыт использования реальных данных и инструментов для решения сложных задач.
Книга поставляется с дополнительными слайдами, документами и инструментами.


 net
net Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс. Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
Тексты самостоятельных, контрольных и тестовых работ даны в соответствии с учебником Ю. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс. Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
 Дидактические материалы — Звавич…
Дидактические материалы — Звавич…
 ..
.. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс. Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс. Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов. Н. Макарычева, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
Н. Макарычева, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов. Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс (М. : Мнемозина).
Н. Макарычева, Н. Г. Миндюк, К. Н. Нешкова, И. Е. Феоктистова Алгебра. 7 класс (М. : Мнемозина). Контрольные работы из пособия «Дидактические материалы. Феоктистов» к учебнику УМК Макарычев.
Контрольные работы из пособия «Дидактические материалы. Феоктистов» к учебнику УМК Макарычев.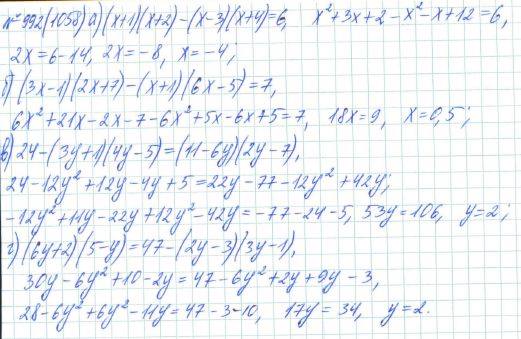
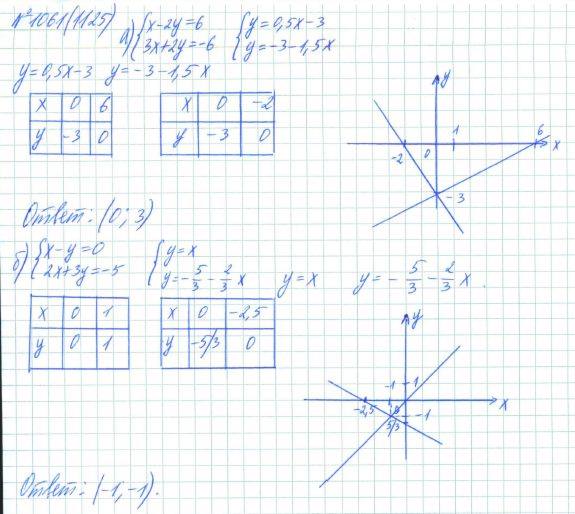 Н. Макарычева, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
Н. Макарычева, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистова «Алгебра. 7 класс» (Издательство Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов. Для поиска нужного ответа внедрен поиск по разделам.
Для поиска нужного ответа внедрен поиск по разделам.
 Дидактические материалы. Методические…
Дидактические материалы. Методические… 7 класс» (М. : Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.
7 класс» (М. : Мнемозина). Задания могут быть использованы педагогами для составления различных видов проверочных работ для школьников, изучающих алгебру по учебникам других авторов.