Страница 29 №89-90 ГДЗ к учебнику «Алгебра» 7 класс Дорофеев, Суворова, Бунимович
Задание 89. а) В школе 16% девочек и 28% мальчиков занимаются в спортивных секциях. Сколько всего процентов школьников занимается в спортивных секциях, если число мальчиков и число девочек в школе одинаково?
б) В школьном оркестре играют 12% всех мальчиков, которые учатся в школе, и 8% всех девочек. Сколько всего процентов учащихся школы играет в оркестре, если мальчики составляют $\frac{3}{5}$ всех учащихся школы?
Решение 7 гуру
а) Пусть x − мальчиков и x − девочек в школе, тогда:
1) 0,16x (девочек) − занимаются спортом;
2) 0,28x (мальчиков) − занимаются спортом;
3) 0,16x + 0,28x = 0,44x (школьников) − занимаются спортом;
4) 0,44x : (x + x) * 100% = 0,44 : 2 * 100% = 22% (школьников) − занимаются спортом.
Ответ: 22%.б) Пусть x − учащихся в школе, тогда:
1) $\frac{3}{5}x$ (мальчиков) − в школе;
2) $(1 — \frac{3}{5})x = \frac{2}{5}x$ (девочек) − в школе;
3) $0,12 * \frac{3}{5}x = \frac{12}{100} * \frac{3}{5}x = \frac{9}{125}x$ (мальчиков) − играют в оркестре;4) $0,08 * \frac{2}{5}x = \frac{8}{100} * \frac{2}{5}x = \frac{4}{125}x$ (девочек) − играют в оркестре;
5) $\frac{9}{125}x + \frac{4}{125}x = \frac{13}{125}x$ (учащихся) − играют в оркестре;
6) $\frac{13}{125}x : x * 100$% = 0,104 * 100% = 10,4% (учащихся) − школы играют в оркестре.
Ответ: 10,4%.
-(Itogovoe-povtorenie)-reshenie-89.jpg)
Задание 90. Решите задачу, используя схематические рисунки.
а) Книга дороже альбома на 25%. На сколько процентов альбом дешевле книги?
Решение.
Цена альбома − 100%. Изобразим ее каким−либо отрезком. Увеличим этот отрезок на 25%, то есть на $\frac{1}{4}$ его длины; получим отрезок, соответствующий цене книги (рис.1.9).
Теперь цена книги составляет 100% (рис.1.10). Она изображена большим отрезком. Цена альбома меньше цены книги на $\frac{1}{5}$ этого отрезка. Так как $\frac{1}{5}$ составляют 20%, то альбом дешевле книги на 20%.
в) Чашка на 20% дороже блюдца. Какую часть стоимости чашки составляет стоимость блюдца? На сколько процентов блюдце дешевле чашки?
г) Цена книги была повышена на 10%. В конце года вновь была установлена старая цена. На сколько процентов снизили цену книги в конце года?
Решение задач
а)
$\frac{1}{5}$ − это 20%.
Ответ: на 20% альбом дешевле книги.б)
$\frac{1}{4}$ − это 25%.
Ответ: на 25% тарелка дороже блюдца.в)
1) $\frac{1}{6} * 5 = \frac{5}{6}$;
$\frac{1}{6} * 100$% ≈ 16,67%
Ответ: $\frac{5}{6}$ стоимости чашки составляет стоимость блюдца; на 16,67% блюдце дешевле чашки.г)
$\frac{1}{11}$ * 100% ≈ 9,09%
Ответ: на 9,09% снизили цену книгу в конце года.
-(Chislovye-i-algebraicheskie-vyrazhenija)-reshenie-1.9.jpg)
ГДЗ по Алгебре для 7 класса Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров на 5
Авторы: Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров.
Издательство: Просвещение 2015
«ГДЗ по алгебре 7 класс Алимов, Колягин, Сидоров (Просвещение)» было создано лучшими учителями страны с целью улучшения качества образования.
Ни для кого не секрет, что программа по этому и остальным предметам усложняется с каждым годом. Ребятам все труднее справиться с нагрузками в одиночку. Некоторые обращаются за помощью к частным педагогам. Другие записываются на дополнительные курсы. А остальные уже успели убедиться в эффективности данного методического пособия, выпущенного издательством «Просвещение».
Начиная с этого года, подростки больше не будут изучать математику. Она разделится на алгебру и геометрию. А это значит, что на уроках придется усваивать в два раза больше информации. Темы очень сложные, но интересные. К примеру, на уроках алгебры учащиеся будут проходить следующие параграфы учебника:
- Числовые выражения.
- Математическая запись.
- Координатная прямая.
- Умножение и деление степеней с одинаковыми показателями.
- Стандартный вид одночлена.
- Что такое разложение многочленов на множители, и зачем оно нужно?
Если на уроках почти всем ученикам понятна теоретическая часть материала, так как преподаватель старается максимально подробно ее объяснить, то вот при решении практических заданий у многих возникают трудности.
Алгоритм работы с решебником по алгебре для 7 класса от Алимова
Чтобы улучшить оценки по предмету и подтянуть академическую успеваемость, подросток должен регулярно совершать следующие действия:
- – прочтение параграфа;
- – изучение формул и правил;
- – самостоятельное выполнение заданных на дом номеров;
- – сверка ответов;
- – проведение качественной работы над ошибками.
Учащимся среднего звена может показаться, что все эти процессы отнимут много времени, но это вовсе не так. Ребятам не стоит переживать об этом.
ГДЗ для всех школьников
Вне зависимости от того, какой уровень подготовки у подростка, он может смело использовать материалы сборника верных ответов для реализации собственных планов. «ГДЗ по алгебре за 7 класс Алимов Ш.
А., Колягин Ю. М., Сидоров Ю. В. (Просвещение)» превосходно справится с ролью качественного помощника. Онлайн-сборник пригодится отличникам и хорошистам при устранении часто повторяющихся ошибок. А школьники, которым крайне тяжело дается изучение этого предмета, смогут с помощью книги улучшить оценки по нему.
ГДЗ Алгебра 7 класс Колягин, Ткачева
Алгебра 7 класс
Тип пособия: Рабочая тетрадь
Авторы: Колягин, Ткачева
Издательство: «Просвещение»
Похожие ГДЗ Алгебра 7 класс
Часть 1. Задания: стр.4
Предыдущее
Следующее
Предыдущее
Следующее
Рабочая тетрадь по алгебре для 7 класса под редакцией Колягина дополняет учебник. В ней собраны дополнительные задания по теме. Упражнения направлены на:
- Развитие логического мышления, решение нестандартных задач.
- Закрепление новых тем. Здесь содержится больше номеров, которые соответсвуют разному уровню знаний.
- Лучшее усвоение тем. В учебнике содержится теория и немного упражнений. Рабочая тетрадь позволяет продолжить работу дома и организовать активную деятельность на уроке.
Структура рабочей тетради
Пособие развито на разделы и параграфы идентично учебнику. Упражнения делятся на 3 части. Первая направлена на подготовку учеников к изучению нового материала. Вторая часть содержит упражнения, дополняющие номера из книги. Третья – это проверочные, самостоятельные и контрольные работы, которые позволяют оценить уровень знаний ребенка. Тетрадь содержит задания разной сложности – от базовой до высокой и позволяет адекватно выставить оценки.
Что даст ГДЗ
Решебник к учебнику «Алгебра 7 класс Рабочая тетрадь Колягин, Ткачева, Просвещение» — это вспомогательное пособие. Оно используется для самопроверки знаний. ГДЗ помогает вникнуть в тему и лучше понять материал. Особые трудности вызывают темы, связанные с алгебраическими выражениями, одночленами и многочленами, уравнениями с двумя неизвестными и разложением многочленов на множители.
Поэтому иногда лучше проверить, насколько правильно вы выполнили задания, и в случае необходимости исправить ошибки.
Все ГДЗ в одном месте
На нашем сайте собраны решебники к большинству школьных учебников. Мы предлагаем онлайн-версии. Для того чтобы посмотреть решение и ответ, кликните мышкой на необходимый раздел и номер упражнения. Эта рабочая тетрадь издается в 2 частях. Откройте изображение и сравните ответ с собственным. Готовьтесь к урокам вместе с нами!
ГДЗ Алгебра 7 класс Миндюк, Шлыкова
Алгебра 7 класс
Тип пособия: Рабочая тетрадь
Авторы: Миндюк, Шлыкова
Издательство: «Просвещение»
Похожие ГДЗ Алгебра 7 класс
Часть 1. Задания: стр.4
Предыдущее
Следующее
Предыдущее
Следующее
Рабочая тетрадь по алгебре для 7 класса под редакцией Миндюка – это дополнение к учебнику Макарычева. Сюда входит 40 работ и дополнительный материал для тех, кто хочет знать больше.
Автор включил разноуровневые задания, которые позволяют адекватно оценить знания учащихся. Здесь содержатся номера на повторение материала, изученного ранее.
Структура тетради
Рабочая тетрадь имеет следующие разделы:
- Первая часть с заданиям к темам «Выражения, тождества, уравнения», «Функции», «Степень с натуральным показателем».
- Вторая часть с упражнениями, посвященным многочленам, формулам сокращенного умножения и системам линейных уравнений.
- Каждая работа условно разделена на 2 части. В первую часть входят несложные задания. Во вторую – задачи, требующие высокого уровня знаний.
Особенности заданий
Автор разработал самые разнообразные номера. Ученикам предлагается выбрать правильный ответ, продолжить решение или последовательность, установить соответствие и пр. В издании много таблиц, схем и рисунков, которые помогают в решении номеров. Даются упражнения, которые нужно решить по образцу. Все это формирует математические навыки и умения учеников, позволяет закрепить материал на практике.
Онлайн помощник
Для самостоятельной подготовки к урокам создан онлайн-решебник к учебнику «Алгебра 7 класс Рабочая тетрадь, Миндюк, Шлыкова, Просвещение». Это пособие, в котором расписано условие, решение и ответ к каждому заданию. Пользуйтесь им с умом, проверяя собственные знания, а не просто переписывая ответ. И совсем скоро вы сможете повысить балл по математике! Пособие поможет ученикам, родителям, учителям и студентам педагогических ВУЗов для проверки знаний. Учитесь вместе с нашими решебниками! Открывайте любой номер онлайн!
Wolfram | Alpha Примеры: Common Core Math: Grade 7
Другие примеры
Система счисления Выполняет арифметические операции с целыми, дробными и десятичными знаками, в том числе с несколькими операциями в одном выражении.
Сложить и вычесть рациональные числа (CCSS.Math.Content.7.NS.A.1):
Выполните несколько операций с рациональными числами (CCSS.
Math.Content.7.NS.A.2c):
Другие примеры
Другие примеры
Выражения и уравнения Управляйте выражениями и решайте уравнения и неравенства, в том числе с отрицательными числами.
Упростите выражения (CCSS.Math.Content.7.EE.A.1):
Факторные выражения (CCSS.Math.Content.7.EE.A.1):
Решите уравнение (CCSS.
Math.Content.7.EE.B.4a):
Решите неравенство (CCSS.Math.Content.7.EE.B.4b):
Другие примеры
Другие примеры
Соотношения и пропорции Вычисление с отношениями и процентами в различных контекстах.
Определите удельную стоимость, связанную с соотношением (CCSS.Math.Content.7.RP.A.1):
Представьте изменения количеств в процентах (CCSS.Math.Content.7.RP.A.3):
Определите цены и чаевые, используя проценты (CCSS.
Math.Content.7.RP.A.3):
Другие примеры
Другие примеры
Статистика и вероятностьАнализируйте и сравнивайте наборы данных, в том числе полученные из вероятностных экспериментов.
Сравните центры двух наборов данных (CCSS.
Math.Content.7.SP.B.4):
Сравните изменчивость двух наборов данных (CCSS.Math.Content.7.SP.B.4):
Проведите вероятностные эксперименты (CCSS.
Math.Content.7.SP.C.6):
Другие примеры
Другие примеры
ГеометрияРисование фигур и вычисление геометрических размеров.
Если возможно, нарисуйте треугольник с заданной длиной сторон (CCSS.Math.Content.7.G.A.2):
Рисование фигур с заданными условиями (CCSS.
Math.Content.7.G.A.2):
Решите для измерения кругов (CCSS.Math.Content.7.G.B.4):
Решение для измерений трехмерных тел (CCSS.Math.Content.7.G.B.6):
Другие примеры
Страница не найдена | Движение с математикой — RTI Math Leader
Движение с математикой НовостиИнформационный бюллетень для учителей математики
Прочтите последний выпуск нашего информационного бюллетеня FocalPoint!
Информационный бюллетень весны 2017
Пирсон получает награду выдающихся выпускников Колледжа образования и человеческого развития Миннесотского университета
Ее компания помогла более пяти миллионам студентов выучить математику по всей стране.
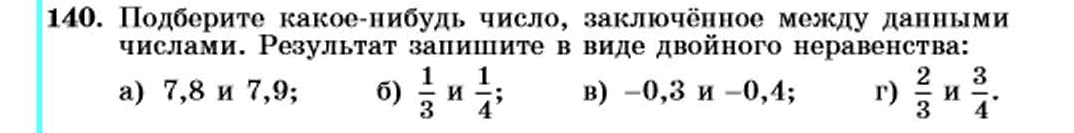
Кэрил Пирсон, единственная женщина в выпускном классе преподавателей математики 1957 года, является лауреатом в 2010 году награды Колледжа образования и развития человеческого потенциала Миннесотского университета.
Пирсон была отмечена своей альма-матер за ее новаторскую работу в качестве преподавателя математики и ее влияние на математическое образование. Проработав 20 лет учителем математики, она основала Math Teacher’s Press Inc., которая сегодня является ведущим издателем дополнительных материалов, призванных помочь ученикам преуспеть в математике.
«Для меня большая честь получить эту награду от Колледжа образования и человеческого развития», — сказал Пирсон.«Замечательные профессора, с которыми я работал в Университете М, вдохновили мою любовь к математике и мою любовь к преподаванию. Основа, которую они мне дали, позволила мне обратиться к ученикам всех уровней способностей и помочь им добиться успеха.
В 1980 году, когда Пирсон преподавал в Юго-Западной средней школе в Миннеаполисе, в школу прибыла большая группа студентов Юго-Восточной Азии из пяти стран в возрасте от 12 до 20 лет, не получивших формального образования и не знающих английского языка.
Когда ее директор попросил ее подготовить этих студентов к алгебре I, она попросила доктораУильяма Барта, руководителя отдела педагогической психологии Университета Массачусетса, за советом. Он сказал ей, что она должна разработать тест, чтобы определить, где находятся ученики, а затем обучить каждой цели с помощью манипулятивных действий.
Пирсон принял его совет близко к сердцу: преподавал днем, а по ночам читал Жана Пиаже и составлял программу по математике. Ее ученики выучили три-четыре года математики всего за шесть месяцев. Позже Пирсон разработала первые эталонные тесты для государственных школ Миннеаполиса, опыт, который помог ей увидеть, что, если она продолжит преподавать математику абстрактно, как в течение 20 лет, она никогда не достигнет учеников из нижнего квартиля.
Оба этих опыта явились новаторской основой для Math Teacher’s Press, которая разрабатывает и распространяет ее учебные программы Moving with Math по всей стране. Сегодня, имея 45 сотрудников, статистически значимые показатели улучшения и долгосрочные рабочие отношения с некоторыми из самых нуждающихся государственных школ страны, Math Teacher’s Press может с гордостью заявить, что помогает более пяти миллионам учеников изучать математику.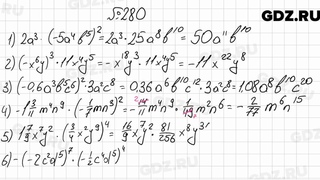
Конечная мечта Пирсона — это всех студентов в U.С. изучает математику, необходимую для продуктивной жизни.
«В знак признания образовательной и деловой карьеры Кэрил в области математического образования и ее поддержки студентов из групп риска, мы рады вручить ей нашу награду« Выдающиеся выпускники », — сказала Джин К. Куам, декан Педагогического и гуманитарного колледжа. Разработка на У М.
В этом году награду «Выдающиеся выпускники колледжа образования и человеческого развития» получили 37 из более чем 70 000 ныне живущих выпускников колледжа.По данным колледжа, впервые в этом году награда присуждается выпускникам, которые проявили себя в своей карьере и в обществе, а также положительно изменили жизнь детей, молодежи, семей, школ, учреждений и организаций.
Пресс-релиз Пирсона (декабрь 2010 г.)
Что работает Информационная служба публикует рекомендации для RTI
Движение с математикой объединяет эти рекомендации Веб-сайт информационного центра «Что работает» http: // ies.
ed.gov/ncee/wwc/ недавно опубликовал восемь рекомендуемых передовых методов реагирования на вмешательство. Эти рекомендации включены в программу Moving with Math , опубликованную Math Teachers Press, Inc.
Ответ на вмешательство
Создание или выбор программ вмешательства
Набор вопросов, разработанный NCTM
«В ответ на призыв сообщества математиков о помощи в создании или выборе эффективных программ вмешательства NCTM разработала ряд вопросов, которые помогут педагогам пройти этот сложный процесс.Учителя и администраторы должны учитывать следующее при выборе программы вмешательства: диагностическая оценка, учебные мероприятия, постоценка, организационная структура вмешательства и исследования, поддерживающие вмешательство. Полная версия PDF-файла NCTM Создание или выбор программ вмешательства приведена ниже.
Выбор программы вмешательства
открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Класс 7A
Марка 7Б
7 класс (A и B вместе)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 8A
Оценка 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 4A
Класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 6А
Марка 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.
Вы можете делать ксерокопии, распечатывать и распространять их сколь угодно часто. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (безымянные версии)
Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
числовых предложений: язык математики
Согласно стандартам, смысл равенства — это то, что учащиеся усваивают в первом классе.А студенты, свободно владеющие языком числовых предложений, понимают, что равенство означает баланс. Но для многих учеников, даже в средней и старшей школе, знак равенства означает «Ответ здесь».
Студенты, которым не хватает этого понимания, год за годом сталкиваются с проблемами. Они борются с переменными, значением операций, распределительными и ассоциативными свойствами, одно- и двухшаговыми уравнениями и даже функциями.
И это лишь некоторые из основных стандартов, основанных на твердом понимании равенства.
Хотя концепция равенства является основой более поздних стандартов, она редко оценивается после первого класса. Учащиеся, неправильно понимающие равенство, могут делать ошибки, которые кажутся небрежными или поспешными.
Другие могут прийти к правильным ответам, но используют неточные обозначения и изо всех сил пытаются составить свои собственные уравнения для решения словесных задач.
Если вы преподаватель математики, в вашем классе почти наверняка есть ученики, которые не на самом деле понимают знак равенства. Трудно оценить, поскольку заблуждения у разных учеников разные.Рассмотрим следующее:
Х + 7 = 10 = 10-7 = 3
В этом примере ученик не балансирует уравнение. Скорее всего, они решают в уме и записывают свою работу запоздало. Хотя ответ правильный, эта стратегия будет работать только для простейших уравнений.
Доказательства числовых предложений помогут вашим ученикам избежать ошибок такого типа. И что самое приятное, вам не нужно добавлять еще одну тему в свой учебный план. Вы можете легко превратить большинство стандартов в доказательство числовых предложений.
Почему имеет значение свободное владение числовыми предложениями Термин номер предложение часто ассоциируется с начальной школой.
Но его полезность выходит за рамки элементарного, поскольку включает в себя как уравнения, так и неравенства. Числовое предложение — это математическое утверждение, состоящее из двух выражений и символа отношения (=,>, <и т. Д.).
Уравнение — это числовое предложение, символом отношения которого является знак равенства. Неравенство — это числовое предложение, символом отношения которого является что-то еще.Подчеркивание связи между уравнениями и неравенствами способствует осмыслению. Это также помогает студентам увидеть сходство в работе с уравнениями и неравенствами.
Доказывая и опровергая числовые предложения, учащиеся углубляют свое понимание равенства как баланса. Это понимание лежит в основе алгебраического мышления и полезно задолго до того, как студенты пойдут на курс алгебры.
Есть три важные причины, по которым учащимся необходимо , чтобы свободно владеть языком числовых предложений, чтобы добиться успеха в математике.
1. Арифметика не концептуальна
Когда я учился в школе, математика в начальной и средней школе была связана с арифметикой. Считалось, что студентам необходимо научиться считать, прежде чем они смогут выполнять более «продвинутую» работу по рассуждению.
Мы запоминали «математические факты» и выполняли сложенные алгоритмы. С возрастом числа становились больше (сотни, тысячи и т. Д.) И меньше (дроби, десятичные знаки). Но концепции остались почти такими же.
Запоминание таблиц умножения и способность переносить, брать взаймы и выполнять деление в столбик имеет свои преимущества.Но многие студенты , кажется, владеют определенными темами, когда на самом деле они просто повторяют процедуры. Сто лет назад умение считать арифметикой могло обеспечить вам хорошо оплачиваемую работу. Сегодня не так много. Использование математики в вашей карьере требует понимания математики и применения ее в реальном мире. Просто научиться имитировать калькулятор уже недостаточно.
2. Отличники математики могут бороться по алгебре
Когда ученики сосредотачиваются на математических фактах и алгоритмах, многие оказываются крайне неподготовленными к высшей математике.Каждый пятый студент в США бросает среднюю школу. Основная причина? Невозможность пройти алгебру.
Странно то, что алгебра не должна быть такой сложной. Школы на самом деле усложняют алгебру, делая упор на вычисления в младших классах и экономя на рассуждениях. Многие студенты вырастают с верой в то, что математика требует быстрого выполнения расчетов.
Некоторые студенты от природы любопытны. Они исследуют концепции, лежащие в основе вычислений, без явного обучения.Эти студенты плавно переходят к алгебре. Но есть большая группа учеников, которые хорошо успевают по математике до 7-8 класса. Как только они сталкиваются с переменными и функциями, они попадают в стену.
3. Числовые предложения помогают учащимся увидеть связи
Современные математические стандарты направлены на устранение трудностей, с которыми сталкиваются многие студенты при переходе на алгебру. Это включает в себя включение алгебраического мышления в математику начальной и средней школы.
Когда учащиеся выполняют операции с алгоритмами, гибкости мало.Они повторяют процесс, часто не понимая, почему этот процесс работает. Например, ученик может сложить 27 и 89, не осознавая, что когда они объединяют 9 и 7, они создают новые 10 и 6. Или что они складывают 8 десятков и 2 десятков, чтобы получить сотню.
Но, используя числовые предложения, студенты могут разбивать числа на части, чтобы увидеть значение каждой цифры. Они могут составлять и разлагать числа по разряду или использовать другие стратегии, развивая свои логические и математические навыки.
Это всего лишь один пример того, как числовые предложения могут помочь учащимся развить навыки счета и математического мышления — в данном случае на основе понимания основы 10. Подобные примеры имеются в большом количестве для дробей, десятичных знаков, минусов, процентов, функций и т. Д.
Математическое мышление, постоянная задача для преподавателей
Стандарты математики адаптированы, чтобы усилить упор на математические рассуждения. И числовые предложения могут оказать существенную поддержку в совершении перехода.
Но стандарты не обязательно приводят к эффективному обучению. Частично проблема заключается в том, что многие школы по-прежнему полагаются на учебники для внесения изменений, несмотря на свидетельства того, что выбор учебника практически не влияет на успеваемость учащихся.
Преподавание концептуальной математики требует высокого профессионального уровня и более эффективных ресурсов. Педагоги, привыкшие обучать арифметике, не могут внезапно перейти к обучению алгебраическому мышлению. Многим нужно выучить алгебраические предметы для своего класса — темы, которым никогда не преподавали, когда мы учились в школе.
Педагогам также необходимо выходить за рамки «Я делаю, мы делаем, ты делаешь». Хотя моделирование и повторение могут работать для обучения вычислениям и другим задачам с низким DOK, они не способствуют глубокому обучению. Чтобы развивать математические рассуждения, преподаватели должны предлагать обучение, ориентированное на учащихся и основанное на запросах.
Привлекайте студентов с помощью числовых доказательствОтличный способ вызвать интерес и поддержать глубокое обучение — это числовые предложения. Практически любой стандарт математики можно преподать с помощью числовых предложений.Первый шаг — просто разложить алгоритмы.
Доказательства числовых предложений помогают учащимся выйти за рамки разрозненных «математических фактов» и увидеть связи между числами. Например, учение «34 x Y = 68» помогает укрепить концепцию равенства. Он также показывает взаимосвязь между умножением и делением. Обучение «4 x 7 = (2 X 7) + (2 X 7)» не только помогает студентам освоить свои таблицы умножения, но также усиливает визуальное моделирование и свойство распределения.
По мере того, как учащиеся развивают свободное владение числовыми предложениями, навык становится «средством» для обучения ряду стандартов.Числовые предложения могут поддерживать сложение нескольких цифр, эквивалентные дроби, соотношения и пропорции, а также практически любой стандарт, о котором вы только можете подумать.
Но сначала студенты должны усвоить условные обозначения. Им следует начать с проверки концепций, которые они уже усвоили. Затем используйте их понимание числовых предложений, чтобы представить новый контент.
Учите равенству как равновесию
Это может быть наиболее важным основанием для беглости числовых предложений. Покажите учащимся, что знак равенства подобен шкале.Я протягиваю руки и делаю вид, что что-то добавляется или удаляется. Чтобы оставаться уравновешенным, все, что происходит с одной стороной, должно происходить с другой.
Это относится к идее обратных операций. Возьмем x + 5 = 8. Чтобы найти x, я вычитаю 5 с обеих сторон. Это показывает, что сложение и вычитание противоположны. Его также можно расширить, чтобы показать, что деление противоположно умножению.
Читать слева направо и упрощать вниз
Изучение правил для работы с числовыми предложениями позволит студентам упростить сложные многоступенчатые уравнения.Одним из таких правил является чтение числовых предложений слева направо. Другой пишет каждый шаг под предыдущим.
Эти соглашения усиливают смысл и цель математических операций. Начните со значения. Сделайте что-нибудь с этим значением (сложите, вычтите, умножьте или разделите). Найдите результат операции.
Сначала мы хотим, чтобы учащиеся привыкли к простым числовым предложениям. Одна операция с результатом справа от знака равенства. Затем мы можем постепенно вводить числовые предложения с несколькими операциями, переменными, группирующими символами и т. Д.
Хотя в целом важно поддерживать творческие способности и исследования учащихся, это неприменимо к соглашениям. Студентов следует научить строго придерживаться подходов «слева направо» и «упрощать нисходящие» при работе с числовыми предложениями.
Не имеет значения, предпочитает ли учащийся размещать свои шаги в беспорядке на странице. Студентам необходимо усвоить, что математика — это язык. Если кто-то не может легко понять свои шаги, значит, он не общается эффективно.
Работа вниз (один шаг на строку) также является важной привычкой, которая позволяет учащимся систематизировать свои мысли при выполнении более сложных, многошаговых задач.
Один знак равенства в каждой строке
Многие студенты, которые не развили беглость с числовыми предложениями, будут работать поперек, а не упрощать вниз.
Вы можете увидеть, как учащиеся используют несколько знаков равенства в каждой строке. Эта привычка проявляется даже в математике высокого уровня. Но в то время как профессор колледжа может нарушать правила, студенты, которые все еще учатся работать с уравнениями, не должны увлекаться.
Непонимание равенстваСохранение одного знака равенства в каждой строке усиливает идею баланса. В конце концов, мы учим студентов думать о числовом предложении как о шкале.
Попробуйте представить шкалу с тремя или четырьмя точками равновесия — как именно это будет работать?
Оставить числовое предложение неизменным
Еще одна привычка, которую развивают некоторые ученики, — это разбивать числовые предложения вместо того, чтобы работать вниз. Например:
х — 14 = 17 + 20
17 + 20 = 37
х-14 = 37
37 + 14 = 51
На первом этапе ученик берет выражение справа от знака равенства и создает новое уравнение.На следующем этапе они объединяют упрощенное выражение (37) с исходным выражением (x-14) с левой стороны.
Окончательный «ответ» почти правильный (мы потеряли нашу переменную по пути) и демонстрирует скромный уровень владения языком. Но этот подход показывает, что учащийся не может упростить, оставив уравнение неизменным.
Сначала вы можете разрешить студентам работать таким образом. Но если с этой привычкой быстро не избавиться (дни или недели), ученик не сможет перейти к более сложным уравнениям.
Кроме того, многие студенты, которые так разбивают уравнения, запутаются, пытаясь «перестроить» в одно уравнение, и сделают небрежные ошибки.
Доказательства приговора с закрытым номером
При введении доказательств числовых предложений начните с «закрытых» числовых предложений. Это числовые предложения без переменных. Студентам дается полное математическое утверждение, и они должны решить, истинно оно или ложно. Например, «⅔ — ⅓ = 1.»
Это похоже на «анализ ошибок», который может быть эффективным способом развития критического мышления.Это также стандарт математической практики (CCSS.MATH.PRACTICE.MP3) и проблема, которая часто встречается в стандартных тестах.
Студенты сначала доказывают или опровергают числовое предложение вычислением. Доказательство расчетом состоит в упрощении обеих сторон до очевидной истины.
Например, уравнение, которое упрощается до «1 = 1», будет истинным. Уравнение, которое упрощается до «2 = 1», окажется ложным.
Затем студенты завершают доказательство рассуждением.Здесь студенты объясняют , почему уравнение истинно или ложно. Это показывает, что они понимают концепции, лежащие в основе вычислений, и что они могут делать общие выводы о свойствах чисел и операций.
Ученик может доказать 3 x (10 + 13) = 30 + 39 вычислением. Но если они не могут объяснить, почему это работает, они не узнают другие экземпляры свойства распределения.
Иногда учащиеся понимают концепцию, но с трудом могут выразить свое понимание в письменной форме.По этой причине учащимся может быть полезно использовать визуальные модели в качестве доказательства путем рассуждений. Если они могут нарисовать сценарий, это явный признак того, что они понимают концепцию.
Профессиональное обучение
Товаров, соответствующих вашему запросу, не обнаружено.
Доказательства предложения открытого числа
Когда учащиеся научатся работать с закрытыми числовыми предложениями, мы можем ввести открытые числовые предложения — числовые предложения с переменными.
Поскольку у них есть переменные, многие предложения с открытыми числами не будут « всегда истинно» или «всегда ложно ». »Некоторые будут, но теперь нам нужна третья категория для числовых предложений, которые« иногда верны ».
Доказательства позволяют студентам более гибко думать о переменных. Многих студентов смущают переменные, потому что они настолько абстрактны. Они сосредотачиваются на «поиске x», что подтверждает идею о том, что математика — это получение ответов. Многие учатся выполнять математику с переменными, но до сих пор не понимают их смысла.
Но когда студенты завершают доказательство открытого числового предложения, они получают более достоверное понимание того, как математики используют переменные. Математики изобретали переменные не для того, чтобы учащиеся могли «решать относительно x».
переменных были разработаны для того, чтобы мы могли разрабатывать, изучать и манипулировать математическими сценариями, когда у нас нет всей информации. Завершение доказательств приближает учащихся к первоначальной цели, делая их обучение более достоверным.
Поддержка свободного владения числовыми предложениямиМне потребовалось время, чтобы сделать числовые предложения регулярной частью моей школьной практики.Основная причина заключалась в том, что я не мог найти достаточно ресурсов для их эффективного обучения.
Со временем я разработал планы уроков, примеры задач и графические органайзеры, которые упростили обучение числовым доказательствам предложений. Планы уроков и примеры задач обеспечивали привязку занятий к стандартам, которые я преподаю. А организаторы помогли студентам структурировать свое мышление.
Вы можете скачать эти занятия в нашем интернет-магазине. Если вы хотите развить свой опыт в обучении числовым предложениям и алгебраическому переосмыслению, запишитесь на один из наших онлайн-семинаров.Это интерактивные занятия в реальном времени с ведущим в реальном времени. Вы можете выбрать из числовых предложений начальной школы или выражений и уравнений средней школы .
ПОСМОТРЕТЬ РЕСУРСЫ
Интервенционное исследование в 7 классе по JSTOR
АбстрактныйНемногие ученики проявляют чувство числа при решении арифметических задач в школе. В этом исследовании изучались эффекты вмешательства в обучение учеников седьмого класса с целью развития чувства числа.Классный руководитель из экспериментальных подразделений обучал студентов числовой величине, мысленному вычислению и вычислительной оценке. Инструкции были разработаны, чтобы предоставить широкие возможности для изучения чисел, числовых отношений и числовых операций, а также для открытия правил и изобретения алгоритмов. Письменные измерения и собеседования до обучения, сразу после обучения и несколько месяцев спустя показали, что после обучения студенты с большей вероятностью выберут стратегии, отражающие числовое чувство, и что это изменение было долгосрочным.Исследователям показалось, что студенты реорганизовали и использовали существующие знания, а не приобрели новые структуры знаний.
Информация о журналеОфициальный журнал Национального совета учителей математики (NCTM), JRME является ведущим исследовательским журналом в области математического образования и посвящен интересам учителей и исследователей на всех уровнях — от дошкольного до колледжа.
Информация об издателеНациональный совет учителей математики — это общественный голос в области математического образования, обеспечивающий видение, руководство и профессиональное развитие для поддержки учителей в обеспечении высочайшего качества обучения математике для всех учащихся.NCTM, насчитывающая около 90 000 членов и 250 аффилированных лиц, является крупнейшей в мире организацией, занимающейся улучшением математического образования в классах от дошкольного до 12-го класса. «Принципы и стандарты школьной математики» Совета являются руководящими принципами для достижения совершенства в математическом образовании и призывают всех учащихся. заниматься более сложной математикой. NCTM нацелен на постоянный диалог и конструктивное обсуждение со всеми заинтересованными сторонами того, что лучше всего для студентов нашей страны.
.