мир издательства | Мир Книги
Опубликовано 13 октября 2018 г. автором The Mitr
В этом посте мы увидим три из пяти томов «Основы проектирования машин» П. Орлова. О книгах: Цель настоящей книги — предложить читателю попытку системного изложения правил рационального … Продолжить чтение →
Рубрика: книги, техника, мир книг, мир издательства | Метки: сборка, литые мембраны, холодное крепление, соединения, циклическая структура, конструкция, долговечность, машиностроение, воображение, машина, обслуживание, механика, методы, надежность, жесткость, заклепочные соединения, деформация, напряжение, поверхность, сварные соединения | 6 комментариев
Опубликовано 13.10.2018 автором The Mitr
В этом посте мы увидим книгу В. П. Маслова «Операционные методы». …Эта книга посвящена одному, но достаточно общему операционному методу, который поглощает многие известные на сегодняшний день операционные методы и позволяет единообразно решать … Продолжить чтение →
Опубликовано в книги, математика, мир книг, издательство мир | Метки: алгебра, асимптотические методы, исчисление, канонические преобразования, задача Коши, диссипация, собственные функции, функции, уравнения Гамильтона-Якоби, гомоморфизм, лаграниан, нильпотентная алгебра Ли, математика, некоммутативность, операционное исчисление, операционный метод, операторы, пространство Шмидта, спектр, t-произведения, теорема | Оставить комментарий
Опубликовано 13. 10.2018 автором The Mitr
10.2018 автором The Mitr
В этом посте мы увидим книгу «Сопротивление материалов» Н. М. Беляева. О книге: Спустя 11 лет вышло новое издание книги Н. М. Беляева «Сопротивление материалов». За 33 года, прошедших между … Продолжить чтение →
Posted in книги, техника, мир книг, мир издательства, физика | Tagged анализ, стержни, балки, изгиб, сжатие, ползучесть, деформации, проектирование, проектирование, нагрузка, материал, физика, столбы, сдвиг, сопротивление материалов, напряжение, конструкции, растяжение, кручение, стены | 1 комментарий
Опубликовано 13.10.2018 автором The Mitr
В этом посте мы увидим серию книг (6/7) из серии «Механизмы в современном инженерном проектировании: Справочник для инженеров, конструкторов и изобретателей» И. И. Артоболевского. О книгах (Из предисловия первого тома): Одна из проблем… Продолжить чтение →
Рубрика: книги, машиностроение, мир книг, мир издательства | Метки: кулачок, конструкция, электротехника, электроника, машиностроение, гибкие связи, трение, шестерня, гидравлика, изобретатели, кинематические цепи, рычаг, механика, механизмы, мир книги, издательство мир, пневматика | 4 комментария
Опубликовано 13. 10.2018 автором The Mitr
10.2018 автором The Mitr
В этом посте мы увидим книгу «Тихое солнце» Н. Пушкова и Б. Силкина. О книге: Как события за 150 миллионов километров могут повлиять на нас здесь, на Земле? Но если вы когда-нибудь жаловались на плохое радио… Продолжить чтение →
Рубрика: Астрономия, книги, техника, геология, история, метеорология, мир книги, издательство мир, физика, наука, советская | Tagged астрономия, полярные сияния, земля, галилео, история, международный год тихого солнца, иксы, магнитные поля, магнетизм, северное сияние, физика, солнце, солнечное излучение, солнечные пятна | Оставить комментарий
Опубликовано 13.10.2018 автором The Mitr
В этом посте мы увидим книгу Планета загадок Е. Новикова. О книге (с задней обложки): Эта книга о нашей планете, Земле, которую мы так хорошо знаем. Но так ли это планета загадок? … Продолжить чтение →
Рубрика: астрономия, книги, геология, мир книги, мир издательства, физика, наука, советская | Tagged астрономия, земля, землетрясения, геология, полезные ископаемые, добыча полезных ископаемых, мир книги, океаны, вечная мерзлота, физика, планета, разведка, горные породы, времена года, почва, советские, приливы | Оставить комментарий
Опубликовано 12. 10.2018 автором The Mitr
10.2018 автором The Mitr
В этом посте мы увидим книгу «Решение задач по алгебре и тригонометрии» — В. Литвиненко, А. Мордкович. В предыдущем посте мы видели сопутствующий том этой книги «Решение задач по геометрии». В сопутствующем томе также есть … Продолжить чтение →
Posted in книги, математика, мир книг, мир издательства, задачники | Метки: алгебра, уравнения, показательная, факторизация, функции, неравенства, логарифмические, числовые выражения, полиномы, задачники, задачи, задачи и решения, преобразования, тригонометрия | 6 комментариев
Опубликовано 9 октября 2018 г. автором The Mitr
В этом посте мы увидим книгу А. Штайнхауса «Девять цветов радуги». О книге (с парадного пиджака) Вы когда-нибудь задумывались, сколько цветов в радуге? Семь или, может, девять… Продолжить чтение →
Рубрика: астрономия, книги, электроника, мир книг, мир издательств, физика, наука, техника | Tagged камера, кинематография, электроника, глаз, лазеры, свет, мир книги, мир издательства, оптика, фотография, фотоны, физика, Steinhaus, телевидение, зрение | Оставить комментарий
Опубликовано 7 октября 2018 г.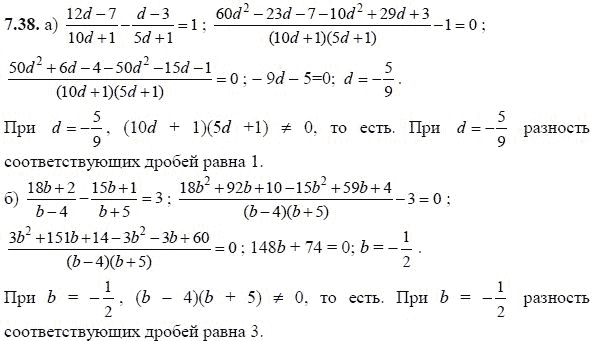 автором The Mitr
автором The Mitr
В этом посте мы увидим книгу «Задачи по геометрии» П. С. Моденова. О книге Этот текст предлагает некоторые общие методы решения задач по элементарной геометрии и предназначен для учителей математики в общеобразовательных школах, а также … Продолжить чтение →
Опубликовано в книги, математика, мир книг, мир издательства, задачники | Tagged аналитическая геометрия, комплексные числа, геометрия, геометрия Маскерони, ячейка Харта, инверсия, математика, механические инверторы, ячейка Поселье, плоская геометрия, задачи и решения, проблемы инверсии, стереометрия, векторы | 2 комментария
Опубликовано 13 сентября 2018 г. автором The Mitr
В этом посте мы увидим долгожданную и несколько редкую книгу «Проблемы теоретической физики» Л. Г. Гречко, В. И. Сугакова, О. Ф. Томасевича А. М. Федорченко. О книге: From the Front Jacket Эта книга представляет собой сборник … Продолжить чтение →
Рубрика: книги, мир книги, издательство мир, физика, задачники | Tagged классическая механика, курс теоретической физики, электродинамика, ландо, лифшиц, физика, задачники, задачи, квантовая механика, решения, статистическая физика, теоретическая физика | 3 комментария
Решение по абстрактной алгебре Даммита и Фута, 3-е издание
- Линейность
- Абстрактная алгебра Даммит Футе
Мы хотели бы предоставить полное руководство по решению этой книги Абстрактная алгебра Даммита и Фута, 3-е издание. Он будет регулярно обновляться. Пожалуйста, также оставьте комментарий, если вы хотите, чтобы какая-то конкретная проблема была обновлена.
Он будет регулярно обновляться. Пожалуйста, также оставьте комментарий, если вы хотите, чтобы какая-то конкретная проблема была обновлена.
Глава 0: Предварительные приготовления
- §0.1: Основы
(#1) (#2) (#3) (#4) (#5) (#6) (#7) - §0.2: Свойства целых чисел
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) - §0.3: Z/(n) – Целые числа по модулю n
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16)
Глава 1: Введение в группы
- §1.1: Основные аксиомы и примеры
(#1) (#2) (# 3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) (#28) (#29) (#30) (#31) ( #32) (#33) (#34) (#35) (#36) - §1.2: Двугранные группы
(#1) (#2) (#3) (#4) (#5) (#6 ) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) - §1.
 3: Симметричные группы
3: Симметричные группы
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11 ) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) - §1.4: Группы матриц
(#1) ( #2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) - §1.5: Группа кватернионов
(#1) (#2) (#3) - §1.6: Гомоморфизмы и изоморфизмы
(#1) (#2) (#3) (#4) (#5) ( #6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) ) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) - §1.7: Групповые действия
(#1) (#2) ( #3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) ) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23)
Глава 2: Подгруппы
- §2.1: Определение и примеры
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) ( #13) (#14) (#15) (#16) (#17) - §2.2: Централизаторы и нормализаторы, стабилизаторы и ядра
(#1) (#2) (#3) (#4) (# 5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) - §2.
 3: Циклические группы и циклические подгруппы
3: Циклические группы и циклические подгруппы
( #1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) ) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) ( #26) - §2.4: Подгруппы, генерируемые подмножествами группы
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) ( #13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) - §2.5: Решетка подгрупп группы
(#1) (# 2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20)
Глава 3. Факторгруппы и гомоморфизмы
- §3.1: Определения и примеры
(#1) (# 2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) (#28) (#29) (#30) (#31) ( #32) (#33) (#34) (#35) (#36) (#37) (#38) (#39) (#40) (#41) (#42) (#43) - § 3.2: Еще о смежных классах и теореме Лагранжа
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) ( #11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) ) - §3.
 3: Теоремы изоморфизма
3: Теоремы изоморфизма
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) - §3.4: Композиционный ряд и программа Гёльдера
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) - §3.5: Транспозиции и чередующаяся группа
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17)
Глава 4: Групповые действия
- §4.1: Групповые действия и представления перестановок
(# 1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) - §4.2: Группы, действующие сами на себя левым умножением – Теорема Кэли
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) - §4.3: Группы, действующие сами на себя посредством сопряжения – уравнение класса
(#1) (#2) (#3) ( #4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) ) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) (#28) ( #29) (#30) (#31) (#32) (#33) (#34) (#35) (#36) - §4.
 4: Автоморфизмы
4: Автоморфизмы
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (# 16) (#17) (#18) (#19) (#20) - §4.5: Теоремы Силова
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) ( #13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) ) (#26) (#27) (#28) (#29) (#30) (#31) (#32) (#33) (#34) (#35) (#36) (#37) ( #38) (#39) (#40) (#41) (#42) (#43) (#44) (#45) (#46) (#47) (#48) (#49) (#50 ) (#51) (#52) (#53) (#54) (#55) (#56) - §4.6: Простота A_n
(#1) (#2) (#3) (#4 ) (#5) (#6) (#7) (#8)
Глава 5. Прямые и полупрямые произведения и абелевы группы
- §5.1: Прямые продукты
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) ( #11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) - §5.2: Основная теорема о конечно порожденных абелевых группах
(#1) ( #2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) ) (#15) (#16) - §5.3: Таблица групп малого порядка
(#1) - §5.
 4: Распознавание прямых произведений
4: Распознавание прямых произведений
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (# 17) (#18) (#19) (#20) - §5.5: Полупрямые продукты
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) ( #10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) ) (#23) (#24) (#25)
Глава 6. Дальнейшие вопросы теории групп
- §6.1: p-группы, нильпотентные группы и разрешимые группы
(#1) (#2) ( #3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) ) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) ( #28) (#29) (#30) (#31) (#32) (#33) (#34) (#35) (#36) (#37) (#38) - §6.2: Приложения в группах среднего порядка
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (# 10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) (#28) (#29) (#30) - §6.3: Несколько слов о свободных группах
(#1) (#2 ) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14)
Глава 7: Знакомство с кольцами
- §7.
 1: Основные определения и примеры
1: Основные определения и примеры
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8 ) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) ( #22) (#23) (#24) (#25) (#26) (#27) (#28) (#29) (#30) - §7.2: Примеры: полиномиальные кольца, матричные кольца и группы Кольца
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) - §7.3: Кольцевые гомоморфизмы и частные кольца
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9 ) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) ( #22) (#23) (#24) (#25) (#26) (#27) (#28) (#29)) (#30) (#31) (#32) (#33) (#34) (#35) (#36) (#37) - §7.4: Свойства идеалов
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (# 15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) (#28) (#29) (#30) (#31) (#32) (#33) (#34) (#35) (#36) (#37) (#38) (#39) (# 40) (#41) - §7.5: Кольца дробей
(#1) (#2) (#3) (#4) (#5) (#6) - §7.
 6: Китайская теорема об остатках
6: Китайская теорема об остатках
( #1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11)
Глава 8. Евклидовы области, главные идеальные области и области уникальной факторизации
- §8.1: Евклидовы области
(#1) (#2) (#3) (#4 ) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) - §8.2: Главные идеальные области
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) - §8.3: Уникальные домены факторизации
(#1) (#2) (#3) (#4) ( #5) (#6) (#7) (#8) (#9) (#10) (#11)
Глава 9: Полиномиальные кольца
- §9.1: Определения и основные свойства
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (# 11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) - §9.2: Кольца многочленов над полями I
(#1) (#2) ( #3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) - §9.3: Полиномиальные кольца которые являются уникальными доменами факторизации
(#1) (#2) (#3) (#4) (#5) - §9.4: Критерии несводимости
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (# 17) (#18) (#19) (#20) - §9.
 5: Кольца многочленов над полями II
5: Кольца многочленов над полями II
(#1) (#2) (#3) (#4) (#5) (#6) (#7) - §9.6: Многочлены в нескольких переменных над полем и основаниями Грёбнера
(# 1) (# 2) (# 3) (# 4) (# 5) (# 6) (# 7) (# 8) (# 9) (# 10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (# 23) (#24) (#25) (#26) (#27) (#28) (#29) (#30) (#31) (#32) (#33) (#34) (#35) (#36) (#37) (#38) (#39) (#40) (#41) (#42) (#43) (#44) (#45)
Глава 10: Введение в теорию модулей
- §10.1: Основные определения и примеры
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10 ) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) ( #23) - §10.2: Фактормодули и модульные гомоморфизмы
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) - §10.3: Создание модулей, прямых сумм и свободных модулей
(#1) (#2) (#3) (# 4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) - §10.
 4: Тензорные произведения модулей
4: Тензорные произведения модулей
(#1) (#2 ) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) ( #15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) ) - §10.5: Точные последовательности – проективные, инъективные и плоские модули
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) ( #9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) ) (#22) (#23) (#24) (#25) (#26) (#27) (#28)
Глава 11: Векторные пространства
- §11.1: Определения и основная теория
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) - §11.2: Матрица линейного преобразования
(#1) (#2) (#3) (# 4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) (#28) (# 29) (#30) (#31) (#32) (#33) (#34) (#35) (#36) (#37) (#38) (#39) - §11.3: Двойные векторные пространства
(#1) (#2) (#3) (#4) (#5) - §11.
 4: Определители
4: Определители
(#1) (#2) (#3) (#4) (#5) (# 6) - §11.5: Тензорные алгебры, симметричные и внешние алгебры
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9 ) (#10) (#11) (#12) (#13) (#14)
Глава 12. Модули над главными идеальными областями
- §12.1: Основная теория
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (# 15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) - §12.2: Рациональная каноническая форма
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) ( #13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) ) - §12.3: Иорданская каноническая форма
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10 ) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) ( #23) (#24) (#25) (#26) (#27) (#28) (#29) (#30) (#31) (#32) (#33) (#34) (#35) ) (#36) (#37) (#38) (#39) (#40) (#41) (#42) (#43) (#44) (#45) (#46) (#47) ( #48) (#49) (#50) (#51) (#52) (#53) (#54) (#55) (#56) (#57) (#58) (#59))
Глава 13: Теория поля
- §13.
 1: Базовая теория расширений поля
1: Базовая теория расширений поля
(#1) (#2) (#3) (#4) (#5) (#6) (#7) ( #8) - §13.2: Алгебраические расширения
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10 ) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) - §13.3: Классические конструкции линейки и компаса
(#1) (#2) (#3) (#4) (#5) - §13.4: Разделяющие поля и алгебраические замыкания
(#1) (#2) ( #3) (#4) (#5) (#6) - §13.5: Отделяемые и неотделимые расширения
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) - §13.6: Циклотомические полиномы и расширения
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17)
Глава 14: Теория Галуа
- §14.1: Основные определения
( #1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) - §14.2: Основная теорема теории Галуа
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) ( #22) (#23) (#24) (#25) (#26) (#27) (#28) (#29) (#30) (#31) - §14.
 3: Конечные поля
3: Конечные поля
(#1 ) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) ( #14) (#15) (#16) (#17) - §14.4: Составные расширения и простые расширения
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) - §14.5: Циклотомические расширения и абелевы расширения над \mathbb{Q}
(#1) (#2) (#3) (#4) (#5) (#6) ( #7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) - §14.6: Группы Галуа многочленов
(#1 ) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) ( #14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) ) (#27) (#28) (#29) (#30) (#31) (#32) (#33) (#34) (#35) (#36) (#37) (#38) ( #39) (#40) (#41) (#42) (#43) (#44) (#45) (#46) (#47) (#48) (#49) (#50) (#51 ) - §14.7: Разрешимые и радикальные расширения: неразрешимость квинтики
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (# 9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) - §14.8: Вычисление групп Галуа над \mathbb{Q}
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9 ) (#10) - §14.
 9: Трансцендентальные расширения, неразделимые расширения, бесконечные группы Галуа
9: Трансцендентальные расширения, неразделимые расширения, бесконечные группы Галуа
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (# 8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19)
Глава 15: Коммутативные кольца и алгебраическая геометрия
- §15.1: Нётеровы кольца и аффинные алгебраические множества
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) ( #13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) ) (#26) (#27) (#28) (#29) (#30) (#31) (#32) (#33) (#34) (#35) (#36) (#37) ( #38) (#39) (#40) (#41) (#42) (#43) (#44) (#45) (#46) (#47) (#48) - §15.2: Радикалы и Аффинные разновидности
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12 ) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) ( #25) (#26) (#27) (#28) (#29)) (#30) (#31) (#32) (#33) (#34) (#35) (#36) (#37) (#38) (#39) (#40) (#41) ( #42) (#43) (#44) (#45) (#46) (#47) (#48) (#49) (#50) (#51) (#52) (#53) (#54) ) - §15.
 3: Интегральные расширения и Nullstellensatz Гильберта
3: Интегральные расширения и Nullstellensatz Гильберта
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (# 10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) (#28) - §15.4: Локализация
(#1) (#2) (#3) (#4) (#5 ) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) ( №18) (№19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) (#28) (#29) (#30) (#31) ( #32) (#33) (#34) (#35) (#36) (#37) (#38) (#39) (#40) - §15.5: Основной спектр кольца
(#1 ) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) ( #14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) ) (#27) (#28) (#29) (#30) (#31)
(#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14)
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9)
(#1) (#2) (#3) (#4) (#5) (#6) (# 7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25)
Глава 17.
 Введение в гомологическую алгебру и групповые когомологии
Введение в гомологическую алгебру и групповые когомологии- §17.1: Введение в гомологическую алгебру – Ext и Тор
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#92(G,A)
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10)
Глава 18: Теория представлений и теория символов
- §18.1: Линейные действия и модули над групповыми кольцами
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (# 20) (#21) (#22) (#23) (#24) - §18.2: Теорема Веддерберна и некоторые следствия
(#1) (#2) (#3) (#4) (#5) ( #6) (#7) (#8) (#9) (#10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) ) - §18.3: Теория персонажей и отношения ортогональности
(#1) (#2) (#3) (#4) (#5) (#6) (#7) (#8) (#9) (# 10) (#11) (#12) (#13) (#14) (#15) (#16) (#17) (#18) (#19) (#20) (#21) (#22) (#23) (#24) (#25) (#26) (#27) (#28)
Глава 19: Примеры и приложения теории характеров
- §19.



 3: Симметричные группы
3: Симметричные группы  3: Циклические группы и циклические подгруппы
3: Циклические группы и циклические подгруппы  3: Теоремы изоморфизма
3: Теоремы изоморфизма  4: Автоморфизмы
4: Автоморфизмы  4: Распознавание прямых произведений
4: Распознавание прямых произведений  1: Основные определения и примеры
1: Основные определения и примеры  6: Китайская теорема об остатках
6: Китайская теорема об остатках  5: Кольца многочленов над полями II
5: Кольца многочленов над полями II  4: Тензорные произведения модулей
4: Тензорные произведения модулей  4: Определители
4: Определители 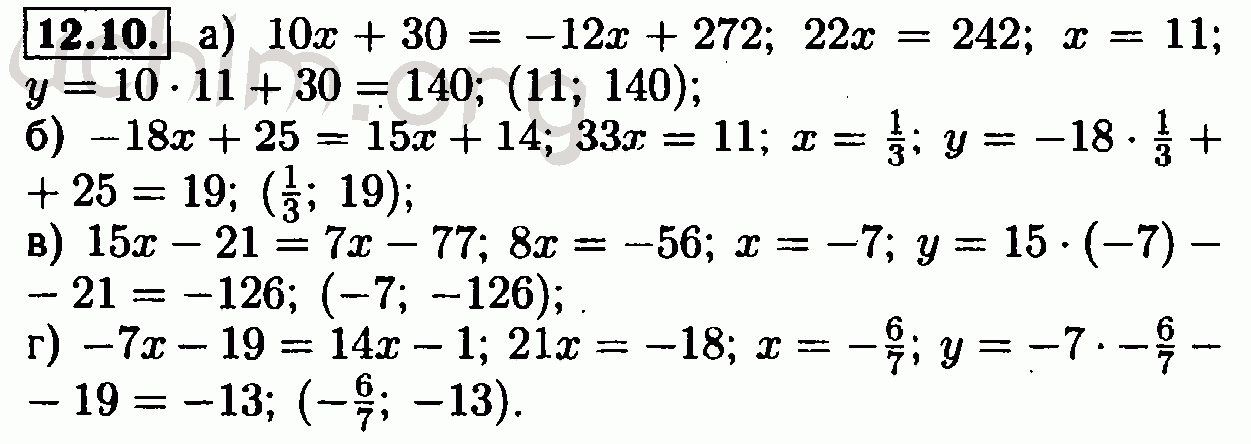 1: Базовая теория расширений поля
1: Базовая теория расширений поля  3: Конечные поля
3: Конечные поля 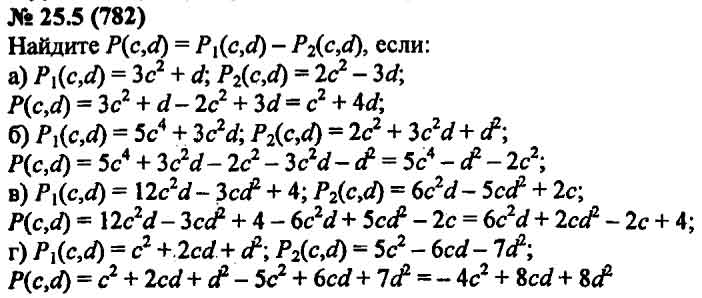 9: Трансцендентальные расширения, неразделимые расширения, бесконечные группы Галуа
9: Трансцендентальные расширения, неразделимые расширения, бесконечные группы Галуа  3: Интегральные расширения и Nullstellensatz Гильберта
3: Интегральные расширения и Nullstellensatz Гильберта 